| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Сложение энергии
Перейдем
теперь к более общему случаю и рассмотрим, что произойдет, если тел много.
Предположим, что имеется несколько тел; пронумеруем их: ![]() и пусть все они
притягивают друг друга. Что тогда произойдет? Можно доказать, что если сложить
кинетические энергии всех тел и добавить сюда сумму (по всем парам частиц) их
взаимных потенциальных энергий тяготения
и пусть все они
притягивают друг друга. Что тогда произойдет? Можно доказать, что если сложить
кинетические энергии всех тел и добавить сюда сумму (по всем парам частиц) их
взаимных потенциальных энергий тяготения ![]() , то все вместе даст постоянную:
, то все вместе даст постоянную:
 . (13.14)
. (13.14)
Как же
это доказать? Мы продифференцируем обе стороны по времени и докажем, что получится
нуль. При дифференцировании ![]() мы получим производные скорости —
силы [как в (13.5)], а потом эти силы заменим их величиной, известной нам из
закона тяготения, и увидим в конце концов, что останется как раз производная по
времени от
мы получим производные скорости —
силы [как в (13.5)], а потом эти силы заменим их величиной, известной нам из
закона тяготения, и увидим в конце концов, что останется как раз производная по
времени от
 .
.
Начинаем доказательство. Производная кинетической энергии по времени есть
 . (13.15)
. (13.15)
Производная по времени от потенциальной энергии есть
 ,
,
но
![]() ,
,
так что
 ,
,
потому что ![]() , хотя
, хотя ![]() . Итак,
. Итак,
 . (13.16)
. (13.16)
Теперь внимательно посмотрим, что
значит  и
и
![]() . В
(13.15)
. В
(13.15)  означает, что
означает, что ![]() принимает по порядку все
значения
принимает по порядку все
значения ![]() ,
и для каждого
,
и для каждого ![]() индекс
индекс
![]() принимает
все значения, кроме
принимает
все значения, кроме ![]() . Если, например,
. Если, например, ![]() , то
, то ![]() принимает значении
принимает значении ![]() .
.
С другой
стороны, в (13.16) ![]() означает, что каждая пара
означает, что каждая пара ![]() и
и ![]() встречается лишь
однажды. Скажем, частицы
встречается лишь
однажды. Скажем, частицы ![]() и
и ![]() дают только один член в сумме. Чтобы
отметить это, можно договориться, что
дают только один член в сумме. Чтобы
отметить это, можно договориться, что ![]() принимает значения
принимает значения ![]() , а
, а ![]() для каждого
для каждого ![]() — только значении,
большие чем
— только значении,
большие чем ![]() .
Если, скажем,
.
Если, скажем, ![]() ,
то
,
то ![]() равно
равно
![]() . Но
вспомним, что каждая пара
. Но
вспомним, что каждая пара ![]() дает два слагаемых в сумме, одно с
дает два слагаемых в сумме, одно с ![]() , а другое с
, а другое с ![]() , и что оба эти члена
выглядят так же, как член в уравнении (13.14) [но только в последнем в сумму
входят все значения
, и что оба эти члена
выглядят так же, как член в уравнении (13.14) [но только в последнем в сумму
входят все значения ![]() и
и ![]() (кроме
(кроме ![]() ) ]. В уравнениях (13.16) и (13.15)
член за членом совпадут по величине. Знаки их, однако, будут противоположны,
так что производная по времени от суммы потенциальной и кинетической энергии
действительно равна нулю. Итак, мы видим, что и в системе многих тел кинетическая
энергия составляется из
суммы энергий отдельных тел и что потенциальная энергия тоже состоит из взаимных потенциальных
энергий пар частиц. Почему она складывается из энергии пар? Это можно уяснить
себе следующим образом: положим, мы хотим найти всю работу, которую нужно совершить,
чтобы развести тела на определенные расстояния друг от друга. Можно это сделать
не за один раз, а постепенно, доставляя их одно за другим из бесконечности, где
на них никакие силы не влияли. Сперва мы приведем тело
) ]. В уравнениях (13.16) и (13.15)
член за членом совпадут по величине. Знаки их, однако, будут противоположны,
так что производная по времени от суммы потенциальной и кинетической энергии
действительно равна нулю. Итак, мы видим, что и в системе многих тел кинетическая
энергия составляется из
суммы энергий отдельных тел и что потенциальная энергия тоже состоит из взаимных потенциальных
энергий пар частиц. Почему она складывается из энергии пар? Это можно уяснить
себе следующим образом: положим, мы хотим найти всю работу, которую нужно совершить,
чтобы развести тела на определенные расстояния друг от друга. Можно это сделать
не за один раз, а постепенно, доставляя их одно за другим из бесконечности, где
на них никакие силы не влияли. Сперва мы приведем тело ![]() , на что работы не
потребуется, потому что, пока нет других тел, силы отсутствуют. Доставка тела
, на что работы не
потребуется, потому что, пока нет других тел, силы отсутствуют. Доставка тела ![]() потребует работы
потребует работы ![]() . И вот теперь
самый существенный момент: мы доставляем тело
. И вот теперь
самый существенный момент: мы доставляем тело ![]() в точку
в точку ![]() . В любой момент сила, действующая
на
. В любой момент сила, действующая
на ![]() ,
слагается из двух частей: из силы, действующей со стороны
,
слагается из двух частей: из силы, действующей со стороны ![]() , и силы со стороны
, и силы со стороны ![]() . Значит, и вся произведенная работа равна сумме
работ каждой из сил, потому
что раз
. Значит, и вся произведенная работа равна сумме
работ каждой из сил, потому
что раз ![]() разбивается
на сумму сил
разбивается
на сумму сил
![]() ,
,
то работа равна
![]() .
.
Стало
быть, вся работа равна сумме работ, произведенных против силы ![]() и против силы
и против силы ![]() , как если бы они
действовали независимо. Продолжая рассуждать, таким образом, мы увидим, что
полная работа, которую необходимо выполнить, чтобы собрать данную конфигурацию
тел, в точности равна значению (13.14) для потенциальной энергии. Именно из-за
того, что тяготение подчиняется принципу наложения сил, можно потенциальную
энергию представить в виде суммы по всем парам частиц.
, как если бы они
действовали независимо. Продолжая рассуждать, таким образом, мы увидим, что
полная работа, которую необходимо выполнить, чтобы собрать данную конфигурацию
тел, в точности равна значению (13.14) для потенциальной энергии. Именно из-за
того, что тяготение подчиняется принципу наложения сил, можно потенциальную
энергию представить в виде суммы по всем парам частиц.
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
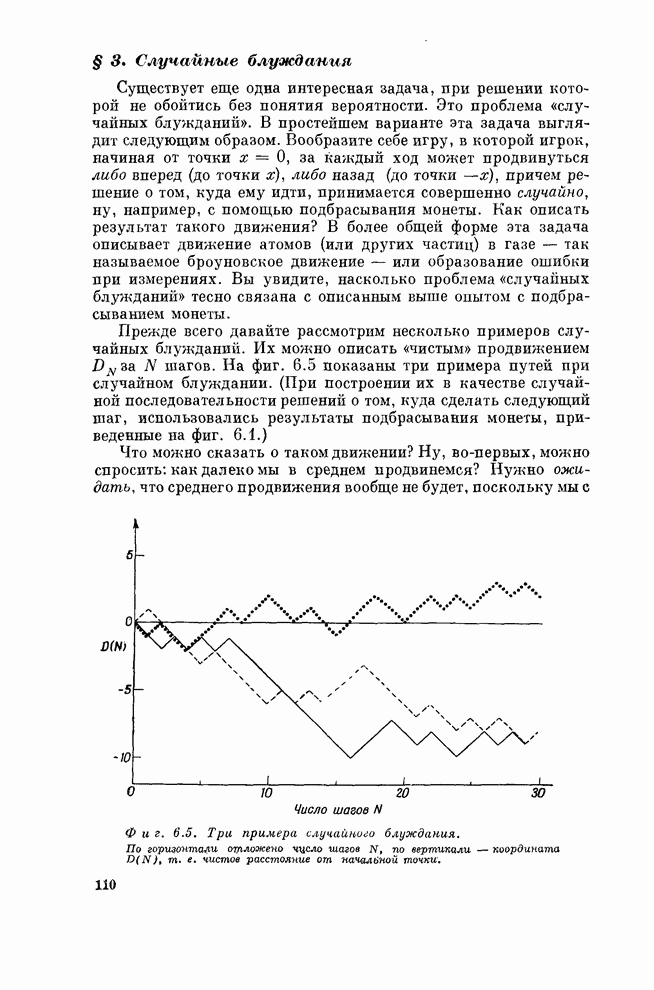
- § 3. Случайные блуждания
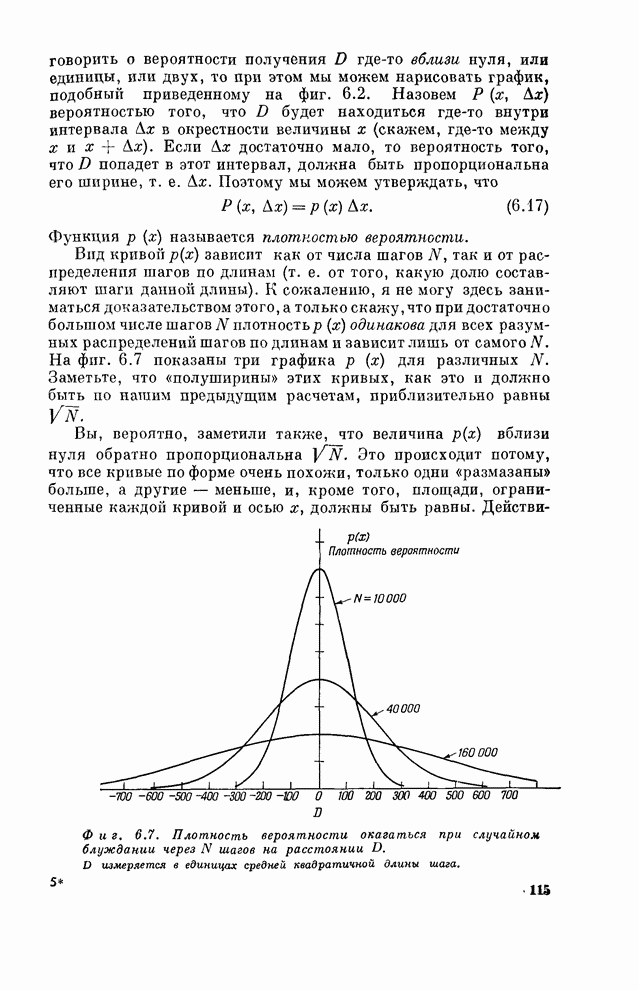
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
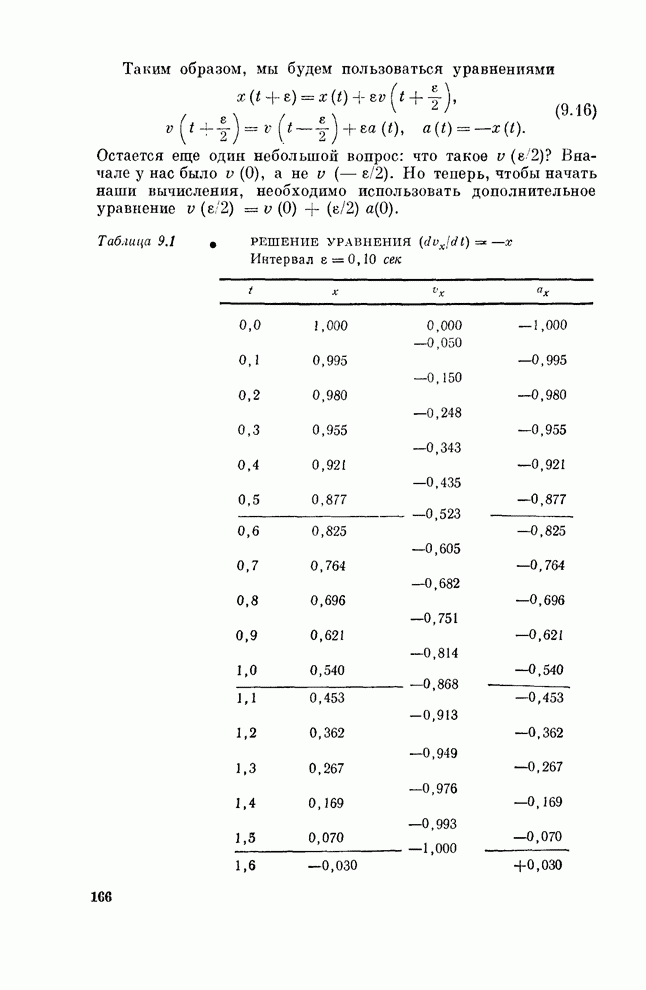
- § 5. Численное решение уравнений
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля