| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 13. Работа и потенциальная энергия (I)
§ 1 Работа падающего тела
В гл. 4 мы разобрали вопрос о сохранении энергии. При этом законами Ньютона мы не пользовались. Интересно теперь посмотреть, как возникает сохранение энергии из-за того, что действуют эти законы. Для ясности мы начнем с самых простых примеров и постепенно будем их усложнять.
Простейший
пример сохранения энергии — это тело, падающее вниз, т. е. тело, движущееся
только в вертикальном направлении. Если оно меняет свою высоту под влиянием только
тяжести, то из-за движения оно обладает кинетической энергией ![]() (или
(или ![]() ) Кроме того, у
него есть потенциальная энергия
) Кроме того, у
него есть потенциальная энергия ![]() (сокращенно
(сокращенно ![]() , или
, или ![]() ). Их сумма постоянна:
). Их сумма постоянна:
![]() ,
,
или
![]() . (13.1)
. (13.1)
Мы хотим показать, что это утверждение правильно. Что значит доказать его правильность? Второй закон Ньютона говорит, как движется тело, как со временем изменяется его скорость (а именно, что в падении она растет пропорционально времени, а высота падения меняется как квадрат времени). Если поэтому отмерять высоту от нулевой точки (где тело покоилось), то не будет ничего странного в том, что она окажется равной квадрату скорости, умноженному на какие-то постоянные. Однако все же рассмотрим это повнимательней.
Попробуем
вычислить прямо из второго закона Ньютона, как обязана меняться кинетическая
энергия; мы продифференцируем кинетическую энергию по времени и потом применим
закон Ньютона. Дифференцируя ![]() по времени, получаем
по времени, получаем
![]() , (13.2)
, (13.2)
потому
что ![]() считается
постоянной. Но по второму закону Ньютона
считается
постоянной. Но по второму закону Ньютона ![]() так что
так что
![]() . (13.3)
. (13.3)
В общем случае получается ![]() , но для нашего
одномерного случая лучше оставить просто произведение силы на скорость.
, но для нашего
одномерного случая лучше оставить просто произведение силы на скорость.
Сила в
нашем простом примере постоянна, равна — ![]() и направлена вниз (знак минус именно
это и показывает), а скорость есть степень изменения положения по вертикали
(высоты
и направлена вниз (знак минус именно
это и показывает), а скорость есть степень изменения положения по вертикали
(высоты ![]() )
со временем. Поэтому степень изменения кинетической энергии равна
)
со временем. Поэтому степень изменения кинетической энергии равна ![]() . Взгляните: что
за чудо! Перед нами снова чья-то скорость изменения — скорость изменения со
временем величины
. Взгляните: что
за чудо! Перед нами снова чья-то скорость изменения — скорость изменения со
временем величины ![]() ! Поэтому выходит, что с течением
времени изменения в кинетической энергии и в величине
! Поэтому выходит, что с течением
времени изменения в кинетической энергии и в величине ![]() остаются равными и
противоположными, так что их сумма остается неизменной. Что и требовалось
доказать.
остаются равными и
противоположными, так что их сумма остается неизменной. Что и требовалось
доказать.
Мы
только что показали, пользуясь Вторым законом Ньютона, что для постоянных сил
энергия сохраняется, если только прибавлять потенциальную энергию ![]() к кинетической
к кинетической ![]() . Исследуем этот
вопрос дальше; посмотрим, можно ли его обобщить, можно ли еще продвинуться в
его понимании. Действует ли этот закон только для свободно падающих тел или
является более общим? Из того, что мы знаем о сохранении энергии, можно
ожидать, что он будет верен для тела, движущегося из одной точки в другую по
кривой без трения и под действием одной лишь тяжести (фиг. 13.1). Когда тело,
начав двигаться с высоты
. Исследуем этот
вопрос дальше; посмотрим, можно ли его обобщить, можно ли еще продвинуться в
его понимании. Действует ли этот закон только для свободно падающих тел или
является более общим? Из того, что мы знаем о сохранении энергии, можно
ожидать, что он будет верен для тела, движущегося из одной точки в другую по
кривой без трения и под действием одной лишь тяжести (фиг. 13.1). Когда тело,
начав двигаться с высоты ![]() , достигает высоты
, достигает высоты ![]() , то опять должна
быть верной та же формула, хотя бы скорость уже не была направлена по
вертикали. Нам надо понять, почему она все еще правильна. Проведем тот же
анализ; отыщем скорость изменения кинетической энергии во времени. Опять будет
получаться
, то опять должна
быть верной та же формула, хотя бы скорость уже не была направлена по
вертикали. Нам надо понять, почему она все еще правильна. Проведем тот же
анализ; отыщем скорость изменения кинетической энергии во времени. Опять будет
получаться ![]() —
скорость изменения величины импульса, т. е. сила в направлении движения —
касательная сила
—
скорость изменения величины импульса, т. е. сила в направлении движения —
касательная сила ![]() Итак,
Итак,
![]()

Фигура 13.1. Тело, движущееся под действием тяжести по кривой без трения.
Скорость—это
скорость изменения расстояния вдоль кривой ![]() , а касательная сила
, а касательная сила ![]() теперь
оказывается меньше
теперь
оказывается меньше ![]() в отношении, равном отношению
расстояния
в отношении, равном отношению
расстояния ![]() вдоль
пути к вертикальному расстоянию
вдоль
пути к вертикальному расстоянию ![]() . Иными словами,
. Иными словами,
![]()
так что
![]()
(![]() выпадает). И
опять, как прежде, мы получили величину
выпадает). И
опять, как прежде, мы получили величину ![]() равную скорости изменения
равную скорости изменения ![]() .
.
Чтобы точно уяснить себе, как вообще соблюдается сохранение энергии в механике, рассмотрим сейчас некоторые полезные понятия.
Во-первых, рассмотрим скорость изменения кинетической энергии в общем трехмерном случае. Кинетическая энергия, когда движение имеет три измерения, равна
![]() .
.
Дифференцируя ее по времени, получаем три устрашающих члена:
 . (13.4)
. (13.4)
Но ведь ![]() — это сила
— это сила ![]() , действующая на
тело в направлении
, действующая на
тело в направлении ![]() . Значит, в правой части формулы
(13.4) стоит
. Значит, в правой части формулы
(13.4) стоит ![]() .
Призвав на помощь векторный анализ, вспоминаем, что это
.
Призвав на помощь векторный анализ, вспоминаем, что это ![]() . Итак,
. Итак,
![]() . (13.5)
. (13.5)
А можно
это вывести и быстрей: если ![]() и
и ![]() — два вектора, зависящих от времени,
то производная от
— два вектора, зависящих от времени,
то производная от ![]() равна
равна
![]() . (13.6)
. (13.6)
Подставим
сюда ![]() :
:
 . (13.7)
. (13.7)
Так как
понятие кинетической энергии и вообще энергии очень важно, то различным
величинам в этих уравнениях присвоены разные имена: ![]() называется, как известно, кинетической
энергией;
называется, как известно, кинетической
энергией; ![]() называется мощностью: сила,
действующая на тело, умноженная («скалярно») на скорость тела,— это мощность,
сообщаемая телу этой силой. Получается великолепная теорема: скорость изменения
кинетической энергии тела равна мощности, затраченной силами, действующими на
тело.
называется мощностью: сила,
действующая на тело, умноженная («скалярно») на скорость тела,— это мощность,
сообщаемая телу этой силой. Получается великолепная теорема: скорость изменения
кинетической энергии тела равна мощности, затраченной силами, действующими на
тело.
Но для
изучения сохранения энергии анализ следует продолжить. Давайте оценим изменение
кинетической энергии за очень короткое время ![]() . Умножив обе части уравнения (13.7)
на
. Умножив обе части уравнения (13.7)
на ![]() , найдем,
что изменение кинетической энергии равно силе, скалярно умноженной на
дифференциал пройденного расстояния
, найдем,
что изменение кинетической энергии равно силе, скалярно умноженной на
дифференциал пройденного расстояния
![]() (13.8)
(13.8)
А интегрируя, получаем
 . (13.9)
. (13.9)
Что это значит? Это значит, что, как
бы и по какой бы кривой траектории ни двигалось тело под действием силы, все
равно изменение в ![]() при переходе от одной точки кривой к
другой равно интегралу от компоненты силы вдоль кривой, умноженной на
дифференциал смещения
при переходе от одной точки кривой к
другой равно интегралу от компоненты силы вдоль кривой, умноженной на
дифференциал смещения ![]() (интегрирование от первой точки до
второй). И у этого интеграла есть имя: его называют работой, совершенной силой
над телом. Немедленно мы обнаруживаем, что мощность — это работа за секунду. И
еще мы замечаем, что работу производит только составляющая силы вдоль
направления движения. В нашем первом простом примере участвовали только
вертикальные силы с одной-единственной составляющей
(интегрирование от первой точки до
второй). И у этого интеграла есть имя: его называют работой, совершенной силой
над телом. Немедленно мы обнаруживаем, что мощность — это работа за секунду. И
еще мы замечаем, что работу производит только составляющая силы вдоль
направления движения. В нашем первом простом примере участвовали только
вертикальные силы с одной-единственной составляющей ![]() равной
равной ![]() . В этих обстоятельствах
совершенно неважно, как тело движется, прямо вниз или но параболе, все равно от
. В этих обстоятельствах
совершенно неважно, как тело движется, прямо вниз или но параболе, все равно от
![]() (которое
можно написать как
(которое
можно написать как ![]() ) остается только
) остается только ![]() , потому что прочие
составляющие силы — нули. Значит, в этом случае
, потому что прочие
составляющие силы — нули. Значит, в этом случае
 , (13.10)
, (13.10)
так что в потенциальную энергию входит только высота, с которой тело падает.
Несколько
слов о единицах. Так как сила измеряется в ньютонах, а для получения работы ее
умножают на расстояние, то работу измеряют в единицах ньютон метр, но
большинство людей этого названия не любит, предпочитая название ![]() . Это только
другое слово, а единица та же. Итак, работу измеряют в джоулях. Мощность же — в
джоулях в секунду; эту единицу называют
. Это только
другое слово, а единица та же. Итак, работу измеряют в джоулях. Мощность же — в
джоулях в секунду; эту единицу называют ![]() . Если умножить ватты на время, то
получим произведенную работу. Работу, которую местная энергосистема производит
в наших квартирах (в техническом смысле), оценивается в ваттах, умноженных на
время. Например, киловатт-час — это
. Если умножить ватты на время, то
получим произведенную работу. Работу, которую местная энергосистема производит
в наших квартирах (в техническом смысле), оценивается в ваттах, умноженных на
время. Например, киловатт-час — это ![]() , т.е.
, т.е. ![]() .
.
Приведем
еще несколько примеров работы и сохранения энергии. Рассмотрим тело, которое
вначале имеет кинетическую энергию и быстро двигается, скользя по полу с
трением. Оно останавливается. В начале кинетическая энергия не равна нулю, а в
конце она равна нулю; существует работа, произведенная силами, потому что раз
есть трение, то есть и составляющая силы в направлении, противоположном
направлению движения, и энергия постепенно теряется. Теперь рассмотрим массу на
конце маятника, который качается в вертикальной плоскости в поле тяжести без
трения. Здесь наблюдается нечто другое, потому что, когда масса опускается,
сила направлена тоже вниз, а когда подымается, сила направлена в обратную
сторону, так что у ![]() на спуске и па подъеме разные знаки.
В соответствующих точках спуска и подъема значения
на спуске и па подъеме разные знаки.
В соответствующих точках спуска и подъема значения ![]() равны по величине, но противоположны
по знаку, так что в итоге интеграл есть чистый нуль. Поэтому кинетическая
энергия в конце спуска в точности такая же, какой она была в начале подъема;
это и есть принцип сохранения энергии. (Заметьте, что в присутствии сил трения
сохранение энергии на первый взгляд не выполняется. Значит, нужно искать другую
форму энергии. И действительно, оказывается, что когда два тела трутся друг о
друга, то возникает тепло, мы же сейчас делаем вид, что об этом не знаем.)
равны по величине, но противоположны
по знаку, так что в итоге интеграл есть чистый нуль. Поэтому кинетическая
энергия в конце спуска в точности такая же, какой она была в начале подъема;
это и есть принцип сохранения энергии. (Заметьте, что в присутствии сил трения
сохранение энергии на первый взгляд не выполняется. Значит, нужно искать другую
форму энергии. И действительно, оказывается, что когда два тела трутся друг о
друга, то возникает тепло, мы же сейчас делаем вид, что об этом не знаем.)
| << Предыдущий параграф | Следующий параграф >> |
- К читателям русского издания
- ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
- ПРЕДИСЛОВИЕ
- Глава 1. АТОМЫ В ДВИЖЕНИИ
- § 1. Введение
- § 2. Вещество состоит из атомов
- § 3. Атомные процессы
- § 4. Химические реакции
- Глава 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
- § 1. Введение
- § 2. Физика до 1920 года
- § 3. Квантовая физика
- § 4. Ядра и частицы
- Глава 3. Физика и другие науки
- § 1. Введение
- § 2. Химия
- § 3. Биология
- § 4. Астрономия
- § 5. Геология
- § 6. Психология
- § 7. С чего все пошло?
- Глава 4. Сохранение энергии
- § 1. Что такое энергия?
- § 2. Потенциальная энергии тяготения
- § 3. Кинетическая энергия
- § 4. Прочие формы энергии
- Глава 5. Время и расстояние
- § 1. Движение
- § 2. Время
- § 3. Короткие времена
- § 4. Большие времена
- § 5. Единицы и стандарты времени
- § 6. Большие расстояния
- § 7. Малые расстояния
- Глава 6. Вероятность
- § 1. Вероятность и правдоподобие
- § 2. Флуктуации
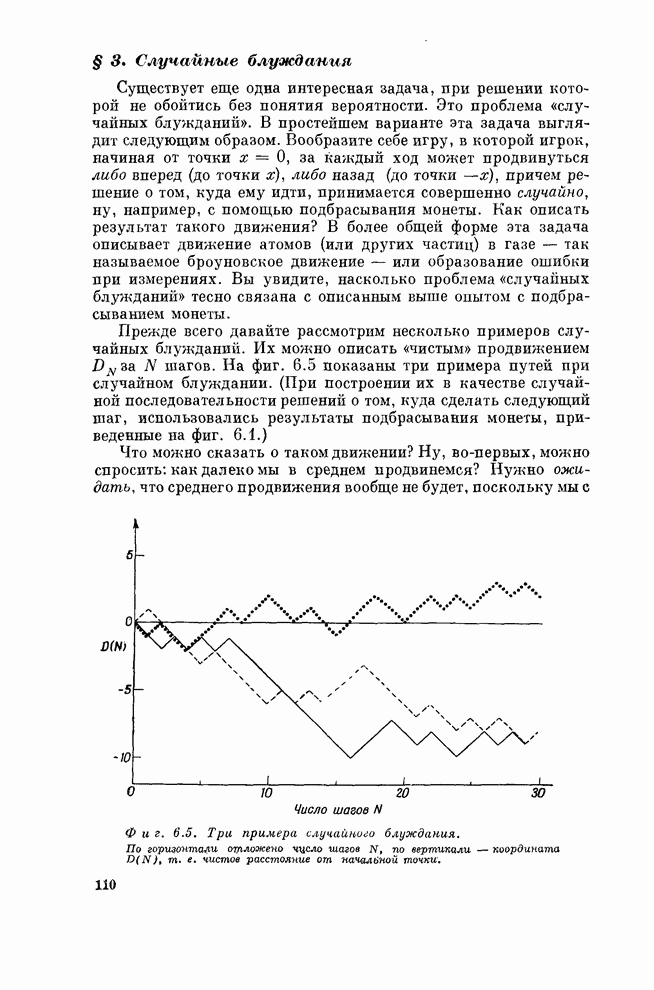
- § 3. Случайные блуждания
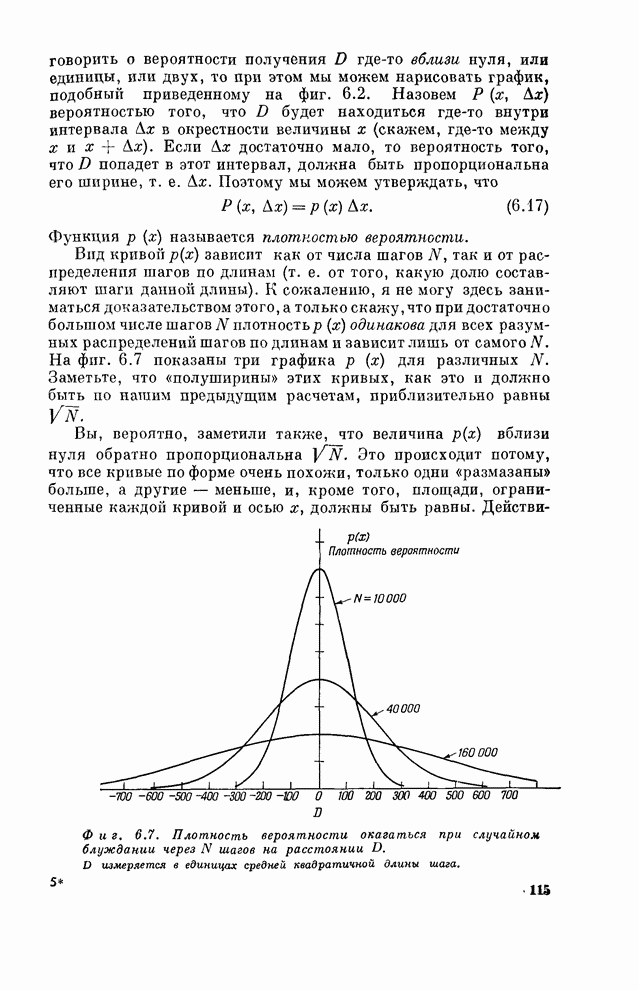
- § 4. Распределение вероятностей
- § 5. Принцип неопределенности
- Глава 7. Теория тяготения
- § 1. Движение планет
- § 2. Законы Кеплера
- § 3. Развитие динамики
- § 4. Ньютонов закон тяготения
- § 5. Всемирное тяготение
- § 6. Опыт Кавендиша
- § 7. Что такое тяготение?
- § 8. Тяготение и относительность
- Глава 8. Движение
- § 1. Описание движения
- § 2. Скорость
- § 3. Скорость как производная
- § 4. Расстояние как интеграл
- § 5. Ускорение
- Глава 9. Динамические законы Ньютона
- § 1. Импульс и сила
- § 2. Компоненты скорости, ускорения и силы
- § 3. Что такое сила?
- § 4. Смысл динамических уравнений
- § 5. Численное решение уравнений
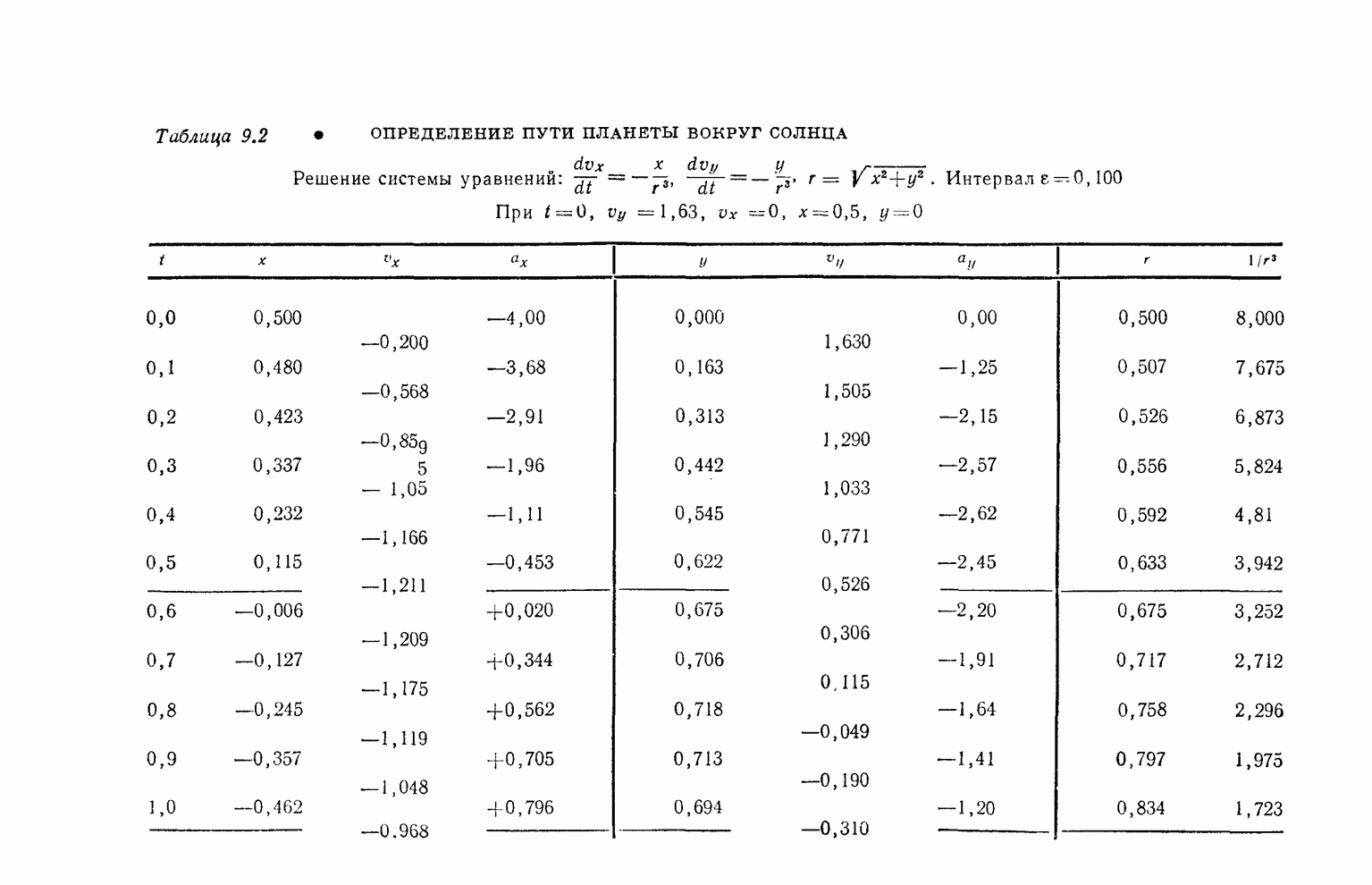
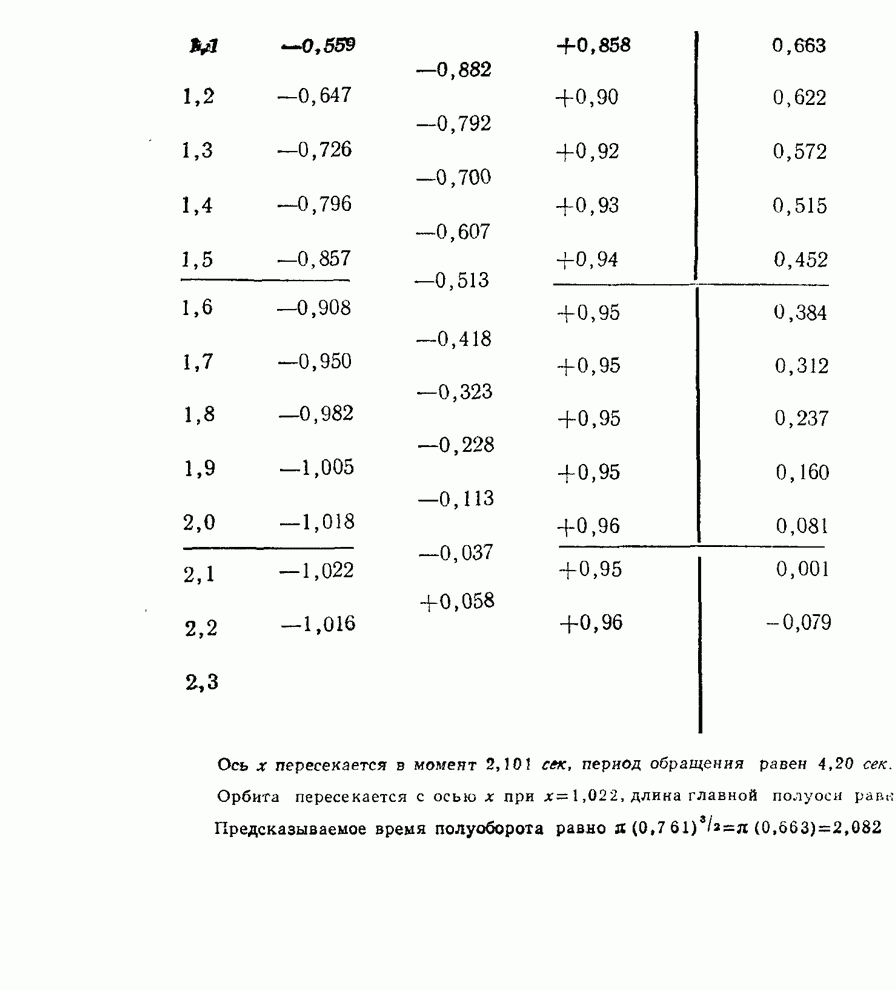
- § 6. Движение планет
- Глава 10. Закон сохранения импульса
- § 1. Третий закон Ньютона
- § 2. Закон сохранения импульса
- § 3. Импульс все-таки сохраняется!
- § 4. Импульс и энергия
- § 5 Релятивистский импульс
- Глава 11. Векторы
- § 1. Симметрия в физике
- § 2. Переносы начала
- § 3. Вращения
- § 4. Векторы
- § 5. Векторная алгебра
- § 6. Законы Ньютона в векторной записи
- § 7. Скалярное произведение векторов
- Глава 12. Характеристики силы
- § 1. Что есть сила?
- § 2. Трение
- § 3. Молекулярные силы
- § 4. Фундаментальные силы. Поля
- § 5. Псевдосилы
- § 6. Ядерные силы
- Глава 13. Работа и потенциальная энергия (I)
- § 1 Работа падающего тела
- § 2. Работа, выполняемая тяжестью
- § 3. Сложение энергии
- § 4. Поле тяготения больших тел
- Глава 14. Работа и потенциальная энергия (II)
- § 1. Работа
- § 2. Движение при наложенных связях
- § 3. Консервативные силы
- § 4. Неконсервативные силы
- § 5. Потенциалы и поля