| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Методика расчета ПН СПП в циклических режимах.
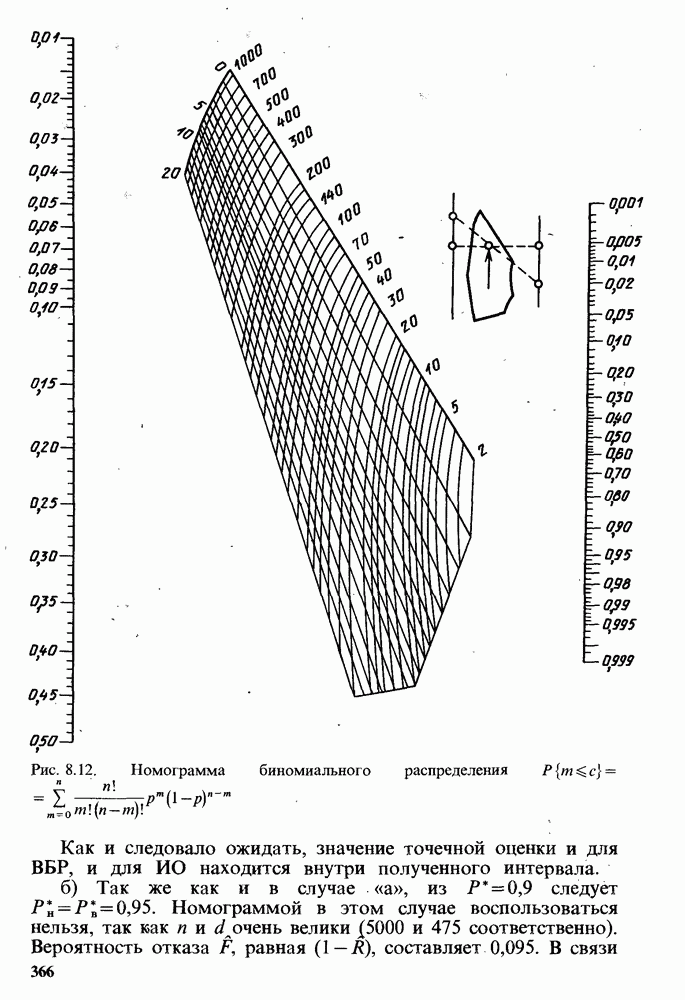
Число циклов до отказа в режиме термоциклирования  может быгь определено по приводимым в информационных материалах кривым, по формулам (8.6), (8.7) или по номограмме рис. 8.25.
может быгь определено по приводимым в информационных материалах кривым, по формулам (8.6), (8.7) или по номограмме рис. 8.25.
Эта номограмма соответствует формуле (8.6). Знания констант  должны быть известны по результатам эксплуатации или испытаний. В § 8.2 отмечалось, что определяемая формулами (8.6), (8.7) величина
должны быть известны по результатам эксплуатации или испытаний. В § 8.2 отмечалось, что определяемая формулами (8.6), (8.7) величина  часто представляет собой среднее значение. Чтобы определить по нему медианную циклостойкость в случае распределения Вейбулла, следует воспользоваться выражением
часто представляет собой среднее значение. Чтобы определить по нему медианную циклостойкость в случае распределения Вейбулла, следует воспользоваться выражением

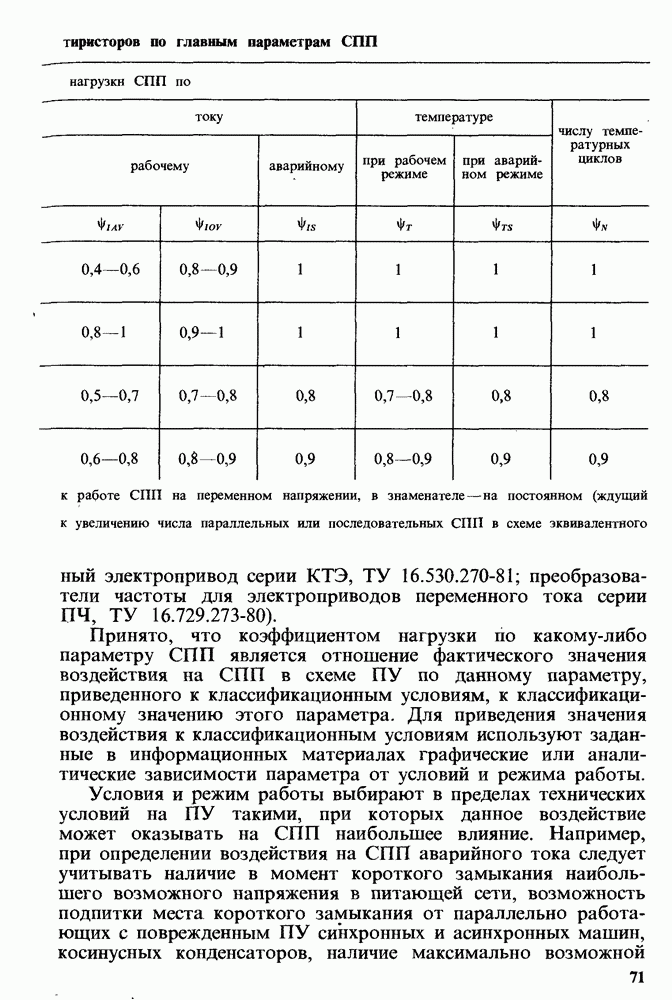
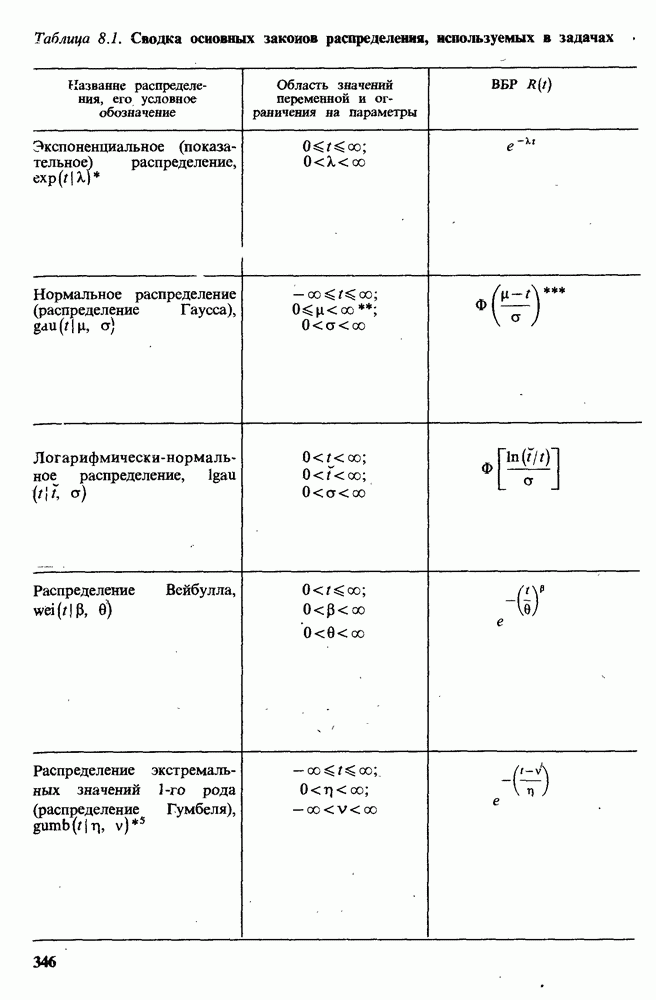
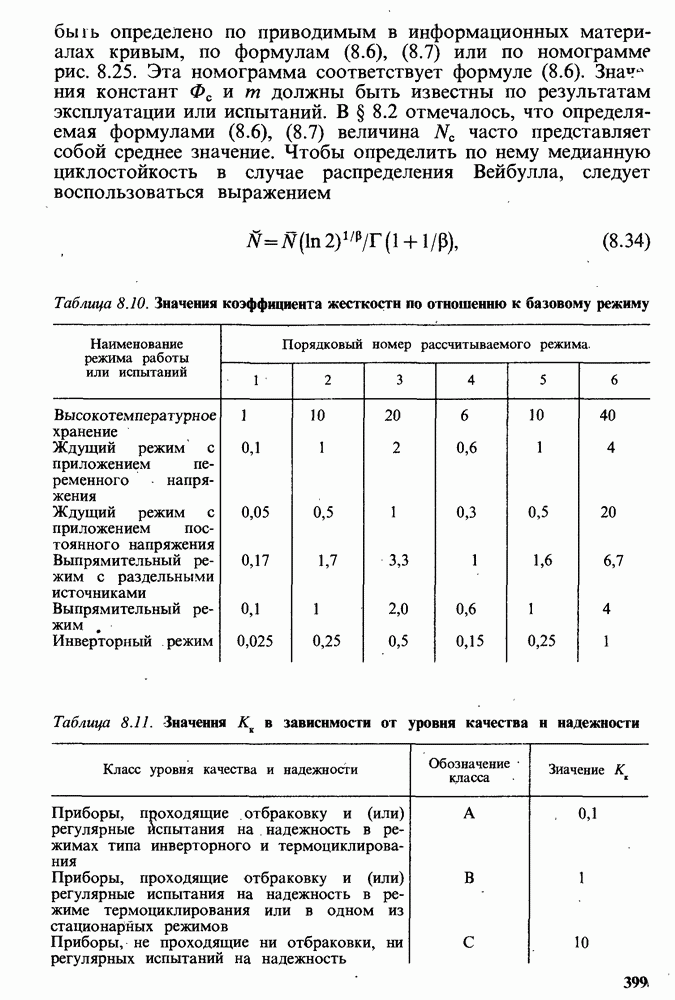
Таблица 8.10. Значения коэффициента жесткости по отношению к базовому режиму

Таблица 8.11. Значения  в зависимости от уровня качества и надежности
в зависимости от уровня качества и надежности

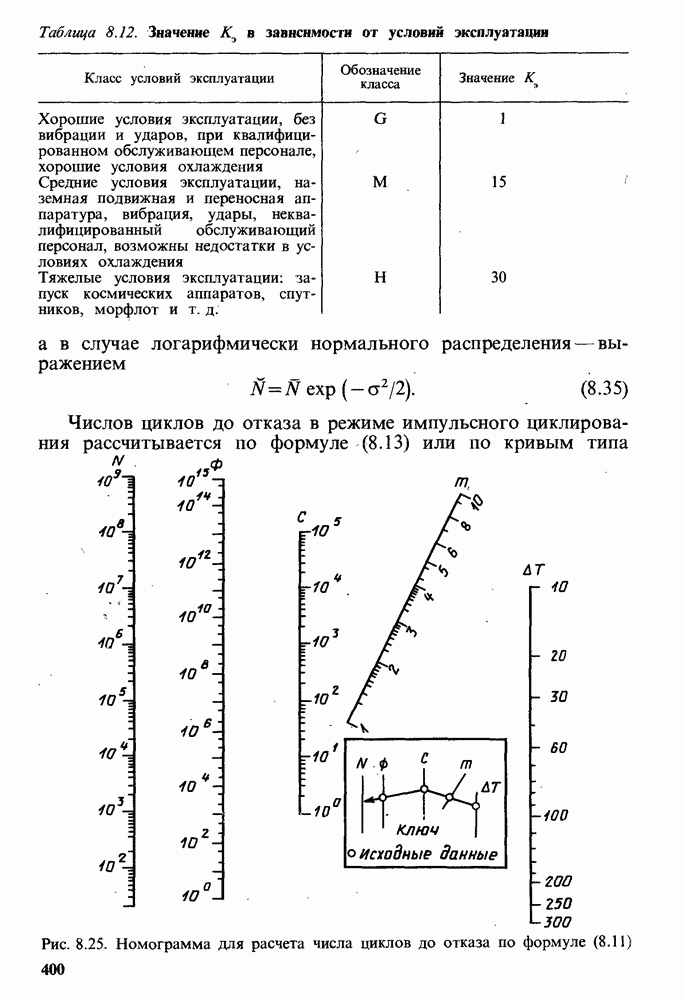
Таблица 8.12. Значение  в зависимости от условий эксплуатации
в зависимости от условий эксплуатации

А в случае логарифмически нормального распределения — выражением

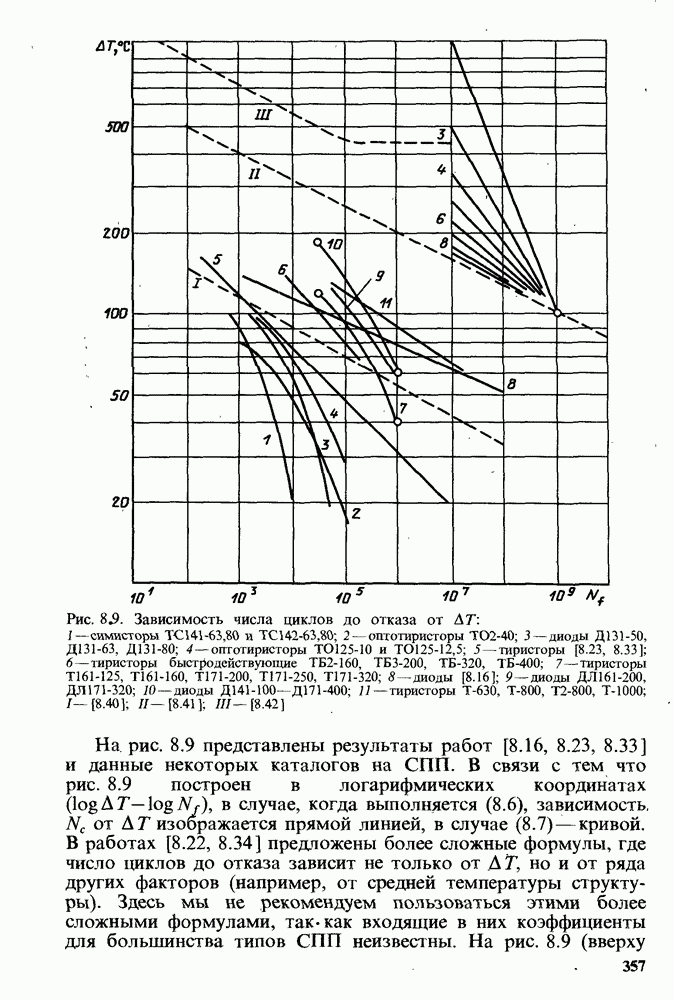
Числов циклов до отказа в режиме импульсного циклирования рассчитывается по формуле (8.13) или по кривым типа I—III на рис. 8.9.

Рис. 8.25. Номограмма для расчета числа циклов до отказа по формуле (8.11)
Константы  должны быть известны по результатам предшествующих эксплуатации или испытаний. В том случае, когда определенное по (8.8) значение
должны быть известны по результатам предшествующих эксплуатации или испытаний. В том случае, когда определенное по (8.8) значение  является средним, пересчет к медианной циклостойкости следует проводить по формулам (8.34) или (8.35) (если распределение отказов согласуется с вейбулловским или логарифмически нормальным распределением).
является средним, пересчет к медианной циклостойкости следует проводить по формулам (8.34) или (8.35) (если распределение отказов согласуется с вейбулловским или логарифмически нормальным распределением).
В ряде случаев для циклических РЭ могут понадобиться значения таких ПН, как ИО, ВБР и т.п. В частности, знание ИО необходимо для аналитического определения класса РЭ. В § 8.2 отмечалось, что плотность распределения числа циклов до отказа чаще всего соответствует вейбулловскому или логарифмически нормальному законам. Поэтому ниже приведены номограммы, позволяющие рассчитывать указанные величины именно для этих двух случаев. Мы построили обе номограммы относительно медианной наработки N, а не относительно 0, поскольку  а на практике чаще задается и ищется именно медианная наработка. Учитывая, что
а на практике чаще задается и ищется именно медианная наработка. Учитывая, что

и заменяя  формулах табл. 8.1
формулах табл. 8.1  на
на  , имеем
, имеем

Выражения (8.36) положены в основу рис. 8.26 и 8.27.
Номограмма на рис. 8.26 позволяет определить ИО для вейбулловского распределения в диапазоне  и для
и для  от 0,15 до 4.; Определение величины А, ведется следующим образом. Соединяем заданную точку на шкале P с рассчитанным значением
от 0,15 до 4.; Определение величины А, ведется следующим образом. Соединяем заданную точку на шкале P с рассчитанным значением  на соответствующей шкале прямой линией и на пересечении этой прямой со
на соответствующей шкале прямой линией и на пересечении этой прямой со  , шкалой
, шкалой  ) делаем засечку. Соединив эту точку с заданным значением
) делаем засечку. Соединив эту точку с заданным значением  на шкале
на шкале  прямой линией, на пересечении ее со шкалой X найдем ответ. Если значение
прямой линией, на пересечении ее со шкалой X найдем ответ. Если значение  является целой. степенью десяти с множителем 1, то, получив значение
является целой. степенью десяти с множителем 1, то, получив значение  на w соответствующей шкале, найдем величину ИО. Пусть
на w соответствующей шкале, найдем величину ИО. Пусть  , требуется найти ИО при
, требуется найти ИО при  . Тогда, соединив значение 0,8 на криволинейной шкапе
. Тогда, соединив значение 0,8 на криволинейной шкапе  с
с  на шкале
на шкале  , найдем на шкале ответ:
, найдем на шкале ответ:  , откуда имеем
, откуда имеем  . То же значение ИО получим на шкале X, соединив значение 3 на шкале
. То же значение ИО получим на шкале X, соединив значение 3 на шкале  со значением
со значением  на шкале
на шкале 
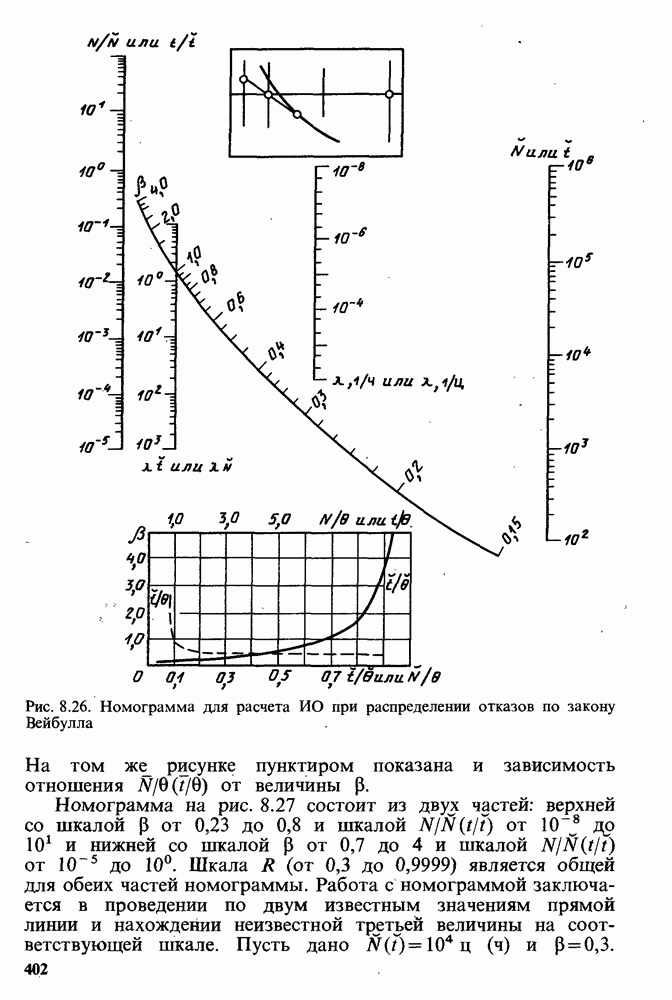
Внизу на рис. 8.26 приведена зависимость отношения  от p. Она позволяет по известным N и P определить параметр 0, входящий в стандартную форму распределения Вейбулла.
от p. Она позволяет по известным N и P определить параметр 0, входящий в стандартную форму распределения Вейбулла.

Рис. 8.26. Номограмма для расчета ИО при распределении отказов по закону Вейбулла
На том  рисунке пунктиром показана и зависимость отношения
рисунке пунктиром показана и зависимость отношения  от величины
от величины  .
.
Номограмма на рис. 8.27 состоит из двух частей: верхней со шкалой p от 0,23 до 0,8 и шкалой  от
от  до
до  и нижней со шкалой (3 от 0,7 до 4 и шкалой
и нижней со шкалой (3 от 0,7 до 4 и шкалой  ) от
) от  до 10°. Шкала R (от 0,3 до 0,9999) является общей для обеих частей номограммы. Работа с номограммой заключается в проведении по двум известным значениям прямой линии и нахождении неизвестной третьей величины на соответствующей шкале. Пусть дано
до 10°. Шкала R (от 0,3 до 0,9999) является общей для обеих частей номограммы. Работа с номограммой заключается в проведении по двум известным значениям прямой линии и нахождении неизвестной третьей величины на соответствующей шкале. Пусть дано  .
.

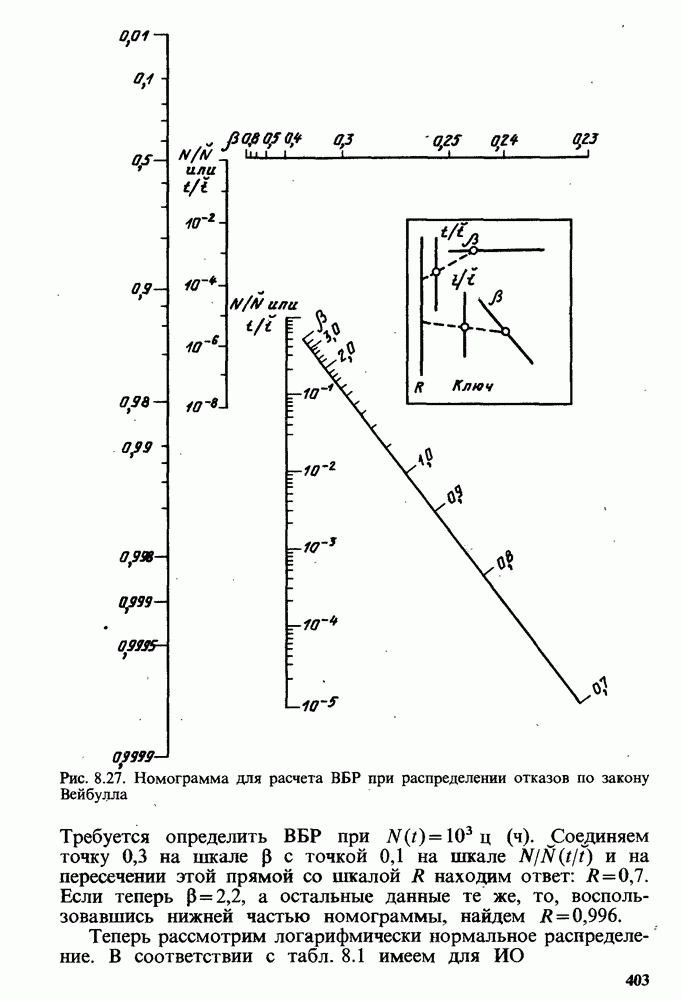
Рис. 8.27. Номограмма для расчета ВБР при распределении отказов по закону Вейбулла
Требуется определить ВБР при  . Соединяем точку 0,3 на шкале (3 с точкой 0,1 на шкале
. Соединяем точку 0,3 на шкале (3 с точкой 0,1 на шкале  ) и на пересечении этой прямой со шкалой R находим ответ:
) и на пересечении этой прямой со шкалой R находим ответ:  . Если теперь
. Если теперь  , а остальные данные те же, то, воспользовавшись нижней частью номограммы, найдем
, а остальные данные те же, то, воспользовавшись нижней частью номограммы, найдем 
Теперь рассмотрим логарифмически нормальное распределение. В соответствии с табл. 8.1 имеем для ИО

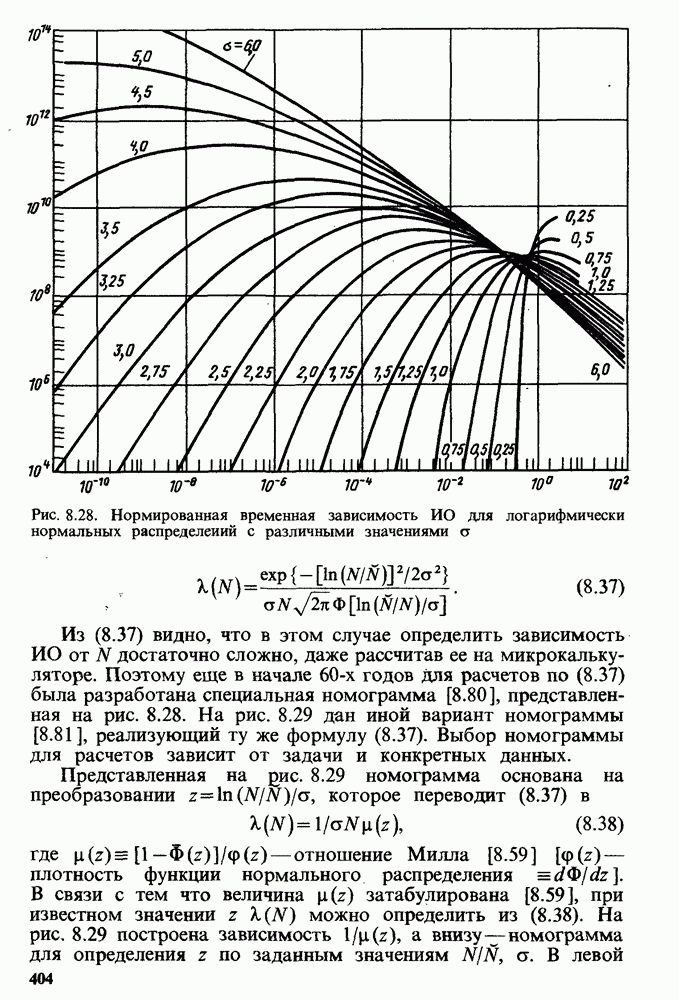
Рис. 8.28. Нормированная временная зависимость ИО для логарифмически нормальных распределений с различными значениями 

Из (8.37) видно, что в этом случае определить зависимость ИО от N достаточно сложно, даже рассчитав ее на микрокалькуляторе. Поэтому еще в начале  годов для расчетов по (8.37) была разработана специальная номограмма [8.80], представленная на рис. 8.28. На рис. 8.29 дан иной вариант номограммы [8.81], реализующий ту же формулу (8.37). Выбор номограммы для расчетов зависит от задачи и конкретных данных.
годов для расчетов по (8.37) была разработана специальная номограмма [8.80], представленная на рис. 8.28. На рис. 8.29 дан иной вариант номограммы [8.81], реализующий ту же формулу (8.37). Выбор номограммы для расчетов зависит от задачи и конкретных данных.
Представленная на рис. 8.29 номограмма основана на преобразовании  , которое переводит (8.37) в
, которое переводит (8.37) в

где  — отношение Милла
— отношение Милла  плотность функции нормального распределения
плотность функции нормального распределения  . В связи с тем что величина
. В связи с тем что величина  затабулирована [8.59], при известном значении
затабулирована [8.59], при известном значении  можно определить из (8.38). На рис. 8.29 построена зависимость
можно определить из (8.38). На рис. 8.29 построена зависимость  , а внизу — номограмма для определения z по заданным значениям
, а внизу — номограмма для определения z по заданным значениям  .
.

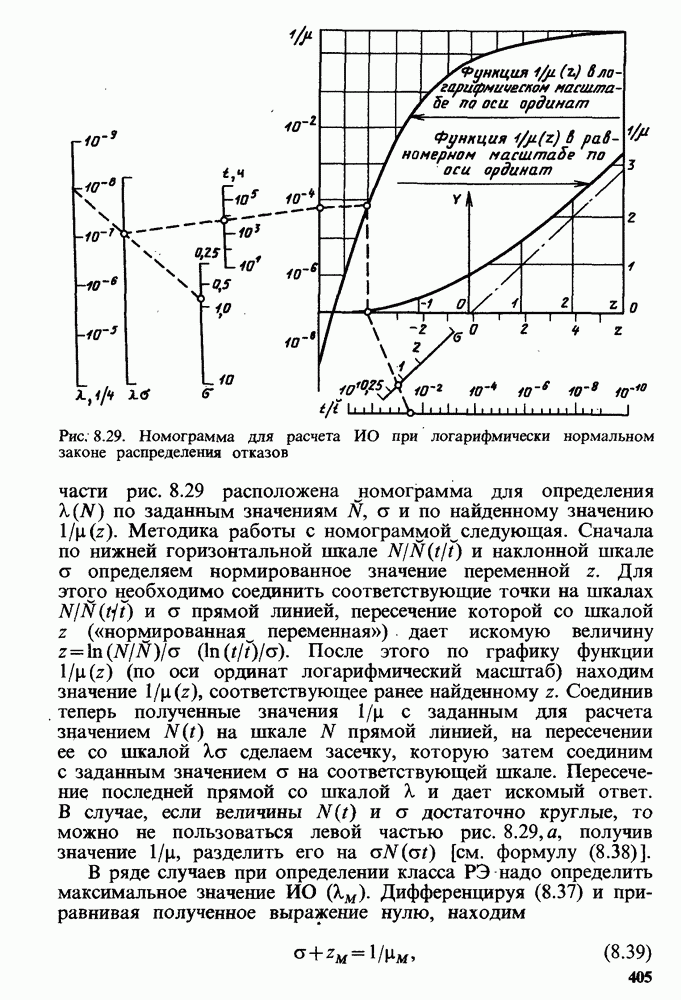
Рис. 8.29. Номограмма для расчета ИО при логарифмически нормальном законе распределения отказов
В левой части рис. 8.29 расположена номограмма для определения  по заданным значениям
по заданным значениям  и по найденному значению
и по найденному значению  . Методика работы с номограммой следующая. Сначала по нижней горизонтальной шкале
. Методика работы с номограммой следующая. Сначала по нижней горизонтальной шкале  и наклонной шкале а определяем нормированное значение переменной z. Для этого необходимо соединить соответствующие точки на шкалах
и наклонной шкале а определяем нормированное значение переменной z. Для этого необходимо соединить соответствующие точки на шкалах  прямой линией, пересечение которой со шкалой
прямой линией, пересечение которой со шкалой  переменная») дает искомую величину
переменная») дает искомую величину  . После этого по графику функции
. После этого по графику функции  (по оси ординат логарифмический масштаб) находим значение
(по оси ординат логарифмический масштаб) находим значение  , соответствующее ранее найденному z. Соединив
, соответствующее ранее найденному z. Соединив  . теперь полученные значения
. теперь полученные значения  с заданным для расчета значением
с заданным для расчета значением  на шкале N прямой линией, на пересечении ее со шкалой
на шкале N прямой линией, на пересечении ее со шкалой  сделаем засечку, которую затем соединим с заданным значением а на соответствующей шкале. Пересечение последней прямой со шкалой
сделаем засечку, которую затем соединим с заданным значением а на соответствующей шкале. Пересечение последней прямой со шкалой  и дает искомый ответ. В случае, если величины
и дает искомый ответ. В случае, если величины  достаточно круглые, то можно не пользоваться левой частью рис. 8.29, а, получив значение
достаточно круглые, то можно не пользоваться левой частью рис. 8.29, а, получив значение  , разделить его на
, разделить его на  [см. формулу (8.38)].
[см. формулу (8.38)].
В ряде случаев при определении класса РЭ надо определить максимальное значение ИО  . Дифференцируя (8.37) и приравнивая полученное выражение нулю, находим
. Дифференцируя (8.37) и приравнивая полученное выражение нулю, находим

где  .
.
Если учесть, что [8.59]

то приближенное решение уравнения (8.39) имеет вид

Для  решение уравнения (8.39) проще всего найти графически. Для этого на рис. 8.29 под графиком функции
решение уравнения (8.39) проще всего найти графически. Для этого на рис. 8.29 под графиком функции  (по оси ординат логарифмический масштаб) приведен график той же функции в равномерном масштабе по оси ординат. Для определения
(по оси ординат логарифмический масштаб) приведен график той же функции в равномерном масштабе по оси ординат. Для определения  через точку заданного значения а на оси
через точку заданного значения а на оси  надо провести прямую, параллельную штрихпунктирной линии
надо провести прямую, параллельную штрихпунктирной линии  , до пересечения с функцией
, до пересечения с функцией  . Точка пересечения и дает искомое значение
. Точка пересечения и дает искомое значение  , откуда
, откуда  .
.
Пример 8.6. Пусть требуется найти ИО приборов в момент  , если известно, что закон распределения отказов логарифмически нормальный,
, если известно, что закон распределения отказов логарифмически нормальный,  .
.
Находим:  , откуда по номограмме рис. 8.29 получаем (см. пунктир)
, откуда по номограмме рис. 8.29 получаем (см. пунктир)  .
.
Если бы нам надо было найти  , то в данном случае для
, то в данном случае для  соответствующая точка на оси OV лежит на кривой
соответствующая точка на оси OV лежит на кривой  , т. е. в данном случае
, т. е. в данном случае  . Это означает, что максимальное значение ИО достигается при
. Это означает, что максимальное значение ИО достигается при  . В этом случае для нахождения
. В этом случае для нахождения  нельзя использовать соотношение
нельзя использовать соотношение  , а надо воспользоваться номограммой в обычном порядке, что дает
, а надо воспользоваться номограммой в обычном порядке, что дает  . Можно убедиться, что применение номограммы, изображенной на рис. 8.28, приводит практически к тем же значениям.
. Можно убедиться, что применение номограммы, изображенной на рис. 8.28, приводит практически к тем же значениям.
Хотя в формулах  в качестве аргумента - мы записали переменную N, они справедливы, если в качестве аргумента будет t. Следовательно, номограммы, изображенные на рис.
в качестве аргумента - мы записали переменную N, они справедливы, если в качестве аргумента будет t. Следовательно, номограммы, изображенные на рис.  , можно использовать при расчетах величин
, можно использовать при расчетах величин  или
или  . Это обстоятельство отражено на всех указанных номограммах, для чего соответствующие шкалы имеют двойное обозначение:
. Это обстоятельство отражено на всех указанных номограммах, для чего соответствующие шкалы имеют двойное обозначение:  и т. д.
и т. д.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ПРИНЦИП ДЕЙСТВИЯ И ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ ДИОДОВ И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
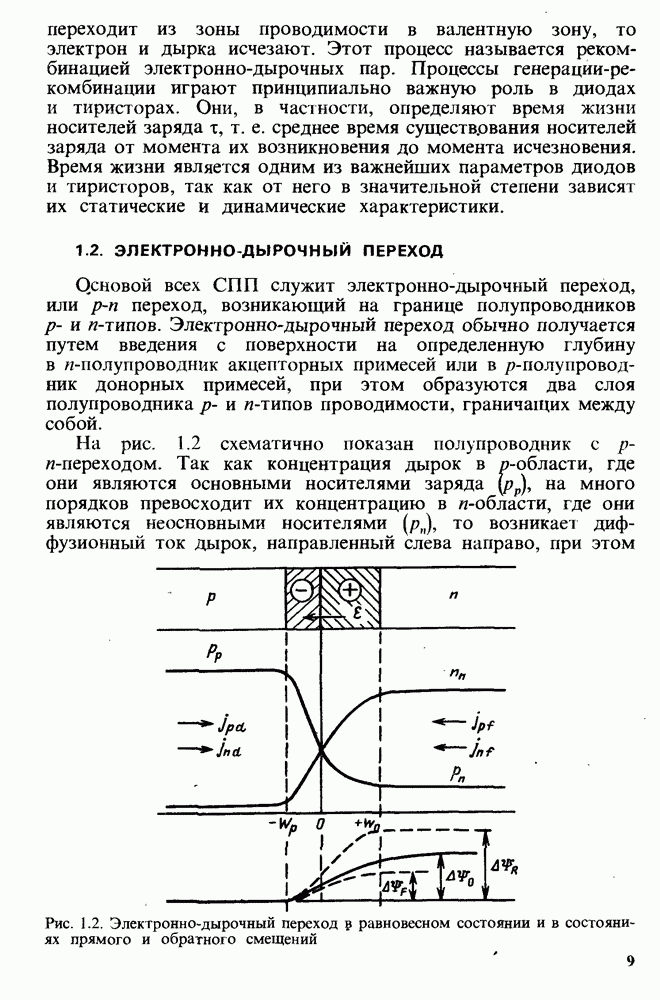
- 1.2. ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД
- 1.3.СИЛОВОЙ ПОЛУПРОВОДНИКОВЫЙ ВЫПРЯМИТЕЛЬНЫЙ ДИОД
- Проводящее состояние силового диода.
- Переходный процесс включения силового полупроводникового диода.
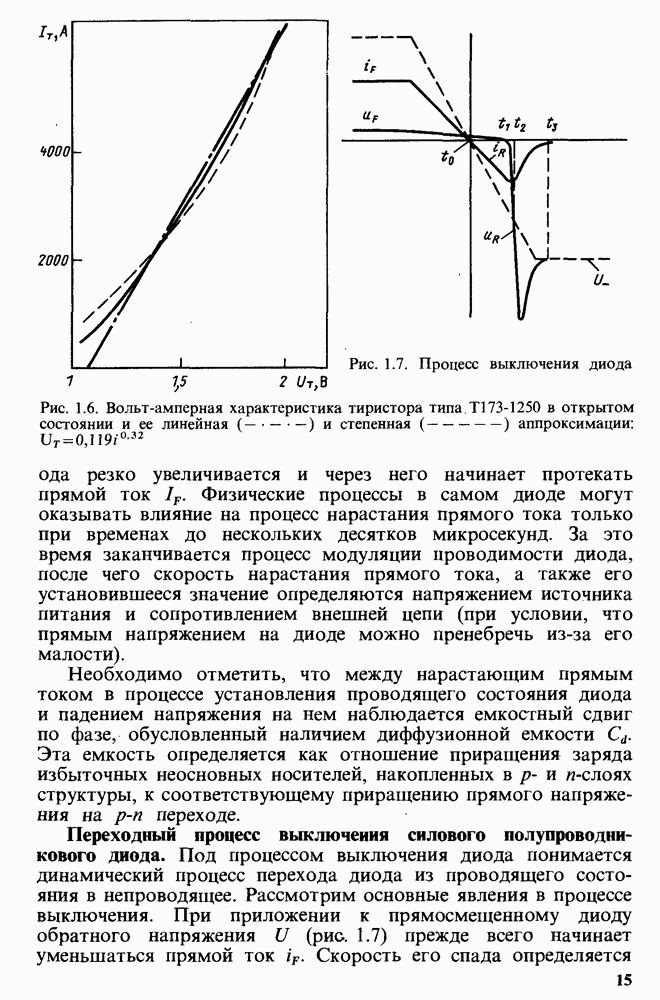
- Переходный процесс выключения силового полупроводникового диода.
- 1.4. СИЛОВОЙ ТРИОДНЫЙ ТИРИСТОР, НЕ ПРОВОДЯЩИЙ В ОБРАТНОМ НАПРАВЛЕНИИ
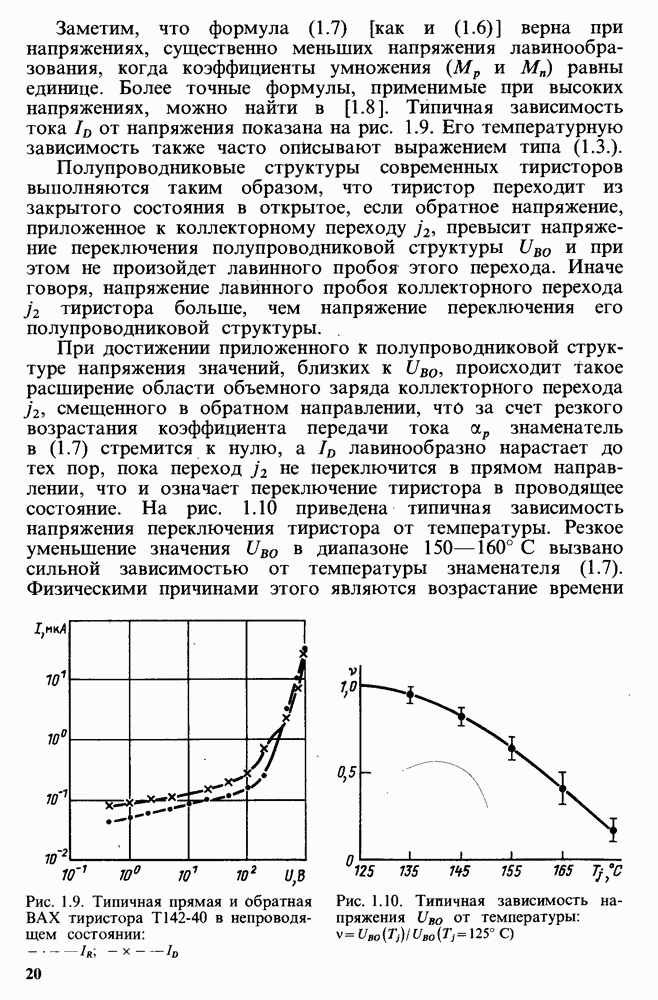
- Обратное непроводящее состояние тиристора.
- Закрытое состояние тиристора.
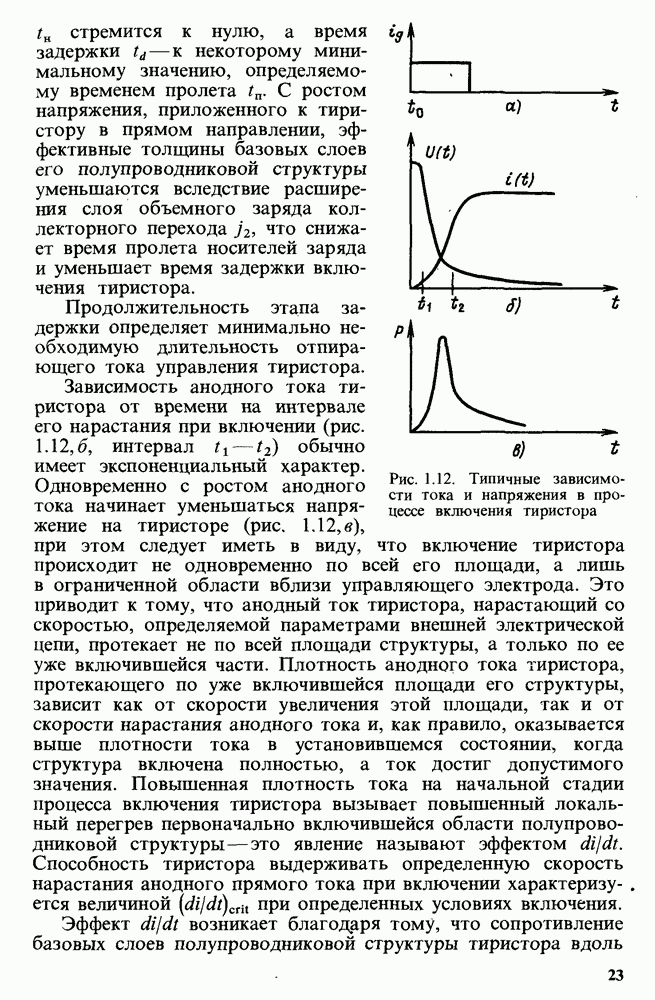
- Процесс включения тиристора. Эффект di/dt. Открытое состояние тиристора.
- Процесс выключения тиристора. Эффект dU/dt.
- Глава 2. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- 2.2. ОСНОВНЫЕ ПАРАМЕТРЫ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Основные электрические параметры силовых тиристоров.
- 2.3. ОСНОВНЫЕ ТЕПЛОВЫЕ ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ДИОДОВ И ТИРИСТОРОВ
- 2.4. КЛАССИФИКАЦИЯ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Классификация силовых полупроводниковых диодов и тиристоров по конструкции.
- 2.5. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ диодов И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
- Условное обозначение типоисполнения диодов и тиристоров.
- 2.6. ОСОБЕННОСТИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ КАК ЭЛЕКТРОТЕХНИЧЕСКИХ ИЗДЕЛИЙ, КОМПЛЕКТУЮЩИХ СХЕМУ СИЛОВОГО ПОЛУПРОВОДНИКОВОГО ПРЕОБРАЗОВАТЕЛЬНОГО УСТРОЙСТВА
- Глава 3. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ И УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ
- 3.1. РЕЖИМЫ И УСЛОВИЯ РАБОТЫ ДИОДОВ И ТИРИСТОРОВ
- 3.2. КЛАССИФИКАЦИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 3.3. ОСОБЕННОСТИ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ
- Рекомендуемая нагрузка диодов и тиристоров.
- Исходные данные и последовательность расчета.
- Глава 4. РАСЧЕТ И ВЫБОР ДИОДОВ И ТИРИСТОРОВ. УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ И РАСЧЕТ СИСТЕМЫ УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 4.1. РАСЧЕТ И ВЫБОР ТИПА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО РАБОЧЕМУ ТОКУ
- Тепловые параметры СПП и выбор условий охлаждения.
- Определение режима нагрузки СПП рабочим током.
- Расчет и выбор типа СПП, типа охладителя и скорости охлаждающей среды при неизменном рабочем токе.
- Расчет и выбор типа прибора, типа охладителя и скорости охлаждающей среды при изменяющемся рабочем токе.
- 4.2. ВЫБОР КЛАССА СПП ПО РАБОЧЕМУ НАПРЯЖЕНИЮ
- Определение класса СПП.
- 4.3. ПРОВЕРКА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО ТЕМПЕРАТУРЕ НАГРЕВА РАБОЧИМ ТОКОМ
- Расчет температур перегрева перехода СПП в рабочем режиме.
- 4.4. ПРОВЕРКА СПП ПО АВАРИЙНОМУ ТОКУ
- Проверка СПП при синусоидальной форме импульса аварийного тока.
- Проверка СПП при несинусоидальной форме аварийного тока.
- 4.5. ВЫБОР КОММУТАЦИОННЫХ ПАРАМЕТРОВ СПП
- Время выключения.
- Критическая скорость нарастания тока при включении.
- Критическая скорость нарастания напряжения в закрытом состоянии СПП.
- Время обратного восстановления.
- 4.6. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УПРАВЛЯЮЩИХ ИМПУЛЬСОВ И СХЕМЫ УПРАВЛЕНИЯ ТИРИСТОРОМ
- Выбор параметров управляющих импульсов.
- Расчет мощности потерь на управляющем электроде.
- 4.7. ПРИМЕР РАСЧЕТА И ВЫБОРА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ
- Расчет и выбор типа СПП и условий его охлаждения но рабочему току.
- Проверка выбранного СПП и условий охлаждения по температуре нагрева перехода рабочим током.
- Проверка СПП по аварийному току.
- Выбор коммутационных параметров СПП.
- Определение параметров управляющих импульсов и источника управления.
- Глава 5. МЕТОДЫ И СРЕДСТВА ОГРАНИЧЕНИЯ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ ПО ТОКУ И НАПРЯЖЕНИЮ В НОРМАЛЬНЫХ И АВАРИЙНЫХ РЕЖИМАХ РАБОТЫ
- 5.1. ТРЕБОВАНИЯ К МЕТОДАМ И СРЕДСТВАМ ОГРАНИЧЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ
- 5.2. ВЫБОР ВИДА И РАСЧЕТ ЭЛЕМЕНТОВ ДЛЯ ОГРАНИЧЕНИЯ АВАРИЙНОГО ТОКА
- 5.3. ОГРАНИЧЕНИЕ КОММУТАЦИОННЫХ ПЕРЕНАПРЯЖЕНИЙ НА СПП
- Получение исходных данных для выбора схем и расчета параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Расчет параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Воздействие перенапряжений, возникающих при запирании СПП, на другие тиристоры преобразовательных схем.
- 5.4. ОГРАНИЧЕНИЕ СХЕМНЫХ И СЕТЕВЫХ ПЕРЕНАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- Схемные перенапряжения
- Уменьшение уровня переиапряжения на вентилях
- Схемные перенапряжения эпизодического характера
- Расчет параметров устройства для ограничения сетевых и схемных перенапряжений.
- Расчет ограничительных устройств для подавления схемных перенапряжений.
- Ограничение скорости нарастания и спадания тока СПП.
- Некоторые явления, связанные с процессом отпирания тиристоров.
- Расчет коммутационных потерь в СПП.
- 5.5. ГРУППОВОЕ СОЕДИНЕНИЕ СПП
- Последовательное соединение СПП
- Групповое соединение СПП
- 5.6. НЕКОТОРЫЕ СХЕМЫ ПОДКЛЮЧЕНИЯ ОГРАНИЧИТЕЛЬНЫХ УСТРОЙСТВ
- Глава 6. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ В СХЕМАХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТАНОВОК
- 6.1. ТРЕБОВАНИЯ К МЕТОДАМ ИЗМЕРЕНИЙ
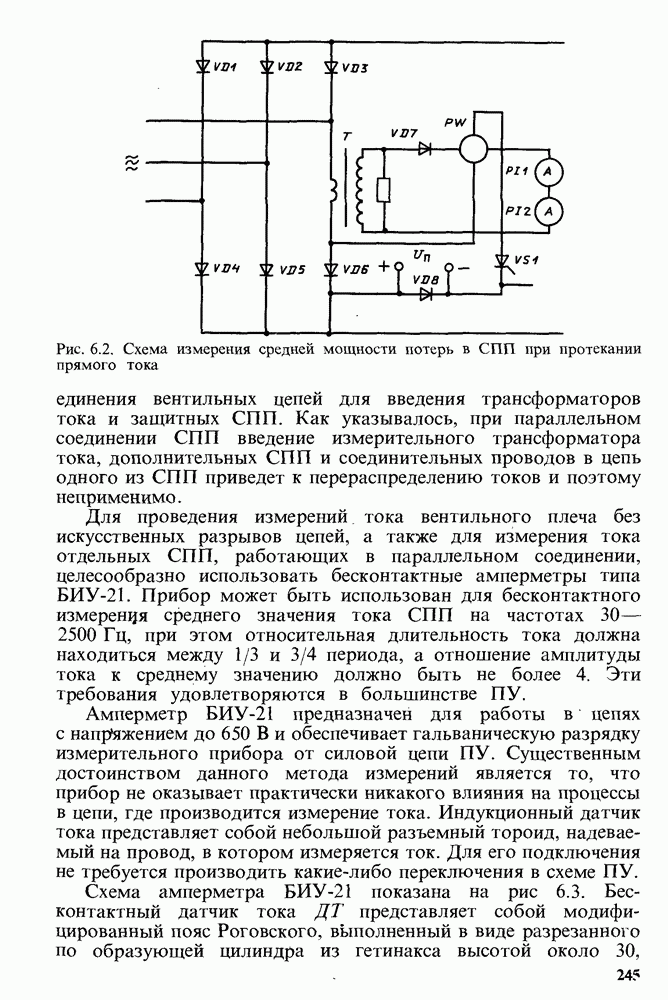
- 6.2. ИЗМЕРЕНИЕ СРЕДНЕГО И ЭФФЕКТИВНОГО ТОКА, ПРОХОДЯЩЕГО ЧЕРЕЗ СПП, И МОЩНОСТИ ПОТЕРЬ В СТАЦИОНАРНОМ РЕЖИМЕ
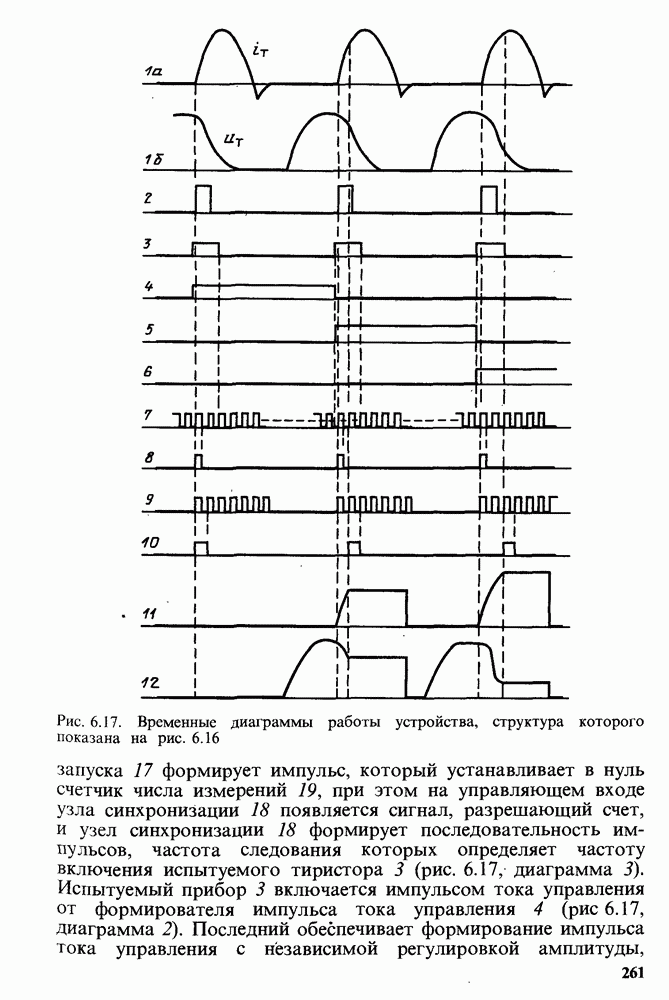
- 6.3. ИЗМЕРЕНИЕ МГНОВЕННЫХ ЗНАЧЕНИЙ ТОКА В ПРОЦЕССЕ ВКЛЮЧЕНИЯ И ВЫКЛЮЧЕНИЯ СПП
- 6.4. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- 6.5. КОНТРОЛЬ ПАРАМЕТРОВ СИГНАЛОВ УПРАВЛЕНИЯ ТИРИСТОРОВ И ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ СПП
- 6.6. СОВРЕМЕННЫЕ МЕТОДЫ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ
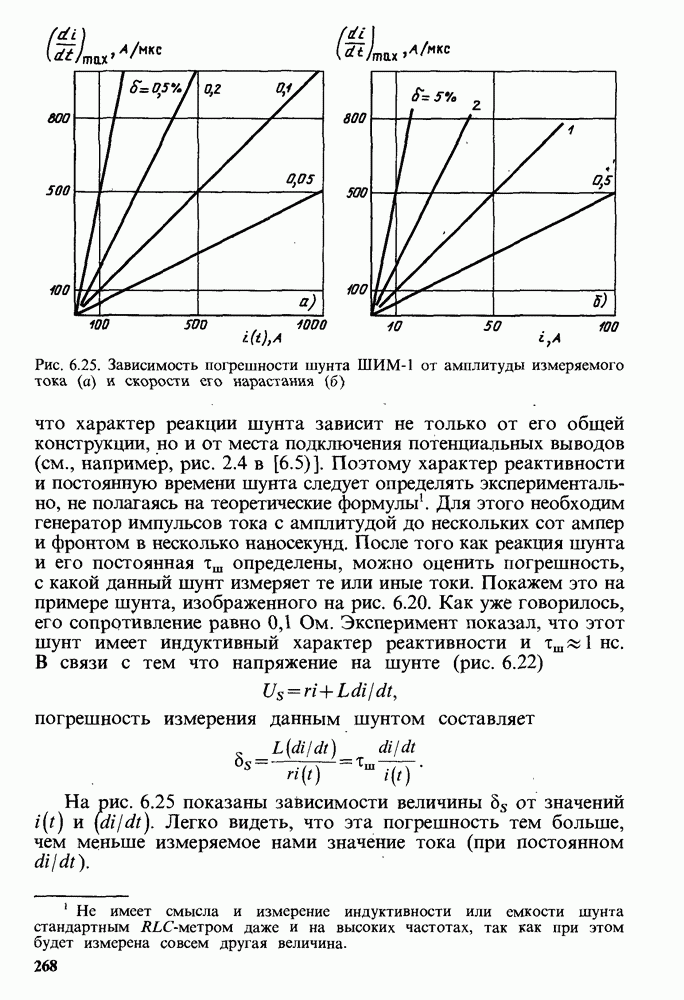
- 6.7. ПОГРЕШНОСТИ ИЗМЕРЕНИЯ БЫСТРОМЕНЯЮЩИХСЯ ТОКОВ С ПОМОЩЬЮ БЕЗЫНДУКТИВНЫХ (МАЛОИНДУКТИВНЫХ) ШУНТОВ
- Глава 7. ОХЛАЖДЕНИЕ ДИОДОВ И ТИРИСТОРОВ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 7.1. ОБЩИЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ. ПРЕДЪЯВЛЯЕМЫЕ К ОХЛАДИТЕЛЯМ СПП
- Классификация охладителей.
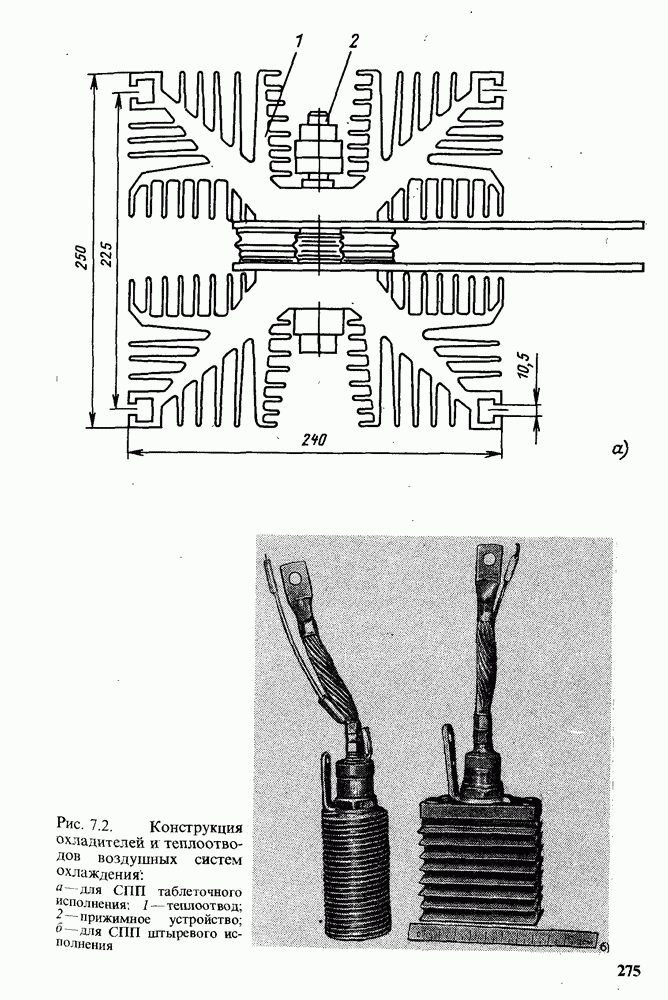
- 7.2. КОНСТРУКЦИИ ОХЛАДИТЕЛЕЙ
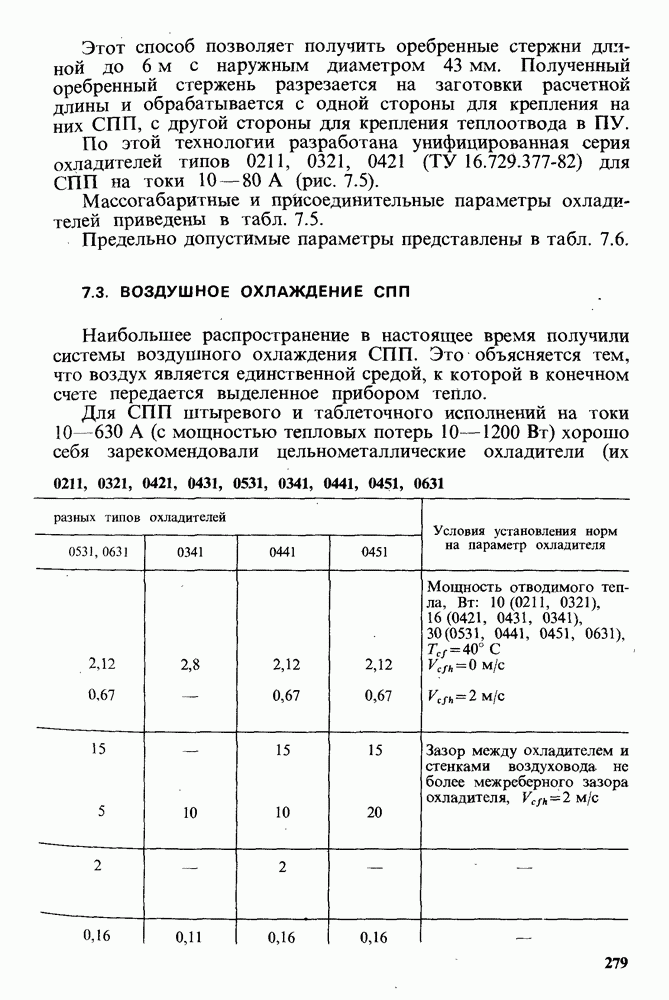
- 7.3. ВОЗДУШНОЕ ОХЛАЖДЕНИЕ СПП
- Прижимные устройства системы «СПП—охладитель».
- Компоновка системы «СПП — охладитель» в ПУ с естественным воздушным охлаждением.
- Температурное поле среды вокруг нагретых СПП с охладителями при наличии в вентильной секции ПУ воздухоотводящих экранов и перфораций.
- Переходное тепловое сопротивление «контактная поверхность — охлаждающая среда» теплоотводов СПП.
- Аэродинамическое сопротивление теплоотводов.
- Потери напора на преодоление сил трения в прямоугольных межреберных каналах теплоотвода охладителя на участке безотрывного течения.
- 7.4. ЖИДКОСТНОЕ ОХЛАЖДЕНИЕ СПП
- Выбор электроизоляционных материалов для охладителей СПП.
- 7.5. ИСПАРИТЕЛЬНОЕ ПОГРУЖНОЕ ОХЛАЖДЕНИЕ СПП
- Критические плотности теплового потока и коэффициенты теплоотдачи.
- Конструкции систем испарительного погружного охлаждения СПП.
- Глава 8. НАДЕЖНОСТЬ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ
- 8.1. ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ ТЕОРИИ НАДЕЖНОСТИ
- 8.2. ПОКАЗАТЕЛИ НАДЕЖНОСТИ СПП И ИХ ЗАВИСИМОСТИ ОТ РЕЖИМОВ РАБОТЫ
- Зависимости ПН от режимов работы.
- 8.3. МЕТОДЫ ОЦЕНКИ И КОНТРОЛЯ ПН СПП
- Режимы проведения испытаний СПП на надежность.
- Методы неразрушающего контроля СПП.
- 8.4. ВИДЫ И МЕХАНИЗМЫ ОТКАЗОВ СПП
- 8.5. МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СПП В РАЗЛИЧНЫХ РЕЖИМАХ
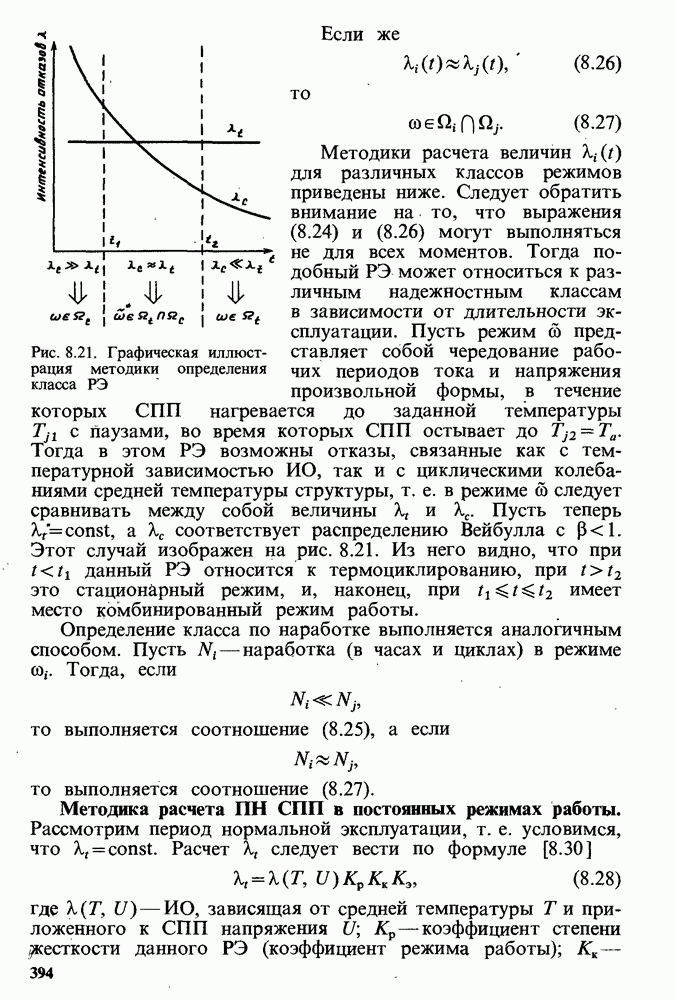
- Методика определения класса РЭ.
- Методика расчета ПН СПП в постоянных режимах работы.
- Методика расчета ПН СПП в циклических режимах.
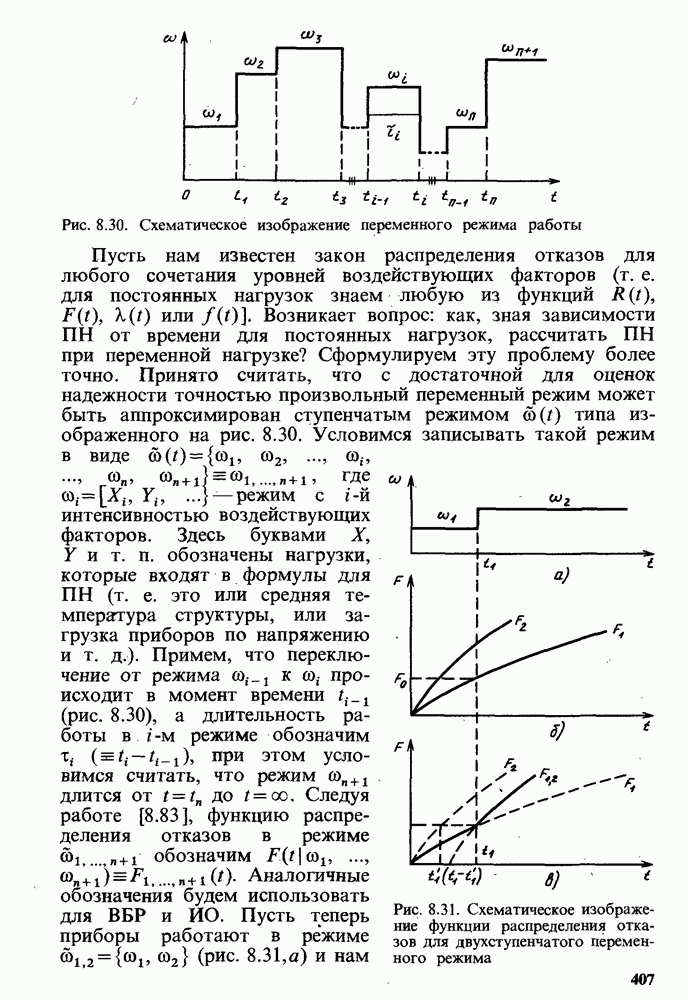
- Методика расчета ПН СПП в переменных и комбинированных режимах.
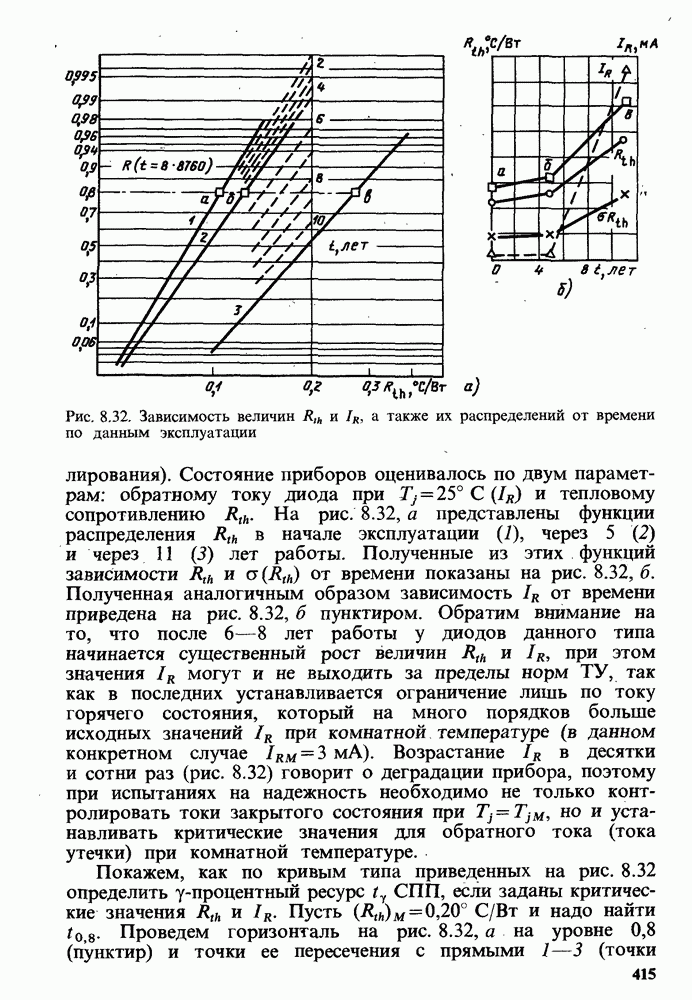
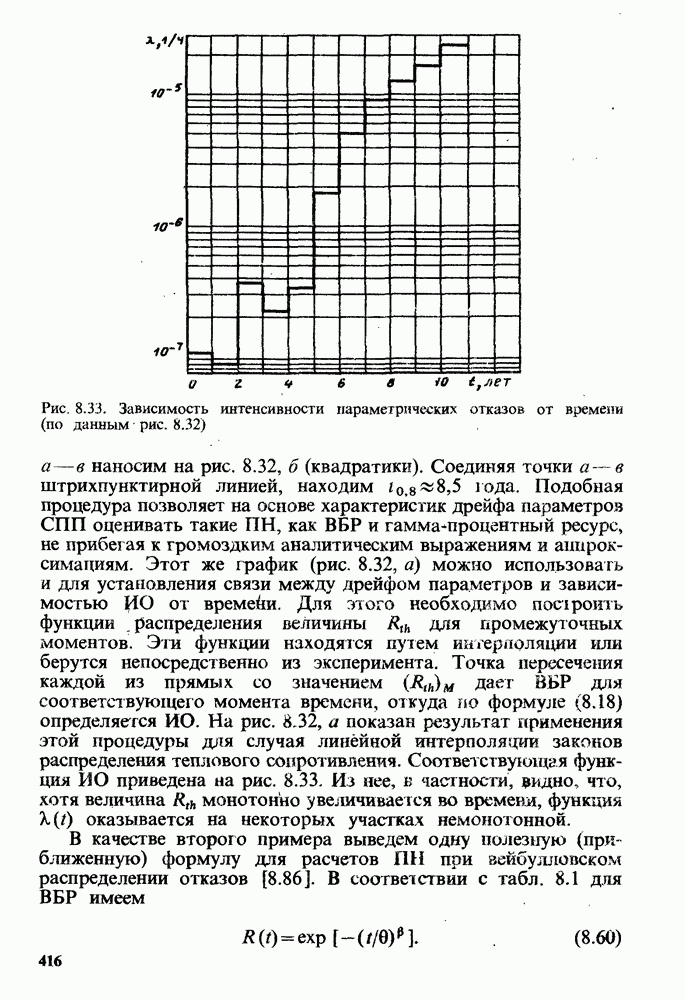
- Некоторые практические рекомендации по расчетам ПН СПП.
- СПИСОК ЛИТЕРАТУРЫ