| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Зависимости ПН от режимов работы.
Для успешного решения проблемы обеспечения и повышения уровня надежности ПУ необходимо прежде всего ответить на следующие вопросы:
1. Как распределены во времени отказы СПП в том или ином режиме?
2. Как зависит распределение отказов от режимов эксплуатации (РЭ) приборов?
На принятом в теории надежности языке эти вопросы могут быть сформулированы следующим образом:
1. Каков(а) закон (функция) распределения отказов СПП в том или ином режиме?
2. Как параметры закона (функции) распределения отказов зависят от РЭ приборов?

Рис. 8.3. Классификация моделей надежности СПП
В том случае, когда ответы на эти вопросы для какого-то класса РЭ нам известны, будем говорить, что в данном классе режимов построена модель надежности СПП. На рис. 8.3 показана возможная классификация моделей надежности, применимая к дискретным полупроводниковым приборам (идея подобной классификации взята из работы [8.4]).
В соответствии с предлагаемой классификацией все модели имеют своей целью решение трех задач: расчет ПН в различных РЭ, пересчет ПН от одних режимов к другим, ускоренные испытания приборов на надежность. Подробно об этих задачах будем говорить ниже, здесь же отметим следующее. Под физическими моделями надежности понимаем такие методы описания закономерностей возникновения отказов, которые основаны на выяснении физических причин и процессов, ведущих к нарушению работоспособности СПП. Другими словами, это модели, с помощью которых можно объяснить, откуда берутся и как в процессе эксплуатации развиваются дефекты прибора, которые рано или поздно приводят к его отказу. Под обобщенно-статистическими моделями надежности понимаем такие математические методы описания поведения совокупности приборов, которые на основе статистических данных о характере изменения некоторых параметров (или характеристик) в процессе эксплуатации (подробнее см. в § 8.5.3) позволяют рассчитать их ПН. Под функциональными моделями надежности понимаем математическую зависимость того или иного ПН от времени и условий эксплуатации [именно это и отражено в символической записи  , РЭ)]. В соответствии с упоминавшимся выше вероятностным подходом исчерпывающее описание надежности любого элемента, в том числе и СПП, дает любая из функций
, РЭ)]. В соответствии с упоминавшимся выше вероятностным подходом исчерпывающее описание надежности любого элемента, в том числе и СПП, дает любая из функций  , поскольку в математическом отношении они полностью эквивалентны. Тем не менее в полупроводниковой электронике чаще всего для построения функциональных моделей надежности используют функцию ИО. Этому есть по крайней мере две причины, на которых остановимся подробнее.
, поскольку в математическом отношении они полностью эквивалентны. Тем не менее в полупроводниковой электронике чаще всего для построения функциональных моделей надежности используют функцию ИО. Этому есть по крайней мере две причины, на которых остановимся подробнее.
Во-первых, по характеру зависимости ИО от времени принято классифицировать различные этапы «жизни» изделий. Так, уже в ранних работах по надежности обнаружено [8.5, 8.6], что при стационарных внешних воздействиях функция  имеет весьма характерный «ваннообразный» вид (рис. 8.4). Эту кривую обычно разбивают на три участка: период приработки, где ИО монотонно убывает; период нормальной эксплуатации, где ИО примерно постоянна; период старения, где ИО монотонно возрастает. Высокое первоначальное значение ИО во время периода приработки обычно связывают с наличием приборов, имеющих скрытые технологические дефекты, которые, с одной стороны, не так грубы, чтобы выявиться на этапе приемо-сдаточного контроля, но, с другой стороны, достаточно велики, чтобы выявляться практически сразу в условиях эксплуатации (или испытаний). Поскольку предполагается, что таких приборов обычно сравнительно немного, то по мере их изъятия из совокупности («выжигание» дефектов) надежность всей партии улучшается.
имеет весьма характерный «ваннообразный» вид (рис. 8.4). Эту кривую обычно разбивают на три участка: период приработки, где ИО монотонно убывает; период нормальной эксплуатации, где ИО примерно постоянна; период старения, где ИО монотонно возрастает. Высокое первоначальное значение ИО во время периода приработки обычно связывают с наличием приборов, имеющих скрытые технологические дефекты, которые, с одной стороны, не так грубы, чтобы выявиться на этапе приемо-сдаточного контроля, но, с другой стороны, достаточно велики, чтобы выявляться практически сразу в условиях эксплуатации (или испытаний). Поскольку предполагается, что таких приборов обычно сравнительно немного, то по мере их изъятия из совокупности («выжигание» дефектов) надежность всей партии улучшается.

Рис. 8.4. Общий вид зависимости ИО элементов от времени
Отказы в течение периода нормальной эксплуатации принято объяснять причинами случайного характера (перегрузки и т. п.), а также скрытыми производственными дефектами или несовершенством конструкции, и, наконец, отказы во время периода старения чаще всего связывают с износом и старением элементов. Момент окончания периода приработки будем обозначать символом  (от английского burn —
(от английского burn —  — выжигание), а момент начала периода старения —
— выжигание), а момент начала периода старения —  (от английского wear
(от английского wear  — износ).
— износ).
Во-вторых, в отличие от функции ИО графические изображения других функций  не обладают такой наглядностью. Так, если на рис. 8.4 изобразить функцию
не обладают такой наглядностью. Так, если на рис. 8.4 изобразить функцию  , то она на всех участках будет монотонно убывающей и для определения наличия периодов приработки и старения, а также для определения моментов
, то она на всех участках будет монотонно убывающей и для определения наличия периодов приработки и старения, а также для определения моментов  потребуется применение специального математического аппарата, тогда как по графику зависимости
потребуется применение специального математического аппарата, тогда как по графику зависимости  ответы на эти вопросы во многих случаях очевидны.
ответы на эти вопросы во многих случаях очевидны.
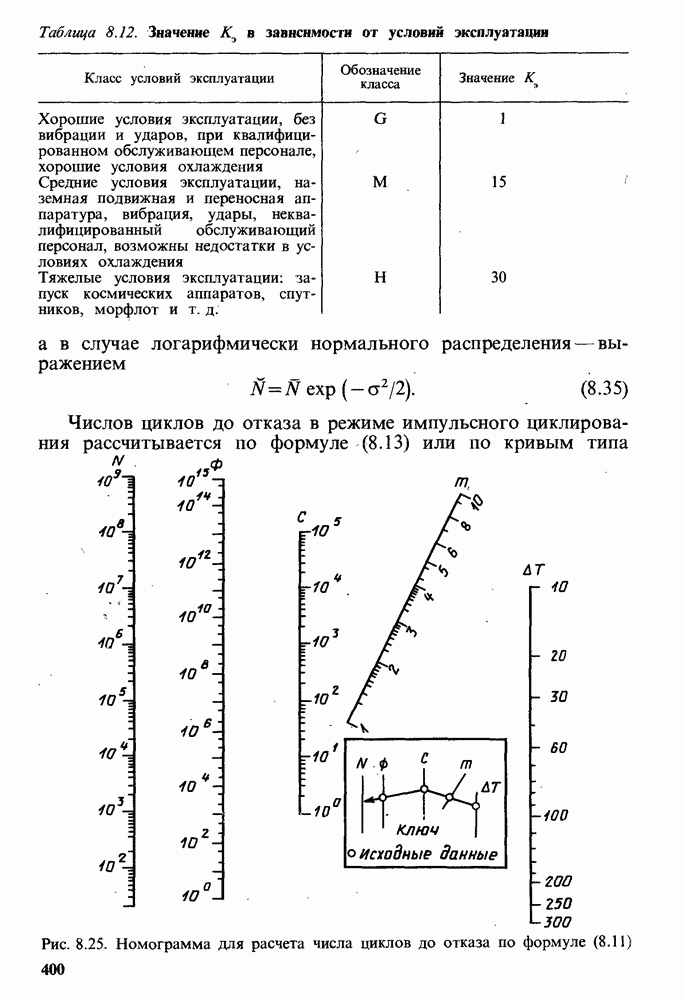
Классификация режимов работы СПП по критерию надежности. Для того чтобы разобраться с многообразием перечисленных ПН, а также для успешного решения задач расчета надежности СПП в различных режимах необходимо ввести классификацию РЭ СПП с точки зрения их надежности. В соответствии с [8.7] все РЭ делят прежде всего на циклические и нециклические (стационарные). В циклических РЭ в качестве ПН выступает число циклов или повторений тех или иных воздействий, выдерживаемых приборами до отказа. В нециклических РЭ в качестве ПН выступает ВБР или ИО. Это деление отражает реально существующую систему ПН СПП. Объективной причиной ее возникновения является тот факт, что в нециклических режимах ПН есть функции непрерывного параметра — времени работы, тогда как значения ПН в циклических режимах зависят от дискретной переменной — числа циклов.

Рис. 8.5. Классификация режимов эксплуатации СПП с точки зрения их надежности. (В нижнем ряду прямоугольников даны показатели, которые наиболее удобны для расчета надежности СПП в эксплуатации).
Физической основой данной классификации является отсутствие в нециклических режимах работы доминирующих механизмов отказа, т. е. эти режимы характеризуются многообразием видов и причин отказов, их взаимодействием и взаимоналожением. В циклических режимах, напротив, существуют преобладающие механизмы отказов, причем по тому, какие именно механизмы являются доминирующими, циклические режимы удается разделить еще на три подгруппы. В итоге приходим к схеме классификации, в соответствии с которой все РЭ СПП делят на следующие режимы (рис.  ):
):
стационарный (или нециклический);
электротермоциклирования (далее просто термоциклирование);
импульсного циклирования;
токовых перегрузок.
Под стационарным режимом понимают режим работы, в котором в качестве ПН используют ВБР или ИО, зависящую в первую очередь от средней температуры структуры  и загрузки приборов по напряжению
и загрузки приборов по напряжению  :
:

где  — амплитудное значение напряжения рабочей частоты, прикладываемого к прибору. Если к прибору прикладывается и прямое
— амплитудное значение напряжения рабочей частоты, прикладываемого к прибору. Если к прибору прикладывается и прямое  , и обратное
, и обратное  напряжения, то
напряжения, то  .
.
Под режимом термоциклирования понимают режим работы, в котором в качестве ПН используют число циклов  средней температуры структуры, выдерживаемое приборами до отказа и зависящее от амплитуды колебаний средней температуры за один цикл
средней температуры структуры, выдерживаемое приборами до отказа и зависящее от амплитуды колебаний средней температуры за один цикл  :
:

Под режимом импульсного циклирования понимают режим работы, в котором в качестве ПН используют число циклов  мгновенной температуры структуры, выдерживаемое приборами до отказа и зависящее от амплитуды колебаний температуры «горячей точки»
мгновенной температуры структуры, выдерживаемое приборами до отказа и зависящее от амплитуды колебаний температуры «горячей точки»  за один цикл:
за один цикл:

Под режимом токовых перегрузок понимают режим работы, в котором в качестве ПН используют число импульсов тока или тока аварийной перегрузки  , выдерживаемое приборами до отказа и зависящее от амплитуды импульса тока
, выдерживаемое приборами до отказа и зависящее от амплитуды импульса тока  :
:

Связь последних трех режимов с механизмами отказов следующая. Отказы в режиме термоциклирования определяются усталостными явлениями в контактных соединениях приборов, отказы в режиме импульсного циклирования — усталостными явлениями в «горячей точке» в окрестности управляющего электрода, отказы в режиме токовых  - накоплением повреждений в объеме структуры и в области контакта структуры с термокомпенсатором.
- накоплением повреждений в объеме структуры и в области контакта структуры с термокомпенсатором.
Рассмотрим последовательно зависимости ПН СПП от режимов работы сначала для нециклических, а затем для циклических режимов применения.
Нециклические режимы. Модели зависимости ИО СПП от времени и нагрузки. Как уже отмечалось, при стационарных внешних условиях зависимость функции ИО от времени имеет вид кривой, показанной на рис. 8.4. Создание модели надежности для функции ИО означает определение вида и параметров закона распределения отказов для каждого из участков кривой  . Прежде чем перейти к рассмотрению конкретных данных о моделях ИО для СПП, рассмотрим некоторые наиболее употребительные в теории и практике надежности законы распределения отказов.
. Прежде чем перейти к рассмотрению конкретных данных о моделях ИО для СПП, рассмотрим некоторые наиболее употребительные в теории и практике надежности законы распределения отказов.
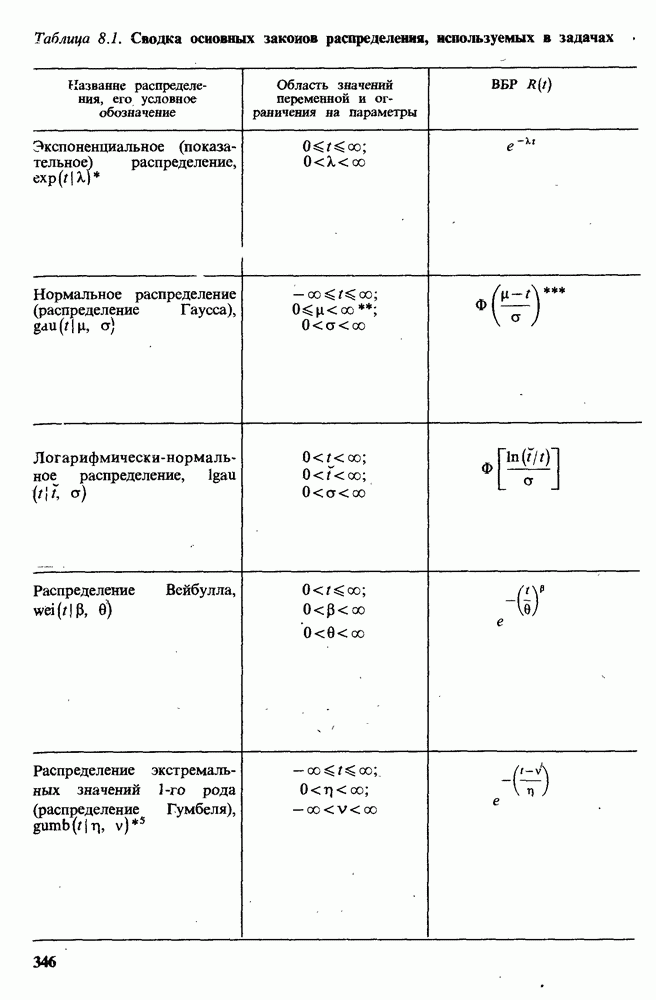
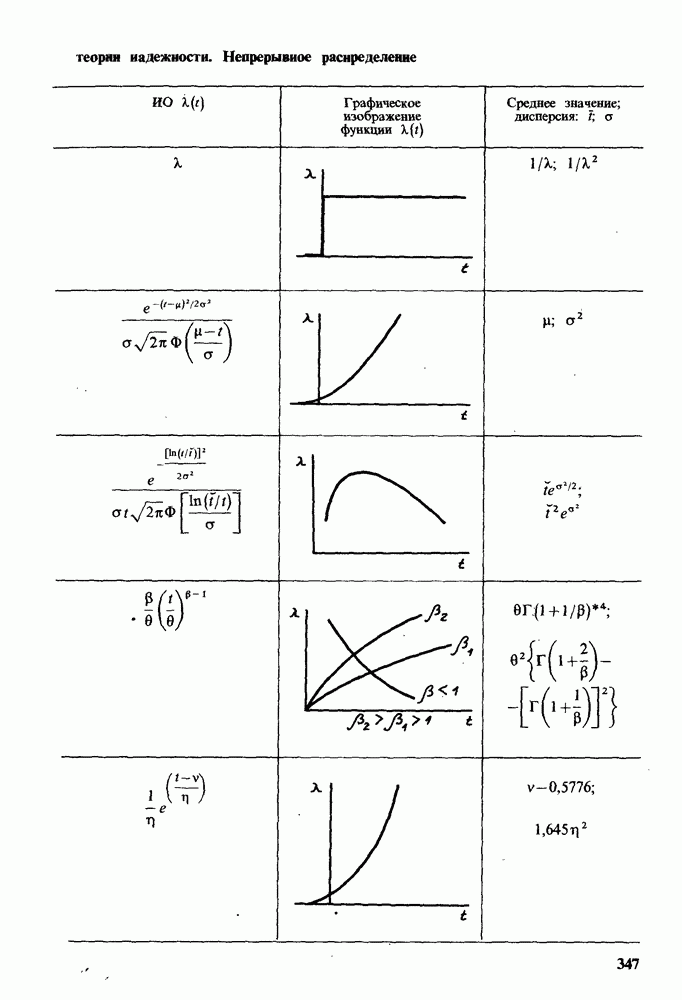
В табл. 8.1 приведен необходимый минимум сведений о наиболее часто встречающихся функциях распределения. В левой колонке дано название распределения и его условное обозначение. Во второй колонке приведены пределы, в которых может изменяться переменная t, и ограничения на параметры данного распределения. В третьей и четвертой колонках даны формулы для ВБР и ИО соответственно. В пятой колонке показан качественный характер функции Ц?) для данного распределения. В шестой колонке приведены среднее значение и дисперсия наработки до отказа, выраженные через параметры распределения. Заметим, что во всех распределениях вместо t всегда можно записать  , где
, где  — параметр сдвига.
— параметр сдвига.
Математически это означает, что соответствующее распределение (т. е. любая из функций  ) сдвинуто вправо на
) сдвинуто вправо на  .
.
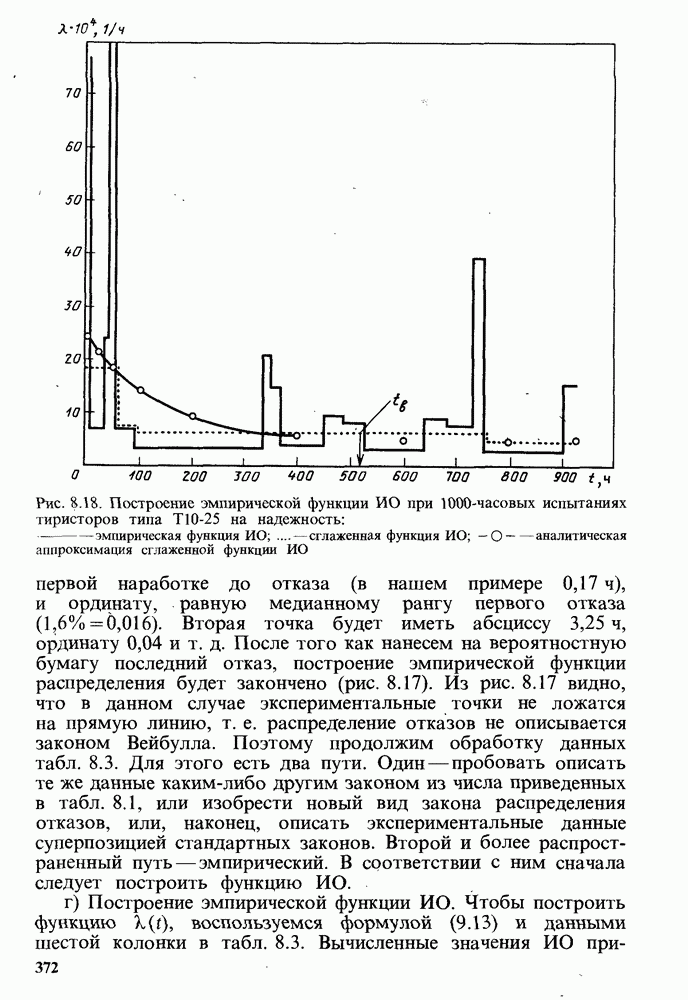
Рассмотрим ряд конкретных данных по моделям ИО СПП. Типичные зависимости ИО от времени приведены на рис. 8.6. В табл. 8.2 представлены данные результатов работ различных авторов, которые включают сведения как об эксплуатационной, так и о лабораторной надежности. В целом о моделях надежности СПП во время периода приработки можно сказать следующее.
Длительность периода приработки для СПП колеблется от 100 до  , причем значение его в целом уменьшается при ужесточении режима работы приборов. Для построения моделей функции ИО в отечественной практике используются два распределения: Вейбулла и Макегама. В случае применимости распределения Вейбулла параметр формы (3 находится в диапазоне
, причем значение его в целом уменьшается при ужесточении режима работы приборов. Для построения моделей функции ИО в отечественной практике используются два распределения: Вейбулла и Макегама. В случае применимости распределения Вейбулла параметр формы (3 находится в диапазоне  Анализ публикации [8.9] показывает, что при лабораторных испытаниях в выпрямительном режиме длительность периода приработки у зарубежных приборов аналогична отечественной. Вопрос о том, как практически определить, есть или нет период приработки, каким законом распределения он лучше описывается, каковы параметры этого распределения и т. п., будет рассмотрен далее. Здесь следует лишь подчеркнуть, что модели надежности, описывающие ход функций ИО во время периода приработки, применимы только при
Анализ публикации [8.9] показывает, что при лабораторных испытаниях в выпрямительном режиме длительность периода приработки у зарубежных приборов аналогична отечественной. Вопрос о том, как практически определить, есть или нет период приработки, каким законом распределения он лучше описывается, каковы параметры этого распределения и т. п., будет рассмотрен далее. Здесь следует лишь подчеркнуть, что модели надежности, описывающие ход функций ИО во время периода приработки, применимы только при  .
.
Для описания периода нормальной эксплуатации используют самое популярное в надежности распределение — экспоненциальное. Из табл. 8.1 видно, что ему соответствует постоянная ИО. Этот период жизни прибора, как правило, много больше периода приработки  , и поэтому он представляет максимальный интерес для потребителя.
, и поэтому он представляет максимальный интерес для потребителя.
Что же касается периода старения, то его для СПП, по-видимому, никто не наблюдал. Это может быть вызвано тем, что значение  в правильно выбранных схемах и РЭ для хороших приборов превышает
в правильно выбранных схемах и РЭ для хороших приборов превышает  , что составляет более 11 лет непрерывной эксплуатации. За это время обычно оборудование устаревает, и приборы заменяют на новые. Отсутствие конкретных данных о периоде старения СПП означает, что нам неизвестны ни отечественные, ни зарубежные публикации, в. которых наблюдалось бы изменение характера функции ИО от постоянной (или убывающей) к монотонно возрастающей. В отличие от этого данные о процессах деградации параметров приборов достаточно многочисленны [8.14]. Как правило, на основе этих данных устанавливают численные значения таких показателей долговечности, как
, что составляет более 11 лет непрерывной эксплуатации. За это время обычно оборудование устаревает, и приборы заменяют на новые. Отсутствие конкретных данных о периоде старения СПП означает, что нам неизвестны ни отечественные, ни зарубежные публикации, в. которых наблюдалось бы изменение характера функции ИО от постоянной (или убывающей) к монотонно возрастающей. В отличие от этого данные о процессах деградации параметров приборов достаточно многочисленны [8.14]. Как правило, на основе этих данных устанавливают численные значения таких показателей долговечности, как  - процентный ресурс и (или) срок службы. В частности, для тиристоров типа
- процентный ресурс и (или) срок службы. В частности, для тиристоров типа  на основании данных многолетних наблюдений можно утверждать, что в выпрямительно-инверторном режиме работы их 90%-ный ресурс превышает 70000 ч.
на основании данных многолетних наблюдений можно утверждать, что в выпрямительно-инверторном режиме работы их 90%-ный ресурс превышает 70000 ч.
Таблица 8.1.
(см. оригинал)
Таблица 8.1. (продолжение)
(см. оригинал)
Таблица 8.1. (продолжение)
(см. оригинал)
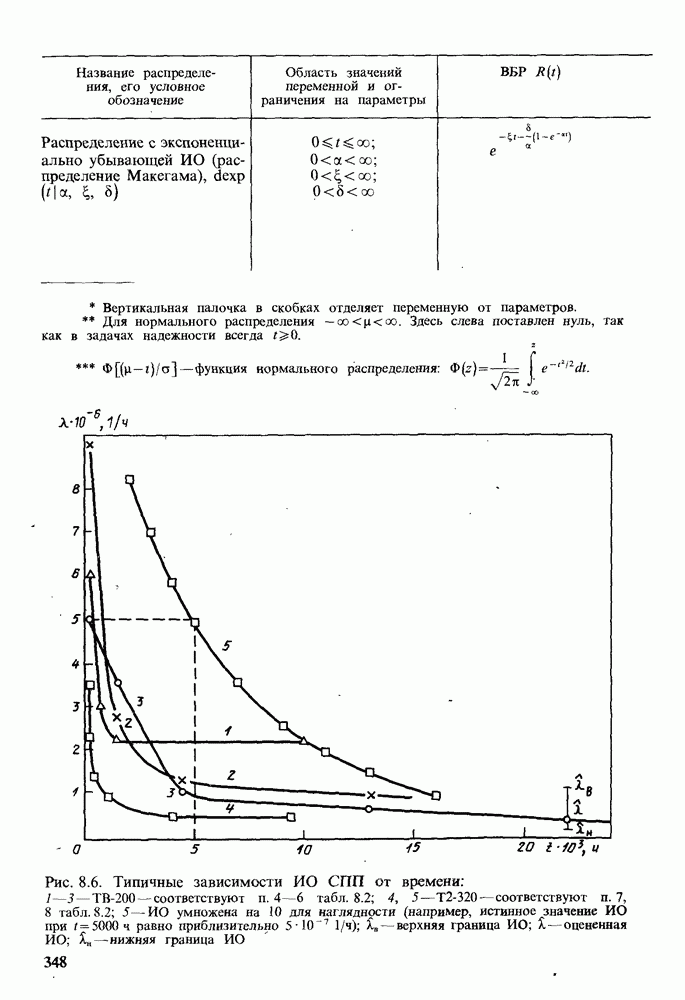
Рис. 8.6. Типичные зависимости ИО СПП от времени:
1—3 — ТВ-200 соответствуют п. 4—6 табл. 8.2; 4, 5 — Т2-320 — соотвсгствуюг п. 7, 8 табл. 8.2; 5 — ИО умножена на 10 для наглядности (например, истинное значение ИО при  равно приблизительно
равно приблизительно  );
);  — верхняя граница ИО; к - оцененная ИО;
— верхняя граница ИО; к - оцененная ИО;  — нижняя граница ИО
— нижняя граница ИО
Таблица 8.1. (окончание)
Таблица 8.2.
(см. оригинал)
Продолжение табл. 8.2.

Для диодов типа  -ный срок службы в выпрямителях тяговых подстанций городского транспорта составляет примерно 8,5 года.
-ный срок службы в выпрямителях тяговых подстанций городского транспорта составляет примерно 8,5 года.
К сожалению, объем статистической информации, имеющийся у инженеров по надежности, как правило, недостаточен для уверенного определения вида закона распределения отказов.  тем многие законы, будучи весьма близкими при значениях ВБР, соответствующих отказу примерно 50% приборов, могут значительно различаться на «хвостах» распределений, что при неправильном выборе вида закона приводит к существенным погрешностям в оценках моментов наступления первых и последних отказов. Поэтому в практике определения вида функции распределения наработки до отказа важное значение имеет использование априорных соображений. В частности, из рис. 8.4 и табл. 8.1 видно, что для описания периода приработки СПП целесообразно использовать такие функции, как распределение Вейбулла с параметром
тем многие законы, будучи весьма близкими при значениях ВБР, соответствующих отказу примерно 50% приборов, могут значительно различаться на «хвостах» распределений, что при неправильном выборе вида закона приводит к существенным погрешностям в оценках моментов наступления первых и последних отказов. Поэтому в практике определения вида функции распределения наработки до отказа важное значение имеет использование априорных соображений. В частности, из рис. 8.4 и табл. 8.1 видно, что для описания периода приработки СПП целесообразно использовать такие функции, как распределение Вейбулла с параметром  , распределение Макегама, для описания периода нормальной эксплуатации — экспоненциальное распределение, для описания периода старения — распределение Вейбулла с параметром
, распределение Макегама, для описания периода нормальной эксплуатации — экспоненциальное распределение, для описания периода старения — распределение Вейбулла с параметром  , нормальное распределение, распределение Гумбеля. Наконец, для описания немонотонной функции ИО пригодно логарифмически нормальное распределение. При этом необходимо учитывать следующее. Экспоненциальное распределение соответствует элементам с постоянной от
, нормальное распределение, распределение Гумбеля. Наконец, для описания немонотонной функции ИО пригодно логарифмически нормальное распределение. При этом необходимо учитывать следующее. Экспоненциальное распределение соответствует элементам с постоянной от  до
до  ИО.
ИО.
Так как реально таких элементов в природе не существует (всегда  ), то область применения этого распределения обязательно должна быть ограничена величиной
), то область применения этого распределения обязательно должна быть ограничена величиной  справа. В противном случае легко получить неверный, а иногда и абсурдный результат. Покажем это на примере. Пусть некоторые приборы имеют постоянную ИО
справа. В противном случае легко получить неверный, а иногда и абсурдный результат. Покажем это на примере. Пусть некоторые приборы имеют постоянную ИО  и
и  -ный ресурс
-ный ресурс  , равный 50 000. Применяя формулу для средней наработки (7) при экспоненциальном распределении (табл. 8.1), получаем
, равный 50 000. Применяя формулу для средней наработки (7) при экспоненциальном распределении (табл. 8.1), получаем

ВБР при 

Покажем, что с учетом значения  все эти значения к этому прибору не могут иметь ни малейшего отношения. В самом деле, если бы ИО была постоянной до
все эти значения к этому прибору не могут иметь ни малейшего отношения. В самом деле, если бы ИО была постоянной до  , то мы бы имели
, то мы бы имели

В связи с тем что  , ИО приборов не могла быть постоянной, а возрастала уже при
, ИО приборов не могла быть постоянной, а возрастала уже при  . Более того, убедившись, что ИО возросла от
. Более того, убедившись, что ИО возросла от  до какого-то другого большего значения, предположим, что после
до какого-то другого большего значения, предположим, что после  она не возрастала. Тогда для оценки ВБР при t — T можно ввести такую постоянную ИО
она не возрастала. Тогда для оценки ВБР при t — T можно ввести такую постоянную ИО  , которая при
, которая при  дала бы ВБР, равную 60%. Имеем
дала бы ВБР, равную 60%. Имеем

откуда для  получаем
получаем  . Если это значение подставить в формулу для ВБР, получим
. Если это значение подставить в формулу для ВБР, получим

т. е. во всех случаях, когда экспоненциальное распределение применяется за пределами интервала  , оно приводит к противоречиям.
, оно приводит к противоречиям.
Нормальное распределение возникает при решении различных задач, когда отказ связывают с достижением каким-либо параметром критического уровня, а исходное распределение этого параметра описывается функцией нормального распределения. Логарифмически нормальное распределение [8.15] возникает при наличии большого числа мультипликативно накапливающихся дефектов (модель пропорционального эффекта), вклады которых сравнимы между собой.
Распределение Вейбулла является одним из распределений экстремальных значений. Оно возникает в модели «слабейшего звена», согласно которой прибор (объект) состоит из большого числа однотипных элементарных объемов, причем отказ происходит в том из них, который обладает минимальным сопротивлением (прочностью) по отношению к внешнему воздействию («слабейшее звено», «горячая точка» и т. п.). Аналогичное происхождение имеет и распределение Гумбеля [8.15]. Разница между этими двумя распределениями вызвана тем, что распределение Вейбулла возникает при ограниченной переменной (т.е. когда прочность заведомо меньше некоторого значения), а распределение Гумбеля — для неограниченной переменной (прочность элемента лежит в диапазоне от нуля и до бесконечности).
Приведенные краткие сведения о схемах возникновения различных распределений призваны способствовать сужению класса функций, среди которых ищется подходящая аналитическая аппроксимация опытных данных. Не следует абсолютизировать значимость приведенных сведений. Все они являются, скорее, математическими иллюстрациями того, как может возникнуть тот или иной вид закона распределения наработки до отказа, чем их обоснованием. Для последнего чисто математические методы, как правило, недостаточны, необходимо привлекать сведения о физике отказов.
Рассмотрим зависимость ИО СПП от температуры, напряжения и других факторов нагрузки. Ранее отмечалось, что и поэтому наибольший интерес для потребителя представляет период нормальной эксплуатации  . Во многих режимах работы ИО СПП в течение этого периода может считаться постоянной. Это означает, что, говоря о безотказности приборов, можно оперировать величиной X без указания момента, к которому это значение относится. Поэтому в общей формуле
. Во многих режимах работы ИО СПП в течение этого периода может считаться постоянной. Это означает, что, говоря о безотказности приборов, можно оперировать величиной X без указания момента, к которому это значение относится. Поэтому в общей формуле

где  - температура Т, напряжение U, ток I, влажность H и т. п., можно избавиться от переменной
- температура Т, напряжение U, ток I, влажность H и т. п., можно избавиться от переменной  .
.
Таким образом, имеем

Оказывается [8.14], что во многих режимах применение ИО СПП является функцией в первую очередь средней температуры структуры, причем эта зависимость имеет вид закона Аррениуса:

где  — ИО при температурах
— ИО при температурах  ;
;  — энергия активации;
— энергия активации;  — постоянная Больцмана. Из формулы (8.1) видно, что в координатах
— постоянная Больцмана. Из формулы (8.1) видно, что в координатах  зависимость ИО от температуры представляет прямую линию, наклон которой определяется величиной
зависимость ИО от температуры представляет прямую линию, наклон которой определяется величиной  . На рис. 8.7 приведены графики функции
. На рис. 8.7 приведены графики функции  , построенные по данным зарубежных и отечественных работ
, построенные по данным зарубежных и отечественных работ  . Пунктиром на рис. 8.7 показаны результаты, относящиеся к приборам малой мощности [8.26, 8.27], штрих-пунктиром — отечественные данные по зависимости ИО СПП от температуры. Отметим, что приведенные на рис. 8.7 графики исчерпывают всю обнаруженную нами в литературе конкретную информацию по функциональной зависимости
. Пунктиром на рис. 8.7 показаны результаты, относящиеся к приборам малой мощности [8.26, 8.27], штрих-пунктиром — отечественные данные по зависимости ИО СПП от температуры. Отметим, что приведенные на рис. 8.7 графики исчерпывают всю обнаруженную нами в литературе конкретную информацию по функциональной зависимости  для
для  , при этом данные работы [8.22] относятся к режиму хранения, а результаты работы
, при этом данные работы [8.22] относятся к режиму хранения, а результаты работы  периоду приработки при испытаниях в «ждущем» режиме. Слева внизу на рис. 8.7 приведены вспомогательные прямые, по которым можно определить значения
периоду приработки при испытаниях в «ждущем» режиме. Слева внизу на рис. 8.7 приведены вспомогательные прямые, по которым можно определить значения  для всех представленных данных. Эти значения указаны в подписи к рис. 8.7 (цифры в круглых скобках непосредственно после номера кривой). Из анализа результатов указанных выше работ и рис. 8.7 следует, что энергия активации для отечественных СПП лежит в пределах
для всех представленных данных. Эти значения указаны в подписи к рис. 8.7 (цифры в круглых скобках непосредственно после номера кривой). Из анализа результатов указанных выше работ и рис. 8.7 следует, что энергия активации для отечественных СПП лежит в пределах  эВ, тогда как для приборов зарубежных фирм этот диапазон составляет
эВ, тогда как для приборов зарубежных фирм этот диапазон составляет  эВ (без учета данных [9.18], относящихся к приборам в пластмассовых корпусах). Это важно при расчетах ПН отечественных СПП, так как использование данных [8.16,
эВ (без учета данных [9.18], относящихся к приборам в пластмассовых корпусах). Это важно при расчетах ПН отечественных СПП, так как использование данных [8.16,  8.25] может приводить к неправильным результатам.
8.25] может приводить к неправильным результатам.
Следует подчеркнуть, что указание для того или иного СПП определенного значения энергии активации не следует интерпретировать как наличие у данного СПП конкретного механизма отказа, обладающего именно таким значением  . Фактически в приборах одновременно протекают различные физико-химические процессы деградации с различными значениями
. Фактически в приборах одновременно протекают различные физико-химические процессы деградации с различными значениями  , и поэтому наблюдаемое нами значение
, и поэтому наблюдаемое нами значение  есть результирующая всех этих процессов.
есть результирующая всех этих процессов.
Остановимся на зависимости ИО от приложенного к прибору напряжения. Согласно, ряду теоретических моделей надежности эта зависимость может иметь вид [8.14].

Рис. 8.7. Зависимость ИО СПП от температуры: 1 (0,6) — диоды [8.16]; 2 (0,7) — транзисторы [8.27]; 3 (0,75) — тиристоры [8.17]; 4 (1,7) — тиристоры и симисторы в пластмассовых корпусах [8.18]; 5 (0,62) — диоды [8.19]; 6 ( -диоды
-диоды  -стандарт США
-стандарт США  В по данным [8.20]; 8
В по данным [8.20]; 8  9
9  10 (0,5) — тиристоры
10 (0,5) — тиристоры  11 (0,73) — диоды [8.26]; 12 (0,3) — тиристоры [8.22]; 13
11 (0,73) — диоды [8.26]; 12 (0,3) — тиристоры [8.22]; 13  14 (
14 ( -тиристоры
-тиристоры 

где с и  -константы.
-константы.
Формула (8.2) соответствует модели Эйринга, из которой (8.1) вытекает как частный случай.
В ряде работ используется более простая степенная зависимость ИО от напряжения [8.28]:

где  .
.
Значение  согласно [8.28] равно 4,5. Однако в [8.28] это значение взято из работы [8.29], анализ которой показывает, что соответствующие данные получены на основе
согласно [8.28] равно 4,5. Однако в [8.28] это значение взято из работы [8.29], анализ которой показывает, что соответствующие данные получены на основе  -часовых испытаний маломощных тиристоров типов
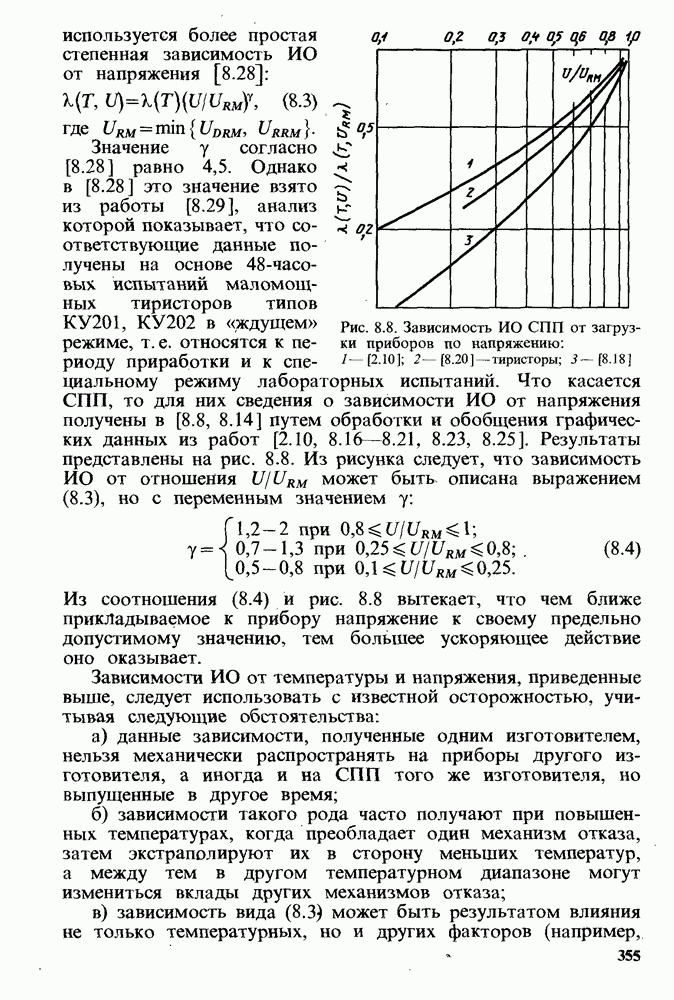
-часовых испытаний маломощных тиристоров типов  в «ждущем» режиме, т.е. относятся к периоду приработки и к специальному режиму лабораторных испытаний. Что касается СПП, то для них сведения о зависимости ИО от напряжения получены в [8.8, 8.14] путем обработки и обобщения графических данных из работ [8.25]. Результаты представлены на рис. 8.8. Из рисунка следует, что зависимость ИО от отношения
в «ждущем» режиме, т.е. относятся к периоду приработки и к специальному режиму лабораторных испытаний. Что касается СПП, то для них сведения о зависимости ИО от напряжения получены в [8.8, 8.14] путем обработки и обобщения графических данных из работ [8.25]. Результаты представлены на рис. 8.8. Из рисунка следует, что зависимость ИО от отношения  может быть описана выражением (8.3), но с переменным значением
может быть описана выражением (8.3), но с переменным значением  :
:

Из соотношения (8.4) и рис. 8.8 вытекает, что чем ближе прикладываемое к прибору напряжение к своему предельно допустимому значению, тем большее ускоряющее действие оно оказывает.

Рис. 8.8. Зависимость ИО СПП от загрузки приборов по напряжению: 1 — [2.10]; 2 —  - тиристоры; 3 — [8.18]
- тиристоры; 3 — [8.18]
Зависимости ИО от температуры и напряжения, приведенные выше, следует использовать с известной осторожностью, учитывая следующие обстоятельства:
а) данные зависимости, полученные одним изготовителем, нельзя механически распространять на приборы другого изготовителя, а иногда и на СПП того же изготовителя, но выпущенные в другое время;
б) зависимости такого рода часто получают при повышенных температурах, когда преобладает один механизм отказа, затем экстраполируют их в сторону меньших температур, а между тем в другом температурном диапазоне могут измениться вклады других механизмов отказа;
в) зависимость вида (8.3) может быть результатом влияния не только температурных, но и других факторов (например, механических воздействий, влажности и пр.), при этом дополнительные факторы могут существенно изменять «кажущуюся» энергию активации.
Вопрос о влиянии других (кроме температуры и напряжения) факторов внешних воздействий на ПН для СПП рассматривался в работах [8.20, 8.31]. В [8.20] зависящая от температуры и напряжения ИО  для учета влияния других факторов умножается на некоторые коэффициенты:
для учета влияния других факторов умножается на некоторые коэффициенты:

где  — коэффициент, учитывающий влияние коммутационных потерь (для диодов
— коэффициент, учитывающий влияние коммутационных потерь (для диодов  отсутствует);
отсутствует);  — коэффициент, учитывающий влияние циклирования;
— коэффициент, учитывающий влияние циклирования;  — коэффициент уровня качества;
— коэффициент уровня качества;  — коэффициент, учитывающий влияние окружающей среды на ИО.
— коэффициент, учитывающий влияние окружающей среды на ИО.
Согласно данным [8.20] коэффициент  можно считать равным 1 практически до конца полезной жйзни прибора, а значение фактора
можно считать равным 1 практически до конца полезной жйзни прибора, а значение фактора  близко к 0,1 для многих областей применения СПП. Заметим, что это заведомо не так для приборов в пластмассовых корпусах, где влажность увеличивает ИО. так же, как и температура
близко к 0,1 для многих областей применения СПП. Заметим, что это заведомо не так для приборов в пластмассовых корпусах, где влажность увеличивает ИО. так же, как и температура  . Что же касается фактора
. Что же касается фактора  , то его значение лежит в диапазоне 1—100. Подчеркнем, что значение
, то его значение лежит в диапазоне 1—100. Подчеркнем, что значение  , являющееся исходным для (8.5), соответствует режимам работы с
, являющееся исходным для (8.5), соответствует режимам работы с  . В таких же больших пределах (1 —100), как и
. В таких же больших пределах (1 —100), как и  , изменяется по данным [8.20] и коэффициент
, изменяется по данным [8.20] и коэффициент  . Формула (8.5) представляет собой один из вариантов применения коэффициентного метода расчета ИО. Другой вариант изложен в работе [8.30], которую подробно рассмотрим в § 8.5.
. Формула (8.5) представляет собой один из вариантов применения коэффициентного метода расчета ИО. Другой вариант изложен в работе [8.30], которую подробно рассмотрим в § 8.5.
Показатели надежности СПП в циклических режимах работы. В соответствии с классификацией РЭ СПП основным ПН в циклических режимах является число циклов тех или иных воздействий, выдерживаемое приборами до отказа (общее обозначение  ). Рассмотрим сначала режим термоциклирования. Этот режим был изучен одним из первых, поскольку приборы первого поколения имели паяные контактные соединения, которые в условиях термоциклирования сравнительно быстро разрушались. Было установлено [1.2], что
). Рассмотрим сначала режим термоциклирования. Этот режим был изучен одним из первых, поскольку приборы первого поколения имели паяные контактные соединения, которые в условиях термоциклирования сравнительно быстро разрушались. Было установлено [1.2], что

где  — константы, зависящие от типа СПП и диапазона циклирования;
— константы, зависящие от типа СПП и диапазона циклирования;  — перепад средней температуры за один цикл. Кроме степенной возможна и экспоненциальная зависимость величины
— перепад средней температуры за один цикл. Кроме степенной возможна и экспоненциальная зависимость величины  от
от  [8.32]
[8.32]

где  — константы, зависящие от типа СПП.
— константы, зависящие от типа СПП.

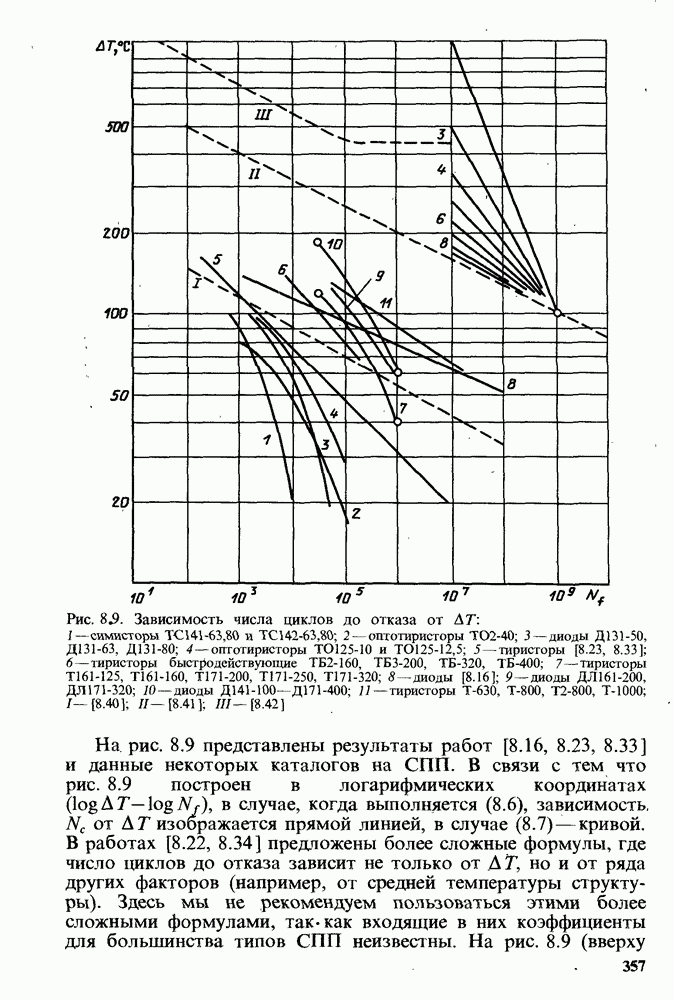
Рис. 8.9. Зависимость числа циклов до отказа от  — симисторы
— симисторы  — оатотиристоры
— оатотиристоры  — диоды
— диоды  — оптотиристоры
— оптотиристоры  — тиристоры [8.23, 8.33]; 6 — тиристоры быстродействующие
— тиристоры [8.23, 8.33]; 6 — тиристоры быстродействующие  — тиристоры
— тиристоры  — диоды [8.16]; 9 — диоды
— диоды [8.16]; 9 — диоды  — диоды
— диоды  — тиристоры
— тиристоры 
На рис. 8.9 представлены результаты работ [8.16, 8.23, 8.33] и данные некоторых каталогов на СПП. В связи с тем что рис. 8.9 построен в логарифмических координатах  , в случае, когда выполняется (8.6), зависимость,
, в случае, когда выполняется (8.6), зависимость,  от ДГ изображается прямой линией, в случае (
от ДГ изображается прямой линией, в случае ( -кривой. В работах [8.22, 8.34] предложены более сложные формулы, где число циклов до отказа зависит не только от А Т, но и от ряда других факторов (например, от средней температуры структуры). Здесь мы не рекомендуем пользоваться этими более сложными формулами, так-как входящие в них коэффициенты для большинства типов СПП неизвестны. На рис. 8.9 (вверху справа) приведены прямые, наклон которых соответствует различным значениям параметра
-кривой. В работах [8.22, 8.34] предложены более сложные формулы, где число циклов до отказа зависит не только от А Т, но и от ряда других факторов (например, от средней температуры структуры). Здесь мы не рекомендуем пользоваться этими более сложными формулами, так-как входящие в них коэффициенты для большинства типов СПП неизвестны. На рис. 8.9 (вверху справа) приведены прямые, наклон которых соответствует различным значениям параметра  (от 9 до 2).
(от 9 до 2).
С помощью этих прямых можно определить наклон (т. е. значение m) для любой из приведенных на рис. 8.9 зависимостей.
Следует рассмотреть, как отказы в циклических режимах распределены во времени. Обычно для этого используют функцию плотности распределения  . В общем случае переход от N к
. В общем случае переход от N к  невозможен, поскольку циклы могут следовать нерегулярно во времени. Для
невозможен, поскольку циклы могут следовать нерегулярно во времени. Для  известны две основные параметризации: логарифмически нормальная [8.10, 8.22, 8.35] и вейбулловская [8.23, 8.33]. Известна также работа [8.36], где при определении
известны две основные параметризации: логарифмически нормальная [8.10, 8.22, 8.35] и вейбулловская [8.23, 8.33]. Известна также работа [8.36], где при определении  использовано дисперсионное распределение Бернштейна. Подчеркнем еще раз, что в большинстве работ рассматривались СПП с паяными контактами. Для современных мощных СПП прижимной конструкции можно указать лишь на работы [8.35, 8.37].
использовано дисперсионное распределение Бернштейна. Подчеркнем еще раз, что в большинстве работ рассматривались СПП с паяными контактами. Для современных мощных СПП прижимной конструкции можно указать лишь на работы [8.35, 8.37].
В [8.35] показано, что для тиристоров  функция
функция  может быть описана логарифмически нормальным распределением с ненулевым параметром сдвига
может быть описана логарифмически нормальным распределением с ненулевым параметром сдвига  Значение
Значение  по данным [8.35] составило 2422 цикла для тиристоров, испытывавшихся при токе нагрузки 1200 А, и 8010 для тиристоров, испытывавшихся при токе
по данным [8.35] составило 2422 цикла для тиристоров, испытывавшихся при токе нагрузки 1200 А, и 8010 для тиристоров, испытывавшихся при токе  . В [8.37] приведены данные, согласно которым приборы типа
. В [8.37] приведены данные, согласно которым приборы типа  выдерживают без отказов 10 млн. циклов при амплитуде перепада температуры структуры, равной 55° С. Там же указано, что таблеточные тиристоры с диаметром шайбы 25 мм без ухудшения параметров выдерживают 240000 циклов при
выдерживают без отказов 10 млн. циклов при амплитуде перепада температуры структуры, равной 55° С. Там же указано, что таблеточные тиристоры с диаметром шайбы 25 мм без ухудшения параметров выдерживают 240000 циклов при  (число испытанных приборов в [8.37] не приведено).
(число испытанных приборов в [8.37] не приведено).
Теперь следует вернуться к формулам (8.6) и (8.7) и ответить на вопрос: какой характеристикой распределения является в этих формулах величина  Действительно, поскольку существует функция
Действительно, поскольку существует функция  , то в выражениях подобного типа необходимо обязательно указывать, что именно понимается под величиной
, то в выражениях подобного типа необходимо обязательно указывать, что именно понимается под величиной  : среднее значение, медиана распределения или его мода. Несмотря на то что в большинстве работ под
: среднее значение, медиана распределения или его мода. Несмотря на то что в большинстве работ под  понимают среднее значение
понимают среднее значение  , в качестве ПН мы рекомендуем применять не
, в качестве ПН мы рекомендуем применять не  , а медиану распределения —
, а медиану распределения —  Причиной этого являются следующие обстоятельства. Во-первых, функция
Причиной этого являются следующие обстоятельства. Во-первых, функция  во многих случаях существенно асимметрична. При этом среднее значение оказывается плохим показателем, так как дает искаженное представление о циклостойкости изделий. Например, если
во многих случаях существенно асимметрична. При этом среднее значение оказывается плохим показателем, так как дает искаженное представление о циклостойкости изделий. Например, если  соответствует логарифмически нормальному распределению, то ВБР для
соответствует логарифмически нормальному распределению, то ВБР для  при а
при а  составит
составит  т. е. такое число циклов выдержат всего лишь 20% СПП. Причиной этого оказывается увеличение М. за счет вклада (хотя и небольшого числа) очень стойких СПП.
т. е. такое число циклов выдержат всего лишь 20% СПП. Причиной этого оказывается увеличение М. за счет вклада (хотя и небольшого числа) очень стойких СПП.

Рис. 8.10. Соотношение между модой, медианой и средним значением для симметричного (а) и асимметричного (б) распределений. [Мода — значение, соответствующее максимуму  . Медиана — значение, соответствующее ВБР, равной 50% (площадь слева от медианы равна площади справа). Среднее значение —
. Медиана — значение, соответствующее ВБР, равной 50% (площадь слева от медианы равна площади справа). Среднее значение — 
В то же время, если распределение близко к симметричному, то все равно, чем пользоваться в качестве ПН, так как среднее значение, медиана и мода близки между собой (на рис. 8.10 оба рассмотренных случая проиллюстрированы графически). Во-вторых, медиана в качестве ПН намного практичнее, чем среднее значение. В самом деле, для определения и подтверждения величины N надо довести до отказа все изделия, в том числе и самые стойкие. В то же время для определения и подтверждения величины N надо довести до отказа лишь 50% приборов. Это может существенно уменьшить время, необходимое для испытаний на надежность.
Обращает на себя внимание малочисленность данных по циклостойкости СПП с прижимными контактами. Причиной этого является тот факт, что в связи с отказом от использования мягких припоев в конструкции СПП повысилась (см. выше) циклостойкость СПП на несколько порядков. Такое существенное  данного ПН было принято изготовителями и разработчиками приборов за полное снятие проблемы, вследствие чего работы в этом направлении прекратились, а сам параметр даже не попал в число приводимых в технических условиях и каталогах. Между тем циклостойкость современных приборов хотя и велика, но небесконечна, и поэтому считать данную проблему решенной окончательно нельзя.
данного ПН было принято изготовителями и разработчиками приборов за полное снятие проблемы, вследствие чего работы в этом направлении прекратились, а сам параметр даже не попал в число приводимых в технических условиях и каталогах. Между тем циклостойкость современных приборов хотя и велика, но небесконечна, и поэтому считать данную проблему решенной окончательно нельзя.
Рассмотрим режим импульсного циклирования. В более традиционной терминологии это тот режим, где существенна проблема  - стойкости силовых тиристоров. Строго говоря, следует четко различать, о каком
- стойкости силовых тиристоров. Строго говоря, следует четко различать, о каком  идет речь. Дело в том, что когда рассматривают любое разрушающее воздействие, то существуют две возможные схемы для отказа прибора:
идет речь. Дело в том, что когда рассматривают любое разрушающее воздействие, то существуют две возможные схемы для отказа прибора:
а) прибор может выйти из строя при однократном приложении данного воздействия;
б) прибор может выйти из строя при многократном приложении данного воздействия.
В соответствии с этим в случае  целесообразно говорить о таком максимальном значении
целесообразно говорить о таком максимальном значении  , которое СПП может выдержать лишь ограниченное число раз (в пределе — 1 раз). Будем называть это значение аварийным и обозначим его как
, которое СПП может выдержать лишь ограниченное число раз (в пределе — 1 раз). Будем называть это значение аварийным и обозначим его как  . В случае
. В случае  целесообразно говорить о таком максимальном значении
целесообразно говорить о таком максимальном значении  , которое прибор выдержит в течение всего своего срока службы при приложении с предельно допустимой частотой. Назовем это значение повторяющимся
, которое прибор выдержит в течение всего своего срока службы при приложении с предельно допустимой частотой. Назовем это значение повторяющимся  . Вопрос о необходимости четко разграничивать эти величины в отечественной литературе независимо друг от друга был одновременно поставлен в работах [8.38, 8.39]. В [8.39] показано, что проблема
. Вопрос о необходимости четко разграничивать эти величины в отечественной литературе независимо друг от друга был одновременно поставлен в работах [8.38, 8.39]. В [8.39] показано, что проблема  - стойкости тиристоров — это, по существу, проблема надежности силовых тиристоров в тех режимах, где преобладают механизмы отказов, связанные с быстрым и локальным выделением энергии в окрестности управляющего электрода. При этом средняя температура структуры
- стойкости тиристоров — это, по существу, проблема надежности силовых тиристоров в тех режимах, где преобладают механизмы отказов, связанные с быстрым и локальным выделением энергии в окрестности управляющего электрода. При этом средняя температура структуры  может быть постоянной или слабоменяющейся функцией времени, а температура «горячей точки» (Ты) совершает значительные колебания (
может быть постоянной или слабоменяющейся функцией времени, а температура «горячей точки» (Ты) совершает значительные колебания ( ). Число импульсных циклов до отказа обозначим
). Число импульсных циклов до отказа обозначим  . Величина
. Величина  согласно данным работ
согласно данным работ  зависит от
зависит от  соответствий с выражением
соответствий с выражением

где  — константы, зависящие от типа прибора. Графическое изображение результатов указанных работ дано на рис. 8.9 пунктиром
— константы, зависящие от типа прибора. Графическое изображение результатов указанных работ дано на рис. 8.9 пунктиром  . В [8.40] формула (8.8) приведена в следующем виде;
. В [8.40] формула (8.8) приведена в следующем виде;

В работе [8.43] на основе одной из моделей длительной прочности [8.44] теоретически обосновано выражение, аналогичное (8.8). Другие полученные в [8.43] теоретические формулы использовать не будем, так как значения входящих в них констант неизвестны. Следует отметить еще две работы, посвященные проблеме  -стойкости. В [8.45] показано, что снижение
-стойкости. В [8.45] показано, что снижение  с 720 до
с 720 до  увеличивает
увеличивает  для тиристоров типа
для тиристоров типа  от 22 650 примерно до
от 22 650 примерно до  циклов. В работе [8.46] приведены данные, показывающие зависимость числа циклов до отказа от величины
циклов. В работе [8.46] приведены данные, показывающие зависимость числа циклов до отказа от величины  для быстродействующих тиристоров типа ТБ 143-320 (400). Согласно этим данным аварийное
для быстродействующих тиристоров типа ТБ 143-320 (400). Согласно этим данным аварийное  для СПП этого типа близко к
для СПП этого типа близко к  .
.
Так же как и в случае с обычной циклостойкостью, необходимо указывать, что понимают под величиной  . По тем же причинам, какие изложены выше, в качестве ПН рекомендуем применять медианное число циклов до отказа
. По тем же причинам, какие изложены выше, в качестве ПН рекомендуем применять медианное число циклов до отказа  .
.

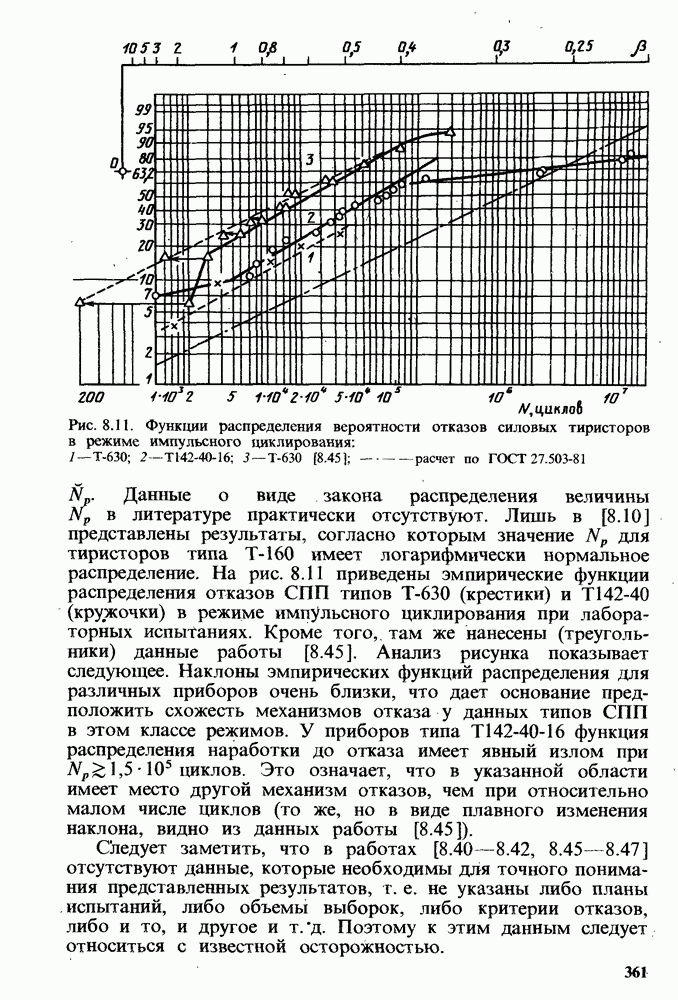
Рис. 8.11. Функции распределения вероятности отказов силовых тиристоров в режиме импульсного циклирования: 1 —  по ГОСТ
по ГОСТ 
Данные о виде закона распределения величины  в литературе практически отсутствуют. Лишь в [8.10] представлены результаты, согласно которым значение
в литературе практически отсутствуют. Лишь в [8.10] представлены результаты, согласно которым значение  для тиристоров типа
для тиристоров типа  имеет логарифмически нормальное распределение. На рис. 8.11 приведены эмпирические функции распределения отказов СПП типов
имеет логарифмически нормальное распределение. На рис. 8.11 приведены эмпирические функции распределения отказов СПП типов  (крестики) и
(крестики) и  (кружочки) в режиме импульсного циклирования при лабораторных испытаниях. Кроме того, там же нанесены (треугольники) данные работы [8.45]. Анализ рисунка показывает следующее. Наклоны эмпирических функций распределения для различных приборов очень близки, что дает основание предположить схожесть механизмов отказа у данных типов СПП в этом классе режимов. У приборов типа
(кружочки) в режиме импульсного циклирования при лабораторных испытаниях. Кроме того, там же нанесены (треугольники) данные работы [8.45]. Анализ рисунка показывает следующее. Наклоны эмпирических функций распределения для различных приборов очень близки, что дает основание предположить схожесть механизмов отказа у данных типов СПП в этом классе режимов. У приборов типа  функция распределения наработки до отказа имеет явный излом при
функция распределения наработки до отказа имеет явный излом при  циклов. Это означает, что в указанной области имеет место другой механизм отказов, чем при относительно малом числе циклов (то же, но в виде плавного изменения наклона, видно из данных работы [8.45]).
циклов. Это означает, что в указанной области имеет место другой механизм отказов, чем при относительно малом числе циклов (то же, но в виде плавного изменения наклона, видно из данных работы [8.45]).
Следует заметить, что в работах  отсутствуют данные, которые необходимы для точного понимания представленных результатов, т. е. не указаны либо планы испытаний, либо объемы выборок, либо критерии отказов, либо и то, и другое и т. д. Поэтому к этим данным следует относиться с известной осторожностью.
отсутствуют данные, которые необходимы для точного понимания представленных результатов, т. е. не указаны либо планы испытаний, либо объемы выборок, либо критерии отказов, либо и то, и другое и т. д. Поэтому к этим данным следует относиться с известной осторожностью.
Рассмотрим режим, который назван режимом токовых перегрузок. Так же как и выше, можно задать два вопроса:
а) при какой амплитуде тока прибор выйдет из строя за один импульс?
б) сколько импульсов тока заданной амплитуды выдержит прибор?
Анализ литературы (см. [8.14]) показывает, что большинство работ, посвященных ударным токам СПП, направлено на решение первого вопроса. Физические процессы, приводящие к отказам СПП при многократном воздействии ударного тока, в настоящее время практически не изучены. Исследованию поведения силовых тиристоров в режимах токовых перегрузок посвящено лишь несколько экспериментальных работ  . В [8.10] приведены результаты испытаний тиристоров типа
. В [8.10] приведены результаты испытаний тиристоров типа  . Показано, что функция плотности распределения отказов во времени удовлетворительно описывается суммой двух логарифмически нормальных кривых. В [8.49] исследовалась возможность прогнозирования числа импульсов тока заданной амплитуды, которое выдержат тиристоры до отказа. Заметим, что в зарубежной нормативно-технической документации существует ограничение на это число. Оно составляет несколько сотен импульсов [2.10]. Попытки построения модельных представлений о надежности СПП при многократном воздействии импульсов тока перегрузки предпринимались в работах [8.51, 8.52]. Вероятность безотказной работы в этом РЭ сильно зависит от амплитуды тока [8.48, 8.50], однако аналитический вид этой зависимости в настоящее время отсутствует.
. Показано, что функция плотности распределения отказов во времени удовлетворительно описывается суммой двух логарифмически нормальных кривых. В [8.49] исследовалась возможность прогнозирования числа импульсов тока заданной амплитуды, которое выдержат тиристоры до отказа. Заметим, что в зарубежной нормативно-технической документации существует ограничение на это число. Оно составляет несколько сотен импульсов [2.10]. Попытки построения модельных представлений о надежности СПП при многократном воздействии импульсов тока перегрузки предпринимались в работах [8.51, 8.52]. Вероятность безотказной работы в этом РЭ сильно зависит от амплитуды тока [8.48, 8.50], однако аналитический вид этой зависимости в настоящее время отсутствует.
Наконец, для тиристоров типа  одним из авторов обзора [8.14] показано, что в зависимости от сочетания таких параметров тиристоров, как
одним из авторов обзора [8.14] показано, что в зависимости от сочетания таких параметров тиристоров, как  и
и  , можно с определенной вероятностью (см. [8.14]) прогнозировать СПП, выдерживающие 100 и более импульсов ударного тока без приложения напряжения.
, можно с определенной вероятностью (см. [8.14]) прогнозировать СПП, выдерживающие 100 и более импульсов ударного тока без приложения напряжения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ПРИНЦИП ДЕЙСТВИЯ И ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ ДИОДОВ И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
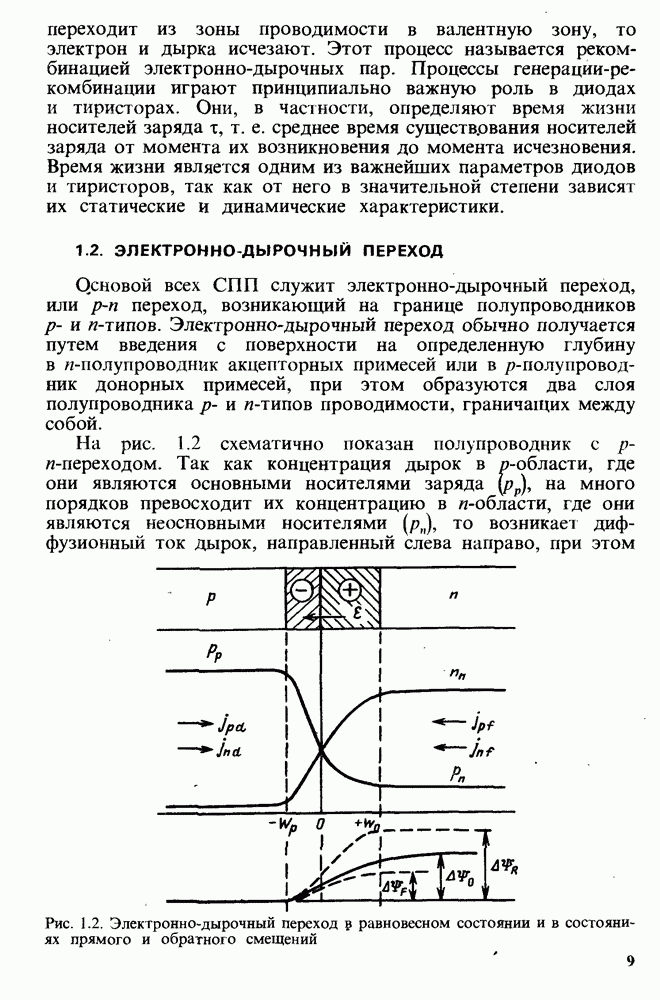
- 1.2. ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД
- 1.3.СИЛОВОЙ ПОЛУПРОВОДНИКОВЫЙ ВЫПРЯМИТЕЛЬНЫЙ ДИОД
- Проводящее состояние силового диода.
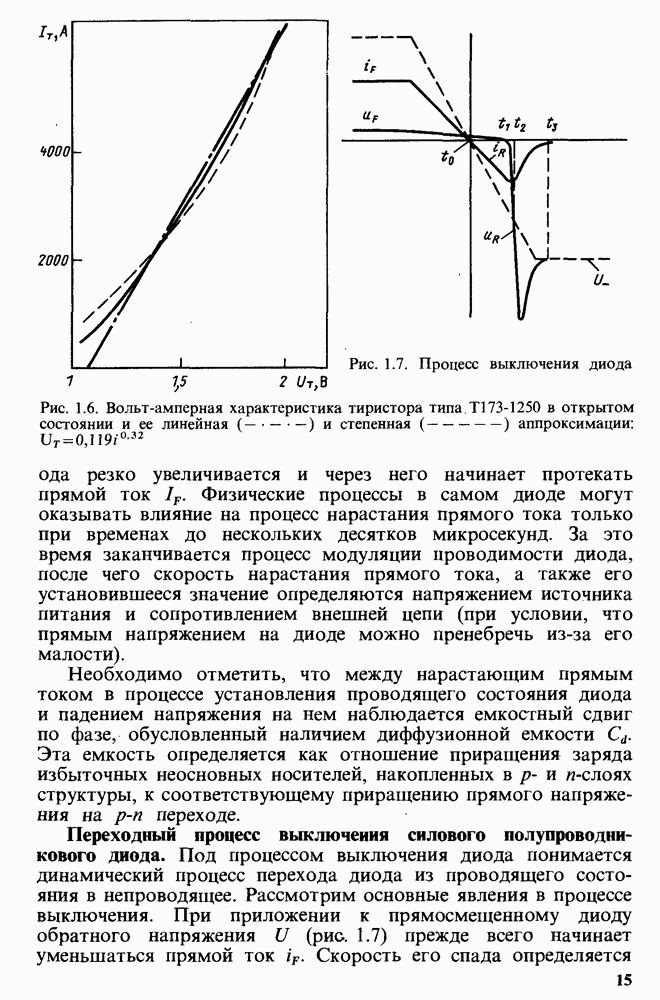
- Переходный процесс включения силового полупроводникового диода.
- Переходный процесс выключения силового полупроводникового диода.
- 1.4. СИЛОВОЙ ТРИОДНЫЙ ТИРИСТОР, НЕ ПРОВОДЯЩИЙ В ОБРАТНОМ НАПРАВЛЕНИИ
- Обратное непроводящее состояние тиристора.
- Закрытое состояние тиристора.
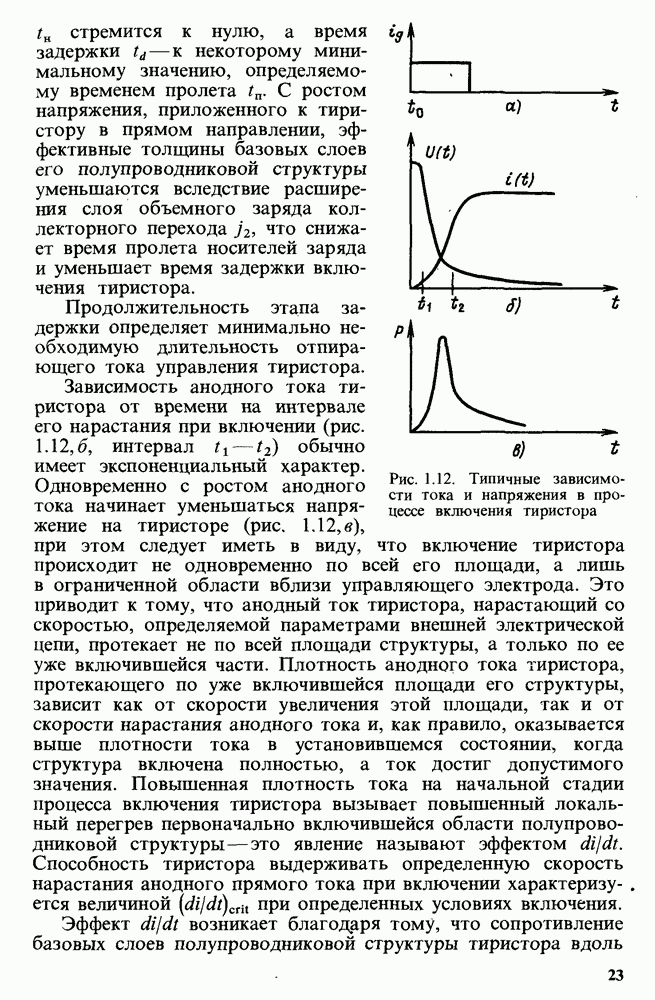
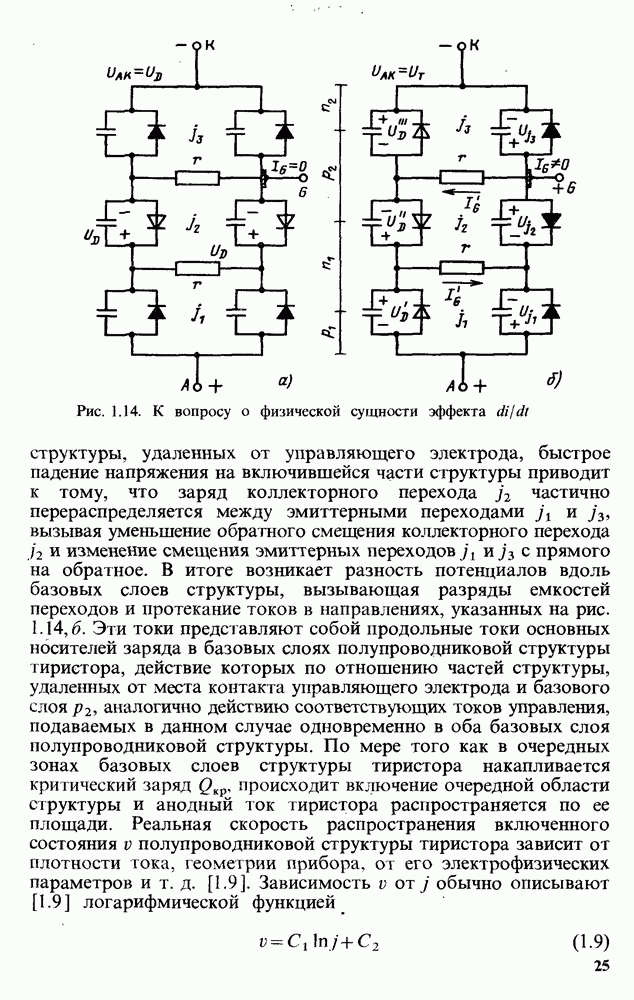
- Процесс включения тиристора. Эффект di/dt. Открытое состояние тиристора.
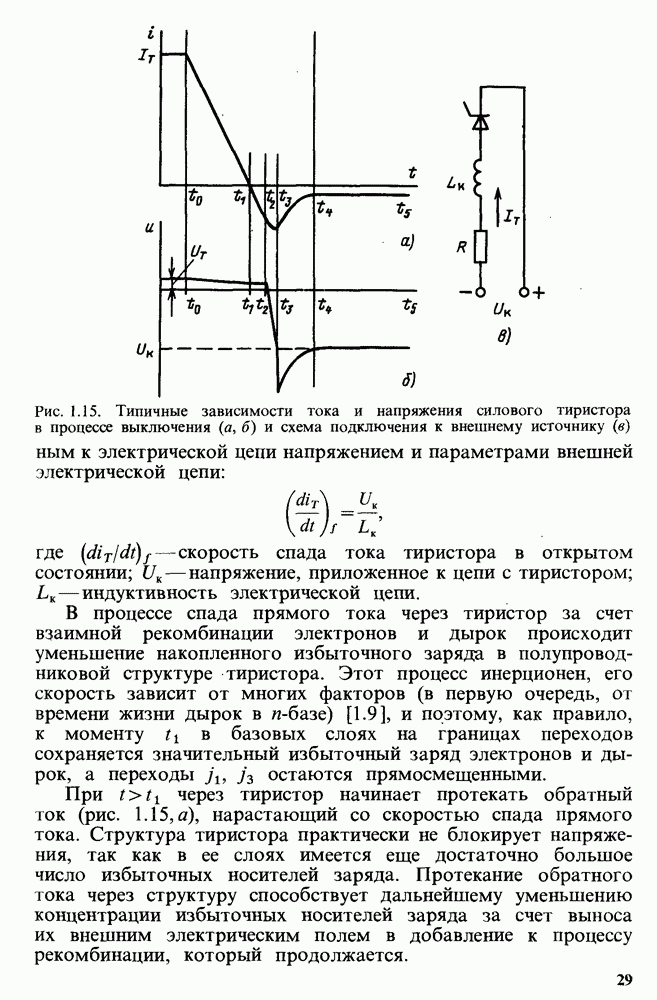
- Процесс выключения тиристора. Эффект dU/dt.
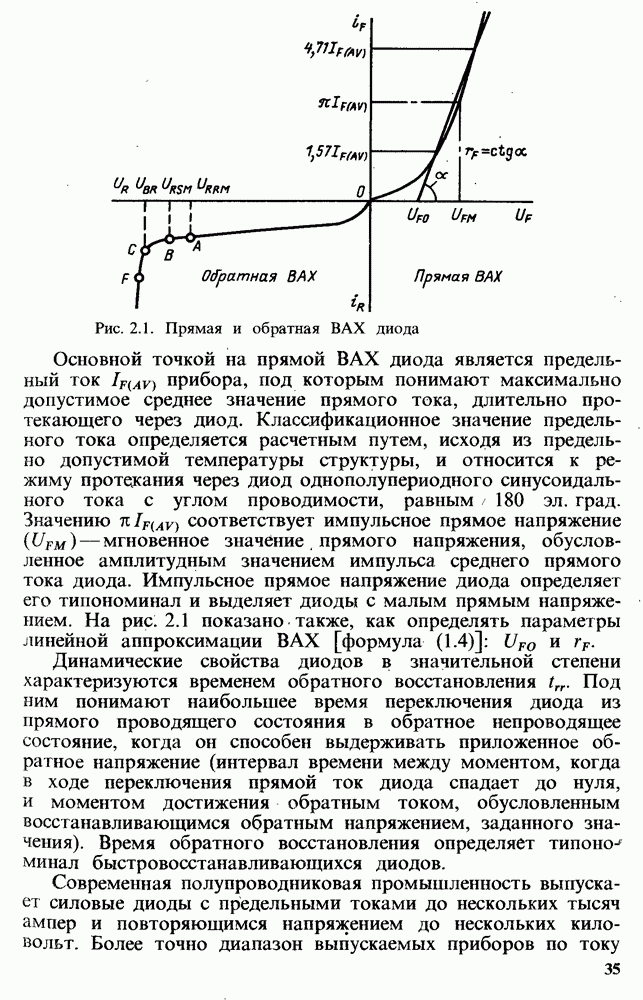
- Глава 2. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- 2.2. ОСНОВНЫЕ ПАРАМЕТРЫ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Основные электрические параметры силовых тиристоров.
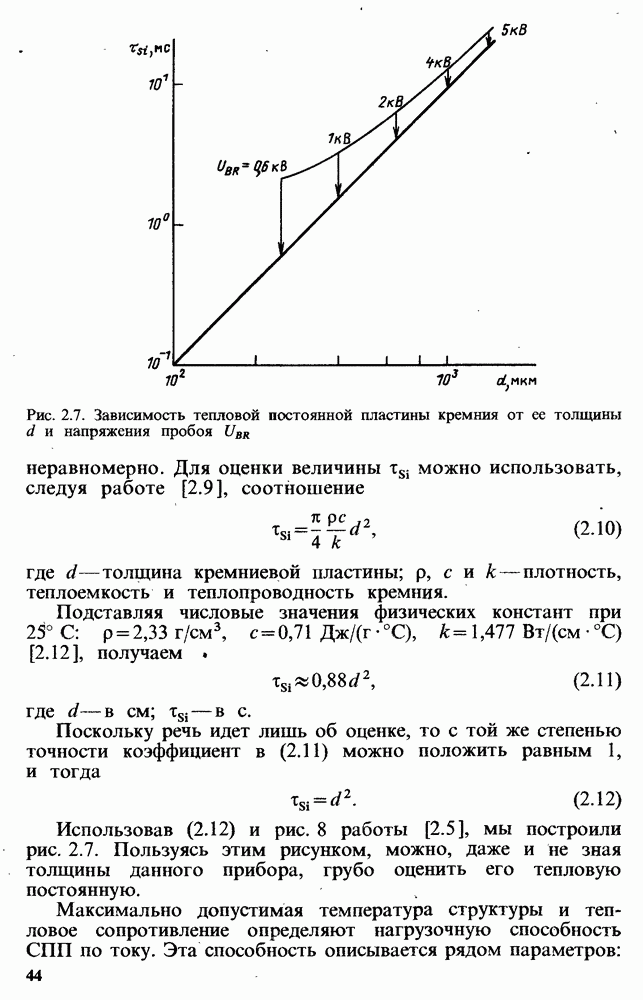
- 2.3. ОСНОВНЫЕ ТЕПЛОВЫЕ ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ДИОДОВ И ТИРИСТОРОВ
- 2.4. КЛАССИФИКАЦИЯ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Классификация силовых полупроводниковых диодов и тиристоров по конструкции.
- 2.5. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ диодов И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
- Условное обозначение типоисполнения диодов и тиристоров.
- 2.6. ОСОБЕННОСТИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ КАК ЭЛЕКТРОТЕХНИЧЕСКИХ ИЗДЕЛИЙ, КОМПЛЕКТУЮЩИХ СХЕМУ СИЛОВОГО ПОЛУПРОВОДНИКОВОГО ПРЕОБРАЗОВАТЕЛЬНОГО УСТРОЙСТВА
- Глава 3. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ И УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ
- 3.1. РЕЖИМЫ И УСЛОВИЯ РАБОТЫ ДИОДОВ И ТИРИСТОРОВ
- 3.2. КЛАССИФИКАЦИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 3.3. ОСОБЕННОСТИ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ
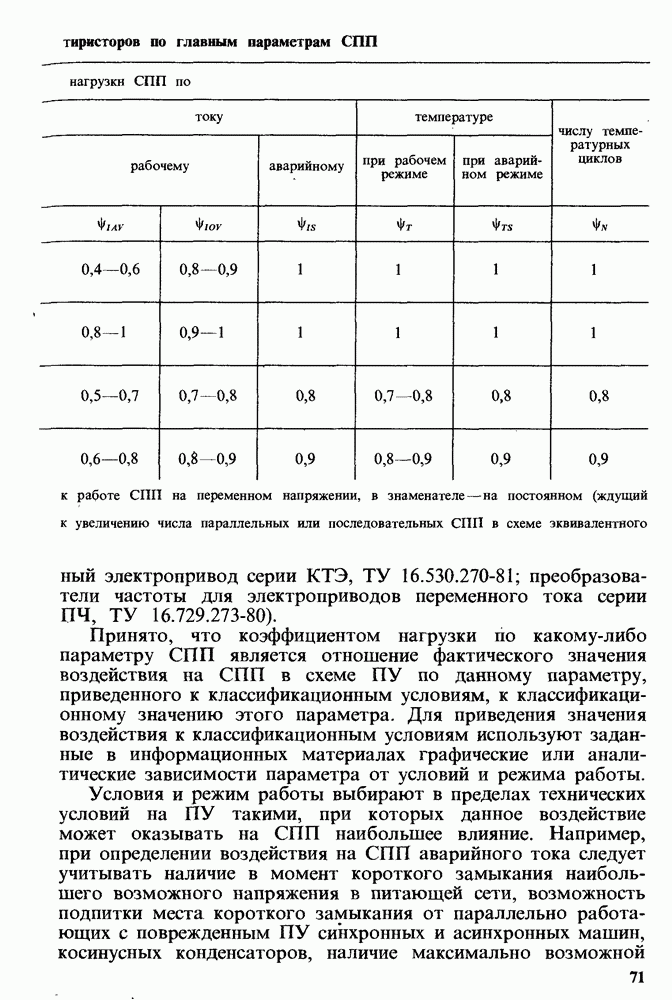
- Рекомендуемая нагрузка диодов и тиристоров.
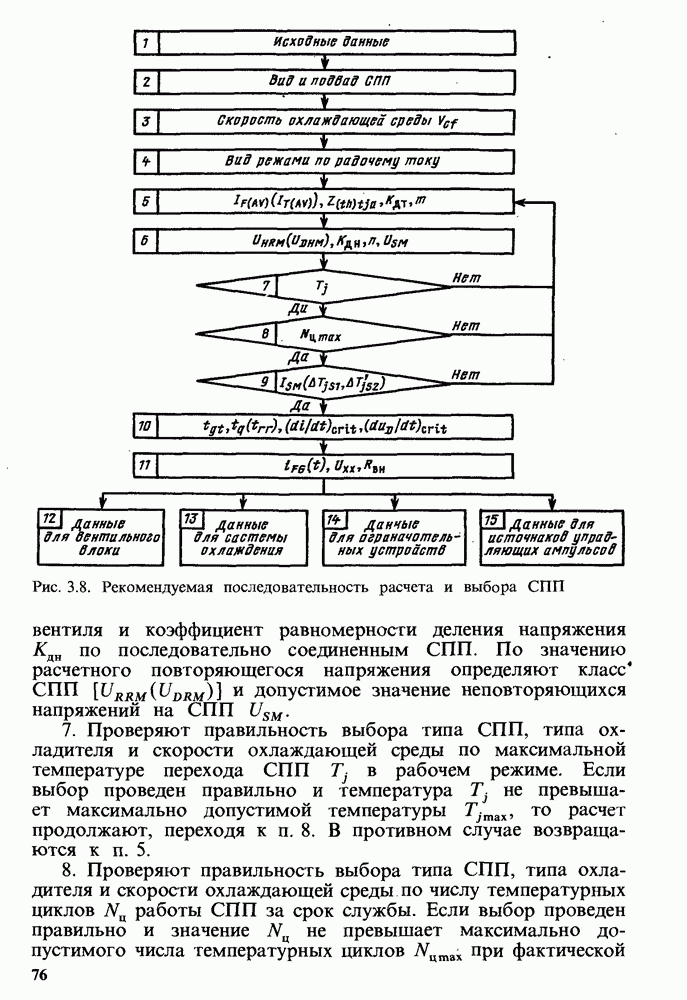
- Исходные данные и последовательность расчета.
- Глава 4. РАСЧЕТ И ВЫБОР ДИОДОВ И ТИРИСТОРОВ. УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ И РАСЧЕТ СИСТЕМЫ УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 4.1. РАСЧЕТ И ВЫБОР ТИПА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО РАБОЧЕМУ ТОКУ
- Тепловые параметры СПП и выбор условий охлаждения.
- Определение режима нагрузки СПП рабочим током.
- Расчет и выбор типа СПП, типа охладителя и скорости охлаждающей среды при неизменном рабочем токе.
- Расчет и выбор типа прибора, типа охладителя и скорости охлаждающей среды при изменяющемся рабочем токе.
- 4.2. ВЫБОР КЛАССА СПП ПО РАБОЧЕМУ НАПРЯЖЕНИЮ
- Определение класса СПП.
- 4.3. ПРОВЕРКА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО ТЕМПЕРАТУРЕ НАГРЕВА РАБОЧИМ ТОКОМ
- Расчет температур перегрева перехода СПП в рабочем режиме.
- 4.4. ПРОВЕРКА СПП ПО АВАРИЙНОМУ ТОКУ
- Проверка СПП при синусоидальной форме импульса аварийного тока.
- Проверка СПП при несинусоидальной форме аварийного тока.
- 4.5. ВЫБОР КОММУТАЦИОННЫХ ПАРАМЕТРОВ СПП
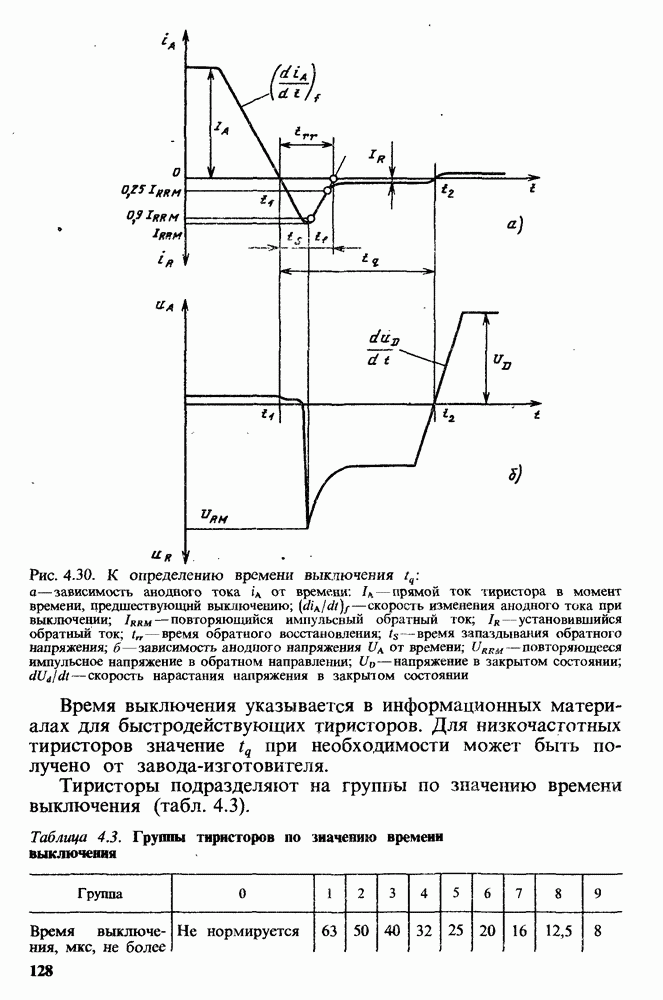
- Время выключения.
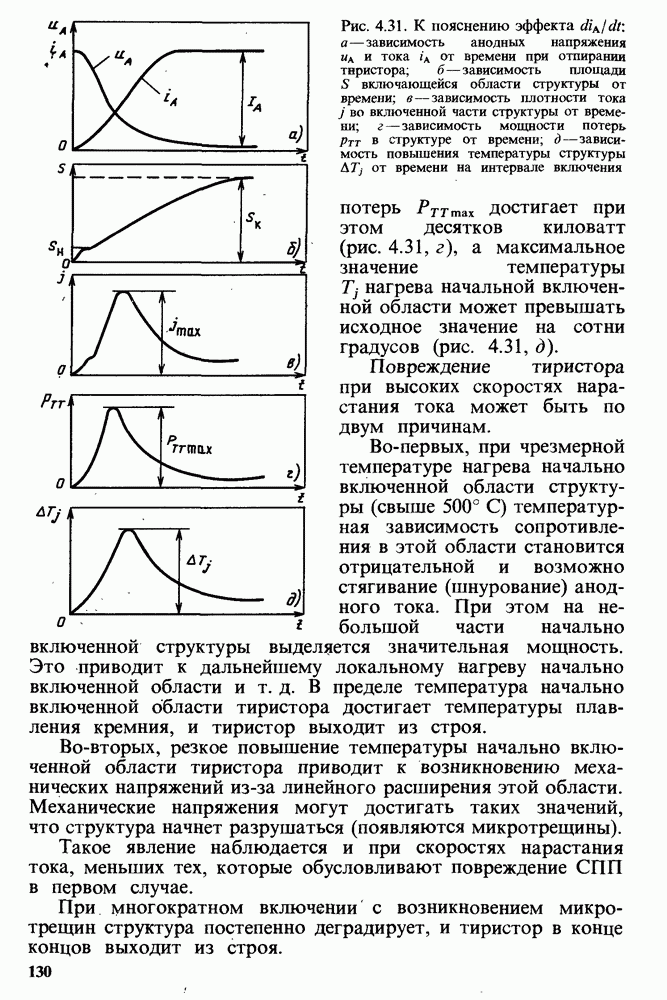
- Критическая скорость нарастания тока при включении.
- Критическая скорость нарастания напряжения в закрытом состоянии СПП.
- Время обратного восстановления.
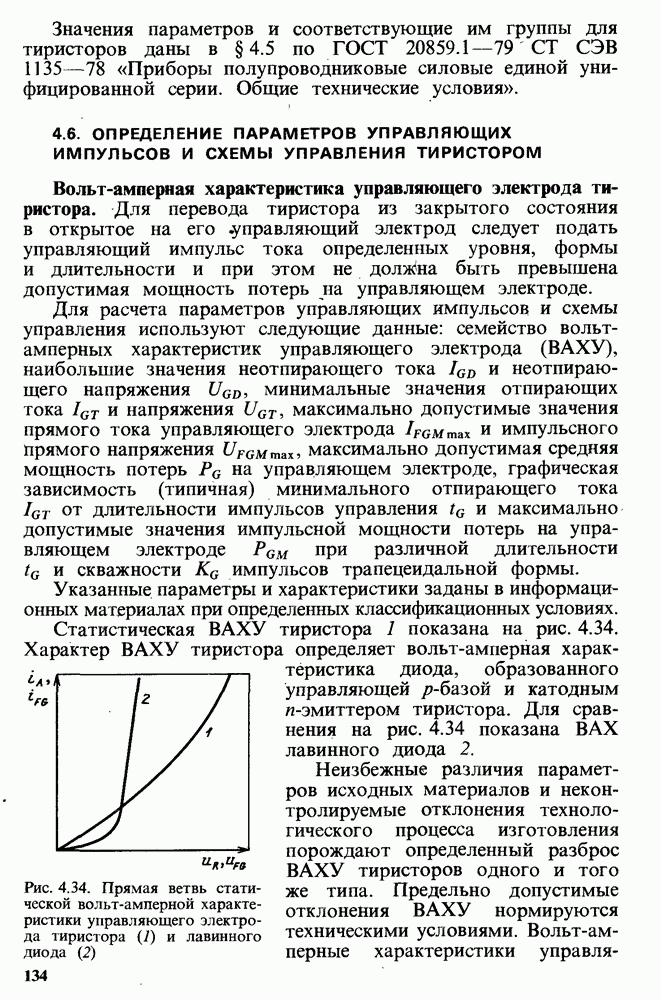
- 4.6. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УПРАВЛЯЮЩИХ ИМПУЛЬСОВ И СХЕМЫ УПРАВЛЕНИЯ ТИРИСТОРОМ
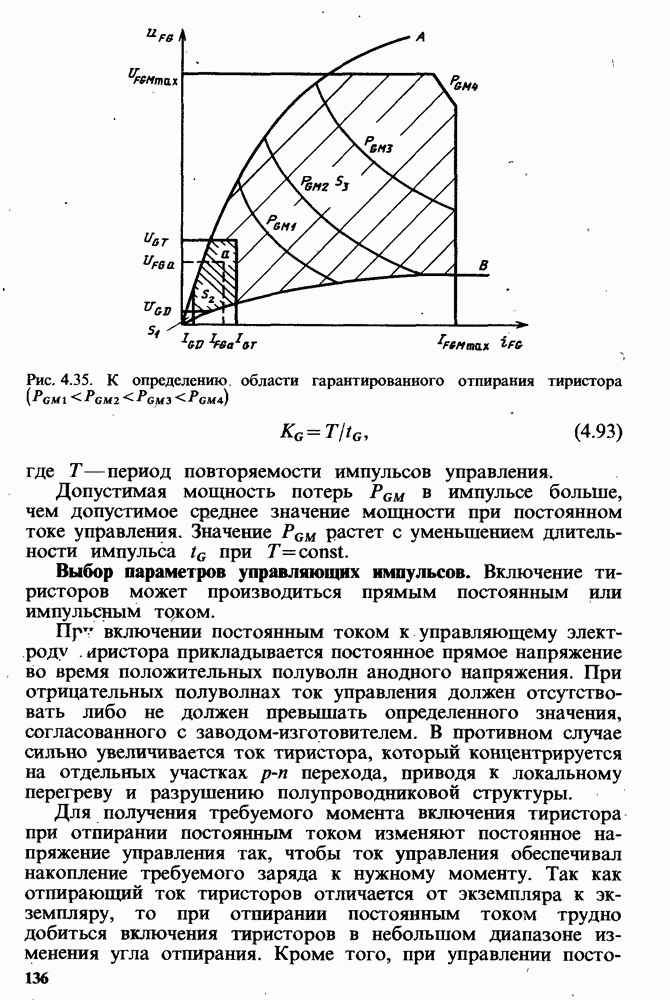
- Выбор параметров управляющих импульсов.
- Расчет мощности потерь на управляющем электроде.
- 4.7. ПРИМЕР РАСЧЕТА И ВЫБОРА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ
- Расчет и выбор типа СПП и условий его охлаждения но рабочему току.
- Проверка выбранного СПП и условий охлаждения по температуре нагрева перехода рабочим током.
- Проверка СПП по аварийному току.
- Выбор коммутационных параметров СПП.
- Определение параметров управляющих импульсов и источника управления.
- Глава 5. МЕТОДЫ И СРЕДСТВА ОГРАНИЧЕНИЯ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ ПО ТОКУ И НАПРЯЖЕНИЮ В НОРМАЛЬНЫХ И АВАРИЙНЫХ РЕЖИМАХ РАБОТЫ
- 5.1. ТРЕБОВАНИЯ К МЕТОДАМ И СРЕДСТВАМ ОГРАНИЧЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ
- 5.2. ВЫБОР ВИДА И РАСЧЕТ ЭЛЕМЕНТОВ ДЛЯ ОГРАНИЧЕНИЯ АВАРИЙНОГО ТОКА
- 5.3. ОГРАНИЧЕНИЕ КОММУТАЦИОННЫХ ПЕРЕНАПРЯЖЕНИЙ НА СПП
- Получение исходных данных для выбора схем и расчета параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Расчет параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Воздействие перенапряжений, возникающих при запирании СПП, на другие тиристоры преобразовательных схем.
- 5.4. ОГРАНИЧЕНИЕ СХЕМНЫХ И СЕТЕВЫХ ПЕРЕНАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- Схемные перенапряжения
- Уменьшение уровня переиапряжения на вентилях
- Схемные перенапряжения эпизодического характера
- Расчет параметров устройства для ограничения сетевых и схемных перенапряжений.
- Расчет ограничительных устройств для подавления схемных перенапряжений.
- Ограничение скорости нарастания и спадания тока СПП.
- Некоторые явления, связанные с процессом отпирания тиристоров.
- Расчет коммутационных потерь в СПП.
- 5.5. ГРУППОВОЕ СОЕДИНЕНИЕ СПП
- Последовательное соединение СПП
- Групповое соединение СПП
- 5.6. НЕКОТОРЫЕ СХЕМЫ ПОДКЛЮЧЕНИЯ ОГРАНИЧИТЕЛЬНЫХ УСТРОЙСТВ
- Глава 6. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ В СХЕМАХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТАНОВОК
- 6.1. ТРЕБОВАНИЯ К МЕТОДАМ ИЗМЕРЕНИЙ
- 6.2. ИЗМЕРЕНИЕ СРЕДНЕГО И ЭФФЕКТИВНОГО ТОКА, ПРОХОДЯЩЕГО ЧЕРЕЗ СПП, И МОЩНОСТИ ПОТЕРЬ В СТАЦИОНАРНОМ РЕЖИМЕ
- 6.3. ИЗМЕРЕНИЕ МГНОВЕННЫХ ЗНАЧЕНИЙ ТОКА В ПРОЦЕССЕ ВКЛЮЧЕНИЯ И ВЫКЛЮЧЕНИЯ СПП
- 6.4. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- 6.5. КОНТРОЛЬ ПАРАМЕТРОВ СИГНАЛОВ УПРАВЛЕНИЯ ТИРИСТОРОВ И ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ СПП
- 6.6. СОВРЕМЕННЫЕ МЕТОДЫ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ
- 6.7. ПОГРЕШНОСТИ ИЗМЕРЕНИЯ БЫСТРОМЕНЯЮЩИХСЯ ТОКОВ С ПОМОЩЬЮ БЕЗЫНДУКТИВНЫХ (МАЛОИНДУКТИВНЫХ) ШУНТОВ
- Глава 7. ОХЛАЖДЕНИЕ ДИОДОВ И ТИРИСТОРОВ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 7.1. ОБЩИЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ. ПРЕДЪЯВЛЯЕМЫЕ К ОХЛАДИТЕЛЯМ СПП
- Классификация охладителей.
- 7.2. КОНСТРУКЦИИ ОХЛАДИТЕЛЕЙ
- 7.3. ВОЗДУШНОЕ ОХЛАЖДЕНИЕ СПП
- Прижимные устройства системы «СПП—охладитель».
- Компоновка системы «СПП — охладитель» в ПУ с естественным воздушным охлаждением.
- Температурное поле среды вокруг нагретых СПП с охладителями при наличии в вентильной секции ПУ воздухоотводящих экранов и перфораций.
- Переходное тепловое сопротивление «контактная поверхность — охлаждающая среда» теплоотводов СПП.
- Аэродинамическое сопротивление теплоотводов.
- Потери напора на преодоление сил трения в прямоугольных межреберных каналах теплоотвода охладителя на участке безотрывного течения.
- 7.4. ЖИДКОСТНОЕ ОХЛАЖДЕНИЕ СПП
- Выбор электроизоляционных материалов для охладителей СПП.
- 7.5. ИСПАРИТЕЛЬНОЕ ПОГРУЖНОЕ ОХЛАЖДЕНИЕ СПП
- Критические плотности теплового потока и коэффициенты теплоотдачи.
- Конструкции систем испарительного погружного охлаждения СПП.
- Глава 8. НАДЕЖНОСТЬ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ
- 8.1. ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ ТЕОРИИ НАДЕЖНОСТИ
- 8.2. ПОКАЗАТЕЛИ НАДЕЖНОСТИ СПП И ИХ ЗАВИСИМОСТИ ОТ РЕЖИМОВ РАБОТЫ
- Зависимости ПН от режимов работы.
- 8.3. МЕТОДЫ ОЦЕНКИ И КОНТРОЛЯ ПН СПП
- Режимы проведения испытаний СПП на надежность.
- Методы неразрушающего контроля СПП.
- 8.4. ВИДЫ И МЕХАНИЗМЫ ОТКАЗОВ СПП
- 8.5. МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СПП В РАЗЛИЧНЫХ РЕЖИМАХ
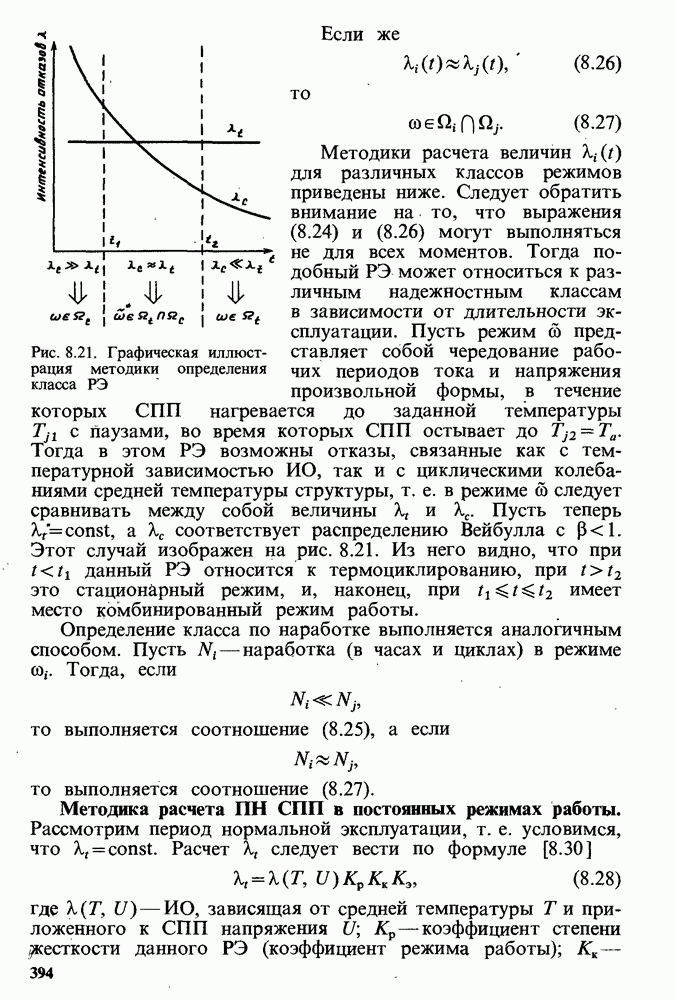
- Методика определения класса РЭ.
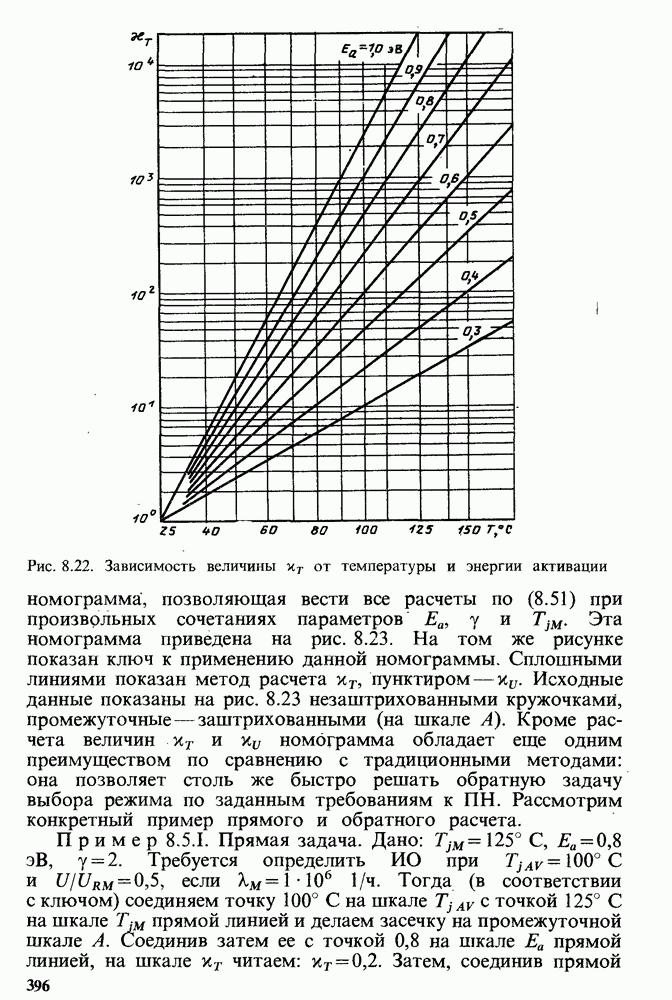
- Методика расчета ПН СПП в постоянных режимах работы.
- Методика расчета ПН СПП в циклических режимах.
- Методика расчета ПН СПП в переменных и комбинированных режимах.
- Некоторые практические рекомендации по расчетам ПН СПП.
- СПИСОК ЛИТЕРАТУРЫ