| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Методика расчета ПН СПП в переменных и комбинированных режимах.
Методы расчета ПН в переменных и комбинированных режимах весьма сложны и недостаточно освещены в литературе. Достаточно заметить, что к этой проблеме нет ни единого подхода, ни установившейся терминологии, ни системы обозначений. Поэтому прежде всего остановимся на тех принципах, которые лежат в основе последующих расчетов.

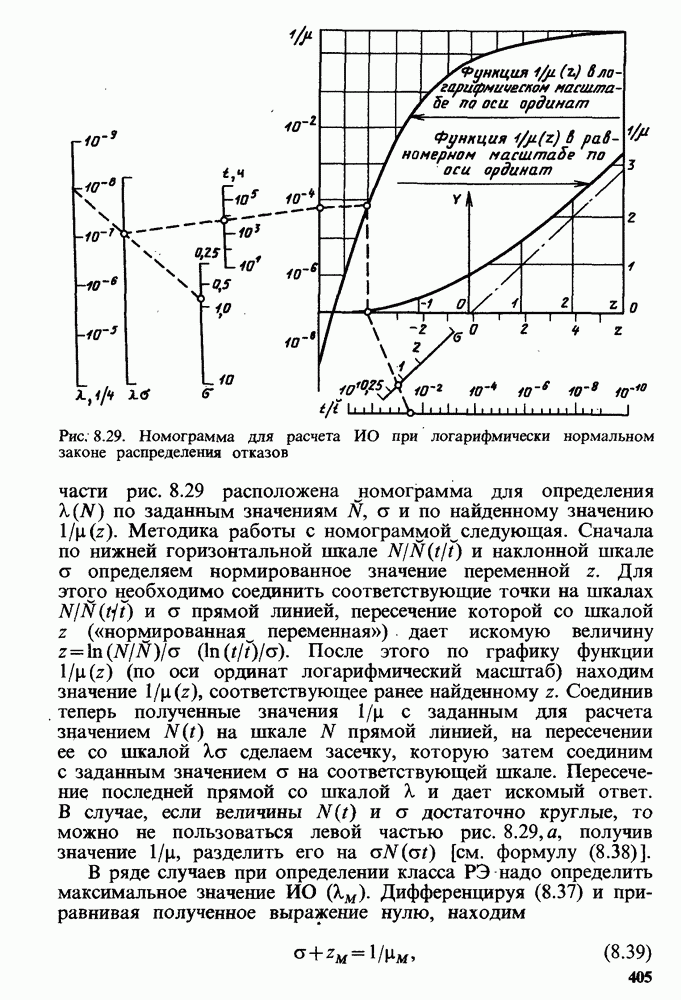
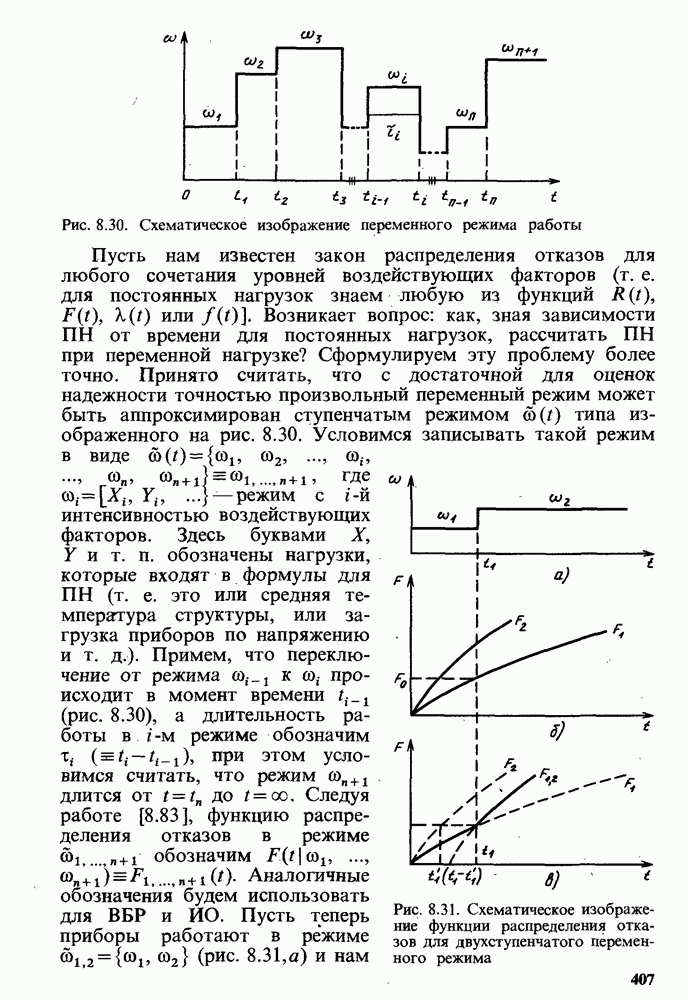
Рис. 8.30. Схематическое изображение переменного режима работы
Пусть нам известен закон распределения отказов для любого сочетания уровней воздействующих факторов (т. е. для постоянных нагрузок знаем любую из функций  ),
),  или
или  Возникает вопрос: как, зная зависимости ПН от времени для постоянных нагрузок, рассчитать ПН при переменной нагрузке? Сформулируем эту проблему более точно. Принято считать, что с достаточной для оценок надежности точностью произвольный переменный режим может быть аппроксимирован ступенчатым режимом со
Возникает вопрос: как, зная зависимости ПН от времени для постоянных нагрузок, рассчитать ПН при переменной нагрузке? Сформулируем эту проблему более точно. Принято считать, что с достаточной для оценок надежности точностью произвольный переменный режим может быть аппроксимирован ступенчатым режимом со  типа изображенного на рис. 8.30. Условимся записывать такой режим в виде
типа изображенного на рис. 8.30. Условимся записывать такой режим в виде  ,
,  - режим с
- режим с  интенсивностью воздействующих факторов. Здесь буквами X,
интенсивностью воздействующих факторов. Здесь буквами X,  и т. п. обозначены нагрузки, которые входят в формулы для ПН (т. е. это или средняя темпераггура структуры, или загрузка приборов по напряжению и т. д.). Примем, что переключение от режима
и т. п. обозначены нагрузки, которые входят в формулы для ПН (т. е. это или средняя темпераггура структуры, или загрузка приборов по напряжению и т. д.). Примем, что переключение от режима  происходит в момент времени
происходит в момент времени  (рис. 8.30), а длительность работы в
(рис. 8.30), а длительность работы в  режиме обозначим
режиме обозначим  , при этом условимся считать, что режим
, при этом условимся считать, что режим  длится от
длится от  до
до  . Следуя работе [8.83], функцию распределения отказов в режиме
. Следуя работе [8.83], функцию распределения отказов в режиме  обозначим
обозначим  ,
,
Аналогичные обозначения будем использовать для ВБР и ИО. Пусть теперь приборы работают в режиме  (Рис. 8.31,а) и нам известны функции
(Рис. 8.31,а) и нам известны функции  и
и  (рис. 8.31,б).
(рис. 8.31,б).

Рис. 8.31. Схематическое изображение функции распределения отказов для двухступенчатого переменного режима
Проблема заключается в следующем: можно ли выразить закон распределения отказов в режиме  через функции
через функции  , и, если можно, как это сделать? Оказывается, что без привлечения некоторых постулатов эта задача не имеет
, и, если можно, как это сделать? Оказывается, что без привлечения некоторых постулатов эта задача не имеет  , так как в общем случае [8.82]
, так как в общем случае [8.82]

где  может быть никак не связана ни с
может быть никак не связана ни с  , ни с
, ни с  . Другими словами, если не пользоваться дополнительными постулатами, то для определения функций вида
. Другими словами, если не пользоваться дополнительными постулатами, то для определения функций вида  необходимо проводить испытания в соответствующем режиме. Задача эта явно безнадежна, особенно если учесть, что даже при одинаковых уровнях нагрузки
необходимо проводить испытания в соответствующем режиме. Задача эта явно безнадежна, особенно если учесть, что даже при одинаковых уровнях нагрузки  изменение хотя бы одного момента переключения
изменение хотя бы одного момента переключения  ведет к изменению функции
ведет к изменению функции  для всех
для всех  . Наиболее подходящим принципом, позволяющим выразить
. Наиболее подходящим принципом, позволяющим выразить  через
через  , представляется так называемый принцип Седякина [8.83]. Он заключается в том, что функция
, представляется так называемый принцип Седякина [8.83]. Он заключается в том, что функция  в (8.41) совпадает со сдвинутой на величину
в (8.41) совпадает со сдвинутой на величину  кривой
кривой  , причем
, причем  (рис. 8.31,в). Из принципа Седякина следует, что [8.84]
(рис. 8.31,в). Из принципа Седякина следует, что [8.84]

где  определяется из уравнения
определяется из уравнения

Именно выражения (8.42), (8.43) будут в дальнейшем использованы наиболее часто. В дополнение к принципу Седякина при расчетах ПН в переменных режимах часто используют постулат о линейной связи между моментами отказов при различных уровнях нагрузки. Его смысл заключается в следующем. На рис. 8.31 видно, что каждому значению вероятности отказа  соответствуют определенные моменты
соответствуют определенные моменты  в режиме
в режиме  , и
, и  в режиме
в режиме  . В общем случае можно записать
. В общем случае можно записать  , где
, где  - неубывающая функция m [8.82]. Если же
- неубывающая функция m [8.82]. Если же

где  не зависящая от времени, но зависящая от соотношения нагрузок в режимах
не зависящая от времени, но зависящая от соотношения нагрузок в режимах  , то говорят о линейной связи моментов отказов в этих режимах.
, то говорят о линейной связи моментов отказов в этих режимах.
В [8.82] показано, что если выполняется (8.44), то  , т. е. вероятность отказа (ВБР или ИО) в момент
, т. е. вероятность отказа (ВБР или ИО) в момент  не зависит от порядка следования режимов работы. Это позволяет упростить расчет ПН за счет суммирования тех
не зависит от порядка следования режимов работы. Это позволяет упростить расчет ПН за счет суммирования тех  , которые отвечают одинаковым уровням нагрузки.
, которые отвечают одинаковым уровням нагрузки.
Наконец, в циклических РЭ в некоторых, оговоренных далее, случаях для расчетов будет использован принцип Пальмгрена-Майнера. Его детерминистическая трактовка имеет следующий вид. Пусть  — число циклов до отказа, выдерживаемых приборами в режиме
— число циклов до отказа, выдерживаемых приборами в режиме  для режима термоциклирования или
для режима термоциклирования или  для режима импульсного циклирования). Тогда
для режима импульсного циклирования). Тогда

где  - число циклов до отказа, определяемое в режиме
- число циклов до отказа, определяемое в режиме  ; где
; где  — число циклов при нагрузке
— число циклов при нагрузке  , причем
, причем  . Заметим, что при экспоненциальном законе распределения наработки до отказа принцип Седякина совпадает с принципом Пальмгрена-Майнера, причем в этом случае выполняются равенство (8.44) и вытекающие из него следствия.
. Заметим, что при экспоненциальном законе распределения наработки до отказа принцип Седякина совпадает с принципом Пальмгрена-Майнера, причем в этом случае выполняются равенство (8.44) и вытекающие из него следствия.
Вернемся к рассмотрению собственно методов расчета ПН СПП в переменных режимах. Во избежание возможных недоразумений заметим следующее. Произвольный РЭ, принадлежащий одному классу, будет постоянным или переменным в зависимости от того, постоянны или переменны во времени величины  , причем мгновенные значения температуры
, причем мгновенные значения температуры  загрузки приборов по напряжению и т. д. могут быть периодическими функциями времени.
загрузки приборов по напряжению и т. д. могут быть периодическими функциями времени.
Приведем методику расчета ЙО в стационарных РЭ.
Пусть  , причем
, причем  и требуется определить ВБР при
и требуется определить ВБР при  , а также среднюю за время t ИО X. Из формулы (8.43) имеем
, а также среднюю за время t ИО X. Из формулы (8.43) имеем  , где
, где  . Отсюда находим
. Отсюда находим

Легко показать, что для режима средняя к моменту  ИО
ИО

Пусть РЭ имеет вид со  , где
, где  заданы так же, как и раньше. Тогда из (8.48) вытекает, что
заданы так же, как и раньше. Тогда из (8.48) вытекает, что

где  — суммарное время работы в режиме
— суммарное время работы в режиме  и
и  соответственно.
соответственно.
Перепишем теперь (8.49) с учетом формулы (8.29) в следующем виде:

В тех случаях, когда вместо (8.50) имеем

Рассмотрим методику расчета ПН в циклических режимах.
Пусть  , причем
, причем  . Требуется определить число циклов
. Требуется определить число циклов  , которое приборы проработают в режиме
, которое приборы проработают в режиме  после того, как они проработали и, циклов в режиме
после того, как они проработали и, циклов в режиме  . При такой постановке задачи целесообразно использовать принцип Пальмгрена-Майнера. Из соотношения (8.45) имеем
. При такой постановке задачи целесообразно использовать принцип Пальмгрена-Майнера. Из соотношения (8.45) имеем

откуда с учетом связи между  и
и  [см. формулу (8.6)] получаем
[см. формулу (8.6)] получаем

Здесь, как и раньше,  . Легко видеть, что этот расчет позволяет оценить число циклов до отказа в одном РЭ по известному количеству циклов, проработанных в другом режиме. Данный метод рекомендуется использовать при отсутствии сведений о законе распределения величины
. Легко видеть, что этот расчет позволяет оценить число циклов до отказа в одном РЭ по известному количеству циклов, проработанных в другом режиме. Данный метод рекомендуется использовать при отсутствии сведений о законе распределения величины  .
.
Рассмотрим методику расчета ИО в переменных режимах при непостоянной функции интенсивности.
Пусть  , причем
, причем  . Применяя последовательно (8.42) и (8.43) к режиму
. Применяя последовательно (8.42) и (8.43) к режиму  , получаем
, получаем

где  находится из решения рекуррентной системы уравнений
находится из решения рекуррентной системы уравнений

Чтобы вывести из (8.50), (8.54) явные аналитические выражения, надо задаться конкретным видом функций Примем, что в переменных режимах работы выполняются не только соотношения (8.42), (8.43), но и (8.44). Основанием для этого является допущение о том, что изменение интенсивности тех или иных внешних воздействий не меняет доминирующего механизма отказов (или их совокупности). Это означает, что закон распределения отказов меняет не свою форму, а лишь масштаб по времени. Иначе, моменты отказов одних и тех же изделий в различных режимах отличаются постоянным множителем, одинаковым для всех элементов партии и зависящим от вида функциональной модели надежности и соотношения нагрузок в этих режимах.
Это предположение используется повсеместно в теории ускоренных испытаний для пересчета к нормальному режиму [8.82] (если же форма распределения изменяется, то считают, что нарушается условие автомодельности). Дальнейший анализ показывает, что предположение (8.44) накладывает довольно жесткие ограничения на варьирование параметров законов распределений от режима к режиму. Продемонстрируем это на примере распределения Вейбулла. Из формулы (8.43) находим  откуда
откуда  Для того чтобы выполнялось еще и условие (8.44), надо потребовать, чтобы
Для того чтобы выполнялось еще и условие (8.44), надо потребовать, чтобы  . Это означает, что при изменении нагрузок варьируется только параметр в, а параметр формы
. Это означает, что при изменении нагрузок варьируется только параметр в, а параметр формы  остается постоянным. Аналогичным образом можно найти и ограничения на параметры для других законов распределения. Полученные результаты для самых распространенных распределений сведены в табл. 8.13. С учетом этих ограничений из (8.53), (8.54) легко вывести формулы для
остается постоянным. Аналогичным образом можно найти и ограничения на параметры для других законов распределения. Полученные результаты для самых распространенных распределений сведены в табл. 8.13. С учетом этих ограничений из (8.53), (8.54) легко вывести формулы для  , которые приведены во второй колонке табл. 8.13. Таким образом, при переменной во времеци ИО ее значение на
, которые приведены во второй колонке табл. 8.13. Таким образом, при переменной во времеци ИО ее значение на  ступени дается формулой (8.53), где
ступени дается формулой (8.53), где  определяется по приведенным в табл. 8.13 выражениям. Для вейбулловского и логарифмически нормального распределений приведенные формулы обобщают результаты работы
определяется по приведенным в табл. 8.13 выражениям. Для вейбулловского и логарифмически нормального распределений приведенные формулы обобщают результаты работы  на произвольный РЭ. Для циклических режимов в формулах этого параграфа надо t заменить на
на произвольный РЭ. Для циклических режимов в формулах этого параграфа надо t заменить на  .
.
Таблица 8.13. Формулы  расчета ИО в переменных РЭ
расчета ИО в переменных РЭ

Рассмотрим методику расчета ПН СПП в комбинированных режимах.
Как отмечалось, если режим может быть одновременно отнесен к  классам, то он называется комбинированным
классам, то он называется комбинированным  . Предположение о том, что действует один и тот же механизм отказа, становится в этом случае весьма сомнительным, и потому от допущения (8.44) следует отказаться. Возможен случай, когда ресурс расходуется независимо в различных областях структуры, и тогда соответствующие ИО можно просто складывать. Рассмотрим различные варианты комбинированных режимов более подробно.
. Предположение о том, что действует один и тот же механизм отказа, становится в этом случае весьма сомнительным, и потому от допущения (8.44) следует отказаться. Возможен случай, когда ресурс расходуется независимо в различных областях структуры, и тогда соответствующие ИО можно просто складывать. Рассмотрим различные варианты комбинированных режимов более подробно.
Пусть  Физически такой режим представляет чередование рабочих периодов тока и напряжения произвольной формы, в течение которых структура нагревается до заданной температуры
Физически такой режим представляет чередование рабочих периодов тока и напряжения произвольной формы, в течение которых структура нагревается до заданной температуры  с паузами, во время которых прибор остывает до
с паузами, во время которых прибор остывает до  . Требуется определить ИО в произвольный момент
. Требуется определить ИО в произвольный момент  , причем длительность работы под нагрузкой равна и длительность паузы
, причем длительность работы под нагрузкой равна и длительность паузы  . Во введенных обозначениях
. Во введенных обозначениях  , причем
, причем  .
.
В связи с тем что механизмы отказов в нециклическом режиме и режиме термоциклирования различны, то до тех пор, пока  , ресурс в этих режимах будет расходоваться независимо. Поэтому полный ресурс, израсходованный в режиме
, ресурс в этих режимах будет расходоваться независимо. Поэтому полный ресурс, израсходованный в режиме 

откуда для ИО в момент  получаем
получаем

Здесь в формуле (8.56) мы перешли от переменной  в функции
в функции  к переменной
к переменной  . Этот переход осуществляется либо через среднюю частоту циклирования, либо через среднюю длительность цикла. В частности, для распределения Вейбулла
. Этот переход осуществляется либо через среднюю частоту циклирования, либо через среднюю длительность цикла. В частности, для распределения Вейбулла  перейдет в
перейдет в  просто при замене 0 на
просто при замене 0 на  и одновременной замене N на
и одновременной замене N на  , для логарифмически нормального распределения надо вместо
, для логарифмически нормального распределения надо вместо  подставить
подставить  и т. п.
и т. п.
Если ввести среднюю ИО  , такую, чтобы ВБР при
, такую, чтобы ВБР при  в режиме
в режиме  была равна
была равна  , то
, то

где  . Стоит обратить внимание на то, что формула (8.57) формально аналогична широко известному выражению [8.84].
. Стоит обратить внимание на то, что формула (8.57) формально аналогична широко известному выражению [8.84].

где  ИО при работе и во время пауз;
ИО при работе и во время пауз;  и
и  длительность работы и паузы соответственно;
длительность работы и паузы соответственно;  — длительность цикла;
— длительность цикла;  - частота циклирования.
- частота циклирования.
Заметим, что выражение (8.57) получено для средней ИО при предположении о независимом расходовании ресурса в этих РЭ и, кроме того,  (т. е.
(т. е.  также
также  ).
).
Пусть  . Физически это соответствует стационарному режиму с высоким значением
. Физически это соответствует стационарному режиму с высоким значением  . Здесь уже нельзя априори предполагать независимость расходования ресурса, а, напротив, он будет вырабатываться в «горячей точке» структуры. Пусть для определенности РЭ имеет вид
. Здесь уже нельзя априори предполагать независимость расходования ресурса, а, напротив, он будет вырабатываться в «горячей точке» структуры. Пусть для определенности РЭ имеет вид  , где режим
, где режим  , и имеет постоянную ИО, равную
, и имеет постоянную ИО, равную  , а режим
, а режим  и имеет ИО
и имеет ИО  . Тогда, применяя последовательно формулу (8.54), получаем
. Тогда, применяя последовательно формулу (8.54), получаем

причем число слагаемых каждого вида в (8.59) одинаково и равно к. Зная  , сразу находим
, сразу находим  и далее любые нужные ПН. Аналогичным образом следует поступать и в случае
и далее любые нужные ПН. Аналогичным образом следует поступать и в случае 
Наконец, еще один режим, представляющий  - это
- это  . Физически это может быть, например, серия из
. Физически это может быть, например, серия из  коротких импульсов с большими
коротких импульсов с большими  , затем пауза, во время которой прибор остывает, и т. д. Тогда, чтобы определить число циклов, которые выдержит прибор до отказа
, затем пауза, во время которой прибор остывает, и т. д. Тогда, чтобы определить число циклов, которые выдержит прибор до отказа  , надо вычислить величины
, надо вычислить величины  по формулам типов
по формулам типов  для соответствующих значений
для соответствующих значений  и выбрать искомое
и выбрать искомое  Так же следует поступать и для режимов типов
Так же следует поступать и для режимов типов  .
.
Пример 8.7. а) Пусть в каком-то ПУ в пусковых режимах 2 раза в сутки (к примеру) средняя температура приборов в течение 10 с составляет 120° С, а в остальное время  — 85° С. Будет ли это кратковременное повышение
— 85° С. Будет ли это кратковременное повышение  влиять на ИО? Для получения ответа вычисляем величину
влиять на ИО? Для получения ответа вычисляем величину  . Пусть
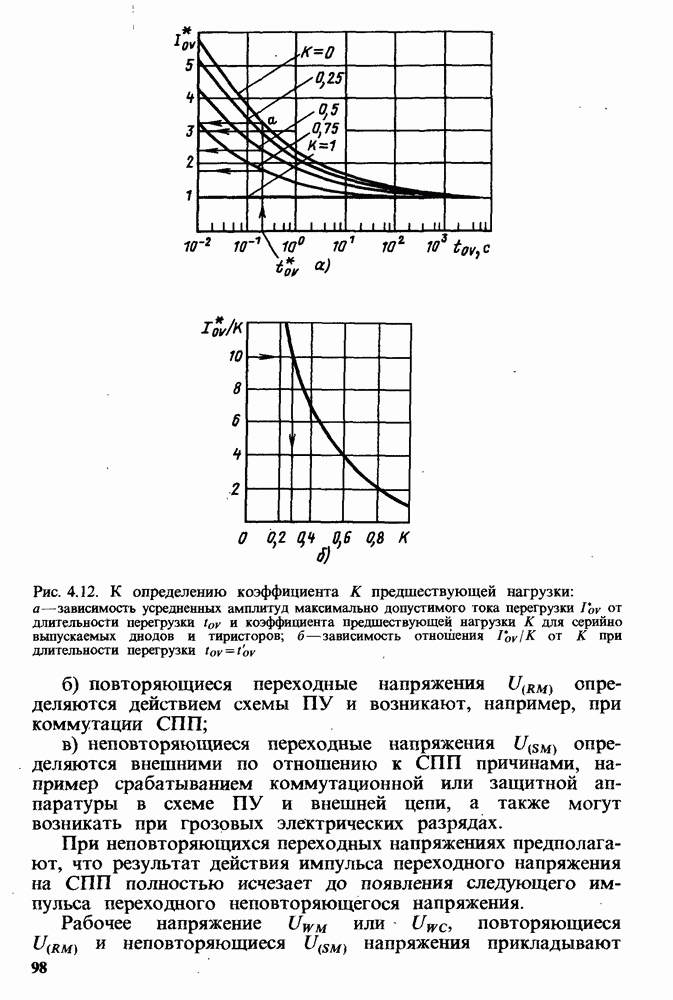
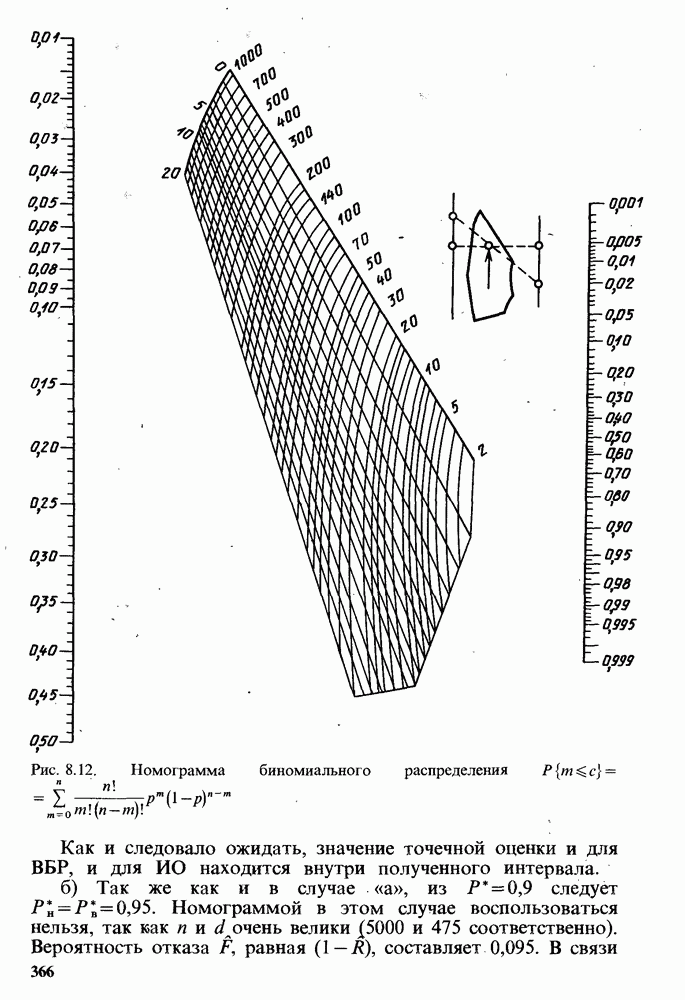
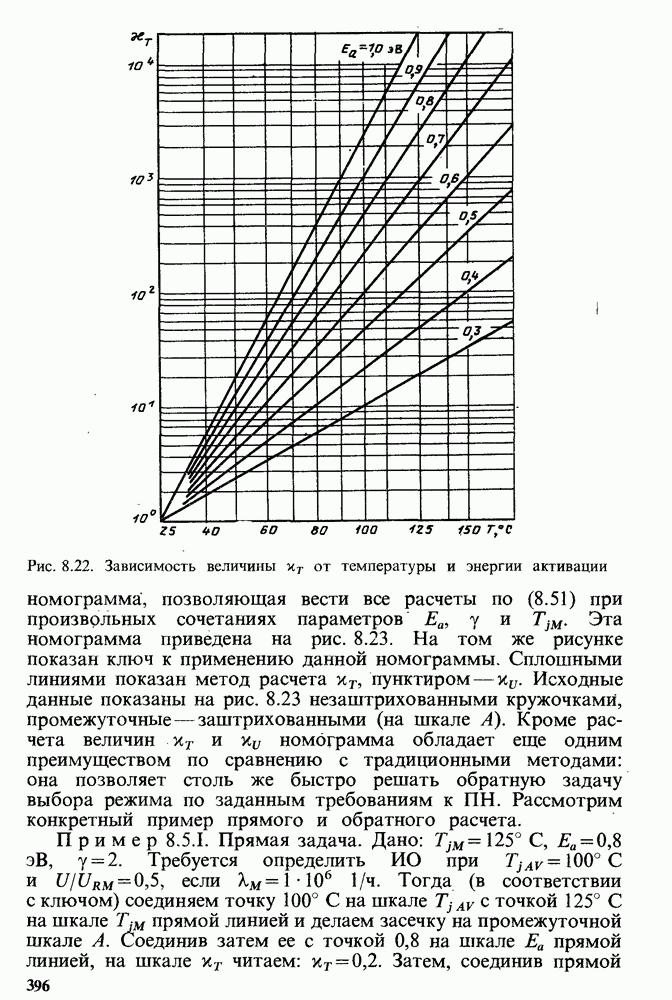
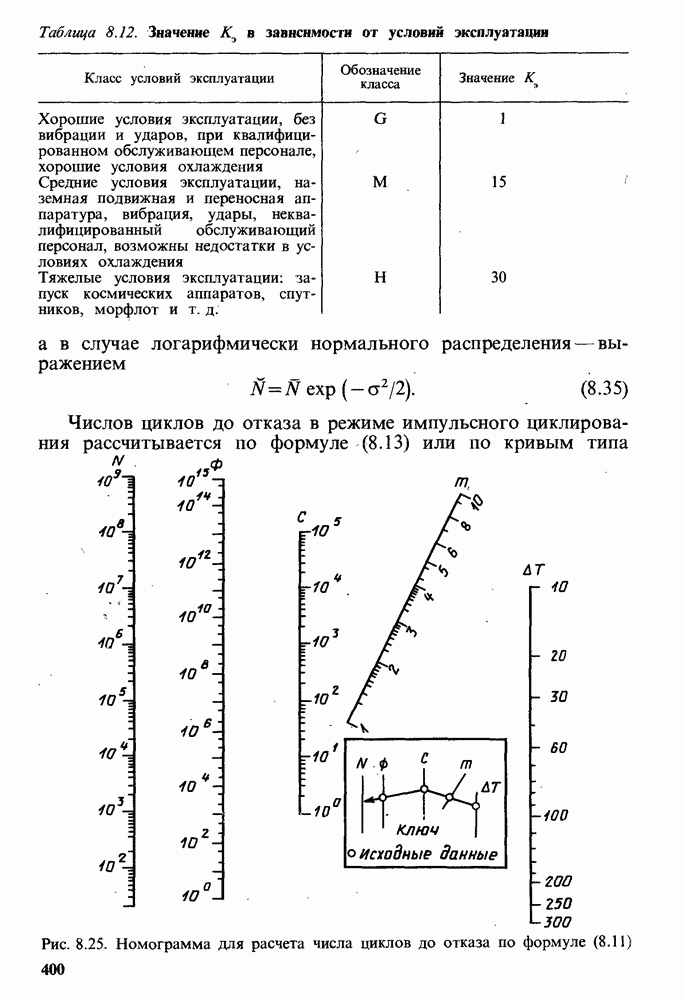
. Пусть  . Тогда по номограмме
. Тогда по номограмме  ). Так как
). Так как  то в итоге получаем, что
то в итоге получаем, что  , т. е. такие пусковые режимы не влияют на ИО. Если бы пусковой режим протекал каждый раз в течение 10 мин, то
, т. е. такие пусковые режимы не влияют на ИО. Если бы пусковой режим протекал каждый раз в течение 10 мин, то  и, следовательно, ИО возросла бы за счет этих режимов почти на 1/3.
и, следовательно, ИО возросла бы за счет этих режимов почти на 1/3.
б) Пусть длительность. периода приработки равна  и ИО на этом участке
и ИО на этом участке  описывается распределением Вейбулла с параметрами
описывается распределением Вейбулла с параметрами  .
.
При  интенсивность отказов постоянна и равна
интенсивность отказов постоянна и равна  . Определим ВБР в момент
. Определим ВБР в момент  и какой наработке в режиме
и какой наработке в режиме  эквивалентны первые
эквивалентны первые  .
.
Из (8.5) имеем  да
да  куда
куда  . Вероятность безотказной работы
. Вероятность безотказной работы  да 0,67.
да 0,67.
в) Пусть  , причем
, причем  . Определить ИО через
. Определить ИО через  циклов и среднюю ИО
циклов и среднюю ИО  за это время.
за это время.
Заменяя  на
на  , имеем для ИО выражение
, имеем для ИО выражение  , откуда для
, откуда для  получим да
получим да  . Так как
. Так как  в этом случае постоянна, то окончательно имеем
в этом случае постоянна, то окончательно имеем  .
.
г) Пусть при тех же исходных данных, которые даны в п.  примера 8.7, требуется определить класс РЭ. Тогда, в силу того, что
примера 8.7, требуется определить класс РЭ. Тогда, в силу того, что  . Последнее, однако, верно не всегда, поскольку
. Последнее, однако, верно не всегда, поскольку  уменьшается во времени. Поэтому, если заданное число циклов
уменьшается во времени. Поэтому, если заданное число циклов  будет не 104, а, например, 105, то
будет не 104, а, например, 105, то  , что уже сравнимо с
, что уже сравнимо с  и потому
и потому  и т. д.
и т. д.
д) Определение класса по наработке проиллюстрируем на следующем примере. Пусть в нециклическом режиме приборы подвергаются воздействию такого  , что локальный перегрев
, что локальный перегрев  15° С, и пусть частота приложения этих воздействий равна 50 Гц. Тогда в соответствии со значениями параметров
15° С, и пусть частота приложения этих воздействий равна 50 Гц. Тогда в соответствии со значениями параметров  , или
, или  непрерывной работы. Если X, для этих приборов примерно равно
непрерывной работы. Если X, для этих приборов примерно равно  , то средняя наработка до отказа (при
, то средняя наработка до отказа (при  ) составит
) составит  .
.
В связи с тем что  , то
, то  . Если бы
. Если бы  было равно 60° С, то
было равно 60° С, то  или примерно
или примерно  непрерывной работы, т. е. в этом случае
непрерывной работы, т. е. в этом случае  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ПРИНЦИП ДЕЙСТВИЯ И ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ ДИОДОВ И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
- 1.2. ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД
- 1.3.СИЛОВОЙ ПОЛУПРОВОДНИКОВЫЙ ВЫПРЯМИТЕЛЬНЫЙ ДИОД
- Проводящее состояние силового диода.
- Переходный процесс включения силового полупроводникового диода.
- Переходный процесс выключения силового полупроводникового диода.
- 1.4. СИЛОВОЙ ТРИОДНЫЙ ТИРИСТОР, НЕ ПРОВОДЯЩИЙ В ОБРАТНОМ НАПРАВЛЕНИИ
- Обратное непроводящее состояние тиристора.
- Закрытое состояние тиристора.
- Процесс включения тиристора. Эффект di/dt. Открытое состояние тиристора.
- Процесс выключения тиристора. Эффект dU/dt.
- Глава 2. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- 2.2. ОСНОВНЫЕ ПАРАМЕТРЫ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Основные электрические параметры силовых тиристоров.
- 2.3. ОСНОВНЫЕ ТЕПЛОВЫЕ ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ДИОДОВ И ТИРИСТОРОВ
- 2.4. КЛАССИФИКАЦИЯ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Классификация силовых полупроводниковых диодов и тиристоров по конструкции.
- 2.5. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ диодов И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
- Условное обозначение типоисполнения диодов и тиристоров.
- 2.6. ОСОБЕННОСТИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ КАК ЭЛЕКТРОТЕХНИЧЕСКИХ ИЗДЕЛИЙ, КОМПЛЕКТУЮЩИХ СХЕМУ СИЛОВОГО ПОЛУПРОВОДНИКОВОГО ПРЕОБРАЗОВАТЕЛЬНОГО УСТРОЙСТВА
- Глава 3. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ И УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ
- 3.1. РЕЖИМЫ И УСЛОВИЯ РАБОТЫ ДИОДОВ И ТИРИСТОРОВ
- 3.2. КЛАССИФИКАЦИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 3.3. ОСОБЕННОСТИ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ
- Рекомендуемая нагрузка диодов и тиристоров.
- Исходные данные и последовательность расчета.
- Глава 4. РАСЧЕТ И ВЫБОР ДИОДОВ И ТИРИСТОРОВ. УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ И РАСЧЕТ СИСТЕМЫ УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 4.1. РАСЧЕТ И ВЫБОР ТИПА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО РАБОЧЕМУ ТОКУ
- Тепловые параметры СПП и выбор условий охлаждения.
- Определение режима нагрузки СПП рабочим током.
- Расчет и выбор типа СПП, типа охладителя и скорости охлаждающей среды при неизменном рабочем токе.
- Расчет и выбор типа прибора, типа охладителя и скорости охлаждающей среды при изменяющемся рабочем токе.
- 4.2. ВЫБОР КЛАССА СПП ПО РАБОЧЕМУ НАПРЯЖЕНИЮ
- Определение класса СПП.
- 4.3. ПРОВЕРКА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО ТЕМПЕРАТУРЕ НАГРЕВА РАБОЧИМ ТОКОМ
- Расчет температур перегрева перехода СПП в рабочем режиме.
- 4.4. ПРОВЕРКА СПП ПО АВАРИЙНОМУ ТОКУ
- Проверка СПП при синусоидальной форме импульса аварийного тока.
- Проверка СПП при несинусоидальной форме аварийного тока.
- 4.5. ВЫБОР КОММУТАЦИОННЫХ ПАРАМЕТРОВ СПП
- Время выключения.
- Критическая скорость нарастания тока при включении.
- Критическая скорость нарастания напряжения в закрытом состоянии СПП.
- Время обратного восстановления.
- 4.6. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УПРАВЛЯЮЩИХ ИМПУЛЬСОВ И СХЕМЫ УПРАВЛЕНИЯ ТИРИСТОРОМ
- Выбор параметров управляющих импульсов.
- Расчет мощности потерь на управляющем электроде.
- 4.7. ПРИМЕР РАСЧЕТА И ВЫБОРА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ
- Расчет и выбор типа СПП и условий его охлаждения но рабочему току.
- Проверка выбранного СПП и условий охлаждения по температуре нагрева перехода рабочим током.
- Проверка СПП по аварийному току.
- Выбор коммутационных параметров СПП.
- Определение параметров управляющих импульсов и источника управления.
- Глава 5. МЕТОДЫ И СРЕДСТВА ОГРАНИЧЕНИЯ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ ПО ТОКУ И НАПРЯЖЕНИЮ В НОРМАЛЬНЫХ И АВАРИЙНЫХ РЕЖИМАХ РАБОТЫ
- 5.1. ТРЕБОВАНИЯ К МЕТОДАМ И СРЕДСТВАМ ОГРАНИЧЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ
- 5.2. ВЫБОР ВИДА И РАСЧЕТ ЭЛЕМЕНТОВ ДЛЯ ОГРАНИЧЕНИЯ АВАРИЙНОГО ТОКА
- 5.3. ОГРАНИЧЕНИЕ КОММУТАЦИОННЫХ ПЕРЕНАПРЯЖЕНИЙ НА СПП
- Получение исходных данных для выбора схем и расчета параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Расчет параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Воздействие перенапряжений, возникающих при запирании СПП, на другие тиристоры преобразовательных схем.
- 5.4. ОГРАНИЧЕНИЕ СХЕМНЫХ И СЕТЕВЫХ ПЕРЕНАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- Схемные перенапряжения
- Уменьшение уровня переиапряжения на вентилях
- Схемные перенапряжения эпизодического характера
- Расчет параметров устройства для ограничения сетевых и схемных перенапряжений.
- Расчет ограничительных устройств для подавления схемных перенапряжений.
- Ограничение скорости нарастания и спадания тока СПП.
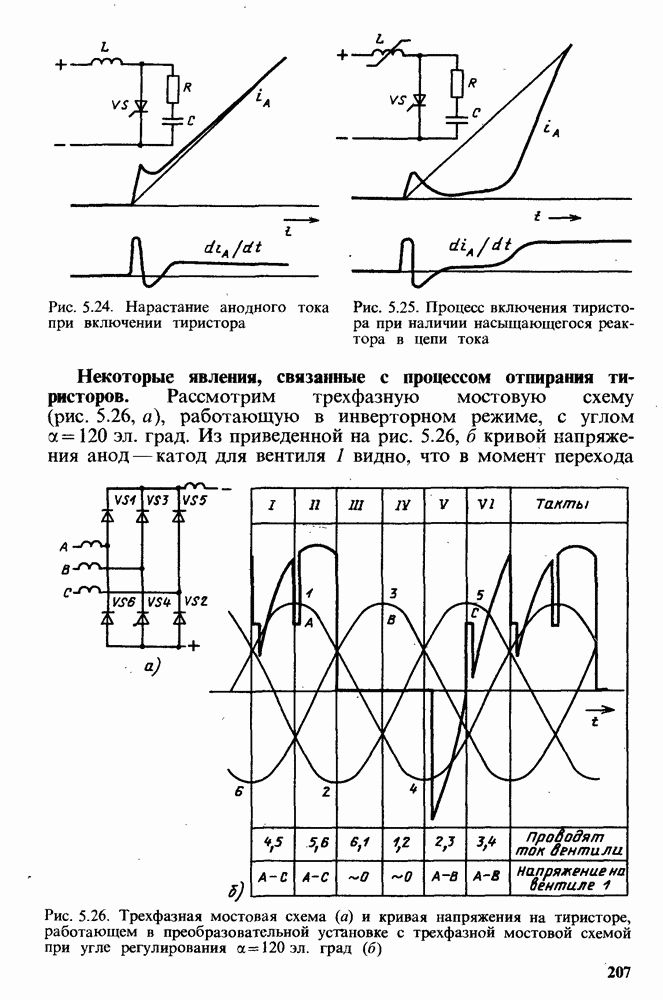
- Некоторые явления, связанные с процессом отпирания тиристоров.
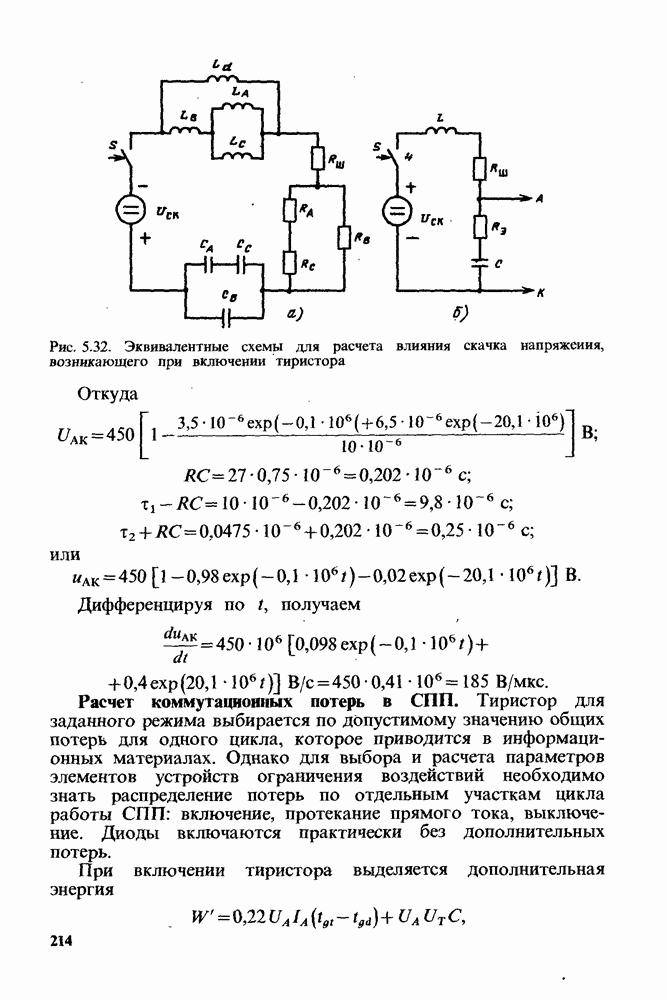
- Расчет коммутационных потерь в СПП.
- 5.5. ГРУППОВОЕ СОЕДИНЕНИЕ СПП
- Последовательное соединение СПП
- Групповое соединение СПП
- 5.6. НЕКОТОРЫЕ СХЕМЫ ПОДКЛЮЧЕНИЯ ОГРАНИЧИТЕЛЬНЫХ УСТРОЙСТВ
- Глава 6. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ В СХЕМАХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТАНОВОК
- 6.1. ТРЕБОВАНИЯ К МЕТОДАМ ИЗМЕРЕНИЙ
- 6.2. ИЗМЕРЕНИЕ СРЕДНЕГО И ЭФФЕКТИВНОГО ТОКА, ПРОХОДЯЩЕГО ЧЕРЕЗ СПП, И МОЩНОСТИ ПОТЕРЬ В СТАЦИОНАРНОМ РЕЖИМЕ
- 6.3. ИЗМЕРЕНИЕ МГНОВЕННЫХ ЗНАЧЕНИЙ ТОКА В ПРОЦЕССЕ ВКЛЮЧЕНИЯ И ВЫКЛЮЧЕНИЯ СПП
- 6.4. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- 6.5. КОНТРОЛЬ ПАРАМЕТРОВ СИГНАЛОВ УПРАВЛЕНИЯ ТИРИСТОРОВ И ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ СПП
- 6.6. СОВРЕМЕННЫЕ МЕТОДЫ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ
- 6.7. ПОГРЕШНОСТИ ИЗМЕРЕНИЯ БЫСТРОМЕНЯЮЩИХСЯ ТОКОВ С ПОМОЩЬЮ БЕЗЫНДУКТИВНЫХ (МАЛОИНДУКТИВНЫХ) ШУНТОВ
- Глава 7. ОХЛАЖДЕНИЕ ДИОДОВ И ТИРИСТОРОВ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 7.1. ОБЩИЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ. ПРЕДЪЯВЛЯЕМЫЕ К ОХЛАДИТЕЛЯМ СПП
- Классификация охладителей.
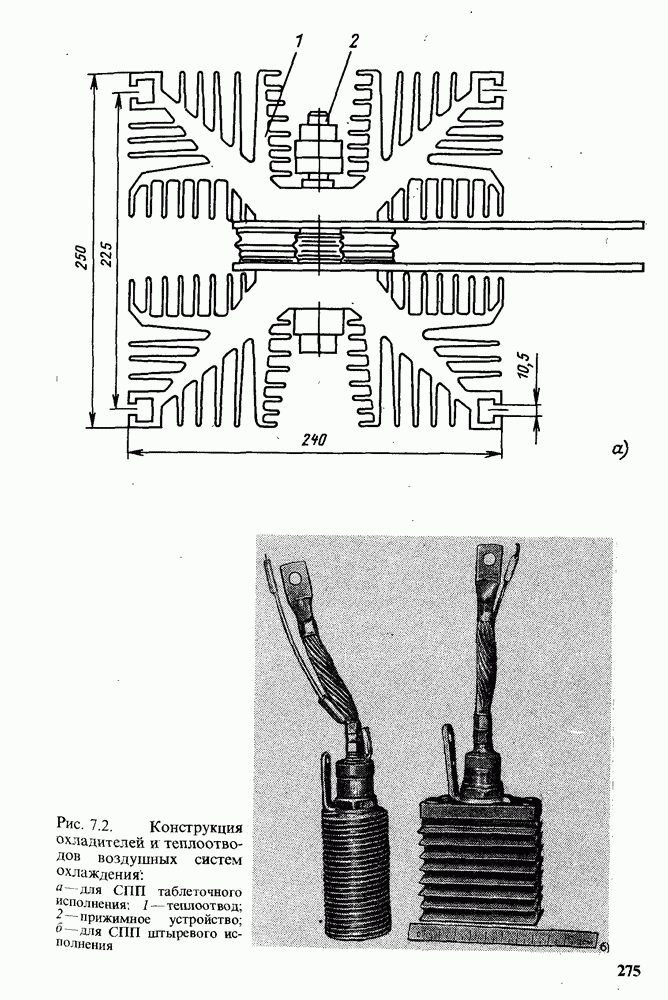
- 7.2. КОНСТРУКЦИИ ОХЛАДИТЕЛЕЙ
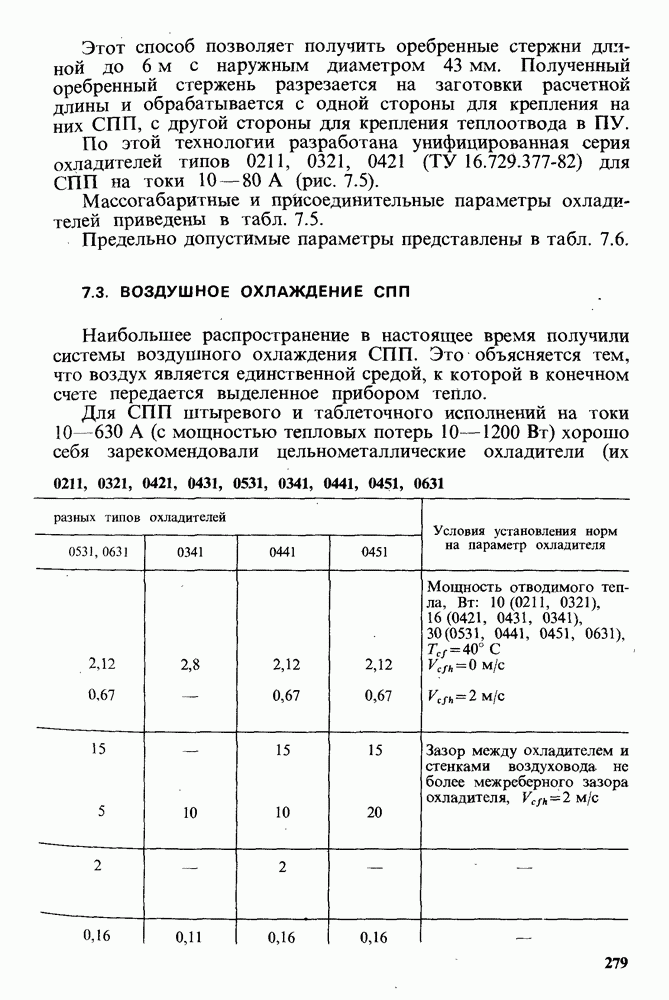
- 7.3. ВОЗДУШНОЕ ОХЛАЖДЕНИЕ СПП
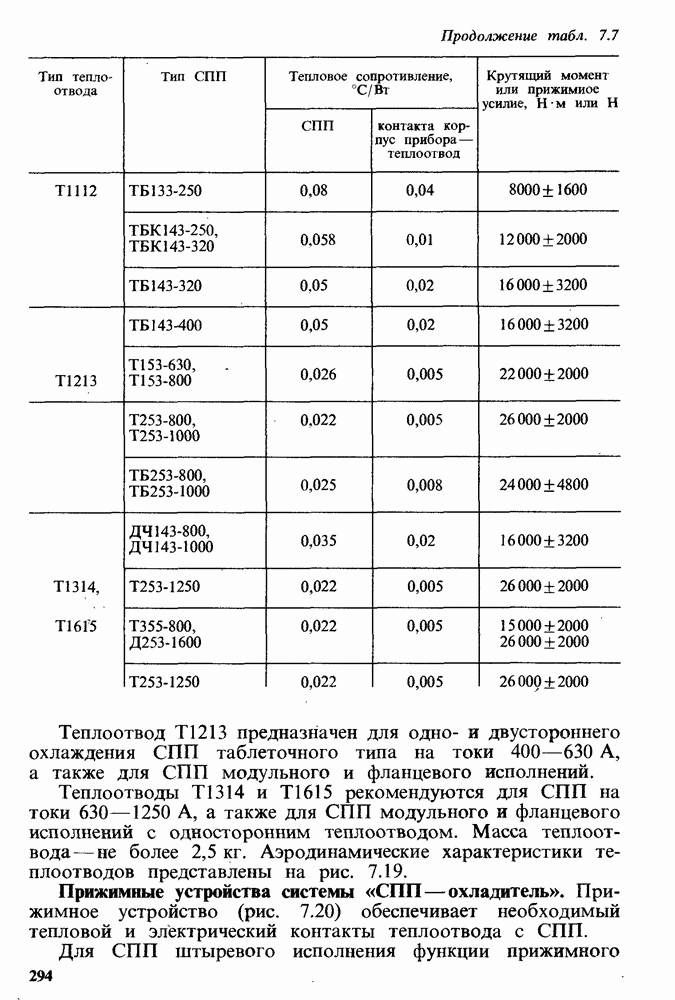
- Прижимные устройства системы «СПП—охладитель».
- Компоновка системы «СПП — охладитель» в ПУ с естественным воздушным охлаждением.
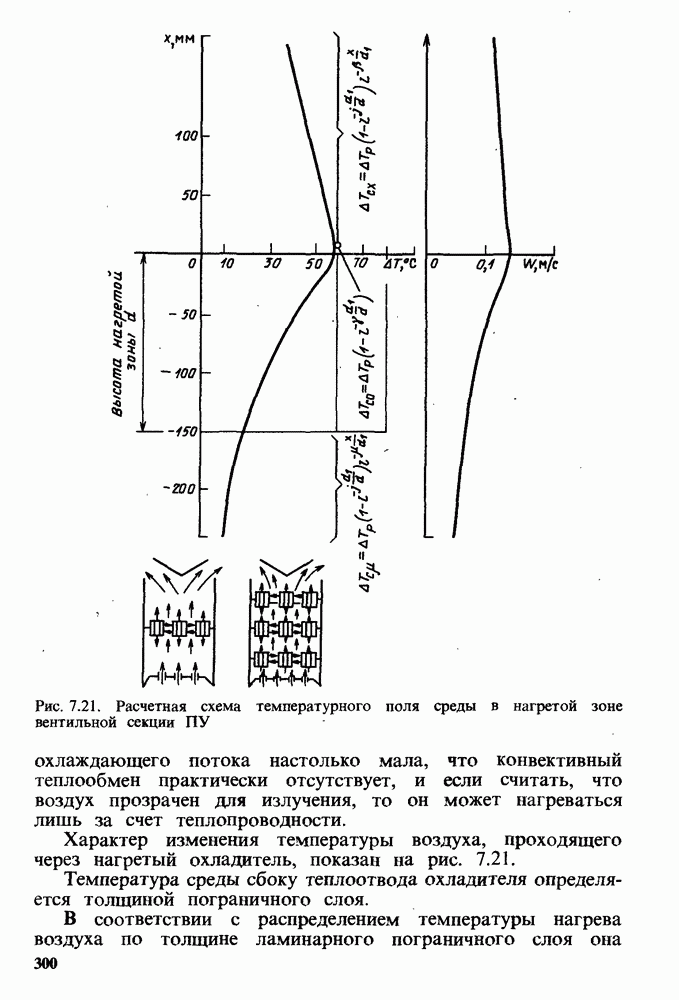
- Температурное поле среды вокруг нагретых СПП с охладителями при наличии в вентильной секции ПУ воздухоотводящих экранов и перфораций.
- Переходное тепловое сопротивление «контактная поверхность — охлаждающая среда» теплоотводов СПП.
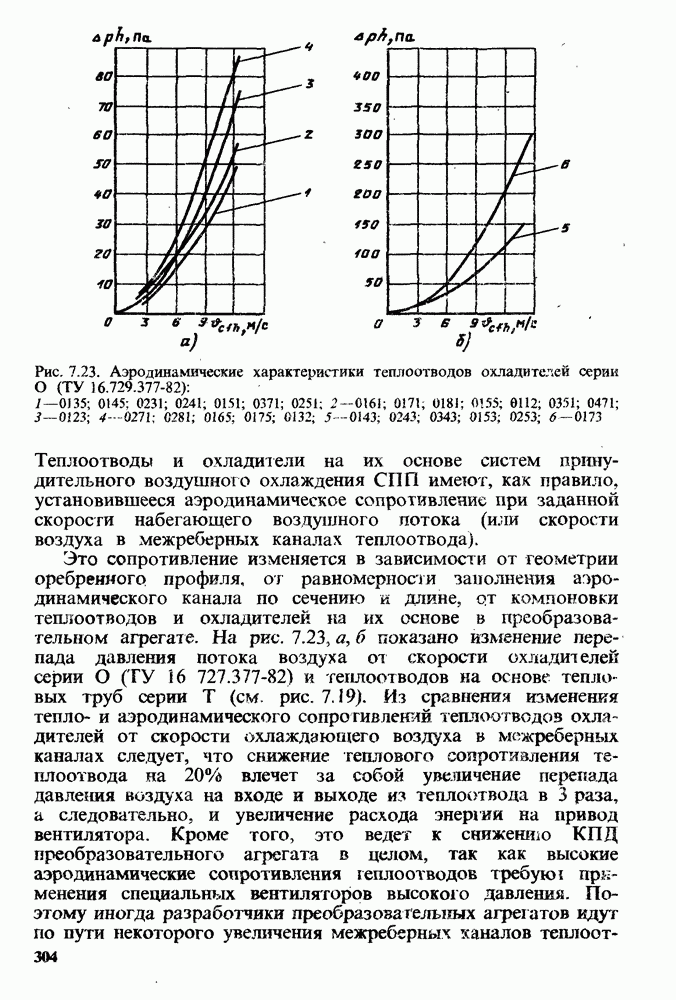
- Аэродинамическое сопротивление теплоотводов.
- Потери напора на преодоление сил трения в прямоугольных межреберных каналах теплоотвода охладителя на участке безотрывного течения.
- 7.4. ЖИДКОСТНОЕ ОХЛАЖДЕНИЕ СПП
- Выбор электроизоляционных материалов для охладителей СПП.
- 7.5. ИСПАРИТЕЛЬНОЕ ПОГРУЖНОЕ ОХЛАЖДЕНИЕ СПП
- Критические плотности теплового потока и коэффициенты теплоотдачи.
- Конструкции систем испарительного погружного охлаждения СПП.
- Глава 8. НАДЕЖНОСТЬ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ
- 8.1. ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ ТЕОРИИ НАДЕЖНОСТИ
- 8.2. ПОКАЗАТЕЛИ НАДЕЖНОСТИ СПП И ИХ ЗАВИСИМОСТИ ОТ РЕЖИМОВ РАБОТЫ
- Зависимости ПН от режимов работы.
- 8.3. МЕТОДЫ ОЦЕНКИ И КОНТРОЛЯ ПН СПП
- Режимы проведения испытаний СПП на надежность.
- Методы неразрушающего контроля СПП.
- 8.4. ВИДЫ И МЕХАНИЗМЫ ОТКАЗОВ СПП
- 8.5. МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СПП В РАЗЛИЧНЫХ РЕЖИМАХ
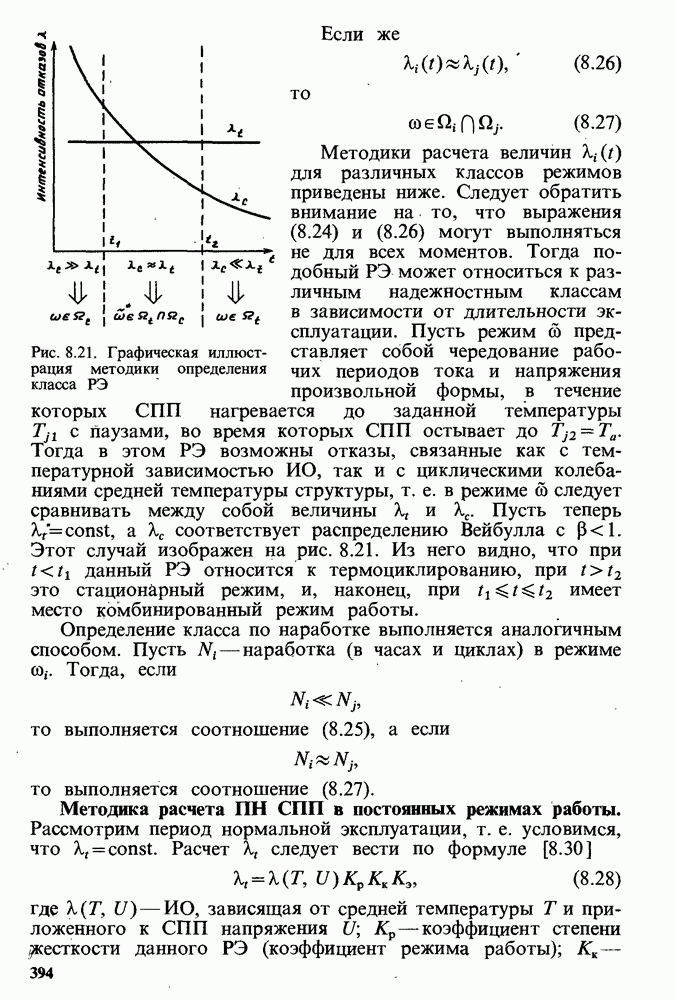
- Методика определения класса РЭ.
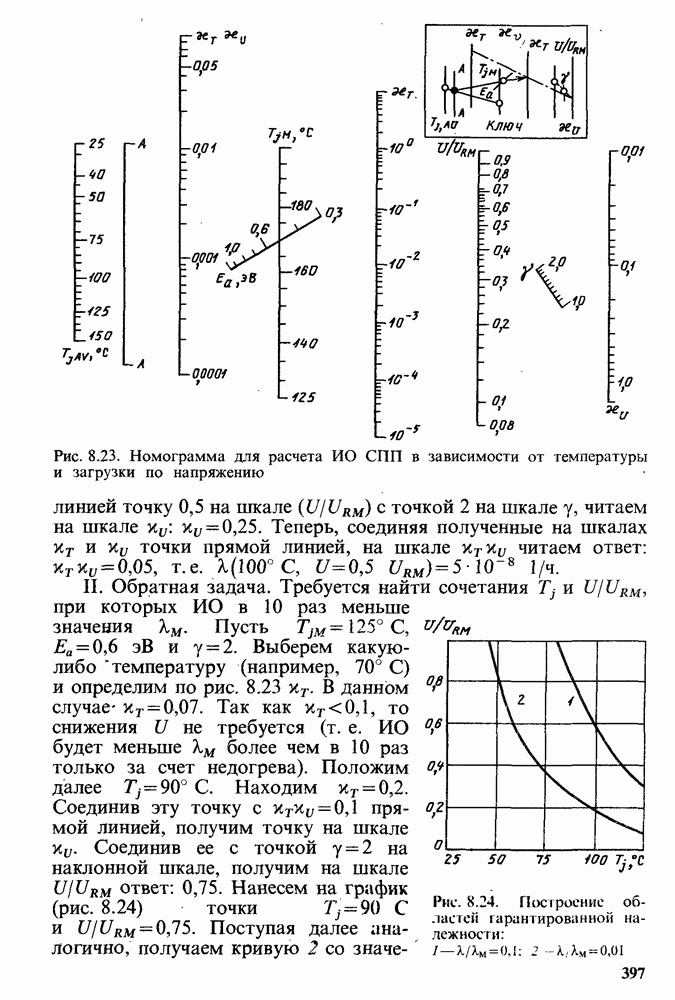
- Методика расчета ПН СПП в постоянных режимах работы.
- Методика расчета ПН СПП в циклических режимах.
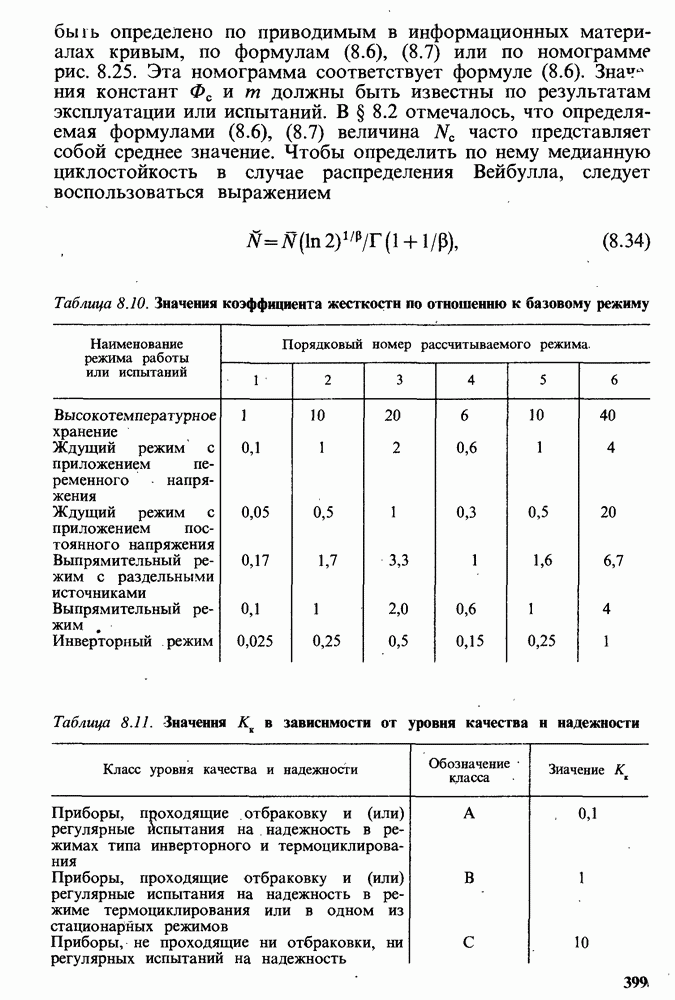
- Методика расчета ПН СПП в переменных и комбинированных режимах.
- Некоторые практические рекомендации по расчетам ПН СПП.
- СПИСОК ЛИТЕРАТУРЫ