| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
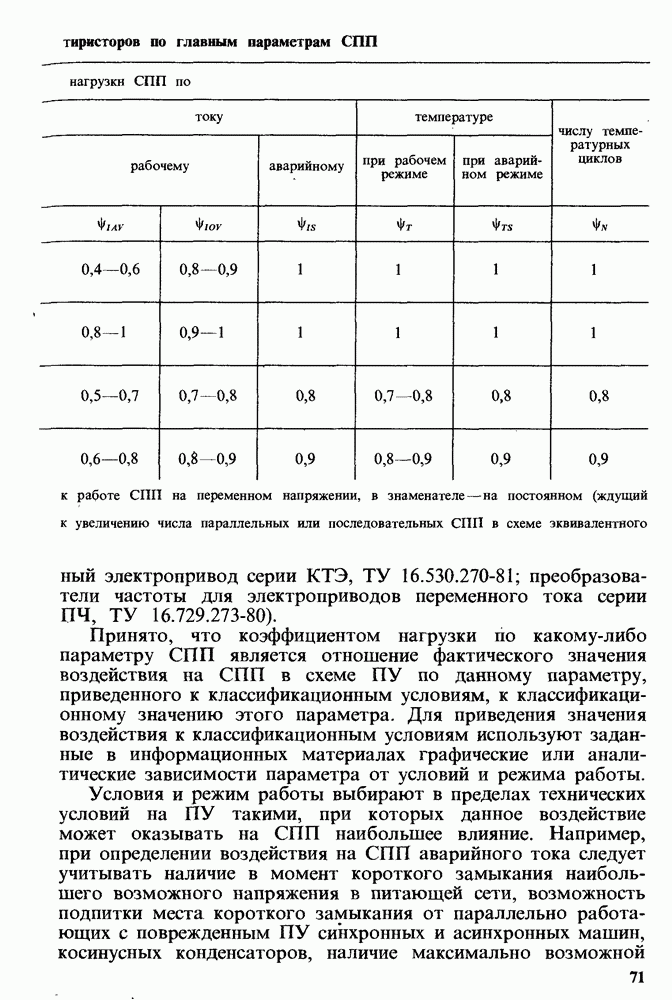
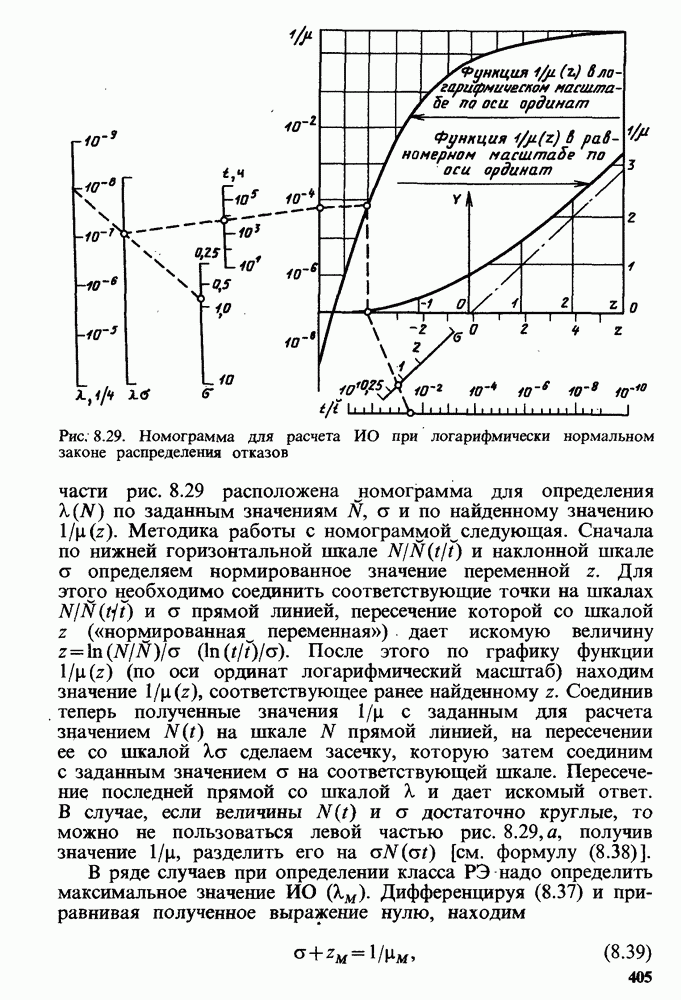
Некоторые практические рекомендации по расчетам ПН СПП.
Ниже показано, как можно вычислять ПН СПП, используя имеющиеся реальные данные и не прибегая к громоздким формулам. Кроме того, приведены приближенные формулы для расчета некоторых ПН.
Первый пример, который рассмотрим, относится к одному из наиболее распространенных вариантов обобщенно-статистических моделей, а именно к модели дрейфа параметров (см. рис. 8.3). Исходными являются данные по долговечности диодов типа  Изучались приборы, проработавшие от 0 до 12 лет в выпрямителях тяговых подстанций городского электрифицированного транспорта г. Москвы (режим термоциклирования).
Изучались приборы, проработавшие от 0 до 12 лет в выпрямителях тяговых подстанций городского электрифицированного транспорта г. Москвы (режим термоциклирования).

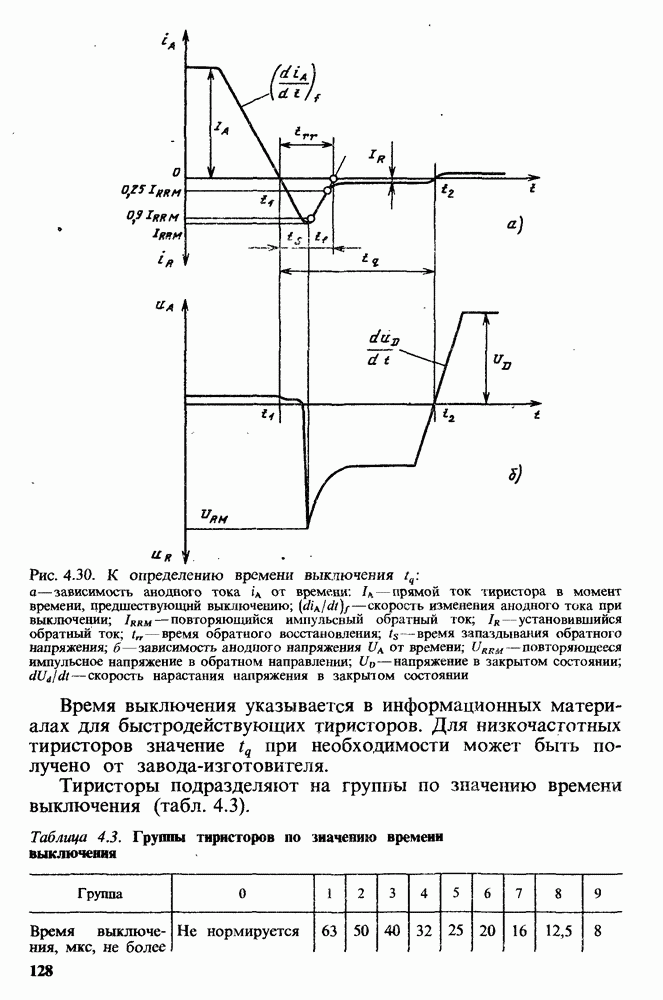
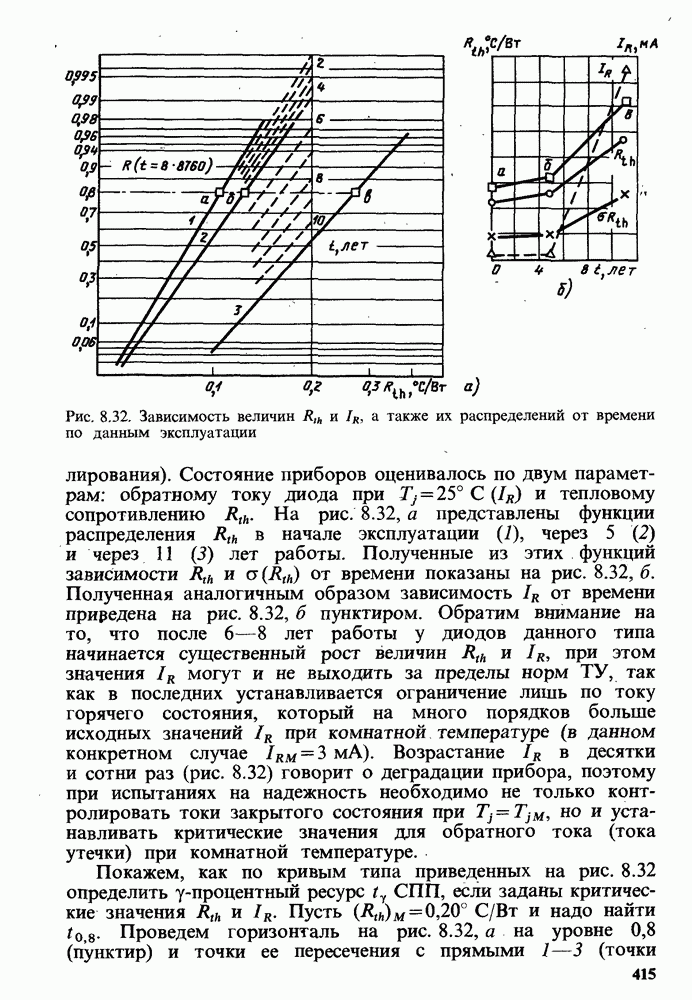
Рис. 8.32. Зависимость величин  и
и  , а также их распределений от времени по данным эксплуатации
, а также их распределений от времени по данным эксплуатации
Состояние приборов оценивалось по двум параметрам: обратному току диода при  25° С (
25° С ( ) и тепловому сопротивлению
) и тепловому сопротивлению  . На рис. 8.32, а представлены функции распределения
. На рис. 8.32, а представлены функции распределения  в начале эксплуатации
в начале эксплуатации  , через 5 (2) и через 11 (3) лет работы. Полученные из этих функций зависимости
, через 5 (2) и через 11 (3) лет работы. Полученные из этих функций зависимости  от времени показаны на рис. 8.32, б. Полученная аналогичным образом зависимость
от времени показаны на рис. 8.32, б. Полученная аналогичным образом зависимость  от времени приредена на рис. 8.32, б пунктиром. Обратим внимание на то, что после 6—8 лет работы у диодов данного типа начинается существенный рост величин
от времени приредена на рис. 8.32, б пунктиром. Обратим внимание на то, что после 6—8 лет работы у диодов данного типа начинается существенный рост величин  , при этом значения
, при этом значения  могут и не выходить за пределы норм ТУ, так как в последних устанавливается ограничение лишь по току горячего состояния, который на много порядков больше исходных значений
могут и не выходить за пределы норм ТУ, так как в последних устанавливается ограничение лишь по току горячего состояния, который на много порядков больше исходных значений  при комнатной температуре (в данном конкретном случае
при комнатной температуре (в данном конкретном случае  ). Возрастание
). Возрастание  в десятки и сотни раз (рис. 8.32) говорит о деградации прибора, поэтому при испытаниях на надежность необходимо не только контролировать токи закрытого состояния при
в десятки и сотни раз (рис. 8.32) говорит о деградации прибора, поэтому при испытаниях на надежность необходимо не только контролировать токи закрытого состояния при  , но и устанавливать критические значения для обратного тока (тока утечки) при комнатной температуре.
, но и устанавливать критические значения для обратного тока (тока утечки) при комнатной температуре.
Покажем, как по кривым типа приведенных на рис. 8.32 определить у - процентный ресурс  СПП, если заданы критические значения
СПП, если заданы критические значения  и
и  . Пусть
. Пусть  и надо найти
и надо найти  . Проведем горизонталь на рис. 8.32, а на уровне 0,8 (пунктир) и точки ее пересечения с прямыми 1—3 (точки а — в наносим на рис. 8.32, б (квадратики).
. Проведем горизонталь на рис. 8.32, а на уровне 0,8 (пунктир) и точки ее пересечения с прямыми 1—3 (точки а — в наносим на рис. 8.32, б (квадратики).

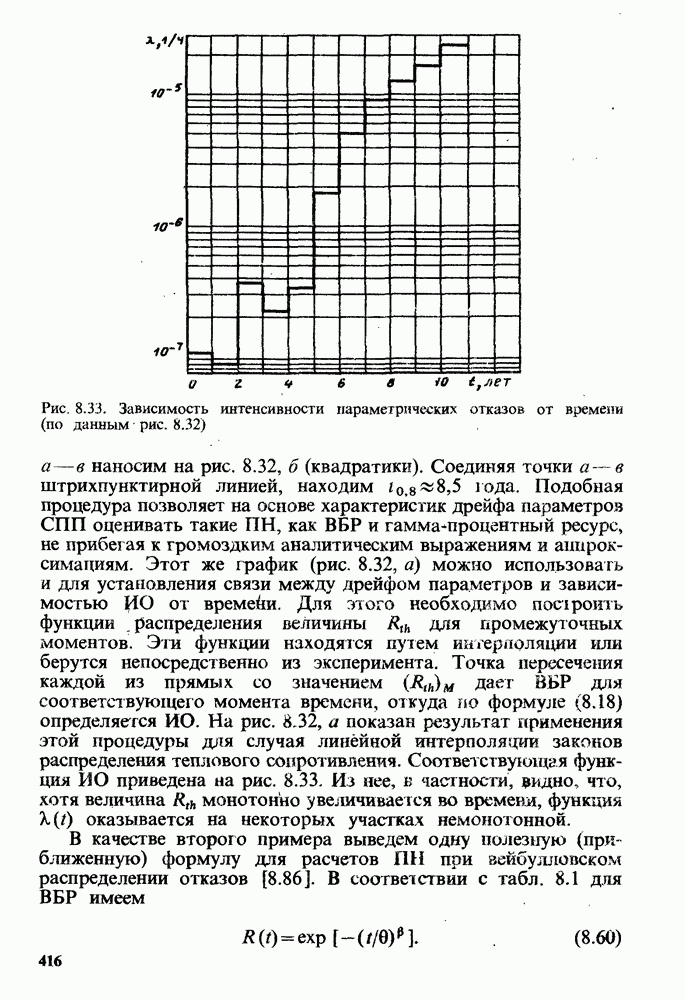
Рис. 8.33. Зависимость интенсивности параметрических отказов от времени (по данным рис. 8.32)
Соединяя точки а — в штрихпунктирной линией, находим  года. Подобная процедура позволяет на основе характеристик дрейфа параметров СПП оценивать такие ПН, как ВБР и гамма - процентный ресурс, не прибегая к громоздким аналитическим выражениям и аппроксимациям. Этот же график (рис. 8.32, а) можно использовать и для установления связи между дрейфом параметров и зависимостью ИО от времени. Для этого необходимо построить функции распределения величины
года. Подобная процедура позволяет на основе характеристик дрейфа параметров СПП оценивать такие ПН, как ВБР и гамма - процентный ресурс, не прибегая к громоздким аналитическим выражениям и аппроксимациям. Этот же график (рис. 8.32, а) можно использовать и для установления связи между дрейфом параметров и зависимостью ИО от времени. Для этого необходимо построить функции распределения величины  для промежуточных моментов. Эти функции находятся путем интерполяции или берутся непосредственно из эксперимента. Точка пересечения каждой из прямых со значением
для промежуточных моментов. Эти функции находятся путем интерполяции или берутся непосредственно из эксперимента. Точка пересечения каждой из прямых со значением  дает ВБР для соответствуюхцего момента времени, откуда по формуле (8.18) определяется ИО. На рис. 8.32, а показан результат применения этой процедуры для случая линейной интерполяции законов распределения теплового сопротивления. Соответствующая функция ИО приведена на рис. 8.33. Из нее, в частности, видно, что, хотя величина
дает ВБР для соответствуюхцего момента времени, откуда по формуле (8.18) определяется ИО. На рис. 8.32, а показан результат применения этой процедуры для случая линейной интерполяции законов распределения теплового сопротивления. Соответствующая функция ИО приведена на рис. 8.33. Из нее, в частности, видно, что, хотя величина  монотонно увеличивается во времени, функция
монотонно увеличивается во времени, функция  оказывается на некоторых участках немонотонной.
оказывается на некоторых участках немонотонной.
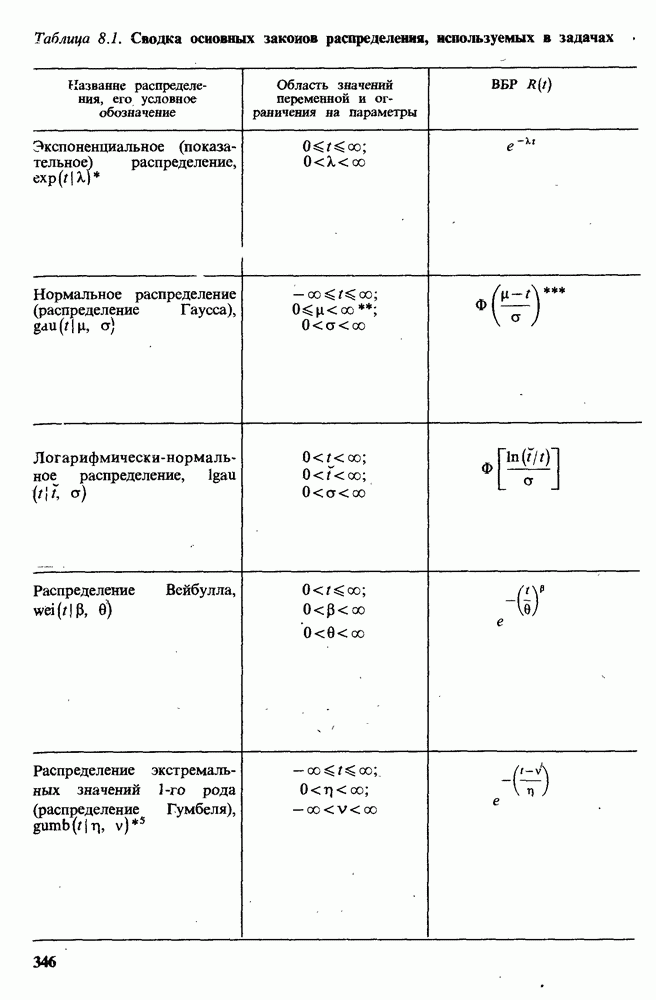
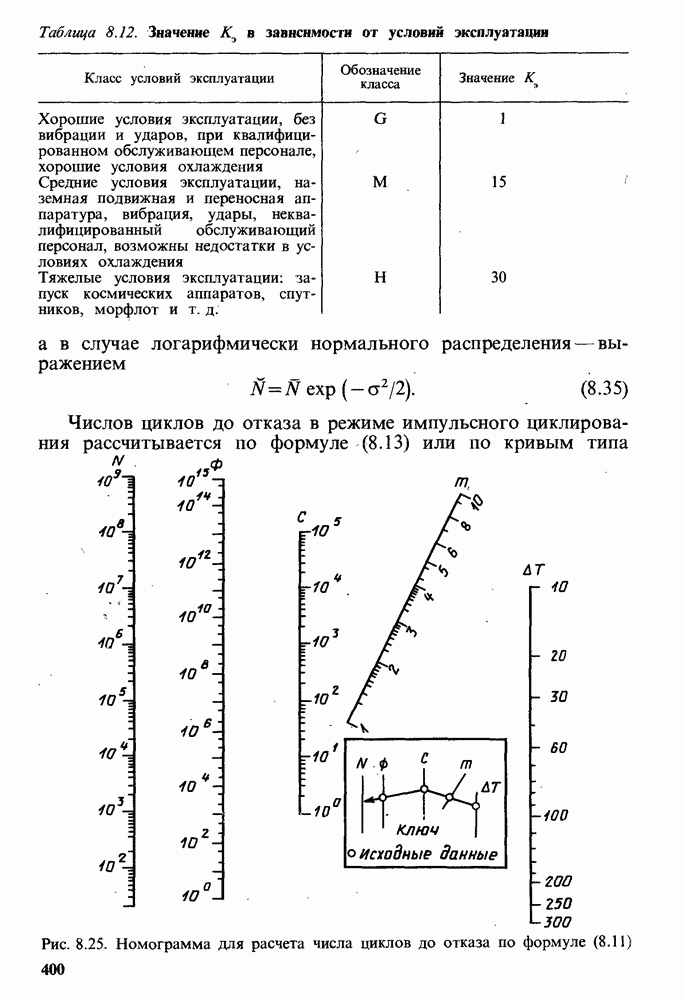
В качестве второго примера выведем одну полезную (приближенную) формулу для расчетов ПН при вейбулловском распределении отказов [8.86]. В соответствии с табл. 8.1 для ВБР имеем

Если рассматриваются времена t, много меньшие  (т. е. пока процент отказов еще мал), то вместо (8.86) можно записать
(т. е. пока процент отказов еще мал), то вместо (8.86) можно записать

Логарифмируя (8.86) и учитывая, что  при
при  , имеем
, имеем

Положим, что нам известно значение ВБР в одном режиме и необходимо рассчитать ВБР в другом. Это означает, что нам известно значение  и надо найти
и надо найти  при условии, что отказы распределены по вейбулловскому закону и
при условии, что отказы распределены по вейбулловскому закону и  . Тогда
. Тогда  малых вероятностей отказа) из (8.62) получаем
малых вероятностей отказа) из (8.62) получаем

Если теперь принять, что для этих двух режимов применим закон Аррениуса, то можно в (8.63) заменить отношение  через экспоненциальный множитель аррениусовского типа. Для этого надо учесть следующее обстоятельство. В § 8.2 и 8.5 отмечалось, что зависимости типа
через экспоненциальный множитель аррениусовского типа. Для этого надо учесть следующее обстоятельство. В § 8.2 и 8.5 отмечалось, что зависимости типа  обычно относятся к экспоненциальному закону распределения отказов
обычно относятся к экспоненциальному закону распределения отказов  ). Однако на практике закон Аррениуса применяют и при других законах распределения. Однако здесь возникает проблема: к какому моменту относить температурный множитель? В самом деле, ведь
). Однако на практике закон Аррениуса применяют и при других законах распределения. Однако здесь возникает проблема: к какому моменту относить температурный множитель? В самом деле, ведь  не может быть равно
не может быть равно  Более того, даже если
Более того, даже если  , то все равно
, то все равно  произвольного момента
произвольного момента

Оказывается, что в подобных случаях соотношение Аррениуса следует относить либо к средней или медианной наработке до отказа, либо к параметру масштаба, либо к какому-то фиксированному квантилю ВБР (это вытекает из принципа равной вероятности). Следовательно,

В соответствие с (8.29) обозначим величину

как  . Тогда
. Тогда

Подставив (8.65) в (8.63), получим формулу

которая может быть использована для пересчета ВБР от одних режима и момента к другим. Рассмотрим пример использования (8.66).
Пример 8.8. Пусть в технических условиях на прибор указано, что ВБР на  равна 0,995. Требуется найти ВБР приборов данного типа при температуре
равна 0,995. Требуется найти ВБР приборов данного типа при температуре  перехода 90° С в момент
перехода 90° С в момент  . Известно также, что закон распределения отказов вейбулловский и значение
. Известно также, что закон распределения отказов вейбулловский и значение  .
.
В связи с тем что в условии не указано, к какой температуре относится значение ВБР  то будем считать, что оно соответствует максимально допустимой температуре структуры. Пусть
то будем считать, что оно соответствует максимально допустимой температуре структуры. Пусть  для данного типа приборов равна 125° С. Тогда
для данного типа приборов равна 125° С. Тогда  Следовательно, надо определить
Следовательно, надо определить  Для этого надо сначала определить величину
Для этого надо сначала определить величину  . Так как в условиях примера ничего не сказано об
. Так как в условиях примера ничего не сказано об  , то берем значение
, то берем значение  эВ. По рис. 8.23 или 8.22 находим
эВ. По рис. 8.23 или 8.22 находим  . Теперь имеем в соответствии с (8.66)
. Теперь имеем в соответствии с (8.66)

откуда  . Так как это соответствует всего лишь 5% отказов, то условия, при которых выведено соотношение (8.66), соблюдены.
. Так как это соответствует всего лишь 5% отказов, то условия, при которых выведено соотношение (8.66), соблюдены.
Следующий практический совет относится к вопросам планирования испытаний. Предположим, что необходимо, хотя бы грубо, оценить объем испытаний на надежность, не имея никаких таблиц, справочников и т. п. Тогда следует перевести требуемый ПН в значение ВБР. (Если задана ВБР, то ничего переводить не надо.) Если задана ИО, то

Найдя значение R, вычислим вероятность отказа  :
:

Полученное значение F записываем в виде дроби  . Эта дробь означает, что из
. Эта дробь означает, что из  приборов в среднем откажут А штук. Находим величину, обратную
приборов в среднем откажут А штук. Находим величину, обратную  . Эта величина и будет давать примерный минимальный объем испытаний, необходимых для подтверждения
. Эта величина и будет давать примерный минимальный объем испытаний, необходимых для подтверждения  .
.
Пример 8.9. Определим примерный объем испытаний, требуемый для подтверждения следующих ПН: 
Решение, a) t — медианная наработка, т. е.  , т. е. надо два прибора испытывать в течение
, т. е. надо два прибора испытывать в течение  .
.
б)  . Пусть возможная длительность испытаний составляет
. Пусть возможная длительность испытаний составляет  . Тогда
. Тогда  .
.
Соответственно  Следовательно,
Следовательно,  .
.
в)  . Следовательно,
. Следовательно,  .
.
Можно убедиться в том, что для определенных параметров планов испытаний планирование по точным формулам дает в случае  , в случае
, в случае  и да 350 и в случае
и да 350 и в случае  да 60.
да 60.
В заключение рассмотрим ряд публикаций, содержащих методические погрешности в расчетах ПН СПП [8.88].
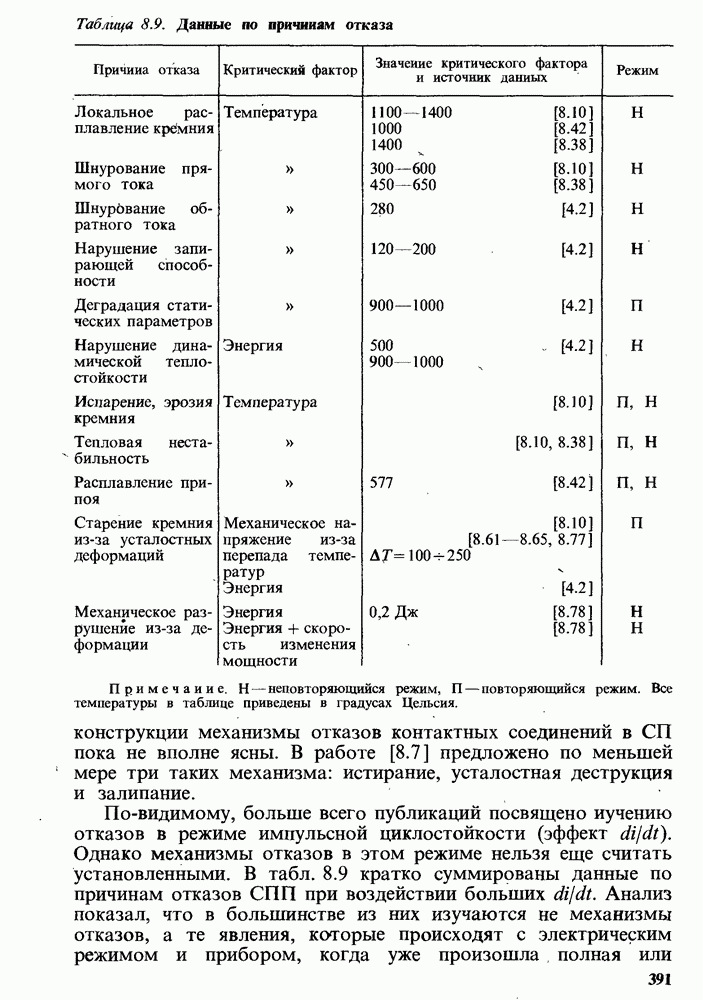
В [8.89] приведены данные о том, что СПП имеют два вида отказов: пробои (замыкания), составляющие 80% повреждений, и обрывы, на долю которых приходится около 20% отказов. Отсюда автор делает вывод, что ИО СПП есть сумма интенсивностей замыканий  и обрывов
и обрывов  , причем
, причем  , где
, где  — некоторая базовая (расчетная) ИО. Дальнейшие расчеты в [8.89] построены на соотношении
— некоторая базовая (расчетная) ИО. Дальнейшие расчеты в [8.89] построены на соотношении

где  - полная ИО силового ПП.
- полная ИО силового ПП.
Между тем соотношение (8.67) неверно, так как ИО является условной, а не безусловной вероятностью. Поэтому правильное соотношение между  может быть найдено следующим образом. В связи с тем что вероятность замыкания составляет 80%, вероятность безотказной работы (ВБР) за фиксированное время t для замыканий
может быть найдено следующим образом. В связи с тем что вероятность замыкания составляет 80%, вероятность безотказной работы (ВБР) за фиксированное время t для замыканий  составляет 0,2. Соответственно ВБР для обрывов
составляет 0,2. Соответственно ВБР для обрывов  за то же время равна 0,8. Приняв экспоненциальный закон распределения наработки до отказа (см. табл. 8.1), имеем соотношения
за то же время равна 0,8. Приняв экспоненциальный закон распределения наработки до отказа (см. табл. 8.1), имеем соотношения

Из (8.68) можно получить, что  (а не 4, как в [8.89]) и вместо формулы (8.67) запишем
(а не 4, как в [8.89]) и вместо формулы (8.67) запишем

В работе [8.90] предлагается модель надежности для двухступенчатых испытаний, при которых одну и ту же партию изделий в интервале времени  испытывают при температуре
испытывают при температуре  , а в интервале
, а в интервале  — при температуре
— при температуре  . Предполагается также, что справедлива экспоненциальная модель надежности и
. Предполагается также, что справедлива экспоненциальная модель надежности и  . Предложенное авторами решение в интервале
. Предложенное авторами решение в интервале  совпадает с результатом, вытекающим из принципа Седякина [8.83]. Однако распространение его на интервал
совпадает с результатом, вытекающим из принципа Седякина [8.83]. Однако распространение его на интервал  , что сделано в названной работе [см. формулу (6) и текст пёред ней], неправомерно. Это видно хотя бы из того, что ВБР при
, что сделано в названной работе [см. формулу (6) и текст пёред ней], неправомерно. Это видно хотя бы из того, что ВБР при  по второй из формул (6) в [8.90] равна константе а, которая не равна 1. В результате этой неточности окончательная формула модели надежности для двухступенчатых испытаний, имеющая в [8.90] вид
по второй из формул (6) в [8.90] равна константе а, которая не равна 1. В результате этой неточности окончательная формула модели надежности для двухступенчатых испытаний, имеющая в [8.90] вид

тоже неверна, так как она не учитывает наличие двух ступеней с разными значениями ИО и противоречит всему предшествующему рассмотрению.
В работе [8.45] определяется зависимость числа циклов до отказа внешних воздействий и параметров приборов. Определив зависимости циклостойкости сначала от фактора  , а потом — от фактора
, а потом — от фактора  , авторы далее утверждают следующее: «Поскольку величины и
, авторы далее утверждают следующее: «Поскольку величины и  являются событиями независимыми, то вероятное число воздействий до отказа в зависимости от значений
являются событиями независимыми, то вероятное число воздействий до отказа в зависимости от значений  и
и  определяется как произведение величин
определяется как произведение величин  :
:

где  — есть импульсное сопротивление тиристора, измеренное в некотором режиме». Данное утверждение является ошибочным, так как из независимости событий отказ под действием заданного
— есть импульсное сопротивление тиристора, измеренное в некотором режиме». Данное утверждение является ошибочным, так как из независимости событий отказ под действием заданного  при
при  и отказ приборов, ймеющих заданное значение
и отказ приборов, ймеющих заданное значение  при
при  , не вытекает необходимость перемножать
, не вытекает необходимость перемножать  и
и  . Перемножать надо вероятности соответствующих событий, которые должны быть предварительно введены. Следовательно, готовую формулу (11) работы [8.45] нельзя считать обоснованной и применять при прогнозе циклостойкости силовых тиристоров.
. Перемножать надо вероятности соответствующих событий, которые должны быть предварительно введены. Следовательно, готовую формулу (11) работы [8.45] нельзя считать обоснованной и применять при прогнозе циклостойкости силовых тиристоров.
В  автор исследовал вопрос о том, какой из законов распределения (вейбулловский или логарифмически-нормальный) предпочтителен для расчетов ВБР некоторой технической системы, состоящей из СПП. При этом сравнение проводится при условии равенства двух первых моментов распределений
автор исследовал вопрос о том, какой из законов распределения (вейбулловский или логарифмически-нормальный) предпочтителен для расчетов ВБР некоторой технической системы, состоящей из СПП. При этом сравнение проводится при условии равенства двух первых моментов распределений  .
.
Однако из приведенных в [8.91] исходных данных следует, что для  - распределения параметр формы был больше единицы (1.79), т. е. ИО в этом случае была монотонно возрастающей функцией времени (см. табл. 8.1). В то же время ИО
- распределения параметр формы был больше единицы (1.79), т. е. ИО в этом случае была монотонно возрастающей функцией времени (см. табл. 8.1). В то же время ИО  - распределения есть немонотонная функция, которая сначала растет, а затем, пройдя максимум, падает. Следовательно, выводы, полученные в [8.91], относятся к распределениям, описывающим в принципе различное поведение элементов во времени. Это в свою очередь вызывает вопрос: а стоит ли сравнивать друг с другом такие расчеты, когда надежность элементов в одном случае со временем повышается, а в другом — понижается?
- распределения есть немонотонная функция, которая сначала растет, а затем, пройдя максимум, падает. Следовательно, выводы, полученные в [8.91], относятся к распределениям, описывающим в принципе различное поведение элементов во времени. Это в свою очередь вызывает вопрос: а стоит ли сравнивать друг с другом такие расчеты, когда надежность элементов в одном случае со временем повышается, а в другом — понижается?
В работе [8.92] предлагается считать, что ВБР изделий есть функция их качества  :
:

где  - ВБР при заданном качестве q. Далее, взяв для функций
- ВБР при заданном качестве q. Далее, взяв для функций  экспоненциальное распределение, автор с помощью преобразования Эфроса получил, что
экспоненциальное распределение, автор с помощью преобразования Эфроса получил, что

где 10 — функция Бесселя первого рода нулевого порядка  и b — параметры функций
и b — параметры функций  . Использование (8.69) для ВБР вызывает, как минимум, два возражения. Во-первых, функция
. Использование (8.69) для ВБР вызывает, как минимум, два возражения. Во-первых, функция  при
при  становится отрицательной, т. е.
становится отрицательной, т. е.  должно быть меньше 2,4, а, следовательно,
должно быть меньше 2,4, а, следовательно,  . Во-вторых, ИО, отвечающая формуле (8.69), оказывается возрастающей функцией, стремящейся к бесконечности при
. Во-вторых, ИО, отвечающая формуле (8.69), оказывается возрастающей функцией, стремящейся к бесконечности при  . Это означает, что ИО изделий, имеющих одинаковое качество — быстро возрастающая функция времени. Это не согласуется с имеющимися данными по эксплуатационной надежности, согласно которой для СПП в основном наблюдается постоянная или уменьшающаяся ИО.
. Это означает, что ИО изделий, имеющих одинаковое качество — быстро возрастающая функция времени. Это не согласуется с имеющимися данными по эксплуатационной надежности, согласно которой для СПП в основном наблюдается постоянная или уменьшающаяся ИО.
В работе [8.32] предложен метод ускоренной оценки надежности ПП, основанной на объединении испытаний на долговечность при постоянной температуре с испытаниями на термоциклостойкость. Предложенная автором [8.32] расчетная модель основана на следующих соотношениях. Распределение отказов в режиме температурного воздействия считается экспоненциальным, причем ИО зависит от температуры по закону Аррениуса. Это означает, что средняя наработка до отказа

(в [8.32] автор все время использует обозначение MTBF — среднее время между отказами, но так как ПП являются невосстанавливаемыми элементами, то точнее говорить о MTTF, а не о MTBF, что для дальнейшего рассуждения непринципиально).
Распределение отказов при термоциклировании считается нормальным  , а среднее число циклов до отказа (N) экспоненциально зависит от перепада температуры за цикл. Далее автор [8.32] вводйт величину
, а среднее число циклов до отказа (N) экспоненциально зависит от перепада температуры за цикл. Далее автор [8.32] вводйт величину

после чего основное уравнение предлагаемой модели надежности имеет вид

где  - среднее время до отказа в условиях последовательных испытаний на термоциклирование и долговечность;
- среднее время до отказа в условиях последовательных испытаний на термоциклирование и долговечность;  - тот же параметр, но при отсутствии испытаний на циклостойкость; n — число циклов при испытаниях на циклостойкость. Смысл формулы (8.72) сводится к тому, что испытания на термоциклостойкость вырабатывают ресурс прибора, уменьшая время до его отказа. Здесь хотелось бы обратить внимание на следующие обстоятельства.
- тот же параметр, но при отсутствии испытаний на циклостойкость; n — число циклов при испытаниях на циклостойкость. Смысл формулы (8.72) сводится к тому, что испытания на термоциклостойкость вырабатывают ресурс прибора, уменьшая время до его отказа. Здесь хотелось бы обратить внимание на следующие обстоятельства. 
Во-первых, из (8.7), (8.72) видно, что  если
если  . Это означает, что в (8.72) неявно заложено предположение о равенстве числа отказавших приборов за время
. Это означает, что в (8.72) неявно заложено предположение о равенстве числа отказавших приборов за время  и за N температурных циклов. Между тем это не так, из-за того что за время
и за N температурных циклов. Между тем это не так, из-за того что за время  отказывает
отказывает  приборов, а N (как следует из текста статьи) соответствует отказу 50% приборов.
приборов, а N (как следует из текста статьи) соответствует отказу 50% приборов.
Во вторых, обозначив  , имеем
, имеем

откуда

В то же время есть все основания считать, что при испытаниях на долговечность и при термоциклировании работают различные механизмы отказов, так как в одном случае мы ускоряем различные физико-химические процессы в объеме и на поверхности ПП, а в другом усталостные явления на контакте разнородных материалов. При этом ИО в комбинации из двух вышеописанных режимов должна быть равна сумме соответствующих ИО, т. е.

где  — ИО в режиме термоциклирования.
— ИО в режиме термоциклирования.
Сравнивая (8.74) с (8173), видим, что

Однако (8.75) противоречит тому условию, что отказы приборов при термоциклировании распределены нормально. И наоборот. Если известен закон распределения отказов, мы знаем функцию  , и тогда из (8.74) можно вычислить полную ИО в данном комбинированном режиме и оценить MTTF. При этом выражения (8.72) мы, естественно, не получим. Стоит отметить, что по данным автора среднее число отказов при испытаниях на долговечность равно 2,8. В то же время из рис.
, и тогда из (8.74) можно вычислить полную ИО в данном комбинированном режиме и оценить MTTF. При этом выражения (8.72) мы, естественно, не получим. Стоит отметить, что по данным автора среднее число отказов при испытаниях на долговечность равно 2,8. В то же время из рис.  и ВБР за
и ВБР за  таким образом вероятность отказа приблизительно равна 0,06, т. е. около трех приборов на партию в
таким образом вероятность отказа приблизительно равна 0,06, т. е. около трех приборов на партию в  . Это означает, что данные испытания, по-видимому, независимы друг от друга.
. Это означает, что данные испытания, по-видимому, независимы друг от друга.
В [8.93] предпринята попытка рассчитать зависимость интенсивности параметрических отказов от времени для силовых ПП. Идея работы состоит в следующем: по мере циклирования растет тепловое сопротивление приборов, что приводит к росту температуры структуры этих приборов  и отказу прибора при
и отказу прибора при  . Однако, хотя авторы утверждают, что интересующие их режимы эксплуатации являются циклическими, они нигде не используют зависимость числа циклов до отказа
. Однако, хотя авторы утверждают, что интересующие их режимы эксплуатации являются циклическими, они нигде не используют зависимость числа циклов до отказа  от
от  и потому возникает вопрос: а не может ли так оказаться, что величина N с учетом длительности цикла и его частоты ограничит жизнь прибора гораздо раньше, чем его средняя температура превысит
и потому возникает вопрос: а не может ли так оказаться, что величина N с учетом длительности цикла и его частоты ограничит жизнь прибора гораздо раньше, чем его средняя температура превысит  . К тому же из рис. 3 [8.93] следует, что при
. К тому же из рис. 3 [8.93] следует, что при  (что соответствует техническим условиям), ИО равна нулю вплоть до
(что соответствует техническим условиям), ИО равна нулю вплоть до  (это противоречит данным по эксплуатационной надежности [8.8, 8.87]).
(это противоречит данным по эксплуатационной надежности [8.8, 8.87]).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ПРИНЦИП ДЕЙСТВИЯ И ОСНОВНЫЕ СВОЙСТВА ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ ДИОДОВ И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
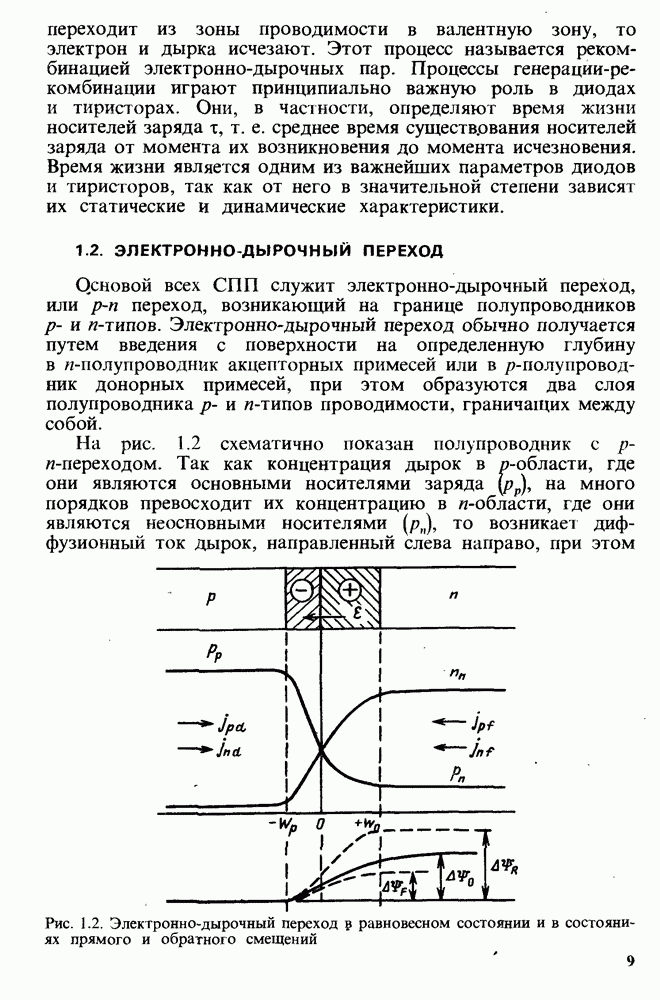
- 1.2. ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД
- 1.3.СИЛОВОЙ ПОЛУПРОВОДНИКОВЫЙ ВЫПРЯМИТЕЛЬНЫЙ ДИОД
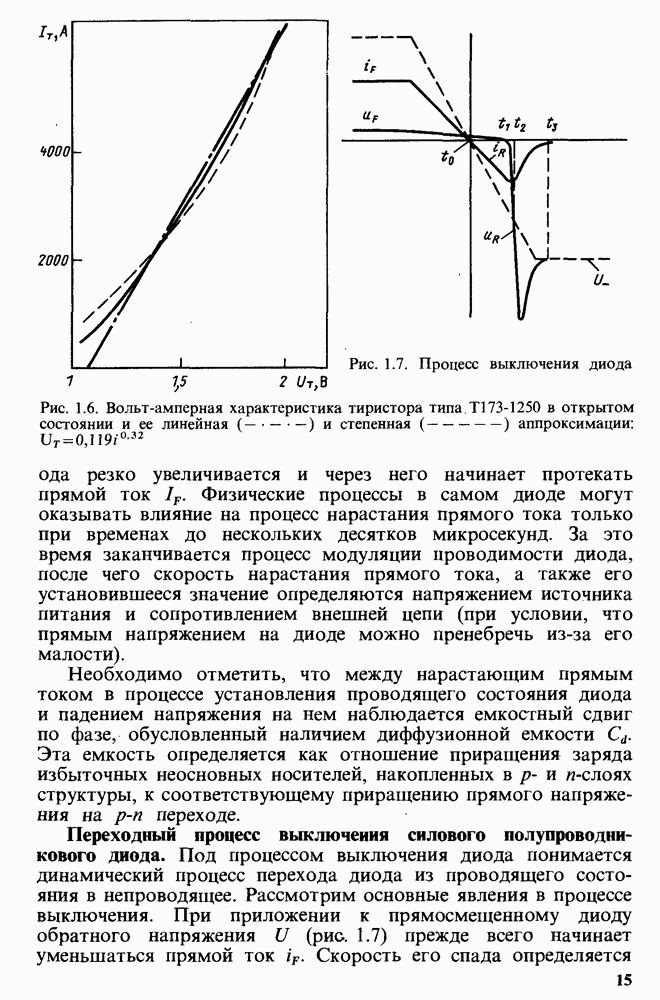
- Проводящее состояние силового диода.
- Переходный процесс включения силового полупроводникового диода.
- Переходный процесс выключения силового полупроводникового диода.
- 1.4. СИЛОВОЙ ТРИОДНЫЙ ТИРИСТОР, НЕ ПРОВОДЯЩИЙ В ОБРАТНОМ НАПРАВЛЕНИИ
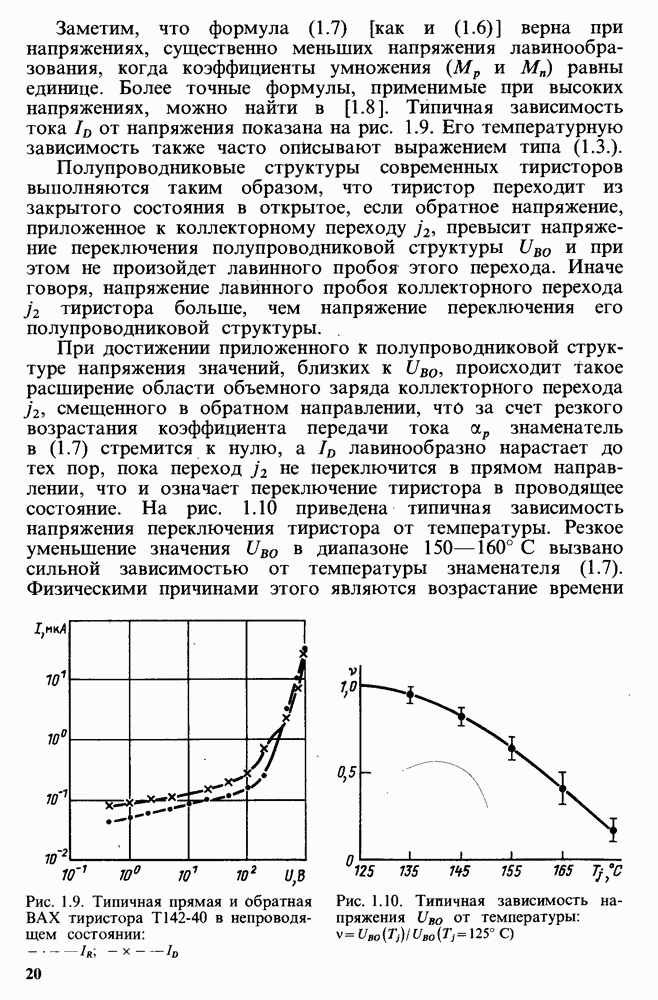
- Обратное непроводящее состояние тиристора.
- Закрытое состояние тиристора.
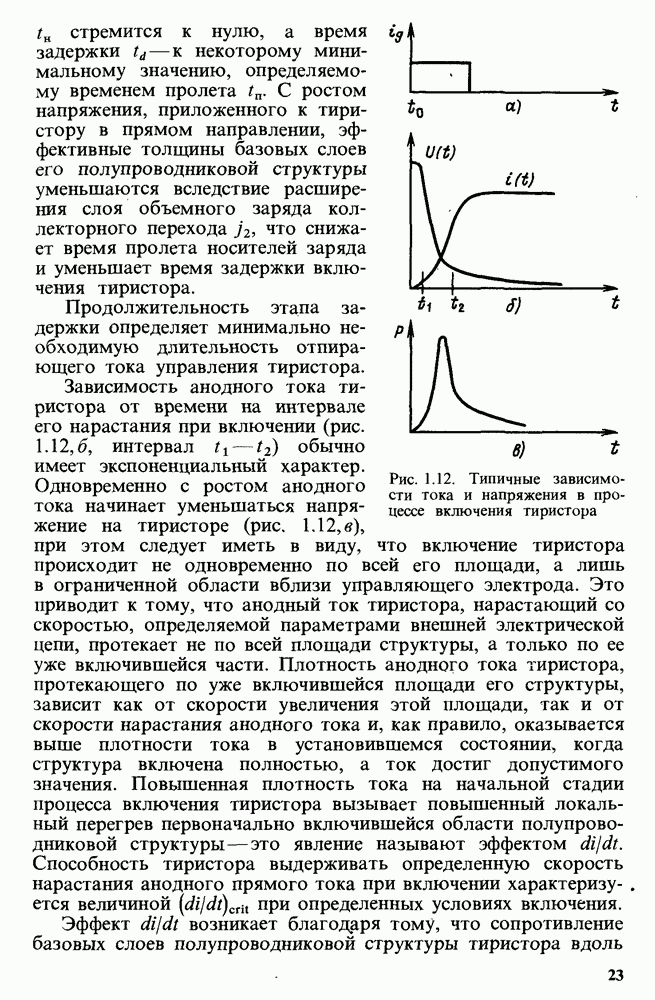
- Процесс включения тиристора. Эффект di/dt. Открытое состояние тиристора.
- Процесс выключения тиристора. Эффект dU/dt.
- Глава 2. ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- 2.2. ОСНОВНЫЕ ПАРАМЕТРЫ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Основные электрические параметры силовых тиристоров.
- 2.3. ОСНОВНЫЕ ТЕПЛОВЫЕ ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ДИОДОВ И ТИРИСТОРОВ
- 2.4. КЛАССИФИКАЦИЯ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ
- Классификация силовых полупроводниковых диодов и тиристоров по конструкции.
- 2.5. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ВЫПРЯМИТЕЛЬНЫХ диодов И ТРИОДНЫХ ТИРИСТОРОВ, НЕ ПРОВОДЯЩИХ В ОБРАТНОМ НАПРАВЛЕНИИ
- Условное обозначение типоисполнения диодов и тиристоров.
- 2.6. ОСОБЕННОСТИ СИЛОВЫХ ДИОДОВ И ТИРИСТОРОВ КАК ЭЛЕКТРОТЕХНИЧЕСКИХ ИЗДЕЛИЙ, КОМПЛЕКТУЮЩИХ СХЕМУ СИЛОВОГО ПОЛУПРОВОДНИКОВОГО ПРЕОБРАЗОВАТЕЛЬНОГО УСТРОЙСТВА
- Глава 3. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ И УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ
- 3.1. РЕЖИМЫ И УСЛОВИЯ РАБОТЫ ДИОДОВ И ТИРИСТОРОВ
- 3.2. КЛАССИФИКАЦИЯ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 3.3. ОСОБЕННОСТИ РАСЧЕТА И ВЫБОРА ДИОДОВ И ТИРИСТОРОВ
- Рекомендуемая нагрузка диодов и тиристоров.
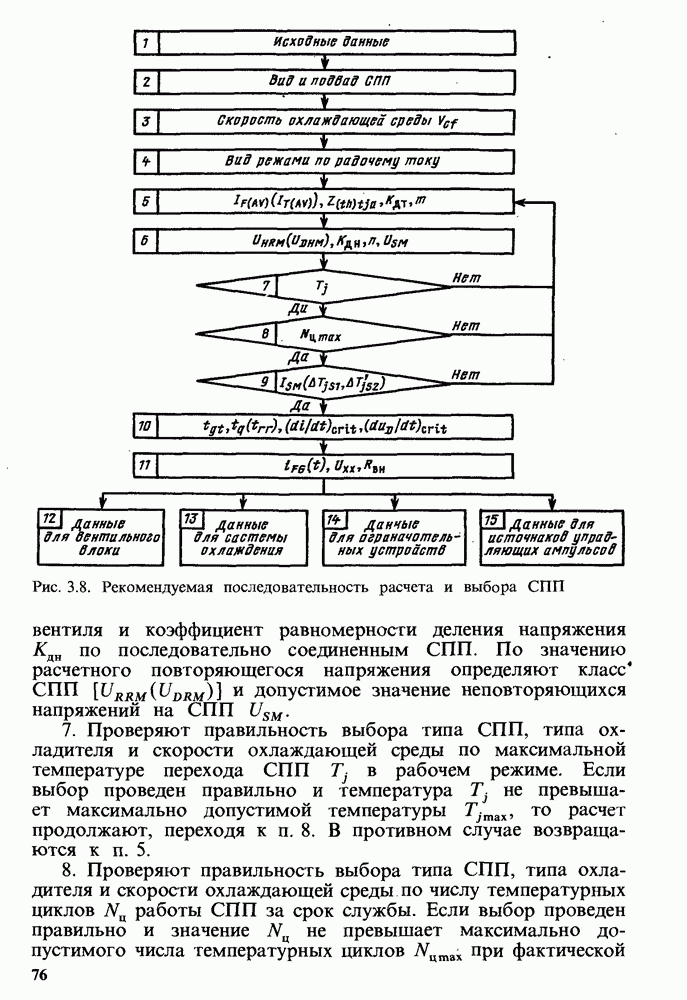
- Исходные данные и последовательность расчета.
- Глава 4. РАСЧЕТ И ВЫБОР ДИОДОВ И ТИРИСТОРОВ. УСЛОВИЙ ИХ ОХЛАЖДЕНИЯ И РАСЧЕТ СИСТЕМЫ УПРАВЛЕНИЯ ТИРИСТОРАМИ
- 4.1. РАСЧЕТ И ВЫБОР ТИПА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО РАБОЧЕМУ ТОКУ
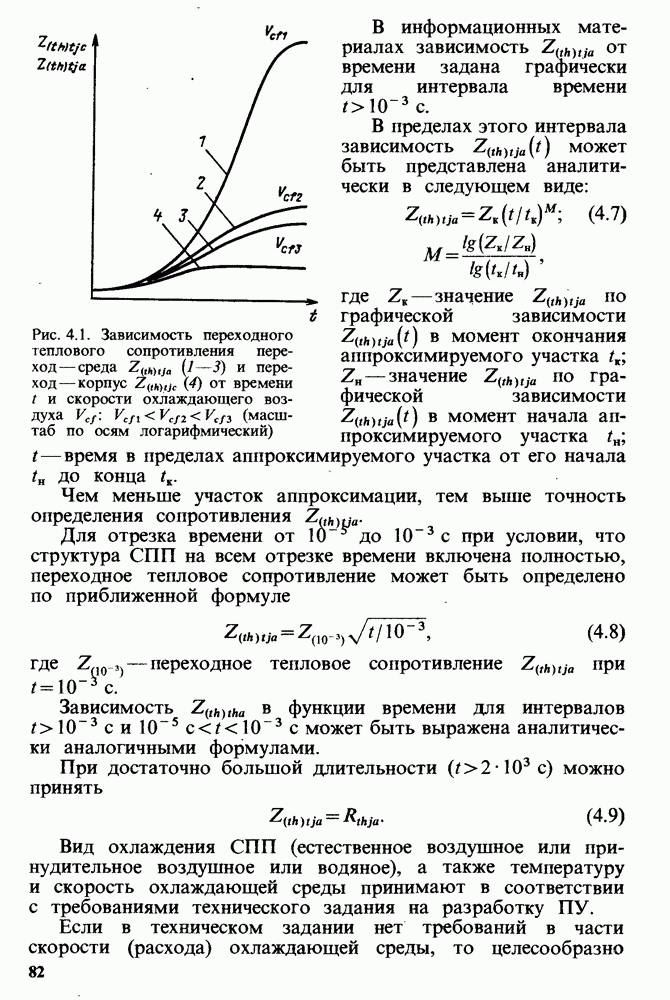
- Тепловые параметры СПП и выбор условий охлаждения.
- Определение режима нагрузки СПП рабочим током.
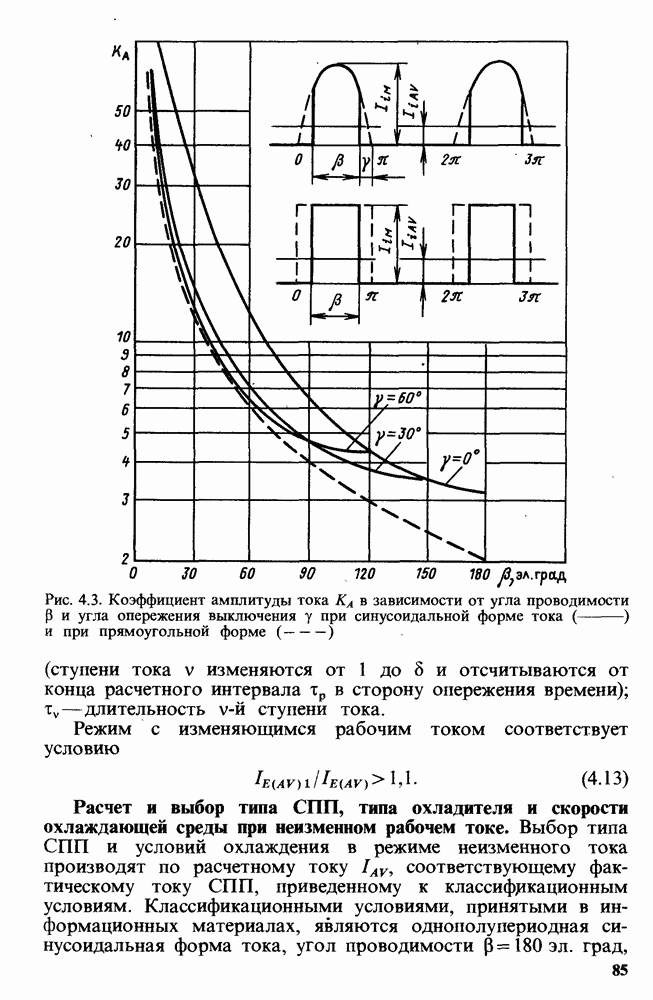
- Расчет и выбор типа СПП, типа охладителя и скорости охлаждающей среды при неизменном рабочем токе.
- Расчет и выбор типа прибора, типа охладителя и скорости охлаждающей среды при изменяющемся рабочем токе.
- 4.2. ВЫБОР КЛАССА СПП ПО РАБОЧЕМУ НАПРЯЖЕНИЮ
- Определение класса СПП.
- 4.3. ПРОВЕРКА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ ПО ТЕМПЕРАТУРЕ НАГРЕВА РАБОЧИМ ТОКОМ
- Расчет температур перегрева перехода СПП в рабочем режиме.
- 4.4. ПРОВЕРКА СПП ПО АВАРИЙНОМУ ТОКУ
- Проверка СПП при синусоидальной форме импульса аварийного тока.
- Проверка СПП при несинусоидальной форме аварийного тока.
- 4.5. ВЫБОР КОММУТАЦИОННЫХ ПАРАМЕТРОВ СПП
- Время выключения.
- Критическая скорость нарастания тока при включении.
- Критическая скорость нарастания напряжения в закрытом состоянии СПП.
- Время обратного восстановления.
- 4.6. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ УПРАВЛЯЮЩИХ ИМПУЛЬСОВ И СХЕМЫ УПРАВЛЕНИЯ ТИРИСТОРОМ
- Выбор параметров управляющих импульсов.
- Расчет мощности потерь на управляющем электроде.
- 4.7. ПРИМЕР РАСЧЕТА И ВЫБОРА СПП И УСЛОВИЙ ЕГО ОХЛАЖДЕНИЯ
- Расчет и выбор типа СПП и условий его охлаждения но рабочему току.
- Проверка выбранного СПП и условий охлаждения по температуре нагрева перехода рабочим током.
- Проверка СПП по аварийному току.
- Выбор коммутационных параметров СПП.
- Определение параметров управляющих импульсов и источника управления.
- Глава 5. МЕТОДЫ И СРЕДСТВА ОГРАНИЧЕНИЯ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ ПО ТОКУ И НАПРЯЖЕНИЮ В НОРМАЛЬНЫХ И АВАРИЙНЫХ РЕЖИМАХ РАБОТЫ
- 5.1. ТРЕБОВАНИЯ К МЕТОДАМ И СРЕДСТВАМ ОГРАНИЧЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ
- 5.2. ВЫБОР ВИДА И РАСЧЕТ ЭЛЕМЕНТОВ ДЛЯ ОГРАНИЧЕНИЯ АВАРИЙНОГО ТОКА
- 5.3. ОГРАНИЧЕНИЕ КОММУТАЦИОННЫХ ПЕРЕНАПРЯЖЕНИЙ НА СПП
- Получение исходных данных для выбора схем и расчета параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Расчет параметров элементов устройств ограничения коммутационных перенапряжений, создаваемых СПП.
- Воздействие перенапряжений, возникающих при запирании СПП, на другие тиристоры преобразовательных схем.
- 5.4. ОГРАНИЧЕНИЕ СХЕМНЫХ И СЕТЕВЫХ ПЕРЕНАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- Схемные перенапряжения
- Уменьшение уровня переиапряжения на вентилях
- Схемные перенапряжения эпизодического характера
- Расчет параметров устройства для ограничения сетевых и схемных перенапряжений.
- Расчет ограничительных устройств для подавления схемных перенапряжений.
- Ограничение скорости нарастания и спадания тока СПП.
- Некоторые явления, связанные с процессом отпирания тиристоров.
- Расчет коммутационных потерь в СПП.
- 5.5. ГРУППОВОЕ СОЕДИНЕНИЕ СПП
- Последовательное соединение СПП
- Групповое соединение СПП
- 5.6. НЕКОТОРЫЕ СХЕМЫ ПОДКЛЮЧЕНИЯ ОГРАНИЧИТЕЛЬНЫХ УСТРОЙСТВ
- Глава 6. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ В СХЕМАХ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТАНОВОК
- 6.1. ТРЕБОВАНИЯ К МЕТОДАМ ИЗМЕРЕНИЙ
- 6.2. ИЗМЕРЕНИЕ СРЕДНЕГО И ЭФФЕКТИВНОГО ТОКА, ПРОХОДЯЩЕГО ЧЕРЕЗ СПП, И МОЩНОСТИ ПОТЕРЬ В СТАЦИОНАРНОМ РЕЖИМЕ
- 6.3. ИЗМЕРЕНИЕ МГНОВЕННЫХ ЗНАЧЕНИЙ ТОКА В ПРОЦЕССЕ ВКЛЮЧЕНИЯ И ВЫКЛЮЧЕНИЯ СПП
- 6.4. ИЗМЕРЕНИЕ НАПРЯЖЕНИЙ, ВОЗДЕЙСТВУЮЩИХ НА СПП
- 6.5. КОНТРОЛЬ ПАРАМЕТРОВ СИГНАЛОВ УПРАВЛЕНИЯ ТИРИСТОРОВ И ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ СПП
- 6.6. СОВРЕМЕННЫЕ МЕТОДЫ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ДИОДЫ И ТИРИСТОРЫ
- 6.7. ПОГРЕШНОСТИ ИЗМЕРЕНИЯ БЫСТРОМЕНЯЮЩИХСЯ ТОКОВ С ПОМОЩЬЮ БЕЗЫНДУКТИВНЫХ (МАЛОИНДУКТИВНЫХ) ШУНТОВ
- Глава 7. ОХЛАЖДЕНИЕ ДИОДОВ И ТИРИСТОРОВ ПРЕОБРАЗОВАТЕЛЬНЫХ УСТРОЙСТВ
- 7.1. ОБЩИЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ. ПРЕДЪЯВЛЯЕМЫЕ К ОХЛАДИТЕЛЯМ СПП
- Классификация охладителей.
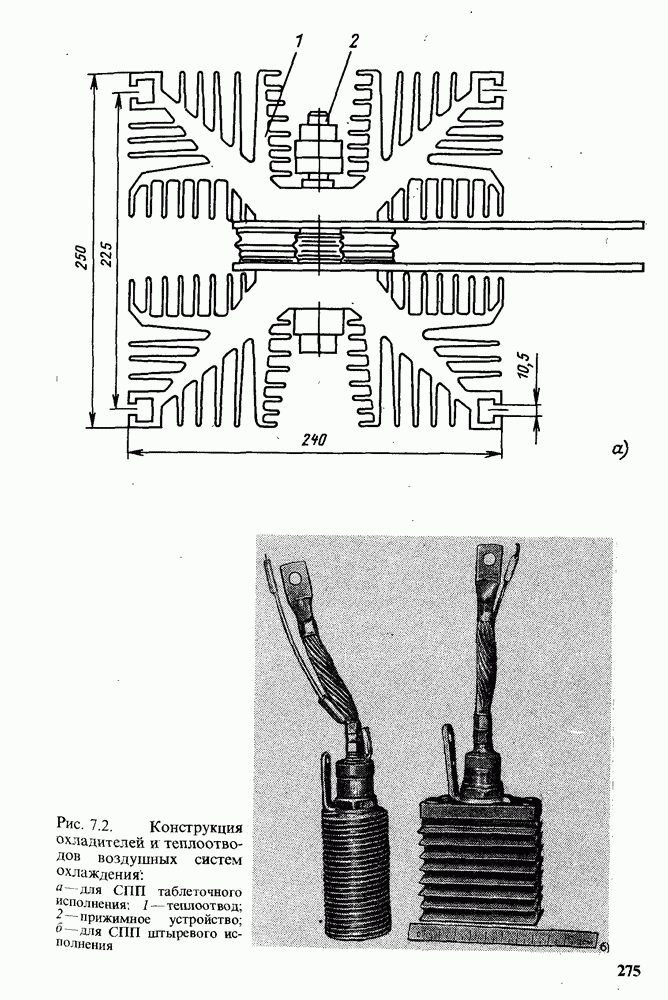
- 7.2. КОНСТРУКЦИИ ОХЛАДИТЕЛЕЙ
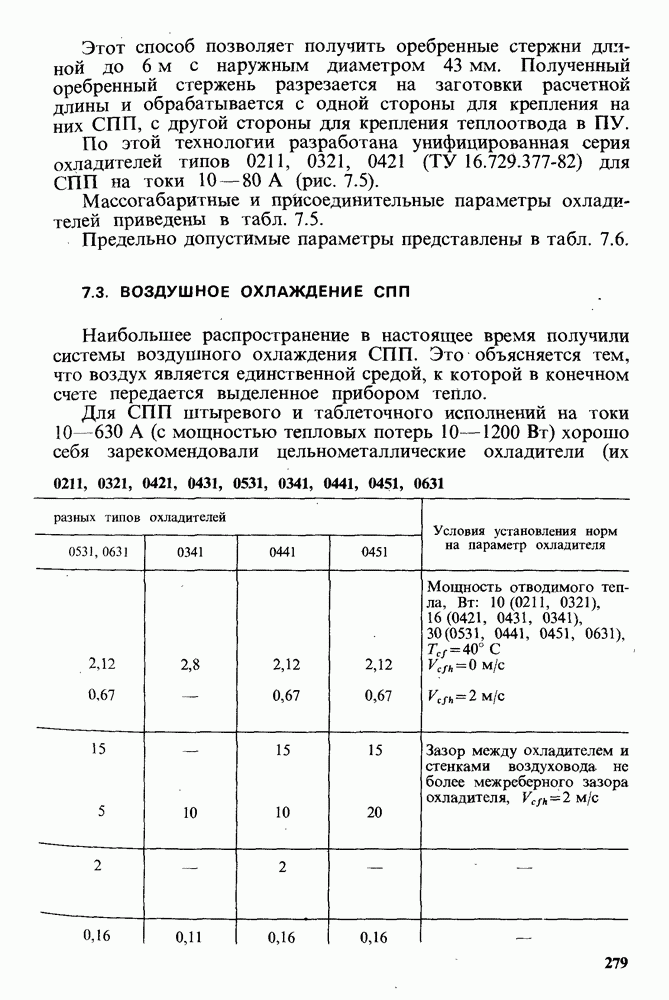
- 7.3. ВОЗДУШНОЕ ОХЛАЖДЕНИЕ СПП
- Прижимные устройства системы «СПП—охладитель».
- Компоновка системы «СПП — охладитель» в ПУ с естественным воздушным охлаждением.
- Температурное поле среды вокруг нагретых СПП с охладителями при наличии в вентильной секции ПУ воздухоотводящих экранов и перфораций.
- Переходное тепловое сопротивление «контактная поверхность — охлаждающая среда» теплоотводов СПП.
- Аэродинамическое сопротивление теплоотводов.
- Потери напора на преодоление сил трения в прямоугольных межреберных каналах теплоотвода охладителя на участке безотрывного течения.
- 7.4. ЖИДКОСТНОЕ ОХЛАЖДЕНИЕ СПП
- Выбор электроизоляционных материалов для охладителей СПП.
- 7.5. ИСПАРИТЕЛЬНОЕ ПОГРУЖНОЕ ОХЛАЖДЕНИЕ СПП
- Критические плотности теплового потока и коэффициенты теплоотдачи.
- Конструкции систем испарительного погружного охлаждения СПП.
- Глава 8. НАДЕЖНОСТЬ СИЛОВЫХ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ
- 8.1. ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ ТЕОРИИ НАДЕЖНОСТИ
- 8.2. ПОКАЗАТЕЛИ НАДЕЖНОСТИ СПП И ИХ ЗАВИСИМОСТИ ОТ РЕЖИМОВ РАБОТЫ
- Зависимости ПН от режимов работы.
- 8.3. МЕТОДЫ ОЦЕНКИ И КОНТРОЛЯ ПН СПП
- Режимы проведения испытаний СПП на надежность.
- Методы неразрушающего контроля СПП.
- 8.4. ВИДЫ И МЕХАНИЗМЫ ОТКАЗОВ СПП
- 8.5. МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СПП В РАЗЛИЧНЫХ РЕЖИМАХ
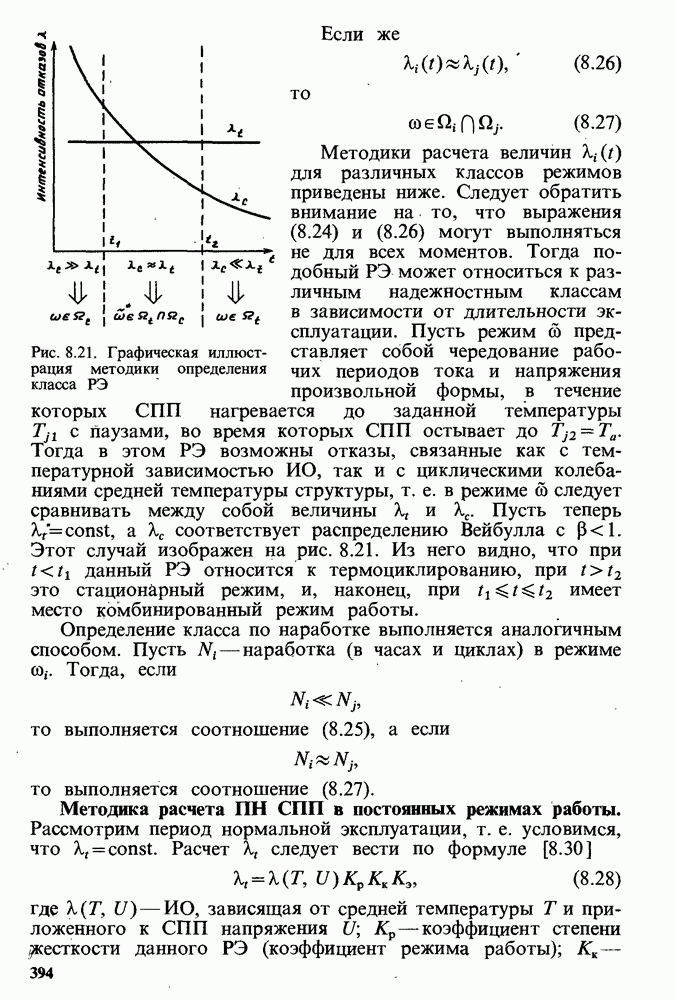
- Методика определения класса РЭ.
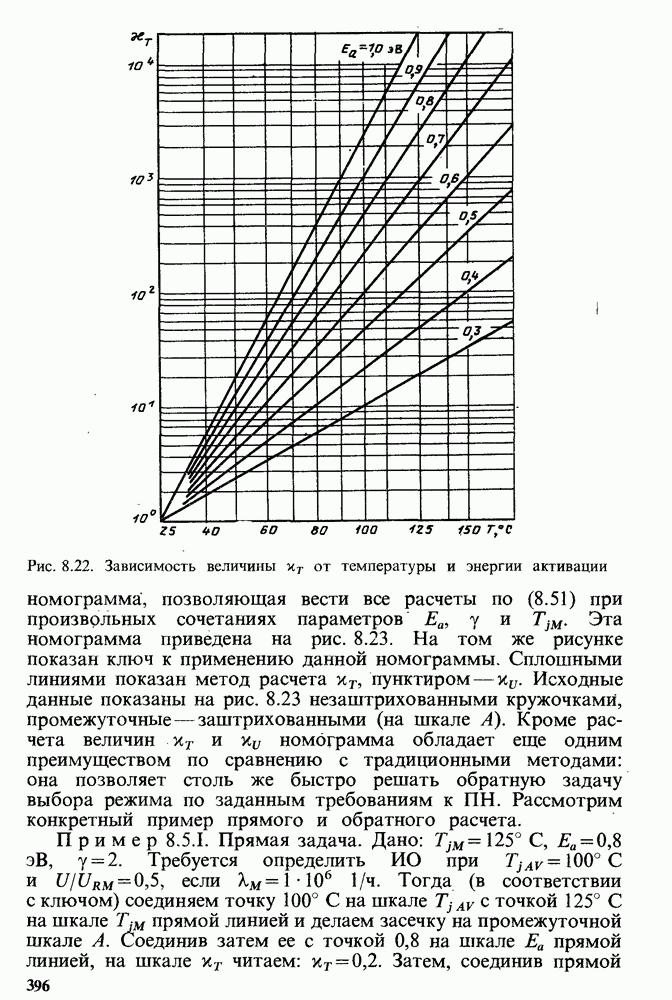
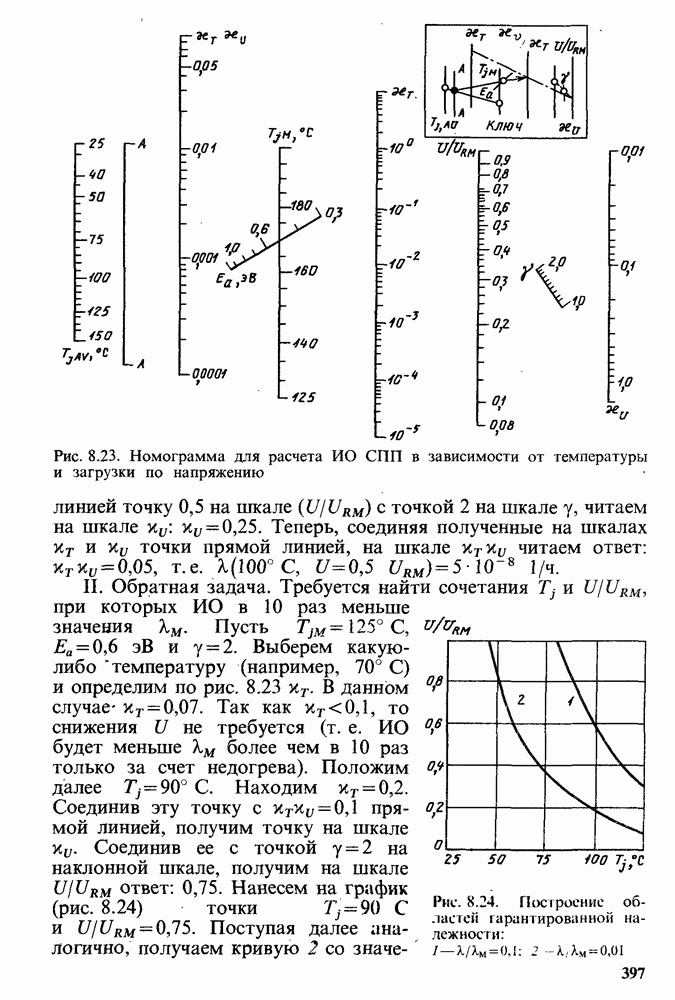
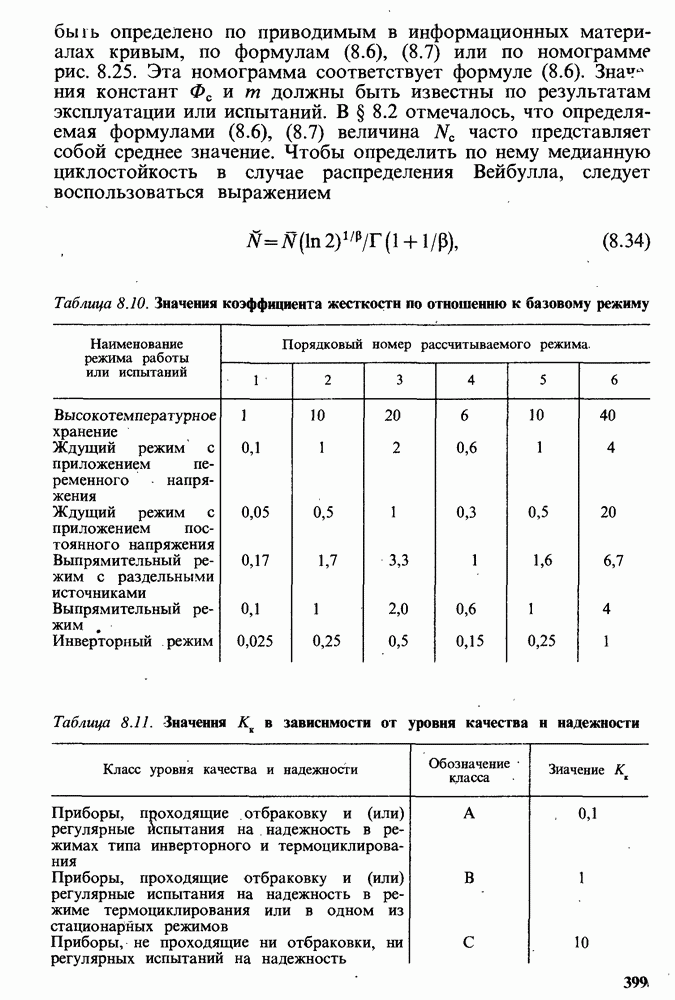
- Методика расчета ПН СПП в постоянных режимах работы.
- Методика расчета ПН СПП в циклических режимах.
- Методика расчета ПН СПП в переменных и комбинированных режимах.
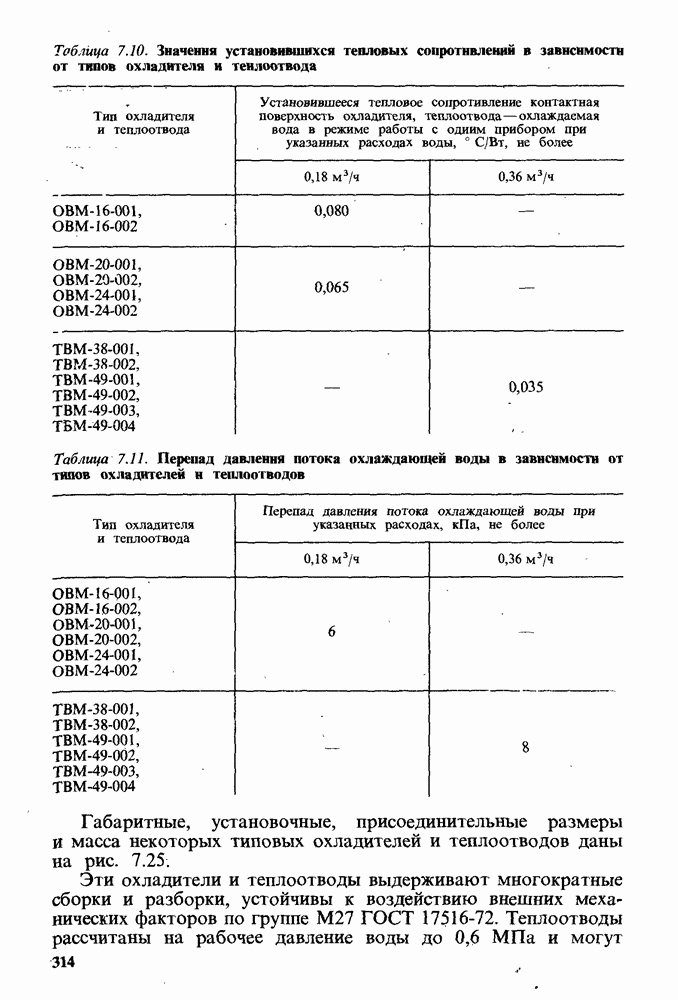
- Некоторые практические рекомендации по расчетам ПН СПП.
- СПИСОК ЛИТЕРАТУРЫ