| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 11. КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ
§ 11.1. Свободные колебания в контуре
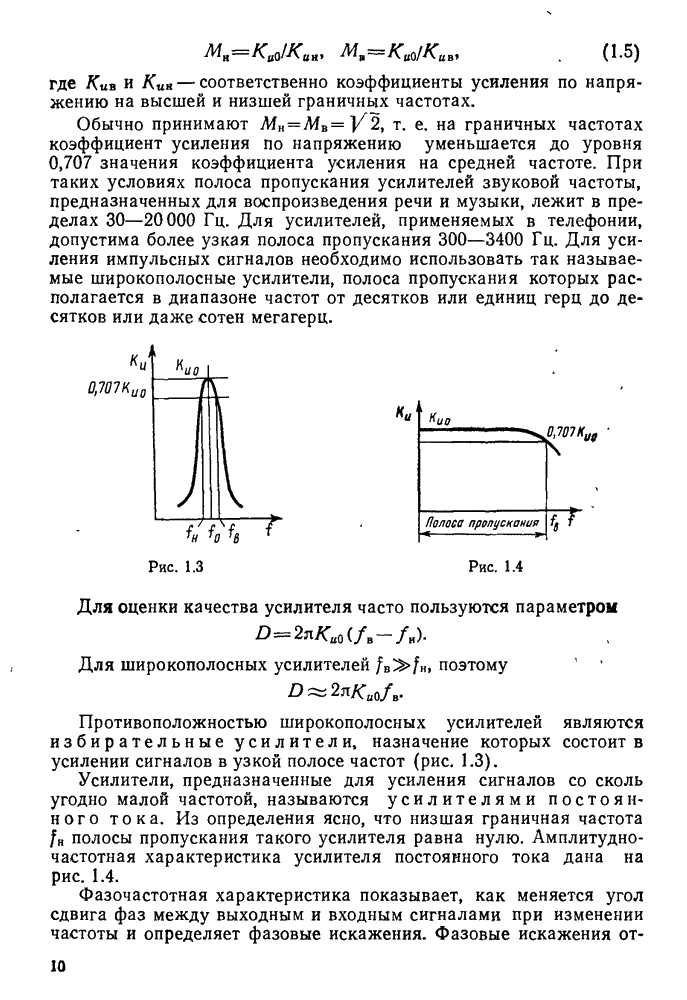
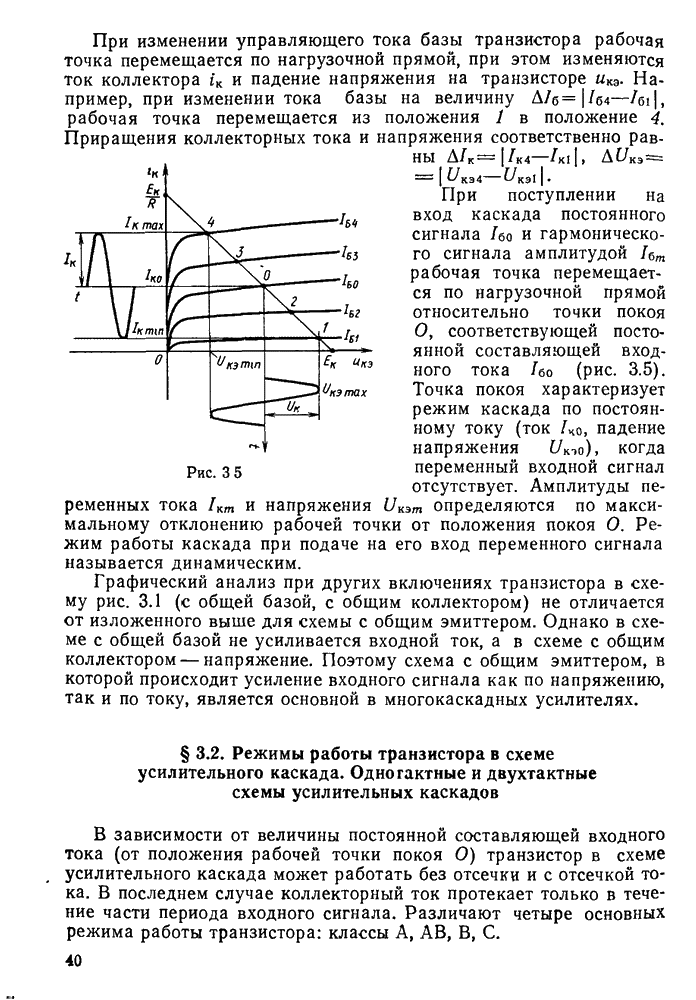
Функции резонансных фильтров, выделяющих необходимый спектр частот при прохождении сигнала в устройствах радиосвязи, выполняют колебательные контуры.
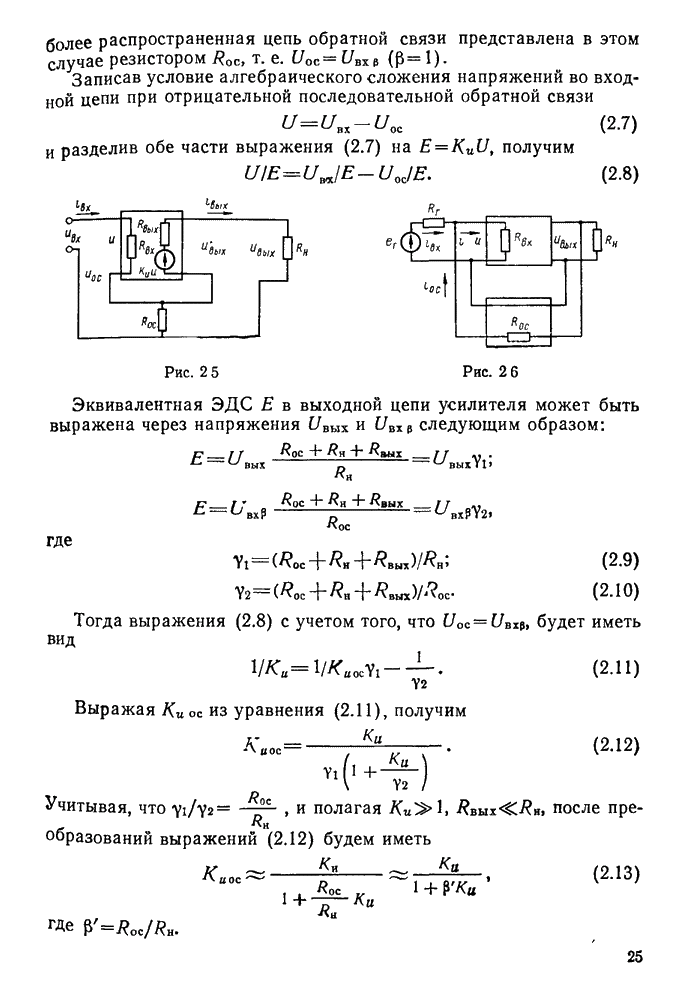
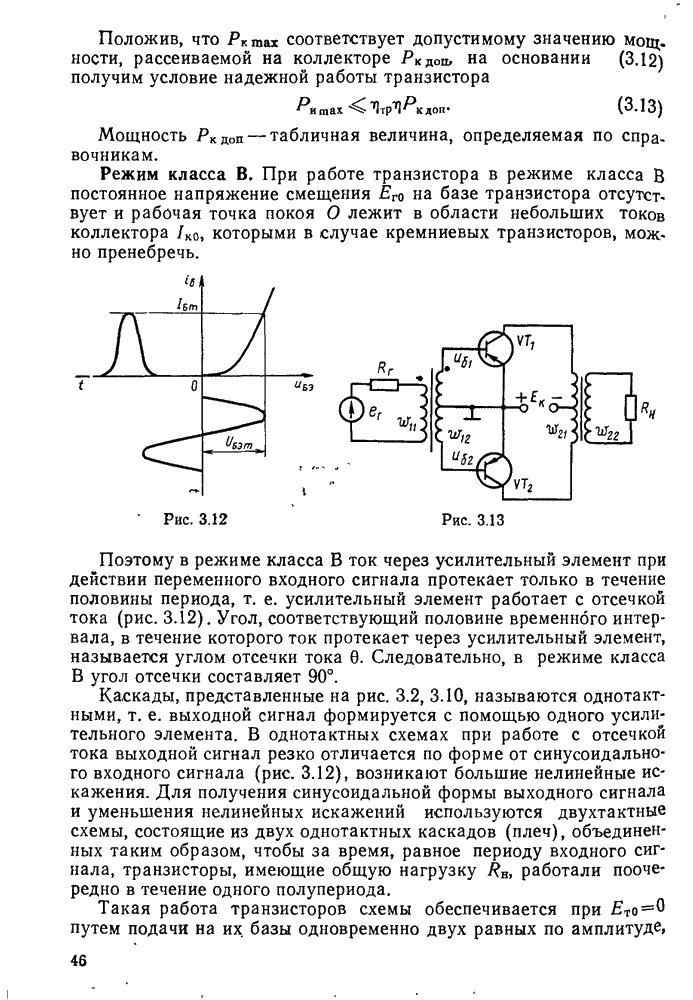
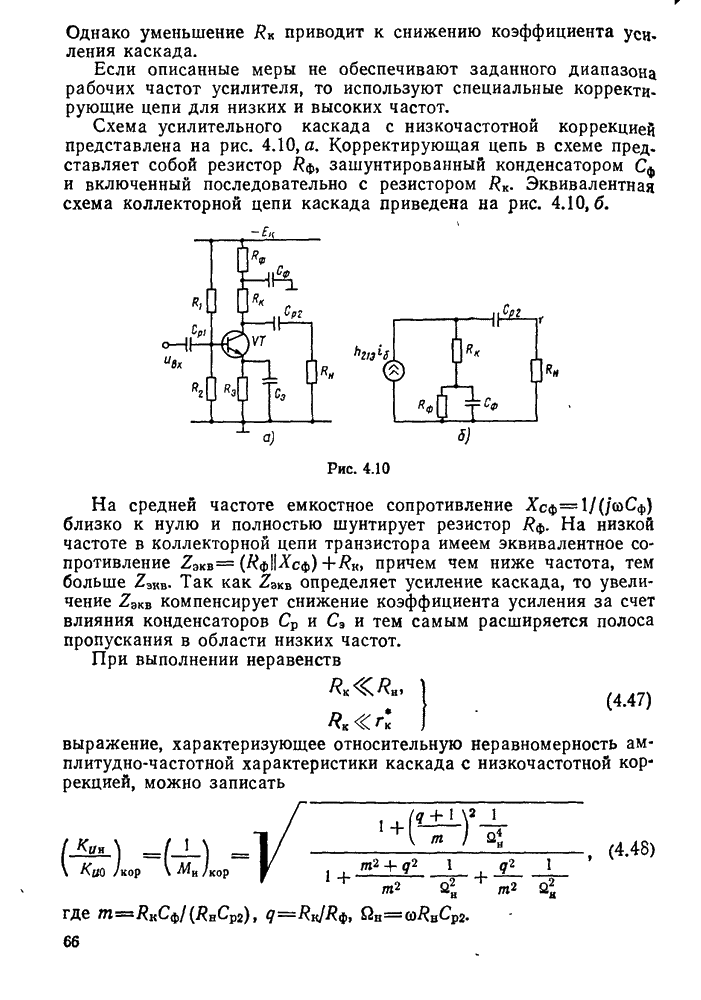
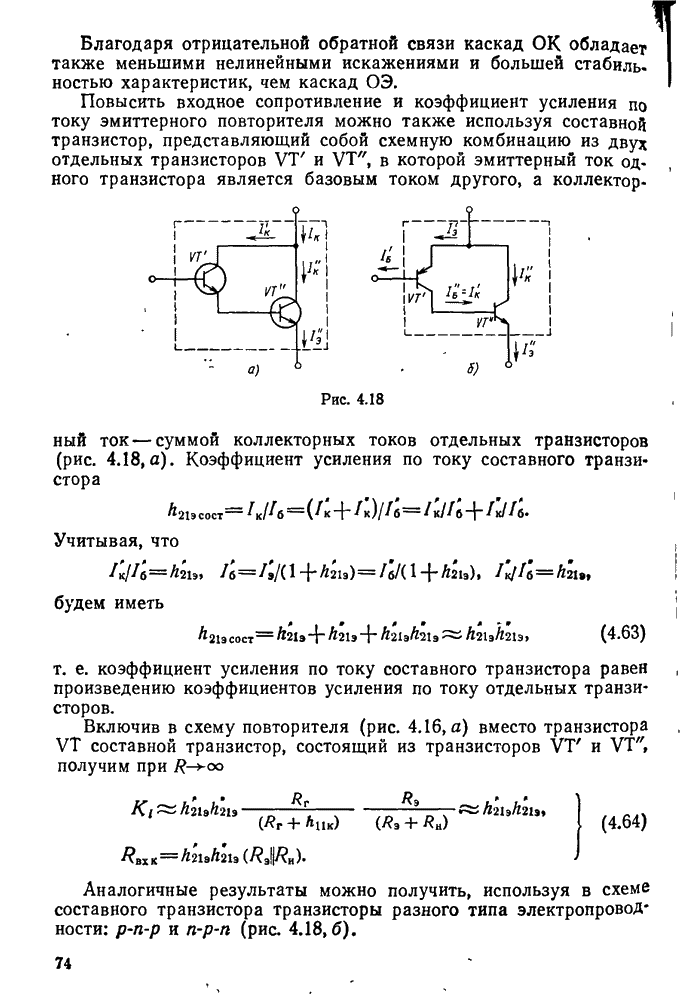
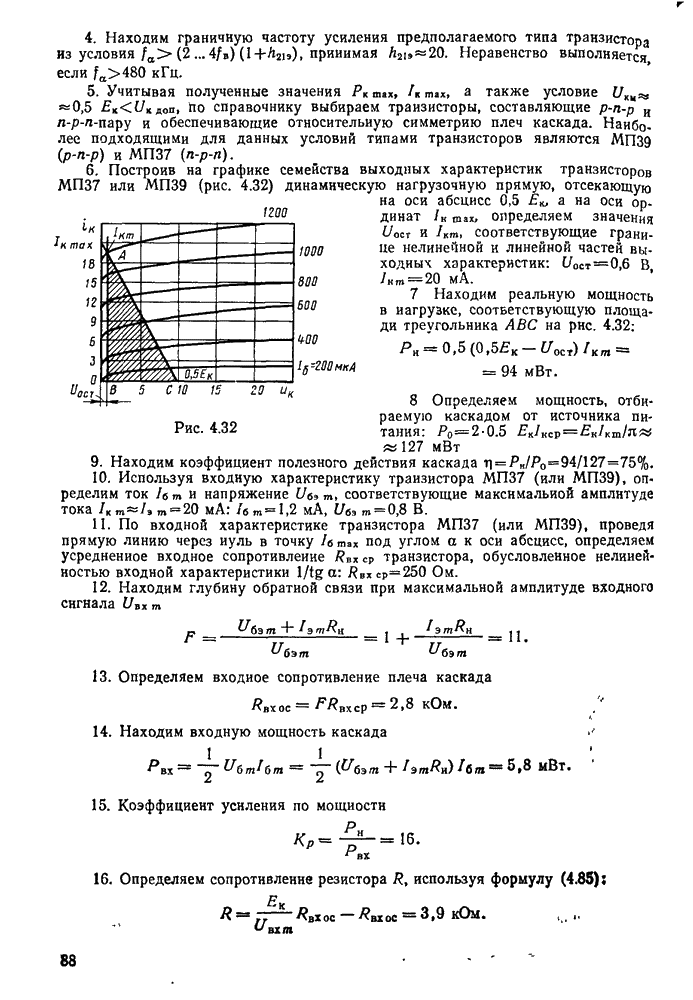
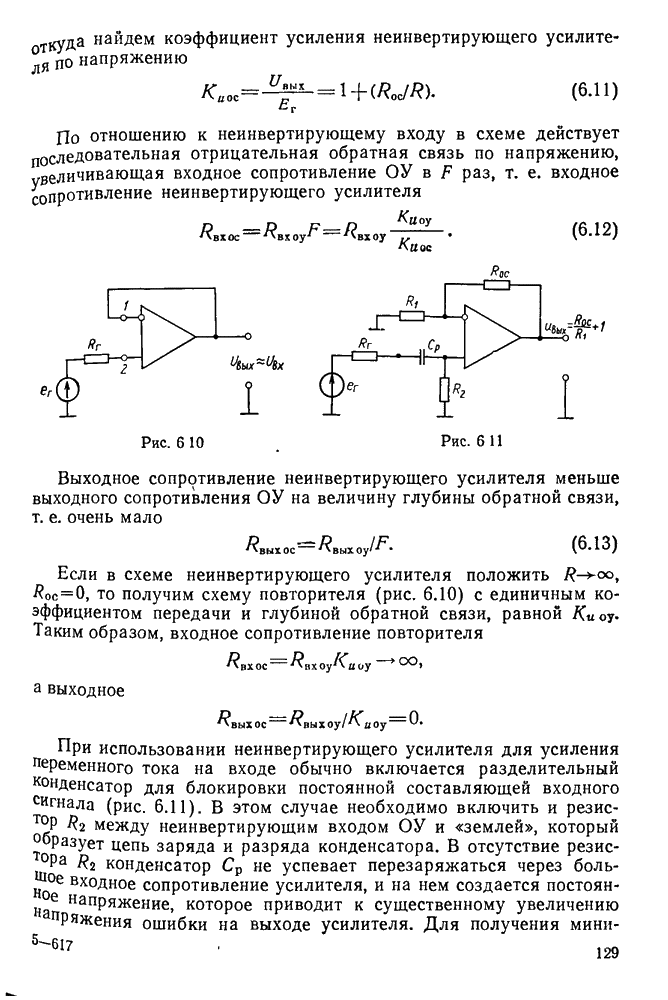
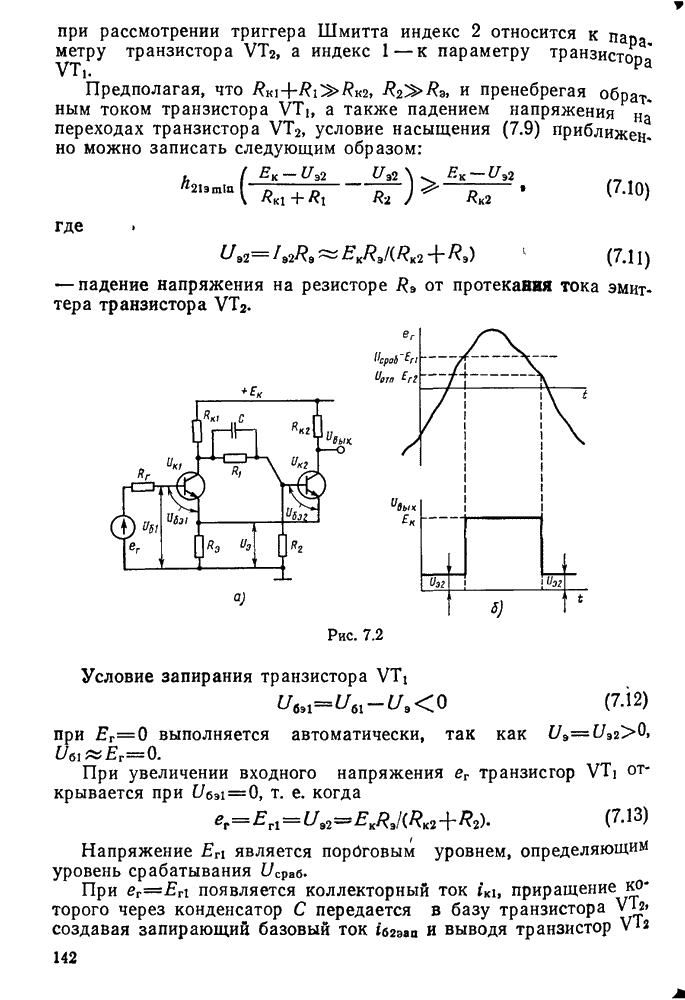
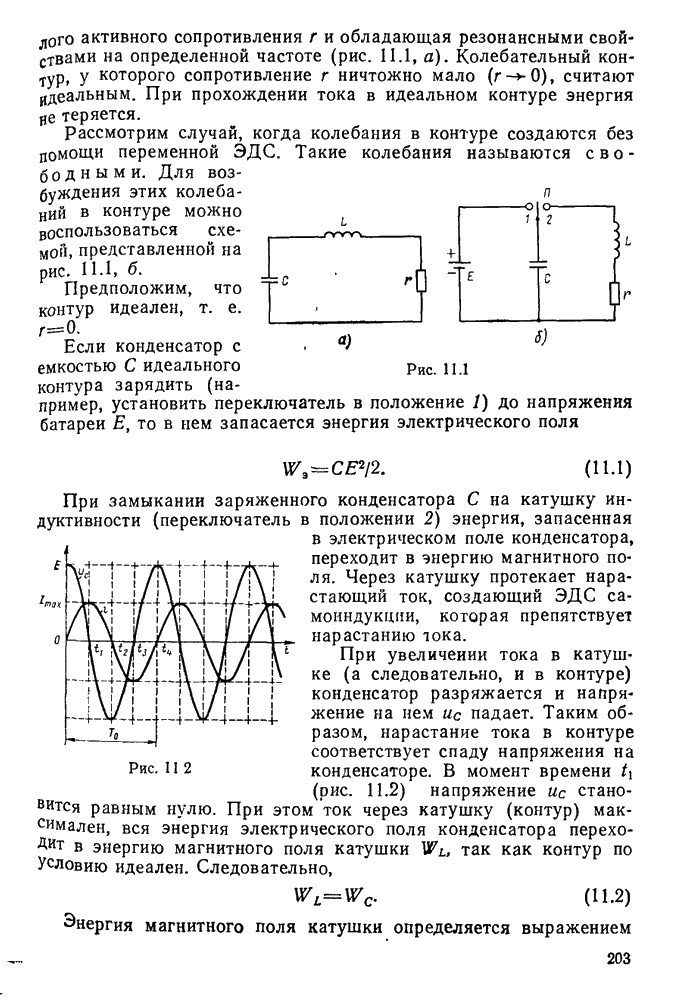
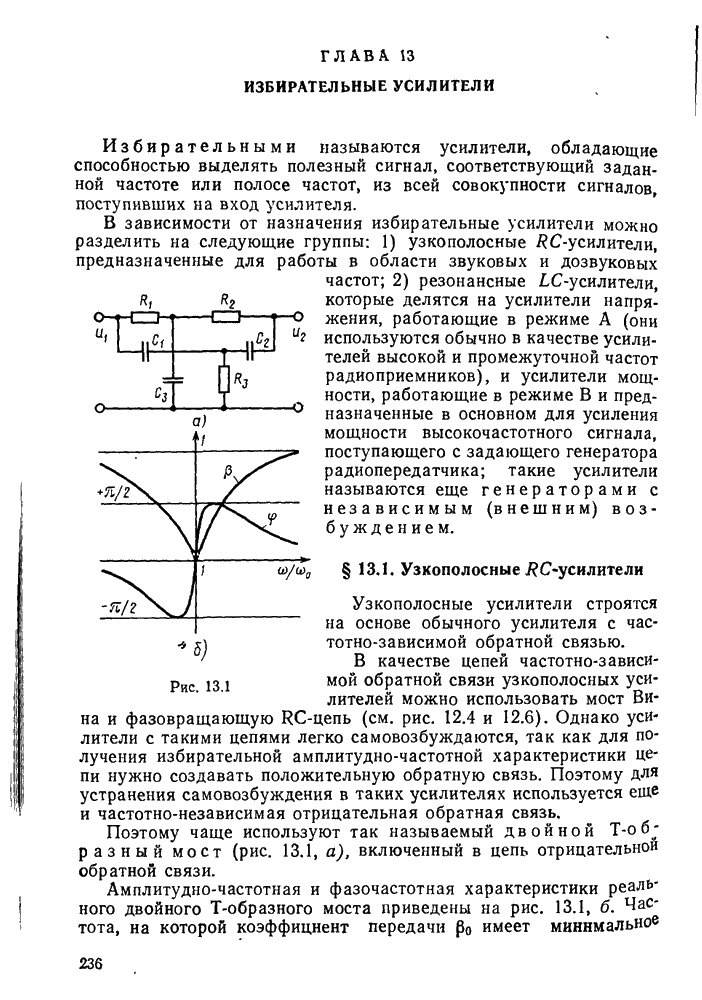
Колебательным контуром называется замкнутая цепь, состоящая из катушки индуктивности L, конденсатора С, малого активного сопротивления  и обладающая резонансными свойствами на определенной частоте (рис. 11.1, а).
и обладающая резонансными свойствами на определенной частоте (рис. 11.1, а).
Колебательный  у которого сопротивление
у которого сопротивление  ничтожно мало
ничтожно мало  , считают идеальным. При прохождении тока в идеальном контуре энергия не теряется.
, считают идеальным. При прохождении тока в идеальном контуре энергия не теряется.
Рассмотрим случай, когда колебания в контуре создаются без ломощи переменной ЭДС. Такие колебания называются свободными. Для возбуждения этих колебаний в контуре можно воспользоваться схемой, представленной на рис. 11.1. б.
Предположим, что контур идеален, т. е.  .
.
Если конденсатор с емкостью С идеального контура зарядить (например, установить переключатель в положение 1) до напряжения батареи Е, то в нем запасается энергия электрического поля

При замыкании заряженного конденсатора С на катушку индуктивности (переключатель в положении 2) энергия, запасенная в электрическом поле конденсатора, переходит в энергию магнитного поля. Через катушку протекает нарастающий ток, создающий ЭДС самоиндукцни, которая препятствует нарастанию тока.
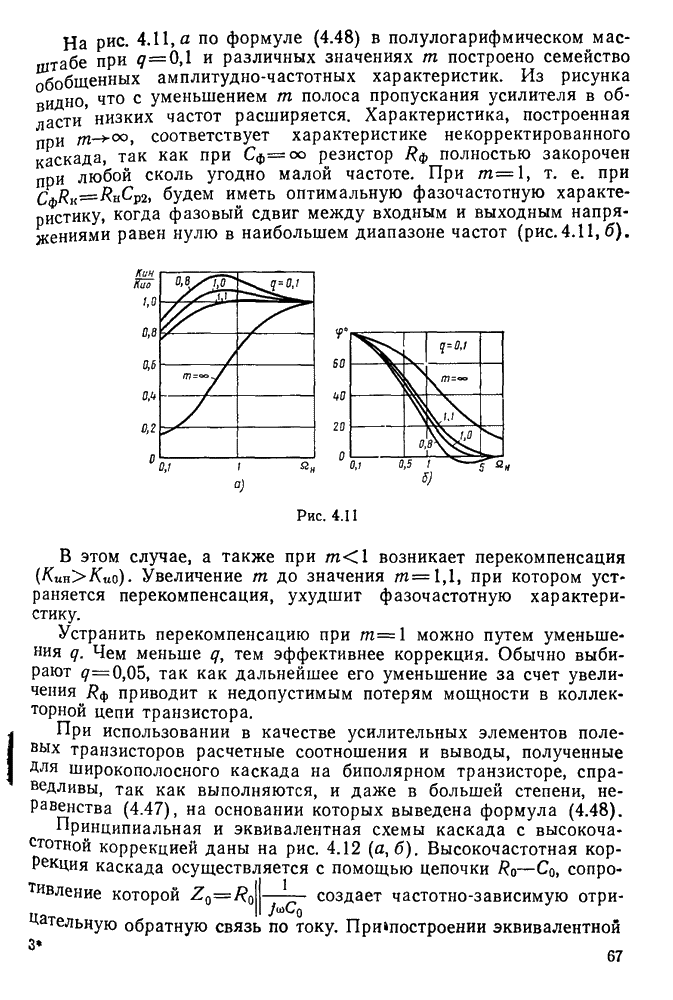
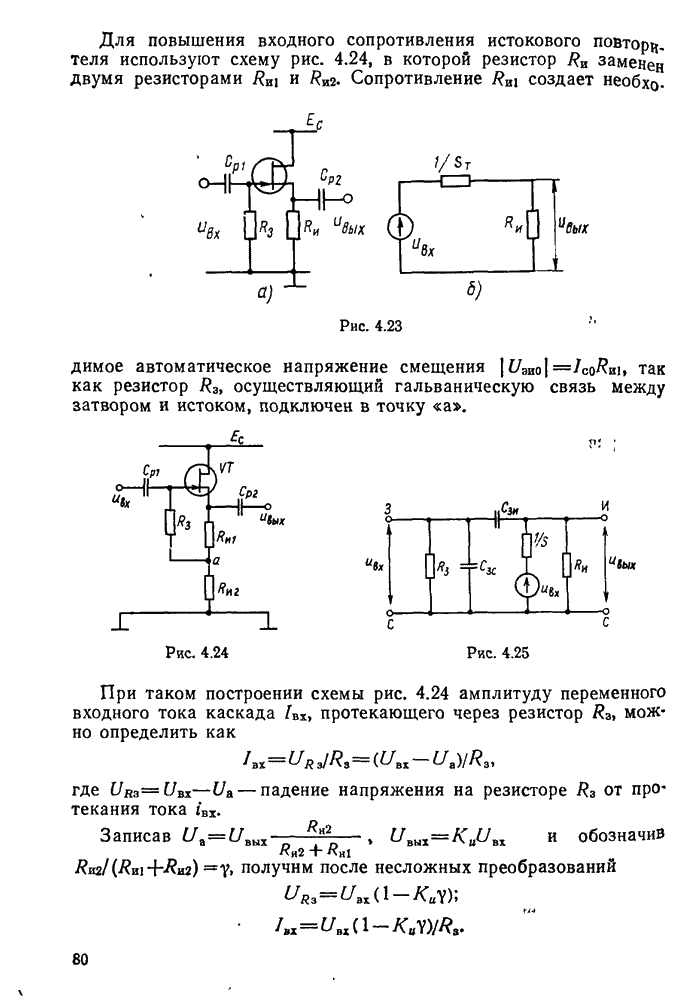
При увеличении тока в катушке (а следовательно, и в контуре) конденсатор разряжается и напряжение на нем «с падает. Таким образом, нарастание тока в контуре соответствует спаду напряжения на конденсаторе. В момент времени  (рис. 11.2) напряжение
(рис. 11.2) напряжение  становится равным нулю. При этом ток через катушку (контур) максимален, вся энергия электрического поля конденсатора переходит в энергию магнитного поля катушки
становится равным нулю. При этом ток через катушку (контур) максимален, вся энергия электрического поля конденсатора переходит в энергию магнитного поля катушки  , так как контур по условию идеален. Следовательно,
, так как контур по условию идеален. Следовательно,


Рис. 11.1.

Рис. 11.2.
Энергия магнитного поля катушки определяется выражением

где  — ток контура в момент
— ток контура в момент  , соответствующий его максимальному значению.
, соответствующий его максимальному значению.
Следовательно, равенство (11.2) с учетом выражений (11.1) и (11.3) можно записать так:

После момента времени  энергия магнитного поля снова переходит в энергию электрического поля и ток катушки убывает.
энергия магнитного поля снова переходит в энергию электрического поля и ток катушки убывает.
ЭДС самоиндукции направлена теперь таким образом, что препятствует убыванию тока. Конденсатор С заряжается. Напряжение на его обкладках возрастает, но имеет полярность, противоположную первоначальной.
В момент времени вся энергия магнитного поля снова переходит в энергию электрического поля. Напряжение на конденсаторе достигает максимального значения Е, а ток в контуре прекращается.
В течение времени  конденсатор разряжается и напряжение на нем падает. Ток в контуре возрастает, но в направлении, противоположном первоначальному. С момента времени процесс колебаний повторяется и носит гармонический характер. Так как потерь энергии в идеальном контуре не происходит, то возникшие в нем свободные гармонические колебания являются незатухающими.
конденсатор разряжается и напряжение на нем падает. Ток в контуре возрастает, но в направлении, противоположном первоначальному. С момента времени процесс колебаний повторяется и носит гармонический характер. Так как потерь энергии в идеальном контуре не происходит, то возникшие в нем свободные гармонические колебания являются незатухающими.
Частоту свободных колебаний в контуре  можно определить из следующих соображений.
можно определить из следующих соображений.
При свободных колебаниях к элементам контура (катушка индуктивности и конденсатор) приложено одно и то же напряжение  и через них протекает один и тот же переменный ток
и через них протекает один и тот же переменный ток  .
.
Следовательно, емкостное  и индуктивное
и индуктивное  сопротивления элементов контура на частоте
сопротивления элементов контура на частоте  также должны быть равны между собой, т. е.
также должны быть равны между собой, т. е.

где  — круговая частота свободных колебаний.
— круговая частота свободных колебаний.
Из этого равенства получим

или

Время  за которое протекает один цикл колебаний напряжения и тока в контуре, т. е. период свободных колебаний, является величиной, обратной частоте:
за которое протекает один цикл колебаний напряжения и тока в контуре, т. е. период свободных колебаний, является величиной, обратной частоте:

Отсюда с учетом выражения (11.7) будем иметь

Реактивное сопротивление элементов контура на частоте  называют характеристическим или волновым сопротивлением контура
называют характеристическим или волновым сопротивлением контура  . Учитывая выражение (11.6), получим
. Учитывая выражение (11.6), получим
 (11.10)
(11.10)
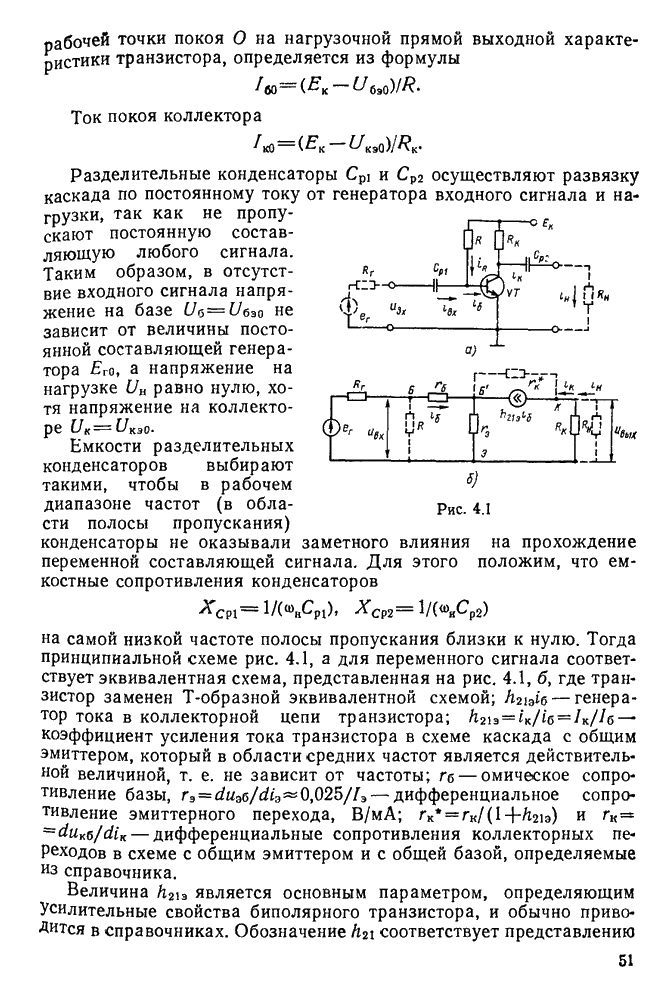
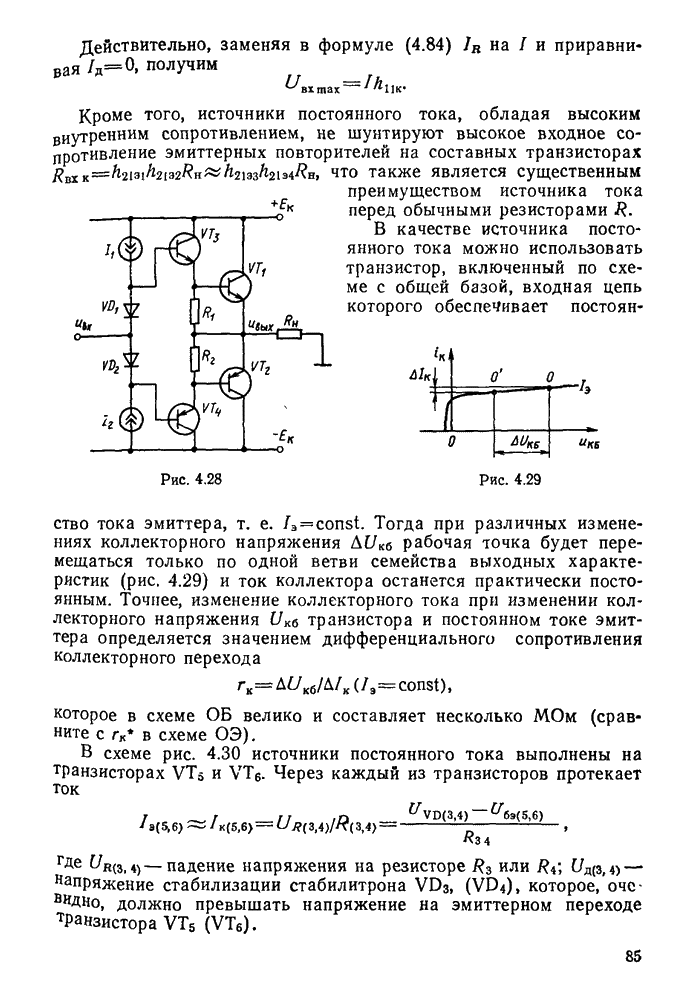
Теперь предположим, что свободные колебания за счет энергии, запасенной первоначально в конденсаторе, происходят в реальном контуре, т. е. активное сопротивление контура  не равно нулю.
не равно нулю.

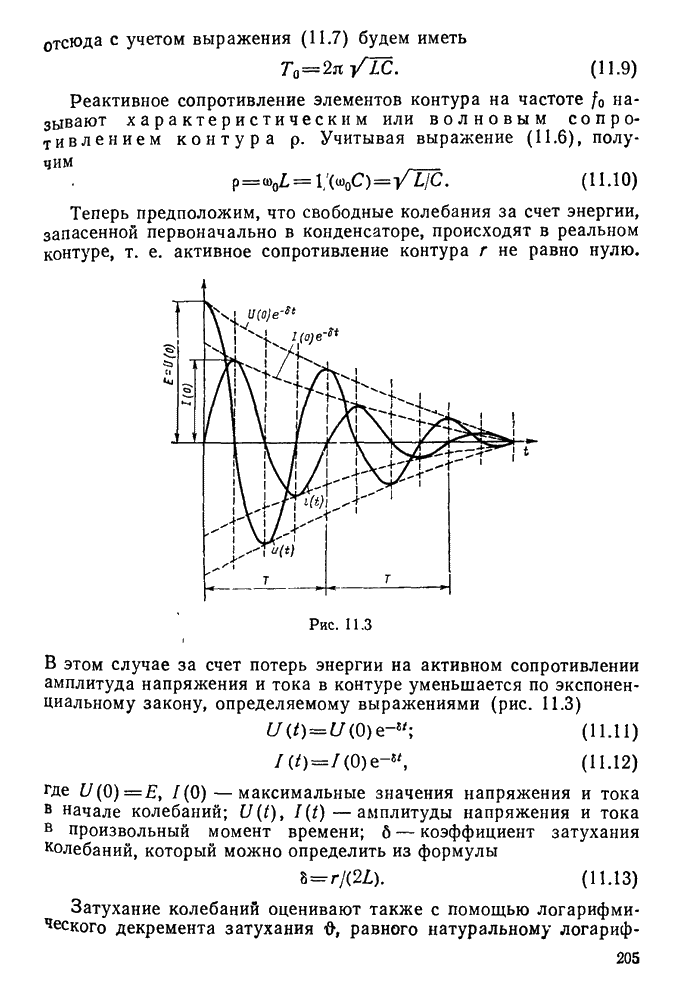
Рис. 11.3.
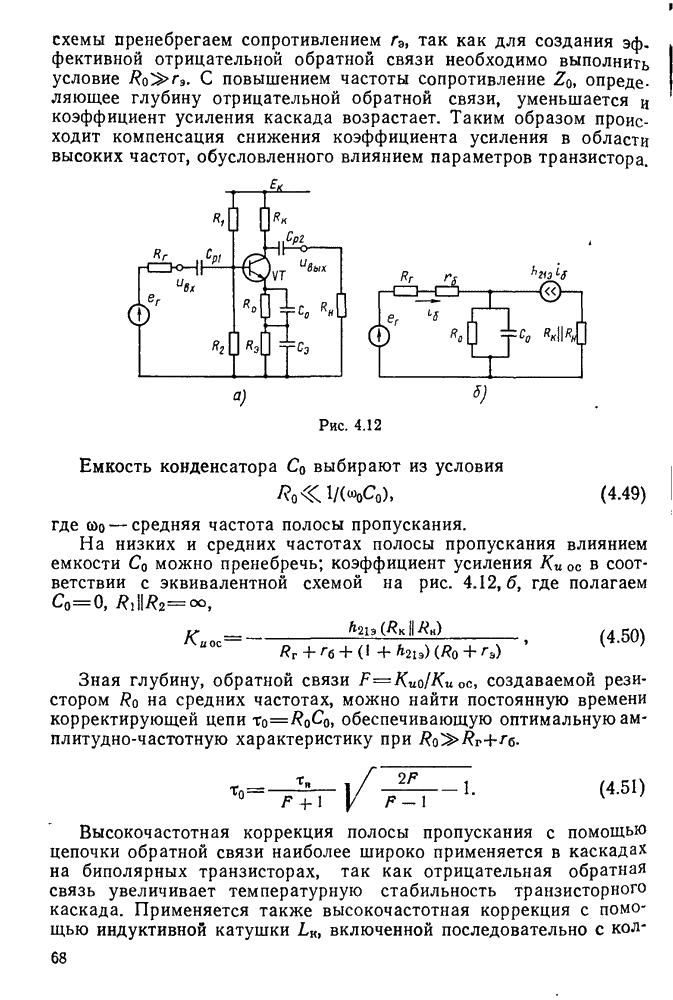
В этом случае за счет потерь энергии на активном сопротивлении амплитуда напряжения и тока в контуре уменьшается по экспоненциальному закону, определяемому выражениями (рис. 11.3)
 (11.11)
(11.11)
где  - максимальные значения напряжения и тока в начале колебаний;
- максимальные значения напряжения и тока в начале колебаний;  - амплитуды напряжения и тока в произвольный момент времени;
- амплитуды напряжения и тока в произвольный момент времени;  — коэффициент затухания колебаний, который можно определить из формулы
— коэффициент затухания колебаний, который можно определить из формулы
 (11.13)
(11.13)
Затухание колебаний оценивают также с помощью логарифмического декремента затухания  , равного натуральному логарифму отношения амплитуд напряжения (тока), разделенных во времени на период
, равного натуральному логарифму отношения амплитуд напряжения (тока), разделенных во времени на период  , т. е.
, т. е.

Подставляя в формулу (11.14) выражения для  из (11.9) и (11.12) и учитывая (11.10), получим
из (11.9) и (11.12) и учитывая (11.10), получим
 (11.15)
(11.15)
Чем меньше отношение  , тем медленнее затухают свободные колебания в контуре. Величина, обратная d, называется добротностью контура:
, тем медленнее затухают свободные колебания в контуре. Величина, обратная d, называется добротностью контура:
 (11.16)
(11.16)
Добротность является важной характеристикой колебательного контура, определяющей его качество. Добротность  -контуров, применяемых в системах радиосвязи, лежит в пределах 20—300.
-контуров, применяемых в системах радиосвязи, лежит в пределах 20—300.

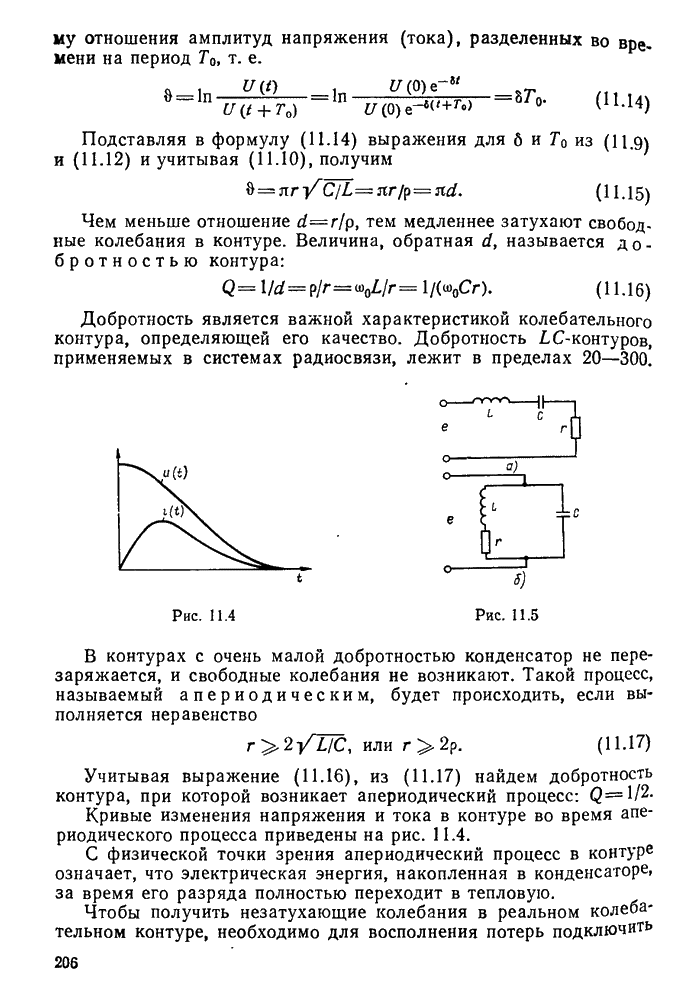
Рис. 11.4.
В контурах с очень малой добротностью конденсатор не перезаряжается, и свободные колебания не возникают. Такой процесс, называемый апериодическим, будет происходить, если выполняется неравенство
 (11.17)
(11.17)
Учитывая выражение (11.16), из (11.17) найдем добротность контура, при которой возникает апериодический процесс: 
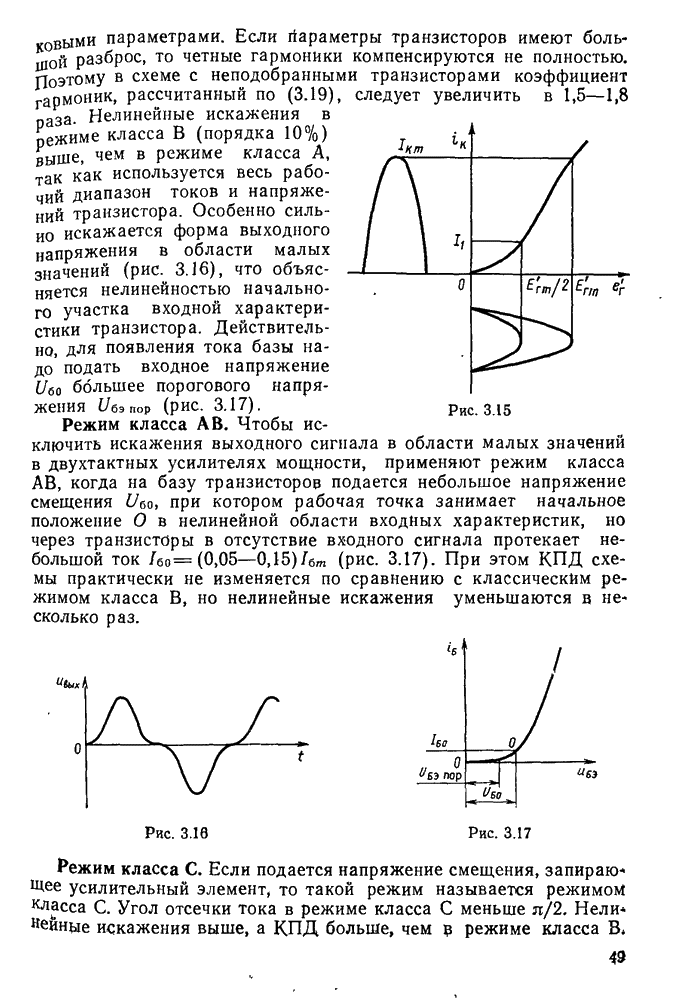
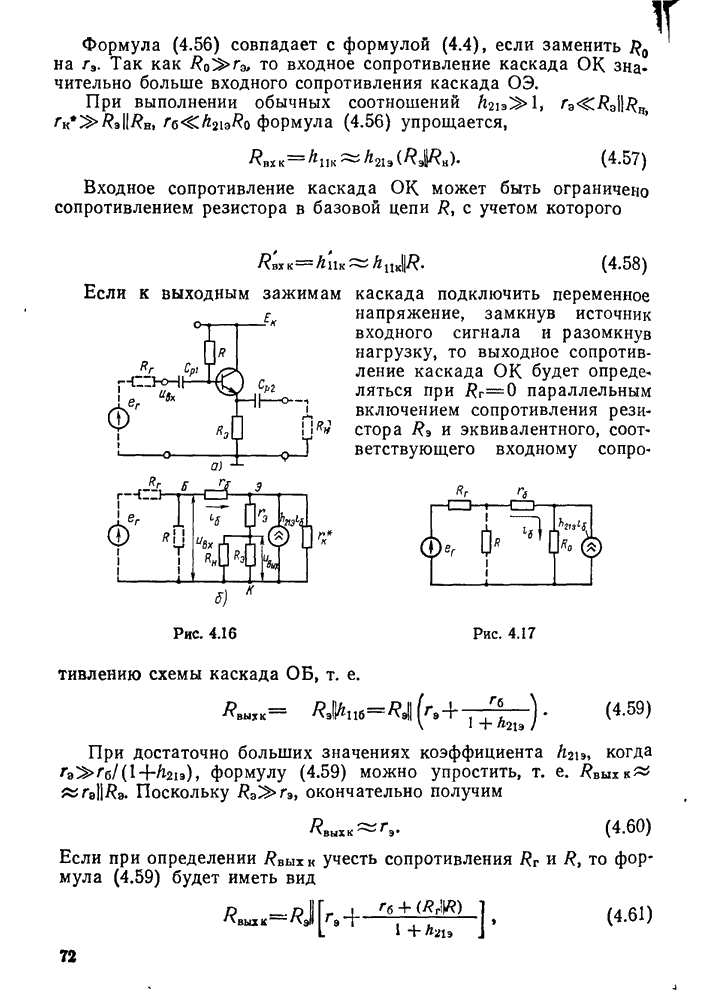
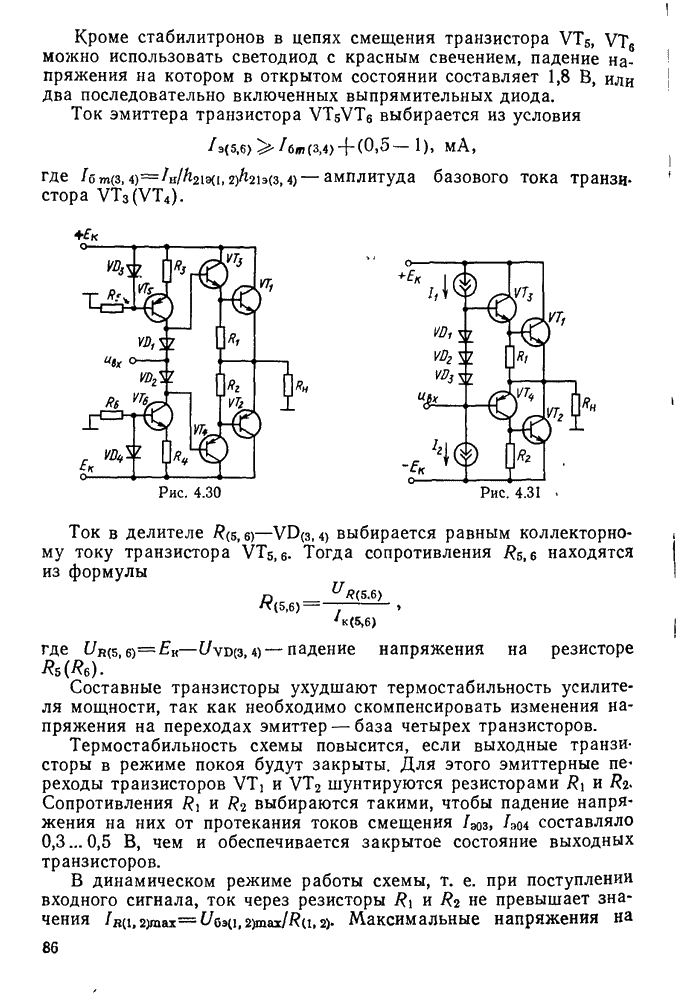
Кривые изменения напряжения и тока в контуре во время апериодического процесса приведены на рис. 11.4.

Рис. 11.5.
С физической точки зрения апериодический процесс в контуре означает, что электрическая энергия, накопленная в конденсаторе, за время его разряда полностью переходит в тепловую.
Чтобы получить незатухающие колебания в реальном колебательном контуре, необходимо для восполнения потерь подключить к контуру источник переменной ЭДС.
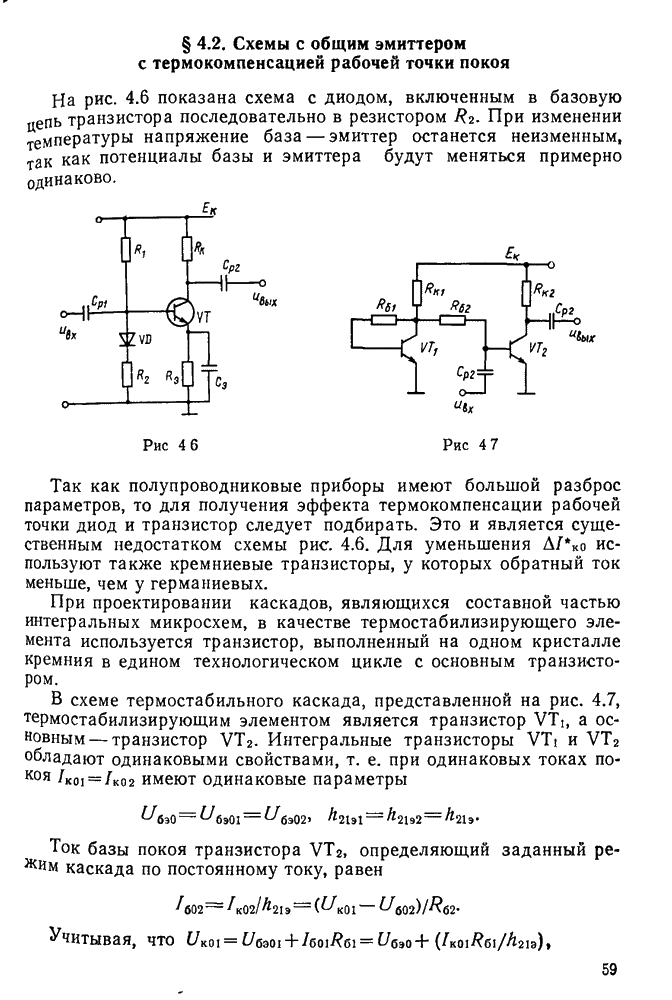
Колебания в контуре, возникшие под действием подключенного к нему источника переменной ЭДС, называются вынужденными. Если источник ЭДС включают последовательно с катушкой индуктивности и конденсатором, то образованный таким образом контур называют последовательным (рис. 11.5, а).
Контур, в котором источник переменной ЭДС включен параллельно с катушкой и конденсатором, называется параллельным (рис. 11.5, б).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ И РЕЛЕЙНЫЕ СХЕМЫ
- ГЛАВА 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ УСИЛИТЕЛЕЙ
- § 1.2. Коэффициент усиления. Линейные и нелинейные искажения
- § 1.3. Эквивалентная схема усилителя. Входное и выходное сопротивления
- § 1.4. Показатели многокаскадных усилителей
- § 1.5. Шумы в усилителях
- Вопросы и задачи для самопроверки
- ГЛАВА 2. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
- § 2.1. Виды обратных связей
- § 2.2. Влияние обратной связи на коэффициент усиления и искажения сигнала
- § 2.3. Влияние отрицательной обратной связи на входное сопротивление усилителя
- § 2.4. Влияние отрицательной обратной связи на выходное сопротивление усилителя
- Вопросы и задачи для самопроверки
- ГЛАВА 3. ПРИНЦИПЫ ПОСТРОЕНИЯ УСИЛИТЕЛЬНЫХ КАСКАДОВ НА ТРАНЗИСТОРАХ
- § 3.1. Включение транзистора в схему усилительного каскада. Графический анализ работы каскада
- § 3.2. Режимы работы транзистора в схеме усилительного каскада. Однотактные и двухтактные схемы усилительных каскадов
- Вопросы и задачи для самопроверки
- ГЛАВА 4. ПРАКТИЧЕСКИЕ СХЕМЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ НА ТРАНЗИСТОРАХ
- § 4.1. Каскад с общим эмиттером
- § 4.2. Схемы с общим эмиттером с термокомпенсацией рабочей точки покоя
- § 4.3. Частотные искажения в схеме с общим эмиттером. Область низких частот
- § 4.4. Широкополосные каскады с общим эмиттером
- § 4.5. Каскад с общей базой (повторитель тока)
- § 4.6. Каскад с общим коллектором (повторитель напряжения)
- § 4.7. Каскад с общим истоком
- § 4.8. Каскад с общим стоком (истоковыб повторитель)
- § 4.9. Выходные каскады (усилители мощности)
- Расчет бестрансформаторного двухтактного усилителя мощности
- Вопросы и задачи для самопроверки
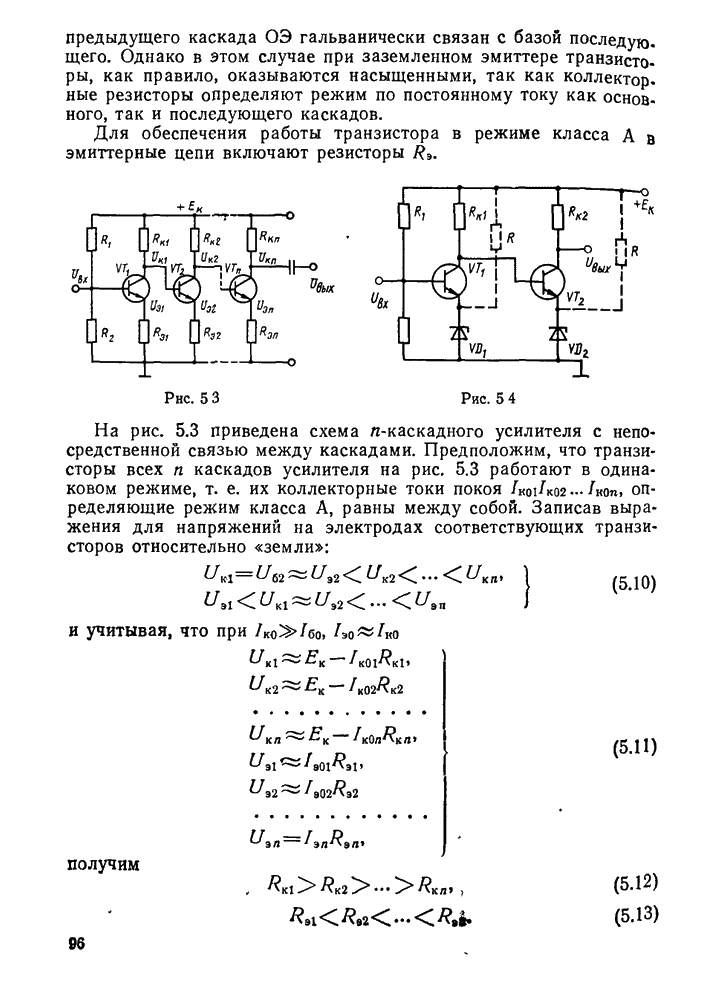
- ГЛАВА 5. ПРАКТИЧЕСКИЕ СХЕМЫ МНОГОКАСКАДНЫХ УСИЛИТЕЛЕЙ
- § 5.1. Усилители с резистивно-емкостной связью
- § 5.2. Усилители с непосредственной связью (усилители постоянного тока)
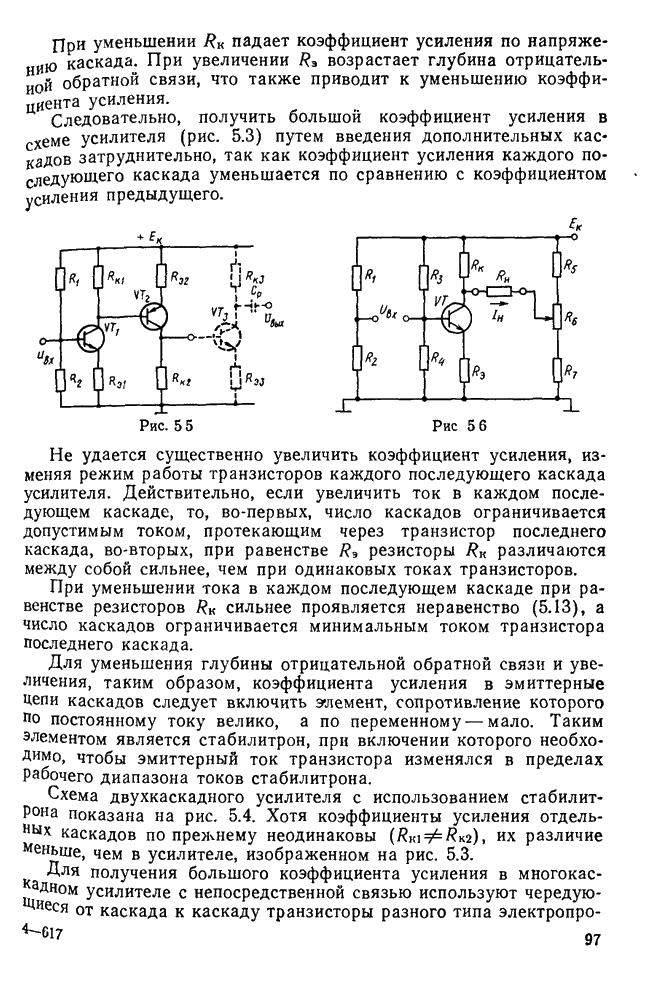
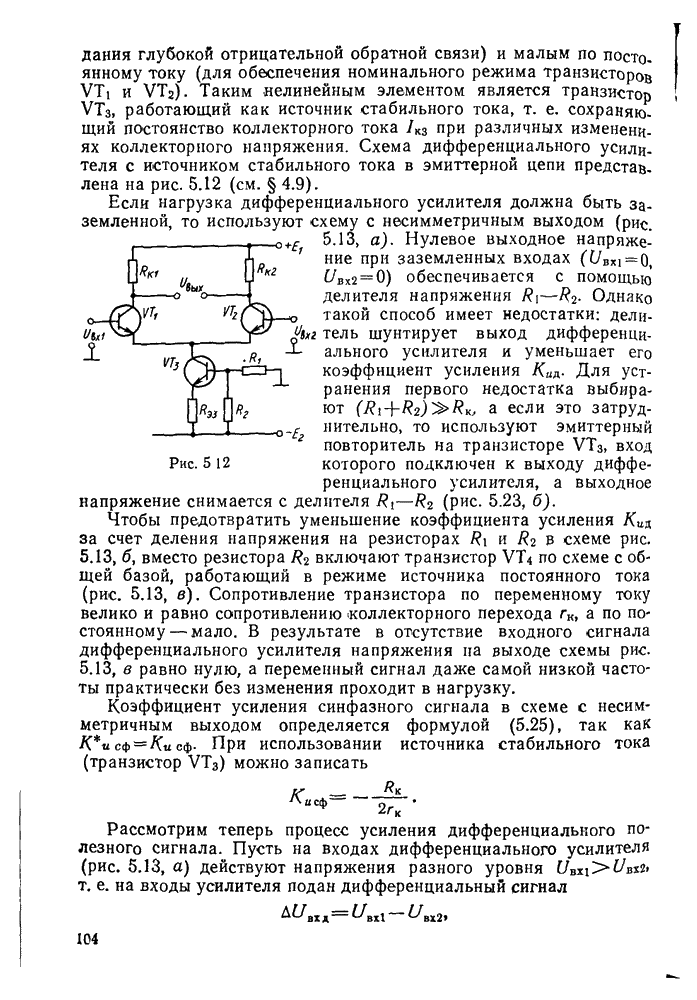
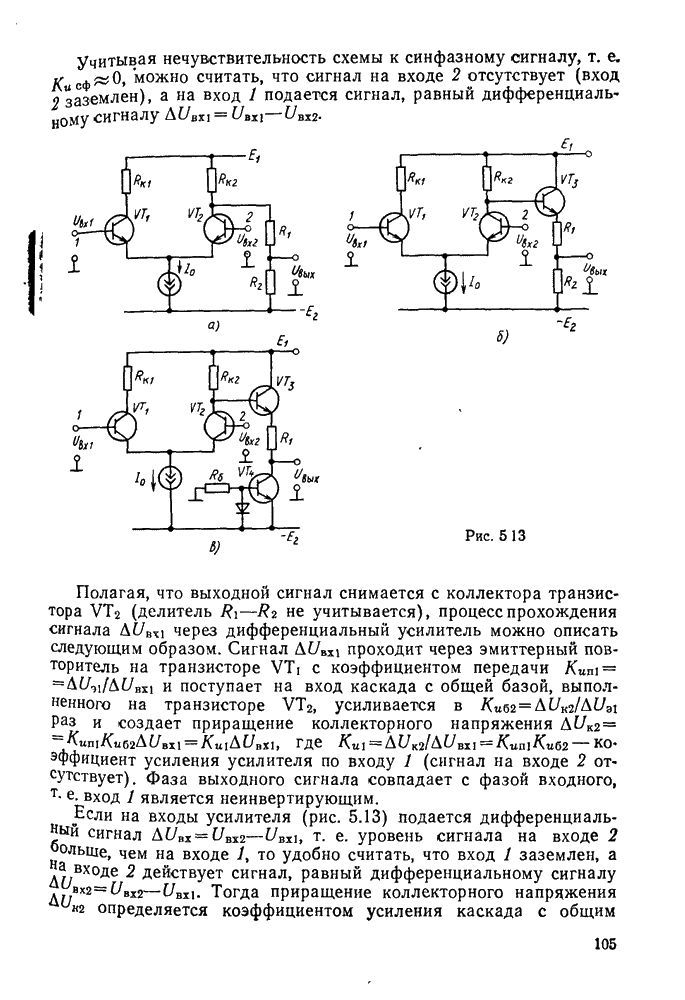
- § 5.3. Дифференциальные усилители
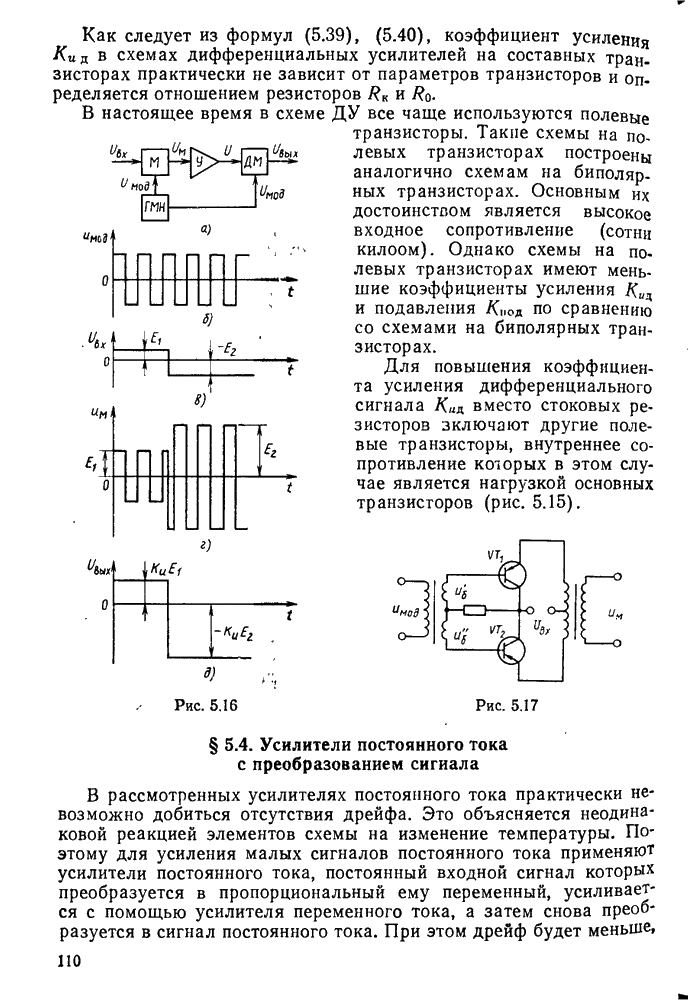
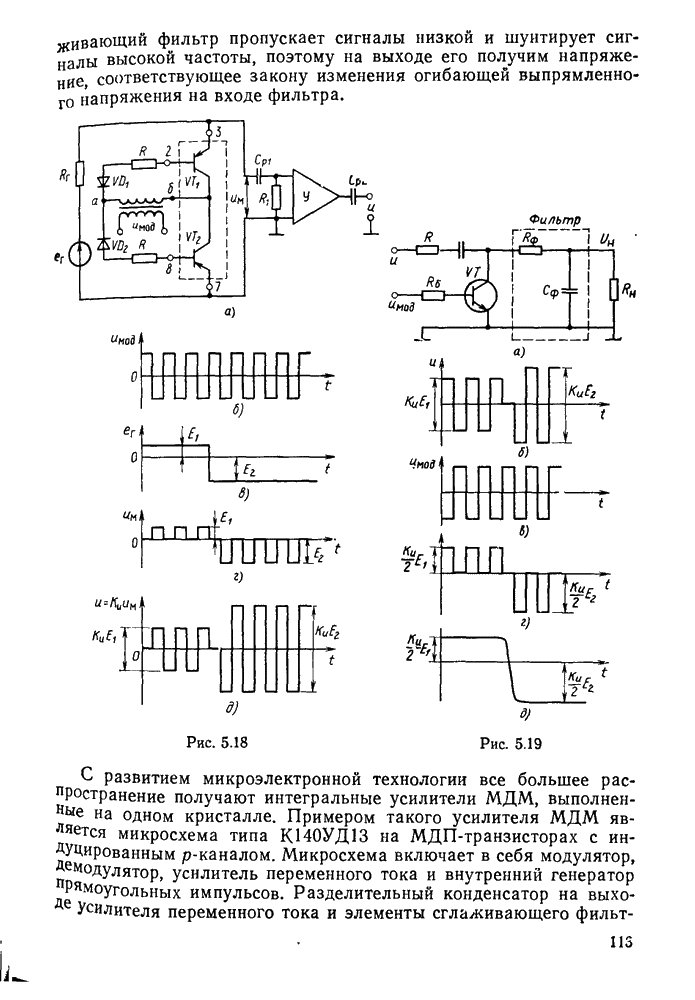
- § 5.4. Усилители постоянного тока с преобразованием сигнала
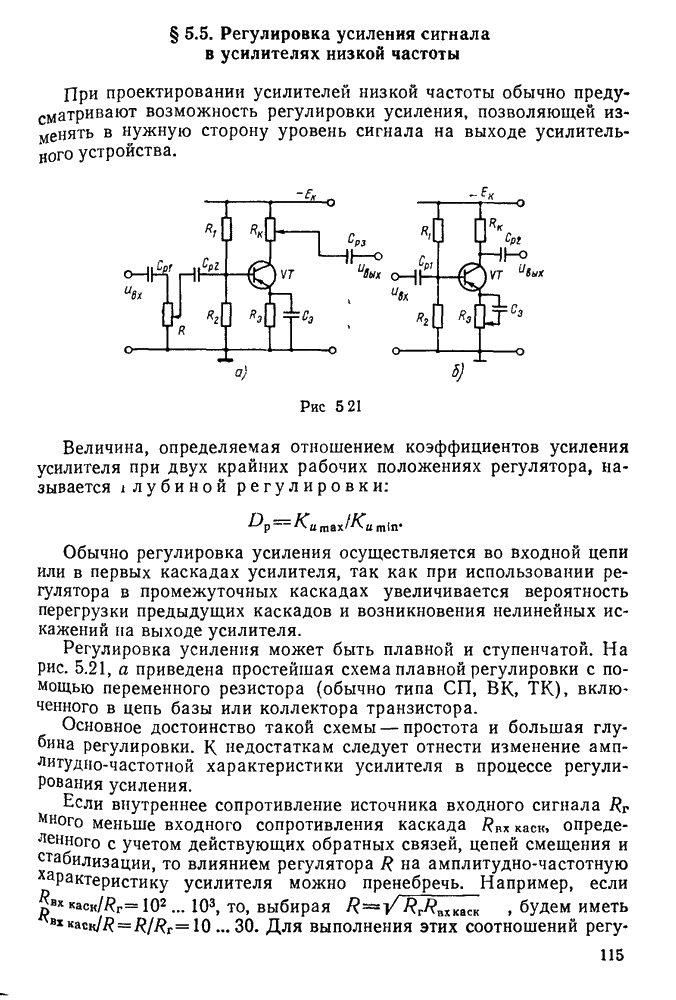
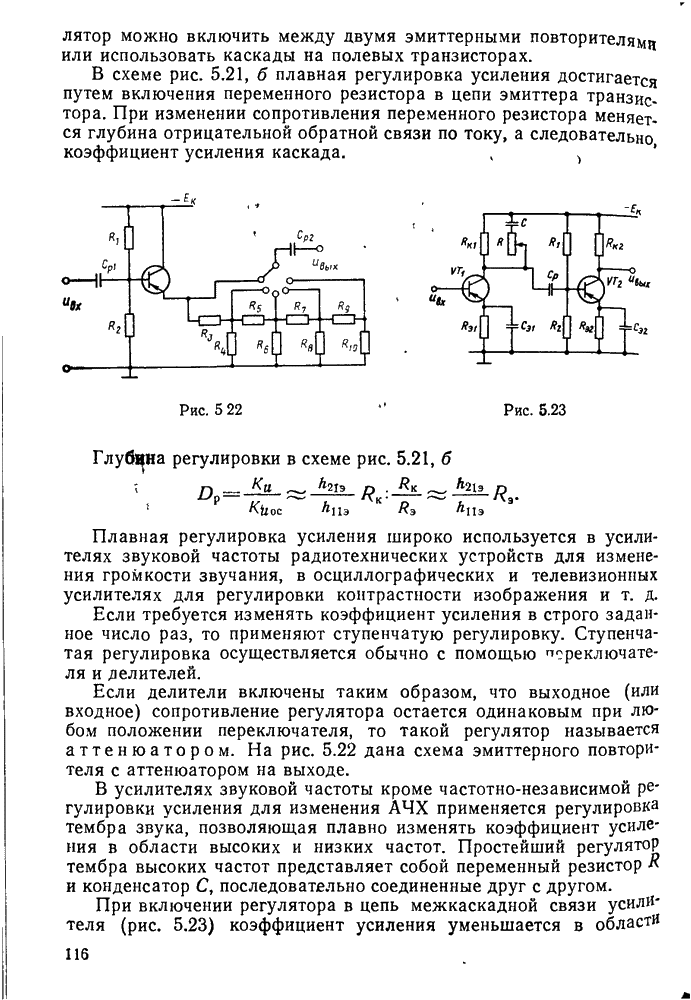
- § 5.5. Регулировка усиления сигнала в усилителях низкой частоты
- Вопросы и задачи для самопроверки
- ГЛАВА 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- § 6.2. Эквивалентная схема и основные параметры
- Области применения операционных усилителей
- § 6.3. Линейные схемы на операционных усилителях
- § 6.4. Устойчисвость и частотная коррекция операционных усилителей
- § 6.5. Работа операционного усилителя на низкоомную нагрузку
- Вопросы и задачи для самопроверки
- ГЛАВА 7. РЕЛЕЙНЫЕ СХЕМЫ
- § 7.1. Электромагнитные контактные реле. Общие сведения и основные параметры
- § 7.2. Электронные реле
- § 7.3. Электронные реле времени
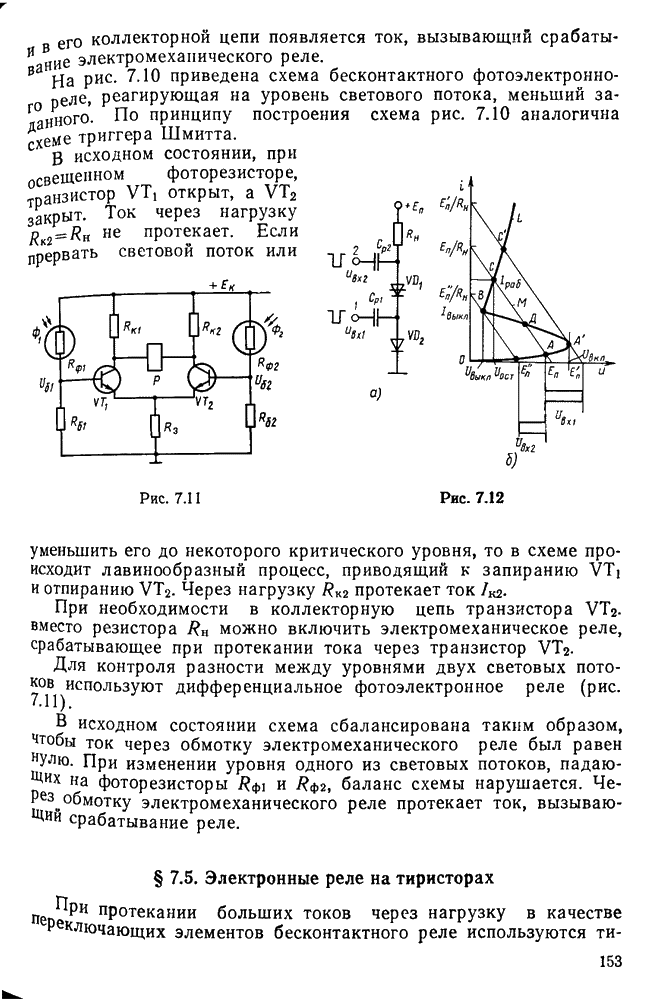
- § 7.4. Фотоэлектронные реле
- § 7.5. Электронные реле на тиристорах
- РАЗДЕЛ II. ВЫПРЯМИТЕЛИ И СТАБИЛИЗАТОРЫ
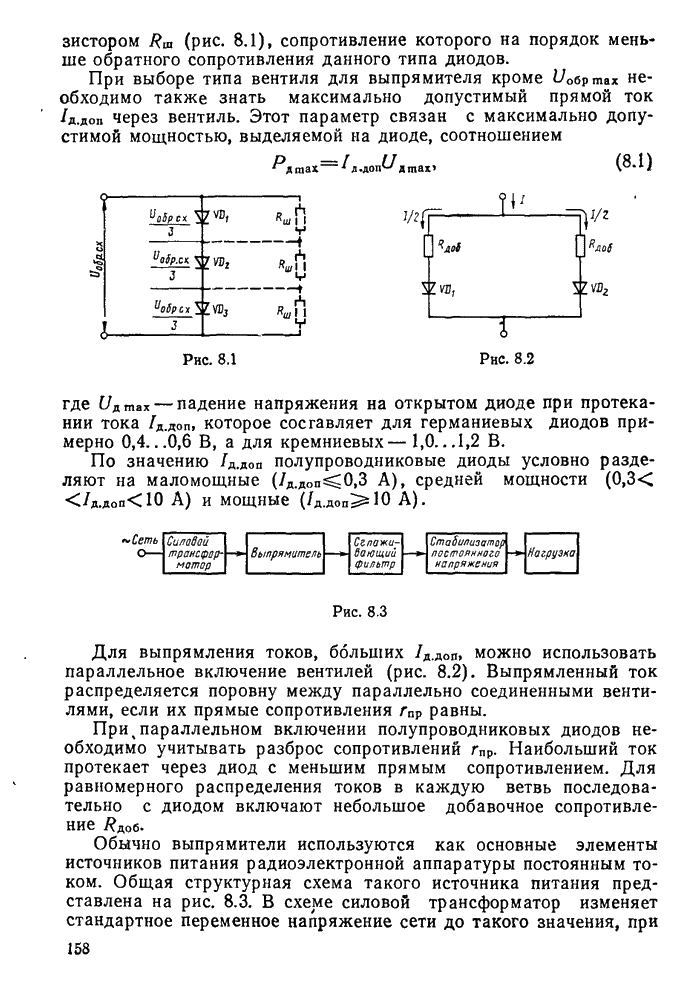
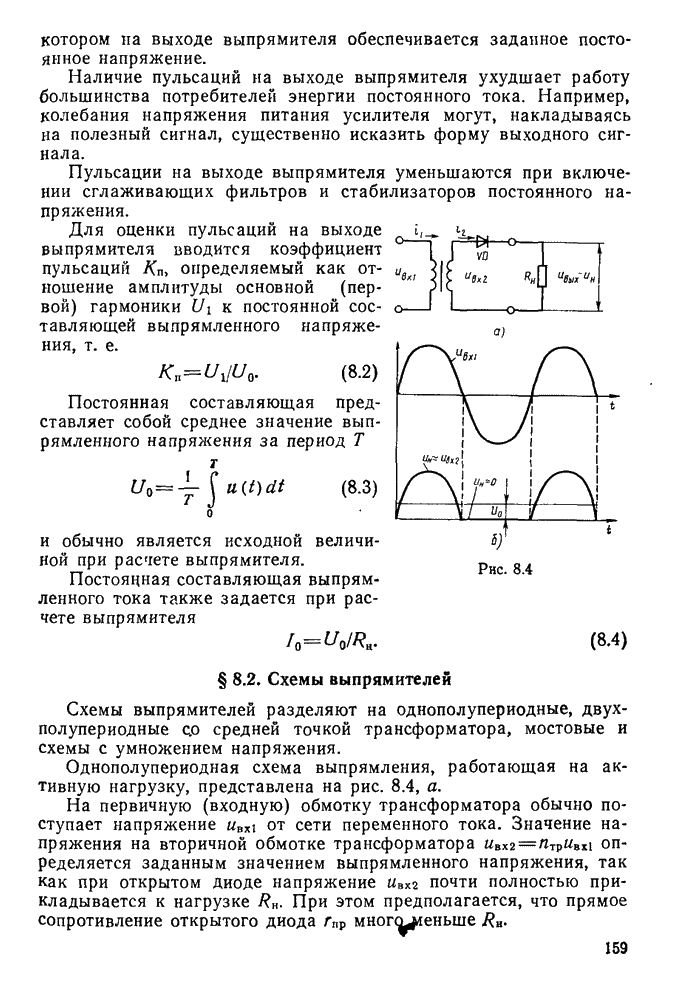
- § 8.1. Определение и параметры выпрямителя
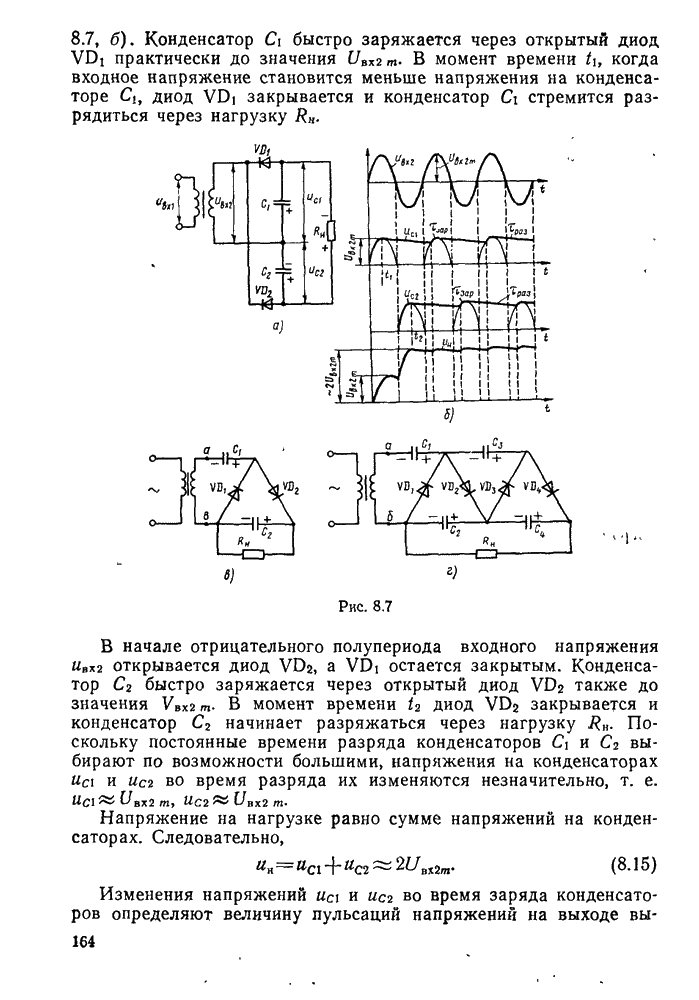
- § 8.2. Схемы выпрямителей
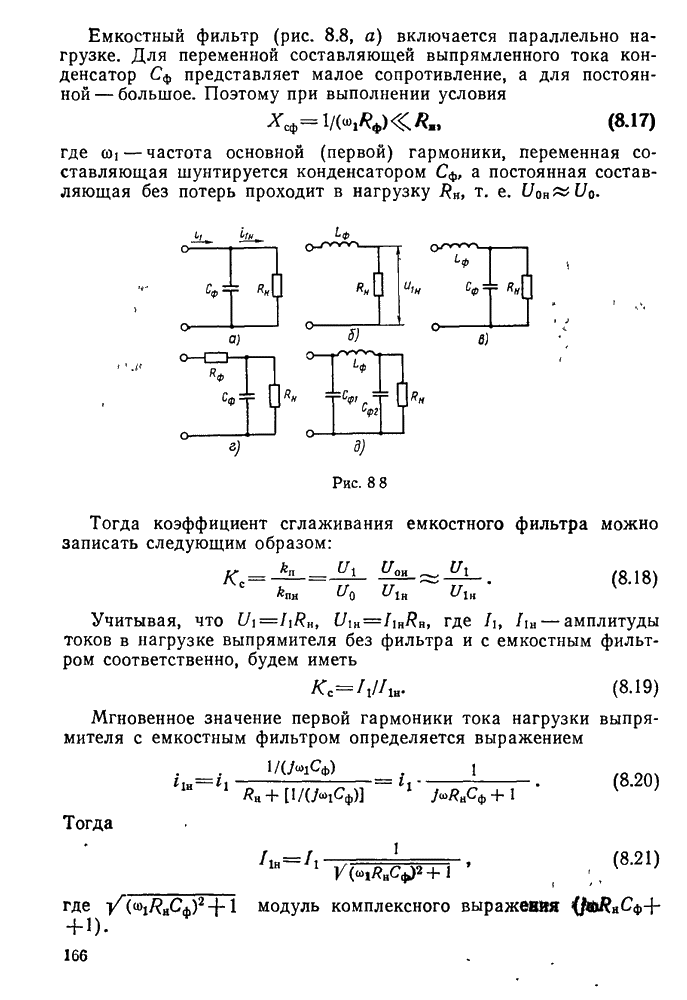
- § 8.3. Сглаживающие фильтры
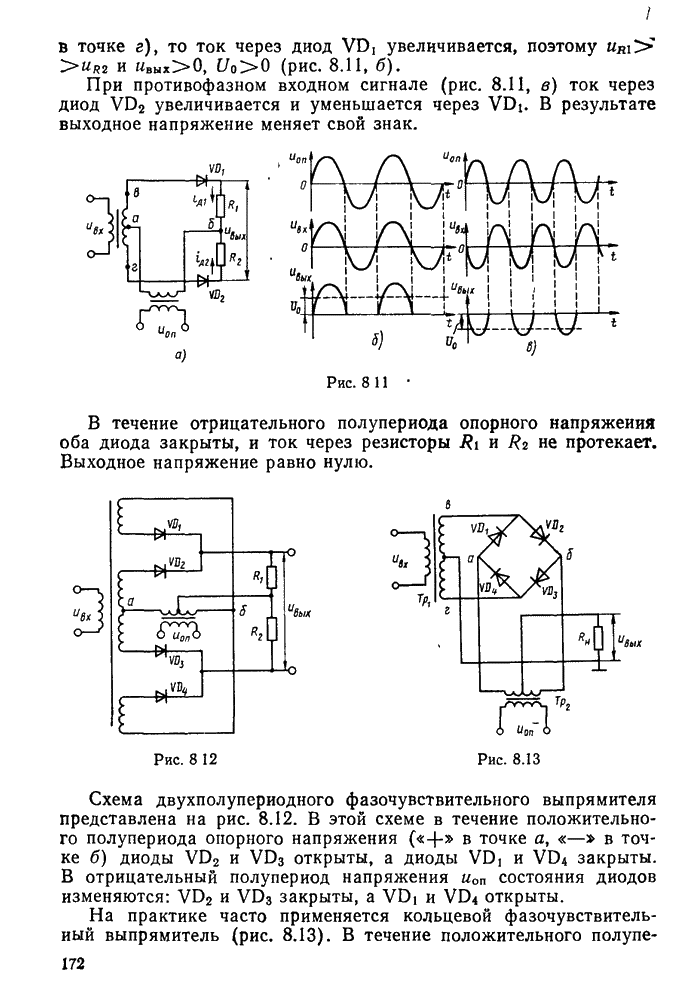
- § 8.4. Фазочувстительные выпрямители и усилители
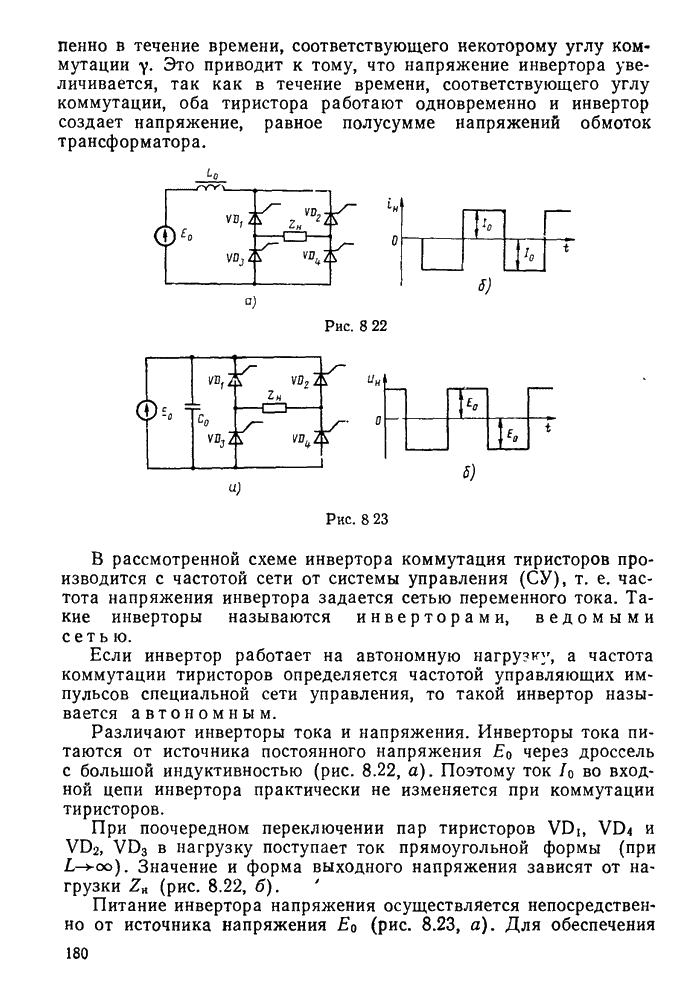
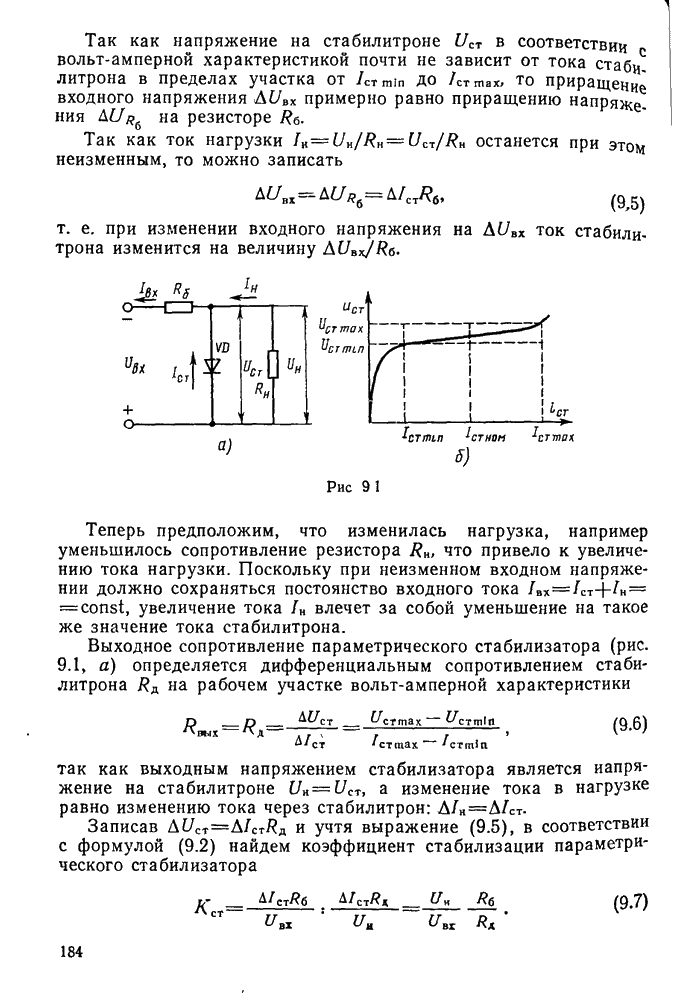
- § 8.5. Управляемые выпрямители и инверторы
- Вопросы и задачи для самопроверки
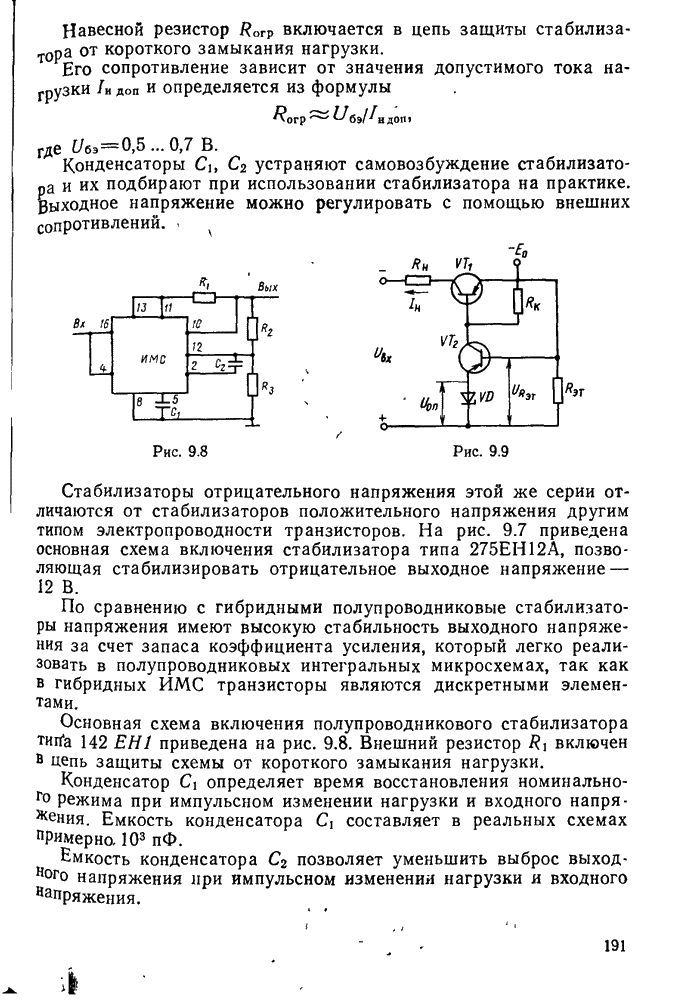
- ГЛАВА 9. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ И ТОКА
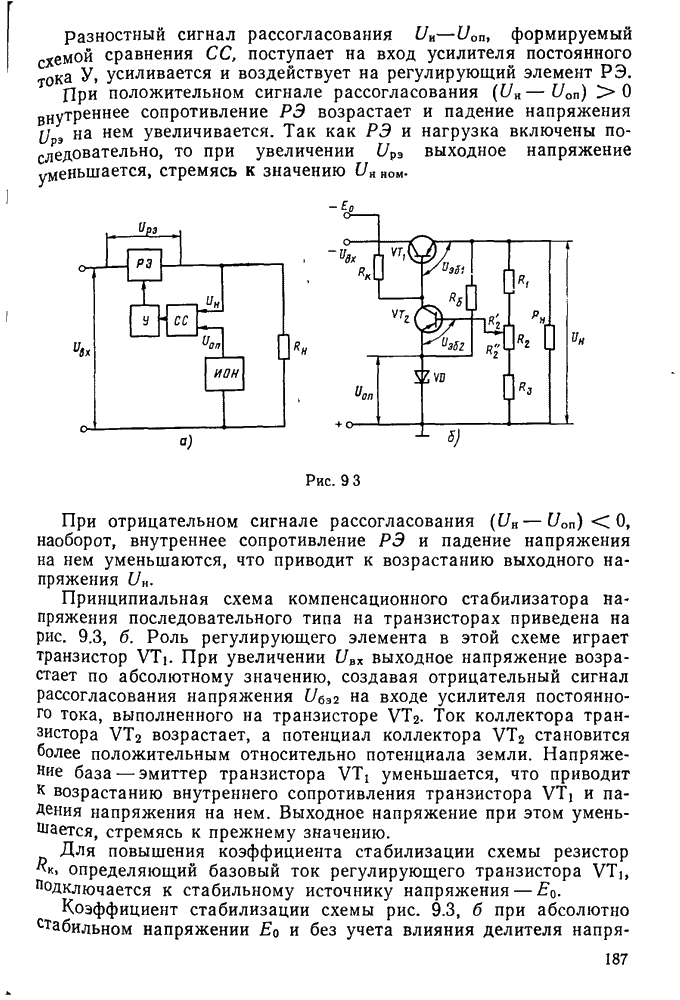
- § 9.1. Параметрические стабилизаторы
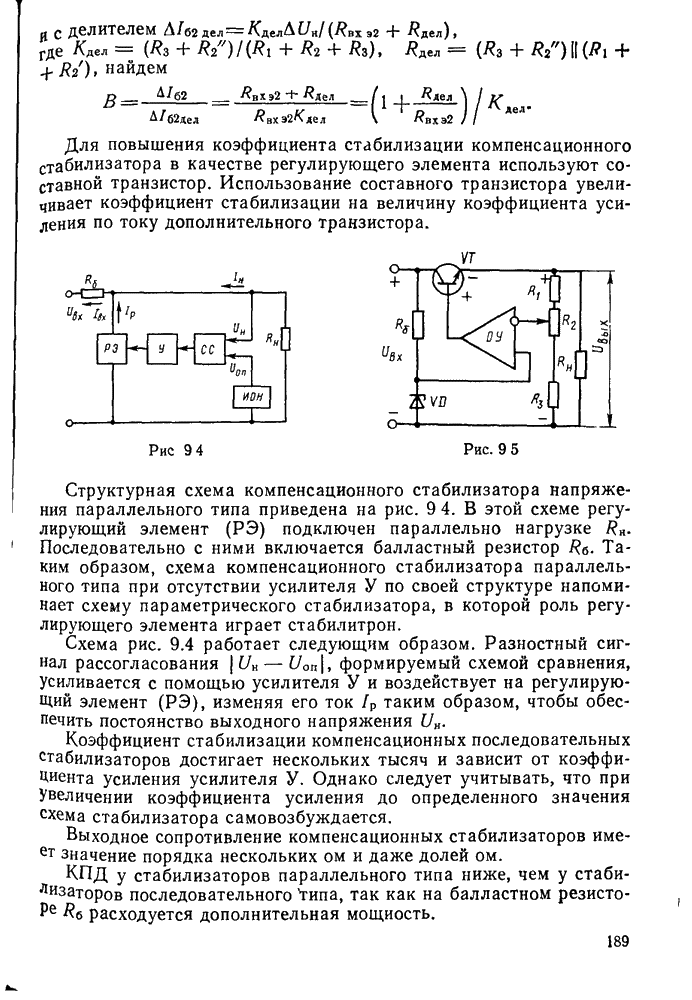
- § 9.2. Компенсационные стабилизаторы
- Расчет компенсационного стабилизатора непрерывного действия
- Вопросы и задачи для самопроверки
- РАЗДЕЛ III. ПРИНЦИП РАДИОСВЯЗИ. ИЗБИРАТЕЛЬНЫЕ СХЕМЫ
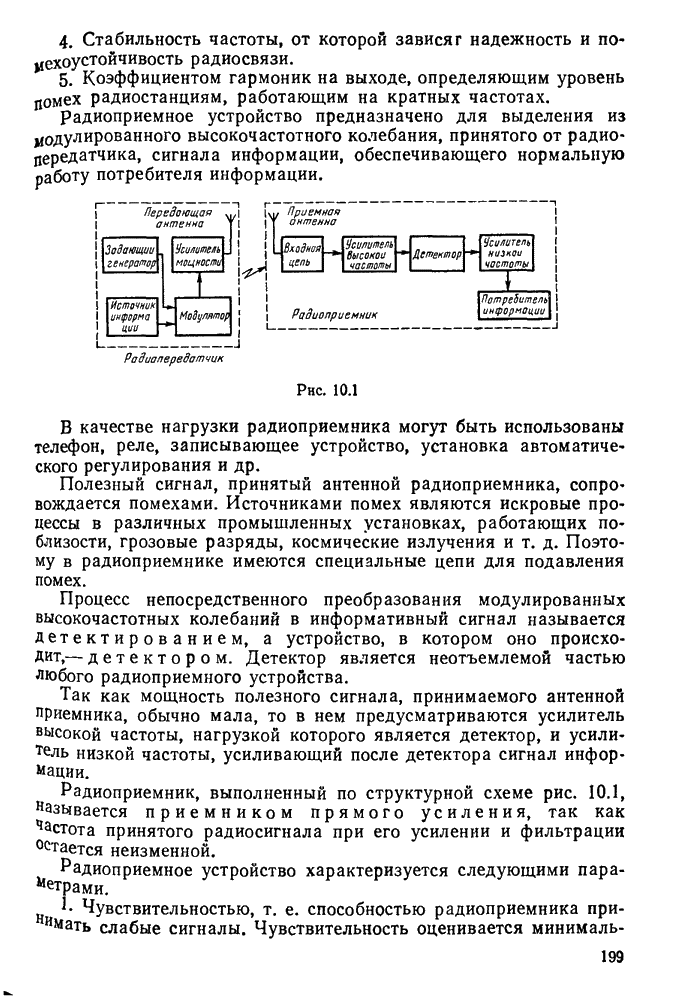
- § 10.1. Основные параметры радиопередающих и радиоприемных устройств
- § 10.2. Радиоприемник супергетеродинного типа
- Вопросы и задачи для самопроверки
- ГЛАВА 11. КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ
- § 11.1. Свободные колебания в контуре
- § 11.2. Вынужденные колебания в последовательном контуре
- § 11.3. Вынужденные колебания в параллельном контуре
- § 11.4. Вынужденные колебания в связанных контурах
- Вопросы и задачи для самопроверки
- ГЛАВА 12. ГЕНЕРАТОРЫ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- § 12.1. Принципы построения генераторов
- § 12.2. Генератор с фазовращающей RC-цепью
- Расчет генератора низкой частоты
- § 12.3. Генератор с мостом Вина в цепи обратной связи
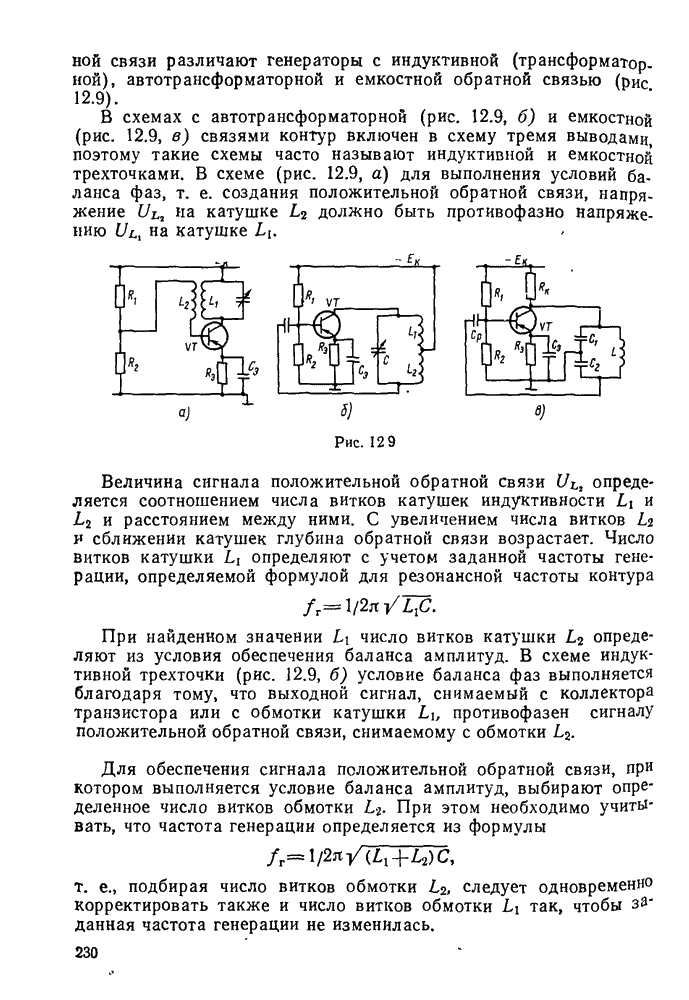
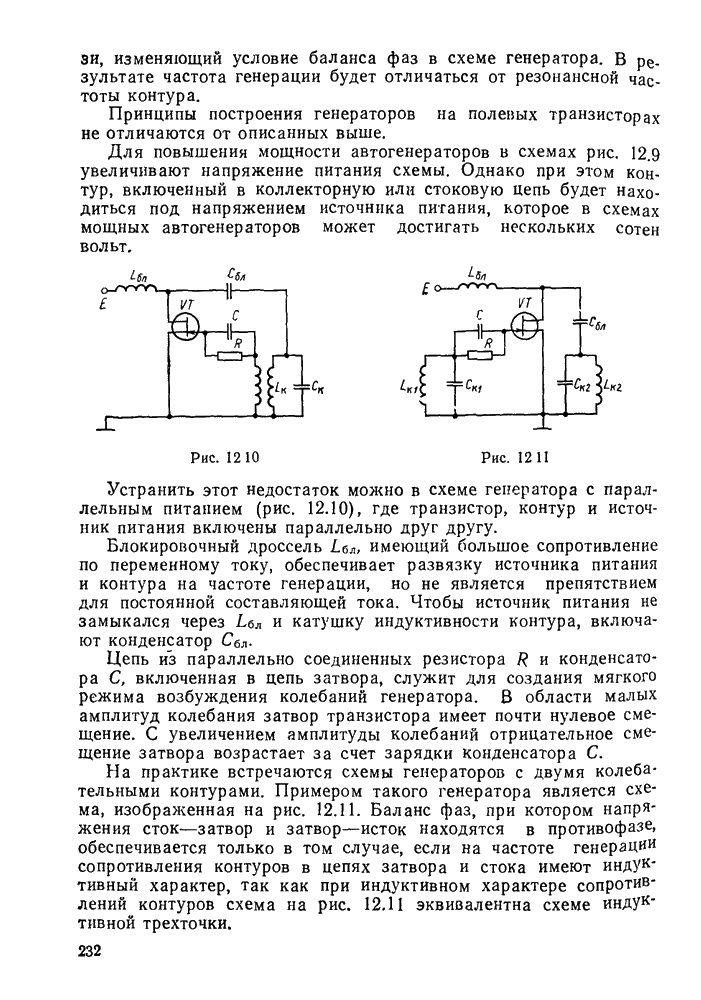
- § 12.4. Генераторы с колебательными контурами
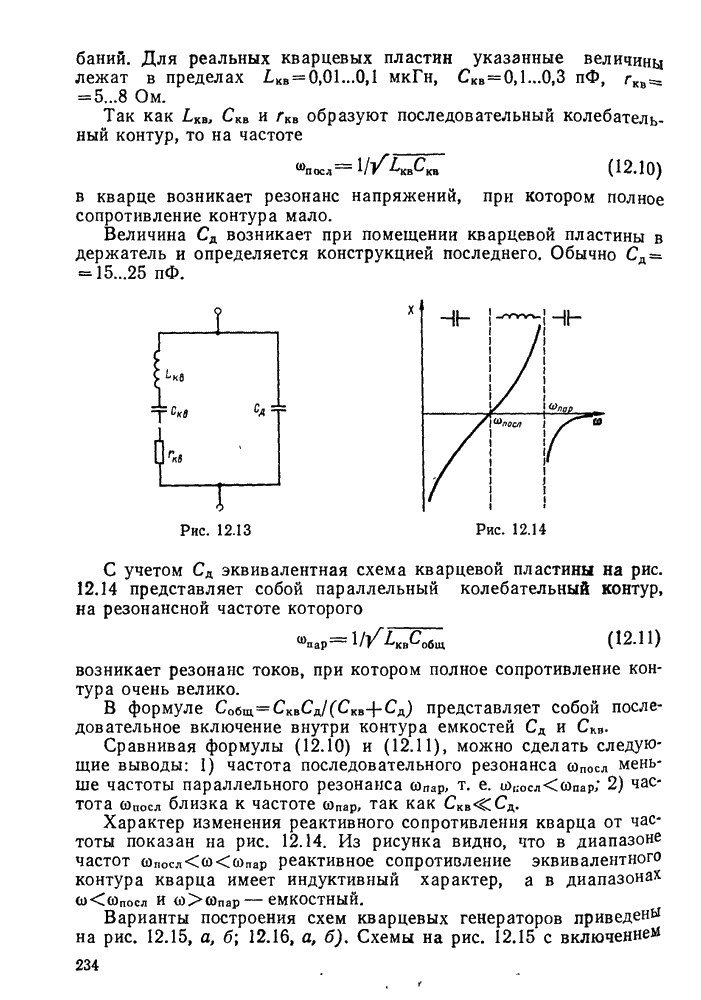
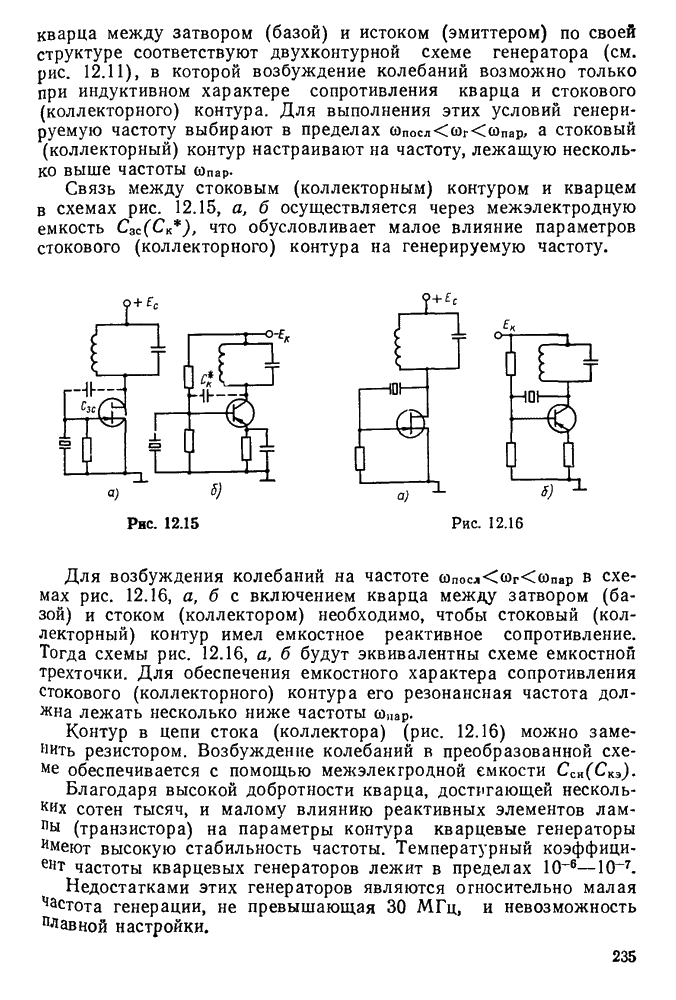
- § 12.5. Стабилизация частоты LC-генераторов. Кварцевые генераторы
- ГЛАВА 13. ИЗБИРАТЕЛЬНЫЕ УСИЛИТЕЛИ
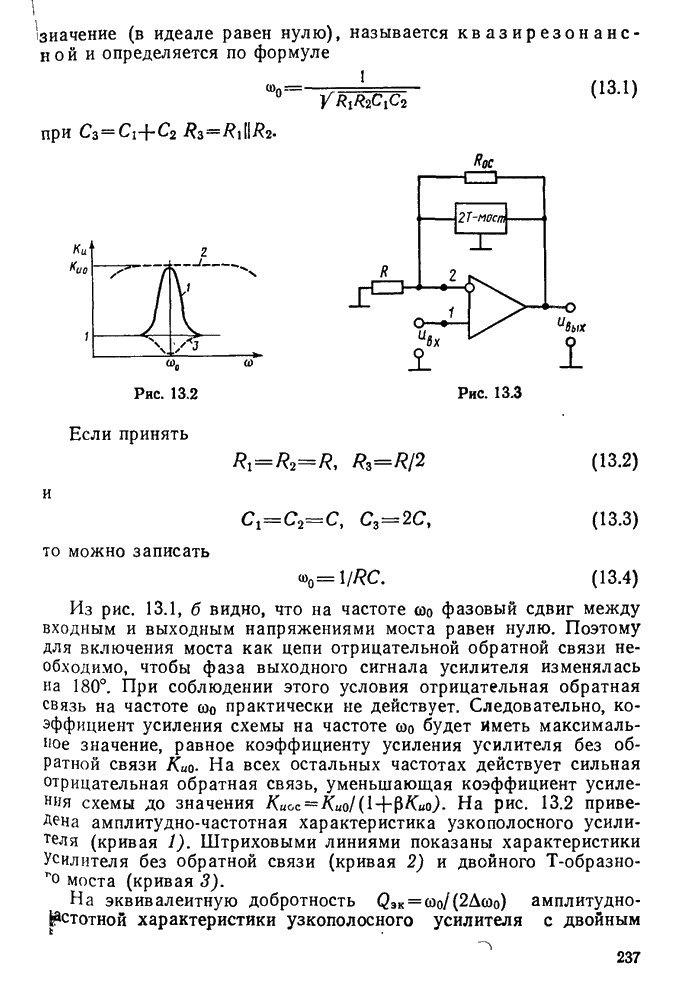
- § 13.1. Узкополосные RC-усилители
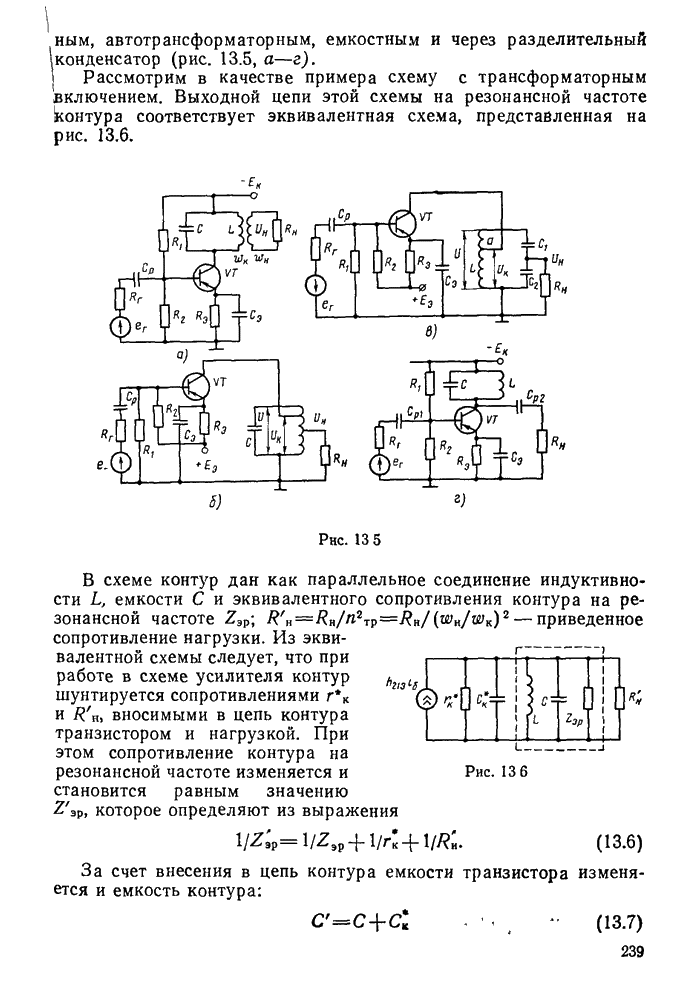
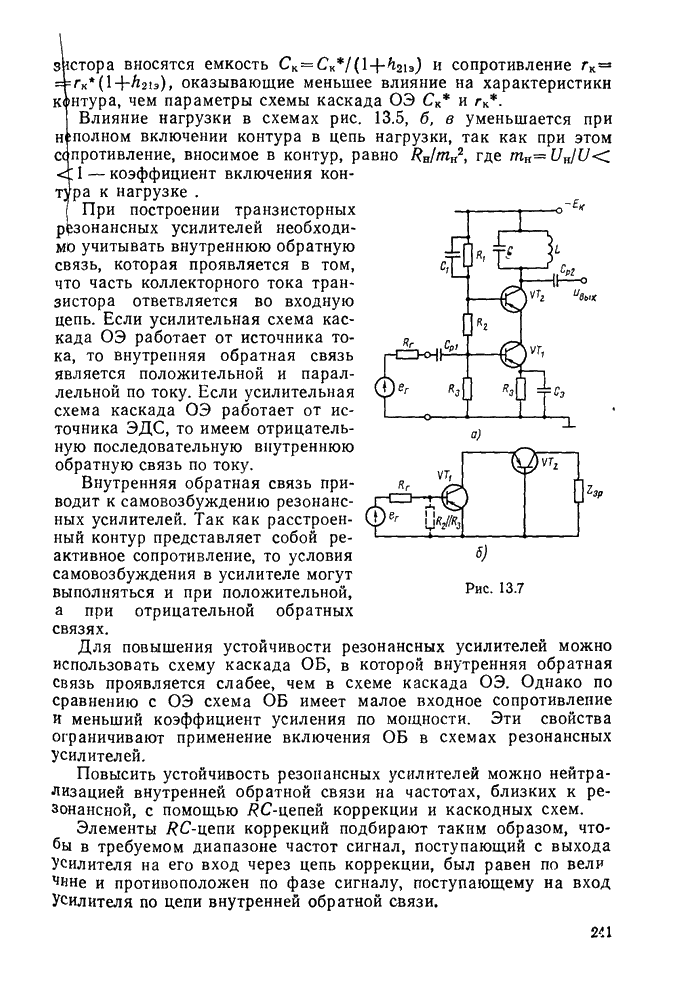
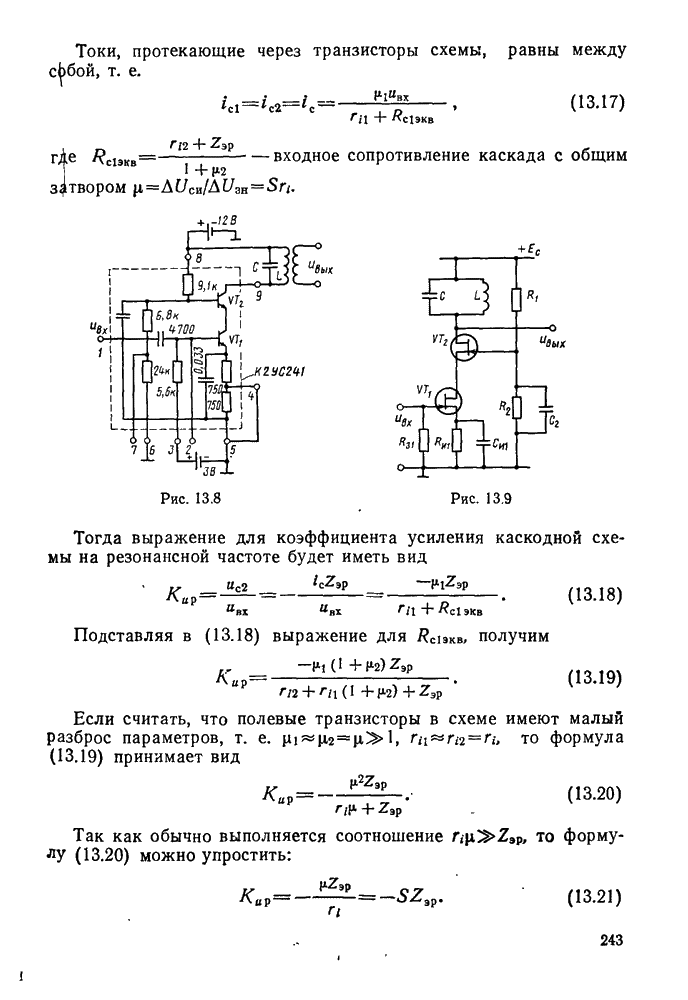
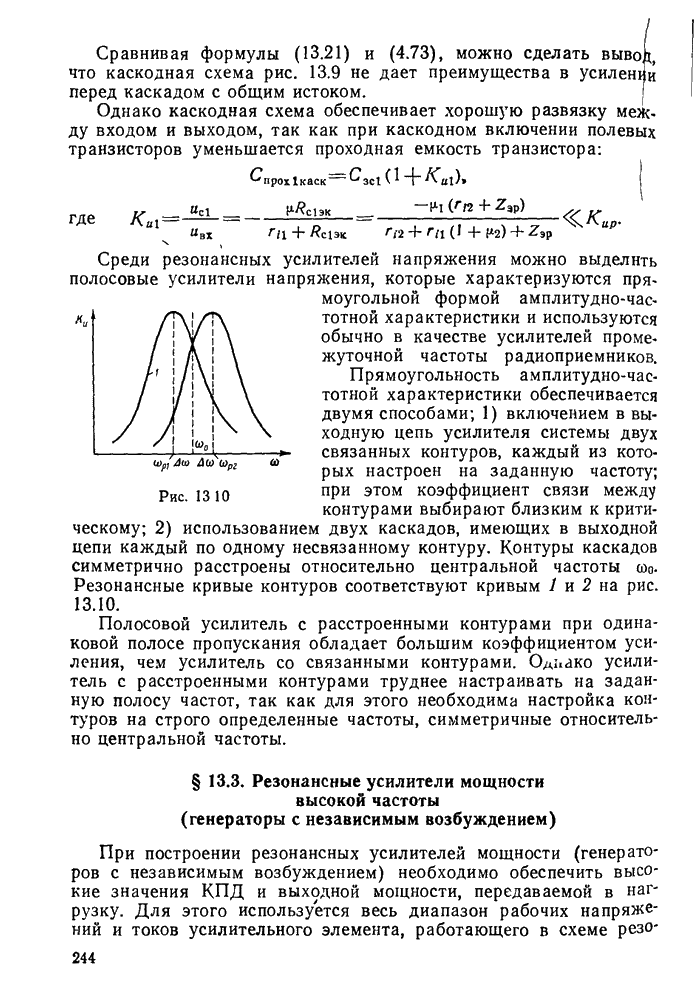
- § 13.2. Резонансные усилители напряжения высокой частоты
- § 13.3. Резонансные усилители мощности высокой частоты (генераторы с независимым возбуждением)
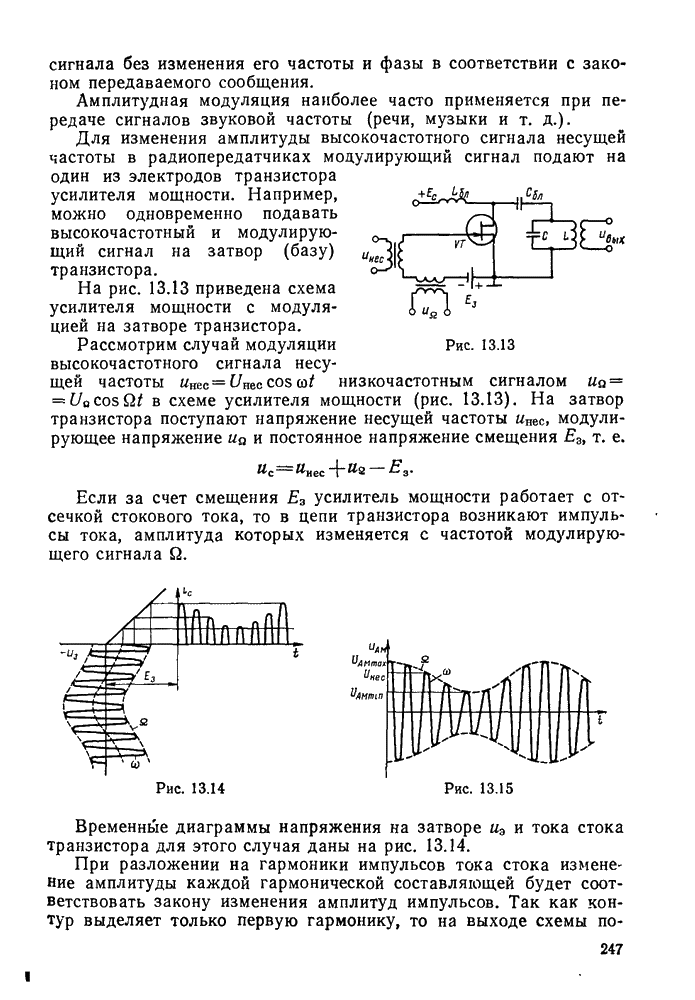
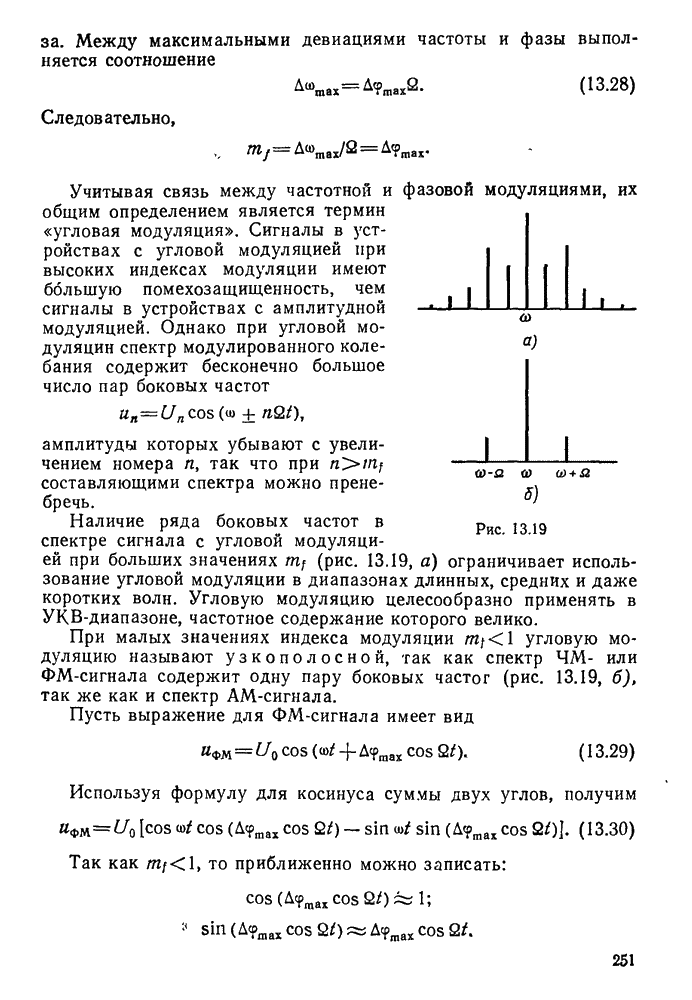
- § 13.4. Модуляция высокочастотного сигнала
- ЛИТЕРАТУРА