| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
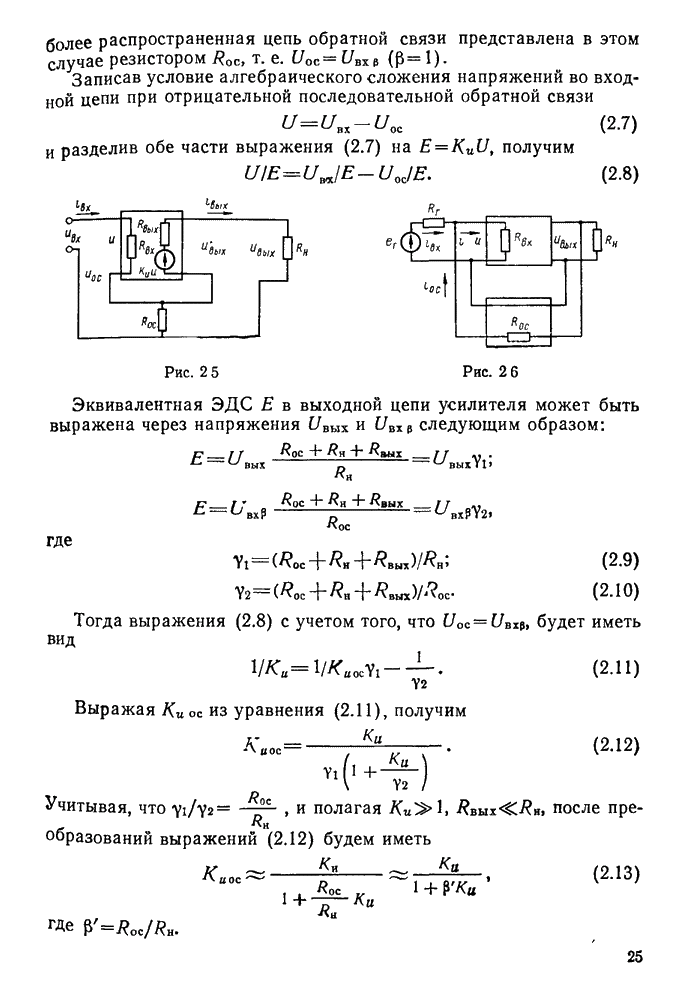
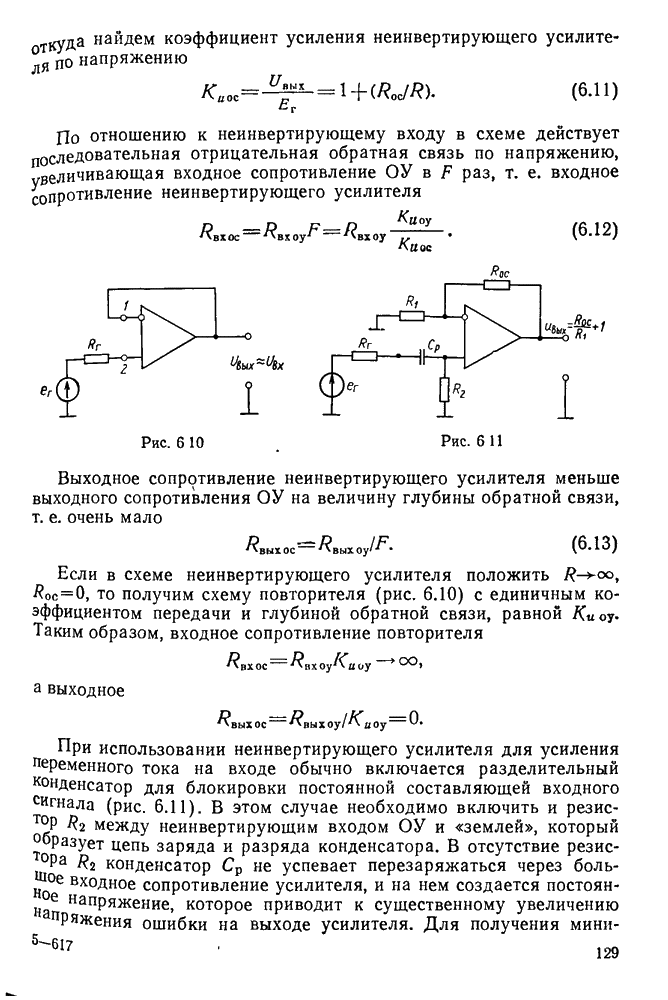
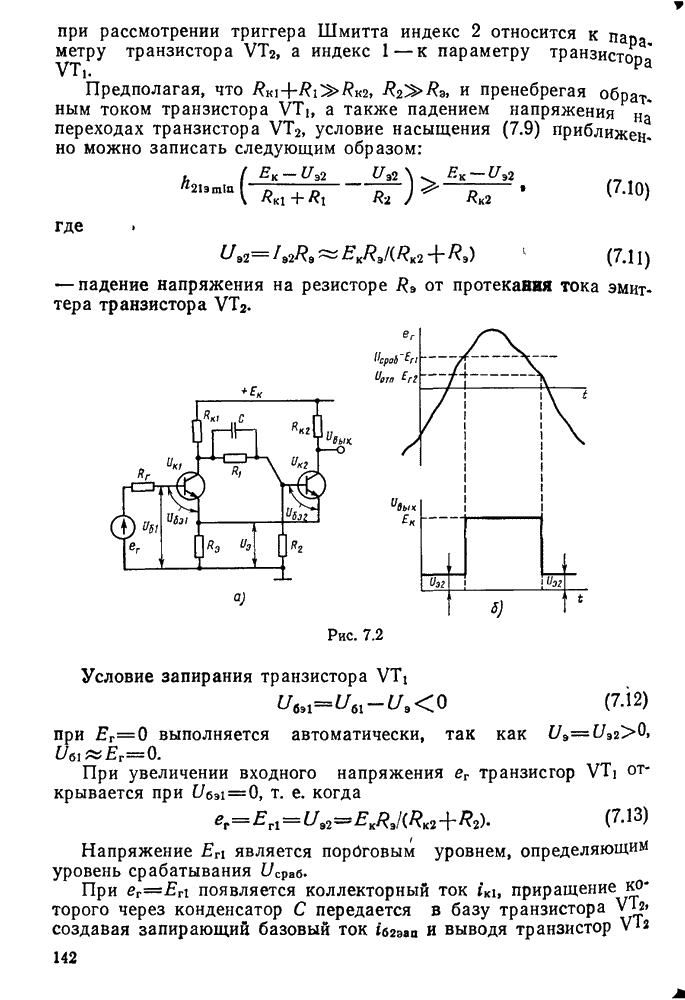
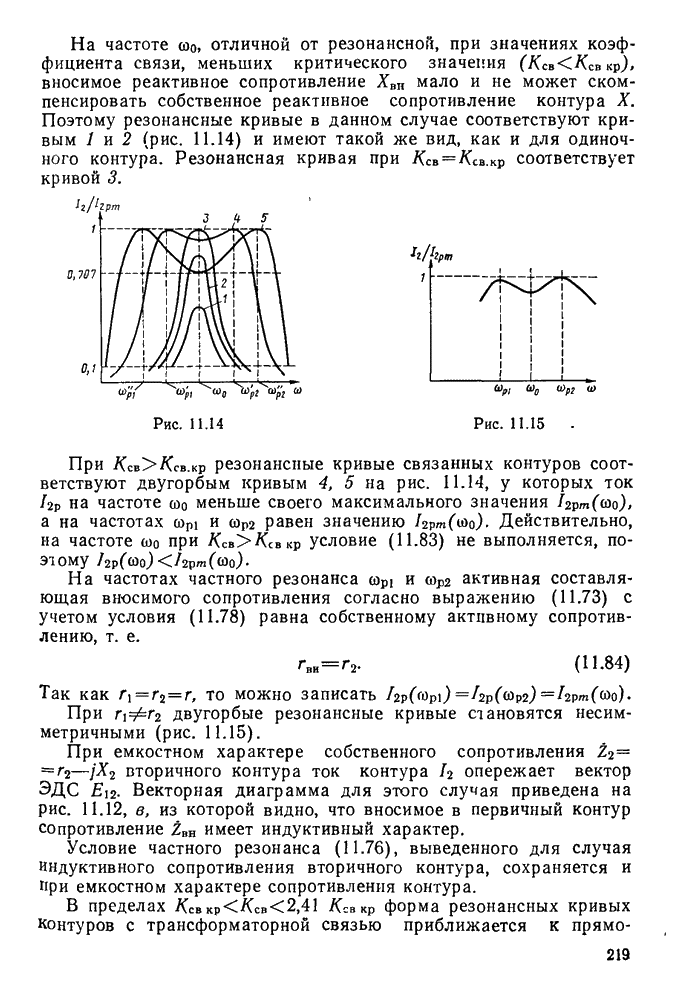
§ 11.2. Вынужденные колебания в последовательном контуре
Под действием переменной ЭДС  в последовательном контуре протекает переменный ток
в последовательном контуре протекает переменный ток
 (11.18)
(11.18)
где
 (11.19)
(11.19)
 — полное сопротивление контура);
— полное сопротивление контура);  — реактивные сопротивления катушки индуктивности и конденсатора. Полное реактивное сопротивление контура
— реактивные сопротивления катушки индуктивности и конденсатора. Полное реактивное сопротивление контура
 (11.20)
(11.20)
Амплитуда тока в контуре определяется выражением
 (11.21)
(11.21)
где
 (11.22)
(11.22)
— модуль полного сопротивления.
По закону Кирхгофа, напряжение  , приложенное к контуру, складывается из напряжения на конденсаторе
, приложенное к контуру, складывается из напряжения на конденсаторе  , катушке индуктивности
, катушке индуктивности  и активном сопротивлении
и активном сопротивлении  . Амплитуды этих напряжений соответственно равны
. Амплитуды этих напряжений соответственно равны
 (11.23)
(11.23)
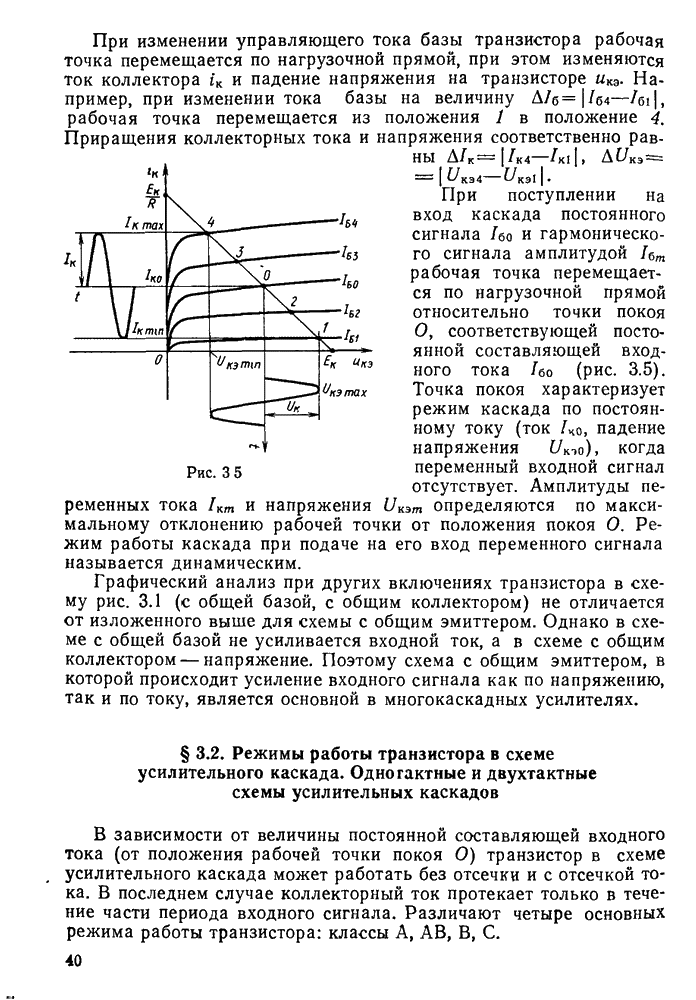
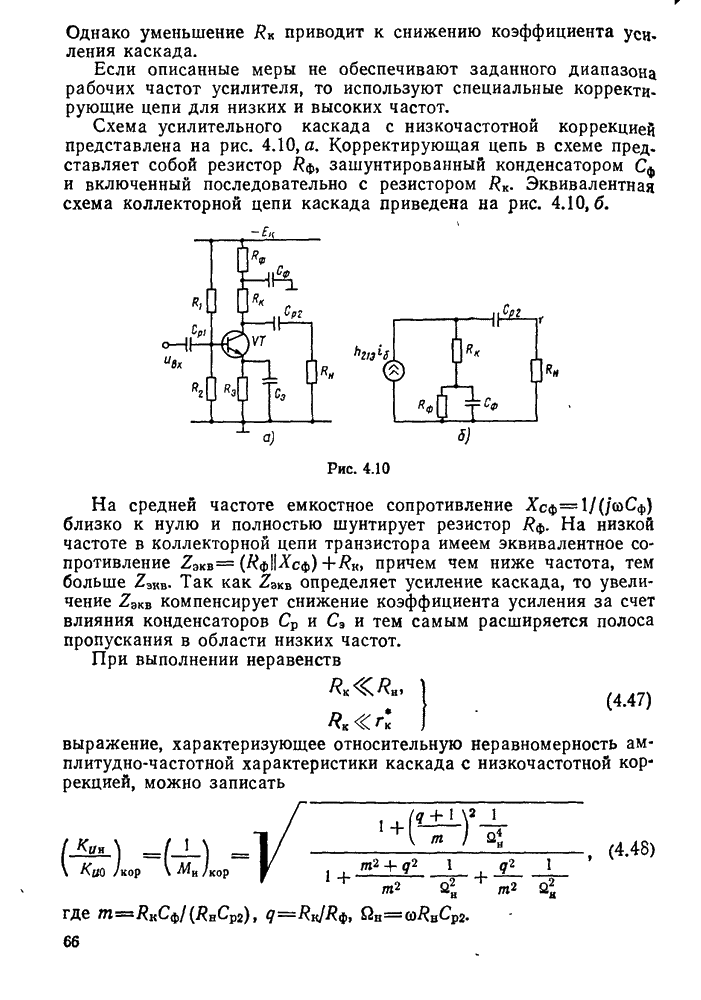
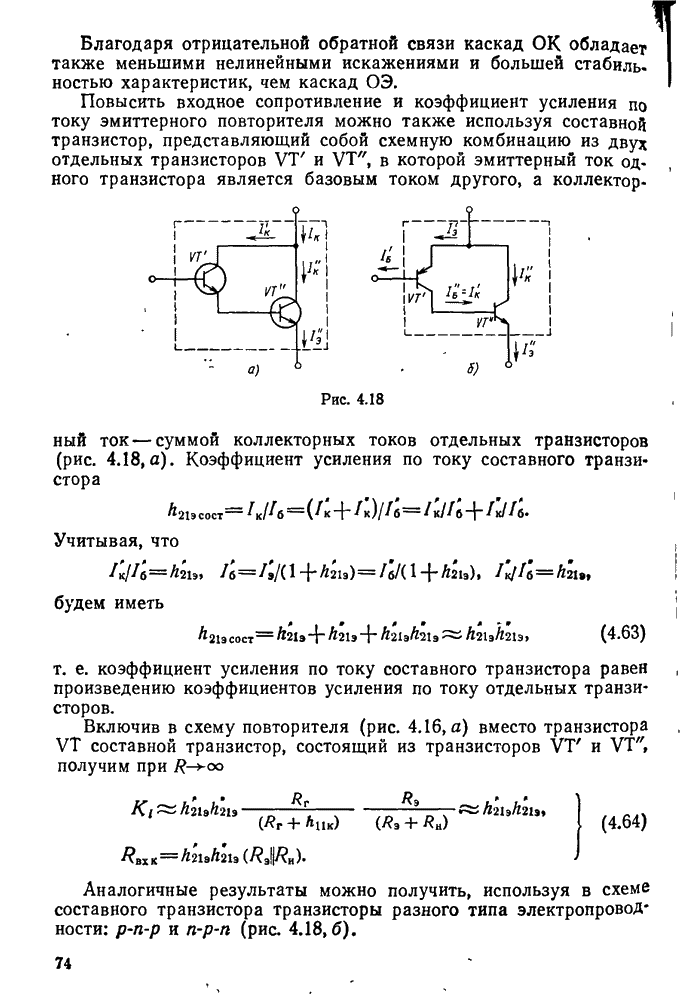
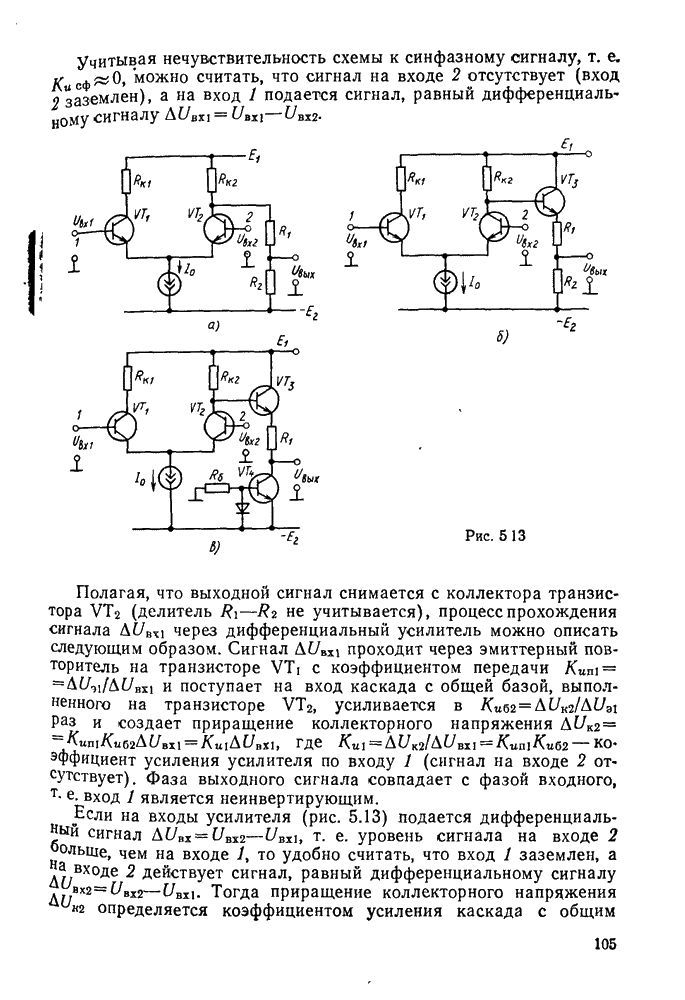
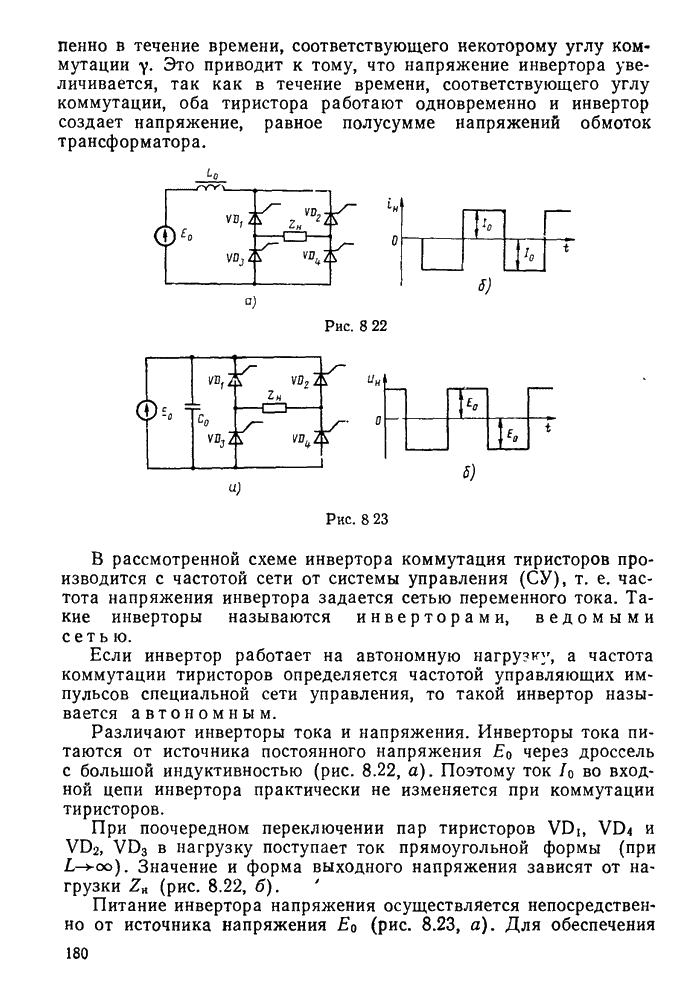
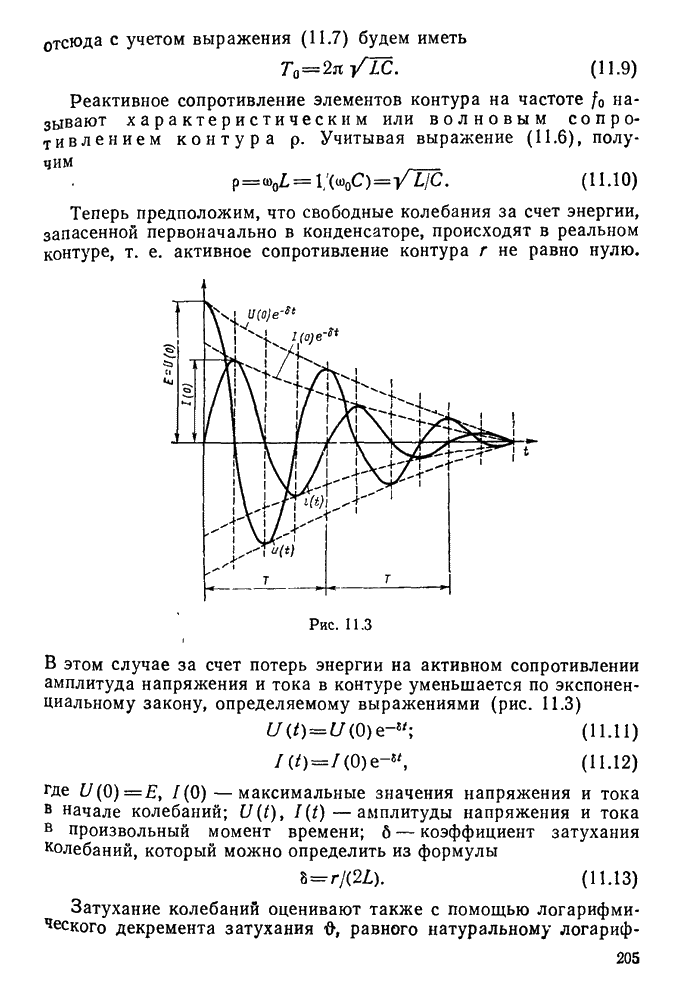
Наглядное представление о характере изменений напряжений и токов в контуре может дать векторная диаграмма (рис. 11.6), построенная на основании следующих положений. Напряжение на активном сопротивлении совпадает по фазе с током, на конденсаторе оно отстает от тока на 90°, а на индуктивности опережает ток тоже на 90°. Вектор напряжения Е равен геометрической сумме векторов  .
.
При изменении частоты со источника переменной ЭДС, приложенного к контуру, меняется реактивное сопротивление X контура.
На низких частотах реактивное сопротивление контура имеет емкостный характер, потому что в формуле (11.19) можно пренебречь членом  , а на высоких частотах — индуктивный, так как в этом случае можно пренебречь членом
, а на высоких частотах — индуктивный, так как в этом случае можно пренебречь членом  .
.
На некоторой частоте  , называемой резонансной, реактивное сопротивление контура
, называемой резонансной, реактивное сопротивление контура
 (11.24)
(11.24)
а полное сопротивление в соотпетствии с формулой (11.19)
 (11.25)
(11.25)
Тогда амплитуда резонансного тока в контуре будет максимальной
 (11.26)
(11.26)
Идеальный последовательный контур  при резонансе можно считать цепью, замкнутой накоротко.
при резонансе можно считать цепью, замкнутой накоротко.
Из уравнения (11.24) легко найти выражение для резонансной частоты
 (11.27)
(11.27)
Сравнивая формулы (11.6) и (11.27), видим, что резонансная частота вынужденных колебаний в последовательном контуре равна частоте собственных колебаний, т. е.
 (11.28)
(11.28)
Запишем уравнение (11.24) в виде равенства
 (11.29)
(11.29)
Равенство (11.29) показывает, что при резонансе индуктивное сопротивление последовательного контура по величине равно емкостному.
Умножая левую и правую части равенства на ток  , получим
, получим
 (11.30)
(11.30)
или, учитывая выражения (11.23), будем иметь
 (11.31)
(11.31)
Таким образом, при резонансе в последовательном контуре амплитуды напряжений на конденсаторе контура  и катушке индуктивности
и катушке индуктивности  равны между собой.
равны между собой.

Рис. 11.6.
Разделив обе части равенства (11.31) на  , с учетом выражений (11.16), (11.23) и (11.26) получим
, с учетом выражений (11.16), (11.23) и (11.26) получим
 (11.32)
(11.32)
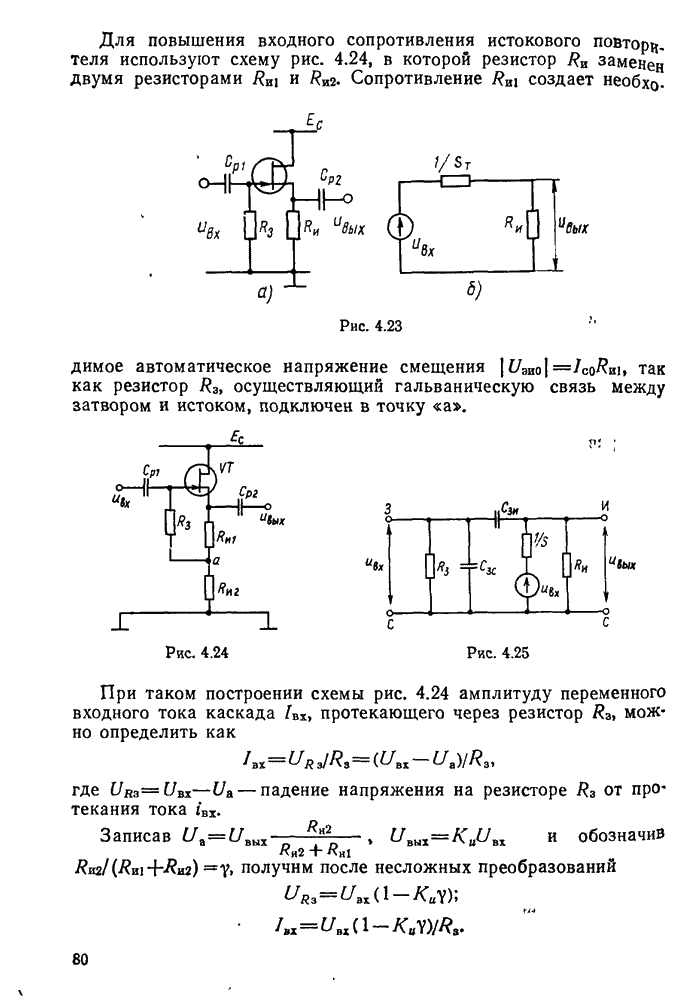
Выражение (11.32) показывает, что напряжение на катушке индуктивности или конденсаторе последовательного контура при резонансе превышает в Q раз ЭДС источника вынужденных колебаний.

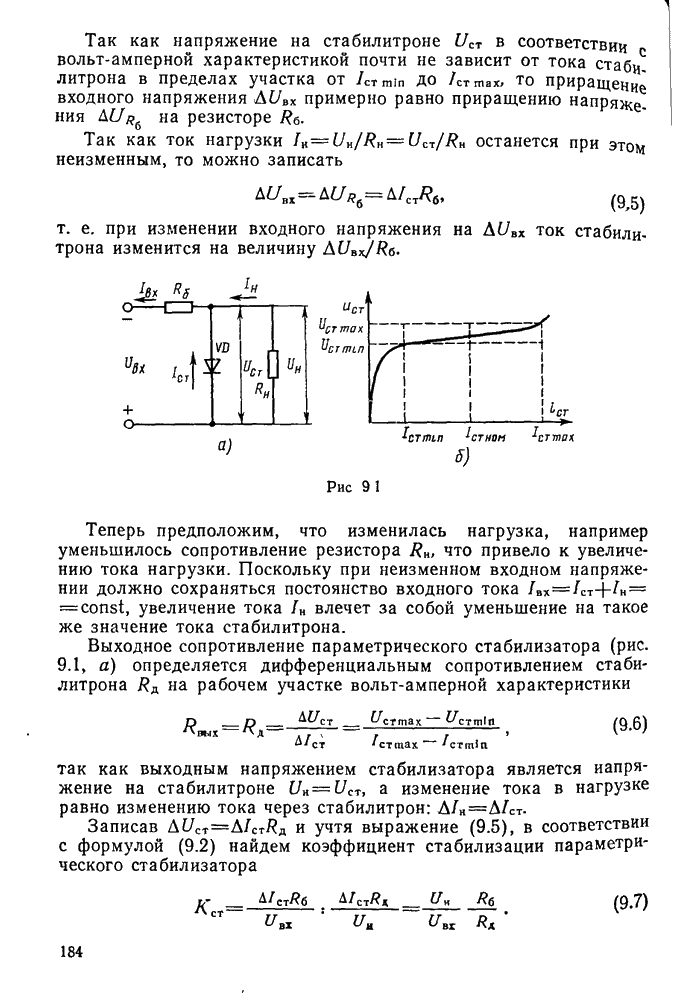
Рис. 11.7.
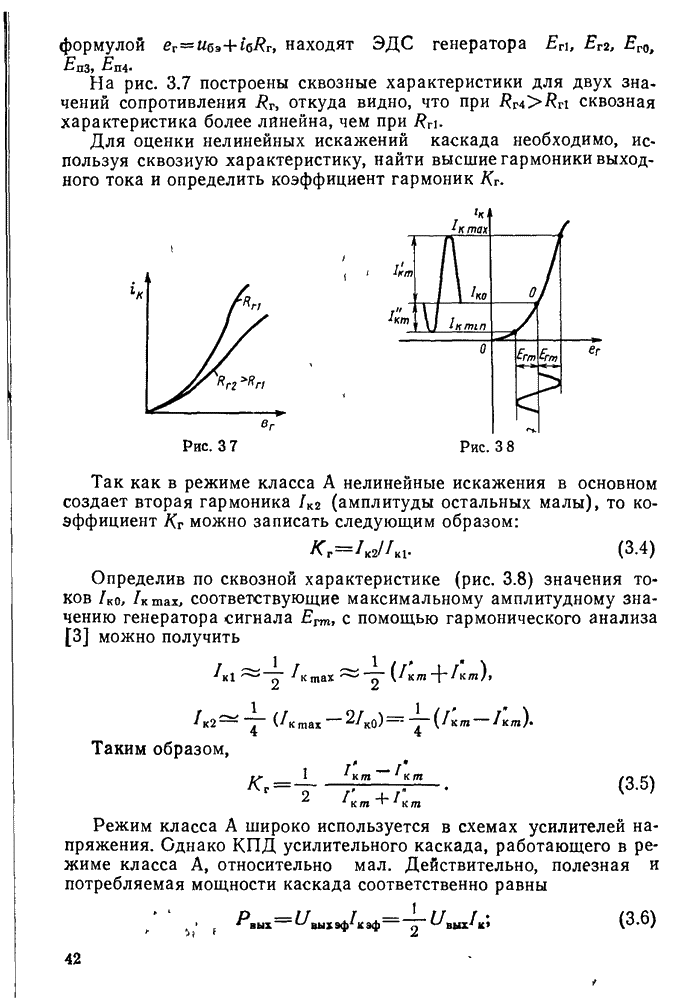
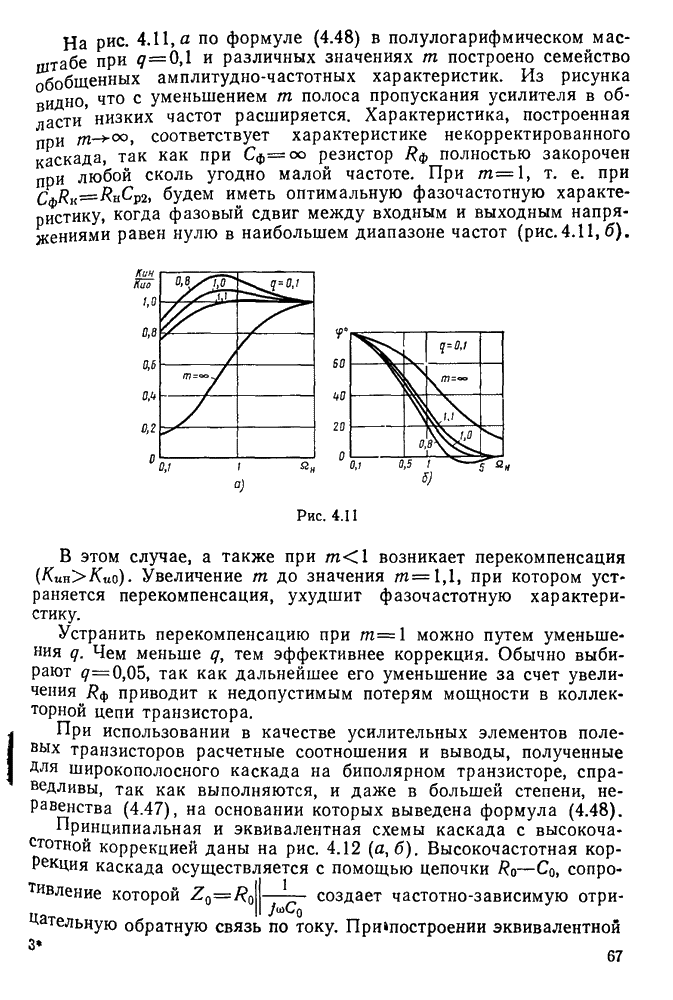
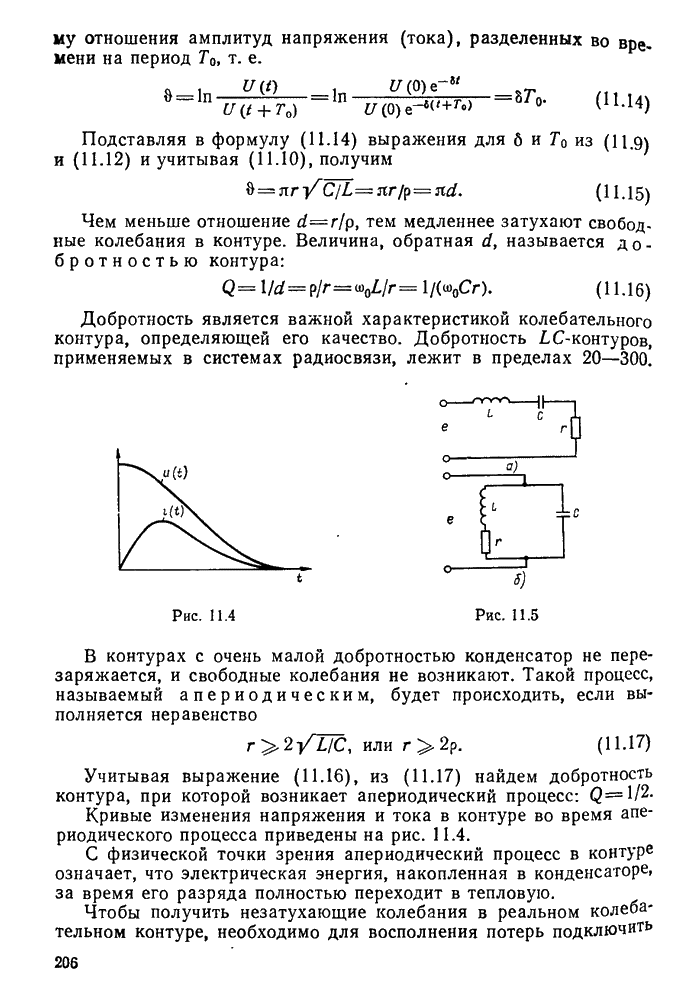
Векторная диаграмма напряжений и токов в последовательном контуре при резонансе приведена на рис. 11.7. Векторы напряжений  равны по величине и противоположны по направлению. Последнее означает, что переменные напряжения
равны по величине и противоположны по направлению. Последнее означает, что переменные напряжения  сдвинуты по фазе друг относительно друга на 180°. Вектор напряжения Е совпадает по направлению с вектором тока
сдвинуты по фазе друг относительно друга на 180°. Вектор напряжения Е совпадает по направлению с вектором тока  .
.

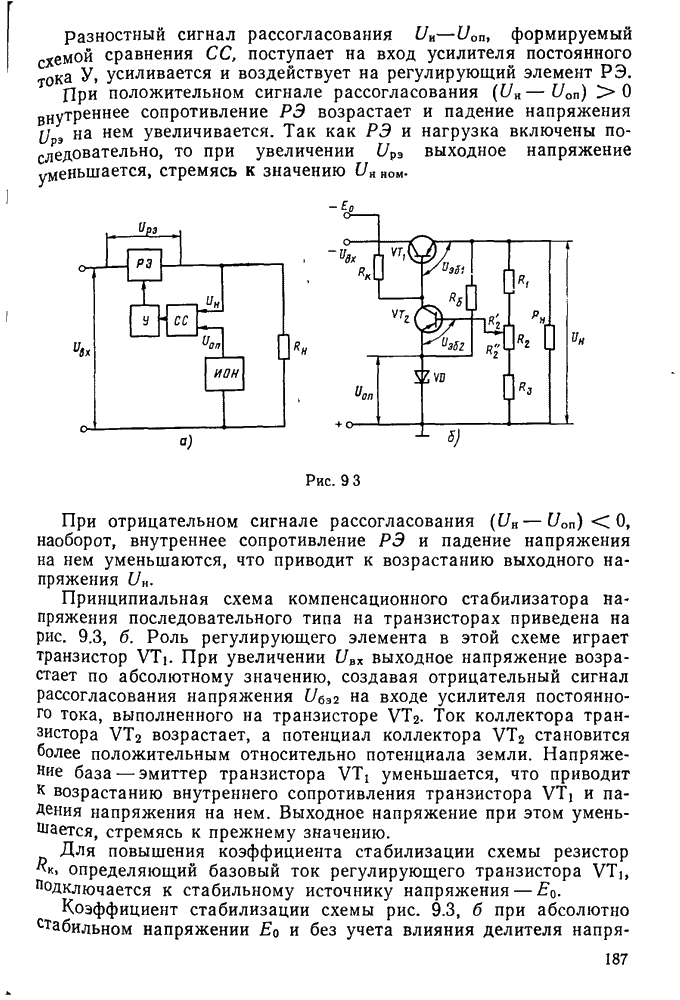
Рис. 11.8.
Резонансные свойства последовательного контура часто оценивают с помощью коэффициента избирательности по току  , показывающего, во сколько раз уменьшается ток в контуре при отклонении частоты на величину
, показывающего, во сколько раз уменьшается ток в контуре при отклонении частоты на величину  от резонансного значения
от резонансного значения  .
.
Учитывая выражения (11.21), (11.22) и (11.26), можно записать

или, разделив числитель и знаменатель на  , получаем
, получаем
 (11.34)
(11.34)
Подставляя в формулу (11.34) выражения для Q и  из (11.16) и (11.27), находим
из (11.16) и (11.27), находим

или после несложных преобразований
 (11.35)
(11.35)
При небольших отклонениях частоты  от резонансного значения можно записать
от резонансного значения можно записать
 (11.36)
(11.36)
С учетом принятого допущения выражение (11.35) будет иметь вид
 (11.37)
(11.37)
где  — так называемая расстройка контура.
— так называемая расстройка контура.
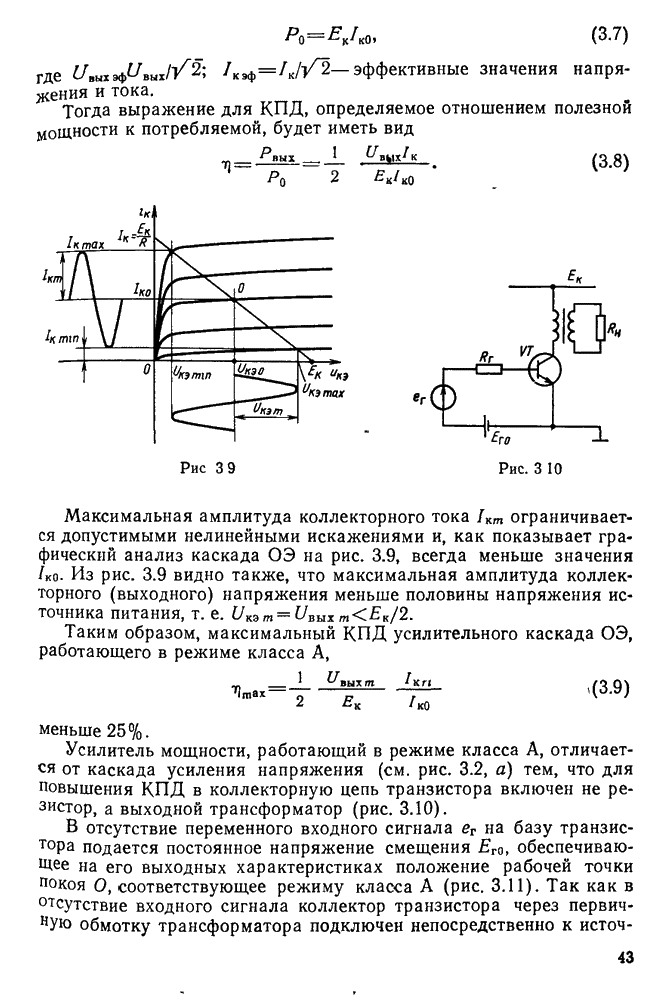
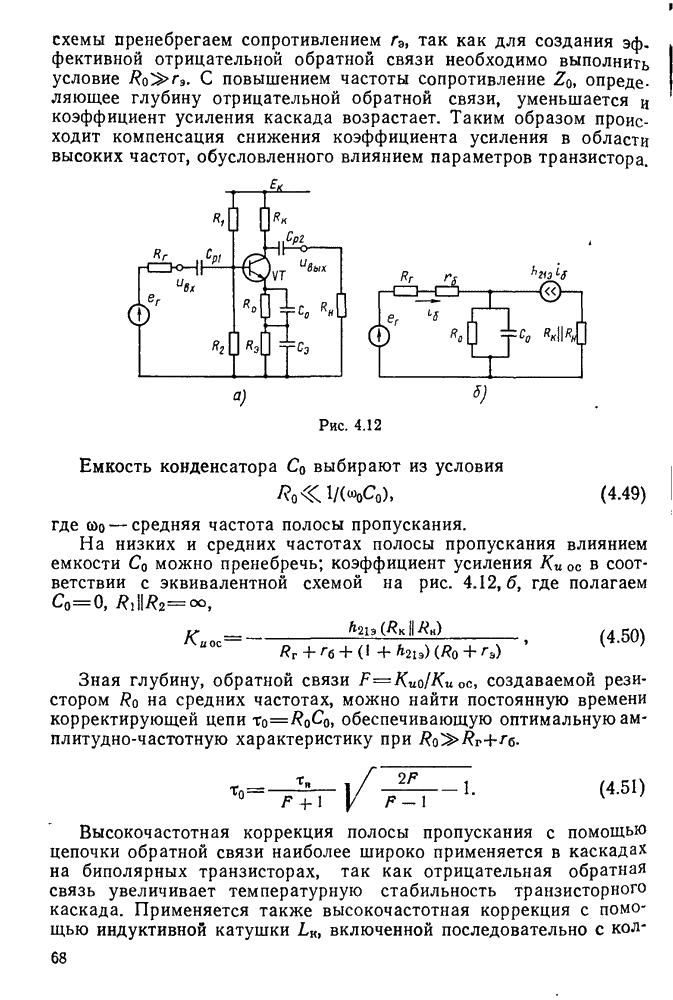
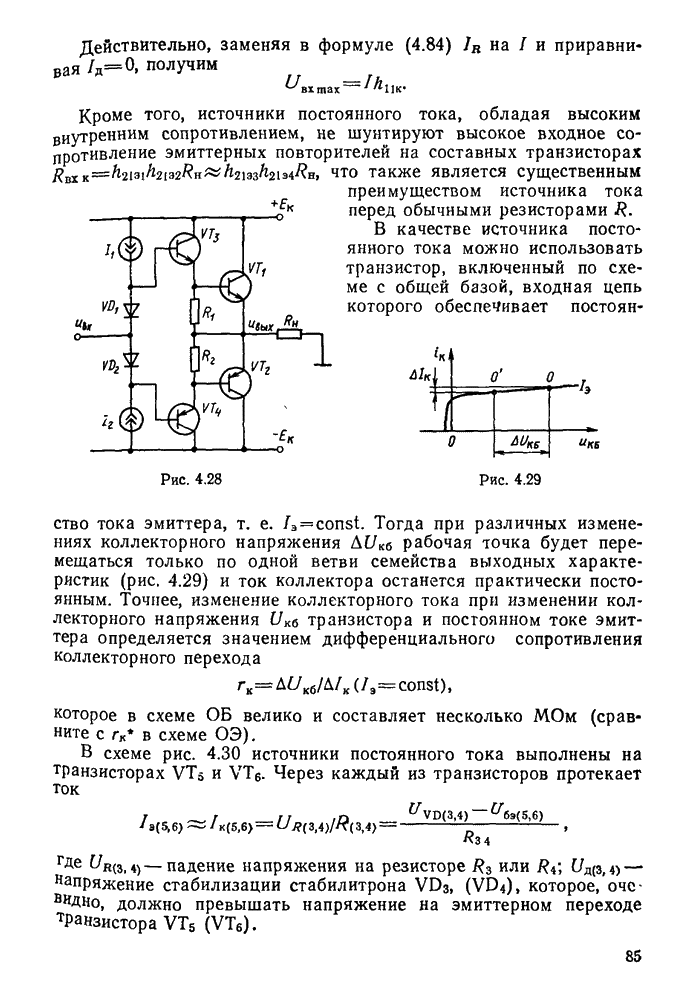
На основании выражения (11.37) можно построить резонансную кривую контура, характеризующую относительное изменение тока в контуре при его расстройке.
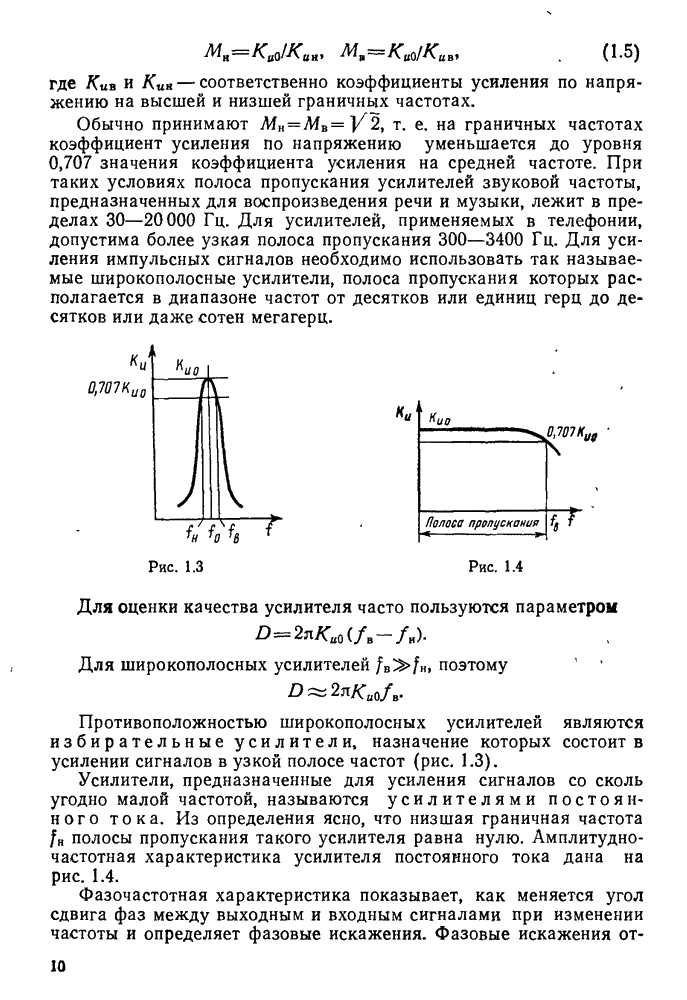
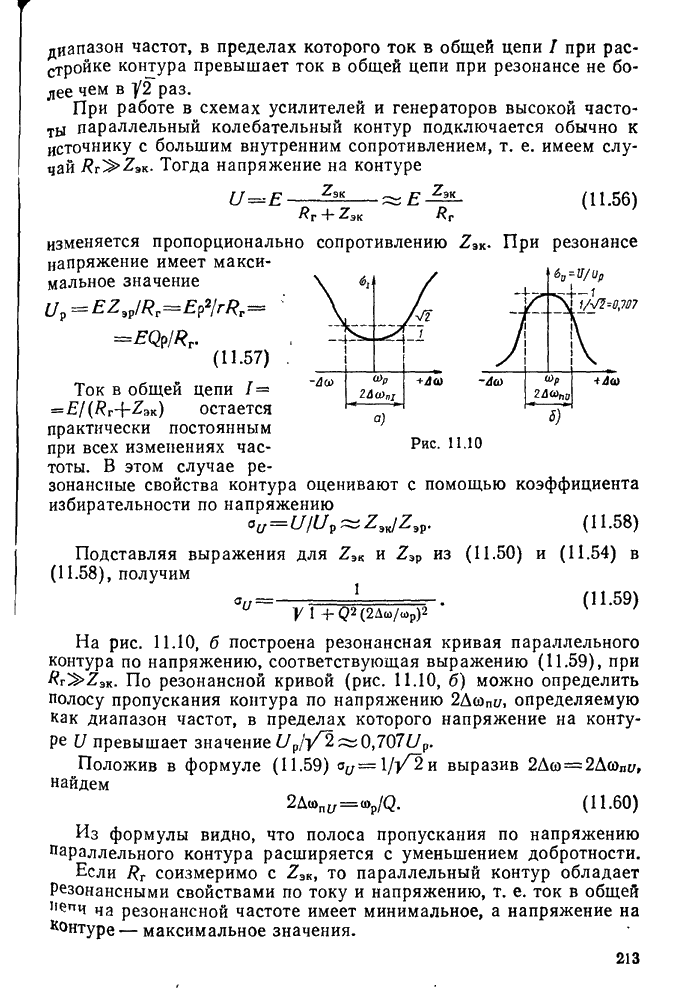
На рис. 11.8 приведено семейство резонансных кривых последовательного контура при различных значениях добротности Q. По этим кривым можно определить полосу пропускания контура  , т. е. диапазон частот, в пределах которого ток в контуре превышает значение
, т. е. диапазон частот, в пределах которого ток в контуре превышает значение  . Из рисунка видно, что полоса пропускания расширяется с уменьшением добротности. Действительно, положив в формуле
. Из рисунка видно, что полоса пропускания расширяется с уменьшением добротности. Действительно, положив в формуле  и выразив
и выразив  , получаем
, получаем
 (11.38)
(11.38)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. УСИЛИТЕЛЬНЫЕ И РЕЛЕЙНЫЕ СХЕМЫ
- ГЛАВА 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ УСИЛИТЕЛЕЙ
- § 1.2. Коэффициент усиления. Линейные и нелинейные искажения
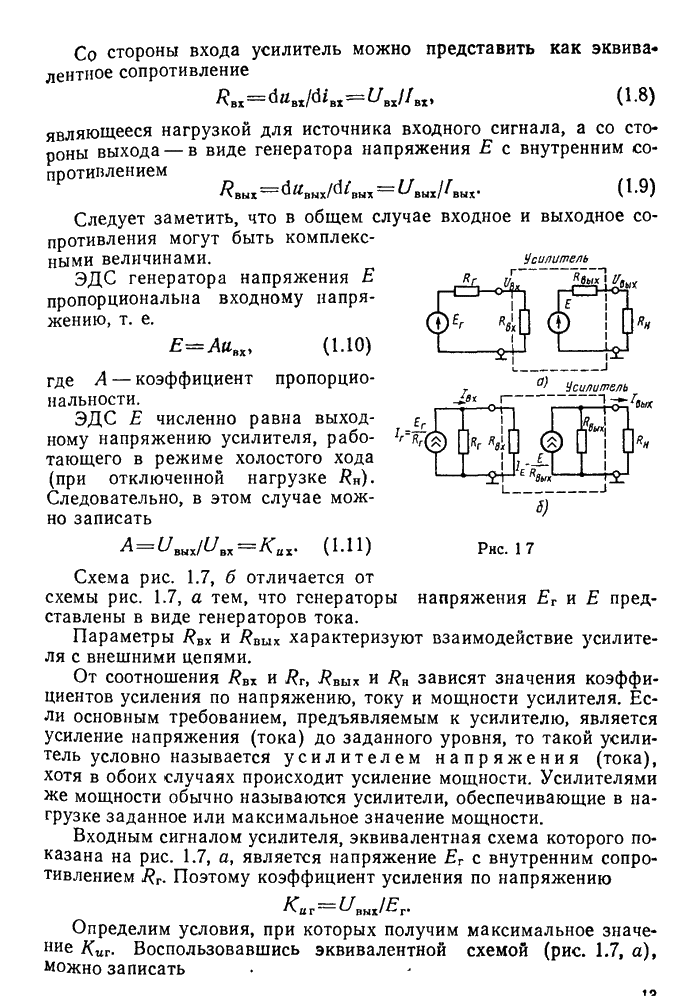
- § 1.3. Эквивалентная схема усилителя. Входное и выходное сопротивления
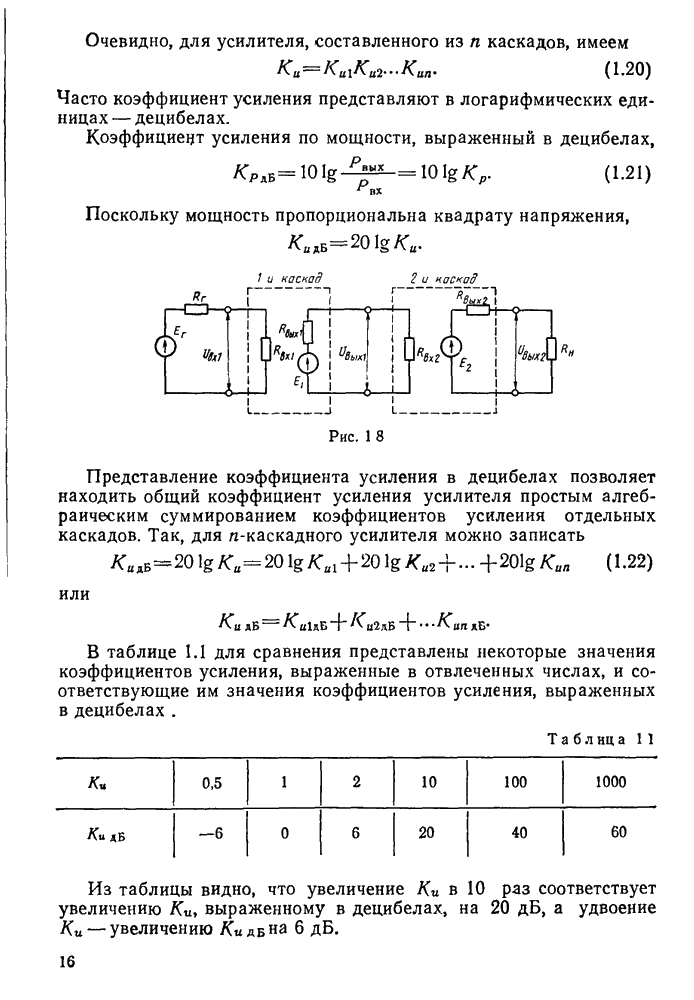
- § 1.4. Показатели многокаскадных усилителей
- § 1.5. Шумы в усилителях
- Вопросы и задачи для самопроверки
- ГЛАВА 2. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ
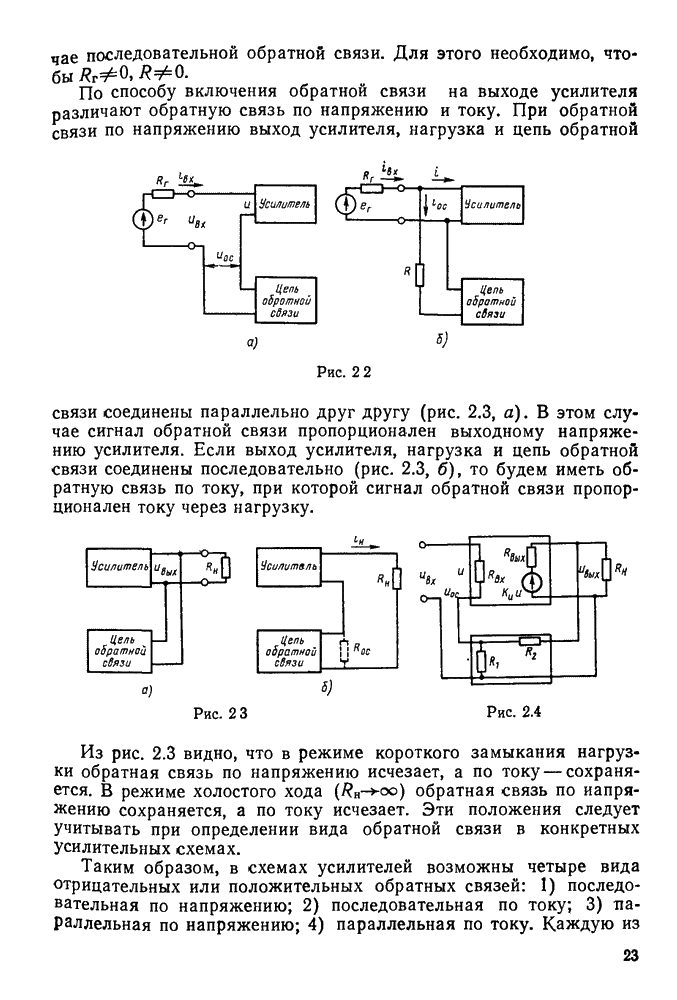
- § 2.1. Виды обратных связей
- § 2.2. Влияние обратной связи на коэффициент усиления и искажения сигнала
- § 2.3. Влияние отрицательной обратной связи на входное сопротивление усилителя
- § 2.4. Влияние отрицательной обратной связи на выходное сопротивление усилителя
- Вопросы и задачи для самопроверки
- ГЛАВА 3. ПРИНЦИПЫ ПОСТРОЕНИЯ УСИЛИТЕЛЬНЫХ КАСКАДОВ НА ТРАНЗИСТОРАХ
- § 3.1. Включение транзистора в схему усилительного каскада. Графический анализ работы каскада
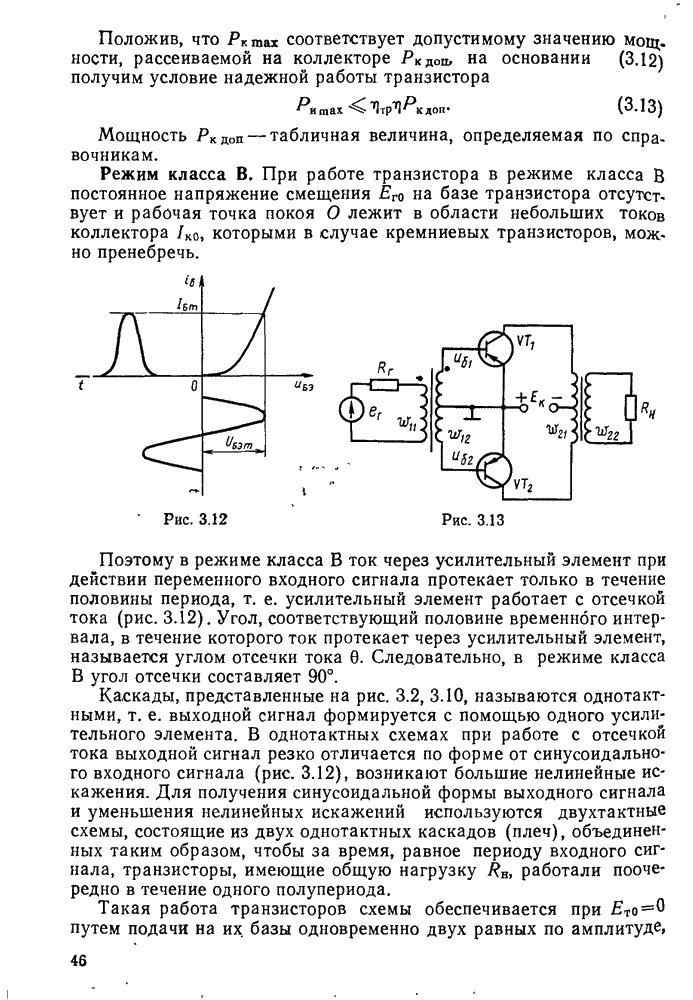
- § 3.2. Режимы работы транзистора в схеме усилительного каскада. Однотактные и двухтактные схемы усилительных каскадов
- Вопросы и задачи для самопроверки
- ГЛАВА 4. ПРАКТИЧЕСКИЕ СХЕМЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ НА ТРАНЗИСТОРАХ
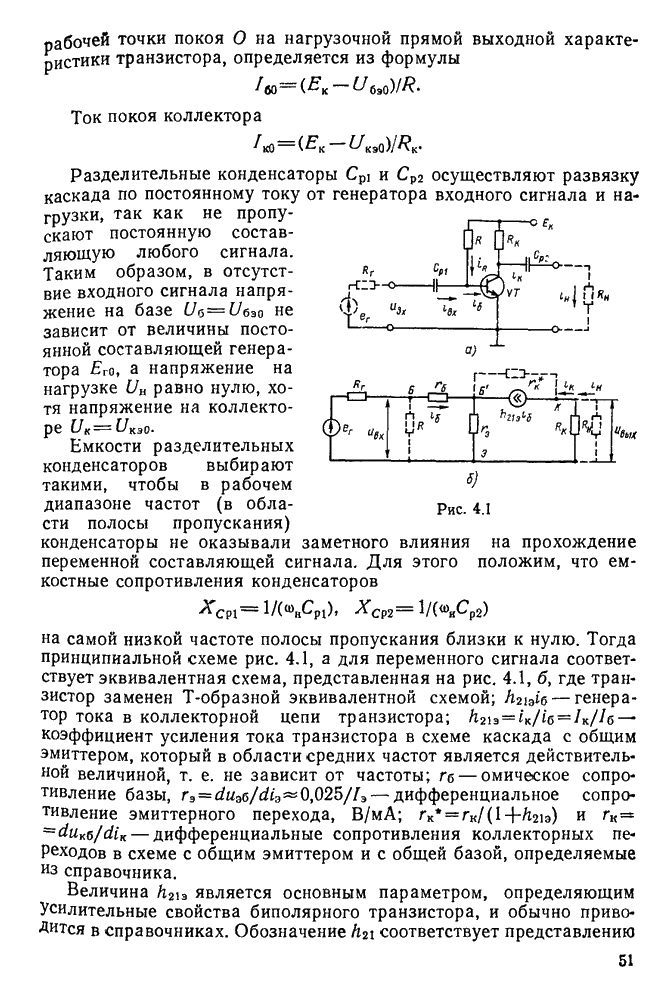
- § 4.1. Каскад с общим эмиттером
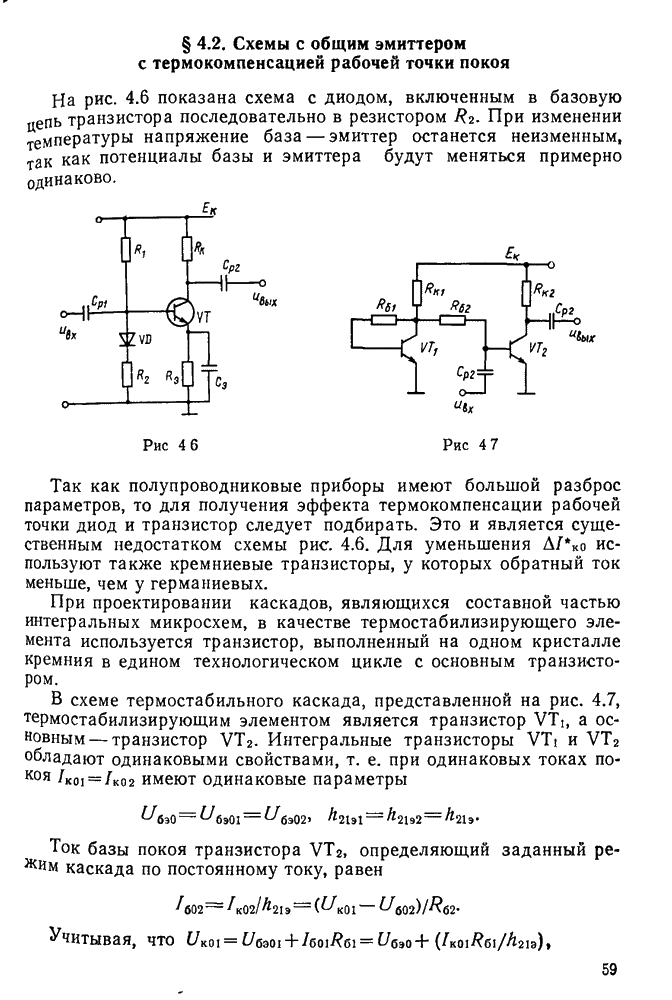
- § 4.2. Схемы с общим эмиттером с термокомпенсацией рабочей точки покоя
- § 4.3. Частотные искажения в схеме с общим эмиттером. Область низких частот
- § 4.4. Широкополосные каскады с общим эмиттером
- § 4.5. Каскад с общей базой (повторитель тока)
- § 4.6. Каскад с общим коллектором (повторитель напряжения)
- § 4.7. Каскад с общим истоком
- § 4.8. Каскад с общим стоком (истоковыб повторитель)
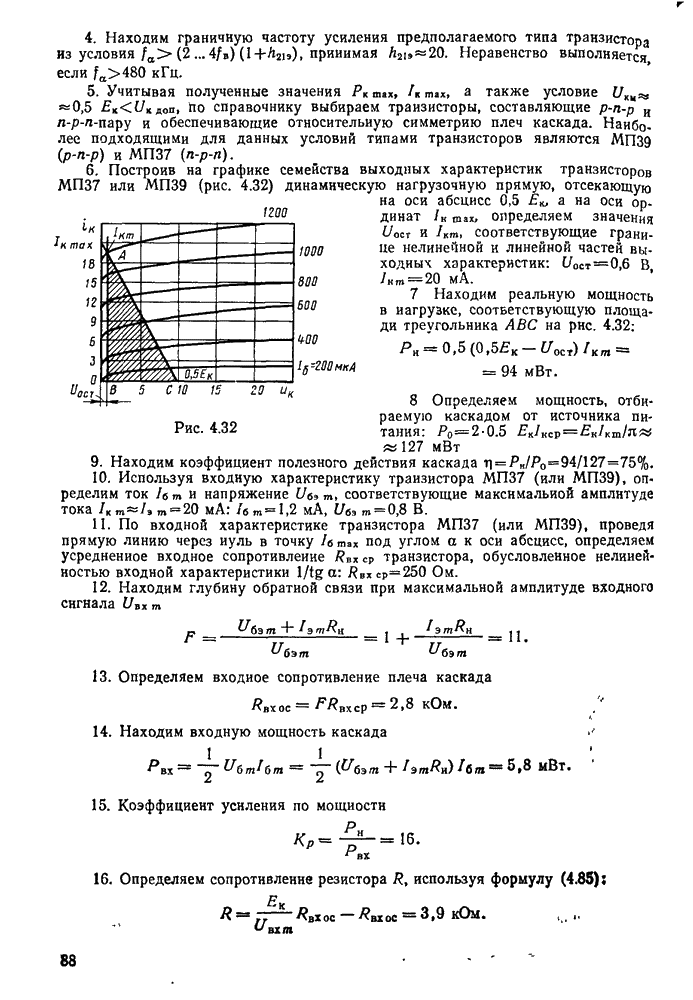
- § 4.9. Выходные каскады (усилители мощности)
- Расчет бестрансформаторного двухтактного усилителя мощности
- Вопросы и задачи для самопроверки
- ГЛАВА 5. ПРАКТИЧЕСКИЕ СХЕМЫ МНОГОКАСКАДНЫХ УСИЛИТЕЛЕЙ
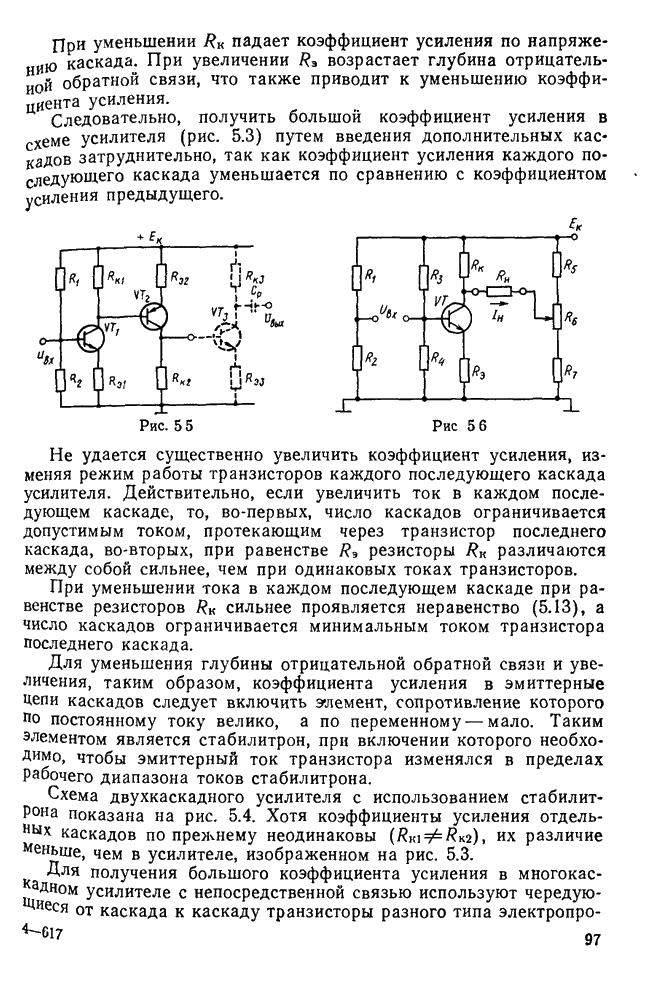
- § 5.1. Усилители с резистивно-емкостной связью
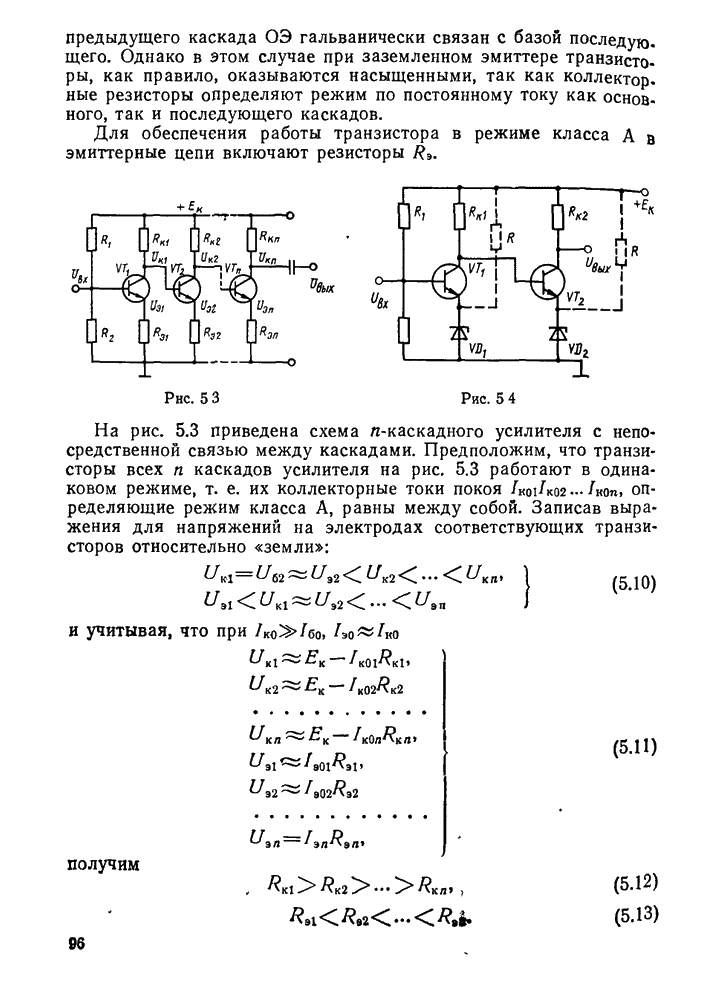
- § 5.2. Усилители с непосредственной связью (усилители постоянного тока)
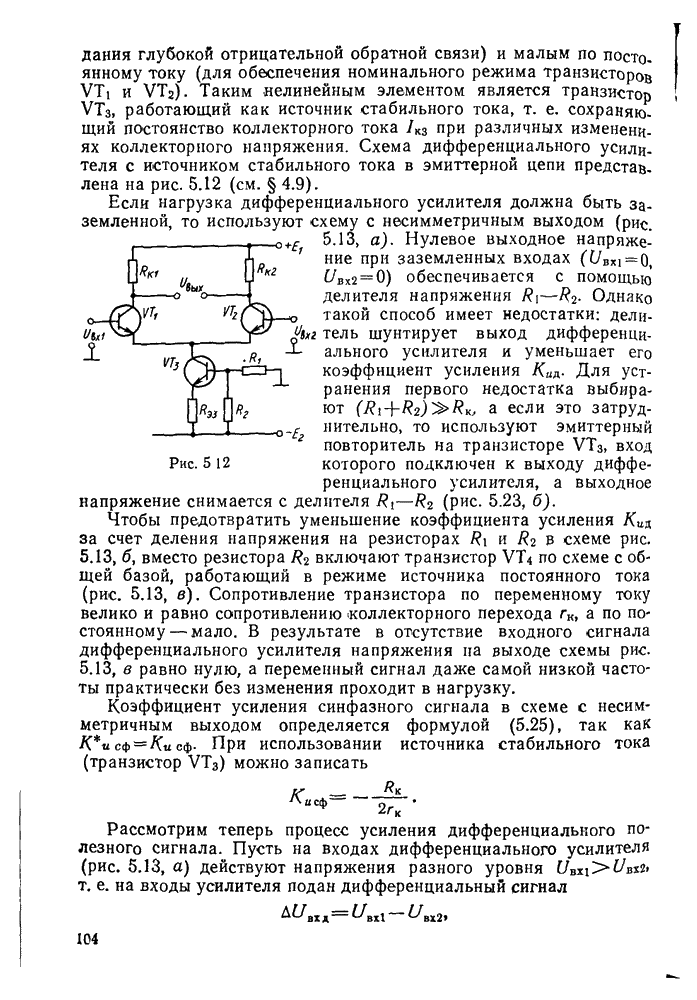
- § 5.3. Дифференциальные усилители
- § 5.4. Усилители постоянного тока с преобразованием сигнала
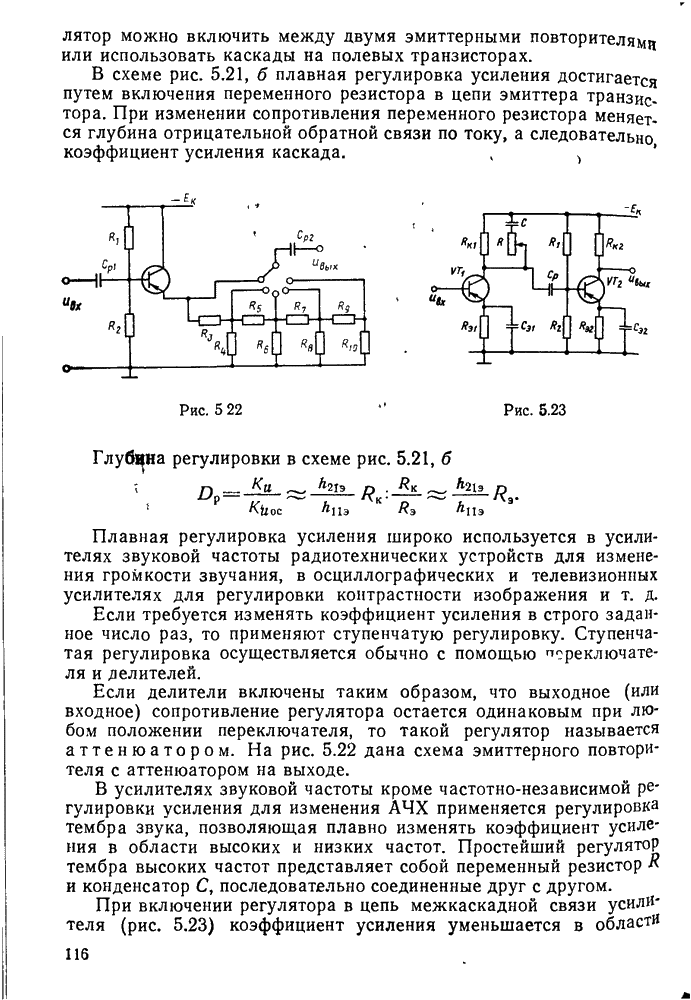
- § 5.5. Регулировка усиления сигнала в усилителях низкой частоты
- Вопросы и задачи для самопроверки
- ГЛАВА 6. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- § 6.2. Эквивалентная схема и основные параметры
- Области применения операционных усилителей
- § 6.3. Линейные схемы на операционных усилителях
- § 6.4. Устойчисвость и частотная коррекция операционных усилителей
- § 6.5. Работа операционного усилителя на низкоомную нагрузку
- Вопросы и задачи для самопроверки
- ГЛАВА 7. РЕЛЕЙНЫЕ СХЕМЫ
- § 7.1. Электромагнитные контактные реле. Общие сведения и основные параметры
- § 7.2. Электронные реле
- § 7.3. Электронные реле времени
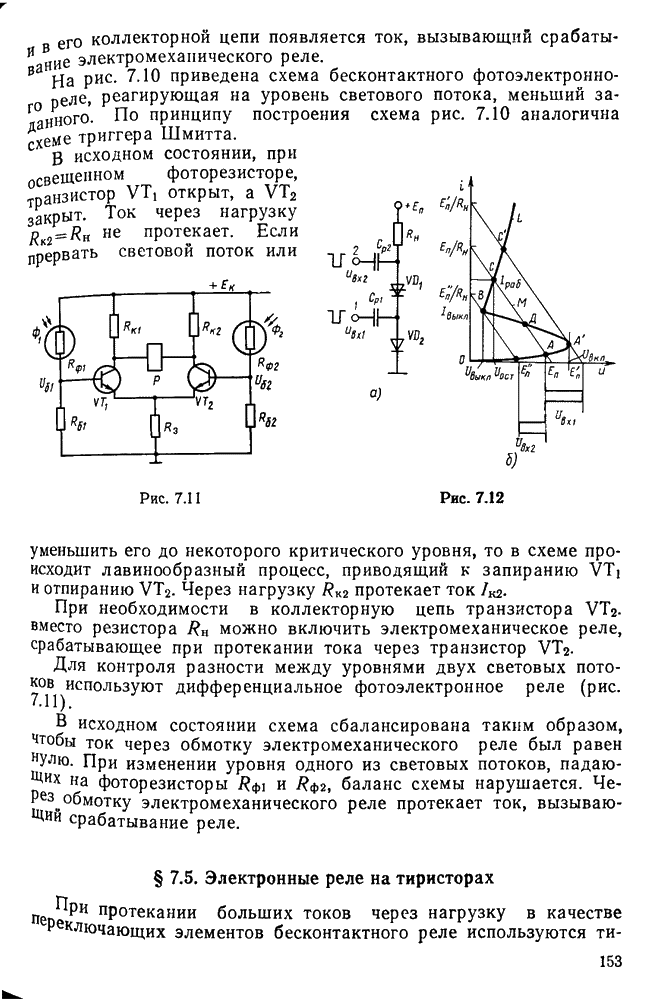
- § 7.4. Фотоэлектронные реле
- § 7.5. Электронные реле на тиристорах
- РАЗДЕЛ II. ВЫПРЯМИТЕЛИ И СТАБИЛИЗАТОРЫ
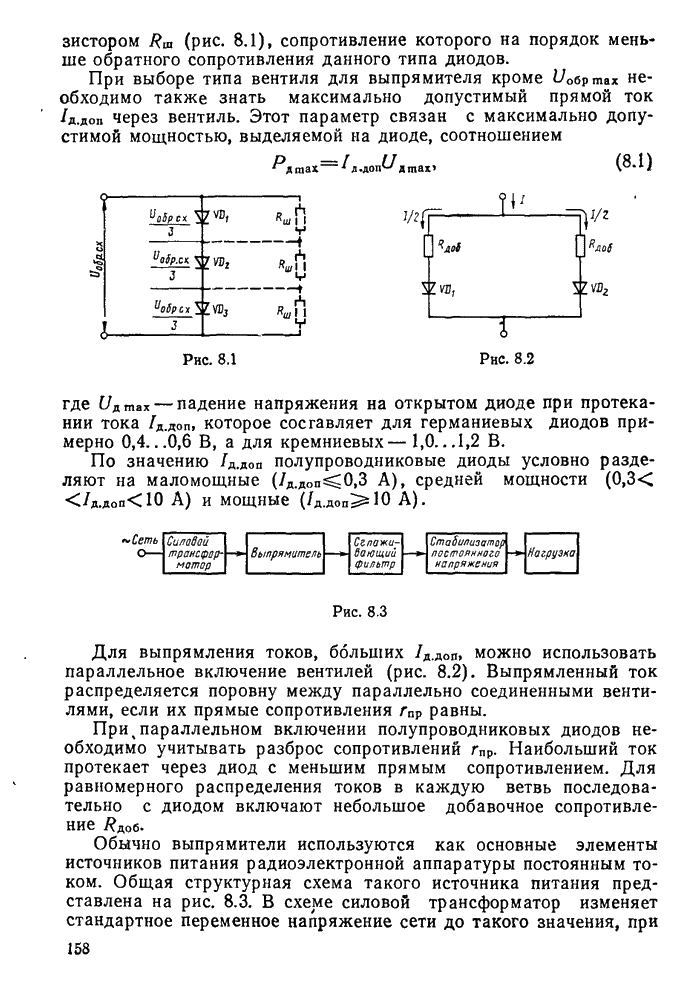
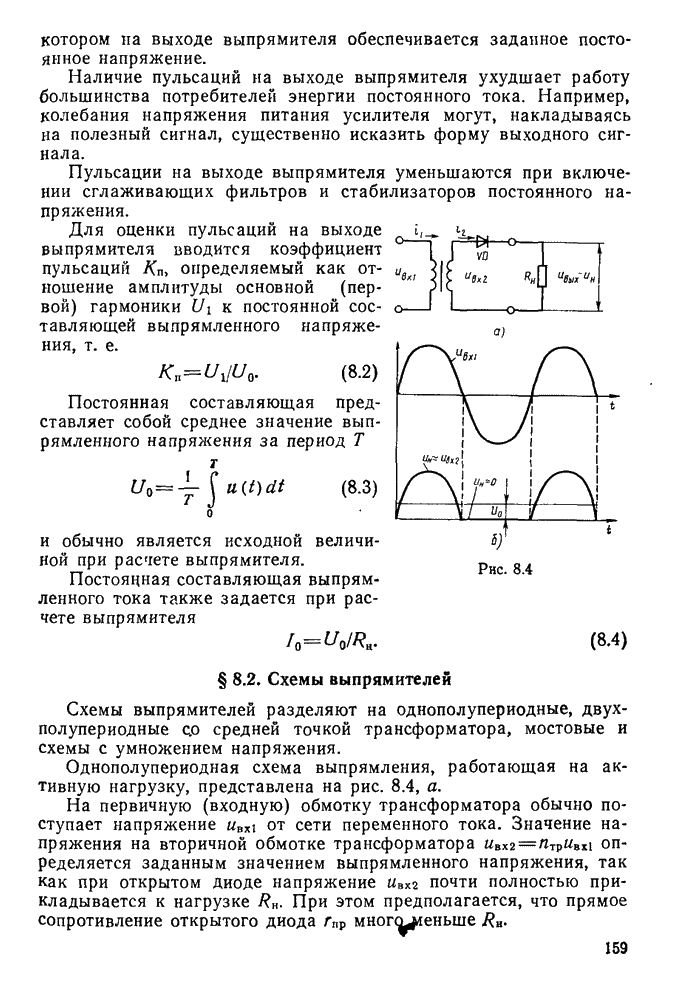
- § 8.1. Определение и параметры выпрямителя
- § 8.2. Схемы выпрямителей
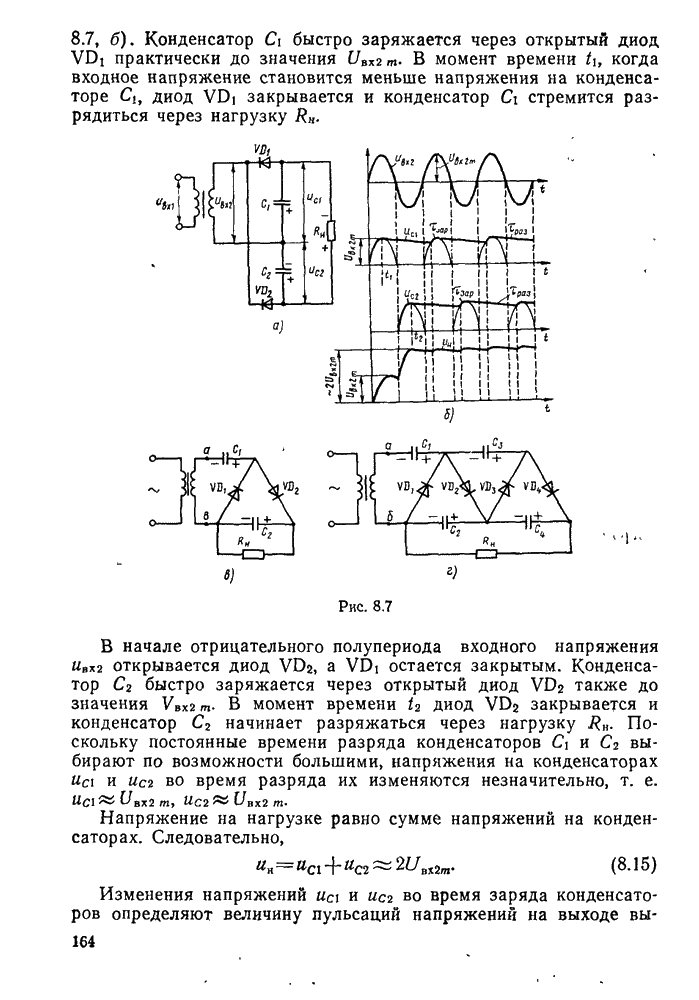
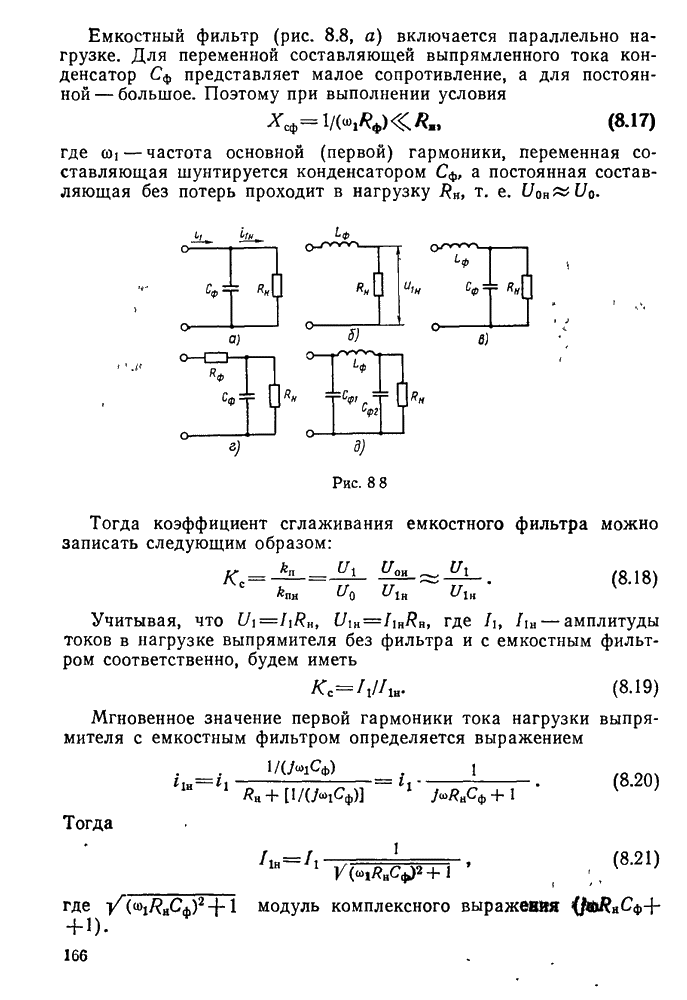
- § 8.3. Сглаживающие фильтры
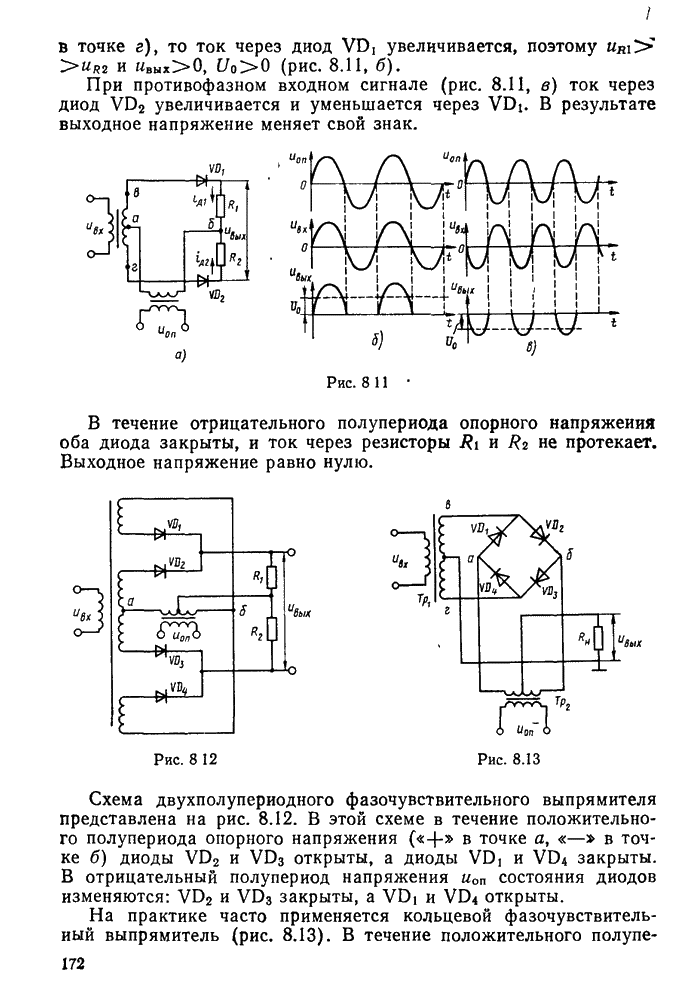
- § 8.4. Фазочувстительные выпрямители и усилители
- § 8.5. Управляемые выпрямители и инверторы
- Вопросы и задачи для самопроверки
- ГЛАВА 9. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ И ТОКА
- § 9.1. Параметрические стабилизаторы
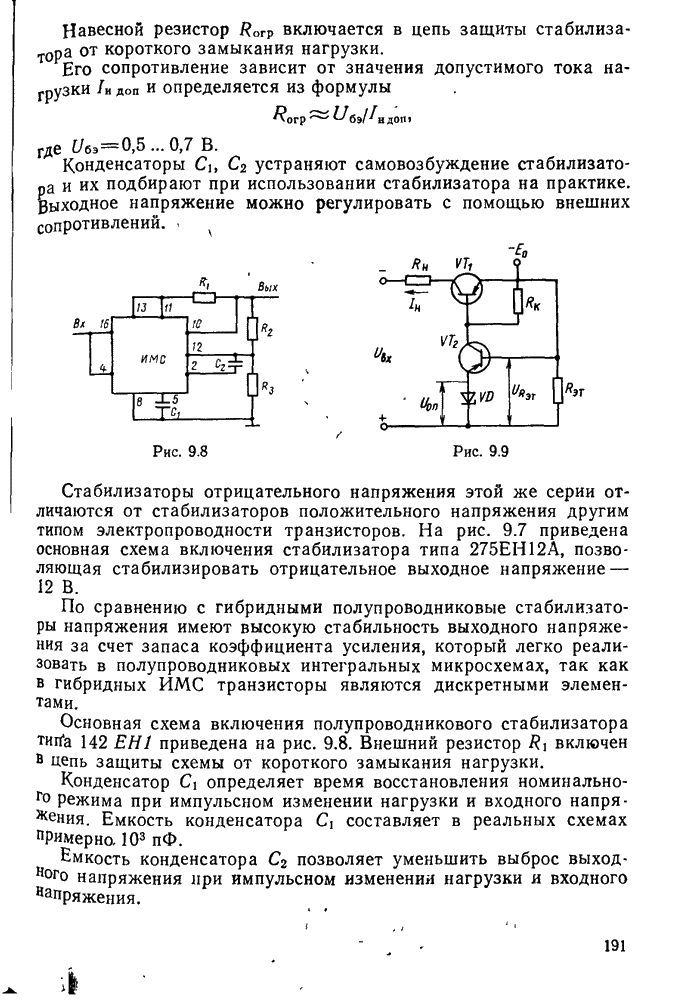
- § 9.2. Компенсационные стабилизаторы
- Расчет компенсационного стабилизатора непрерывного действия
- Вопросы и задачи для самопроверки
- РАЗДЕЛ III. ПРИНЦИП РАДИОСВЯЗИ. ИЗБИРАТЕЛЬНЫЕ СХЕМЫ
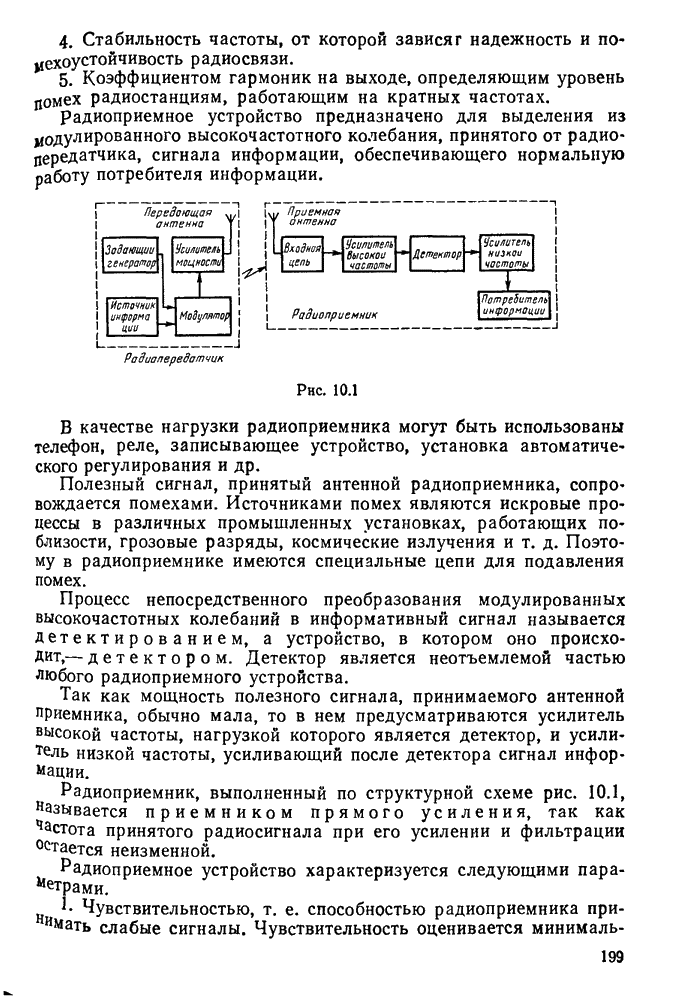
- § 10.1. Основные параметры радиопередающих и радиоприемных устройств
- § 10.2. Радиоприемник супергетеродинного типа
- Вопросы и задачи для самопроверки
- ГЛАВА 11. КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ
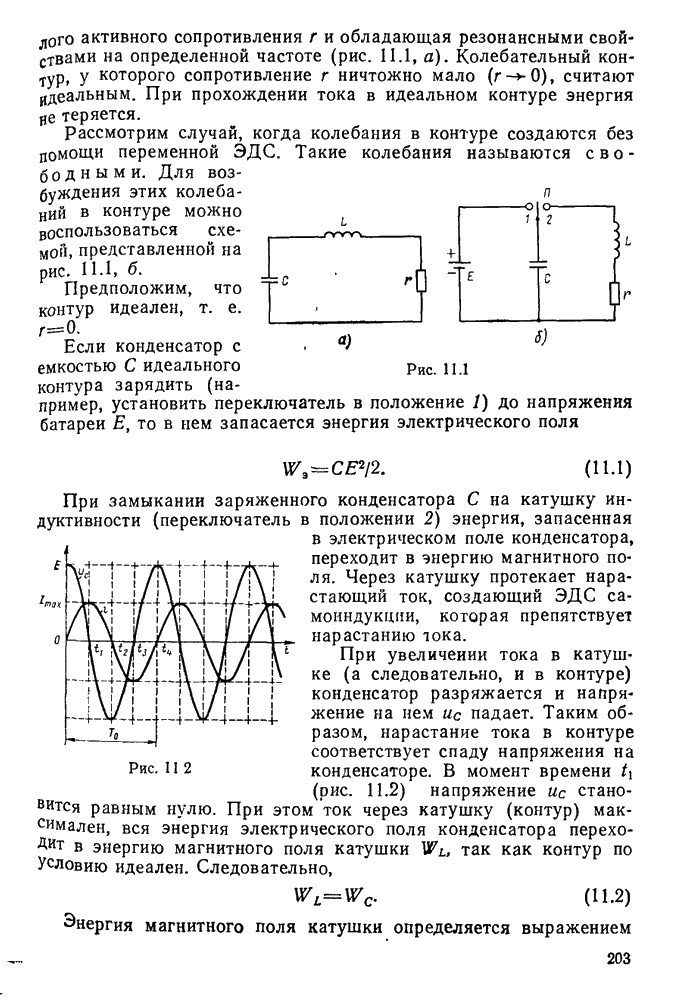
- § 11.1. Свободные колебания в контуре
- § 11.2. Вынужденные колебания в последовательном контуре
- § 11.3. Вынужденные колебания в параллельном контуре
- § 11.4. Вынужденные колебания в связанных контурах
- Вопросы и задачи для самопроверки
- ГЛАВА 12. ГЕНЕРАТОРЫ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ
- § 12.1. Принципы построения генераторов
- § 12.2. Генератор с фазовращающей RC-цепью
- Расчет генератора низкой частоты
- § 12.3. Генератор с мостом Вина в цепи обратной связи
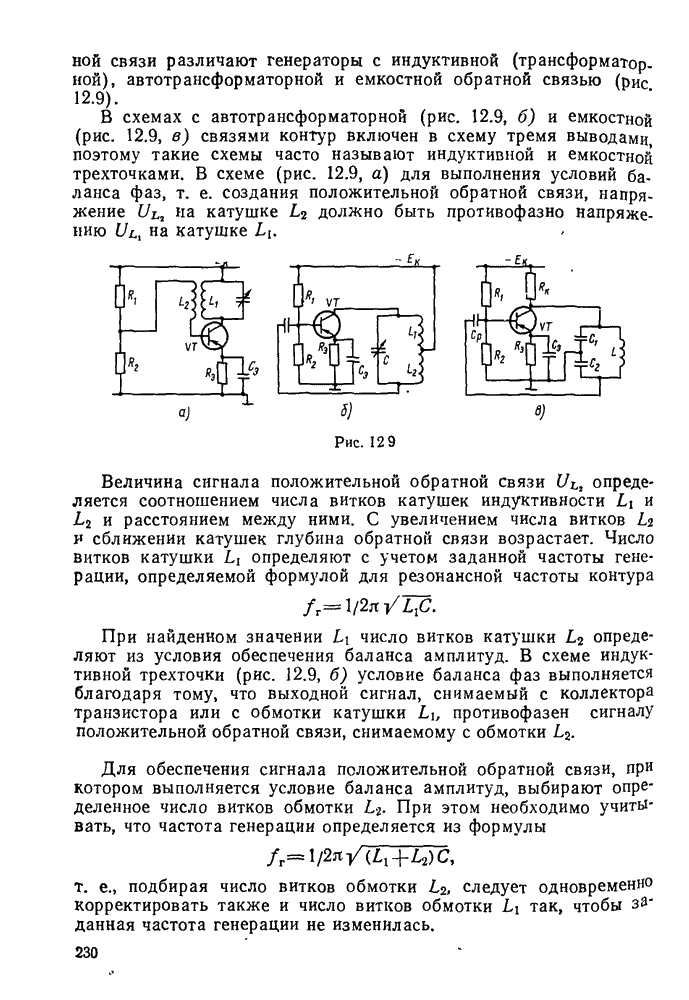
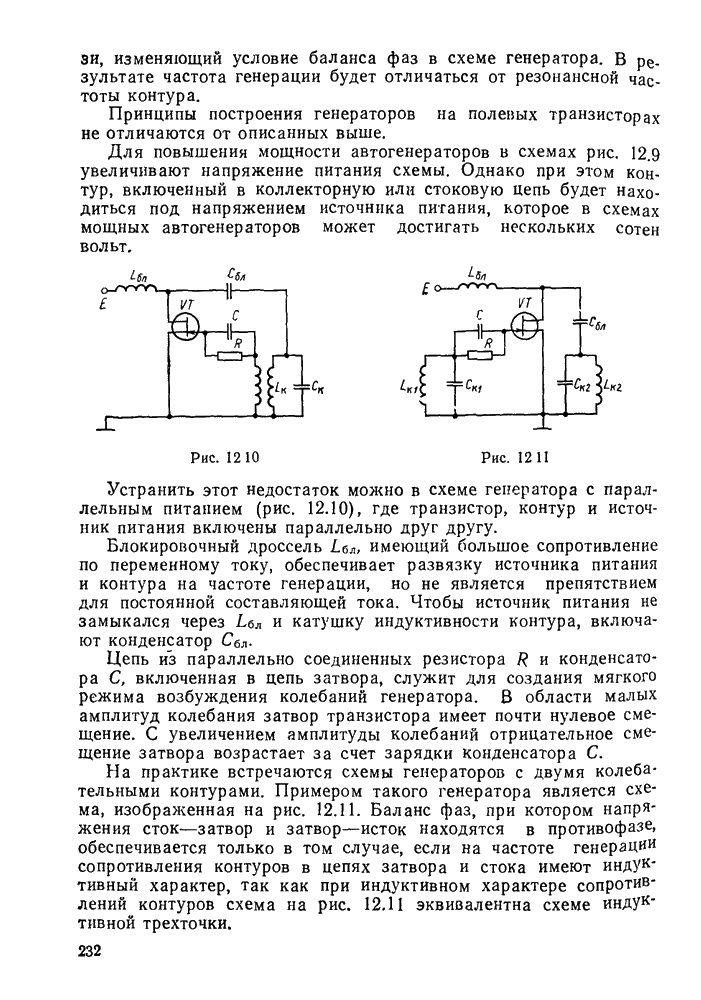
- § 12.4. Генераторы с колебательными контурами
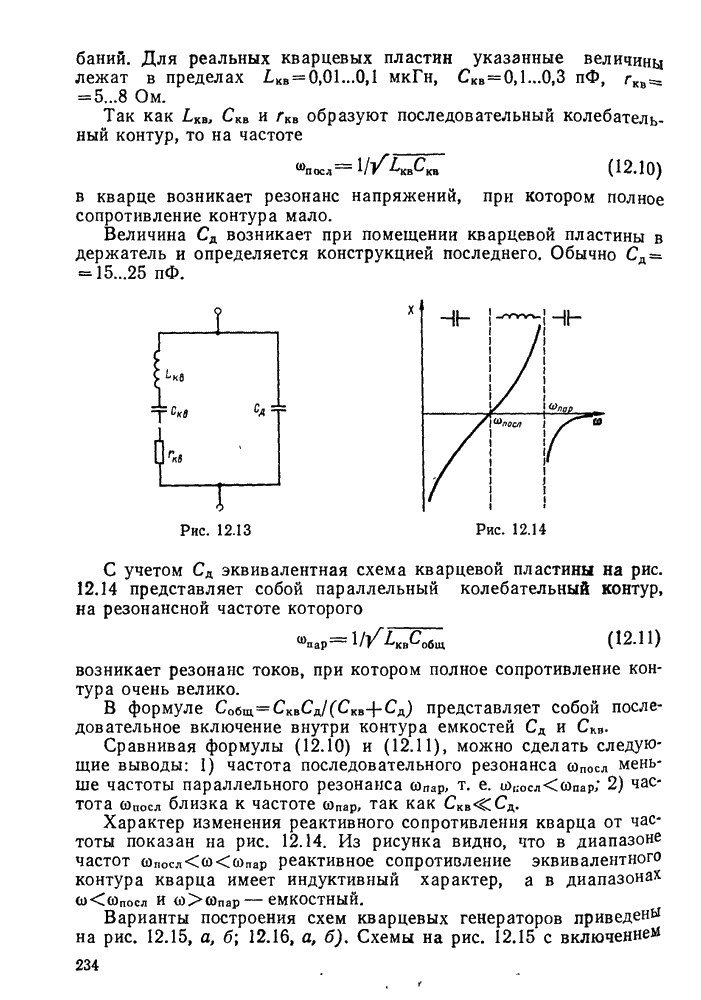
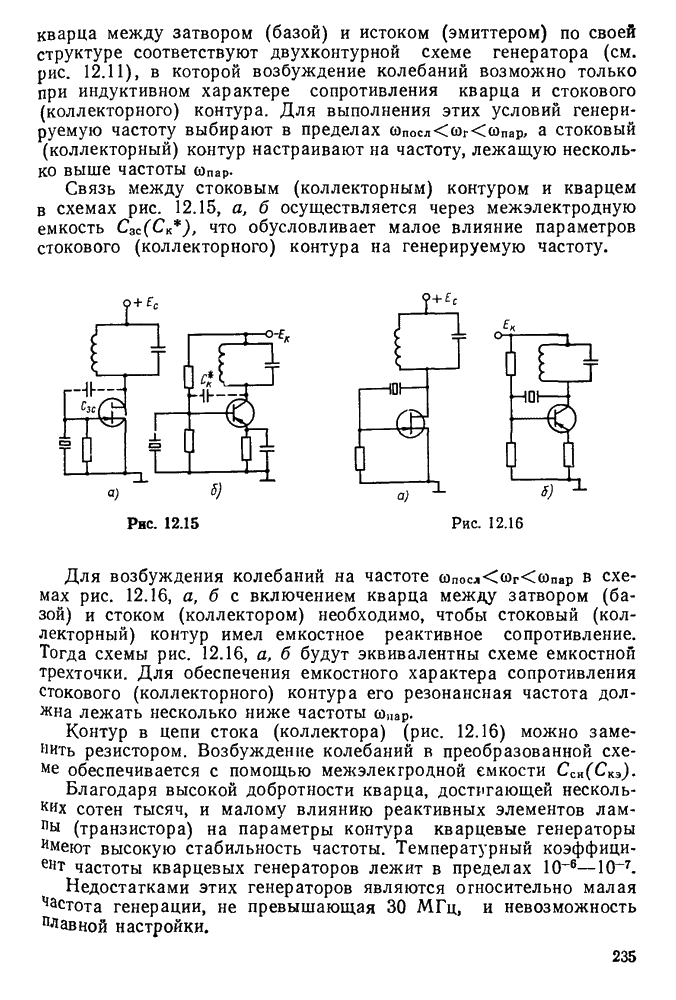
- § 12.5. Стабилизация частоты LC-генераторов. Кварцевые генераторы
- ГЛАВА 13. ИЗБИРАТЕЛЬНЫЕ УСИЛИТЕЛИ
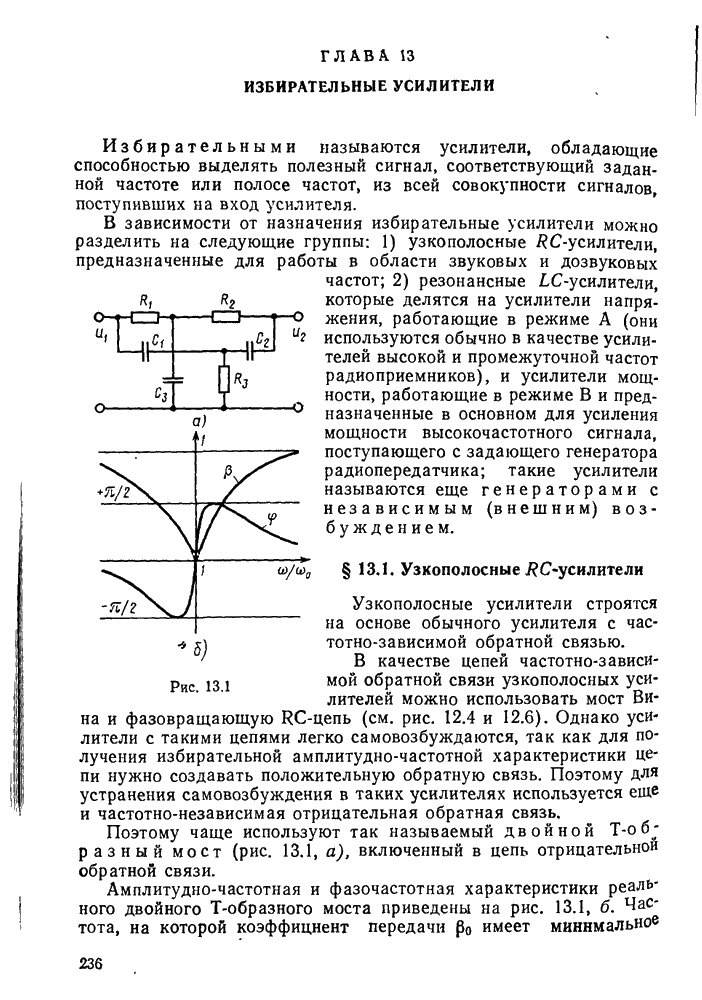
- § 13.1. Узкополосные RC-усилители
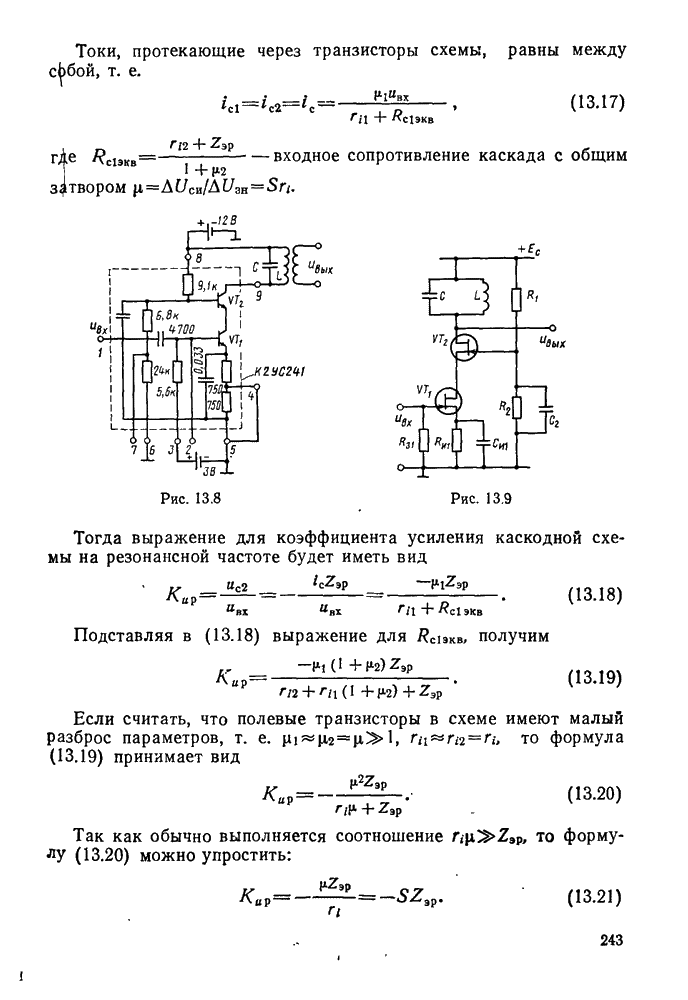
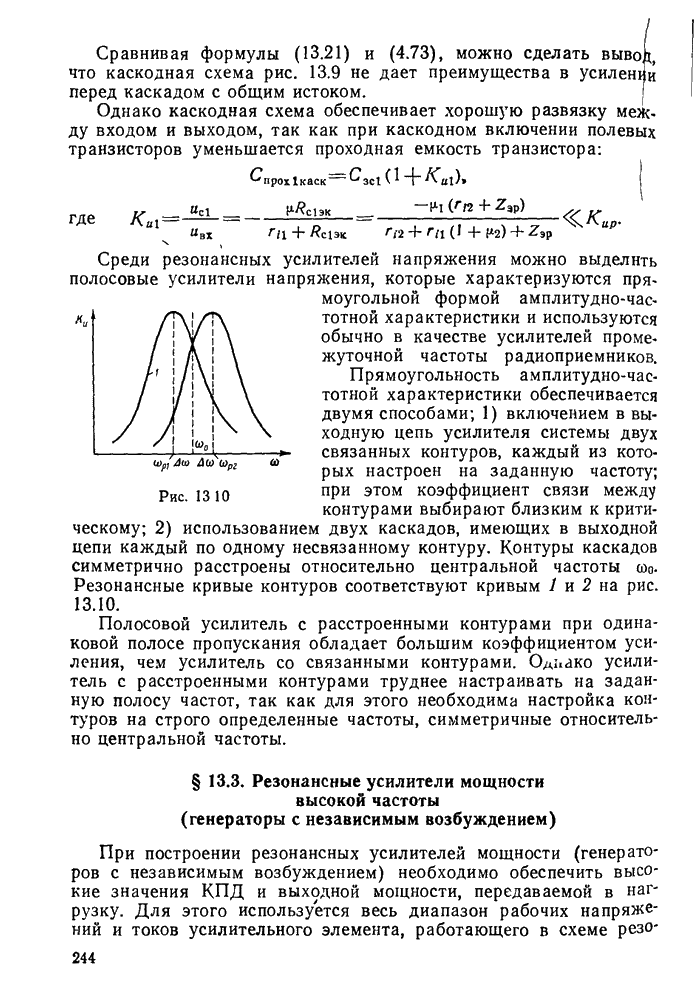
- § 13.2. Резонансные усилители напряжения высокой частоты
- § 13.3. Резонансные усилители мощности высокой частоты (генераторы с независимым возбуждением)
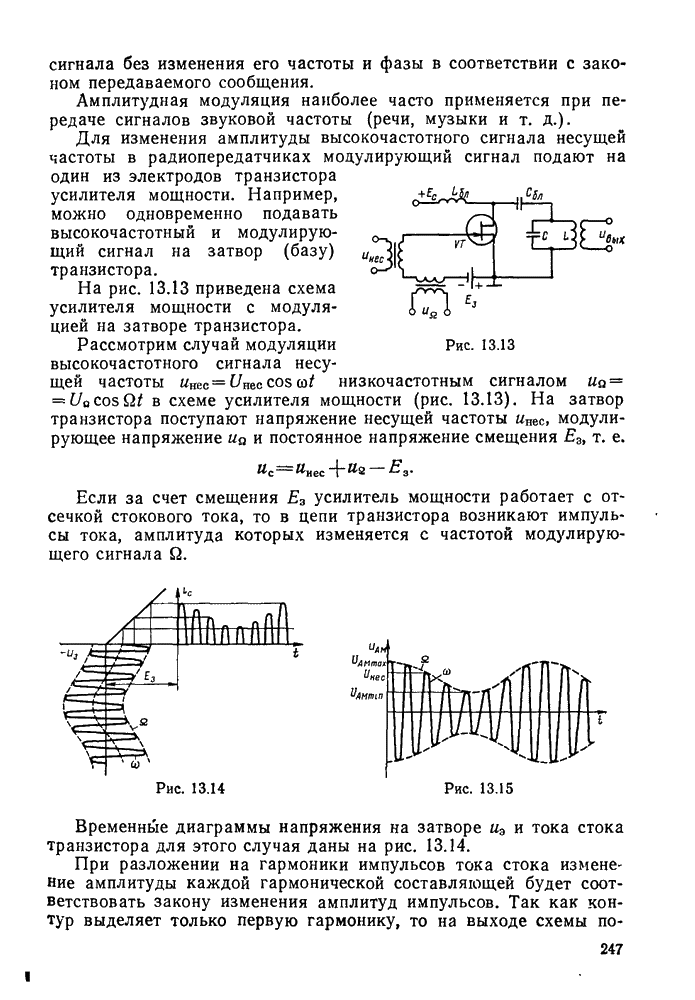
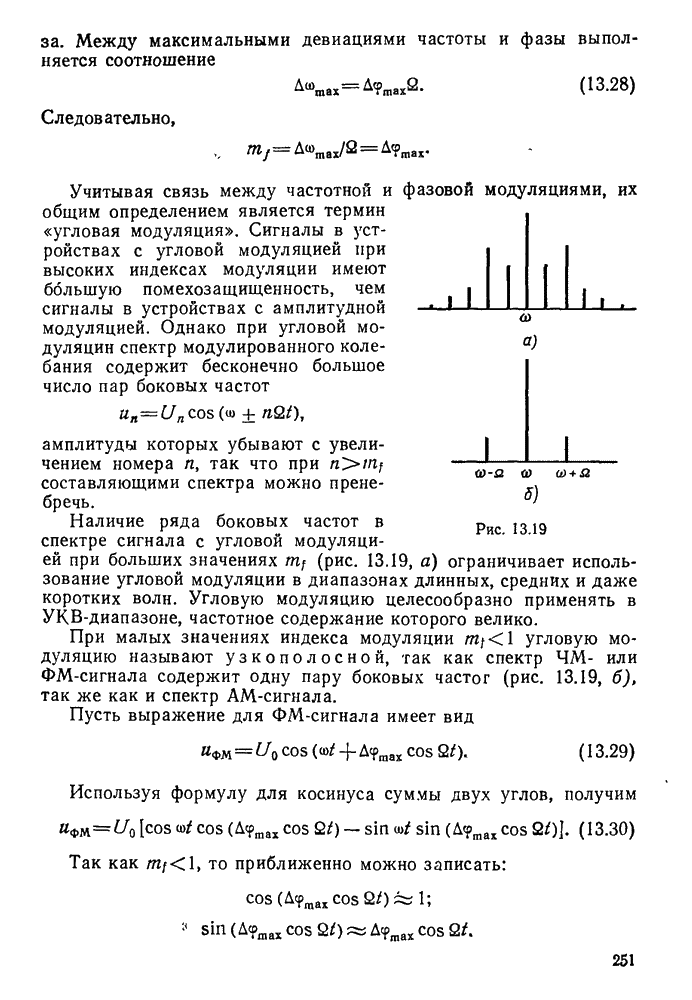
- § 13.4. Модуляция высокочастотного сигнала
- ЛИТЕРАТУРА