| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.16. Квадратные генераторы
Время от времени возникает потребность в генераторах, которые формируют одновременно пару одинаковых по амплитуде колебаний синусоидальной формы, но сдвинутых по фазе на 90°. Эту пару сигналов можно рассматривать как синусоидальное и косинусоидальное колебания, мы же будем придерживаться термина квадратурная пара сигналов (сигналы «в квадратуре»). Наиболее важны такие сигналы в радиосвязи (квадратурные смесители, схемы формирования однополосных сигналов). Кроме того, дальше будет показано, что такая квадратурная пара сигналов всегда необходима для формирования сигнала с любой произвольной фазой.
Первая мысль, которая сразу  это как подавать сигнал синусоидальной формы на интегратор (или дифференциатор), чтобы на его выходе появился сдвинутый на 90° сигнал косинусоидальной формы. При этом сигнал имеет правильный фазовый сдвиг, но его амплитуда испорчена (поймите почему). Далее предлагаются некоторые способы решения этой задачи.
это как подавать сигнал синусоидальной формы на интегратор (или дифференциатор), чтобы на его выходе появился сдвинутый на 90° сигнал косинусоидальной формы. При этом сигнал имеет правильный фазовый сдвиг, но его амплитуда испорчена (поймите почему). Далее предлагаются некоторые способы решения этой задачи.
Резонатор на переключаемых конденсаторах.
Таблица 5.4. ГУН

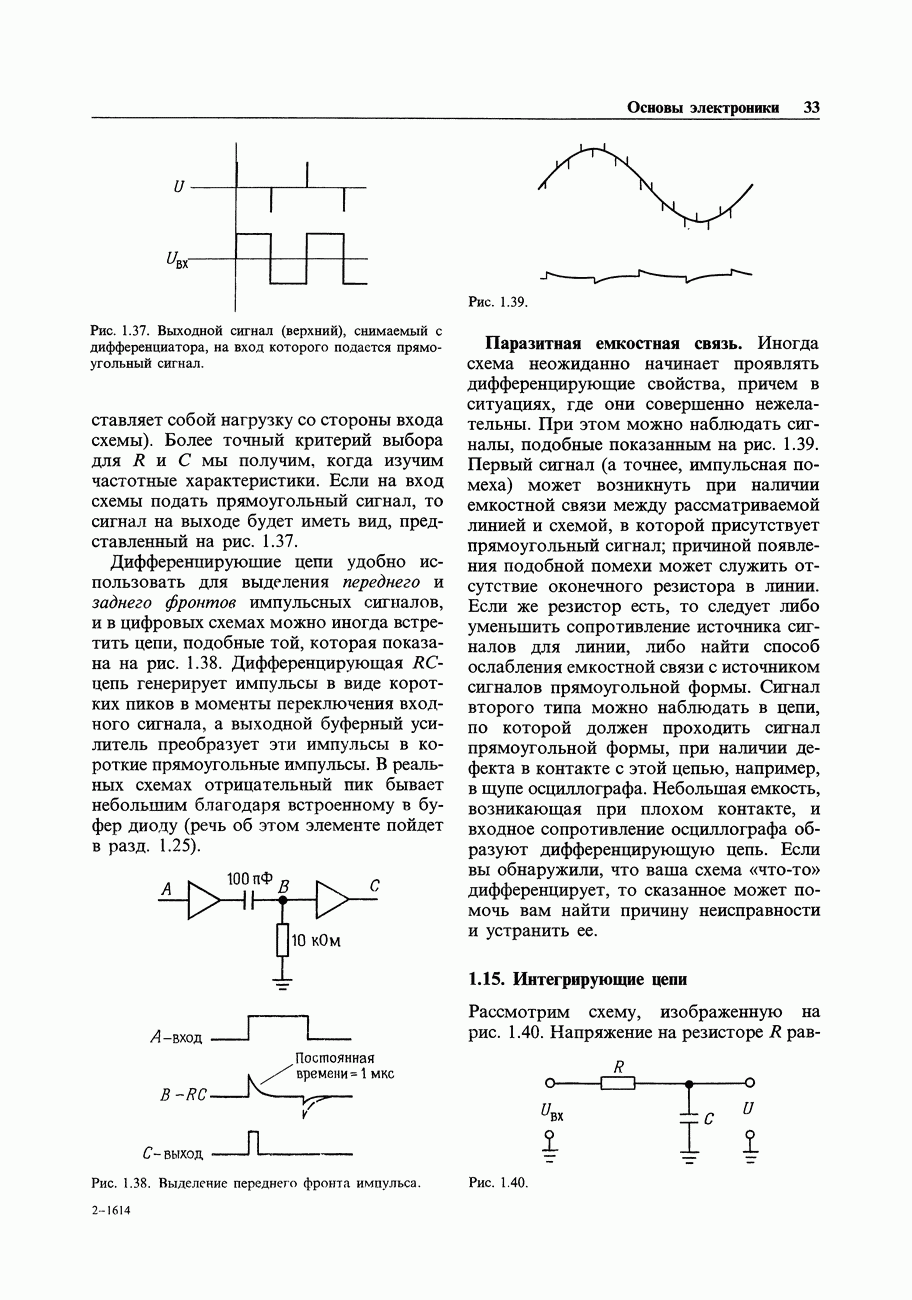
На рис. 5.38 показан способ использования ИС фильтра на переключаемых конденсаторах  в режиме самовозбуждающегося полосового фильтра, который формирует пару квадратурных сигналов синусоидальной формы. Наиболее простой способ понять ее работу - это предположить, что на выходе уже присутствует сигнал синусоидальной формы; далее компаратор преобразует его в прямоугольное колебание с небольшой амплитудой (падение напряжения на одном диоде), которое снова подается на вход фильтра. Фильтр обладает узкой полосой пропускания
в режиме самовозбуждающегося полосового фильтра, который формирует пару квадратурных сигналов синусоидальной формы. Наиболее простой способ понять ее работу - это предположить, что на выходе уже присутствует сигнал синусоидальной формы; далее компаратор преобразует его в прямоугольное колебание с небольшой амплитудой (падение напряжения на одном диоде), которое снова подается на вход фильтра. Фильтр обладает узкой полосой пропускания  , так что он преобразует это прямоугольное колебание в выходной синусоидальный сигнал и таким образом поддерживается генерация. Входное прямоугольное колебание тактовой частоты (такт) задает центральную частоту полосы пропускания, следовательно, сама частота генерации в этом случае
, так что он преобразует это прямоугольное колебание в выходной синусоидальный сигнал и таким образом поддерживается генерация. Входное прямоугольное колебание тактовой частоты (такт) задает центральную частоту полосы пропускания, следовательно, сама частота генерации в этом случае  . Эта схема пригодна для работы в диапазоне частот от нескольких герц до приблизительно
. Эта схема пригодна для работы в диапазоне частот от нескольких герц до приблизительно  и формирует квадратурную пару синусоидальных сигналов с равными амплитудами.
и формирует квадратурную пару синусоидальных сигналов с равными амплитудами.
Следует отметить, что эта схема дает «ступенчатую» аппроксимацию синусоидальной формы выходного сигнала вследствие того, что переключаемый фильтр дает квантованный выходной сигнал.
Генератор колебаний специальной формы (аналоговые тригонометрические функции).
Фирма Analog Devices изготовляет интересную нелинейную «функциональную ИС», которая преобразует входное напряжение в выходной сигнал, пропорциональный , где коэффициент усиления А имеет фиксированное значение, равное
, где коэффициент усиления А имеет фиксированное значение, равное  . Как правило, этот кристалл
. Как правило, этот кристалл  может на самом деле выполнять гораздо больше функций. Он вырабатывает четыре выходных сигнала, называемые
может на самом деле выполнять гораздо больше функций. Он вырабатывает четыре выходных сигнала, называемые  , и формирует выходной сигнал, напряжение которого определяется следующим образом:
, и формирует выходной сигнал, напряжение которого определяется следующим образом:  . Таким образом, если например, установить
. Таким образом, если например, установить  (закоротка на
(закоротка на  ), а входное напряжение подавать на вход
), а входное напряжение подавать на вход  , то вырабатывается сигнал вида
, то вырабатывается сигнал вида  .
.
Упражнение 5.10. Докажите последнее утверждение.
У схемы  имеется также выход прецизионного опорного напряжения
имеется также выход прецизионного опорного напряжения  , что существенно облегчает ее применение. Следовательно, если на пару ИС
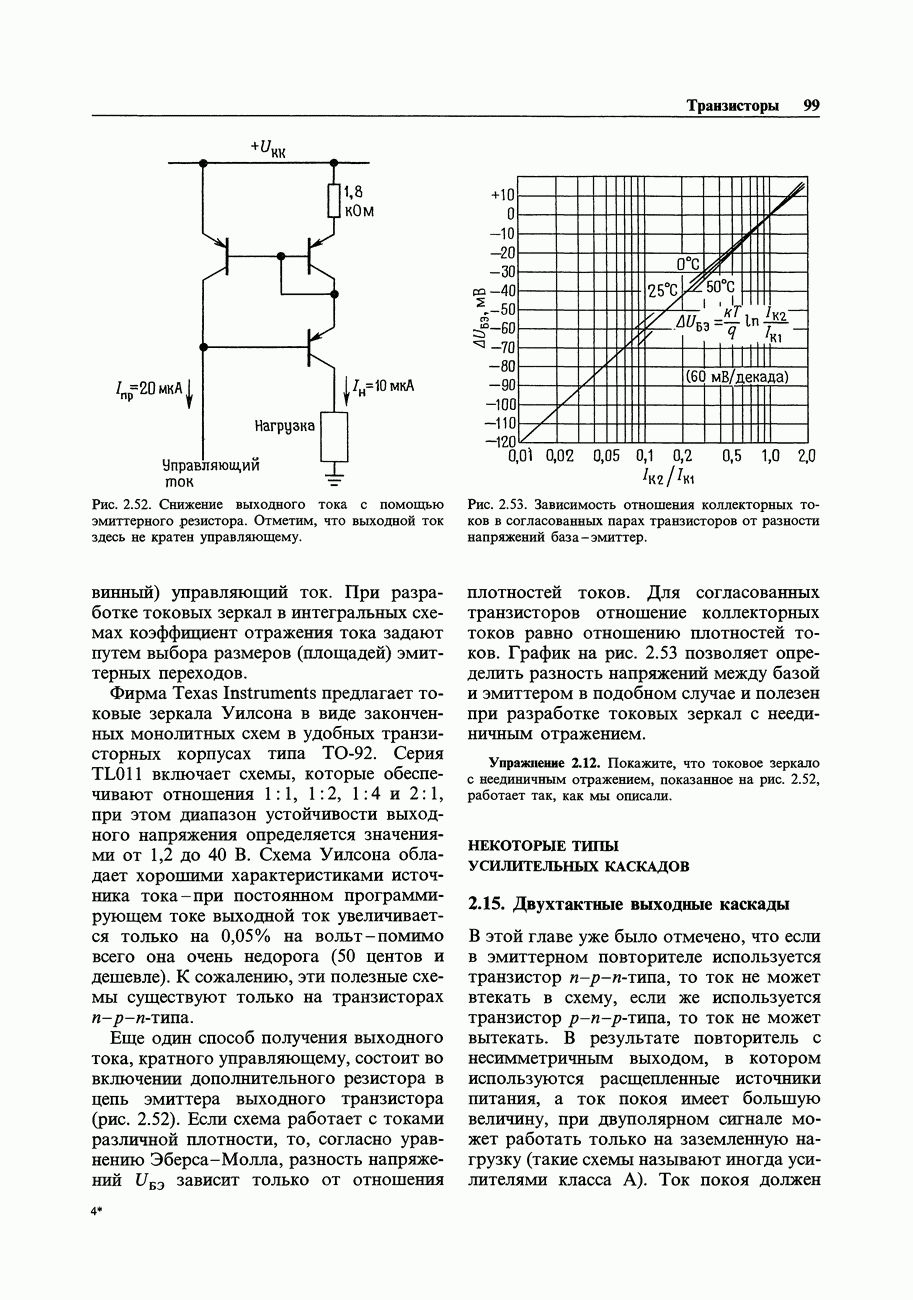
, что существенно облегчает ее применение. Следовательно, если на пару ИС  подать треугольное колебание с амплитудой 1,8 В, то можно получить пару квадратурных сигналов синусоидальной формы, как это показано на рис. 5.39. Рабочий диапазон частот этой ИС лежит в пределах от постоянного тока до приблизительно 1 МГц.
подать треугольное колебание с амплитудой 1,8 В, то можно получить пару квадратурных сигналов синусоидальной формы, как это показано на рис. 5.39. Рабочий диапазон частот этой ИС лежит в пределах от постоянного тока до приблизительно 1 МГц.
Просмотровая таблица (поиск элементов при помощи просмотра).
Это цифровая методика, которую вы полностью освоите только после изучения гл. 9. Основная идея состоит в том, чтобы запрограммировать цифровую память большого объема цифровыми значениями (выборками) синуса и косинуса, аргументы которых выбираются через равноотстоящие угловые промежутки (скажем, через 1°).
Рис. 5.38. Квадратурный генератор на переключаемых конденсаторах.

Рис. 5.39. Генератор тригонометрических функций.
Тогда, быстро последовательно перебирая адреса этой памяти, можно получить колебание синусоидальной формы, для этого считанные из памяти по каждому адресу цифровые значения (т. е. для последовательности угловых аргументов) подаются на пару цифро-аналоговых преобразователей (ЦАП).
Этот метод имеет следующие недостатки. Как и в случае резонатора на переключаемых конденсаторах, выходной сигнал имеет ступенчатую форму, поскольку он формируется из набора дискретных напряжений, по одному на содержимое каждой ячейки памяти. Можно, конечно, для сглаживания выходного сигнала поставить фильтр нижних частот, но, делая это, нельзя перекрыть широкий диапазон частот, поскольку нужно выбирать такой фильтр нижних частот, чтобы он пропускал само синусоидальное колебание и в то же время подавлял более высокую частоту выборки (такая же проблема характерна и для резонатора на переключаемых конденсаторах). В этом случае помогает сокращение углового интервала между соседними значениями, но тогда соответственно снижается максимальная частота вырабатываемого выходного колебания. При использовании стандартных ЦАП с временем преобразования не более одной микросекунды, можно получить синусоидальные сигналы с частотами вплоть до нескольких десятков килогерц, полагая, что шаг углового аргумента составляет порядка одного градуса. Для самих же ЦАП характерно наличие в момент переключения больших остроконечных выбросов напряжения («кратковременная импульсная помеха»). Эти полноразрядные кратковременные импульсные помехи возникают даже, если переключение происходит между смежными (ближайшими) уровнями выходного напряжения! В гл. 9 будут предложены способы решения этой проблемы. Разрядность имеющихся в распоряжении ЦАП достигает 16 (в этом случае разрешающая способность составляет единицу из 65536 значений).
Генератор на основе метода переменных состояния.
Все предложенные ранее методы требуют выполнения некоторой тяжелой работы.
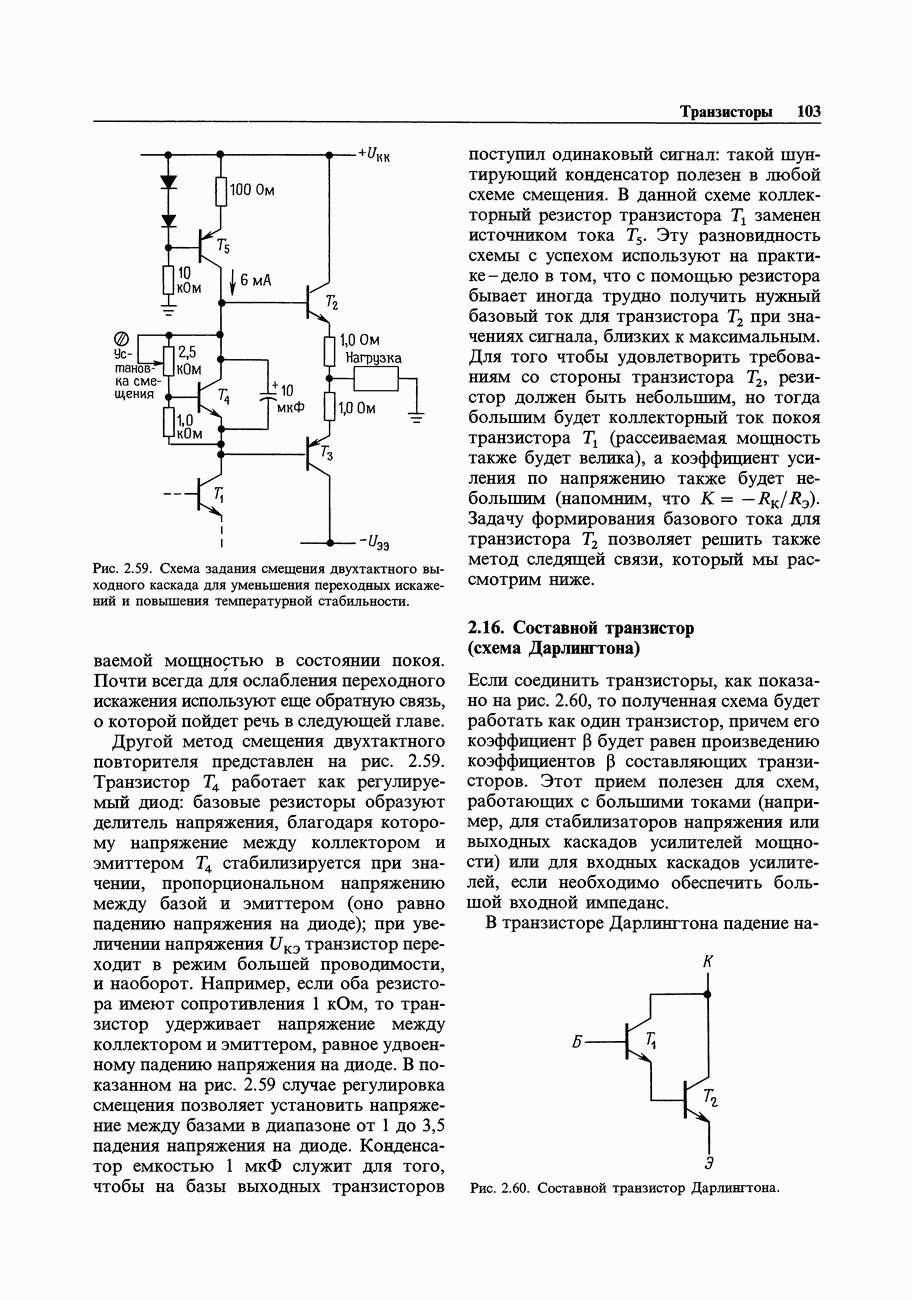
Рис. 5.40.
К счастью, сотрудники дружественной фирмы Burr-Brown провели эту работу дома и вышли на рынок с моделью 4423, которая представляет собой «прецизионный квадратурный генератор». В нем используется стандартная схема полосового фильтра на основе метода переменных состояния, выполненная на трех ОУ (рис. 5.18), где выходной сигнал через диодный ограничитель подается на вход (см. рис. 5.40). Она предназначена для работы в диапазоне частот от 0,002 Гц до  и при этом она демонстрирует высокую стабильность фазового сдвига, амплитуды и частоты (максимально
и при этом она демонстрирует высокую стабильность фазового сдвига, амплитуды и частоты (максимально  ). Схема 4432 является модульной (а не монолитной ИС) и выпускается. в
). Схема 4432 является модульной (а не монолитной ИС) и выпускается. в  -выводном стандартном
-выводном стандартном  -корпусе при цене 24 долл. в малых партиях.
-корпусе при цене 24 долл. в малых партиях.
Фильтры на схеме с упорядоченными фазовыми сдвигами.
Известны изощренные схемы -фильтров, которые обладают способностью при подаче на их вход сигнала синусоидальной формы формировать на выходе пару синусоидальных сигналов, имеющих разность фаз приблизительно 90°. В радиотехнике это называется «фазовым» методом формирования однополосного сигнала (благодаря Weaver), где предназначенный для передачи входной сигнал состоит из сигналов речевого диапазона.
-фильтров, которые обладают способностью при подаче на их вход сигнала синусоидальной формы формировать на выходе пару синусоидальных сигналов, имеющих разность фаз приблизительно 90°. В радиотехнике это называется «фазовым» методом формирования однополосного сигнала (благодаря Weaver), где предназначенный для передачи входной сигнал состоит из сигналов речевого диапазона.
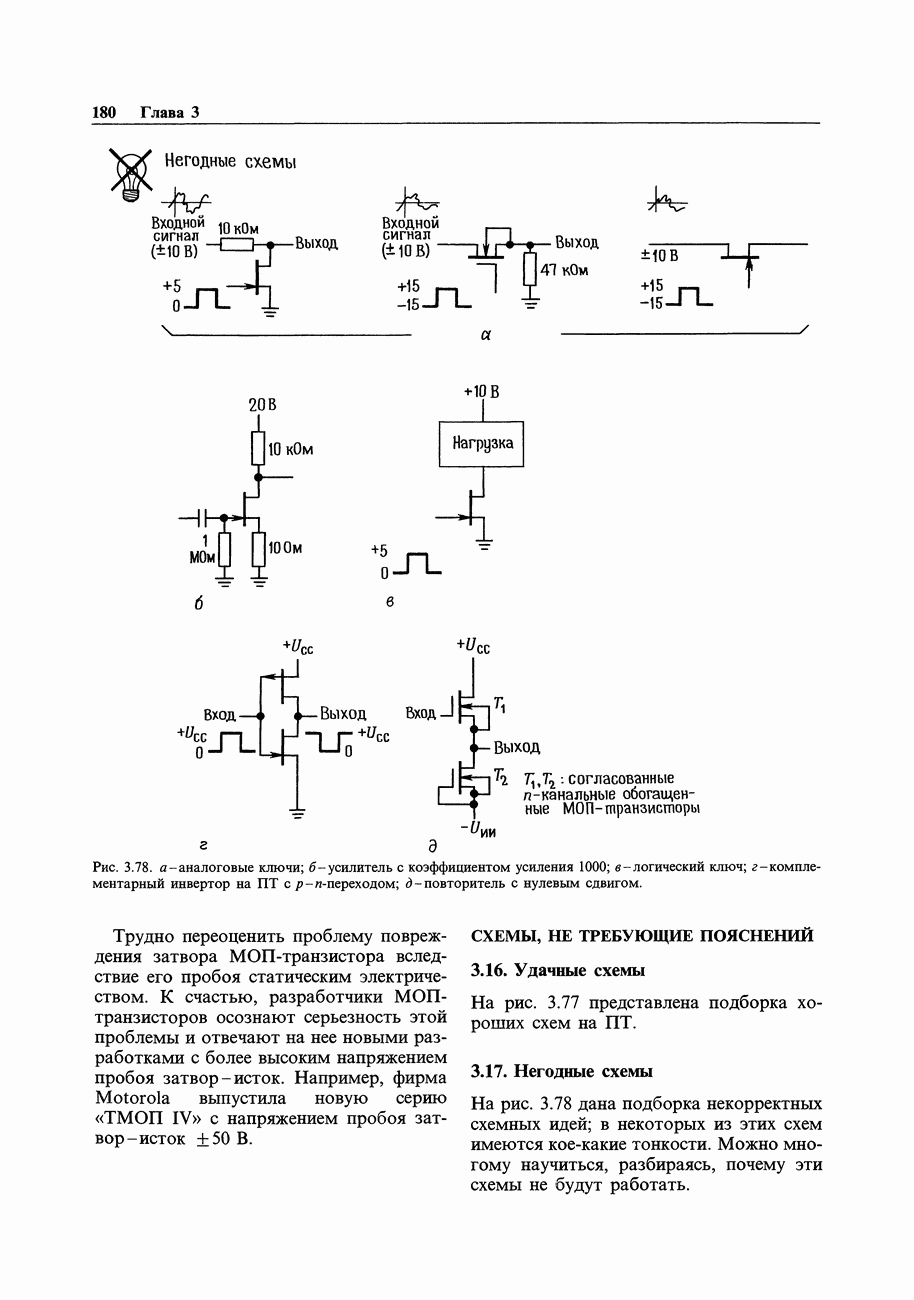
К сожалению, этот метод работает удовлетворительно только в ограниченном диапазоне частот и требует точного подбора номиналов резисторов и конденсаторов. Более приемлемый способ формирования широкополосных квадратурных сигналов основан на использовании «цепи с упорядоченными фазовыми сдвигами», которая представляет собой регулярную структуру, состоящую из резисторов с равными номиналами, а номиналы конденсаторов уменьшаются в геометрической прогрессии, как это указано на рис. 5.41. На вход этой цепи подаются два сигнала, а именно прямой и сдвинутый на 180° (это легко сделать с помощью инвертора с единичным коэффициентом передачи). Выходной сигнал представляет собой набор из четырех квадратурных сигналов и при использовании  -секцион-ной цепи их погрешность составляет
-секцион-ной цепи их погрешность составляет  0,5° в диапазоне частот
0,5° в диапазоне частот  .
.
Квадратурные колебания прямоугольной формы.
В некоторых случаях формирование квадратурных сигналов прямоугольной формы является несложной задачей.
Рис. 5.41. Цепь с упорядоченными фазовыми сдвигами.
Основная идея заключается в том, чтобы сформировать сигнал удвоенной частоты, затем поделить его в два раза с помощью цифрового триггера (гл. 8) и декодировать на вентилях (снова гл. 8). Это наиболее совершенный способ формирования квадратурных прямоугольных колебаний в диапазоне частот от постоянного тока до по крайней мере 100 МГц.
Квадратурные сигналы диапазона радиочастот.
В диапазоне радиочастот (выше нескольких мегагерц) формирование пары квадратурных сигналов синусоидальной формы снова достаточно тривиальная задача; в этом случае используются приборы, которые называются квадратурными гибридными схемами (или квадратурные расщепитель/объединитель). На низкочастотной границе радиочастотного диапазона (от нескольких мегагерц до, может быть, ) они принимают форму небольших трансформаторов с магнитным сердечником, в то время как на более высоких частотах нужно найти их воплощение в форме полосковых линий передачи (полоски и печатные проводники, изолированные от заземленной подложки) или световодов (полая прямоугольная трубка). Эти вопросы снова будут рассмотрены в гл. 13. Методика достаточно узкополосная, типовая ширина рабочей частоты не превышает октаву (т. е. соотношение частот
) они принимают форму небольших трансформаторов с магнитным сердечником, в то время как на более высоких частотах нужно найти их воплощение в форме полосковых линий передачи (полоски и печатные проводники, изолированные от заземленной подложки) или световодов (полая прямоугольная трубка). Эти вопросы снова будут рассмотрены в гл. 13. Методика достаточно узкополосная, типовая ширина рабочей частоты не превышает октаву (т. е. соотношение частот  ).
).
Формирование синусоидального колебания с произвольной фазой.
Поскольку у нас уже имеется пара квадратурных сигналов, достаточно просто сформировать синусоидальное колебание с произвольной фазой. В этом случае требуется просто объединить синфазный и квадратурные сигналы
и квадратурные сигналы  на резистивном сумматоре, что наиболее просто реализуется с помощью потенциометра, включенного между I и Q сигналами. При вращении движка потенциометра эти сигналы
на резистивном сумматоре, что наиболее просто реализуется с помощью потенциометра, включенного между I и Q сигналами. При вращении движка потенциометра эти сигналы  и Q) суммируются в различных соотношениях, при этом удается получить плавное изменение фазы в диапазоне от 0 до 90°. Если же рассматривать эту проблему с точки зрения векторов, то можно показать, что фаза результирующего колебания совершенно не зависит от частоты; однако его амплитуда при регулировке фазы меняется, спадая на 3 дБ при фазе 45°. Метод достаточно просто можно распространить и на случай формирования колебания, фаза которого должна лежать в диапазоне от 0 до 360°, при этом используются противоположные сигналы (фазовый сдвиг 180°) Г и Q, которые получаются с помощью инвертирующих усилителей с коэффициентом передачи -1.
и Q) суммируются в различных соотношениях, при этом удается получить плавное изменение фазы в диапазоне от 0 до 90°. Если же рассматривать эту проблему с точки зрения векторов, то можно показать, что фаза результирующего колебания совершенно не зависит от частоты; однако его амплитуда при регулировке фазы меняется, спадая на 3 дБ при фазе 45°. Метод достаточно просто можно распространить и на случай формирования колебания, фаза которого должна лежать в диапазоне от 0 до 360°, при этом используются противоположные сигналы (фазовый сдвиг 180°) Г и Q, которые получаются с помощью инвертирующих усилителей с коэффициентом передачи -1.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. ОСНОВЫ ЭЛЕКТРОНИКИ
- НАПРЯЖЕНИЕ, ТОК И СОПРОТИВЛЕНИЕ
- 1.01. Напряжение и ток
- 1.02. Взаимосвязь напряжения и тока: резисторы
- ПРИСТАВКИ ДЛЯ ОБРАЗОВАНИЯ КРАТНЫХ И ДОЛЬНЫХ ЕДИНИЦ ИЗМЕРЕНИЯ
- РЕЗИСТОРЫ
- ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ ФИРМЫ ALLEN BRADLEY, (СЕРИЯ АВ, ТИП СВ)
- 1.03. Делители напряжения
- 1.04. Источники тока и напряжения
- 1.05. Теорема об эквивалентном преобразовании источников (генераторов)
- УНИВЕРСАЛЬНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1.06. Динамическое сопротивление
- СИГНАЛЫ
- 1.07. Синусоидальные сигналы
- 1.08. Измерение амплитуды сигналов
- 1.09. Другие типы сигналов
- 1.10. Логические уровни
- 1.11. Источники сигналов
- КОНДЕНСАТОРЫ И ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 1.12. Конденсаторы
- КОНДЕНСАТОРЫ
- 1.13. RС-цепи: изменения во времени напряжения и тока
- 1.14. Дифференцирующие цепи
- 1.15. Интегрирующие цепи
- ИНДУКТИВНОСТИ и ТРАНСФОРМАТОРЫ
- 1.16. Индуктивности
- 1.17. Трансформаторы
- ПОЛНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ
- 1.18. Частотный анализ реактивных схем
- 1.19. RC-фильтры
- 1.20. Векторные диаграммы
- 1.21. «Полюсы» и наклон в пределах октавы
- 1.22. Резонансные схемы и активные фильтры
- 1.23. Другие примеры использования конденсаторов
- 1.24. Обобщенная теорема Тевенина об эквивалентном преобразовании (эквивалентном генераторе)
- ДИОДЫ И ДИОДНЫЕ СХЕМЫ
- 1.25. Диоды
- 1.26. Выпрямление
- 1.27. Фильтрация в источниках питания
- 1.28. Схемы выпрямителей для источников питания
- 1.29. Стабилизаторы напряжения
- 1.30. Примеры использования диодов
- 1.31. Индуктивные нагрузки и диодная защита
- ДРУГИЕ ПАССИВНЫЕ КОМПОНЕНТЫ
- 1.32. Электромеханические элементы
- 1.33. Индикаторы
- 1.34. Переменные компоненты
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 2. ТРАНЗИСТОРЫ
- 2.01. Первая модель транзистора: усилитель тока
- НЕКОТОРЫЕ ОСНОВНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.02. Транзисторный переключатель
- 2.03. Эмиттерный повторитель
- 2.04. Использование эмиттерных повторителей в качестве стабилизаторов напряжения
- 2.05. Смещение в эмиттерном повторителе
- 2.06. Транзисторный источник тока
- 2.07. Усилитель с общим эмиттером
- 2.08. Схема расщепления фазы с единичным коэффициентом усиления
- 2.09. Крутизна
- МОДЕЛЬ ЭБЕРСА-МОЛЛА ДЛЯ ОСНОВНЫХ ТРАНЗИСТОРНЫХ СХЕМ
- 2.10. Улучшенная модель транзистора: усилитель с передаточной проводимостью (крутизной)
- 2.11. Еще раз об эмиттерном повторителе
- 2.13. Еще раз об усилителе с общим эмиттером
- 2.13. Смещение в усилителе с общим эмиттером
- 2.14. Токовые зеркала
- НЕКОТОРЫЕ ТИПЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ
- 2.15. Двухтактные выходные каскады
- 2.16. Составной транзистор (схема Дарлингтона)
- 2.17. Следящая связь
- 2.18. Дифференциальные усилители
- 2.19. Емкость и эффект Миллера
- 2.20. Полевые транзисторы
- НЕКОТОРЫЕ ТИПИЧНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.21. Стабилизированный источник напряжения
- 2.22. Терморегулятор
- 2.23. Простая логическая схема на транзисторах и диодах
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 2.24. Удачные схемы
- 2.25. Негодные схемы
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 3. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- 3.01. Характеристики полевых транзисторов
- 3.02. Типы ПТ
- 3.03. Общая классификация ПТ
- 3.04. Выходные характеристики ПТ
- 3.05. Производственный разброс характеристик ПТ
- ОСНОВНЫЕ СХЕМЫ НА ПТ
- 3.06. Источники тока на ПТ с р-n-переходом
- 3.07. Усилители на ПТ
- 3.08. Истоковые повторители
- 3.09. Ток затвора ПТ
- 3.10. ПТ в качестве переменных резисторов
- КЛЮЧИ НА ПТ
- 3.11. Аналоговые ключи на ПТ
- 3.12. Недостатки ПТ-ключей
- 3.13. Несколько схем на ПТ-ключах
- 3.14. Логические и мощные ключи на МОП-транзисторах
- 3.15. Необходимые предосторожности в обращении с МОП-транзисторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 4. ОБРАТНАЯ СВЯЗЬ И ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 4.01. Предварительные сведения об обратной связи
- 4.02. Операционные усилители
- 4.03. Важнейшие правила
- ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.04. Инвертирующий усилитель
- 4.05. Неинвертирующий усилитель
- 4.06. Повторитель
- 4.07. Источники тока
- 4.08. Основные предостережения по работе с ОУ
- КАЛЕЙДОСКОП СХЕМ НА ОПЕРАЦИОННЫХ УСИЛИТЕЛЯХ
- 4.09. Линейные схемы
- 4.10. Нелинейные схемы
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.11. Отличие характеристик идеального ОУ от реального
- 4.12. Эффекты ограничений ОУ на работу схем на их основе
- 4.13. Микромощные и программируемые ОУ
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ НЕКОТОРЫХ СХЕМ НА ОУ
- 4.14. Логарифмический усилитель
- 4.15. Активный пиковый детектор
- 4.16. Выборка-запоминание
- ДИЭЛЕКТРИЧЕСКОЕ ПОГЛОЩЕНИЕ
- 4.17. Активный ограничитель
- 4.18. Схема выделения модуля абсолютного значения сигнала
- 4.19. Интеграторы
- 4.20. Дифференциаторы
- РАБОТА ОУ С ОДНИМ ИСТОЧНИКОМ ПИТАНИЯ
- 4.21. Смещение усилителей переменного тока, использующих один источник питания.
- 4.22. Операционные усилители с одним источником питания.
- КОМПАРАТОРЫ И ТРИГГЕР ШМИТТА
- 4.23. Компараторы
- 4.24. Триггер Шмитта
- ОБРАТНАЯ СВЯЗЬ И УСИЛИТЕЛИ С КОНЕЧНЫМ УСИЛЕНИЕМ
- 4.25. Уравнение для коэффициента усиления
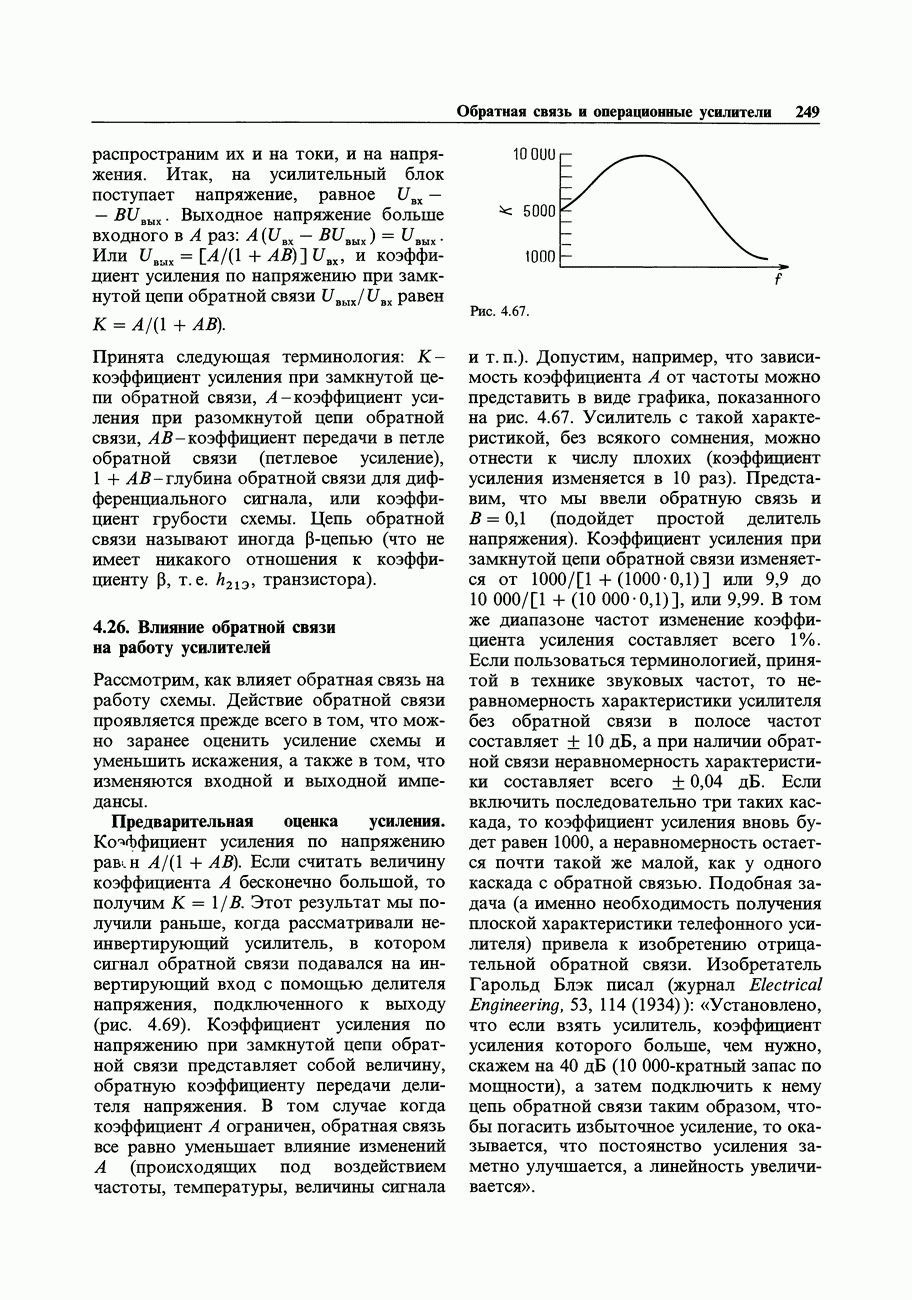
- 4.26. Влияние обратной связи на работу усилителей
- 4.27. Два примера транзисторных усилителей с обратной связью
- НЕКОТОРЫЕ ТИПИЧНЫЕ СХЕМЫ С ОПЕРАЦИОННЫМИ УСИЛИТЕЛЯМИ
- 4.28. Лабораторный усилитель общего назначения
- 4.29. Генератор, управляемый напряжением
- 4.30. Линейный переключатель на полевом транзисторе с p-n-переходом, с компенсацией.
- 4.31. Детектор нуля для ТТЛ-схем
- 4.32. Схема измерения тока в нагрузке
- ЧАСТОТНАЯ КОРРЕКЦИЯ УСИЛИТЕЛЕЙ С ОБРАТНОЙ СВЯЗЬЮ
- 4.33. Зависимость коэффициента усиления и фазового сдвига от частоты
- 4.34. Методы коррекции усилителей
- 4.35. Частотная характеристика цепи обратной связи
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 4.36. Некоторые полезные идеи
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 5. АКТИВНЫЕ ФИЛЬТРЫ И ГЕНЕРАТОРЫ
- АКТИВНЫЕ ФИЛЬТРЫ
- 5.01. Частотная характеристика RC-фильтров
- 5.02. Идеальный рабочий режим LC-фильтров
- 5.03. Введение в активные фильтры: обзор
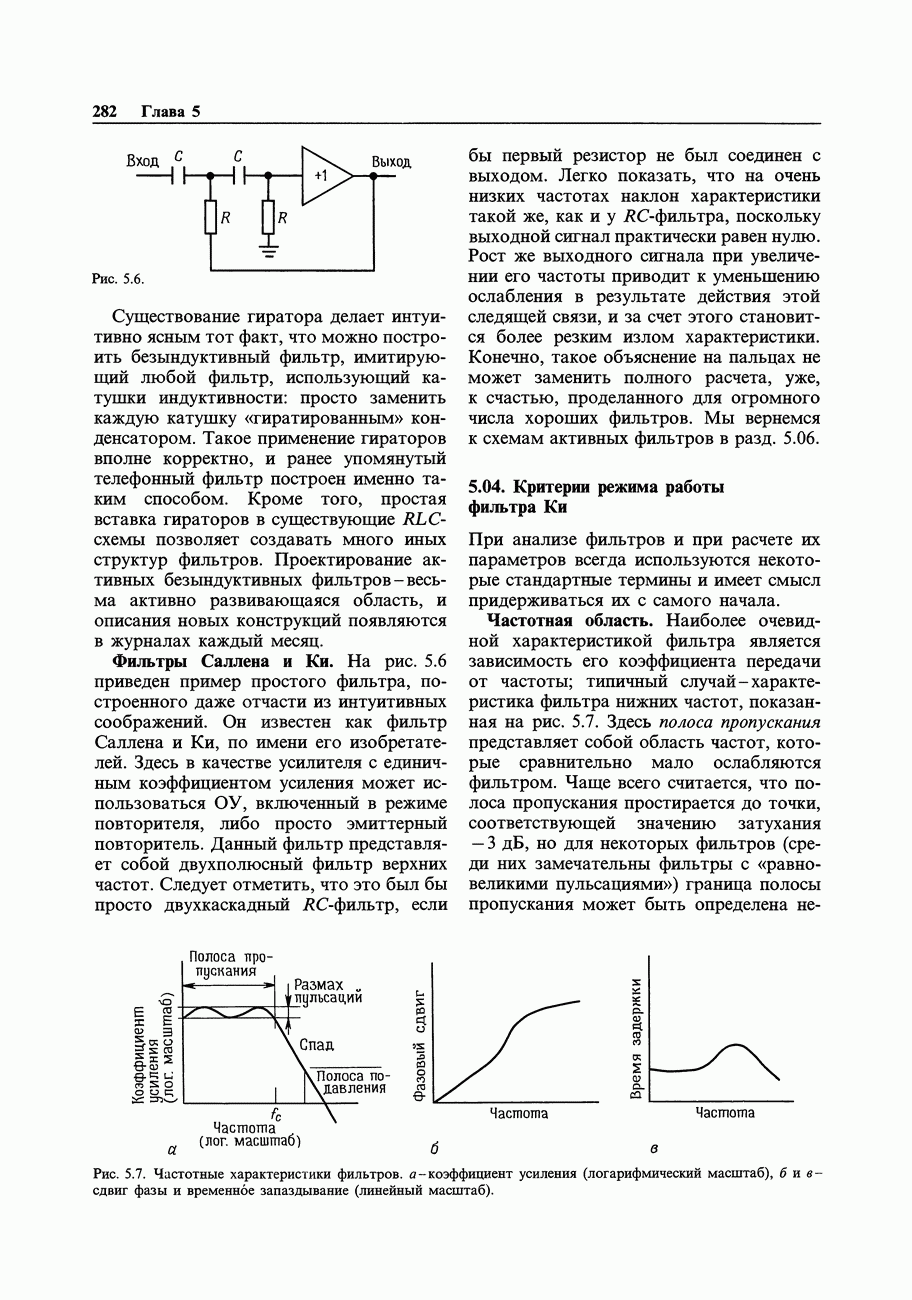
- 5.04. Критерии режима работы фильтра Ки
- 5.05. Типы фильтров
- СХЕМЫ АКТИВНЫХ ФИЛЬТРОВ
- 5.06. Схемы на ИНУН
- 5.07. Проектирование фильтров на ИНУН с использованием наших упрощенных таблиц
- 5.08. Фильтры, построенные на основе метода переменных состояния
- 5.09. Двойной Т-образный фильтр-пробка
- 5.10. Построение фильтров на гираторах
- 5.11. Фильтры на переключаемых конденсаторах
- ГЕНЕРАТОРЫ
- 5.13. Релаксационные генераторы
- 5.14. Классическая ИС таймера-555
- 5.15. Генераторы, управляемые напряжением
- 5.16. Квадратные генераторы
- 5.17. Мостовые генераторы Вина и L С-генераторы
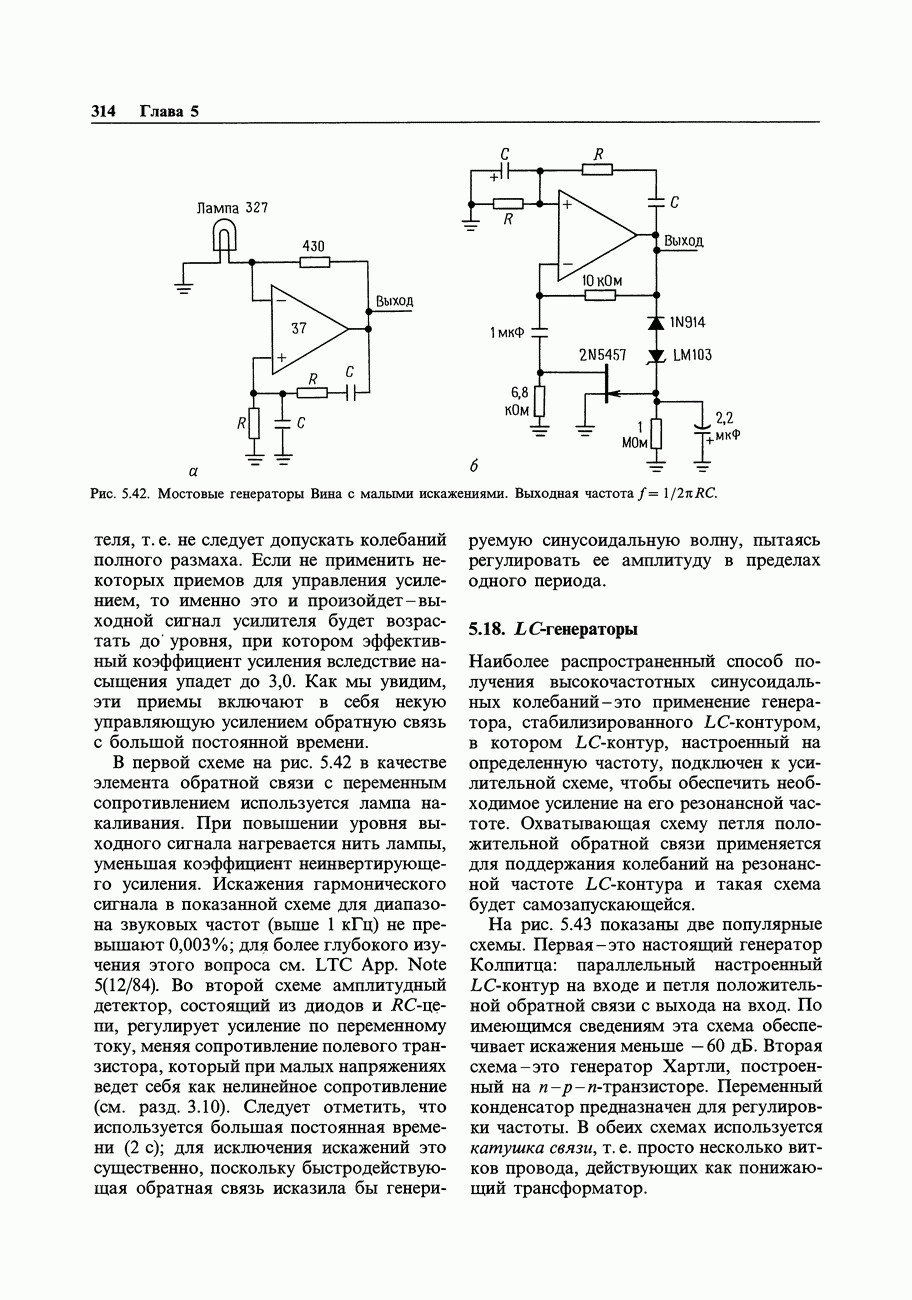
- 5.18. LС-генераторы
- 5.19. Генераторы с кварцевыми резонаторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 6. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ И ИСТОЧНИКИ ПИТАНИЯ
- БАЗОВЫЕ СХЕМЫ СТАБИЛИЗАТОРОВ НА ОСНОВЕ КЛАССИЧЕСКОЙ ИМС 723
- 6.01. ИМС стабилизатора 723
- 6.02. Стабилизатор положительного напряжения
- 6.03. Стабилизаторы с большими выходными токами
- ПРОЕКТИРОВАНИЕ ТЕПЛООТВОДА МОЩНЫХ СХЕМ
- 6.04. Мощные транзисторы и отвод тепла
- 6.05. Ограничители тока с обратным наклоном характеристики
- 6.06. Защита от больших напряжений
- 6.07. Специальные вопросы проектирования сильноточных источников питания
- 6.08. Программируемые источники питания
- 6.09. Пример схемы источника питания
- 6.10. Другие ИМС стабилизатора
- НЕСТАБИЛИЗИРОВАННЫЕ ИСТОЧНИКИ ПИТАНИЯ
- 6.11. Компоненты линии переменного тока
- 6.12. Трансформаторы
- 6.13 Элементы схемы, работающие на постоянном токе
- ИСТОЧНИКИ ОПОРНОГО НАПРЯЖЕНИЯ
- 6.14. Стабилитроны
- 6.15. Источник опорного напряжения на стабилитроне
- ТРЕХВЫВОДНЫЕ И ЧЕТЫРЕХВЫВОДНЫЕ СТАБИЛИЗАТОРЫ
- 6.16. Трехвыводные стабилизаторы
- 6.17. Трехвыводные регулируемые стабилизаторы
- 6.18. Дополнительные замечания относительно трехвыводных стабилизаторов
- 6.19. Импульсные стабилизаторы и преобразователи постоянного тока
- ИСТОЧНИКИ ПИТАНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ
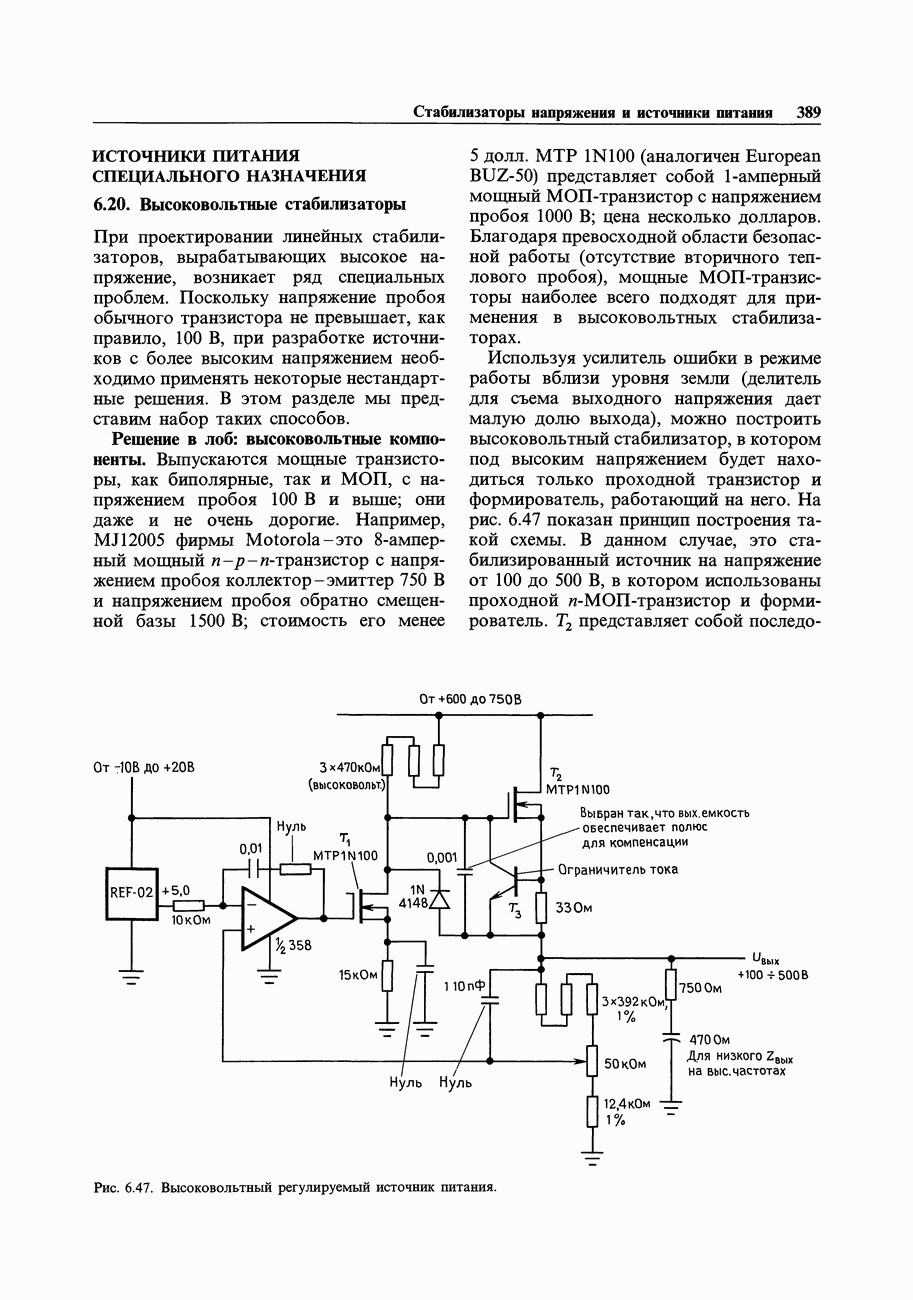
- 6.20. Высоковольтные стабилизаторы
- 6.21. Источники питания с малым уровнем помех и малым дрейфом
- 6.22. Микромощные стабилизаторы
- 6.23. Преобразователи напряжения с переключаемыми конденсаторами (зарядовый насос)
- 6.24. Источники стабилизированного постоянного тока
- 6.25. Коммерческие модули источников питания
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ