| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ ФИРМЫ ALLEN BRADLEY, (СЕРИЯ АВ, ТИП СВ)
Стандартный допуск в номинальных условиях составляет 5%. Максимальная мощность при температуре окружающей среды  составляет
составляет  , при этом внутренняя температура повышается до
, при этом внутренняя температура повышается до  . Максимальное приложенное напряжение составляет (
. Максимальное приложенное напряжение составляет ( или 250 В (меньшее из двух значений). И это на самом деле так! (см. рис. 6.53). Однократное превышение напряжения до 400 В в течение 5 с вызывает необратимое изменение сопротивления на 2%.
или 250 В (меньшее из двух значений). И это на самом деле так! (см. рис. 6.53). Однократное превышение напряжения до 400 В в течение 5 с вызывает необратимое изменение сопротивления на 2%.

В схемах, где требуется высокая точность или стабильность, следует использовать резисторы из металлической пленки с допуском 1% (см. приложение Г). Они обеспечивают стабильность не хуже  в нормальных условиях и не хуже
в нормальных условиях и не хуже  в самых жестких условиях. Прецизионные проволочные резисторы способны удовлетворить наиболее высоким требованиям.
в самых жестких условиях. Прецизионные проволочные резисторы способны удовлетворить наиболее высоким требованиям.
Если ожидается, что мощность, рассеиваемая в схеме, будет составлять более  , то следует выбрать резистор с большим значением рассеиваемой мощности. Композиционные углеродистые резисторы характеризуются мощностью до
, то следует выбрать резистор с большим значением рассеиваемой мощности. Композиционные углеродистые резисторы характеризуются мощностью до  , а мощные проволочные резисторы - более высокими значениями. Для мощных схем наилучшие характеристики обеспечивает резистор с отводом тепла. Резисторы этого типа выпускаются с допуском 1% и могут надежно работать при собственной температуре до
, а мощные проволочные резисторы - более высокими значениями. Для мощных схем наилучшие характеристики обеспечивает резистор с отводом тепла. Резисторы этого типа выпускаются с допуском 1% и могут надежно работать при собственной температуре до  в течение длительного периода времени. Допустимая рассеиваемая мощность зависит от воздушного потока, температурных условий на выводах и плотности схемы; следовательно, мощность на резисторе следует рассматривать как грубую ориентировочную величину. Отметим также, что мощность резистора связана со средним значением мощности, рассеиваемой в схеме, и может существенно превышаться в короткие интервалы времени (в зависимости от «тепловой массы» эти интервалы могут длиться несколько секунд или более).
в течение длительного периода времени. Допустимая рассеиваемая мощность зависит от воздушного потока, температурных условий на выводах и плотности схемы; следовательно, мощность на резисторе следует рассматривать как грубую ориентировочную величину. Отметим также, что мощность резистора связана со средним значением мощности, рассеиваемой в схеме, и может существенно превышаться в короткие интервалы времени (в зависимости от «тепловой массы» эти интервалы могут длиться несколько секунд или более).
Упражнение 1.1. Возьмем два резистора сопротивлением 5 и 10 кОм. Чему равно сопротивление при (а) последовательном и (б) параллельном их соединении?
Упражнение 1.2. Какую мощность будет рассеивать в пространство резистор с сопротивлением 1 Ом, подключенный к батарее автомобиля с напряжением 1 В?
Упражнение 1.3. Докажите справедливость формул для сопротивления последовательного и параллельного соединения резисторов.
Упражнение 1.4. Покажите, что сопротивление нескольких параллельно соединенных резисторов определяется следующим образом:

Секрет резисторов, соединенных параллельно: начинающие часто приступают к сложным алгебраическим выкладкам или углубляются в законы электроники, а здесь как раз лучше всего воспользоваться интуитивным правилом. Приступим теперь к освоению интуитивных правил и развитию интуиции.
Правило 1. Сопротивление двух резисторов, один из которых обладает большим сопротивлением, а другой малым, соединенных между собой последовательно (параллельно), приблизительно равно большему (меньшему) из двух сопротивлений.
Правило 2. Допустим, вы хотите узнать, чему равно сопротивление двух параллельно соединенных резисторов, обладающих сопротивлением 5 и 10 кОм. Если вообразить, что резистор сопротивлением 5 кОм представляет собой параллельное соединение двух резисторов сопротивлением 10 кОм, то схема будет представлена параллельным соединением трех резисторов с сопротивлением 10 кОм. Так как сопротивление одинаковых параллельно соединенных резисторов равно  части сопротивления одного из них, то ответ в нашей задаче будет
части сопротивления одного из них, то ответ в нашей задаче будет  , или 3,33 кОм. Это правило полезно усвоить, так как с его помощью можно быстро проанализировать схему «в
, или 3,33 кОм. Это правило полезно усвоить, так как с его помощью можно быстро проанализировать схему «в  . Мы хотим, чтобы вы научились решать стоящие перед вами задачи, имея под рукой минимум - оборотную сторону почтового конверта и ручку. Тогда блестящие идеи, возникшие у вас в любой момент, не будут встречать препятствий на пути своего развития.
. Мы хотим, чтобы вы научились решать стоящие перед вами задачи, имея под рукой минимум - оборотную сторону почтового конверта и ручку. Тогда блестящие идеи, возникшие у вас в любой момент, не будут встречать препятствий на пути своего развития.
И еще несколько принципов нашей доморощенной философии: среди начинающих наблюдается тенденция вычислять значения сопротивлений резисторов и характеристики других компонентов схем с большой точностью, доступность же карманных калькуляторов в наше время помогает развитию этой тенденции. Поддаваться ей не следует по двум причинам: во-первых, компоненты сами по себе имеют определенную конечную точность (наиболее распространенные  характеристики транзисторов, например часто задаются одним - двумя коэффициентами); во-вторых, одним из признаков хорошей схемы является ее нечувствительность к точности величин компонентов (бывают, конечно, и исключения). И еще: вы скорее придете к интуитивному пониманию схем, если разовьете в себе способность быстро прикидывать «в
характеристики транзисторов, например часто задаются одним - двумя коэффициентами); во-вторых, одним из признаков хорошей схемы является ее нечувствительность к точности величин компонентов (бывают, конечно, и исключения). И еще: вы скорее придете к интуитивному пониманию схем, если разовьете в себе способность быстро прикидывать «в  , а не будете увлекаться вычислениями с ненужной точностью на красивых калькуляторах.
, а не будете увлекаться вычислениями с ненужной точностью на красивых калькуляторах.
Некоторые считают, что для того чтобы скорее научиться оценивать величину сопротивления, полезно вводить понятие проводимость,  . Ток, протекающий через элемент с проводимостью G, к которому приложено напряжение U, определяется как
. Ток, протекающий через элемент с проводимостью G, к которому приложено напряжение U, определяется как  (это закон Ома).
(это закон Ома).
Чем меньше сопротивление проводника, тем больше его проводимость и тем больше ток, протекающий под воздействием напряжения, приложенного между концами проводника.
С этой точки зрения формула для определения сопротивления параллельно соединенных проводников вполне очевидна: если несколько резисторов или проводящих участков подключены к одному и тому же напряжению, то полный ток равен сумме токов, протекающих в отдельных ветвях. В связи с этим проводимость соединения равна сумме отдельных проводимостей составных элементов:  , а это выражение эквивалентно выражению для параллельно соединенных резисторов, приведенному выше.
, а это выражение эквивалентно выражению для параллельно соединенных резисторов, приведенному выше.
Инженеры неравнодушны к обратным величинам, и в качестве единицы измерения проводимости они установили 1 сименс (1 См  Ом), который иногда называют
Ом), который иногда называют  («ом» наоборот). Хотя понятие проводимости и помогает развить интуицию в отношении сопротивления резисторов, широкого применения оно не находит, и большинство предпочитает иметь дело с величинами сопротивления, а не проводимости.
(«ом» наоборот). Хотя понятие проводимости и помогает развить интуицию в отношении сопротивления резисторов, широкого применения оно не находит, и большинство предпочитает иметь дело с величинами сопротивления, а не проводимости.
Мощность и резисторы.
Мощность, рассеиваемая резистором или любым другим элементом, определяются как . Пользуясь законом
. Пользуясь законом  , эту формулу можно записать в эквивалентном виде:
, эту формулу можно записать в эквивалентном виде:

Упражнение 1.5. Возьмем схему, работающую от батареи с напряжением 15 В. Докажите, что независимо от того, как будет включен в схему резистор, обладающий сопротивлением более 1 кОм, мощность на нем не превысит  .
.
Упражнение 1.6. Дополнительное упражнение: для Нью-Йорка требуется  электрической энергии при напряжении 110 В (цифры вполне правдоподобны:
электрической энергии при напряжении 110 В (цифры вполне правдоподобны:  . жителей, каждый потребляет в среднем
. жителей, каждый потребляет в среднем  электроэнергии). Высоковольтный кабель может иметь диаметр 25,4 мм. Давайте подсчитаем, что произойдет, если в качестве кабеля взять провод из чистой меди диаметром
электроэнергии). Высоковольтный кабель может иметь диаметр 25,4 мм. Давайте подсчитаем, что произойдет, если в качестве кабеля взять провод из чистой меди диаметром  . Сопротивление такого провода составляет
. Сопротивление такого провода составляет  Ом) в расчете на
Ом) в расчете на  . Определите: а) потери мощности в расчете на
. Определите: а) потери мощности в расчете на  , исходя из того, что потери оцениваются величиной
, исходя из того, что потери оцениваются величиной  длину кабеля, на которой будут потеряны все
длину кабеля, на которой будут потеряны все  если вы знаете физику, определите, до какой температуры нагреется кабель
если вы знаете физику, определите, до какой температуры нагреется кабель  .
.
Если расчет выполнен правильно, то результат, вероятно, удивил вас. Как же разрешить проблему?
Вход и выход. Практически во всех электронных схемах что-либо подается на вход (обычно это напряжение) и соответственно снимается с выхода (это также чаще всего напряжение). Например, с выхода усилителя звуковой частоты снимается напряжение (оно имеет переменное значение), которое в 100 раз превышает входное напряжение (изменяющееся аналогично). В этом усилителе выходное напряжение рассматривается для данного значения напряжения, действующего на входе. Инженеры пользуются понятием передаточной функции Н, которая представляет собой отношение напряжения, измеренного на выходе, к напряжению, действующему на входе; для вышеупомянутого усилителя звуковой частоты Н-это постоянная величина  . К изучению усилителей мы приступим в следующей главе. Однако, уже сейчас, имея представление только о резисторах, мы рассмотрим делитель напряжения (по сути он является
. К изучению усилителей мы приступим в следующей главе. Однако, уже сейчас, имея представление только о резисторах, мы рассмотрим делитель напряжения (по сути он является  ), который играет немаловажную роль в электронных схемах.
), который играет немаловажную роль в электронных схемах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. ОСНОВЫ ЭЛЕКТРОНИКИ
- НАПРЯЖЕНИЕ, ТОК И СОПРОТИВЛЕНИЕ
- 1.01. Напряжение и ток
- 1.02. Взаимосвязь напряжения и тока: резисторы
- ПРИСТАВКИ ДЛЯ ОБРАЗОВАНИЯ КРАТНЫХ И ДОЛЬНЫХ ЕДИНИЦ ИЗМЕРЕНИЯ
- РЕЗИСТОРЫ
- ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ ФИРМЫ ALLEN BRADLEY, (СЕРИЯ АВ, ТИП СВ)
- 1.03. Делители напряжения
- 1.04. Источники тока и напряжения
- 1.05. Теорема об эквивалентном преобразовании источников (генераторов)
- УНИВЕРСАЛЬНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1.06. Динамическое сопротивление
- СИГНАЛЫ
- 1.07. Синусоидальные сигналы
- 1.08. Измерение амплитуды сигналов
- 1.09. Другие типы сигналов
- 1.10. Логические уровни
- 1.11. Источники сигналов
- КОНДЕНСАТОРЫ И ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 1.12. Конденсаторы
- КОНДЕНСАТОРЫ
- 1.13. RС-цепи: изменения во времени напряжения и тока
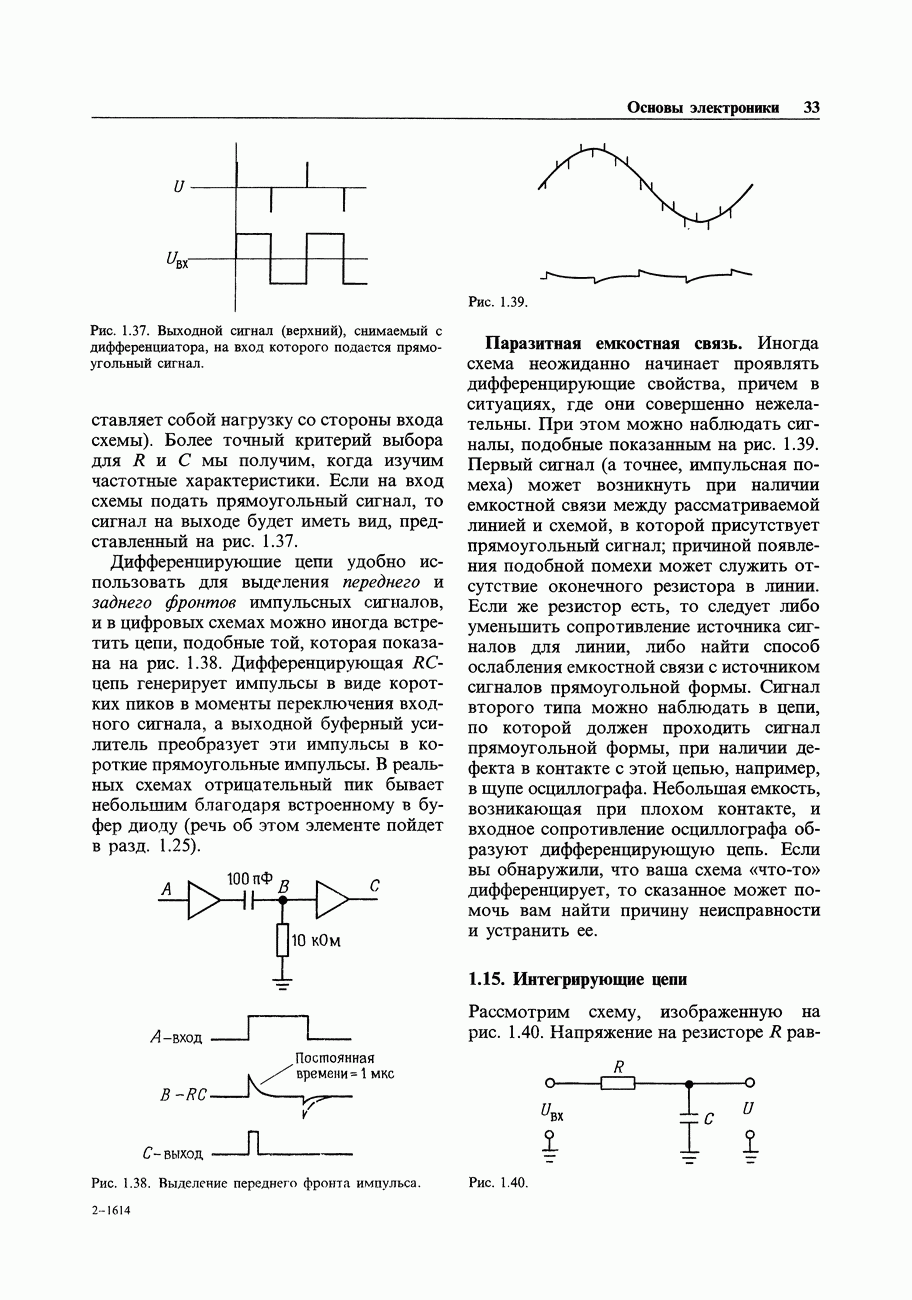
- 1.14. Дифференцирующие цепи
- 1.15. Интегрирующие цепи
- ИНДУКТИВНОСТИ и ТРАНСФОРМАТОРЫ
- 1.16. Индуктивности
- 1.17. Трансформаторы
- ПОЛНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ
- 1.18. Частотный анализ реактивных схем
- 1.19. RC-фильтры
- 1.20. Векторные диаграммы
- 1.21. «Полюсы» и наклон в пределах октавы
- 1.22. Резонансные схемы и активные фильтры
- 1.23. Другие примеры использования конденсаторов
- 1.24. Обобщенная теорема Тевенина об эквивалентном преобразовании (эквивалентном генераторе)
- ДИОДЫ И ДИОДНЫЕ СХЕМЫ
- 1.25. Диоды
- 1.26. Выпрямление
- 1.27. Фильтрация в источниках питания
- 1.28. Схемы выпрямителей для источников питания
- 1.29. Стабилизаторы напряжения
- 1.30. Примеры использования диодов
- 1.31. Индуктивные нагрузки и диодная защита
- ДРУГИЕ ПАССИВНЫЕ КОМПОНЕНТЫ
- 1.32. Электромеханические элементы
- 1.33. Индикаторы
- 1.34. Переменные компоненты
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 2. ТРАНЗИСТОРЫ
- 2.01. Первая модель транзистора: усилитель тока
- НЕКОТОРЫЕ ОСНОВНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.02. Транзисторный переключатель
- 2.03. Эмиттерный повторитель
- 2.04. Использование эмиттерных повторителей в качестве стабилизаторов напряжения
- 2.05. Смещение в эмиттерном повторителе
- 2.06. Транзисторный источник тока
- 2.07. Усилитель с общим эмиттером
- 2.08. Схема расщепления фазы с единичным коэффициентом усиления
- 2.09. Крутизна
- МОДЕЛЬ ЭБЕРСА-МОЛЛА ДЛЯ ОСНОВНЫХ ТРАНЗИСТОРНЫХ СХЕМ
- 2.10. Улучшенная модель транзистора: усилитель с передаточной проводимостью (крутизной)
- 2.11. Еще раз об эмиттерном повторителе
- 2.13. Еще раз об усилителе с общим эмиттером
- 2.13. Смещение в усилителе с общим эмиттером
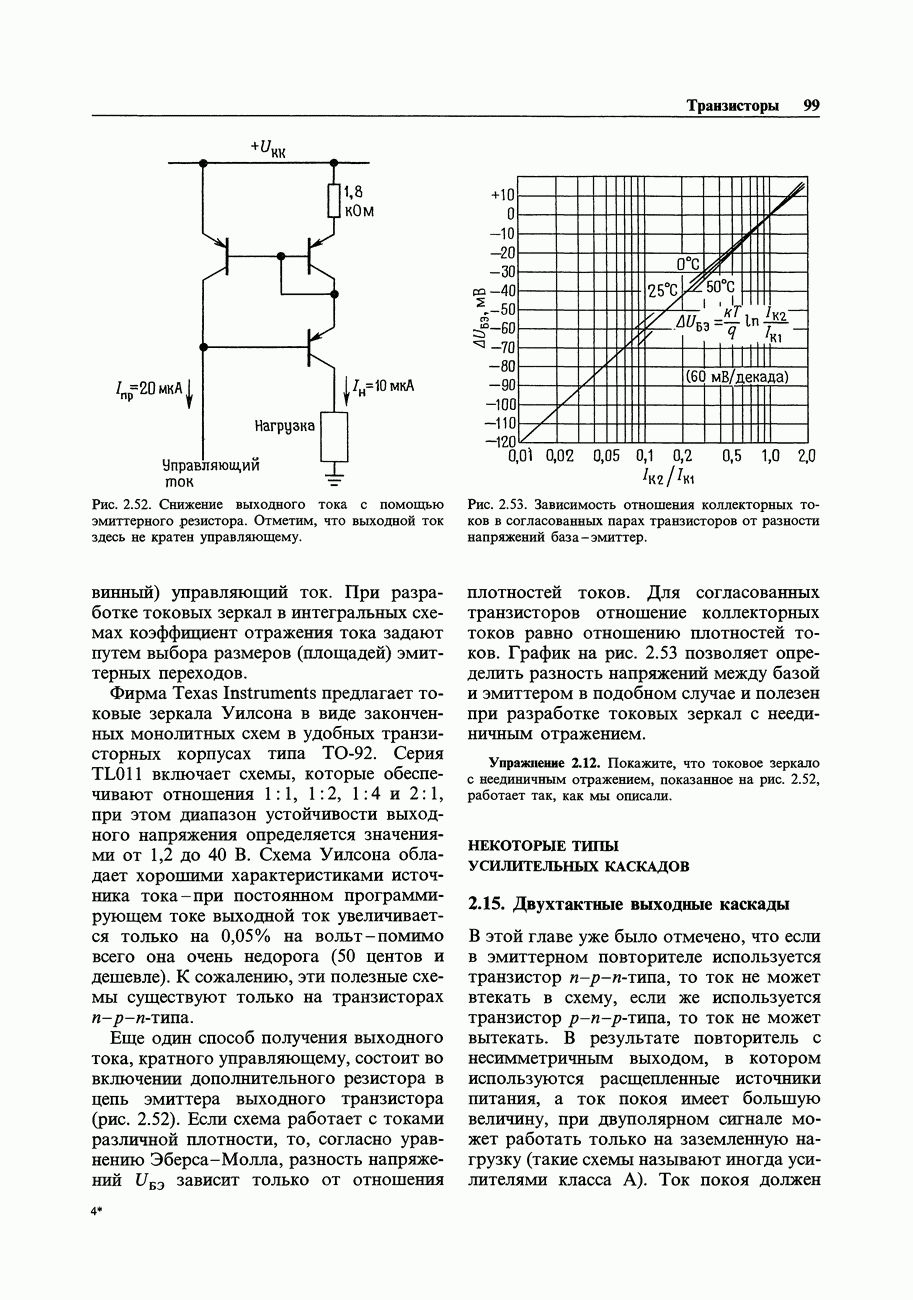
- 2.14. Токовые зеркала
- НЕКОТОРЫЕ ТИПЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ
- 2.15. Двухтактные выходные каскады
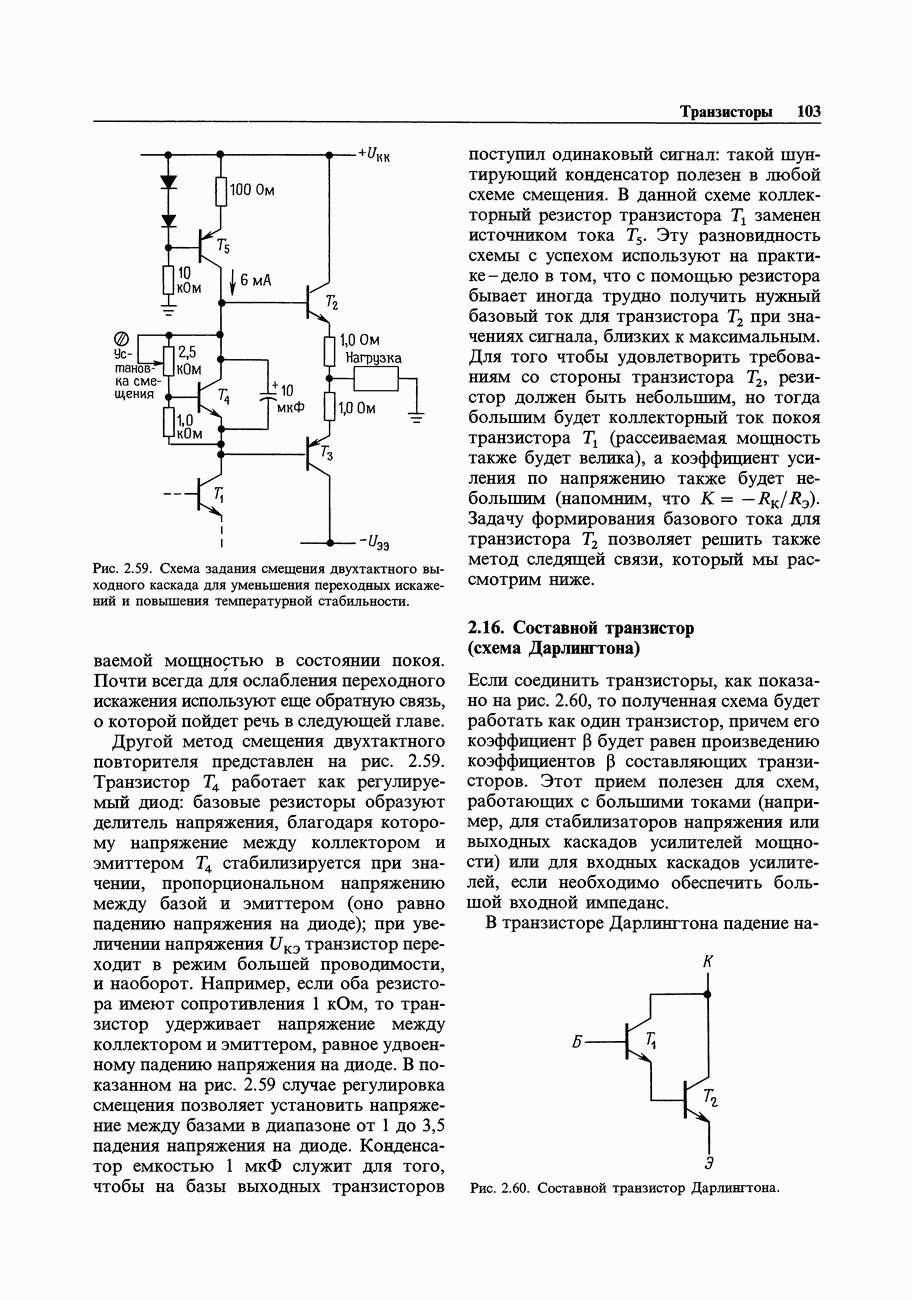
- 2.16. Составной транзистор (схема Дарлингтона)
- 2.17. Следящая связь
- 2.18. Дифференциальные усилители
- 2.19. Емкость и эффект Миллера
- 2.20. Полевые транзисторы
- НЕКОТОРЫЕ ТИПИЧНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.21. Стабилизированный источник напряжения
- 2.22. Терморегулятор
- 2.23. Простая логическая схема на транзисторах и диодах
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 2.24. Удачные схемы
- 2.25. Негодные схемы
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 3. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- 3.01. Характеристики полевых транзисторов
- 3.02. Типы ПТ
- 3.03. Общая классификация ПТ
- 3.04. Выходные характеристики ПТ
- 3.05. Производственный разброс характеристик ПТ
- ОСНОВНЫЕ СХЕМЫ НА ПТ
- 3.06. Источники тока на ПТ с р-n-переходом
- 3.07. Усилители на ПТ
- 3.08. Истоковые повторители
- 3.09. Ток затвора ПТ
- 3.10. ПТ в качестве переменных резисторов
- КЛЮЧИ НА ПТ
- 3.11. Аналоговые ключи на ПТ
- 3.12. Недостатки ПТ-ключей
- 3.13. Несколько схем на ПТ-ключах
- 3.14. Логические и мощные ключи на МОП-транзисторах
- 3.15. Необходимые предосторожности в обращении с МОП-транзисторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 4. ОБРАТНАЯ СВЯЗЬ И ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 4.01. Предварительные сведения об обратной связи
- 4.02. Операционные усилители
- 4.03. Важнейшие правила
- ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.04. Инвертирующий усилитель
- 4.05. Неинвертирующий усилитель
- 4.06. Повторитель
- 4.07. Источники тока
- 4.08. Основные предостережения по работе с ОУ
- КАЛЕЙДОСКОП СХЕМ НА ОПЕРАЦИОННЫХ УСИЛИТЕЛЯХ
- 4.09. Линейные схемы
- 4.10. Нелинейные схемы
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.11. Отличие характеристик идеального ОУ от реального
- 4.12. Эффекты ограничений ОУ на работу схем на их основе
- 4.13. Микромощные и программируемые ОУ
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ НЕКОТОРЫХ СХЕМ НА ОУ
- 4.14. Логарифмический усилитель
- 4.15. Активный пиковый детектор
- 4.16. Выборка-запоминание
- ДИЭЛЕКТРИЧЕСКОЕ ПОГЛОЩЕНИЕ
- 4.17. Активный ограничитель
- 4.18. Схема выделения модуля абсолютного значения сигнала
- 4.19. Интеграторы
- 4.20. Дифференциаторы
- РАБОТА ОУ С ОДНИМ ИСТОЧНИКОМ ПИТАНИЯ
- 4.21. Смещение усилителей переменного тока, использующих один источник питания.
- 4.22. Операционные усилители с одним источником питания.
- КОМПАРАТОРЫ И ТРИГГЕР ШМИТТА
- 4.23. Компараторы
- 4.24. Триггер Шмитта
- ОБРАТНАЯ СВЯЗЬ И УСИЛИТЕЛИ С КОНЕЧНЫМ УСИЛЕНИЕМ
- 4.25. Уравнение для коэффициента усиления
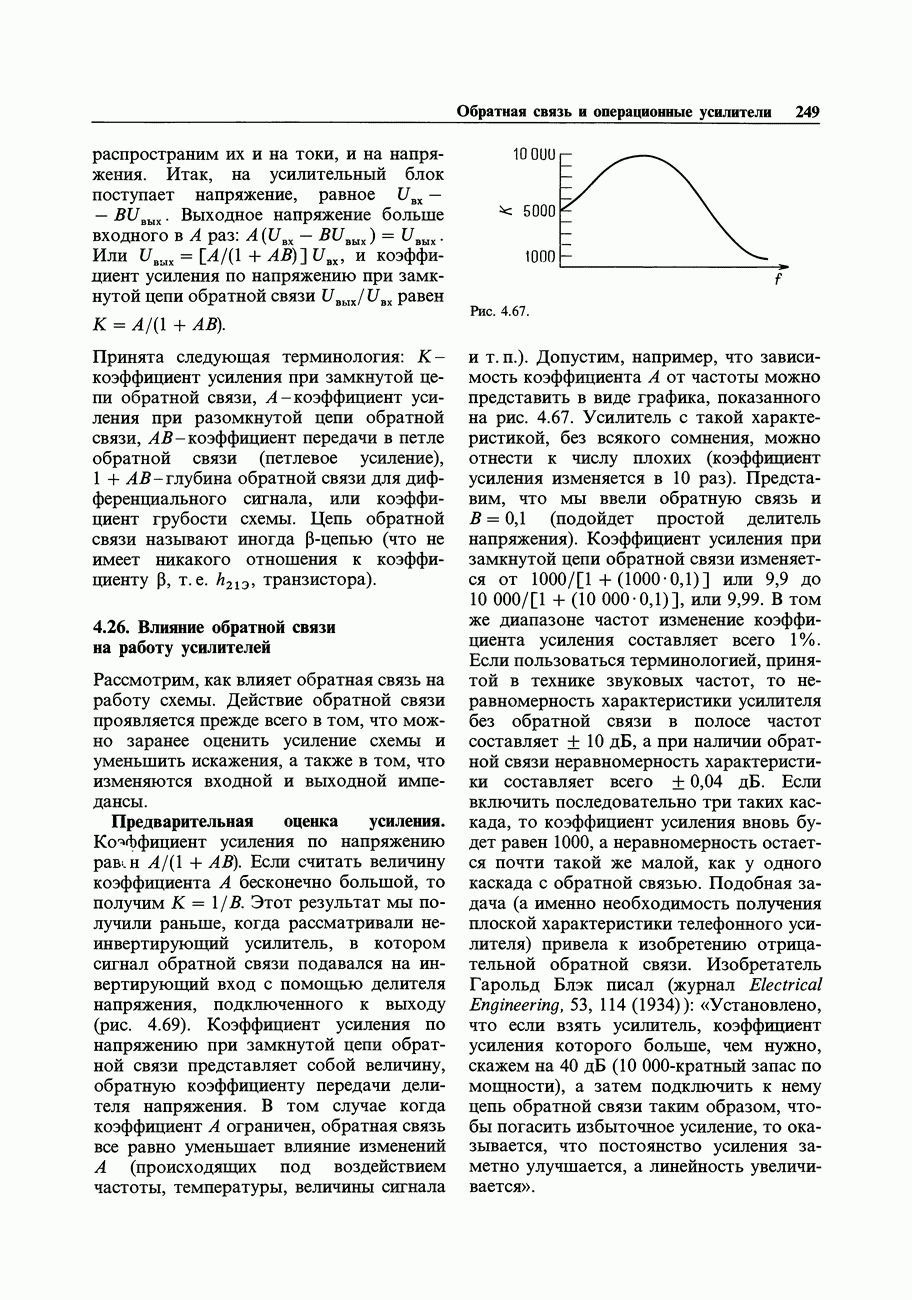
- 4.26. Влияние обратной связи на работу усилителей
- 4.27. Два примера транзисторных усилителей с обратной связью
- НЕКОТОРЫЕ ТИПИЧНЫЕ СХЕМЫ С ОПЕРАЦИОННЫМИ УСИЛИТЕЛЯМИ
- 4.28. Лабораторный усилитель общего назначения
- 4.29. Генератор, управляемый напряжением
- 4.30. Линейный переключатель на полевом транзисторе с p-n-переходом, с компенсацией.
- 4.31. Детектор нуля для ТТЛ-схем
- 4.32. Схема измерения тока в нагрузке
- ЧАСТОТНАЯ КОРРЕКЦИЯ УСИЛИТЕЛЕЙ С ОБРАТНОЙ СВЯЗЬЮ
- 4.33. Зависимость коэффициента усиления и фазового сдвига от частоты
- 4.34. Методы коррекции усилителей
- 4.35. Частотная характеристика цепи обратной связи
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 4.36. Некоторые полезные идеи
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 5. АКТИВНЫЕ ФИЛЬТРЫ И ГЕНЕРАТОРЫ
- АКТИВНЫЕ ФИЛЬТРЫ
- 5.01. Частотная характеристика RC-фильтров
- 5.02. Идеальный рабочий режим LC-фильтров
- 5.03. Введение в активные фильтры: обзор
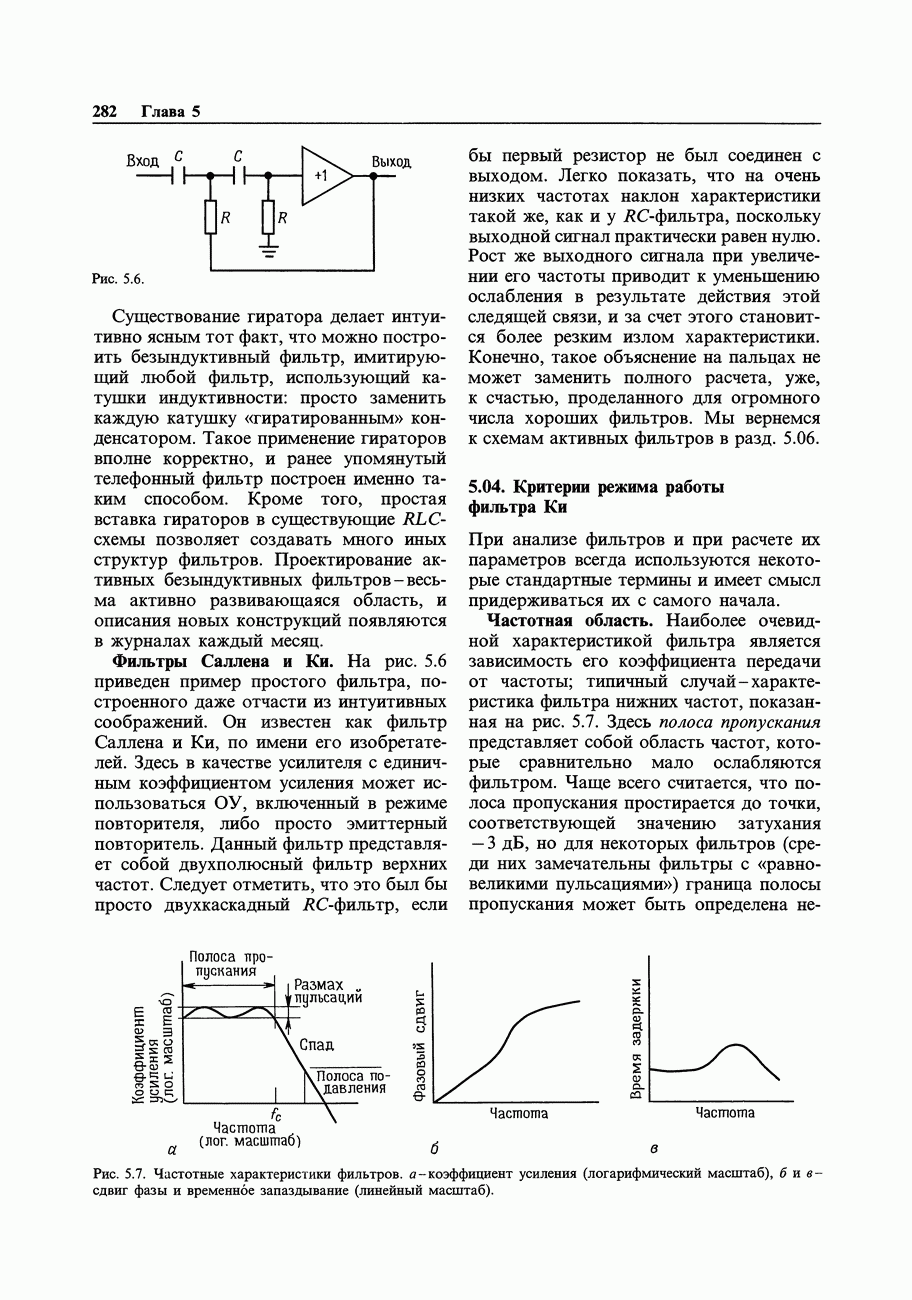
- 5.04. Критерии режима работы фильтра Ки
- 5.05. Типы фильтров
- СХЕМЫ АКТИВНЫХ ФИЛЬТРОВ
- 5.06. Схемы на ИНУН
- 5.07. Проектирование фильтров на ИНУН с использованием наших упрощенных таблиц
- 5.08. Фильтры, построенные на основе метода переменных состояния
- 5.09. Двойной Т-образный фильтр-пробка
- 5.10. Построение фильтров на гираторах
- 5.11. Фильтры на переключаемых конденсаторах
- ГЕНЕРАТОРЫ
- 5.13. Релаксационные генераторы
- 5.14. Классическая ИС таймера-555
- 5.15. Генераторы, управляемые напряжением
- 5.16. Квадратные генераторы
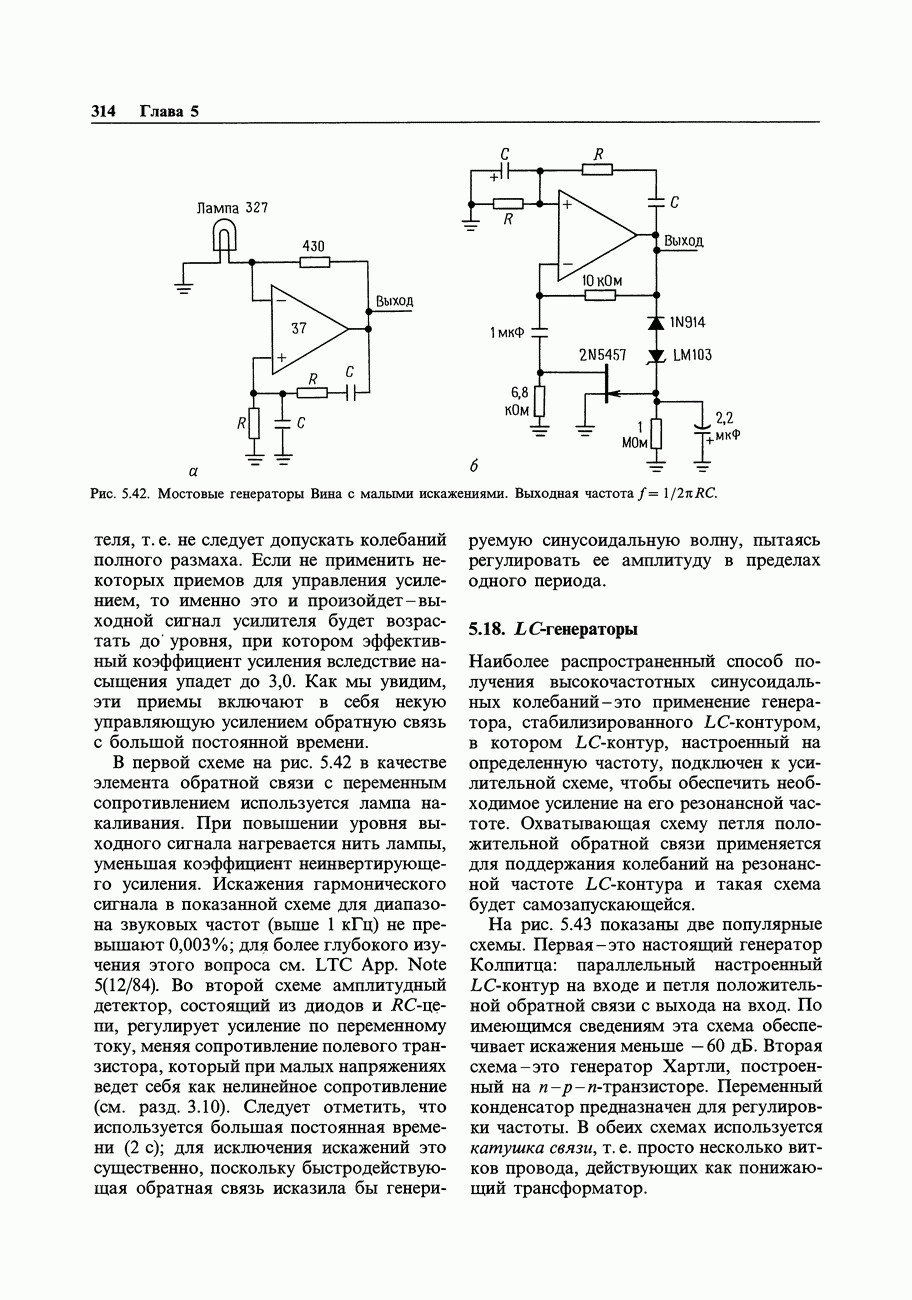
- 5.17. Мостовые генераторы Вина и L С-генераторы
- 5.18. LС-генераторы
- 5.19. Генераторы с кварцевыми резонаторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 6. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ И ИСТОЧНИКИ ПИТАНИЯ
- БАЗОВЫЕ СХЕМЫ СТАБИЛИЗАТОРОВ НА ОСНОВЕ КЛАССИЧЕСКОЙ ИМС 723
- 6.01. ИМС стабилизатора 723
- 6.02. Стабилизатор положительного напряжения
- 6.03. Стабилизаторы с большими выходными токами
- ПРОЕКТИРОВАНИЕ ТЕПЛООТВОДА МОЩНЫХ СХЕМ
- 6.04. Мощные транзисторы и отвод тепла
- 6.05. Ограничители тока с обратным наклоном характеристики
- 6.06. Защита от больших напряжений
- 6.07. Специальные вопросы проектирования сильноточных источников питания
- 6.08. Программируемые источники питания
- 6.09. Пример схемы источника питания
- 6.10. Другие ИМС стабилизатора
- НЕСТАБИЛИЗИРОВАННЫЕ ИСТОЧНИКИ ПИТАНИЯ
- 6.11. Компоненты линии переменного тока
- 6.12. Трансформаторы
- 6.13 Элементы схемы, работающие на постоянном токе
- ИСТОЧНИКИ ОПОРНОГО НАПРЯЖЕНИЯ
- 6.14. Стабилитроны
- 6.15. Источник опорного напряжения на стабилитроне
- ТРЕХВЫВОДНЫЕ И ЧЕТЫРЕХВЫВОДНЫЕ СТАБИЛИЗАТОРЫ
- 6.16. Трехвыводные стабилизаторы
- 6.17. Трехвыводные регулируемые стабилизаторы
- 6.18. Дополнительные замечания относительно трехвыводных стабилизаторов
- 6.19. Импульсные стабилизаторы и преобразователи постоянного тока
- ИСТОЧНИКИ ПИТАНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ
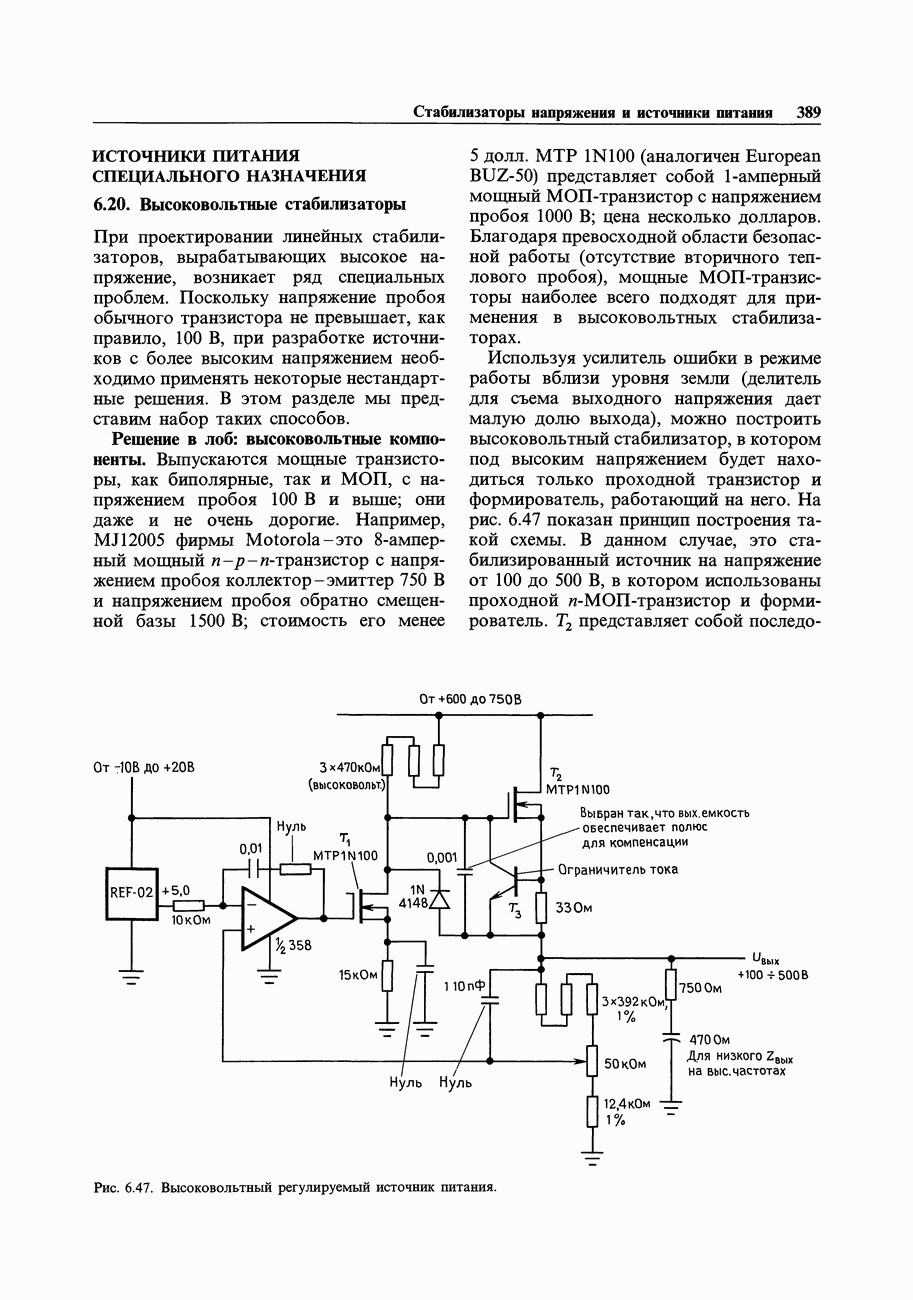
- 6.20. Высоковольтные стабилизаторы
- 6.21. Источники питания с малым уровнем помех и малым дрейфом
- 6.22. Микромощные стабилизаторы
- 6.23. Преобразователи напряжения с переключаемыми конденсаторами (зарядовый насос)
- 6.24. Источники стабилизированного постоянного тока
- 6.25. Коммерческие модули источников питания
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ