| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.18. Частотный анализ реактивных схем
Для начала рассмотрим конденсатор, на который подается синусоидальное напряжение источника питания (рис. 1.47). Ток в схеме определяется следующим образом:

Из этого уравнения следует, что ток имеет амплитуду 7 и опережает входное напряжение по фазе на 90°. Если не принимать во внимание соотношение фаз, то


Рис. 1.47.

Рис. 1.48.
(Напомним, что  ) Конденсатор ведет себя как резистор, сопротивление которого зависит от частоты и определяется выражением
) Конденсатор ведет себя как резистор, сопротивление которого зависит от частоты и определяется выражением  , и, кроме того, ток, протекающий через конденсатор, сдвинут по фазе на
, и, кроме того, ток, протекающий через конденсатор, сдвинут по фазе на  относительно напряжения (рис. 1.48). Например, через конденсатор емкостью
относительно напряжения (рис. 1.48). Например, через конденсатор емкостью  , подключенный к силовой сети с напряжением 110 В (эффективное значение) и частотой 60 Гц, будет протекать ток, эффективная амплитуда которого определяется следующим образом:
, подключенный к силовой сети с напряжением 110 В (эффективное значение) и частотой 60 Гц, будет протекать ток, эффективная амплитуда которого определяется следующим образом:  (эффективное значение).
(эффективное значение).
Замечание: сейчас нам необходимо воспользоваться комплексными переменными; при желании вы можете пропустить математические выкладки, приводимые в последующих разделах, и принять на веру полученные результаты (они выделены в тексте). Не думайте, что подробные алгебраические преобразования, приводимые в этих разделах, необходимы для понимания всего остального материала книги. Это не так - глубокое знание математики похвально, но совсем не обязательно. Следующий раздел, пожалуй, наиболее труден для тех, у кого нет достаточной математической подготовки. Но пусть это вас не огорчает.
Определение напряжения и тока с помощью комплексных чисел.
Только что вы убедились в том, что в цепи переменного тока, работающей с синусоидальным сигналом некоторой частоты, возможен сдвиг по фазе между напряжением и током. Тем не менее если схема содержит только линейные элементы (резисторы, конденсаторы, индуктивности), то амплитуда токов на всех участках схемы пропорциональна амплитуде питающего напряжения.В связи с этим можно попытаться найти некоторые общие выражения тока, напряжения и сопротивления и обобщить тем самым закон  . Очевидно, что для того, чтобы определить ток в какой-либо точке схемы, недостаточно задать одно значение - дело в том, что ток характеризуется как амплитудой, так и сдвигом фазы.
. Очевидно, что для того, чтобы определить ток в какой-либо точке схемы, недостаточно задать одно значение - дело в том, что ток характеризуется как амплитудой, так и сдвигом фазы.
Конечно, можно определять амплитуды и фазовые сдвиги напряжений и токов явно, например  но оказывается, что проще это делать с помощью комплексных чисел. Вместо того чтобы тратить время и силы на сложение и вычитание синусоидальных функций, можно легко и просто складывать и вычитать комплексные числа. Так как действующие значения напряжения и тока представляют собой реальные количественные величины, изменяющиеся во времени, следует вывести правило для перевода реальных количественных величин в комплексное представление и наоборот. Напомним еще раз, что мы имеем дело с частотой синусоидального колебания
но оказывается, что проще это делать с помощью комплексных чисел. Вместо того чтобы тратить время и силы на сложение и вычитание синусоидальных функций, можно легко и просто складывать и вычитать комплексные числа. Так как действующие значения напряжения и тока представляют собой реальные количественные величины, изменяющиеся во времени, следует вывести правило для перевода реальных количественных величин в комплексное представление и наоборот. Напомним еще раз, что мы имеем дело с частотой синусоидального колебания  , и сформулируем следующие правила:
, и сформулируем следующие правила:
1. Напряжение и ток представляются комплексными величинами U и I. Напряжение  представляется комплексным числом
представляется комплексным числом  . Напомним, что
. Напомним, что  где
где 
2. Для того чтобы получить выражение для действующего напряжения и тока, нужно умножить соответствующие комплексные представления на  и выделить действительную часть. Это записывается следующим образом:
и выделить действительную часть. Это записывается следующим образом:  Иначе говоря,
Иначе говоря,

(В электронике символ j используется вместо принятого в алгебре для комплексной переменной символа  , с тем чтобы избежать путаницы с током, который также обозначают символом i). Итак, в общем случае действующие напряжения и токи определяются следующим образом:
, с тем чтобы избежать путаницы с током, который также обозначают символом i). Итак, в общем случае действующие напряжения и токи определяются следующим образом:

Например, комплексному напряжению  соответствует реальное напряжение
соответствует реальное напряжение

Реактивное сопротивление конденсаторов и индуктивностей.
Принятое соглашение позволяет применять закон для схем, содержащих как резисторы, так и конденсаторы, и индуктивности. Определим реактивное сопротивление конденсатора и индуктивности. Нам известно, что
для схем, содержащих как резисторы, так и конденсаторы, и индуктивности. Определим реактивное сопротивление конденсатора и индуктивности. Нам известно, что  . Так как в случае конденсатора справедливо выражение
. Так как в случае конденсатора справедливо выражение  , получим
, получим

т. е. для конденсатора

 - это реактивное сопротивление конденсатора на частоте со. Конденсатор емкостью
- это реактивное сопротивление конденсатора на частоте со. Конденсатор емкостью  , например, имеет реактивное сопротивление
, например, имеет реактивное сопротивление  Ом на частоте 60 Гц и —
Ом на частоте 60 Гц и —  Ом на частоте 1 МГц. Для постоянного тока реактивное сопротивление равно бесконечности.
Ом на частоте 1 МГц. Для постоянного тока реактивное сопротивление равно бесконечности.
Аналогичные рассуждения для индуктивности дают следующий результат:

Схема, содержащая только конденсаторы и индуктивности, всегда обладает мнимым импедансом; это значит, что напряжение и ток всегда сдвинуты по фазе друг относительно друга на  -схема абсолютно реактивна. Если в схеме присутствуют резисторы, то импеданс имеет и действительную часть.
-схема абсолютно реактивна. Если в схеме присутствуют резисторы, то импеданс имеет и действительную часть.
Под реактивным сопротивлением подразумевается при этом только мнимая часть импеданса.
Обобщенный закон Ома.
Соглашения, принятые для представления напряжений и токов, позволяют записать закон Ома в следующей простой форме:
означающей, что напряжение U, приложенное к схеме с импедансом Z, порождает ток I. Импеданс последовательно и параллельно соединенных элементов определяется по тем же правилам, что и сопротивление последовательно и параллельно соединенных резисторов:

(для последовательного соединения),

(для параллельного соединения).
И в заключение приведем формулы для определения импеданса резисторов, конденсаторов и индуктивностей:

Полученные зависимости позволяют анализировать любые схемы переменного тока с помощью методов, принятых для схем постоянного тока, а именно с помощью закона Ома и формул для последовательного и параллельного соединения элементов. Результаты, которые мы получили при анализе таких схем, как, например, делитель напряжения, сохраняют почти такой же вид. Так же как и для схем постоянного тока, для сложных разветвленных схем переменного тока справедливы законы Кирхгофа; отличие состоит в том, что вместо токов I и напряжений U здесь следует использовать их комплексные представления: сумма падений напряжения (комплексного) в замкнутом контуре равна нулю; сумма токов (комплексных), втекающих в узел, равна сумме токов (комплексных), вытекающих из него. Из последнего правила, как и в случае с цепями постоянного тока, вытекает, что ток (комплексный) в последовательной цепи всюду одинаков.
Упражнение 1.16. Используя формулы для импеданса параллельного и последовательного соединения элементов, выведите формулы (разд. 1.12) для емкости двух конденсаторов, соединенных (а) параллельно, (б) последовательно. Подсказка: допустим, что в каждом случае конденсаторы имеют емкость и  . Запишите выражение для импеданса параллельно и последовательно соединенных элементов и приравняйте его импедансу конденсатора с емкостью С. Найдите С.
. Запишите выражение для импеданса параллельно и последовательно соединенных элементов и приравняйте его импедансу конденсатора с емкостью С. Найдите С.
Попробуем воспользоваться рекомендованным методом для анализа простейшей цепи переменного тока, которая состоит из конденсатора, к которому приложено напряжение перменного тока. После этого кратко остановимся на вопросе о мощности в реактивных схемах (это будет последний кирпич в фундаменте наших знаний) и рассмотрим простую, но очень полезную схему  -фильтра.
-фильтра.
Представим себе, что к силовой сети с напряжением 110 В (эффективное значение) и частотой 60 Гц подключен конденсатор емкостью  . Какой ток протекает при этом через конденсатор? Воспользуемся обобщенным законом
. Какой ток протекает при этом через конденсатор? Воспользуемся обобщенным законом  . Следовательно, ток можно определить следующим образом:
. Следовательно, ток можно определить следующим образом:  . Фаза напряжения произвольна, допустим
. Фаза напряжения произвольна, допустим  , где амплитуда
, где амплитуда  , тогда
, тогда  . Искомый ток имеет амплитуду
. Искомый ток имеет амплитуду  (эффективное значение составляет
(эффективное значение составляет  ) и опережает напряжение по фазе на 90°. Результат соответствует полученным ранее выводам. Отметим, что если бы нас интересовала только амплитуда тока, то можно было бы не прибегать к комплексным числам: если
) и опережает напряжение по фазе на 90°. Результат соответствует полученным ранее выводам. Отметим, что если бы нас интересовала только амплитуда тока, то можно было бы не прибегать к комплексным числам: если  , то
, то  , где А, В, С-амплитуды комплексных чисел. То же самое справедливо и для произведения (см. упражнение 1.17). Для нашего случая
, где А, В, С-амплитуды комплексных чисел. То же самое справедливо и для произведения (см. упражнение 1.17). Для нашего случая

Иногда этот прием очень полезен.
Как ни странно, конденсатор в нашем примере мощность не рассеивает.
Его подключение к сети не приводит к увеличению показаний счетчика электроэнергии. Разгадку этой «тайны» вы узнаете, прочитав следующий раздел. А затем мы продолжим анализ схем, содержащих резисторы и конденсаторы, с помощью обобщенного закона Ома.

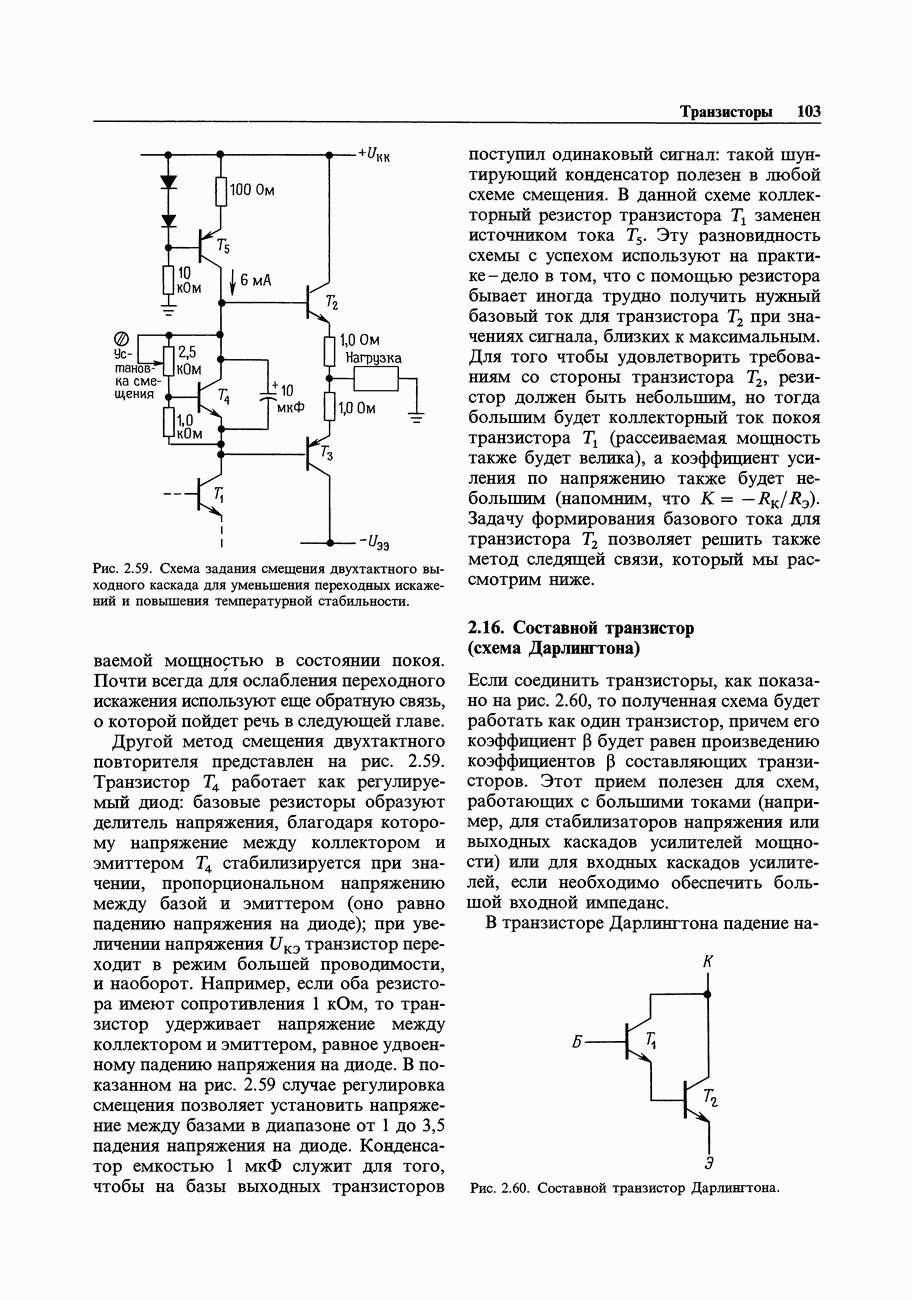
Рис. 1.49. При использовании синусоидального сигнала ток через конденсатор опережает напряжение по фазе на 90°.
Упражнение 1.17. Докажите, что  , то
, то  , где А, В, С-амплитуды комплексных чисел. Подсказка: представьте каждое комплексное число в форме
, где А, В, С-амплитуды комплексных чисел. Подсказка: представьте каждое комплексное число в форме  .
.
Мощность в реактивных схемах.
Мгновенное значение мощности, потребляемой любым элементом схемы, определяется произведением . Однако в реактивных схемах, где напряжение U и ток I связаны между собой не простой пропорциональной зависимостью, просто перемножить их нельзя. Дело в том, что могут возникать странные явления, например, знак произведения может изменяться в течение одного периода сигнала переменного тока. Такой пример показан на рис. 1.49. На интервалах А и С на конденсатор поступает некоторая мощность (правда, скорость ее изменения переменна), и благодаря этому он заряжается: накапливаемая конденсатором энергия увеличивается (мощность - это скорость изменения энергии). На интервалах В и D потребляемая мощность имеет отрицательный знак - конденсатор разряжается. Средняя мощность за период для нашего примера равна нулю; этим свойством обладают все реактивные элементы (индуктивности, конденсаторы и всевозможные их комбинации). Если вы знакомы с интегралами от тригонометрических функций, то следующее упражнение поможет вам доказать это свойство.
. Однако в реактивных схемах, где напряжение U и ток I связаны между собой не простой пропорциональной зависимостью, просто перемножить их нельзя. Дело в том, что могут возникать странные явления, например, знак произведения может изменяться в течение одного периода сигнала переменного тока. Такой пример показан на рис. 1.49. На интервалах А и С на конденсатор поступает некоторая мощность (правда, скорость ее изменения переменна), и благодаря этому он заряжается: накапливаемая конденсатором энергия увеличивается (мощность - это скорость изменения энергии). На интервалах В и D потребляемая мощность имеет отрицательный знак - конденсатор разряжается. Средняя мощность за период для нашего примера равна нулю; этим свойством обладают все реактивные элементы (индуктивности, конденсаторы и всевозможные их комбинации). Если вы знакомы с интегралами от тригонометрических функций, то следующее упражнение поможет вам доказать это свойство.
Упражнение 1.18. (дополнительное). Докажите, что схема в среднем за полный период не потребляет мощности, если протекающий через нее ток сдвинут по фазе относительно питающего напряжения на  .
.
Как определить среднюю потребляемую мощность для произвольной схемы? В общем случае можно просуммировать произведения UI и разделить сумму на длительность истекшего интервала времени. Иными словами.

где  - полный период времени. Практически так мощность почти никогда не определяют. Нетрудно доказать, что средняя мощность определяется следующим выражением:
- полный период времени. Практически так мощность почти никогда не определяют. Нетрудно доказать, что средняя мощность определяется следующим выражением:

где U и I - эффективные комплексные значения напряжения и тока.
Рассмотрим пример. Допустим, что в предыдущей схеме конденсатор питается синусоидальным напряжением, эффективное значение которого равно 1 В. Для простоты будем выполнять все преобразования с эффективными значениями. Итак:  . Мы получили, что средняя мощность, как и утверждалось, равна нулю.
. Мы получили, что средняя мощность, как и утверждалось, равна нулю.
А теперь рассмотрим схему, показанную на рис. 1.50. Выполним ряд преобразований:


Рис. 1.50.
В третьей строке преобразований при определении тока I мы умножили числитель и знаменатель на комплексное число, сопряженное знаменателю, для того чтобы получить в знаменателе действительное число. Полученная величина меньше, чем произведение амплитуд U и I; ее отношение к этому произведению называют коэффициентом мощности:

Коэффициент мощности - это косинус угла, определяющего сдвиг фаз напряжения и тока, он лежит в диапазоне от 0 (для реактивной схемы) до 1 (для резистивной схемы). Если коэффициент мощности меньше 1, то это значит, что в схеме присутствует реактивный элемент.
Упражнение 1.19. Докажите, что вся средняя мощность предыдущей схемы рассеивается на резисторе. Для того, чтобы решить эту задачу, нужно определить величину отношения  . Определите, чему будет равна эта мощность в ваттах, если цепь, состоящая из последовательно соединенных конденсатора емкостью
. Определите, чему будет равна эта мощность в ваттах, если цепь, состоящая из последовательно соединенных конденсатора емкостью  и резистора сопротивлением 1 кОм, подключена к силовой сети с эффективным напряжением 110 В (частота 60 Гц).
и резистора сопротивлением 1 кОм, подключена к силовой сети с эффективным напряжением 110 В (частота 60 Гц).
Коэффициент мощности играет немаловажную роль в распределении больших мощностей, так как реактивные токи не передают нагрузке никакой полезной мощности, зато вызывают нагрев в сопротивлениях проводов генераторов и трансформаторов (температура нагрева пропорциональна  ). Бытовые потребители электроэнергии платят только за «действительную» потребляемую мощность
). Бытовые потребители электроэнергии платят только за «действительную» потребляемую мощность  , а промышленные потребители с учетом коэффициента мощности. Вот почему большие предприятия для погашения влияния индуктивных реактивных сопротивлений производственного оборудования (моторов) сооружают специальные конденсаторные блоки.
, а промышленные потребители с учетом коэффициента мощности. Вот почему большие предприятия для погашения влияния индуктивных реактивных сопротивлений производственного оборудования (моторов) сооружают специальные конденсаторные блоки.
Упражнение 1.20. Покажите, что последовательное подключение конденсатора емкостью  к последовательной RL-цепи делает коэффициент мощности этой цепи равным единице. Затем рассмотрите параллельную цепь и параллельно подключенный конденсатор.
к последовательной RL-цепи делает коэффициент мощности этой цепи равным единице. Затем рассмотрите параллельную цепь и параллельно подключенный конденсатор.

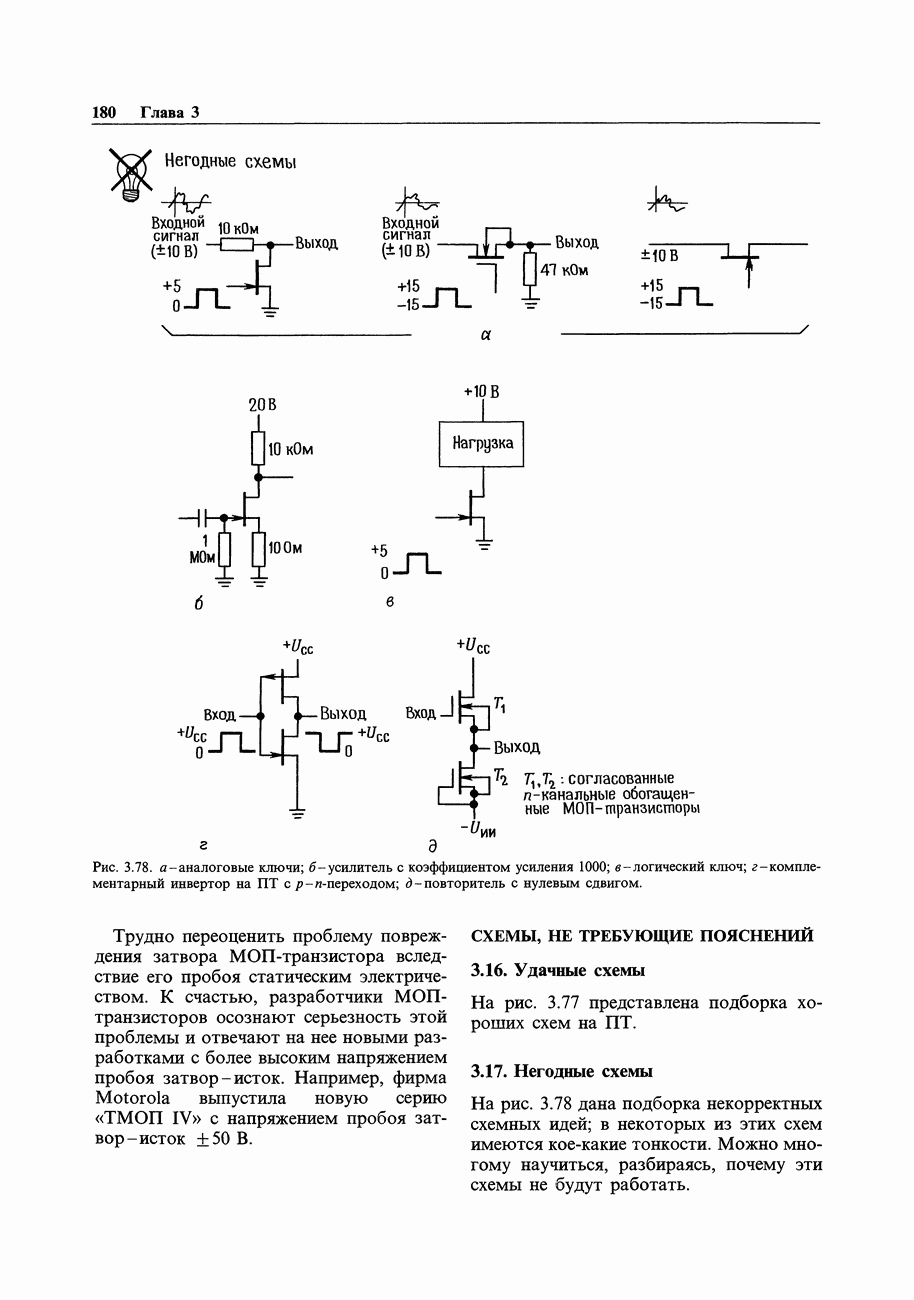
Рис. 1.51. Обобщенная схема делителя напряжения: пара электрических цепей с произвольным импедансом.
Делители напряжения: обобщение.
Простейший делитель напряжения (рис. 1.5) состоит из пары последовательно соединенных резисторов. Входное напряжение измеряется в верхней точке относительно земли, а выходное в точке соединения резисторов относительно земли. От простейшего резистивного делителя перейдем к более общей схеме делителя, если один или оба резистора заменим на конденсатор или индуктивность, как на рис. 1.51 (в более сложной схеме присутствуют и R, и L, и С). Вообще говоря, в таком делителе отношение не является постоянной величиной, а зависит от частоты. Анализ схемы выполняется без всяких хитроумных приемов:
не является постоянной величиной, а зависит от частоты. Анализ схемы выполняется без всяких хитроумных приемов:

Не будем сосредоточивать внимание на полученном результате, рассмотрим лучше некоторые простые, но очень важные примеры.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. ОСНОВЫ ЭЛЕКТРОНИКИ
- НАПРЯЖЕНИЕ, ТОК И СОПРОТИВЛЕНИЕ
- 1.01. Напряжение и ток
- 1.02. Взаимосвязь напряжения и тока: резисторы
- ПРИСТАВКИ ДЛЯ ОБРАЗОВАНИЯ КРАТНЫХ И ДОЛЬНЫХ ЕДИНИЦ ИЗМЕРЕНИЯ
- РЕЗИСТОРЫ
- ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ ФИРМЫ ALLEN BRADLEY, (СЕРИЯ АВ, ТИП СВ)
- 1.03. Делители напряжения
- 1.04. Источники тока и напряжения
- 1.05. Теорема об эквивалентном преобразовании источников (генераторов)
- УНИВЕРСАЛЬНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1.06. Динамическое сопротивление
- СИГНАЛЫ
- 1.07. Синусоидальные сигналы
- 1.08. Измерение амплитуды сигналов
- 1.09. Другие типы сигналов
- 1.10. Логические уровни
- 1.11. Источники сигналов
- КОНДЕНСАТОРЫ И ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 1.12. Конденсаторы
- КОНДЕНСАТОРЫ
- 1.13. RС-цепи: изменения во времени напряжения и тока
- 1.14. Дифференцирующие цепи
- 1.15. Интегрирующие цепи
- ИНДУКТИВНОСТИ и ТРАНСФОРМАТОРЫ
- 1.16. Индуктивности
- 1.17. Трансформаторы
- ПОЛНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ
- 1.18. Частотный анализ реактивных схем
- 1.19. RC-фильтры
- 1.20. Векторные диаграммы
- 1.21. «Полюсы» и наклон в пределах октавы
- 1.22. Резонансные схемы и активные фильтры
- 1.23. Другие примеры использования конденсаторов
- 1.24. Обобщенная теорема Тевенина об эквивалентном преобразовании (эквивалентном генераторе)
- ДИОДЫ И ДИОДНЫЕ СХЕМЫ
- 1.25. Диоды
- 1.26. Выпрямление
- 1.27. Фильтрация в источниках питания
- 1.28. Схемы выпрямителей для источников питания
- 1.29. Стабилизаторы напряжения
- 1.30. Примеры использования диодов
- 1.31. Индуктивные нагрузки и диодная защита
- ДРУГИЕ ПАССИВНЫЕ КОМПОНЕНТЫ
- 1.32. Электромеханические элементы
- 1.33. Индикаторы
- 1.34. Переменные компоненты
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 2. ТРАНЗИСТОРЫ
- 2.01. Первая модель транзистора: усилитель тока
- НЕКОТОРЫЕ ОСНОВНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.02. Транзисторный переключатель
- 2.03. Эмиттерный повторитель
- 2.04. Использование эмиттерных повторителей в качестве стабилизаторов напряжения
- 2.05. Смещение в эмиттерном повторителе
- 2.06. Транзисторный источник тока
- 2.07. Усилитель с общим эмиттером
- 2.08. Схема расщепления фазы с единичным коэффициентом усиления
- 2.09. Крутизна
- МОДЕЛЬ ЭБЕРСА-МОЛЛА ДЛЯ ОСНОВНЫХ ТРАНЗИСТОРНЫХ СХЕМ
- 2.10. Улучшенная модель транзистора: усилитель с передаточной проводимостью (крутизной)
- 2.11. Еще раз об эмиттерном повторителе
- 2.13. Еще раз об усилителе с общим эмиттером
- 2.13. Смещение в усилителе с общим эмиттером
- 2.14. Токовые зеркала
- НЕКОТОРЫЕ ТИПЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ
- 2.15. Двухтактные выходные каскады
- 2.16. Составной транзистор (схема Дарлингтона)
- 2.17. Следящая связь
- 2.18. Дифференциальные усилители
- 2.19. Емкость и эффект Миллера
- 2.20. Полевые транзисторы
- НЕКОТОРЫЕ ТИПИЧНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.21. Стабилизированный источник напряжения
- 2.22. Терморегулятор
- 2.23. Простая логическая схема на транзисторах и диодах
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 2.24. Удачные схемы
- 2.25. Негодные схемы
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 3. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- 3.01. Характеристики полевых транзисторов
- 3.02. Типы ПТ
- 3.03. Общая классификация ПТ
- 3.04. Выходные характеристики ПТ
- 3.05. Производственный разброс характеристик ПТ
- ОСНОВНЫЕ СХЕМЫ НА ПТ
- 3.06. Источники тока на ПТ с р-n-переходом
- 3.07. Усилители на ПТ
- 3.08. Истоковые повторители
- 3.09. Ток затвора ПТ
- 3.10. ПТ в качестве переменных резисторов
- КЛЮЧИ НА ПТ
- 3.11. Аналоговые ключи на ПТ
- 3.12. Недостатки ПТ-ключей
- 3.13. Несколько схем на ПТ-ключах
- 3.14. Логические и мощные ключи на МОП-транзисторах
- 3.15. Необходимые предосторожности в обращении с МОП-транзисторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 4. ОБРАТНАЯ СВЯЗЬ И ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 4.01. Предварительные сведения об обратной связи
- 4.02. Операционные усилители
- 4.03. Важнейшие правила
- ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.04. Инвертирующий усилитель
- 4.05. Неинвертирующий усилитель
- 4.06. Повторитель
- 4.07. Источники тока
- 4.08. Основные предостережения по работе с ОУ
- КАЛЕЙДОСКОП СХЕМ НА ОПЕРАЦИОННЫХ УСИЛИТЕЛЯХ
- 4.09. Линейные схемы
- 4.10. Нелинейные схемы
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.11. Отличие характеристик идеального ОУ от реального
- 4.12. Эффекты ограничений ОУ на работу схем на их основе
- 4.13. Микромощные и программируемые ОУ
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ НЕКОТОРЫХ СХЕМ НА ОУ
- 4.14. Логарифмический усилитель
- 4.15. Активный пиковый детектор
- 4.16. Выборка-запоминание
- ДИЭЛЕКТРИЧЕСКОЕ ПОГЛОЩЕНИЕ
- 4.17. Активный ограничитель
- 4.18. Схема выделения модуля абсолютного значения сигнала
- 4.19. Интеграторы
- 4.20. Дифференциаторы
- РАБОТА ОУ С ОДНИМ ИСТОЧНИКОМ ПИТАНИЯ
- 4.21. Смещение усилителей переменного тока, использующих один источник питания.
- 4.22. Операционные усилители с одним источником питания.
- КОМПАРАТОРЫ И ТРИГГЕР ШМИТТА
- 4.23. Компараторы
- 4.24. Триггер Шмитта
- ОБРАТНАЯ СВЯЗЬ И УСИЛИТЕЛИ С КОНЕЧНЫМ УСИЛЕНИЕМ
- 4.25. Уравнение для коэффициента усиления
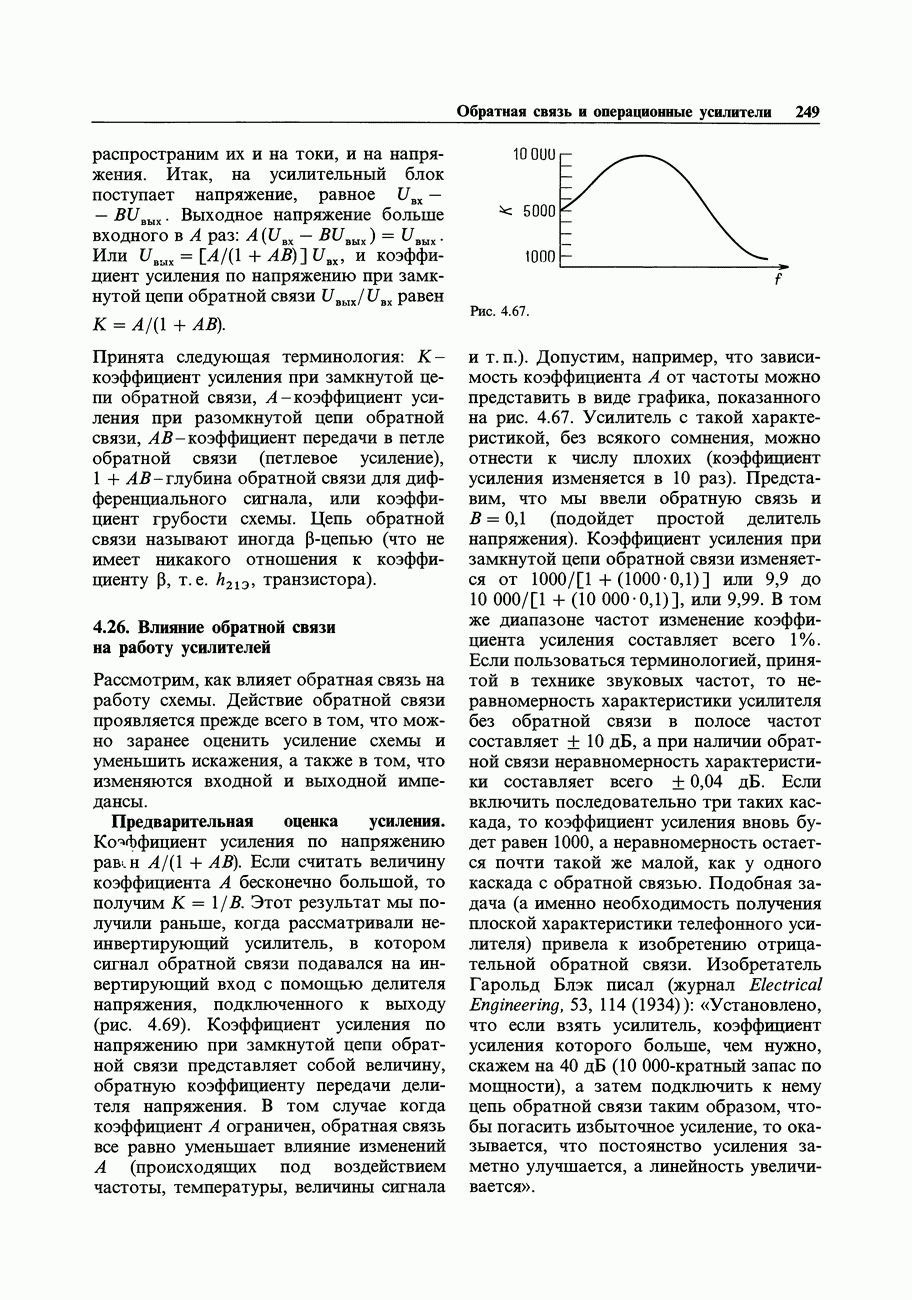
- 4.26. Влияние обратной связи на работу усилителей
- 4.27. Два примера транзисторных усилителей с обратной связью
- НЕКОТОРЫЕ ТИПИЧНЫЕ СХЕМЫ С ОПЕРАЦИОННЫМИ УСИЛИТЕЛЯМИ
- 4.28. Лабораторный усилитель общего назначения
- 4.29. Генератор, управляемый напряжением
- 4.30. Линейный переключатель на полевом транзисторе с p-n-переходом, с компенсацией.
- 4.31. Детектор нуля для ТТЛ-схем
- 4.32. Схема измерения тока в нагрузке
- ЧАСТОТНАЯ КОРРЕКЦИЯ УСИЛИТЕЛЕЙ С ОБРАТНОЙ СВЯЗЬЮ
- 4.33. Зависимость коэффициента усиления и фазового сдвига от частоты
- 4.34. Методы коррекции усилителей
- 4.35. Частотная характеристика цепи обратной связи
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 4.36. Некоторые полезные идеи
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 5. АКТИВНЫЕ ФИЛЬТРЫ И ГЕНЕРАТОРЫ
- АКТИВНЫЕ ФИЛЬТРЫ
- 5.01. Частотная характеристика RC-фильтров
- 5.02. Идеальный рабочий режим LC-фильтров
- 5.03. Введение в активные фильтры: обзор
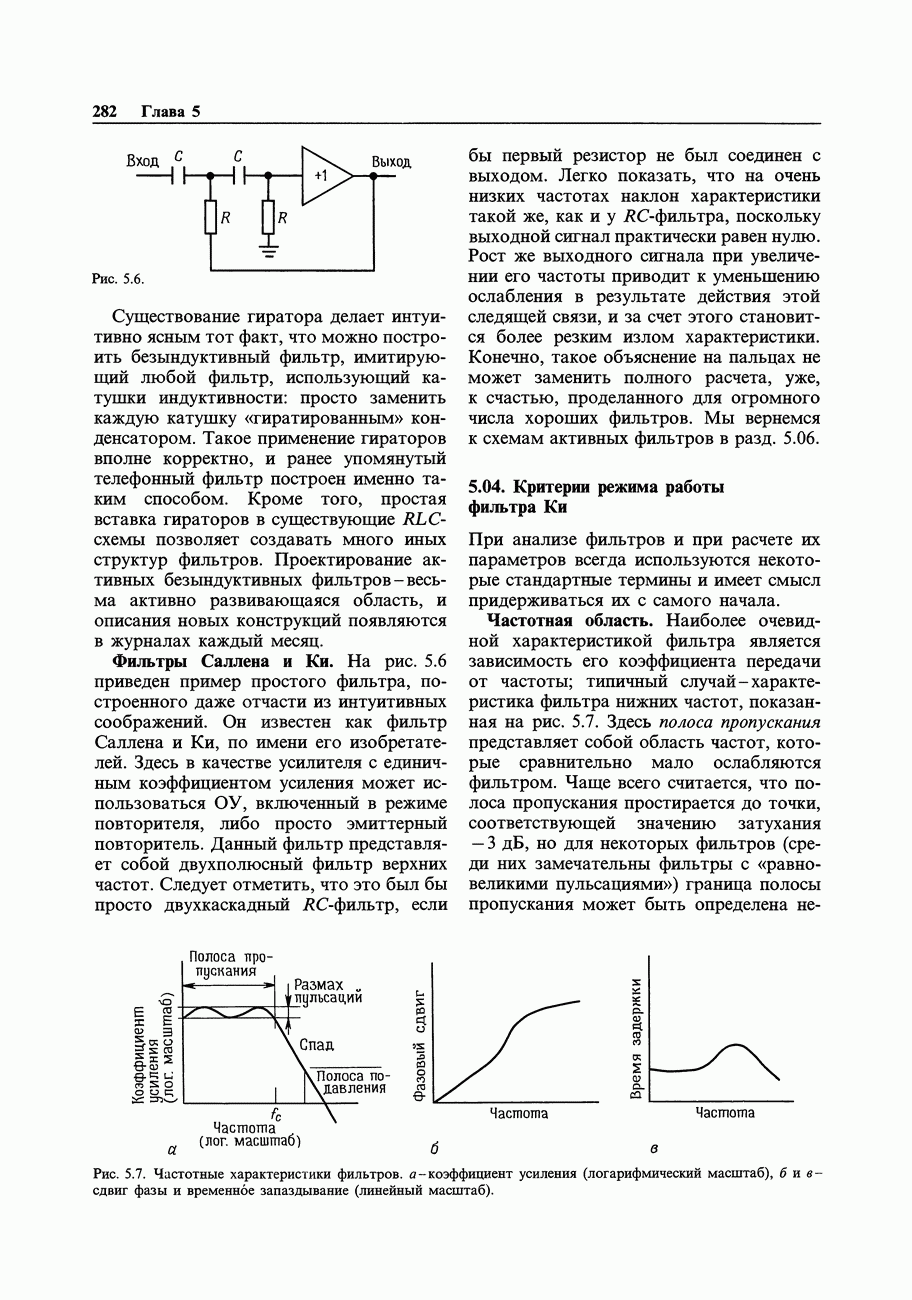
- 5.04. Критерии режима работы фильтра Ки
- 5.05. Типы фильтров
- СХЕМЫ АКТИВНЫХ ФИЛЬТРОВ
- 5.06. Схемы на ИНУН
- 5.07. Проектирование фильтров на ИНУН с использованием наших упрощенных таблиц
- 5.08. Фильтры, построенные на основе метода переменных состояния
- 5.09. Двойной Т-образный фильтр-пробка
- 5.10. Построение фильтров на гираторах
- 5.11. Фильтры на переключаемых конденсаторах
- ГЕНЕРАТОРЫ
- 5.13. Релаксационные генераторы
- 5.14. Классическая ИС таймера-555
- 5.15. Генераторы, управляемые напряжением
- 5.16. Квадратные генераторы
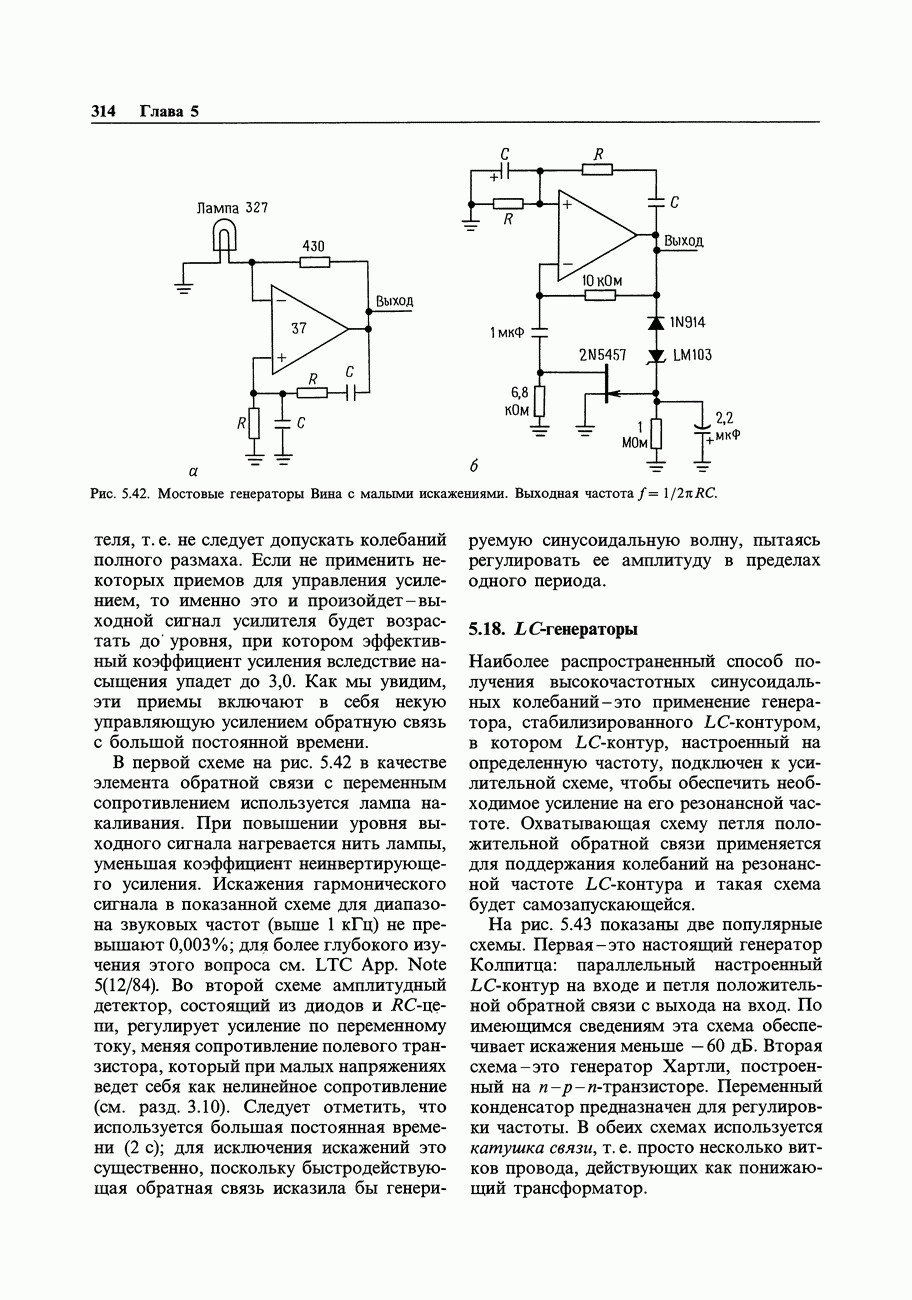
- 5.17. Мостовые генераторы Вина и L С-генераторы
- 5.18. LС-генераторы
- 5.19. Генераторы с кварцевыми резонаторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 6. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ И ИСТОЧНИКИ ПИТАНИЯ
- БАЗОВЫЕ СХЕМЫ СТАБИЛИЗАТОРОВ НА ОСНОВЕ КЛАССИЧЕСКОЙ ИМС 723
- 6.01. ИМС стабилизатора 723
- 6.02. Стабилизатор положительного напряжения
- 6.03. Стабилизаторы с большими выходными токами
- ПРОЕКТИРОВАНИЕ ТЕПЛООТВОДА МОЩНЫХ СХЕМ
- 6.04. Мощные транзисторы и отвод тепла
- 6.05. Ограничители тока с обратным наклоном характеристики
- 6.06. Защита от больших напряжений
- 6.07. Специальные вопросы проектирования сильноточных источников питания
- 6.08. Программируемые источники питания
- 6.09. Пример схемы источника питания
- 6.10. Другие ИМС стабилизатора
- НЕСТАБИЛИЗИРОВАННЫЕ ИСТОЧНИКИ ПИТАНИЯ
- 6.11. Компоненты линии переменного тока
- 6.12. Трансформаторы
- 6.13 Элементы схемы, работающие на постоянном токе
- ИСТОЧНИКИ ОПОРНОГО НАПРЯЖЕНИЯ
- 6.14. Стабилитроны
- 6.15. Источник опорного напряжения на стабилитроне
- ТРЕХВЫВОДНЫЕ И ЧЕТЫРЕХВЫВОДНЫЕ СТАБИЛИЗАТОРЫ
- 6.16. Трехвыводные стабилизаторы
- 6.17. Трехвыводные регулируемые стабилизаторы
- 6.18. Дополнительные замечания относительно трехвыводных стабилизаторов
- 6.19. Импульсные стабилизаторы и преобразователи постоянного тока
- ИСТОЧНИКИ ПИТАНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ
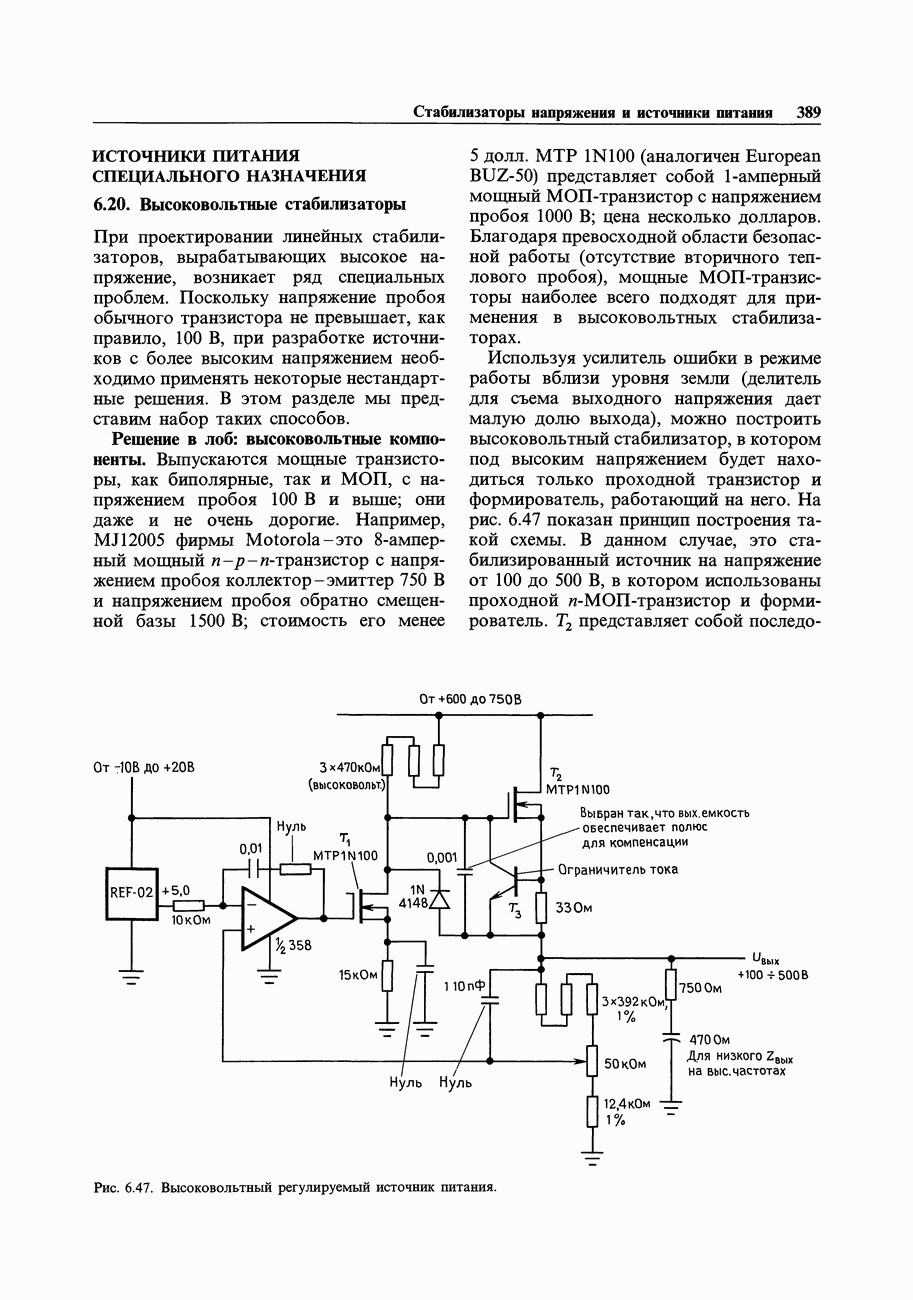
- 6.20. Высоковольтные стабилизаторы
- 6.21. Источники питания с малым уровнем помех и малым дрейфом
- 6.22. Микромощные стабилизаторы
- 6.23. Преобразователи напряжения с переключаемыми конденсаторами (зарядовый насос)
- 6.24. Источники стабилизированного постоянного тока
- 6.25. Коммерческие модули источников питания
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ