| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
МОДЕЛЬ ЭБЕРСА-МОЛЛА ДЛЯ ОСНОВНЫХ ТРАНЗИСТОРНЫХ СХЕМ
2.10. Улучшенная модель транзистора: усилитель с передаточной проводимостью (крутизной)
Существенную поправку следует внести в правило 4 (разд. 2.01), которое определяет, что  . Мы рассматривали транзистор как усилитель тока, вход которого работает как диод. Это приближение является грубым, но для некоторых практических случаев большей точности и не требуется. Однако для того чтобы понять, как работают дифференциальные усилители, логарифмические преобразователи, схемы температурной компенсации и некоторые другие практически полезные схемы, следует рассматривать транзистор как элемент с передаточной проводимостью - коллекторный ток в нем определяется напряжением между базой и эмиттером.
. Мы рассматривали транзистор как усилитель тока, вход которого работает как диод. Это приближение является грубым, но для некоторых практических случаев большей точности и не требуется. Однако для того чтобы понять, как работают дифференциальные усилители, логарифмические преобразователи, схемы температурной компенсации и некоторые другие практически полезные схемы, следует рассматривать транзистор как элемент с передаточной проводимостью - коллекторный ток в нем определяется напряжением между базой и эмиттером.
Итак, правило 4 в измененном виде:
4. Если правила 1-3 соблюдены (разд. 2.01), то ток  связан с напряжением
связан с напряжением  следующей зависимостью:
следующей зависимостью:

где  при комнатной температуре
при комнатной температуре  заряд электрона (
заряд электрона ( Кл),
Кл),  - постоянная Больцмана
- постоянная Больцмана  ), Т - абсолютная температура в кельвинах
), Т - абсолютная температура в кельвинах  - ток насыщения транзистора (зависит от Т). Тогда ток базы, который также зависит от
- ток насыщения транзистора (зависит от Т). Тогда ток базы, который также зависит от  , можно приблизительно определить так:
, можно приблизительно определить так:

где «постоянная»  обычно принимает значения от 20 до 1000 и зависит от транзистора,
обычно принимает значения от 20 до 1000 и зависит от транзистора,  и температуры. Ток
и температуры. Ток  представляет собой обратный ток эмиттерного перехода. В активной области
представляет собой обратный ток эмиттерного перехода. В активной области  и членом — 1 можно пренебречь.
и членом — 1 можно пренебречь.

Рис. 2.32. Зависимость базового и коллекторного токов транзистора от напряжения между базой и эмиттером.
Уравнение для  известно под названием «уравнение Эберса-Молла». Оно приблизительно описывает также зависимость тока от напряжения для диода, если
известно под названием «уравнение Эберса-Молла». Оно приблизительно описывает также зависимость тока от напряжения для диода, если  умножается на корректировочный коэффициент m со значением между 1 и 2. Следует запомнить, что в транзисторе коллекторный ток зависит от напряжения между базой и эмиттером, а не от тока базы (ток базы в грубом приближении определяется коэффициентом
умножается на корректировочный коэффициент m со значением между 1 и 2. Следует запомнить, что в транзисторе коллекторный ток зависит от напряжения между базой и эмиттером, а не от тока базы (ток базы в грубом приближении определяется коэффициентом  ). Экспоненциальная зависимость между током
). Экспоненциальная зависимость между током  и напряжением
и напряжением  точно соблюдается в большом диапазоне токов, обычно от наноампер до миллиампер. На рис. 2.32 приведен график этой зависимости. Если измерить ток базы при различных значениях коллекторного тока, то получим график зависимости
точно соблюдается в большом диапазоне токов, обычно от наноампер до миллиампер. На рис. 2.32 приведен график этой зависимости. Если измерить ток базы при различных значениях коллекторного тока, то получим график зависимости  от
от  (рис. 2.33).
(рис. 2.33).

Рис. 2.33. Типичная зависимость коэффициента усиления по току для транзистора  от коллекторною тока.
от коллекторною тока.
Согласно уравнению Эберса-Молла, напряжение между базой и эмиттером «управляет» коллекторным током, однако это свойство нельзя использовать непосредственно на практике (создавать смещение в транзисторе с помощью напряжения, подаваемого на базу), так как велик температурный коэффициент напряжения между базой и эмиттером. В дальнейшем вы увидите, как уравнение Эберса-Молла помогает решить эту проблему.
Практические правила для разработки транзисторных схем.
На основании уравнения Эберса-Молла получены некоторые зависимости, которые часто используют при разработке схем:1. Ступенчатая характеристика диода. На сколько нужно увеличить напряжение  , чтобы ток
, чтобы ток  увеличился в 10 раз? Из уравнения Эберса-Молла следует, что
увеличился в 10 раз? Из уравнения Эберса-Молла следует, что  нужно увеличить на
нужно увеличить на  , или на
, или на  при комнатной температуре. Напряжение на базе увеличивается на
при комнатной температуре. Напряжение на базе увеличивается на  при увеличении коллекторного тока в 10 раз. Эквивалентным является следующее выражение
при увеличении коллекторного тока в 10 раз. Эквивалентным является следующее выражение  , где A U измеряется в милливольтах.
, где A U измеряется в милливольтах.
2. Импеданс для малого сигнала со стороны эмиттера при фиксированном напряжении на базе. Возьмем производную от  по
по  , где ток
, где ток  измеряется в миллиамперах. Величина
измеряется в миллиамперах. Величина  соответствует комнатной температуре. Это собственное сопротивление эмиттера
соответствует комнатной температуре. Это собственное сопротивление эмиттера  выступает в качестве последовательного для эмиттерной цепи во всех транзисторных схемах. Оно ограничивает усиление усилителя с заземленным эмиттером, приводит к тому, что коэффициент усиления эмиттерного повторителя имеет значение чуть меньше единицы и не позволяет выходному сопротивлению эмиттерного повторителя стать равным нулю. Этот параметр относится к параметрам малого сигнала. Отметим, что крутизна для усилителя с заземленным эмиттером определяется следующим образом:
выступает в качестве последовательного для эмиттерной цепи во всех транзисторных схемах. Оно ограничивает усиление усилителя с заземленным эмиттером, приводит к тому, что коэффициент усиления эмиттерного повторителя имеет значение чуть меньше единицы и не позволяет выходному сопротивлению эмиттерного повторителя стать равным нулю. Этот параметр относится к параметрам малого сигнала. Отметим, что крутизна для усилителя с заземленным эмиттером определяется следующим образом:  .
.
3. Температурная зависимость. Глядя на уравнение Эберса-Молла, можно предположить, что  имеет положительный температурный коэффициент.
имеет положительный температурный коэффициент.
Однако, в связи с тем что ток  зависит от температуры, напряжение
зависит от температуры, напряжение  уменьшается на
уменьшается на  . В грубом приближении оно пропорционально
. В грубом приближении оно пропорционально  , где
, где  - абсолютная температура.
- абсолютная температура.
И еще одна зависимость пригодится нам на практике, правда, она не связана с уравнением Эберса-Молла. Речь идет об эффекте Эрли, описанном в разд. 2.06, который накладывает ограничения на выходную характеристику транзистора как источника тока.
4. Эффект Эрли.  хоть и в слабой мере, но зависит от
хоть и в слабой мере, но зависит от  при постоянном токе
при постоянном токе  . Этот эффект обусловлен изменением эффективной ширины базы и описывается следующей приблизительной зависимостью:
. Этот эффект обусловлен изменением эффективной ширины базы и описывается следующей приблизительной зависимостью:  , где
, где  . Мы перечислили основные соотношения, которые могут быть полезны на практике. Эти соотношения, а не сами уравнения Эберса-Молла, используются при разработке транзисторных схем.
. Мы перечислили основные соотношения, которые могут быть полезны на практике. Эти соотношения, а не сами уравнения Эберса-Молла, используются при разработке транзисторных схем.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. ОСНОВЫ ЭЛЕКТРОНИКИ
- НАПРЯЖЕНИЕ, ТОК И СОПРОТИВЛЕНИЕ
- 1.01. Напряжение и ток
- 1.02. Взаимосвязь напряжения и тока: резисторы
- ПРИСТАВКИ ДЛЯ ОБРАЗОВАНИЯ КРАТНЫХ И ДОЛЬНЫХ ЕДИНИЦ ИЗМЕРЕНИЯ
- РЕЗИСТОРЫ
- ХАРАКТЕРИСТИКИ РЕЗИСТОРОВ ФИРМЫ ALLEN BRADLEY, (СЕРИЯ АВ, ТИП СВ)
- 1.03. Делители напряжения
- 1.04. Источники тока и напряжения
- 1.05. Теорема об эквивалентном преобразовании источников (генераторов)
- УНИВЕРСАЛЬНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- 1.06. Динамическое сопротивление
- СИГНАЛЫ
- 1.07. Синусоидальные сигналы
- 1.08. Измерение амплитуды сигналов
- 1.09. Другие типы сигналов
- 1.10. Логические уровни
- 1.11. Источники сигналов
- КОНДЕНСАТОРЫ И ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 1.12. Конденсаторы
- КОНДЕНСАТОРЫ
- 1.13. RС-цепи: изменения во времени напряжения и тока
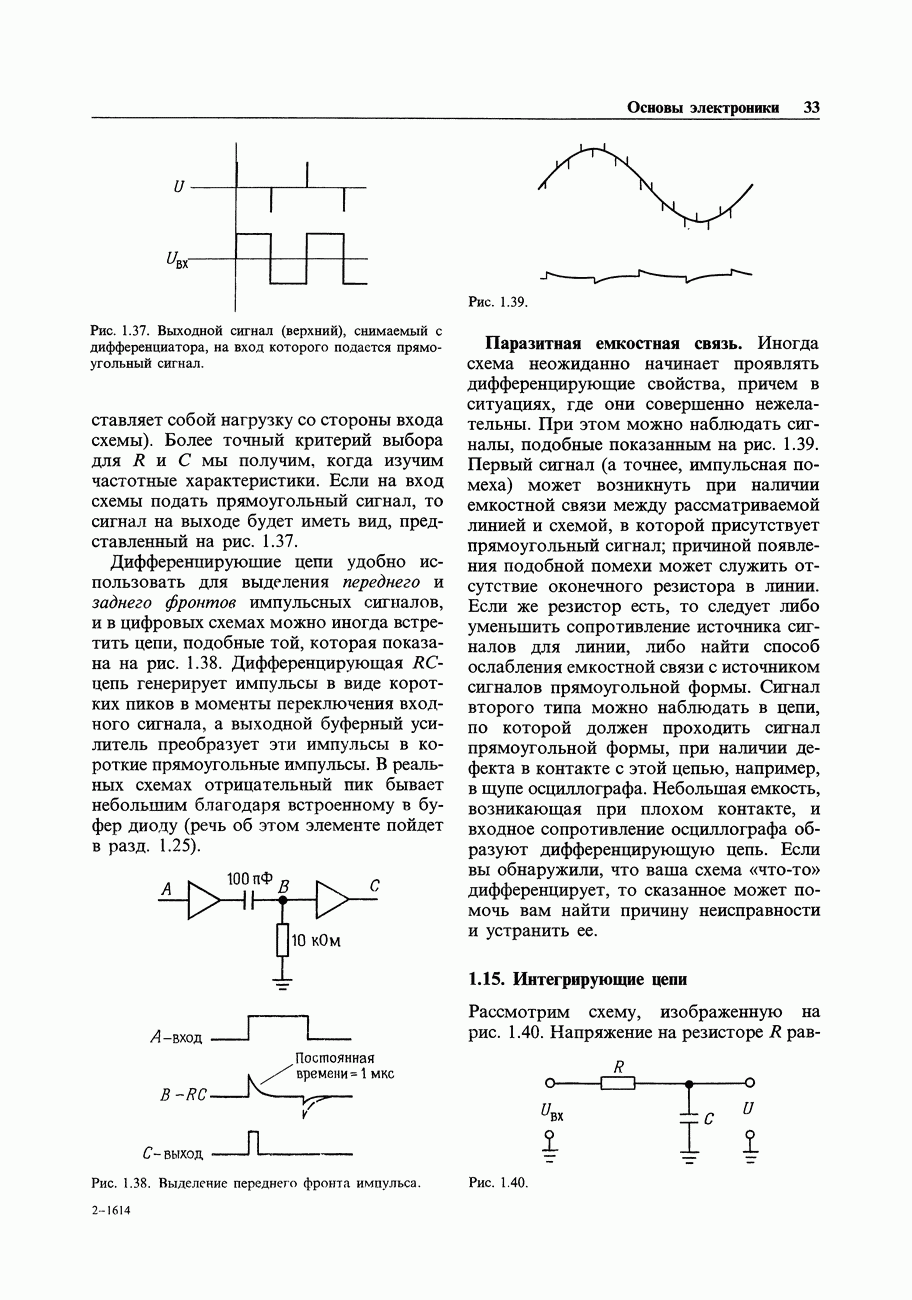
- 1.14. Дифференцирующие цепи
- 1.15. Интегрирующие цепи
- ИНДУКТИВНОСТИ и ТРАНСФОРМАТОРЫ
- 1.16. Индуктивности
- 1.17. Трансформаторы
- ПОЛНОЕ И РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ
- 1.18. Частотный анализ реактивных схем
- 1.19. RC-фильтры
- 1.20. Векторные диаграммы
- 1.21. «Полюсы» и наклон в пределах октавы
- 1.22. Резонансные схемы и активные фильтры
- 1.23. Другие примеры использования конденсаторов
- 1.24. Обобщенная теорема Тевенина об эквивалентном преобразовании (эквивалентном генераторе)
- ДИОДЫ И ДИОДНЫЕ СХЕМЫ
- 1.25. Диоды
- 1.26. Выпрямление
- 1.27. Фильтрация в источниках питания
- 1.28. Схемы выпрямителей для источников питания
- 1.29. Стабилизаторы напряжения
- 1.30. Примеры использования диодов
- 1.31. Индуктивные нагрузки и диодная защита
- ДРУГИЕ ПАССИВНЫЕ КОМПОНЕНТЫ
- 1.32. Электромеханические элементы
- 1.33. Индикаторы
- 1.34. Переменные компоненты
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 2. ТРАНЗИСТОРЫ
- 2.01. Первая модель транзистора: усилитель тока
- НЕКОТОРЫЕ ОСНОВНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.02. Транзисторный переключатель
- 2.03. Эмиттерный повторитель
- 2.04. Использование эмиттерных повторителей в качестве стабилизаторов напряжения
- 2.05. Смещение в эмиттерном повторителе
- 2.06. Транзисторный источник тока
- 2.07. Усилитель с общим эмиттером
- 2.08. Схема расщепления фазы с единичным коэффициентом усиления
- 2.09. Крутизна
- МОДЕЛЬ ЭБЕРСА-МОЛЛА ДЛЯ ОСНОВНЫХ ТРАНЗИСТОРНЫХ СХЕМ
- 2.10. Улучшенная модель транзистора: усилитель с передаточной проводимостью (крутизной)
- 2.11. Еще раз об эмиттерном повторителе
- 2.13. Еще раз об усилителе с общим эмиттером
- 2.13. Смещение в усилителе с общим эмиттером
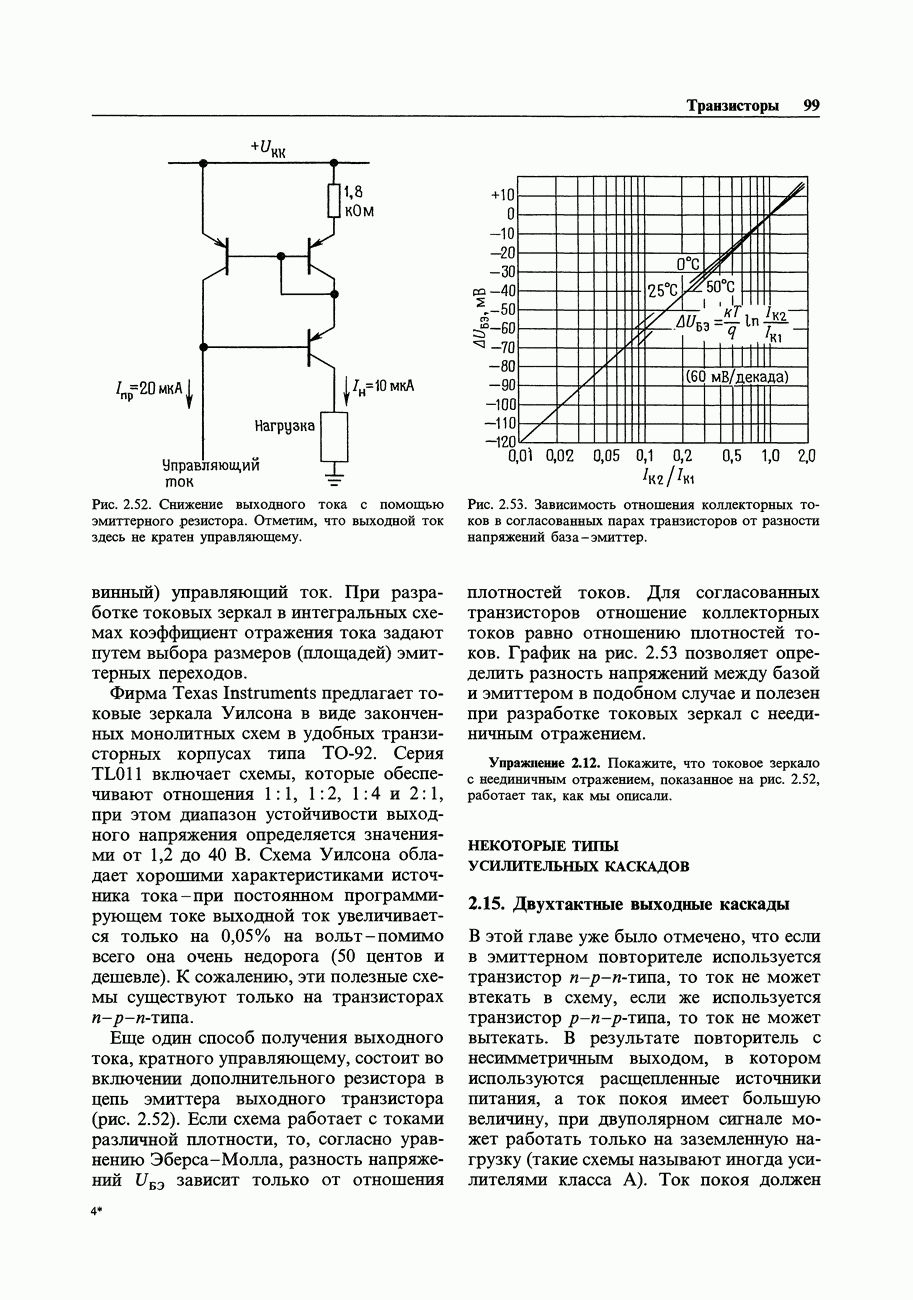
- 2.14. Токовые зеркала
- НЕКОТОРЫЕ ТИПЫ УСИЛИТЕЛЬНЫХ КАСКАДОВ
- 2.15. Двухтактные выходные каскады
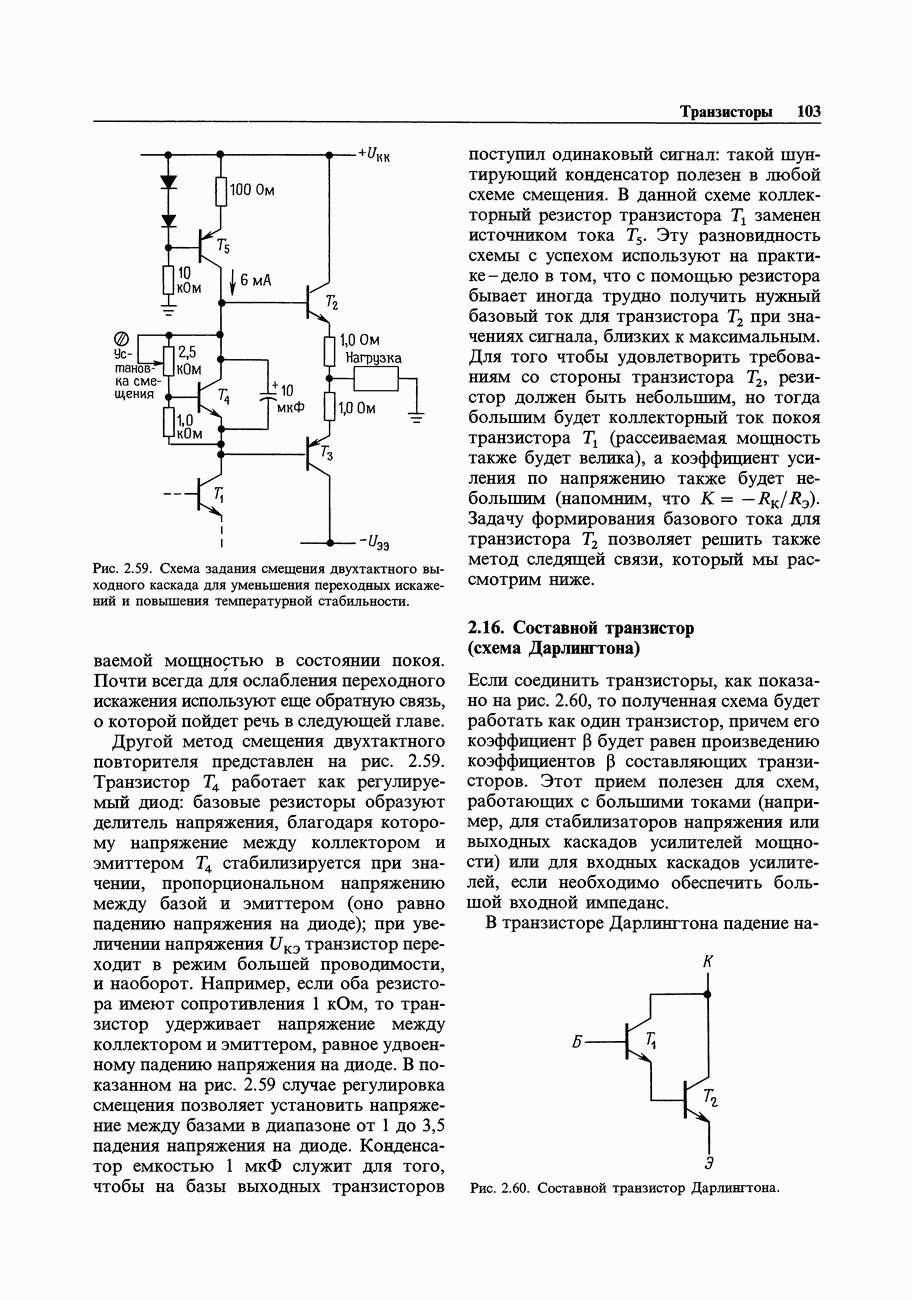
- 2.16. Составной транзистор (схема Дарлингтона)
- 2.17. Следящая связь
- 2.18. Дифференциальные усилители
- 2.19. Емкость и эффект Миллера
- 2.20. Полевые транзисторы
- НЕКОТОРЫЕ ТИПИЧНЫЕ ТРАНЗИСТОРНЫЕ СХЕМЫ
- 2.21. Стабилизированный источник напряжения
- 2.22. Терморегулятор
- 2.23. Простая логическая схема на транзисторах и диодах
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 2.24. Удачные схемы
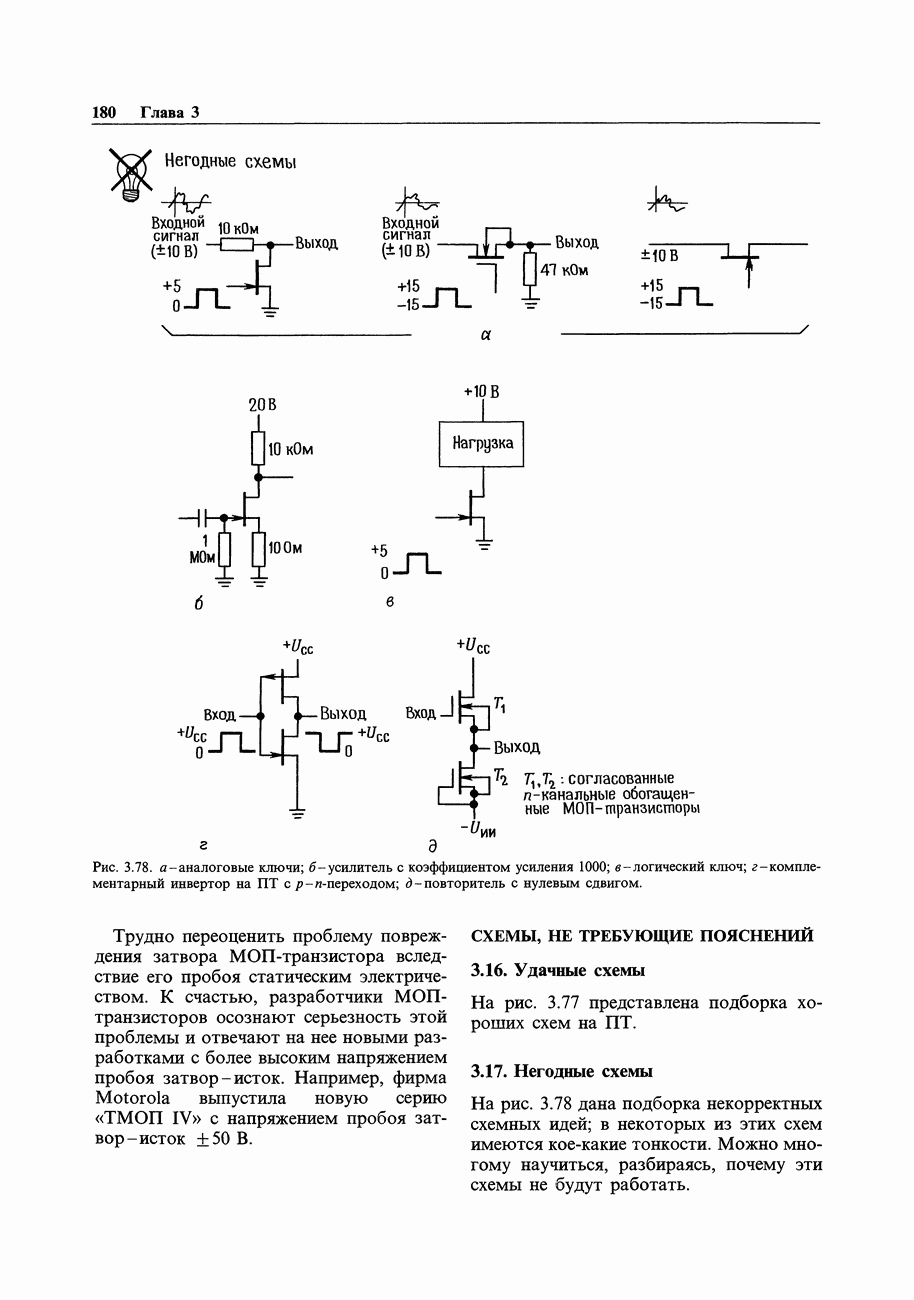
- 2.25. Негодные схемы
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 3. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- 3.01. Характеристики полевых транзисторов
- 3.02. Типы ПТ
- 3.03. Общая классификация ПТ
- 3.04. Выходные характеристики ПТ
- 3.05. Производственный разброс характеристик ПТ
- ОСНОВНЫЕ СХЕМЫ НА ПТ
- 3.06. Источники тока на ПТ с р-n-переходом
- 3.07. Усилители на ПТ
- 3.08. Истоковые повторители
- 3.09. Ток затвора ПТ
- 3.10. ПТ в качестве переменных резисторов
- КЛЮЧИ НА ПТ
- 3.11. Аналоговые ключи на ПТ
- 3.12. Недостатки ПТ-ключей
- 3.13. Несколько схем на ПТ-ключах
- 3.14. Логические и мощные ключи на МОП-транзисторах
- 3.15. Необходимые предосторожности в обращении с МОП-транзисторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 4. ОБРАТНАЯ СВЯЗЬ И ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ
- 4.01. Предварительные сведения об обратной связи
- 4.02. Операционные усилители
- 4.03. Важнейшие правила
- ОСНОВНЫЕ СХЕМЫ ВКЛЮЧЕНИЯ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.04. Инвертирующий усилитель
- 4.05. Неинвертирующий усилитель
- 4.06. Повторитель
- 4.07. Источники тока
- 4.08. Основные предостережения по работе с ОУ
- КАЛЕЙДОСКОП СХЕМ НА ОПЕРАЦИОННЫХ УСИЛИТЕЛЯХ
- 4.09. Линейные схемы
- 4.10. Нелинейные схемы
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ
- 4.11. Отличие характеристик идеального ОУ от реального
- 4.12. Эффекты ограничений ОУ на работу схем на их основе
- 4.13. Микромощные и программируемые ОУ
- ПОДРОБНЫЙ АНАЛИЗ РАБОТЫ НЕКОТОРЫХ СХЕМ НА ОУ
- 4.14. Логарифмический усилитель
- 4.15. Активный пиковый детектор
- 4.16. Выборка-запоминание
- ДИЭЛЕКТРИЧЕСКОЕ ПОГЛОЩЕНИЕ
- 4.17. Активный ограничитель
- 4.18. Схема выделения модуля абсолютного значения сигнала
- 4.19. Интеграторы
- 4.20. Дифференциаторы
- РАБОТА ОУ С ОДНИМ ИСТОЧНИКОМ ПИТАНИЯ
- 4.21. Смещение усилителей переменного тока, использующих один источник питания.
- 4.22. Операционные усилители с одним источником питания.
- КОМПАРАТОРЫ И ТРИГГЕР ШМИТТА
- 4.23. Компараторы
- 4.24. Триггер Шмитта
- ОБРАТНАЯ СВЯЗЬ И УСИЛИТЕЛИ С КОНЕЧНЫМ УСИЛЕНИЕМ
- 4.25. Уравнение для коэффициента усиления
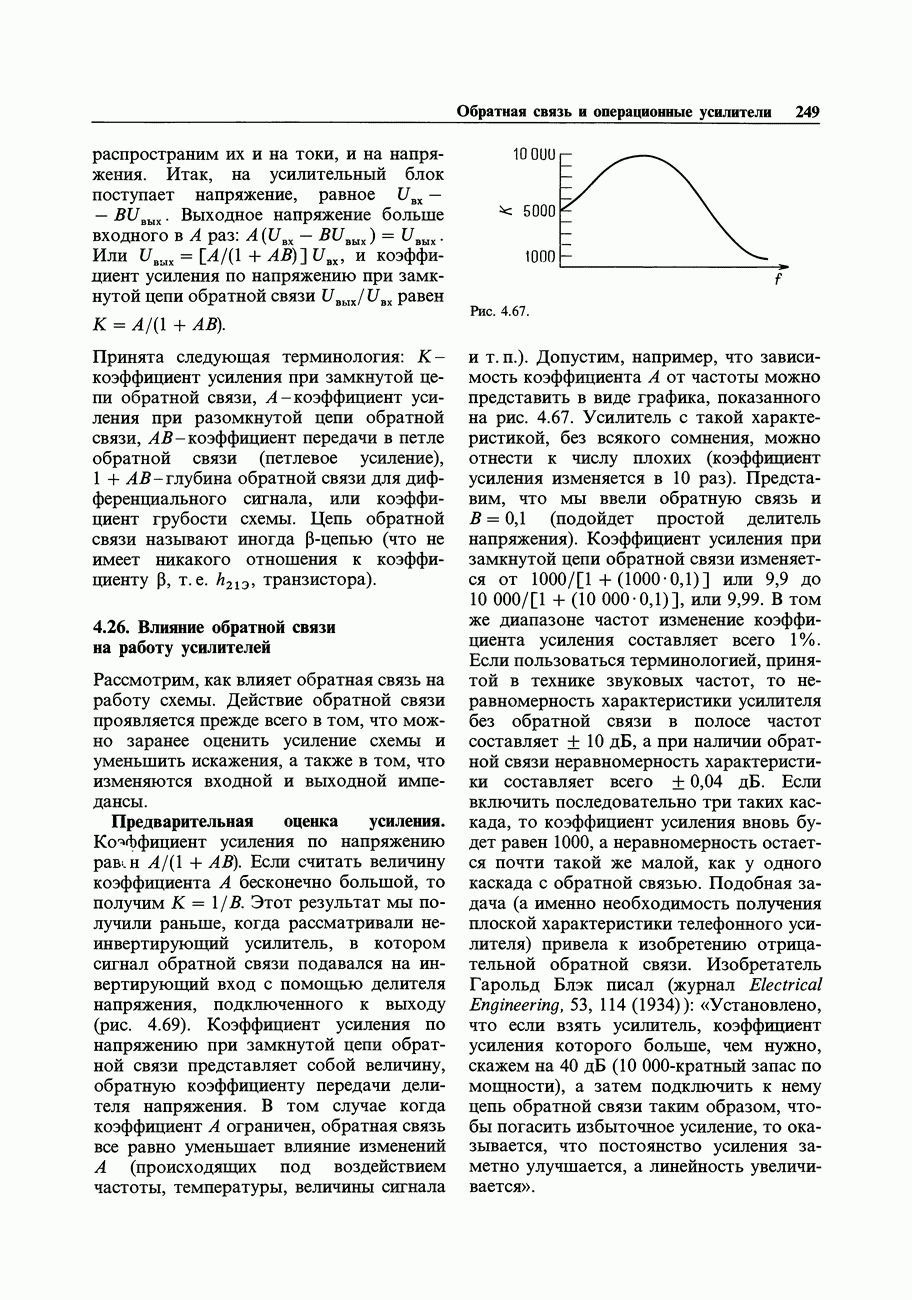
- 4.26. Влияние обратной связи на работу усилителей
- 4.27. Два примера транзисторных усилителей с обратной связью
- НЕКОТОРЫЕ ТИПИЧНЫЕ СХЕМЫ С ОПЕРАЦИОННЫМИ УСИЛИТЕЛЯМИ
- 4.28. Лабораторный усилитель общего назначения
- 4.29. Генератор, управляемый напряжением
- 4.30. Линейный переключатель на полевом транзисторе с p-n-переходом, с компенсацией.
- 4.31. Детектор нуля для ТТЛ-схем
- 4.32. Схема измерения тока в нагрузке
- ЧАСТОТНАЯ КОРРЕКЦИЯ УСИЛИТЕЛЕЙ С ОБРАТНОЙ СВЯЗЬЮ
- 4.33. Зависимость коэффициента усиления и фазового сдвига от частоты
- 4.34. Методы коррекции усилителей
- 4.35. Частотная характеристика цепи обратной связи
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- 4.36. Некоторые полезные идеи
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 5. АКТИВНЫЕ ФИЛЬТРЫ И ГЕНЕРАТОРЫ
- АКТИВНЫЕ ФИЛЬТРЫ
- 5.01. Частотная характеристика RC-фильтров
- 5.02. Идеальный рабочий режим LC-фильтров
- 5.03. Введение в активные фильтры: обзор
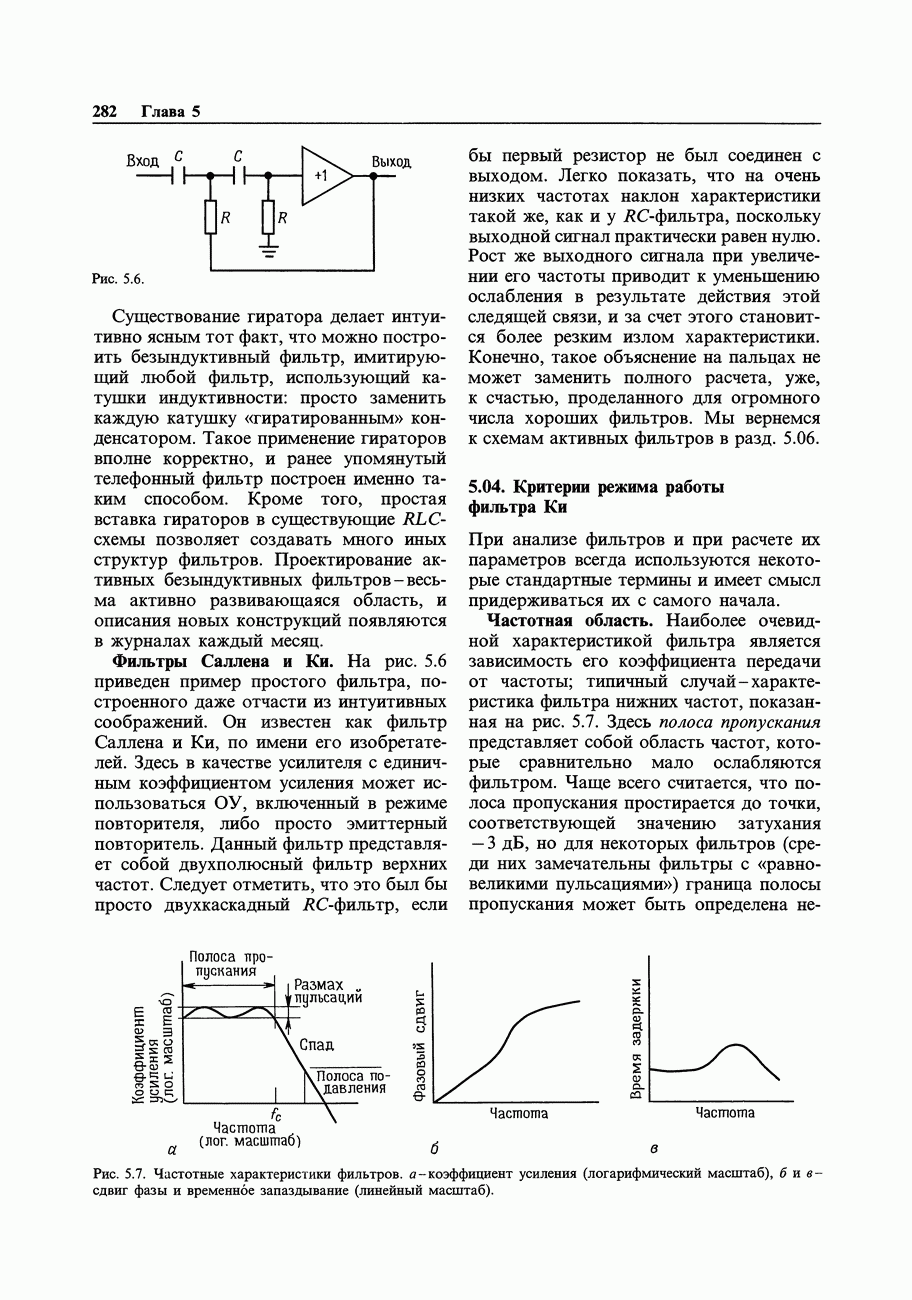
- 5.04. Критерии режима работы фильтра Ки
- 5.05. Типы фильтров
- СХЕМЫ АКТИВНЫХ ФИЛЬТРОВ
- 5.06. Схемы на ИНУН
- 5.07. Проектирование фильтров на ИНУН с использованием наших упрощенных таблиц
- 5.08. Фильтры, построенные на основе метода переменных состояния
- 5.09. Двойной Т-образный фильтр-пробка
- 5.10. Построение фильтров на гираторах
- 5.11. Фильтры на переключаемых конденсаторах
- ГЕНЕРАТОРЫ
- 5.13. Релаксационные генераторы
- 5.14. Классическая ИС таймера-555
- 5.15. Генераторы, управляемые напряжением
- 5.16. Квадратные генераторы
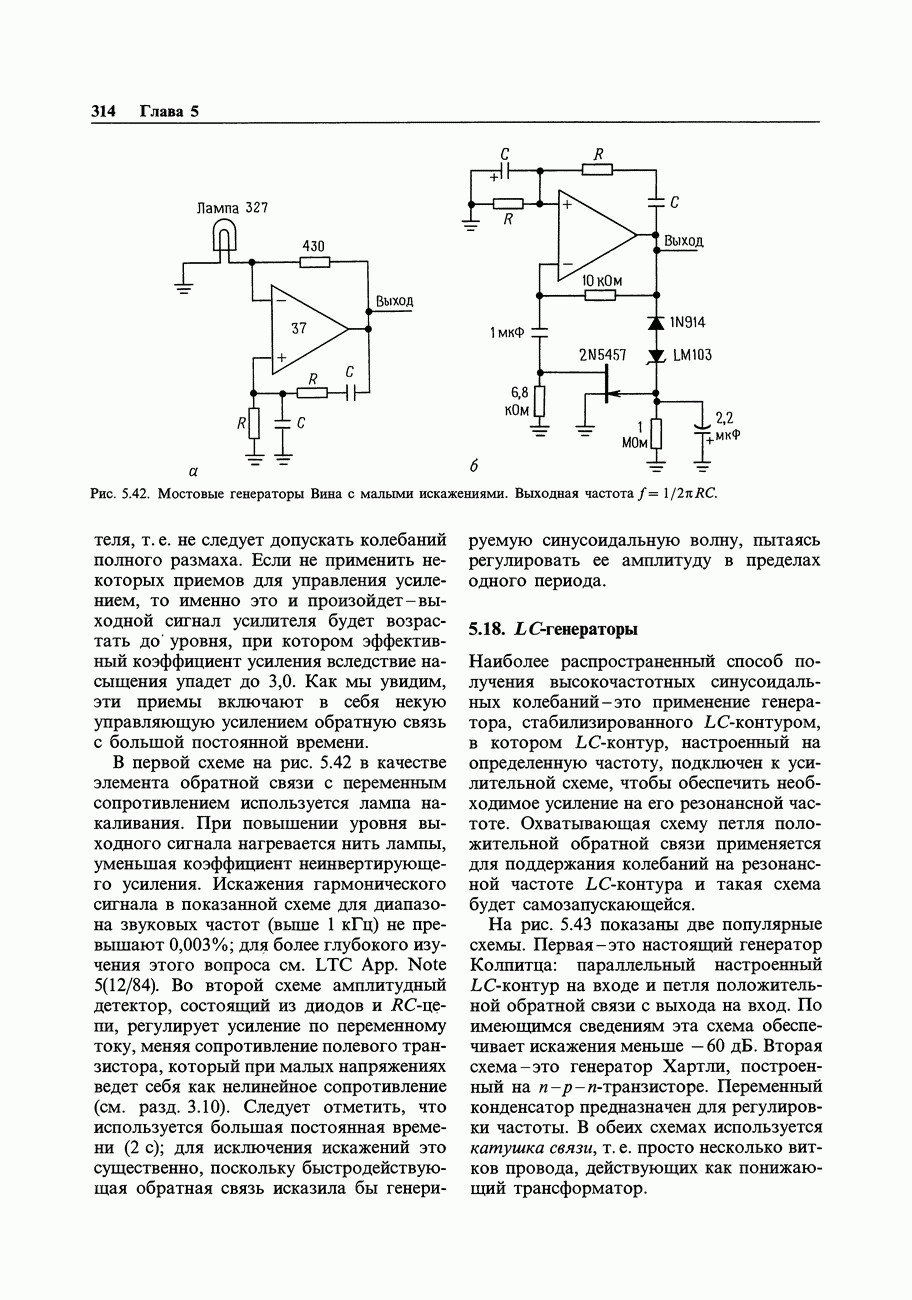
- 5.17. Мостовые генераторы Вина и L С-генераторы
- 5.18. LС-генераторы
- 5.19. Генераторы с кварцевыми резонаторами
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 6. СТАБИЛИЗАТОРЫ НАПРЯЖЕНИЯ И ИСТОЧНИКИ ПИТАНИЯ
- БАЗОВЫЕ СХЕМЫ СТАБИЛИЗАТОРОВ НА ОСНОВЕ КЛАССИЧЕСКОЙ ИМС 723
- 6.01. ИМС стабилизатора 723
- 6.02. Стабилизатор положительного напряжения
- 6.03. Стабилизаторы с большими выходными токами
- ПРОЕКТИРОВАНИЕ ТЕПЛООТВОДА МОЩНЫХ СХЕМ
- 6.04. Мощные транзисторы и отвод тепла
- 6.05. Ограничители тока с обратным наклоном характеристики
- 6.06. Защита от больших напряжений
- 6.07. Специальные вопросы проектирования сильноточных источников питания
- 6.08. Программируемые источники питания
- 6.09. Пример схемы источника питания
- 6.10. Другие ИМС стабилизатора
- НЕСТАБИЛИЗИРОВАННЫЕ ИСТОЧНИКИ ПИТАНИЯ
- 6.11. Компоненты линии переменного тока
- 6.12. Трансформаторы
- 6.13 Элементы схемы, работающие на постоянном токе
- ИСТОЧНИКИ ОПОРНОГО НАПРЯЖЕНИЯ
- 6.14. Стабилитроны
- 6.15. Источник опорного напряжения на стабилитроне
- ТРЕХВЫВОДНЫЕ И ЧЕТЫРЕХВЫВОДНЫЕ СТАБИЛИЗАТОРЫ
- 6.16. Трехвыводные стабилизаторы
- 6.17. Трехвыводные регулируемые стабилизаторы
- 6.18. Дополнительные замечания относительно трехвыводных стабилизаторов
- 6.19. Импульсные стабилизаторы и преобразователи постоянного тока
- ИСТОЧНИКИ ПИТАНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ
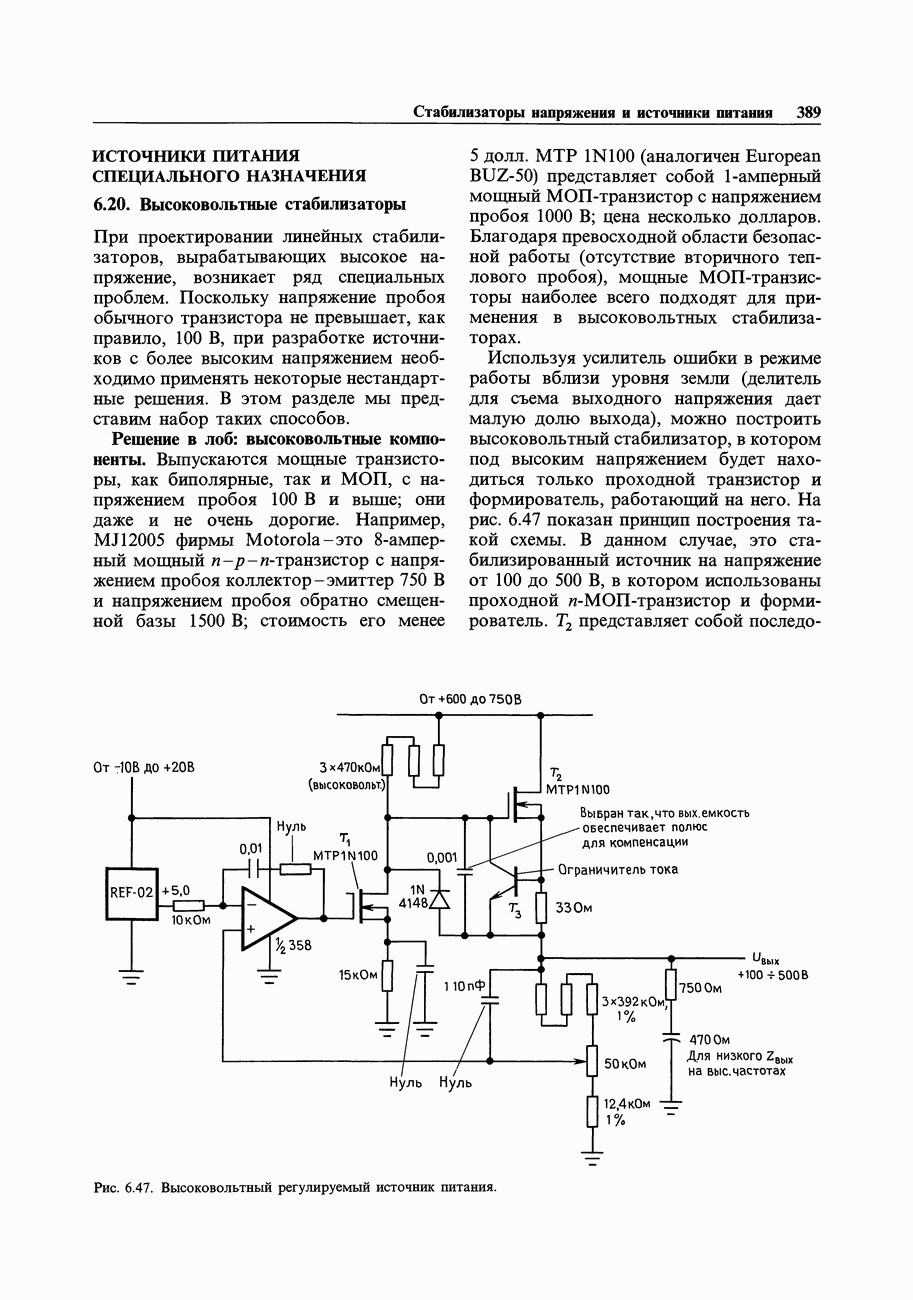
- 6.20. Высоковольтные стабилизаторы
- 6.21. Источники питания с малым уровнем помех и малым дрейфом
- 6.22. Микромощные стабилизаторы
- 6.23. Преобразователи напряжения с переключаемыми конденсаторами (зарядовый насос)
- 6.24. Источники стабилизированного постоянного тока
- 6.25. Коммерческие модули источников питания
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ