ГЛАВА 11. ПАРНЫЕ СРАВНЕНИЯ

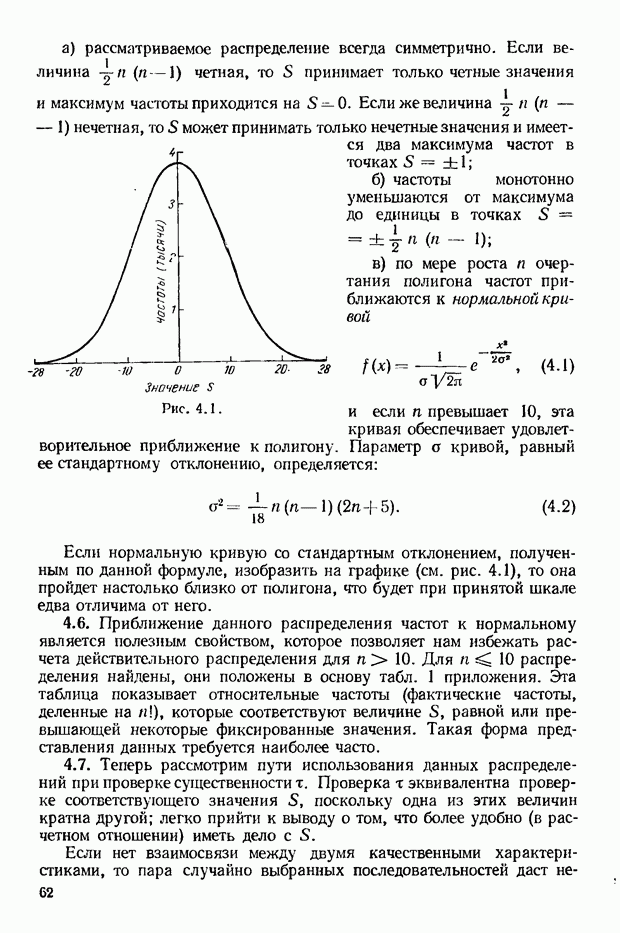
11.1. До сих пор предполагалось, что последовательности рангов содержатся в самой постановке задачи, и мы не задавались вопросом о том, в какой степени рассматриваемые данные удовлетворяют требованиям, предъявляемым к последовательностям рангов. Однако во многих случаях (особенно часто — в психологических исследованиях) возникают некоторые сомнения относительно правомерности такой постановки вопроса. Допустим, мы попросили эксперта ранжировать десять человек по степени развития их интеллектуальных способностей. Предположим даже, что эксперт смог справиться с этой задачей (хотя, вообще говоря, природа интеллекта настолько неясна, что мы не можем быть уверенными в самой возможности адекватного упорядочения индивидуумов по этому признаку). Мы допускаем какую-то произвольность в наших рассуждениях, предполагая, что переменная, характеризующая интеллектуальные способности, линейна. Другой пример: мы можем предложить эксперту упорядочить некоторое число географических районов в соответствии со своими предпочтениями: насколько привлекателен каждый из них в качестве места жительства. Однако в этом случае предпочтения будут зависеть от взаимодействия различных факторов, таких, как стоимость жизни, наличие удобного транспорта, высота над уровнем моря, близость к торговым центрам; поэтому нет никакой уверенности в том, что наблюдатель сможет выразить свои окончательные предпочтения с помощью линейной шкалы. Даже в тех случаях, когда мы настаиваем на том, чтобы эксперт упорядочил свои предпочтения, а он стремится выполнить указанную просьбу, будучи уверенным в том, что располагает соответствующими возможностями, эти попытки могут свестись к тому, что мы будем, так сказать, втискивать наши данные в рамки чрезмерно узкой схемы, которая исказит реальную действительность. В этой главе рассматривается метод, с помощью которого можно преодолеть подобные трудности.

11.2. Предположим, что имеется объектов и эксперту поочередно представляют каждую из пар объектов. Эксперт сопоставляет между собой представленные объекты и по каждой паре записывает свои предпочтения. Если объект А предпочитают объекту В, мы можем записать это следующим образом: или

Пример 11.1.

В экспериментальных целях было подготовлено шесть различных видов корма для собак. Собаке поочередно предлагалась каждая из возможных пар, составленных из этих видов корма; при этом каждый раз фиксировалось, какую пищу собака ест в первую очередь. (Подобный опыт проводился с целью иллюстрации справедливости некоторых предположений, и к нему, разумеется, нельзя относиться как к некой серьезной попытке выявить собачьи предпочтения.) Обозначив виды корма с помощью букв латинского алфавита от А до объединим полученные результаты в таблицу:

Таблица 11.1

Реакции собаки при сопоставлении шести видов корма

Запись 1 в клетке, находящейся на пересечении, скажем, столбца и строки X, означает разумеется, в клетке, находящейся на пересечении строки и столбца X, должен стоять 0. Таким образом, в нашей таблице Диагональные элементы таблицы исключены.

Последовательность, в которой различные виды корма записываются по строкам и столбцам таблицы, произвольна; понятно, однако, что удобнее всего располагать объекты по строкам и по столбцам в одинаковом порядке.

Всю систему предпочтений можно охарактеризовать с помощью диаграммы. Для этого расположим шесть объектов от А до по вершинам правильного многоугольника (как показано на рис. 11.1). Проведем все возможные линии, соединяющие вершины этого многоугольника, и если направим стрелку из вдоль линии

11.3. Предположим, что нам даны три объекта и эксперт высказал следующие предпочтения: или . В этом случае будем говорить, что предпочтения по трем объектам характеризуются цикличностью или что предпочтения «несовместны». С помощью диаграммы (подобной 11.1) можно показать, что цикличные предпочтения по трем объектам позволяют, двигаясь вдоль стрелок, последовательно обойти все вершины треугольника На рис. 11.1 цикличными оказываются предпочтения по объектам и (можно найти также три другие цикличные тройки объектов).

Ясно, что цикличность предпочтений не может возникать в обычных последовательностях рангов, так как если то Необходимым и достаточным условием того, что предпочтения могут быть выражены с помощью последовательности рангов, служит отсутствие цикличных предпочтений по трем объектам. Чем более интенсивно (если можно так выразиться) проявляется цикличность предпочтений по трем объектам, тем меньше возможностей составить последовательность рангов и тем ближе мы оказываемся к «несовместной» ситуации, когда объект X может предпочитаться объекту объект объекту и тем не менее объект предпочитается объекту

Рис. 11.1

11.4. Иногда встречаются циклы предпочтений, содержащие более трех объектов. Например, пусть здесь цикличностью характеризуются предпочтения по четырем объектам. Цикл предпочтений по объектам должен содержать по крайней мере циклов по трем объектам (их может быть и больше); но если в состав системы предпочтений, включающей объектов, входят циклы по трем объектам, из этого еще не следует, что цикличны предпочтения по всей системе. Предположим, например, что предпочтения по объектам образуют цикл. Тогда или или первом случае цикличны предпочтения по объектам во втором — по объектам Рассуждая аналогично, можно показать, что должны быть цикличны предпочтения либо по объектам либо по объектам Таким образом, цикл предпочтений по четырем объектам должен включать по меньшей мере два цикла предпочтений по трем объектам. Допустим теперь, что имеют место соотношения следующего типа: такая система предпочтений содержит циклы по трем объектам: и однако предпочтения по всей системе нецикличны.

В дальнейшем изложении мы будем рассматривать прежде всего циклы предпочтений по трем объектам (поскольку они образуют «элементарные клеточки» несовместной ситуации). Мы не будем прибегать к более сложным (и менее определенным) критериям выявления циклов по совокупностям высшего порядка.

11.5. В следующей главе будет показано, что когда величина нечетна, максимальное количество циклов по трем объектам равно а при четном равно Минимальное их число равно нулю. Исходя из этих соображений, можно ввести коэффициент

совместности, определив его с помощью следующих уравнений:

где число обнаружившихся циклов предпочтений по трем объектам. Циклы предпочтений по трем объектам отсутствуют и ранговые оценки удается упорядочить тогда и только тогда, когда коэффициент равен единице.

Например, оценки, приведенные в примере 11.1, содержат 5 циклов предпочтений по трем объектам. Максимальное число таких циклов равно 8, следовательно,

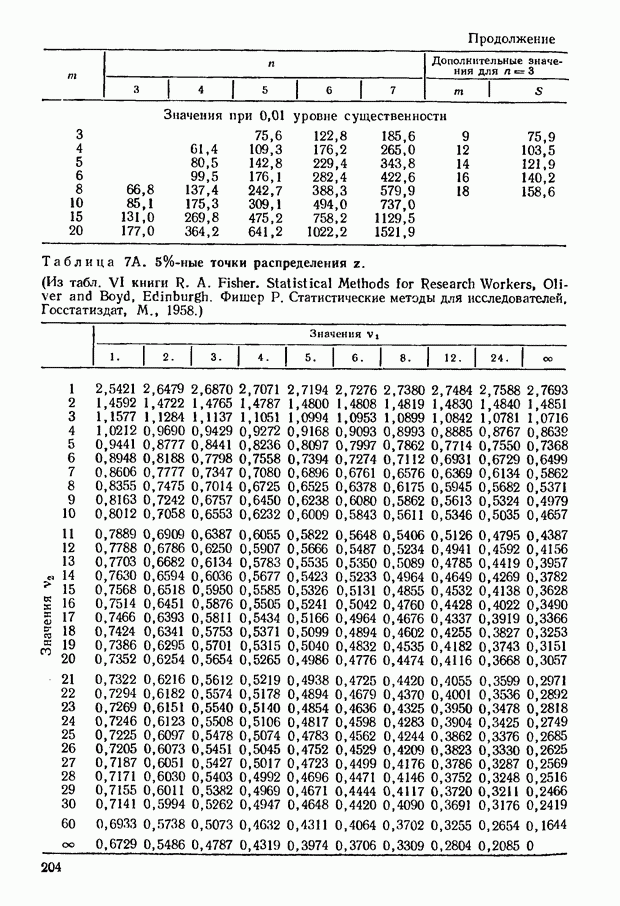
11.6. Для того чтобы как-то проверить существенность коэффициента выясним, как будут распределены эти величины в том случае, когда все предпочтения складываются случайным образом. Благодаря этому мы сможем узнать, может ли наблюдаемое значение коэффициента представлять собой случайную величину (такая ситуация имеет место, когда эксперт совершенно некомпетентен), либо же, напротив, предпочтения эксперта характеризуются некоторой, хотя, возможно, и не идеальной согласованностью.

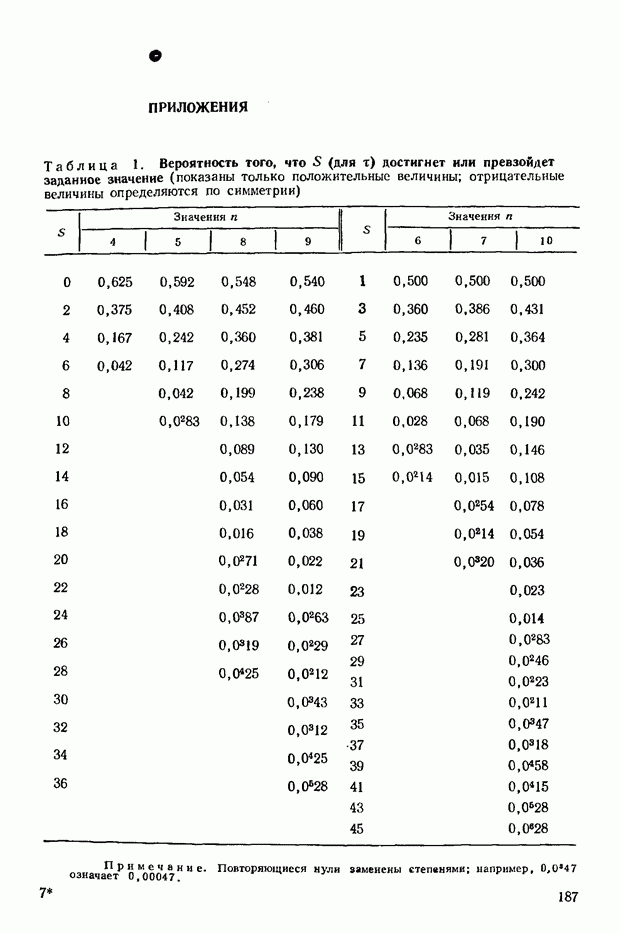
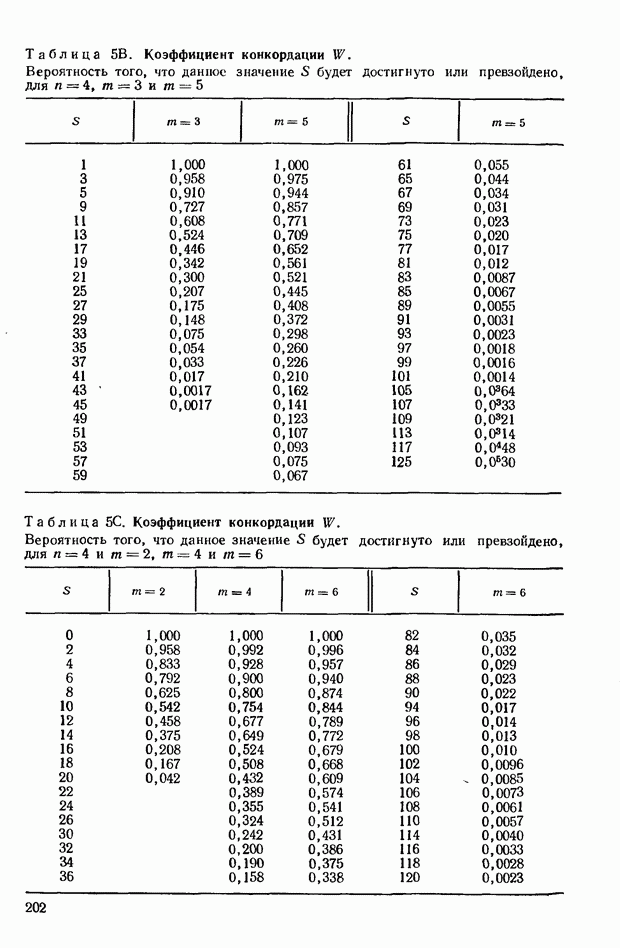
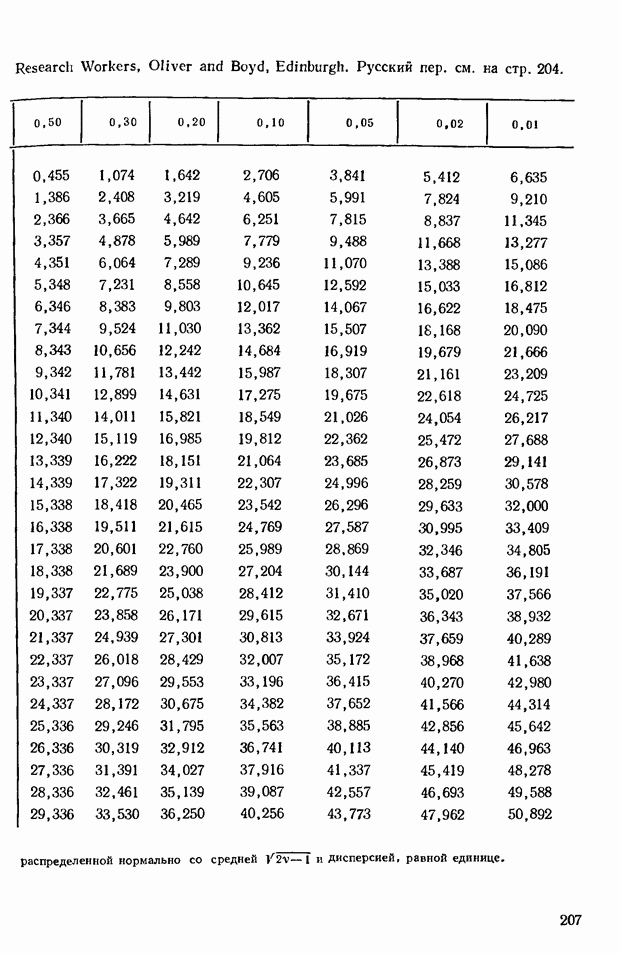
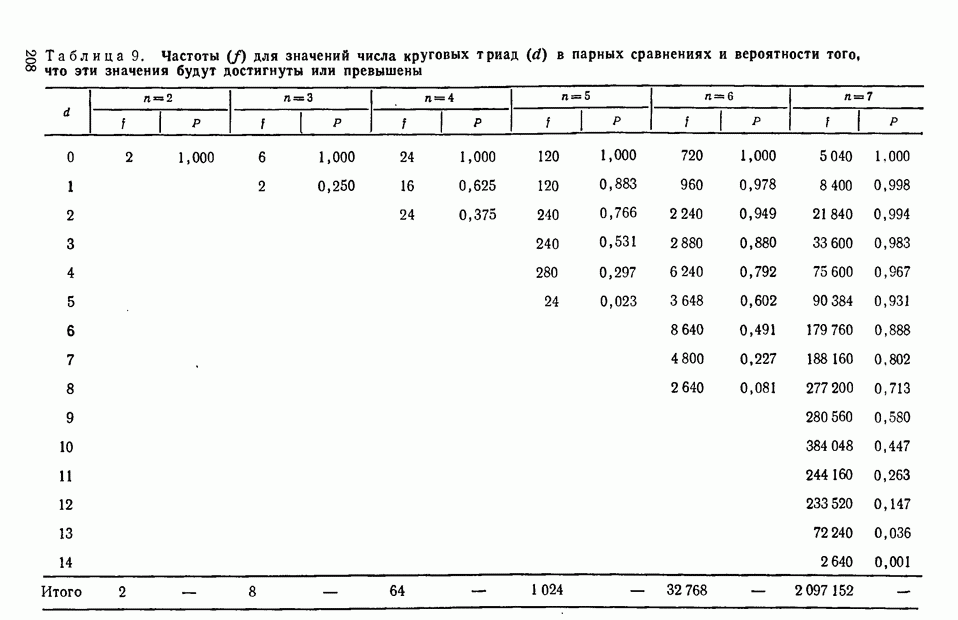
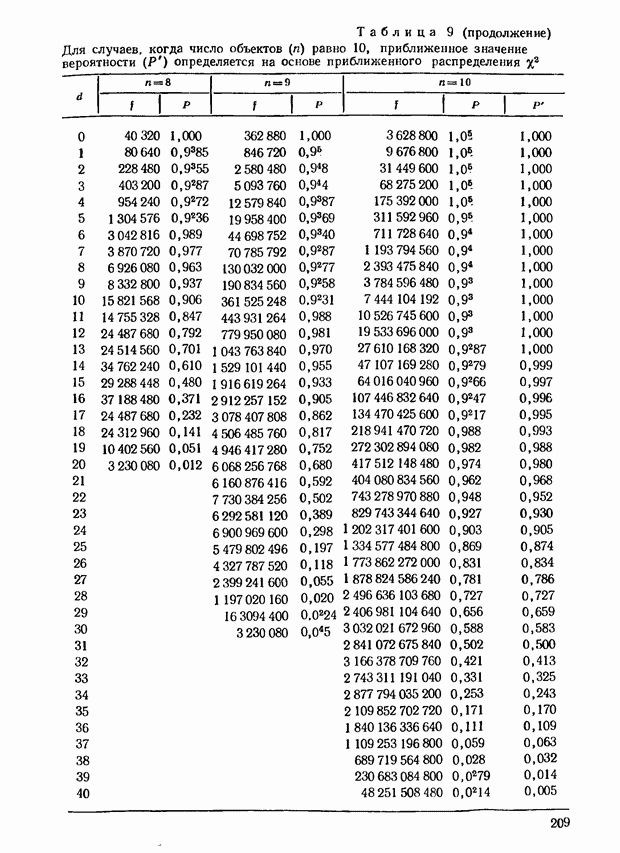
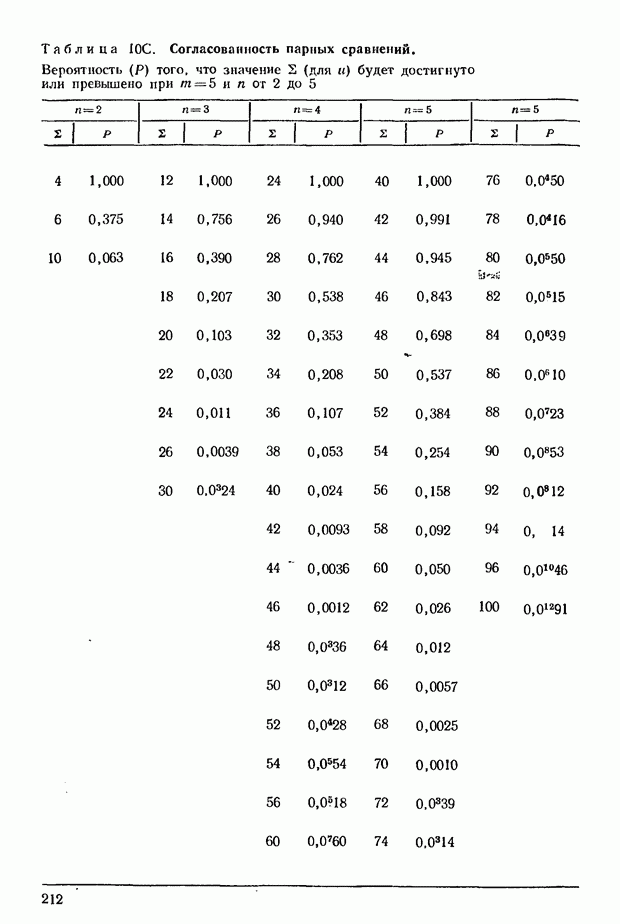
Предположив, что предпочтения носят чисто случайный характер (и, следовательно, одна система предпочтений столь же вероятна, как и любая другая), можно подсчитать вероятности, характеризующие различные значения коэффициента . В приложении в табл. 9 приведены вероятности того, что будут достигнуты или превышены некоторые величины при меняющем значения от 2 до 7. На практике редко приходится иметь дело с большими значениями Допустим, однако, что нам требуется провести статистическую проверку при больших значениях поскольку расчет подобных распределений — дело довольно трудоемкое, можно воспользоваться распределением к которому с ростом стремится распределение Действительно, выписав значения

можно видеть, что величины степенями свободы распределены примерно таким же образом. Однако в распределении величин отсчет ведется от большего значения к меньшему, поэтому и вероятность того, что достигает некоторой величины или превосходит ее, не совпадает с соответствующей вероятностью для а представляет собой ее дополнение единицы). Следующий пример поможет лучше понять технику вычислений.

Пример 11.2

Предположим, что мы имеем дело с системой, состоящей из 7 объектов, причем На основании (11.2) можно записать:

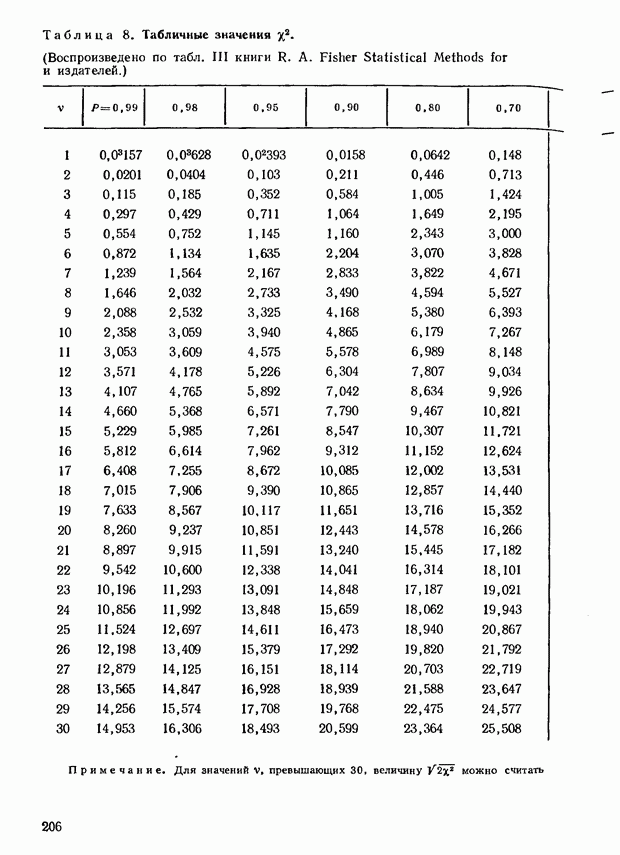
В приведенной в приложении табл. 8, найдем, что этим значениям примерно соответствует уровень существенности, равный 0,95. В таком случае соответствующий уровень существенности для равен Приведенное в табл. 9 приложения точное значение вероятности равно 0,36. Следовательно, даже для столь малого значения как 7, результаты аппроксимации вполне удовлетворительны.

11.7. Если мы располагаем таблицей, подобной 11.1, общую численность циклов предпочтений по трем объектам можно определить более простым путем. Обозначим, например, суммы чисел по строкам с помощью букв Тогда

Так, в табл. 11.1 суммы оценок, исчисленные по строкам, соответственно равны 4, 2, 4, 1, 2, 2, итого единиц. Таким образом,

и, следовательно,

Можно использовать эту же формулу применительно к суммам оценок по столбцам (обозначим эти суммы буквами Исходя из самого построения таблицы, можно записать:

Таким образом,

и, следовательно,

Соотношение (11.3) можно записать также в следующем виде:

Вероятно, это простейший путь исчисления

Коэффициент согласия

11.8. Предположим, опыте участвуют экспертов, каждый из которых рассмотрел все возможные пары из объектов и высказал предпочтений. Построим таблицу, подобную 11.1, причем во всех случаях, когда мы будем вписывать единицу в клетку, расположенную на пересечении строки и столбца, а затем подсчитаем количество единиц в каждой клетке. В ней может оказаться любое число единиц — от до Если наблюдатели единодушны, то клеток будут содержать по единиц, а остальные клетки — нули. Согласие между наблюдателями может быть полным даже в том случае, когда встречаются циклы предпочтений.

Предположим, что в клетке, находящейся на пересечении строки и столбца, вписано число . Введем теперь следующее соотношение:

причем суммирование ведется по клеткам таблицы (диагональные клетки не учитываются). Тогда 2 будет представлять собой общее число случаев, в которых пара экспертов согласна между собой. Положим

Величину и мы будем называть коэффициентом согласия в том и только в том случае, когда имеет место полная согласованность в предпочтениях экспертов. Чем меньше степень согласованности (измеряемая совпадением или несовпадением предпочтений каждой пары экспертов), тем меньшие значения принимает коэффициент и. В таком случае число единиц в клетке, характеризующее минимальную согласованность предпочтении, составляет если величина четна, а в противном случае Тогда в первом случае и равно во втором —

Только при и достигает своего минимального значения, равного —1. Поскольку в опыте участвуют всего два эксперта, наша формула принимает следующий вид:

В этом случае и можно представить как некое обобщение коэффициента

Пример 11.3.

В классе мальчиков (в возрасте от 11 до 13 лет) был проведен опрос, в ходе которого им предложили сформулировать свой предпочтения относительно некоторых учебных дисциплин. Каждый из опрашиваемых получил лист бумаги, на котором были выписаны все возможные пары дисциплин; в каждом случае требовалось подчеркнуть название дисциплины, которой оказывалось предпочтение. В классе насчитывался 21 ученик, а число учебных дисциплин равно 13. В результате опроса были получены результаты, сведенные в табл. 11.2.

Таблица 11.2. Предпочтения, высказанные 21 учеником относительно 13 предметов

(см. скан)

Наименования учебных дисциплин в этой таблице упорядочены в соответствии с общим числом выявленных предпочтений, поэтому величину 2 легче вычислить следующим образом: соотношение (11.5) можно привести к виду

а суммирование будем проводить по той половине таблицы, что лежит ниже диагонали. Благодаря тому, что расположенные здесь числа меньше, чем числа в верхней половине таблицы, удается несколько облегчить соответствующие арифметические операции. Подсчеты показывают, что

и, следовательно,

Таким образом, мы исчислили некоторую величину, характеризующую степень согласованности между предпочтениями учеников; она измеряется положительным значением коэффициента .

Циклы предпочтений по трем объектам в этом примере распределяются следующим образом:

(см. скан)

Общее число таких циклов предпочтений равно 242, а их среднее значение — 11,5. Лишь у одного ученика была выявлена полностью совместная (непротиворечивая) система предпочтений. С другой стороны, для максимальное число циклов предпочтений по трем объектам равно 91 при среднем значении, равном 71,5. Ясно, что за исключением, быть может, одного ученика, все остальные высказывали такие предпочтения, которые нельзя полагать случайными. Следовательно, мы вновь можем убедиться в том, что ребята действительно способны формулировать свои предпочтения. Это проявилось, в частности, в том, что у половины мальчиков значения коэффициента превышают 0,92.

Пример 11.4

На практике часто встречается ситуация, когда эксперты отказываются высказать отчетливое предпочтение одному из двух рассматриваемых объектов. В этом случае мы сталкиваемся с такими же трудностями, как при анализе связанных рангов. Для того чтобы каким-то образом преодолеть затруднения, мы при составлении таблицы типа 11.1 будем использовать следующий прием. Если при сравнении объектов не выявлено никакого предпочтения, будем вписывать величину как в клетку, находящуюся на пересечении строки X и столбца У, так и в клетку, находящуюся на пересечении строки У и столбца Проиллюстрируем этот метод.

На предприятии был проведен опрос 46 работников: им предложили сравнить между собой попарно ряд возможных улучшений (всего 66 пар), выделив в каждой паре ту перспективу, которая каждому из них представляется более важной.

(см. скан)

Результаты опроса сведены в таблицу (см. стр. 166).

Подсчитав суммы квадратов приведенных в таблице значений мы найдем:

Таким образом,

Если, невзирая на то, что у теперь может принимать дробные значения, мы будем пользоваться прежней формулой (11.6), то получим:

Рассмотрим теперь одну из оценок, например число, которое записано в клетке, находящейся на пересечении строки и столбца а также его дополнение — число, которое расположено в клетке, находящейся на пересечении столбца и строки В т. е. Эти дробные величины дадут следующие оценки, включаемые в общие результаты наших расчетов:

Итак, применяемый метод приближенного оценивания в случае отсутствия четкого предпочтения эквивалентен определению среднего значения, причем сначала мы полагаем, что (в данном случае соответствующие мнения характеризуются числами 25 и 21, а затем, что и число предпочтений соответственно равно 24 и 22; при этом мы не принимаем в расчет слагаемое, равное , но его влияние

(см. скан)

сравнительно невелико. Это согласуется с изложенным выше методом изучения случаев, когда существуют связи между рангами.

В нашей таблице в клетке, находящейся на пересечении строки В и столбца Г, стоит число 21. Оно равно 20, т. е. включает две дроби, каждая из которых равна Аналогично на пересечении столбца В и строки записано число, которое фактически составляло Если бы и в этом случае нам потребовалось рассчитать соответствующие средние значения, то они были бы равны

Разность между этой суммой и числами, которые мы действительно использовали в расчетах (21; 25), составляет:

Такая разность вновь очень невелика.

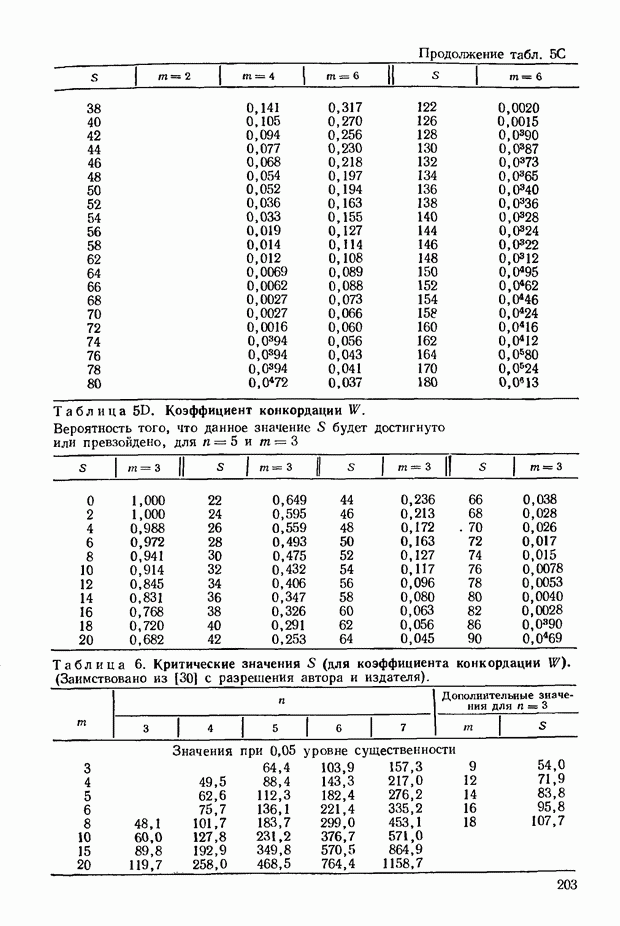
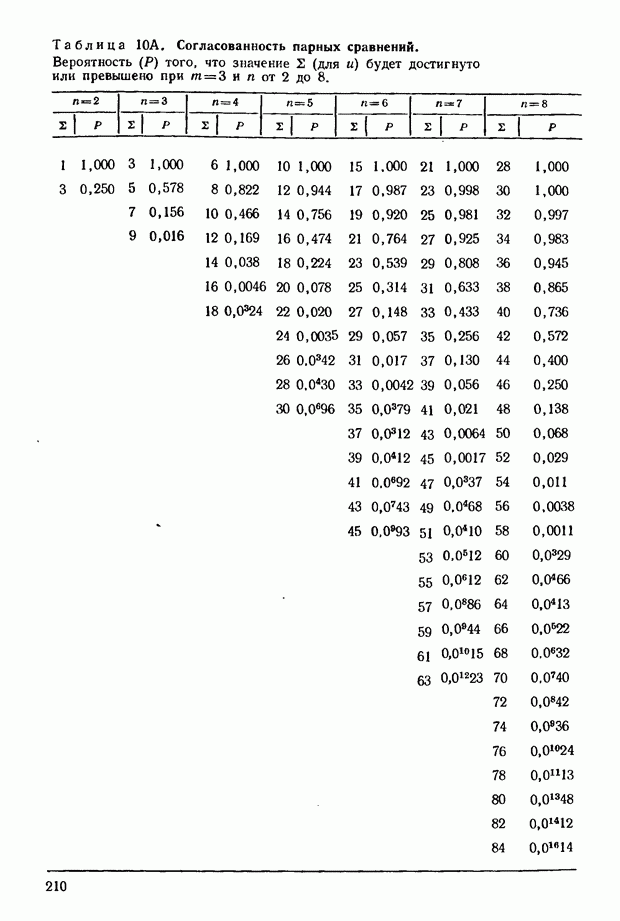
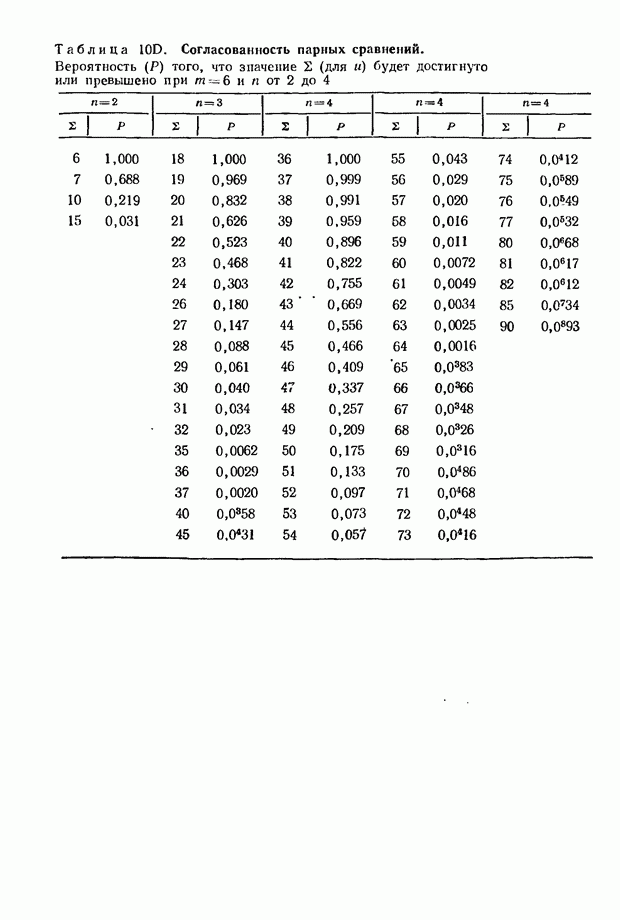
11.9. Попытаемся найти способ для проверки статистической существенности. Для этого рассмотрим распределение и в том случае, когда все предпочтения носят случайный характер. Такие распределения построены для На основе этих расчетов исчислены данные, приведенные в приложении в табл. 10.

Для больших значений вполне удовлетворительные результаты обеспечивает аппроксимация с помощью распределения В таком случае можно записать:

и провести проверку статистической существенности по критериям распределения степенями свободы. Можно ввести поправку на непрерывность, для этого из нужно соответственно вычитать единицу.

Например, при мы получили следующие значения и

В приведенной в приложении табл. мы находим:

Соответствующие этим значениям 2 (поправка на непрерывность введена) величины равны 212 и 228. При мы можем полагать, что величина распределена по нормальному закону с единичной дисперсией, составляющей примерно так что наши отклонения равны:

и

С помощью приведенной в приложении табл. 3 можно установить, что такие отклонения соответствуют вероятностям 0,011 и 0,00114, т. е. полученные результаты весьма близки к истинным значениям.

Допустим теперь, что тогда с помощью соотношений (11.8) и (11.9) можно аналогичным образом найти, что распределение величины (2 — 33,75) характеризуется 11, 25 степенями свободы. С помощью табл. (см. приложение) мы можем определить, что -ный уровень существенности предполагает значения 2, лежащие между числами 59 и 60. Тогда (введя поправку на непрерывность) мы сможем отыскать соответствующие значения они равны 24, 25 и 25, 25. Обратившись к приведенной в приложении табл. 8, мы увидим, что эти значения действительно вполне соответствуют уровню существенности, поскольку соответствующая величина при должна находиться в следующих границах: Пример 11.5

В примере 11.3 мы рассчитали значения соответствующие Это свидетельствовало о том, что имеет место некоторая (хотя и не очень большая) согласованность предпочтений. Прибегнем теперь к проверке статистической существенности полученных величин.

С помощью формул (11.8) и (11.9) можно рассчитать значения

Полученные величины значительно превосходят любые общепринятые стандарты статистической значимости. Из этого можно заключить, что коэффициент и не мог бы принять значение, подобное тому, которое мы рассчитали, если бы совокупность всех высказываемых учениками предпочтений действительно содержала лишь случайные величины. Этот расчет еще раз подтверждает справедливость выводов, сформулированных на основе анализа примера 11.3.

Проделав аналогичные расчеты в примере получаем:

И здесь полученные результаты свидетельствуют о том, что лишь с ничтожной вероятностью можно предполагать чисто случайный характер предпочтений. Поэтому можно сделать следующий вывод: рассчитанное значение коэффициента и существенно.

Библиография

См. [57], а также [65]. Парные сравнения (ненулевой случай) рассматриваются в [85] и [23].

В [23], кроме того, приводится уточнение предложенного Кендэлом и Бэбингтоном Смитом метода, с помощью которого проводится статистическая проверка существенности коэффициента и в случае упорядоченности исходных данных. Если можно провести статистическую проверку существенности коэффициента , используя для этого распределение в таком случае

с степенями свободы.

См. также монографию Н. A. D a v i d «The Method of Paired Comparisons» (Griffin and Co., London, 1963, 1969).