| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 6 ПРОБЛЕМА m ПОСЛЕДОВАТЕЛЬНОСТЕЙ
6.1. До сих пор мы рассматривали корреляцию двух последовательностей рангов. Теперь рассмотрим случай, когда имеется несколько последовательностей; их число обозначим буквой  , а количество рангов в каждой последовательности — буквой
, а количество рангов в каждой последовательности — буквой  Рассмотрим общие соотношения между указанными последовательностями, Предположим, что четыре эксперта упорядочили шесть объектов следующим образом:
Рассмотрим общие соотношения между указанными последовательностями, Предположим, что четыре эксперта упорядочили шесть объектов следующим образом:

Воспользовавшись рассмотренными ранее методами, мы можем рассчитать коэффициенты корреляции между рангами каждых двух экспертов; следуя по этому пути, можно получить  коэффициентов корреляции. Однако обычно нам требуются не такие показатели. Нас интересует общая мера согласованности (конкордации) внутои группы экспертов.
коэффициентов корреляции. Однако обычно нам требуются не такие показатели. Нас интересует общая мера согласованности (конкордации) внутои группы экспертов.
6.2. Наиболее наглядно такую меру, вероятно, можно было бы получить, усреднив все возможные значения коэффициентов тир, исчисленные для каждой пары экспертов, но когда число  велико, такая процедура, понятно, потребует чрезвычайно больших затрат труда. В случаях, подобных описанному выше, проще всего сопоставить суммы рангов, приписываемых каждому объекту различными экспертами; такие данные приведены в последней строке (6.1). Сумма этих чисел составляет 84; в общем случае она равна
велико, такая процедура, понятно, потребует чрезвычайно больших затрат труда. В случаях, подобных описанному выше, проще всего сопоставить суммы рангов, приписываемых каждому объекту различными экспертами; такие данные приведены в последней строке (6.1). Сумма этих чисел составляет 84; в общем случае она равна 
Эта величина получена путем суммирования  слагаемых, каждое из которых представляет собой сумму натуральных чисел от 1 до
слагаемых, каждое из которых представляет собой сумму натуральных чисел от 1 до 
Тогда среднее значение суммы рангов одного объекта составляет  в нашем примере оно равно 14. Рассмотрим индивидуальные отклонения от этого среднего значения:
в нашем примере оно равно 14. Рассмотрим индивидуальные отклонения от этого среднего значения:

Если бы все последовательности совпадали, суммы рангов в (6.1) выглядели бы следующим образом:

(эти суммы, разумеется, необязательно располагались бы именно в таком порядке), а их отклонения равнялись бы соответственно

Сумма квадратов этих отклонений составляет:

Это максимальное значение, которое может принимать сумма квадратов рассматриваемых отклонений. Другое экстремальное значение может быть равно нулю, когда  «етьо либо
«етьо либо  нечетно (либо и то и другое одновременно), в остальных случаях значение суммы квадра
нечетно (либо и то и другое одновременно), в остальных случаях значение суммы квадра  в хотя и не равно нулю, но сравнительно мало.
в хотя и не равно нулю, но сравнительно мало.
Обозначим буквой  сумму квадратов фактически встречающихся отклонений, в нашем примере (см.
сумму квадратов фактически встречающихся отклонений, в нашем примере (см.  она составляет 64. В таком случае величину
она составляет 64. В таком случае величину

будем называть коэффициентом конкороаиии (коэффициентом согласованности). В нашем примере

6.3. В некотором смысле  служит мерой общность суждений
служит мерой общность суждений  экспертов. Если все эти суждения совпадаю то
экспертов. Если все эти суждения совпадаю то  Если различия между ними очень велики, суммы рангов окажутся более или
Если различия между ними очень велики, суммы рангов окажутся более или  близки друг к другу по своей величине и поэтому сумма квадратов
близки друг к другу по своей величине и поэтому сумма квадратов  будет меньше ее возможного максимального значения, а следовательно, и коэффициент
будет меньше ее возможного максимального значения, а следовательно, и коэффициент  составит малую величину. Увеличение
составит малую величину. Увеличение  от
от  до 1 означает, что различия между отклонениями «усиливаются», и в это! проявляется все большая согласованность рангов.
до 1 означает, что различия между отклонениями «усиливаются», и в это! проявляется все большая согласованность рангов.
6.4. Читатель может спросить: почему выбранный нами коэффициент меняет свои значения в границах от  до 1, а не от —1 до
до 1, а не от —1 до  как, например, коэффициент ранговой корреляции? Ответ заключается в следующем: когда имеется более двух экспертов, противоположные понятия согласованности и несогласованности утрачивают прежнюю
как, например, коэффициент ранговой корреляции? Ответ заключается в следующем: когда имеется более двух экспертов, противоположные понятия согласованности и несогласованности утрачивают прежнюю
Пример 6.1
Рассмотрим три последовательности рангов:
(см. скан)
Сумма квадратов отклонений равна 591. Подсчитаем теперь соответствующие величины Т:

Таким образом, из (6.8) получим:

Из этого непосредственно следует, что вносимая нами поправка на наличие связей в данном случае не оказывает существенного влияния на результаты.
6.8. Перейдем теперь к вопросу о том, как проверить существенность наблюдаемого значения  Если эксперты независимы друг от друга в своих суждениях, то та или иная система рангов столь же вероятна, как и любая другая. В связи с этим будем рассматривать распределения
Если эксперты независимы друг от друга в своих суждениях, то та или иная система рангов столь же вероятна, как и любая другая. В связи с этим будем рассматривать распределения  на множестве, состоящем из
на множестве, состоящем из  возможных систем рангов. Прибегая к обычным методам проверки статистических гипотез, будем полагать, что суждения экспертов не характеризуются общностью предпочтений.
возможных систем рангов. Прибегая к обычным методам проверки статистических гипотез, будем полагать, что суждения экспертов не характеризуются общностью предпочтений.
Действительно, существующие распределения  были исследованы лишь для малых
были исследованы лишь для малых  например, при
например, при  изменяющемся от 2 до 10; при
изменяющемся от 2 до 10; при  принимающем значения от 2 до 6; при
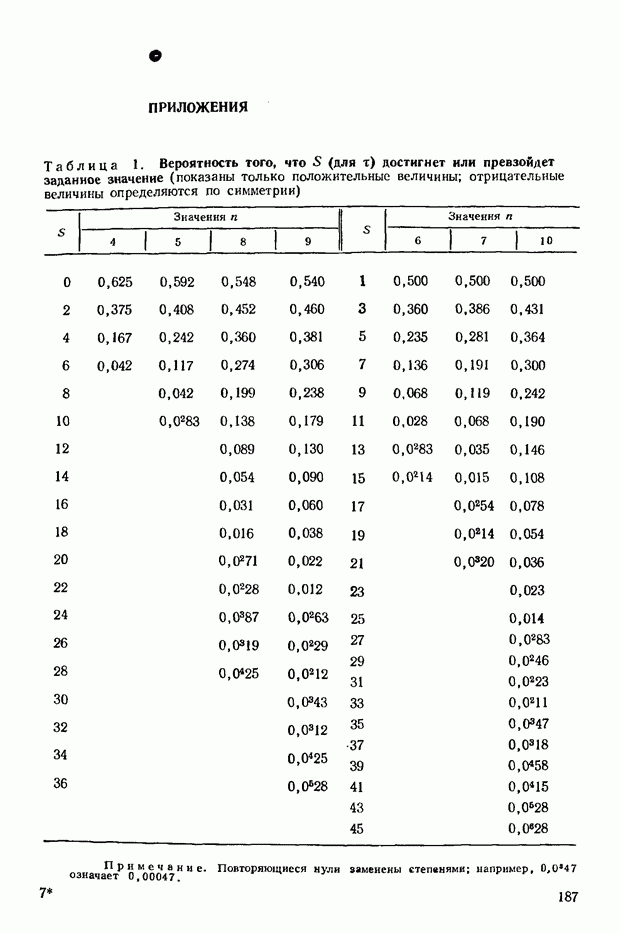
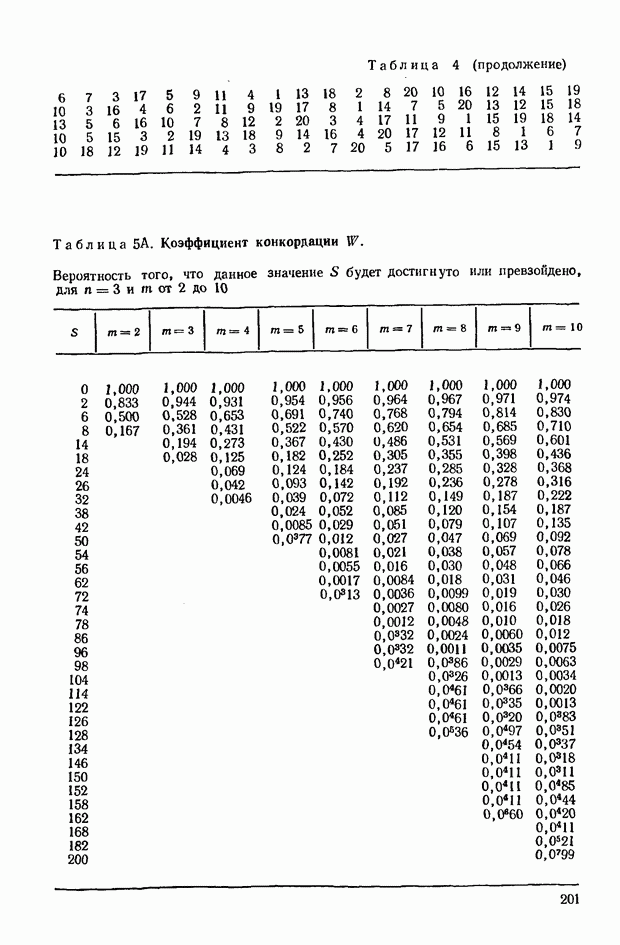
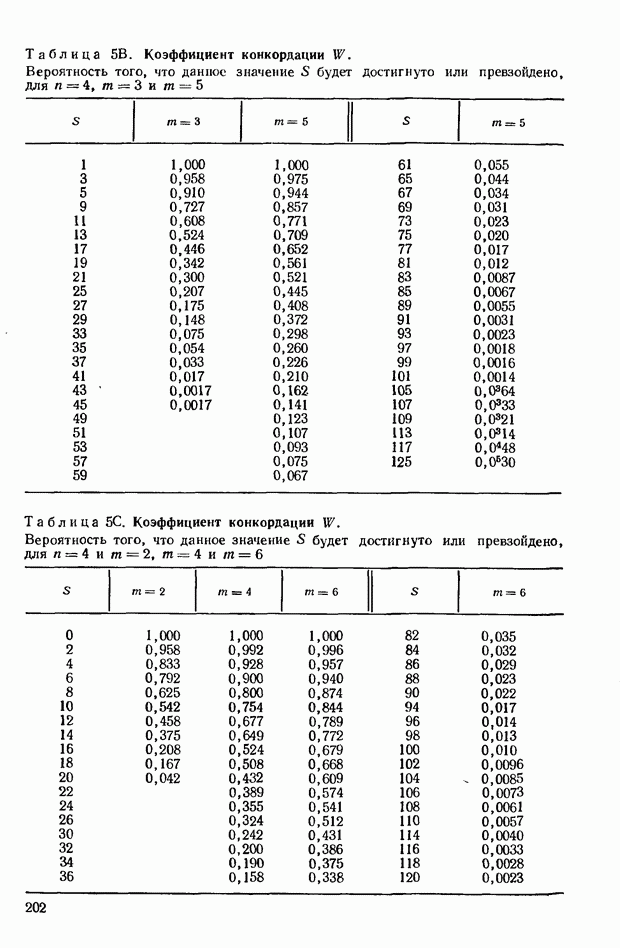
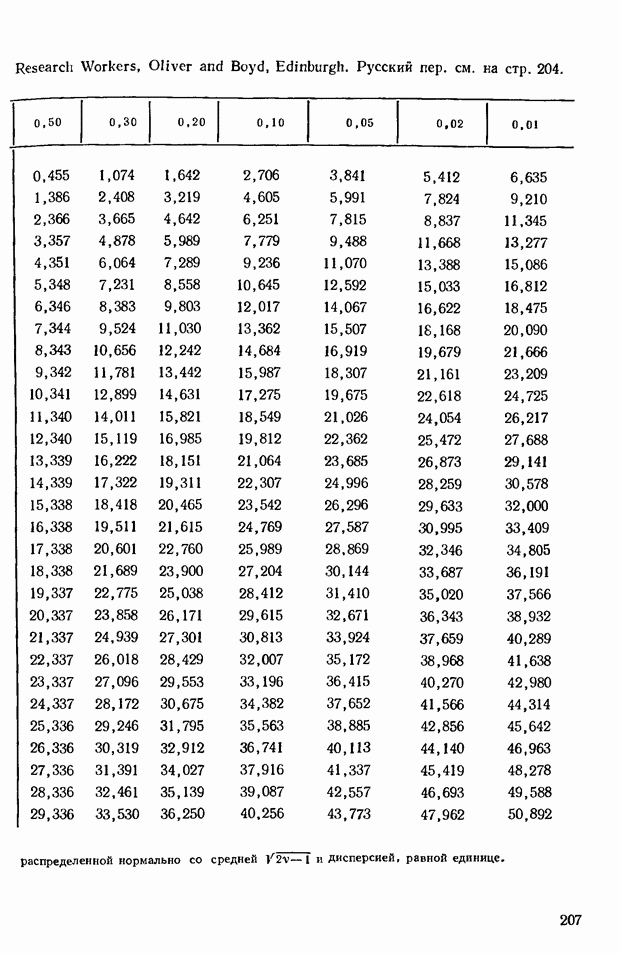
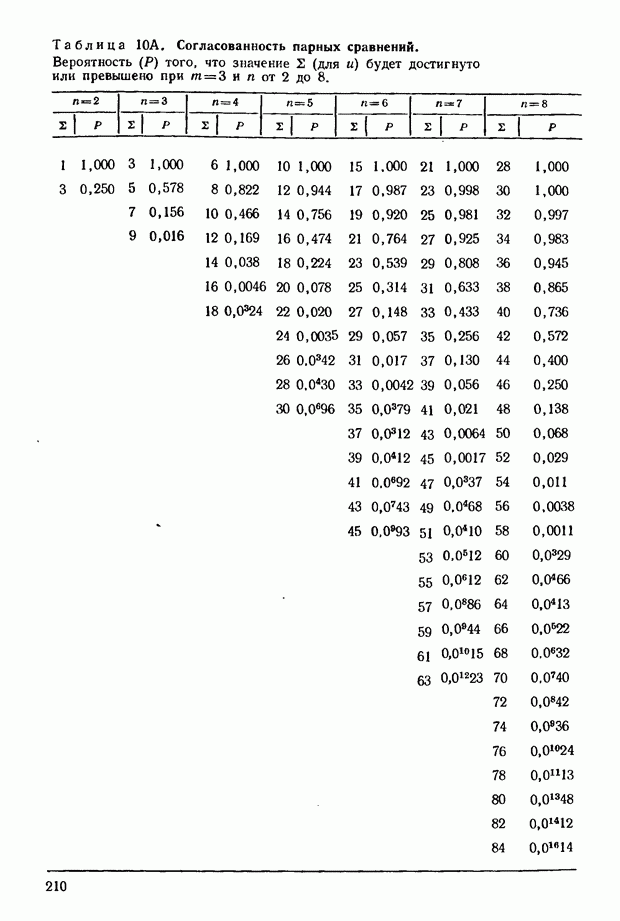
принимающем значения от 2 до 6; при  Соответствующие данные можно найти в табл. 5, приведенной в приложении.
Соответствующие данные можно найти в табл. 5, приведенной в приложении.
Для характеристики распределения при больших значениях  можно использовать следующие два приближенных метода вычислений.
можно использовать следующие два приближенных метода вычислений.
1. Если нам приходится иметь дело с любыми значениями, отличными от приведенных в табл. 5 приложения, мы можем прибегнуть к аппроксимации, основанной на использовании известного в статистике  -распределения Фишера. Будем полагать
-распределения Фишера. Будем полагать

Тогда, зная «степени свободы» и  можно проверить значение
можно проверить значение  пользуясь приведенными в ряде источников таблицами распределения Фишера. Можно, однако, обойтись без этого, прибегнув непосредственно к данным приведенной в приложении табл. 5; в ней содержатся значения
пользуясь приведенными в ряде источников таблицами распределения Фишера. Можно, однако, обойтись без этого, прибегнув непосредственно к данным приведенной в приложении табл. 5; в ней содержатся значения  соответствующие
соответствующие  уровням существенности величины
уровням существенности величины  если при этом
если при этом  принимает значения от 3 до
принимает значения от 3 до  от 3 до 7. Несколько ниже будет приведен пример, показывающий, как пользоваться этой таблицей.
от 3 до 7. Несколько ниже будет приведен пример, показывающий, как пользоваться этой таблицей.
2. Выше был предложен общий метод проверки; однако, если  можно прибегнуть к более простой процедуре. Будем полагать
можно прибегнуть к более простой процедуре. Будем полагать

В таком случае распределение  совпадает с известным в статистике распределением
совпадает с известным в статистике распределением  степенями свободы. Пример 6.2
степенями свободы. Пример 6.2
Предположим, что мы имеем дело с 18 последовательностями, каждая из которых содержит по 7 рангов. При этом значение  равно 1620, следовательно,
равно 1620, следовательно,

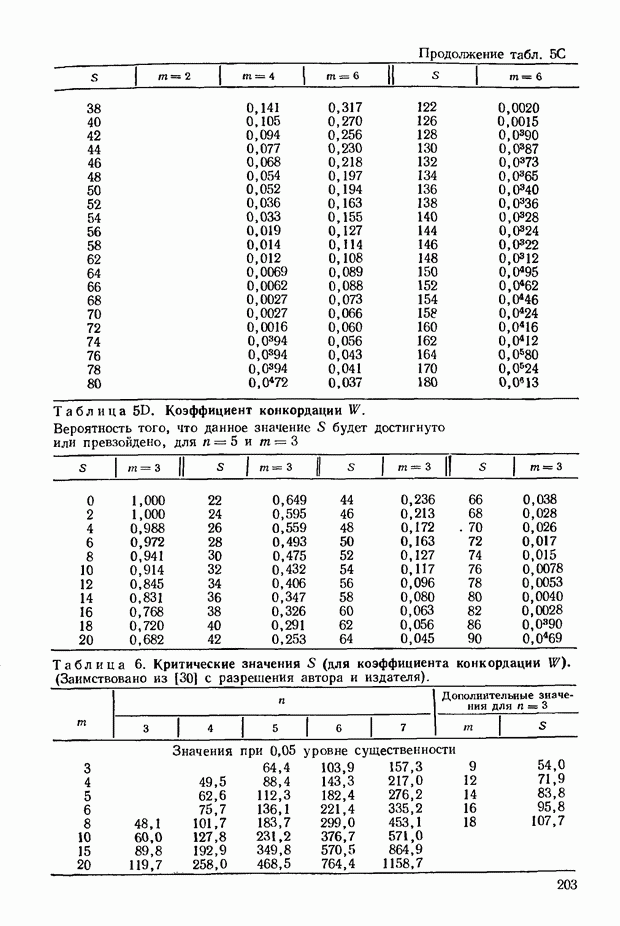
В табл. 6, приведенной в приложении, можно найти следующие величины  соответствующие
соответствующие  уровню существенности:
уровню существенности:

и величины 5, соответствующие  уровню существенности:
уровню существенности:

Величина  при
при  лежит между значениями, соответствующими
лежит между значениями, соответствующими  стало быть, рассчитанная нами величина
стало быть, рассчитанная нами величина  оказывается больше, чем табличное значение
оказывается больше, чем табличное значение  соответствующее
соответствующее  уровню существенности. Из этого следует, что вероятность получения числа, равного наблюдаемому или превосходящего его, составляет менее 0,01, или, как иногда говорят, значение лежит выше
уровню существенности. Из этого следует, что вероятность получения числа, равного наблюдаемому или превосходящего его, составляет менее 0,01, или, как иногда говорят, значение лежит выше  уровня. Таким образом, исчисленная величина существенна, если мы исходим из того, что столь малые вероятности могут характеризовать статистическую существенность. Пример 6.3
уровня. Таким образом, исчисленная величина существенна, если мы исходим из того, что столь малые вероятности могут характеризовать статистическую существенность. Пример 6.3
Пусть даны 28 последовательностей, каждая из которых содержит по 13 членов. При этом величина  и, следовательно,
и, следовательно,

Мы можем проверить эти вычисления, пользуясь методом (6.13). Действительно,

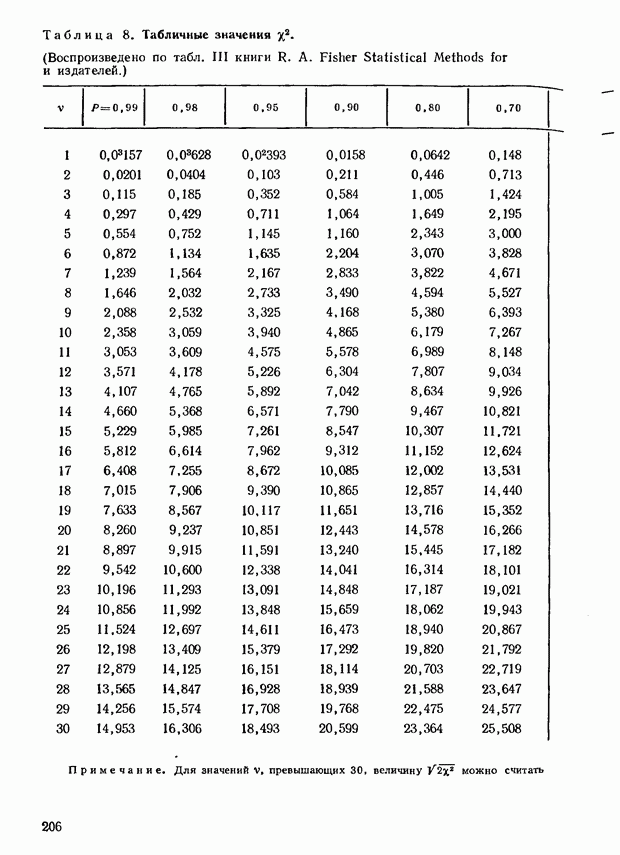
В приведенной в приложении табл. 8 можно найти соответствующую  уровню существенности величину при
уровню существенности величину при  степенях свободы
степенях свободы  Полученное нами значение несколько больше этого числа, стало быть, оно «в точности существенно» при уровне существенности в 1%. Пример 6.4
Полученное нами значение несколько больше этого числа, стало быть, оно «в точности существенно» при уровне существенности в 1%. Пример 6.4
На практике часто приходится иметь дело с ситуациями, когда  столь Еелико, что не имеет смысла делать поправки для всех промежуточных значений
столь Еелико, что не имеет смысла делать поправки для всех промежуточных значений  Если поправка все же требуется, ее можно ввести, добавив 2 к знаменателю и уменьшив на 1 числитель в формуле
Если поправка все же требуется, ее можно ввести, добавив 2 к знаменателю и уменьшив на 1 числитель в формуле

Рассмотрим в качестве примера случай, когда  предположим, что
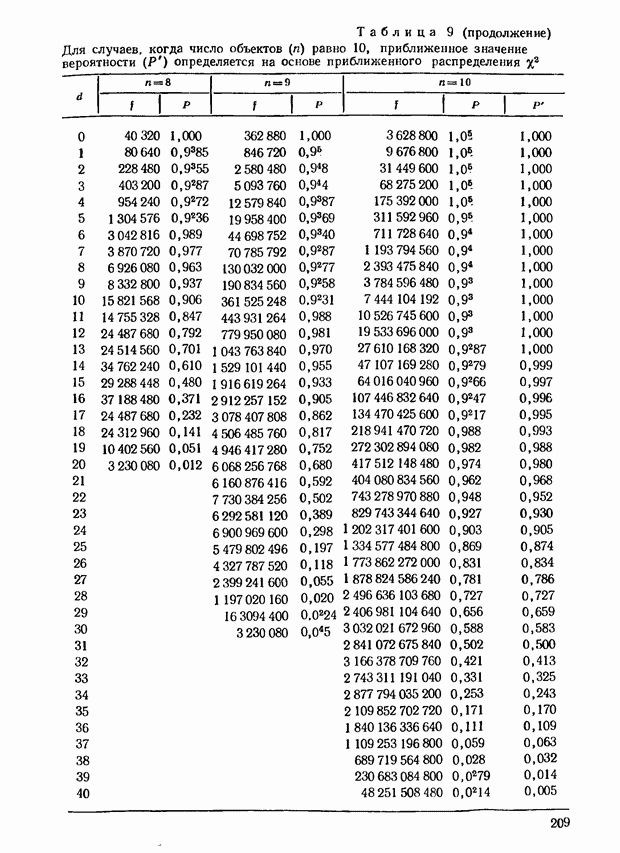
предположим, что  . С помощью приведенной в приложении табл.
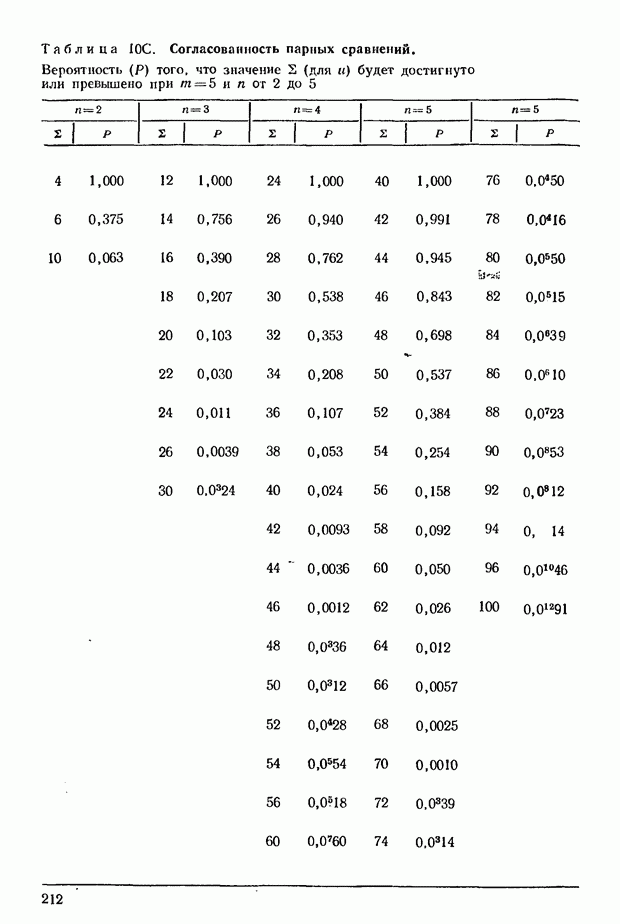
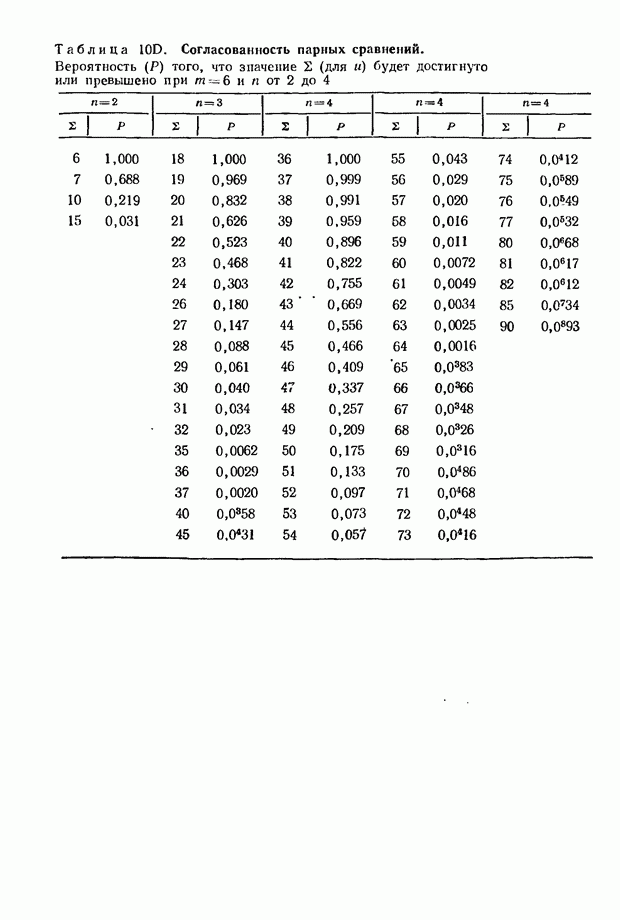
. С помощью приведенной в приложении табл.  можно выяснить, что вероятность такого или большего значения 5 равна 0,010, так что это приблизительно соответствует
можно выяснить, что вероятность такого или большего значения 5 равна 0,010, так что это приблизительно соответствует  уровню существенности. Предположим теперь, что, проверяя существенность этих данных, мы воспользовались
уровню существенности. Предположим теперь, что, проверяя существенность этих данных, мы воспользовались  -критерием. Тогда, введя поправку
-критерием. Тогда, введя поправку
на непрерывность значений, можно получить:

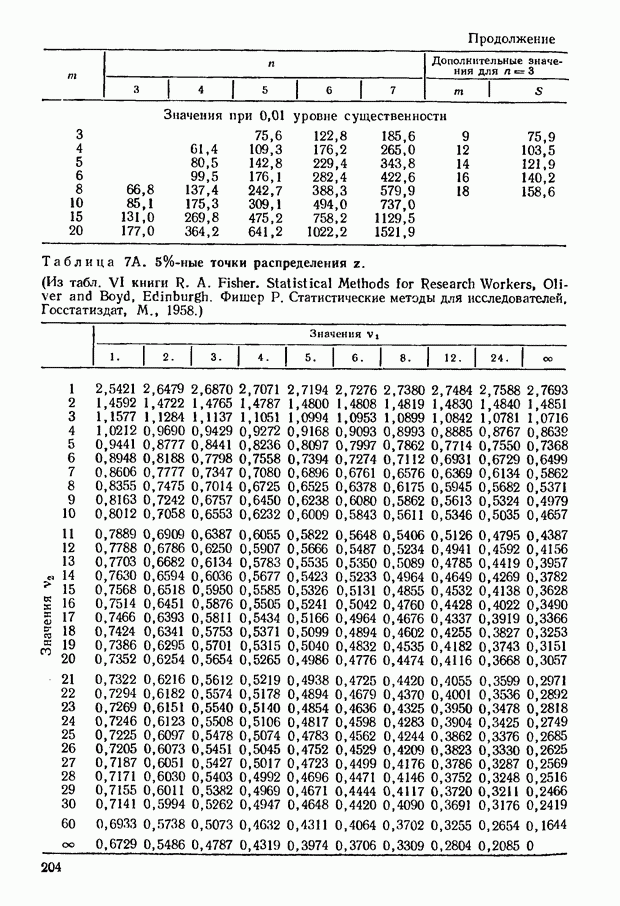
Проведя линейную интерполяцию указанных в приведенной в приложении табл. 7В обратных величин, мы можем по значениям  отыскать табличную величину
отыскать табличную величину  равную 0,954 (в то время как вычисленное нами значение равно 0,979). Даже при столь малом значении
равную 0,954 (в то время как вычисленное нами значение равно 0,979). Даже при столь малом значении  проверка по
проверка по  -критерию обеспечивает удовлетворительную аппроксимацию.
-критерию обеспечивает удовлетворительную аппроксимацию.
6.9. Наличие связей в последовательностях рангов не требует изменений в методах проверки по  -критерию, за исключением тех случаев, когда число связей велико или значительна их протяженность. В последнем случае процедура проверки усложняется. Обозначим через дисперсию, исчисленную для
-критерию, за исключением тех случаев, когда число связей велико или значительна их протяженность. В последнем случае процедура проверки усложняется. Обозначим через дисперсию, исчисленную для  последовательности, характеризуемой выражением
последовательности, характеризуемой выражением  Запишем выражение
Запишем выражение

причем суммирование производится по  значениям
значениям 
Тогда статистическая существенность  может быть проверена с помощью
может быть проверена с помощью  -критерия по формуле (6.11), причем в расчет числа степеней свободы вносятся следующие изменения:
-критерия по формуле (6.11), причем в расчет числа степеней свободы вносятся следующие изменения:

В таком случае соответствующее значение  может быть определено из формулы
может быть определено из формулы

Статистическая оценка
6.10. Теперь предположим, что исчисленный нами коэффициент  обладает статистической существенностью и, следовательно, можно полагать, что между оценками экспертов существует некоторая согласованность. Попытаемся сделать еще один шаг в указанном направлении: предположим, что можно более или менее точно упорядочить суждения экспертов в соответствии с некоторой объективной шкалой.
обладает статистической существенностью и, следовательно, можно полагать, что между оценками экспертов существует некоторая согласованность. Попытаемся сделать еще один шаг в указанном направлении: предположим, что можно более или менее точно упорядочить суждения экспертов в соответствии с некоторой объективной шкалой.
Тогда мы можем поставить следующий вопрос: как установить «подлинную» последовательность объектов или как можно получить наилучшую оценку такой «подлинной» последовательности?
6.11. Предположим, что мы имеем дело с тремя последовательностями, каждая из которых содержит по восемь рангов.

Нельзя ли упорядочить объекты, исходя из числа «первых мест», «вторых мест» и т. д., занимаемых каждым объектом в последовательностях различных экспертов? Например, мы могли бы приписать объекту С общую ранговую оценку 1, поскольку этот объект у двух экспертов был выдвинут на первое место. Объект  один раз занял первое место, и мы могли бы приписать ему общую ранговую оценку, равную 2. Затем обратимся к объектам, занявшим вторые места: объект В занял второе место у двух экспертов; поэтому ему приписывается общая ранговая оценка, равна трем. Один из экспертов отвел второе место С, но этот объект уже проранжирован. Затем переходим к объектам, занявшим третьи места, и т. д. В конечном счете получаем ряд:
один раз занял первое место, и мы могли бы приписать ему общую ранговую оценку, равную 2. Затем обратимся к объектам, занявшим вторые места: объект В занял второе место у двух экспертов; поэтому ему приписывается общая ранговая оценка, равна трем. Один из экспертов отвел второе место С, но этот объект уже проранжирован. Затем переходим к объектам, занявшим третьи места, и т. д. В конечном счете получаем ряд:

Два объекта  заняли четвертое место по одному разу, однако мы поставили
заняли четвертое место по одному разу, однако мы поставили  перед А, поскольку
перед А, поскольку  одного из оставшихся экспертов занял пятое место, а объект А у двух оставшихся экспертов занял лишь седьмое место.
одного из оставшихся экспертов занял пятое место, а объект А у двух оставшихся экспертов занял лишь седьмое место.
Однако от такого подхода приходится отказаться, поскольку он содержит внутренние противоречия. Предположим, мы начали упорядочение с другого конца, так что ранг 8 присвоен объекту, занявшему наибольшее число раз восьмое место. В таком случае рассматривавшиеся ранее объекты в конце концов окажутся расположенными в такой последовательности:

Полученные последовательности отличаются друг от друга. Вообще говоря, у нас нет особых причин для того, чтобы всегда начинать упорядочение с какого-то одного конца (а не с другого). Поскольку два способа применения рассмотренной процедуры упорядочения приводят к различным результатам, эту процедуру, разумеется, приходится признать неудовлетворительной.
6.12. Более эффективным оказывается метод упорядочения, основанный на использовании сумм рангов, приписываемых каждому
объекту. Следуя такой процедуре, можно заключить, что объект С в (6.17) обладает наименьшей суммой рангов, так что общий ранг можно положить равным единице, объект В занимает следующее место и т. д. В итоге получаем последовательность

которая, как нетрудно заметить, отличается от последовательности (6.18) и от последовательности (6.19).
Можно доказать (мы докажем это утверждение в следующей главе), что с точки зрения некоторого критерия, используемого обычно в расчетах по методу наименьших квадратов, такая оценка является «наилучшей».
Действительно, рассмотрим сумму квадратов разностей между действительно наблюдаемыми суммами рангов и значениями таких величин в ситуации, когда все последовательности совпадают между собой; эта сумма принимает минимальное значение в том случае, когда совокупные ранги оцениваются в соответствии с описанной выше процедурой. Кроме того, если измерить соответствие между построенной таким образом последовательностью рангов и наблюдаемыми последовательностями с помощью коэффициента  Спирмэна, среднее значение этого коэффициента окажется больше, чем при сравнении наблюдаемых последовательностей с любой другой построенной последовательностью рангов. Сравнение указанных последовательностей с помощью коэффициента
Спирмэна, среднее значение этого коэффициента окажется больше, чем при сравнении наблюдаемых последовательностей с любой другой построенной последовательностью рангов. Сравнение указанных последовательностей с помощью коэффициента  может не обнаружить такого свойства, однако если число сравниваемых между собой объектов не слишком велико, то приведенное выше утверждение оказывается верным и применительно к коэффициенту
может не обнаружить такого свойства, однако если число сравниваемых между собой объектов не слишком велико, то приведенное выше утверждение оказывается верным и применительно к коэффициенту 
6.13. Несколько слов следует сказать также в отношении проблемы связей рангов.
а. Если наблюдаемые последовательности не содержат связей и мы исключаем возможность, что такие связи все же существуют, в некоторых случаях могут возникать дополнительные проблемы.
Предположим, что некоторые три объекта были упорядочены следующим образом:

Сумма рангов всех трех объектов совпадает, наш метод не дает критерия, с помощью которого можно провести упорядочение. Если мы Допускаем наличие связей между рангами, то правомерно полагать, что все объекты имеют одинаковый ранг. Если все же возможность существования связей отвергается, то наиболее логичным
представляется следующее решение: мы отдаем предпочтение тому объекту, у которого ранги в наименьшей степени различаются. Так как суммы рангов одинаковы, приведенное выше утверждение эквивалентно такому: первое место приписывается объекту с наименьшей суммой квадратов рангов. В примере (6.21) суммы квадратов рангов для объектов  соответственно равны 164, 178, 176, так что их можно упорядочить следующим образом:
соответственно равны 164, 178, 176, так что их можно упорядочить следующим образом: 
Если рассматривать ранг объекта, равный  как выражение того факта, что
как выражение того факта, что  элементов последовательности получили предпочтение, то сумма рангов (за вычетом
элементов последовательности получили предпочтение, то сумма рангов (за вычетом  характеризует как бы сумму предпочтений и, следовательно, описанный метод позволяет ранжировать объекты в соответствии с предпочтениями. Если некоторые ранги связаны между собой, то замещение суммы рангов связями не искажает соотношений с другими членами группы, а просто снимает Еопрос о соотношении предпочтений внутри связанной группы. Таким образом, описанный метод позволяет упорядочить объекты в соответствии с предпочтениями даже в тех случаях, когда существуют связи.
характеризует как бы сумму предпочтений и, следовательно, описанный метод позволяет ранжировать объекты в соответствии с предпочтениями. Если некоторые ранги связаны между собой, то замещение суммы рангов связями не искажает соотношений с другими членами группы, а просто снимает Еопрос о соотношении предпочтений внутри связанной группы. Таким образом, описанный метод позволяет упорядочить объекты в соответствии с предпочтениями даже в тех случаях, когда существуют связи.
6.14. Мало разработана следующая проблема: как распределена величина  в случае, когда существует некоторая общность предпочтений. Поэтому мы не можем проверить статистическую существенность различий между системами, каждая из которых содержит несколько последовательностей рангов. Предположим, что каждый из 8 преподавателей-мужчин ранжировал учащихся в классе, состоящем из 30 мальчиков; результирующее значение
в случае, когда существует некоторая общность предпочтений. Поэтому мы не можем проверить статистическую существенность различий между системами, каждая из которых содержит несколько последовательностей рангов. Предположим, что каждый из 8 преподавателей-мужчин ранжировал учащихся в классе, состоящем из 30 мальчиков; результирующее значение  для всех последовательностей оказалось равным 0,5. Предположим также, что 6 преподавателей-женщин проранжировали учащихся того же класса, величина
для всех последовательностей оказалось равным 0,5. Предположим также, что 6 преподавателей-женщин проранжировали учащихся того же класса, величина  в этом случае оказалась равной 0,7. Приведенные значения показывают, что преподаватели-женщины обладают более общей системой предпочтений, чем преподаватели-мужчины; однако если мы будем рассматривать этих мужчин как выборку из всей совокупности учителей-мужчин (то же самое относится и к женщинам), то нет способа, с помощью которого удалось бы проверить статистическую существенность гипотезы о большей общности суждений преподавателей-женщин по сравнению с преподавателями-мужчинами. Здесь налицо пробел в наших знаниях, и было бы весьма полезным его заполнить.
в этом случае оказалась равной 0,7. Приведенные значения показывают, что преподаватели-женщины обладают более общей системой предпочтений, чем преподаватели-мужчины; однако если мы будем рассматривать этих мужчин как выборку из всей совокупности учителей-мужчин (то же самое относится и к женщинам), то нет способа, с помощью которого удалось бы проверить статистическую существенность гипотезы о большей общности суждений преподавателей-женщин по сравнению с преподавателями-мужчинами. Здесь налицо пробел в наших знаниях, и было бы весьма полезным его заполнить.
6.15. Методы статистической проверки гипотез в условиях существования связей между рангами пока, как отмечалось выше, мало разработаны; но в ряде случаев удается обнаружить важные эффекты, прибегнув к непосредственному анализу исходных данных. Если заранее (a priori) существует «подозрение», что вкусы внутри некоторой группы экспертов совершенно разнородны, объединение оценок различных экспертов в одну группу может привести к искажению выявленных предпочтений. Рассмотрим, например, предельный случай: десять экспертов оказались единодушными в своих оценках шести объектов, суммы рангов соответственно составляют:

так что  Предположим при этом, что десять других экспертов также совершенно одинаково оценили эти объекты, но суммы рангов оценки теперь расположены в противоположном порядке:
Предположим при этом, что десять других экспертов также совершенно одинаково оценили эти объекты, но суммы рангов оценки теперь расположены в противоположном порядке:

причем вновь  Рассмотрим теперь суммарные ранговые оценки всех 20 экспертов: для каждого объекта оценка, разумеется, равна
Рассмотрим теперь суммарные ранговые оценки всех 20 экспертов: для каждого объекта оценка, разумеется, равна  Из последнего расчета должен следовать вывод о том, что среди группы экспертов не существует никакой общности предпочтений, тогда как в действительности единодушие одной части экспертов полностью скрадывается общностью суждений другой группы экспертов.
Из последнего расчета должен следовать вывод о том, что среди группы экспертов не существует никакой общности предпочтений, тогда как в действительности единодушие одной части экспертов полностью скрадывается общностью суждений другой группы экспертов.
Неполные последовательности рангов
6.16. В ряде случаев приходится иметь дело с неполными последовательностями рангов. Представляют интерес, в частности, проблемы использования неполных последовательностей при планировании эксперимента, поскольку мы можем «сконструировать» такие неполные последовательности, которые будут обладать свойством симметрии.
Рассмотрим, например, стратегию предпринимателя, выпускающего мороженое. Он хотел бы выявить предпочтения покупателей относительно семи сортов мороженого, исходя из упорядочения суждений нескольких потребителей. При этом предприниматель может не захотеть давать на пробу каждому дегустатору все сорта мороженого — то ли потому, что он стремится экономить время, то ли потому, что вкус человека как бы «притупляется» после дегустации нескольких сортов мороженого. Назовем сорта  и образуем следующие группы, каждая из которых включает три сорта мороженого:
и образуем следующие группы, каждая из которых включает три сорта мороженого:

Будем полагать, что каждая группа, содержащая по три сорта, выражает предпочтения одного из семи дегустаторов. Смысл такого разбиения состоит в следующем: каждый объект подвергается экспериментальной оценке одинаковое число раз (в нашем случае оценивается трижды), кроме того, в эксперименте сопоставляется каждая пара объектов по одному разу, так что все элементы охвачены сопоставлением одинаковое число раз. Указанную систему можно рассматривать как семь последовательностей рангов семи объектов, но при этом в каждой последовательности отсутствуют оценки четырех элементов.
6.17. Предположим, что дегустаторы расположили свои оценки указанных выше сортов следующим образом:

Выпишем суммы рангов каждого из семи объектов:

Если бы индивидуальные ранговые оценки были случайно распределены между объектами, то существовала бы тенденция к выравниванию сумм рангов по различным группам; с другой стороны, если бы ранги однозначно соответствовали месту данного объекта при строгом упорядочении системы, то суммы рангов были бы равны соответственно  и различались бы между собой настолько, насколько это вообще возможно. Поэтому, как обычно, будем полагать, что
и различались бы между собой настолько, насколько это вообще возможно. Поэтому, как обычно, будем полагать, что  представляет собой сумму квадратов отклонений чисел, приведенных в последовательности (6.24), от их среднего значения; тогда можно построить коэффициент
представляет собой сумму квадратов отклонений чисел, приведенных в последовательности (6.24), от их среднего значения; тогда можно построить коэффициент  разделив эту сумму на максимальное значение
разделив эту сумму на максимальное значение  . В нашем примере численная величина
. В нашем примере численная величина  может быть определена следующим образом:
может быть определена следующим образом:

6.18. Схему эксперимента, подобную (6.22), называют квадратом Юдена. Если из общего числа объектов, равного  в эксперименте каждый раз представлено
в эксперименте каждый раз представлено  объектов и при этом любой из объектов участвует в эксперименте в общей сложности
объектов и при этом любой из объектов участвует в эксперименте в общей сложности  раз, то всего потребуется образовать
раз, то всего потребуется образовать  групп. При этом в каждой группе будет сопоставляться между собой
групп. При этом в каждой группе будет сопоставляться между собой  пар, следовательно, общее число таких сопоставлений составит
пар, следовательно, общее число таких сопоставлений составит  . Буквой
. Буквой  обозначим общее число групп, в которых встречается некая заданная пара элементов. В таком случае
обозначим общее число групп, в которых встречается некая заданная пара элементов. В таком случае

или

X — это целое число и поэтому произведение  должно содержать в качестве множителя число
должно содержать в качестве множителя число  Кроме того,
Кроме того,  должно нацело делиться на
должно нацело делиться на  Эти условия налагают существенные ограничения на числа, используемые при составлении такого рода
Эти условия налагают существенные ограничения на числа, используемые при составлении такого рода
схем. В приведенном выше примере  следовательно, должно делиться на 3 (в нашем примере оно просто было равно 3); поэтому из соотношения (6.25) следовало:
следовательно, должно делиться на 3 (в нашем примере оно просто было равно 3); поэтому из соотношения (6.25) следовало: 
Допустим, что в последовательностях рангов нет связей, обозначим через  ранг, приписанный
ранг, приписанный  объекту
объекту  экспертом (тем самым предполагается наличие
экспертом (тем самым предполагается наличие  блока, если данное разбиение на блоки однократно используется в эксперименте, и 1-х блоков, если эксперимент повторяется).
блока, если данное разбиение на блоки однократно используется в эксперименте, и 1-х блоков, если эксперимент повторяется).  будет означать сумму квадратов отклонений от среднего значения этих величин. Она принимает максимальное значение в том случае, когда суммы рангов распределяются по объектам следующим образом:
будет означать сумму квадратов отклонений от среднего значения этих величин. Она принимает максимальное значение в том случае, когда суммы рангов распределяются по объектам следующим образом:  следовательно, максимальное значение
следовательно, максимальное значение 
Таким образом, в общем случае

Не всегда легко ввести поправку, когда имеются связи, поэтому нам остается либо игнорировать их, если они не слишком многочисленны, либо просто «на глаз» приписать им некоторые суммарные ранги. Это не отразится на проверке существенности.
6.19. При ограниченном  и больших
и больших  статистическую существенность
статистическую существенность  можно проверить следующим образом: будем полагать, что величина
можно проверить следующим образом: будем полагать, что величина

распределена как  степенью свободы. Для более точной проверки можно использовать
степенью свободы. Для более точной проверки можно использовать  -распределение.
-распределение.

при

степенях свободы.
Если  следовательно,
следовательно,  эти выражения, как и следовало ожидать, сводятся к соотношениям (6.11) и (6.13). Пример 6.5 [19]
эти выражения, как и следовало ожидать, сводятся к соотношениям (6.11) и (6.13). Пример 6.5 [19]
Предположим, что мы трижды воспользовались планом эксперимента (6.22) и что в результате мы будем располагать 21 блоком оценок, каждый из этих блоков принадлежит соответствующему эксперту. Суммы рангов равны:

Исчисленная на основе этих данных средняя ранговая оценка равна  и, следовательно,
и, следовательно,  Таким образом,
Таким образом,

Для проверки существенности подставляем соответствующие числовые значения в (6.29) и (6.30).

В приведенной в приложении таблице  находим следующие значения для
находим следующие значения для 

Следовательно, полученная оценка характеризуется  -ным уровнем статистической существенности. Отсюда следует вывод, что такое упорядочение предпочтений не является случайным.
-ным уровнем статистической существенности. Отсюда следует вывод, что такое упорядочение предпочтений не является случайным.
Библиография
Квадраты Юдена списываются в [19]; в этой работе показано также, что «истинное» упорядочение в использовании сбалансированных планов указанного типа можно получить методом, описанным в 6.10 (упорядочение объектов проводится в соответствии с суммой приписанных им рангов). Подобная процедура обеспечивает минимизацию суммы взвешенных инверсий в наблюдаемых последовательностях рангов относительно оцененной последовательности.
Общий случай (когда в каждой из последовательностей может отсутствовать любое количество рангов) описан в работе [1].
Методы, изложенные в  применимы не только к квадратам Юдена, но ко всяким планам проведения эксперимента с неполными блоками, включая планы попарных сопоставлений. Более подробно эти вопросы рассматриваются в [19]. Эффективность этих методов анализируется в [109].
применимы не только к квадратам Юдена, но ко всяким планам проведения эксперимента с неполными блоками, включая планы попарных сопоставлений. Более подробно эти вопросы рассматриваются в [19]. Эффективность этих методов анализируется в [109].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ГЛАВА 1. ИЗМЕРЕНИЕ РАНГОВОЙ КОРРЕЛЯЦИИ
- ГЛАВА 2. ВВЕДЕНИЕ В ОБЩУЮ ТЕОРИЮ РАНГОВОЙ КОРРЕЛЯЦИИ
- ГЛАВА 3. СВЯЗАННЫЕ РАНГИ
- ГЛАВА 4. ПРОВЕРКА СУЩЕСТВЕННОСТИ
- ГЛАВА 5. ДОКАЗАТЕЛЬСТВА РЕЗУЛЬТАТОВ ГЛАВЫ 4
- ГЛАВА 6 ПРОБЛЕМА m ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- ГЛАВЛ 7. ДОКАЗАТЕЛЬСТВО РЕЗУЛЬТАТОВ ГЛАВЫ 6
- ГЛАВА 8. ЧАСТНАЯ РАНГОВАЯ КОРРЕЛЯЦИЯ
- ГЛАВА 9. РАНГИ И ЗНАЧЕНИЯ ПРИЗНАКА
- ГЛАВА 10. ДОКАЗАТЕЛЬСТВО РЕЗУЛЬТАТОВ ГЛАВЫ 9
- ГЛАВА 11. ПАРНЫЕ СРАВНЕНИЯ
- ГЛАВА 12. ДОКАЗАТЕЛЬСТВО ТЕОРЕМ, ПРИВЕДЕННЫХ В ГЛАВЕ 11
- ГЛАЗА 13. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЯ