ГЛАВЛ 7. ДОКАЗАТЕЛЬСТВО РЕЗУЛЬТАТОВ ГЛАВЫ 6

7.1. Рассмотрим следующий вопрос: насколько правомерно использовать -распределение для статистической проверки существенности коэффициента конкордации на множестве возможных последовательностей рангов. Поскольку нам потребуются некоторые общие результаты, предполагающие наличие связанных последовательностей, мы приведем здесь, следуя [78], постановку задачи в общем виде.

7.2. Предположим, что нам дано последовательностей чисел:

В дальнейшем будем полагать, что каждое число характеризует отклонение от среднего значения элементов соответствующей строки, следовательно, средняя из элементов любой строки и среднее значение всех чисел данного массива равны нулю. В таком случае мы можем записать:

Знаменатель этой дроби представляет собой постоянную величину, так что изменения коэффициента могут быть связаны только с изменениями в числителе дроби. Обозначим через вторые моменты строк, содержащих элементы с и в этом случае знаменатель рассматриваемой дроби можно записать так: Кроме того, введем

следующие обозначения:

причем представляет собой обозначение любого при всех возможных сочетаниях элементов Тогда записывается следующим образом:

Теперь определим моменты: сначала для затем для наконец, для

7.3. Буквой будем обозначать математическое ожидание соответствующих величин. В этом случае

Аналогично можно показать (промежуточные вычисления опущены), что

где символ обозначает третий момент а и где характеризуют ее третью и четвертую -статистику, которые можно выразить через соответствующие моменты:

Смысл применения -статистик состоит в следующем: для совокупностей нормально распределенных величин все -статистики выше второго порядка обращаются в нуль; поэтому можно полагать, что для достаточно близких к нормальному распределений значения -статистик будут малы.

7.4. Прежде чем приступить к вычислению моментов для отметим, что всех значениях индексов, за исключением случаев, когда если только значения индексов не образуют «замкнутой» последовательности типа Если рассматривается произведение, содержащее четыре множителя, то аналогичным образом в нуль не будут обращаться лишь те из них, индексы которых образуют замкнутую последовательность Следовательно,

Далее

Следовательно,

и, опуская промежуточные вычисления, выпишем конечные результаты:

Наконец, перейдем к рассмотрению моментов

обозначим эту величину

Пренебрегая слагаемыми, содержащими (поскольку они представляют собой величины меньшего порядка относительно можно утверждать, что

7.6. Теперь рассмотрим случай, когда не существует связей. В таком случае дисперсии всех последовательностей равны между собой и, следовательно,

Рассмотрим теперь распределение

Первые два момента равны:

Приравняв между собой соотношения (7.17) и (7.22), а также (7.18) и (7.23), можно найти, что

Таким образом, распределение служит аппроксимацией распределения (7.21), если принимают указанные значения Для (7.21) третий момент равен.

Сопоставляя это выражение с (7.19), можно видеть, что для величин, характеризующихся распределением (7.21), третий момент можно полагать приблизительно равным третьему моменту если только произведение не представляет собой малой величины. Аналогичным образом вычисляем четвертый момент для (7.21), равный

где Это выражение приблизительно равно четвертому моменту если только произведение принимает достаточно большие значения.

7.6. Таким образом, два первых момента распределения (7.21) всегда в точности совпадают с соответствующими моментами действительного распределения а третий и четвертый моменты распределения (7.21) приблизительно равны соответствующим моментам в связи с этим мы предполагаем, что распределение (7.21) достаточно хорошо аппроксимирует действительное распределение На самом деле точность аппроксимации выше, чем можно было бы предположить, глядя на приведенные выше довольно громоздкие доказательства.

В теоретической статистике распределение (7.21) называют -распределением или распределением типа . С помощью несложных преобразований можно свести это распределение к -распределению Фишера. Действительно, полагая

находим, что выражение (7.21) приводится к виду:

т. е. к распределению Фишера, при

Таким образом, из (7.24) следует

что совпадает со значениями, которые были приведены в формуле (6.12).

7.7. Более подробно следует рассмотреть случай, когда имеют место связи.

а. В предыдущих рассуждениях мы пользовались отсутствием связей лишь тогда, когда вычисляли величины так что если последовательности имеют одинаковые связи, то дисперсии по-прежнему будут оставаться равными друг другу и наши выводы сохраняют справедливость.

б. Если числа соответствующие связям, малы по сравнению с величиной то процедура статистической проверки не требует изменений. Тогда, ограничиваясь лишь теми слагаемыми, которые содержат в первой степени, можно записать:

Таким образом, с указанной выше степенью точности можно полагать, что второй момент остается неизменным. Влияние связей на величину третьего и четвертого моментов при заданном порядке величин также пренебрежимо мало. Из этого следует, что приведенные выше выводы сохраняют свое значение.

в. Если числа велики, то нам придется вычислить . В таком случае

Следовательно, можно использовать описанную выше процедуру статистической проверки, подставив соответствующие значения и Докажем теперь, что распределение величин

с ростом стремится к распределению

при

Обратимся к суммам элементов любого столбца из (7.1). Рассмотрим, например, сумму элементов первого столбца, обозначив ее буквой Тогда

Порядок равен а порядок равен . С помощью рассуждений, аналогичных приведенным в (5.21), можно показать, что выражение имеет меньший порядок и что главный член в выражении образует сумма Таким образом, в пределе нечетные моменты обращаются в нуль и

Если все элементы а равны между собой или близки к этому, то

и, следовательно, распределение величин стремится к нормальному распределению с нулевой средней.

Обозначим через сумму случайных величин подчиненных только одному ограничению: Тогда значения распределены как степенями свободы, причем представляет собой коэффициент, определяемый из следующего условия: средняя величина равна среднему значению Однако

таким образом,

и, следовательно, величины

распределены по закону

Если последовательности рангов не содержат связей, то дисперсия любой из них равна откуда следует, что

что совпадает с выражением (7.26).

Если имеют место связи, характеризующиеся соответствующими числами то определяется из следующего выражения:

Если связи не имеют широкого распространения, то второй член в знаменателе оказывает сравнительно малое влияние на величину

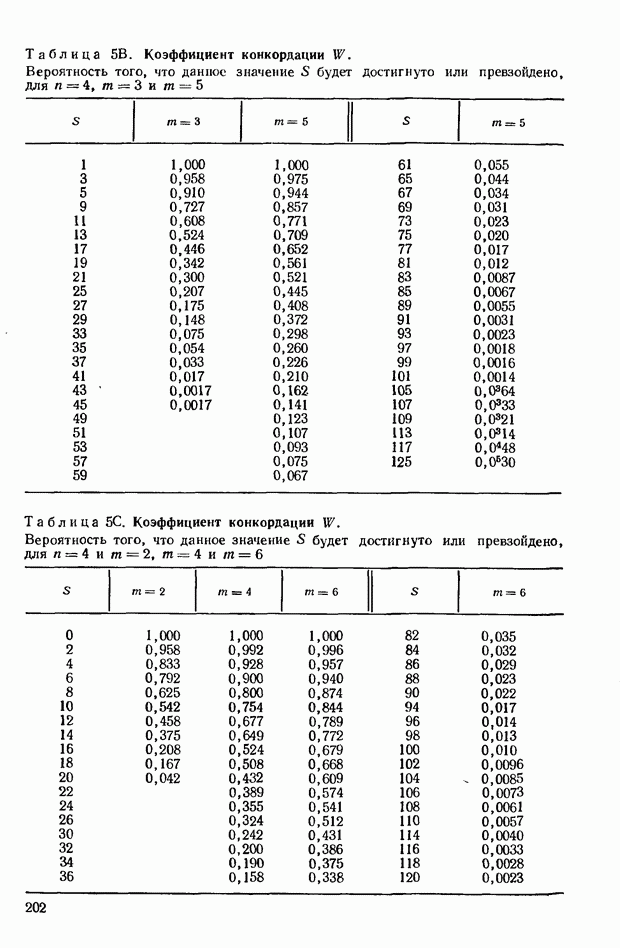
7.9. Теперь изложим основное содержание методов, с помощью которых рассчитывается действительное распределение или — эквивалентная задача — распределение 5 при условии, что значения невелики.

Заметим, что при можно воспользоваться -распределением Спирмэна. Будем исходить из того, что нам даны требуется рассмотреть переход к значениям Пусть, например, при заданы следующие значения сумм рангов (измеренных относительно средней):

Здесь —2; 1; 1 и 2; —1; —1 можно полагать идентичными, поскольку величины рассчитанные для этих последовательностей, совпадают между собой; они будут играть одинаковую роль и после рассматриваемого ниже перехода к

При приведенные выше типы могут быть прибавлены к шести перестановкам из —1, 0, 1; например, на основе типа —2, 0,2 появятся следующие типы: . Эти типы будут появляться также при переходе каждого из остальных «базисных» типов к . В результате мы получили

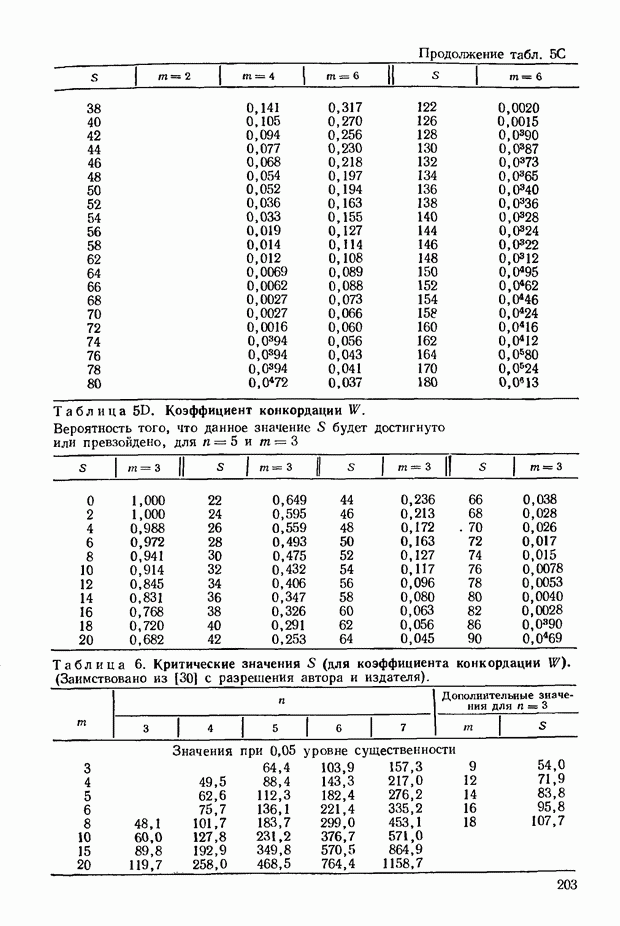
При равном пяти или превышающем 5, трудоемкость расчетов резко возрастает в связи с тем, что на каждом этапе приходится принимать во внимание все большее число различных типов. И все же в обычных

задачах, связанных со статистической проверкой существенности, вероятно, можно полагать, что при достаточно больших значениях -распределение служит достаточно точной аппроксимацией.

7.10. Теперь мы можем показать, что предложенный метод оценивания (как отмечалось в 6.12) максимизирует среднее значение коэффициента корреляции между оцениваемыми и наблюдаемыми последовательностями.

Предположим, что оцениваемая последовательность имеет вид а суммарные ранги равны Тогда среднее значение коэффициента можно получить из следующего выражения:

где представляет собой ранг объекта в последовательности. Это выражение равносильно следующему:

Ясно, что это выражение достигает максимальной величины в том случае, когда наибольшее значение принимает т. е. когда наибольшее 5 умножается на наибольшее X, затем эта процедура продолжается до тех пор, пока наименьшее не умножается на наибольшую величину Предполагавшееся выше правило оценивания, по существу, обеспечивает необходимый для максимизации порядок умножения, а отсюда непосредственно следует требуемый результат.

Рассмотрим теперь сумму

Поскольку первые два члена в правой части представляют собой постоянные величины, достигает минимума в том случае, когда принимает максимальное значение. Поэтому наш метод оценивания основан на минимизации или, другими словами, мы минимизируем сумму квадратов разностей между действительными значениями сумм и значениями которые они принимают в том случае, когда все последовательности совпадают между собой.

7.11. Теперь выясним методы статистической проверки существенности в случае неполных последовательностей рангов, рассматривавшихся в 6.16. Придерживаясь прежних обозначений, будем исходить из того, что

Тогда, поскольку

можно определить с помощью следующего выражения:

В приведенном выражении объект встречается дважды: он фигурирует в оценках экспертов причем величина любого элемента из одной группы не зависит от элементов содержащихся в любой другой группе. Следовательно,

и

Первая сумма в этом выражении содержит слагаемых, математическое ожидание каждого из этих слагаемых равно Во вторую сумму, фигурирующую в выражении (7.34), входят произведения таких элементов х, у которых и 1-й объекты совместно встречаются лишь в различных группах.

Далее,

в тех случаях, когда и 1-й объекты входят в одну и ту же группу; вместе с тем равно нулю во всех остальных случаях. Общее число случаев, когда и 1-й объекты входят в одну группу, равно Подставив приведенные данные в выражение (7.34), можно получить

Таким образом,

7.12. Следует отметить, что третий и четвертый моменты мы не можем вычислить тем же способом, который использовался при определении обычных коэффициентов. Ведь ранее можно было воспользоваться свойством симметрии, поскольку объекты или пары объектов

появлялись одинаково часто. При переходе к наборам, содержащим три объекта, или к более сложным системам симметричность исчезает, однако по аналогии с величинами можно полагать (отчасти исходя из эвристических соображений), что в обычном случае рассматриваемое нами распределение совпадает с распределением (7.21), а первый и второй моменты нашей совокупности можно приравнять соответственно (7.36) и (7.37). В таком случае можно записать следующие соотношения:

Из этого непосредственно вытекает методика проверки, предлагавшаяся в 6.19.

7.13. Положим, с тем, чтобы обеспечить наибольшее соответствие распределения величин -распределению с степенями свободы. В таком случае

Из этого следует, что, исключив а, мы можем записать выражение для

Отсюда видно, что распределение этих величин стремится к распределению степенями свободы. Дисперсия нашего выражения равна:

т. е. приблизительно равна:

При больших этой формуле будет соответствовать соотношение (7.37).

Библиография

Здесь можно вновь сослаться на статьи, упоминавшиеся в библиографии к предшествующей главе, а также указать работы [78], 1113], [50] и [51].