ГЛАВА 4. ПРОВЕРКА СУЩЕСТВЕННОСТИ

4.1. Последовательности, с которыми мы имеем дело на практике, обычно основываются на совокупности объектов, которая сама является лишь выборкой из более многочисленной совокупности. Так, возможность измерения взаимосвязи между математическими и музыкальными способностями в данной группе учеников представляет определенный интерес, однако существенно больший интерес заключается в возможности ответить на вопрос, в какой мере результат, полученный на основе выборки, проливает свет на взаимосвязь в исходной совокупности, если данная группа учеников отобрана случайно. В этой главе рассмотрим следующий вопрос: с какой степенью надежности мы можем полагаться на заключение о том, что в совокупности, из которой произведен отбор, существует корреляция, если получен некоторый выборочный коэффициент корреляции рангов. Короче, мы попытаемся проверить существенность наблюдавшихся корреляций рангов в свете статистической теории выборки.

4.2. Предположим, что в представленной совокупности нет взаимозависимости между двумя изучаемыми качествами. Тогда, если выборка случайная, какая-либо последовательность качественных характеристик А должна появиться в сочетании с данной последовательностью В как, вероятно, любая другая последовательность. Если мы приняли любое произвольное расположение В (не имеет значения, какое, поэтому возьмем натуральный ряд чисел, т. е. то все возможных последовательностей чисел от 1 до для А являются одинаково вероятными. Соответственно каждое из них имеет вероятность (в данном случае ограничимся случаем, когда связи отсутствуют).

Каждой возможной последовательности А теперь корреспондирует некоторое значение тир. Совокупность таких величин, общим числом может быть сгруппирована в соответствии с действительными значениями или которые охватывают диапазон от —1 до Результат такой группировки называют распределением частот. Это распределение является фундаментальным в настоящем исследовании, и мы рассмотрим некоторые его частные свойства.

4.3. При ранжировании четырех единиц наблюдения существует 24 возможных последовательности. Если читатель выпишет их и сопоставит с натуральным рядом чисел 1, 2, 3, 4, то получит следующие значения

Таким образом, наибольшая частота значений равная 6, соответствует Данное распределение симметрично относительно этой величины; когда абсолютное значение превышает 0, частоты падают до единицы.

4.4. Такого же рода распределение для имеет следующий вид (ниже приводится только нулевое и положительные значения 5, частоты отрицательных значений симметричны относительно приведенных ниже величин).

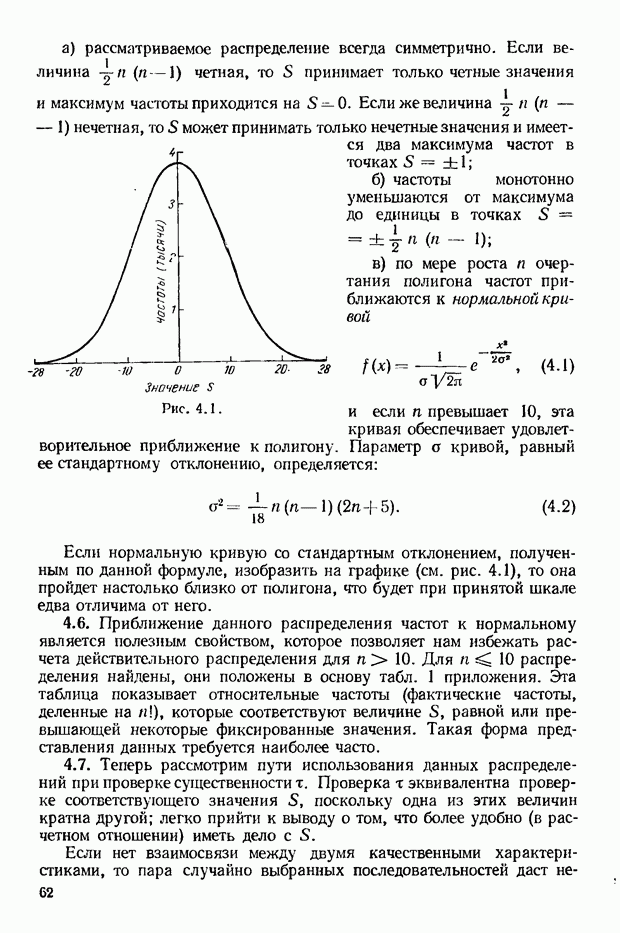
На рис. 4.1 показан график частот этого распределения; здесь частоты показаны в виде ординат соответствующих абсцисс

Опять нами найдено, что максимальное значение приходится на затем при росте 5 значение частоты неуклонно падает.

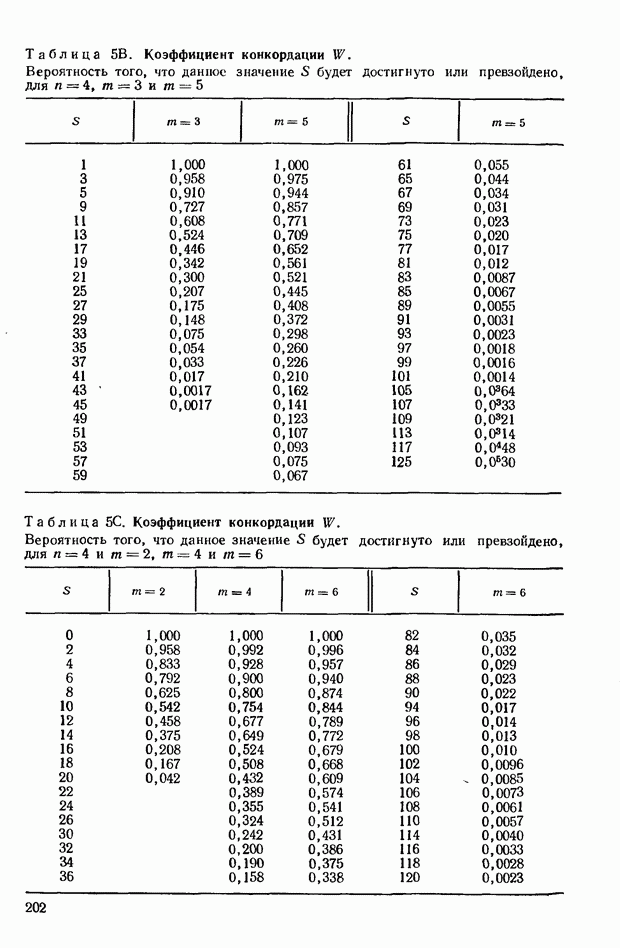
4.5. В следующей главе мы покажем, как получить такие распределения для различных значений Здесь же мы утверждаем без доказательства следующее:

а) рассматриваемое распределение всегда симметрично. Если величина четная, то принимает только четные значения и максимум частоты приходится на Если же величина нечетная, то может принимать только нечетные значения и имеется два максимума частот в точках

б) частоты монотонно уменьшаются от максимума до единицы в точках

в) по мере роста очертания полигона частот приближаются к нормальной кривой

и если превышает 10, эта кривая обеспечивает удовлетворительное приближение к полигону. Параметр о кривой, равный ее стандартному отклонению, определяется:

Если нормальную кривую со стандартным отклонением, полученным по данной формуле, изобразить на графике (см. рис. 4.1), то она пройдет настолько близко от полигона, что будет при принятой шкале едва отличима от него.

Рис. 4.1.

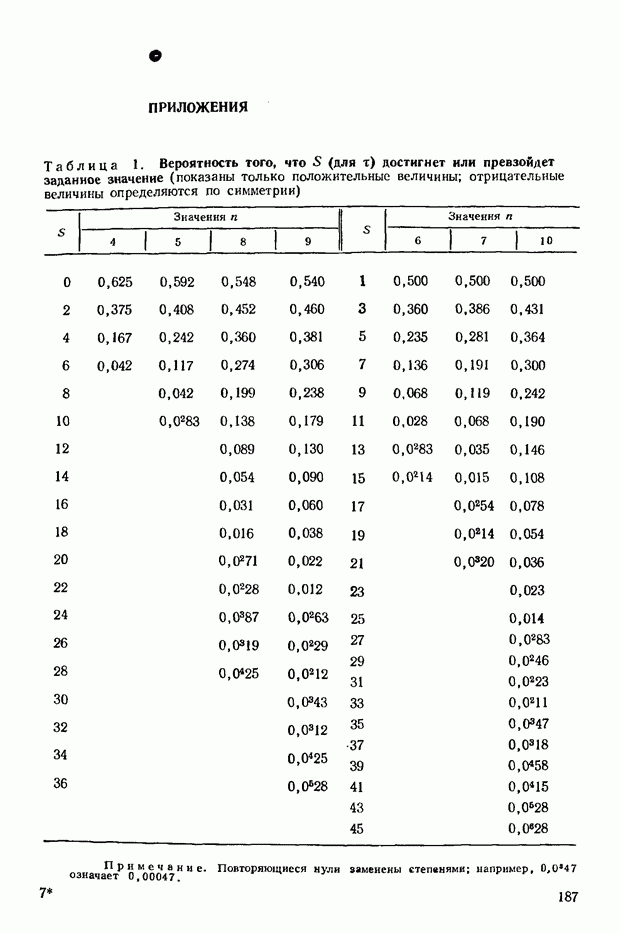
4.6. Приближение данного распределения частот к нормальному является полезным свойством, которое позволяет нам избежать расчета действительного распределения для Для распределения найдены, они положены в основу табл. 1 приложения. Эта таблица показывает относительные частоты (фактические частоты, деленные на которые соответствуют величине равной или превышающей некоторые фиксированные значения. Такая форма представления данных требуется наиболее часто.

4.7. Теперь рассмотрим пути использования данных распределений при проверке существенности Проверка эквивалентна проверке соответствующего значения 5, поскольку одна из этих величин кратна другой; легко прийти к выводу о том, что более удобно (в расчетном отношении) иметь дело с

Если нет взаимосвязи между двумя качественными характеристиками, то пара случайно выбранных последовательностей даст

некоторое значение лежащее в пределах . Подавляющая часть таких значений будет концентрироваться вокруг нуля. Примем следующий критерий: если наблюдаемые значения таковы, что весьма маловероятно, чтобы такое или большее абсолютное значение могло появиться случайно, то мы отклоняем гипотезу о том, что данные две качественные характеристики являются независимыми. Иначе говоря, если наблюдаемое значение 5 лежит в «хвостах» распределения далеко от средней, то мы отвергнем эту гипотезу. Решение вопроса о том, где провести линии, для того чтобы отделить «хвосты», или, что является весьма маловероятным, дело соглашения. Обычно вероятность 0,05 или 0,01 считают малой, очень малой. Иногда говорят «пятипроцентный уровень вероятности Это означает, что некоторое значение 5 достигают или превышают с вероятностью 0,05, аналогично употребляют выражения «однопроцентный уровень вероятности» и -процентный уровень вероятности». Соответствующие значения 5 могут быть определены, например, как «пятипроцентный предел существенности». Фраза «наблюденные 5 лежат вне пятипроцентного предела существенности» означает, что вероятность появления такого или большего (абсолютного) значения 5 меньше, чем 0,05.

Если мы заранее подозреваем существование положительной корреляции, то можно рассматривать вероятность того, что 5 лежит только в верхнем «хвосте» распределения; аналогично можно ограничиться только нижним «хвостом», если ожидается отрицательная корреляция. Это равнозначно расчету вероятности того, что 5 достигает некоторого заданного значения его, или превышает, или, как это иногда бывает, падает ниже какой-нибудь величины вместо того, чтобы достигать или превышать некоторое число без учета его знака.

Пример 4.1

Для случайной выборки, давшей последовательность из 10 объектов, найдено значение равное —0,11. Является ли эта величина существенной?

Соответствующее значение равно —5. Из табл. 1 приложения видно, что доля последовательностей, которые дают значение —5 и меньше, и больше составляет 0,364, взятое дважды, т. е. 0,728. Эта значительная величина, и мы не можем отвергнуть гипотезу независимости двух качественных характеристик. Другими словами, наблюденная величина не является существенной. Она могла появиться случайно в ходе выборки из исходной совокупности, в которой математические и музыкальные способности не находятся во взаимосвязи.

Если найденное значение было бы равно что соответствует то вероятность того, что (больше или равно 25 по абсолютной величине) составит 0,028. Это незначительная вероятность; следовало бы прийти к выводу о том, что способности не являются независимыми в исходной совокупности.

Мы основывали наше заключение на абсолютных значениях представляется, что такой подход является наилучшим, осооенно тогда, когда выборочное распределение симметрично. Однако, если необходимо, заключение можно основывать на фактических значениях. Если вероятность того, что 5 больше, чем некоторая абсолютная величина равна то это записывается так:

Вероятность Тогда вероятность того, что (где положительная величина), равна этому равна и вероятность того, что отрицательная величина). Например, для вероятность а для вероятность

Пользуясь таблицами вероятностей, читатель должен помнить, какая вероятность рассматривается. Так, -ный предел, который применяется для абсолютного значения, представляет собой лишь -ный предел для фактической величины.

Поправка на непрерывность

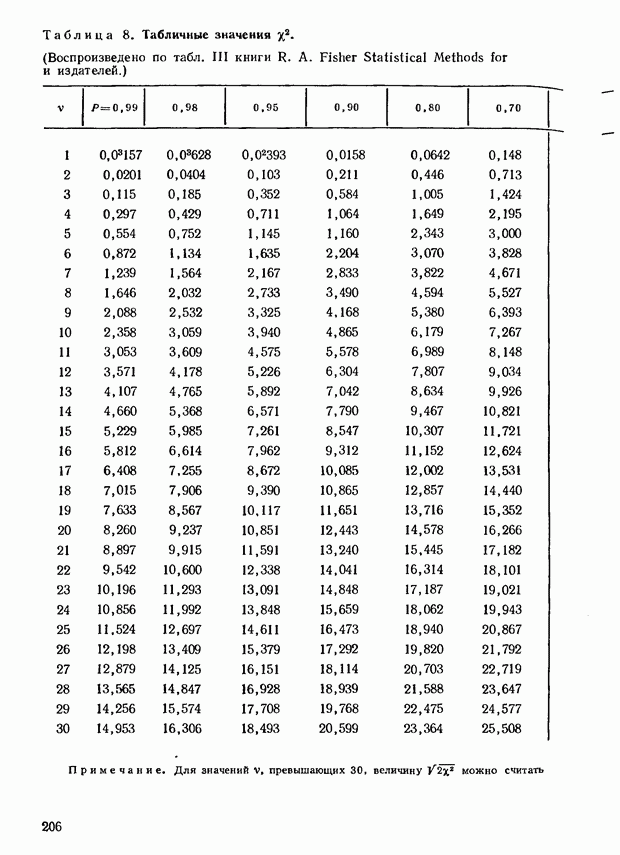
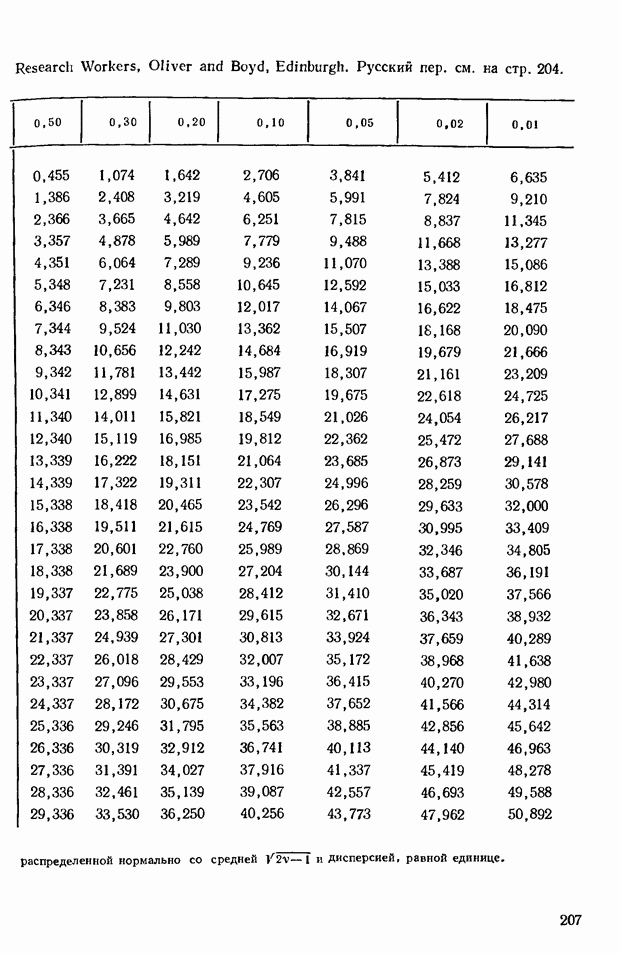
4.8. Если больше 10, то мы применяем таблицу площадей под нормальной кривей как приближение к точным значениям распределения Соотгегствующие площади даны в табл. 3 приложения. Они характеризуют вероятность гого, что данное число стандартных отклонений (а не абсолютная величина) будет достигнуто или превышено. Полезно запомнить, что у нормального распределения вероятность превышения в 1,96 раза абсолютного значения стандгртного отклонения равна 0,05, вероятность превышения стандартного отклонения в 2,58 раза составит 0,01 и превышения в 3,3 раза — 0,001.

При применении этой таблицы следует помнить, что мы заменяем распределение которое дискретно, непрерывным распределением, отличающимся от первого "на две единицы. Для того чтобы улучшить приближение, будем считать, что частота относящаяся к не сконцентрирована в точке а равномерно распределена на протяжении с до Для того чтебы сопоставить с площадями нормальной кривой, примем, что «хвост» распределения начинается в точке иначе говоря, мы вычтем единицу из наблюдаемого 5, если оно положительно (и прибавим единицу, если оно отрицательно), прежде чем выразим этот показатель в стандартных отклонениях. Данная процедура

известна как «поправка на непрерывность». Следующий пример прояснит эту процедуру.

Пример 4.2.

Для двух ранжирований 20 объектов получено значение равное 58, соответственно Является ли эта величина существенной?

На основе (4.2) находим:

Для скорректированного на непрерывность, получим величину 57, и, следовательно,

В табл. 3 приложения находим, что вероятность отклонения меньшего чем 1,85 а составляет около 0,9678. Вероятность того, что отклонение будет равно или превысит эту величину, найдем как Эта величина небольшая, но не очень. Мы подозреваем, что наблюдаемое значение является существенным, однако мы не можем прийти к вполне определенному решению.

Попробуем теперь сравнить величину, которую дает нормальное приближение при Предположим, что наблюдаемое 5 равно 20, соответственно На основе (4.2) имеем:

При корректировке на непрерывность получим:

Как видно из табл. 3 приложения, вероятность того, что эта величина будет достигнута или превзойдена по абсолютному значению, равна примерно 0,048. Точное значение, взятое из табл. 1 приложения, равно 0,044. Если бы мы не произвели поправку на непрерывность, то нашли бы, что искомое значение равно 0,037.

4.9. Формула (4.2) для стандартной ошибки требует некоторой перестройки для случаев, когда имеются связи. Если связи охватывают членов в одной последовательности и и в другой, то дисперсия распределения, полученного коррелированием одной последовательности со всеми возможными вариантами второй

последовательности, определяется как

Если связи содержатся только в одной последовательности и, соответственно, все и суть нули, то

Мы докажем это в следующей главе.

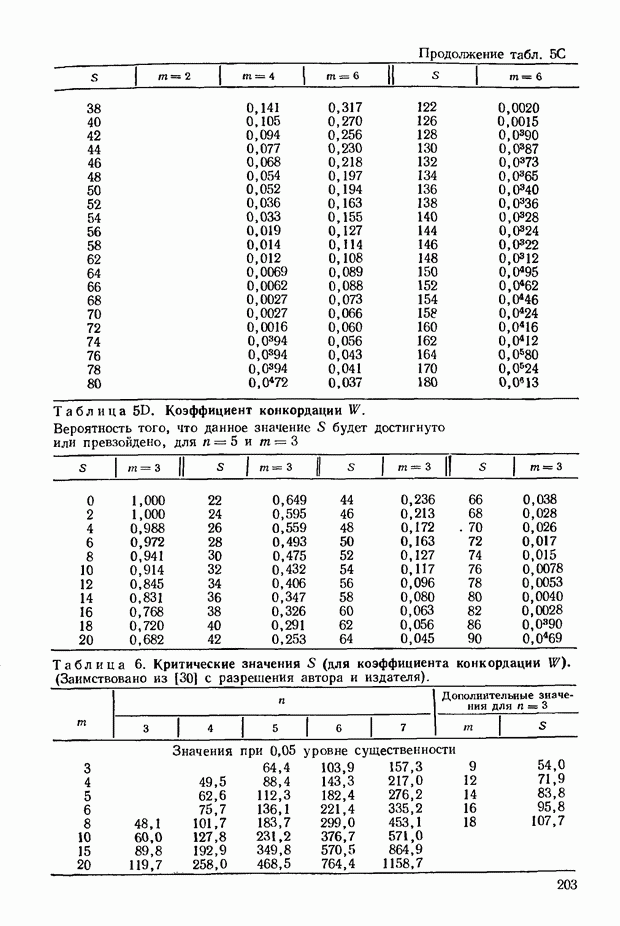
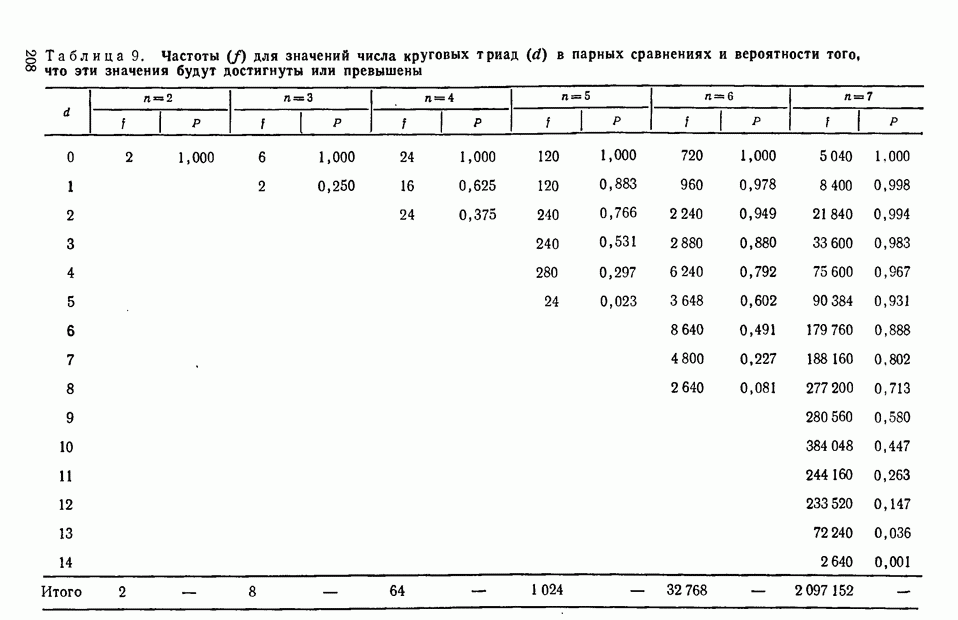
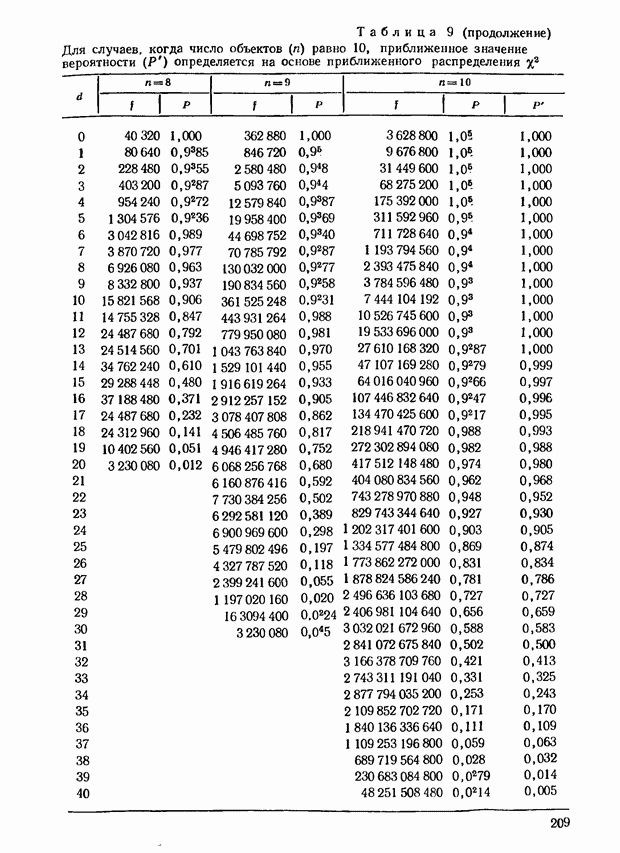
4.10. По мере увеличения распределение для любого фиксированного числа связей, как и при отсутствии связей, стремится к нормальному. По-видимому, возникает не очень серьезная ошибка при применении нормального приближения для тем не менее если связи многочисленны, то, может быть, следует предпринять специальное исследование. Для случаев, когда полных таблиц для большого числа вариантов нет. Однако Силлито [82] создал таблицы для любого числа связанных пар или связанных троек до включительно.

Пример 4.3

Рассмотрим две последовательности, состоящие из двенадцати членов:

Находим

В первой последовательности связи охватывают 2, 2 и 3 члена, во второй и 2 члена. Теперь на основе (4.3) получим:

Таким образом, с поправкой на непрерывность

Шанс достигнуть или превзойти эту величину по абсолютному значению составит около 0,021. Это незначительная вероятность, и мы склоняемся считать величину существенной. 11. Если оцна последовательность вырождается в дихотомию числом членов ли как, например, в 3.13 и со связями в другой последовательности, представляемыми членами, то после ановки в (4.3) соответствующих величин получим уравнение

Наконец, если в обеих последовательностях, как, например, в 3.14, наблюдается дихотомия, то после подстановки в 4.5 соответствующих величин имеэм:

4.12. Эти уравнения позволяют нам проверить существенность коэффициентов та, или значений на основе которых они получены. Имеется, однако, одно затруднение, связанное с поправкой на непрерывность, а именно:

а) и случае, когда имеется дихотомия и несвязанная последовательность, интервал между соседними значениями равен двум. Поправка на непрерывность равна половине этого интервала, т. е. единице;

б) для дихотомии и последовательности, целиком состс ящей из связей, охватывающих членов, интервал равен 21 и соответствующая поправка на непрерывность составляет величину

в) когда обе переменные представлены дихотомиями, интервал равен и поправка на непрерывность составляет

г) если последовательность дня одной переменной расчленена на две группы, а вторая содержит связи различной протяженности, то в различных частях диапазона наблюдений интервалы между соседними значениями 5 будут варьировать. В этом случае мы можем прибегнуть к приближенному методу, как это показано ниже в примере 4.5.

Пример 4.4

В примере 3 5 мы нашли величину

которая базировалась на На основе (4.6) определяем дисперсию:

Поправка на непрерывность равна 17/2, следовательно, имеем:

Вероятность того, что эта величина будет достигнута пли превышена по абсолютному значению, равна не является существенным.

Пример 4.5

Для данных примера 3.4 при условии, что одна переменная не разбита на две группы, находим, что На основе (4.5) определим дисперсию:

Приступая к определению поправки на непрерывность, заметим, что в последовательности А имеется «прыжок» с 2 на 5, а это приводит к интервалу в значении равному 5. Если же мы заменим одно из на О, которое корреспондирует рангу 5 в последовательности то 5 сократится на 5 и первые пять параметров составят вместо Аналогично «прыжок» с 5 до дает интервал 3 и т. д. Мы можем подсчитать средний интервал без расчета каждого отдельного интервала. Общий интервал параметра 5 равен удвоенному числу членов в последовательности минус продолжительность связей, включающих первый и последний член. В рассматриваемом случае он составит Таким образом, средний интервал равен . В качестве поправки на непрерывность возьмем половину этой величины, откуда

Это дает возможность установить, что вероятность того, что будет равно данной величине или превысит ее по абсолютному значению, составит 0,089. Величина опять-таки является несущественной.

В предыдущем примере для таблицы мы нашли, что и что эта величина не является существенной. Результат, вообще говоря, мало чего стоит. В примере, который был только что рассмотрен, т. е. несколько меньшая величина, вероятность превзойти которую по абсолютному значению равна 0,089, в то время как для этой же величины, полученной для таблицы вероятность составила 0,24. Здесь нет расхождения. В настоящем примере мы не расчленили на две группы вторую последовательность и приняли во внимание все ранги. Наш метод позволил проявить себя величинам, которые могли сформироваться случайно, и, следовательно, вероятность превышения данной величины в этой, более обширной области, может отличаться от величины, полученной для более ограниченной области определения при дихотомии.

Существенность «ро»

4.13. Совокупность величин, полученных коррелированием всех возможных (несвязанных) последовательностей с произвольной последовательностью, дает множество значений которое может быть использовано для проверки существенности этого коэффициента так же, как это было сделано для Распределение симметрично и имеет тенденцию к нормальному при больших однако его менее удобно применять, чем распределение по следующим причинам:

а) действительное распределение значительно труднее определить; полностью оно получено только для включительно;

б) распределение приближается к нормальному медленнее, чем распределение и необходима некоторая промежуточная форма, для того чтобы восполнить разрыв между значениями для (довольно сомнительным), при котором приближение к нормальному распределению достаточно;

в) для такой промежуточной области не разработаны простые методы расчета, учитывающие связи.

4.14. При отсутствии связей стандартное отклонение распределения рассчитывается по простой формуле

Соответствующее выражение для имеет вид:

Если то, вероятно, применение этих выражений при предположении о наличии нормального выборочного распределения будет вполне правильным. Пример 4.6

При ранжировании 20 объектов наблюденное значение составило 840. Имеем:

Стандартная ошибка по формуле (4.7) равна Таким образом, наблюденное значение равно стандартной ошибки и едва ли может быть существенным.

Для такой большой величины поправка на непрерывность не представляет большой важности, однако если мы все же хотим ее осуществить, то должны вычесть единицу из Тогда по формуле .8) получим стандартную ошибку

Теперь варьирует от 0 до со средней в данном случае она равна 1330. Получим следующее отклонение наблюденной величины от средней: Абсолютное отклонение с учетом поправки на непрерывность составит: стандартного отклонения, что приводит к тому же заключению, к которому мы пришли относительно

На рис. 4.2 показано распределение в виде полигона частот для Пилообразный профиль графика является необычным, однако соответствие нормальной кривой умеренно хорошее, хотя не вполне хорошее для наших целей, поскольку при проверке существенности нас интересует, главным образом, соответствие кривой в области «хвостов» распределения.

Рис. 4.2

Поправка на непрерывность для «ро»

4.15. Подобно поправкам на непрерывность для рассмотренным в 4.12, можо предложить следующие поправки для при наличии связей:

а) если имеются дихотомия и последовательность без связей, то интервал между последовательными величинами равен , и поэтому мы вычитаем из

б) если имеются дихотомия и последовательность, которая целиком состоит из связей, охватывающих членов, то интервал равен и соответственно надо вычитать

в) при наличии двойной дихотомии поправка на непрерывность равна

Однако эта поправка мало чего стоит, поскольку при двойной дихотомии точно такое же, что и формула для последней характеристики обычно и применяется в расчетах.

Если в последовательности присутствуют связи, то не требуется никакой корректировки в значении дисперсии она остается равной

Проверка в нулевом случае

4.16. До сих пор мы применяли проверки, основанные на распределении корреляций в совокупности величин, полученных при перестановке рангов всеми возможными путями. Такой подход эффективен, если проверяется гипотеза о том, что исследуемые качественные признаки в генеральной совокупности независимы. Тогда наша проверка покажет, является ли наблюдаемая корреляция существенным указанием на отличие корреляции генеральной совокупности от нуля. Однако нам может понадобиться испытать корреляции с другой точки зрения или приписать пределы в вероятностном смысле этой генеральной величине. Например, предположим, что мы получили значение равное 0,6, и найдено, что оно существенно. Можем ли мы сказать, в каких пределах находится величина корреляции? Допустим еще раз, что для другой выборки эта величина равна 0,8, причем она также существенна. Можем ли мы сказать, что второе значение более существенно, чем первое, или разность между ними можно приписать действию случая?

4.17. Предположим, что целая совокупность, охватывающая членов, ранжирована по первой переменной в порядке Очевидно, что это можно допустить без потери общности доказательства. Расположим теперь в этой последовательности данную совокупность. Пусть ранг члена, соответствующий второй переменной, будет равен Тогда в соответствии с нашим обычным методом подсчитаем значение для этой совокупности.

Теперь предположим, что из выбрано членов. Эти члены будут иметь натуральный порядок по первой переменной. Тогда можно определить величину, допустим, которая будет означать выборочный коэффициент Итак, вместо запишем для обозначения того, что мы рассматриваем выборочную величину, а не показатель, относящийся к генеральной совокупности. Для каждой возможной выборки имеется соответствующая величина и поскольку существует выборок то имеется равное количество значений

4.18. В следующей главе мы покажем, что для любой совокупности распределение стремится к нормальному распределению, по мере того как размер выборки возрастает при условии, что генеральное не очень близко к единице и удовлетворяются некоторые условия, не носящие характер ограничений. Мы также покажем, что средняя этого распределения равна До сих пор все шло хорошо. Однако дальше мы сталкиваемся с рядом затруднений. Если бы стандартное отклонение распределения зависело только от то мы легко могли бы проверить наблюдаемую величину так, как нам нужно; однако в действительности стандартное отклонение зависит от других неизвестных величин.

4.19. Простая иллюстрация прояснит эту мысль. Рассмотрим последовательность из 9 членов (в соответствии со значением второй переменной):

Имеется возможных варианта выборок, состоящих из 3 членов Найдем значение для каждого варианта ьыборки. Получим следующее распределение:

Находим, что средняя этого распределения равна 13/6, отсюда среднее значение для величин составит:

Можно найти, что для генерального значения следовательно,

Таким образом проверяется наше утверждение о том, что сред! ее значение равно генеральному Последовательность

также имеет однако распределение для выборок по 3 члена теперь следующее:

Опять среднее значение равно генеральному распределение во втором случае отличается от распределения в нервом примере, его диспсрсия равна то время как дисперсия в первом примере составила 0,639.

4.20. Мы находимся в трудном положении, поскольку, если мы ничего не знаем о последовательности рангов в исходной совокупности (обычно так и бывает), не можем выразить дисперсию через известные факторы. В следующей главе, тем не менее, мы покажем, что для любой исходной совокупности дисперсия не может превышать определенное значение, а именно:

Этот результат можно с большой надежностью применить для проверки. Данное выражение также пригодно для случаев, когда имеются Соответствующее приближенное выражение для при (здесь означает выборочное значение ) имеет вид:

Однако это выражение нельзя считать обоснованным для случаев, когда имеются связи. Данное замечание будет более понятным при рассмотрении следующего примера.

Пример 4.7

Найдено, что для последовательности из 30 рангов величина равна 0,816. Допустим, что этот ранжированный ряд является случайной выборкой. Что можно сказать теперь о значении в исходной совокупности?

Для выборок, состоящих из 30 единиц, распределение можно принять нормальным и взять в виде оценки среднего значения величину 0,816. Из (1.9) находим:

иначе говоря, стандартная ошибка меньше или раьна 0,149.

Вероятность отклонения от средней на 1,96 стандартного отклонения или больше (по абсолютной величине) равна 0,05. Поэтому мы можем сказать, что в худшем случае вероятность того, что действительная величина лежит в пределах вокруг 0,816, равна Иначе говоря, вероятность того, что действительная величина лежит вне интервала 0,524 1,0, меньше или равна 0,05, Вместо определения пределов обычным статистическим путем с соответствующей степенью вероятности, мы устанавливаем пределы с максимальной вероятностью; ииаче говоря, мы устанавливаем внешние границы для диапазона генерального Это может привести к излишней строгости: мы делаем ошибку, повышающую надежность в том смысле, что избегаем опасность приписывания существенности несущественным результатам. Правда, и некоторых случаях мы можем не выявить существенность там, где она действительно имеется.

4.21. связь со стандартной ошибкой была показана так, как это обычно практикуется в элементарном курсе статистики. Для того чтобы применить формулу (4.9), нам нужно заменить неизвестное генеральное значение на выборочное как это было сделано в предыдущем примере. Этой процедуры можно избежать, если к теории доверительных интервалов. Если нормированное отклонение, соответствующее уровню вероятности

процентов (т. е. вероятность того, что отклонение от средней на стандартных отклонений или больше но абсолютному значению возникнет в связи со случайным отбором, равна то самое большее с этой вероятностью можно утверждать, что

где корни следующего выражения:

Отсюда

Пример 4.8

По данным примера 4.7 имеем Нормированное отклонение, соответствующее вероятности 0,05, равно 1,96. Подстановка данных в (4.12) дает:

Таким образом, можно утверждать, что лежит между 0,34 и 0,96, причем можно быть уверенным, что это справедливо в среднем по крайней мере в 95% случаев. Этот метод более точен, чем метод, рассмотренный в 4.20. Ограничения, разумеется, здесь остаются максимальными.

Пример 4.9

Для выборки из 20 объектов получено значение равное 0,8. Вторая выборка дала значение этого коэффициента, равное 0,6. Имеется ли указание на то, что выборки принадлежат различным совокупностям; иначе говоря, могут или нет различные значения возникнуть благодаря случайности?

Имеем следующую величину максимальной дисперсии для первого случая:

Стандартная ошибка равна 0,19. Значение стандартной ошибки для второго случая отличается примерно на эту же величину и, следовательно, мы не может признать существенность различия.

Альтернативный подход заключается в следующем. Найдем дисперсию для второго коэффициента, она равна 0,064. Таким образом,

максимальная дисперсия разности коэффициентов (равна сумме дисперсий) составит 0,109, а стандартная ошибка - 0,32. Эта величина пресышает действительную разность, равную 0,2. Отсюда опять следует, что различие коэффициентов не является существенным.

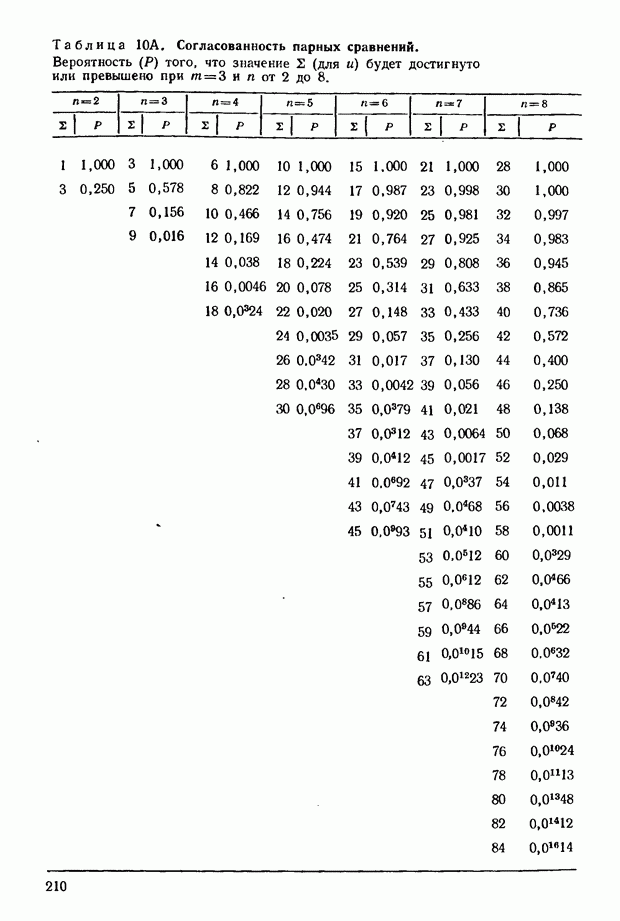
Вообще, если имеется ряд значений 5 (даже для последовательностей различной протяженности), то можно суммировать их и проверить существенность всей совокупности, сопоставляя с суммой дисперсий отдельных последовательностей. Ценность этой процедуры основывается на том факте, что дисперсия суммы независимых переменных равна сумме их дисперсий. Она оказывается очень полезной в экспериментальной работе

4.22. Предыдущий пример подчеркнул одну довольно разочаро Бывающую особенность коэффициента ранговой корреляции — ему свойственны относительно большие стандартные ошибки. Какой бы ни была величина стандартная ошибка имеет величину порядка Этот недостаток характерен для большинства коэффициентов корреляции. Так, например, стандартная ошибка коэффициента парной корреляции в выборках, следующих нормальному закону распределения, равна таким образом, имеет в общем величину порядка Очевидно, что невозможно оценить коэффициент корреляции для генеральной совокупности очень точно, если ранжированный ряд состоит менее чем из 30 или 40 членов. В связи с этим необходима осторожность при приписывании реального смысла коэффициентам корреляиии, подсчитанным для последовательностей небольшой протяженности, если нет нескольких выборочных величин.

Например, при ранжировании 32 объектов максимальная стандартная ошибка раина Если в этом случае близко к нулю, то на этой основе мы не можем определить генеральное в пределах, меньших чем удвоенная стандартная ошибка, т. е. ±0,5. Если же, допустим, равно 0,8, то пределы сужаются, однако область неопределенности, охватывающая действительное значение, все еще простирается от 0,5 до 1,0

4.23. Как будет показано в следующей главе, нельзя значительно уменьшать максимальные пределы, получаемые на основе (4.9) или (4.11). Однако мы увчдим, что весьма существенное улучшение возможно, если имеется персичное ранжирование и исследователь обладает терпением для выполнения необходимых расчетов. Если не принимать во внимание сказанное выше, то представляется невероятным, что возможно какое лиоо простое улучшение без принятия предположений о существе переменной и ее генеральном распределении, как это и будет показано в гл. 9

Библиография

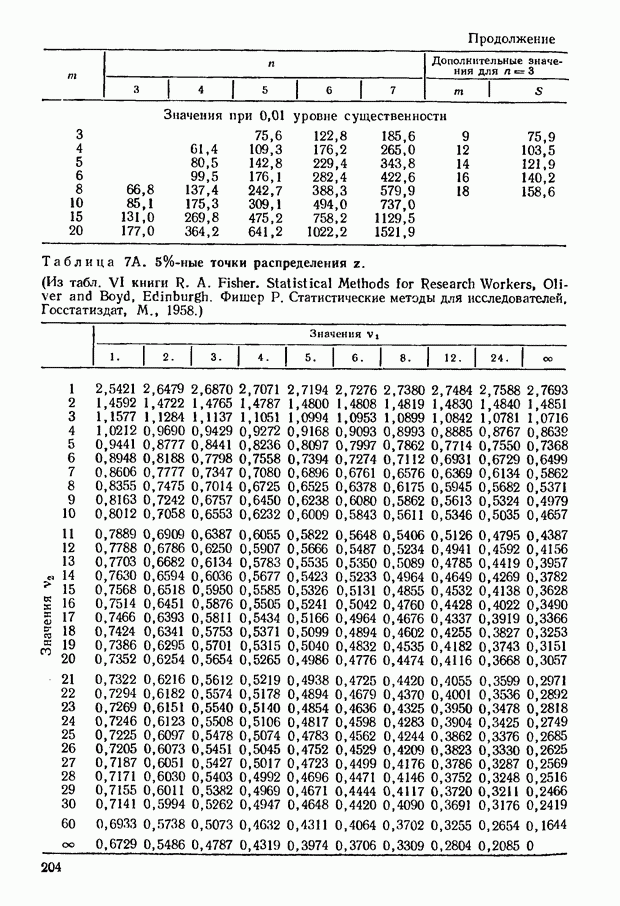
О распределении - см. [48], [14], [9], [82]; о распределении см. Об общем совместном распределении коэффициентов корреляции см [9], [131 и [39].

Более полные таблицы распределения для достигающие 40 единиц, опубликованы в [47].

Формула (4.10) является следствием более общей формулы, полученной Хоффдингом [39]. Если есть выборочные значения то

и

где коэффициент ранговой корреляции Спирмэна для непрерывной совокупности (см. 9.5). Для больших имеет тенденцию быть равным См. также [6], [31], [27], [28] и [74].