ГЛАЗА 13. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ

13.1. В данной, заключительной главе необходимо кратко обрисовать ряд недавних достижений в теории ранжирования. Некоторые из идей и методов, которые будут здесь затронуты, являются новыми и еще не полностью разработаны. Развитию других препятствует сложность возникающих математических проблем. Поэтому данная глава, в отличие от предыдущих, не содержит систематического введения в раздел статистической теории, который исследован в такой степени, что может быть применен на практике в качестве рутинной процедуры. Скорее это обзор последних достижений и руководство для дальнейшего чтения.

Ситуации, требующие применения рангов

13.2. До сих пор мы имели дело главным образом с применением рангов в ситуациях, в которых не было генеральной корреляции (так называемый нулевой случай), или с одной особенной моделью (5.17), в которой наши наблюдения рассматривались как извлечение из исходной последовательности большего объема. В некоторых условиях ни один из этих подходов не является пригодным. Например, пусть нам известно, что имеется некоторая исходная взаимосвязь, тогда больший интерес представляет характеристика ее степени, чем выявление факта существования. В иных случаях мы можем изучать генеральную совокупность последовательностей, имеющих одинаковую протяженность, причем некоторые из них представлены в выборке.

13.3. В двух ситуациях, имеющих довольно общий характер, был достигнут некоторый прогресс.

а. Модель Стюарта

Стюарт [92] изучил проблемы выборки из группы экспертов. Предположим, что каждый член группы располагает ооъектов в порядке предпочтения; например, совокупность видов деятельности может быть упорядочена в соответствии с общественным престижем каждого из них. Если случайным образом из множества отобрано членов, получим совокупностей последовательностей, состоящих из объектов. Наша проблема теперь заключается не в испытании

независимости (подобно тому, как это изложено в гл. 6), хотя эта проблема также возникает, а главным образом в том, чтобы увидеть, насколько подобная общность предпочтений, существующая в наблюденных членах, может быть принята в качестве представителя предпочтений множества

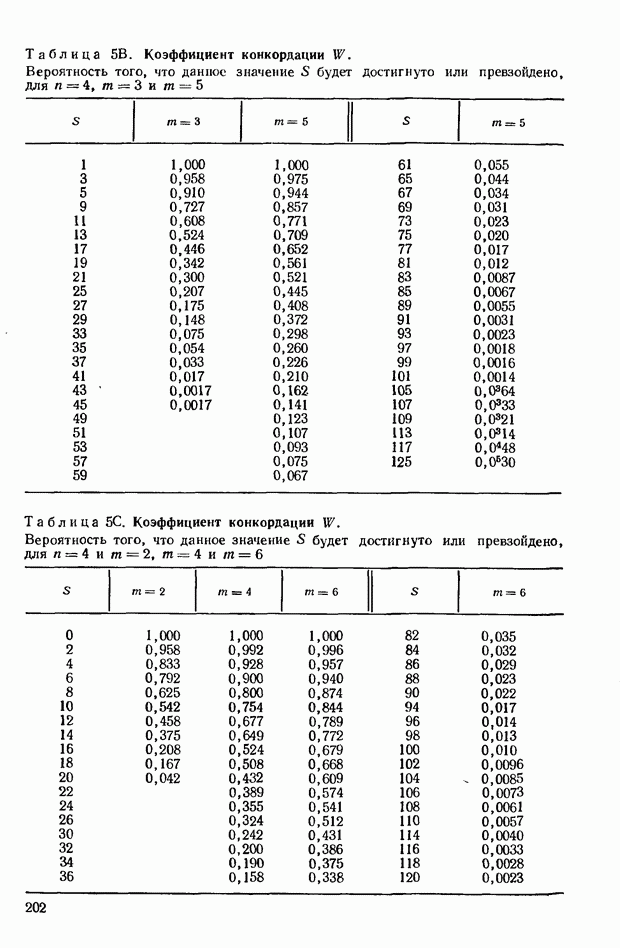
13.4. При исследовании этой проблемы Стюарт применил коэффициент конкордации рангов . В ненулевом случае распределение подобной функции весьма сложно и для оценивания даже первых четырех моментов требует трудоемких расчетов. Однако затраты труда не являются непреодолимым препятствием, и соответствующие результаты были успешно использованы для решения практических задач, связанных с социальными группировками. Так, в результате опроса примерно 1000 человек, охваченных выборкой, были получены ранги, характеризующие 30 видов занятий в соответствии с их неопределимым качественным признаком, отражающим «общественное положение». Далее был подсчитан средний ранг, приписанный каждому занятию. Возникает вопрос: насколько существенно расхождения в выборочных средних рангах отражают реальные расхождения в совокупности? Подробности об этом можно найти в работе Стюарта.

13.5. В этой связи можно упомянуть об одной важной проблеме в теории конкордации. Предположим, что у нас имеется два набора, содержащих последовательностей. Испытания, рассмотренные в гл. 6, могут показать, что коэффициенты конкордации каждого из них, скажем и являются существенными. Как нам проверить, является или нет разность — существенной, или, что более обще, может ли какой-либо метод быть использован в качестве инструмента проверки того, существенно или нет степень согласованности между последовательностями отличается от степени согласованности между последовательностями? Представляется, что по этой проблеме еще ничего не сделано.

6. Модель Тэрстоуна-Мостеллера-Дэниелса.

13.6. Допустим, что одна последовательность определяется на основе объективного критерия, например, объекты могут быть упорядочены во времени или в пространстве в соответствии с некоторым измеримым критерием. Отдельный эксперт, не зная истинного порядка объектов, выносит суждения о них и приписывает им некоторый порядок. Совокупность значений, с которой теперь мы имеем дело, представляет собой (бесконечное) множество последовательностей, которое мог воспроизвести эксперт при повторении опыта; элементы этого множества различаются между собой, поскольку он мог допускать ошибки или неправильные суждения, или, более обще, последовательности рангов могут быть воспроизведены разными экспертами. Модель, рассмотренная в предполагает наличие непрерывной переменной у в качестве источника отклонения от истинного значения функция плотности последовательности есть

и проблема заключается в оценивании значения или по крайней мере определении их порядка на основе наблюдений. Таким образом, возникает проблема, связанная с регрессией, и Дэниеле разработал ее значительно дальше, чем можно было ожидать.

Модели парных сравнений

13.7. Весьма обобщенные модели могут быть разработаны для парных сравнений. Однако их практическое применение не легко осуществить. Например, предположим, что у нас имеется объектов и вероятность того, что объекту будет приписан более высокий ранг, чем объекту равна Такая модель была бы пригодна для ситуаций, в которых эксперт выражает предпочтение, причем оно может быть ошибочным, как и в модели последовательности 13.6 или в случае, когда ряд экспертов высказывает различные предпочтения. Такая модель предложена в [23]. Коэффициент согласованности и (11.8) имеет среднее значение, определяемое как

и дисперсию

Трудность применения данного результата заключается в том, что мы не знаем значений .

13.8. Другого рода подход развит в [3]. Предположим, что объектов имеют «истинную» последовательность, охарактеризованную числами (причем Когда объекты сравниваются, то вероятность того, что объект предпочитается равна Данная модель, уже заслужившая определеннее доверие во многих предшествующих работах, связанных с парными сравнениями, проще, чем предыдущая, поскольку в ней представлено параметров вместо параметров ли. 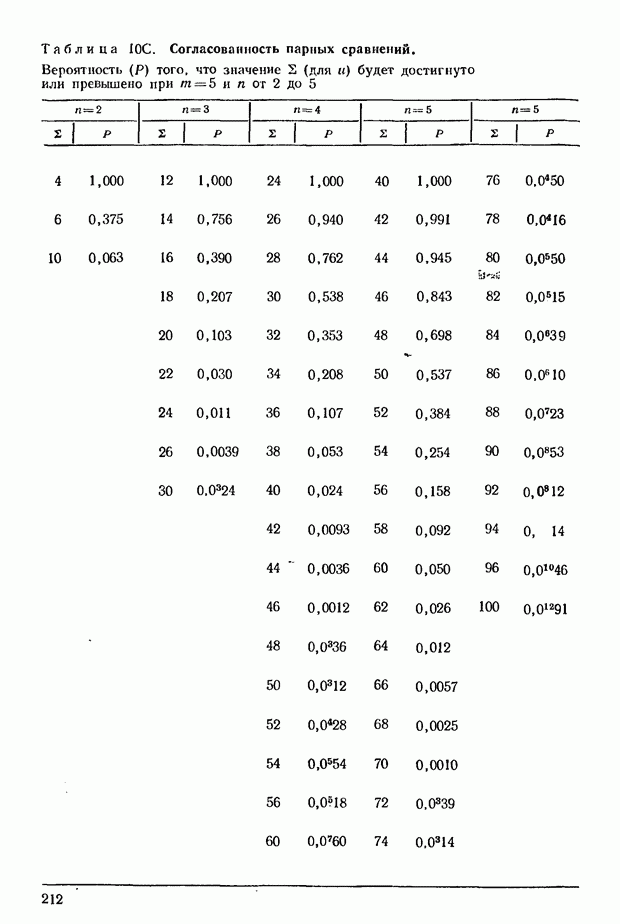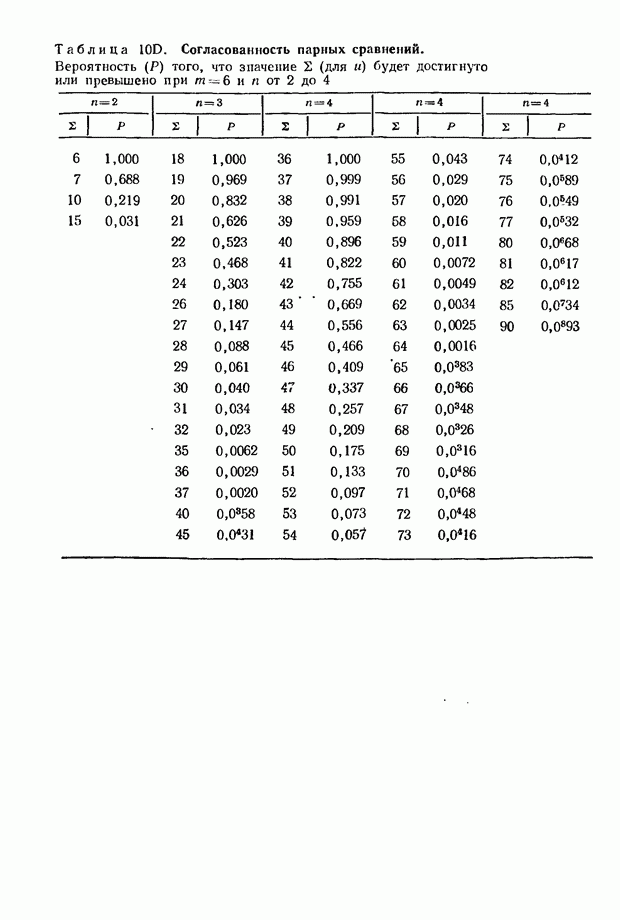разработан метод оценивания параметров на основе наблюдений и проверки существенности полученных результатов. Были опубликованы таблицы, необходимые для практического приложения данного метода (см. [3] и [4]).

Ранговые критерии стандартных статистических ситуаций

13.9. Идеи, лежащие в основе формирования ранговых коэффициентов, особенно коэффициентов могут быть приложимы к ряду ситуаций, с которыми часто сталкиваются в статистическом анализе. Можно выделить следующие пять случаев.

а. Проверка независимости. В случае, когда имеется пар наблюдений может возникнуть необходимость проверки

независимости распределения от распределения у. Для этого может быть применен простой критерий, основанный на или Более сложный критерий разработан в [39].

б. Проверка однородности двух выборок. Критерий, приведенный в 3.12, был разработан в 1116] и [64] исходя из разных соображений. Обычно он называется тестом Уилкоксона. Он эффективен при проверке однородности двух выборок путем рассмотрения доли случаев, в которых значение членов одной выборки превышает значение членов другой. Эта проверка формально может быть связана с проверкой для дихотомии.

в. Проверка однородности для выборок. Метод проверки для двух выборок не может быть с легкостью распространен на случай с числом выборок выше двух. В [102] и [46] некоторым образом обобщен критерий Уилкоксона. В основу полученного критерия положена величина учитывающая связи в одной последовательности. В [60] также рассмотрен этот случай и сделан обзор имевшейся в то время литературы.

г. Проверка на наличие тренда во временных рядах. Совокупность наблюдений, упорядоченных во времени, может быть проверена на наличие тренда путем анализа корреляции между рядом рангов наблюденных величин и показателями времени (см. пример 1.1). В [63] изучены две возможности такого анализа и оценена их относительная эффективность. В [94] и 195] рассмотрены другие подходы. См. также [8].

д. Подбор функциональных взаимосвязей. Одна из наиболее трудных проблем статистики возникает при подгонке функциональных взаимосвязей к переменным, содержащим ошибки. Классические методы решения этой проблемы предполагают принятие определенных допущений относительно дисперсии ошибок. Тейл [104] показал, что эта проблема может быть успешно разрешена без таких допущений с помощью методов, базирующихся на свойствах, связанных с порядком расположения величин.

Довольно полное изложение всех этих методов приводится в [58, гл. 29 и 31].

Преобразование парных сравнений в ранги

13.10. В некоторых ситуациях, когда проводятся многочисленные попарные сравнения, возникает необходимость обобщения окончательных результатов в форме последовательностей. Например, при исследовании вкусов потребителей может оказаться желательным в конце концов ранжировать множество объектов в порядке общего предпочтения. В [112] и [54] обсужден метод, который можно было применить в данном случае. Проблема сокращения числа парных сравнений требует для своего решения применения сбалансированных схем экспериментов.

Эффективность и мощность ранговых методов

13.11. Рамки настоящей книги не позволяют охватить вопросы, связанные с эффективностью и мощностью ранговых методов в свете современной теории проверки гипотез, за исключением эпизодического рассмотрения относительной эффективности тир при оценивании параметров корреляции в двумерных нормальных совокупностях. В последние годы в этой области предприняты большие работы. Вообще говоря, метод оценивания или проверки, использующий ранги, выигрывает в общности, поскольку он не зависит от формы распределения в генеральной совокупности, однако он может быть связан с потерями эффективности и мощности. Это вполне естественно. Средство, употребляемое для многих целей, обычно не так эффективно, как специально созданное ради одной цели. С другой стороны, существуют ситуации, когда мощность проверок, основанных на рангах, удивительно высока и потери от применения ранговых методов незначительны. О некоторых результатах в данной области см. [58, гл. 31].

13.12. Библиография, которая следует далее (см. с. 182), охватывает соответствующую область достаточно полно, однако читатель, который желает пойти дальше в изучении данного предмета, может получить дополнительные сведения в [106] и [80].

Ранжирование и измерение

13.13. Автором разработан метод определения шкал измерения в тех случаях, когда не только объекты, но и различия между ними могут быть ранжированы [Biomeirika, July, 1962]. Некоторые связанные с этим задачи были исследованы Дэниелсом и Пэрри (там же). Все же проблема еще не полностью разработана, однако возможности в этом отношении представляются интересными.

БИБЛИОГРАФИЯ

(см. скан)

(см. скан)

(см. скан)

(см. скан)

(см. скан)