| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
§ 4.1. Применение основных свойств функций
4.1.1. Использование ОДЗ.
Иногда знание ОДЗ позволяет доказать, что уравнение (или неравенство) не имеет решений, а иногда позволяет найти решения уравнения (или неравенства) непосредственной подстановкой чисел из ОДЗ. Пример I. Решить уравнение

Решение. ОДЗ этого уравнения состоит из всех  одновременно удовлетворяющих условиям
одновременно удовлетворяющих условиям  т.е. ОДЗ есть пустое множество. Этим решение уравнения и завершается, так как установлено, что ни одно число не может являться решением, т. е. что уравнение не имеет корней. Ответ: решений нет.
т.е. ОДЗ есть пустое множество. Этим решение уравнения и завершается, так как установлено, что ни одно число не может являться решением, т. е. что уравнение не имеет корней. Ответ: решений нет.
Пример 2. Решить уравнение

Решение. ОДЗ этого уравнения состоит из всех  одновременно удовлетворяющих условиям
одновременно удовлетворяющих условиям 
 т. е. ОДЗ есть
т. е. ОДЗ есть  . Подставляя эти значения
. Подставляя эти значения  в уравнение (1), получаем, что его левая и правая части равны 0, а это означает, что все
в уравнение (1), получаем, что его левая и правая части равны 0, а это означает, что все  являются его решениями.
являются его решениями.
Ответ: 
Пример 3. Решить неравенство

Решение. ОДЗ неравенства (2) состоит из всех х, одновременно удовлетворяющих условиям  т. е. ОДЗ состоит из двух чисел
т. е. ОДЗ состоит из двух чисел  Подставляя
Подставляя  в неравенство (2), получаем, что его левая часть равна 0, правая равна
в неравенство (2), получаем, что его левая часть равна 0, правая равна  есть решение неравенства (2). Подставляя
есть решение неравенства (2). Подставляя  в неравенство (2), получаем, что
в неравенство (2), получаем, что  не является его решением, поскольку левая часть неравенства (2) равна 0, а правая часть равна
не является его решением, поскольку левая часть неравенства (2) равна 0, а правая часть равна 
Ответ: 
Пример 4. Решить неравенство

Решение. ОДЗ неравенства (3) есть все х, удовлетворяющие условию  Ясно, что
Ясно, что  не является решением неравенства (3). Для х из промежутка
не является решением неравенства (3). Для х из промежутка  имеем
имеем  Следовательно, все а: из промежутка
Следовательно, все а: из промежутка  являются решениями неравенства (3).
являются решениями неравенства (3).
Ответ: 
Пример 5. Решить неравенство

Решение. ОДЗ неравенства (4) есть все х из промежутка  Разобьем это множество на два промежутка
Разобьем это множество на два промежутка 
Для х из промежутка —  имеем
имеем  Следовательно,
Следовательно, 
на этом промежутке, и поэтому неравенство (4) не ймеет решений на этом промежутке.
Пусть х принадлежит промежутку  тогда
тогда  Следовательно,
Следовательно,  для таких
для таких  и, значит, на этом промежутке неравенство (4) также не имеет решений.
и, значит, на этом промежутке неравенство (4) также не имеет решений.
Итак, неравенство (4) решений не имеет.
Ответ: решений нет.
Замечания. 1. При решении уравнений необязательно находить ОДЗ. Иногда проще перейти к следствию и проверить найденные корни (соответствующие примеры уже были в предыдущих главах).
2. При решении неравенств иногда можно не находить ОДЗ, а решать неравенство переходом к равносильной ему системе неравенств, в которой либо одно из неравенств не имеет решений, либо знание его решения помогает решить систему неравенств.
Пример 6. Решить неравенство

Решение. Отыскание ОДЗ неравенства есть непростая задача, поэтому поступим иначе. Неравенство (5) равносильно системе неравенств

Третье неравенство этой системы равносильно неравенству  не имеющему решений. Следовательно, система неравенств (6) не имеет решений, значит, и неравенство (5) не имеет решений.
не имеющему решений. Следовательно, система неравенств (6) не имеет решений, значит, и неравенство (5) не имеет решений.
Ответ: нет решений.
Пример 7. Решить неравенство

Решение. Нахождение ОДЗ неравенства (7) есть трудная задача. Поэтому поступим иначе. Неравенство (7) равносильно системе неравенств

Третье неравенство этой системы имеет решениями все х из промежутка —  Первое неравенство системы (8) справедливо не для всех х из этого промежутка, а лишь для х из промежутка
Первое неравенство системы (8) справедливо не для всех х из этого промежутка, а лишь для х из промежутка  Для всех х из промежутка
Для всех х из промежутка  второе неравенство справедливо. Следовательно, множеством решений системы (8) является промежуток
второе неравенство справедливо. Следовательно, множеством решений системы (8) является промежуток 
Ответ: 
4.1.2. Использование ограниченности функции.
При решении уравнений и неравенств свойство ограниченности снизу или сверху функции на некотором множестве часто играет определяющую роль.
Например, если для всех х из некоторого множества М справедливы неравенства  где А некоторое число, то на множестве М уравнение
где А некоторое число, то на множестве М уравнение  и неравенство
и неравенство  решений не имеют.
решений не имеют.
Заметим, что роль числа А часто играет нуль, в этом случае говорят о сохранении знака функций  на множестве М.
на множестве М.
Пример 8. Решить уравнение

Решение. Для любого действительного числа х имеем  Поскольку для любого значения х левая часть уравнения не превосходит единицы, а правая часть всегда не меньше двух, то данное уравнение не имеет решений.
Поскольку для любого значения х левая часть уравнения не превосходит единицы, а правая часть всегда не меньше двух, то данное уравнение не имеет решений. 
Ответ: нет решений.
Пример 9. Решить уравнение

Решение, Очевидно, что  являются решениями уравнения (9). Для нахождения других решений уравнения (9) в силу нечетности функции
являются решениями уравнения (9). Для нахождения других решений уравнения (9) в силу нечетности функции  достаточно найти его решения в области
достаточно найти его решения в области  поскольку если
поскольку если  является его решением, то и
является его решением, то и  ттже ятттсм его решением.
ттже ятттсм его решением.
Разобьем множество  на два промежутка: (0; 1) и
на два промежутка: (0; 1) и 
Перепишем уравнение (9) в виде  На промежутке (0; 1) функция
На промежутке (0; 1) функция  принимает только отрицательные значения, поскольку
принимает только отрицательные значения, поскольку  а функция
а функция  только положительные. Следовательно, на этом промежутке уравнение
только положительные. Следовательно, на этом промежутке уравнение  не имеет решений.
не имеет решений.
Пусть х принадлежит промежутку  Для каждого из таких значений х функция
Для каждого из таких значений х функция  принимает положительное значения, функция
принимает положительное значения, функция  принимает значения разных! знаков, причем на промежутке
принимает значения разных! знаков, причем на промежутке  функция
функция  неположительна. Следовательно, на промежутке (1; 2] уравнение (9) решений не имеет.
неположительна. Следовательно, на промежутке (1; 2] уравнение (9) решений не имеет.
Если же  то
то  а это означает, что и на промежутке
а это означает, что и на промежутке  уравнение (9) также не имеет решении.
уравнение (9) также не имеет решении.
Итак,  и только они являются решениями исходного уравнения.
и только они являются решениями исходного уравнения.
Ответ: 
Пример 10. Решить неравенство

Решение. ОДЗ неравенства (10) есть все действительные х, кроме  Разобьем ОДЗ на три множества:
Разобьем ОДЗ на три множества:  и рассмотрим неравенство (10) на каждом из этих промежутков.
и рассмотрим неравенство (10) на каждом из этих промежутков.
Пусть  Для каждого из этих х имеем
Для каждого из этих х имеем  Следовательно, все эти
Следовательно, все эти  являются решениями неравенства (10).
являются решениями неравенства (10).
Пусть  Для каждого из этих х имеем
Для каждого из этих х имеем  Следовательно, ни одно из этих х не является решением неравенства (10).
Следовательно, ни одно из этих х не является решением неравенства (10).
Пусть  Для каждого из этих х имеем
Для каждого из этих х имеем  Следовательно, все эти
Следовательно, все эти  являются решениями неравенства (10).
являются решениями неравенства (10).
Ответ: 
Пример 11. Решить уравнение

Решение. Обозначим  через
через  Из определения абсолютной величины следует, что
Из определения абсолютной величины следует, что  при
при  при
при  при
при  Поэтому, если
Поэтому, если  то уравнение (11) можно переписать в виде
то уравнение (11) можно переписать в виде  т.е. в виде
т.е. в виде  Это уравнение имеет решения
Это уравнение имеет решения  этих значений
этих значений  условию
условию  удовлетворяют только
удовлетворяют только  то уравнение (11) можно переписать в виде
то уравнение (11) можно переписать в виде  т. е. в виде
т. е. в виде  Это уравнение имеет решения
Это уравнение имеет решения  Из этих значений
Из этих значений  условию
условию  удовлетворяют только
удовлетворяют только 
Рассмотрим  из промежутка
из промежутка  На этом промежутке уравнение (11) можно переписать в виде
На этом промежутке уравнение (11) можно переписать в виде  т. е. в виде
т. е. в виде

Ясно, что  есть решение уравнения (12), а значит, и исходного уравнения. Докажем, что других решений уравнение (12) на промежутке
есть решение уравнения (12), а значит, и исходного уравнения. Докажем, что других решений уравнение (12) на промежутке  не имеет.
не имеет.
Для  уравнение (12) равносильно уравнению
уравнение (12) равносильно уравнению

Для любого значения  функция
функция  принимает только положительные значения, поэтому уравнение (12) не имеет решений на множестве
принимает только положительные значения, поэтому уравнение (12) не имеет решений на множестве 
Ответ: 
Пример 12. Решить уравнение

Решение. Пусть  есть решение уравнения (13), тогда справедливы равенство
есть решение уравнения (13), тогда справедливы равенство

и неравенства  Из справедливости неравенств получаем, что левая часть равенства (14) имеет тот же знак, что и
Из справедливости неравенств получаем, что левая часть равенства (14) имеет тот же знак, что и  т. е. тот же знак, что и
т. е. тот же знак, что и  а правая часть — тот же знак, что и
а правая часть — тот же знак, что и  Но так как
Но так как  и
и  удовлетворяют равенству (14), то они имеют одинаковые знаки.
удовлетворяют равенству (14), то они имеют одинаковые знаки.
Перепишем равенство (14), в виде

Применяя формулу сокращенного умножения

перепишем равенство (15) в виде

где

Так как  и
и  имеют одинаковые знаки, то
имеют одинаковые знаки, то  Поэтому из равенства (16) следует, что для любого решения уравнения (13) справедливо равенство втжа
Поэтому из равенства (16) следует, что для любого решения уравнения (13) справедливо равенство втжа 
Таким образом, любое решение уравнение (13) удовлетворяет уравнению

Очевидно, что любое решение уравнения (17) есть решение уравнения (13). Следовательно, уравнение (13) равносильно уравнению (17). Решения уравнения (17) есть  к
к  они и только они есть решения уравнения (13).
они и только они есть решения уравнения (13).
Ответ: 
Замечание. Точно так же, как в примере 12, можно доказать, что уравнение

где  — любые натуральные числа, равносильно уравнению
— любые натуральные числа, равносильно уравнению  и затем решать это более простое уравнение.
и затем решать это более простое уравнение.
4.1.3. Использование монотонности функции.
Решение уравнений и неравенств с использованием свойства монотонности основывается на следующих утверждениях.
1. Пусть  — непрерывная и строго монотонная функция на промежутке I, тогда уравнение
— непрерывная и строго монотонная функция на промежутке I, тогда уравнение  , где С — данная константа, может иметь не более одного решения на промежутке X.
, где С — данная константа, может иметь не более одного решения на промежутке X.
2. Пусть  - непрерывные на промежутке 1 функции,
- непрерывные на промежутке 1 функции,  строго возрастает, а
строго возрастает, а  строго убывает на этом
строго убывает на этом
промежутке, тогда уравнение  может иметь не более одного решения на промежутке I.
может иметь не более одного решения на промежутке I.
Отметим что в качестве промежутка 1 могут быть бесконечный промежуток  полубесконечные промежутки
полубесконечные промежутки  отрезки, интервалы и полуинтервалы.
отрезки, интервалы и полуинтервалы.
Пример 13. Решить уравнение

Решение. Очевидно, что  не может являться решением уравнения (18), так как тогда
не может являться решением уравнения (18), так как тогда  Для
Для  функция
функция  непрерывна и строго возрастает, как произведение двух непрерывных положительных строго возрастающих для этих х функций
непрерывна и строго возрастает, как произведение двух непрерывных положительных строго возрастающих для этих х функций  Значит, в области
Значит, в области  функция
функция  принимает каждое свое значение ровно в одной точке. Легко видеть, что
принимает каждое свое значение ровно в одной точке. Легко видеть, что  является решением уравнения (18), следовательно, это его единственное решение.
является решением уравнения (18), следовательно, это его единственное решение.
Ответ: 
Пример 14. Решить неравенство

Решение. Каждая из функций  непрерывная и строго возрастающая на всей оси. Значит, такой же является и исходная функция
непрерывная и строго возрастающая на всей оси. Значит, такой же является и исходная функция  Легко видеть, что при
Легко видеть, что при  функция
функция  принимает значение 3. В силу непрерывности и строгой монотонности этой функции при
принимает значение 3. В силу непрерывности и строгой монотонности этой функции при  имеем
имеем  при
при  имеем
имеем  Следовательно, решениями неравенства (19) являются все
Следовательно, решениями неравенства (19) являются все 
Ответ: 
Пример 15. Решить уравнение

Решение. Область допустимых значении уравнения (20) есть промежуток  На ОДЗ функции
На ОДЗ функции  непрерывны и строго убывают, следовательно, непрерывна и убывает функция.
непрерывны и строго убывают, следовательно, непрерывна и убывает функция.  Поэтому каждое свое значение функция
Поэтому каждое свое значение функция  принимает только в одной точке. Так как
принимает только в одной точке. Так как  то
то  является единственным корнем исходного уравнения.
является единственным корнем исходного уравнения.
Ответ: 
Пример 16. Решить неравенство

Решение. ОДЗ неравенства (21) есть промежуток  На ОДЗ функция
На ОДЗ функция  является непрерывной и строго возрастающей. Так как
является непрерывной и строго возрастающей. Так как  то все значения х из множества [0; 1) удовлетворяют исходному неравенству.
то все значения х из множества [0; 1) удовлетворяют исходному неравенству.
Ответ:  .
.
ПРИМЕР 17. Решить уравнение

Решение. Перепишем уравнение (22) в виде

Рассмотрим непрерывные функции  Функция
Функция  убывает на промежутке
убывает на промежутке  и возрастает на промежутке
и возрастает на промежутке  Функция
Функция  убывает на промежутке
убывает на промежутке  и возрастает на промежутке
и возрастает на промежутке  . Так как на промежутке
. Так как на промежутке  функция
функция  возрастает, а функция
возрастает, а функция  убывает и обе функции непрерывны, то на этом промежутке уравнение
убывает и обе функции непрерывны, то на этом промежутке уравнение  может иметь не более одного корня. Легко проверить, что таким корнем является число
может иметь не более одного корня. Легко проверить, что таким корнем является число  Так как на промежутке
Так как на промежутке  функция
функция  убывает, а функция
убывает, а функция  возрастает и обе функции
возрастает и обе функции
непрерывны, то на этом промежутке уравнение  также может иметь не более одного корня. Легко видеть, что таким числом является число
также может иметь не более одного корня. Легко видеть, что таким числом является число  Итак, данное уравнение (22) имеет два корня
Итак, данное уравнение (22) имеет два корня 
Ответ: 
Пример 18. Решить неравенство

Решение. ОДЗ неравенства (23) есть все  из промежутка
из промежутка  Все х из промежутка
Все х из промежутка  являются решениями исходного неравенства (23), так как для каждого такого х имеем, что функция
являются решениями исходного неравенства (23), так как для каждого такого х имеем, что функция  неотрицательна, а функция
неотрицательна, а функция  отрицательна.
отрицательна.
Рассмотрим неравенство (23) на промежутке  Поскольку функция
Поскольку функция  непрерывна и строго возрастает на этом промежутке, а функция
непрерывна и строго возрастает на этом промежутке, а функция  непрерывна и строго убывает, то, если уравнение
непрерывна и строго убывает, то, если уравнение  имеет корень на этом промежутке, то он единственный. Легко видеть, что таким корнем является число
имеет корень на этом промежутке, то он единственный. Легко видеть, что таким корнем является число 
Для каждого х из промежутка  имеем, что
имеем, что  Поэтому все
Поэтому все  из этого промежутка являются решениями исходного неравенства (23).
из этого промежутка являются решениями исходного неравенства (23).
Для каждого х из промежутка  имеем
имеем  Поэтому такие
Поэтому такие  не удовлетворяют данному неравенству (23).
не удовлетворяют данному неравенству (23).
Итак, решениями исходного неравенства (23) являются все  из промежутка
из промежутка 
Ответ: 
Пример 19. Сколько действительных корней имеет уравнение

если числа а и  одного знака?
одного знака?
Решение. Так как числа  одного знака, то
одного знака, то  для любого
для любого  При
При  очевидно,
очевидно,
что уравнение (24) имеет единственный корень  Пусть
Пусть  Перепишем данное уравнение в виде
Перепишем данное уравнение в виде

Функция  для каждого
для каждого  принимает положительные значения и является непрерывной и строго возрастающей на промежутке
принимает положительные значения и является непрерывной и строго возрастающей на промежутке  и непрерывной и строго убывающей на промежутке
и непрерывной и строго убывающей на промежутке  Если
Если  то функция
то функция  непрерывна и строго убывает на всей оси
непрерывна и строго убывает на всей оси  и принимает все положительные значения для
и принимает все положительные значения для  и отрицательные значения для
и отрицательные значения для  Поэтому уравнение (25) имеет единственный корень на про межутке
Поэтому уравнение (25) имеет единственный корень на про межутке  Если
Если  то функция
то функция  непрерывна и строго возрастает на всей оси
непрерывна и строго возрастает на всей оси  и принимает все положительные значения для
и принимает все положительные значения для  и отрицательные значения для
и отрицательные значения для  Поэтому уравнение (25) имеет единственный корень на промежутке
Поэтому уравнение (25) имеет единственный корень на промежутке 
Ответ: единственный корень.
4.1.4. Использование графиков функций.
При решении уравнений или неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно.
Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ еще надо обосновать.
Пример 20. Решить неравенство

Решение. ОДЗ неравенства (26) есть все  из промежутка Эскизы графиков функций
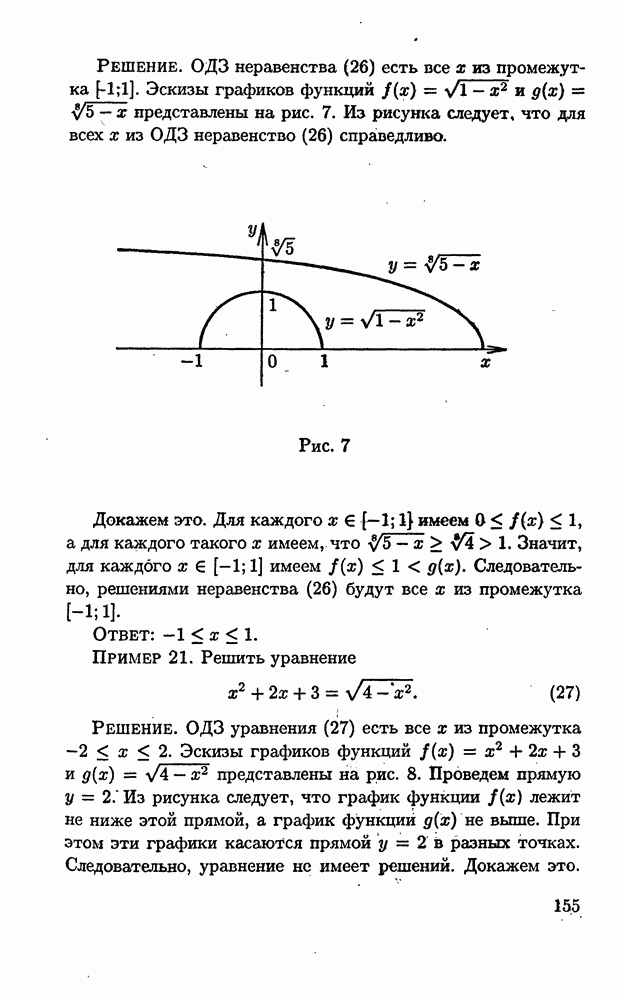
из промежутка Эскизы графиков функций  представлены на рис. 7. Из рисунка следует, что для всех х из ОДЗ неравенство (26) справедливо.
представлены на рис. 7. Из рисунка следует, что для всех х из ОДЗ неравенство (26) справедливо.

Рис. 7
Докажем это. Для каждого  имеем
имеем  а для каждого такого х имеем, что
а для каждого такого х имеем, что  Значит, для каждого
Значит, для каждого  имеем
имеем  Следовательно, решениями неравенства (26) будут все х из промежутка
Следовательно, решениями неравенства (26) будут все х из промежутка 
Ответ: 
Пример 21. Решить уравнение

Решение. ОДЗ уравнения (27) есть все  из промежутка
из промежутка  Эскизы графиков функций
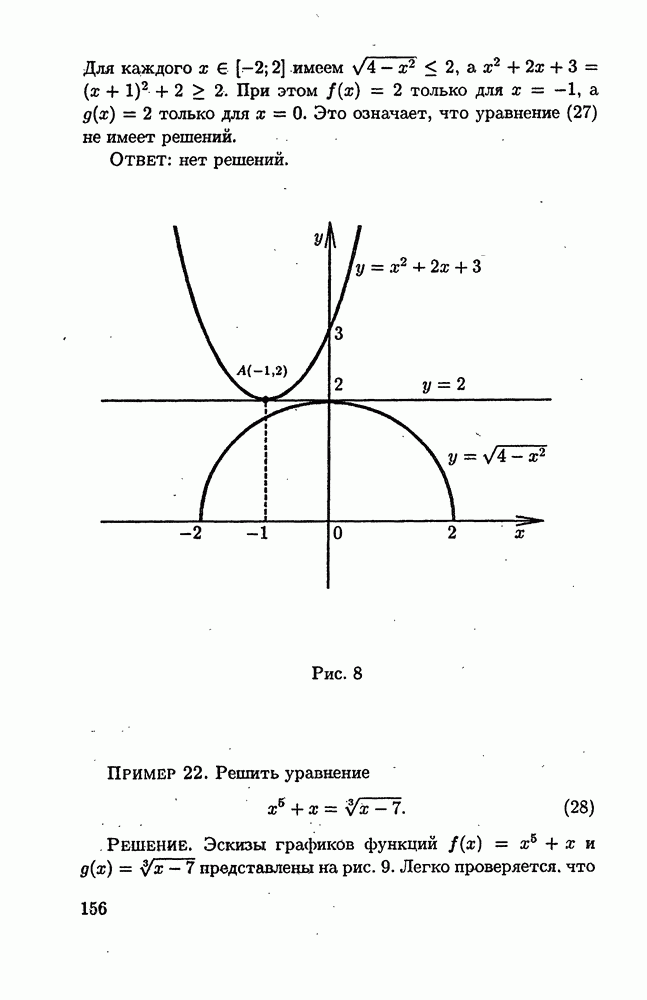
Эскизы графиков функций  представлены на рис. 8. Проведем прямую
представлены на рис. 8. Проведем прямую  Из рисунка следует, что график функции
Из рисунка следует, что график функции  лежит не ниже этой прямой, а график функций
лежит не ниже этой прямой, а график функций  не выше. При этом эти графики касаются прямой
не выше. При этом эти графики касаются прямой  в разных точках. Следовательно, уравнение не имеет решений. Докажем это.
в разных точках. Следовательно, уравнение не имеет решений. Докажем это.
Для каждого  имеем
имеем  При этом
При этом  только для
только для  только для
только для  Это означает, что уравнение (27) не имеет решений.
Это означает, что уравнение (27) не имеет решений.
Ответ: нет решений.

Рис. 8
Пример 22. Решить уравнение

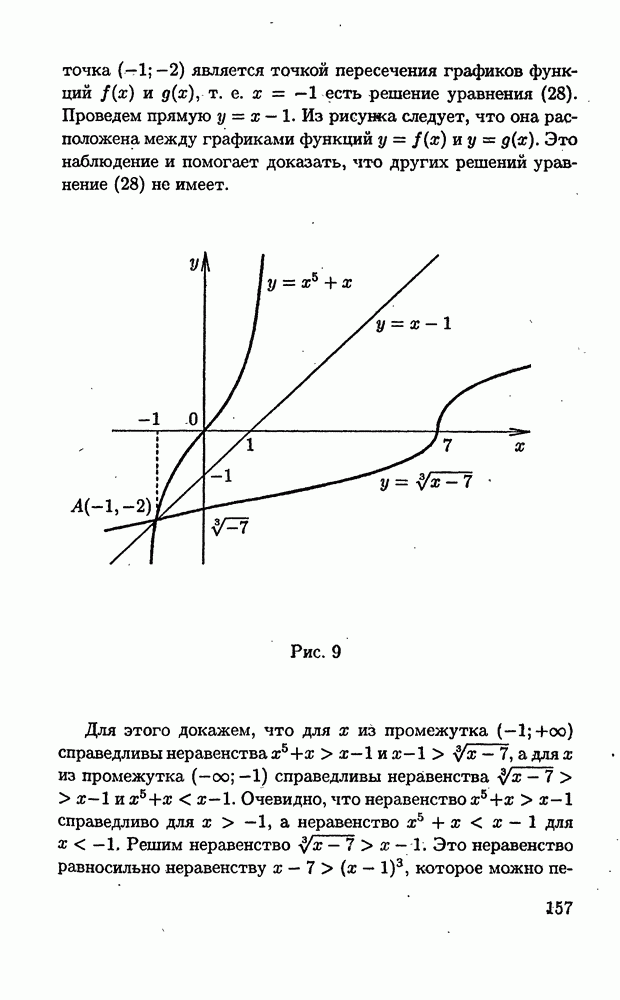
Решение. Эскизы графиков функций  представлены на рис. 9. Легко проверяется, что
представлены на рис. 9. Легко проверяется, что
точка  является точкой пересечения графиков функций
является точкой пересечения графиков функций  есть решение уравнения (28). Проведем прямую
есть решение уравнения (28). Проведем прямую  Из рисунка следует, что она расположена между графиками функций
Из рисунка следует, что она расположена между графиками функций  Это наблюдение и помогает доказать, что других решений уравнение (28) не имеет.
Это наблюдение и помогает доказать, что других решений уравнение (28) не имеет.

Рис. 9
Для этого докажем, что для х из промежутка  справедливы неравенства
справедливы неравенства  дляж из промежутка
дляж из промежутка  справедливы неравенства
справедливы неравенства  Очевидно, что неравенство
Очевидно, что неравенство  справедливо для
справедливо для  а неравенство
а неравенство  для
для  Решим неравенство
Решим неравенство  Это неравенство равносильно неравенству
Это неравенство равносильно неравенству  которое можно
которое можно 
реписать в виде  Решениями этого неравенства являются все
Решениями этого неравенства являются все  Точно так же показывается, что решениями неравенства
Точно так же показывается, что решениями неравенства  являются все
являются все 
Следовательно, требуемое утверждение доказано, и уравнение (28) имеет единственный корень 
Ответ: 
Пример 23. Решить неравенство

Решение. Область допустимых значений данного неравенства состоит из всех х, удовлетворяющих условиям  , т. е. ОДЗ состоит из трех промежутков
, т. е. ОДЗ состоит из трех промежутков  Рассмотрим неравенство (29) на каждом из этих промежутков. Отметим, что в области
Рассмотрим неравенство (29) на каждом из этих промежутков. Отметим, что в области  оно равносильно неравенству
оно равносильно неравенству

а в области  оно равносильно неравенству
оно равносильно неравенству

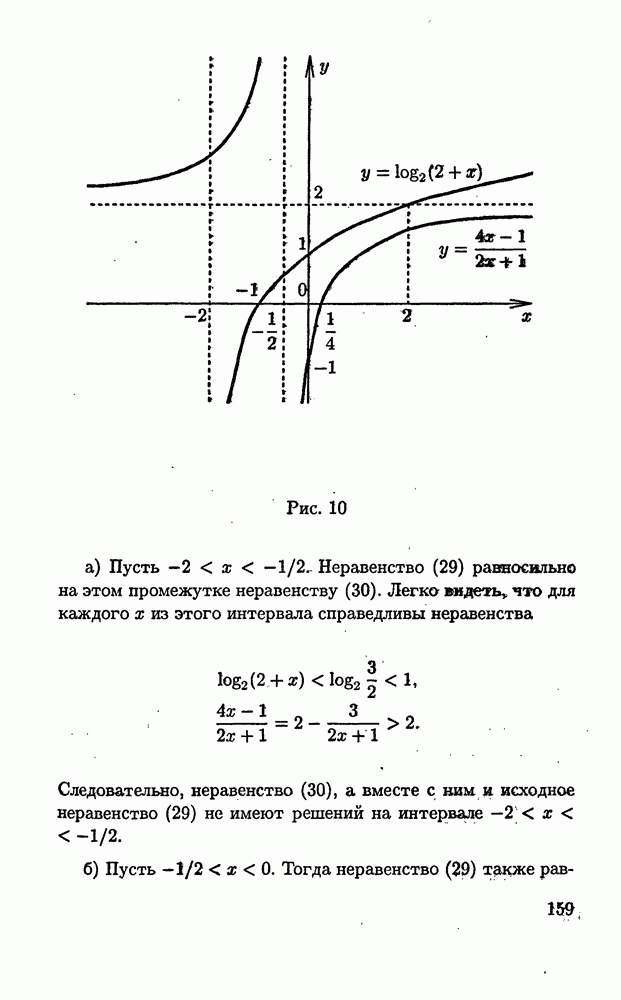
Эскизы графиков функций  приведены «а рис. 10. Из рисунка видно, что
приведены «а рис. 10. Из рисунка видно, что  на промежутке
на промежутке  на каждом из промежутков
на каждом из промежутков  Поэтому неравенство
Поэтому неравенство  не имеет решений, а неравенство (30) будет иметь решениями все х из промежутка
не имеет решений, а неравенство (30) будет иметь решениями все х из промежутка 
Докажем это.

Рис. 10
а) Пусть  Неравенство (29) ранносильно на этом промежутке неравенству (30). Легко видеть что для каждого х из этого интервала справедливы неравенства
Неравенство (29) ранносильно на этом промежутке неравенству (30). Легко видеть что для каждого х из этого интервала справедливы неравенства

Следовательно, неравенство (30), а вместе с ним и исходное неравенство (29) не имеют решений на интервале 
б) Пусть  Тогда неравенство (29) также равносительно
Тогда неравенство (29) также равносительно
неравенству (30). Для каждого х из этого интервала

Следовательно, любое такое х является решением неравенства (30), а поэтому и исходного неравенства (29).
в) Пусть  На этом множестве исходное неравенство равносильно неравенству (31). Очевидно, что для любого х из этого множества справедливы неравенства
На этом множестве исходное неравенство равносильно неравенству (31). Очевидно, что для любого х из этого множества справедливы неравенства

Отсюда следует: 1) неравенство (31) не имеет решений на том множестве, где  т. е. неравенство (31) не имеет решений на множестве
т. е. неравенство (31) не имеет решений на множестве  неравенство (31) не имеет решений на том множестве, где
неравенство (31) не имеет решений на том множестве, где  Учитывая, что в рассматриваемом случае
Учитывая, что в рассматриваемом случае  получаем, что неравен ство (31) не имеет решений на множестве
получаем, что неравен ство (31) не имеет решений на множестве  Остается найти решения неравенства (31), принадлежащие интервалу
Остается найти решения неравенства (31), принадлежащие интервалу 
На этом интервале

Покажем теперь, что справедливо числовое неравенство

Действительно, поскольку  то
то  откуда и очевидна справедливость неравенства (32). Итак, на интервале
откуда и очевидна справедливость неравенства (32). Итак, на интервале  имеем
имеем

Значит, неравенство (31) не имеет решений на интервале  Подводя итог, получаем, что множество решений исходного неравенства есть интервал
Подводя итог, получаем, что множество решений исходного неравенства есть интервал 
Ответ: 
4.1.5. Метод интервалов для непрерывных функций.
Пусть надо решить неравенство  (или неравенство
(или неравенство  Пусть ОДЗ этого неравенства состоит из объединения конечного числа промежутков
Пусть ОДЗ этого неравенства состоит из объединения конечного числа промежутков  занумерованных в порядке следования слева направо. При этом, если
занумерованных в порядке следования слева направо. При этом, если  то
то  могут быть соответственно бесконечными промежутками
могут быть соответственно бесконечными промежутками  Промежутки соответственно могут быть отрезками
Промежутки соответственно могут быть отрезками  интервалами
интервалами  и полуинтервалами
и полуинтервалами  . В случае же
. В случае же  может быть любым из перечисленных промежутков, а также промежутком
может быть любым из перечисленных промежутков, а также промежутком  проверим справедливость неравенства в каждой точке-конце отрезка или полуинтервала. Предположим также, что на каждом из промежутков
проверим справедливость неравенства в каждой точке-конце отрезка или полуинтервала. Предположим также, что на каждом из промежутков  функция
функция  непрерывна и имеет конечное число нулей. Выбросим из ОДЗ неравенства все эти нули и концы отрезков или полуинтервалов
непрерывна и имеет конечное число нулей. Выбросим из ОДЗ неравенства все эти нули и концы отрезков или полуинтервалов  При этом некоторые из промежутков
При этом некоторые из промежутков  могут разбиться на конечное число интервалов. На каждом из них функция
могут разбиться на конечное число интервалов. На каждом из них функция  непрерывна и не обращается в нуль. Значит, на каждом из них она сохраняет постоянный знак, т. е. для каждого х из этого интервала она принимает только либо положительные, либо отрицательные значения. Выбирая в каждом из них некоторую точку
непрерывна и не обращается в нуль. Значит, на каждом из них она сохраняет постоянный знак, т. е. для каждого х из этого интервала она принимает только либо положительные, либо отрицательные значения. Выбирая в каждом из них некоторую точку  и вычисляя знак
и вычисляя знак  этот знак ставят над ним. Тогда решением неравенства
этот знак ставят над ним. Тогда решением неравенства  будет объединение тех интервалов, над которыми поставлен знак плюс, а решением неравенства
будет объединение тех интервалов, над которыми поставлен знак плюс, а решением неравенства  будет объединение тех интервалов,
будет объединение тех интервалов,  которыми поставлен знак минус.
которыми поставлен знак минус.
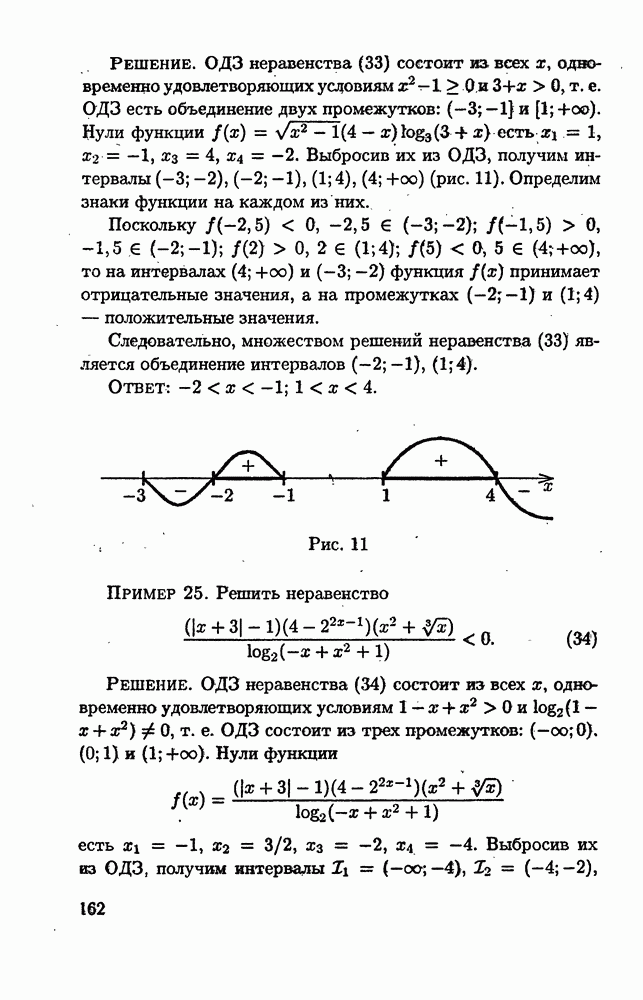
Пример 24. Решить неравенство

Решение. ОДЗ неравенства (33) состоит из всех  одновременно удовлетворяющих условиям
одновременно удовлетворяющих условиям  т. е. ОДЗ есть объединение двух промежутков:
т. е. ОДЗ есть объединение двух промежутков:  Нули функции
Нули функции  естъ
естъ  Выбросив их из ОДЗ, получим интервалы
Выбросив их из ОДЗ, получим интервалы  Определим знаки функции на каждом из них.
Определим знаки функции на каждом из них.
Поскольку  то на интервалах
то на интервалах  функция
функция  принимает отрицательные значения, а на промежутках
принимает отрицательные значения, а на промежутках  — положительные значения.
— положительные значения.
Следовательно, множеством решений неравенства (33) является объединение интервалов 
Ответ: 

Рис. 11
Пример 25. Решить неравенство

Решение. ОДЗ неравенства (34) состоит из всех  одновременна удовлетворяющих условиям
одновременна удовлетворяющих условиям  т. е. ОДЗ состоит из трех промежутков:
т. е. ОДЗ состоит из трех промежутков:  Нули функции
Нули функции

есть  Выбросив их
Выбросив их  получим интервалы
получим интервалы  ,
,
 Легко видеть, что
Легко видеть, что  Следовательно, множеством решений неравенства (34) является объединение интервалов:
Следовательно, множеством решений неравенства (34) является объединение интервалов: 
Ответ: 

Рис. 12
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
- 1.5.2. Метод интервалов.
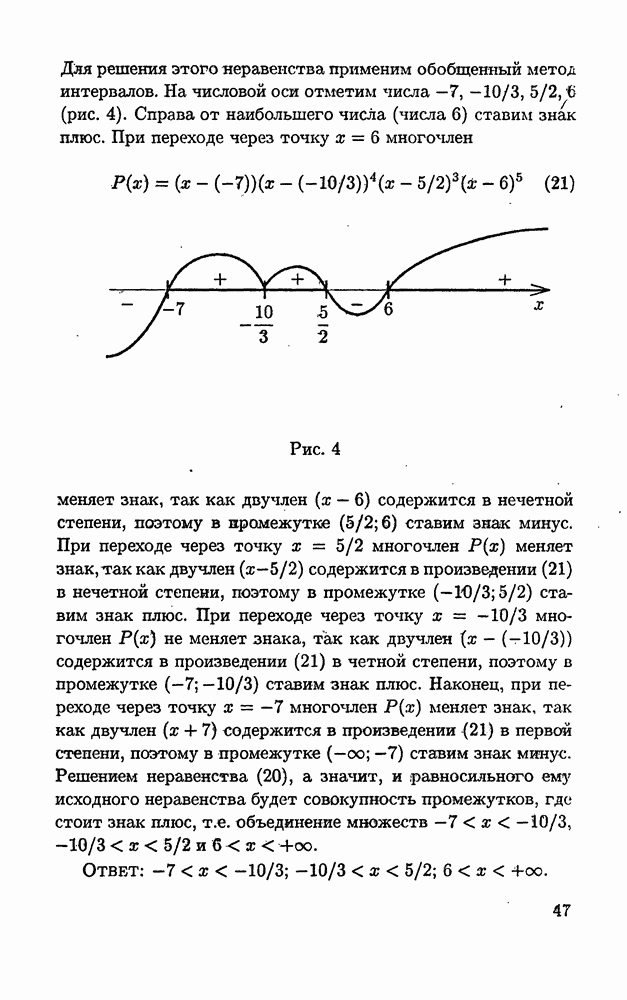
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.