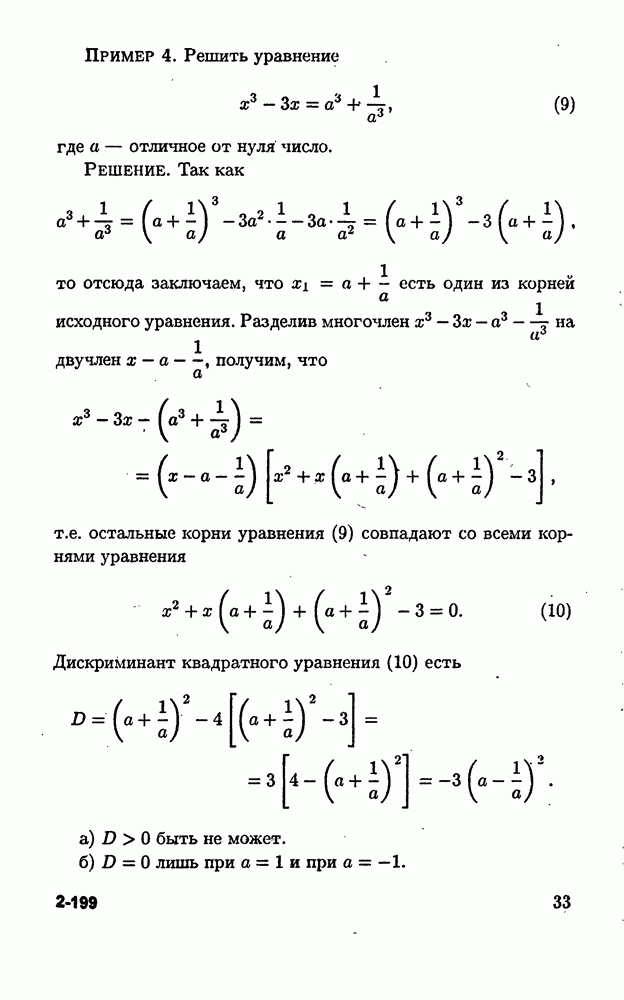| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5.2. Метод интервалов.
В основе этого метода лежигг следующее свойство двучлена х — а: точка а делит числовую ось на две части — справа от точки а двучлен  положителен, а слева от точки а — отрицателен.
положителен, а слева от точки а — отрицателен.
Пусть требуется решить неравенство

где  — фиксированные числа, среди которых нет равных, причем такие, что
— фиксированные числа, среди которых нет равных, причем такие, что 
Рассмотрим многочлен

Для любого числа  такого, что
такого, что  соответствующее числовое значение любого сомножителя в произведении (10) положительно, а значит,
соответствующее числовое значение любого сомножителя в произведении (10) положительно, а значит,  Для любого числа
Для любого числа 
взятого из интервала  соответствующее числовое значение любого из множителей, кроме множителя
соответствующее числовое значение любого из множителей, кроме множителя  положительно, поэтому число
положительно, поэтому число  и т. д.
и т. д.
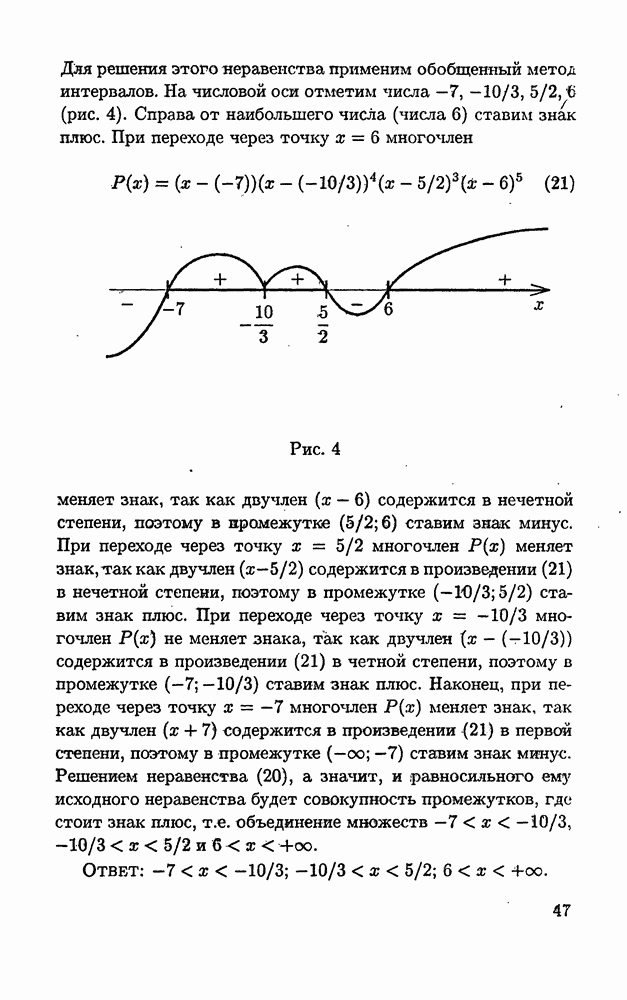
На этом рассуждении и основан метод интервалов, состоящий в следующем: на числовую ось наносят числа  в промежутке справа от наибольшего из них, т.е. числа
в промежутке справа от наибольшего из них, т.е. числа  ставят знак плюс, в следующем за ним справа налево интервале ставят знак минус, затем — знак плюс, затем — знак минус и т.д. Тогда множеством всех решений неравенства (9) будет объединение всех промежутков, в которых стоит знак плюс, а множеством решений неравенства
ставят знак плюс, в следующем за ним справа налево интервале ставят знак минус, затем — знак плюс, затем — знак минус и т.д. Тогда множеством всех решений неравенства (9) будет объединение всех промежутков, в которых стоит знак плюс, а множеством решений неравенства

где  будет объединение всех промежутков, в которых стоит знак минус.
будет объединение всех промежутков, в которых стоит знак минус.
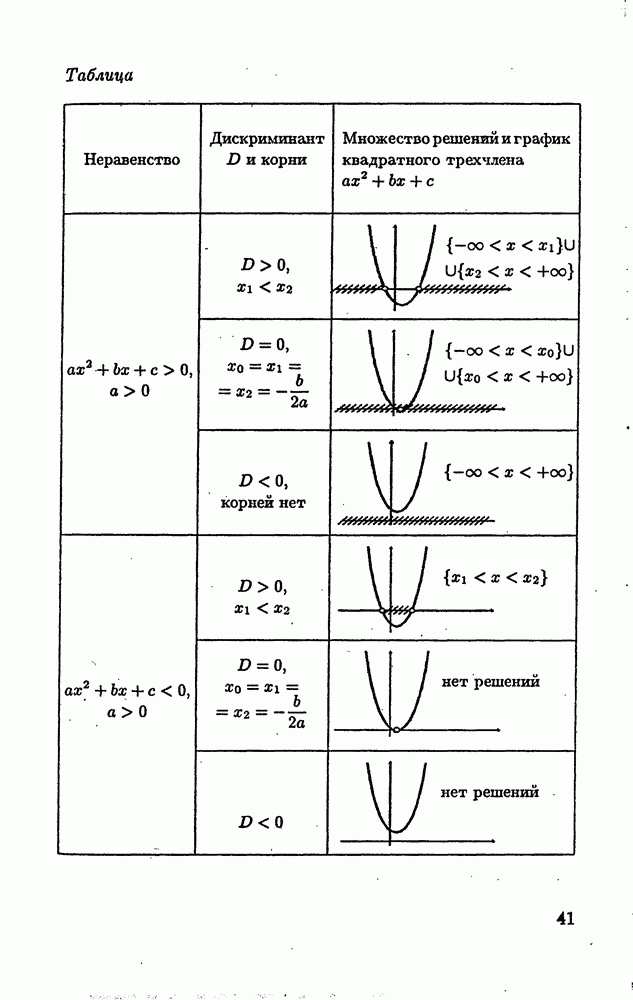
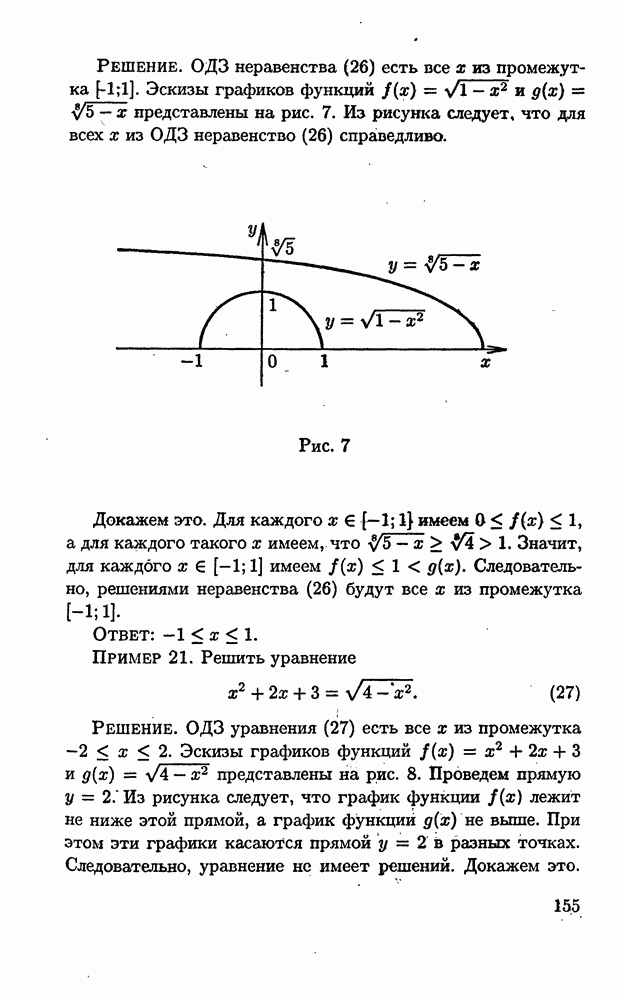
Пример 2. Решить неравенство

Решение. Перепишем неравенство в виде


Рис. 1
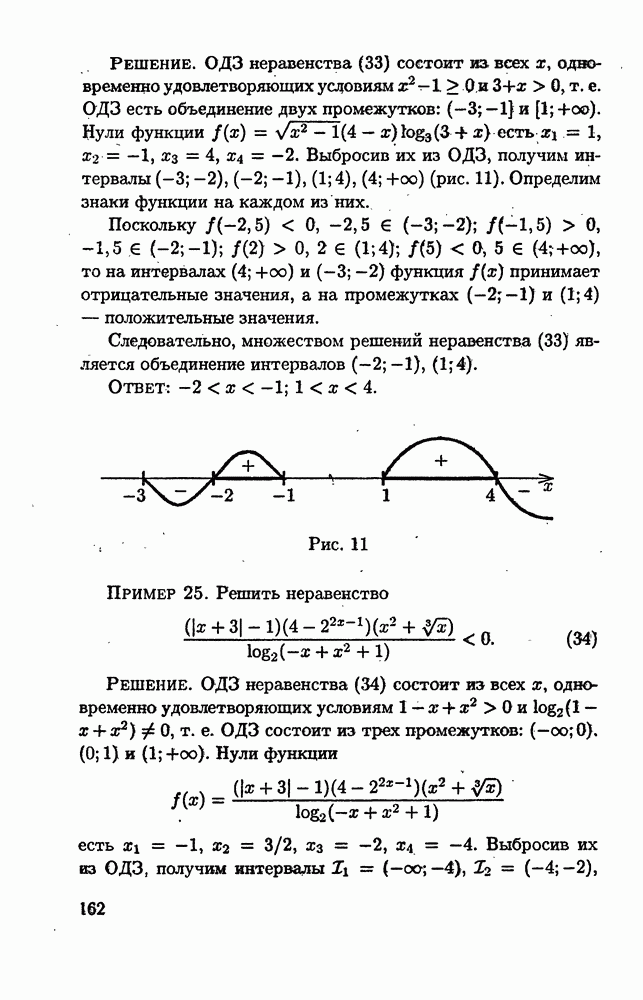
Отметим на координатной оси числа  и 4 и расставим знаки плюс и минус так, как указано на рис. 1.
и 4 и расставим знаки плюс и минус так, как указано на рис. 1.
Решениями неравенства (12) будут все х из объединения промежутков 
Ответ: 
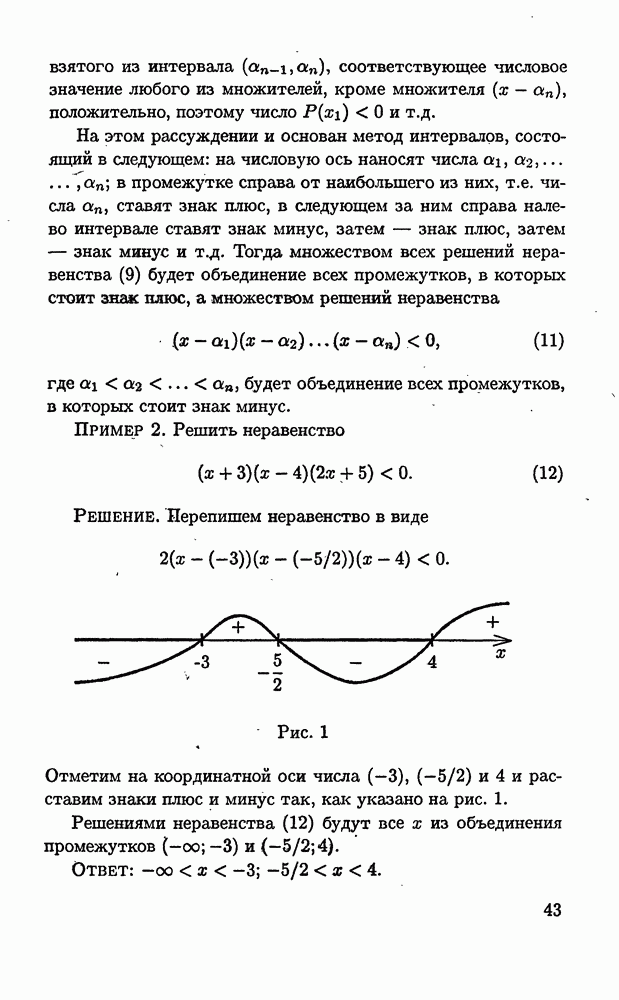
Пример 3. Решить неравенство

Решение. Перепишем неравенство (13) в виде

или

Поскольку  для любого действительного х, то неравенство (14) равносильно неравенству
для любого действительного х, то неравенство (14) равносильно неравенству  Применяя метод интервалов, находим решения последнего, а значит и исходного неравенства: это будут все х из двух промежутков
Применяя метод интервалов, находим решения последнего, а значит и исходного неравенства: это будут все х из двух промежутков  (рис. 2).
(рис. 2).
Ответ: 
Метод интервалов можно применять и при решении неравенств вида

где  — многочлены, если заметить, что на множестве всех действительных чисел неравенство (15) равносильно неравенству
— многочлены, если заметить, что на множестве всех действительных чисел неравенство (15) равносильно неравенству 

Рис. 2
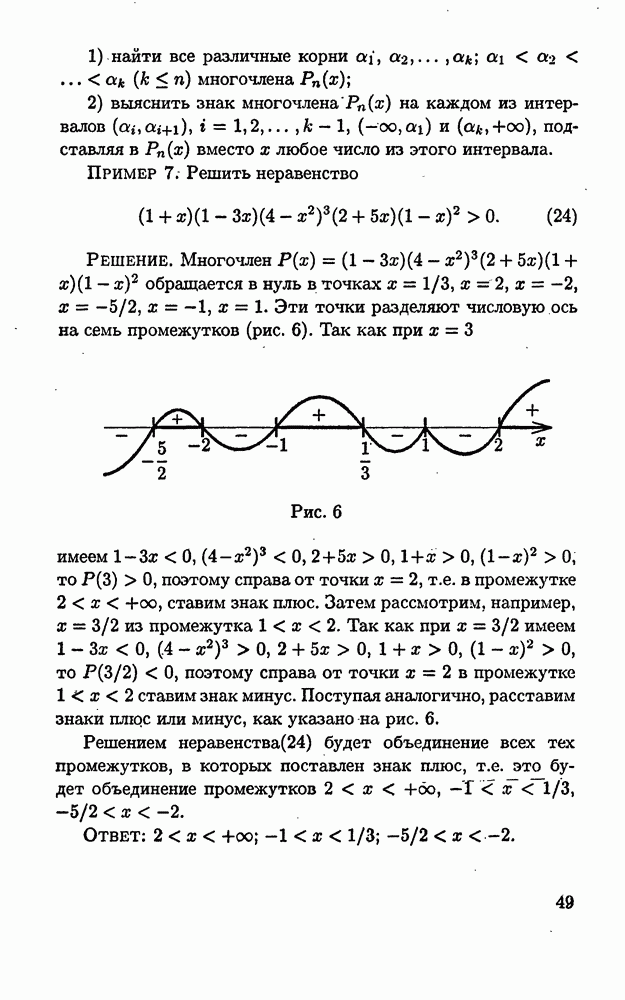
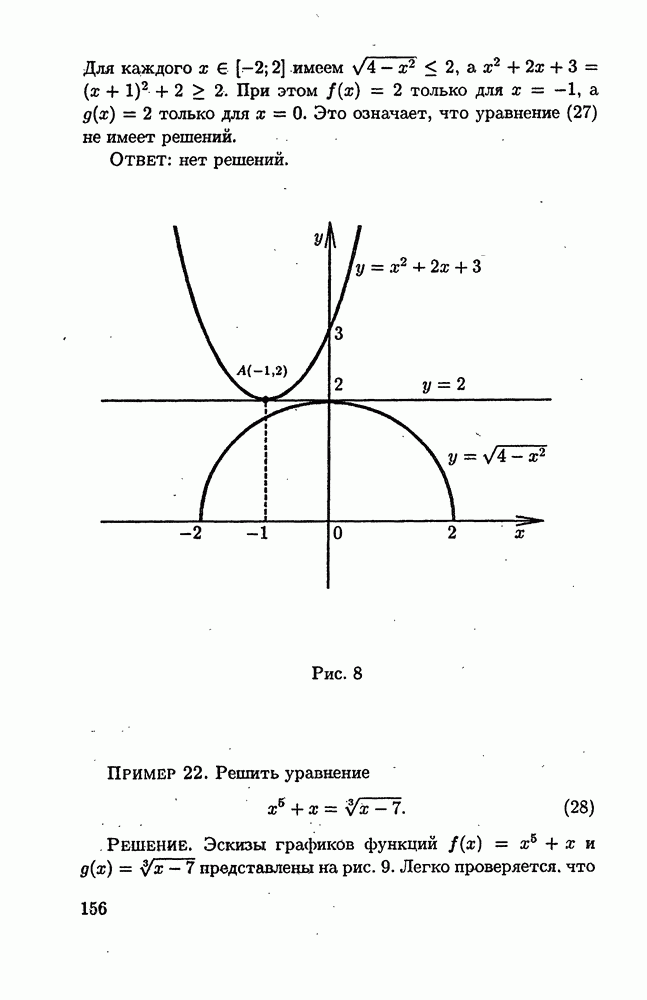
Пример 4. Решить неравенство

Решение. Неравенство (16) равносильно неравенству

Перепишем это неравенство в виде


Рис. 3
Применяя метод интервалов (рис. 3), получим, что решениями неравенства (17), а значит, и решениями исходного неравенства, являются все х из трех промежутков — 
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.