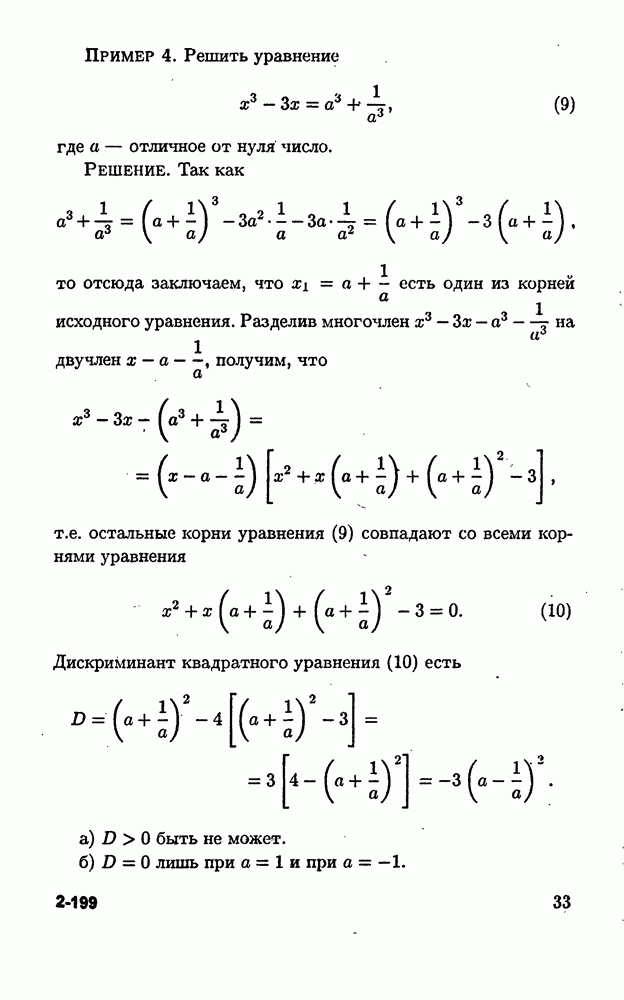| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
§ 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
2.1.1. Возведение в степень.
Основным методом решения уравнений и неравенств, содержащих радикалы, является возведение, возможно даже неоднократное, обеих частей уравнения или неравенства в соответствующую степень.
При возведении обеих частей уравнения или неравенства в степень надо следить за равносильностью преобразований.
Для уравнений можно не следить за равносильностью, тогда в конце решения надо делать проверку найденных корней. Пример 1. Решить неравенство

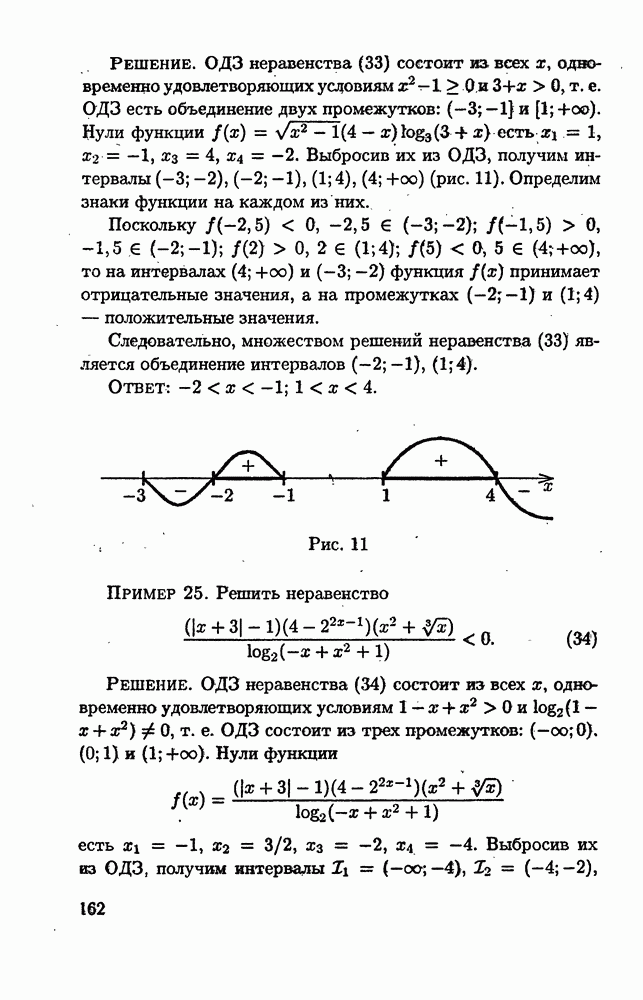
Решение. ОДЗ неравенства состоит из всех х, удовлетворяющих
одновременно условиям

т. е. ОДЗ есть все х из промежутка  Перепишем неравенство (1) в виде
Перепишем неравенство (1) в виде

На ОДЗ обе части неравенства (2) неотрицательны, поэтому, возводя обе части этого неравенства в квадрат, получим на ОДЗ исходного неравенства равносильное ему неравенство

На ОДЗ неравенства выражение  принимает как положительные, так и отрицательные значения, поэтому разобьем ОДЗ на два промежутка
принимает как положительные, так и отрицательные значения, поэтому разобьем ОДЗ на два промежутка  Для любого х, принадлежащего промежутку
Для любого х, принадлежащего промежутку  левая часть неравенства (3) неположительная, а правая — положительная. Это означает, что для каждого из таких х неравенство (3) выполняется.
левая часть неравенства (3) неположительная, а правая — положительная. Это означает, что для каждого из таких х неравенство (3) выполняется.
Если х принадлежит промежутку  то обе части неравенства (3) положительны и оно на это области равносильно неравенству
то обе части неравенства (3) положительны и оно на это области равносильно неравенству

т.е. неравенству

Решениями неравенства (4) являются все х на промежутка  . Для х из этого промежутка условию
. Для х из этого промежутка условию  удовлетворяют только х из промежутка
удовлетворяют только х из промежутка 

Объединяя полученные решения в каждом из двух случаев, получаем, что решениями исходного неравенства являются все  из промежутка
из промежутка 
Ответ: 
Пример 2. Решить уравнение

Решение. ОДЗ уравнения (5) есть все  На ОДЗ обе части уравнения (5) положительны, поэтому после возведения в квадрат получим уравнение
На ОДЗ обе части уравнения (5) положительны, поэтому после возведения в квадрат получим уравнение

равносильное для  уравнению (5). Перепишем уравнение (6) в виде
уравнению (5). Перепишем уравнение (6) в виде

Для любого  левая часть уравнения (7) положительна, а правая отрицательна. Следовательно, среди
левая часть уравнения (7) положительна, а правая отрицательна. Следовательно, среди  нет решений уравнения (7).
нет решений уравнения (7).
Для —  левая часть уравнения (7) неотрицательна, поэтому после возведения в квадрат получим уравнение
левая часть уравнения (7) неотрицательна, поэтому после возведения в квадрат получим уравнение

равносильное для этих х уравнению (7). Уравнение (8) имеет единственный корень  Так как это число
Так как это число  удовлетворяет условию
удовлетворяет условию  то
то  является корнем уравнения (5), равносильного уравнению (8) для этих
является корнем уравнения (5), равносильного уравнению (8) для этих 
Ответ: 
Пример 3. Решить уравнение

Решение. Перепишем уравнение (9) в виде

Возводя обе части уравнения (10) в квадрат, получим уравнение

являющееся следствием исходного уравнения (9). Последнее уравнение можно переписать в виде

Следствием этого уравнения является уравнение

Решения уравнения (11) есть  Так как уравнение (11) — следствие уравнения (9), то надо проверить, являются ли
Так как уравнение (11) — следствие уравнения (9), то надо проверить, являются ли  его корнями. Подставляя эти значения х в исходное уравнение, получаем, что
его корнями. Подставляя эти значения х в исходное уравнение, получаем, что  является его решением, а
является его решением, а  не является.
не является.
Ответ: 
Замечание. Если уравнение (5) решать переходом к следствию, то проверка найденного корня была бы затруднительна. Если уравнение (9) решать с помощью равносильных преобразований, то его решение будет намного сложнее, чем приведенное выше.
Поэтому при решении уравнений с радикалами надо уметь пользовться любым из этих способов.
2.1.2. Уравнения вида ...
Уравнение

можно решить при помощи описанного в пункте 2.1.1 основного метода, но иногда их можно решить следующим образом.
Рассмотрим решение уравнении типа (12) на множестве М — тех значений х, для которых 
Пусть  корень уравнения
корень уравнения

Тогда справедливо числовое равенство

Найдем разность чисел

и запишем равенство (15) в виде

Используя равенство (14), запишем равенство (16) в виде

Равенство (17) означает, что число  есть корень уравнения
есть корень уравнения

Таким образом, уравнение (18) является следствием уравнения (13) на множестве М. Складывая уравнения (13) и (18) и умножая полученное уравнение на  получим уравнение
получим уравнение

также являющееся следствием уравнения (13) на множестве М. Возведя уравнение (19) в квадрат и решив полученное уравнение, надо сделать проверку найденных корней, т.е. проверить, являются ли его корни корнями исходного уравнения (13).
Замечание. Если  корень уравнения (13) и
корень уравнения (13) и  то
то  также есть корень уравнения (19). Следовательно, уравнение (19) есть следствие уравнения (13).
также есть корень уравнения (19). Следовательно, уравнение (19) есть следствие уравнения (13).
Отметим, что точно так же показывается, что уравнение (19) есть следствие уравнения

Пример 4. Решить уравнение

Решение. Поскольку разность подкоренных выражений  есть
есть  и
и

то уравнение

является следствием исходного уравнения. Тогда, складывая уравнения (20) и (21), получим уравнение

также являющееся следствием уравнения (20). Возводя обе части уравнения (22) в квадрат, получим уравнение

являющееся следствием исходного уравнения. Решения уравнения (23) есть  Проверкой убеждаемся, что оба эти числа являются корнями исходного уравнения. Ответ:
Проверкой убеждаемся, что оба эти числа являются корнями исходного уравнения. Ответ: 
2.1.3. Уравнения вида ...
Уравнение

можно решать следующим методом.
Пусть  — корень уравнения (24). Тогда справедливо числовое равенство
— корень уравнения (24). Тогда справедливо числовое равенство

После возведения равенства (25) в куб получим равенство

откуда в силу (25) имеем равенство

Равенство (26) означает, что  есть корень уравнений
есть корень уравнений

Таким образом, уравнение (27) есть следствие уравнения (24). Возведя уравнение (27) в куб и решив полученное уравнение, надо проверить, являются ли найденные корни корнями исходного уравнения.
Пример 5. Решить уравнение

Решение. Возведя обе части уравнения в куб, получим уравнение

равносильное исходному. Подставляя вместо выражения  единицу, получаем уравнение
единицу, получаем уравнение

являющееся следствием исходного уравнения.
Уравнение (29) перепишем так:

Возводя обе части уравнения (30) в куб, получаем уравнение

равносильное уравнению (30). Решения уравнения (31) есть  Проверка показывает, что
Проверка показывает, что  не является корнем исходного уравнения, а
не является корнем исходного уравнения, а  является его корнем. Ответ:
является его корнем. Ответ: 
Частным случаем уравнения (24) является уравнение вида

Уравнение (32) после возведения обеих частей в третью степень и замены выражения  на
на  приводится к уравнению
приводится к уравнению

которое есть следствие исходного уравнения. В некоторых случаях уравнение (33) можно решить и тем самым найти числа, среди которых содержатся корни исходного уравнения (32).
Пример 6. Решить уравнение

Решение. Возведя обе части уравнения (34) в третью степень, имеем уравнение

равносильное исходному. Заменяя выражение  выражением
выражением  получим уравнение, являющееся следствием исходного
получим уравнение, являющееся следствием исходного

Уравнение (36) равносильно совокупности двух уравнении

и

Решения первого уравнения совокупности (37) есть  Решение второго уравнения совокупности (37) есть
Решение второго уравнения совокупности (37) есть 
Проверка показывает, что  являются корнями исходного уравнения.
являются корнями исходного уравнения.
Ответ: 
Замечание. Уравнение вида

можно решать следующим образом. 
Умножая обе части уравнения на  перейдем, к уравнению
перейдем, к уравнению

являющемуся следствием уравнения (38). Далее уравнение (39) можно решать так, как это предлагалось в этом пункте. Только надо помнить, что уравнение (39) есть следствие уравнения (38).
2.1.4. Умножение уравнения или неравенства на функции.
В некоторых случаях полезно умножение обоих
частей уравнения или неравенства, содержащих радикалы, на некоторую функцию, имеющую смысл на их ОДЗ.
При решении уравнения этим способом надо либо следить за равносильностью преобразований на ОДЗ исходного уравнения, либо в конце решения надо делать проверку, так как могут появиться посторонние корни.
При решении неравенства надо следить за равносильностью преобразований неравенства на его ОДЗ, и поэтому можно умножать обе части неравенства на функцию, принимающую на ОДЗ неравенства только значения одного знака, либо разбивать ОДЗ на промежутки, на которых функция знакопостоянна, и делать равносильные преобразования на этих промежутках.
Пример 7. Решить уравнение

Решение. Умножив обе части уравнения на функцию VI  получим уравнение
получим уравнение

являющееся следствием уравнения (40). Перепишем уравнение (41) в виде

Следствием уравнения (42) является уравнение

Решениями уравнения (42) являются  Проверка показывает, что
Проверка показывает, что  является корнем исходного уравнения, а
является корнем исходного уравнения, а  не являются его корнями.
не являются его корнями.
Ответ: 
Пример 8. Решить уравнение

Решение. ОДЗ уравнения состоит из всех х, удовлетворяющих одновременно условиям  т.е. ОДЗ есть все
т.е. ОДЗ есть все  На ОДЗ уравнение (44) можно переписать в виде
На ОДЗ уравнение (44) можно переписать в виде

или в виде

После умножения обеих частей уравнения (45) на функцию  , принимающую на ОДЗ уравнения (44) только положительные значения, получим уравнение
, принимающую на ОДЗ уравнения (44) только положительные значения, получим уравнение

равносильное исходному на его ОДЗ. Поскольку выражение  обращается в нуль при
обращается в нуль при  то разобьем множество
то разобьем множество  на два множества:
на два множества:  Для любого
Для любого  левая часть уравнения (46) неположительна, а правая положительна. Значит, ни одно из этих х не может быть решением уравнения (46), а значит, и исходного уравнения.
левая часть уравнения (46) неположительна, а правая положительна. Значит, ни одно из этих х не может быть решением уравнения (46), а значит, и исходного уравнения.
Для любого  обе части уравнения (46) положи-, тельны, и оно на этом множестве равносильно уравнению
обе части уравнения (46) положи-, тельны, и оно на этом множестве равносильно уравнению

т.е. уравнению

Уравнение (47) на множестве  равносильно уравнению
равносильно уравнению

т.е. уравнению

Решения уравнения (48) есть  Из этих значений х условию
Из этих значений х условию  удовлетворяет только
удовлетворяет только  оно и является решением исходного уравнения.
оно и является решением исходного уравнения.
Ответ: 
Пример 9. Решить неравенство

Решение. ОДЗ неравенства (49) состоит из всех х, для которых  Поскольку на ОДЗ
Поскольку на ОДЗ  , получим неравенство
, получим неравенство

равносильное исходному на множестве 
При  имеем
имеем  и неравенство (50) перепишется в виде
и неравенство (50) перепишется в виде

Решения неравенства (51) составляют промежуток  Поэтому для этих
Поэтому для этих  решения неравенства (50) составляют промежуток
решения неравенства (50) составляют промежуток 
При —  неравенство (50) перепишется в виде
неравенство (50) перепишется в виде

Решения неравенства (52) составляют промежуток  Поэтому решением неравенства (50) при рассматриваемых условиях будет промежуток
Поэтому решением неравенства (50) при рассматриваемых условиях будет промежуток  Следовательно, множеством решений неравенства (49) является объединение промежутков
Следовательно, множеством решений неравенства (49) является объединение промежутков

т.е. интервал

Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
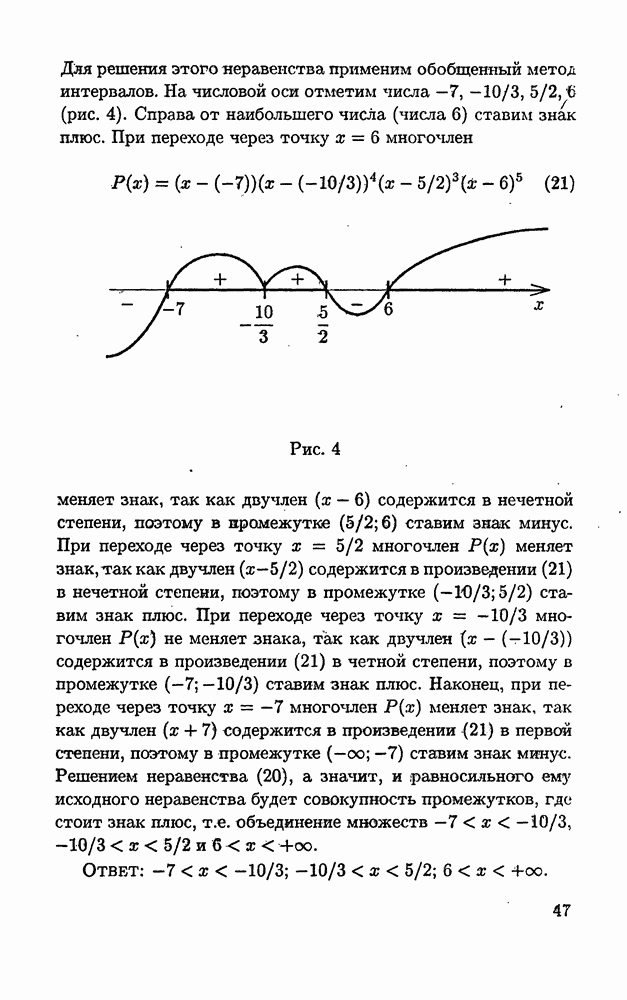
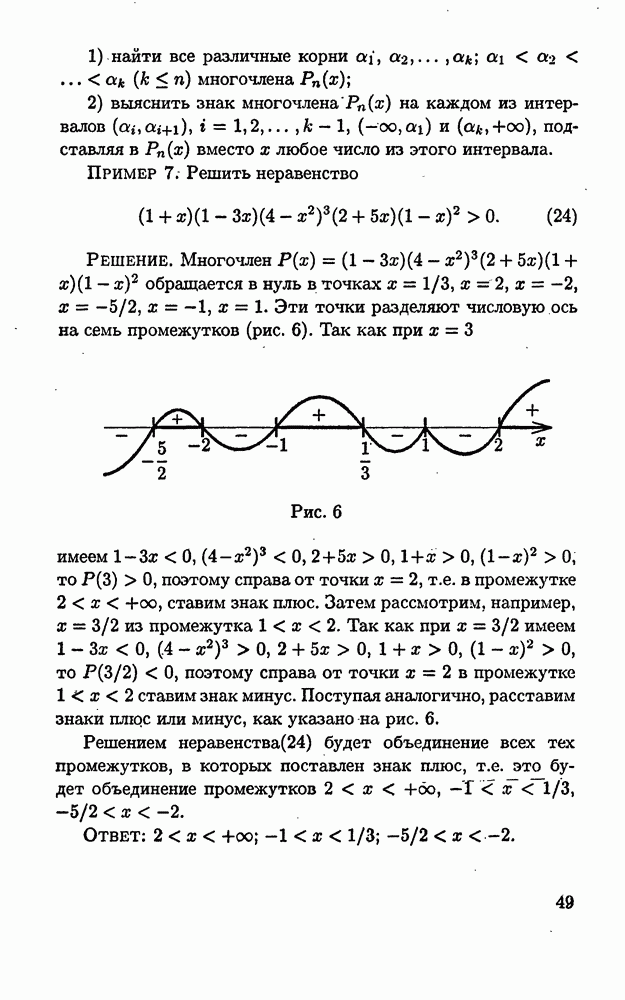
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.