| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1.5. Решение алгебраических неравенств
1.5.1. Простейшие способы решения алгебраических неравенств.
Так как, умножая неравенство (III) на  его можно привести к виду (II), а умножая неравенство (II) на
его можно привести к виду (II), а умножая неравенство (II) на  его можно привести к виду (III), то дальше будем считать, что в неравенствах (II) и (III) положителен коэффициент при старшем члене, т.е. что
его можно привести к виду (III), то дальше будем считать, что в неравенствах (II) и (III) положителен коэффициент при старшем члене, т.е. что 
Таким образом, в этом пункте рассматриваются только неравенства вида

и

где 
В случае  неравенства (1) и (2) обычно записывают в виде
неравенства (1) и (2) обычно записывают в виде

и называют неравенствами первой степени.
Множество решений неравенства (3) есть промежуток  множество решений неравенства (4) есть промежуток
множество решений неравенства (4) есть промежуток 
В случае  неравенства (1) и (2) обычно записывают в виде
неравенства (1) и (2) обычно записывают в виде

и называют квадратными неравенствами.
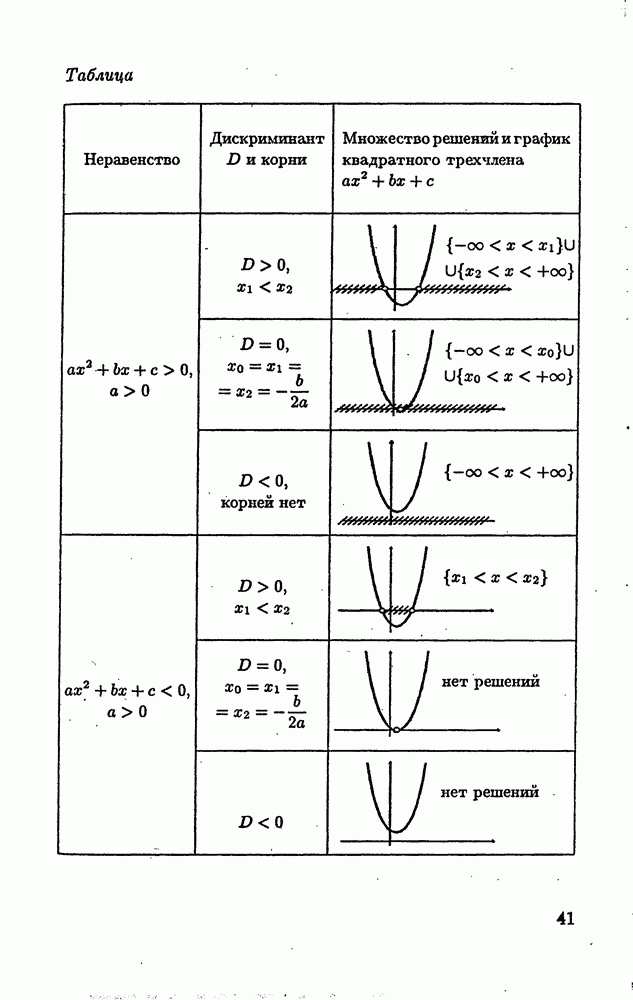
Решения неравенств (5) и (6) зависят от знака дискриминанта  квадратного трехчлена
квадратного трехчлена  с и приведены в таблице.
с и приведены в таблице.
В случае  многочлен (IV) надо сначала разложить на множители и затем либо заменить неравенство равносильной ему совокупностью систем неравенств, либо применить изложенный ниже метод интервалов.
многочлен (IV) надо сначала разложить на множители и затем либо заменить неравенство равносильной ему совокупностью систем неравенств, либо применить изложенный ниже метод интервалов.
Отметим, что при разложении на множители, конечно, можно пользоваться всеми теми же методами, которые были изложены при решении уравнений.
Таблица (см. скан)
Пример 1. Решить неравенство

Решение. Разложим методом группировки на множители многочлен, находящийся в левой части неравенства

Тогда неравенство (Т) можно переписать в виде

Так как  для любого
для любого  то неравенство (8) равносильно неравенству
то неравенство (8) равносильно неравенству 
Решения этого неравенства, а значит, и исходного, есть все 
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- § 1.1. Разложение многочлена на множители
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- § 1.5. Решение алгебраических неравенств
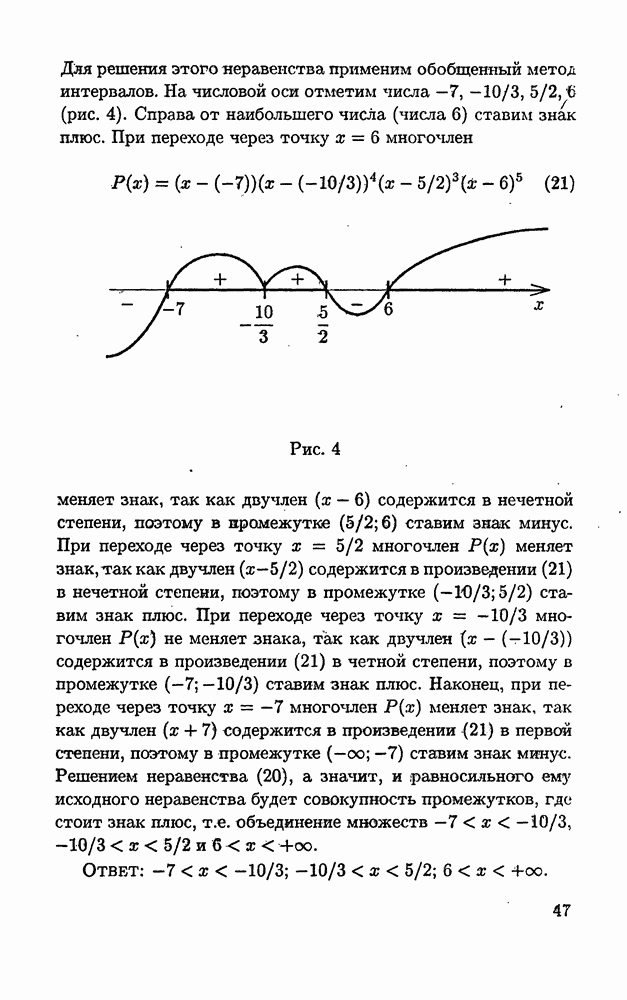
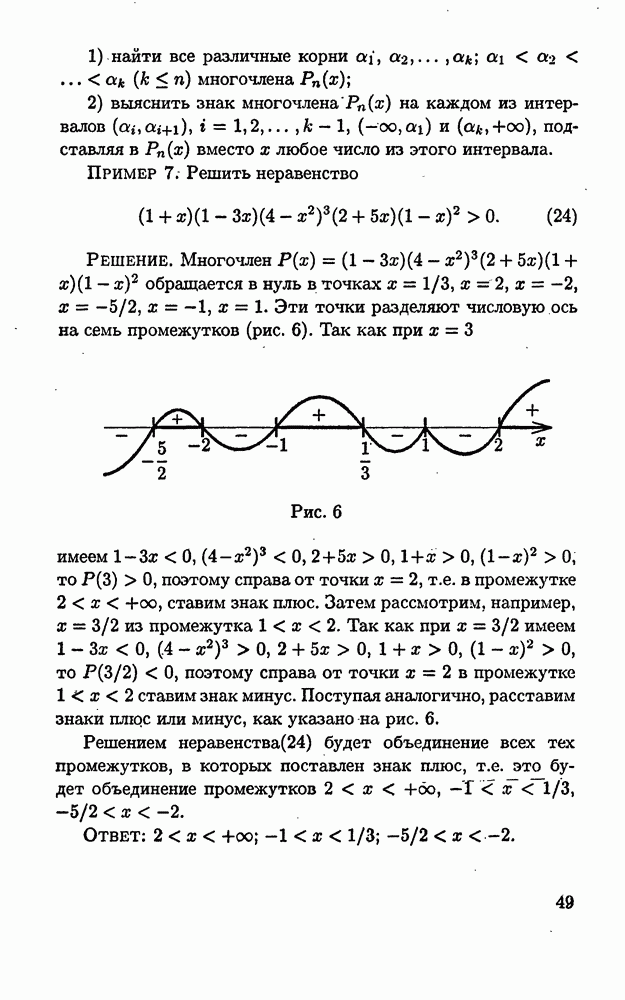
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ РАДИКАЛЫ, СТЕПЕНИ, ЛОГАРИФМЫ И МОДУЛИ
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком радикала
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- Глава III. СПОСОБ ЗАМЕНЫ НЕИЗВЕСТНЫХ ПРИ РЕШЕНИИ УРАВНЕНИЙ
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнении сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ВХОДЯЩИХ В НИХ ФУНКЦИЙ
- § 4.1. Применение основных свойств функций
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- § 4.3. Применение производной.