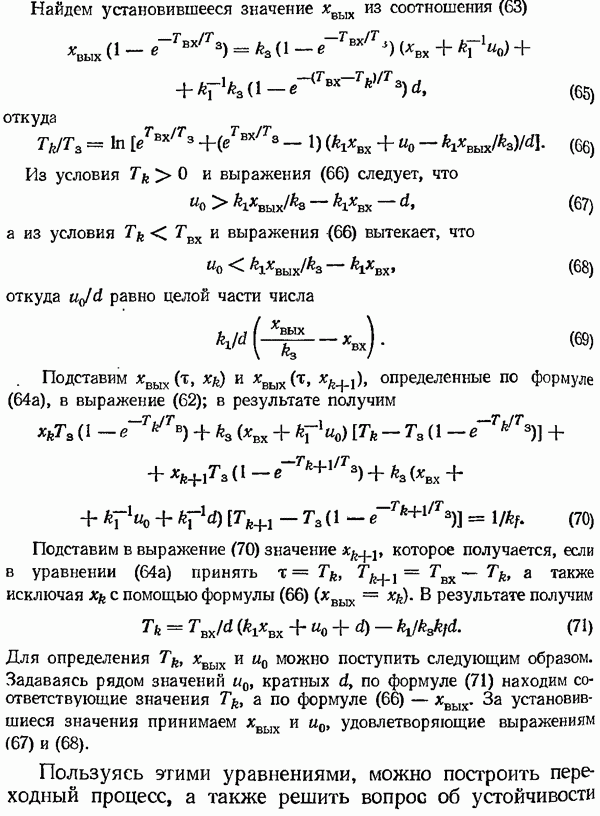| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. САУ С ЦИФРОВЫМ ИНТЕГРАТОРОМ
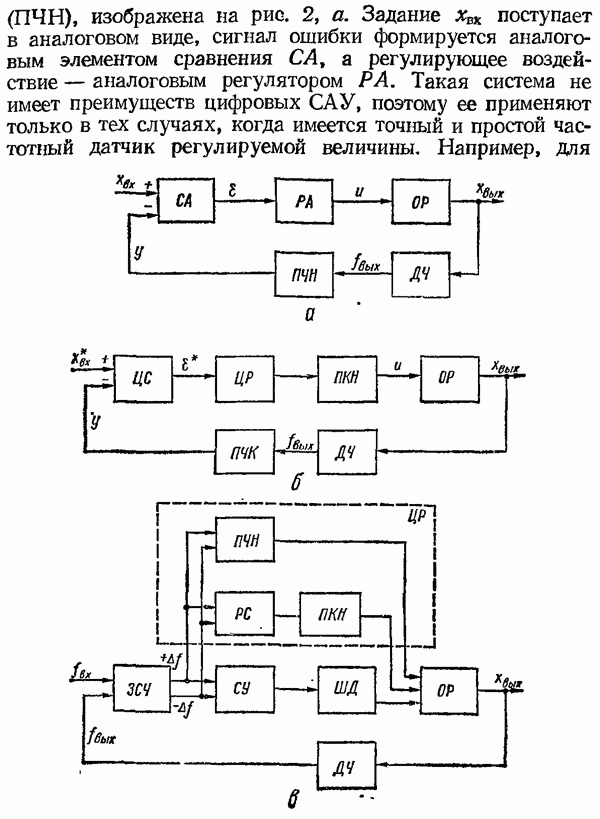
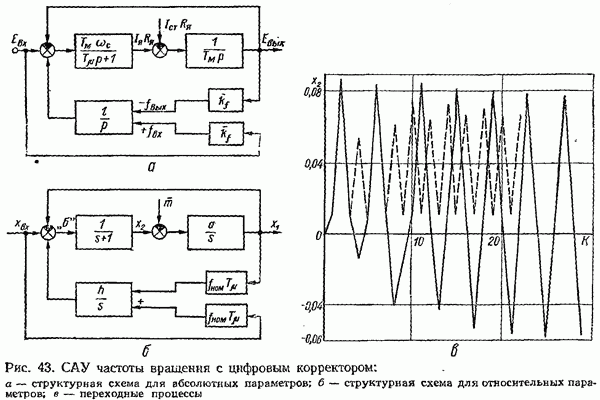
Если выполнено условие (37), то цифровой интегратор и цифровые устройства для введения ПИД-составляющих можно заменить непрерывными и структурные схемы рис. 2, г и д привести к схемам, изображенным на рис. 37, а, б. Здесь  , где
, где  равно изменению выходного напряжения интегратора при изменении его состояния на единицу;
равно изменению выходного напряжения интегратора при изменении его состояния на единицу;  — передаточная функция
— передаточная функция  с фильтром на выходе (без учета интегрирующих свойств ЦИ);
с фильтром на выходе (без учета интегрирующих свойств ЦИ);  — коэффициенты усиления соответственно по пропорциональному и дифференцирующему каналам;
— коэффициенты усиления соответственно по пропорциональному и дифференцирующему каналам;  — учитывает дополнительные инерционности и запаздывания в этих каналах,
— учитывает дополнительные инерционности и запаздывания в этих каналах,  — передаточная функция регулятора без учета канала ЦИ. Коэффициенты и
— передаточная функция регулятора без учета канала ЦИ. Коэффициенты и  определяются схемами узлов, примененных для получения указанных составляющих. Если пропорциональная составляющая образуется с помощью схемы вычитания частот и преобразователя частота — напряжение, основанном на формировании постоянной вольт-секундной площади импульса
определяются схемами узлов, примененных для получения указанных составляющих. Если пропорциональная составляющая образуется с помощью схемы вычитания частот и преобразователя частота — напряжение, основанном на формировании постоянной вольт-секундной площади импульса  то
то  , а при использовании преобразователя, основанного на подсчете числа импульсов за время
, а при использовании преобразователя, основанного на подсчете числа импульсов за время  , где
, где  — напряжение на выходе преобразователя при максимальном заполнении счетчика емкостью
— напряжение на выходе преобразователя при максимальном заполнении счетчика емкостью  . При
. При
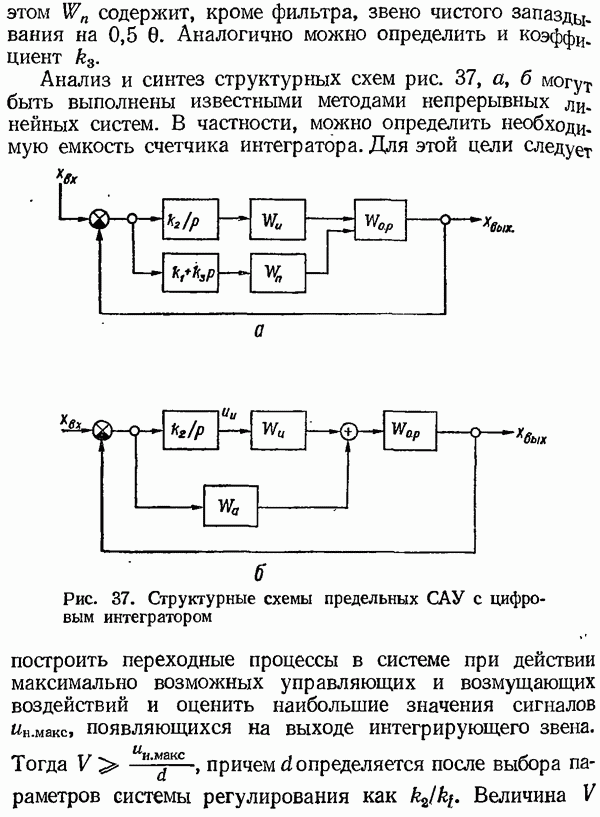
этом  содержит, кроме фильтра, звено чистого запаздц. вания на 0,5 0. Аналогично можно определить и коэффициент
содержит, кроме фильтра, звено чистого запаздц. вания на 0,5 0. Аналогично можно определить и коэффициент 
Рис. 37. (см. скан) Структурные схемы предельных САУ с цифровым
Анализ и синтез структурных схем рис. 37, а, б могут быть выполнены известными методами непрерывных линейных систем. В частности, можно определить необходимую емкость счетчика интегратора. Для этой цели следует интегратором построить переходные процессы в системе при действии максимально возможных управляющих и возмущающих воздействий и оценить наибольшие значения сигналов  появляющихся на выходе интегрирующего звена.
появляющихся на выходе интегрирующего звена.
Тогда  причем
причем  определяется после выбора параметров системы регулирования как
определяется после выбора параметров системы регулирования как  . Величина V
. Величина V
[может быть выбрана меньше, чем  однако в этом [случае при переходных процессах интегратор может выходить из зоны линейности, что приводит к затягиванию
однако в этом [случае при переходных процессах интегратор может выходить из зоны линейности, что приводит к затягиванию  переходных процессов и может вызвать увеличение колебательности и даже неустойчивость. Минимально допустимая величина V должна быть такой, чтобы обеспечить компенсацию возмущений в статическом режиме.
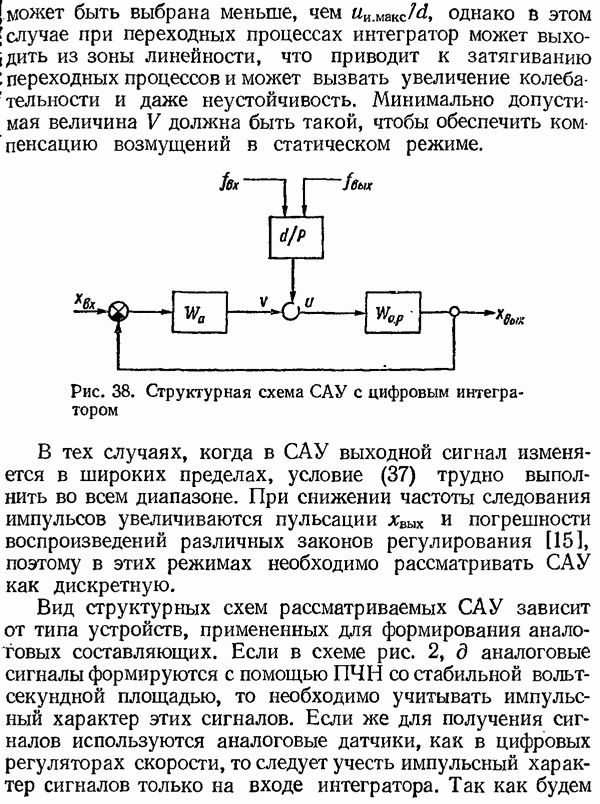
переходных процессов и может вызвать увеличение колебательности и даже неустойчивость. Минимально допустимая величина V должна быть такой, чтобы обеспечить компенсацию возмущений в статическом режиме.

Рис. 38. Структурная схема САУ с цифровым интегратором
В тех случаях, когда в САУ выходной сигнал изменяется в широких пределах, условие (37) трудно выполнить во всем диапазоне. При снижении частоты следования импульсов увеличиваются пульсации  и погрешности воспроизведений различных законов регулирования [15], поэтому в этих режимах необходимо рассматривать САУ как дискретную.
и погрешности воспроизведений различных законов регулирования [15], поэтому в этих режимах необходимо рассматривать САУ как дискретную.
Вид структурных схем рассматриваемых САУ зависит от типа устройств, примененных для формирования аналоговых составляющих. Если в схеме рис. 2, д аналоговые сигналы формируются с помощью ПЧН со стабильной вольт-секундной площадью, то необходимо учитывать импульсный характер этих сигналов. Если же для получения сигналов используются аналоговые датчики, как в цифровых регуляторах скорости, то следует учесть импульсный характер сигналов только на входе интегратора. Так как будем
анализировать режим работы САУ, при котором сигналы на ее выходе меньше максимальных, то можно принять что импульсы аппроксимируются дельта-функциями (период следования импульсов во много раз больше их длительности).
Рассмотрим САУ с использованием аналоговых датчиков, структурная схема которой изображена на рис. 38 (считая что  отнесено к
отнесено к  или пренебрегая
или пренебрегая  ). Тогда
). Тогда

Предположим, что  выполнен по схеме, изображенной на рис. 19. Пусть
выполнен по схеме, изображенной на рис. 19. Пусть  , где
, где  — порядок
— порядок  — порядок
— порядок  . Предположим, что момент
. Предположим, что момент  совпадает с приходом импульса частот
совпадает с приходом импульса частот  или
или  и известны начальные значения
и известны начальные значения  . Так как система линейная, то (51)
. Так как система линейная, то (51)

При  после прихода очередного импульса и
после прихода очередного импульса и  скачком изменяется
скачком изменяется  и до прихода следующего импульса не меняется. Функции
и до прихода следующего импульса не меняется. Функции  являются обратными преобразованиями Лапласа от
являются обратными преобразованиями Лапласа от

Функция  является решением однородного дифференциального уравнения системы с заданными начальными условиями. Она может быть найдена, например, преобразованием Лапласа. Это дифференциальное уравнение в операторной форме можно записать в виде
является решением однородного дифференциального уравнения системы с заданными начальными условиями. Она может быть найдена, например, преобразованием Лапласа. Это дифференциальное уравнение в операторной форме можно записать в виде  , где
, где  — полиномы относительно
— полиномы относительно  соответствующие числителям и знаменателям
соответствующие числителям и знаменателям  . Функция линейна по
. Функция линейна по  поэтому
поэтому

Повторным дифференцированием  по
по  вычислим
вычислим  . Введем вектор
. Введем вектор  , имеющий компоненты
, имеющий компоненты  которой
которой  равны коэффициентам при
равны коэффициентам при  в (формуле для
в (формуле для  ). Аналогично введем векторы
). Аналогично введем векторы  компоненты которых равны коэффициентам при
компоненты которых равны коэффициентам при  и
и  в формулах для
в формулах для  Тогда можно записать следующее
Тогда можно записать следующее  равенство:
равенство:

Будем рассматривать импульсные последовательности  как общую последовательность, причем текущий
как общую последовательность, причем текущий  период этой последовательности обозначим
период этой последовательности обозначим  . Предположим, что сразу же после прихода
. Предположим, что сразу же после прихода  импульса (т. е. в момент
импульса (т. е. в момент  причем
причем  является начальным условием для изменения
является начальным условием для изменения  при
при  . На основании выражения (54) можно записать
. На основании выражения (54) можно записать

причем

где  если
если  импульс является импульсом
импульс является импульсом  если
если  импульс является импульсом
импульс является импульсом  .
.
Для построения переходного процесса необходимо определить  . При этом нужно учитывать, что в переходных процессах несколько импульсов одной частоты
. При этом нужно учитывать, что в переходных процессах несколько импульсов одной частоты  или
или  могут поступать подряд. Будем рассматривать только интегральную частотную модуляцию
могут поступать подряд. Будем рассматривать только интегральную частотную модуляцию  рода, когда
рода, когда  период выходной частоты определяется из уравнения
период выходной частоты определяется из уравнения

Имеем  . Если при
. Если при  был импульс входной частоты
был импульс входной частоты  то
то  является
является
решением уравнения

где суммирование проводится от  до
до  шага, когда последний раз был импульс
шага, когда последний раз был импульс  . При этом, если
. При этом, если  , то
, то  если
если  , то
, то  . При расчетах по формуле (58) интегралы в правой ее части зависят от известных величин.
. При расчетах по формуле (58) интегралы в правой ее части зависят от известных величин.
Если

где определяется как решение уравнения

В формуле  — номер шага, когда последний раз был импульс
— номер шага, когда последний раз был импульс  при этом, если
при этом, если  то
то  если
если 
С помощью полученного соотношения можно построить переходный процесс отработки входного сигнала. Значения фазовых координат находятся только в моменты прихода импульсов. На рис. 39 показана структурная схема алгогоритма для определения  причем
причем


Рис. 39. Структурная схема алгоритма определения 
С помощью приведенных уравнений можно вычислить установившиеся значения координат. В установившемся режиме импульсы входной и выходной частот чередуются, а  принимает значения
принимает значения  . Учитывая, что
. Учитывая, что  и принимая, что первый импульс является импульсом выходной частоты, получаем
и принимая, что первый импульс является импульсом выходной частоты, получаем

Таким образом, для определения  неизвестных
неизвестных  имеем
имеем  уравнений (61), а также уравнение, связывающее
уравнений (61), а также уравнение, связывающее  и
и  в виде
в виде

Учтя свойства переходной матрицы  и вектора
и вектора  согласно выражению (61), можно записать
согласно выражению (61), можно записать

Недостающая зависимость, необходимая для однозначного определения фазовых координат и  установившемуся режиме, получается из ограничивающих условий:
установившемуся режиме, получается из ограничивающих условий:  — целое число.
— целое число.
Пример 2. Пусть  . В соответствии с выражением (51)
. В соответствии с выражением (51)

откуда

Найдем установившееся значение  из соотношения (63)
из соотношения (63)

откуда

Из условия  и выражения (66) следует, что
и выражения (66) следует, что

а из условия  и выражения (66) вытекает, что
и выражения (66) вытекает, что

откуда  равно целой части числа
равно целой части числа

Подставим  определенные по формуле (64а), в выражение (62); в результате получим
определенные по формуле (64а), в выражение (62); в результате получим

Подставим в выражение (70) значение  которое получается, если в уравнении (64а) принять
которое получается, если в уравнении (64а) принять  а также исключая
а также исключая  с помощью формулы
с помощью формулы  . В результате получим
. В результате получим

Для определения  можно поступить следующим образом. Задаваясь рядом значений
можно поступить следующим образом. Задаваясь рядом значений  кратных
кратных  по формуле (71) находим соответствующие значения
по формуле (71) находим соответствующие значения  , а по формуле
, а по формуле  . За установившиеся значения принимаем
. За установившиеся значения принимаем  , удовлетворяющие выражениям (67) и (68).
, удовлетворяющие выражениям (67) и (68).
Пользуясь этими уравнениями, можно построить переходный процесс, а также решить вопрос об устойчивости
системы. Так как рассматриваемая САУ с ЧИМ является (нелинейной, то в ней возможны различные типы устойчивых автоколебательных процессов. Определение устойчивости  общем виде достаточно сложно. Правильно спроектированная система должна удовлетворять условиям устойчивости «в малом» с достаточным запасом.
общем виде достаточно сложно. Правильно спроектированная система должна удовлетворять условиям устойчивости «в малом» с достаточным запасом.

Рис. 40. К расчету устойчивости САУ
Найдем рекуррентное соотношение, связывающее значения фазовых координат в моменты поступления двух соседних импульсов  , причем между этими двумя импульсами поступает один импульс
, причем между этими двумя импульсами поступает один импульс  (рис. 40), как это происходит в установившемся режиме. Если в соотношении (61) заменить
(рис. 40), как это происходит в установившемся режиме. Если в соотношении (61) заменить  на
на  , то получим:
, то получим:

Из рис. 40

Значения  связаны рекуррентным соотношением
связаны рекуррентным соотношением

Учитывая свойства матрицы  векторов
векторов  и
и  и подставляя соотношение (73) в выражение (72), получаем
и подставляя соотношение (73) в выражение (72), получаем

где  и определяется видом модуляции. Уравнения (73) и (74) образуют искомые рекуррентные соотношения порядка
и определяется видом модуляции. Уравнения (73) и (74) образуют искомые рекуррентные соотношения порядка  .
.
Введем квадратную матрицу  порядка
порядка  элементы которой
элементы которой  являются частными производными
являются частными производными  строки системы (73), (74) по
строки системы (73), (74) по  при
при  или по
или по  при
при  причем
причем  вычисляются в точке равновесия. Для устойчивой системы все собственные числа
вычисляются в точке равновесия. Для устойчивой системы все собственные числа  по модулю меньше 1.
по модулю меньше 1.
Пример 3. Пусть на рис. 37, б  . Воспользовавшись соотношениями (64) и (74), запишем
. Воспользовавшись соотношениями (64) и (74), запишем

Продифференцируем правую часть этого равенства по  положив
положив  После подстановки в этот результат координаты точки равновесия
После подстановки в этот результат координаты точки равновесия  получим
получим

Подставляя в выражение  а также из соотношения (66), получаем
а также из соотношения (66), получаем

Аналогично определяем

Условия устойчивости запишем в виде [36]


Ограничивающим является второе неравенство. Подставим в выражение (70) значение  из выражения (64а), а также исключим
из выражения (64а), а также исключим  с помощью соотношения (72а). Получим следующее неявное уравнение, связывающее
с помощью соотношения (72а). Получим следующее неявное уравнение, связывающее  :
:

Производные  находятся по правилам дифференцирования неявных функций:
находятся по правилам дифференцирования неявных функций:

Выполняя дифференцирование и подставляя координаты исследуемой точки из формул (66) и (71), получаем

Подставляя выражения (82) и (83) в соотношения  ратем коэффициенты
ратем коэффициенты  во второе неравенство (80), получаем условие устойчивости в виде
во второе неравенство (80), получаем условие устойчивости в виде

Приведенный выше анализ относится к цифровому интегратору с реверсивным счетчиком с  на его выходе. При использовании цифрового интегратора с ШИМ анализ усложняется, однако следует иметь в виду следующее. Частота колебаний выходного триггера
на его выходе. При использовании цифрового интегратора с ШИМ анализ усложняется, однако следует иметь в виду следующее. Частота колебаний выходного триггера  выбирается значительно большей, чем частота среза системы, поэтому если
выбирается значительно большей, чем частота среза системы, поэтому если  то эффект квантования по времени можно не учитывать. Если же
то эффект квантования по времени можно не учитывать. Если же  то учет квантования по времени можно произвести по приведенным выше формулам.
то учет квантования по времени можно произвести по приведенным выше формулам.
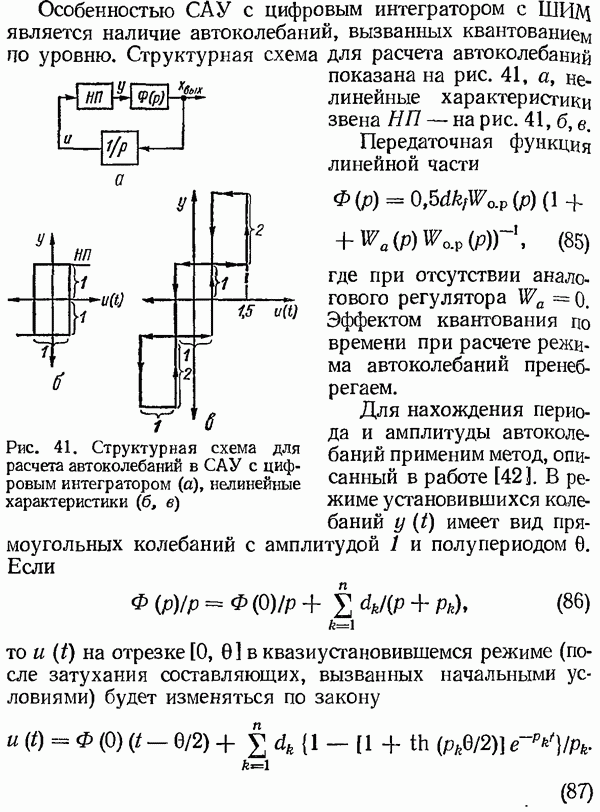
Особенностью САУ с цифровым интегратором с ШИМ является наличие автоколебаний, вызванных квантованием по уровню. Структурная схема для расчета автоколебаний показана на рис. 41, а, нелинейные характеристики звена  — на рис. 41, б, е.
— на рис. 41, б, е.
Передаточная функция линейной части

где при отсутствии аналогового регулятора  . Эффектом квантования по времени при расчете режима автоколебаний пренебрегаем.
. Эффектом квантования по времени при расчете режима автоколебаний пренебрегаем.

Рис. 41. Структурная схема для расчета автоколебаний в САУ с цифровым интегратором (а), нелинейные характеристики (б, е)
Для нахождения периода и амплитуды автоколебаний применим метод, описанный в работе [42]. В режиме установившихся колебаний  имеет вид прямоугольных колебаний с амплитудой 1 и полупериодом 0. Если
имеет вид прямоугольных колебаний с амплитудой 1 и полупериодом 0. Если

то  на отрезке
на отрезке  в квазиустановившемся режиме (после затухания составляющих, вызванных начальными условиями) будет изменяться по закону
в квазиустановившемся режиме (после затухания составляющих, вызванных начальными условиями) будет изменяться по закону

Для определения  служит уравнение периодов
служит уравнение периодов

причем устойчивые колебания возможны только для таких корней  уравнения (88), для которых
уравнения (88), для которых  .
.
Условия переключения имеют вид  .
.
При правильном выборе параметров системы  . Следовательно, учесть квантование по времени, вносимое цифровым интегратором, можно введением запаздывания от момента, когда и
. Следовательно, учесть квантование по времени, вносимое цифровым интегратором, можно введением запаздывания от момента, когда и  станет равным 0,5, до момента переключения. Это запаздывание не превосходит
станет равным 0,5, до момента переключения. Это запаздывание не превосходит  . При этом уравнение (88) запишем в виде
. При этом уравнение (88) запишем в виде

а условия переключения

Пример 4. Пусть  тогда
тогда  . Согласно формуле
. Согласно формуле  или
или  . Решение этого уравнения дано в табл. 3.
. Решение этого уравнения дано в табл. 3.
Таблица 3 (см. скан)
Зная  , подставляем это значение в соотношение (87), вычисляем значения и
, подставляем это значение в соотношение (87), вычисляем значения и  при
при  проверяем, не выходят ли колебания и
проверяем, не выходят ли колебания и  за пределы одного «кванта». Если это явление происходит, то пользуемся более сложной нелинейной характеристикой рис. (41, е).
за пределы одного «кванта». Если это явление происходит, то пользуемся более сложной нелинейной характеристикой рис. (41, е).
Пусть  . По табл. 3
. По табл. 3  откуда
откуда  . Учтем теперь запаздывание
. Учтем теперь запаздывание  Обозначив
Обозначив 
из соотношений (87) и (89), получим уравнение  .
.
Если  , то
, то  , т.е. меньше, чем 1,5, когда происходит переход на следующий участок нелинейности.
, т.е. меньше, чем 1,5, когда происходит переход на следующий участок нелинейности.
Кроме этого можно применить метод, предложенный в работе [42]. Для систем высокого порядка можно найти частоту автоколебаний графически без определения  корней характеристического уравнения.
корней характеристического уравнения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава первая. СТРУКТУРНЫЕ СХЕМЫ И УЗЛЫ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА ЦИФРОАНАЛОГОВЫХ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 2. СТРУКТУРНЫЕ СХЕМЫ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 3. ЭЛЕМЕНТНАЯ БАЗА ЦИФРОАНАЛОГОВЫХ САУ
- Глава вторая. ЧАСТОТНЫЕ ДАТЧИКИ И ЗАДАЮЩИЕ УСТРОЙСТВА
- 1. ЧАСТОТНЫЕ ДАТЧИКИ РЕГУЛИРУЕМЫХ ВЕЛИЧИН
- 2. ЧАСТОТНЫЕ ЗАДАЮЩИЕ УСТРОЙСТВА
- Глава третья. ФУНКЦИОНАЛЬНЫЕ УЗЛЫ ЦИФРОАНАЛОГОВЫХ САУ С ЧАСТОТНЫМИ СИГНАЛАМИ
- 1. ЦИФРОВЫЕ ИНТЕГРАТОРЫ
- 2. ДЕМОДУЛЯТОР ШИРОТНО-ИМПУЛЬСНЫХ КОЛЕБАНИЙ
- 3. ЦИФРОВЫЕ УСТРОЙСТВА СРАВНЕНИЯ ДВУХ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
- 4. ПРЕОБРАЗОВАТЕЛИ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ В НАПРЯЖЕНИЕ ПОСТОЯННОГО ТОКА (ПЧН)
- 5. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
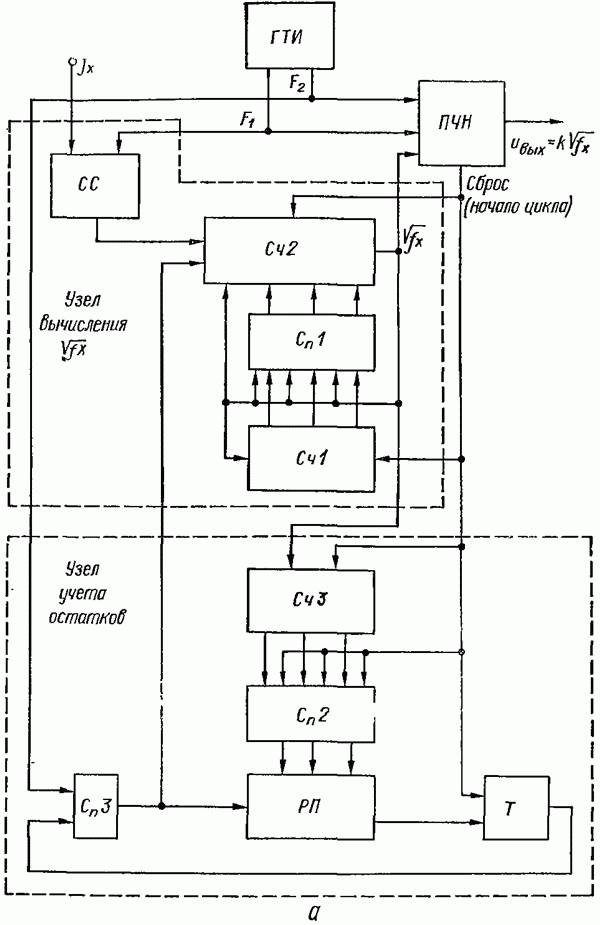
- Цифроаналоговое устройство извлечения квадратного корня
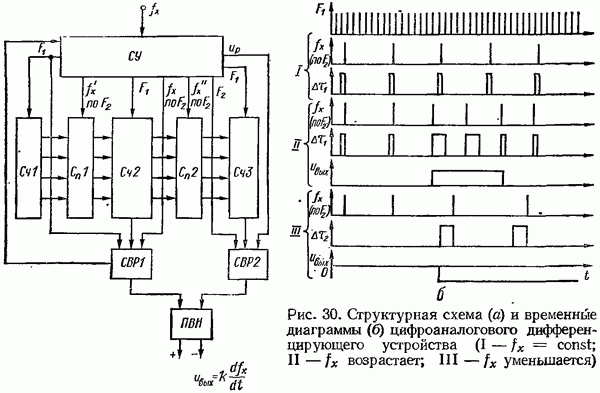
- Цифроаналоговое дифференцирующее устройство
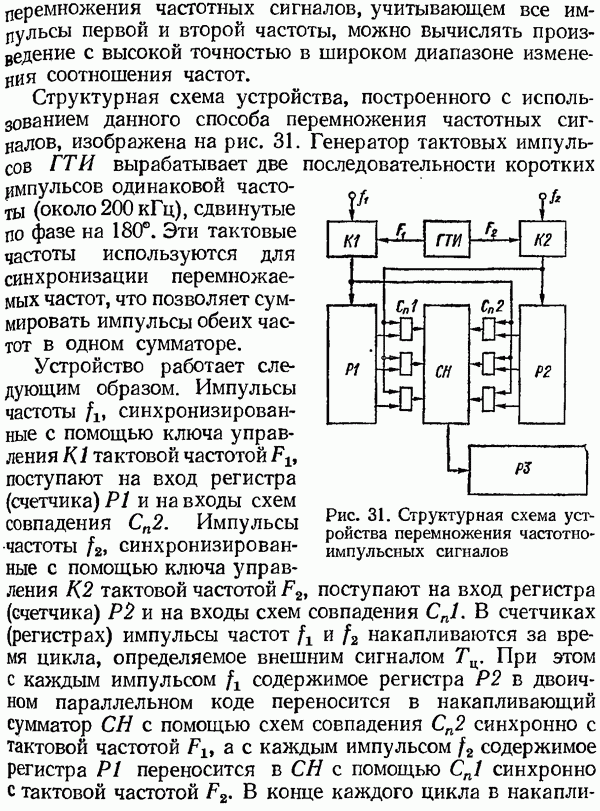
- Устройство для перемножения двух частотно-импульсных сигналов
- Умножитель частоты
- 6. ПРЕОБРАЗОВАТЕЛЬ НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА В ЧАСТОТУ СЛЕДОВАНИЯ ИМПУЛЬСОВ
- Глава четвертая. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ САУ С ЧАСТОТАМ ПРЕДСТАВЛЕНИЕМ СИГНАЛОВ
- 1. САУ С ПРЕОБРАЗОВАТЕЛЕМ ЧАСТОТА—НАПРЯЖЕНИЕ В ОБРАТНОЙ СВЯЗИ
- 2. САУ С ПРЕОБРАЗОВАТЕЛЕМ ЧАСТОТА—КОД В ОБРАТНОЙ СВЯЗИ
- 3. САУ С ЦИФРОВЫМ ИНТЕГРАТОРОМ
- Глава пятая. ПРИМЕРЫ ВЫПОЛНЕНИЯ И РАСЧЕТА ЦИФРОАНАЛОГОВЫХ САУ
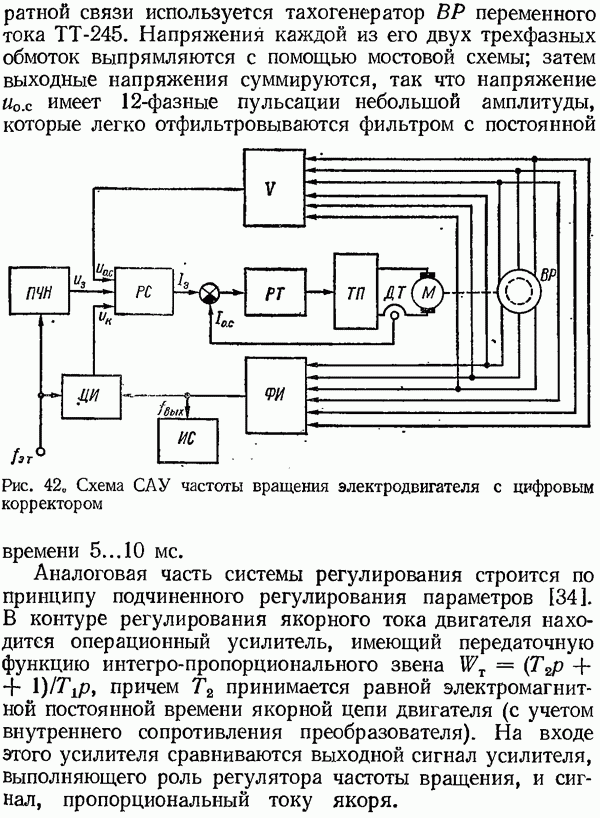
- 1. ЦИФРОАНАЛОГОВАЯ СИСТЕМА РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ
- 2. ЦИФРОВАЯ СИСТЕМА УПРАВЛЕНИЯ СКОРОСТНЫМИ РЕЖИМАМИ РЕДУКЦИОННОГО СТАНА
- 3. ЦИФРОВЫЕ УСТРОЙСТВА ИЗМЕРЕНИЯ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
- 4. ЭКСПЛУАТАЦИОННЫЕ ХАРАКТЕРИСТИКИ ЦИФРОАНАЛОГОВЫХ САУ
- СПИСОК ЛИТЕРАТУРЫ