| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. СТРУКТУРНЫЕ СХЕМЫ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
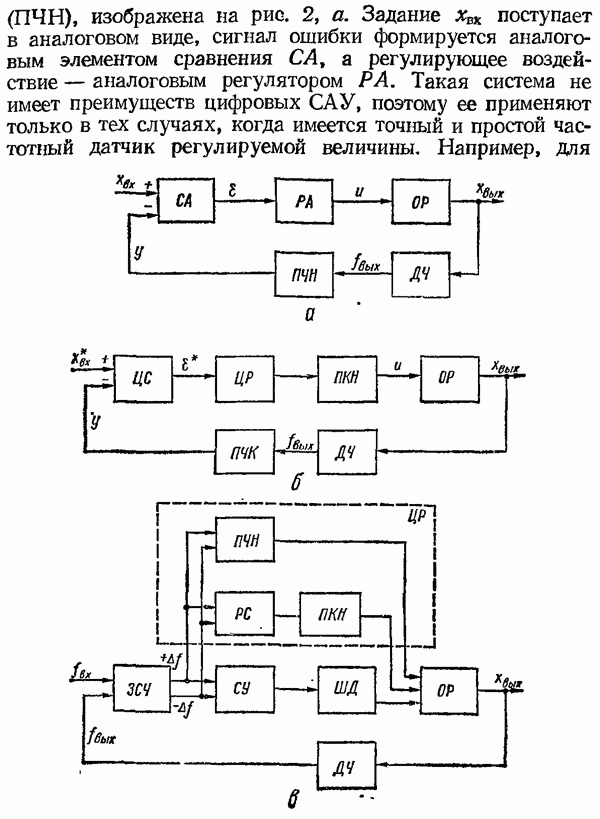
Существуют разнообразные структурные схемы САУ с частотными сигналами, основные из них изображены на рис. 2.
Структурная схема САУ, в цепи обратной связи которой используется преобразователь частота — напряжение
(ПЧН), изображена на рис. 2, а. Задание  поступает в аналоговом виде, сигнал ошибки формируется аналоговым элементом сравнения СА, а регулирующее воздействие — аналоговым регулятором РА. Такая система не имеет преимуществ цифровых САУ, поэтому ее применяют только в тех случаях, когда имеется точный и простой частотный датчик регулируемой величины. Например, для
поступает в аналоговом виде, сигнал ошибки формируется аналоговым элементом сравнения СА, а регулирующее воздействие — аналоговым регулятором РА. Такая система не имеет преимуществ цифровых САУ, поэтому ее применяют только в тех случаях, когда имеется точный и простой частотный датчик регулируемой величины. Например, для
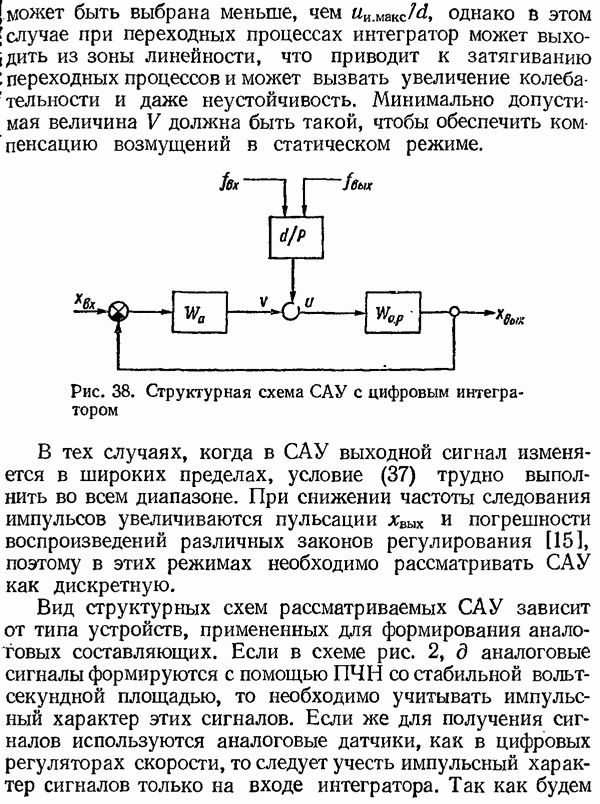
электропривода клети непрерывного стана холодной прокатки фирма «Сименс» (ФРГ) применила следующую схему формирования сигнала обратной связи. С валом двигателя сочленены тахогенератор постоянного тока и импульсный датчик, на выходе которого установлен преобразователь частота — напряжение. Сигнал обратной связи образуется на выходе операционного усилителя, на вход которого поступают выходное напряжение тахогенератора и выходное напряжение интегратора. На вход интегратора подаются с разными знаками напряжение преобразователя частота — напряжение и напряжение обратной связи. Так как при установившейся частоте вращения сумма входных напряжений интегратора равна нулю, то сигнал обратной связи равен выходному напряжению ПЧН, которое с высокой степенью точности пропорционально частоте вращения. В переходных процессах быстрое измерение текущей частоты вращения обеспечивается тахогенератором.

Рис. 2. Структурные схемы САУ: а — с ПЧН в обратной связи; б — цифровой; в — с непрерывным сравнением частот; г — с цифровым интегратором; д — с цифровым интегратором и ПЧН для формирования пропорциональной составляющей;  — датчик частотный; ПЧН — преобразователь частота — напряжение; СА—устройство сравнения аналоговое;
— датчик частотный; ПЧН — преобразователь частота — напряжение; СА—устройство сравнения аналоговое;  — преобразователь код—напряжение;
— преобразователь код—напряжение;  — цифровой регулятор; ПЧК — преобравователь частота — код;
— цифровой регулятор; ПЧК — преобравователь частота — код;  — цифровой регулятор;
— цифровой регулятор;  — преобразователь частота — код;
— преобразователь частота — код;  — цифровое сравнивающее устройство; ЗСЧ — знакочувст-вительиая схема сравнения частот;
— цифровое сравнивающее устройство; ЗСЧ — знакочувст-вительиая схема сравнения частот;  — схема управления шаговым двигателем;
— схема управления шаговым двигателем;  — реверсивный счетчик;
— реверсивный счетчик;  — цифровой интегратор; ЦПБ — цифровой пропорциональный блок с фильтром Ф
— цифровой интегратор; ЦПБ — цифровой пропорциональный блок с фильтром Ф
Кроме того, такая схема может применяться в длинных цепях связи между датчиком измеряемой величины и регулятором для увеличения помехоустойчивости (например, в телеметрических системах). Сравнение аналоговых сигналов задания и обратной связи может производиться также до частотного датчика  . Тогда на выходе
. Тогда на выходе  образуется импульсная последовательность, частота которой зависит от величины ошибки. В этом случае ПЧН может быть выполнен по наиболее распространенной схеме, когда на каждый импульс
образуется импульсная последовательность, частота которой зависит от величины ошибки. В этом случае ПЧН может быть выполнен по наиболее распространенной схеме, когда на каждый импульс  формируется импульс форсированной площади. Такая система не является цифровой, а относится к импульсным с частотно-импульсной модуляцией (ЧИМ) [19].
формируется импульс форсированной площади. Такая система не является цифровой, а относится к импульсным с частотно-импульсной модуляцией (ЧИМ) [19].
Работа схемы рис. 2, а в основном определяется особенностями построения ПЧН. При использовании ПЧН с фиксированной вольт-секундной площадью выходных импульсов также получаем импульсную (не цифровую) САУ с  Использование цифровых ПЧН, основанных на подсчете числа импульсов измеряемой частоты за фиксированный промежуток времени, позволяет отнести данную САУ к цифровым.
Использование цифровых ПЧН, основанных на подсчете числа импульсов измеряемой частоты за фиксированный промежуток времени, позволяет отнести данную САУ к цифровым.
Применяемые в системах ЧИМ датчики по характеру связи между текущей величиной периода  где
где  — моменты выдачи двух последовательных импульсов обратной связи, и величиной
— моменты выдачи двух последовательных импульсов обратной связи, и величиной  бывают двух родов. В ЧИМ 1-го рода
бывают двух родов. В ЧИМ 1-го рода  является функцией
является функцией  а в ЧИМ 2-го рода
а в ЧИМ 2-го рода  является решением уравнения
является решением уравнения

где  — импульсная переходная функция некоторого фильтра, в частности,
— импульсная переходная функция некоторого фильтра, в частности,  - дельта-функция; с — фиксированная величина. Таким образом,
- дельта-функция; с — фиксированная величина. Таким образом,  импульс
импульс
будет выдан, когда

что соответствует интегральной 
В цифровой  сигнал обратной связи с выхода частотного датчика преобразуется в код (рис. 2, б). Сигнал задания также представлен в цифровой форме. Выделение сигнала ошибки
сигнал обратной связи с выхода частотного датчика преобразуется в код (рис. 2, б). Сигнал задания также представлен в цифровой форме. Выделение сигнала ошибки  производится с помощью цифрового сравнивающего устройства
производится с помощью цифрового сравнивающего устройства  Затем
Затем  поступает на цифровой регулятор
поступает на цифровой регулятор  Выходная величина цифрового регулятора через преобразователь код — напряжение
Выходная величина цифрового регулятора через преобразователь код — напряжение  воздействует на объект регулирования ОР. В ЦР формируется нужная передаточная функция ЦСАУ. К недостаткам такой системы следует отнести необходимость интервала времени
воздействует на объект регулирования ОР. В ЦР формируется нужная передаточная функция ЦСАУ. К недостаткам такой системы следует отнести необходимость интервала времени  для преобразования частоты в код, что вводит дополнительное запаздывание в систему и ухудшает ее динамические показатели.
для преобразования частоты в код, что вводит дополнительное запаздывание в систему и ухудшает ее динамические показатели.
Преобразование частоты в код обычно производится одним из двух способов: 1) подсчетом числа импульсов измеряемой частоты за фиксированное время  ; 2) подсчетом числа импульсов высокой эталонной частоты за фиксированное число периодов измеряемой частоты. Однако в ЦСАУ второй способ применяется редко [15, 16].
; 2) подсчетом числа импульсов высокой эталонной частоты за фиксированное число периодов измеряемой частоты. Однако в ЦСАУ второй способ применяется редко [15, 16].
При первом способе преобразования число импульсов, поступивших в счетчик,  , где символ
, где символ  означает целую часть числа
означает целую часть числа  . Методическая относительная погрешность, равная
. Методическая относительная погрешность, равная  всегда отрицательна и уменьшается с увеличением
всегда отрицательна и уменьшается с увеличением  Если
Если  — максимальная входная частота, то емкость счетчика
— максимальная входная частота, то емкость счетчика 
Рассмотрим использование такого способа преобразования частоты в код для системы регулирования частоты вращения двигателя постоянного тока. Пусть угловая частота вращения  а импульсный датчик выдает
а импульсный датчик выдает
 . Тогда
. Тогда  Пусть относительная ошибка
Пусть относительная ошибка  .
.
Частота среза современных систем регулирования частоты вращения электроприводов прокатных станов составляет примерно  откуда следует, что время
откуда следует, что время  не должно превышать 0,01 с. Отсюда находим, что
не должно превышать 0,01 с. Отсюда находим, что  . Это очень высокая величина. Ее можно получить только в некоторых типах современных датчиков. Рассмотренный способ преобразования частоты в код применим в основном для инерционных объектов.
. Это очень высокая величина. Ее можно получить только в некоторых типах современных датчиков. Рассмотренный способ преобразования частоты в код применим в основном для инерционных объектов.
Работа преобразователя частота — код в ЦСАУ протекает в два такта. В первый такт длительностью в происходит подсчет импульсов измеряемой частоты; во второй такт длительностью  (обычно
(обычно  ) поступление импульсов в счетчик прекращается и производится передача выработанного кода в цифровое сравнивающее устройство, а затем сброс счетчика. Таким образом, период дискретности цифрового устройства
) поступление импульсов в счетчик прекращается и производится передача выработанного кода в цифровое сравнивающее устройство, а затем сброс счетчика. Таким образом, период дискретности цифрового устройства  .
.
Часто счетчик преобразователя частота — код и цифровое сравнивающее устройство объединяют. При этом перед началом счета в реверсивный счетчик вводят код задания, а импульсы обратной связи в течение времени  поступают на вычитающий вход счетчика. Спустя время в в счетчике оказывается записанным число, пропорциональное ошибке. В течение
поступают на вычитающий вход счетчика. Спустя время в в счетчике оказывается записанным число, пропорциональное ошибке. В течение  производится перенос кода ошибки в
производится перенос кода ошибки в  сброс счетчика и повторное введение кода задания.
сброс счетчика и повторное введение кода задания.
Цифровой регулятор в этой схеме может иметь достаточно сложный вид. Обычно регулятор принимается линейным. Его работа описывается разностным уравнением вида

где  — значения выходного сигнала цифрового регулятора и сигнала ошибки соответственно в дискретные моменты времени:
— значения выходного сигнала цифрового регулятора и сигнала ошибки соответственно в дискретные моменты времени: 
Чаще всего достаточно ограничиться интегрально-пропорционально-дифференциальным регулятором, выходная величина которого

где  На отрезке
На отрезке  Выражению (4) соответствует разностное уравнение
Выражению (4) соответствует разностное уравнение

и дискретная передаточная функция

В качестве примеров выполнения ДСАУ такого типа можно привести регулятор частоты вращения, описанный в работе [25]. Он предназначен для регулирования угловой частоты вращения в пределах  . Импульсный датчик выдает 720 импульсов на
. Импульсный датчик выдает 720 импульсов на  , а время измерения
, а время измерения  Динамика системы регулирования характеризуется временем отработки толчка задания скорости, которое для данной системы равно 90 мс.
Динамика системы регулирования характеризуется временем отработки толчка задания скорости, которое для данной системы равно 90 мс.
В структурной схеме, изображенной на рис. 2, в, в отличие от предыдущих, производится непосредственное непрерывное сравнение частот задания и обратной связи. В качестве органа сравнения применена знакочувствительная схема сравнения частот (ЗСЧ), на выходе которой образуется последовательность импульсов с частотой, равной разности сравниваемых частот. Эта схема имеет два выхода — для положительной и отрицательной разности. Если разностный сигнал подать на схему управления СУ шаговым двигателем  ротор которого при подаче каждого импульса поворачивается на определенный угол, то суммарный
ротор которого при подаче каждого импульса поворачивается на определенный угол, то суммарный
угол поворота ротора оказывается пропорциональным интегралу от разности частот. Если с ротором ШД [13] связан какой-либо исполнительный орган (потенциометр, заслонка и т. п.), то система, изображенная на рис. 2, в, будет представлять собой интегрирующую ЦСАУ.
На рис. 2, е показан также один из цифровых регуляторов ЦР, который применяется при отсутствии шагового двигателя. Разность количества импульсов поступает на реверсивный счетчик PC, в результате чего на выходе ПКН образуется интегральная составляющая закона регулирования; на выходе ПЧН получаем пропорциональную составляющую.
Так как для данной схемы закон регулирования интегральный (или интегрально-пропорциональный), то постоянная входная величина отрабатывается без ошибки с точностью до одной дискреты квантования по уровню. При наличии шагового двигателя один «квант» выходной величины равен изменению выходной величины, соответствующей перемещению шагового двигателя на один шаг, а при наличии ЦР — изменению содержимого  на единицу.
на единицу.
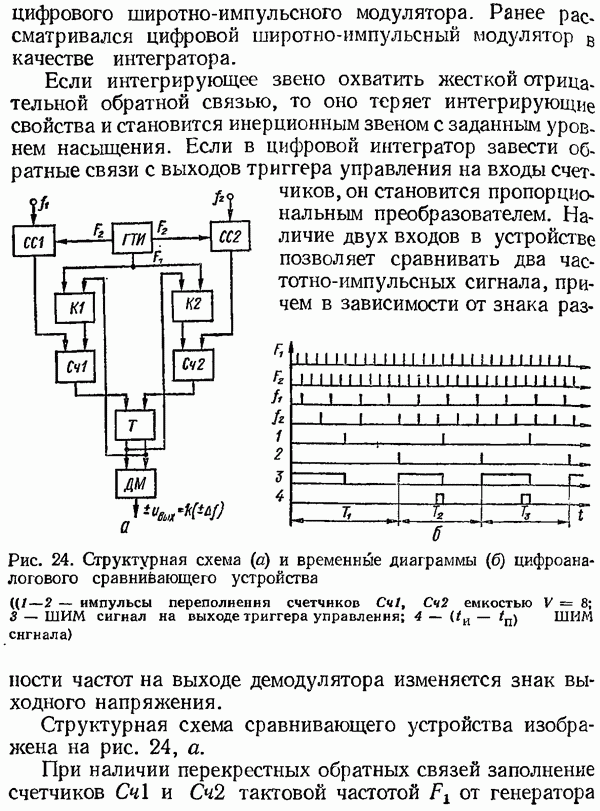
Структурная схема рис. 2, в используется редко ввиду относительной сложности устройства знакочувствитель-ного сравнения частот в широком диапазоне. Чаще используется схема рис. 2, г, в которой с помощью цифрового интегратора ЦП определяется разность между общими числами импульсов частот задания и обратной связи, т. е. сигнал на выходе 
Такие системы, благодаря своей простоте и в то же время высокой статической точности, получили наибольшее распространение.
При необходимости введения в закон регулирования пропорциональной и дифференциальной составляющих можно

поступить различно. В цифровом регуляторе  , описанном в работе [15], пропорциональная составляющая рассчитывается по формуле
, описанном в работе [15], пропорциональная составляющая рассчитывается по формуле

т. е. как средняя величина за время цикла  которое является достаточно малой величиной, так что
которое является достаточно малой величиной, так что  за время Гц меняется мало.
за время Гц меняется мало.
Можно также использовать схему рис. 2, в, вычислив пропорциональную составляющую с помощью ЗСЧ и ПЧН. Однако рациональнее применять комбинированные цифро-аналоговые системы (рис. 2, 5). Здесь сигнал задания и обратной связи представлены в виде последовательностей импульсов частот  , а соответствующие аналоговые сигналы формируются преобразователями ПЧН, и их разность воздействует на аналоговый регулятор РА, передаточная функция которого может иметь любой вид (например, пропорционально-дифференциальный).
, а соответствующие аналоговые сигналы формируются преобразователями ПЧН, и их разность воздействует на аналоговый регулятор РА, передаточная функция которого может иметь любой вид (например, пропорционально-дифференциальный).
Еще один способ выработки сигнала, пропорционального интегралу от разности частот задания и обратной связи, который применяется в настоящее время, заключается в сравнении фаз этих импульсных последовательностей, т. е. измерении временного сдвига между соседними импульсами задания и обратной связи [28]

Если  то сигнал
то сигнал  непрерывно увеличивается (или уменьшается), что приводит к изменению выходного сигнала САУ. Не меняется
непрерывно увеличивается (или уменьшается), что приводит к изменению выходного сигнала САУ. Не меняется  если
если  причем
причем  может быть произвольным (но меньше, чем минимальная длительность периода частот
может быть произвольным (но меньше, чем минимальная длительность периода частот  что определяет астатические свойства САУ. Если измерение
что определяет астатические свойства САУ. Если измерение  производится цифровыми методами, то рассматриваемую
производится цифровыми методами, то рассматриваемую
САУ можно считать цифровой. Если же цифровое измерение  не используется, то эту систему можно рассматривать как чисто импульсную с широтно-импульсной модуляцией.
не используется, то эту систему можно рассматривать как чисто импульсную с широтно-импульсной модуляцией.
Достоинством этой САУ является ее простота. Действительно, если объект управления статический, то им можно управлять последовательностью широтно-модулированных импульсов, причем выходная величина  пропорциональна ширине импульса управления. В качестве импульсов управления можно принять усиленные по мощности сигналы
пропорциональна ширине импульса управления. В качестве импульсов управления можно принять усиленные по мощности сигналы  что существенно упрощает САУ [28, 32]. К недостатку этого способа следует отнести узкий диапазон возможных рассогласований по частоте, так как при этом фазовый сдвиг быстро достигает своих предельных значений. Обычно в САУ такого типа установлен дополнительный «грубый» регулятор, который вводит систему в область выходных значений, близких к
что существенно упрощает САУ [28, 32]. К недостатку этого способа следует отнести узкий диапазон возможных рассогласований по частоте, так как при этом фазовый сдвиг быстро достигает своих предельных значений. Обычно в САУ такого типа установлен дополнительный «грубый» регулятор, который вводит систему в область выходных значений, близких к  (обеспечивает «втягивание в синхронизм»). Ограничение диапазона изменения фазового сдвига для предотвращения «выпадения из синхронизма» приводит к затяжке переходных процессов. Исследование реакции на синусоидальный входной сигнал показало, что такой интегратор нормально работает, если глубина модуляции составляет несколько процентов.
(обеспечивает «втягивание в синхронизм»). Ограничение диапазона изменения фазового сдвига для предотвращения «выпадения из синхронизма» приводит к затяжке переходных процессов. Исследование реакции на синусоидальный входной сигнал показало, что такой интегратор нормально работает, если глубина модуляции составляет несколько процентов.
Для управления линейным объектом регулирования применялись линейные регуляторы (если рассматривать их в непрерывном приближении как предельно непрерывные системы). Однако для управления нелинейными объектами, а также линейными при использовании методов оптимизации, может потребоваться нелинейный регулятор. В этих случаях необходимы различного рода функциональные преобразователи частотных сигналов. Например, для получения оптимального закона отработки рассогласования в следящих системах необходимо сравнивать сигнал ошибки и сигнал, пропорциональный квадрату скорости изменения выходной координаты, или сигнал скорости с сигналом, пропорциональным корню квадратному из рассогласования.
Если сигналы, пропорциональные выходной координате и скорости ее изменения, вырабатываются в частотной форме, то для реализации указанных выше схем необходимы устройства, преобразующие частоту следования импульсов в аналоговый сигнал и код, пропорциональные квадрату или корню квадратному из входной частоты. При построении самонастраивающихся САУ необходимы устройства для умножения сигналов, заданных в виде частоты следования импульсов, на переменный коэффициент и др.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава первая. СТРУКТУРНЫЕ СХЕМЫ И УЗЛЫ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА ЦИФРОАНАЛОГОВЫХ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 2. СТРУКТУРНЫЕ СХЕМЫ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 3. ЭЛЕМЕНТНАЯ БАЗА ЦИФРОАНАЛОГОВЫХ САУ
- Глава вторая. ЧАСТОТНЫЕ ДАТЧИКИ И ЗАДАЮЩИЕ УСТРОЙСТВА
- 1. ЧАСТОТНЫЕ ДАТЧИКИ РЕГУЛИРУЕМЫХ ВЕЛИЧИН
- 2. ЧАСТОТНЫЕ ЗАДАЮЩИЕ УСТРОЙСТВА
- Глава третья. ФУНКЦИОНАЛЬНЫЕ УЗЛЫ ЦИФРОАНАЛОГОВЫХ САУ С ЧАСТОТНЫМИ СИГНАЛАМИ
- 1. ЦИФРОВЫЕ ИНТЕГРАТОРЫ
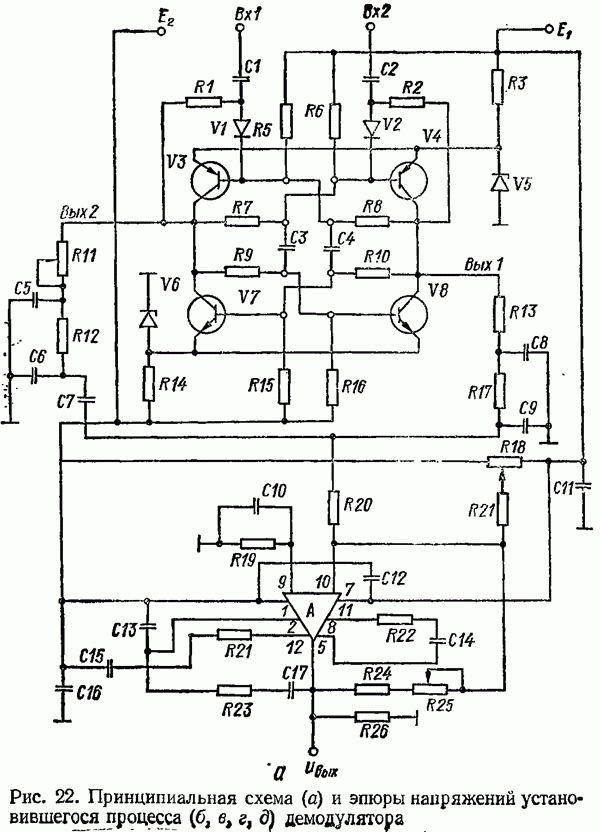
- 2. ДЕМОДУЛЯТОР ШИРОТНО-ИМПУЛЬСНЫХ КОЛЕБАНИЙ
- 3. ЦИФРОВЫЕ УСТРОЙСТВА СРАВНЕНИЯ ДВУХ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
- 4. ПРЕОБРАЗОВАТЕЛИ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ В НАПРЯЖЕНИЕ ПОСТОЯННОГО ТОКА (ПЧН)
- 5. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
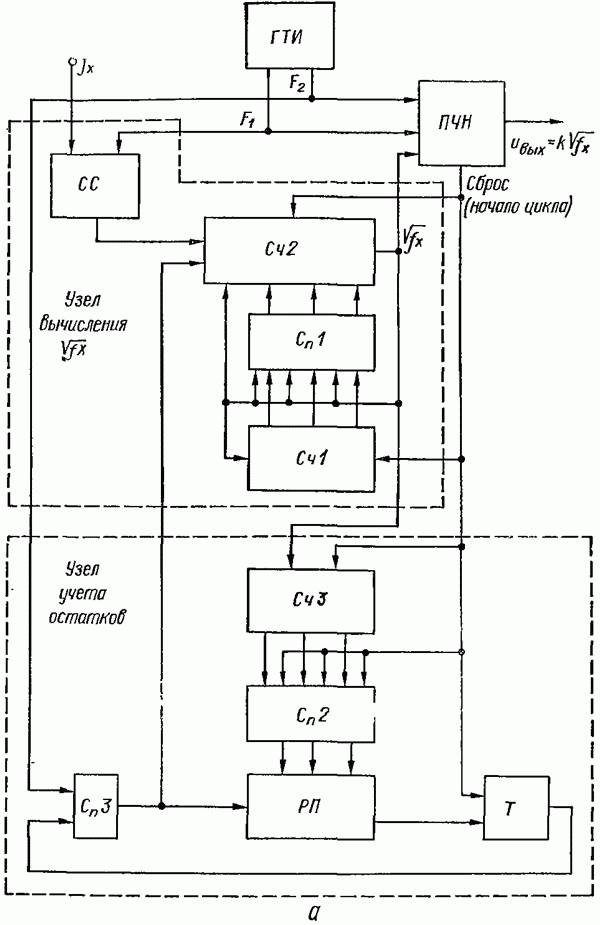
- Цифроаналоговое устройство извлечения квадратного корня
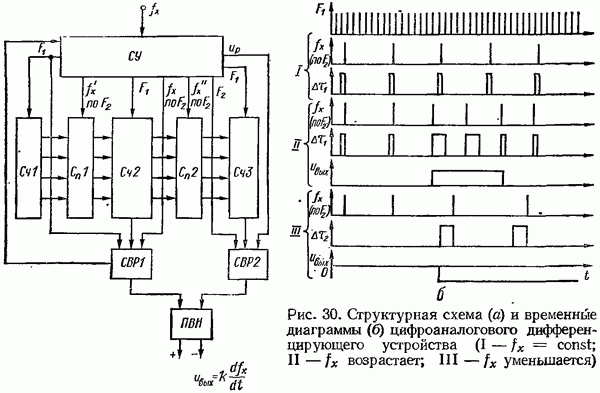
- Цифроаналоговое дифференцирующее устройство
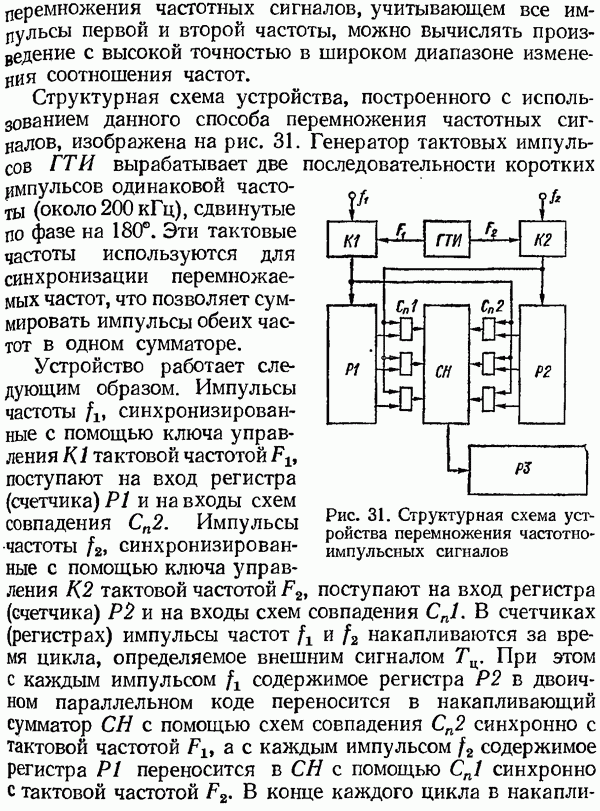
- Устройство для перемножения двух частотно-импульсных сигналов
- Умножитель частоты
- 6. ПРЕОБРАЗОВАТЕЛЬ НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА В ЧАСТОТУ СЛЕДОВАНИЯ ИМПУЛЬСОВ
- Глава четвертая. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ САУ С ЧАСТОТАМ ПРЕДСТАВЛЕНИЕМ СИГНАЛОВ
- 1. САУ С ПРЕОБРАЗОВАТЕЛЕМ ЧАСТОТА—НАПРЯЖЕНИЕ В ОБРАТНОЙ СВЯЗИ
- 2. САУ С ПРЕОБРАЗОВАТЕЛЕМ ЧАСТОТА—КОД В ОБРАТНОЙ СВЯЗИ
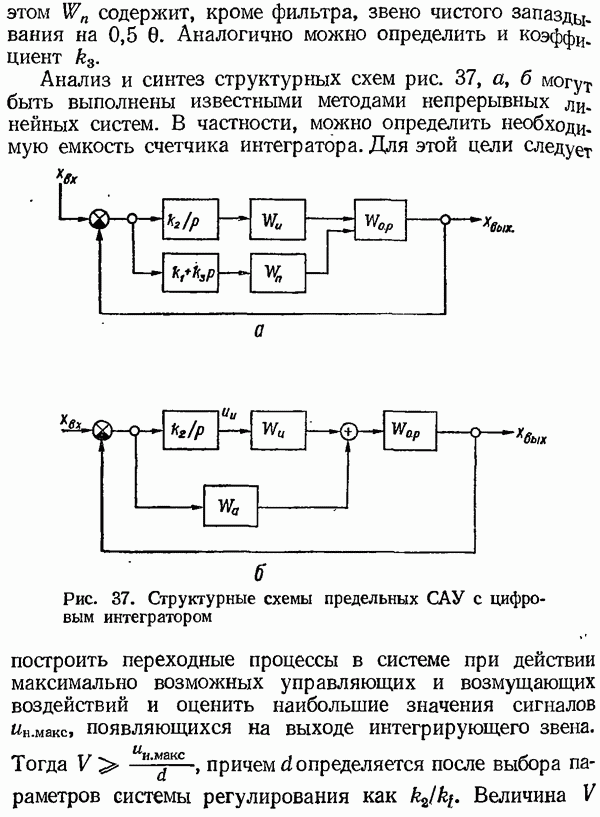
- 3. САУ С ЦИФРОВЫМ ИНТЕГРАТОРОМ
- Глава пятая. ПРИМЕРЫ ВЫПОЛНЕНИЯ И РАСЧЕТА ЦИФРОАНАЛОГОВЫХ САУ
- 1. ЦИФРОАНАЛОГОВАЯ СИСТЕМА РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ
- 2. ЦИФРОВАЯ СИСТЕМА УПРАВЛЕНИЯ СКОРОСТНЫМИ РЕЖИМАМИ РЕДУКЦИОННОГО СТАНА
- 3. ЦИФРОВЫЕ УСТРОЙСТВА ИЗМЕРЕНИЯ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
- 4. ЭКСПЛУАТАЦИОННЫЕ ХАРАКТЕРИСТИКИ ЦИФРОАНАЛОГОВЫХ САУ
- СПИСОК ЛИТЕРАТУРЫ