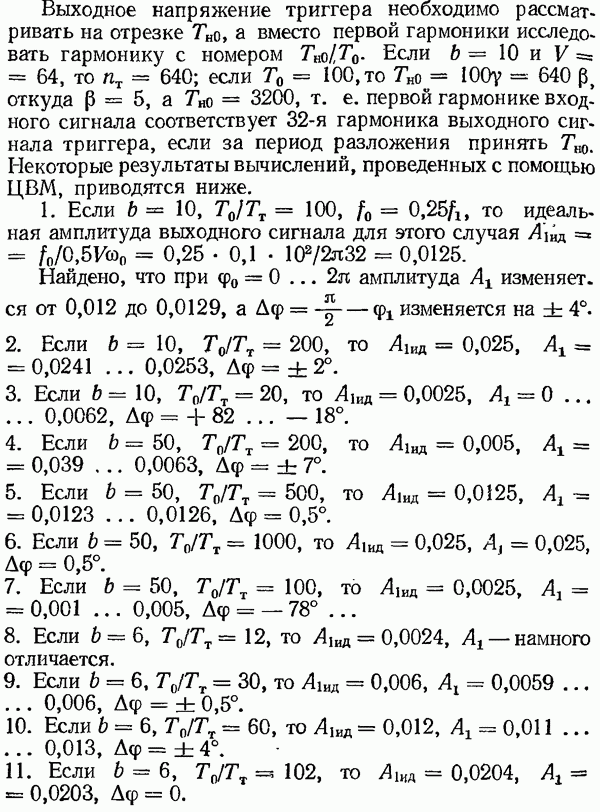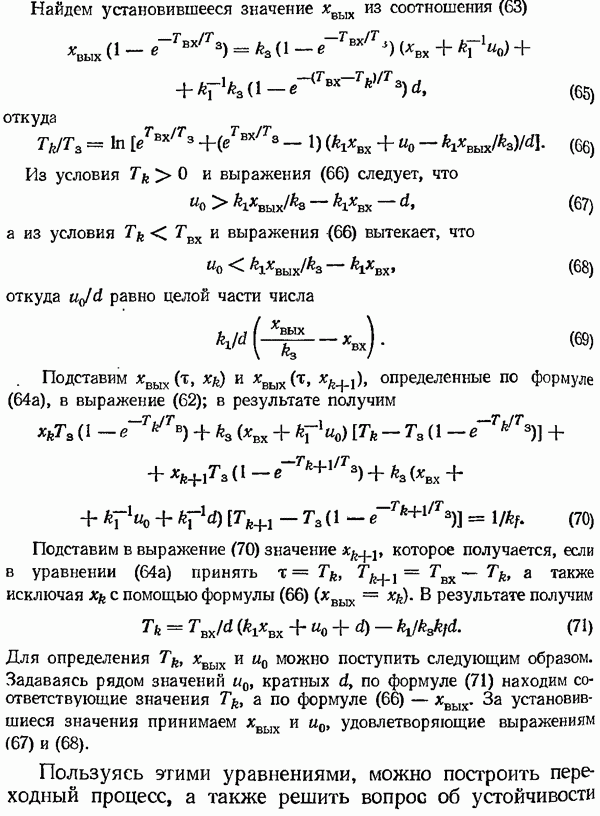| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава пятая. ПРИМЕРЫ ВЫПОЛНЕНИЯ И РАСЧЕТА ЦИФРОАНАЛОГОВЫХ САУ
1. ЦИФРОАНАЛОГОВАЯ СИСТЕМА РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ
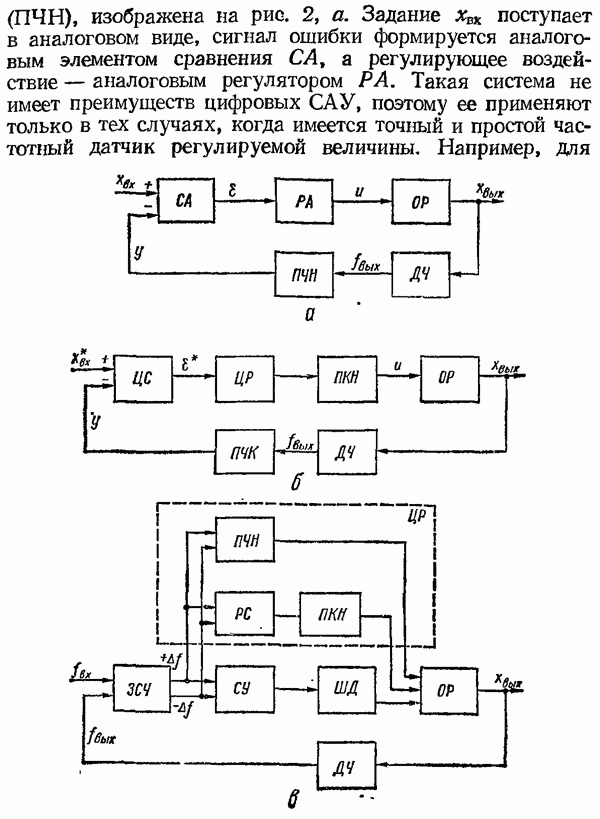
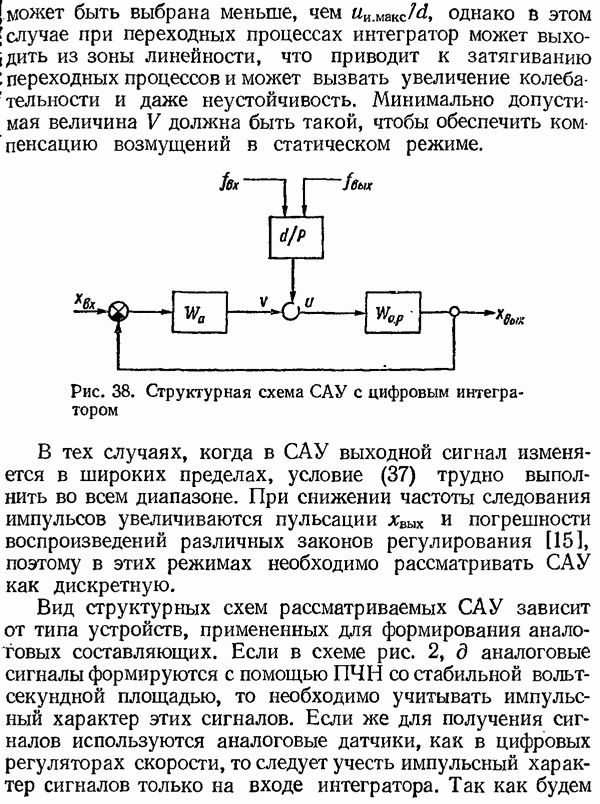
Электродвигатели некоторых производственных механизмов должны поддерживать и регулировать частоту вращения с точностью 0,1 % и выше. Особенно высокие требования к точности поддержания частоты вращения предъявляются в тех случаях, когда обрабатываемый материал находится одновременно в нескольких механизмах (непрерывные прокатные станы, бумагоделательные машины) и когда возникновение небольшого рассогласования может привести к порче материала. Такая точность не может быть обеспечена только аналоговыми системами регулирования, поэтому применяются цифроаналоговые системы (рис. 42).
Электродвигатель постоянного тока М получает питание от регулируемого источника напряжения тиристорного преобразователя  . Частота вращения задается в виде частотного сигнала, частота импульсов которого
. Частота вращения задается в виде частотного сигнала, частота импульсов которого  пропорциональна заданной частоте
пропорциональна заданной частоте  . В качестве датчика обратной
. В качестве датчика обратной
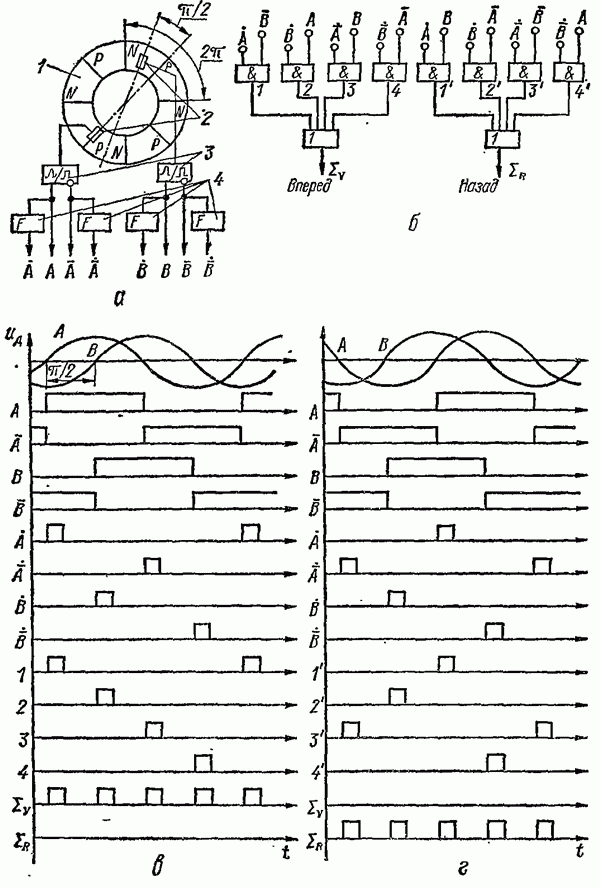
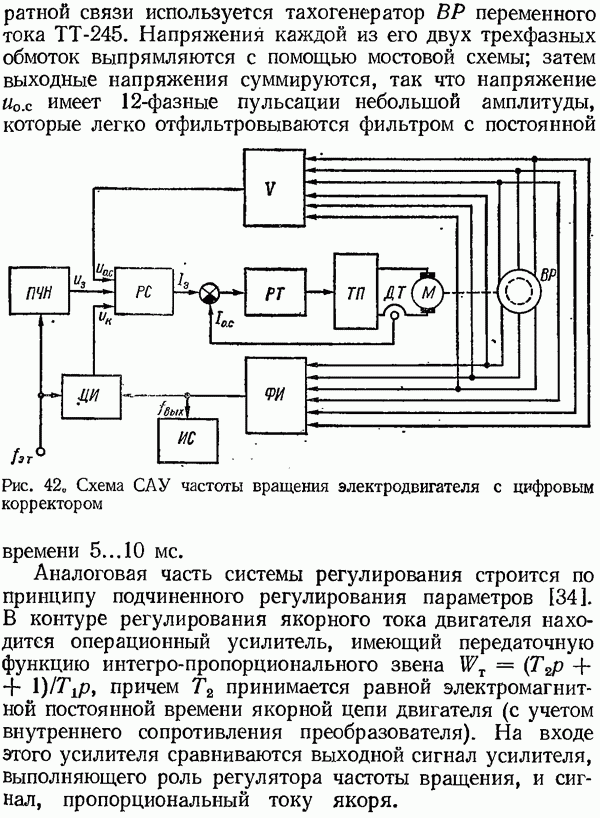
связи используется тахогенератор BP переменного тока  . Напряжения каждой из его двух трехфазных обмоток выпрямляются с помощью мостовой схемы; затем выходные напряжения суммируются, так что напряжение
. Напряжения каждой из его двух трехфазных обмоток выпрямляются с помощью мостовой схемы; затем выходные напряжения суммируются, так что напряжение  имеет 12-фазные пульсации небольшой амплитуды, которые легко отфильтровываются фильтром с постоянной времени
имеет 12-фазные пульсации небольшой амплитуды, которые легко отфильтровываются фильтром с постоянной времени  .
.

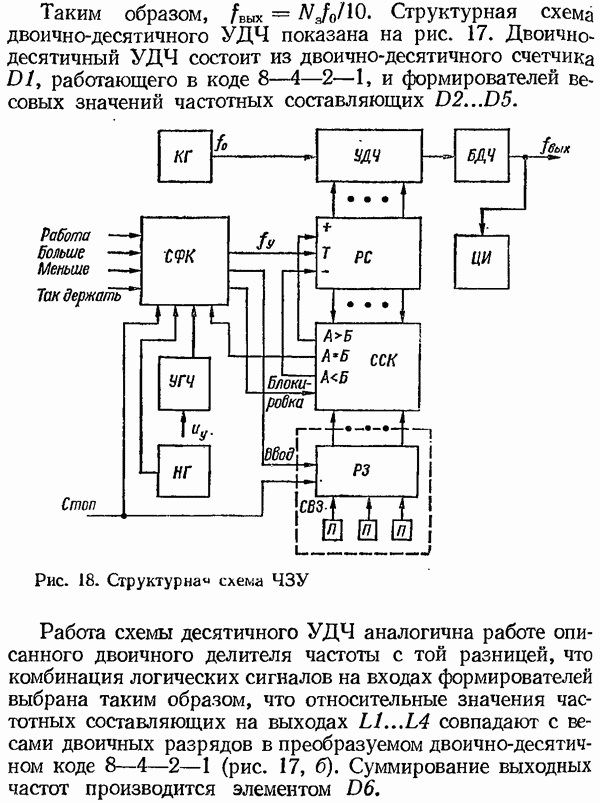
Рис. 42. Схема САУ частоты вращения электродвигателя с цифровым корректором
Аналоговая часть системы регулирования строится по принципу подчиненного регулирования параметров [34]. В контуре регулирования якорного тока двигателя находится операционный усилитель, имеющий передаточную функцию интегро-пропорционального звена  , причем
, причем  принимается равной электромагнитной постоянной времени якорной цепи двигателя (с учетом внутреннего сопротивления преобразователя). На входе этого усилителя сравниваются выходной сигнал усилителя, выполняющего роль регулятора частоты вращения, и сигнал, пропорциональный току якоря.
принимается равной электромагнитной постоянной времени якорной цепи двигателя (с учетом внутреннего сопротивления преобразователя). На входе этого усилителя сравниваются выходной сигнал усилителя, выполняющего роль регулятора частоты вращения, и сигнал, пропорциональный току якоря.
При расчете контура частоты вращения предполагается, что в нем содержится некомпенсируемая постоянная времени равная сумме постоянной времени фильтра на выходе тахогенератора и эквивалентной инерционности замкнутого контура регулирования тока  , где
, где  частота среза контура тока. Операционный усилитель регулятора скорости работает в режиме пропорционального звена, причем его коэффициент усиления
частота среза контура тока. Операционный усилитель регулятора скорости работает в режиме пропорционального звена, причем его коэффициент усиления  выбирается таким, что частота среза контура скорости
выбирается таким, что частота среза контура скорости  , где
, где  .
.
ряжение на выходе аналогового датчика обратной связи по скорости при номинальной скорости вращения;  — относительное падение скорости вращения двигателя при изменении нагрузки от нуля до номинальной величины при отсутствии цифрового корректора;
— относительное падение скорости вращения двигателя при изменении нагрузки от нуля до номинальной величины при отсутствии цифрового корректора;  — напряжение на выходе датчика обратной связи по току
— напряжение на выходе датчика обратной связи по току  при номинальном токе якоря; Ты — электромеханическая постоянная времени двигателя с приводимым им механизмом. При этом реакция аналоговой части системы на толчок задания имеет перерегулирование 4,3%.
при номинальном токе якоря; Ты — электромеханическая постоянная времени двигателя с приводимым им механизмом. При этом реакция аналоговой части системы на толчок задания имеет перерегулирование 4,3%.
При появлении статического момента на валу двигателя возникает ошибка по скорости  причем отношение величины этой ошибки к величине изменения скорости вращения без регулятора
причем отношение величины этой ошибки к величине изменения скорости вращения без регулятора  . Для ликвидации ошибки
. Для ликвидации ошибки  , а также погрешностей аналоговых задающих устройств и датчиков обратных связей применяется цифровой корректор частоты вращения, основную часть которого образует цифровой интегратор разности частот
, а также погрешностей аналоговых задающих устройств и датчиков обратных связей применяется цифровой корректор частоты вращения, основную часть которого образует цифровой интегратор разности частот  . В качестве
. В качестве  на него поступает задающая частота
на него поступает задающая частота  а в качестве
а в качестве  — частота обратной связи
— частота обратной связи  . Эта частота формируется из фазных напряжений тахогенератора. Число импульсов на оборот датчика равно 552, а максимальная частота
. Эта частота формируется из фазных напряжений тахогенератора. Число импульсов на оборот датчика равно 552, а максимальная частота  . С помощью индикатора скорости
. С помощью индикатора скорости  можно визуально наблюдать за точным значением частоты вращения. Выходной сигнал
можно визуально наблюдать за точным значением частоты вращения. Выходной сигнал  поступает на вход усилителя регулятора
поступает на вход усилителя регулятора
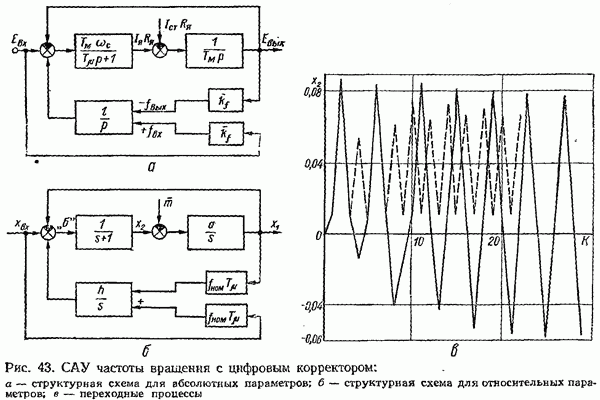
Рис. 43. (см. скан) САУ частоты вращения с цифровым корректором: а — структурная схема для абсолютных параметров; б — структурная схема для относительных параметров; в — переходные процессы
скорости, складываясь алгебраически с напряжением задания  Поскольку напряжение
Поскольку напряжение  будет изменяться до тех пор, пока не будет достигнуто равенство
будет изменяться до тех пор, пока не будет достигнуто равенство  то частота вращения двигателя будет точно равна заданной.
то частота вращения двигателя будет точно равна заданной.
Рассмотрим основные соотношения в цифроаналоговой системе регулирования частоты вращения. Пусть система предельная непрерывная. Явлениями квантования во времени и по уровню пренебрегаем.
Структурная схема системы регулирования САУ частоты с цифровым корректором показана на рис. 43, а. Выходной величиной является  двигателя,
двигателя,  — падение напряжения в якорной цепи под действием статического тока (тока нагрузки)
— падение напряжения в якорной цепи под действием статического тока (тока нагрузки)  — отношение коэффициента усиления регулятора скорости по каналу
— отношение коэффициента усиления регулятора скорости по каналу  к коэффициенту усиления по каналу основной (аналоговой) обратной связи. Для получения более общих результатов введем относительные
к коэффициенту усиления по каналу основной (аналоговой) обратной связи. Для получения более общих результатов введем относительные  , а также относительное время
, а также относительное время  . Из теории преобразования Лапласа известно, что при такой замене передаточная функция системы имеет прежний вид, но оператор
. Из теории преобразования Лапласа известно, что при такой замене передаточная функция системы имеет прежний вид, но оператор  должен быть заменен на оператор
должен быть заменен на оператор 
Структурная схема рис. 43, а сводится к схеме рис. 43, б. Реальные частоты заменяются на относительные, имеющие периоды  . Закон
. Закон  в абсолютных и относительных переменных записывается соответственно в виде
в абсолютных и относительных переменных записывается соответственно в виде

Если разомкнуть систему в точке  , то получим передаточную функцию разомкнутой системы в виде
, то получим передаточную функцию разомкнутой системы в виде

где  выбирается в зависимости от требуемого быстродействия и допустимой величины перерегулирования. Например, при часто практикующейся настройке по так называемому «симметричному оптимуму»
выбирается в зависимости от требуемого быстродействия и допустимой величины перерегулирования. Например, при часто практикующейся настройке по так называемому «симметричному оптимуму»  . Зная
. Зная  находим
находим

являющуюся конструктивным параметром 
Определим необходимую емкость счетчика цифрового интегратора  Будем ее выбирать из того условия, чтобы при максимально возможном толчковом изменении нагрузки
Будем ее выбирать из того условия, чтобы при максимально возможном толчковом изменении нагрузки  счетчик
счетчик  не переполнялся. Составим операторное выражение относительно
не переполнялся. Составим операторное выражение относительно

по этому выражению построим переходный процесс и найдем максимальное значение  кривой
кривой  Тогда
Тогда

Из выражения (93) получаем, что и  обозначим
обозначим  Следовательно,
Следовательно,

Максимально допустимая величина  Для указанной выше настройки на «симметричный оптимум»
Для указанной выше настройки на «симметричный оптимум» 
Пример 5. Пусть  . На основании уравнения
. На основании уравнения  Далее
Далее  откуда
откуда  . Примем
. Примем  , т. е. 5 двоичных разрядов.
, т. е. 5 двоичных разрядов.
Перейдем теперь к уточненному рассмотрению системы с учетом дискретности. Вначале определим установившиеся значения координат, воспользовавшись соотношением, аналогичным соотношению (63). В нашем случае это соотношение
запишем в виде

При записи выражения (96) учтено, что  и
и  приложены к одной точке схемы, и, кроме того, введено слагаемое, учитывающее влияние момента сопротивления.
приложены к одной точке схемы, и, кроме того, введено слагаемое, учитывающее влияние момента сопротивления.
Определим элементы матрицы  и векторов
и векторов  , приняв в качестве компонент вектора
, приняв в качестве компонент вектора  . Дифференциальные уравнения системы имеют вид
. Дифференциальные уравнения системы имеют вид  . Решая их при начальных условиях
. Решая их при начальных условиях  находим закон изменения координат
находим закон изменения координат  откуда следуют форму,
откуда следуют форму,  для
для  . Окончательно получим
. Окончательно получим

Перейдем от координат отклонениям  . Тогда выражение (96) с учетом соотношения (97) запишем в виде
. Тогда выражение (96) с учетом соотношения (97) запишем в виде

Решая систему уравнений (98) относительно  находим установившиеся значения отклонений координат
находим установившиеся значения отклонений координат  в момент прихода импульса частоты
в момент прихода импульса частоты  Значения установившихся отклонений координат в момент прихода импульса частоты
Значения установившихся отклонений координат в момент прихода импульса частоты  определяются из равенства
определяются из равенства

Для нахождения  нужно полученное описанным выше способом выражение для
нужно полученное описанным выше способом выражение для  подставить в уравнение (62) и учесть связь
подставить в уравнение (62) и учесть связь  согласно формуле (99). Учитывая выражение (90), после выполнения интегрирования
согласно формуле (99). Учитывая выражение (90), после выполнения интегрирования
и соответствующих преобразовании получаем

Таким образом, необходимо вначале, зная  и возмущение
и возмущение  определить
определить  и по уравнению
и по уравнению  — целое число и равно целой части числа
— целое число и равно целой части числа  , а затем вычислить
, а затем вычислить  и по уравнениям (98) и (99).
и по уравнениям (98) и (99).
Таблица 4 (см. скан)
Важным показателем цифровой САУ является размах колебаний координат  Непосредственное использование величин
Непосредственное использование величин  и
и  невозможно, так как максимальные отклонения могут происходить между моментами поступления импульсов. Поэтому нужно сначала, зная
невозможно, так как максимальные отклонения могут происходить между моментами поступления импульсов. Поэтому нужно сначала, зная  найти моменты времени
найти моменты времени  когда отклонения максимальны, а затем вычислить это отклонение. Из условия
когда отклонения максимальны, а затем вычислить это отклонение. Из условия  находим
находим  Из условия
Из условия  находим
находим  причем, если
причем, если  то максимальное отклонение
то максимальное отклонение  происходит при
происходит при  Подставляя
Подставляя  в формулы для
в формулы для  определяем максимальное отклонение координат, причем размах колебаний координат
определяем максимальное отклонение координат, причем размах колебаний координат  . В табл. 4 приведены зависимости величин
. В табл. 4 приведены зависимости величин  и
и  от
от  при настройке пропорциональной части регулятора частоты вращения по «модульному» оптимуму
при настройке пропорциональной части регулятора частоты вращения по «модульному» оптимуму 
Пусть в рассмотренном выше примере допустимая по условиям точности величина  . Находим
. Находим  . Таким образом,
. Таким образом,
колебания частоты вращения достигнут допустимой величины при снижении ее в диапазоне  . При этом колебания тока якоря
. При этом колебания тока якоря 
Рассчитаем устойчивость. Для этой дели воспользуемся формулой (93), записав ее в виде

Уравнение (73) сводится к виду

Для получения соотношения, связывающего  и
и  поступим следующим образом. На основании выражений (62) и (90)
поступим следующим образом. На основании выражений (62) и (90)

Подставляя в соотношение (103) выражение для  выполняя интегрирование и учитывая связь
выполняя интегрирование и учитывая связь  в виде (99), получаем неявное уравнение
в виде (99), получаем неявное уравнение

Для расчета устойчивости необходимо вычислить элементы Гц матрицы  причем в данном случае
причем в данном случае  является производной
является производной  строки системы (101), (102) по
строки системы (101), (102) по  аргументу (первый аргумент
аргументу (первый аргумент  , второй —
, второй —  , третий —
, третий —  ). Эти производные должны вычисляться с учетом зависимости
). Эти производные должны вычисляться с учетом зависимости  от этих аргументов в соответствии с выражением (104). После взятия производных необходимо в полученные выражения подставить координаты исследуемой точки
от этих аргументов в соответствии с выражением (104). После взятия производных необходимо в полученные выражения подставить координаты исследуемой точки  увыхь
увыхь  Так как рассматривается устойчивость симметричных колебаний, то принимаем
Так как рассматривается устойчивость симметричных колебаний, то принимаем  . В качестве
. В качестве  принимаются установившиеся
принимаются установившиеся
значения координат по выражению (98) Например,  причем производные вычисляются при
причем производные вычисляются при  элементы матрицы
элементы матрицы  определяются
определяются  , причем
, причем  . Далее применяем критерии: собственные числа
. Далее применяем критерии: собственные числа  по модулю меньше единицы. Вычислим коэффициенты характеристического полинома
по модулю меньше единицы. Вычислим коэффициенты характеристического полинома

Таблица 5 (см. скан)
Для этого нужно диагональные элементы  заменить на
заменить на  а затем раскрыть определитель матрицы. Для устойчивости должны быть одновременно выполнены условия
а затем раскрыть определитель матрицы. Для устойчивости должны быть одновременно выполнены условия 
В связи с громоздкостью получаемых выражений расчеты проводились с помощью ЦВМ. При расчетах, когда заданы  коэффициент
коэффициент  изменялся от нуля до величины, при которой нарушается одно из приведенных неравенств. В результате найдено, что устойчивость определяется величинами
изменялся от нуля до величины, при которой нарушается одно из приведенных неравенств. В результате найдено, что устойчивость определяется величинами  значения
значения  соответствующие границе устойчивости, приведены в табл. 5. Для предельной непрерывной системы
соответствующие границе устойчивости, приведены в табл. 5. Для предельной непрерывной системы  Для
Для  («симметричный оптимум») устойчивость нарушается при
(«симметричный оптимум») устойчивость нарушается при  На рис. 43, в показаны кривые переходных процессов при набросе нагрузки
На рис. 43, в показаны кривые переходных процессов при набросе нагрузки  построенные в функции «номера»
построенные в функции «номера»
импульса  для различных параметров системы регулирования, рассчитанные по алгоритму, описанному в четвертой главе. При этом
для различных параметров системы регулирования, рассчитанные по алгоритму, описанному в четвертой главе. При этом  . При
. При  возникают устойчивые колебания, при которых два импульса одной и той же частоты следуют подряд, а не чередуются, как при
возникают устойчивые колебания, при которых два импульса одной и той же частоты следуют подряд, а не чередуются, как при  например при
например при  (показано штриховой линией).
(показано штриховой линией).
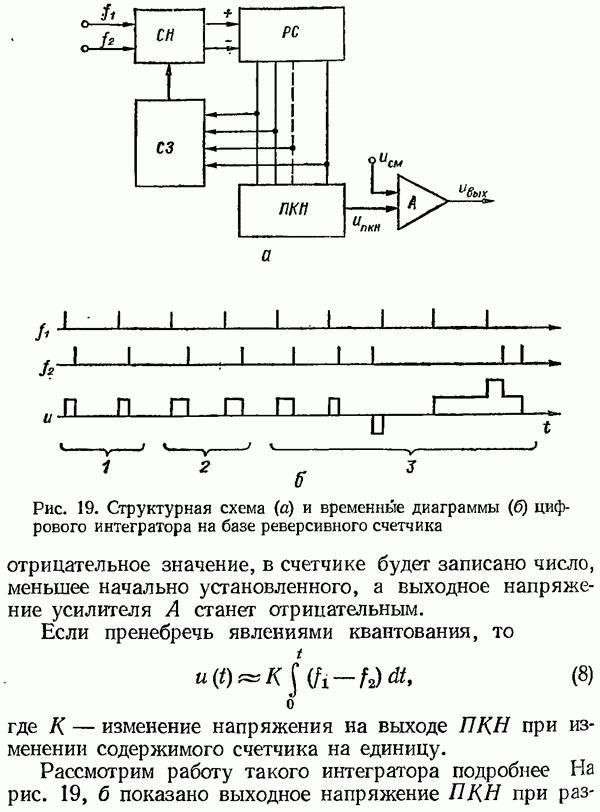
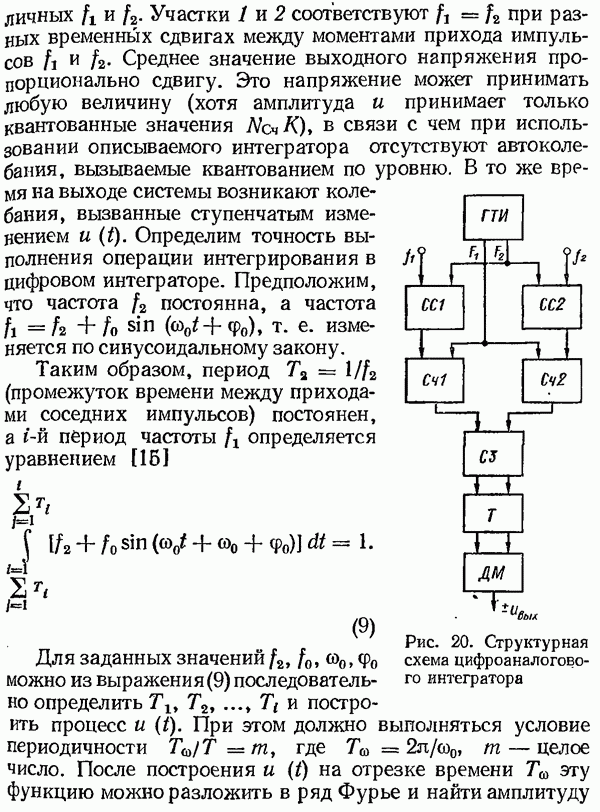
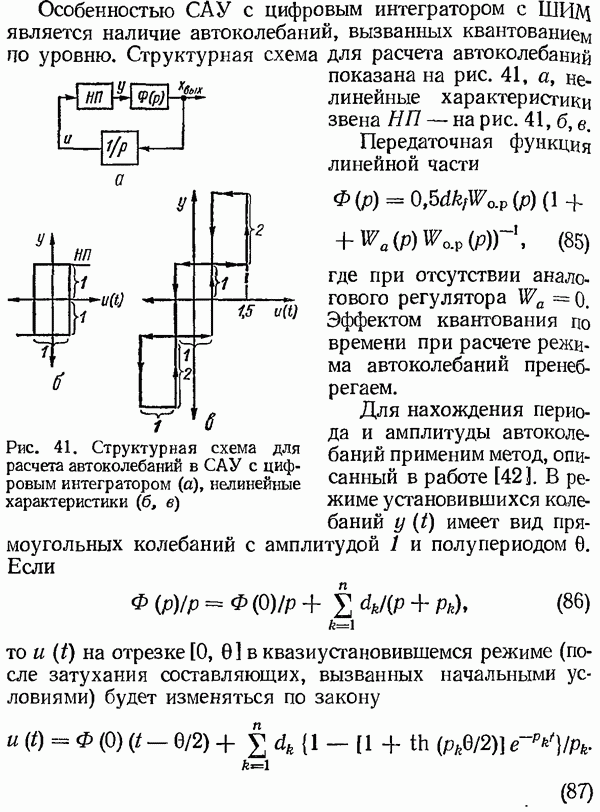
Предположим теперь, что  выполнен по схеме рис. 20. Размах колебаний, вызванных квантованием по уровню
выполнен по схеме рис. 20. Размах колебаний, вызванных квантованием по уровню  определяется приведенными выше соотношениями, однако период колебаний зависит от параметров системы. Для структурной схемы рис. 43, б уравнение периодов запишем в виде
определяется приведенными выше соотношениями, однако период колебаний зависит от параметров системы. Для структурной схемы рис. 43, б уравнение периодов запишем в виде  , где
, где  — реакция системы с передаточной функцией
— реакция системы с передаточной функцией  на прямоугольные колебания единичной амплитуды, или с учетом выражения (91) и
на прямоугольные колебания единичной амплитуды, или с учетом выражения (91) и  . В выражении для передаточной функции разомкнутой системы
. В выражении для передаточной функции разомкнутой системы  пренебрежем сомножителем
пренебрежем сомножителем  Тогда
Тогда  соответствует передаточной функции
соответствует передаточной функции  .
.
Использовав результаты примера 4 и приняв  получим, что при настройке на «симметричный оптимум»
получим, что при настройке на «симметричный оптимум»  При использовании точной формулы для
При использовании точной формулы для  результат отличается на несколько процентов.
результат отличается на несколько процентов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава первая. СТРУКТУРНЫЕ СХЕМЫ И УЗЛЫ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 1. КРАТКАЯ ХАРАКТЕРИСТИКА ЦИФРОАНАЛОГОВЫХ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 2. СТРУКТУРНЫЕ СХЕМЫ САУ С ЧАСТОТНЫМ ПРЕОБРАЗОВАНИЕМ СИГНАЛОВ
- 3. ЭЛЕМЕНТНАЯ БАЗА ЦИФРОАНАЛОГОВЫХ САУ
- Глава вторая. ЧАСТОТНЫЕ ДАТЧИКИ И ЗАДАЮЩИЕ УСТРОЙСТВА
- 1. ЧАСТОТНЫЕ ДАТЧИКИ РЕГУЛИРУЕМЫХ ВЕЛИЧИН
- 2. ЧАСТОТНЫЕ ЗАДАЮЩИЕ УСТРОЙСТВА
- Глава третья. ФУНКЦИОНАЛЬНЫЕ УЗЛЫ ЦИФРОАНАЛОГОВЫХ САУ С ЧАСТОТНЫМИ СИГНАЛАМИ
- 1. ЦИФРОВЫЕ ИНТЕГРАТОРЫ
- 2. ДЕМОДУЛЯТОР ШИРОТНО-ИМПУЛЬСНЫХ КОЛЕБАНИЙ
- 3. ЦИФРОВЫЕ УСТРОЙСТВА СРАВНЕНИЯ ДВУХ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
- 4. ПРЕОБРАЗОВАТЕЛИ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ В НАПРЯЖЕНИЕ ПОСТОЯННОГО ТОКА (ПЧН)
- 5. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
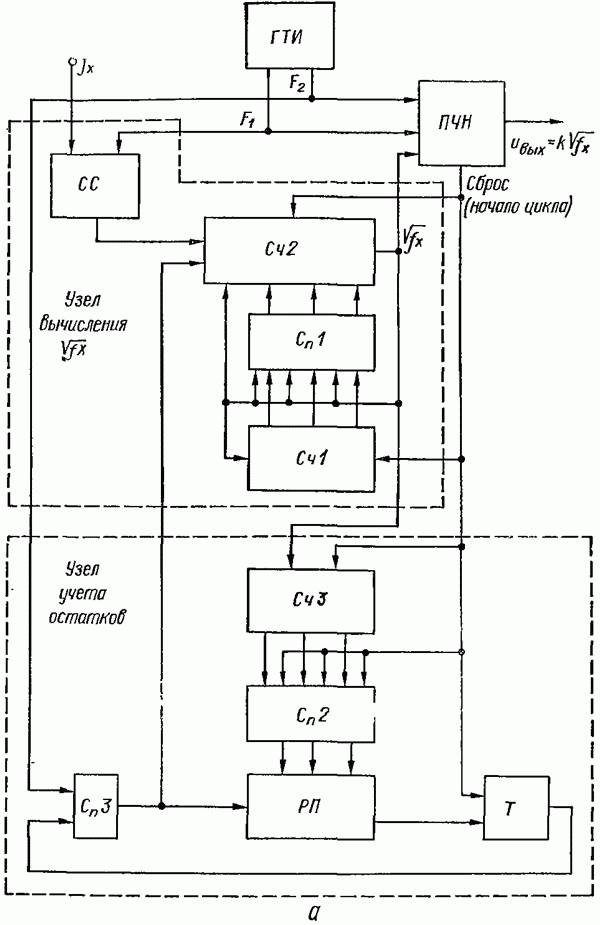
- Цифроаналоговое устройство извлечения квадратного корня
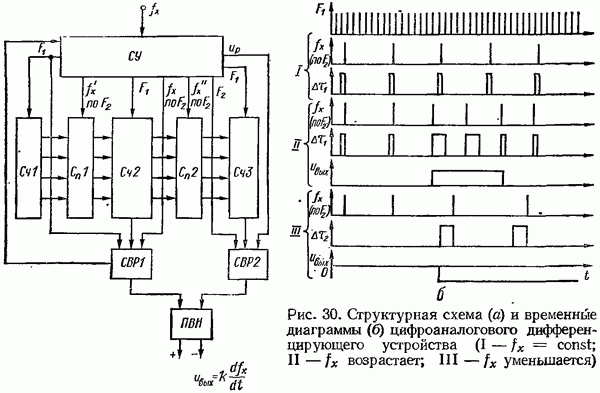
- Цифроаналоговое дифференцирующее устройство
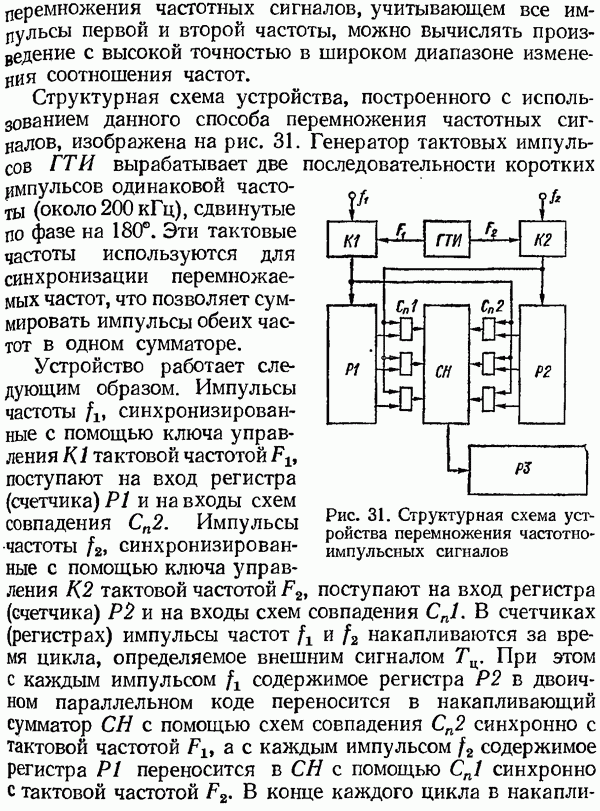
- Устройство для перемножения двух частотно-импульсных сигналов
- Умножитель частоты
- 6. ПРЕОБРАЗОВАТЕЛЬ НАПРЯЖЕНИЯ ПОСТОЯННОГО ТОКА В ЧАСТОТУ СЛЕДОВАНИЯ ИМПУЛЬСОВ
- Глава четвертая. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ САУ С ЧАСТОТАМ ПРЕДСТАВЛЕНИЕМ СИГНАЛОВ
- 1. САУ С ПРЕОБРАЗОВАТЕЛЕМ ЧАСТОТА—НАПРЯЖЕНИЕ В ОБРАТНОЙ СВЯЗИ
- 2. САУ С ПРЕОБРАЗОВАТЕЛЕМ ЧАСТОТА—КОД В ОБРАТНОЙ СВЯЗИ
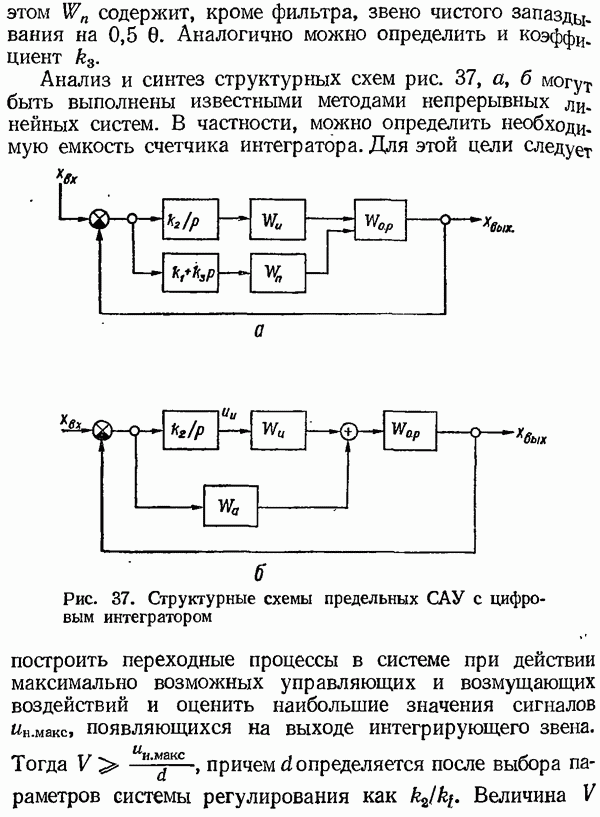
- 3. САУ С ЦИФРОВЫМ ИНТЕГРАТОРОМ
- Глава пятая. ПРИМЕРЫ ВЫПОЛНЕНИЯ И РАСЧЕТА ЦИФРОАНАЛОГОВЫХ САУ
- 1. ЦИФРОАНАЛОГОВАЯ СИСТЕМА РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ
- 2. ЦИФРОВАЯ СИСТЕМА УПРАВЛЕНИЯ СКОРОСТНЫМИ РЕЖИМАМИ РЕДУКЦИОННОГО СТАНА
- 3. ЦИФРОВЫЕ УСТРОЙСТВА ИЗМЕРЕНИЯ ЧАСТОТНО-ИМПУЛЬСНЫХ СИГНАЛОВ
- 4. ЭКСПЛУАТАЦИОННЫЕ ХАРАКТЕРИСТИКИ ЦИФРОАНАЛОГОВЫХ САУ
- СПИСОК ЛИТЕРАТУРЫ