Глава 10. ОБУЧЕНИЕ В СИСТЕМАХ С ДВУХАЛЬТЕРНАТИВНЫМ ВЫБОРОМ

Использование биномиального распределения

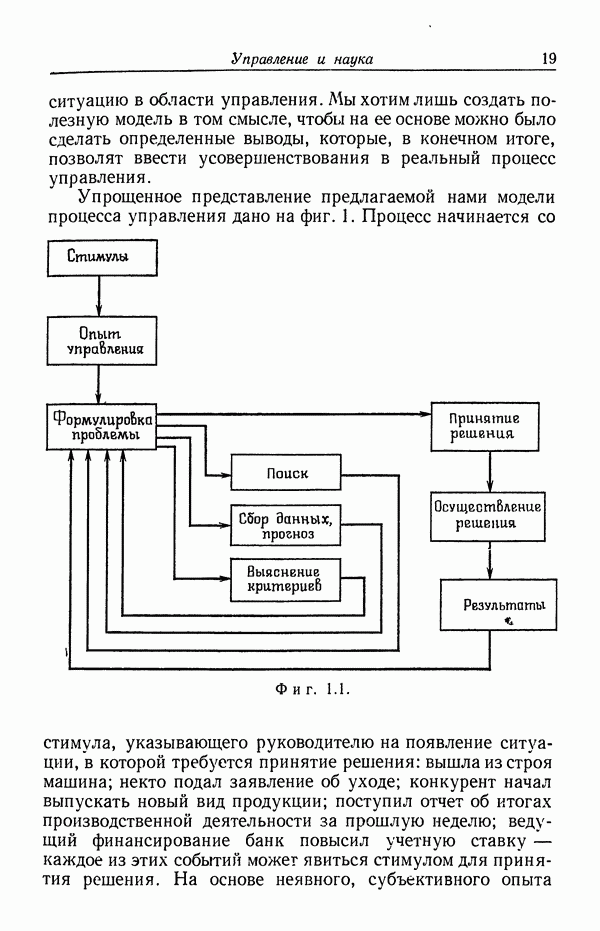
Изложенные ниже вопросы охватывают задачи «обучения» принятию решения, основные принципы которых те же, что и ранее, но форма обрабатываемых данных несколько иная. Если производится обследование какого-либо вида продукции, которую предполагается изготовить или закупить, отдельные единицы продукции могут быть классифицированы как годные или негодные, качественные или дефектные, приемлемые или неприемлемые. Обследование изделия выражается в одном из этих двух возможных сообщений, а данные, полученные из ряда таких наблюдений, могут быть представлены как число дефектных изделий , обнаруженное при обследовании изделий. Если вероятность оказаться дефектными одинакова для всех единиц продукции, то, как хорошо известно, вероятностное распределение величины будет биномиальным. Аналогично, изучая поведение потребителей при покупке товаров, можно всех потребителей классифицировать на покупателей и непокупателей того или иного вида товара. Задания могут выполняться успешно или неуспешно, рабочий может быть загружен или не загружен, машина может работать или простаивать. Все это примеры ситуаций, в которых основные данные имеют двоичный характер, и при подходящих предположениях исходный случайный процесс может в этих случаях моделироваться с помощью биномиального распределения. Задачи такого рода можно проиллюстрировать на примере из области контроля качества.

Пример: проверка с последующим исправлением дефектных изделий

Предположим, что от поставщика поступила партия, состоящая из L изделий, и что относительно их качества существует некоторая неопределенность. Если достоверно известно,

что некоторая доля изделий в этой партии дефектна, легко сделать выбор одного из двух вариантов:

принять партию, разрешив ее передачу в производство;

испытывать каждое изделие в партии, заменяя или исправляя все дефектные изделия, так что передаваемая в производство партия уже будет состоять только из доброкачественных изделий.

Предположим наличие простой структуры затрат, существенно зависящей от процентной доли дефектных изделий. Пусть издержки, связанные с передачей в производство одного дефектного изделия, составляют долл. Затраты на каждое проверяемое изделие в случае, когда партия подвергается 100%-ной проверке, равны долл., а затраты на исправление или замену каждой дефектной единицы равны долл. Тогда, если известно, выбирается минимальное из двух выражений:

Если то, приравняв эти выражения, заключаем, что случай безразличия к выбору имеет место при

Проблема принятия решения здесь представляет интерес только в том случае, когда существует некоторая неопределенность относительно процента бракованных изделий в партии и когда имеется возможность проверки выборки образцов изделий из партии перед принятием решения.

Априорное b-распределение

Предположим, что в типичном случае относительно процентной доли дефектных образцов в партии имеется неопределенность. Если размеры партии велики по отношению к размеру любой рассматриваемой выборки, то для расчета вероятности того, что в выборке из образцов имеется дефектных, можно использовать биномиальное (а не гипер-геометрическое) распределение. Таким образом, возникает необходимость в таком распределении для выражения

априорной неопределенности принимающего решения лица, которое

могло бы быть применено к широкому многообразию исходных состояний;

легко сочеталось бы с биномиальным распределением в выборках согласно логике теоремы Байеса.

Оказывается, что этим требованиям очень хорошо удовлетворяет семейство -распределений. Априорное распределение доли дефектных образцов может быть принято за случайную переменную с (-распределением вида

Априорное среднее значение может быть получено обычным путем:

Это выражение может быть записано в виде

Так как подынтегральное выражение само по себе является -распределением, то этот интеграл равен 1, и мы получаем

Априорная дисперсия величины оказывается равной

Предположим теперь, что при обследовании выборки из образцов среди них обнаружено дефектных. Апостериорное распределение для может быть получено при помощи теоремы Байеса:

Правдоподобность определяется здесь посредством биномиального распределения

Подставляя предыдущие выражения для априорного -распределения и биномиального распределения правдоподобности в апостериорное распределение для , получаем

Сравнивая знаменатель с определением (-распределения, получаем, что значение интеграла должно равняться величине

Отсюда можно видеть, что апостериорное распределение для само является -распределением с параметрами

Тогда апостериорное среднее значение равно

Таким образом, выбрав -распределение для выражения априорной неопределенности принимающего решение лица, можно использовать то весьма удобное обстоятельство, что апостериорное распределение также оказывается (-распределением, параметры которого могут быть получены указанным простым способом. (Немного ниже мы вернемся к задаче выражения поведения принимающего решение лица через априорное (-распределение.)

Предапостериорный анализ

Если было принято решение взять выборку из образцов, но это решение еще не выполнено, то число дефектных образцов, которые будут обнаружены, можно рассматривать

как случайную величину. Для фиксированного значения распределение числа дефектных образцов при наших предположениях является биномиальным распределением. Так как само принимается за случайную величину с априорным (-распределением, безусловное распределение величины имеет вид

Подставляя сюда выражения для биномиального и (-распределений, после комбинирования членов получаем

Сравнивая подынтегральное выражение с формулой, задающей (-распределение, можно найти значение интеграла. В результате получаем для безусловного распределения величины выражение

Это распределение называется бета-биномиальным. Среднее значение и дисперсия величины равны соответственно

Априорное ожидаемое значение апостериорного среднего для тогда равно

Этим подтверждается ранее полученный результат, согласно которому априорно ожидаемое значение апостериорного среднего равно априорному среднему.

Априорная дисперсия апостериорного среднего значения величины равна

Отсюда снова видно, что при возрастании размера выборки априорная дисперсия апостериорного среднего значения приближается к дисперсии априорного распределения.

Ценность полной информации

Возвращаясь к задаче принятия решения в случае, когда имеется возможность проверки и исправления, вычислим сначала ожидаемую ценность полной информации. Пусть на основе априорной информации можно заключить, что в нашем случае

Следовательно, наилучшим априорным действием оказывается принять партию. Если мы обнаружим, что истинное значение величины в действительности превосходит , это может изменить наше мнение относительно наилучшего образа действий, ибо в этом случае нам следовало бы произвести отбор и исправление дефектных изделий. Ожидаемая ценность полной информации равна 1,0

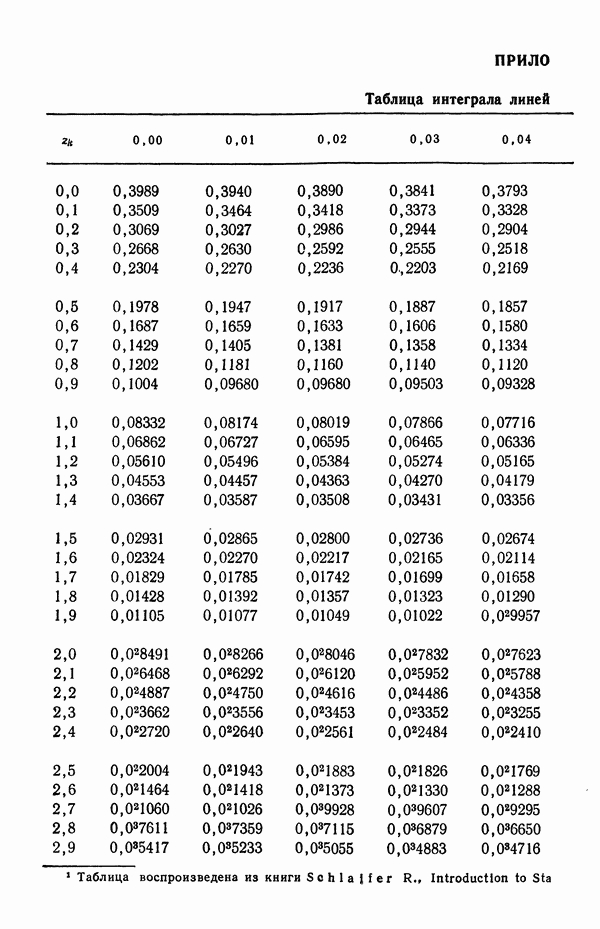
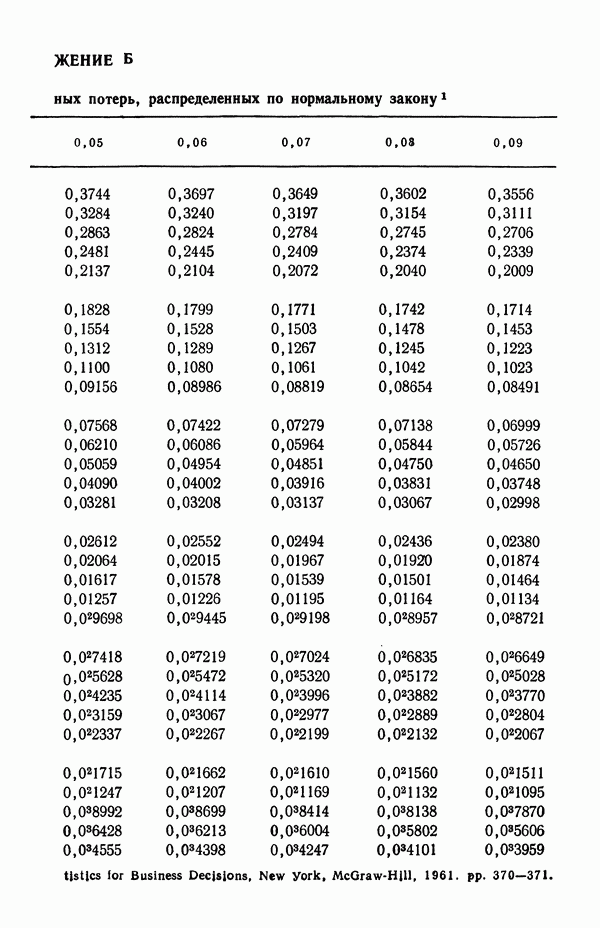
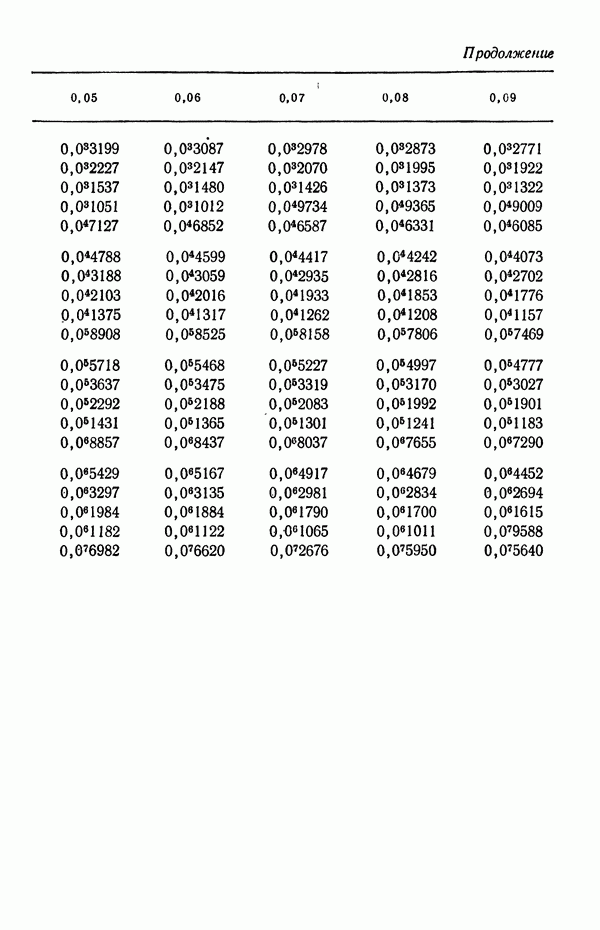
Последнее выражение представляет собой интеграл линейных потерь, описываемых (-распределением

Ценность выборочной информации

Если принимается решение взять выборку из образцов, то наилучшее апостериорное действие определяется апостериорным средним значением величины , т. е. Предположим еще раз, что априорное среднее значение величины меньше или равно и, таким образом, если нельзя получить дальнейшей информации, будет принято решение принять партию. Если апостериорное среднее окажется большим, чем , более предпочтительным будет решение произвести отбор и исправление имеющихся в партии дефектных единиц.

Нам известно, что априорное распределение апостериорного среднего значения является бета-биномиальным; следовательно, ожидаемая ценность выборочной информации равна

Сюда снова входит интеграл линейных потерь, но на этот раз описываемых бета-биномиальным распределением.

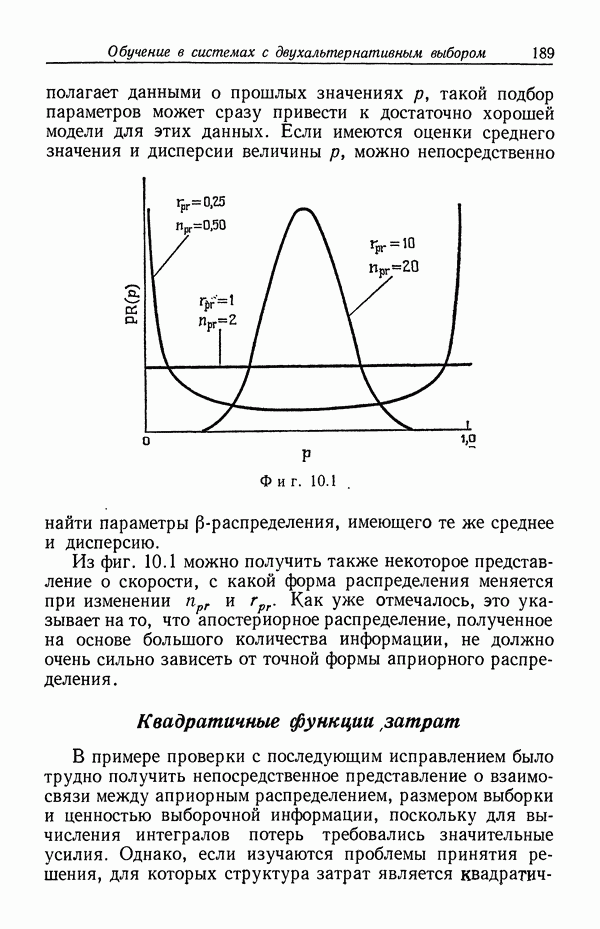
Подбор априорных b-распределений

Некоторые представители семейства -распределений показаны на фиг. 10.1. Ясно, что это — «богатое» семейство, в том смысле, что при надлежащем подборе параметров с его помощью может быть выражено весьма обширное множество разнообразных априорных суждений. Полагая получаем для равномерное априорное распределение. С возрастанием дисперсия априорного распределения убывает, представляя все меньшую неопределенность относительно . Принимающий решения может из таких графиков для различных членов семейства выбрать то априорное распределение, которое будет адекватным образом выражать его мнение относительно . Если он

располагает данными о прошлых значениях р, такой подбор параметров может сразу привести к достаточно хорошей модели для этих данных. Если имеются оценки среднего значения и дисперсии величины можно непосредственно найти параметры (-распределения, имеющего те же среднее и дисперсию.

Фиг. 10.1

Из фиг. 10.1 можно получить также некоторое представление о скорости, с какой форма распределения меняется при изменении Как уже отмечалось, это указывает на то, что апостериорное распределение, полученное на основе большого количества информации, не должно очень сильно зависеть от точной формы априорного распределения

Квадратичные функции затрат

В примере проверки с последующим исправлением было трудно получить непосредственное представление о взаимосвязи между априорным распределением, размером выборки и ценностью выборочной информации, поскольку для вычисления интегралов потерь требовались значительные усилия. Однако, если изучаются проблемы принятия решения, для которых структура затрат является квадратичной,

а не линейной, могут быть сделаны существенные упрощения.

Рассмотрим класс задач, в которых затраты в связи с выполнением некоторого действия выражаются формулой

где а предпринятое действие — параметр биномиального распределения; С — константа.

Пусть, например, доля дефектных изделий, или «ненадежность» партии продукции, оценена равной а. Если эта оценка отлична от истинного значения величины р, то затраты, выраженные через цену, уплаченную за приобретенные изделия и доход от их использования, будут приблизительно пропорциональны квадрату разности между а и р. Или рассмотрим случай, когда руководитель оценивает долю персонала, увольняющегося во время работ по проекту, как . Предвидя это обстоятельство, руководитель проекта может предпринять различные действия, например заранее нанять дополнительное число работников. Если оценка оказалась ошибочной, это может привести к тому, что на работах по проекту будет занято слишком мало или слишком много людей, причем связанные с этим издержки окажутся приближенно пропорциональными квадрату ошибки в оценке. Пусть при планировании производства можно ожидать, что некоторая доля а выпускаемых изделий окажется дефектной. Чтобы удовлетворить заданным требованиям к количеству выпускаемых годных изделий, следует увеличить общий план выпуска продукции с учетом потерь из-за брака. Другой пример из области сбыта. Пусть из числа адресатов, которым непосредственно по почте посланы рекламные объявления, доля будущих покупателей товара оценивается как а. При производстве товаров в количестве, соответствующем этой оценке с учетом проведения рекламной кампании по почте, может оказаться, что будет произведено слишком много или слишком мало товаров. Таковы лишь несколько примеров задач на принятие решения, в которых структуру затрат разумно аппроксимировать квадратичной функцией указанного вида.

Предположим, что относительно величины биномиального параметра существует неопределенность, но что эта

неопределенность может быть выражена в виде некоторого априорного распределения. Априорно ожидаемые затраты в случае выбора некоторого действия (или оценки) а даются выражением

Это выражение можно переписать в виде

Для нахождения априорно наилучшего действия возьмем первую производную от априорно ожидаемых затрат, приравняем ее нулю и решим полученное уравнение:

откуда

Таким образом, априорно наилучшим действием будет взять в качестве оценки среднее значение априорного распределения. В математической статистике величина называлась бы несмещенной оценкой следовательно, одна из интерпретаций несмещенной оценки состоит в том, что она минимизирует ожидаемые затраты в случае квадратичной функции затрат.

Вычисляя ожидаемые затраты с использованием оптимального значения а, получим

Следовательно, ожидаемые затраты на основании наилучшего значения а пропорциональны дисперсии априорного распределения величины . Отсюда непосредственно следует, что при получении дополнительной информации и преобразовании априорных значений в апостериорные наилучшим действием будет положить . В этом случае апостериорно ожидаемые затраты, имеющие место при использовании наилучшего действия, были бы равны . Таким образом, ценность дополнительной информации определяется формулой

откуда

Эти результаты находятся в соответствии с интуитивным предположением, что ожидаемая ценность информации, содержащейся в выборке, будет увеличиваться с уменьшением апостериорной дисперсии, т. е. с увеличением размера выборки. Ценность выборочной информации уменьшается вместе с уменьшением дисперсии априорного распределения. Чем более определенной является для нас ситуация, тем меньше ценность дополнительной информации. Так как в случае полной информации дисперсия апостериорного распределения равна нулю, EVPI оказывается предельным значением EVSI при увеличении размера выборки. Отметим, что ни один из этих результатов не зависит от специальных предположений о виде априорного распределения. Они остаются пригодными как для нормального, так и для -распределения.

Оптимальный размер выборки

В случае квадратичной структуры затрат выражение для оптимального размера выборки может быть получено непосредственно. Рассмотрим ожидаемый чистый выигрыш от получения выборочной информации как функцию размера выборки. Затраты на осуществление выборки полагаются просто пропорциональными размеру выборки. Итак,

Для оценки воспользуемся следующей гипотезой:

Априорная дисперсия апостериорного среднего значения равна дисперсии среднего минус ожидаемое значение апостериорной дисперсии.

Мы не будем здесь приводить доказательства этого утверждения в общем случае, а лишь покажем, что оно справедливо для рассмотренного в гл. 6 нормального распределения. Напомним, что для нормального распределения априорная дисперсия апостериорного среднего дается формулой

Величина по определению является дисперсией априорного распределения. Дисперсия апостериорного распределения равна

а так как эта величина не зависит от наблюдаемого значения среднего по выборке, она равна также ожидаемому значению апостериорной дисперсии. Таким образом, наш результат верен для нормального распределения. Этим еще не доказывается, что он справедлив для общего случая, но мы будем предполагать, что это так.

Применим этот результат для случая априорного -распределения, вспомнив также предыдущий результат. Ранее было найдено, что априорная дисперсия апостериорного среднего равна

Таким образом, мы имеем

или

Ожидаемый чистый выигрыш от получения информации, содержащейся в выборке, можно теперь выразить следующим образом:

Взяв частную производную по и полагая ее равной нулю, получим

где — оптимальный размер выборки.

Из этого выражения мы непосредственно заключаем, что а) чем больше затраты на проведение выборки тем меньше оптимальный размер выборки;

б) чем меньше дисперсия априорного распределения, тем меньше оптимальный размер выборки, т. е. чем больше наша уверенность относительно значения до получения дополнительной информации, тем меньше дополнительных данных нам желательно получить;

в) чем больше затраты, связанные с наличием ошибки (измеряемые величиной С), тем больше оптимальный размер выборки;

г) если выражение для оказывается отрицательным, то это означает, что наилучшее решение — действовать немедленно без поиска какой-либо дополнительной информации.

Последовательные выборки

Большая часть наших рассуждений до сих пор касалась программ сбора данных, основанных на заранее фиксированном размере выборки. Такие программы с фиксированным размером выборки, очевидно, игнорируют то обстоятельство, что в момент поступления данных полученная ранее информация уже может быть достаточно убедительной для составления определенного мнения. Таким образом, может оказаться ненужным тратить усилия на получение дополнительных данных, входящих в заранее запланированную выборку.

Естественное обобщение этой идеи приводит к стратегии последовательных выборок. После получения каждой порции информации вычисляется апостериорное распределение, на основе которого решают, следует ли действовать или надо получить дополнительную порцию информации. В последнем случае предыдущее апостериорное распределение (теперь рассматриваемое уже как априорное) опять преобразуется в новое апостериорное распределение и снова принимается решение, начинать ли действовать или продолжать выборку. Такой план, если он осуществим, очевидно, позволяет наилучшим образом использовать поступающую информацию и обычно обеспечивает наиболее экономную программу сбора.

Рассматривая метод последовательных выборок, мы переходим от единичных, изолированных решений к последовательному принятию решений. Исли сохраняется предположение

о квадратичной структуре затрат, сравнительно легко наметить осуществление программ последовательных выборок. Предположим, что на любом конкретном этапе программы неопределенность относительно , с которой имеет дело лицо, принимающее решения, характеризуется -распределением с параметрами . Отметим, что с точки зрения уже полученной информации это — апостериорное распределение, по отношению же к искомому решению — априорное распределение. Пусть обозначает дисперсию -распределения величины , когда осведомленность принимающего решения выражается величинами . Если он решает остановиться на этом и перейти к действиям, затраты, отвечающие наилучшему в настоящий момент действию, будут равны

Введем теперь следующее определение:

— ожидаемые затраты, если осведомленность лица, принимающего решения, характеризуется величинами гипи если он всегда придерживается наилучшей возможной стратегии.

В этот момент он может либо остановиться и перейти к действиям, либо продолжать поиск, чтобы получить еще одно наблюдение. Следовательно, будет минимальным из двух выражений:

Таким образом, минимальные ожидаемые затраты на каждом этапе могут быть определены лишь тогда, когда известны затраты для всех будущих этапов.

Один из способов решения этой проблемы состоит в «усечении» программы, заранее решая приостановить дальнейшие выборки, когда достигнет какого-то определенного значения если до этого не было решено перейти к действиям. Момент прекращения наблюдений может определяться требованием, чтобы решение было принято до достижения некоторого предельного числа выборок или чтобы

сбор данных производился лишь в пределах некоторого лимита отпущенных на это средств. Посмотрим сначала, какое действие нужно выполнить, если будет равно для каждого возможного значения . После этого мы можем вернуться к этапу, характеризуемому величиной и т. д.

Но даже без такого усечения программы можно быть уверенным, что если получение информации связано с определенными затратами, поиск будет прекращен и после некоторого конечного числа дополнительных выборок будут предприняты действия. Действительно, можно предположить, что существует некоторое значение после которого дополнительные выборки не будут производиться, каково бы ни было в этот момент значение . Другими словами, существует некоторое такое, что для всех

Вспоминая, что

и полагая

подставим эти величины в предыдущее выражение. Рассматривая только случай равенства и разрешая его относительно получим

Это и есть то значение , после которого выборки прекращаются.

Полученный вывод можно проиллюстрировать при помощи весьма простого примера, в котором затраты на выборку предполагаются равными долл. и долл. При этих значениях получаем

На фиг. 10.2 приведена схема относящихся сюда вычислений. При желании читатель может проверить, что при продолжении выборок после ожидаемые затраты могут только увеличиться (или, в лучшем случае, остаться неизменными).

Фиг. 10.2.

Системы контроля и управления

Обратимся теперь к некоторым основным проблемам выработки решения, с которыми сталкивается руководитель, который хочет создать систему контроля и управления и контроля за операциями, относящимися к сфере его ответственности. Основные проблемы будут оставаться структурно-подобными независимо от того, хочет ли он контролировать качество выпускаемой продукции или прибыльность какого-то из подразделений своей фирмы. В общем случае мы имеем некоторую действующую систему, качество работы которой оценивается после выпуска каждой единицы продукции или в определенные моменты времени. Предположим далее, что руководитель в первом приближении разделяет действия на две категории: приемлемые и явно ошибочные. Процесс управления как таковой в конце концов сводится к установлению допусков, критериев приемлемости, заданий по сбыту, пределов ассигнований и т. д., т. е., попросту говоря, критериев приемлемого или неприемлемого качества работы системы. На деле прочно установившаяся традиция «управления по отклонениям» включает процедуру оценки качества

системы, но руководителю представляется информация лишь в случае, когда качество становится неприемлемым.

Проектирование полной системы управления включает

а) установление критериев или стандартов приемлемого качества работы;

б) определение того, насколько часто должно наблюдаться и сравниваться с критериями фактическое качество работы;

в) вскрытие причин появления неприемлемого качества;

г) определение характера необходимого корректирующего воздействия и выбор времени его осуществления.

Проблемы «б» и «г» требуют особого внимания, так как они обычно обсуждаются в общем виде. В нестрогой формулировке эти проблемы выглядят так:

1. Следует ли затрачивать средства на частое наблюдение за качеством работы системы, чтобы можно было сразу вмешаться, когда это окажется необходимым, или же надо экономить средства, прибегая к менее частым наблюдениям, но рискуя зато упустить время, необходимое для исправления возникающих осложнений?

2. Когда появляется информация о возможном нарушении деятельности системы, руководитель должен решить, пойти ли на затраты, которых требует немедленное вмешательство (возможно, и ненужное), или же ждать до тех пор, пока состояние системы не станет более определенным. Конечно, пока он выжидает, могут произойти всякие неприятные события.

Чтобы наглядно проиллюстрировать эти вопросы, рассмотрим задачу управления производственным процессом.

Управление и контроль за выпуском продукции в ходе производственного процесса

Рассмотрим машину, выпускающую некоторые изделия, каждое из которых проверяется на годность или негодность. За основной параметр при разработке системы контроля может быть принято число проверяемых изделий из каждых L единиц продукции. Можно считать размером выборки, a L «интервалом выборки» (говоря точнее, «интервал между выборками»). Основная задача состоит в контроле за долей дефектных изделий, производимых в данном

технологическом процессе. Рассмотрим процесс, непосредственно следующий за осуществлением управляющего воздействия, в результате которого происходит какое-то регулирование или перенастройка системы. Пусть знание доли дефектных изделий характеризуется -распределением с параметрами После указанного регулирования (которое может включать и некоторый тест для подтверждения эффективности управляющего воздействия), возможно, относительно останется лишь небольшая неопределенность или даже неопределенность будет полностью снята.

По мере продолжения производственного процесса возникает все больше возможностей для наступления различных событий, влияющих на его ход и вызывающих его уклонения от того состояния, в которое он был переведен предшествующим управляющим воздействием. Таким образом, по мере продолжения процесса производства растет неопределенность относительно системы. В общем случае после выпуска L единиц продукции неопределенность относительно может быть выражена посредством -распределения с параметрами распределения, которое, как правило, имеет большую «дисперсию», чем в начале «интервала выборки». Возьмем выборку из изделий и подсчитаем число дефектных изделий в ней. Выборка последних произведенных изделий может дать информацию о текущем состоянии системы и может быть использована для упрощения задачи с помощью предположения, что процент брака в данном процессе был фактически постоянным в течение выпуска входящих в выборку изделий. Содержащаяся в выборке информация комбинируется тогда, как обычно, с параметрами , что дает пересмотренное выражение для распределения величины . Тогда можно рассматривать как случайную переменную, распределенную по Р-закону с параметрами и про. Задача проектировщиков системы всегда состоит в подходящем выборе и L. Некоторые из относящихся сюда вопросов можно пояснить на простом примере.

Предположим, что к концу каждого «интервала выборки» затраты на управляющее воздействие умеренны и что система при этом возвращается в то же состояние, в каком она находилась в начале интервала, т. е. состояние с параметрами

Это позволяет рассматривать один «интервал выборки» как характеристический для всех остальных, так как процесс на интервале всегда возобновляется в одинаковых условиях. Предположим далее, что для того, чтобы управляющее воздействие оказалось эффективным, неопределенность относительно должна быть уменьшена до некоторого приемлемого уровня. Это позволит для любого «интервала выборки» L решить, какой фиксированный размер выборки или план последовательных выборок может потребоваться для обеспечения эффективного управляющего воздействия. Вообще говоря, чем больше «интервал выборки» L, тем больше результирующая неопределенность относительно и тем больше размер выборки, необходимый в качестве основы для эффективного управляющего воздействия. Проблема проектирования сводится, таким образом, к проблеме выбора «интервала выборки». В таком случае мы можем попытаться найти такой интервал выборки, который минимизировал бы затраты на единицу продукции при следующей структуре затрат:

1. Затраты на управляющее воздействие могут содержать фиксированную составляющую и могут также зависеть от состояния наших знаний, т. е. от параметров и про.

2. Затраты на осуществление выборки являются некоторой возрастающей функцией размера выборки. С возрастанием L затраты на выборку будут возрастать, так как растет ее размер, но затраты на осуществление выборки, рассчитанные на единицу продукции, могут сильно понизиться. С возрастанием L обычно происходит увеличение количества брака, выпускаемого системой. Таким образом, с увеличением «интервала выборки» растут и расходы на брак.

Проектировщик системы, желающий минимизировать затраты на единицу выпускаемой продукции, обычно обнаруживает, что по мере увеличения

единичные (т. е. рассчитанные на единицу продукции) затраты на управляющие воздействия уменьшаются; единичные затраты на проведение выборки уменьшаются; единичные затраты, связанные с выпуском брака, растут.

Системы с многоинтервальными выборками

Во многих системах контроля и управления руководитель не вырабатывает, как это предполагалось раньше, специальных управляющих воздействий с целью возвращения системы в исходное состояние к началу каждого интервала выборки; после изучения результатов выборки он может принять решение вообще не предпринимать никаких действий. Классическое упрощение состоит в том, чтобы решить, при каких условиях выборочной информацией можно пренебречь, и предполагать, что система действительно находится в состоянии, в котором она находилась в начале интервала. При таком упрощении структура задачи остается такой же, как предполагалось ранее.

Однако более реалистично ожидать, что руководитель изучит результаты выборки, убедится, что система не находится в том же состоянии, что и в начале интервала, и все же решит не прибегать к управляющим воздействиям. Далее, управляющее воздействие, если и будет предпринято, может оказаться не вполне эффективным. Это означает, что оно может перевести систему не в исходное, а какое-то другое состояние, которое может зависеть от знания руководителем текущего значения и от конкретного вида выбранного им управляющего воздействия. В этом случае задача проектировщика системы — найти интервал выборки, размер выборки и подходящее управляющее воздействие (включая, возможно, и отказ от каких-либо действий вообще). При серьезном рассмотрении задача проектирования системы требует заглядывания вперед и предвидения того, что окажется наилучшим в конце будущих интервалов. Например, если не предпринимается вообще никаких действий, результирующие затраты зависят от текущего состояния системы, от того, когда и какого рода управляющие воздействия будут предприняты в будущем и сколько, таким образом, будет произведено бракованных изделий. С другой стороны, если выполнено некоторое управляющее воздействие, это может принести выгоды, которые станут ощутимыми по истечении некоторого числа интервалов, но ценность такого рода действия невозможно определить, не проанализировав эти будущие интервалы. Таким образом, проблема проектирования, как и последовательное проведение

выборок, требует рассмотрения последовательности решений. (Основная структура таких проблем описана в гл. 11).

Другие системы контроля и управления

Хотя разобранный только что пример управления производственным процессом достаточно хорошо иллюстрирует некоторые основные вопросы, возникающие при проектировании большинства систем управления производством, было бы нереалистично думать, что он охватывает все важные проблемы. В случае когда система управления включает в себя как людей, так и технические средства, возникает множество новых затруднений. Когда руководство фиксирует финансовые показатели, задания и нормативы для торговых или промышленных предприятий, эти определения приемлемого качества работы не только образуют основу для систем управления, но и оказывают очень важное стимулирующее воздействие на участников. Если целевое задание очень высоко, так что вероятность его достижения очень мала, участники могут просто отвергнуть его как явно нереалистичное. Если финансовый план настолько занижен, что вероятность его выполнения высока, участники могут работать ниже разумного уровня эффективности, поскольку «приемлемое качество работы» будет и без того легко достижимым. Из этих соображений сразу вытекает, что руководителю следует, не ограничиваясь осуществлением корректирующих воздействий, как в примере с управлением производственным процессом, рассмотреть возможность изменения критериев приемлемого качества работы системы. Такого изменения могут потребовать, например, легко и часто выполнимые финансовые задания, или же финансовые планы, которые редко выполняются или никогда не осуществляются.

Имеются важные указания на то, что, если сотрудники системы имеют возможность устанавливать собственные критерии приемлемого качества работы, такие критерии будут оказывать гораздо большее влияние на их поведение, чем в случае, когда эти показатели устанавливаются руководителями более высокого уровня. Ясно также, что для сотрудников важно иметь четкое представление о том, как определяется приемлемое качество и насколько их собственное

поведение отвечает критериям приемлемости. Вполне может также случиться, что система управления, которая только сообщает об отклонениях от приемлемого поведения и вызывает лишь корректирующие воздействия, может оказать серьезное отрицательное влияние на отношения между руководителем и сотрудниками. Представляется более мудрым сообщать также об успешном достижении целей и обеспечить какие-то формы поощрения в дополнение к корректирующим действиям в ответ на неудовлетворительную работу системы.

Упражнения

10.1. Покажите, что в случае априорного -распределения и биномиального закона для правдоподобности стремится к нулю, когда стремится к бесконечности.

10.2. Руководитель фирмы пытается решить, приступать ли к выпуску новой продукции. Он чувствует, что существует определенное количество потенциальных потребителей этой продукции, но не уверен, какая часть из них будет в действительности ее покупать. Он рассматривает дорогостоящую программу сбора данных о возможных продажах путем изучения выборки из потенциальных потребителей. Укажите, какого рода анализ необходим для того, чтобы помочь ему запланировать наиболее подходящую в этих условиях процедуру.

10.3. Фирма закупает материалы партиями объема L единиц. Когда партия получена, из нее берется выборка размером , и каждое изделие из выборки проверяется на пригодность. На основе этой проверки приобретается или отвергается вся партия. Фирма полагает, что с каждым принятым негодным изделием, с каждым отвергнутым годным изделием и с каждым изделием, подвергнутым проверке, связаны свои особые затраты. Опишите анализ, необходимый для определения оптимального размера выборки, которым следовало бы пользоваться фирме.

10.4. Предположим, что вам приходится выбирать между двумя производственными процессами, практически одинаковыми во всех отношениях, кроме доли дефектных изделий. Однако у вас существует неопределенность относительно этих долей. Можно провести дорогостоящую серию контрольных испытаний, относящихся к одному или к обоим процессам. Вы хотите обосновать ваш выбор, исходя из принципа минимизации ожидаемого процента брака. Предложите план испытаний и анализ их результатов.

10.5. При разборе особенностей системы управления был использован пример, относящийся к управлению производственным процессом. Покажите, каким образом сходные идеи могут быть приложены к какой-либо другой области управления.

10.6. При анализе систем управления с выборками данных по многим интервалам наблюдений указывалось, что при проектировании системы необходимо учитывать и будущие интервалы выборок. Как решить, насколько далеко в будущее было бы важно распространить такое рассмотрение?