Глава 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ПЕРЕМЕННЫЕ

Пример предсказаний

В этой главе теория принятия логически непротиворечивых решений обобщается на ситуации, в которых источники неопределенности, по-видимому, лучше всего моделировать случайными переменными. Выражение неопределенности в виде вероятностей требует привлечения к анализу методов непрерывных случайных переменных. В применениях чаще всего используются нормальное и -распределения; поэтому мы именно на них и сосредоточим свое внимание. Вначале мы проиллюстрируем, каким образом нормальное распределение может быть использовано, чтобы охарактеризовать неопределенность относительно осуществимости прогнозов, на основе которых лицо, принимающее решение, должно основывать свой выбор.

Предположим, что руководитель уверен, что получит какой-то важный контракт, если предложит выполнить требуемую работу по цене R. Однако он не уверен, даст ли ему контракт при такой цене какую-либо прибыль. У его фирмы есть метод оценки стоимости выполнения таких контрактов, но, как часто бывает, руководитель не уверен в точности этих оценок стоимости и, возможно, в какой-то степени не удовлетворен ими.

Эту деятельность по оценке стоимости можно рассматривать как прототип различных систем предсказания или прогнозирования, которые обычно имеются в фирмах. Оценки издержек производства, объема продаж, денежных резервов и т. д. могут быть выполнены традиционными способами и служат в качестве основы для выработки важных решений. Источником этих оценок могут быть отдельные эксперты, комитеты или группы специалистов. К процессу оценки привлекаются как эксперты, полагающиеся в основном на интуицию, так и исследователи

операций, использующие количественные данные и математические модели, или те и другие одновременно.

Согласно сложившейся традиции, содержание получаемых таким образом оценок обычно сводится к однозначным предсказаниям типа: «Стоимость выполнения этого контракта будет я»; «Объем наших продаж на следующие шесть месяцев будет у». В таких предсказаниях не делается попыток выразить неопределенность ситуации. Вся неопределенность этих утверждений, которую, возможно, и сознавали те, кто делал предсказания, изгоняется из них, по мере того как эти однозначные утверждения передаются по организации. Руководители, которые в своей деятельности часто сталкивались с подобными предсказаниями, без труда представляют себе степень их взаимной смещенности, точности или надежности. Мнение о том, что прогнозы о продаже товара, даваемые управляющими отдела сбыта, имеют тенденцию быть «оптимистичными», равносильно утверждению, что в среднем фактический объем продаж оказывается все-таки меньше, чем было обещано этими предсказаниями. Средняя разность между оцениваемым количеством и фактическим результатом измеряет смещение, присущее принятому способу оценки. Если в среднем оценка и фактическая величина оказываются равными, то процесс оценки можно назвать несмещенным.

Существует несколько способов выявления неуверенности руководителя в отношении оценки стоимости (т. е. неопределенность этой оценки) в нашем примере. Допустим, что руководитель представляет себе фактическую стоимость выполнения контракта как сумму оцененной стоимости и некоторой ошибки. В этом случае для нас было бы полезно представить ошибку в виде случайной переменной, среднее значение которой мы примем за меру смещения, а дисперсию — за меру точности процесса оценки. Если среднее значение (математическое ожидание) ошибки равно нулю, мы можем сказать, что процесс дал несмещенные оценки. Если среднее значение ошибки больше нуля, можно было бы вычесть это среднее из каждой оценки и рассматривать исправленные оценки как несмещенные. Но такая простая поправка может улучшить результаты только в том случае, если мы у меем «оценивать» (т. е. определять точность) способ нахождения оценки.

Рассматриваемая нами модель предполагает, что ошибки не зависят от оцениваемых затрат на выполнение контрактов. Ошибки в оценках для крупных контрактов в принципе характеризуются той же степенью неопределенности, что и оценки для контрактов, требующих меньших затрат. Для руководителя может быть разумнее встать на другую точку зрения и рассмотреть относительные ошибки. Он должен чувствовать, что ошибки в долларах будут все-таки больше для крупных контрактов. Можно принять, что фактическая стоимость равна оцененной стоимости, умноженной на некоторую случайную переменную, которая называется коэффициентом ошибки (error ratio). В этом случае несмещенный процесс оценки характеризовался бы коэффициентом ошибки, ожидаемое значение которого равно единице. Подходит ли какая-либо из этих двух моделей и если да, то какая — оставляется на усмотрение руководителя, который руководствуется при этом своим прошлым опытом и фактическими данными относительно качества рассматриваемого процесса оценки. Но какой бы метод он ни выбрал, это, видно, приведет к рассмотрению стоимости выполнения контракта как случайной переменной. Если мы предположим, что руководителю ясно, за какую цену может быть получен контракт, то прибыль становится случайной переменной, определяемой просто как разность между ценой и стоимостью.

Если у руководителя имеется значительный опыт в оценке стоимостей соответствующими методами, он будет склонен действовать так, как если бы он был уверен в величине их смещения и надежности. Используя первую модель, в которой фактическая стоимость полагается равной сумме оценки стоимости и ошибки, руководитель будет склонен действовать так, как если бы он был уверен в величине среднего значения и дисперсии ошибки. При этом мы можем ожидать, что ошибка будет результатом большого числа малых, независимых эффектов, и, таким образом, исходя из теоретических соображений, считать ее распределенной по нормальному закону. Но мы хотим рассмотреть более общий случай, когда опыт руководителя недостаточен для того, чтобы он мог действовать так, как если бы он с уверенностью знал распределение ошибки. Как он может

приобрести этот опыт и как он должен действовать, если он им еще не располагает?

Предположим, что у руководителя есть опыт в выполнении процессов оценки, аналогичных приведенным здесь, и что он, возможно, даже располагает какими-то конкретными данными об их качестве. Тем не менее он может считать рассматриваемый способ оценки источником неопределенности по одной или нескольким из указанных ниже причин.

1. Способ оценки применялся лишь короткое время.

2. В способе оценки произошло какое-то изменение — включение новых лиц, нового метода анализа, дополнительных данных.

3. По прошлому опыту руководитель знает, что способ оценки компенсирует изменения, но ему не ясно, как именно.

4. Возникли новые условия, которые должны быть учтены с помощью принятого способа оценки, но не ясно, как эти условия повлияют на его качество.

5. Способ оценки может быть вполне упрочившимся, но руководителю просто не удается выразить в явном виде замеченные прошлые ошибки.

Проблема разработки программы сбора данных, которую мы собираемся подробнее изучить, предполагает, что руководитель готов действовать так, как если бы ему была известна дисперсия ошибки, но не уверен относительно ее среднего значения. Он может почувствовать, что в процессе что-то изменилось, вследствие чего изменилось смещение оценок, но их надежность осталась прежней. При этом процесс кажется ему похожим на другие, встречавшиеся ранее процессы, которые различались своими смещениями, но имели вполне предсказуемую точность. Для математической теории это предположение очень важно, так как без него решение задачи становится технически очень сложным, хотя и отнюдь не невозможным. Во многих ситуациях, когда можно получить какие-то данные, окончательные результаты довольно нечувствительны к указанному предположению. Обычно оказывается, что 25 наблюдений результатов оценок достаточно для того, чтобы можно было оценить точность используемого способа и тем самым избежать опасности ввести руководителя в заблуждение.

Подбор априорных нормальных распределений

Сосредоточим теперь внимание на смещении оценок, измеряемом с помощью математического ожидания (среднего значения) для распределения ошибок. Не имея полного представления о ситуации, руководитель стремится выразить эту неопределенность в виде вероятностей или рассматривать среднее значение или ошибку процесса оценки как непрерывную случайную переменную. Наша задача состоит в том, чтобы максимально облегчить отыскание такого априорного распределения и помочь руководителю выявить некоторые следствия найденного распределения, полезные с точки зрения выработки логически оправданного поведения.

Рассмотрим сначала случай, когда у руководителя нет конкретных данных о средних ошибках сходных процессов оценки. В этом случае ему приходится всецело полагаться на весь свой опыт и способность к вынесению суждений. Мы предполагаем, что у него имеется некоторый опыт и что он готов тщательно обдумывать его, ибо в противном случае он едва ли занимал бы ответственное положение. Он должен подумать, как он действовал бы в некоторых ситуациях принятия решения, обсуждаемых в гл, 3. Если — математическое ожидание ошибок оценивания, то задача состоит в том, чтобы установить априорное распределение для . Мы можем попросить руководителя рассмотреть следующую ситуацию принятия решения:

существенный выигрыш, если истинное значение больше , и ничего в противном случае;

тот же выигрыш, если истинное значение меньше , и ничего в противном случае.

Если нам удалось установить такое значение , которое вызывает у руководителя безразличие к выбору любой из этих двух возможностей, мы имеем медиану априорного распределения. Аналогично мы можем предложить ему рассмотреть такую задачу на принятие решений;

существенный выигрыш с вероятностью 0,25 (выраженной, например, в терминах нашей базисной лотереи) и ничего с вероятностью 0,75;

тот же выигрыш, если больше и ничего в противном случае.

Если мы установили такое которое оставляет руководителя безразличным по отношению к этим двум возможностям, мы имеем верхний квартиль априорного распределения. Как далеко мы должны продолжать этот процесс, зависит в сильной степени от обстановки, в которой нам приходится действовать. Если представляется возможным получить нужную информацию позже, нам не обязательно тратить усилия на отыскание априорного распределения, так как наши окончательные результаты почти не чувствительны к его точной форме. В других случаях, как мы вскоре убедимся, важное значение имеет достаточно точное знание априорного распределения.

Предположим, что руководитель предпочитает иметь дело с «гладкими» или «хорошо ведущими себя» априорными распределениями, до тех пор пока он не имеет особых причин ожидать появления в таких распределениях «провалов» или «бугров». Таким образом, он будет стремиться «сгладить» распределение, отвечающее его представлениям в процессе принятия решения. Предположим далее, что у него нет возражений против рассмотрения нескольких априорных распределений, из которых все в равной степени хорошо представляют ответы, которые мы получили на такие вопросы. Так как имеются весьма существенные математические соображения, заставляющие стремиться к использованию в качестве априорных нормальные распределения, мы предполагаем, что руководитель часто будет придерживаться распределений именно такой формы, пока они отражают его представление о медианах, квартилях и т. д. Конечно, мы должны тщательно исследовать вместе с ним, не имеется ли каких-либо специальных или необычных следствий выбранного нами априорного распределения.

С другой стороны, если доступны исторические данные из архивов фирмы о смещении, характерном для ряда способов оценки, то руководитель мог бы обратиться к этим данным, положив их в основу своего априорного распределения. Затем мы могли бы начертить гистограмму наблюдавшихся значений и «подогнать» априорное распределение к этим данным. Здесь возникает множество вопросов относительно «наилучшей подгонки» априорного распределения, но снова во многих ситуациях окончательные результаты будут почти не чувствительны к его точной

форме. Мы предполагаем, что априорное распределение будет «сглаживать», или «выравнивать», частоты, соответствующие историческим данным, если нет особых причин предполагать иначе. В таком распределении находят свое выражение знания. руководителя об изучаемом явлении и фактические данные. В нашем примере мы также предполагаем, что для описания имеющихся данных используется нормальное априорное распределение.

Разработка программы сбора данных

Теперь мы подошли к действительно решающей проблеме руководства. Должно ли решение приниматься на основе того, что уже известно о процессе оценки, или до принятия окончательного решения по рассматриваемому контракту должна быть проведена какая-то программа по сбору дополнительных данных? Можно рассмотреть различные программы адаптивного обучения, хотя некоторые из них, безусловно, не относятся к каким-либо ситуациям управления.

1. Если данные о прошлых ошибках процесса оценки могли быть, но не были получены, можно рассмотреть, какое - углубление в архивы было бы разумным для руководителя.

2. Можно провести ряд экспериментов, в которых процесс оценки сводился бы к оценке стоимости контрактов, чья настоящая стоимость уже известна.

3. Можно пытаться находить для контрактов наилучшие решения на основе имеющейся априорной информации, но вместе с тем создать информационную систему, которая регулярно поставляла бы основные данные, необходимые для уменьшения неопределенности руководителя относительно смещения, присущего принятому процессу оценки.

4. Можно полностью отказаться от оценок стоимости с помощью рассматриваемого процесса оценки. Вместо этого руководитель может искать какой-то другой процесс оценки, относительно смещения которого у него было бы меньше неопределенности.

Для простоты предположим, что первые три программы могут дать наблюдения оценок стоимости, которые руководитель склонен приписать данному способу оценки, а также фактическую стоимость работ. Следовательно, каждое такое

наблюдение позволяет вычислить получаемую ошибку в оценке. В четвертом случае задача фактически состоит из сравнения оценки дохода, ожидаемого на основе имеющегося способа оценки, с доходом, которого следует ожидать при использовании какого-то другого способа. Рассмотрим сначала общую проблему, возникающую в связи с первыми тремя случаями.

Процесс оценки считается источником независимых, нормально распределенных ошибок, дисперсия которых известна. Однако принимающий решения не уверен относительно их среднего значения. Он выражает эту неуверенность (неопределенность) в виде нормального априорного распределения. Затем можно получить наблюдения о результатах процесса оценки и вычислить функции правдоподобия этих наблюдений в предположении какого-либо частного значения для средней ошибки. Это дает нам все необходимые элементы для вычисления апостериорного распределения среднего значения ошибки на основе теоремы Байеса, которая служит руководящим принципом для обучения или для усвоения данных. Отсюда мы можем перейти к ожидаемой ценности выборочной информации (EVSI), а при некоторых представлениях о стоимости сбора данных — к разработке оптимальной программы сбора данных или информационной системы для нужд руководства. Изложим теперь основные этапы связанного с этой программой анализа, логические принципы которого совпадают с теми, которые обсуждались в гл. 5.

Переходя к взятому нами примеру оценки контракта, сделаем небольшое упрощение. Предположим, что руководитель хочет максимизировать ожидаемый доход и что последний равен разности между известной ценой и ожидаемыми издержками. Если издержки (себестоимость) считать нормально распределенной случайной величиной, то доход также будет нормально распределенной случайной величиной со средним значением, равным ожидаемому доходу, и стой же дисперсией, что и издержки. Следовательно, мы в этом примере просто принимаем доход от контракта за основную случайную переменную, а ожидаемый доход — за источник неопределенности. Заметим, что очень большое число ситуаций управления можно описать подобным образом.

Связь между априорным и апостериорным распределениями

Мы будем моделировать рассматриваемое нами явление, принимая его за случайный процесс, который порождает последовательность независимых, нормально распределенных случайных величин. Любая из этих величин имеет распределение, обозначаемое следующим образом:

где — математическое ожидание (среднее значение), дисперсия нормального распределения. Мы часто будем называть его распределением процесса, а и v — параметрами процесса. Наиболее подходящая для изучения и вместе с тем типичная ситуация имеется тогда, когда принимающий решение намерен действовать так, как если бы v было известно, а неопределенно. Он выражает эту неопределенность, рассматривая как случайную величину, имеющую нормальное априорное распределение с математическим ожиданием и дисперсией . Следовательно,

Впоследствии мы изучим подробно соображения, которые легли в основу этой важной системы предположений, а пока рассмотрим их дедуктивные следствия.

Предположим, что можно осуществить выборку наблюдений результатов основного нормального процесса в виде Среднее значение этой выборки равно

Среднее значение выборки в этом случае есть нормально распределенная случайная величина. Для любого фиксированного значения математического ожидания процесса функция правдоподобия при реализовавшемся среднем значении выборки будет выражаться в виде

Роль частной выборки наблюдений состоит в преобразовании априорного распределения математического ожидания процесса в апостериорное распределение (РО) согласно формуле Байеса:

Удобно ввести величину

которую можно грубо интерпретировать как меру априорной убежденности или уверенности человека, принимающего решение, относительно величины математического ожидания процесса. Если он вполне убежден или почти уверен относительно величины то с будет большим, так как априорное распределение будет иметь сравнительно малую дисперсию. С другой стороны, малый опыт, отсутствие сильной убежденности и большая неопределенность имеют тенденцию давать большие значения и, следовательно, малые значения с. Возвращаясь к выражению для апостериорного распределения и выписывая нормальные распределения в числителе, получаем

где

Преобразуем теперь выражение для а, прибавив и вычтя величину

и перегруппируем члены. Это дает

Здесь

Апостериорное распределение для можно записать теперь в виде

Так как интеграл от этого выражения в пределах от до должен равняться единице, то

Отсюда видно, что апостериорное распределение математического ожидания процесса также является нормальным и характеризуется параметрами

Вообще говоря, при использовании нормально распределенных выборочных данных нормальное априорное распределение преобразуется в нормальное апостериорное распределение.

Интерпретация апостериорного распределения

Апостериорное значение, для математического ожидания процесса, т. е. величины , является просто взвешенным средним априорного среднего значения математического ожидания процесса и среднего значения по выборке, Весами являются наша приблизительная мера априорной убежденности или уверенности человека, принимающего решение, с и объем выборки п. С увеличением объема выборки среднее значение выборки получает больший вес, а априорное мнение — меньший. Аналогично чем больше дисперсия априорного распределения, тем меньше значение с и тем больше влияние последующих наблюдений. Следовательно, одним из наиболее интересных выводов является тот, что оценка человеком, принимающим решение, своего априорного мнения позволяет ему непосредственно

указать, какой вес должен быть придан априорному мнению, а какой — другим данным, которые будут постепенно становиться доступными. Тот, кто заявляет, что хочет действовать так, как если бы его априорное распределение имело большую дисперсию, одновременно утверждает, что он сильно надеется на поступление дополнительных сведений. Это дает наиболее полезное операциональное определение понятий определенности и неопределенности. Чем больше человек стремится к получению новых данных, тем более неуверенным мы должны его считать в отношении имеющейся ситуации, т. е. тем больше должна быть его неопределенность.

Апостериорная дисперсия математического ожидания процесса уменьшается по мере того, как увеличивается число наблюдений. Если неограниченно возрастает, апостериорная дисперсия будет стремиться к нулю, и человек, принимающий решение, приобретает полную убежденность или уверенность относительно математического ожидания процесса. Заметим, что апостериорная дисперсия становится все меньше с увеличением объема выборки независимо от того, каково среднее значение выборки.

Хотя полезно интерпретировать с как меру неопределенности или недостаточной убежденности, следует проявлять осторожность при использовании термина неопределенный для описания мнения, которое дает малое значение с. Заметим, что, какой бы ни была дисперсия априорного распределения, принимающий решение определил свое мнение, рассматривая, как бы он вел себя в некоторых вполне определенных и четко сформулированных ситуациях принятия решения. Для человека, который дает «широкое» (в противоположность «узкому») априорное распределение, в этих ситуациях нет ничего неопределенного. Широкое априорное распределение не обязательно означает недостаток опыта. Конечно, верно, что по мере приобретения опыта дисперсия апостериорного распределения уменьшается, но широкое (т. е. обладающее большой дисперсией) априорное распределение может очень хорошо выражать мнение опытного в принятии решений руководителя. Большая априорная дисперсия может указывать на неопытность по отношению к рассматриваемому частному

случайному процессу и тем не менее отражать мнение того, кто имеет большой опыт работы со сходными случайными процессами. Такой человек может по опыту знать, что математические ожидания некоторых процессов в действительности могут принимать значения в довольно широком диапазоне величин.

Достаточность

Проведенный нами анализ связи между априорным и апостериорным нормальными распределениями позволил выразить результаты выборки в терминах только одного параметра — среднего значения выборки. Произошла ли какая-либо потеря информации в результате отказа от рассмотрения конкретных значений выборочных наблюдений? Если при использовании фактически полученных значений выборки мы приходим к тому же самому распределению, то среднее может рассматриваться как «достаточная статистика» или «достаточное сообщение». Оно окажет такое же влияние на мнение принимающего решение и в этом смысле содержит всю имеющуюся в данной выборке полезную информацию.

Покажем на простом примере, что среднее значение выборки и в самом деле является достаточной статистикой при рассматриваемых нами условиях. Предположим, что были получены два наблюдения и рассматриваются два возможных сообщения. Сообщение 1 состоит из двух наблюдений сообщение 2 состоит только из среднего значения выборки. Сообщение 1 может рассматриваться как последовательность двух наблюдений, дающая сначала

Это распределение можно далее рассматривать как априорное и вычислить Замечая, что теперь вместо с будем иметь сразу получаем

3 силу того что

это будет то же самое апостериорное распределение, которое получалось бы из сообщения 2.

Если выписать функции правдоподобия сообщений 1 и 2 и взять их отношение, то все члены, содержащие , сократятся. Таким образом, мы можем утверждать, что отношение правдоподобия будет постоянным для всех значений . Это, разумеется, является еще одним частным случаем принципа правдоподобия, изложенного в гл. 5, который указывает, что если отношение правдоподобия двух сообщений постоянно, то сообщения эквивалентны в том смысле, что они приводят к одному и тому же апостериорному распределению.

Предапостериорный анализ

Одна из фундаментальных проблем науки об управлении, безусловно, состоит в том, чтобы заранее решить, должна ли Ьыть предпринята какая-либо программа сбора данных. Сколько данных должно быть собрано в какой-либо ситуации принятия решения, если такой сбор данных оправдан с экономической точки зрения? Какого рода данные лучше всего собирать? Оправдывает ли некоторое конкретное исследование связанные с таким сбором данных издержки? Все эти вопросы требуют рассмотрения стоимости и ценности информации еще до ее получения. В наших терминах сказанное означает, что мы должны рассмотреть как различные наблюдения, которые могут быть сделаны, так и вытекающие из них апостериорные мнения и действия, которые нужно будет предпринять. Все это должно быть рассмотрено до фактического получения данных. Анализ такого рода называется предапостериорным (preposterior) анализом.

Для частного значения выборочного среднего апостериорное среднее дается формулой

Но пока мы не получили каких-либо данных, мы можем рассматривать только как случайную переменную. Если мы уже выбрали объем выборки, то неопределенность, связанная со средним значением выборки, приводит к неопределенности относительно апостериорного среднего. При

этих условиях мы будем говорить об апостериорном среднем как о случайной величине с распределением т. е. априорным распределением апостериорного среднего. Так как есть линейная функция и так как нормально распределено, можно утверждать, что априорное распределение апостериорного среднего также будет нормальным. Хорошо известно также, что если

то

где функция V означает дисперсию. Используя эти результаты, получаем

Но

Подставляя полученное выражение в формулу для имеем

Итак, можно утверждать, что априорное ожидаемое значение апостериорного среднего есть априорное среднее. Иными словами, ожидаемое значение среднего для апостериорного распределения, рассмотренное перед осуществлением выборки, равно среднему априорного распределения.

Читатель поступил бы правильно, если бы тщательно продумал эти утверждения, пытаясь четко запомнить следующие пять распределений, которые участвуют в проводимом анализе:

1) — распределение рассматриваемого случайного процесса;

2) — априорное распределение математического ожидания процесса;

3) — функция правдоподобия выборочного среднего при заданном конкретном значении математического ожидания процесса;

4) апостериорное распределение математического ожидания процесса;

5) — априорпое распределение среднего для апостериорного распределения математического ожидания процесса.

Понимание последующего текста, начиная с этого момента, будет в сильной степени зависеть от того, насколько ясно читатель будет представлять себе различие между указанными распределениями. Это нелегкая задача, потому что при данных условиях все они являются нормальными, хотя и имеют в некоторых (но не во всех) случаях различные параметры.

Возвращаясь к априорному распределению апостериорного среднего, получаем априорную дисперсию апостериорного среднего непосредственно из линейного соотношения между нормальными переменными:

Дисперсия среднего выборки (выборочного среднего) на основании априорной информации может быть получена исходя из определения дисперсии:

Мы предоставляем читателю самому убедиться, что значение третьего слагаемого в последнем выражении равно нулю и что первые два слагаемых дают

Дисперсия среднего выборки представляет собой сумму дисперсии распределения математического ожидания процесса и дисперсии среднего выборки при заданном частном значении математического ожидания процесса. Иными словами, мы можем представлять себе выборочное среднее состоящим из двух независимых аддитивных компонент. Оно равно сумме математического ожидания процесса и

отклонения выборочного среднего от математического ожидания процесса. Так как это отклонение не зависит от величины математического ожидания процесса, то дисперсия суммы просто равна сумме дисперсий, как мы только что и убедились.

Мы можем использовать этот факт, чтобы еще более раскрыть предыдущее выражение для априорной дисперсии апостериорного среднего:

Априорная дисперсия апостериорного среднего равна априорной дисперсии среднего минус апостериорная дисперсия среднего. С ростом объема выборки дисперсия апостериорного среднего стремится к нулю. Следовательно, по мере того как объем информации будет приближаться к полной информации, априорная дисперсия апостериорного среднего будет стремиться к априорной дисперсии среднего.

Экономический анализ

Чтобы проиллюстрировать вычисление ожидаемой ценности выборочной информации и ожидаемой ценности полной информации, снова обратимся к нашему простому примеру. Доход от рассматриваемого контракта можно считать нормально распределенной случайной величиной с известной дисперсией и неопределенным средним значением. Лицо, принимающее решение, выражает свою неуверенность (неопределенность) относительно среднего значения дохода, рассматривая его как случайную величину с нормальным априорным распределением. Ему нужно принять решение — заключить ли этот контракт. Он намерен заключить его только в том случае, если ожидаемый доход будет больше нуля. Ожидаемый доход, связанный с наилучшим априорным действием, равен в силу этого

Предположим сначала, что этому человеку предоставляется возможность получить полную информацию о среднем

доходе. Если полная информация убедит его в том, что ожидаемый доход больше нуля, он заключит контракт, в противном же случае не подпишет его. Следовательно, его выигрыш будет если больше нуля, а в противном случае равен нулю. До получения полной информации его ожидаемый выигрыш от наилучшего действия при наличии полной информации будет равен

где

Ожидаемая ценность полной информации есть ожидаемая прибыль сверх ожидаемого априорного дохода, получаемая в результате использования этой информации:

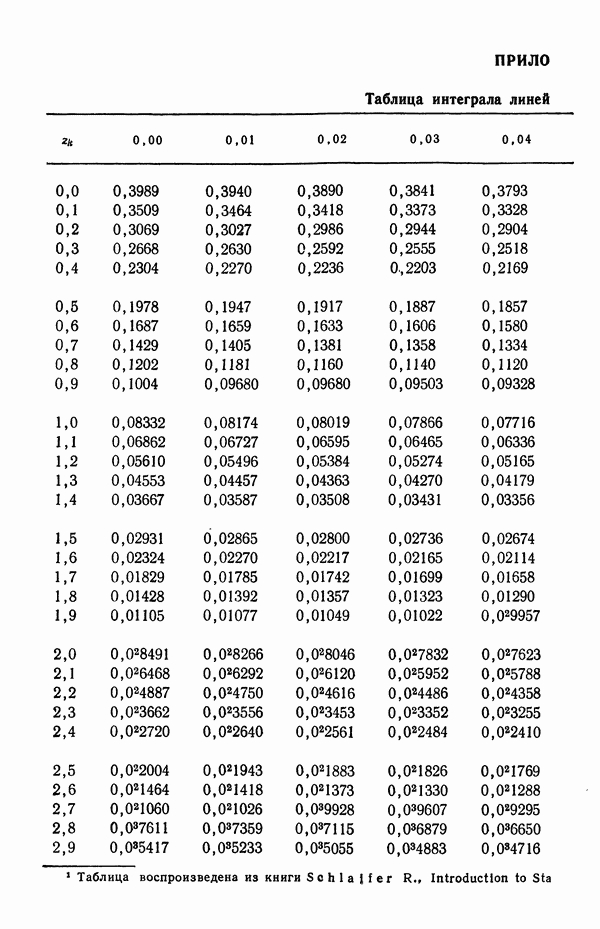
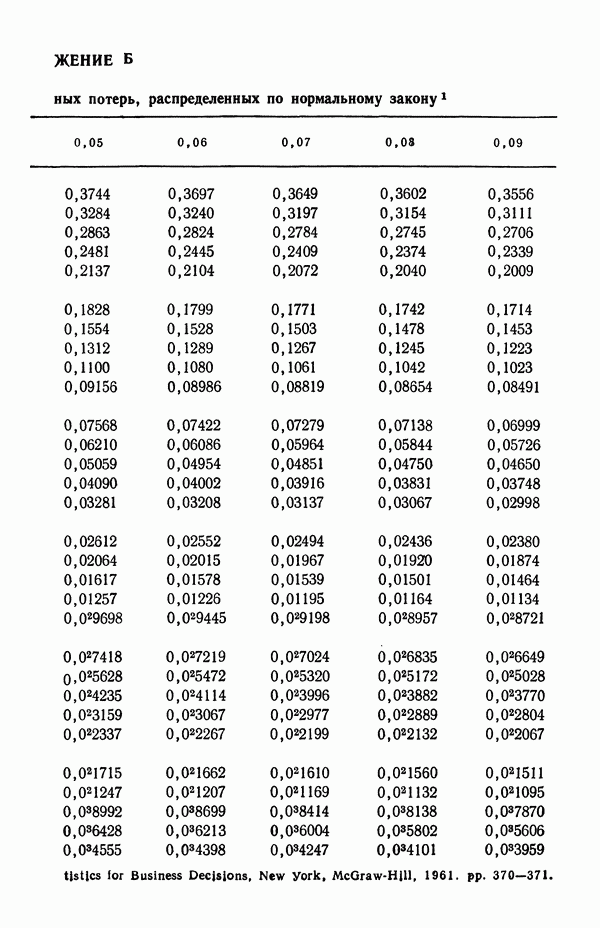
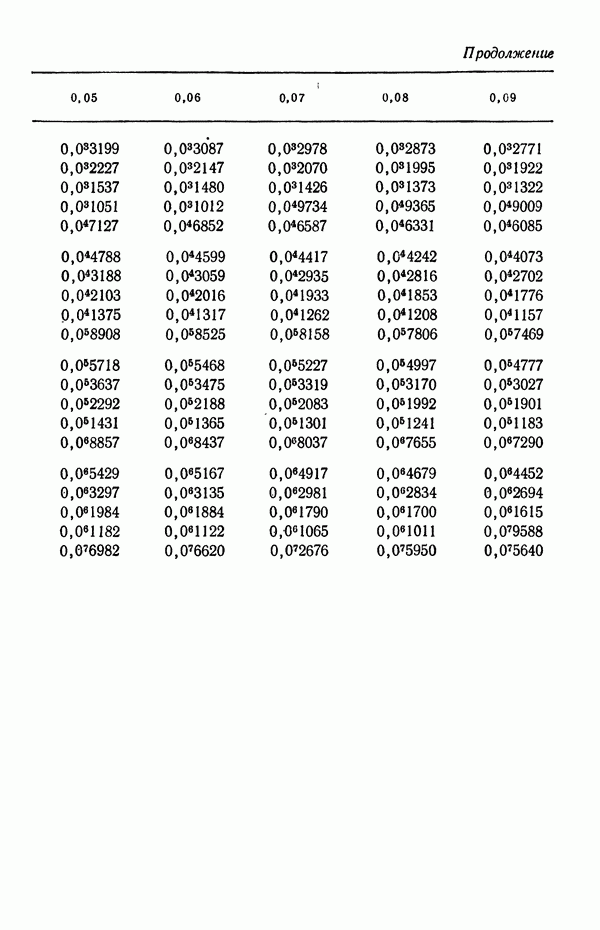
Первый член этого выражения есть частный случай интеграла линейных потерь, распределенных по нормальному закону, который легко можно вычислить методами, указанными в приложении А.

Выражение для ожидаемой ценности выборочной информации имеет ту же форму, хотя, конечно, при выборочных данных дисперсия предапостериорного распределения будет другой:

где

Здесь снова при вычислении интеграла можно воспользоваться методами, указанными в приложении А.

Введем теперь ожидаемую стоимость программы сбора данных, содержащей наблюдений, . Пока мы будем считать, что значение определяется заранее и сами наблюдения не влияют на его выбор, а также что стоимость программы не зависит от того, какие наблюдения фактически

имеют место. Ожидаемая чистая прибыль от выборочной информации ENGSI (Expected Net Gain from Sample Information) выражается в виде

Чтобы представить себе природу этой функции хотя бы на интуитивном уровне, рассмотрим пример, в котором априорное среднее равно нулю, а стоимость информации пропорциональна , т. е. равна . В этом случае (см. приложение А) мы можем написать

Этот пример дает интересное подтверждение некоторым интуитивным представлениям о программах сбора данных.

1. Чем больше дисперсия априорного распределения, тем больше ожидаемая чистая прибыль от выборочной информации. Чем больше неопределенность ситуации принятия решения, тем больше человек будет согласен заплатить за информацию, которая уменьшила бы эту неопределенность.

2. Если стоимость выборки достаточно велика или априорная неопределенность ситуации для принимающего решение достаточно мала, то ENGSI будет отрицательна для всех значений больших нуля. Если принимающий решение, исходя из своего опыта, считает ситуацию достаточно определенной или если данные слишком дороги, ему лучше отказаться от сбора дополнительной информации.

3. Если ENGSI положительна для малых значений , она будет возрастать с убывающей скоростью, и должен существовать такой объем выборки, который максимизирует ENGSI. Информация, полученная вначале, оказывает очень большое влияние на неопределенность, существующую относительно ситуации; каждое последующее наблюдение оказывается все менее эффективным. Если стоимость получения информации постоянна, то в конце концов эффект от каждого дополнительного наблюдения будет приводить к увеличению выигрыша принимающего решение на некоторую величину, которая меньше стоимости ее получения.

Информация о величине дисперсии процесса

Мы везде предполагали, что человек, принимающий решение, склонен действовать так, как если бы дисперсия процесса v была ему известна. Будем надеяться, что это предположение соответствует его убеждениям, если же нет, приходится полагаться на следующую формулу, которую мы приводим здесь без доказательства. Если получение данных возможно, то в качестве оценки v можно использовать следующую величину:

Если объем выборки порядка 25 наблюдений, то в большинстве реальных задач конечные результаты мало различаются между собой, если v полагается известной величиной, равной Если приходится считать v неопределенной величиной, анализ задачи несколько усложняется.

Чувствительность к априорному распределению

Количество усилий, необходимых для получения априорного распределения, зависит от того, насколько чувствительны логически обоснованные действия к форме и параметрам априорного распределения. Принцип определения этой чувствительности является интуитивным. Если можно за умеренную цену получить существенные данные, точное нахождение априорного распределения будет, по-видимому, иметь мало смысла, по крайней мере там, где дело касается определения наилучшего апостериорного действия. Широкое или расплывчатое распределение, имеющее сравнительно большую дисперсию, приводит к возрастанию роли данных и поэтому само оказывает мало влияния на окончательные результаты. Пока дисперсия априорного распределения велика по отношению к дисперсии процесса, можно смело использовать нормальные априорные распределения, преимущество которых состоит в их удобных аналитических свойствах. В этом случае мы склонны ожидать, что выбор точной формы априорного распределения мало повлияет на апостериорное распределение.

Рассмотрим этот эффект на примере. Пусть человек, принимающий решение, должен выбрать в качестве априорного одно из двух нормальных распределений:

Образуем разность апостериорных средних, получающихся на основе указанных априорных распределений. Она равна

Следовательно, если с мало, разность между апостериорными средними будет быстро уменьшаться с увеличением объема выборки. Сходные выводы можно сделать и относительно априорной и апостериорной дисперсий.

Что касается формы апостериорного распределения, то в первом приближении можно принять следующее правило: форма апостериорного распределения будет сравнительно нечувствительна к форме априорного распределения, если

1) полученные данные «благоприятствуют» некоторой частной области значений в том смысле, что они будут иметь сравнительно большие значения функции правдоподобия в указанной области;

2) выбранное априорное распределение является «плоским» в некоторой «благоприятной» области; это означает, что функция распределения не сильно изменяется в этой области;

3) априорное распределение нигде существенно не превышает своего среднего значения в «благоприятной» области.

Если некоторое множество априорных распределений удовлетворяет перечисленным условиям, то любое из них можно использовать без опасения сильно уклониться от наилучшего апостериорного действия, так как форма апостериорного распределения почти одна и та же для всех этих априорных распределений.

Важно подчеркнуть, однако, что все, о чем мы говорим, относится к апостериорному распределению и наилучшему действию при уже выполненной выборке. Более важные аспекты, связанные с созданием программы сбора данных,

могут оказаться не столь нечувствительными к виду априорного распределения, В тех случаях, когда организация сбора данных требует больших затрат или когда мы имеем возможность обратиться к получению данных только один раз, тщательное выяснение априорного распределения может оказаться чрезвычайно важным, так как правильная организация сбора данных может в значительной степени зависеть от априорного распределения. В таких случаях стоит затратить большие усилия на выяснение и проработку априорного распределения. Как бы трудно это ни показалось человеку, принимающему решение, он должен постараться выразить свои мнения в четкой, явно выраженной форме, если хочет извлечь пользу из наших рекомендаций по принятию логически последовательных и обоснованных решений.

Упражнения

6.1. Фирма располагает двумя способами производства некоторого товара. Ежегодные производственные затраты для обоих методов А и В соответственно могут быть представлены следующими функциями (в долл.):

где — число единиц товара, производимое за год. Фирма считает нормально распределенной случайной величиной с дисперсией, равной 2500, и неопределенным средним значением. Среднее значение также является нормально распределенной случайной величиной с ожидаемым значением и дисперсией Можно обратиться к документам и выяснить, сколько единиц товара производилось ежегодно каждым способом, хотя это и дорогостоящий путь поиска информации. Фирма хочет выбрать тот способ производства, который будет минимизировать ожидаемые ежегодные издержки.

Найти ожидаемую ценность полной информации для всех комбинаций следующих значений для и с:

Найти ожидаемую ценность выборочной информации, используя выборки объемом 1 и 4,

Расположить результаты в таблицу и обсудить различные выводы, которые следуют из этих данных,

В качестве примера приводим вычисление EVPI для случая

Так как оба способа имеют равные ожидаемые ежегодные затраты при то наилучшее априорное действие состоит в выборе способа В,

дающего априорные ожидаемые ежегодные затраты

Если апостериорное среднее оказывается больше 1000, мы выбираем способ А, в противном случае — способ В. Итак,

Если учесть, что

то, упрощая выражение для EVPI, получим 00

Для случая полной информации и выбранных нами параметров имеем

Используя методы приложения А, можно написать

6.2. При установлении априорного распределения часто предполагают, что «хвосты» распределения имеют мало значения в случае, когда функция полезности принимающего решение линейна или близка к этому. Обсудить правдоподобность этого предположения.

6.3. Мы уже указывали, что дисперсию или стандартное отклонение процесса можно считать известными, если их оценка основана на выборке объемом 25 или более единиц. Обсудить способы, которыми можно было бы проверить это утверждение. Как можно было бы проанализировать простую задачу принятия решения, не пользуясь предположением о известной дисперсии процесса?

6.4. Обсудить связь между понятием достаточности, изложенным в настоящей главе, и определением достаточной статистики, даваемым в курсах математической статистики.

6.5. Как мы указывали, в задачах принятия решения могут появляться пять видов распределений случайных величин. Какие из этих распределений фигурируют в статистических задачах проверки гипотез?

6.6. Пусть мы хотим сделать выбор между двумя способами производства в условиях неопределенности относительно требуемого объема производства. Затраты по способу 1 даются функцией а по способу 2 — функцией где х — объем производства. Предположим, что Объем производства х рассматривается как нормально распределенная случайная величина с известной дисперсией и неопределенным средним значением. Априорное распределение среднего рассматривается как нормальное. Показать, как можно вычислить ENGSI, включая применение методов приложения А, для получения практических количественных результатов.

Какие из проблем, с которыми вам приходится сталкиваться в процессе руководства, могут иметь такую же линейную структуру затрат?

6.7. Обратимся снова к иллюстративному примеру этой главы, касающемуся принятия решения относительно заключения контракта. Положим априорное среднее равным нулю, а стоимость информации пропорциональной объему выборки. Найти выражение для такого значения объема выборки, которое максимизирует ENGSI.

6.8. Для планирования деятельности фирмы важно оценить средний ежемесячный объем продаж данного товара. Будем считать ежемесячный объем продаж товара нормально распределенной случайной величиной с известной дисперсией и неопределенным средним. Априорное распределение для среднего ежемесячного объема продаж также нормально распределено. Должна быть дана однозначная оценка. Считается, что убытки фирмы пропорциональны квадрату разности между этой оценкой и истинным значением среднего ежемесячного объема продаж. Фирма хочет минимизировать ожидаемые убытки.

Показать, что наилучшая оценка, основанная на априорной информации, будет математическим ожиданием априорного распределения. Показать также, что ожидаемый убыток, использующий эту наилучшую оценку, пропорционален дисперсии априорного распределения.

Каковы были бы наилучшая оценка и ожидаемый убыток, основанные на апостериорном распределении?

Показать, как вы отыскивали бы оптимальный объем выборки, если бы стоимость выборочной информации была пропорциональна объему выборки.