| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
До сих пор вопросы свертки и корреляции теоретически и практически рассматривались только для данных, дискретизованных по времени. Квантованные данные (т. е. данные, дискретизованные, по амплитуде) также были рассмотрены в гл. 5, но при этом каждый отсчет представлялся в виде суммы истинной непрерывной величины и ошибки, а задача состояла в том, чтобы оценить ошибку или минимизировать ее. В данном разделе будет использован совершенно другой подход, а именно будут рассматриваться данные, которые могут принимать только квантованные (целые) значения. Будет изложен интересный метод вычисления сумм произведений сдвигаемых последовательностей (сверток и корреляций) таких чисел, позволяющий в некоторых случаях получить существенную экономию времени счета.
Мы были вынуждены бороться с эффектами округления и переполнения только потому, что при выполнении вычислений без устранения переполнений и без округлений часто нарушается основное требование любой строгой системы счисления, состоящее в том, чтобы в результате выполнения операций над числами получались числа только той же системы счисления.
Предположим, что суммируются два десятиразрядных двоичных целых числа при длине слова 10 разрядов. Правильный результат сложения может быть представлен только 11 разрядами. Таким образом, могут иметь место два случая. В первом из них старший разряд суммы равен нулю, и тогда сумма представляется, очевидно, 10-разрядным словом. Во втором случае старший разряд равен 1, так что результат не может быть размещен в имеющемся регистре. Этот случай называется переполнением. Для математика переполнение указывает на то, что при операции сложения нарушается условие замкнутости, если система возможных чисел включает только 10-разрядные целые числа. При умножении возникают еще большие проблемы подобного рода.
Чтобы удовлетворить условию замкнутости, и были введены операции округления и усечения. Фактически были изменены определения сложения и умножения, которые стали включать операции сдвига и округления. В результате условие замкнутости стало выполняться, однако равенство перестало быть точным.
Совершенно другой подход состоит в том, чтобы выполнять вычисления в соответствии с другими, модифицированными определениями сложения и умножения, которые удовлетворяли бы и условию замкнутости, и условию точного равенства, но за счет допущения о «неправильных» промежуточных результатах. Если и конечный результат такой процедуры вычислений «неправильный», она не представляет интереса. Однако если правильный конечный результат гарантирован, тот факт, что промежуточные результаты были неверны, не имеет никакого значения. Хорошим примером подобного рода вычислений является суммирование знакопеременных целых чисел с использованием фиксированной запятой (в обратном или дополнительном кодах). Если заранее известно, что результирующая сумма может быть корректно представлена при заданной длине слова, любое переполнение в процессе счета можно не учитывать. Для этого примера справедлив новый подход; изучим его более детально для общего случая. Рассмотрим правила сложения и умножения по модулю М, где М — целое, называемое модулем.
Допустимыми числами при выполнении операций будут считаться числа 0, 1, 2, 3, 4, ..., М —1. Два числа а и b называются сравнимыми по модулю М, если их разность в точности кратна М; следовательно, понятия сравнимости и равенства не совпадают, за исключением случая, когда разность между а и b меньше М. В последнем случае единственное число, кратное и меньшее М, может быть только нулем, поэтому а и b должны быть равны. При сложении чисел с использованием слов k-разрядной длины результат в случае переполнения отличается от «обычного» результата на величину, кратную 2. Следовательно, при условии, что  , результат сложения будет сравним по модулю М с обычной суммой (содержащей больше чем k разрядов).
, результат сложения будет сравним по модулю М с обычной суммой (содержащей больше чем k разрядов).
По индукции конечный результат будет сравнимым с обычной суммой, несмотря на возможные многократные переполнения. Если же известно, что конечная обычная сумма представляется k-разрядным числом, то, так как разность между двумя k-разрядными числами меньше, чем  , обычный и получаемый результаты должны быть не только сравнимыми по модулю
, обычный и получаемый результаты должны быть не только сравнимыми по модулю  , но и равными. Ниже будет показано, как, используя другие модули, этот принцип можно успешно применять при выполнении более сложных операций, чем простое суммирование.
, но и равными. Ниже будет показано, как, используя другие модули, этот принцип можно успешно применять при выполнении более сложных операций, чем простое суммирование.
Напомним основные свойства сравнений:
1. Переместительный закон: 
2. Сочетательный закон: 
3. Распределительный закон: 
4. Тождественность:  .
.
5. Отрицание: для каждого  существует элемент
существует элемент  такой, что
такой, что 
6. Замкнутость: оба числа,  являются допустимыми числами рассматриваемой системы счисления.
являются допустимыми числами рассматриваемой системы счисления.
7. Аналогия: если  , то
, то  если
если  , то
, то  если
если  , то
, то  .
.
Необходимо сделать два замечания. Во-первых, при выполнении вычислений по модулю М замкнутость сохраняется всегда, поскольку, если разрядность результата вычисления превышает длину слова, есть возможность, не изменяя результата, вычитать из него любое целое число модулей, так как при этом он остается  сравнимым с исходным результатом арифметической операции. Во-вторых, несмотря на то что существует операция, обратная сложению, с помощью которой можно производить вычитание
сравнимым с исходным результатом арифметической операции. Во-вторых, несмотря на то что существует операция, обратная сложению, с помощью которой можно производить вычитание  нет гарантии, что существует операция, обратная умножению, так что деление не обеспечивается. Это положение справедливо и для целых чисел с обычной арифметикой. Однако в арифметике по модулю М все же имеется ряд взаимно обратных чисел. Так, если М = 14, то целое
нет гарантии, что существует операция, обратная умножению, так что деление не обеспечивается. Это положение справедливо и для целых чисел с обычной арифметикой. Однако в арифметике по модулю М все же имеется ряд взаимно обратных чисел. Так, если М = 14, то целое  не имеет обратного ему числа, но целые
не имеет обратного ему числа, но целые  являются взаимно обратными, поскольку
являются взаимно обратными, поскольку  что сравнимо с 1 по модулю 14.
что сравнимо с 1 по модулю 14.
Так как в дальнейшем будут использоваться и сравнения, и - равенства, необходимо ввести соответствующие обозначения. Обозначим операцию сравнения как  равенство обычным символом
равенство обычным символом  . Если некоторая величина должна быть заменена на другую, сравнимую с исходной и принадлежащую ряду 0, 1, 2,..., М — 1, будет использоваться символ
. Если некоторая величина должна быть заменена на другую, сравнимую с исходной и принадлежащую ряду 0, 1, 2,..., М — 1, будет использоваться символ  , так что
, так что  , где
, где  — целое, и
— целое, и

Операция  называется приведением к остатку. Она используется для обеспечения замкнутости без нарушения сравнения при вычислениях с конечной длиной слова. Один из способов приведения к остатку состоит в делении числа на модуль и сохранении только остатка. Так, если М = 14, то
называется приведением к остатку. Она используется для обеспечения замкнутости без нарушения сравнения при вычислениях с конечной длиной слова. Один из способов приведения к остатку состоит в делении числа на модуль и сохранении только остатка. Так, если М = 14, то  так как
так как

На практике применение этого способа приведения к остатку требует больших затрат времени; к счастью, существуют более простые приемы.
Нас интересует вычисление сверток и корреляций, но, как известно, корреляцию можно представить в виде свертки, поэтому ниже анализируется только вычисление свертки. Поскольку операции умножения и сложения будут рассматриваться по модулю М, имеет смысл говорить о свертке двух последовательностей по модулю М. Пусть при использовании обычной арифметики последовательность  задается соотношением
задается соотношением

При использовании в вычислениях операции  может быть получена последовательность
может быть получена последовательность  так что
так что  Для нас наибольший интерес представляют случаи, когда, вычислив
Для нас наибольший интерес представляют случаи, когда, вычислив  можно получить
можно получить  Пусть наибольшее и наименьшее возможные значения
Пусть наибольшее и наименьшее возможные значения  равны си и
равны си и  соответственно. Тогда, если М больше, чем
соответственно. Тогда, если М больше, чем  может существовать только одно число, сравнимое с
может существовать только одно число, сравнимое с  по модулю М, а именно
по модулю М, а именно  . В этом случае вычисление
. В этом случае вычисление  фактически дает
фактически дает  Конечно, всегда есть возможность увеличить верхний предел значения свертки, выбрав модуль, превосходящий эту величину.
Конечно, всегда есть возможность увеличить верхний предел значения свертки, выбрав модуль, превосходящий эту величину.
Покажем теперь, что между способами вычисления свертки с использованием БПФ и арифметики по модулю М существует полная аналогия, хотя это справедливо лишь для определенных значений модуля М. Чтобы продемонстрировать это утверждение, следует предварительно рассмотреть свойства показательной последовательности по модулю М.
Рассмотрим последовательность  Для нее справедливо соотношение
Для нее справедливо соотношение
 (6.119)
(6.119)
или
 (6.120)
(6.120)
Последнее соотношение соответствует автомату с конечным числом состояний; величина а может принимать только М значений, так что  должна периодически повторяться через самое большее (М — 1) значений n (случай
должна периодически повторяться через самое большее (М — 1) значений n (случай  приводит к его собственной последовательности со значительно более коротким периодом).
приводит к его собственной последовательности со значительно более коротким периодом).
Эта периодичность может быть либо абсолютной, либо с установлением в начале. Приведем два примера:

Второй пример значительно интереснее. Из свойств показательной последовательности следует, что произведение  сравнимо с 1, и, следовательно, они являются взаимно обратными числами, несмотря на отсутствие в общем случае в арифметике по модулю М операции, обратной умножению. В обычной арифметике с целыми числами подобной ситуации не возникает, поэтому здесь нет аналогии с ДПФ, выполняемым с применением обычной арифметики в целых числах. Второй пример представляет по крайней мере один случай такого выбора модуля и вида степенной последовательности, при котором последовательность обладает свойством периодичности, аналогичным свойству
сравнимо с 1, и, следовательно, они являются взаимно обратными числами, несмотря на отсутствие в общем случае в арифметике по модулю М операции, обратной умножению. В обычной арифметике с целыми числами подобной ситуации не возникает, поэтому здесь нет аналогии с ДПФ, выполняемым с применением обычной арифметики в целых числах. Второй пример представляет по крайней мере один случай такого выбора модуля и вида степенной последовательности, при котором последовательность обладает свойством периодичности, аналогичным свойству  в поле комплексных чисел. Чтобы не искать наугад подобные случаи, сформулируем соответствующую теорему:
в поле комплексных чисел. Чтобы не искать наугад подобные случаи, сформулируем соответствующую теорему:
Теорема. Величины р и q являются взаимно обратными по модулю М, если р и М являются взаимно простыми. Доказательство.
Поскольку возможно М значений q, составим следующий набор уравнений:

Существуют две возможности: либо в одном из этих М уравнений вместо вопросительного знака стоит 1 (означающая, что уравнение соответствует правильному значению q, обратному р), либо 1 нет ни в одном из уравнений. В последнем случае, поскольку имеется М уравнений, а величин справа может быть только М — 1 (не больше), должна наблюдаться повторяемость. Пусть повторяемость будет при  Положим, что
Положим, что  , и запишем
, и запишем

или

Следовательно, М является делителем р(а — b). Далее, а — b меньше М и поэтому не может содержать все сомножители М. Однако, согласно условию, р не имеет общих сомножителей с М. Следовательно, вторая из возможностей приводит к противоречию и становится ясно, что pq может быть сравнимо с 1 по модулю М, если только р и М не имеют общих сомножителей. В то же время было показано, что если р не имеет общих сомножителей с М, то в записанных выше уравнениях не может быть повторений, поэтому в одном из них вместо вопросительного знака должна быть 1. Таким образом, доказаны и необходимое, и достаточное условия теоремы.
Из приведенной теоремы непосредственно следует, что произвольное число х, взаимно простое с М, позволяет сформировать степенную последовательность  с периодом, меньшим или равным (М — 1), для всех членов которой существуют обратные им числа по модулю М или, что еще важнее, период последовательности
с периодом, меньшим или равным (М — 1), для всех членов которой существуют обратные им числа по модулю М или, что еще важнее, период последовательности  можно связать с модулем М. Конечно, эта последовательность может содержать лишь члены, взаимно простые с М (поскольку само число х является взаимно простым с М, что согласуется с главным условием периодичности). Количество целых чисел, меньших М и взаимно простых с М, является функцией М и обозначается как
можно связать с модулем М. Конечно, эта последовательность может содержать лишь члены, взаимно простые с М (поскольку само число х является взаимно простым с М, что согласуется с главным условием периодичности). Количество целых чисел, меньших М и взаимно простых с М, является функцией М и обозначается как  . Ясно, что оно дает максимально возможный период последовательности
. Ясно, что оно дает максимально возможный период последовательности  Обозначим действительный период последовательности через N. С математической точки зрения это означает, что
Обозначим действительный период последовательности через N. С математической точки зрения это означает, что  имеет порядок N по модулю
имеет порядок N по модулю  . Эйлер доказал следующую интересную теорему:
. Эйлер доказал следующую интересную теорему:

Докажем ее методом, аналогичным доказательству предыдущей теоремы. Для этого представим, что записаны все целые  меньшие М и взаимно простые с М, и умножим каждое из них на
меньшие М и взаимно простые с М, и умножим каждое из них на  по модулю М. Поскольку все произведения должны отличаться друг от друга и быть взаимно простыми с М, они будут представлять собой переставленные значения исходного набора гг. Перемножим все члены исходного набора и полученных произведений:
по модулю М. Поскольку все произведения должны отличаться друг от друга и быть взаимно простыми с М, они будут представлять собой переставленные значения исходного набора гг. Перемножим все члены исходного набора и полученных произведений:
 (6.122)
(6.122)
Сократив на произведение  , находпм, что сравнимо с 1, что и требовалось доказать. Таким образом, получен очень важный результат: период N последовательности
, находпм, что сравнимо с 1, что и требовалось доказать. Таким образом, получен очень важный результат: период N последовательности  должен быть делителем
должен быть делителем  .
.
Часто в качестве модуля выбирают простое число Р. По определению  , и любое целое, меньшее Р, является взаимно простым с Р, так что
, и любое целое, меньшее Р, является взаимно простым с Р, так что
 (6.123)
(6.123)
Этот результат известен как теорема Ферма. Практически все вопросы теории чисел так или иначе связаны с работами Ферма; ниже мы еще неоднократно будем к ним обращаться.
Изучение свойств последовательности  несколько увело нас в сторону от интересующего вопроса об аналогии между операциями вычисления свертки методом БПФ и с использованием арифметики по модулю М. Чтобы установить ее, проведем сначала аналогию с алгоритмом БПФ и, следовательно, с ДПФ. Определим теоретико-числовое преобразование последовательности из N целых чисел
несколько увело нас в сторону от интересующего вопроса об аналогии между операциями вычисления свертки методом БПФ и с использованием арифметики по модулю М. Чтобы установить ее, проведем сначала аналогию с алгоритмом БПФ и, следовательно, с ДПФ. Определим теоретико-числовое преобразование последовательности из N целых чисел  по мудулю М как некоторую другую последовательность из N целых чисел
по мудулю М как некоторую другую последовательность из N целых чисел  рассчитываемых согласно следующей формуле:
рассчитываемых согласно следующей формуле:
 (6.124)
(6.124)
где а — целое число, взаимно простое с М и имеющее порядок N. Формула (6.124) аналогична ДПФ, но в качестве  здесь используется целое число а,
здесь используется целое число а,  степень которого сравнима с 1, и, кроме того, все вычисления проводятся по модулю М. Напомним, что при выводе алгоритма БПФ использовался тот факт, что
степень которого сравнима с 1, и, кроме того, все вычисления проводятся по модулю М. Напомним, что при выводе алгоритма БПФ использовался тот факт, что  . Поэтому и теоретико-числовое преобразование может быть вычислено с применением аналогичного алгоритма, но с заменой умножений на степени W в БПФ умножениями на степени а. Как и в случае ДПФ, для существования стандартных алгоритмов БПФ N должно быть составным целым числом. Однако в отличие от ДПФ сами теоретико-числовые преобразования не применяются. Ниже они будут использованы лишь для вычисления сверток и корреляций. Правда, при этом придется перемножать соответствующие коэффициенты теоретико-числовых преобразований двух последовательностей, например
. Поэтому и теоретико-числовое преобразование может быть вычислено с применением аналогичного алгоритма, но с заменой умножений на степени W в БПФ умножениями на степени а. Как и в случае ДПФ, для существования стандартных алгоритмов БПФ N должно быть составным целым числом. Однако в отличие от ДПФ сами теоретико-числовые преобразования не применяются. Ниже они будут использованы лишь для вычисления сверток и корреляций. Правда, при этом придется перемножать соответствующие коэффициенты теоретико-числовых преобразований двух последовательностей, например  Для получения круговой свертки исходных последовательностей используется обратное преобразование от последовательности этих произведений. Таким образом, придется определить и обратное теоретико-числовое преобразование. По аналогии с ДПФ оно должно иметь вид
Для получения круговой свертки исходных последовательностей используется обратное преобразование от последовательности этих произведений. Таким образом, придется определить и обратное теоретико-числовое преобразование. По аналогии с ДПФ оно должно иметь вид
 (6.125)
(6.125)
Отрицательный знак в показателе степени а в преобразовании (6.125) имеет определенный смысл, поскольку было показано, что члены периодической степенной последовательности имеют обратные им числа.
При записи преобразования (6.125) были сделаны два предположения. Первое касается существования числа  , обратного числу N. Известно, что оно существует, если N и М не имеют общих сомножителей. Второе предположение состоит в том, что преобразование (6.125) действительно является обратным теоретико-числовым преобразованием. Чтобы показать это, подставим формулу (6.124) в (6.125) и получим таким образом еще одно соотношение между N, М и а. Итак,
, обратного числу N. Известно, что оно существует, если N и М не имеют общих сомножителей. Второе предположение состоит в том, что преобразование (6.125) действительно является обратным теоретико-числовым преобразованием. Чтобы показать это, подставим формулу (6.124) в (6.125) и получим таким образом еще одно соотношение между N, М и а. Итак,
 (6.126)
(6.126)
Меняя порядок суммирования, находим
 (6.127)
(6.127)
Можно показать, что оба эти выражения являются взаимно обратными. Для этого убедимся, что

легко доказывается. Если же  , то умножая на
, то умножая на  , получим
, получим

Все смежные члены суммы взаимно уничтожаются, остаются первый и последний, равные  , которые также взаимно уничтожаются. Следовательно,
, которые также взаимно уничтожаются. Следовательно,
 (6.129)
(6.129)
Отсюда можно легко получить нужный результат, если не учитывать необходимости делить обе части равенства (6.129) на  (деление как операция не определено). Сократить на множитель
(деление как операция не определено). Сократить на множитель  можно только при условии, что существует обратное ему число, и только при этом формула (6.125) действительно представляет обратное теоретико-числовое преобразование. Сформулированное условие, заключающееся в том, что число
можно только при условии, что существует обратное ему число, и только при этом формула (6.125) действительно представляет обратное теоретико-числовое преобразование. Сформулированное условие, заключающееся в том, что число  не должно иметь общих сомножителей с М для
не должно иметь общих сомножителей с М для  , и является последним ограничением.
, и является последним ограничением.
Подведем итог вышеизложенному.
1. Теоретико-числовое преобразование последовательности из N отсчетов определяется следующим образом:

где модуль М и длина последовательности N не имеют общих сомножителей, N является делителем  , а выбирается так, чтобы оно имело порядок N и было взаимно простым с М.
, а выбирается так, чтобы оно имело порядок N и было взаимно простым с М.
2. Обратное теоретико-числовое преобразование последовательности из N отсчетов определяется следующим образом:

где  является взаимно простым с М для всех к, за исключением тех, которые сравнимы с 0 по модулю N.
является взаимно простым с М для всех к, за исключением тех, которые сравнимы с 0 по модулю N.
Все эти условия можно сформулировать в более сжатой форме следующим образом (без доказательства). Преобразование будет обеспечивать вычисление круговой свертки при а, имеющем порядок, равный N, тогда и только тогда, когда Р — 1 делится на N, причем Р — любой из простых сомножителей М.
Доказательство теоремы о свертке для теоретико-числового преобразования очевидно. Математические выкладки будут такими же, как и для ДПФ; читатель может проделать их самостоятельно в качестве упражнения. Поэтому будем считать доказанным, что, вычислив обратное преобразование от произведения теоретико-числовых преобразований, можно получить результат, сравнимый с круговой сверткой исходных последовательностей. Если число N составное, для вычисления прямого и обратного преобразований можно использовать алгоритм БПФ и таким образом очень быстро получить результат, сравнимый с круговой сверткой последовательностей целых чисел.
Здесь, по-видимому, имеет смысл привести практический пример. Чтобы продемонстрировать математическую сторону, а не эффективность вычислений, рассмотрим простейший случай: найдем четырехточечную круговую свертку последовательности 1, 2, 0, 0 саму с собой. Выберем модуль М = 17 и а = 4. Величина N, естественно, равна 4, а  , как легко убедиться, имеет порядок N по модулю М.
, как легко убедиться, имеет порядок N по модулю М.  равно 13. Перепишем для удобства все степени
равно 13. Перепишем для удобства все степени 
Прямое преобразование с применением БПФ:

В итоге получено преобразование исходной последовательности. Возведем его коэффициенты в квадрат по модулю 17:
Преобразование от свертки 9 13 1 15
При обратном преобразовании умножаем на  изменяем
изменяем
знак в показателе степени и выполняем преобразование аналогично предыдущему:

Итак, получен результат круговой свертки исходной последовательности с ней самой. Поскольку максимальное значение истинного результата равно 4, сравнимость полученных значений по модулю 17 обеспечивает равенство. Заметим, что в процессе вычислений все результаты записывались по модулю 17 с приведением к остатку всякий раз, когда результат вычисления выходил за пределы от 0 до 16.
Рассмотрим теперь практические аспекты нового метода. Свертки, полученные с использованием теоретико-числового преобразования, в отличие от обычного метода с применением БПФ являются точными. Поскольку числа по модулю М образуют конечное множество, ни на одном из этапов вычислений приближения не вводились. Действительно, при наличии ошибки даже в одном, самом младшем разряде результат был бы совершенно неверным. К счастью, данная система счисления не требует ни округления, ни усечения даже при самых сложных вычислениях. В практических применениях интерес представляет скорее не сравнимость результатов, а их равенство, поэтому значения свертки должны быть ограничены тем или иным способом, чтобы можно было заменить сравнимость на равенство. Если, например, каждая из двух 64-точечных последовательностей представлена 10-разрядными числами, для точного представления результата необходим 26-разрядный регистр. Таким образом, вычисления с использованием теоретико-числового преобразования потребуют использования модуля М, превышающего  . Было предложено несколько способов совместного использования меньших модулей, но при этом возникают другие трудности.
. Было предложено несколько способов совместного использования меньших модулей, но при этом возникают другие трудности.
Еще одна особенность использования теоретико-числового преобразования состоит в необходимости часто выполнять операции приведения к остатку, чтобы избежать представления промежуточных результатов словами с большим числом разрядов.
В самом деле, фактически после каждой операции необходимо выполнить приведение к остатку. Для этой цели, как было отмечено выше, можно использовать деление числа на модуль и сохранение лишь остатка, однако деление требует больших затрат времени и его стараются избегать, особенно при выполнении совместно со сложением. В действительности, поскольку нам нужен только остаток, выполнять деление нет необходимости. Методы определения остатка зависят от конкретного М, причем простейшие с точки зрения нахождения остатка, но в то же время наиболее важные модули имеют вид  .
.
Арифметика по модулю  известна достаточно хорошо. Все величины представляются g разрядами. Результаты арифметических действий (суммы и произведения), для которых потребуется больше чем g разрядов, могут быть легко приведены к остаткам, если учесть, что
известна достаточно хорошо. Все величины представляются g разрядами. Результаты арифметических действий (суммы и произведения), для которых потребуется больше чем g разрядов, могут быть легко приведены к остаткам, если учесть, что  сравнимо с 1 по модулю
сравнимо с 1 по модулю  , так что при сложении разряд переноса с весом 2s просто добавляется к младшему значащему разряду. Такой перенос называют циклическим, а соответствующую систему счисления — арифметикой с представлением чисел в обратном коде. При умножении получается более одного дополнительного разряда сверх исходных g разрядов. Первый дополнительный разряд имеет вес, сравнимый с 1, последующие разряды имеют веса, сравнимые с 2, 4 и т. д. Следовательно, дополнительные разряды произведения сверх младших g значащих разрядов образуют двоичное число, которое можно добавить к двоичному числу, состоящему из младших g значащих разрядов произведения. Например, при
, так что при сложении разряд переноса с весом 2s просто добавляется к младшему значащему разряду. Такой перенос называют циклическим, а соответствующую систему счисления — арифметикой с представлением чисел в обратном коде. При умножении получается более одного дополнительного разряда сверх исходных g разрядов. Первый дополнительный разряд имеет вес, сравнимый с 1, последующие разряды имеют веса, сравнимые с 2, 4 и т. д. Следовательно, дополнительные разряды произведения сверх младших g значащих разрядов образуют двоичное число, которое можно добавить к двоичному числу, состоящему из младших g значащих разрядов произведения. Например, при  произведение
произведение  можно разложить на два слова: 00000001 и 00000010, сложение которых дает
можно разложить на два слова: 00000001 и 00000010, сложение которых дает  .
.
Проводимые в настоящее время исследования различных М в виде  позволили найти несколько интересных модулей, но ни один из них не представляет такого интереса, как модуль вида
позволили найти несколько интересных модулей, но ни один из них не представляет такого интереса, как модуль вида  .
.
Арифметика по модулю  изучена менее детально. Для представления всех возможных величин здесь требуется
изучена менее детально. Для представления всех возможных величин здесь требуется  разрядов. Это представление в какой-то мере неэффективно, поскольку только для одного числа, а именно для
разрядов. Это представление в какой-то мере неэффективно, поскольку только для одного числа, а именно для  старший значащий разряд равен не нулю, а единице. Но если не учитывать неэффективность использования разрядов, то между данной и рассмотренной выше арифметиками можно обнаружить сходство. Разряд с весом, равным
старший значащий разряд равен не нулю, а единице. Но если не учитывать неэффективность использования разрядов, то между данной и рассмотренной выше арифметиками можно обнаружить сходство. Разряд с весом, равным  представляет величину, сравнимую
представляет величину, сравнимую  по модулю М. Следовательно, вместо циклического переноса для сложения нужно производить циклический перенос для вычитания. В этом и состоит отличие от предыдущего случая, но при этом, помимо обеспечения циклического переноса, не требуется какое-либо дополнительное оборудование.
по модулю М. Следовательно, вместо циклического переноса для сложения нужно производить циклический перенос для вычитания. В этом и состоит отличие от предыдущего случая, но при этом, помимо обеспечения циклического переноса, не требуется какое-либо дополнительное оборудование.
При умножении произведение имеет обычно больше чем g разрядов. Если разложить произведение на два слова, одно из которых представлено младшими разрядами, а другое — остальными разрядами, то второе слово следует вычесть из первого. Например, при  произведение
произведение  раскладывается, как и прежде, на 00000001 и 00000010, т. е. на 1 и 2, и разность между ними равна
раскладывается, как и прежде, на 00000001 и 00000010, т. е. на 1 и 2, и разность между ними равна  . Таким образом, приведение к остатку при модуле
. Таким образом, приведение к остатку при модуле  выполняется почти так же просто, как при модуле
выполняется почти так же просто, как при модуле  . Не следует забывать, что в данном случае есть одна величина
. Не следует забывать, что в данном случае есть одна величина  , которая представляется
, которая представляется  разрядами. Чтобы вычисления выполнялись без ошибки, необходимо принять две меры предосторожности. Во-первых, следует учитывать особый случай, когда результат сравним
разрядами. Чтобы вычисления выполнялись без ошибки, необходимо принять две меры предосторожности. Во-первых, следует учитывать особый случай, когда результат сравним  . Если (снова для М = 257) получен результат 100000000, то его разложение, составленное из старших разрядов, дает +1, а разложение из младших разрядов дает 0. Циклическое вычитание для этого случая дает —1, т. е. результат правильный, но его нельзя представить восьмиразрядным словом. Вторую предосторожность необходимо соблюдать при умножении в том случае, когда численное значение слова, образованного старшими разрядами, превысит численное значение слова из младших разрядов, так что при вычитании получается отрицательный результат. В этом случае к отрицательной величине необходимо добавить М с тем, чтобы результат находился в диапазоне от 0 до М — 1. Конечно, при таком сложении нельзя забывать и о первой предосторожности.
. Если (снова для М = 257) получен результат 100000000, то его разложение, составленное из старших разрядов, дает +1, а разложение из младших разрядов дает 0. Циклическое вычитание для этого случая дает —1, т. е. результат правильный, но его нельзя представить восьмиразрядным словом. Вторую предосторожность необходимо соблюдать при умножении в том случае, когда численное значение слова, образованного старшими разрядами, превысит численное значение слова из младших разрядов, так что при вычитании получается отрицательный результат. В этом случае к отрицательной величине необходимо добавить М с тем, чтобы результат находился в диапазоне от 0 до М — 1. Конечно, при таком сложении нельзя забывать и о первой предосторожности.
Упомянем также и правило изменения знака числа: нужно инвертировать g разрядов и добавить число  (снова используя циклическое вычитание).
(снова используя циклическое вычитание).
Общепризнано, что эта арифметика несколько более сложная, чем обычно используемая система сложений и умножений. С другой стороны, здесь нет необходимости в делении для приведения к остатку, поскольку деление заменяется значительно более простой операцией. Таким образом, среди возможных модулей  будем искать такие g, которые приводят к преобразованиям со свойствами, представляющими для нас интерес, не забывая об ограничивающих соотношениях, связывающих М, N и а. Простейшим из ограничений является случай простых М. Можно поставить вопрос: при каких значениях g модуль
будем искать такие g, которые приводят к преобразованиям со свойствами, представляющими для нас интерес, не забывая об ограничивающих соотношениях, связывающих М, N и а. Простейшим из ограничений является случай простых М. Можно поставить вопрос: при каких значениях g модуль  является простым? Ответ хотя и неполный, но зато удивительно простой, состоит в следующем. Пусть g будет нечетным, скажем
является простым? Ответ хотя и неполный, но зато удивительно простой, состоит в следующем. Пусть g будет нечетным, скажем  . Тогда
. Тогда  и, следовательно,
и, следовательно,  . Это означает, что М делится на 3, т. е. число М не является простым. Исследование четных значений g равносильно рассмотрению модулей
. Это означает, что М делится на 3, т. е. число М не является простым. Исследование четных значений g равносильно рассмотрению модулей  .
.
Теперь, если h нечетное, М будет делиться на 5, поскольку  . Следовательно, М не является простым. Случай четных h соответствует модулю
. Следовательно, М не является простым. Случай четных h соответствует модулю  Здесь, если i нечетное, М имеет сомножитель 17. Методом итераций можно показать, что только те значения М могут быть простыми, у которых g являются степенью двойки. Заметим, что последнее утверждение не доказано; показано лишь, что М является составным, если g имеет какой-либо нечетный сомножитель. Первыми несколькими членами последовательности простых модулей являются
Здесь, если i нечетное, М имеет сомножитель 17. Методом итераций можно показать, что только те значения М могут быть простыми, у которых g являются степенью двойки. Заметим, что последнее утверждение не доказано; показано лишь, что М является составным, если g имеет какой-либо нечетный сомножитель. Первыми несколькими членами последовательности простых модулей являются  . Ферма предположил, но не смог доказать, что все числа вида
. Ферма предположил, но не смог доказать, что все числа вида  являются простыми. На самом же деле число
являются простыми. На самом же деле число  является составным и имеет сомножитель 641, а все последующие числа Ферма тоже, по-видимому, являются составными. Целые числа вида
является составным и имеет сомножитель 641, а все последующие числа Ферма тоже, по-видимому, являются составными. Целые числа вида  , как простые, так и составные, называются числами Ферма. Другое важное для нас свойство известно из работ Лукаса, еще одного известного специалиста в области теории чисел, который показал, что любой простой сомножитель р числа Ферма должен иметь вид
, как простые, так и составные, называются числами Ферма. Другое важное для нас свойство известно из работ Лукаса, еще одного известного специалиста в области теории чисел, который показал, что любой простой сомножитель р числа Ферма должен иметь вид  . Последнее означает, что когда модуль равен числу Ферма, должно существовать теоретико-числовое преобразование для любого N, равного степени двойки и не превышающего
. Последнее означает, что когда модуль равен числу Ферма, должно существовать теоретико-числовое преобразование для любого N, равного степени двойки и не превышающего  , если число Ферма составное, а также для любого N, равного степени двойки и меньшего чем М, если число Ферма простое. Такие размеры преобразований позволяют использовать алгоритмы, подобные простейшим алгоритмам БПФ с основанием два.
, если число Ферма составное, а также для любого N, равного степени двойки и меньшего чем М, если число Ферма простое. Такие размеры преобразований позволяют использовать алгоритмы, подобные простейшим алгоритмам БПФ с основанием два.
Одно интереснейшее свойство преобразования по модулю М, равному числу Ферма, выявляется при анализе возможных значений а. Поскольку  , то
, то  . Из простых соображений ясно, что никакая меньшая, чем
. Из простых соображений ясно, что никакая меньшая, чем  , положительная степень двойки не может быть порядком числа 2 по модулю М. В самом деле, для
, положительная степень двойки не может быть порядком числа 2 по модулю М. В самом деле, для  при
при  все необходимые условия действительно удовлетворяются. Преобразование для этого необычного случая будет иметь
все необходимые условия действительно удовлетворяются. Преобразование для этого необычного случая будет иметь

Обратное преобразование равно

где

Пример,  . Этот особый случай преобразования по модулю чисел Ферма называют числовым преобразованием Ферма. Отметим, что как в прямом, так и в обратном преобразовании используются только умножения на степень двойки. Последнее справедливо и для вычислений числовых преобразований Ферма с помощью алгоритма БПФ. Кроме того, важно, что умножение на степень двойки, достаточно простое в обычно используемой системе счисления с представлением чисел в дополнительном коде, оказывается довольно простым и в системе счисления по модулю чисел Ферма: число сдвигают влево на количество разрядов, равное степени двойки, и затем вычитают слово, образованное старшими разрядами, из слова, образованного младшими разрядами. Поскольку первое из этих слов имеет после сдвига вид 0000хххх (рассматривается случай сдвига восьмиразрядного слова на четыре разряда), а второе имеет вид уууу0000, то вычитание становится чрезвычайно простым и требует меньшего числа логических операций, чем, например, в обычном полном сумматоре. Оно выполняется следующим образом:
. Этот особый случай преобразования по модулю чисел Ферма называют числовым преобразованием Ферма. Отметим, что как в прямом, так и в обратном преобразовании используются только умножения на степень двойки. Последнее справедливо и для вычислений числовых преобразований Ферма с помощью алгоритма БПФ. Кроме того, важно, что умножение на степень двойки, достаточно простое в обычно используемой системе счисления с представлением чисел в дополнительном коде, оказывается довольно простым и в системе счисления по модулю чисел Ферма: число сдвигают влево на количество разрядов, равное степени двойки, и затем вычитают слово, образованное старшими разрядами, из слова, образованного младшими разрядами. Поскольку первое из этих слов имеет после сдвига вид 0000хххх (рассматривается случай сдвига восьмиразрядного слова на четыре разряда), а второе имеет вид уууу0000, то вычитание становится чрезвычайно простым и требует меньшего числа логических операций, чем, например, в обычном полном сумматоре. Оно выполняется следующим образом:

т. е. к младшему значащему разряду представленного в обратном коде слова, сдвинутого за рязрядную сетку, добавляется +1, а к последнему младшему значащему разряду сдвинутого исходного слова добавляется —1. Заметим, что перенос, связанный с добавлением  , будет компенсировать —1, тогда как циклическое вычитание, связанное с добавлением —1, приводит к добавлению еще одной единицы в младший значащий разряд слова.
, будет компенсировать —1, тогда как циклическое вычитание, связанное с добавлением —1, приводит к добавлению еще одной единицы в младший значащий разряд слова.
Ко времени написания книги этап логического проектирования арифметического устройства для выполнения числового преобразования Ферма еще не был завершен, но само преобразование было запрограммировано на ЦВМ IBM 360. Оказалось, что с помощью этого преобразования свертки можно вычислять примерно в три раза быстрее, чем с использованием обычного алгоритма БПФ. Причинами сокращения времени вычисления являются следующие:
1. Числовое преобразование Ферма выполняется без умножений, поэтому для расчета  -точечной свертки требуется всего N умножений. Общее число сложений и вычитаний равно
-точечной свертки требуется всего N умножений. Общее число сложений и вычитаний равно  кроме того, требуется выполнить
кроме того, требуется выполнить  «умножений» на степень двойки.
«умножений» на степень двойки.
2. Используются операции только над действительными числами, что обеспечивает выигрыш во времени преобразования в два раза по сравнению с обычным алгоритмом БПФ;
3. Числовое преобразование Ферма позволяет вычислить точное значение свертки; при этом нет необходимости использовать арифметику с плавающей запятой, делать проверки на переполнение или принимать какие-либо другие меры предосторожности.
Следует, однако, рассмотреть и недостатки нового метода. Один из них связан с ограничениями, накладываемыми на выбор модуля, размера преобразования и величины а, что сильно сужает круг применений. Тот факт, что получаемый результат здесь всегда точный, вынуждает использовать большие модули и, следовательно, оперировать на протяжении всего вычисления преобразования словами большой длины. При аппаратурной реализации стоимость памяти может намного превзойти стоимость умножителей, так что почти полное исключение умножений может все-таки не скомпенсировать увеличения стоимости памяти. В то же время при цифровой обработке сигналов почти никогда не требуется получать абсолютно точный результат.
Другой фактор, способствующий увеличению длины слова, связан с тем, что для чисел Ферма и  размер круговой свертки может быть равен только
размер круговой свертки может быть равен только  Последнее означает, что длина слова должна быть примерно такой же, как и размер самой свертки. В результате для сверток, обычно представляющих интерес, требуемая длина слова составляет сотни разрядов, что совершенно нереально в настоящее время. Ниже будут кратко рассмотрены возможности некоторого смягчения этого ограничения.
Последнее означает, что длина слова должна быть примерно такой же, как и размер самой свертки. В результате для сверток, обычно представляющих интерес, требуемая длина слова составляет сотни разрядов, что совершенно нереально в настоящее время. Ниже будут кратко рассмотрены возможности некоторого смягчения этого ограничения.
На практике в расчет приходится принимать и другие соображения. При обработке сигналов на ЦВМ нет необходимости сводить к минимуму число умножений, если ЦВМ имеет встроенный быстродействующий умножитель. В то же время при всей простоте операций по модулю чисел Ферма для их выполнения требуются несколько команд программы. Более того, возможности программирования операции приведения к остатку существенно зависят от длины слова машины. Читатель может в этом убедиться, написав программу приведения к остатку по модулю  для ЦВМ с длиной слова, равной 12, 16, 18, 24 и 32 разряда, используя аналогичные наборы команд для каждой из ЦВМ. Кроме того, хотя циклический перенос разрядов в слове может показаться более простой операцией, чем умножение, с точки зрения времени выполнения эта операция может оказаться далеко не элементарной, особенно если речь идет об очень простой вычислительной машине, в которой, как правило, за один такт выполняется сдвиг только на один разряд.
для ЦВМ с длиной слова, равной 12, 16, 18, 24 и 32 разряда, используя аналогичные наборы команд для каждой из ЦВМ. Кроме того, хотя циклический перенос разрядов в слове может показаться более простой операцией, чем умножение, с точки зрения времени выполнения эта операция может оказаться далеко не элементарной, особенно если речь идет об очень простой вычислительной машине, в которой, как правило, за один такт выполняется сдвиг только на один разряд.
Ограничение, связанное с размером свертки, можно смягчить двумя способами. Во-первых, заметим, что N можно удвоить, если в качестве а использовать величину, имеющую порядок  .
.
Агарвал и Баррас показали, что величина а, задаваемая формулой

имеет порядок  по модулю
по модулю  Легко показать, что
Легко показать, что  , так что, как и прежде, четные степени а являются степенями двойки. В то же время нечетные степени а не сравнимы с 1, поэтому порядок а будет вдвое превышать порядок числа 2 по модулю М. Умножение на степени числа а, задаваемого формулой (6.130), ненамного сложнее умножения на степени двойки, поскольку а состоит из двух степеней двойки. В то же время оно проще обычного умножения, причем самое важное то, что оно используется либо только на первом, либо на последнем (но не на обоих) из
, так что, как и прежде, четные степени а являются степенями двойки. В то же время нечетные степени а не сравнимы с 1, поэтому порядок а будет вдвое превышать порядок числа 2 по модулю М. Умножение на степени числа а, задаваемого формулой (6.130), ненамного сложнее умножения на степени двойки, поскольку а состоит из двух степеней двойки. В то же время оно проще обычного умножения, причем самое важное то, что оно используется либо только на первом, либо на последнем (но не на обоих) из  этапов алгоритма быстрого числового преобразования по модулю чисел Ферма, поскольку только на этих этапах могут встретиться нечетные степени а.
этапов алгоритма быстрого числового преобразования по модулю чисел Ферма, поскольку только на этих этапах могут встретиться нечетные степени а.
Значительно более существенное смягчение ограничения размера преобразования может быть достигнуто несколько более дорогой ценой за счет того, что любую одномерную свертку можно вычислить, используя алгоритмы свертки двумерных последовательностей. Это, казалось бы, абстрактное утверждение в действительности основано на том, что обычная свертка может быть вычислена методами расчета круговой свертки. Для этого обрабатываемые данные представляются в виде таких двумерных массивов с дополнением нулями и повторением части данных там, где это необходимо, чтобы результат вычисления двумерной свертки совпадал с искомыми значениями одномерной свертки. Читатель может убедиться, что следующую одномерную круговую свертку:

можно найти, вычислив круговую двумерную свертку двух следующих двумерных массивов:

Заметим, что половина результатов дает правильный ответ, а остальные результаты — неверный. Применение двумерной свертки для вычисления одномерной свертки дает возможность использовать двумерное числовое преобразование Ферма. В результате если в одномерном случае модуль ограничивал размер последовательности N точками, то в двумерном случае появляется возможность обрабатывать последовательности из  отсчетов, если, конечно, не возникает проблем, связанных с точностью представления результатов.
отсчетов, если, конечно, не возникает проблем, связанных с точностью представления результатов.
Рассмотрев достоинства и недостатки числового преобразования Ферма, можно остановиться на том, в каких задачах применение нового преобразования представляется целесообразным. Такие задачи должны иметь следующие характеристики: 1) последовательности должны быть достаточно короткими (суммируется около 50 произведений сдвинутых членов); 2) существует необходимость в высокой точности; 3) умножение является значительно более дорогостоящей операцией по сравнению со сложением.
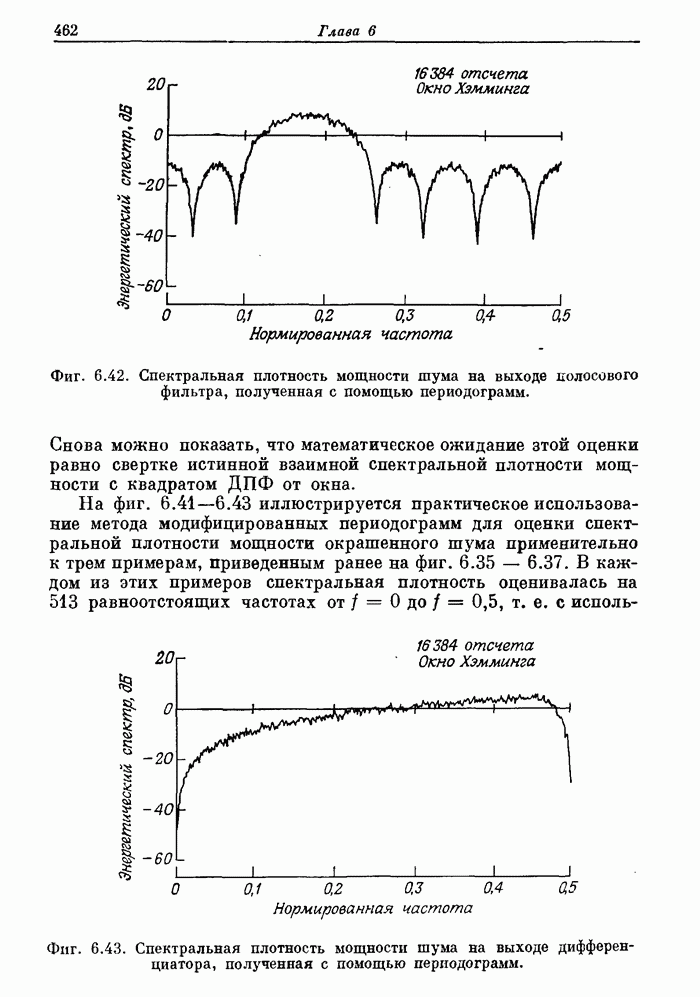
Рассмотрим два возможных применения нового преобразования. Первое относится к оценке спектров (одновременно большого количества) широкополосных сигналов. Из теории спектрального анализа известно, что число сдвигов при расчете корреляционной функции может составлять лишь долю от полного количества обрабатываемых отсчетов. В разд. 6.18 был рассмотрен алгоритм вычисления автокорреляционной функции, основанный на суммировании в частотной области. Но подобное суммирование можно выполнить и в области чисел Ферма. Используя такую методику и применяя 32-разрядные слова, можно рассчитать 65 значений автокорреляционной функции при N = 128 для такого количества исходных отсчетов, которое ограничено лишь однозначным представлением чисел в пределах выбранного модуля. При длине слова в 10 разрядов (включая знак) таким способом можно обработать 2000 отсчетов. Помимо сложений, при расчете коэффициентов преобразований Ферма и накоплении достаточно выполнить лишь одно умножение на каждый входной отсчет вместо 65 умножений при обычном методе вычисления корреляции. Естественно, что получаемый при этом результат будет точным, что в данном случае может быть даже более важным, чем в большинстве других. (Следует отметить, что описанное в данном разделе теоретико-числовое преобразование в равной степени применимо к числам как без знака, так и со знаком.)
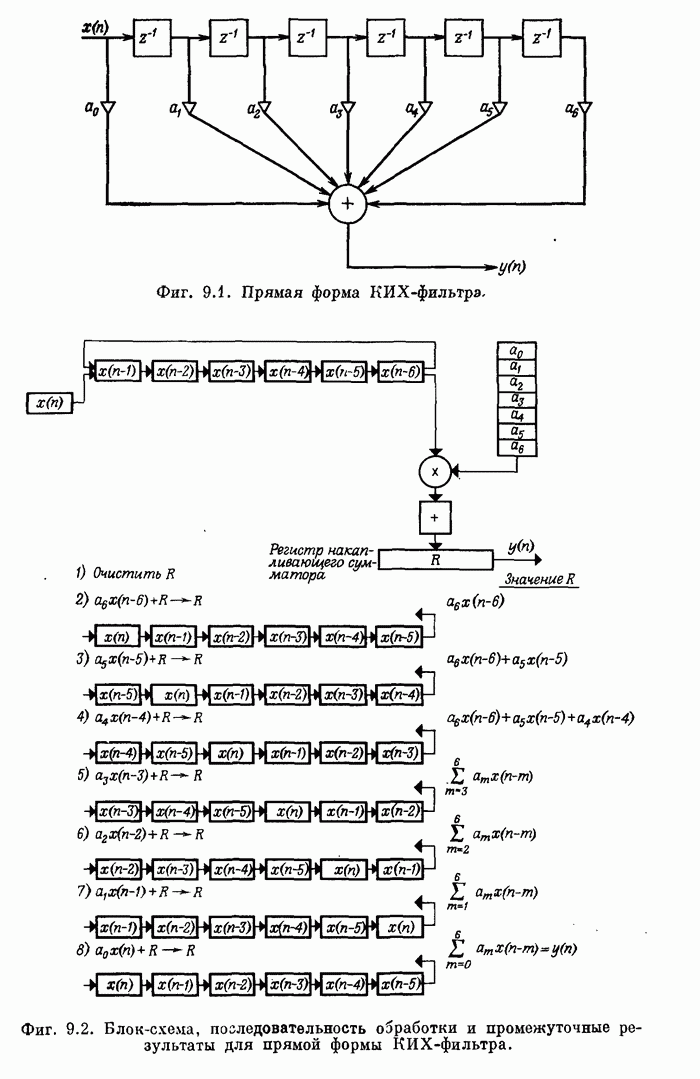
Рассмотрим второе возможное применение теоретико-числового преобразования, относящееся к двумерной КИХ-фильтрации. Речь пойдет, об обработке многоэлементного изображения с использованием произвольной импульсной характеристики размером LxL. Если L имеет величину порядка 5-20, применение БПФ для вычисления свертки будет неэффективным, хотя и более выгодным, чем в одномерном случае. Однако числовое преобразование Ферма будет весьма эффективным. Для импульсной характеристики указанных размеров в отличие от фильтрации прямым методом число умножений сокращается примерно на два порядка за счет увеличения числа сложений, которое тем не менее обычно даже меньше, чем в прямом методе. Таким образом, можно ожидать. что числовое преобразование Ферма вскоре будет использоваться для линейной фильтрации изображений.
Алгоритмы обработки в конечных математических структурах, аналогичные алгоритмам быстрого преобразования Фурье, представляют интересную область исследований, и их применения, несомненно, не ограничиваются лишь вычислением сверток. Как было показано, существует принципиально новый подход к организации вычислений с характерными для него взаимосвязями между разрядностью слова, модулем, величиной а, допустимой неоднозначностью значений результатов и т. д. Возможности этого нового подхода, первоначально казавшегося весьма многообещающим, оказались сильно ограниченными. Можно ожидать, что дальнейшие исследования позволят найти другие математические структуры, которые будут обладать многими достоинствами и в то же время будут целиком или в значительной степени свободны от недостатков структур, рассмотренных в данном разделе. Однако не менее важно и то, что был разработан еще один метод быстрой свертки, о котором мы и не подозревали до тех пор, пока не был исследован аналог обычного метода быстрой свертки в другой системе счисления.
ЛИТЕРАТУРА
Алгоритмы БПФ
1. Cooley J. W., Tukey J. W., An Algorithm for the Machine Computation of Complex Fourier Series, Math. Сотр., 19, 297—301 (April 1965).
2. Bergland G. D., A Guided Tour of the Fast Fourier Transform, IEEE Spectrum, 6, No. 7, 41—52 (1969); есть русский перевод: Бергланд Дж. Д., Руководство к быстрому преобразованию Фурье, Зарубежная радиоэлектроника, № 3 (1971).
3. Cochran W. Т., Cooley J. W., Favin D. L., Helms H. D., Kaenel R. A., Lang W. W., Maling G. C., Nelson D. E., Rader С. M., Welch P. D., What is the Fast Fourier Transform, IEEE Trans, on Audio and Electro-acoustics, 15, No. 2, 45—55 (June 1967); есть русский перевод: Кокрен У. и др., Что такое быстрое преобразование Фурье?, ТИИЭР, 55, № 10 (1967).
4. Cooley J. W., Lewis P., Welch P. D., The Finite Fourier Transform, IEEE Trans, on Audio and Electroacoustics, 17, No. 2, 77—86 (1969).
5. Cooley J. W., Lewis P., Welch P. D., Historical Notes on the Fast Fourier Transform, IEEE Trans, on Audio and Electroacoustics, 15, No. 2, 76—79 (June 1967); есть русский перевод: Кули, Льюис, Уэлч, Исторические замечания относительно быстрого преобразования Фурье, ТИИЭР, 55, № 10 (1967).
6. Singleton R. С., A Method for Computing the Fast Fourier Transform with Auxiliary Memory and Limited High Speed Storage, IEEE Trans, on Audio and Electroacoustics, 15, No. 2, 91—98 (June 1967).
7. Cooley J. W., Lewis P., Welch P. D., The Fast Fourier Transform Algorithm: Programming Considerations in the Calculation of Sine, Cosine, and Laplace Transforms, J. Sound Vib., 12, No. 3, 315—337 (1970).
8. Singleton R. C., An Algorithm for Computing the Mixed Radix Fast Fourier Transform, IEEE Trans, on Audio and Electroacoustics, 17, No. 2, 93—103 (June 1969).
9. Pease M. С., An Adaptation of the Fast Fourier Transform for Parallel Processing, J. Assn. Сотр. Mach., 15, No. 2, 252—264 (April 1968).
10. Rader С. M., Discrete Fourier Transforms When the Number of Data Samples is Prime, Proe. IEEE, 56, No. 6, 1107—1108 (June 1968).
11. Cooley J. W., Lewis P., Welch P. D., The Fast Fourier Transform and Its Applications, IEEE Trans. Education, 12, 27—34 (March 1969).
12. Gold В., Rader С. M., Digital Processing of Signals, McGraw-Hill, N.Y., 1969; есть русский перевод: Голд Б., Рэйдер Ч., Цифровая обработка сигналов, изд-во «Советское радио», 1973.
13. Bluestein L. I., A Linear Filtering Approach to the Computation of Discrete Fourier Transform, IEEE Trans, on Audio and Electroacoustics, 18, No. 4, 451—456 (1970).
14. Rabiner L. R., Schafer R. W., Rader С. M., The Chirp z-Transform Algorithm and Its Application, Bell Syst. Tech. J., 48, No. 5, 1249—1292 (May-June 1969).
Методы статистического спектрального анализа
1. Jenkins G. M., Watts D. G., Spectral Analysis and Its Applications, Hol-den-Day, Inc., Pub., San Francisco, Calif., 1968; есть русский перевод: Дженкинс Г., Ватте Д., Спектральный анализ и его приложения, изд-во «Мир», 1971.
2. Welch P. D., The Use of the FFT for Estimation of Power Spectra: A Method Based on Averaging Over Short, Modified Periodgrams, IEEE Trans, on Audio and Electroacoustics, 15, No. 2, 70—73 (1967).
3. Cooley J. W., Lewis P., Welch P. D., The Use of the Fast Fourier Transform Algorithm for the Estimation of Spectra and Cross Spectra, Proc. of the 1969 Polytechnic Inst, of Brooklyn Symp. on Computer Processing in Communications, 5—20 (1969).
4. Cooley J. W., Lewis P., Welch P. D., The Application of the Fast Fourier Transform Algorithm to the Estimation of Spectra and Cross-Spectra, J. Sound Vib., 12, 339—352 (1970).
5. Rader С. M., An Improved Algorithm for High Speed Autocorrelation with Applications to Spectral Estimation, IEEE Trans, on Audio and Electroacoustics, 18, No. 4, 439—442 (1970).
Теоретико-числовые преобразования и свертка
1. Pollard J. М., The Fast Fourier Transform in a Finite Field, Mathematics of Computation, 25, No. 114, 365—374 (April 1971).
2. Rader С. M., Discrete Convolution Via Mersenne Transforms, IEEE Trans, on Computers, C-21, No. 12, 1269—1273 (Dec. 1972).
3. Agarwal R. C., Burrus C. S., Fast One-Dimensional Convolution by Multidimensional Techniques, IEEE Trans, on Acoustics, Speech, and Signal Processing, ASSP-22, No. 1, 1-10 (Feb. 1974).
4. Agarwal R. C., Burrus C. S., Fast Convolution Using Fermat Number Transforms with Applications to Digital Filtering, IEEE Trans, on Acoustics, Speech, and Signal Processing, ASSP-22, No. 2, 87—97 (April 1974).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
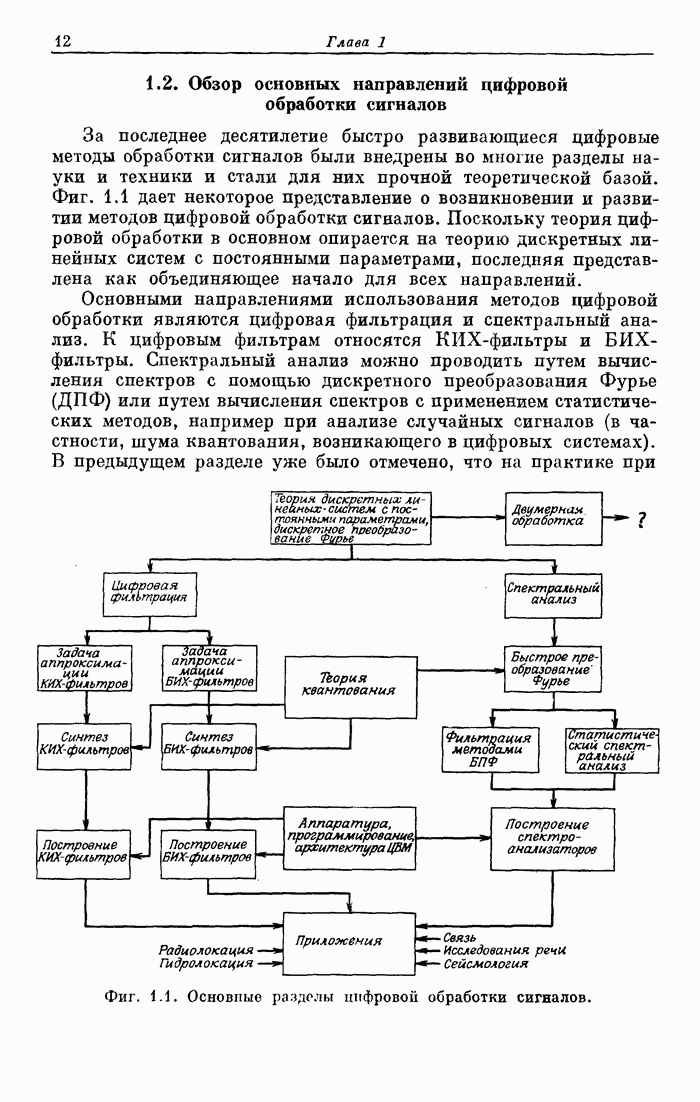
- 1.2. Обзор основных направлений цифровой обработки сигналов
- 1.3. Построение книги
- 2.1. Введение
- 2.2. Последовательности
- 2.3. Представление произвольных последовательностей
- 2.4. Линейные системы с постоянными параметрами
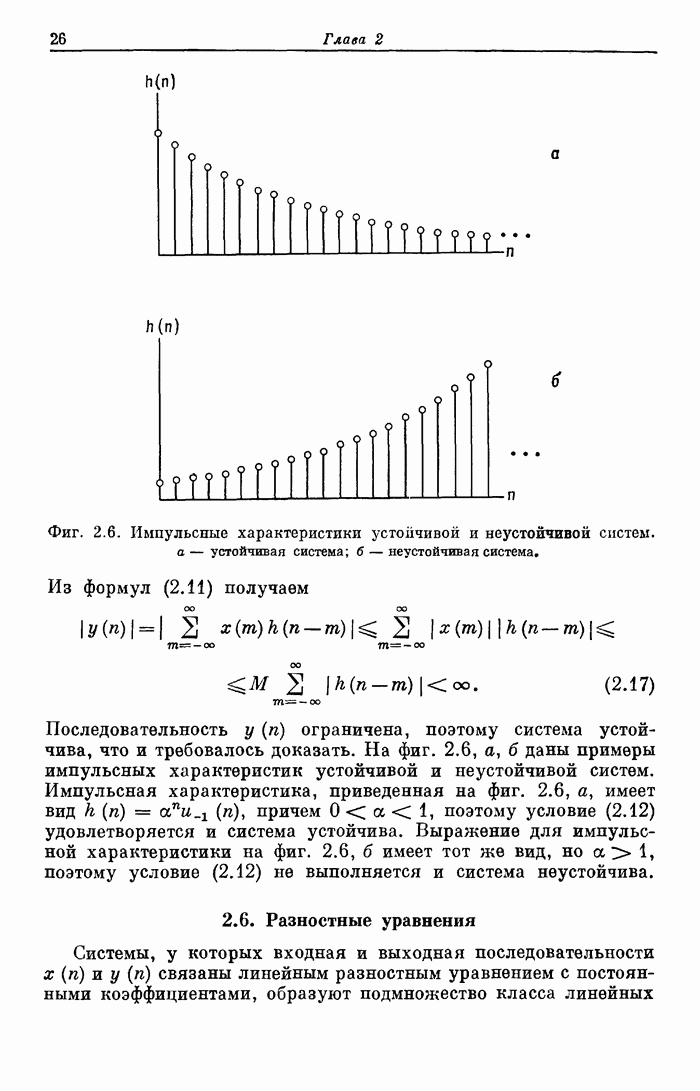
- 2.5. Физическая реализуемость. Устойчивость
- 2.6. Разностные уравнения
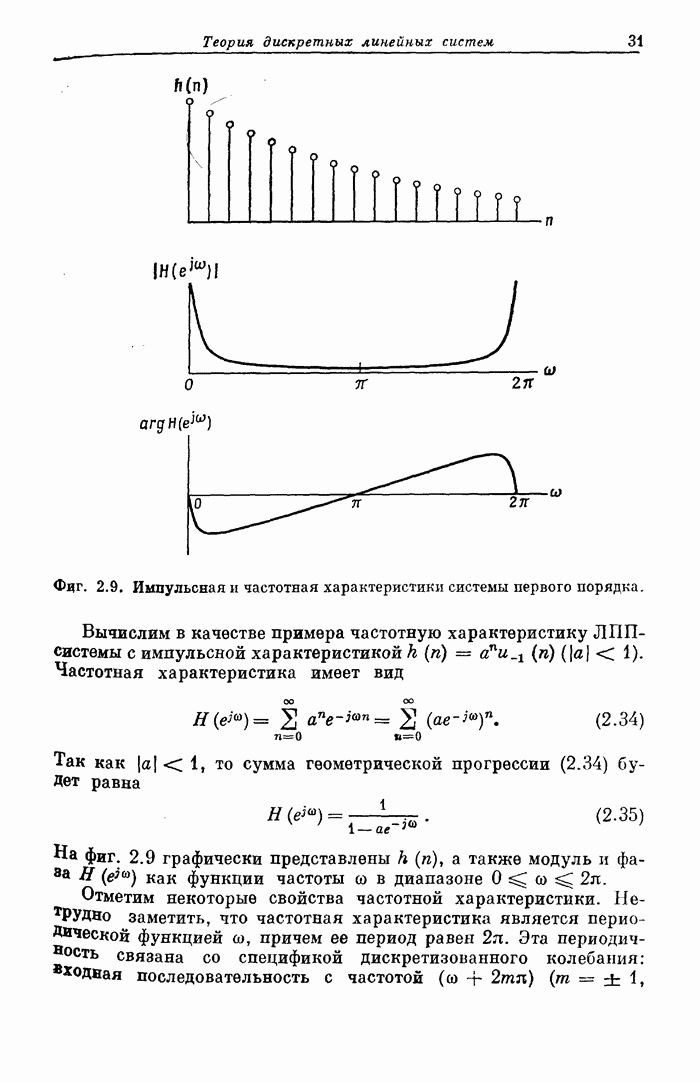
- 2.7. Частотная характеристика
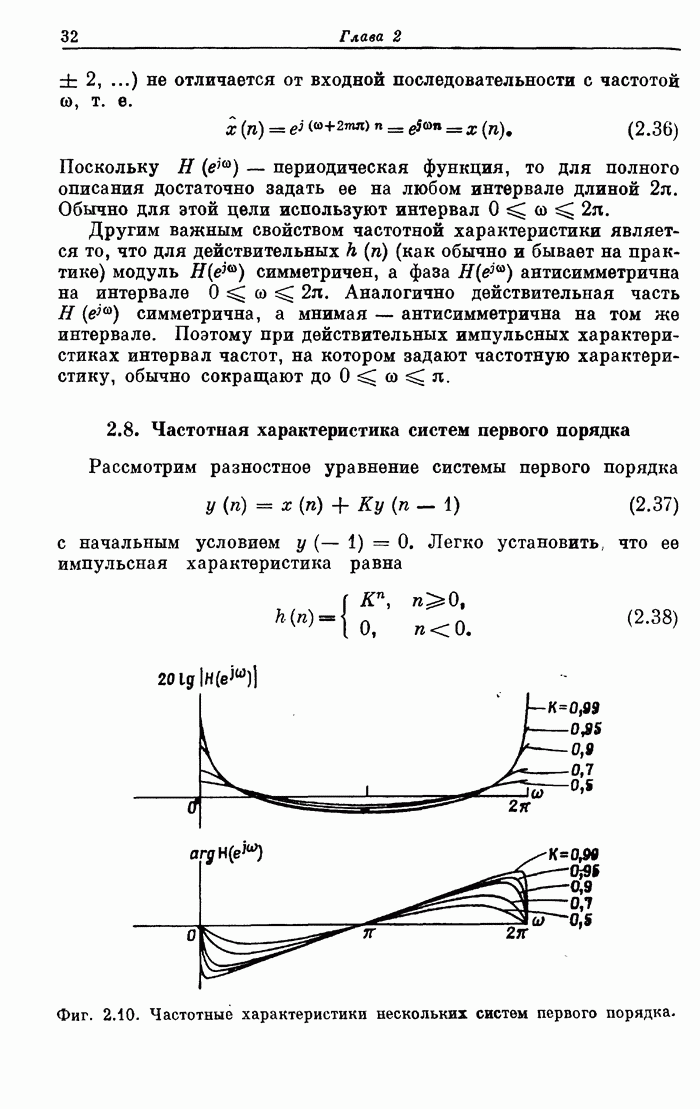
- 2.8. Частотная характеристика систем первого порядка
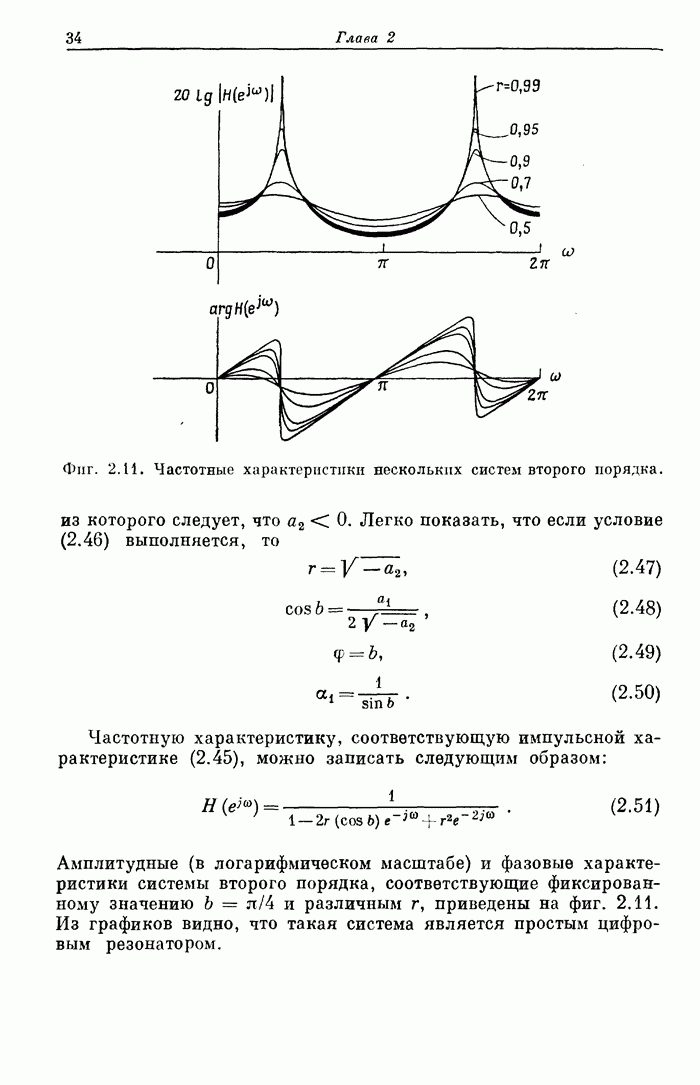
- 2.9. Частотная характеристика систем второго порядка
- 2.10. Дискретный ряд Фурье
- 2.11. Замечания о единицах измерения частоты
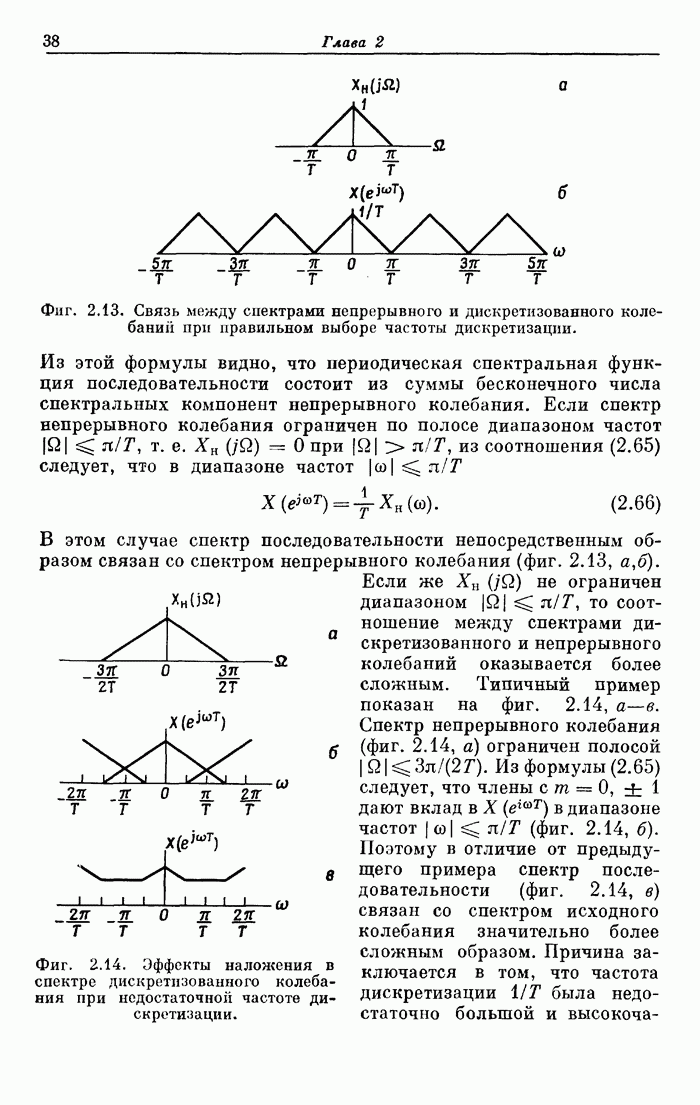
- 2.12. Соотношение между непрерывными и дискретными системами
- 2.13. z-преобразование
- 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности
- 2.15. Обратное z-преобразование
- 2.16. Свойства z-преобразования
- 2.17. Решение разностных уравнений с применением одностороннего z-преобразования
- 2.18. Геометрическая интерпретация преобразования Фурье
- 2.19. Построение цифровых фильтров (структурные схемы фильтров)
- 2.20. Структурные схемы фильтров без полюсов
- 2.21. Дискретное преобразование Фурье
- 2.22. Свойства ДПФ
- 2.23. Свертка последовательностей
- 2.24. Линейная свертка конечных последовательностей
- 2.25. Секционированные свертки
- 2.26. Дискретное преобразование Гильберта
- 2.27. Преобразование Гильберта действительных сигналов
- ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ
- 3.2. Порядок расчета фильтров
- 3.3. Свойства КИХ-фильтров
- 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой
- 3.5. Частотная характеристика КИХ-фильтров с линейной фазой
- 3.6. Расположение нулей КИХ-фильтров с линейной фазой
- 3.7. Методы расчета КИХ-фильтров с линейными фазами
- 3.8. Первый метод расчета — метод взвешивания
- 3.9. Прямоугольное окно
- 3.10. «Обобщенное» окно Хэмминга
- 3.11. Окно Кайзера
- 3.12. Примеры фильтров нижних частот с различными окнами
- 3.13. Особенности использования метода взвешивания
- 3.14. Несколько практических приемов использования окон
- 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания
- 3.16. Общая характеристика окон
- 3.17. Второй метод проектирования — метод частотной выборки
- 3.18. Решение задачи оптимизации
- 3.19. Линейное программирование
- 3.20. Фильтры с частотной выборкой вида 1 и 2
- 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой
- 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой
- 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки
- 3.24. Заключение к описанию метода частотной выборки
- 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой
- 3.26. Аппроксимация по Чебышеву со взвешиванием
- 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой
- 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций
- 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции
- 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров
- 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования
- 3.32. Характеристики оптимальных фильтров нижних частот вида 1
- 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1
- 3.34. Соотношения между параметрами оптимального фильтра нижних частот
- 3.35. Свойства оптимальных фильтров нижних частот вида 2
- 3.36. Характеристики оптимальных дифференциаторов
- 3.37. Характеристики оптимальных преобразователей Гильберта
- 3.38. Многополосные оптимальные КИХ-фильтры
- 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях
- 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот
- Приложение
- Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ
- 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки
- 4.3. Методы расчета коэффициентов БИХ-фильтра
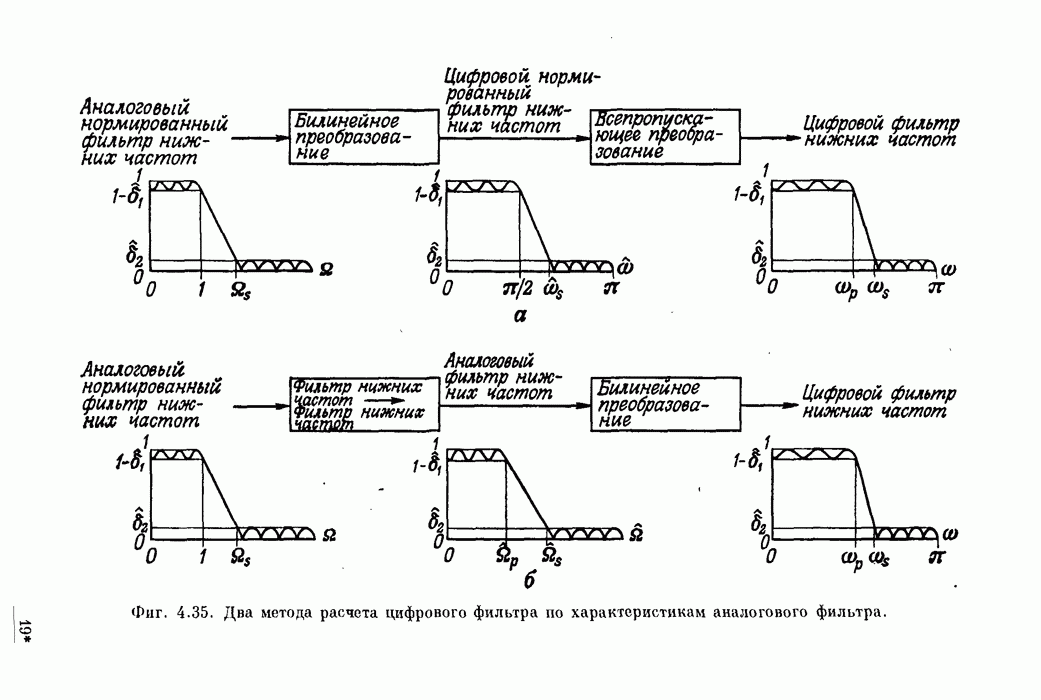
- 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени
- 4.5. Метод отображения дифференциалов
- 4.6. Метод инвариантного преобразования импульсной характеристики
- 4.7. Билинейное z-преобразование
- 4.8. Согласованное z-преобразование
- 4.9. Обзор методов расчета аналоговых фильтров нижних частот
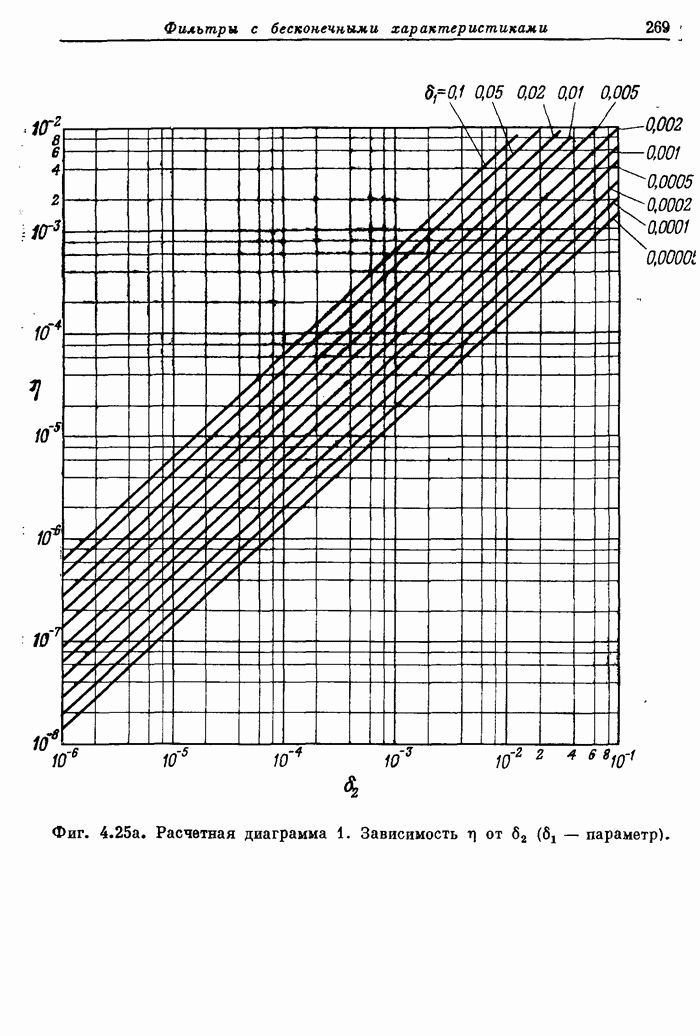
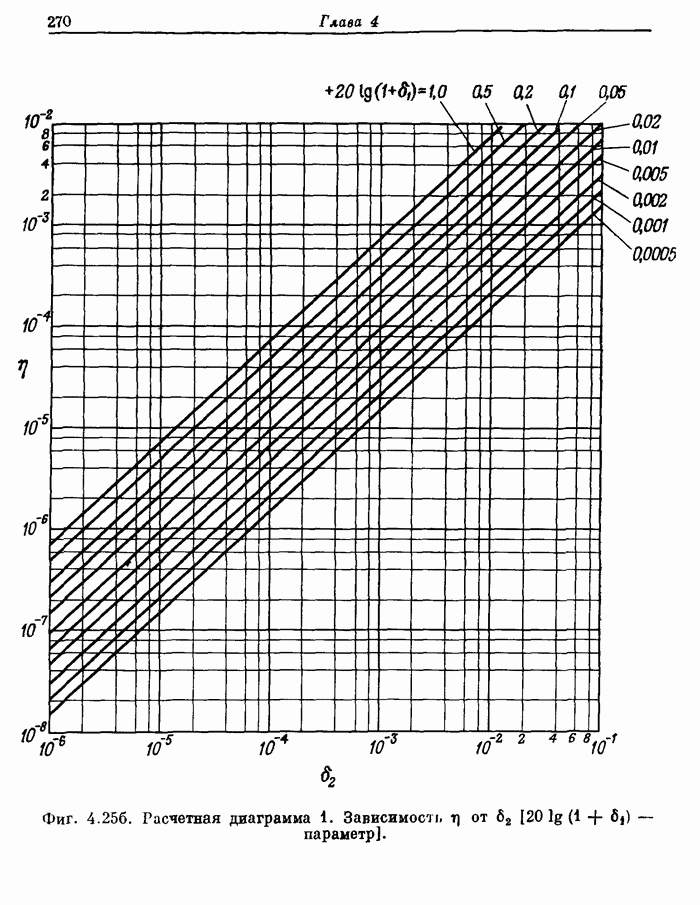
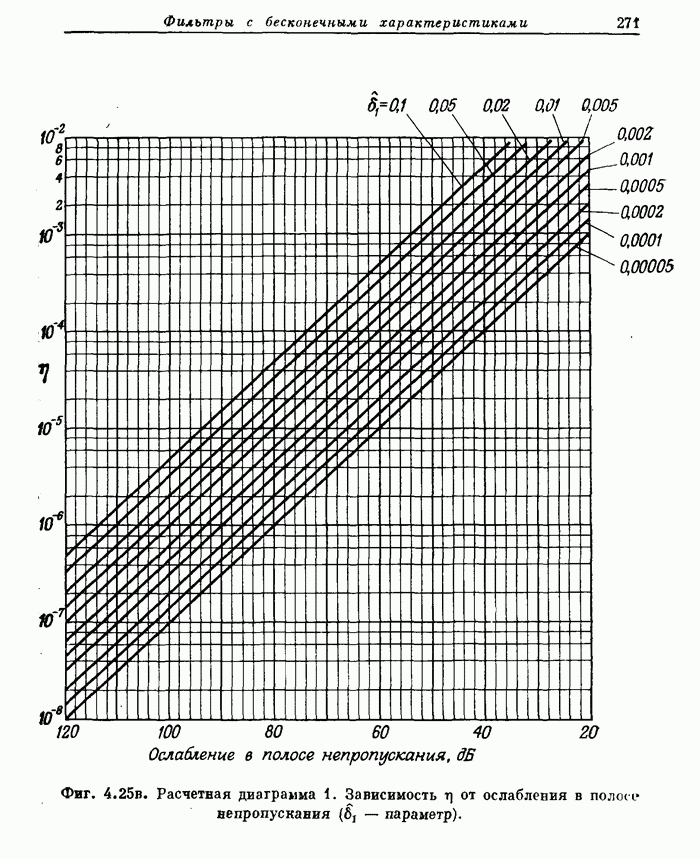
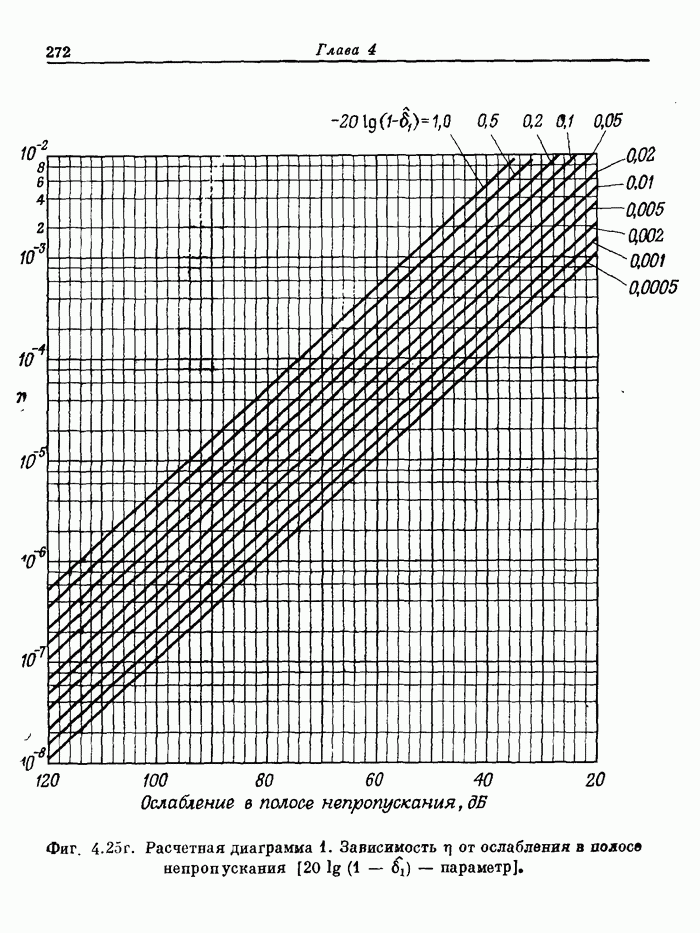
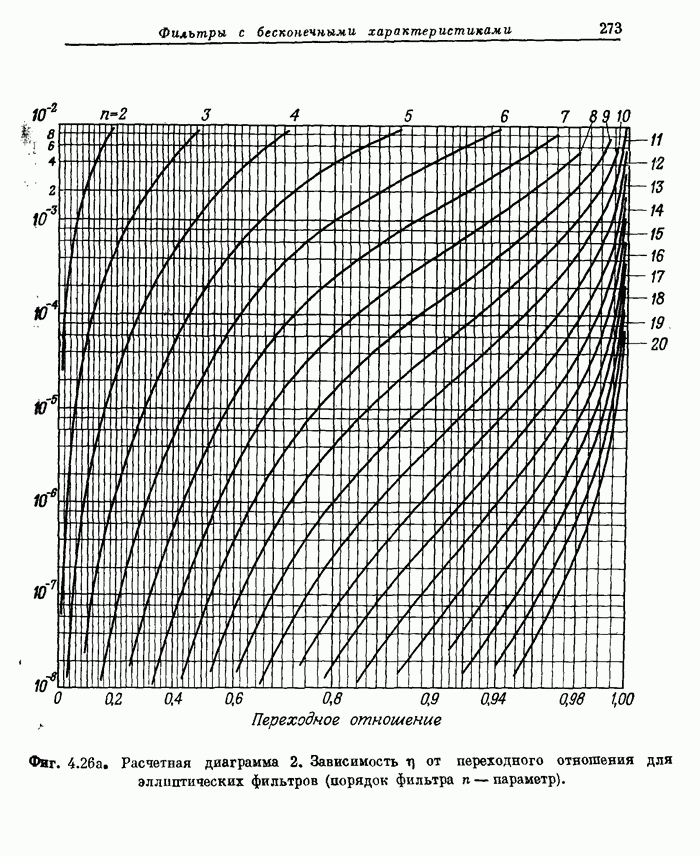
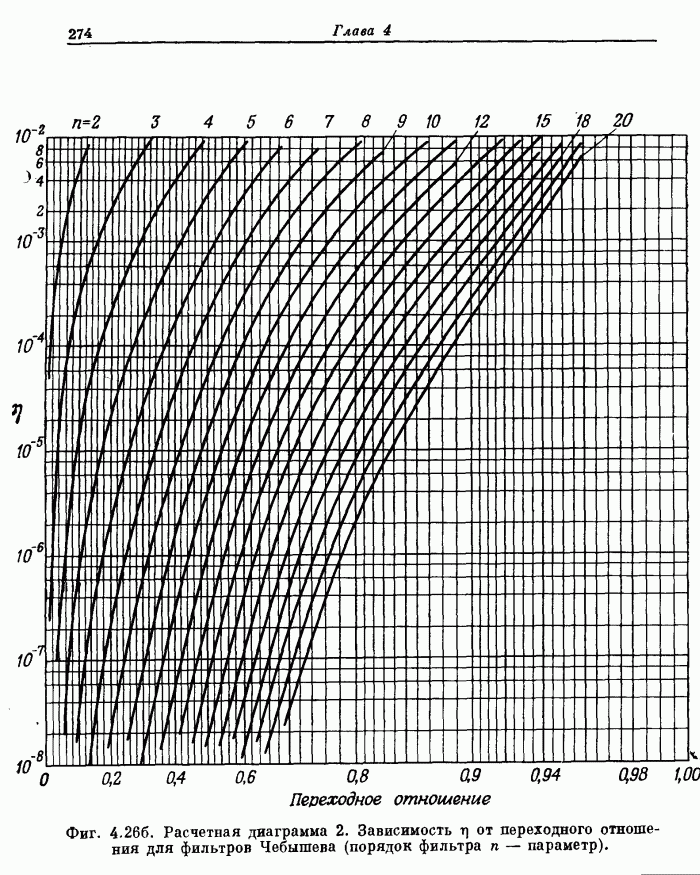
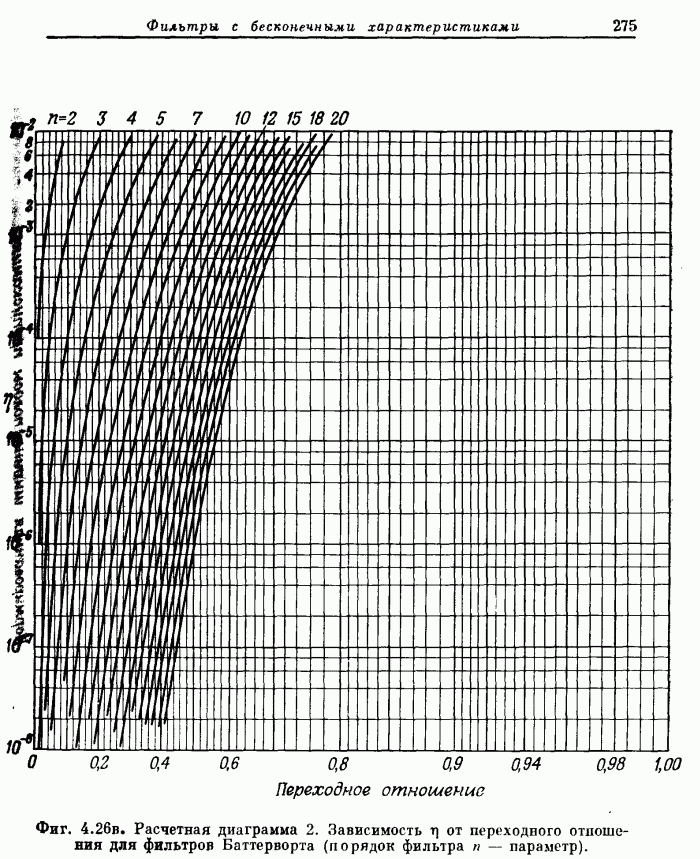
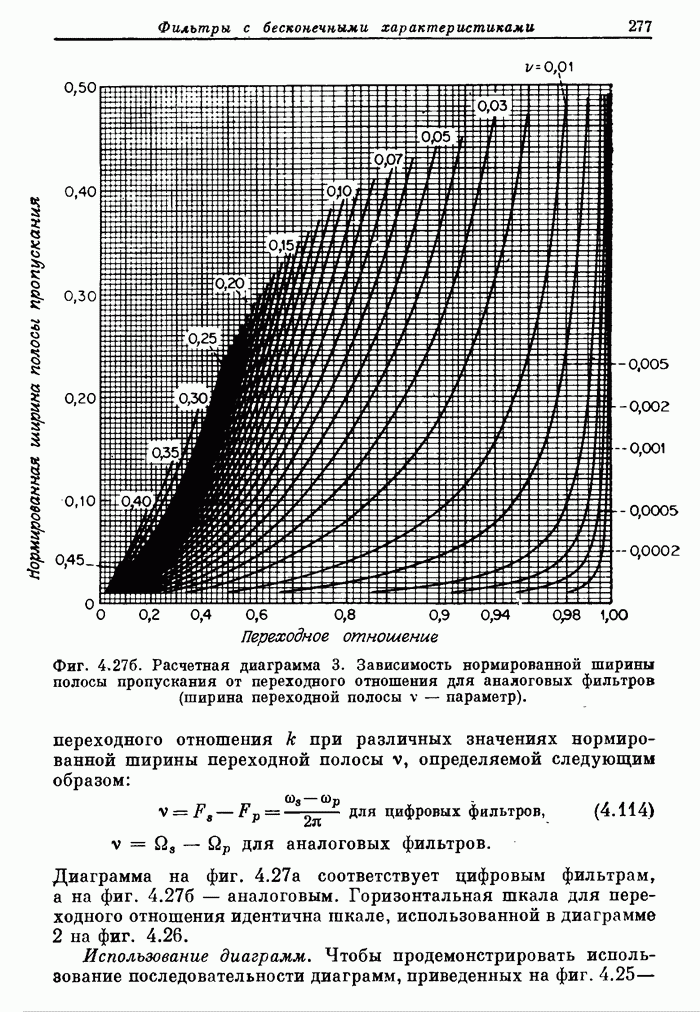
- 4.10. Расчетные диаграммы фильтров нижних частот
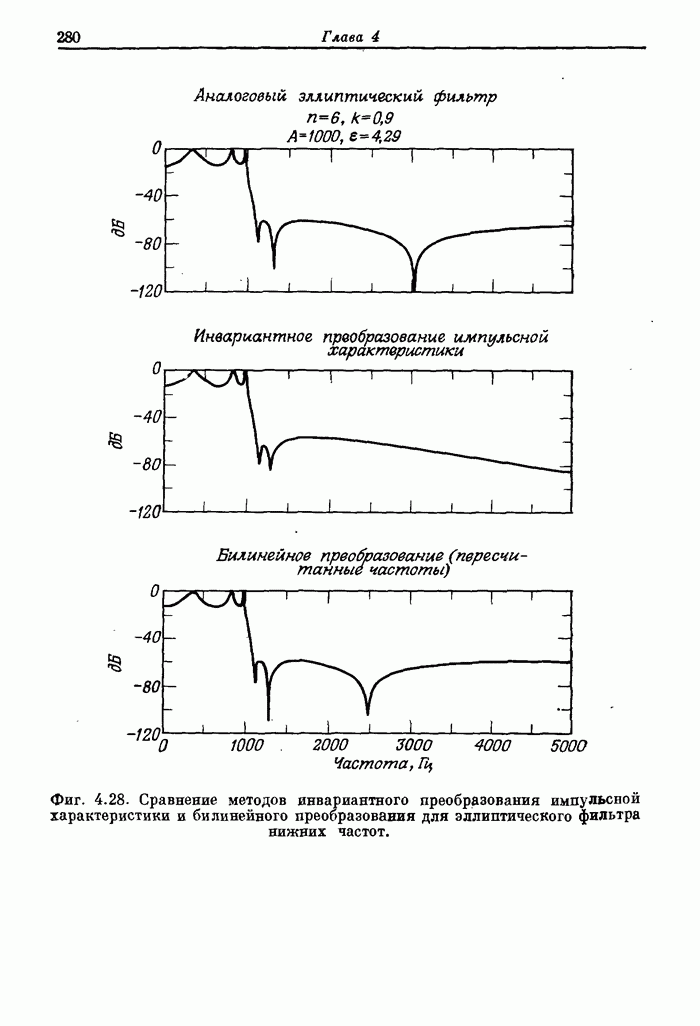
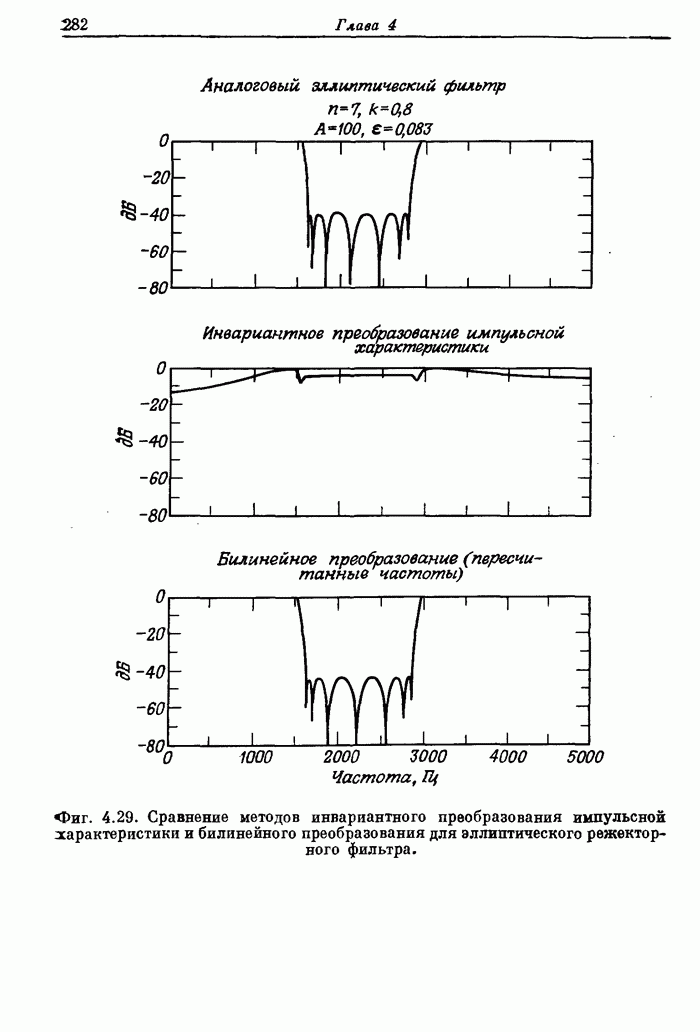
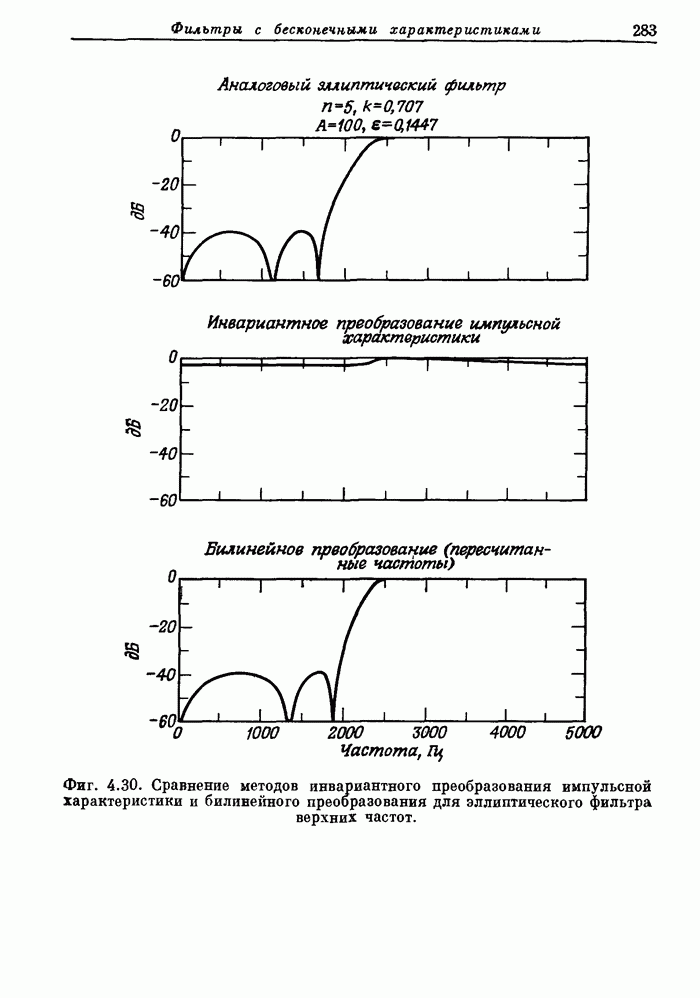
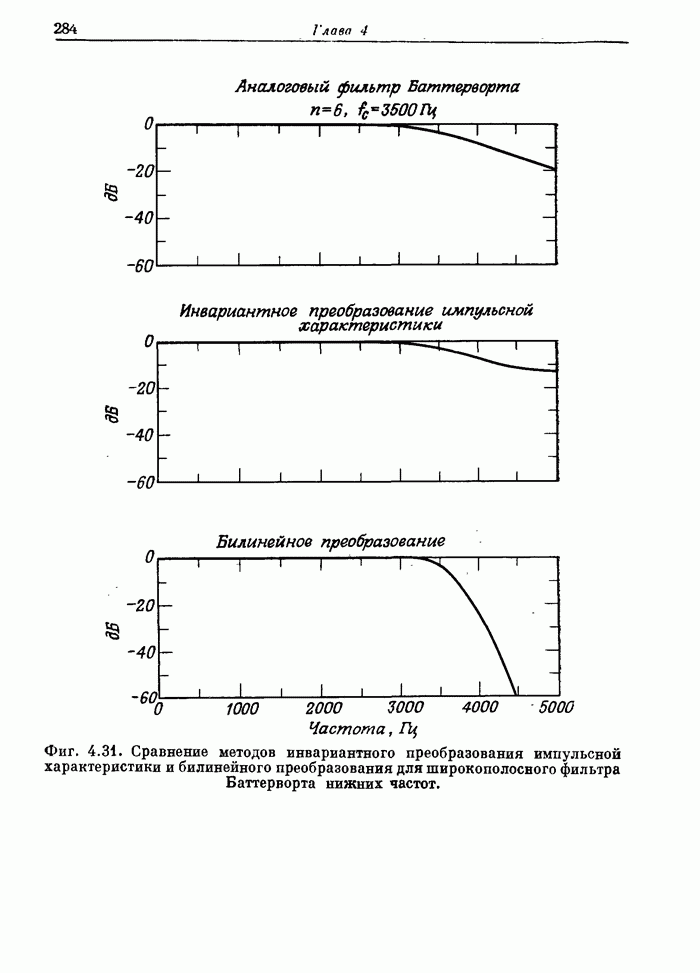
- 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров
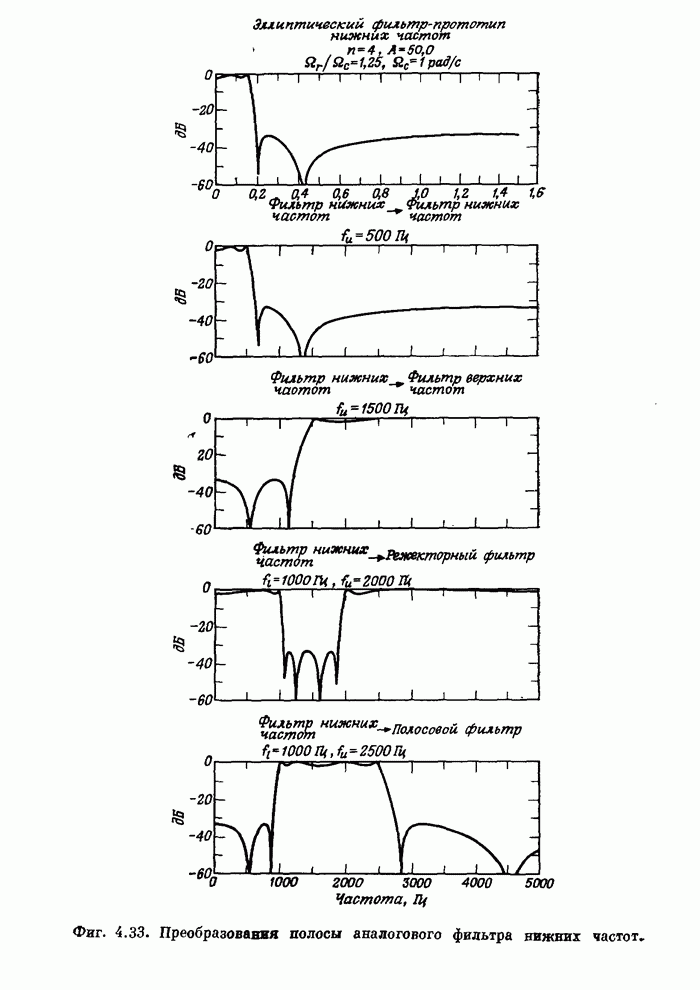
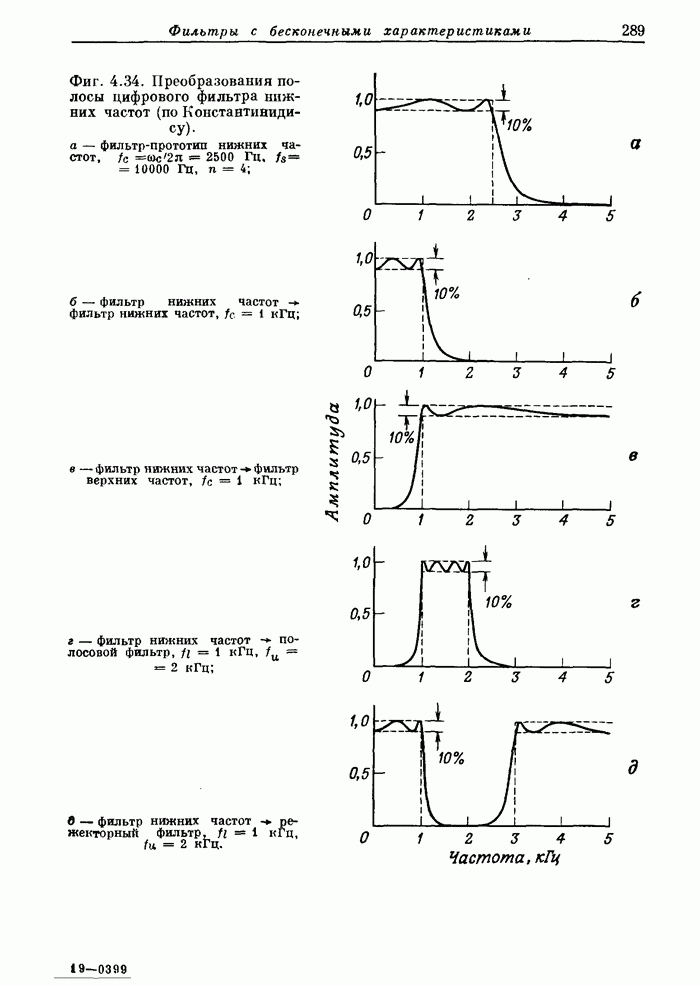
- 4.12. Частотные преобразования
- 4.13. Прямые методы расчета цифровых фильтров
- 4.14. Применение методов оптимизации для расчета БИХ-фильтров
- 4.15. Обзор методов расчета БИХ-фильтров
- 4.16. Сравнение КИХ- и БИХ-фильтров
- 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки
- Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 5.2. Аналого-цифровое преобразование
- 5.3. Цифро-аналоговое преобразование
- 5.4. Системы счисления, применяемые в цифровых устройствах
- 5.5. Система счисления с фиксированной запятой
- 5.6. Системы счисления с плавающей запятой
- 5.7. Система счисления с поблочно плавающей запятой
- 5.8. Виды квантования в цифровых фильтрах
- 5.9. Усечение
- 5.10. Округление
- 5.11. Шум округления в рекурсивных структурах с фиксированной запятой
- 5.12. Ограничение динамического диапазона в системах с фиксированной запятой
- 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме
- 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме
- 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме
- 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме
- 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления
- 5.19. Шум округления в нерекурсивных структурах с фиксированной запятой
- 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме
- 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме
- 5.22. Шум округления в рекурсивных структурах с плавающей запятой
- 5.23. Квантование коэффициентов
- 5.24. Квантование коэффициентов в рекурсивных структурах
- 5.25. Квантование коэффициентов при построении фильтров в прямой форме
- 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов
- 5.27. Оптимальное квантование коэффициентов
- 5.28. Квантование коэффициентов в двухполюсном фильтре
- 5.29. Квантование коэффициентов в нерекурсивных структурах
- 5.30. Квантование коэффициентов при построении КИХ-фильтров
- 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме
- 5.32. Колебания предельного цикла
- Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 6.2. Введение в алгоритмы БПФ с основанием 2
- 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени
- 6.4. Перестановка данных и двоичная инверсия
- 6.5. Программа расчета БПФ на ФОРТРАНе
- 6.6. Алгоритм БПФ с прореживанием по частоте
- 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ
- 6.8. Единый подход к алгоритмам БПФ
- 6.9. Алгоритмы БПФ с основанием 2
- 6.10. Спектральный анализ в одной точке z-плоскости
- 6.11. Спектральный анализ с применением БПФ
- 6.12. Некоторые характеристики спектрального анализа
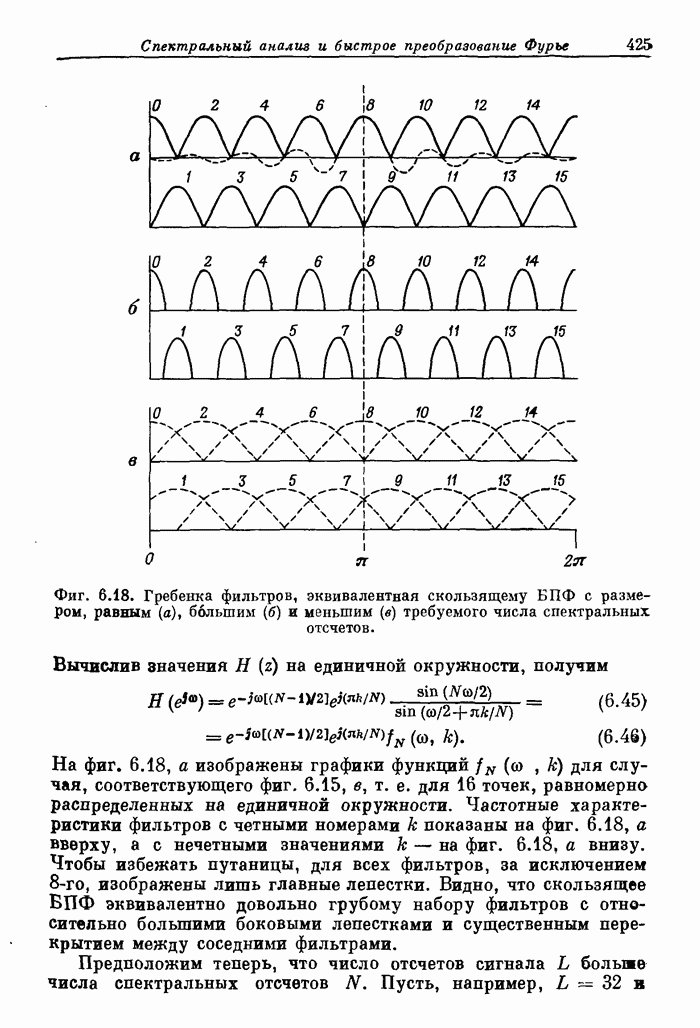
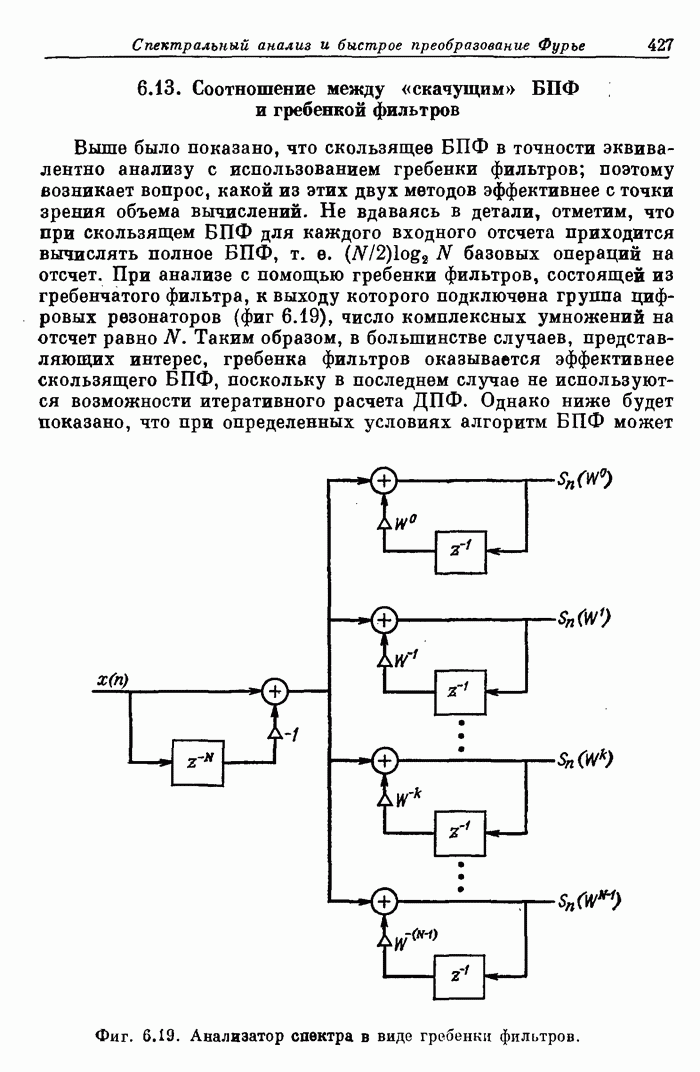
- 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров
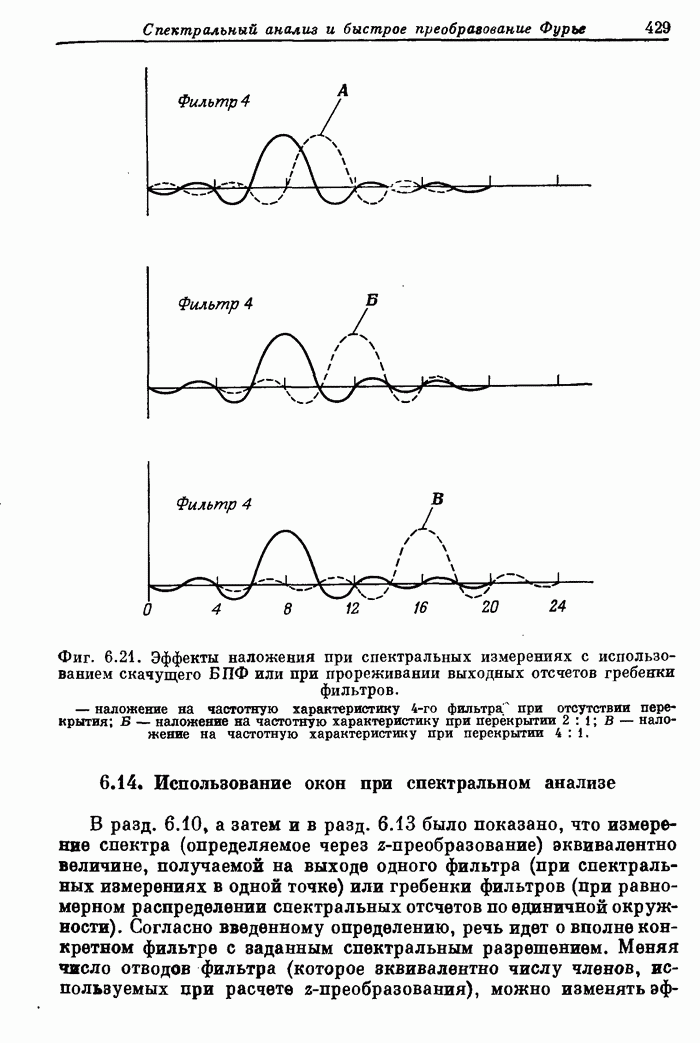
- 6.14. Использование окон при спектральном анализе
- 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ
- 6.16. Алгоритм Блюстейна
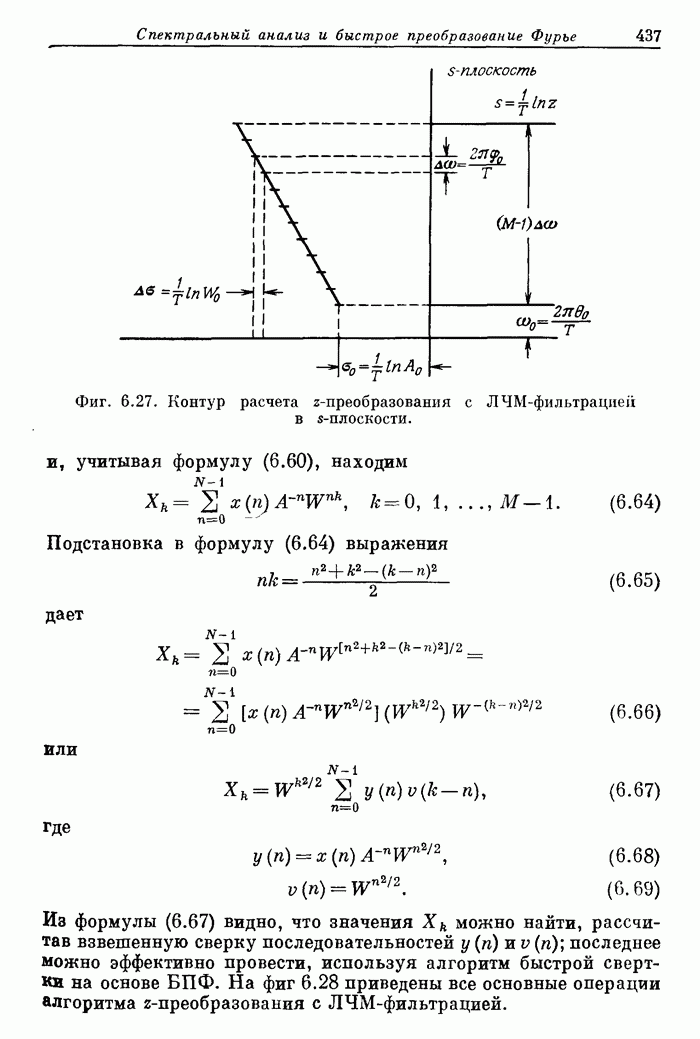
- 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации
- 6.18. Энергетический спектр случайных сигналов
- 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований
- ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ
- Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ
- 7.2. Двумерные сигналы
- 7.3. Двумерные системы
- 7.4. Физическая реализуемость. Разделимость. Устойчивость
- 7.5. Двумерные разностные уравнения
- 7.6. Частотные методы
- 7.7. Двумерное z-преобразование
- 7.8. Конечные последовательности
- 7.9. Свертка последовательностей
- 7.10. Двумерное ДПФ
- 7.11. Расчет двумерных фильтров
- 7.12. БИХ-фильтры
- 7.13. Устойчивость БИХ-фильтров
- 7.14. КИХ-фильтры
- 7.15. Двумерные весовые функции (окна)
- 7.16. Пример расчета фильтра нижних частот методом взвешивания
- 7.17. Фильтры с частотной выборкой
- 7.18. Двумерные фильтры нижних частот с частотной выборкой
- 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров
- 7.20. Частотное преобразование одномерных фильтров в двумерные
- 7.21. Примеры обработки изображений
- Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ
- 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов
- 8.3. Булева алгебра. Примеры простых логических цепей
- 8.4. Основные типы интегральных логических схем
- 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства
- 8.6. Умножители
- 8.7. Делители и устройства с плавающей запятой
- 8.8. Пример: проектирование быстродействующего матричного умножителя
- 8.9. Заключение
- ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ
- 9.2. Аппаратурное построение КИХ-фильтра прямой формы
- 9.3. Параллелизм при построении КИХ-фильтров прямой формы
- 9.4. Каскадная форма КИХ-фильтра
- 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма
- 9.6. Прямая форма построения БИХ-фильтров
- 9.7. Каскадная форма БИХ-фильтров
- 9.8. Мультиплексирование
- 9.9. Цифровой приемник клавишно-тонального вызова
- 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов
- 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах
- 9.12. Специализированный цифровой синтезатор частот
- 9.13. Методы генерации псевдослучайных чисел
- 9.14. Методы генерации гауссовых случайных чисел
- Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ
- 10.2. Обзор теоретических основ БПФ
- 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием
- 10.5. Эффекты квантования в алгоритмах БПФ
- 10.6. Особенности аппаратурной реализации БПФ с основанием 2
- 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2
- 10.9. Выполнение БПФ с использованием сверхоперативной памяти
- 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом
- 10.11. Общие вопросы построения поточных схем БПФ
- 10.12. Поточные схемы БПФ с основанием 2
- 10.13. Поточная схема БПФ с основанием 4
- 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4
- 10.15. Структуры БПФ с повышенным уровнем параллелизма
- 10.16. Общие принципы построения специализированных процессоров БПФ
- 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом
- 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом
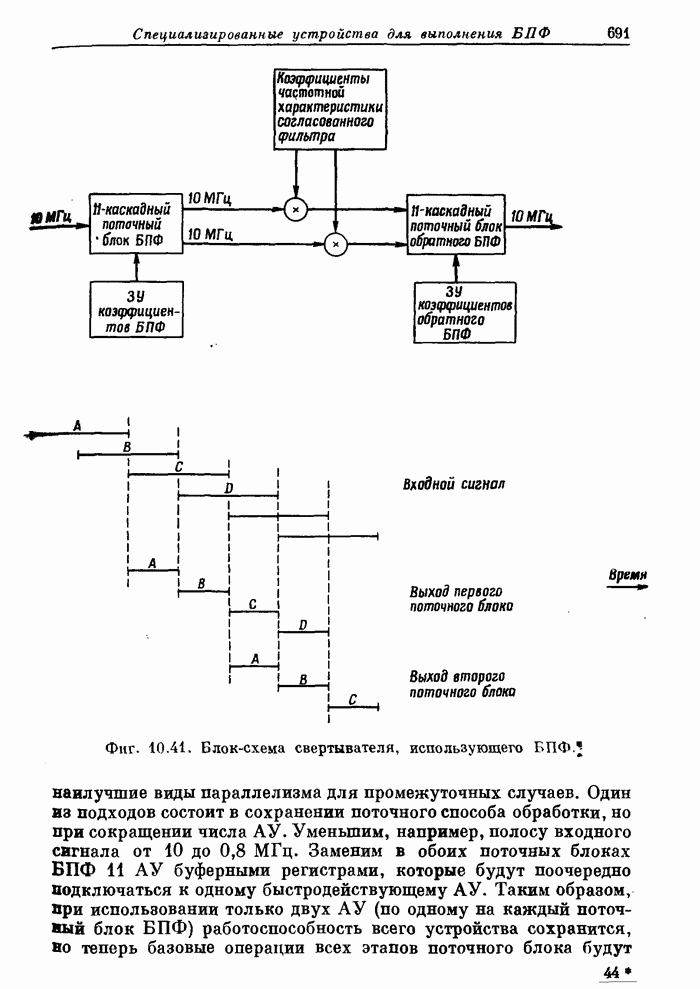
- 10.19. Поточный свертыватель с тактовой частотой 10 МГц
- Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ
- 11.2. Специализированные и универсальные вычислительные машины
- 11.3. Способы описания вычислительных машин
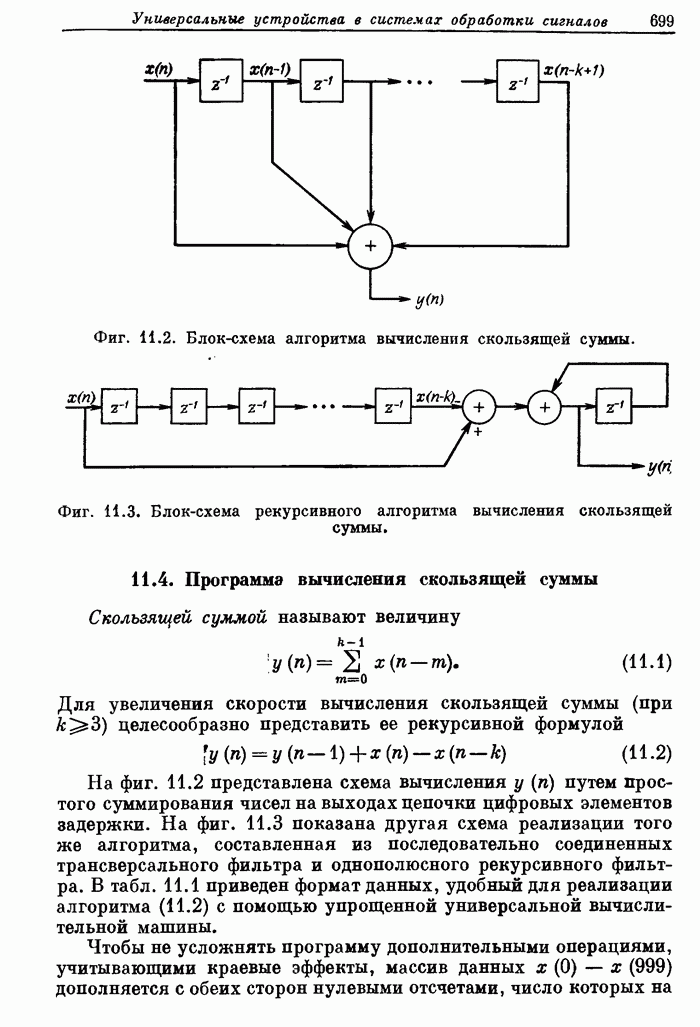
- 11.4. Программа вычисления скользящей суммы
- 11.5. Особенности ввода — вывода при обработке в реальном времени
- 11.6. Методы увеличения быстродействия вычислительной машины
- 11.7. Сверхоперативные ЗУ
- 11.8. Распараллеливание арифметических операций
- 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд
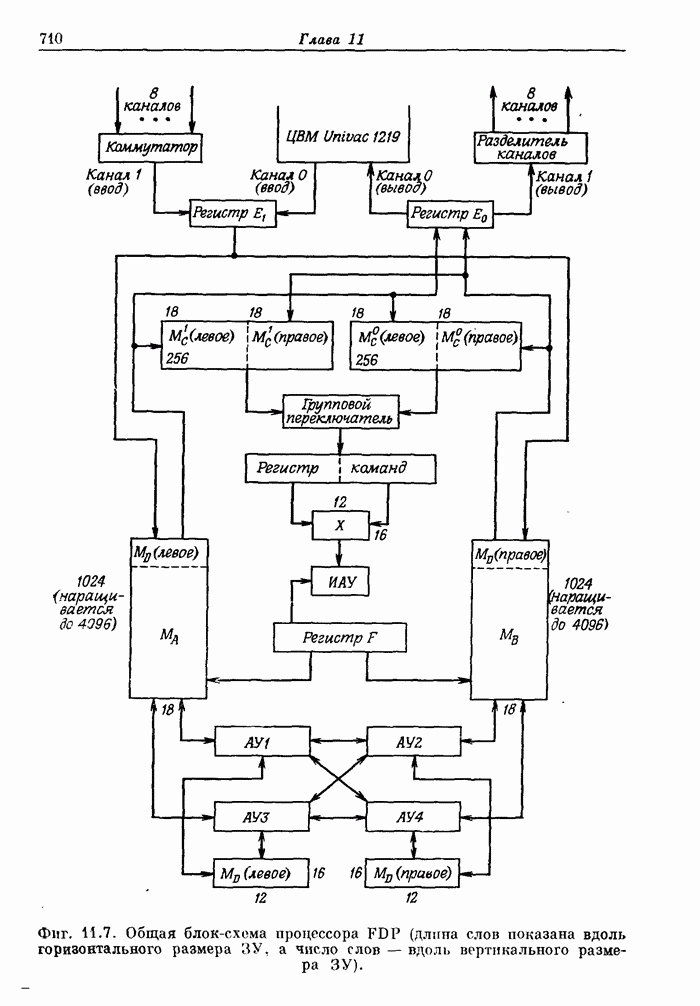
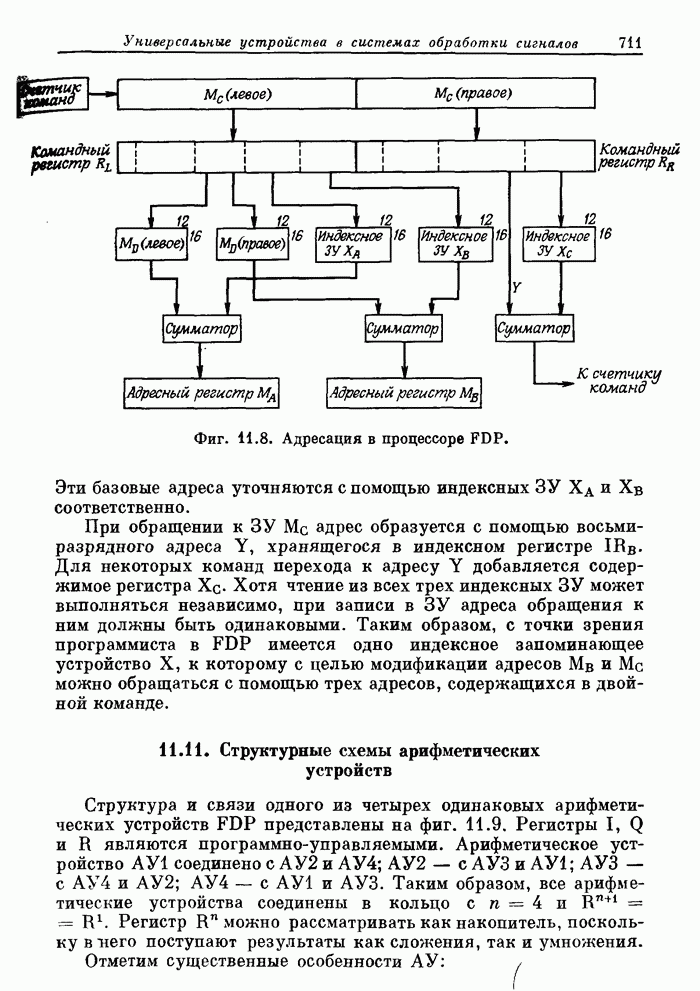
- 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории
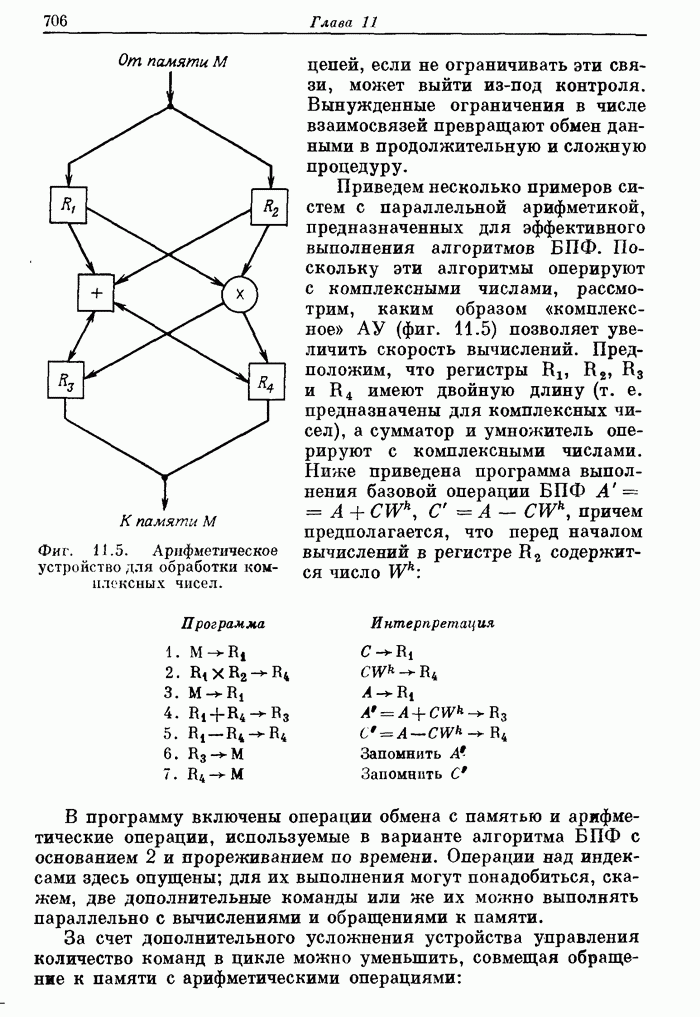
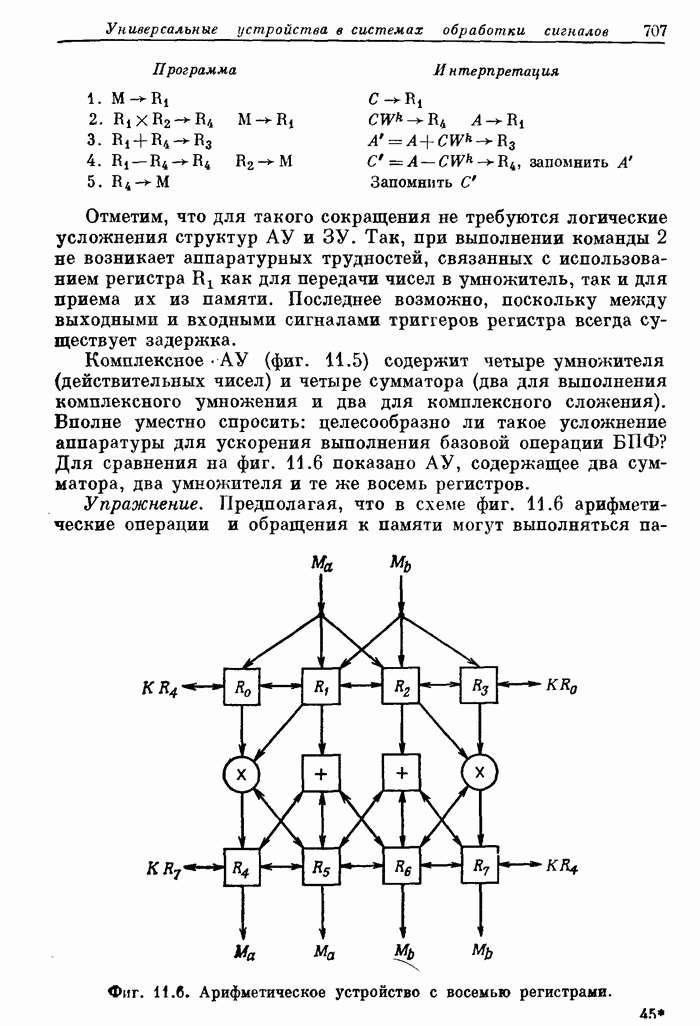
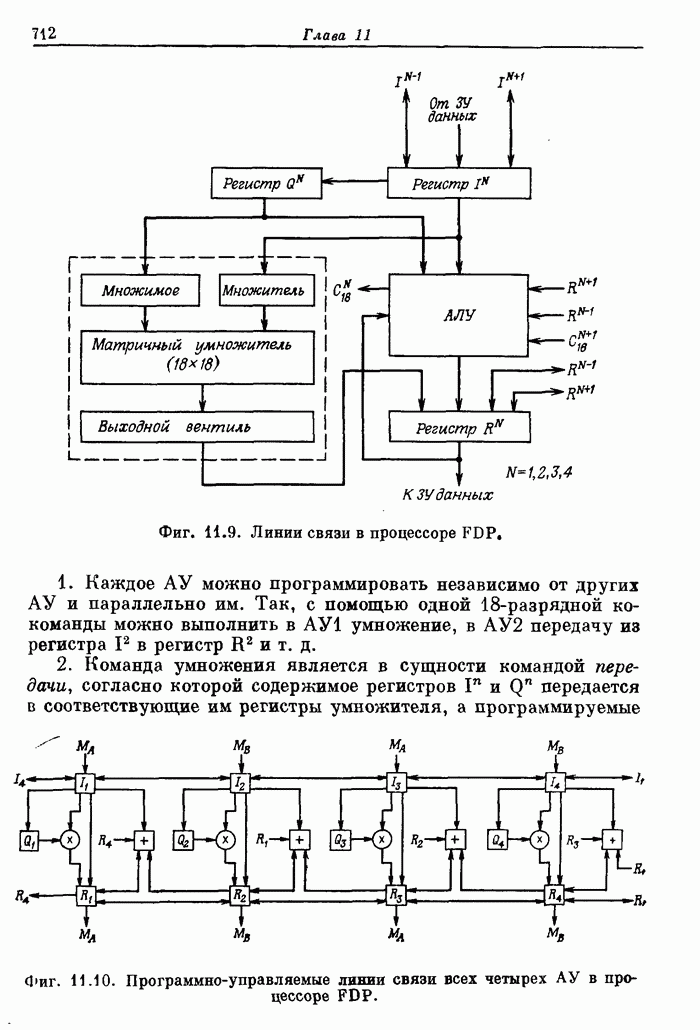
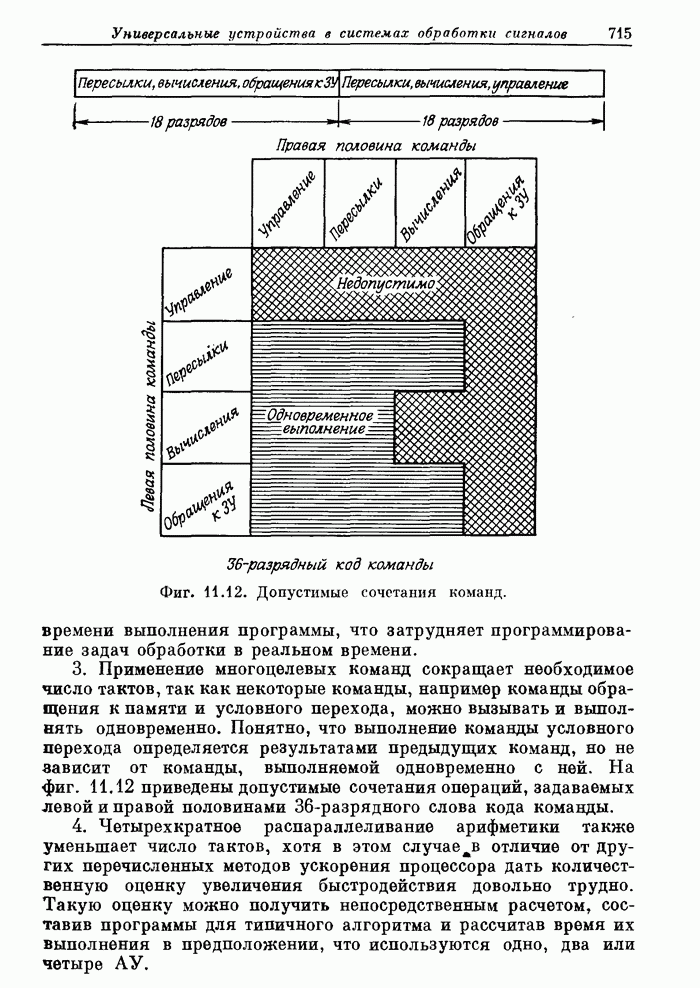
- 11.11. Структурные схемы арифметических устройств
- 11.12. Синхронизация
- 11.13. Обзор методов увеличения быстродействия, использованных в FDP
- 11.14. Выполнение быстрого преобразования Фурье с помощью FDP
- 11.15. Подпрограммы для действий с плавающей запятой
- 11.16. Обзор особенностей FDP, связанных с распараллеливанием
- 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов
- 11.18. Лабораторная вычислительная система для цифровой обработки сигналов
- ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ
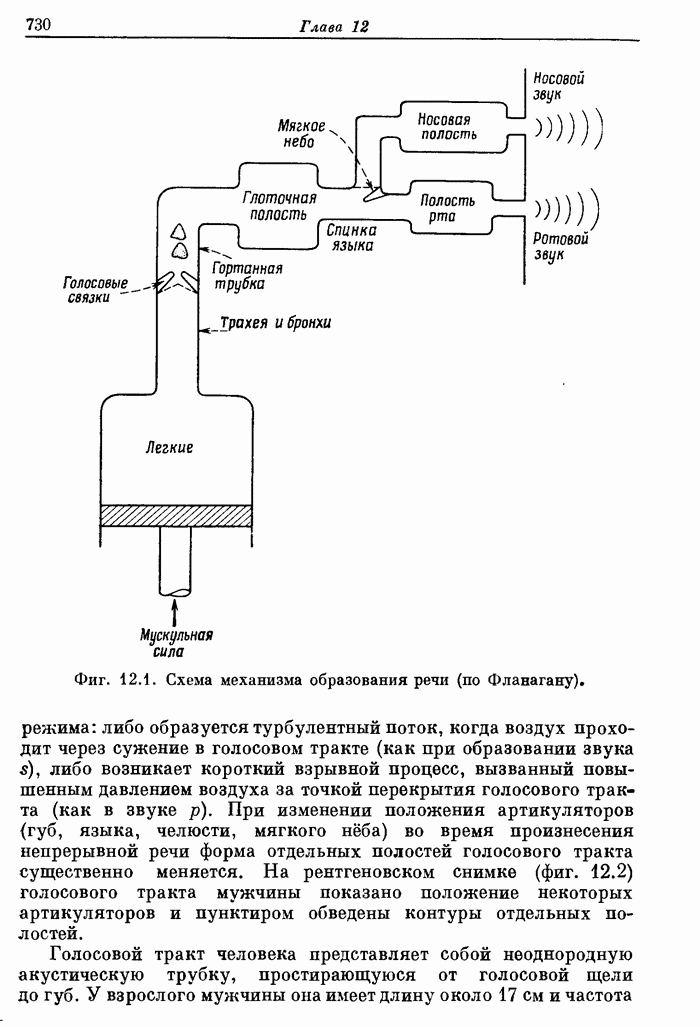
- 12.2. Модель образования речи
- 12.3. Кратковременный спектральный анализ
- 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе
- 12.5. Особенности анализа речи
- 12.6. Система анализа — синтеза
- 12.7. Полосный вокодер
- 12.8. Анализаторы вокодеров. Особенности обработки сигналов
- 12.9. Синтезаторы вокодеров. Особенности обработки сигналов
- 12.10. Другие схемы вокодеров
- 12.11. Выделение высоты основного тона и обнаружение тон — шум
- 12.12. Обнаружитель тон — шум
- 12.13. Гомоморфная обработка речи
- 12.14. Гомоморфный вокодер
- 12.15. Формантный синтез
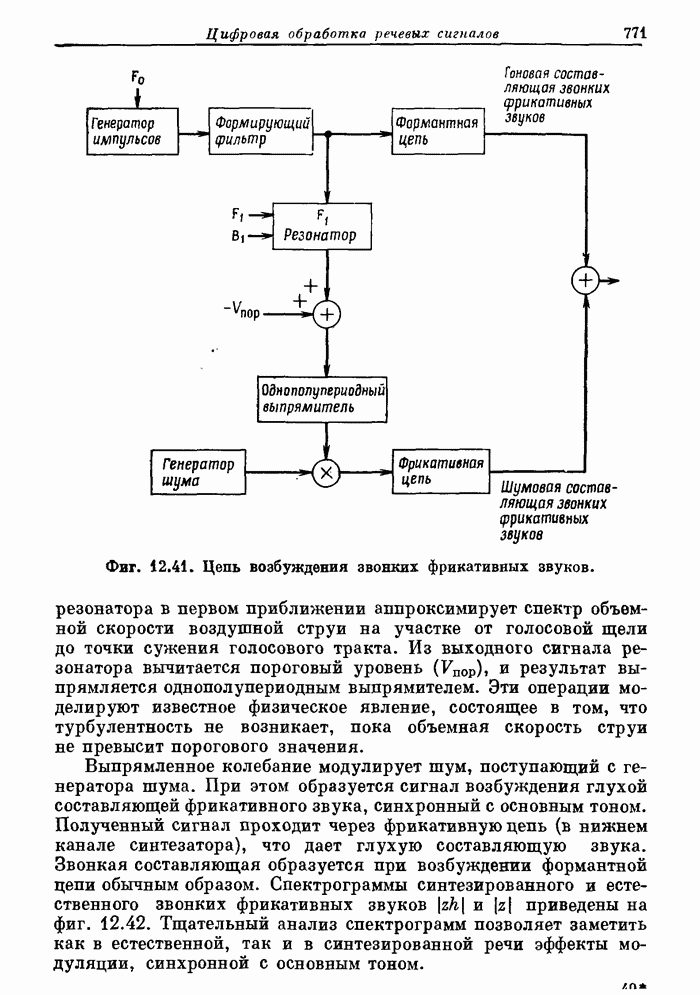
- 12.16. Цепь возбуждения звонких фрикативных звуков
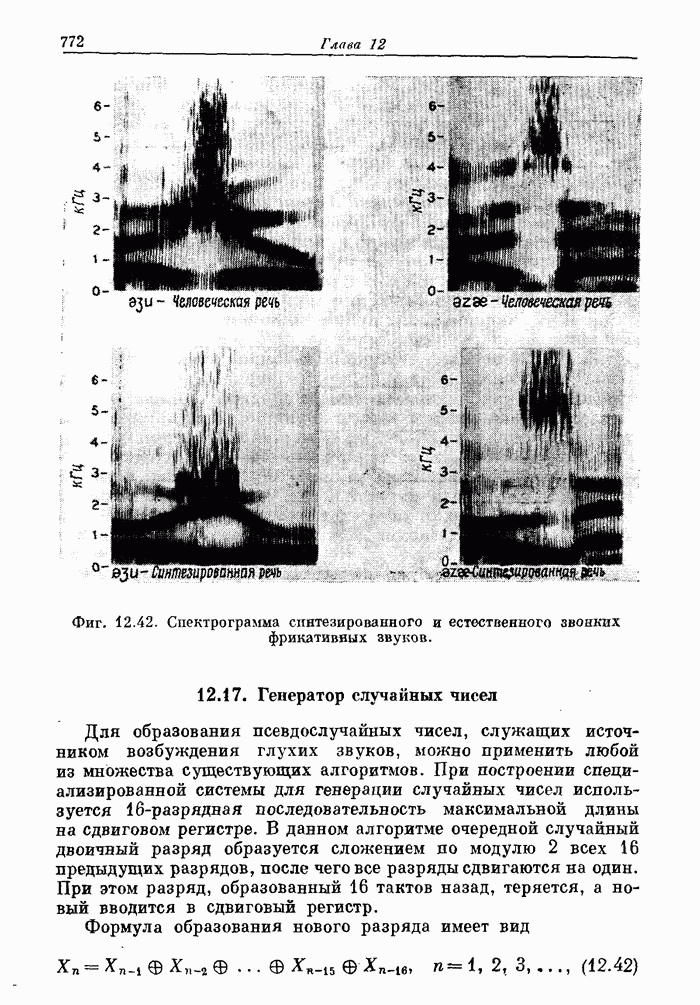
- 12.17. Генератор случайных чисел
- 12.18. Цифровая обработка в формантном синтезаторе
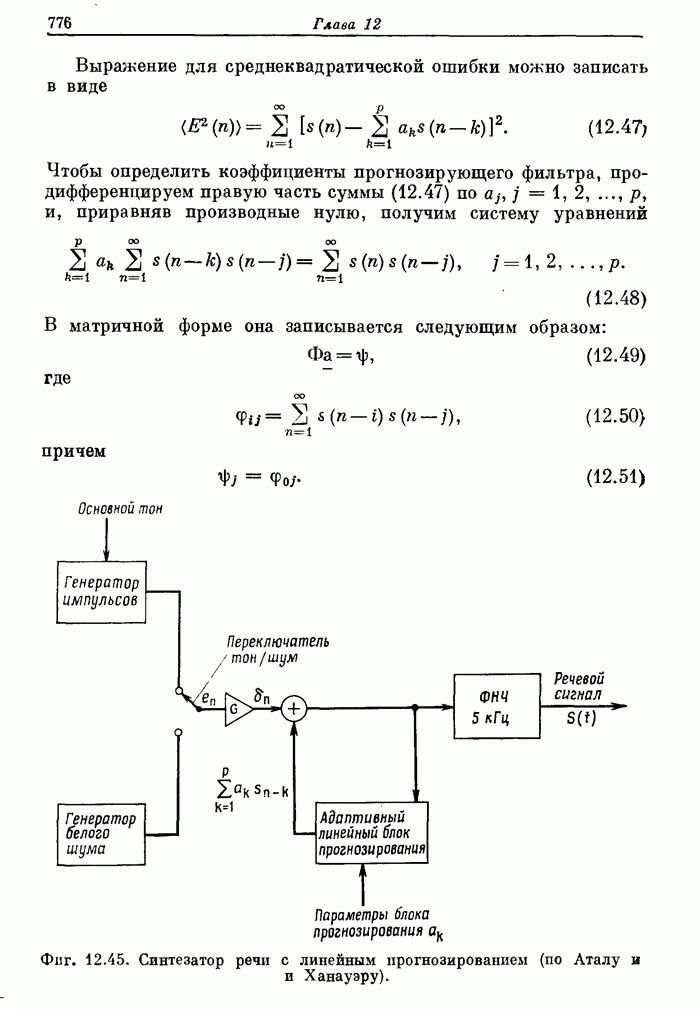
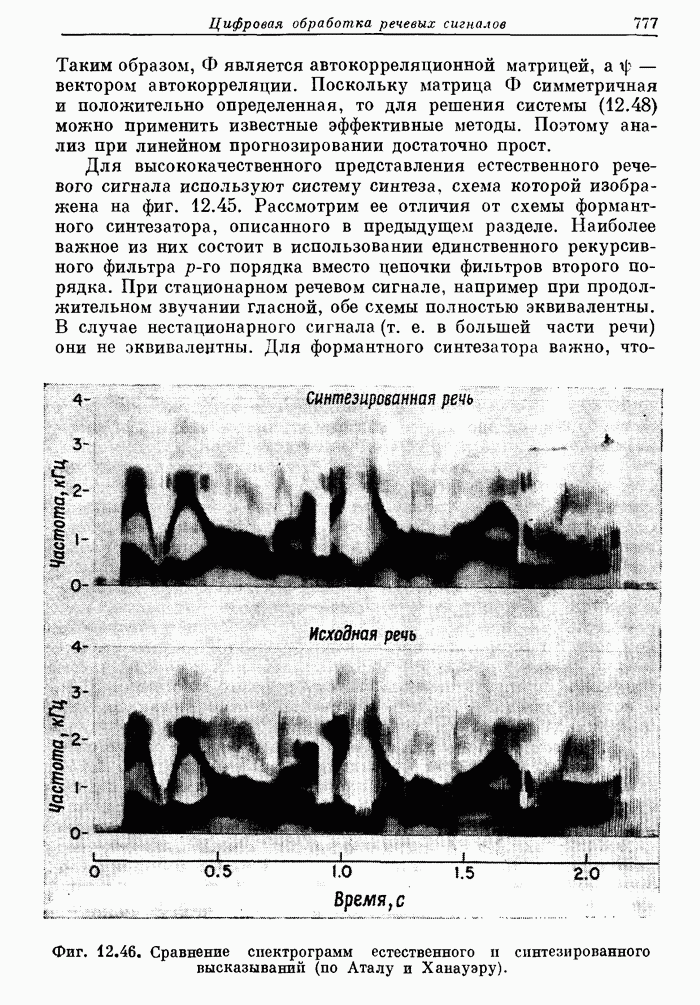
- 12.19. Линейное прогнозирование речи
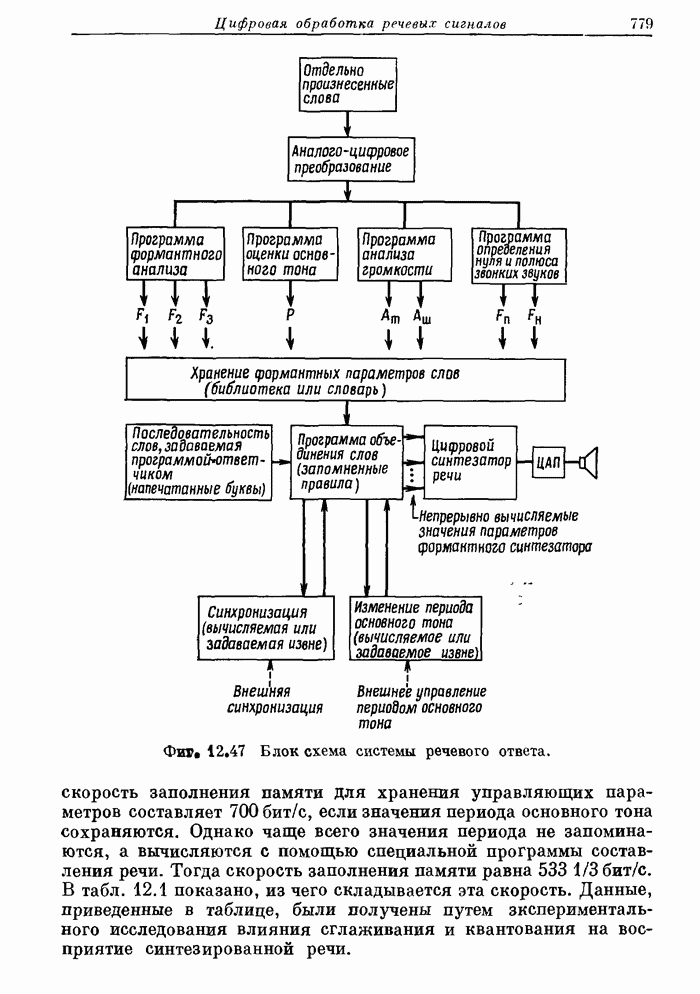
- 12.20. Система речевого ответа для вычислительной машины
- 12.21. Заключение
- 13.1. Вводные замечания о принципах радиолокации и ее применениях
- 13.2. Состав и параметры радиолокационной системы
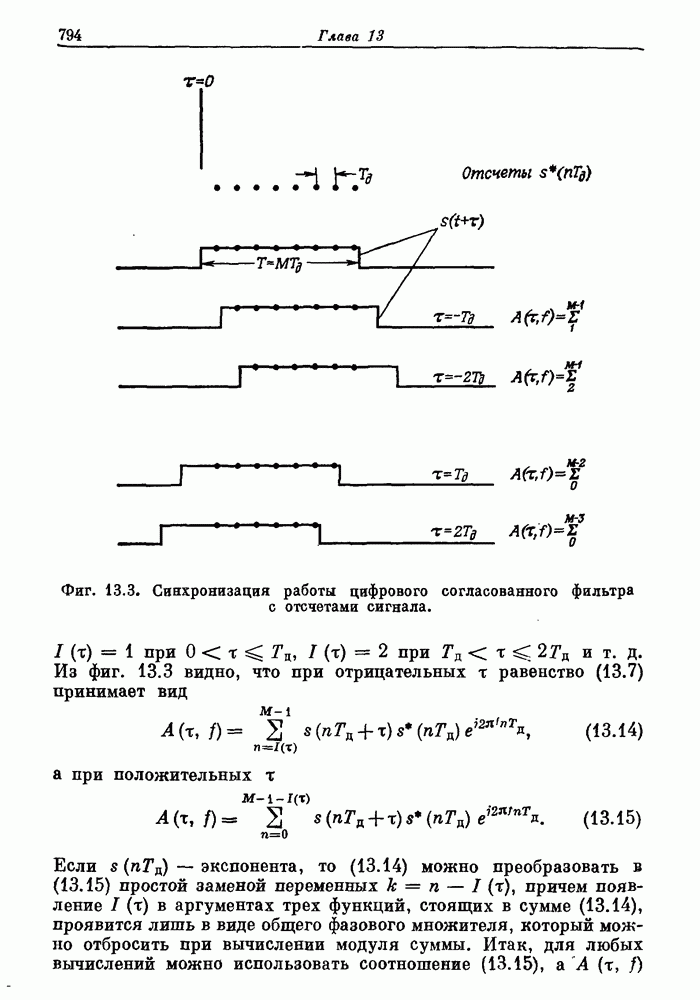
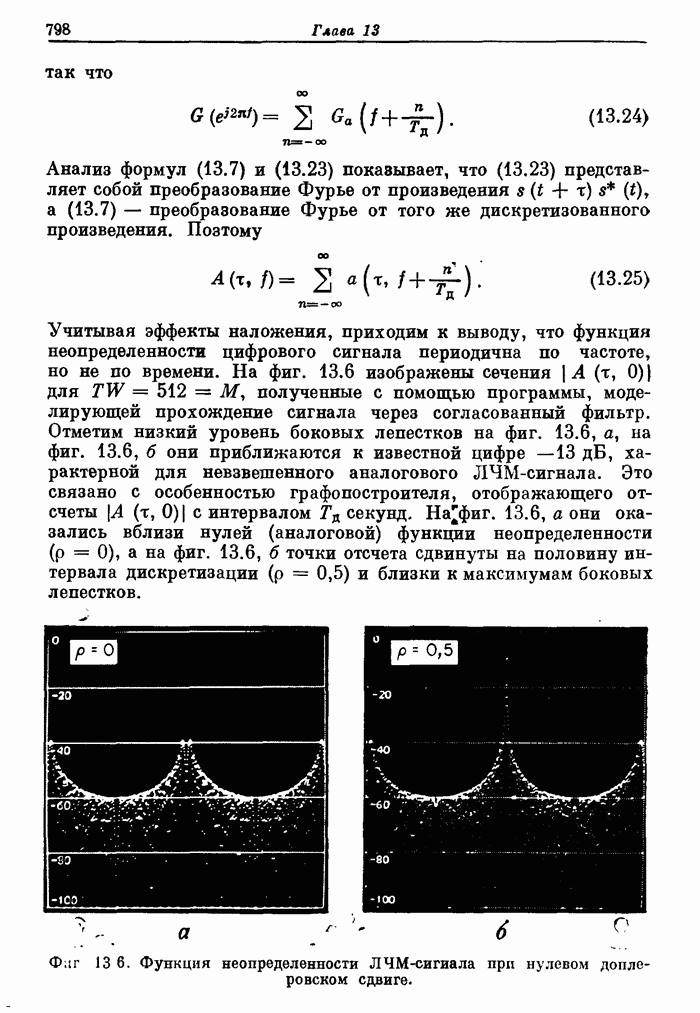
- 13.3. Выбор сигналов и функция неопределенности
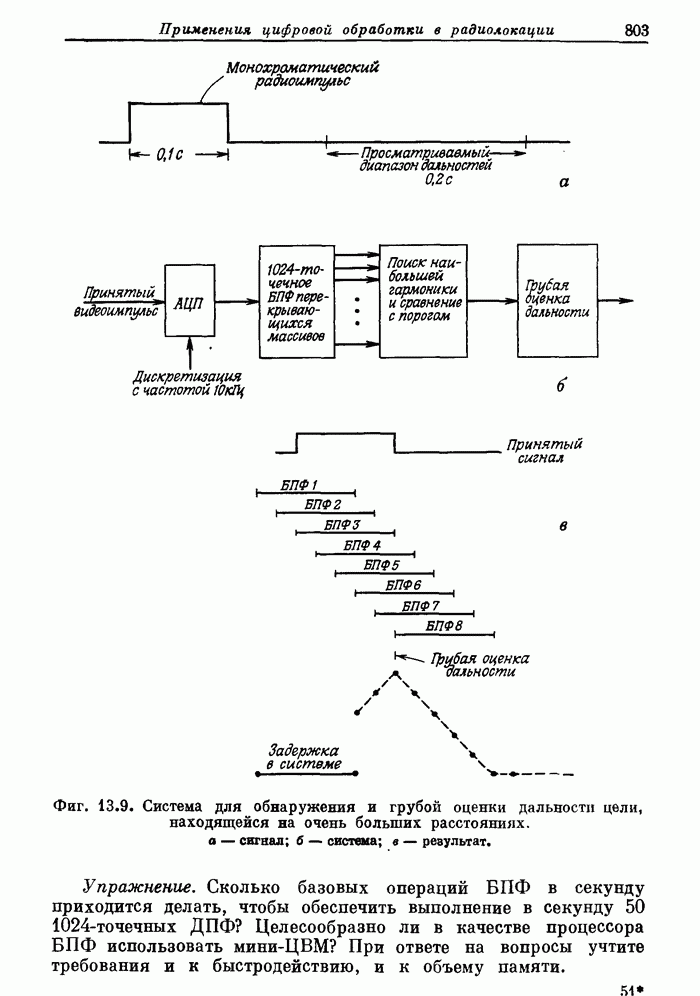
- 13.4. Цифровые согласованные фильтры для радиолокационных сигналов
- 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений
- 13.6. Экспериментальный радиолокатор дальнего действия
- 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора
- 13.8. Заключение