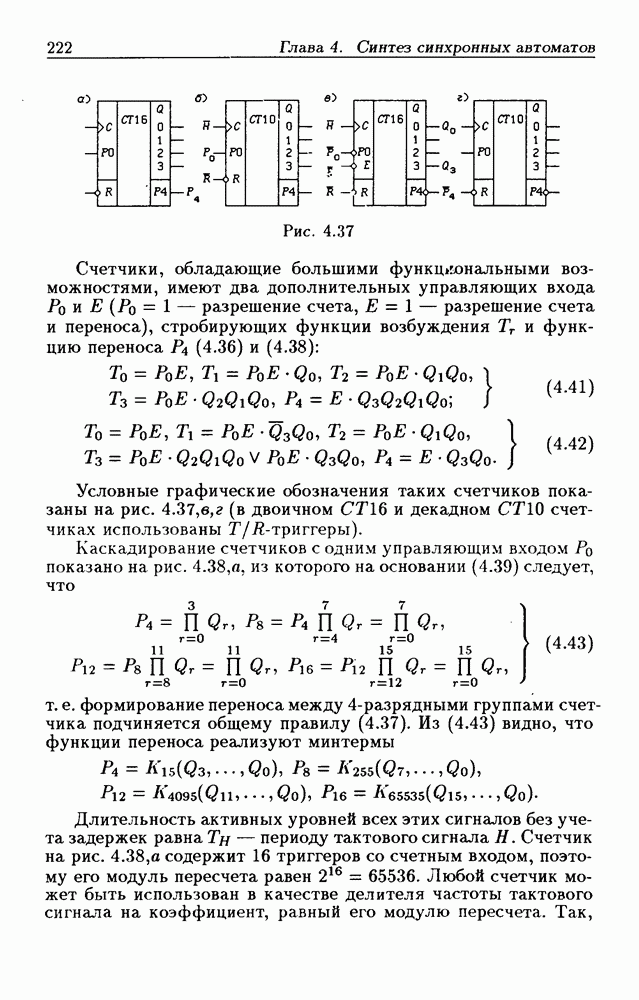| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.15. Линейные функции
В настоящее время наибольшие успехи в развитии теории передачи информации (кодирование сообщений с обнаружением и исправлением ошибок) [13] и теории дискретных сигналов [14, 15] достигнуты благодаря использованию методов абстрактных разделов современной алгебры. Особую роль в технической реализации разработанных методов кодирования и декодирования сообщений, а также генерирования и синтеза сложных сигналов играют линейные автоматы [16], для построения которых достаточно использовать синхронные элементы задержки  -триггеры) и КС, реализующие линейные функции.
-триггеры) и КС, реализующие линейные функции.
Функция  называется линейной [8], если она удовлетворяет принципу суперпозиции
называется линейной [8], если она удовлетворяет принципу суперпозиции

где  константы;
константы;  некоторое поле.
некоторое поле.
Полем  называется множество элементов
называется множество элементов  для которых определены две операции, называемые сложением
для которых определены две операции, называемые сложением  и умножением
и умножением  и выполняются аксиомы:
и выполняются аксиомы:
 - замкнутость;
- замкнутость;
 — ассоциативные законы;
— ассоциативные законы;
 - коммутативные законы;
- коммутативные законы;
 - дистрибутивный закон;
- дистрибутивный закон;
 существование единичных элементов относительно операций сложения и умножения (для операции сложения единичный элемент называется нулем, а для операции умножения — единицей);
существование единичных элементов относительно операций сложения и умножения (для операции сложения единичный элемент называется нулем, а для операции умножения — единицей);
каждый элемент а поля  обладает противоположным элементом
обладает противоположным элементом  относительно операции сложения и обратным элементом
относительно операции сложения и обратным элементом  относительно операции умножения (за исключением нулевого элемента):
относительно операции умножения (за исключением нулевого элемента):

На основании этих аксиом можно доказать, что каждый элемент поля имеет единственный противоположный и единственный обратный элементы, а также, что 
Наиболее известными примерами полей являются множество рациональных и множество действительных чисел, для которых операция  означает арифметическое сложение чисел, а операция
означает арифметическое сложение чисел, а операция  арифметическое умножение. Однако операции
арифметическое умножение. Однако операции  могут иметь и совершенно иной смысл, так как для определения поля имеет значение только выполнение всех вышеперечисленных аксиом.
могут иметь и совершенно иной смысл, так как для определения поля имеет значение только выполнение всех вышеперечисленных аксиом.
В теории цифровых автоматов могут быть использованы только конечные поля, т. е. поля, множество элементов которых конечно. Широкое применение в теории и практике проектирования цифровых устройств находят поля Галуа  в которых в качестве бинарных операций
в которых в качестве бинарных операций  используются операции сложения и умножения целых чисел по модулю
используются операции сложения и умножения целых чисел по модулю  где
где  простое число [13, 16]. Такие поля содержат
простое число [13, 16]. Такие поля содержат  элементов:
элементов:  Напомним, что число X по модулю
Напомним, что число X по модулю  равно остатку от деления данного числа на
равно остатку от деления данного числа на 
Правила сложения и умножения по модулю  определяются табл. 1.7, из которой видно, что операция
определяются табл. 1.7, из которой видно, что операция  совпадает с логической операцией сумма по модулю два
совпадает с логической операцией сумма по модулю два  а операция
а операция  с логической операцией конъюнкция
с логической операцией конъюнкция  Это и является основой для использования алгебраических методов при проектировании линейных цифровых автоматов, КС которых описываются линейными функциями
Это и является основой для использования алгебраических методов при проектировании линейных цифровых автоматов, КС которых описываются линейными функциями

где  или
или  Данные функции удовлетворяют
Данные функции удовлетворяют
Таблица 1.7. (см. скан) Сложение и умножение по модулю 2
Таблица 1.8. (см. скан) Сложение и умножение по модулю 3
Таблица 1.9. (см. скан) Сложение и умножение по модулю 5
определению линейных функций (1.90), если положить 
Правила сложения и умножения по модулю  приведены в табл. 1.8 и 1.9. По этим таблицам легко убедиться, что все аксиомы, входящие в определение поля, удовлетворяются.
приведены в табл. 1.8 и 1.9. По этим таблицам легко убедиться, что все аксиомы, входящие в определение поля, удовлетворяются.
Согласно определению (1.90), линейными функциями являются функции

где  и переменные
и переменные  принимают значения из поля
принимают значения из поля 
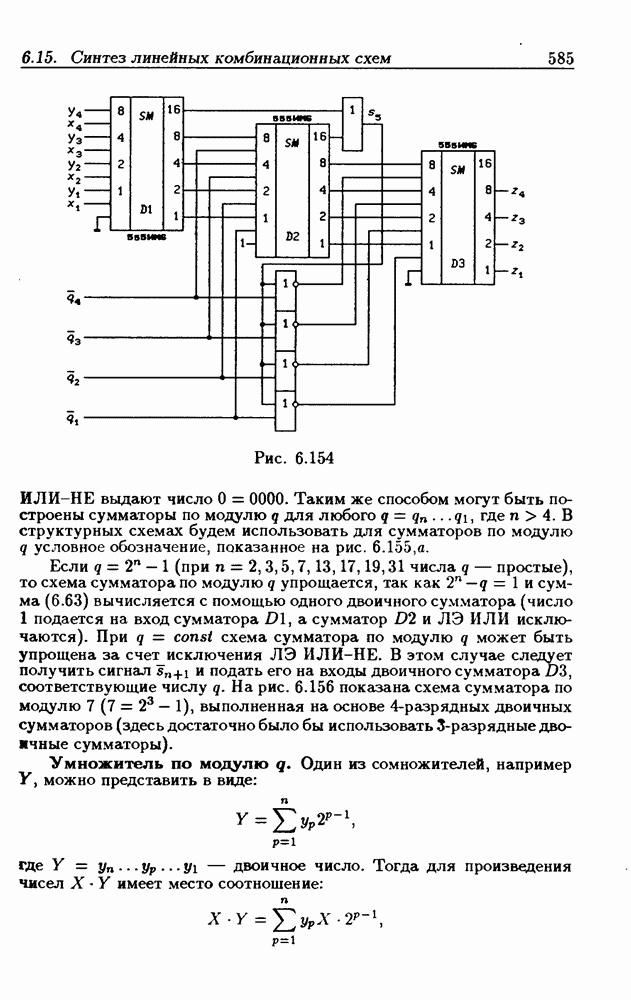
Комбинационные схемы, выполняющие операции сложения и умножения по модулю  называются линейными. При значении
называются линейными. При значении  проблема синтеза линейных КС отсутствует, так как ЛЭ И и сумма по модулю два выпускаются в виде И С. При значениях
проблема синтеза линейных КС отсутствует, так как ЛЭ И и сумма по модулю два выпускаются в виде И С. При значениях  необходимо синтезировать типовые линейные КС, выполняющие операции сложения
необходимо синтезировать типовые линейные КС, выполняющие операции сложения  -ичных чисел и умножения их на константы
-ичных чисел и умножения их на константы  по модулю
по модулю  Данная задача решена в § 6.15.
Данная задача решена в § 6.15.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
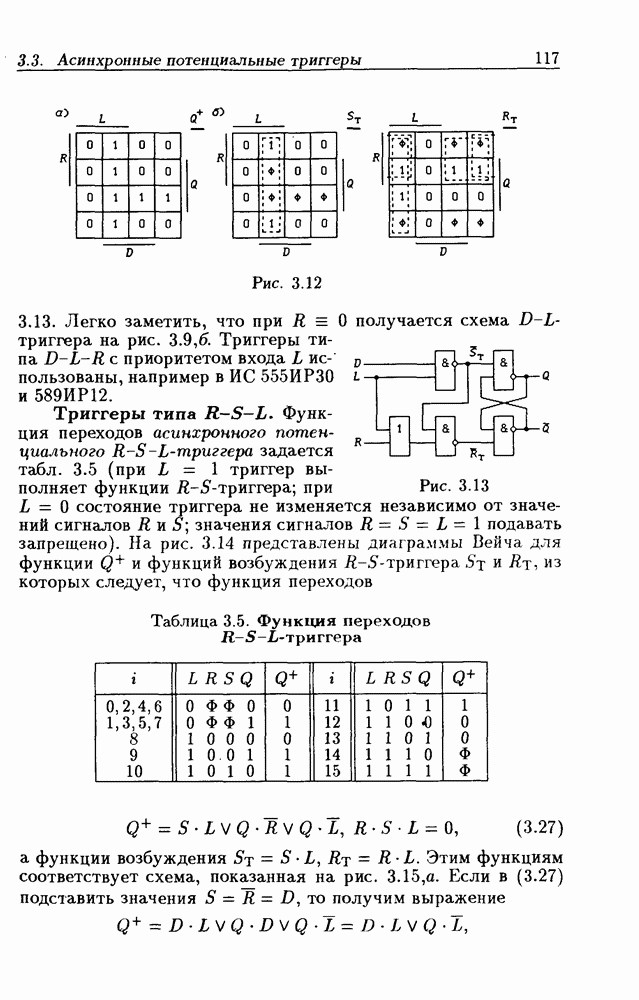
- Триггеры типа R-S-L.
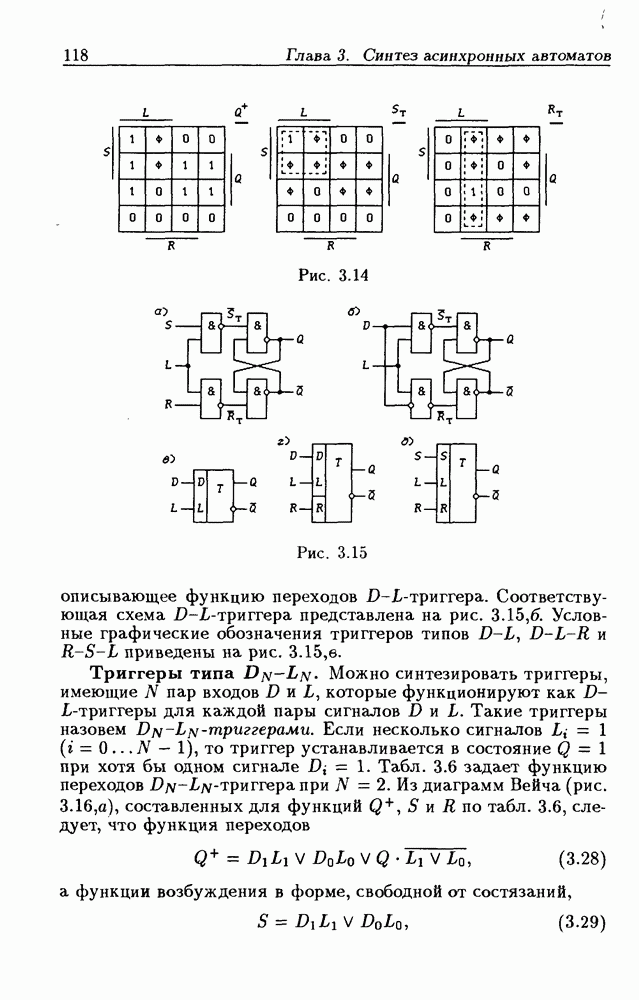
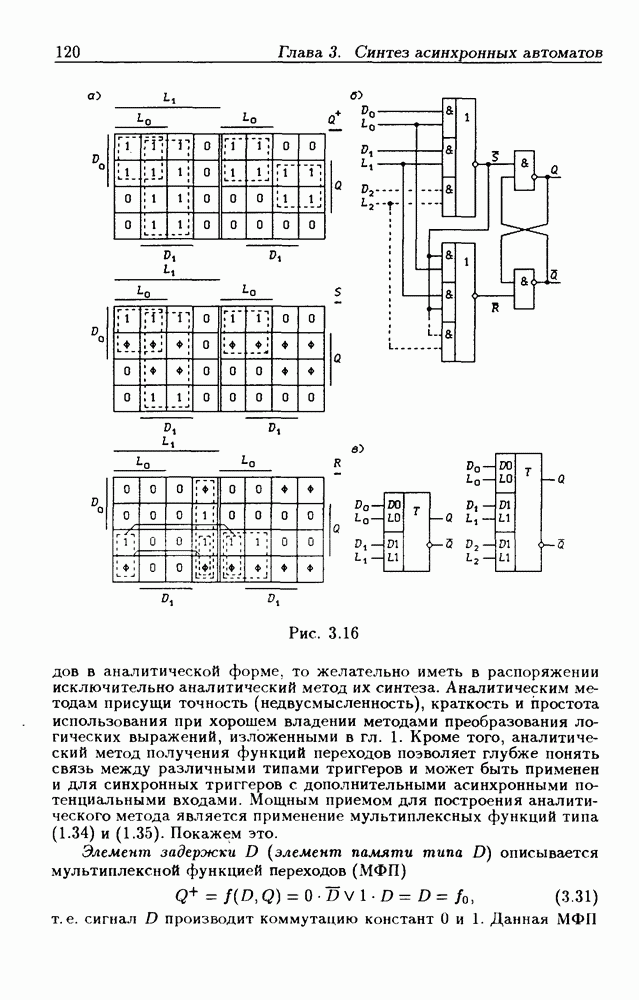
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
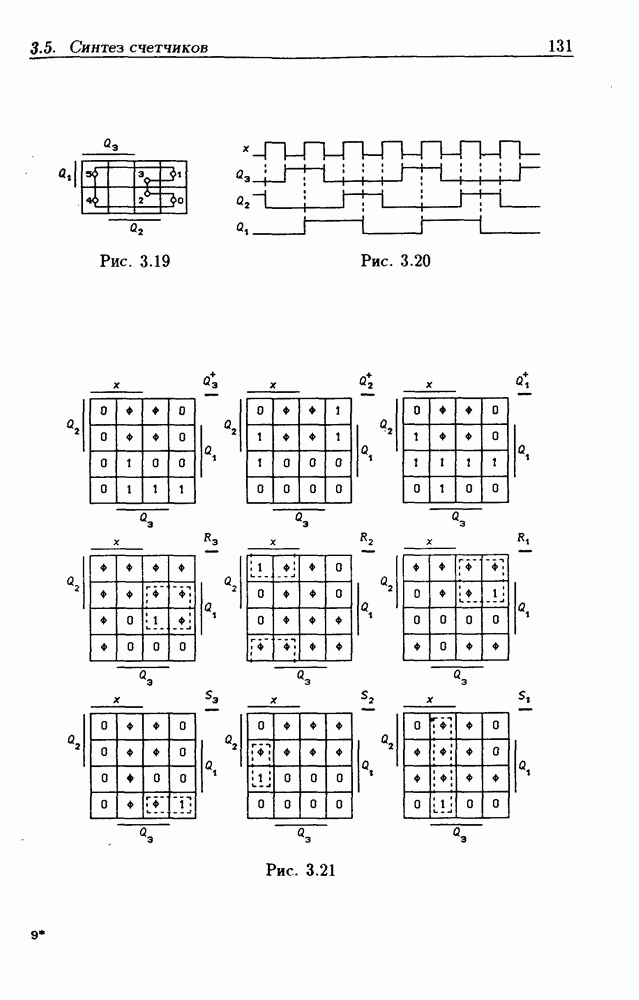
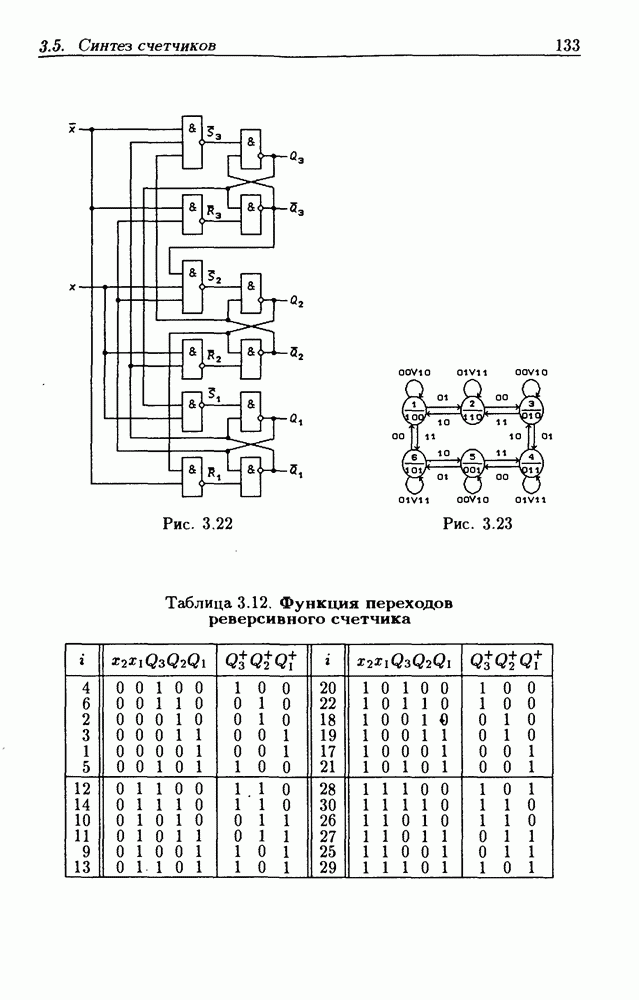
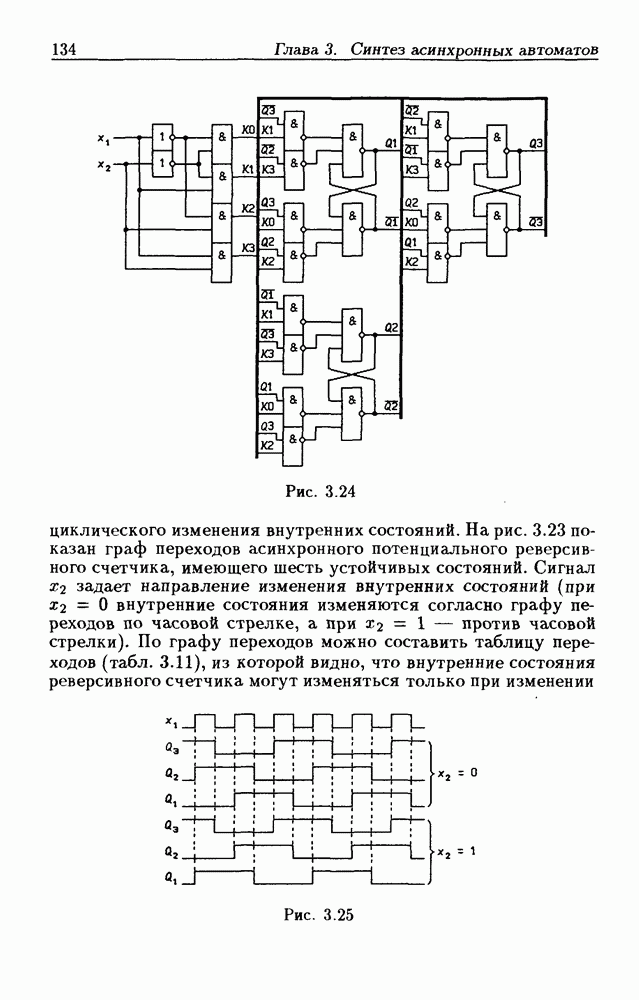
- 3.5. Синтез асинхронных потенциальных счетчиков
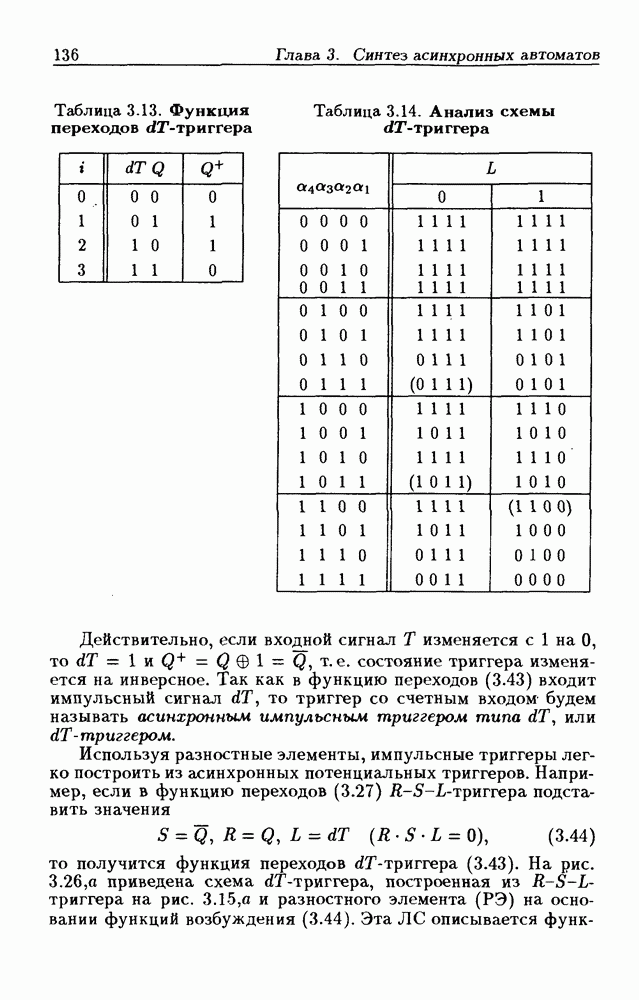
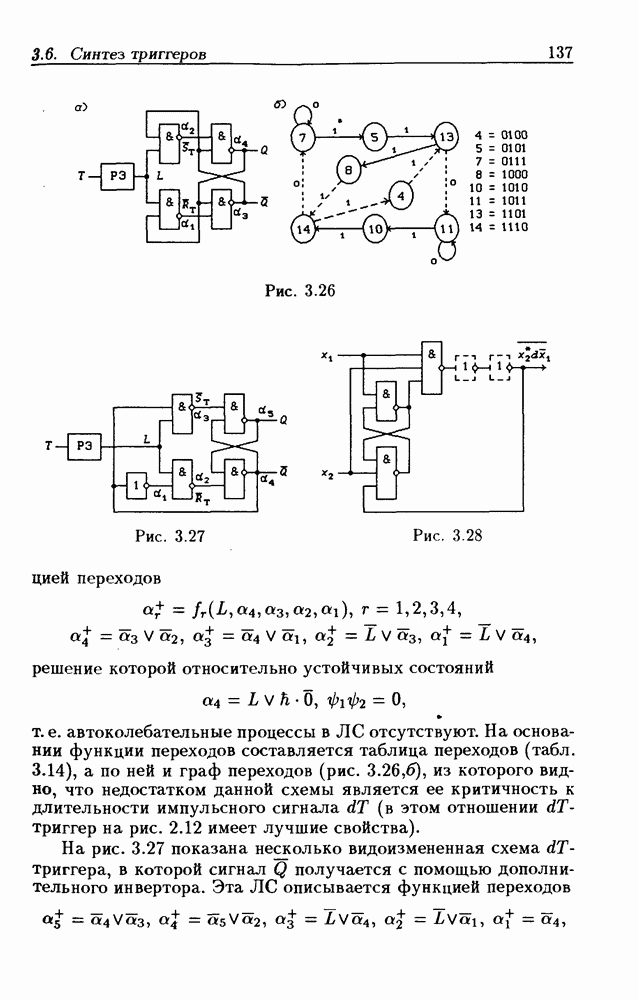
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
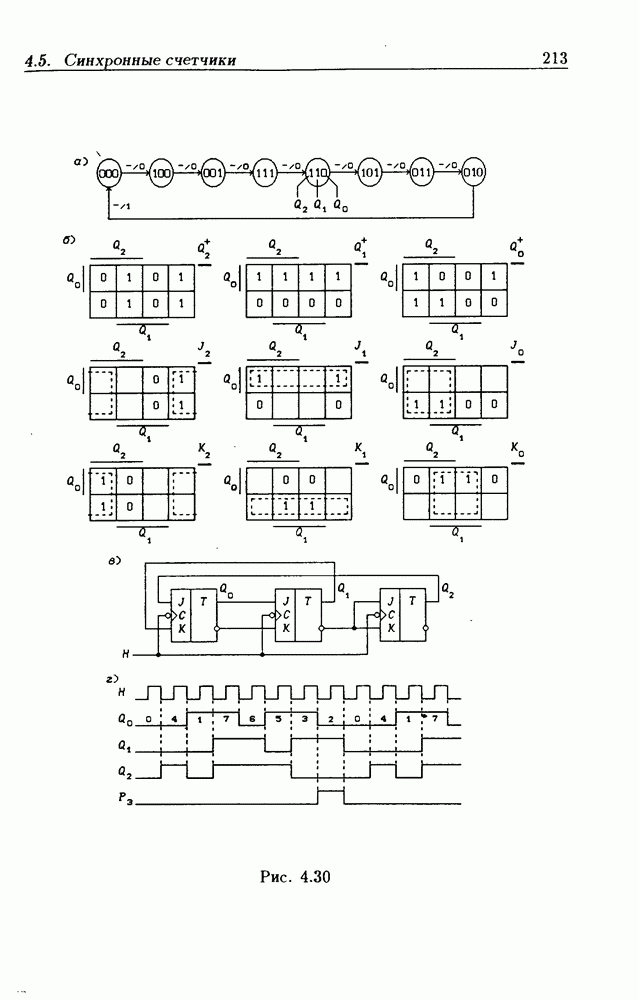
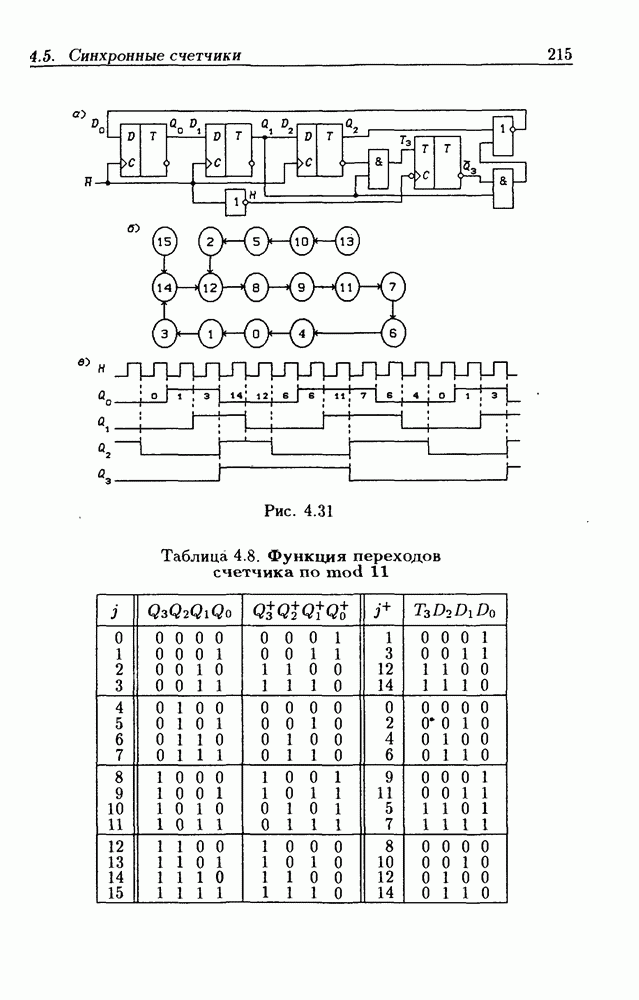
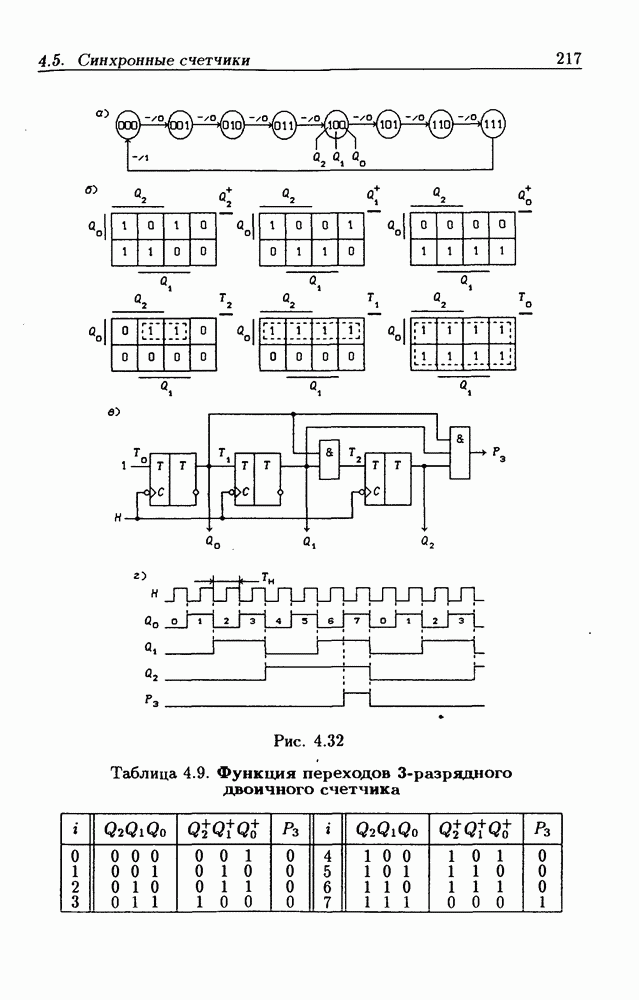
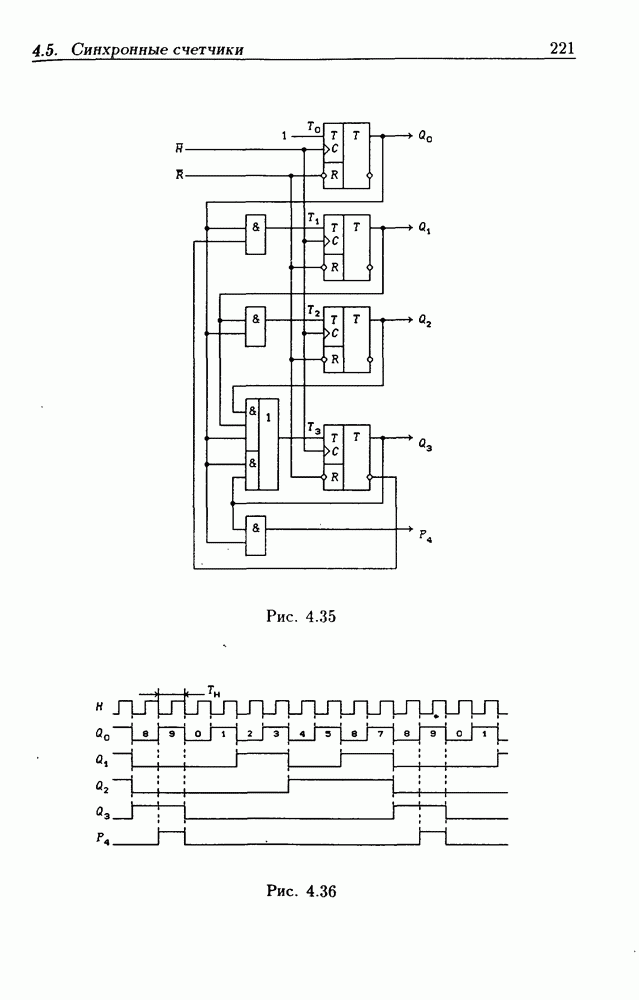
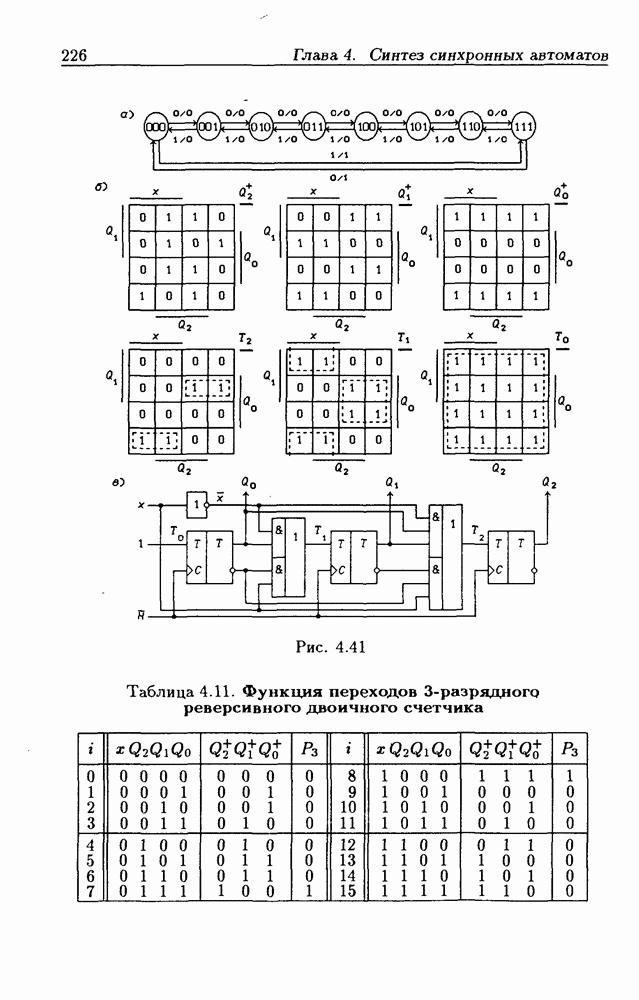
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
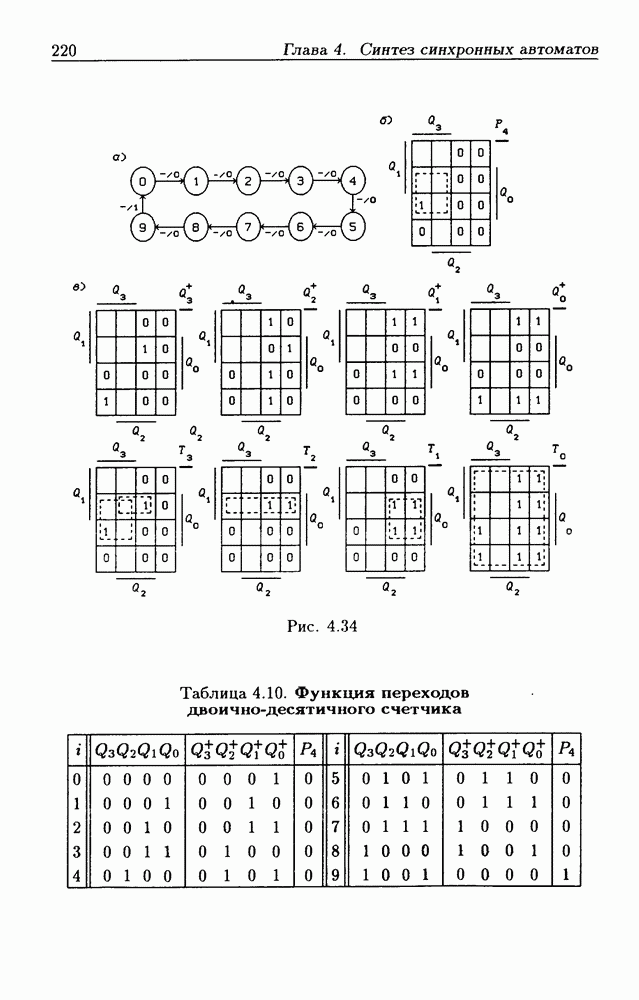
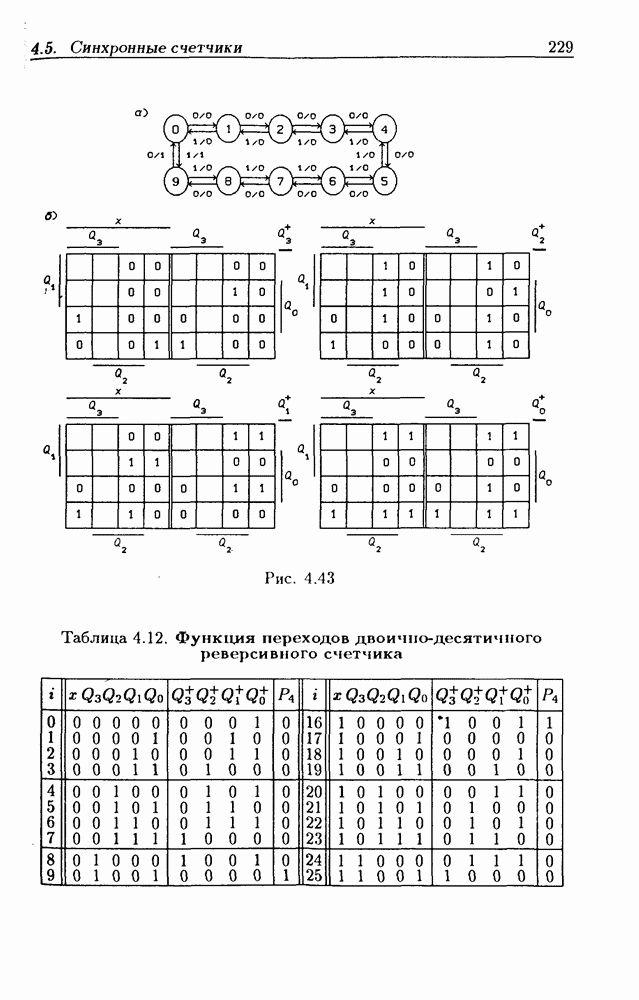
- Синхронные двоично-десятичные счетчики.
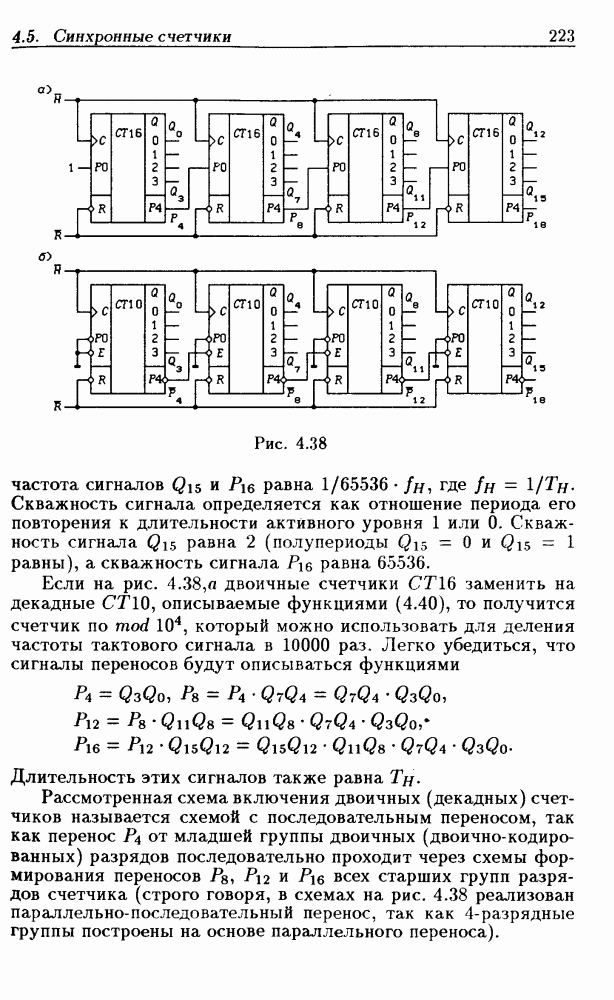
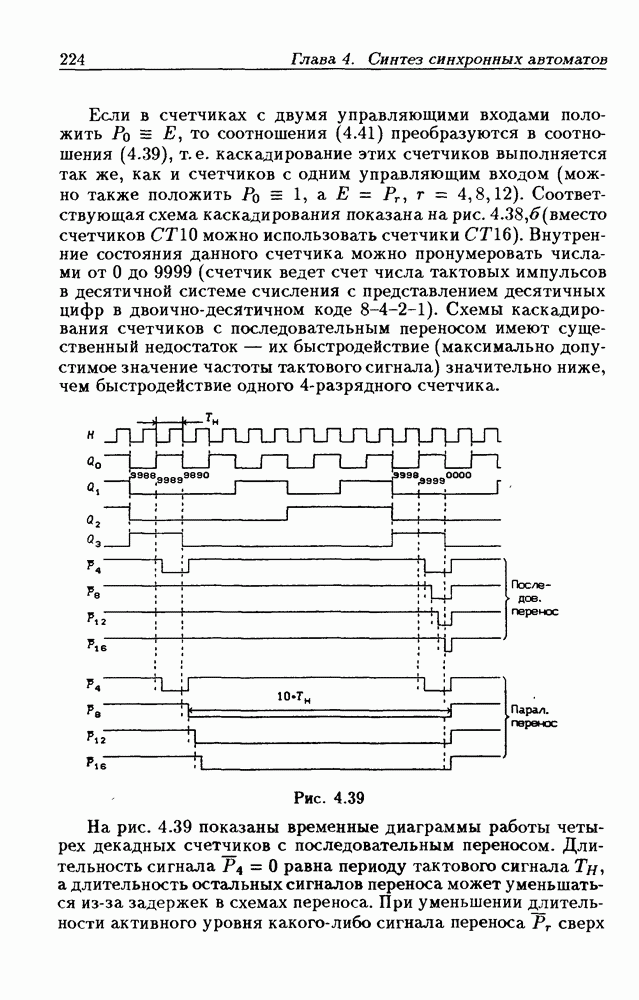
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
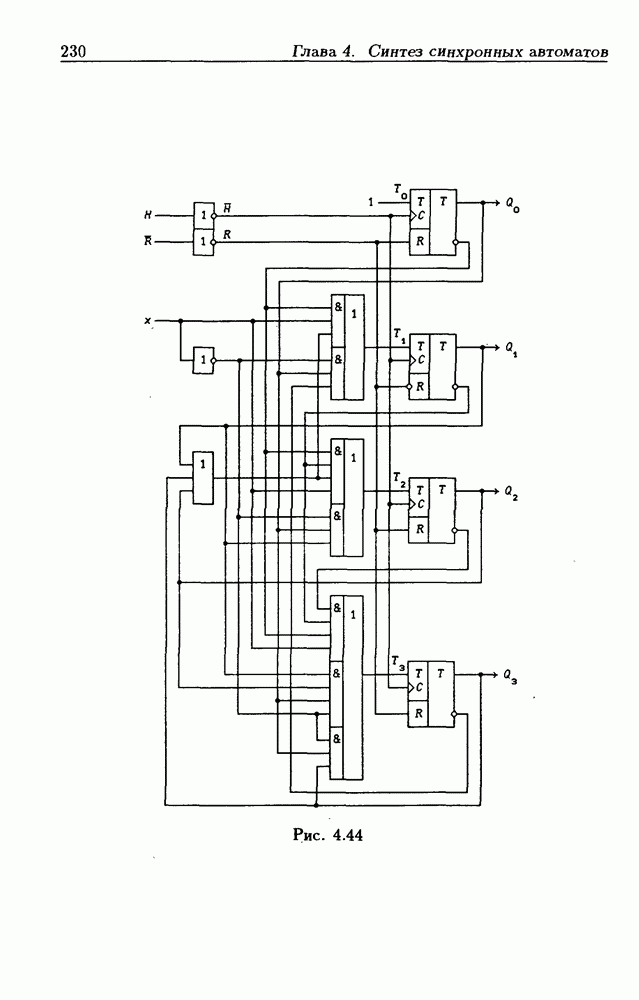
- Реверсивные двоично-десятичные счетчики.
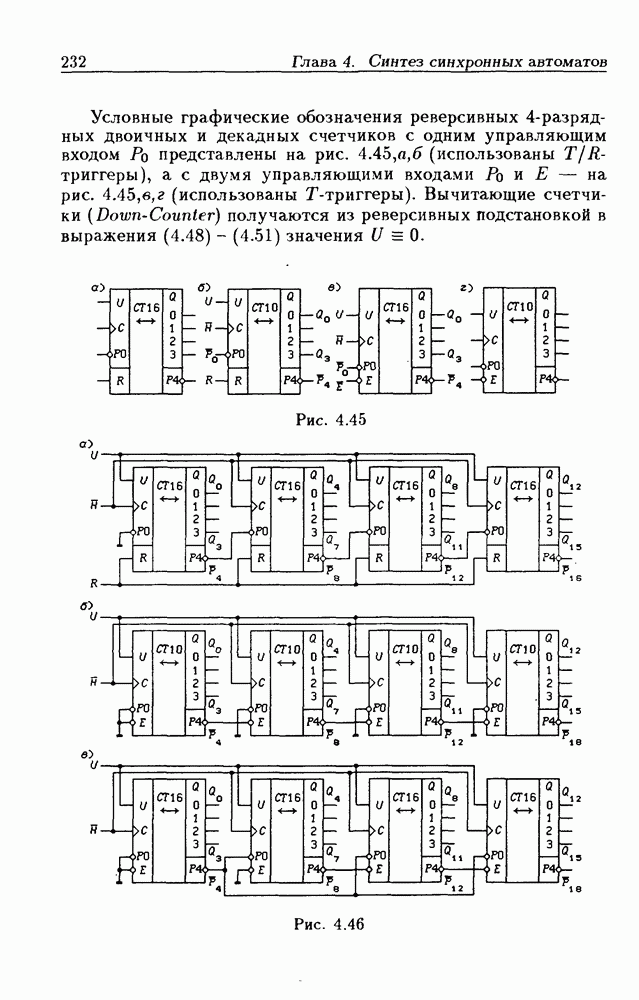
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
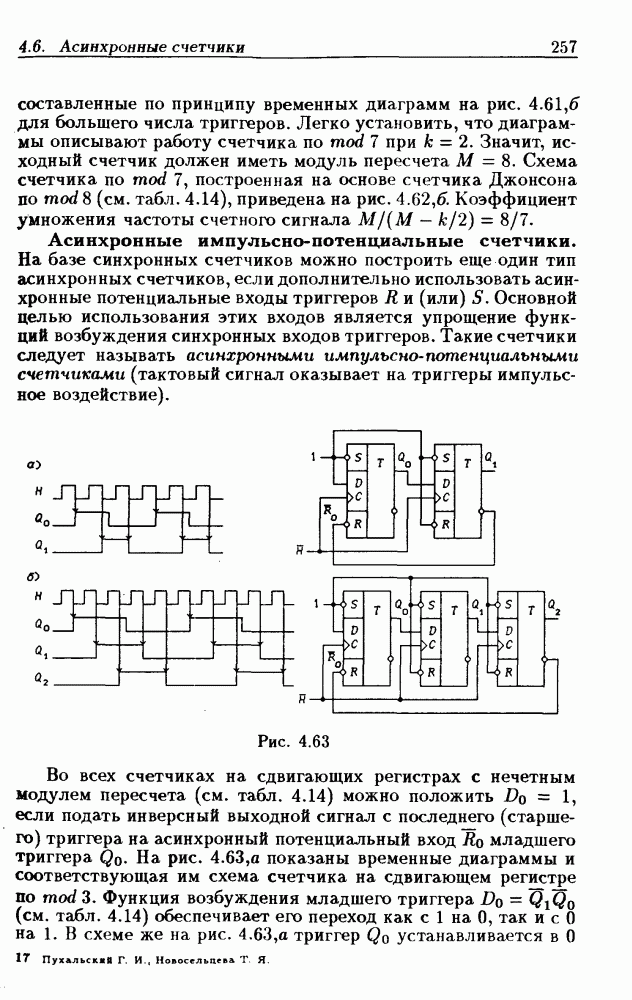
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
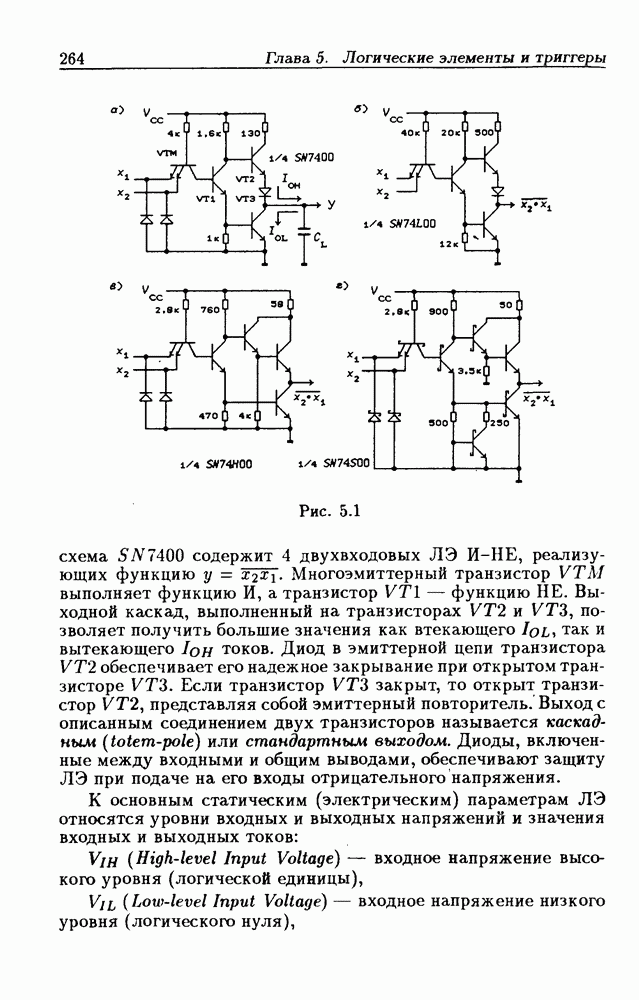
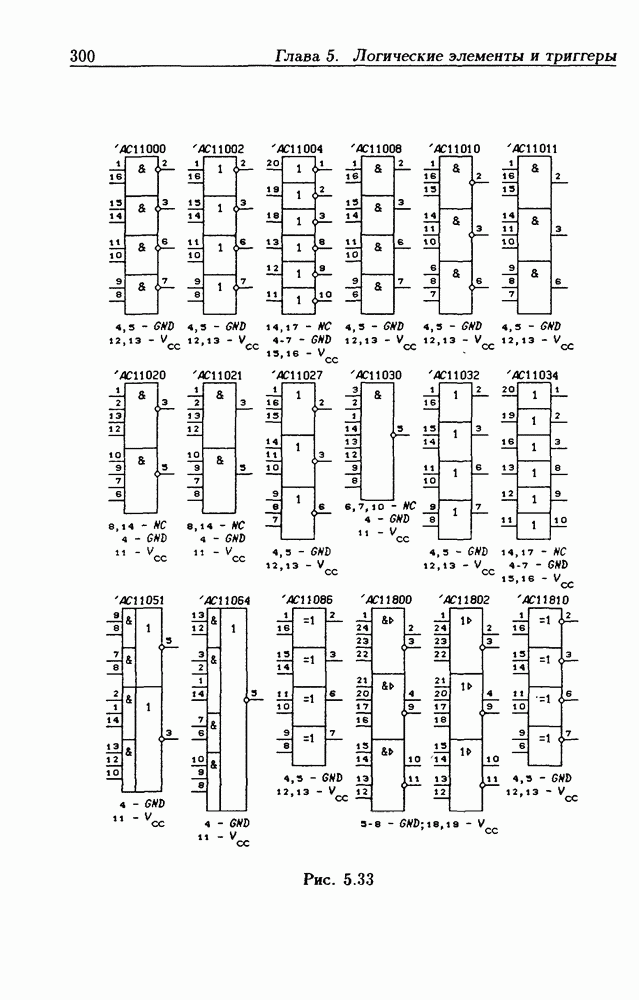
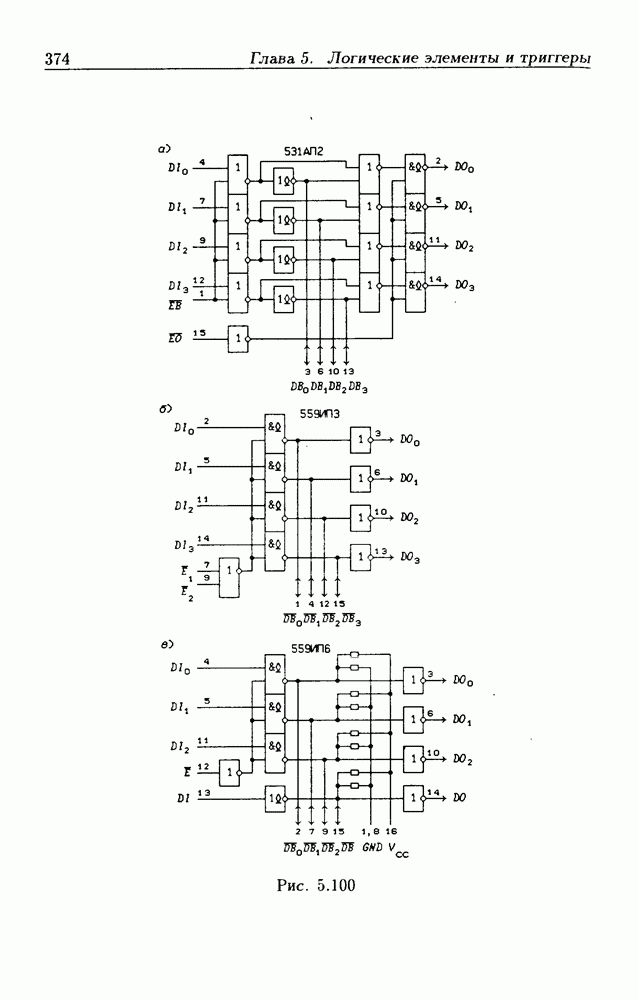
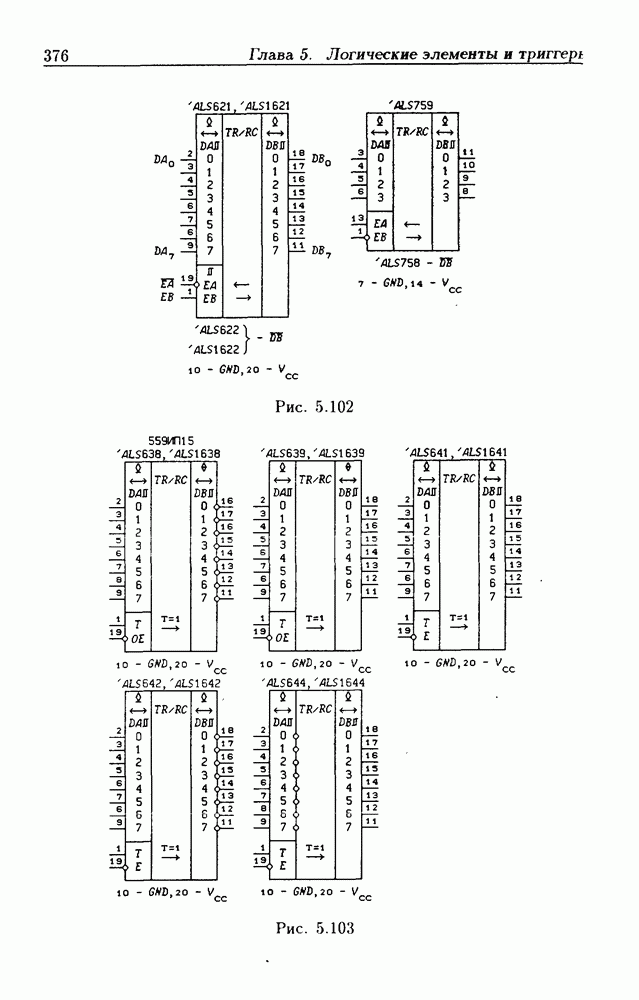
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
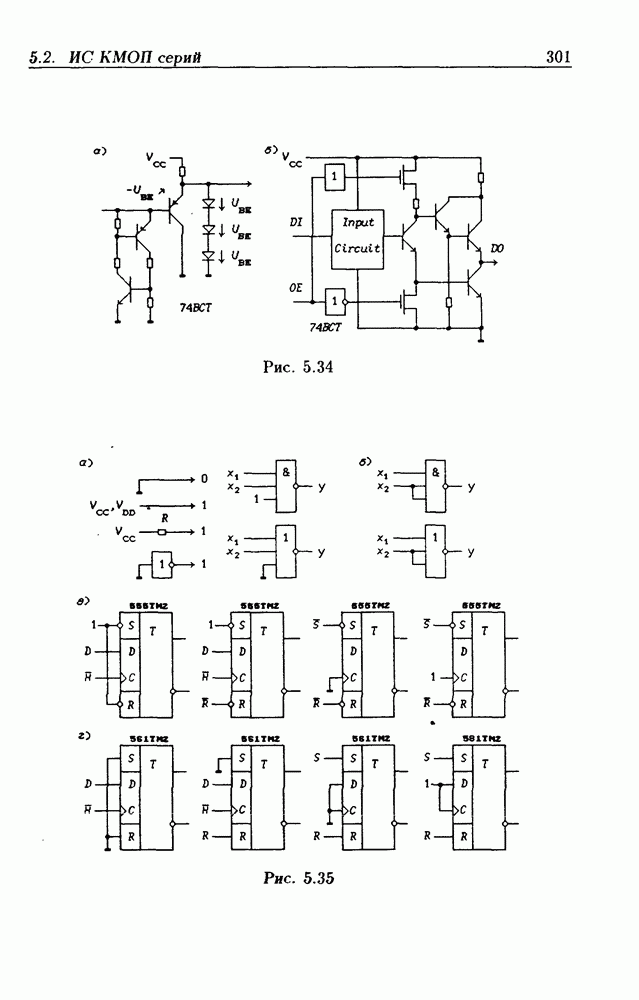
- 5.2. Интегральные схемы КМОП серий
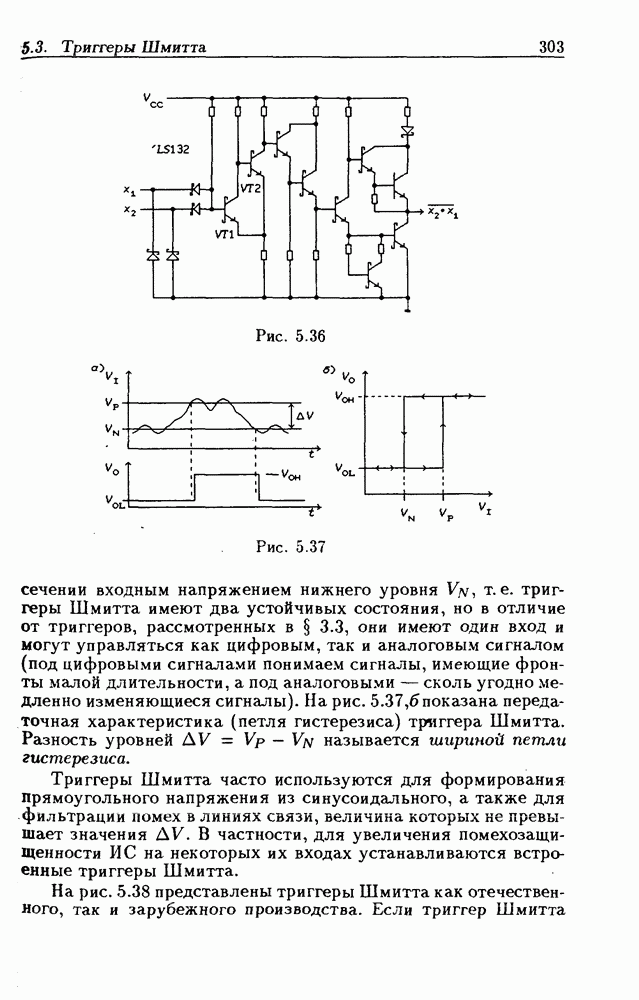
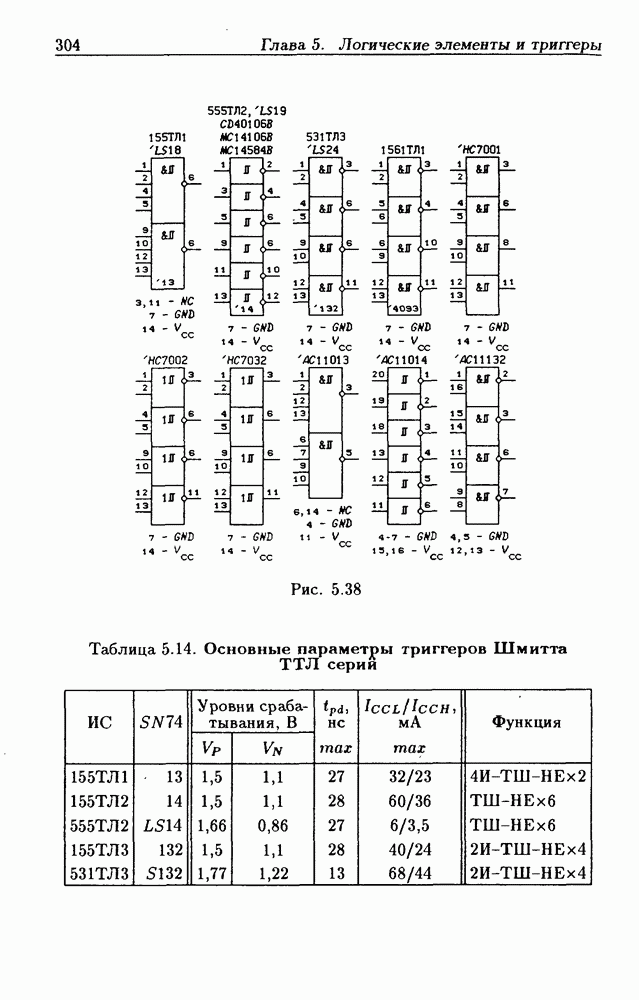
- 5.3. Триггеры Шмитта
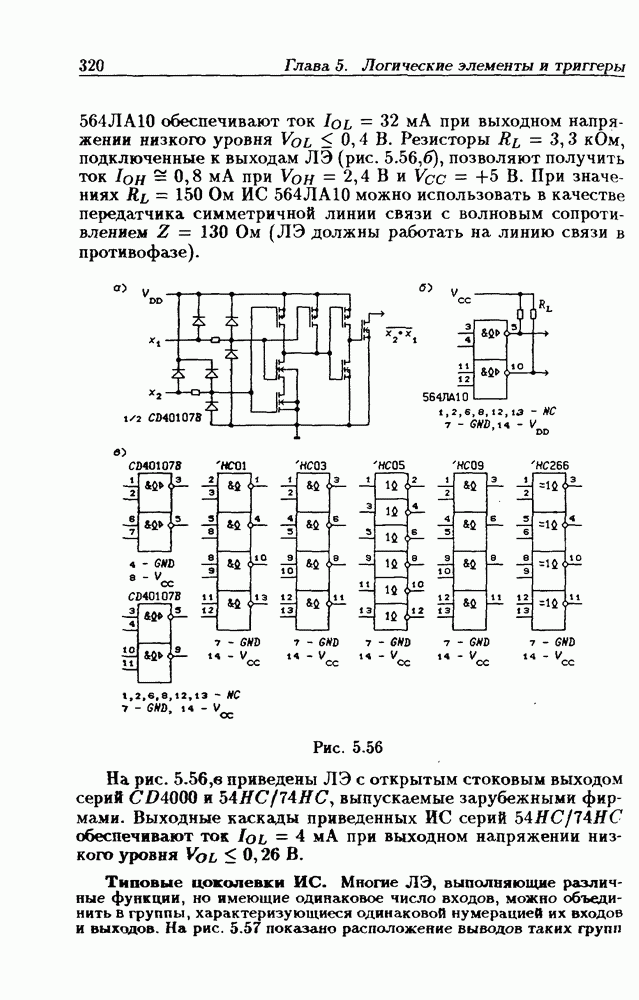
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
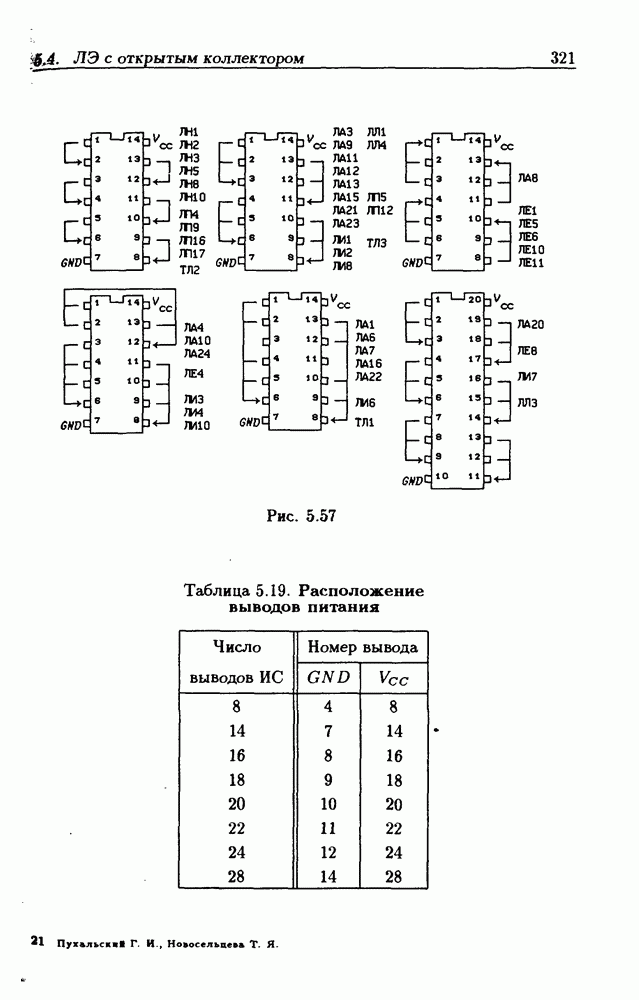
- Типовые цоколевки ИС.
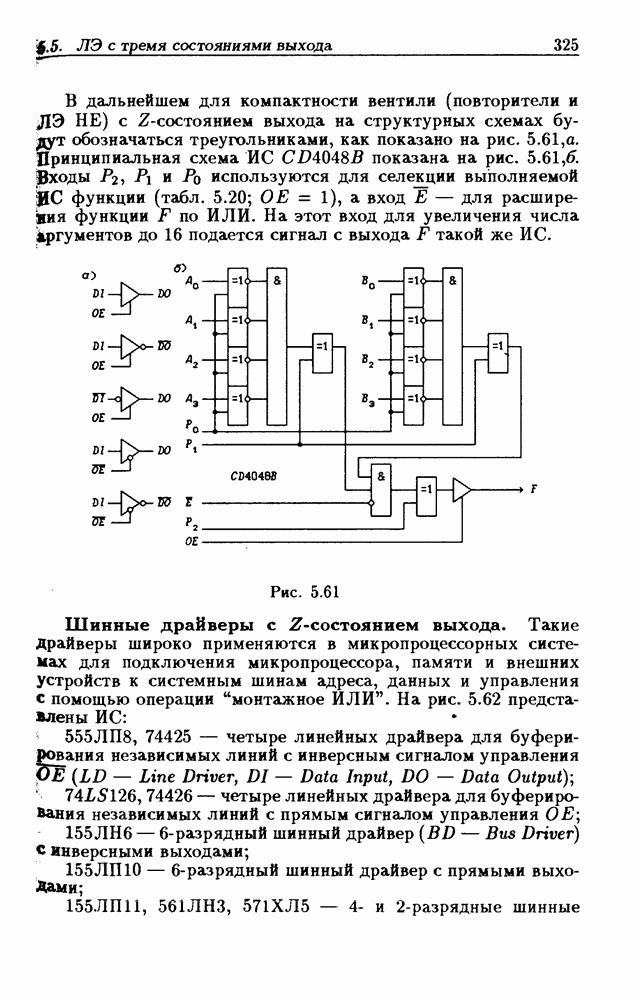
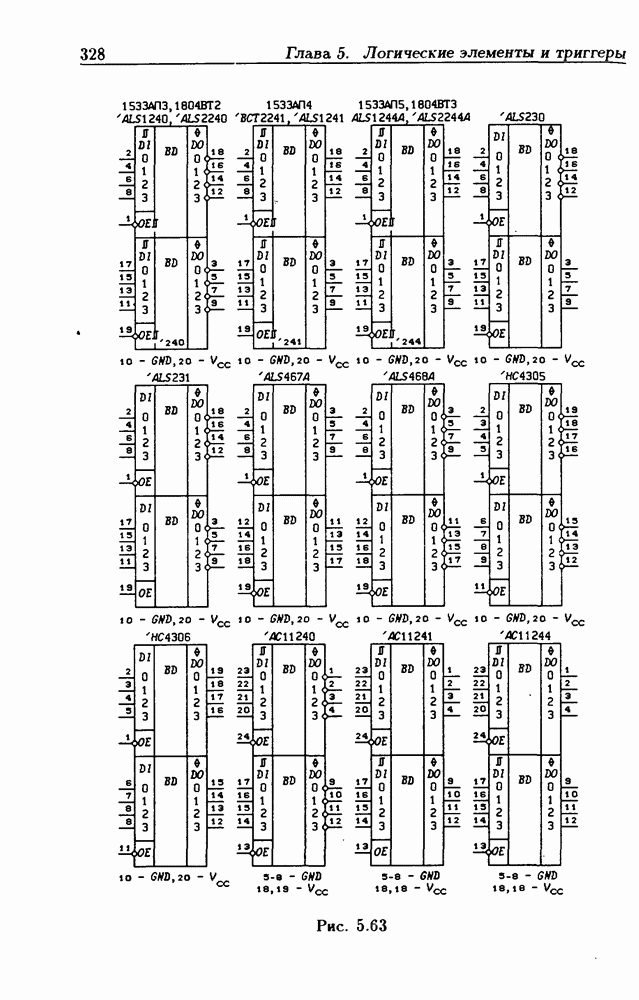
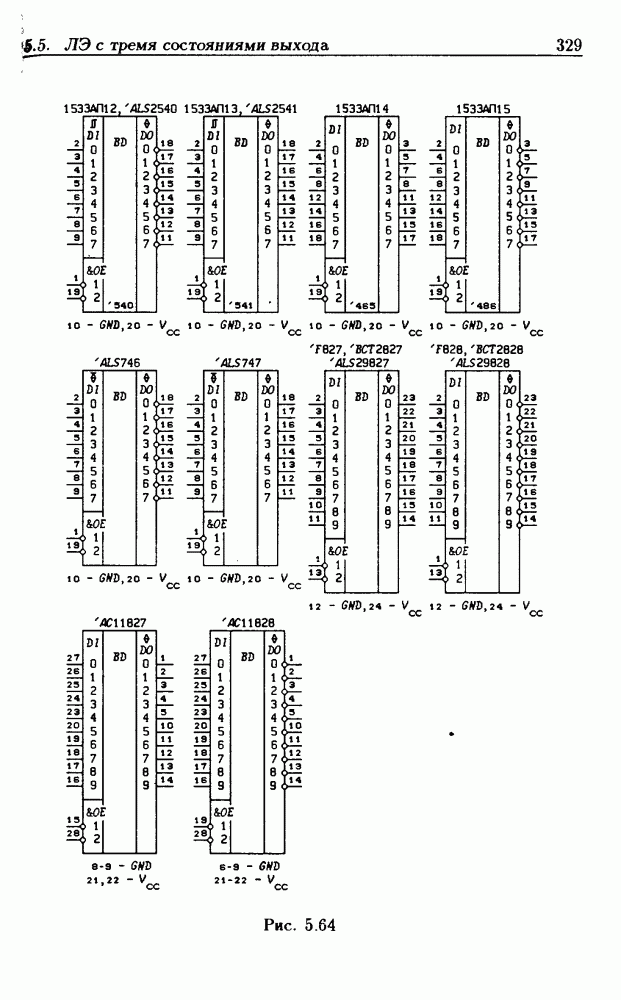
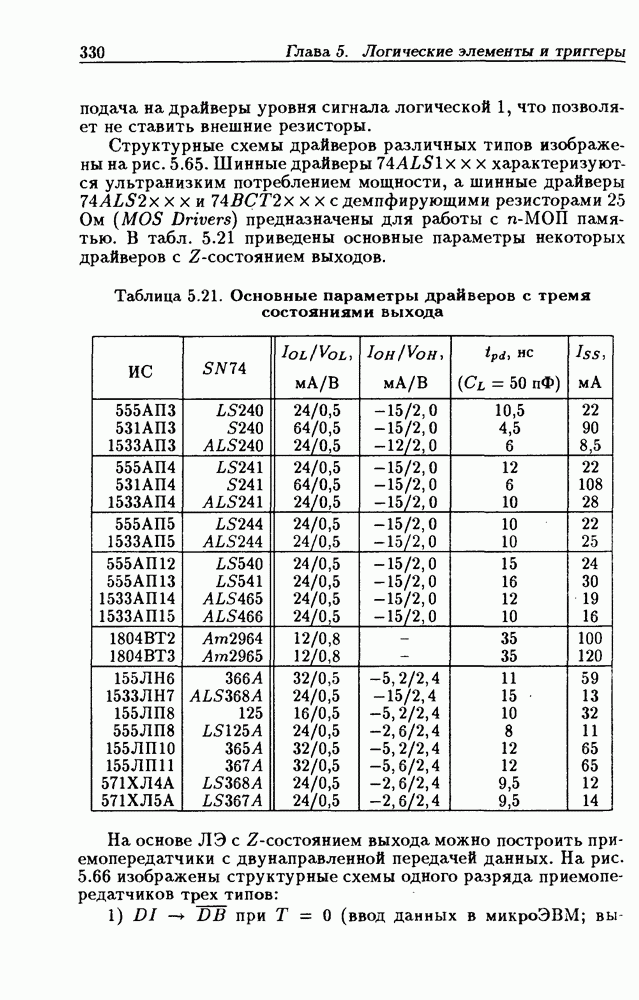
- 5.5. Логические элементы с тремя состояниями выхода
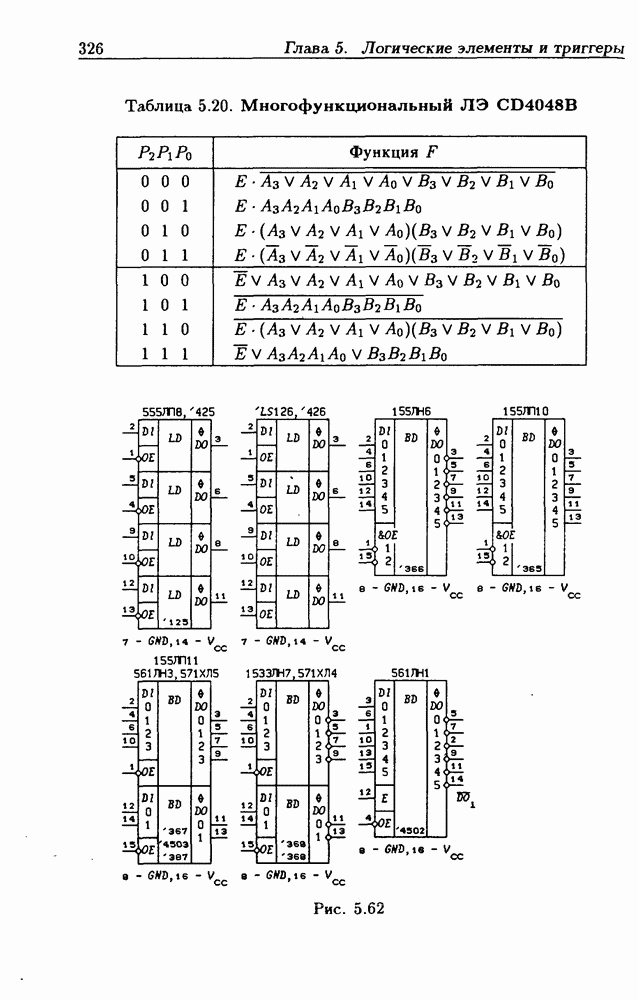
- Шинные драйверы с Z-состоянием выхода.
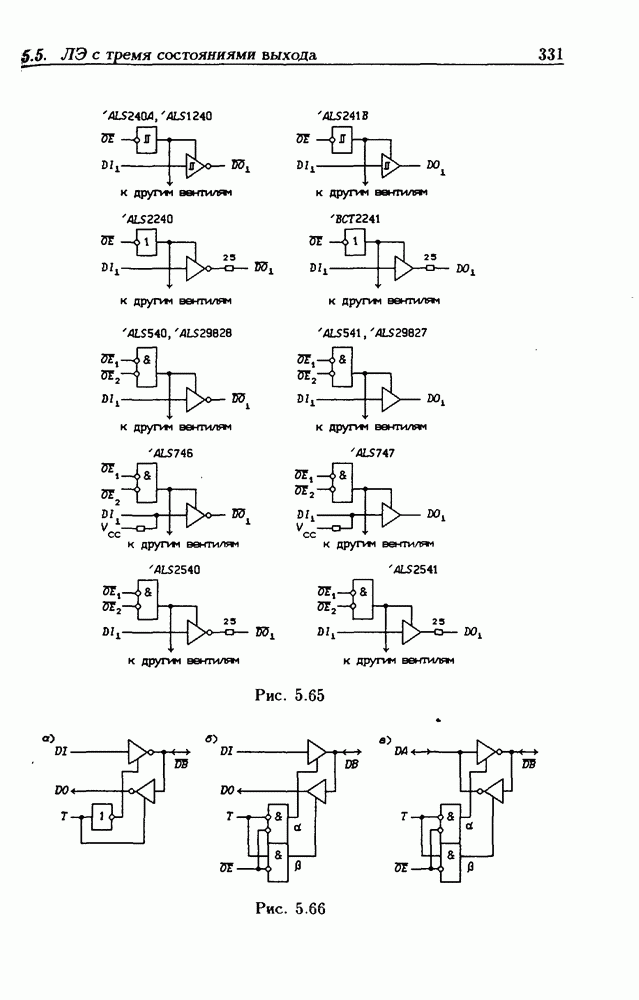
- Основные правила графического изображения ИС.
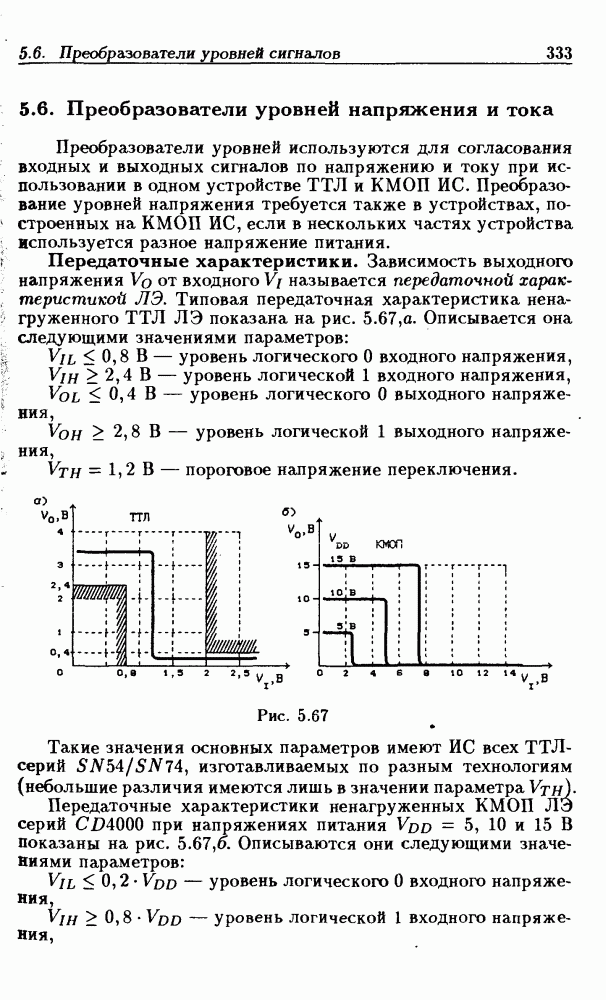
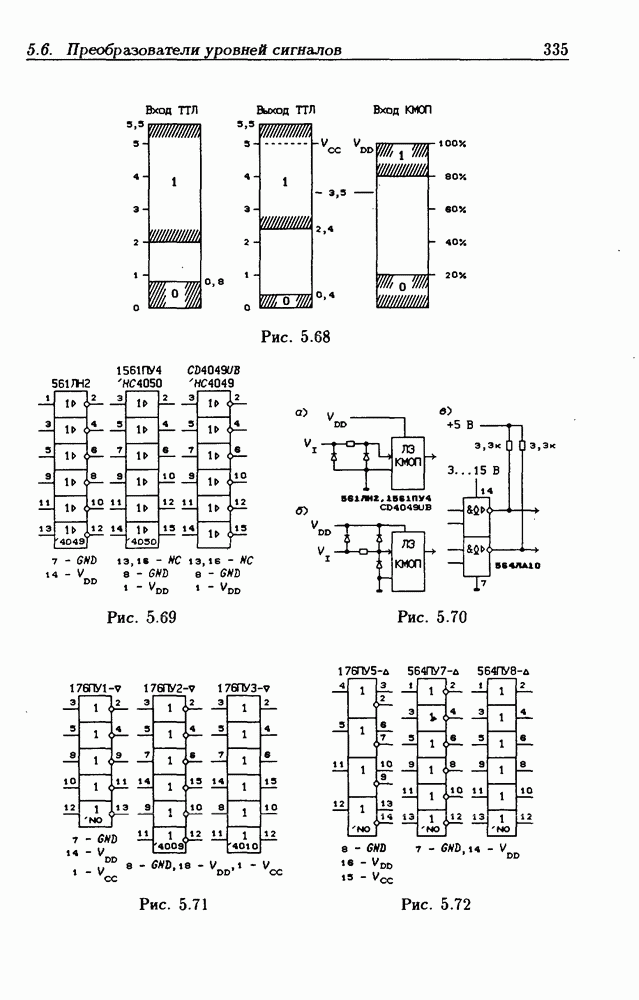
- 5.6. Преобразователи уровней напряжения и тока
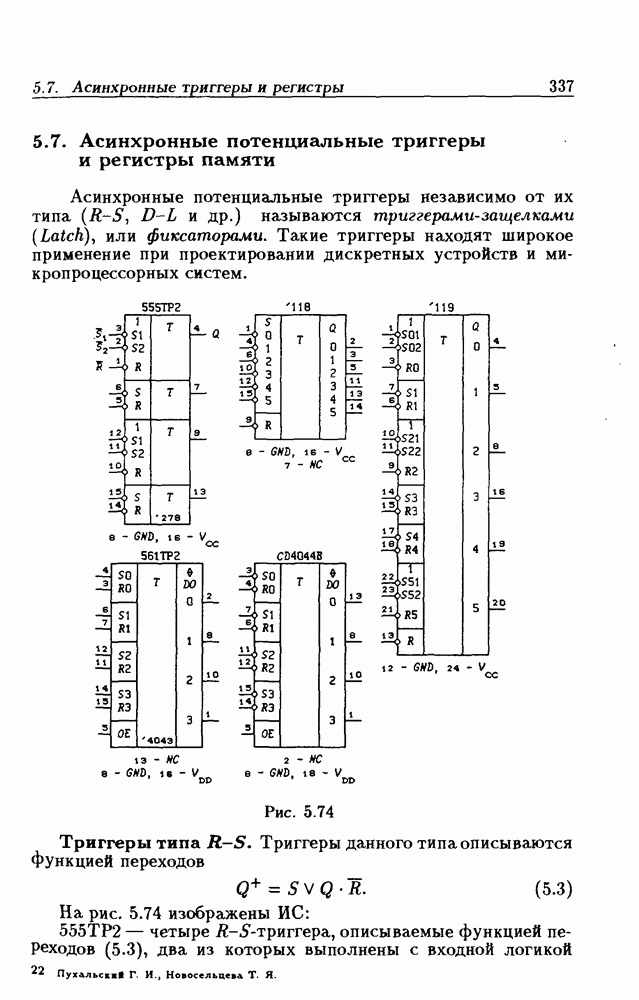
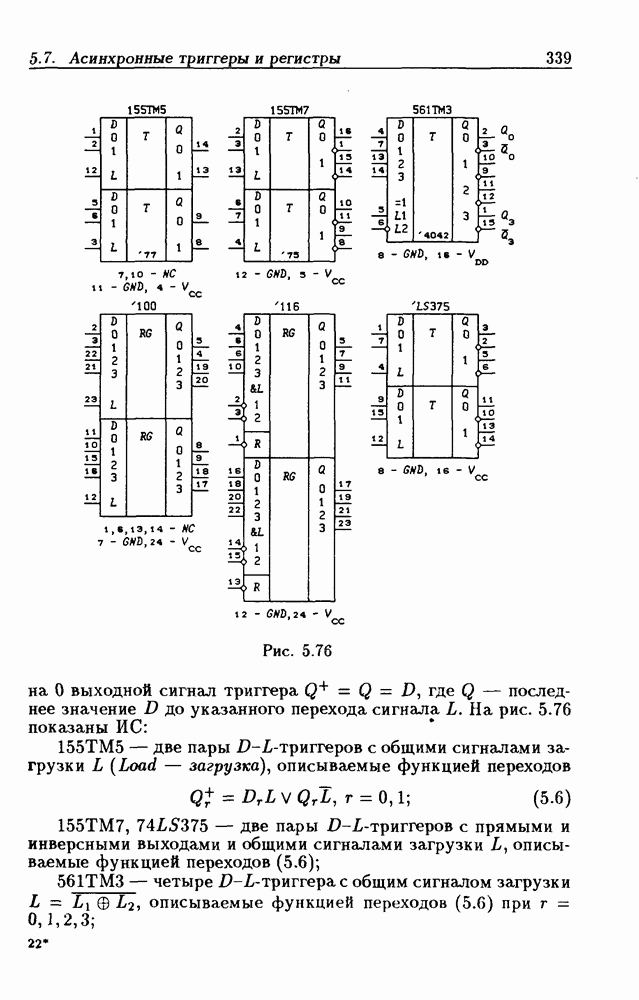
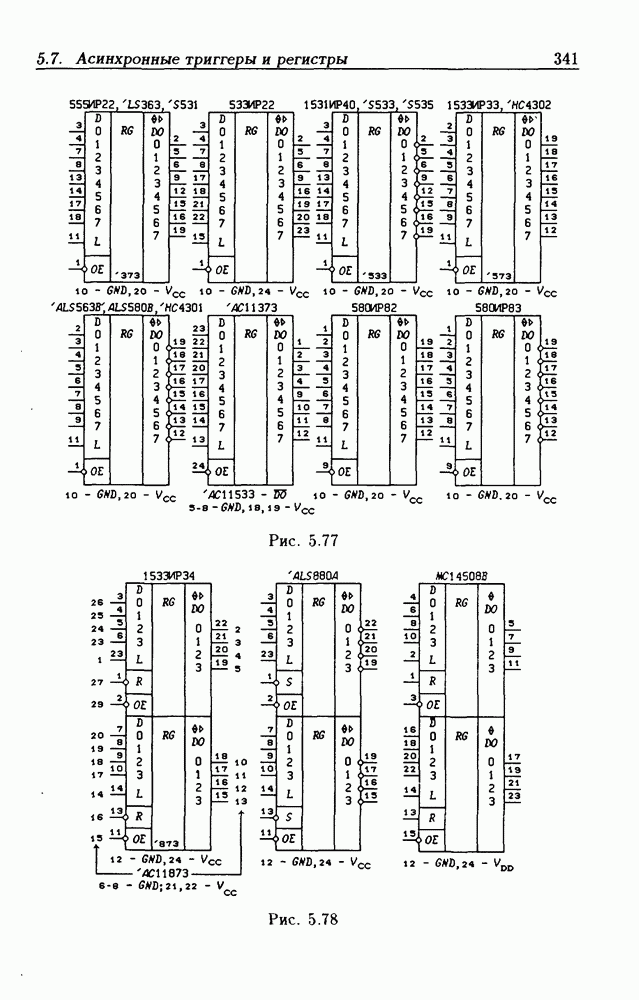
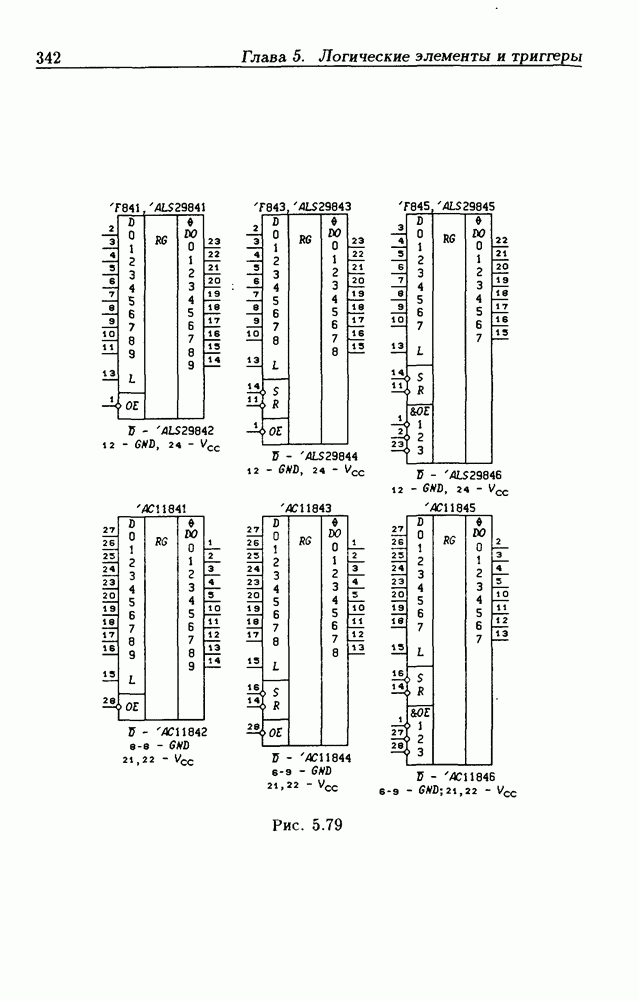
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
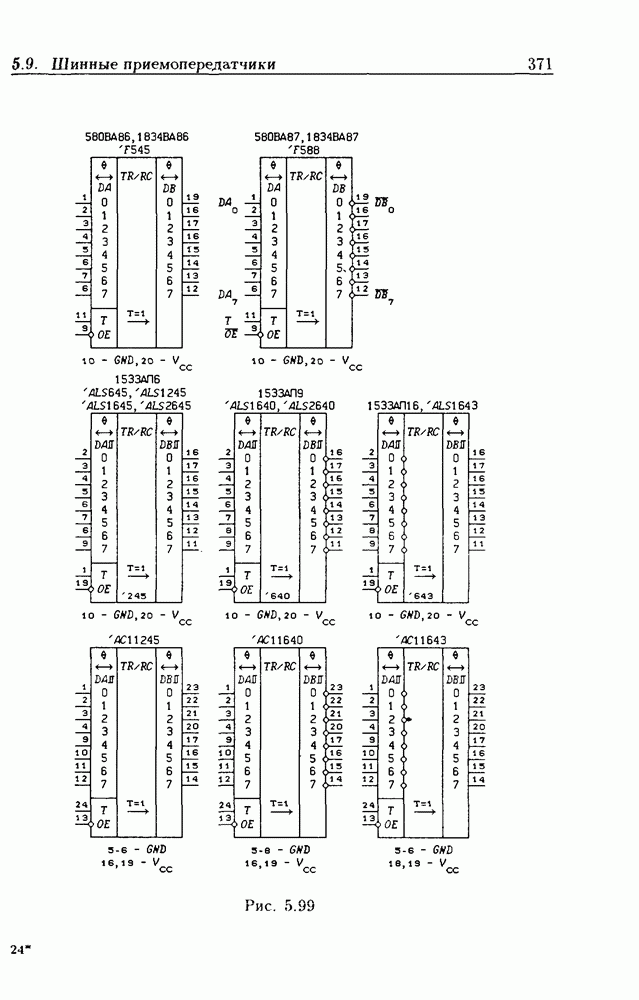
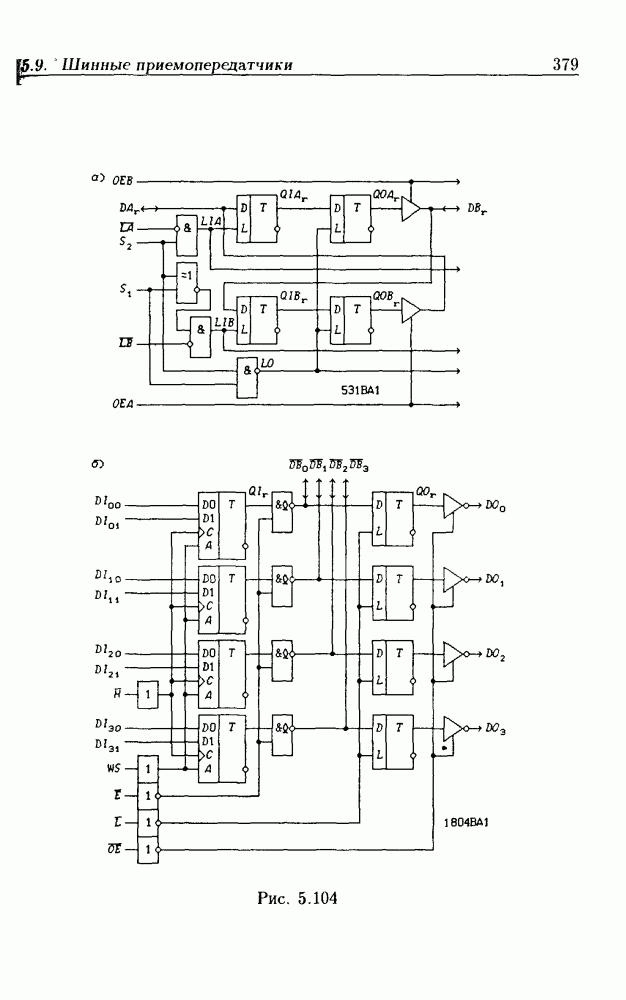
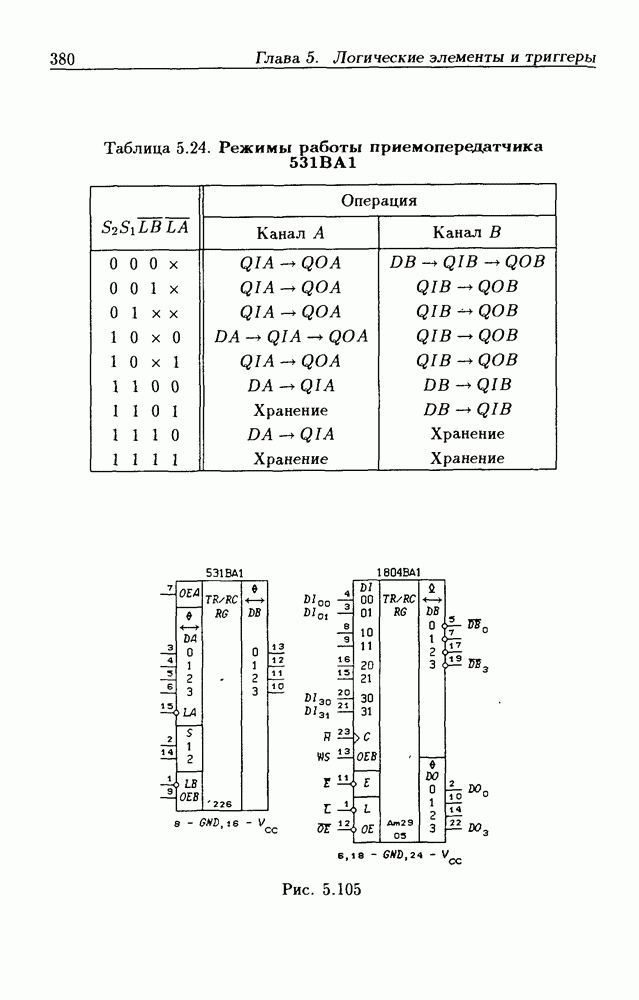
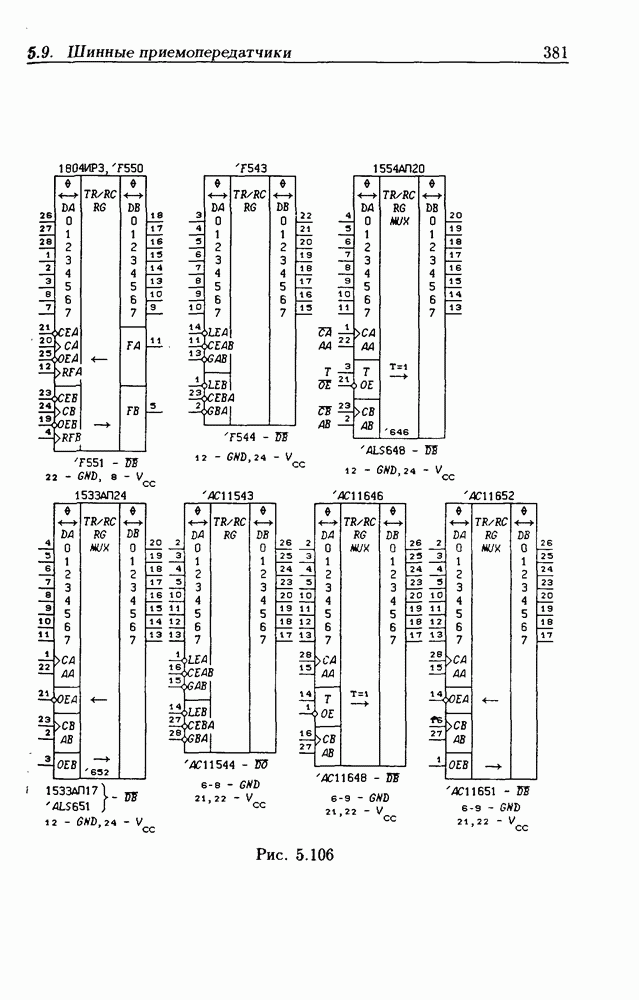
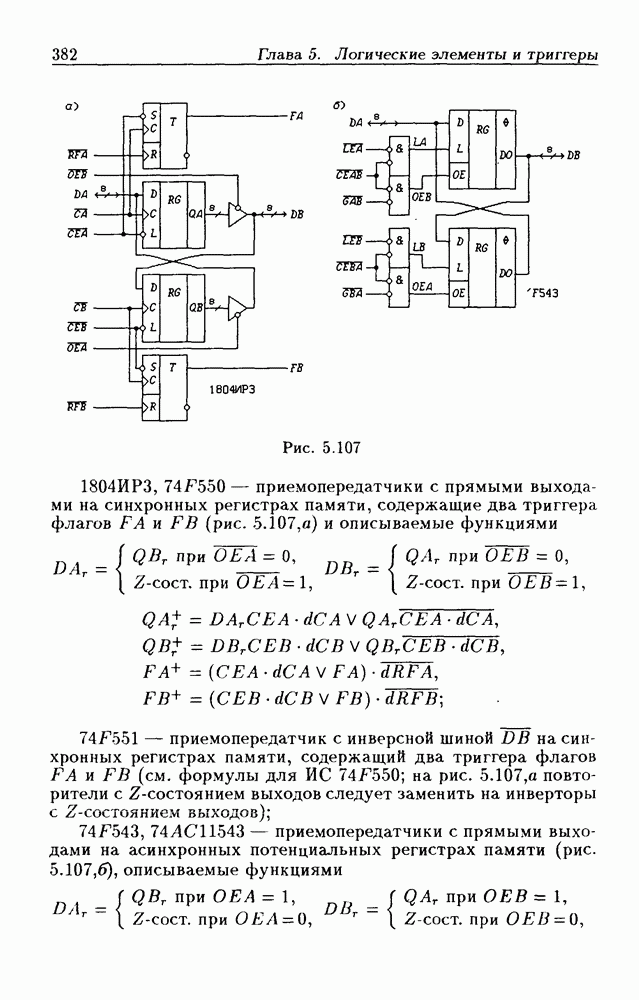
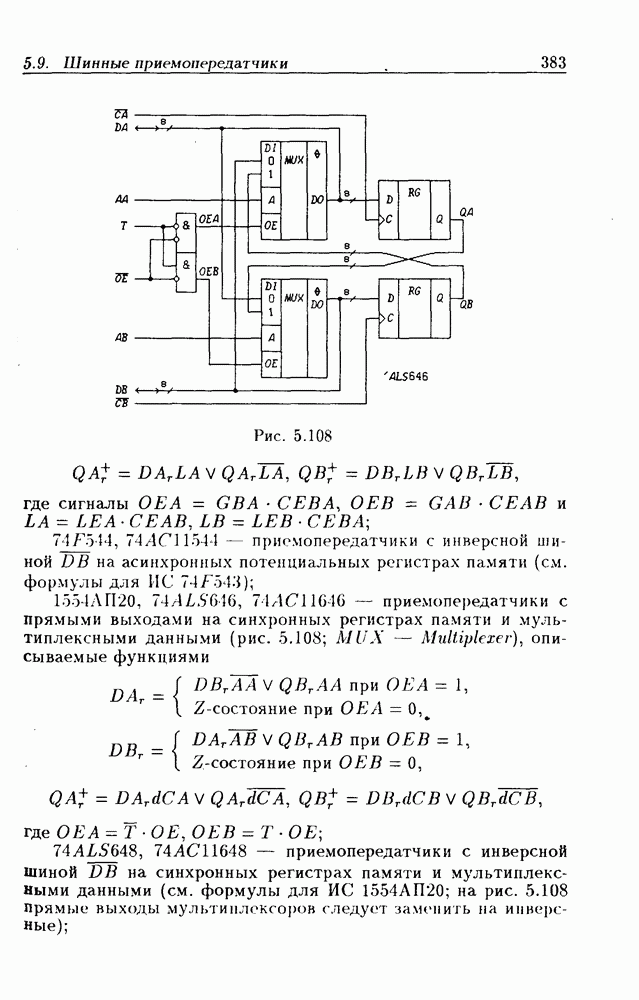
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
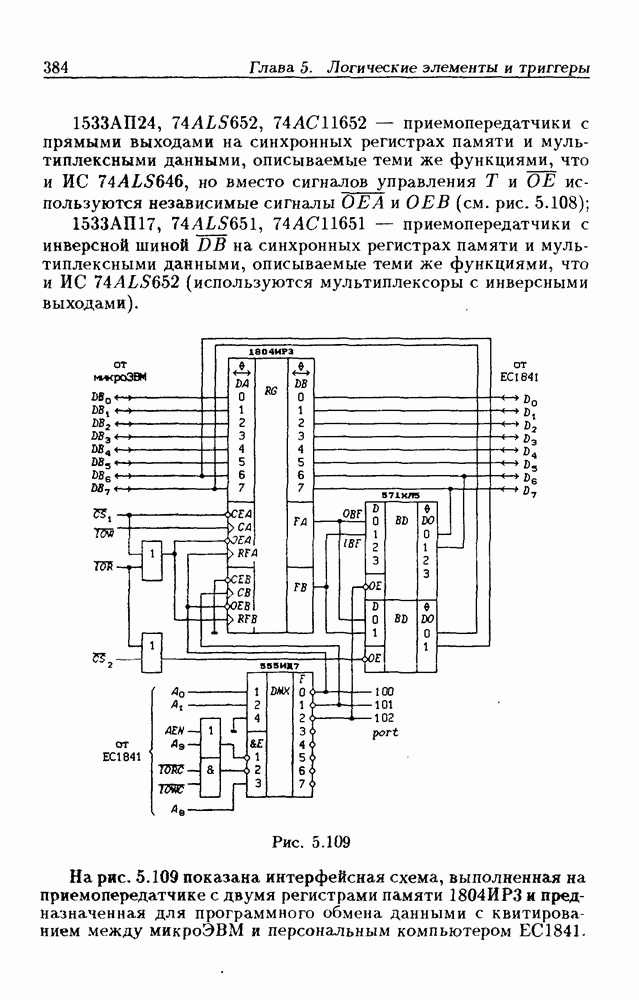
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
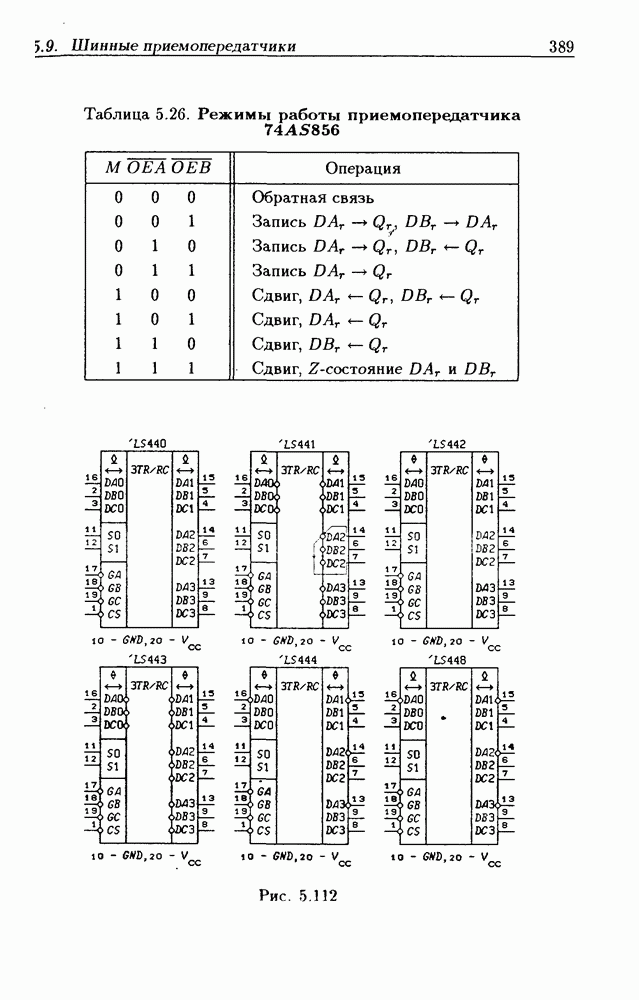
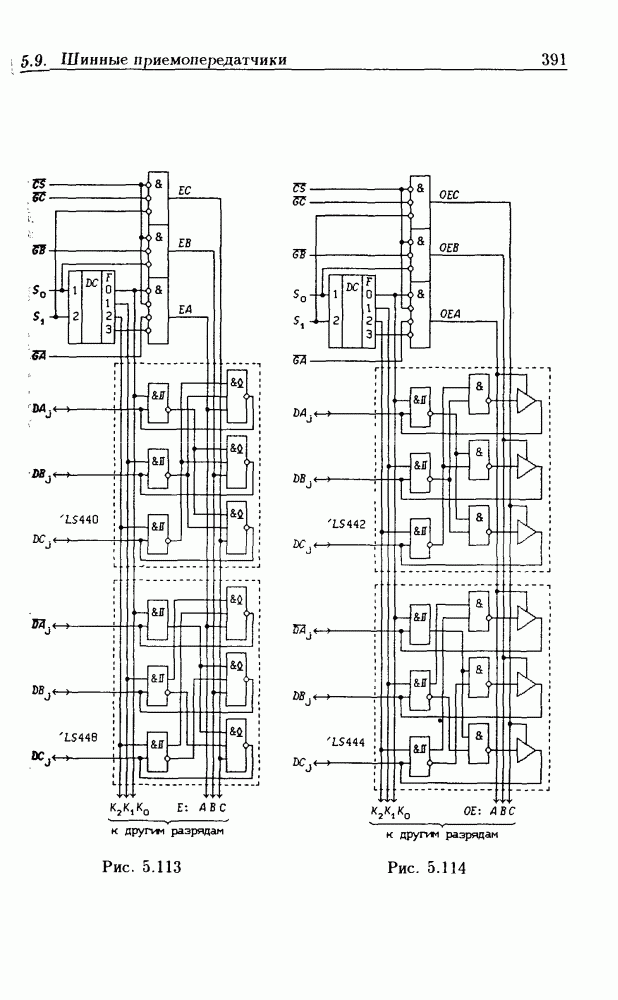
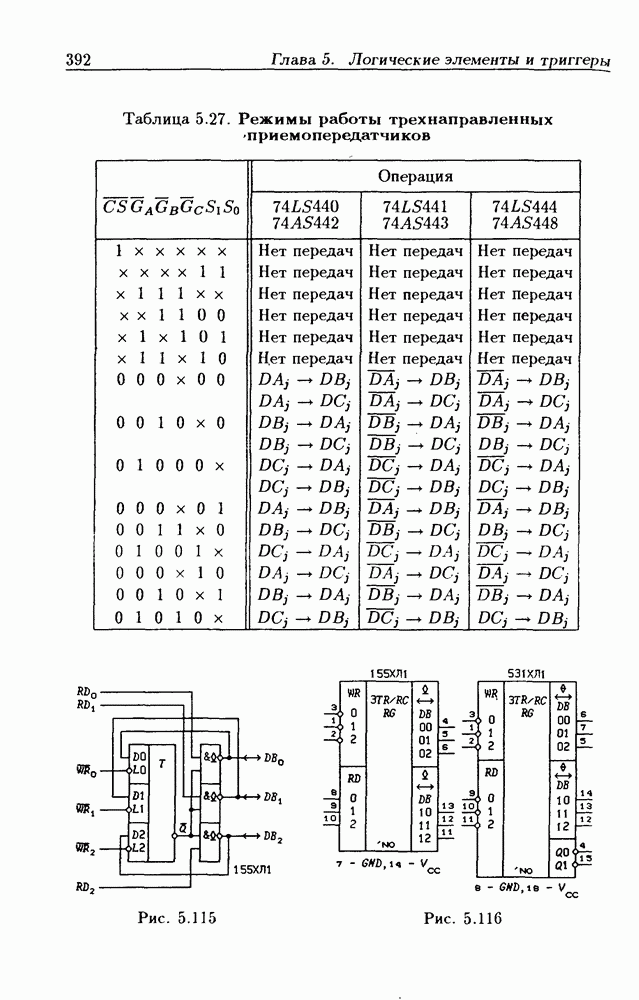
- Шинные трехнаправленные приемопередатчики.
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
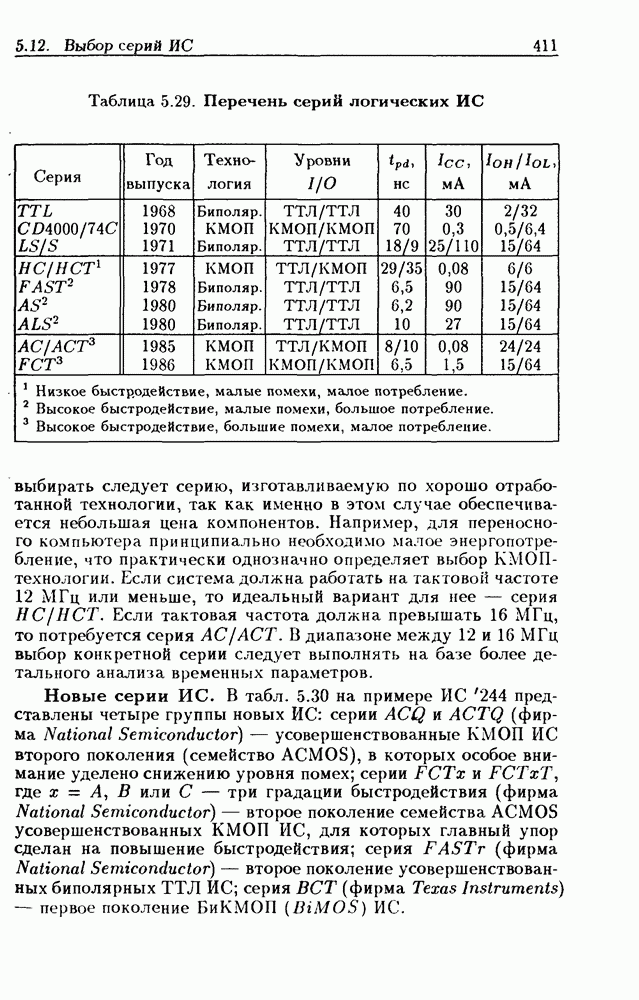
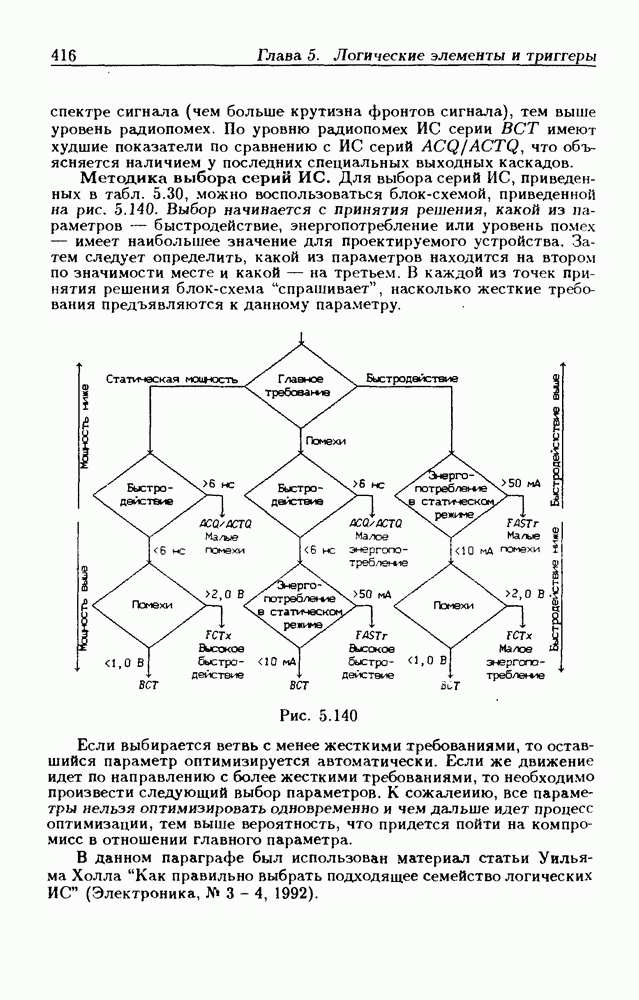
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
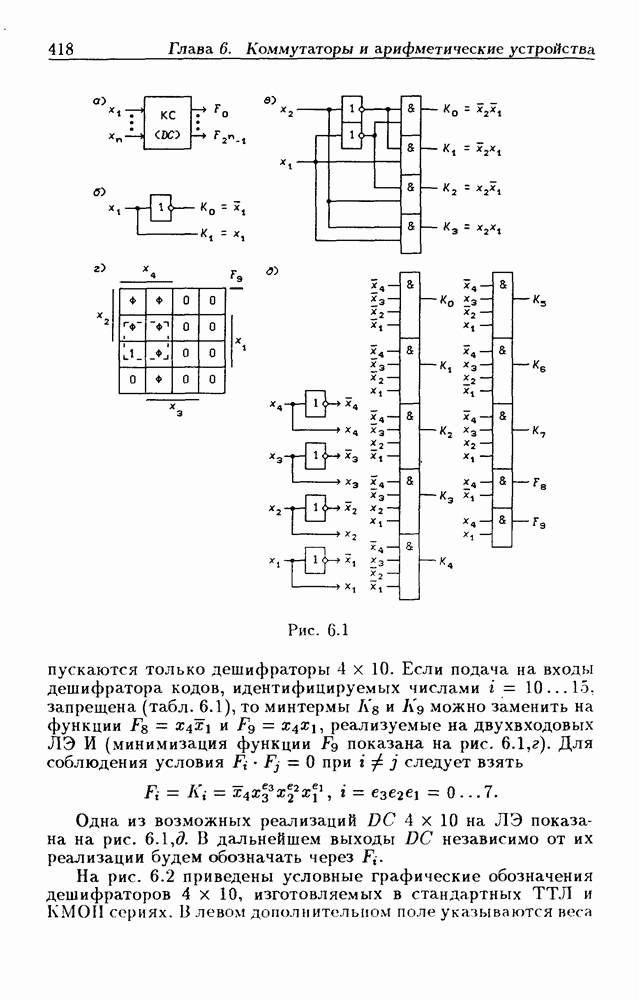
- 6.1. Дешифраторы
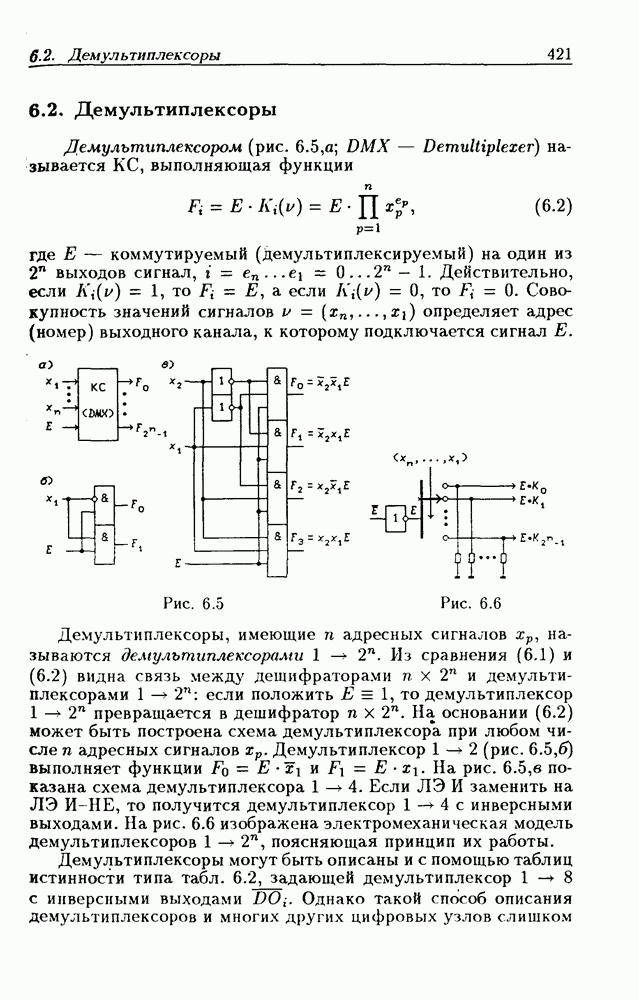
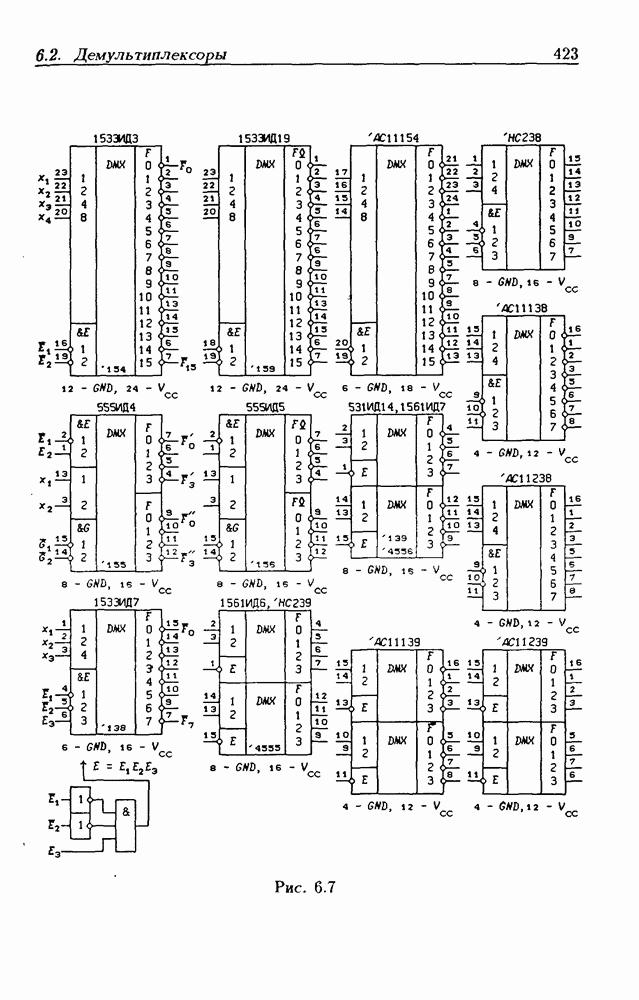
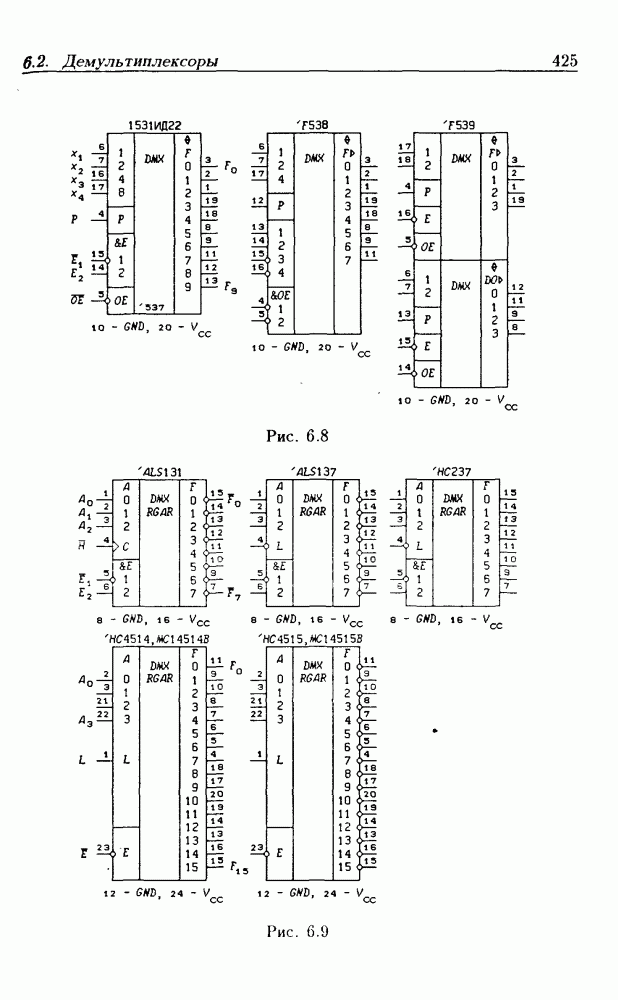
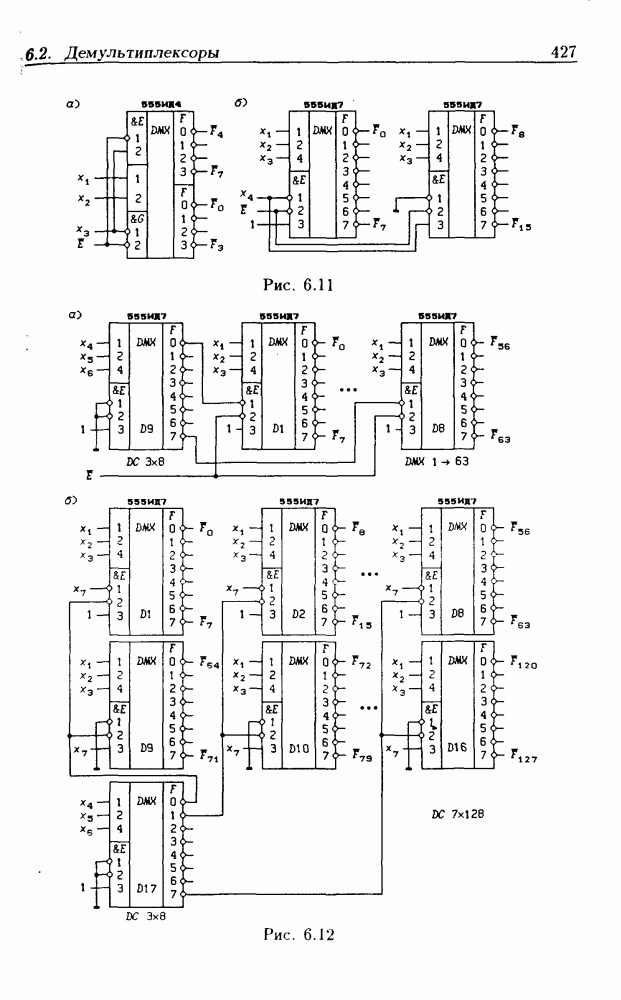
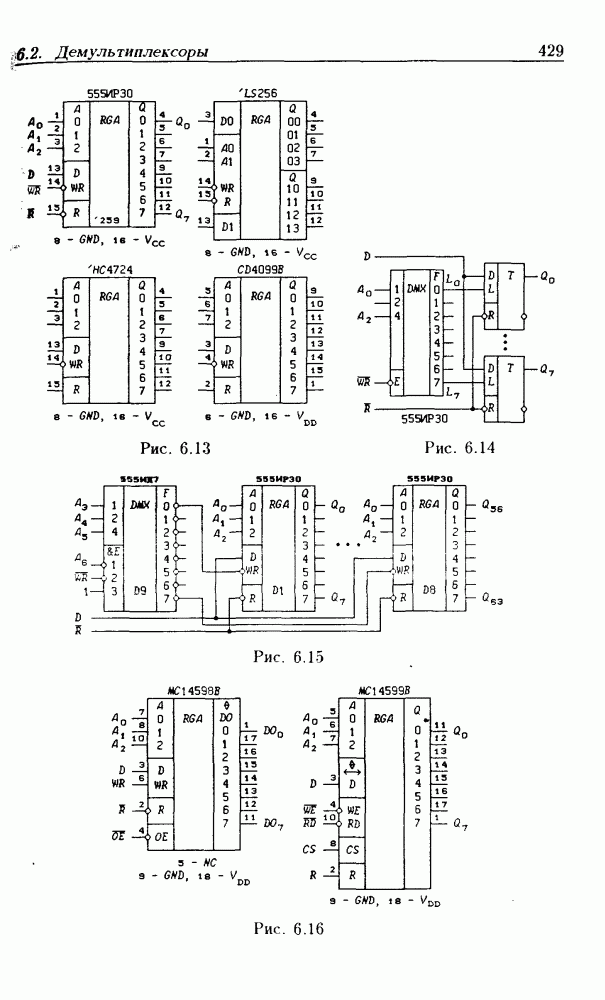
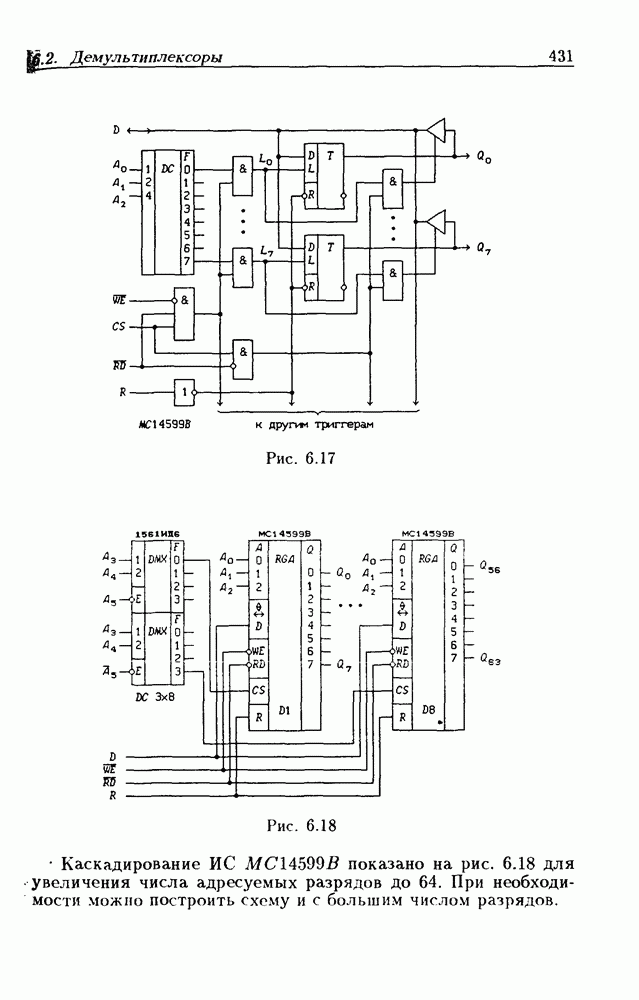
- 6.2. Демультиплексоры
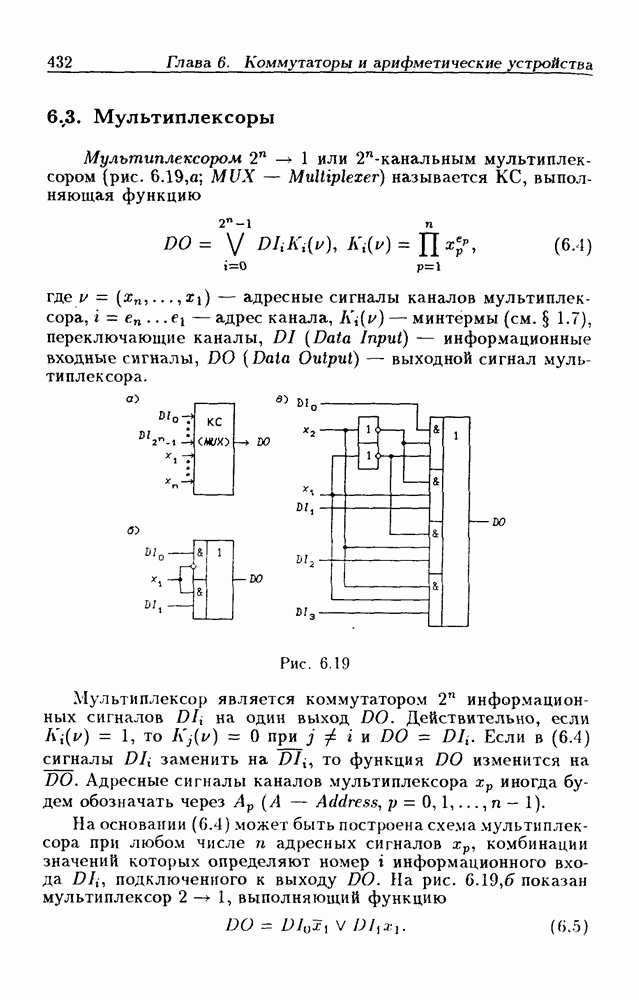
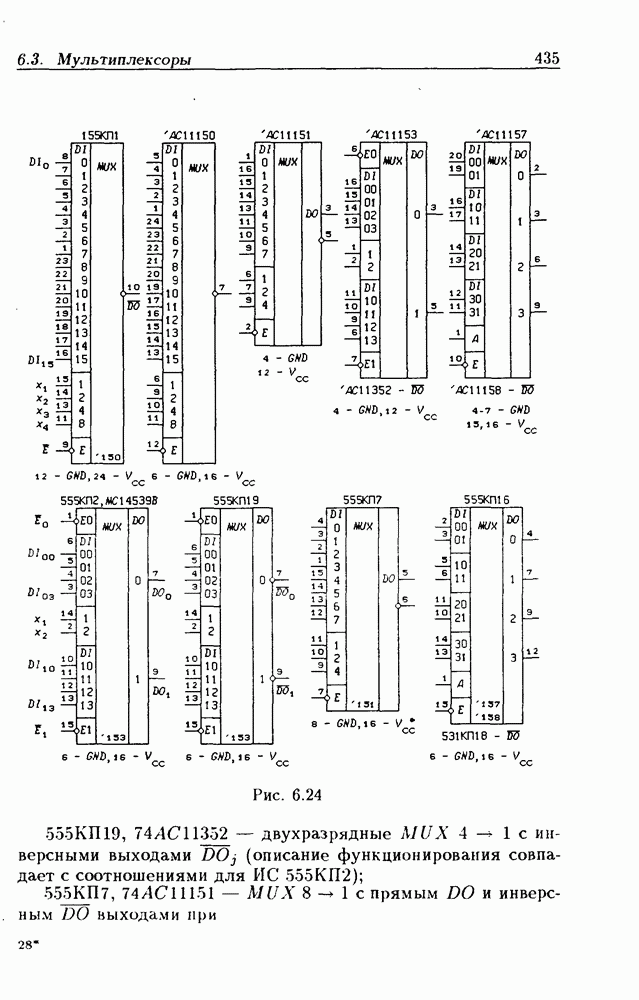
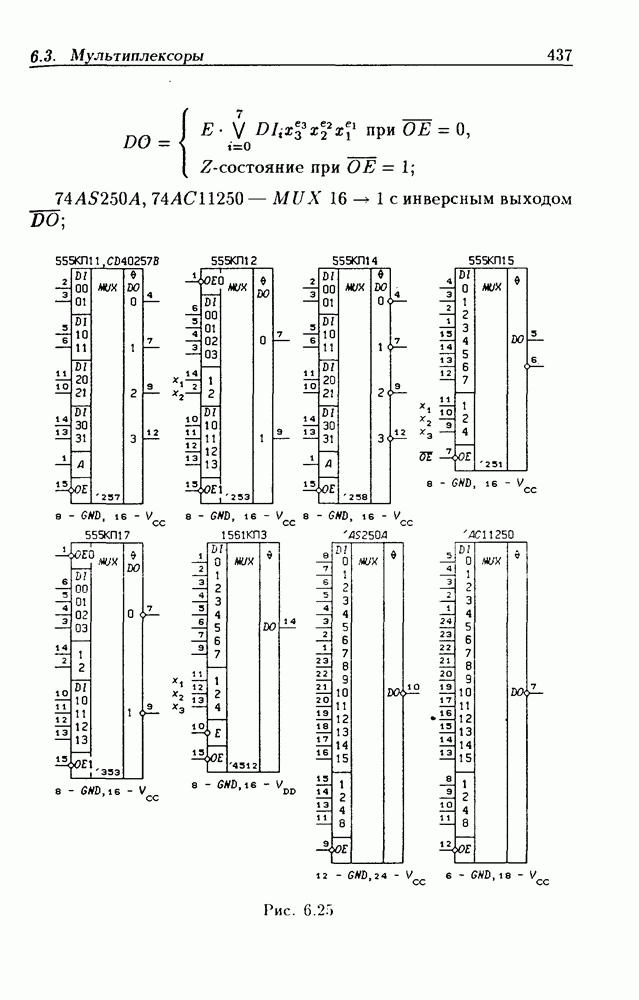
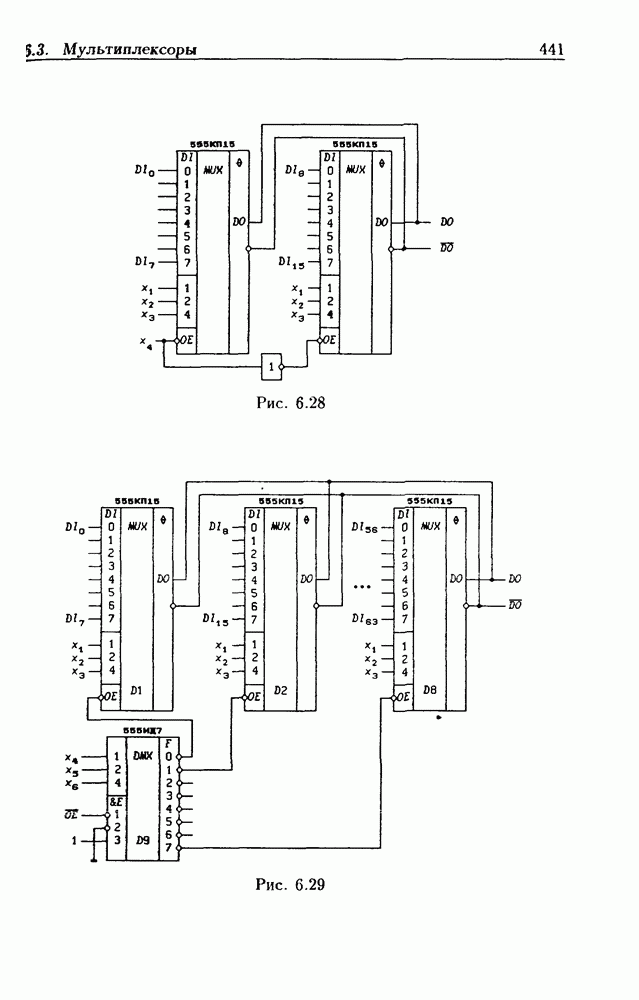
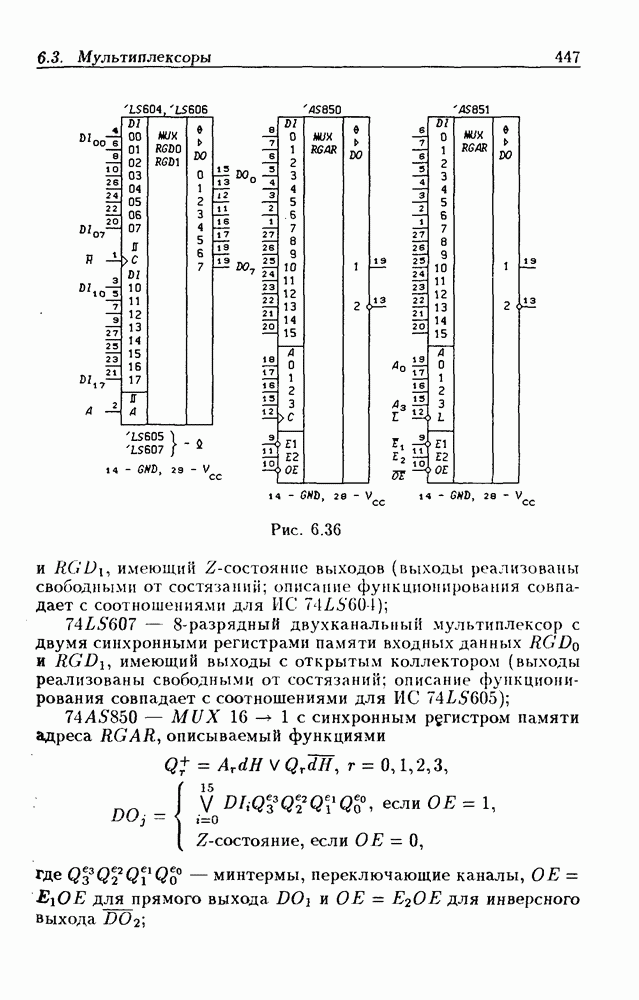
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
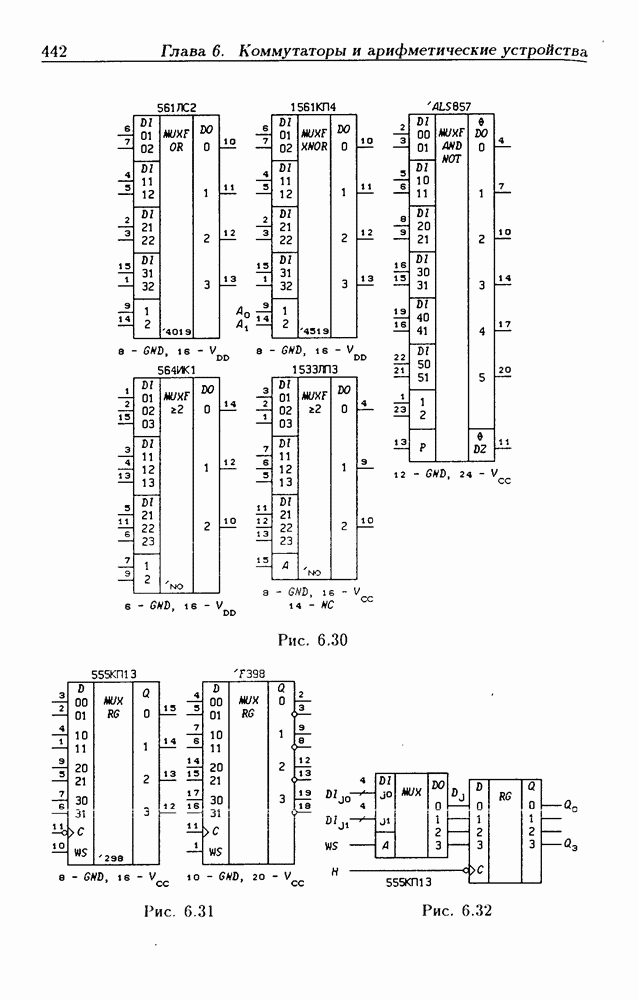
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
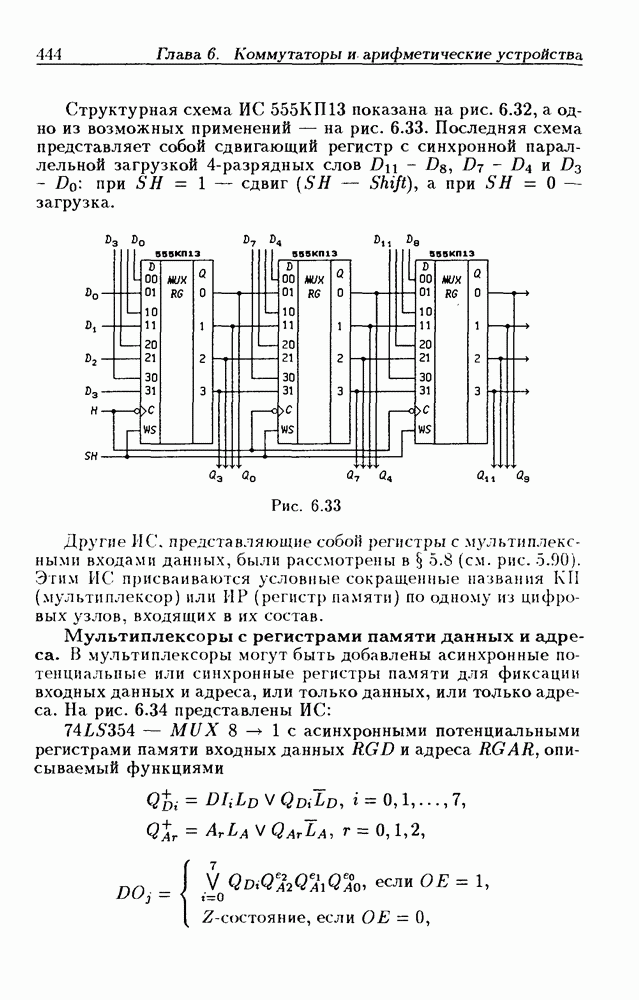
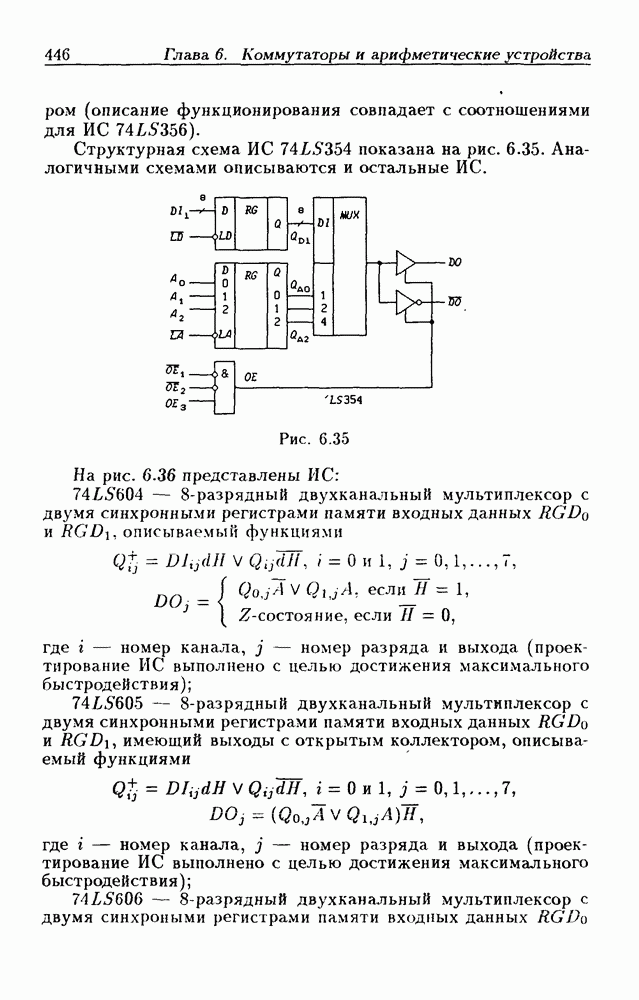
- Мультиплексоры с регистрами памяти данных и адреса.
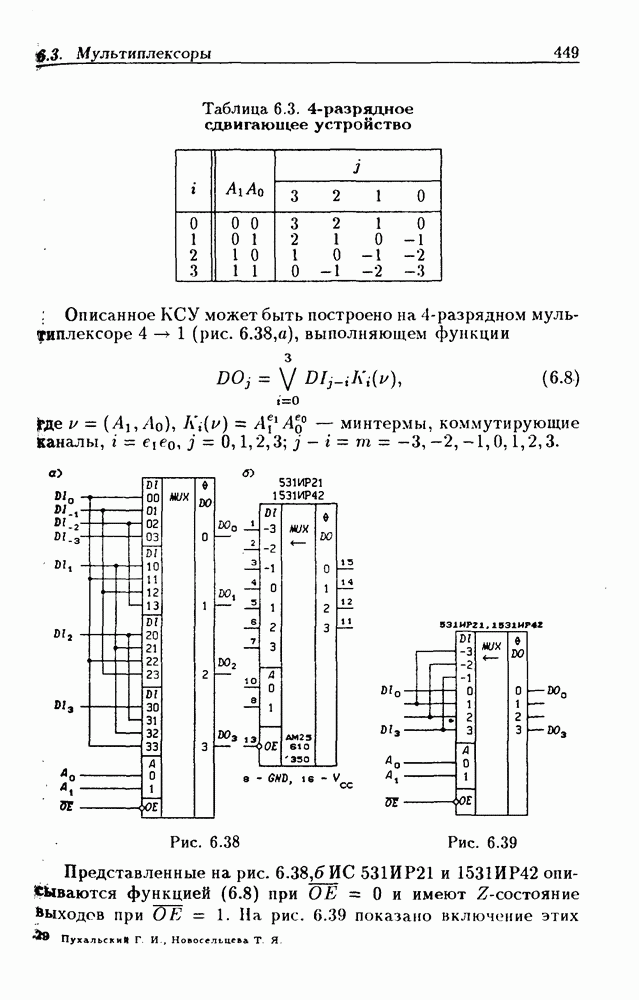
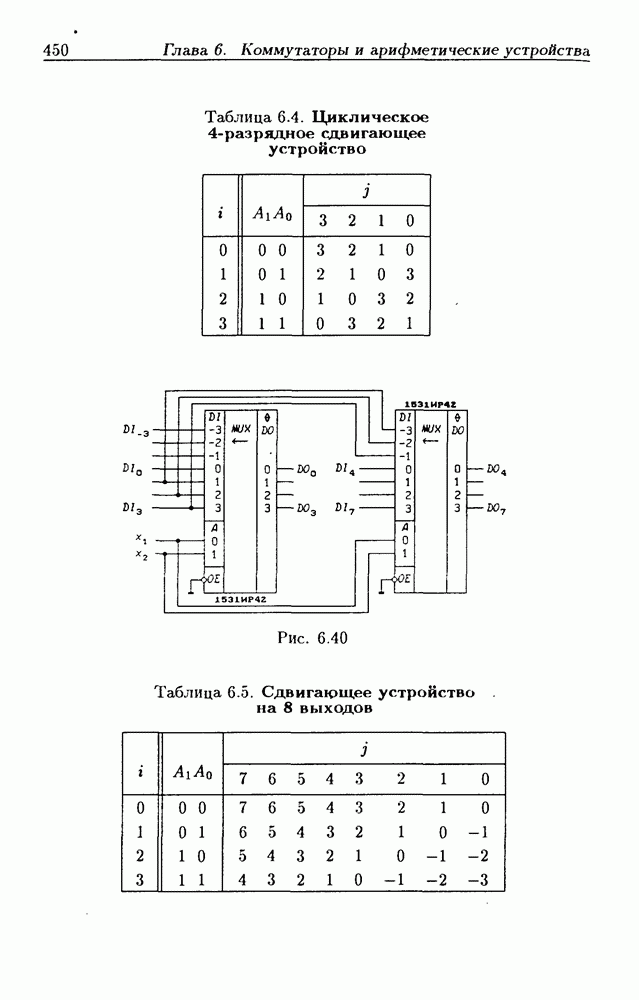
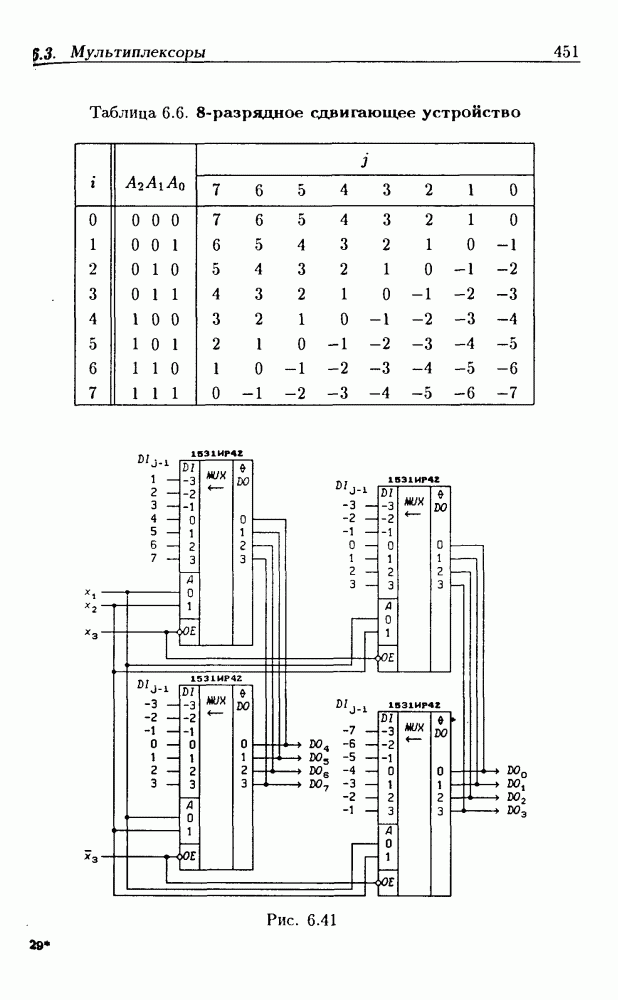
- Сдвигающие мультиплексоры.
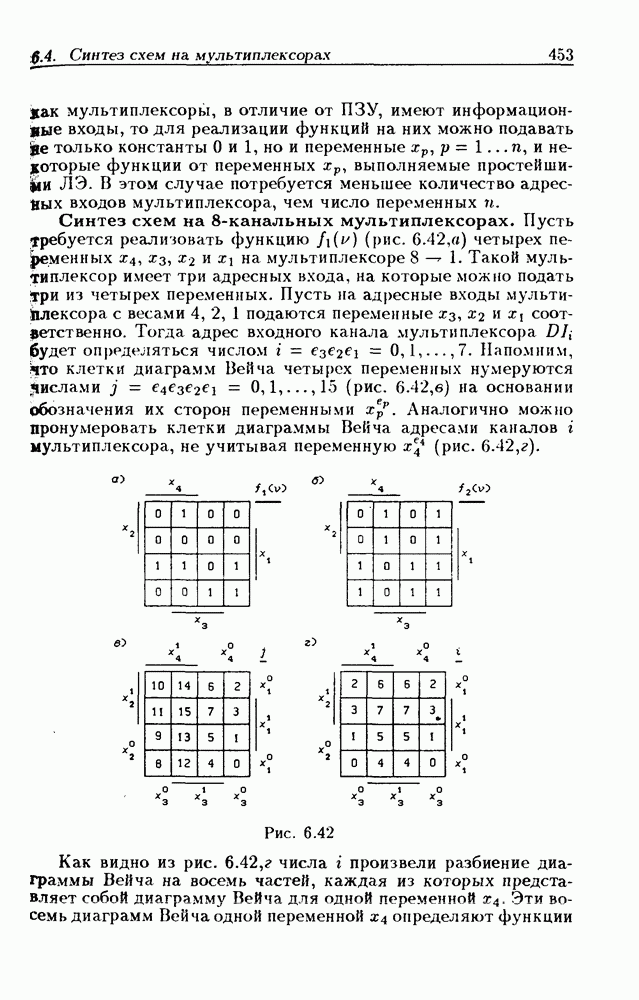
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
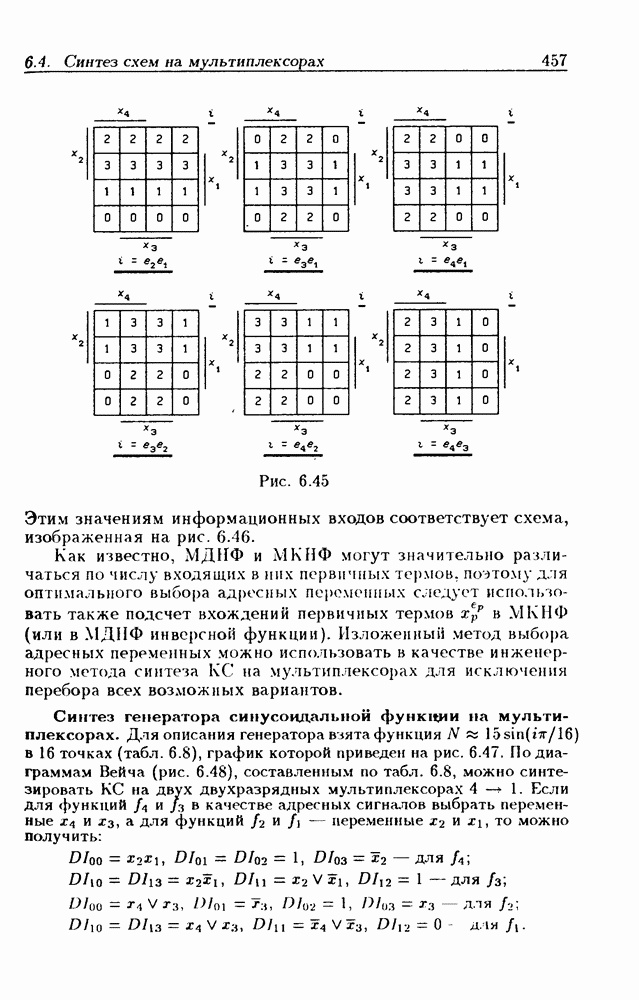
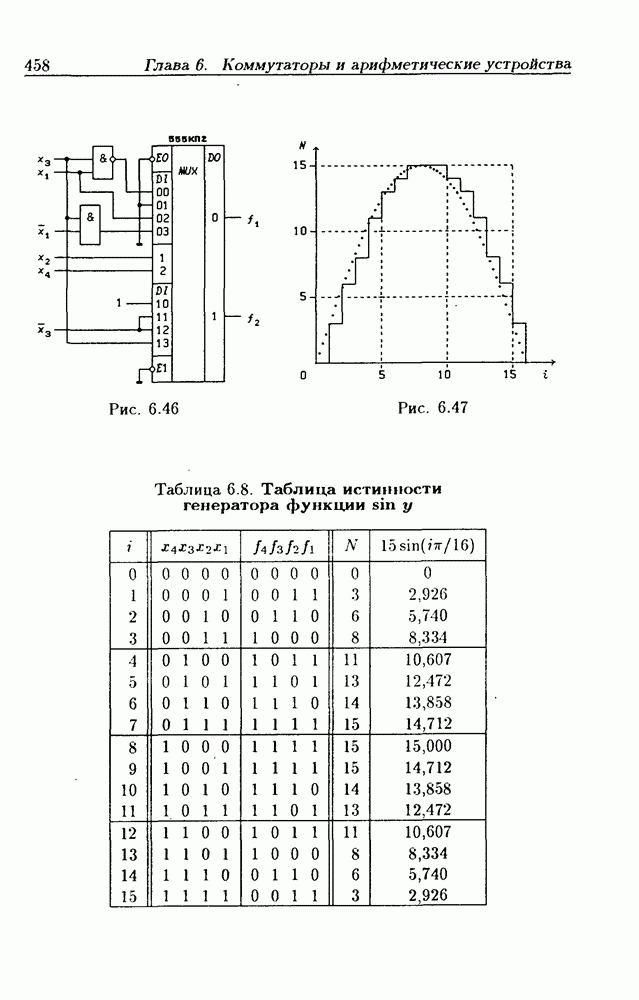
- Синтез генератора синусоидальной функции на мультиплексорах.
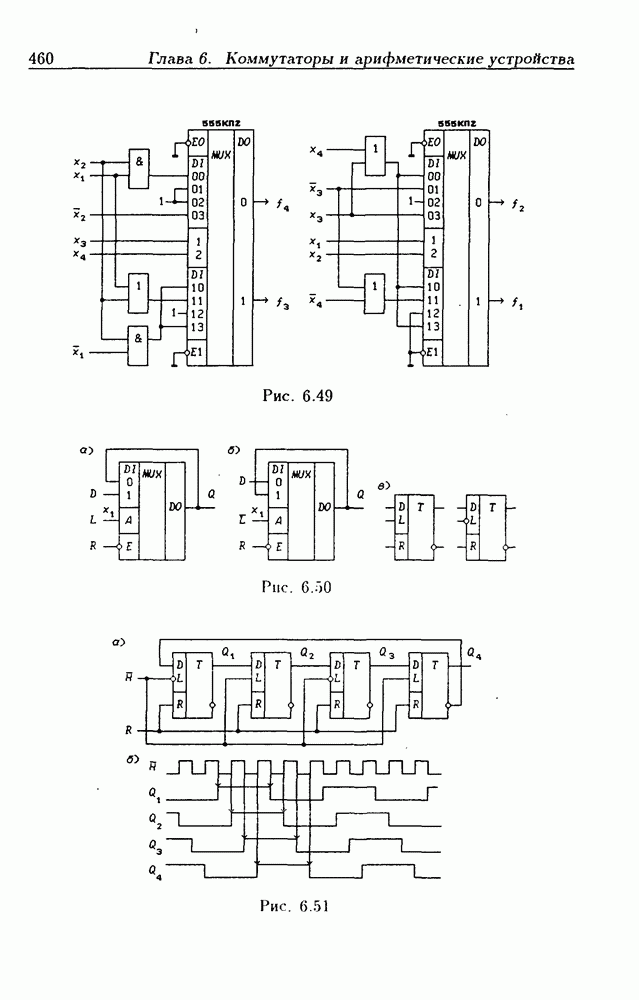
- Синтез триггеров на мультиплексорах.
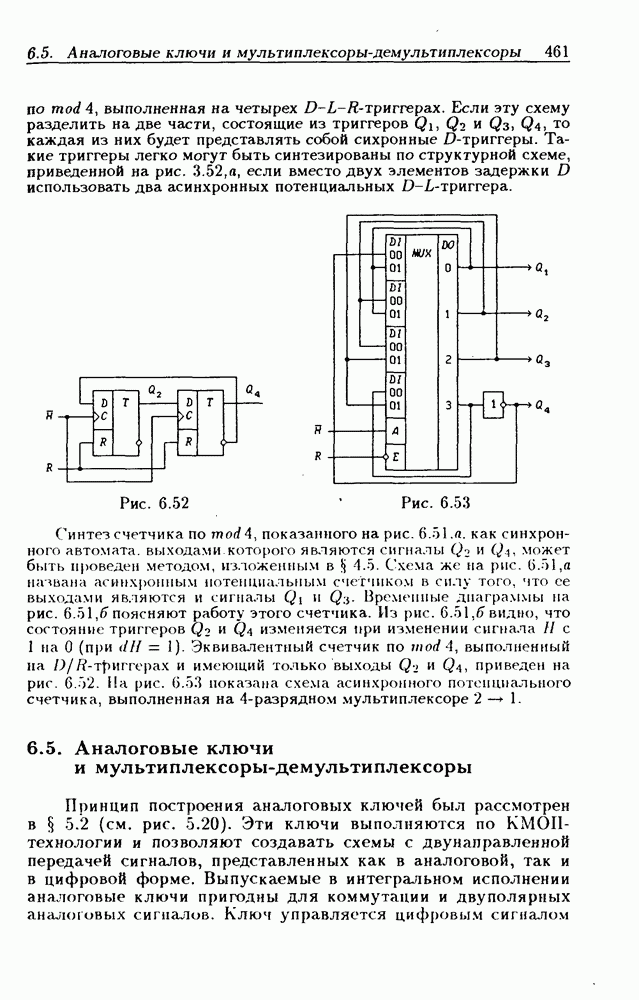
- Синтез счетчиков на мультиплексорах.
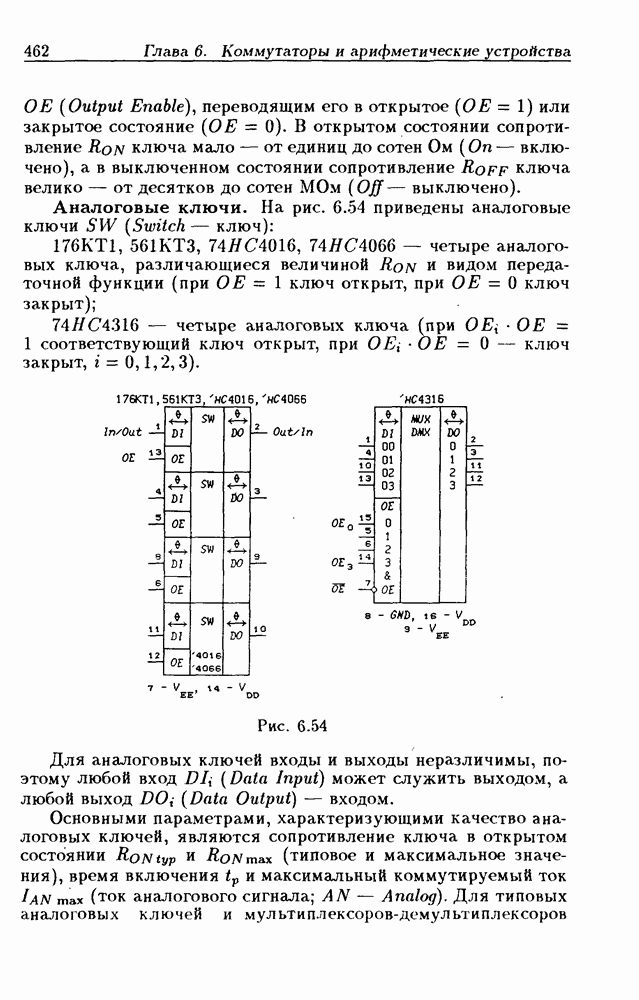
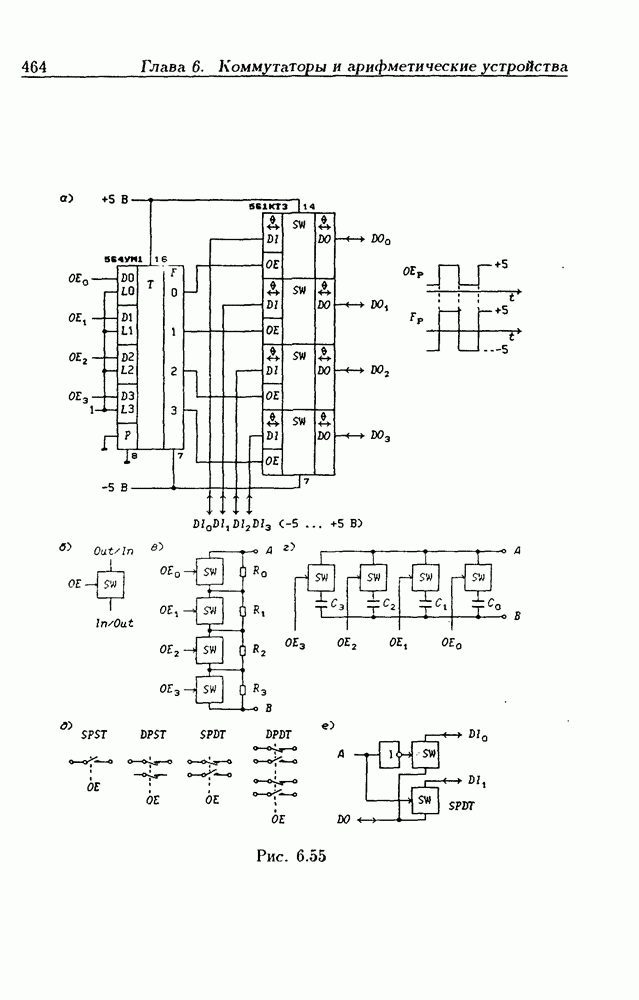
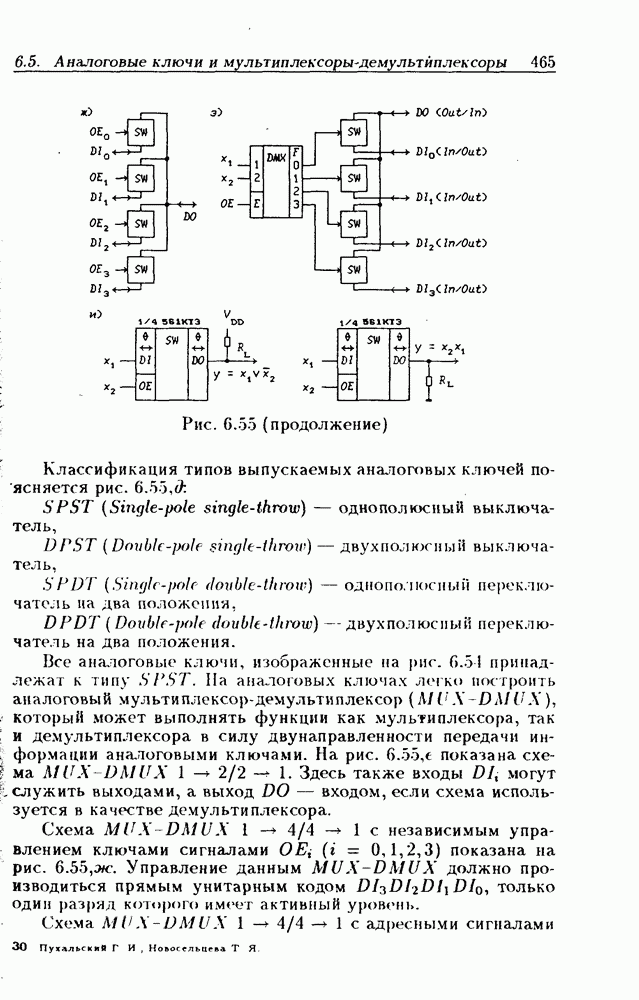
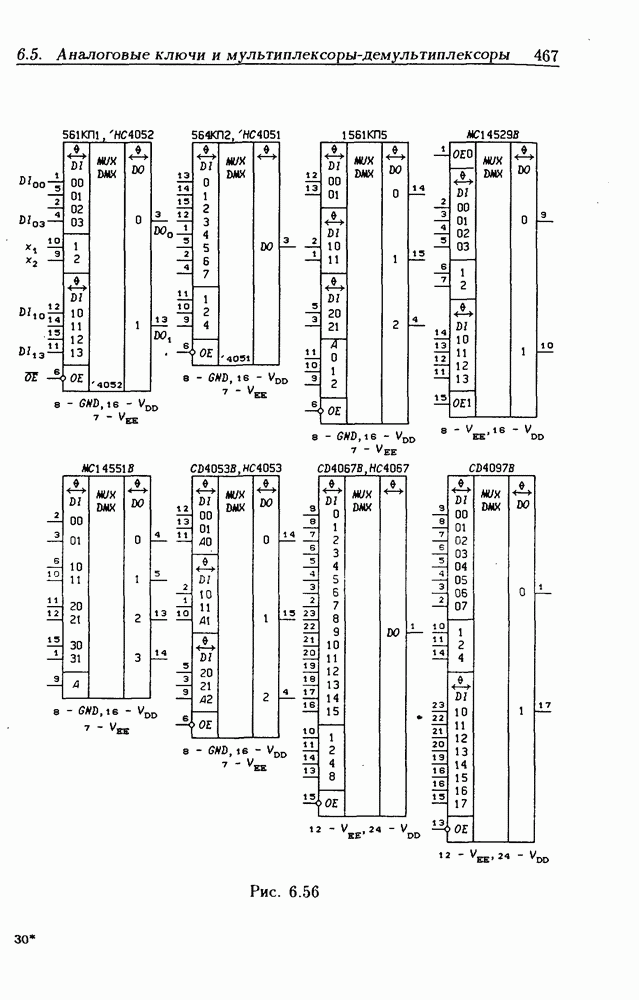
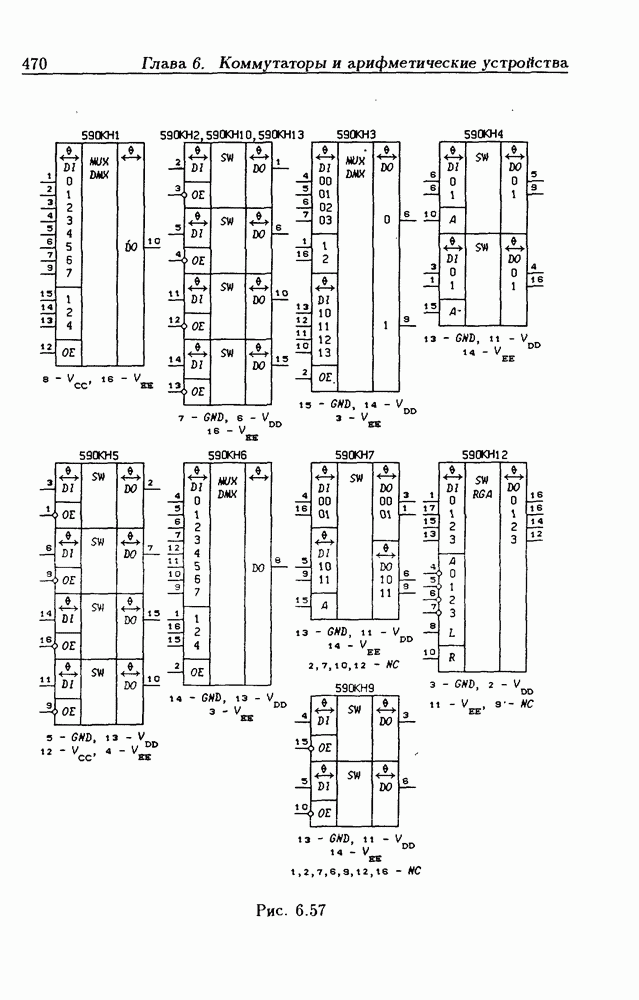
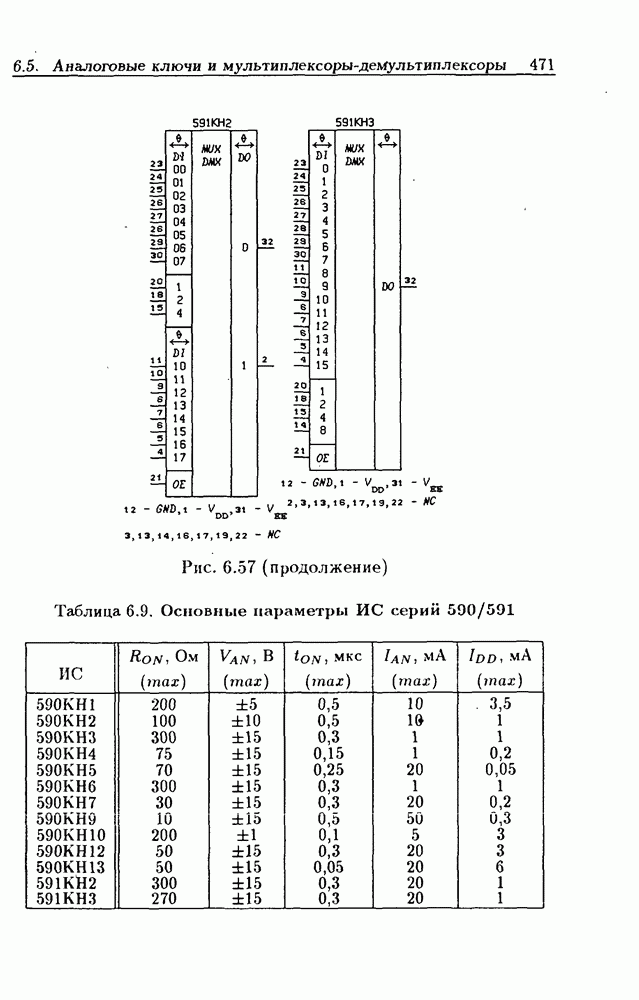
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
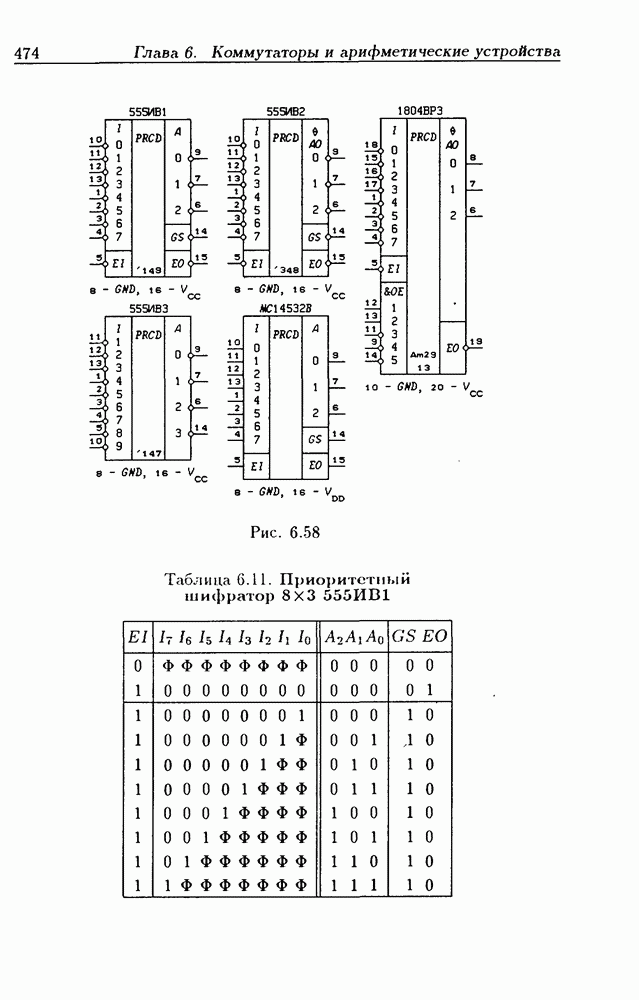
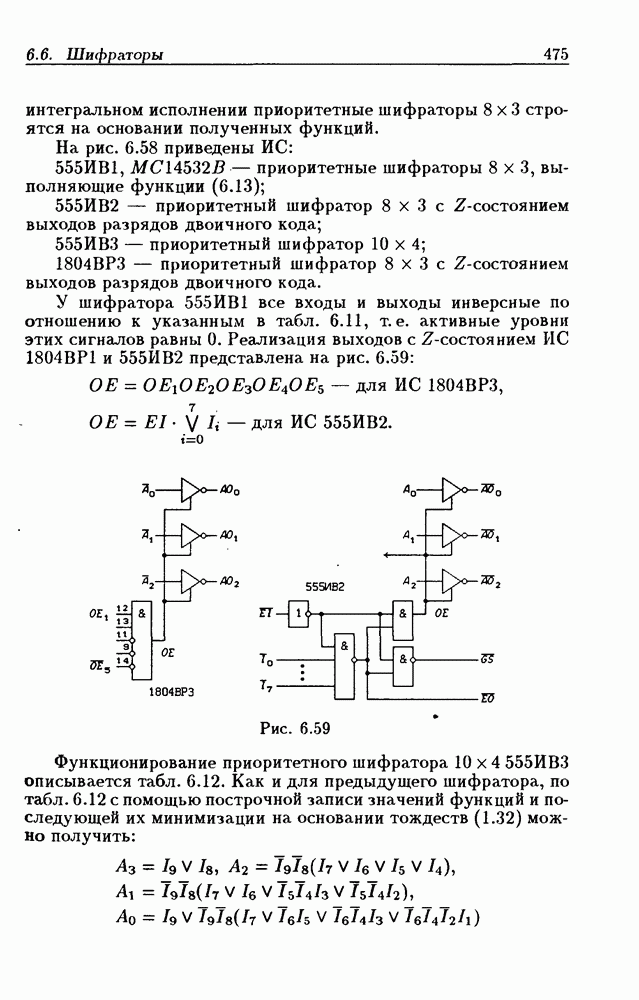
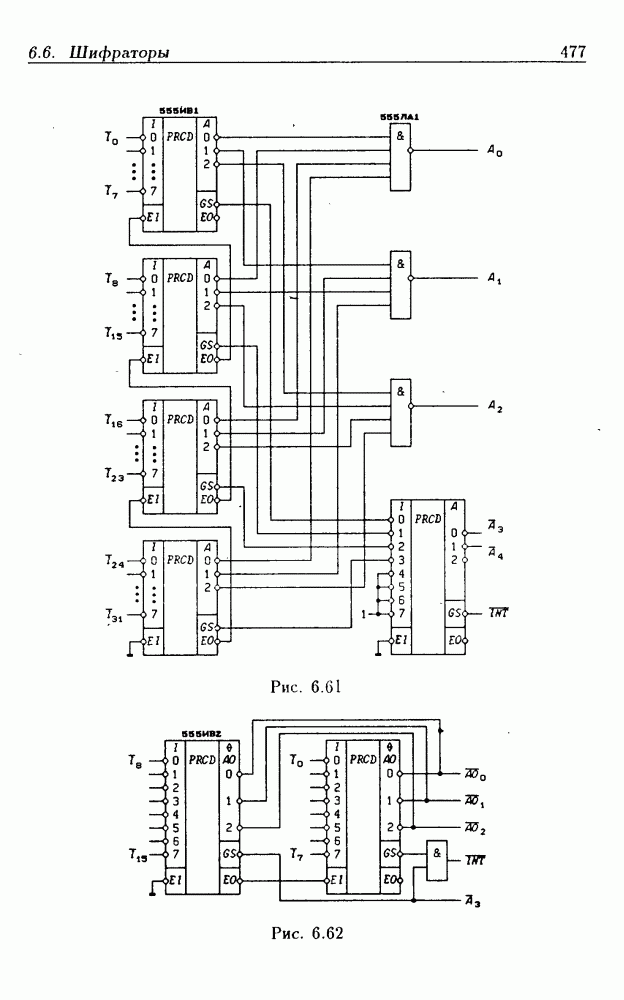
- 6.6. Шифраторы
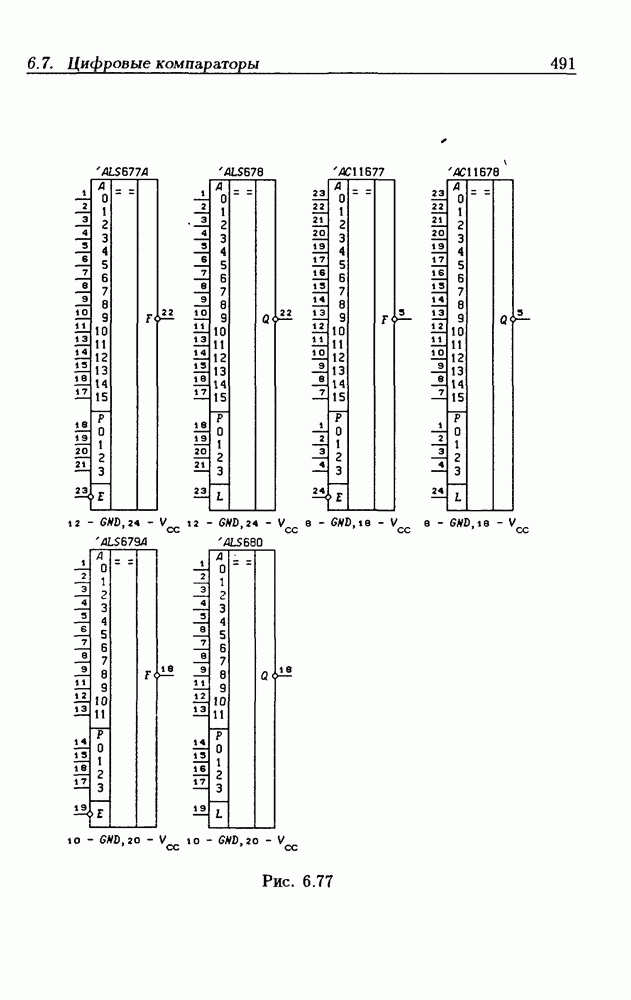
- 6.7. Цифровые компараторы
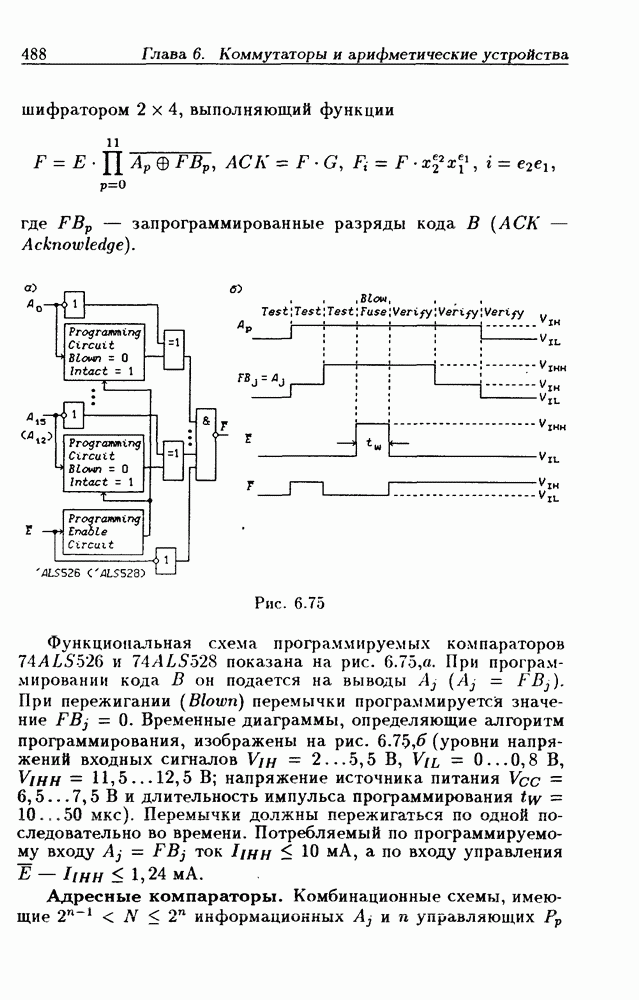
- Программируемые цифровые компараторы.
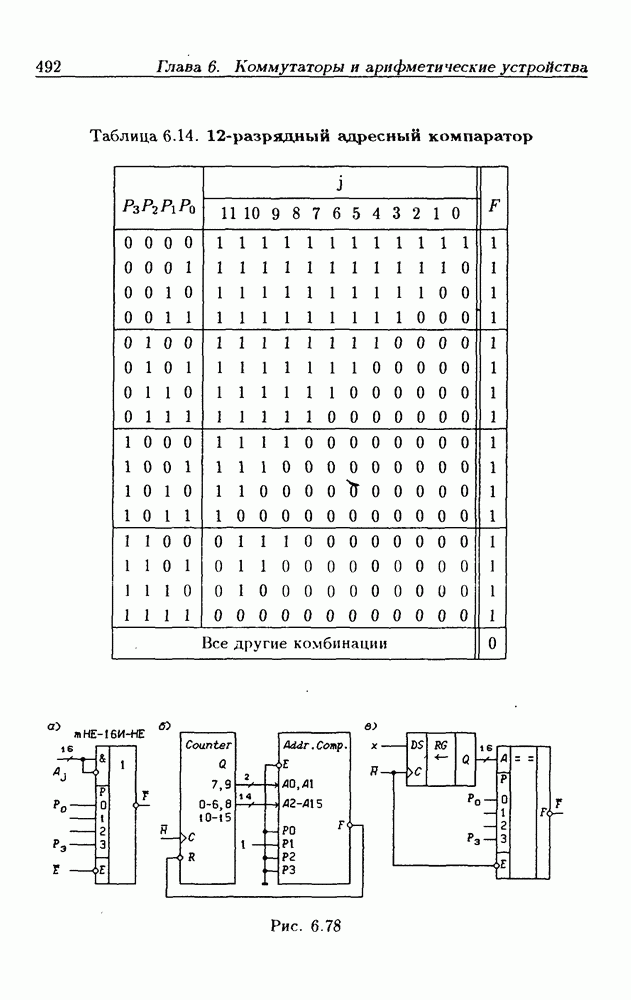
- Адресные компараторы.
- Применения адресных компараторов.
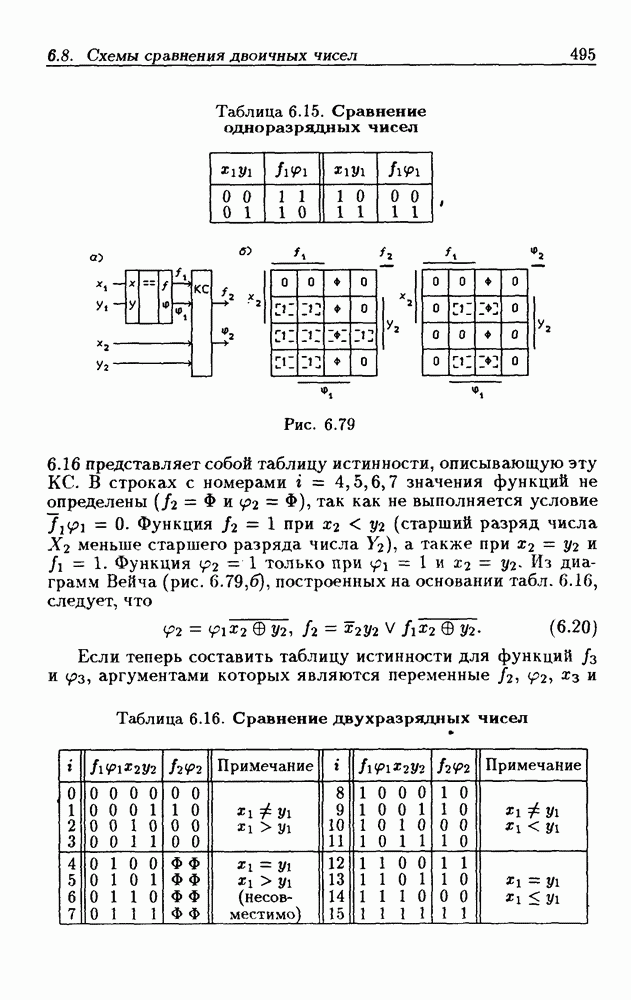
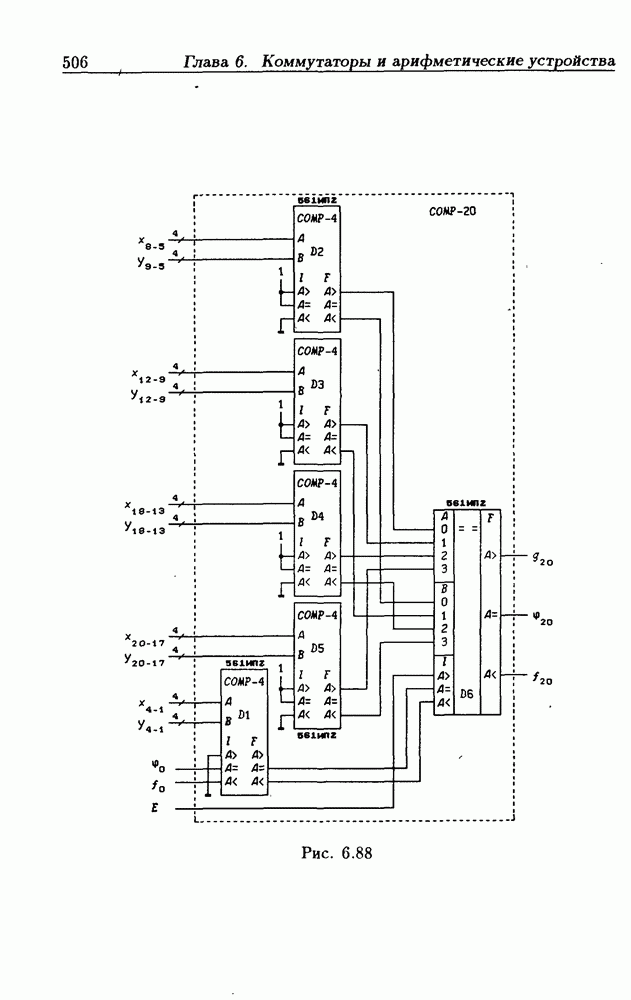
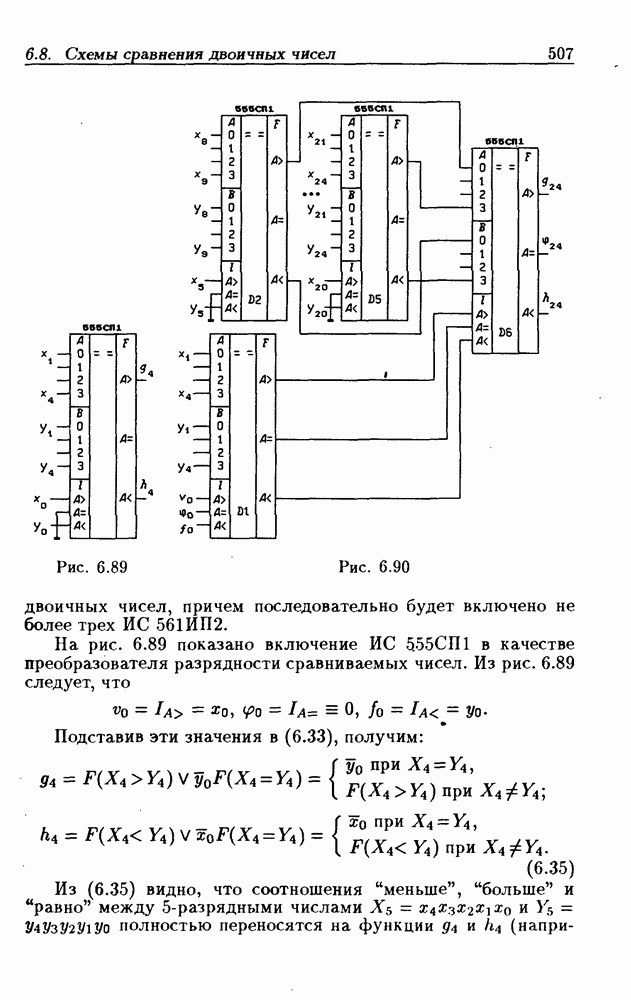
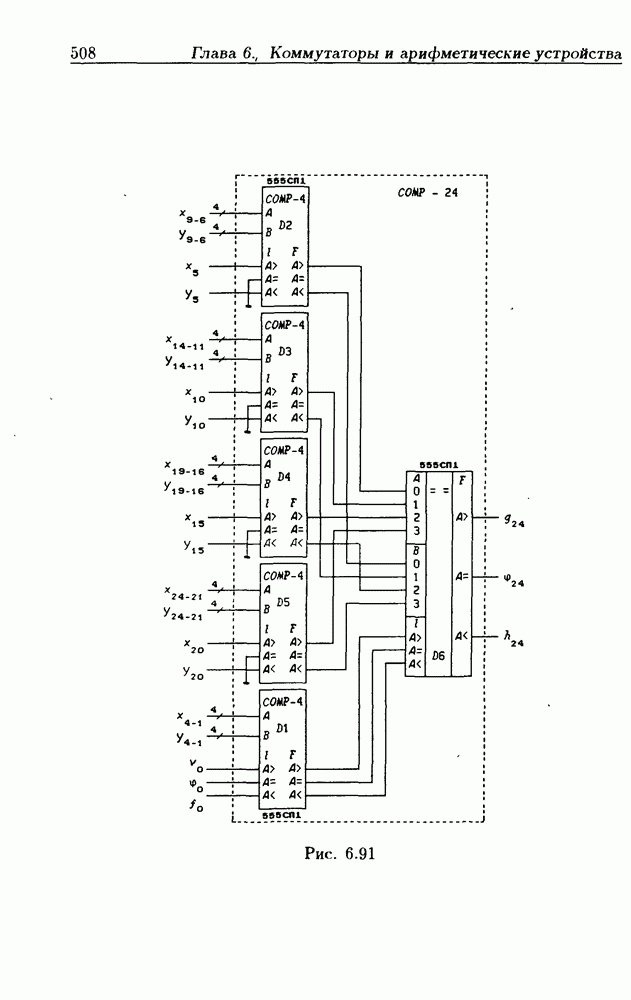
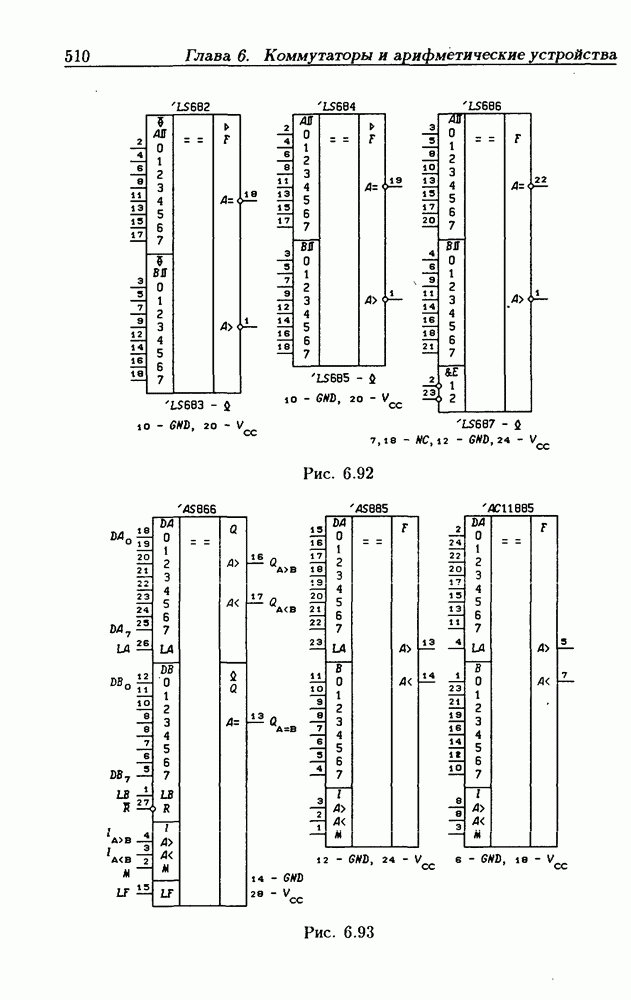
- 6.8. Схемы сравнения двоичных чисел
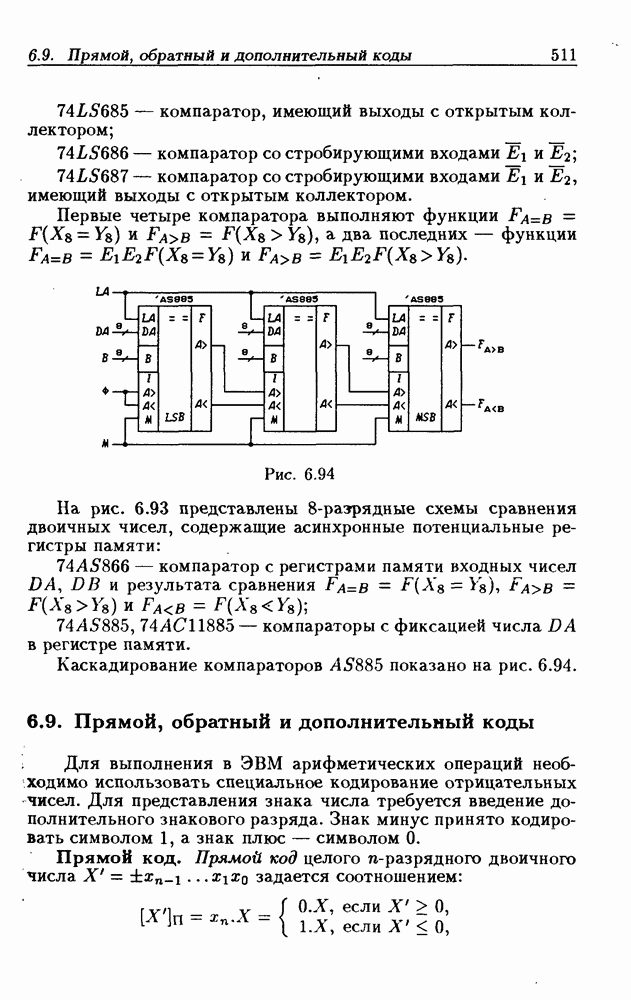
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
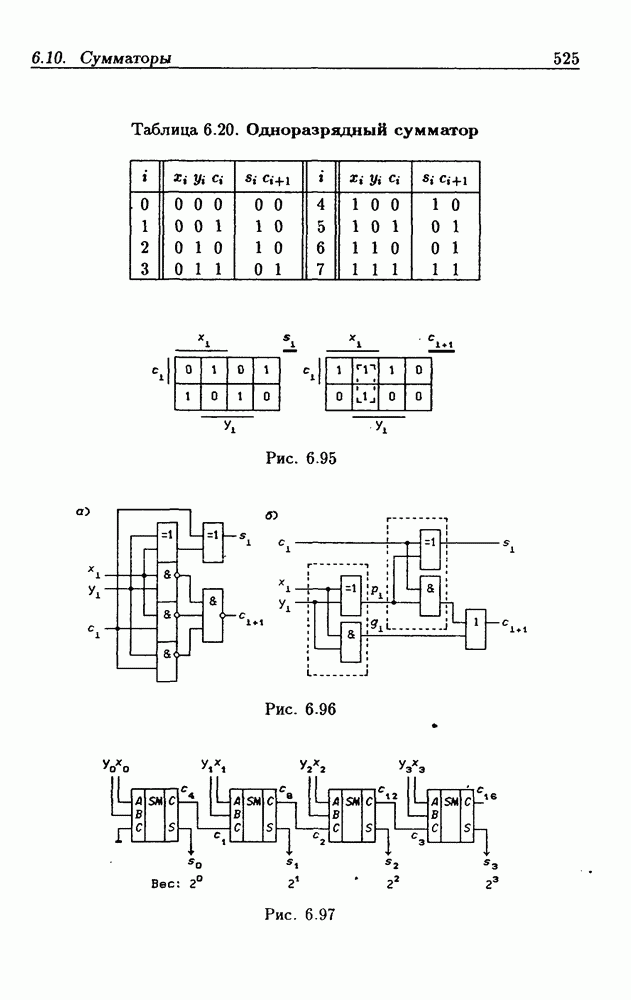
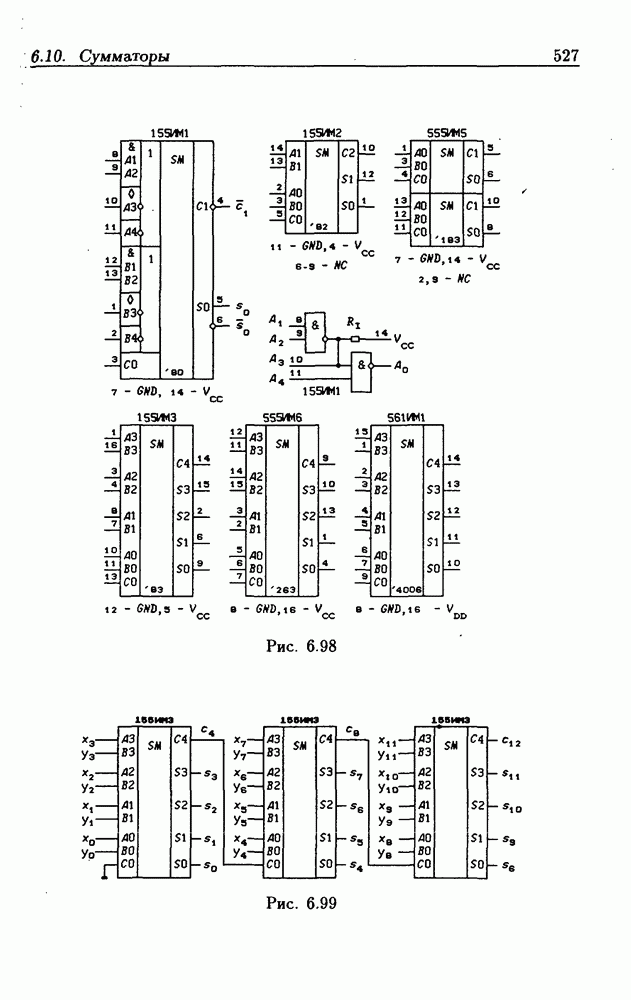
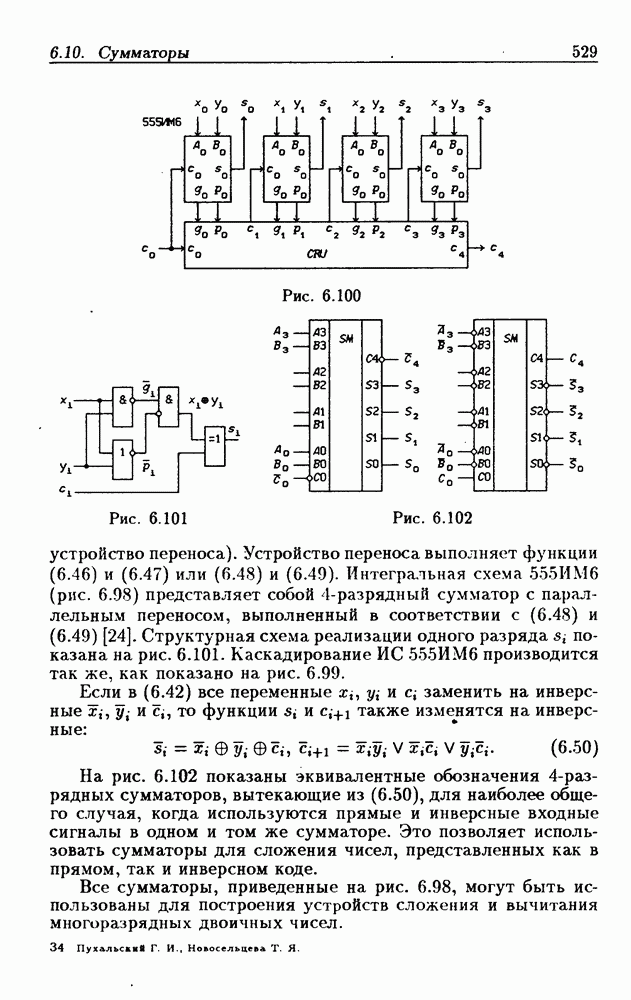
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
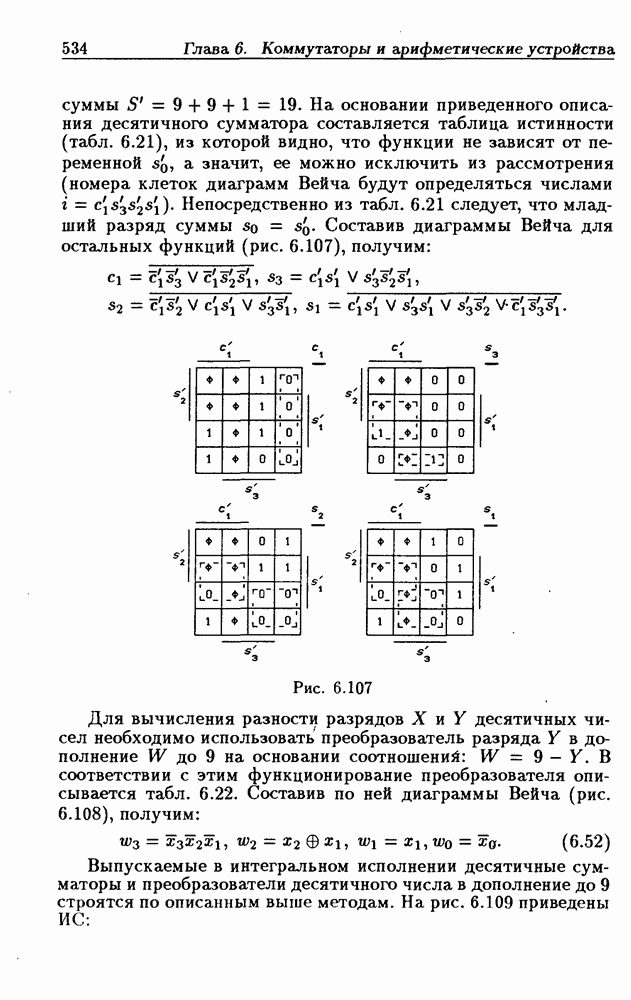
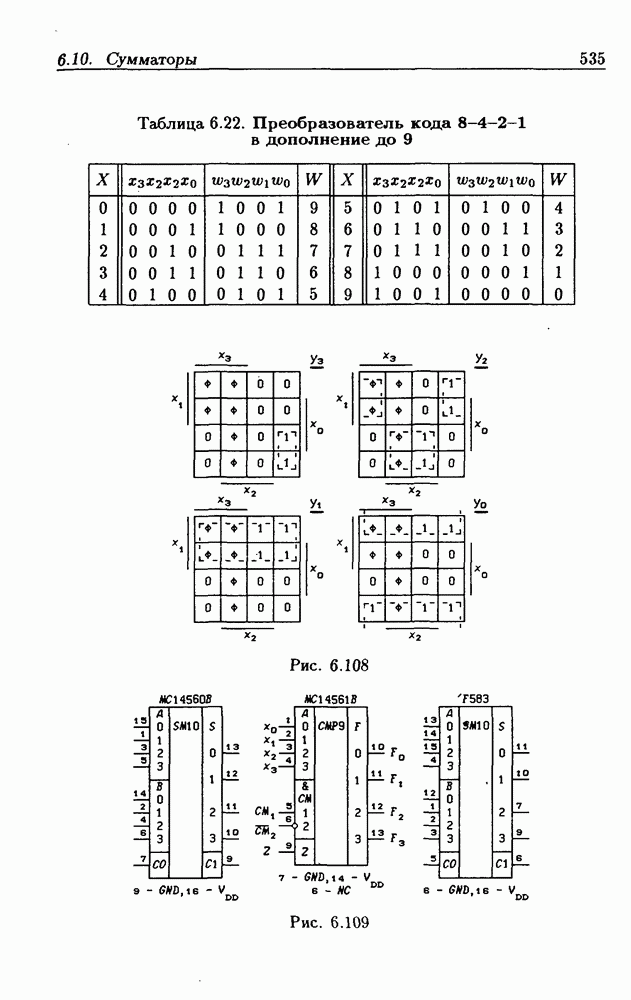
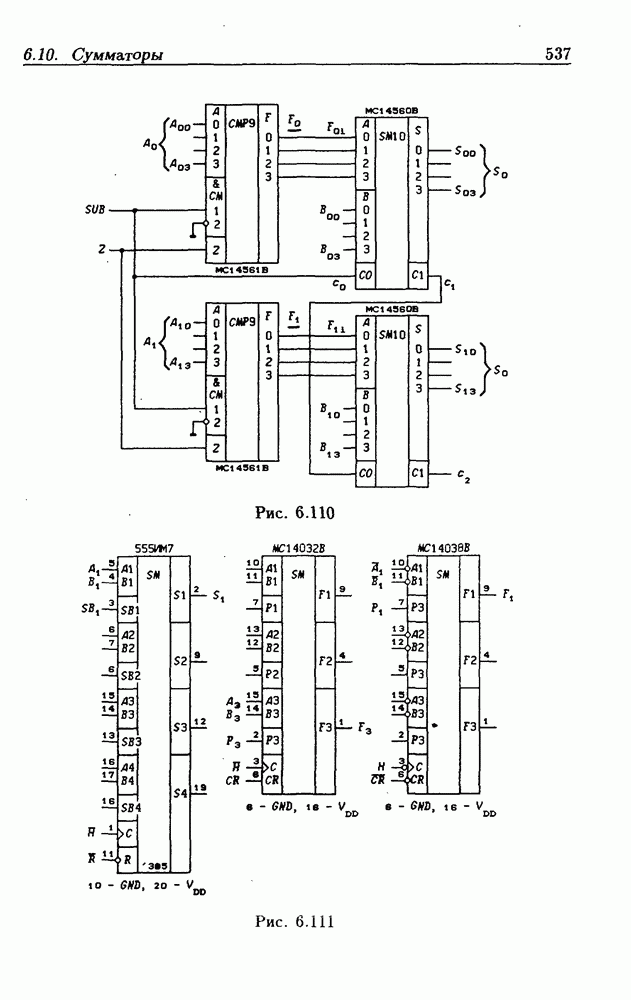
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
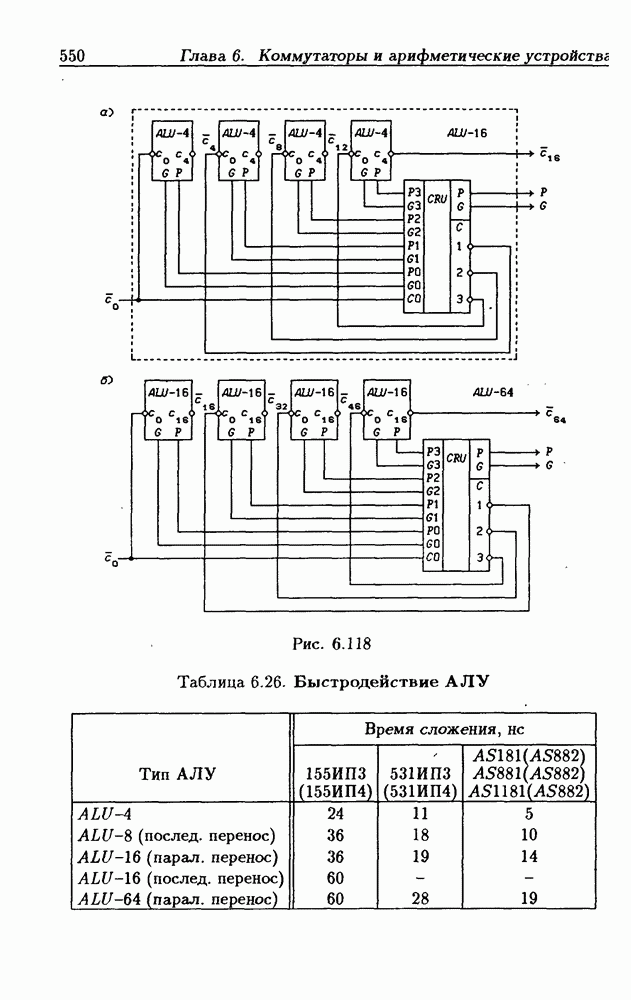
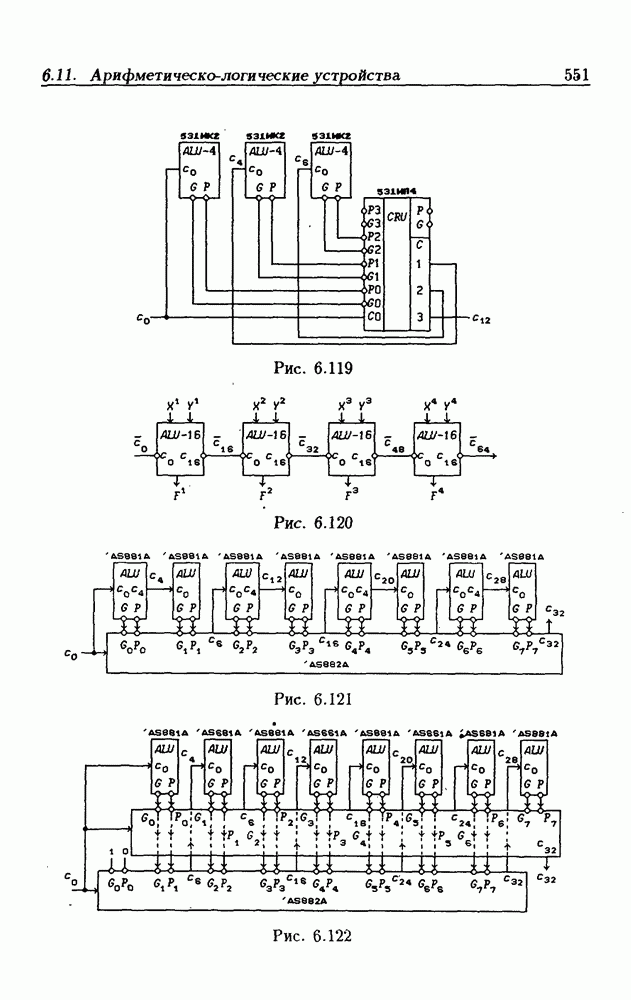
- 6.11. Арифметическо-логические устройства
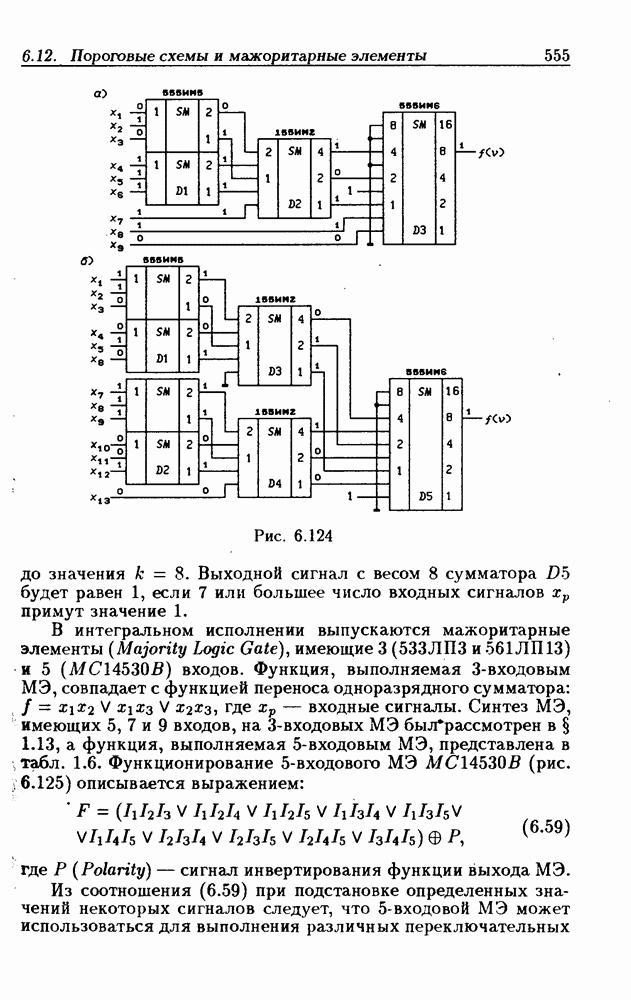
- 6.12. Пороговые схемы и мажоритарные элементы
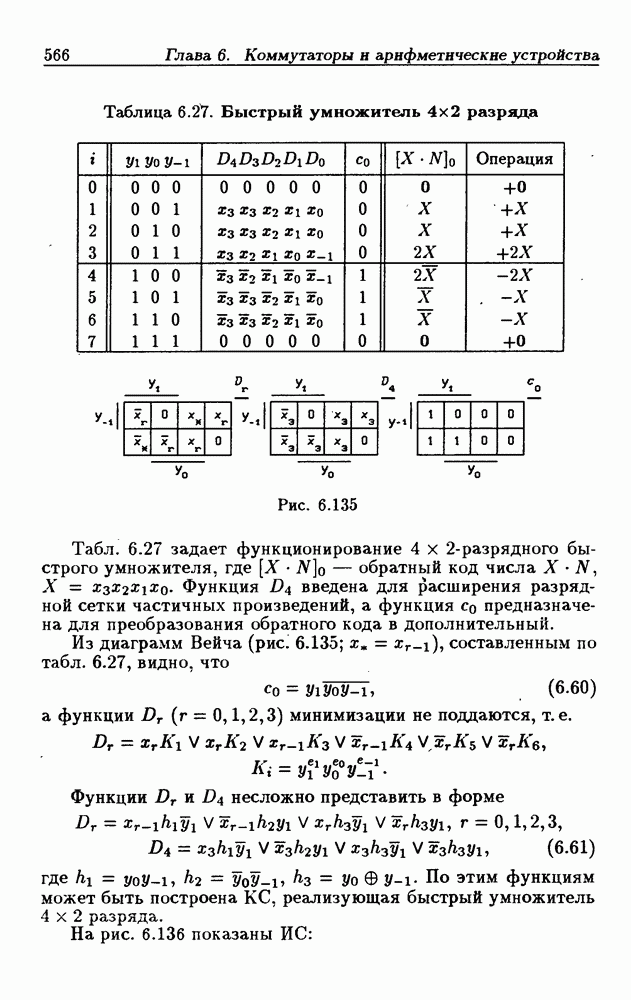
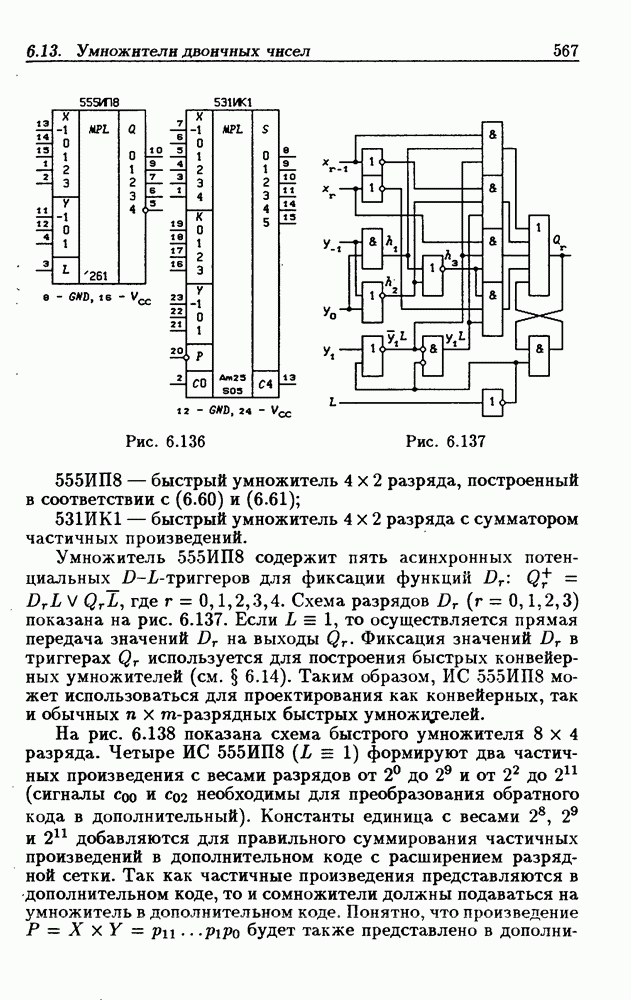
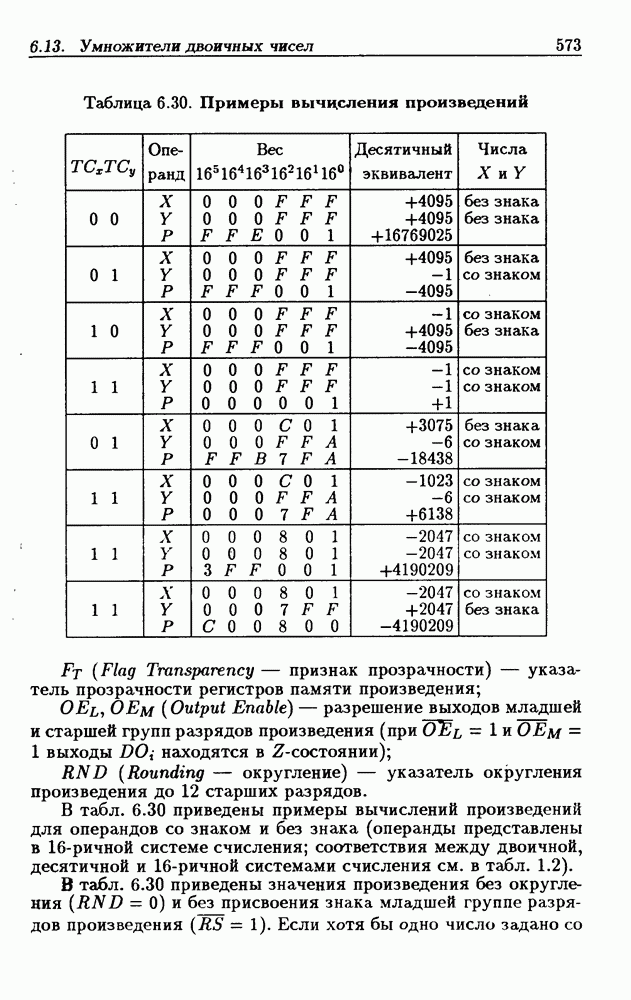
- 6.13. Умножители двоичных чисел
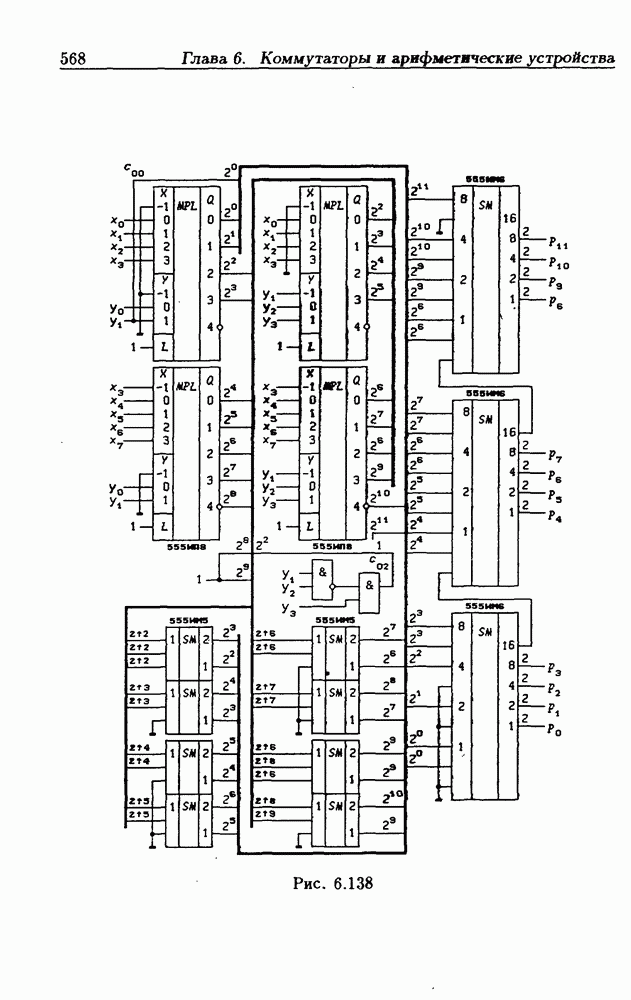
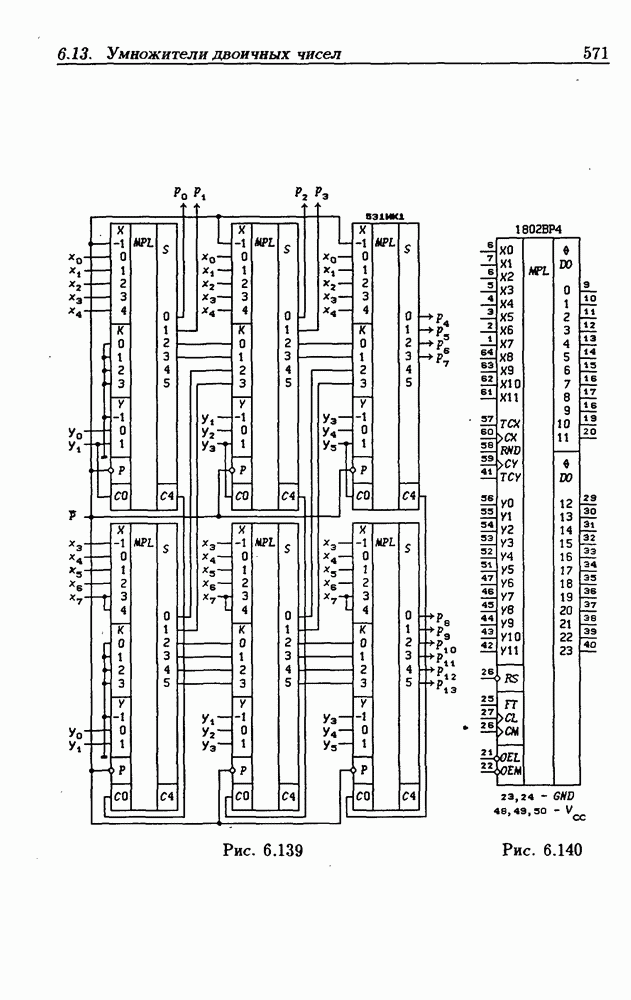
- Быстрые умножители.
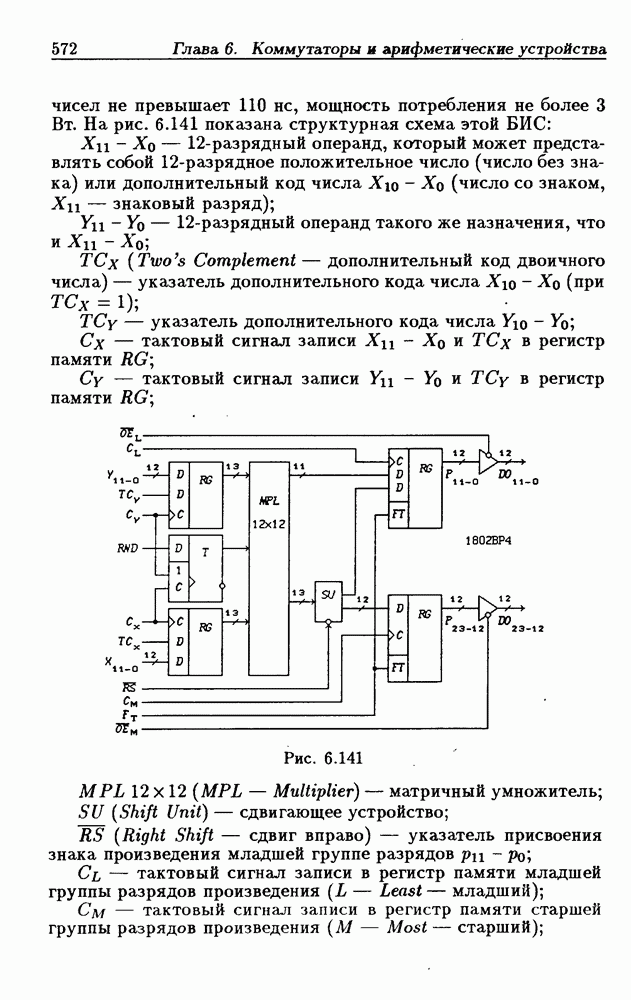
- БИС умножителя 12×12 разрядов 1802ВР4.
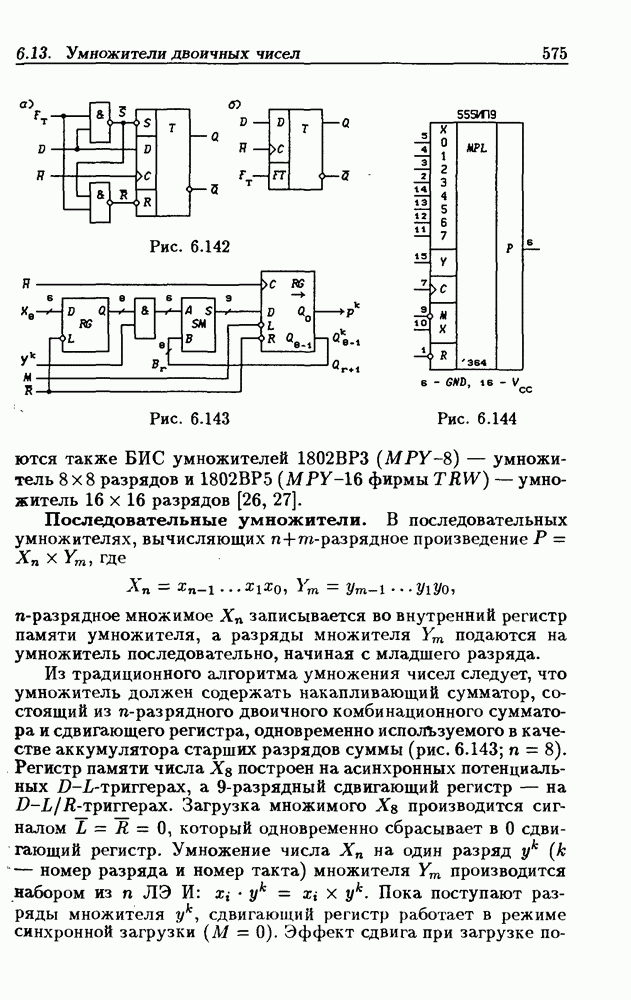
- Последовательные умножители.
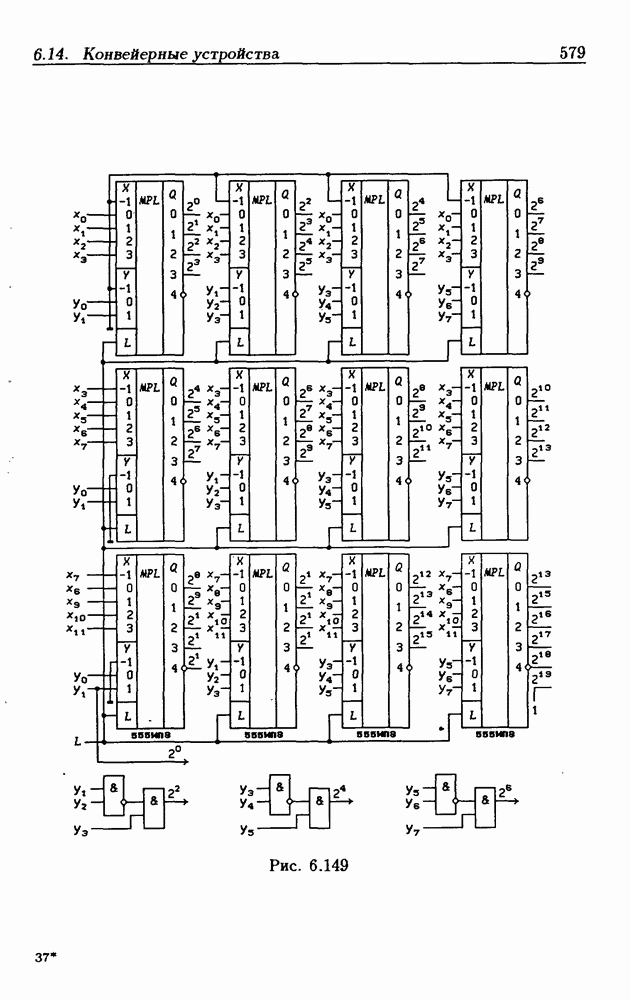
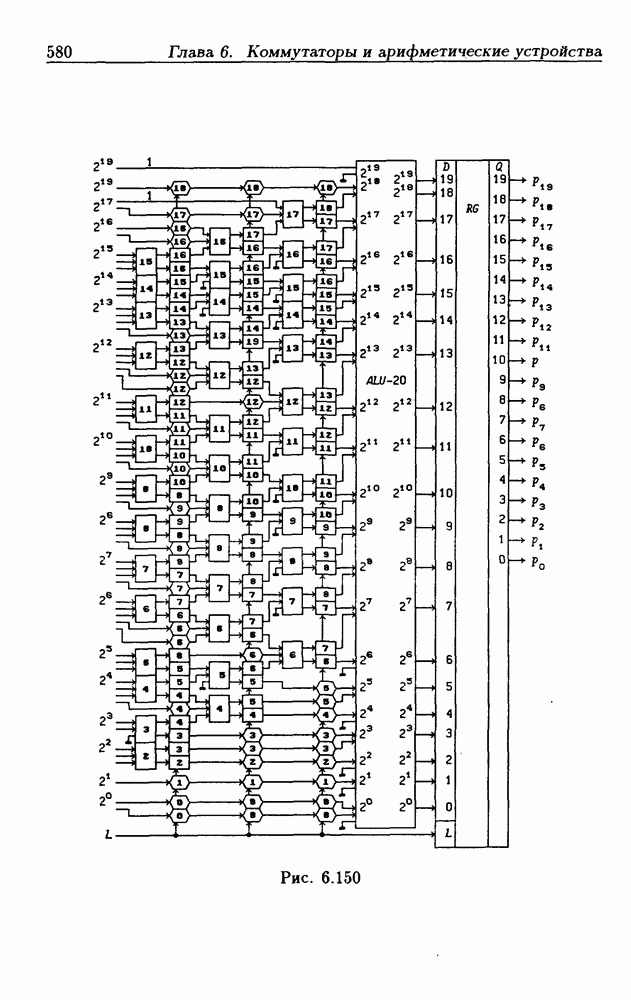
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
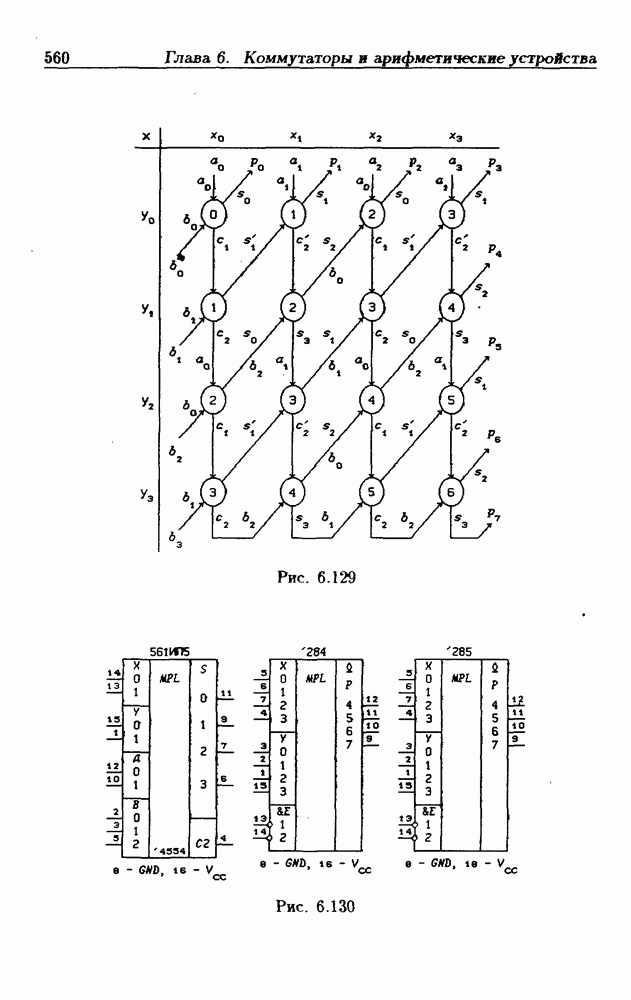
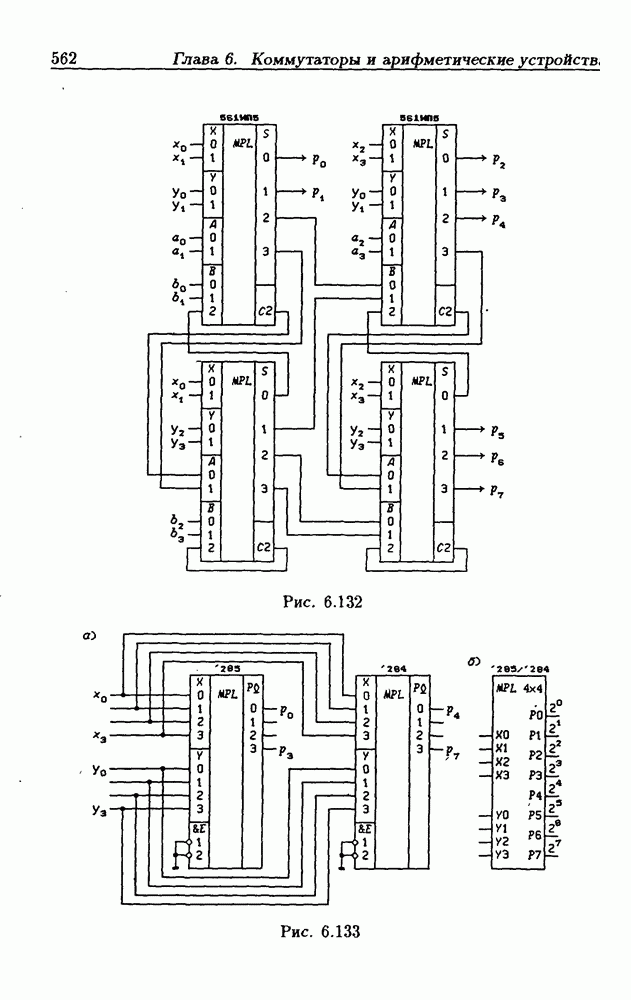
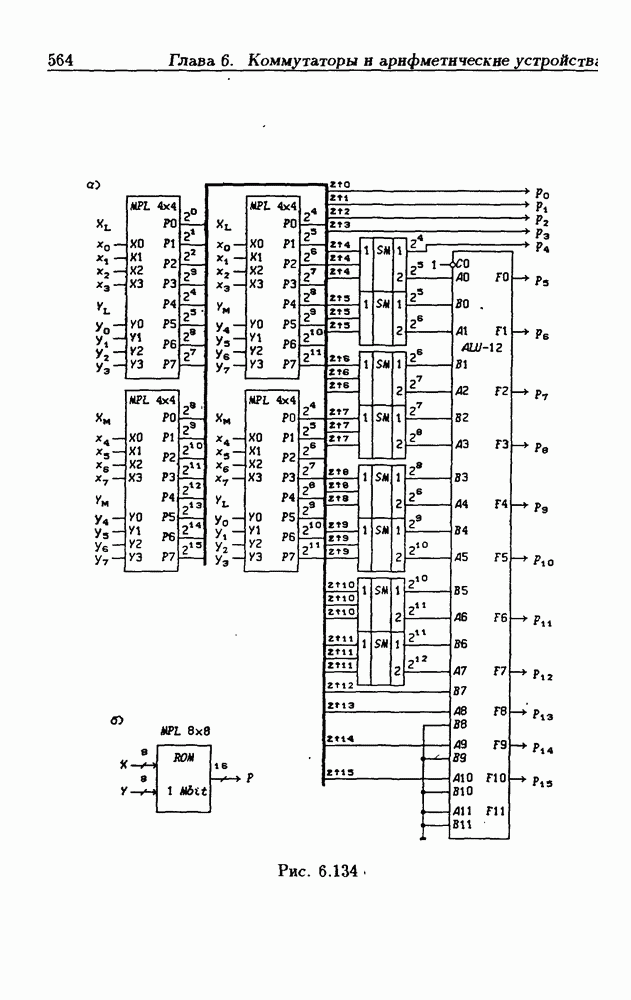
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
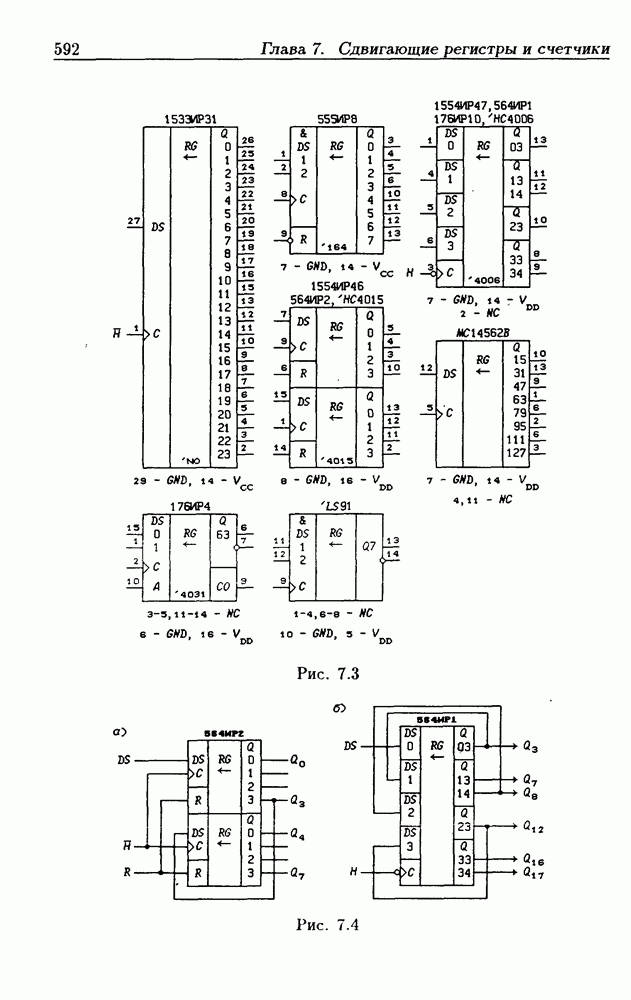
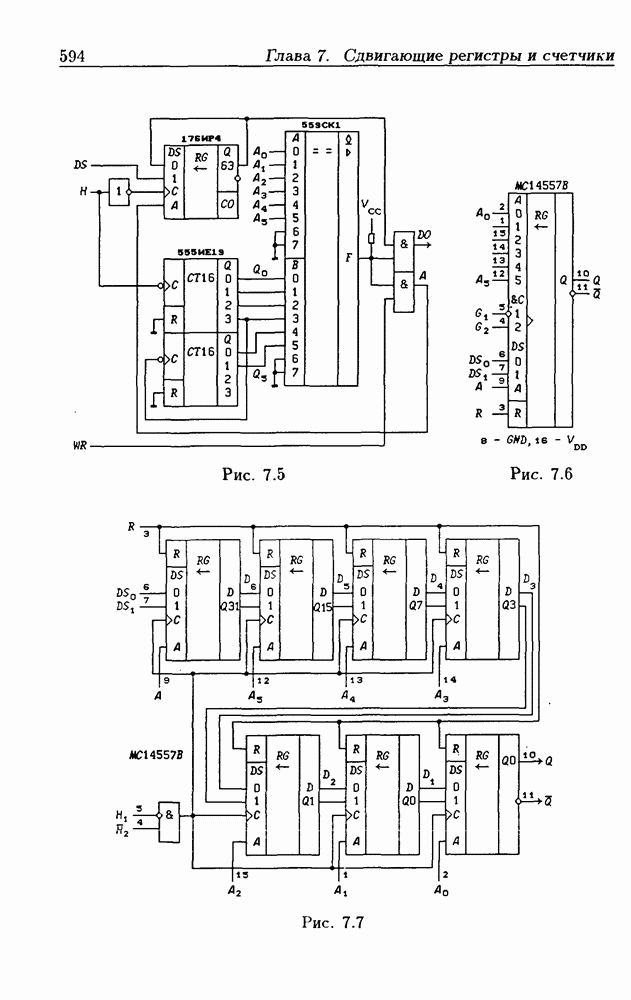
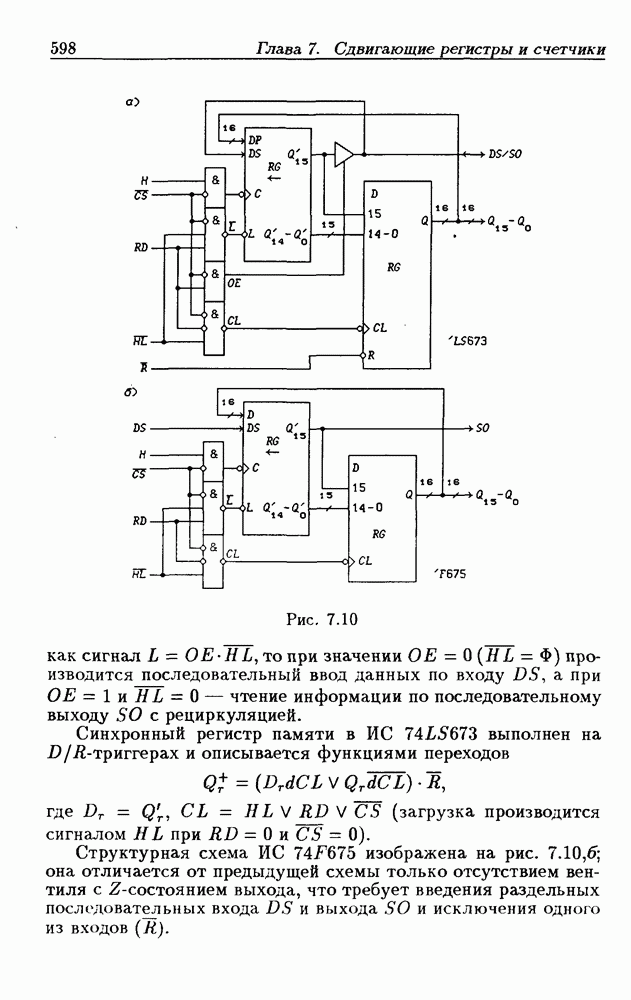
- Глава 7. Сдвигающие регистры и счетчики
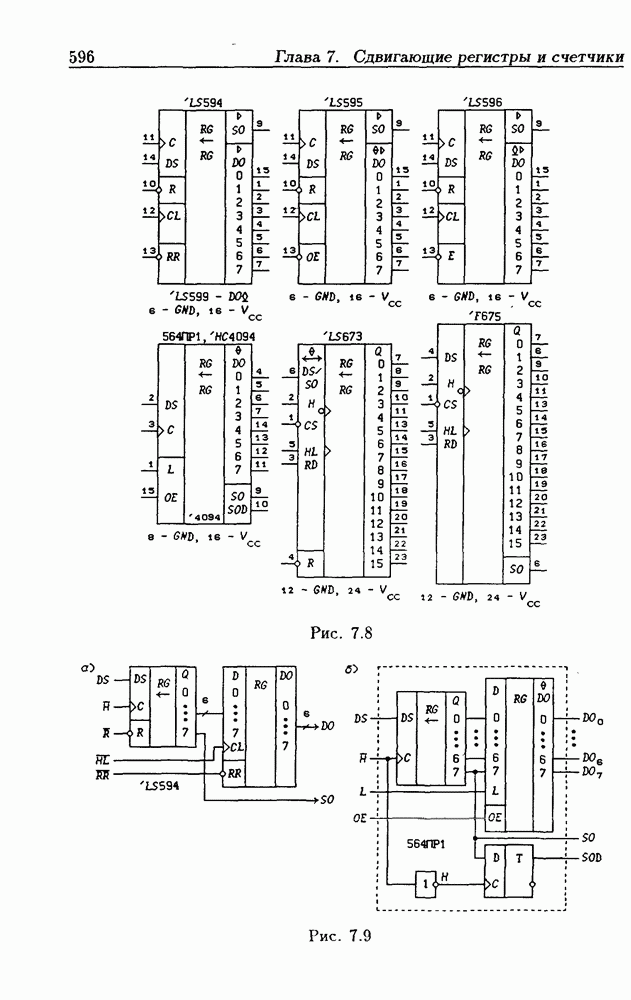
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
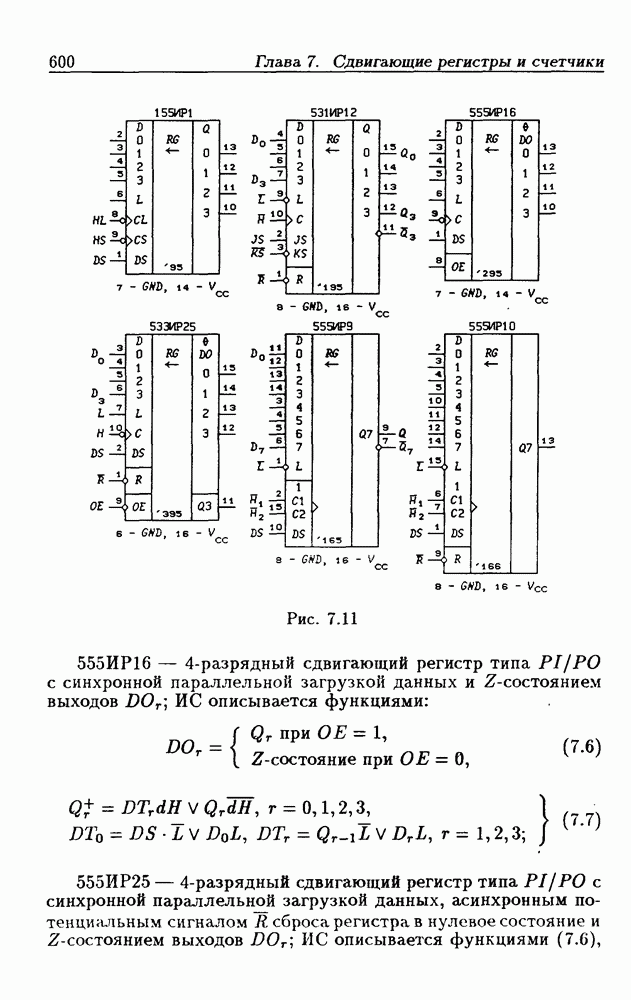
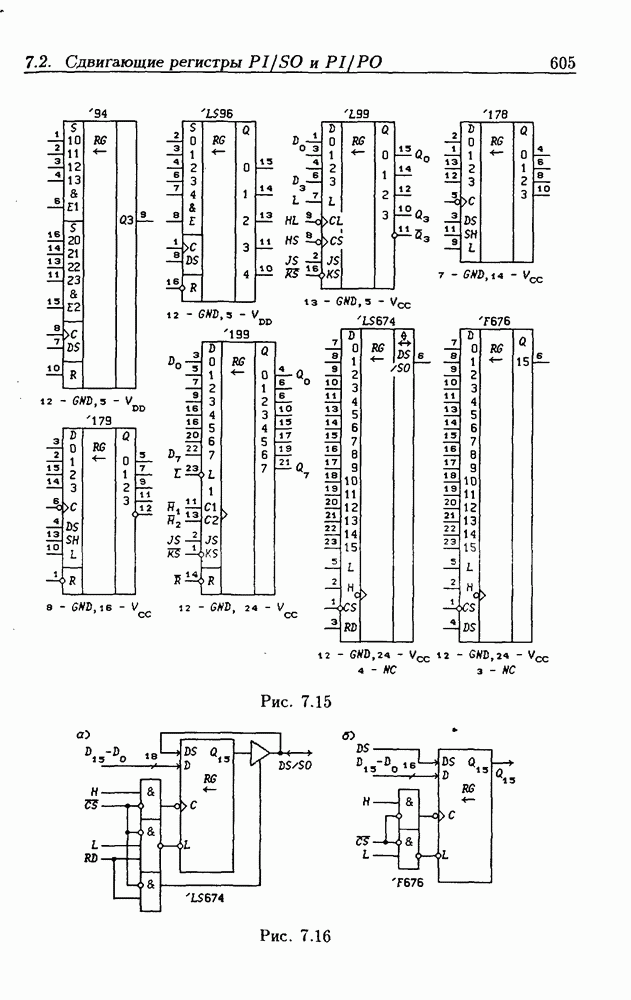
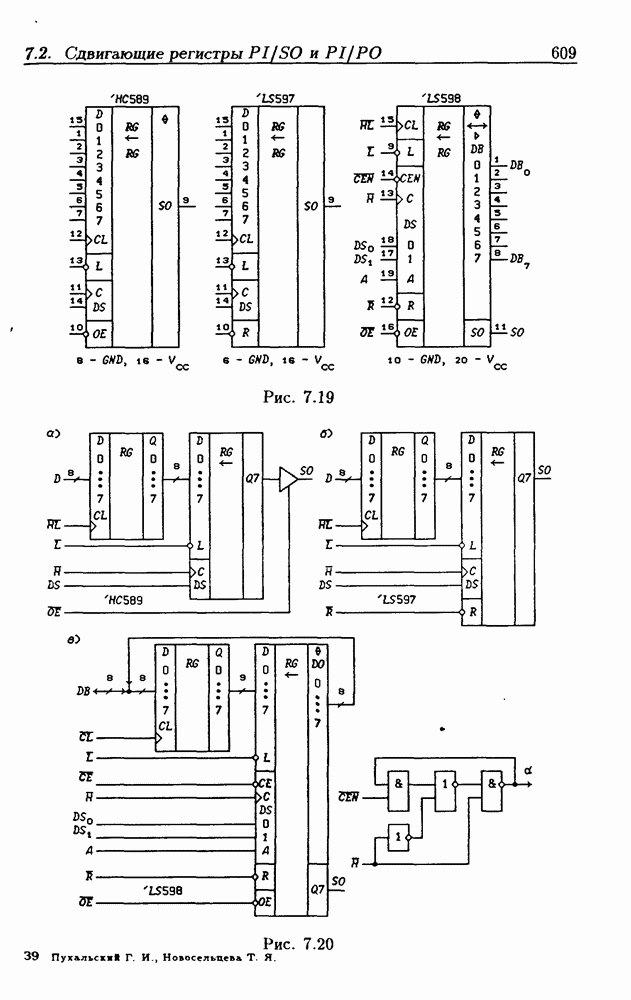
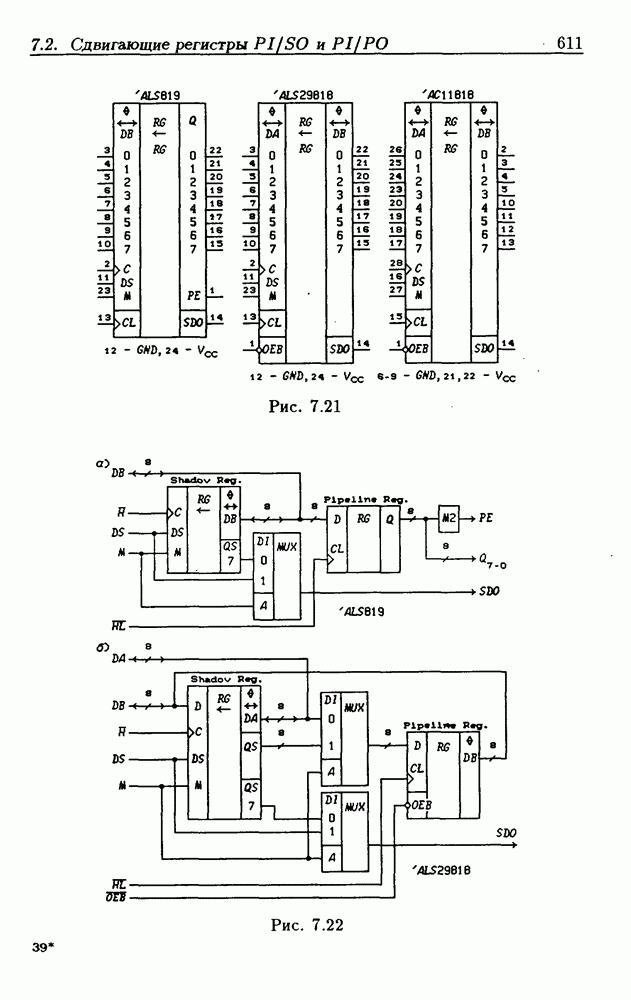
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
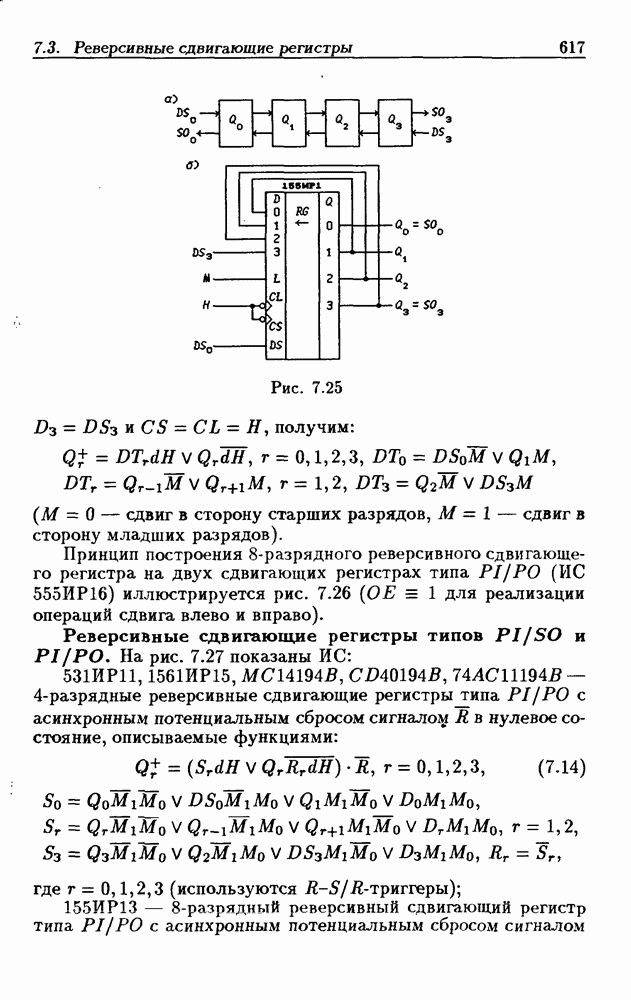
- 7.3. Реверсивные сдвигающие регистры
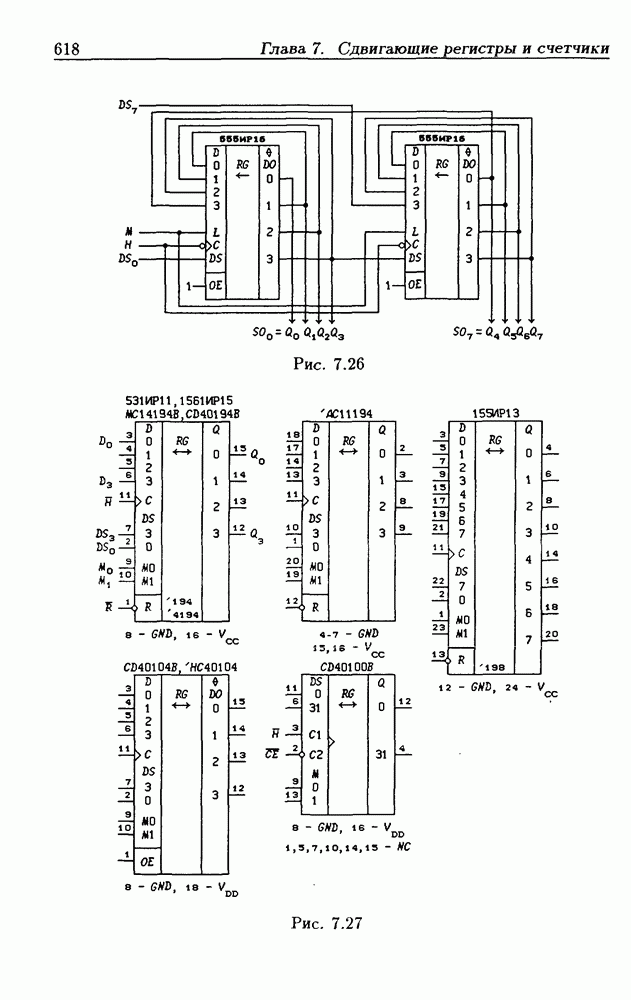
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
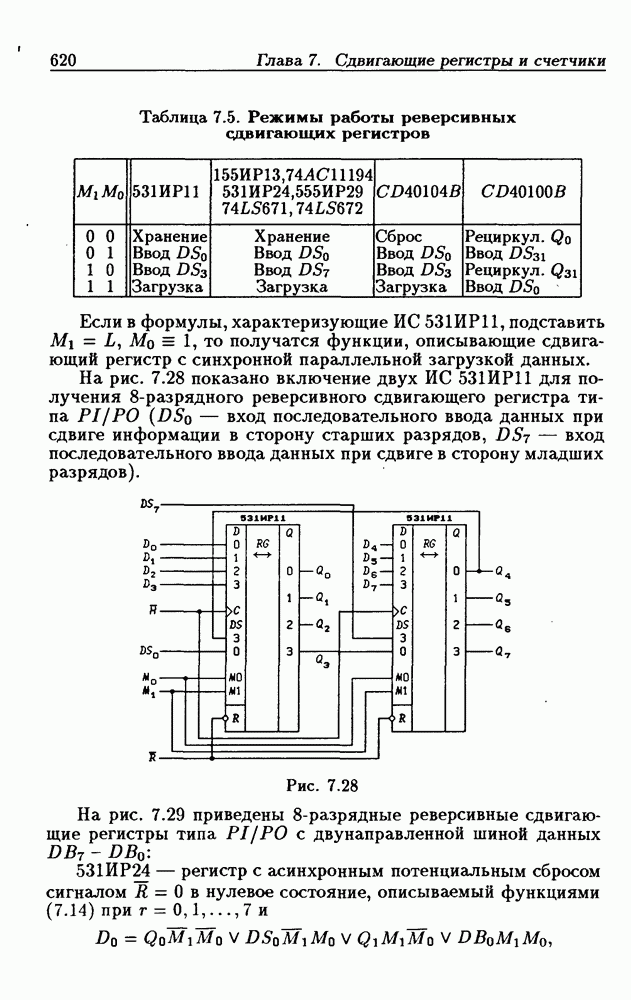
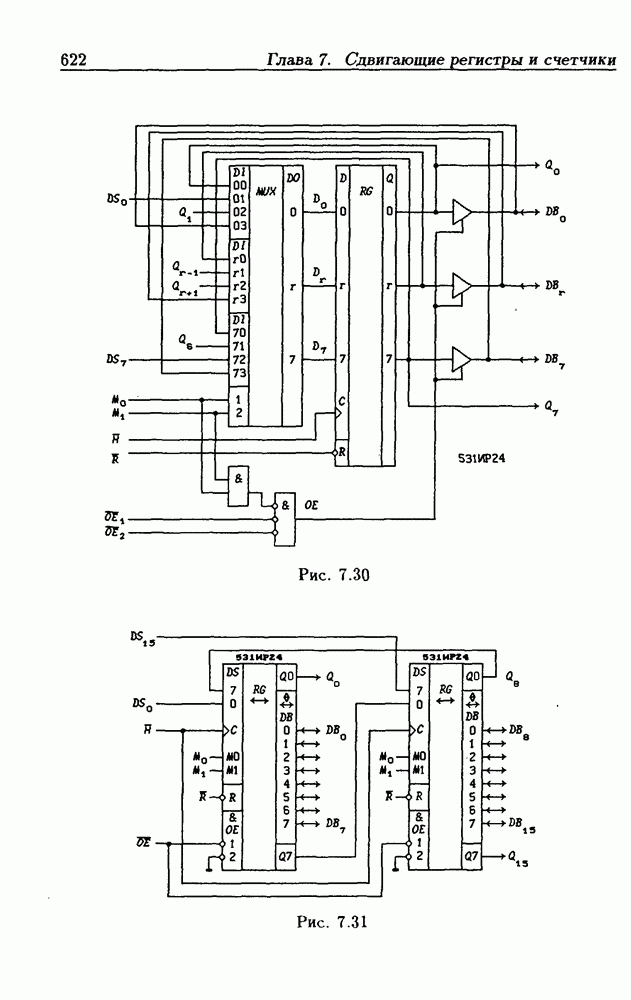
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
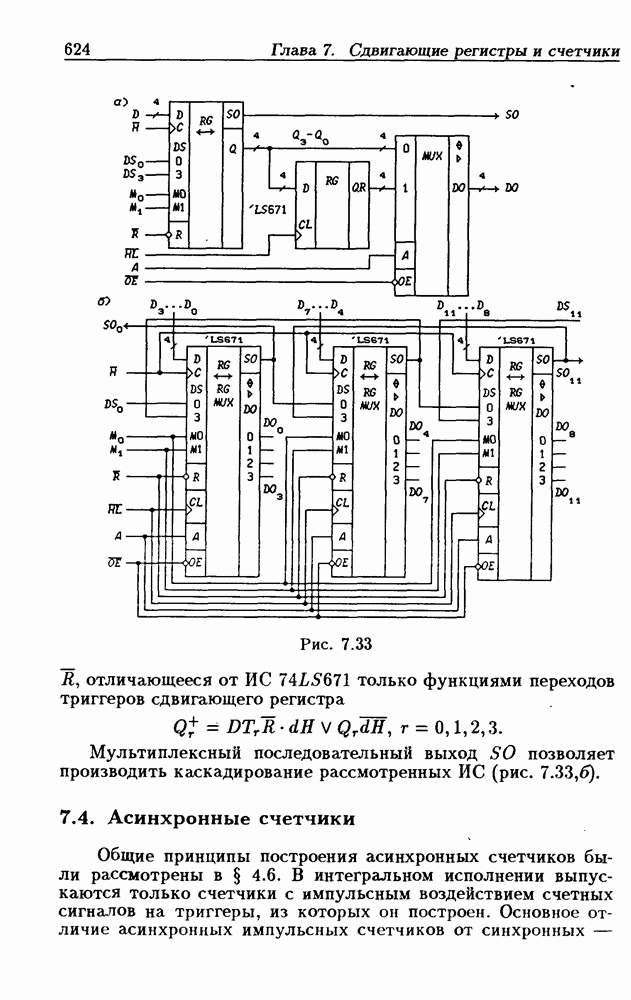
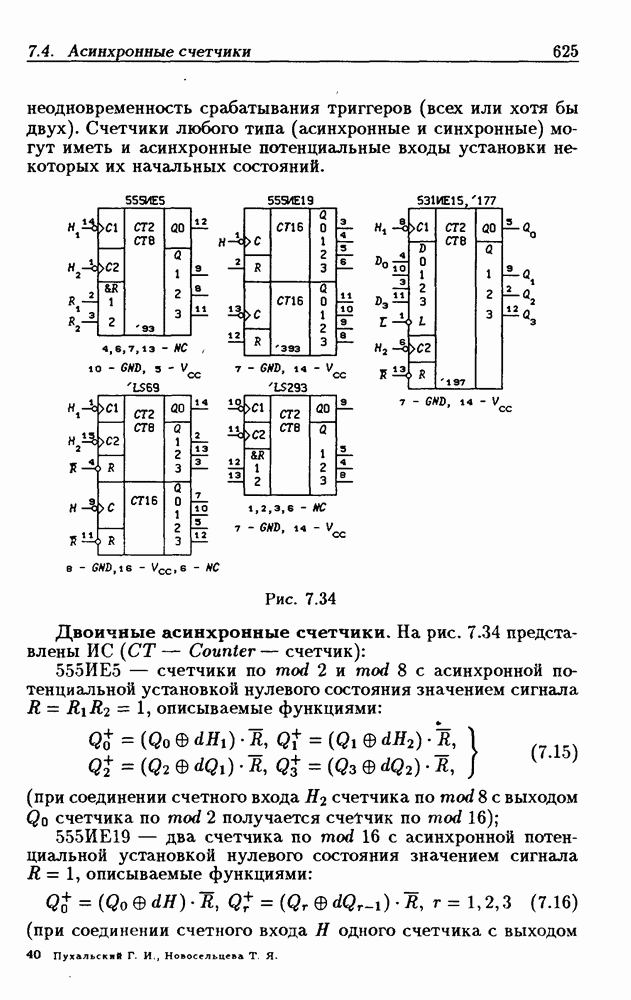
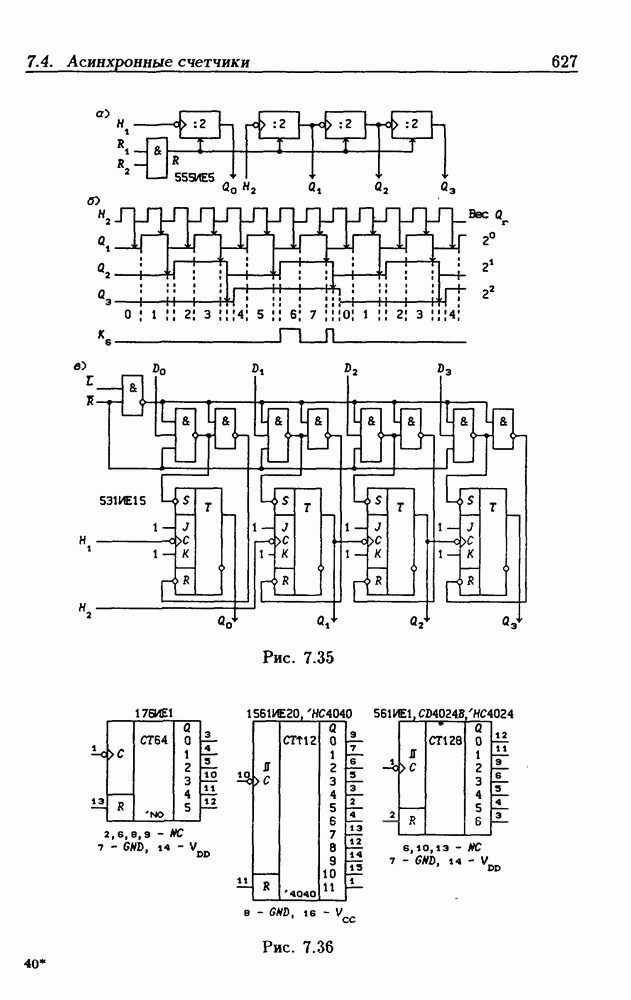
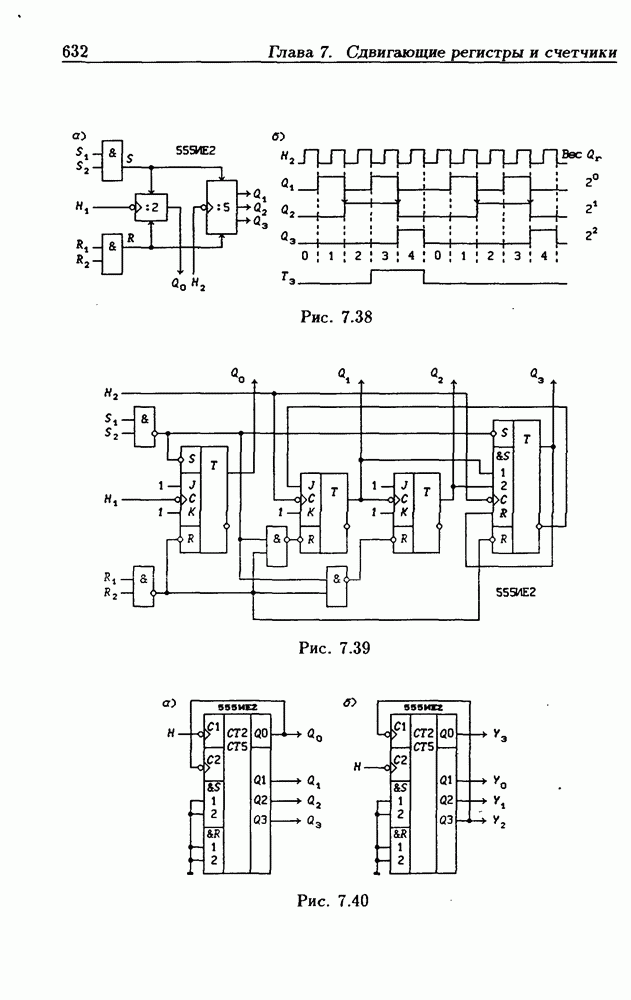
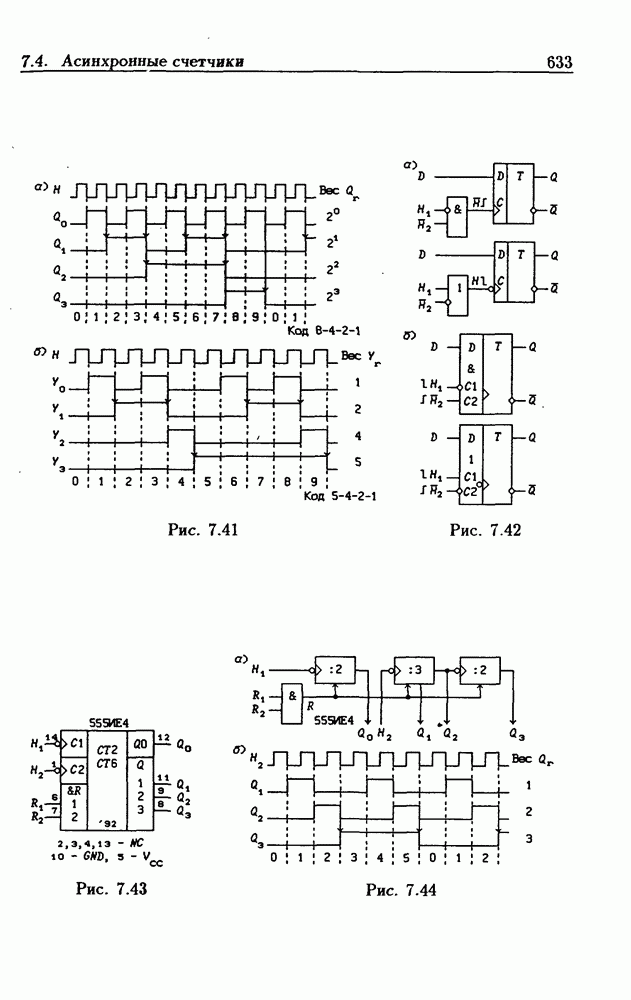
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
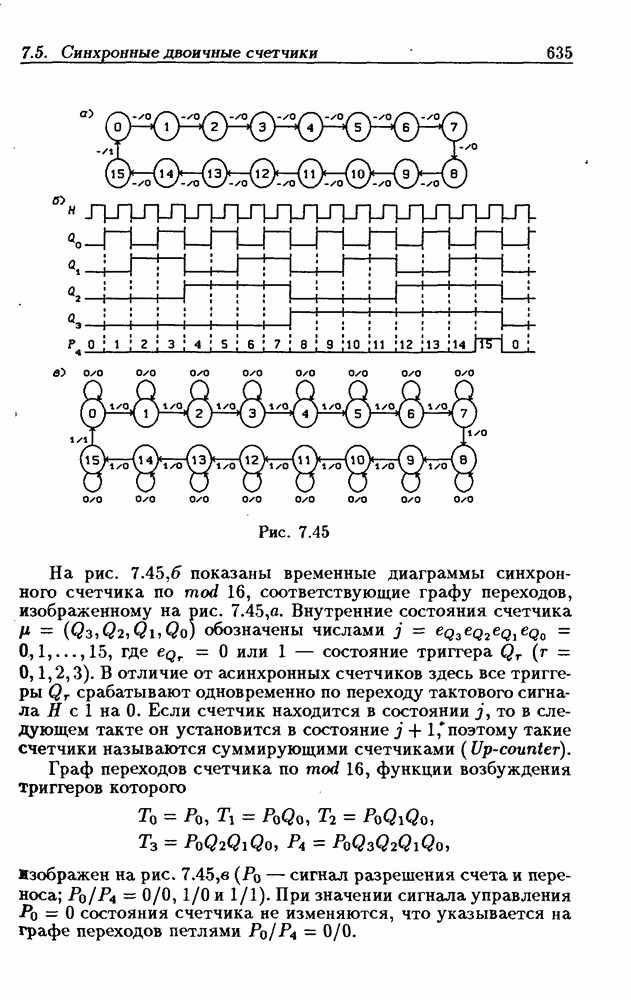
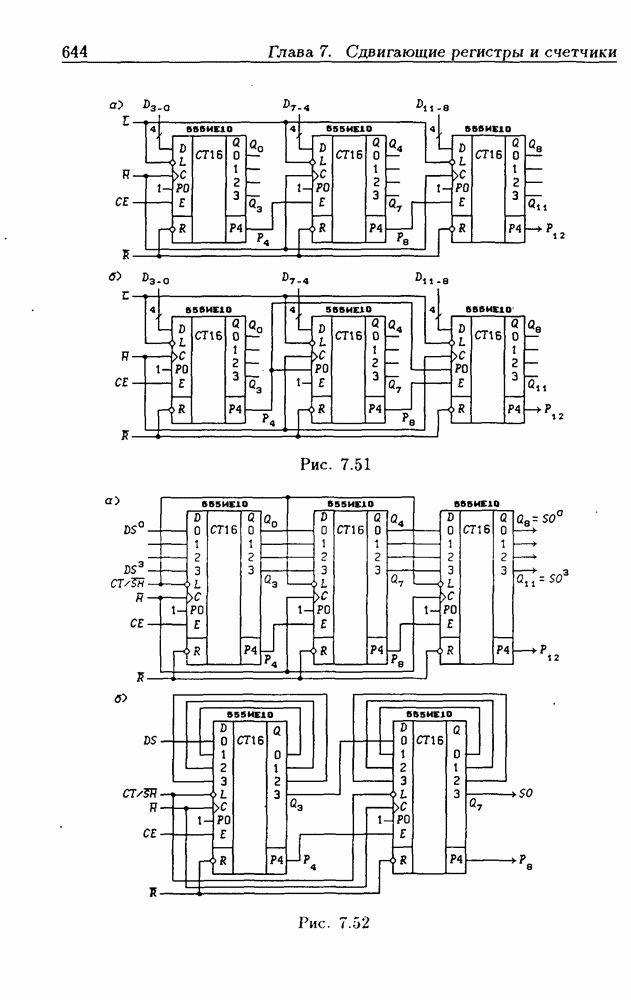
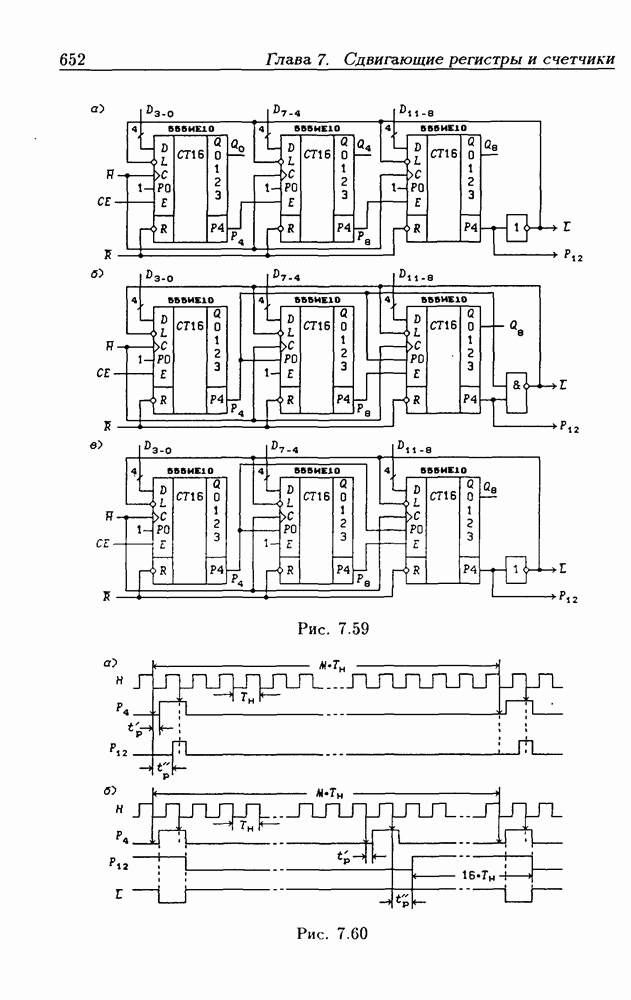
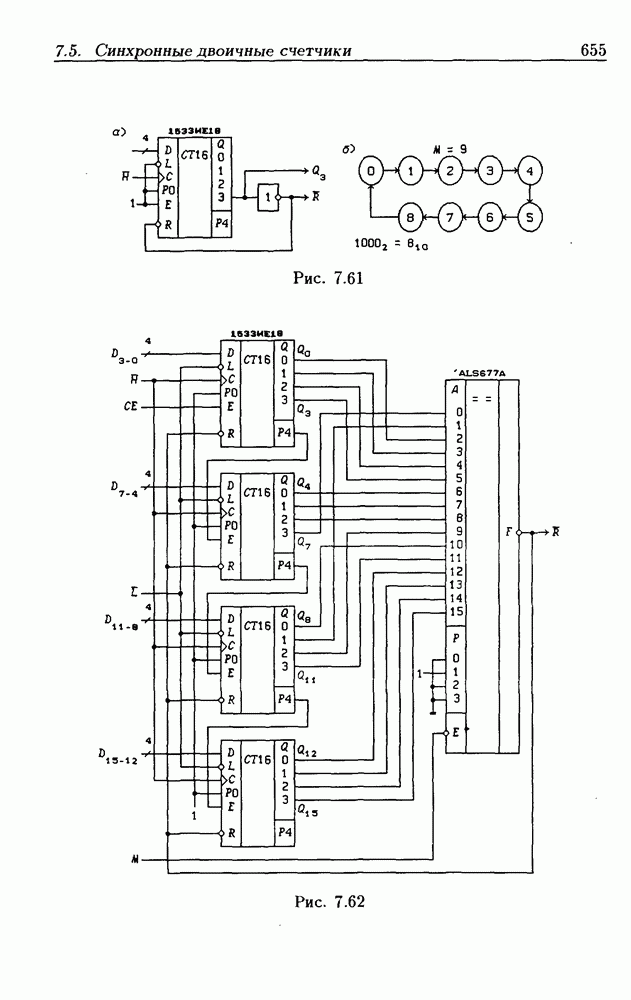
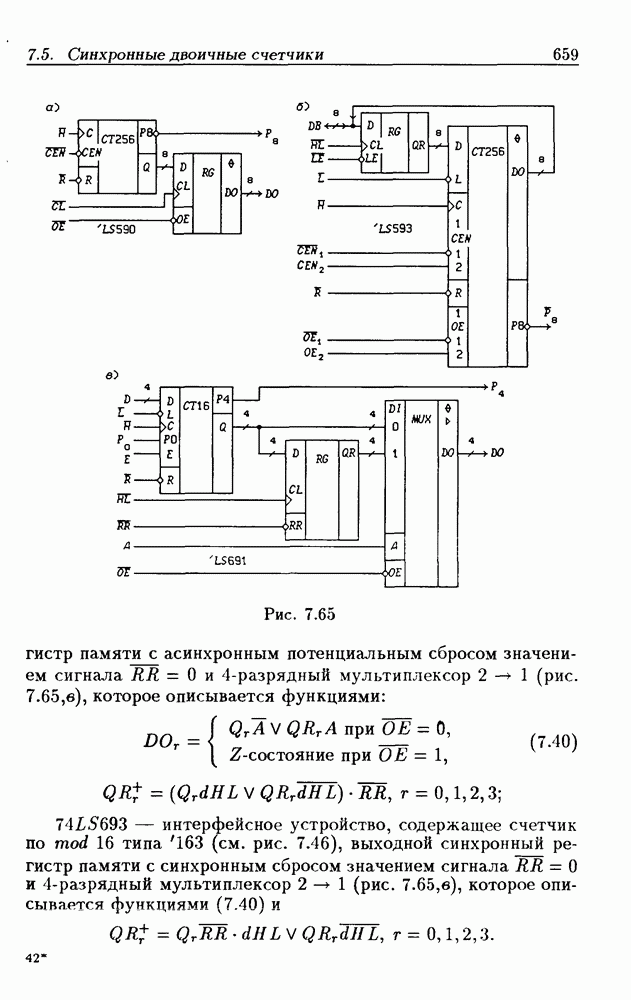
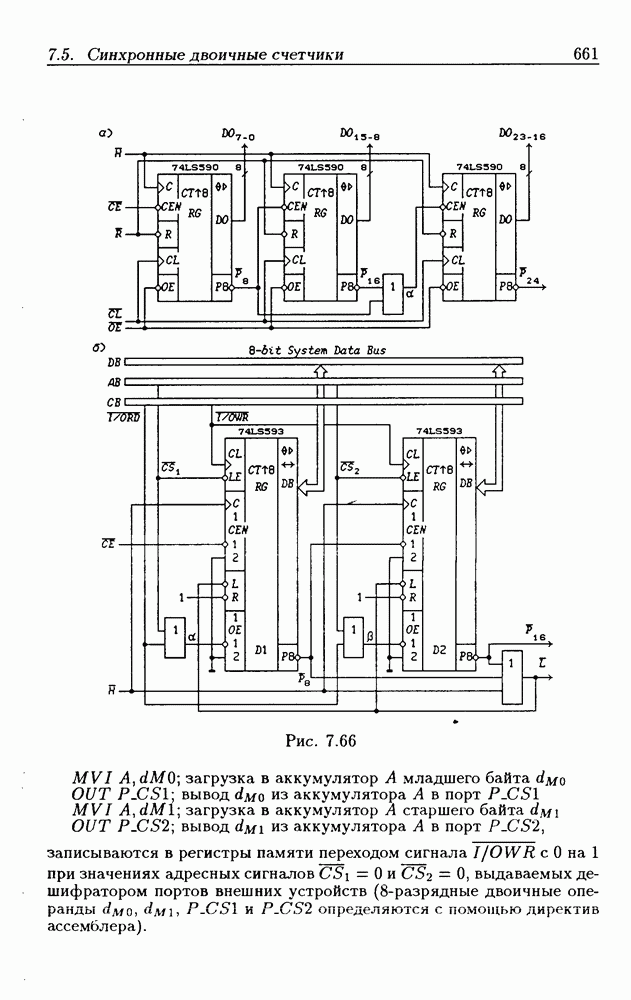
- 7.5. Синхронные двоичные счетчики
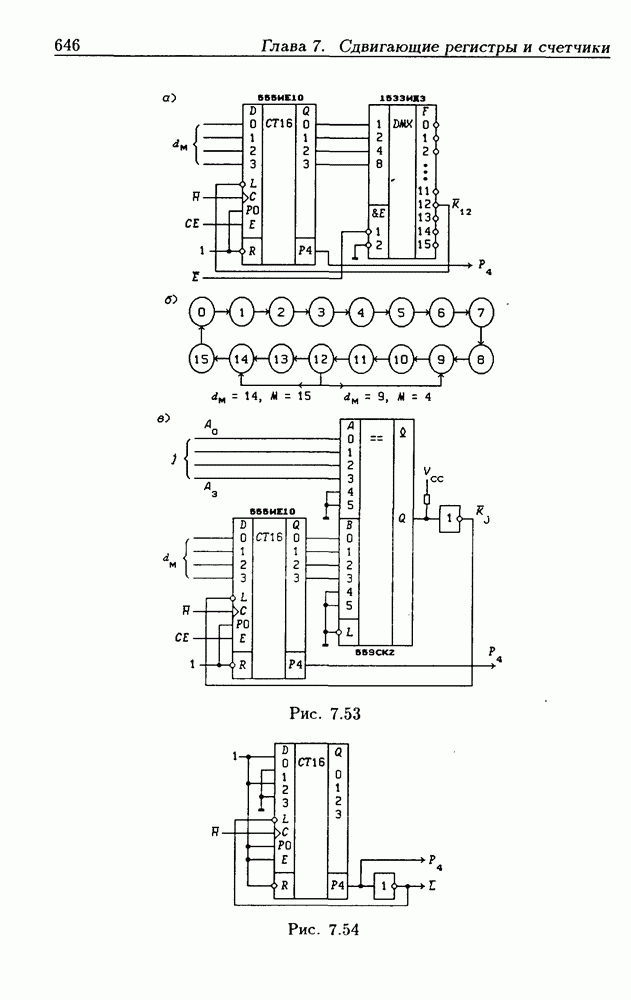
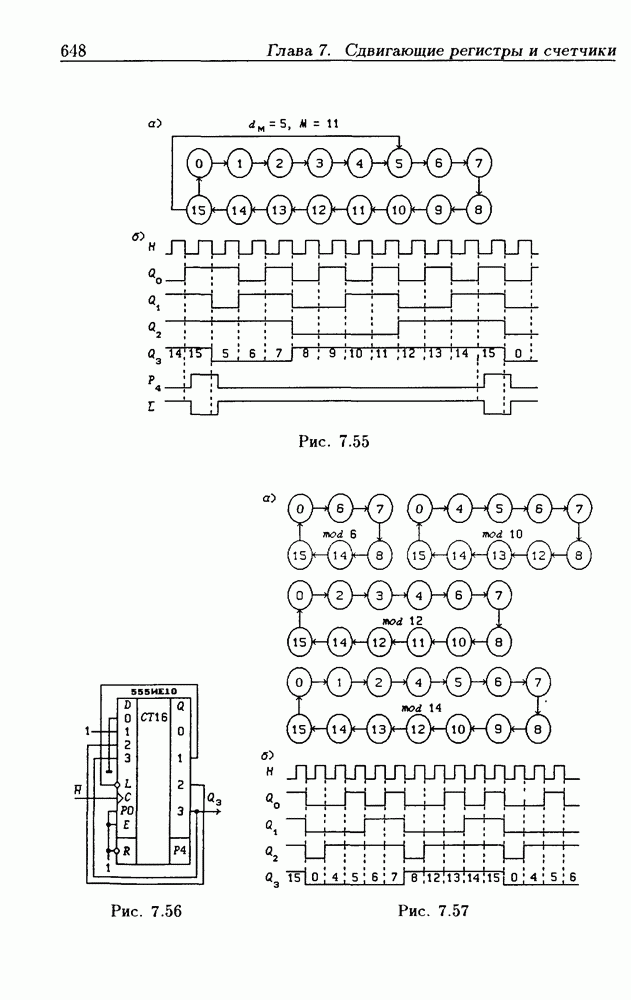
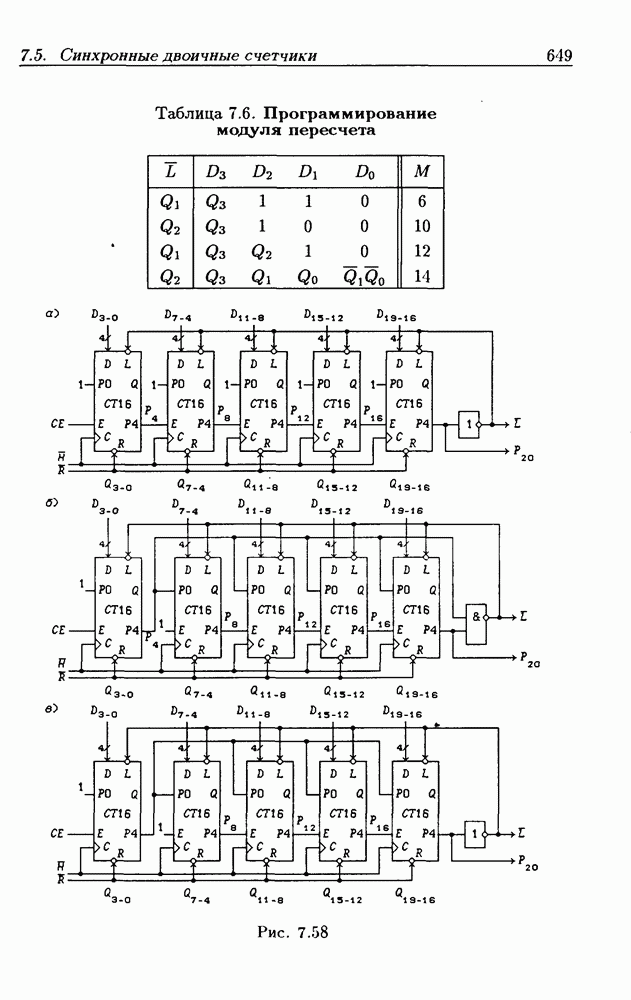
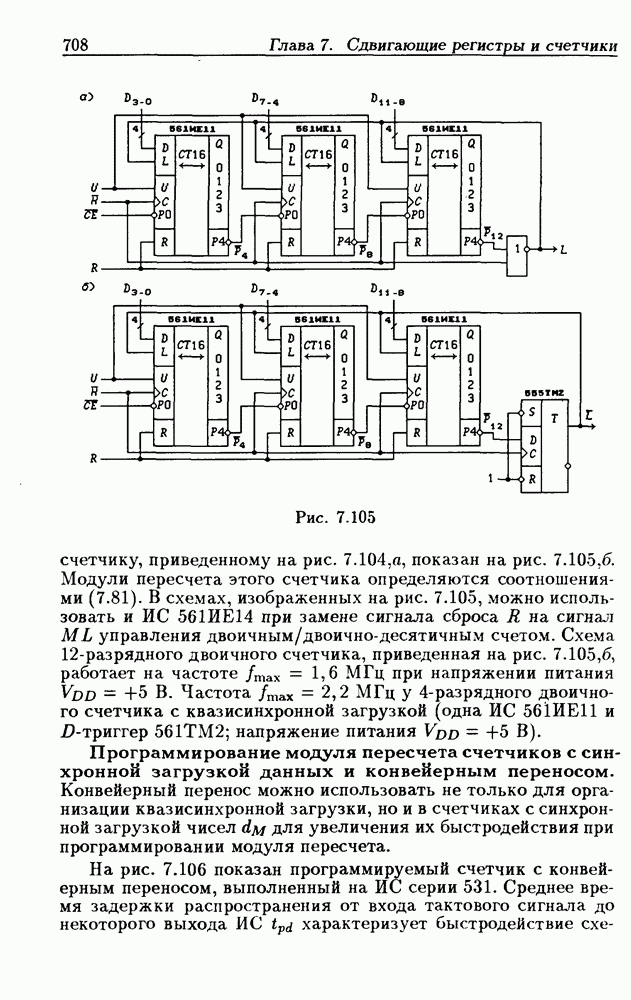
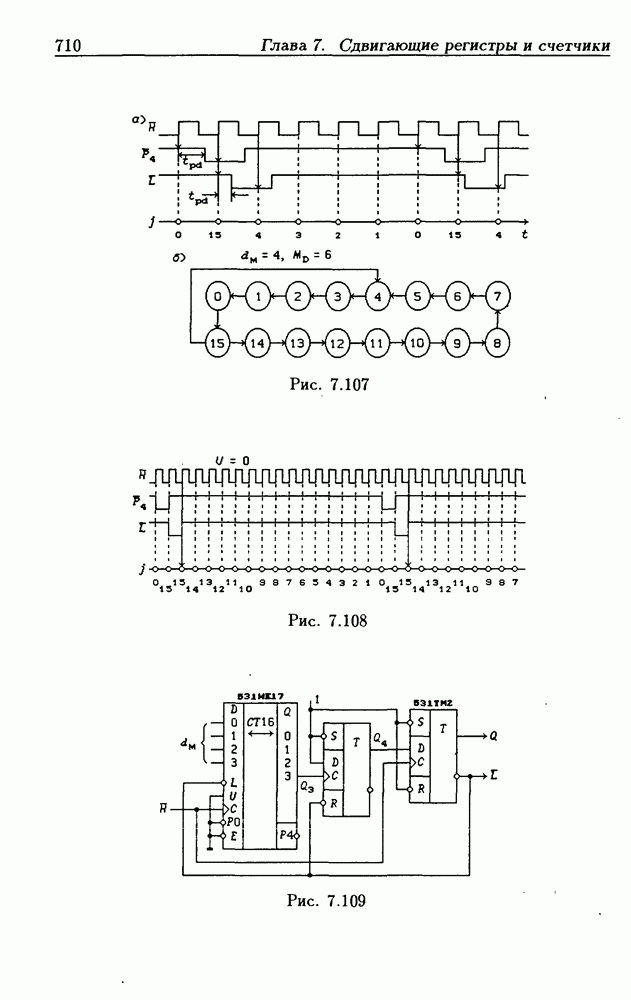
- Программирование модуля пересчета двоичных счетчиков.
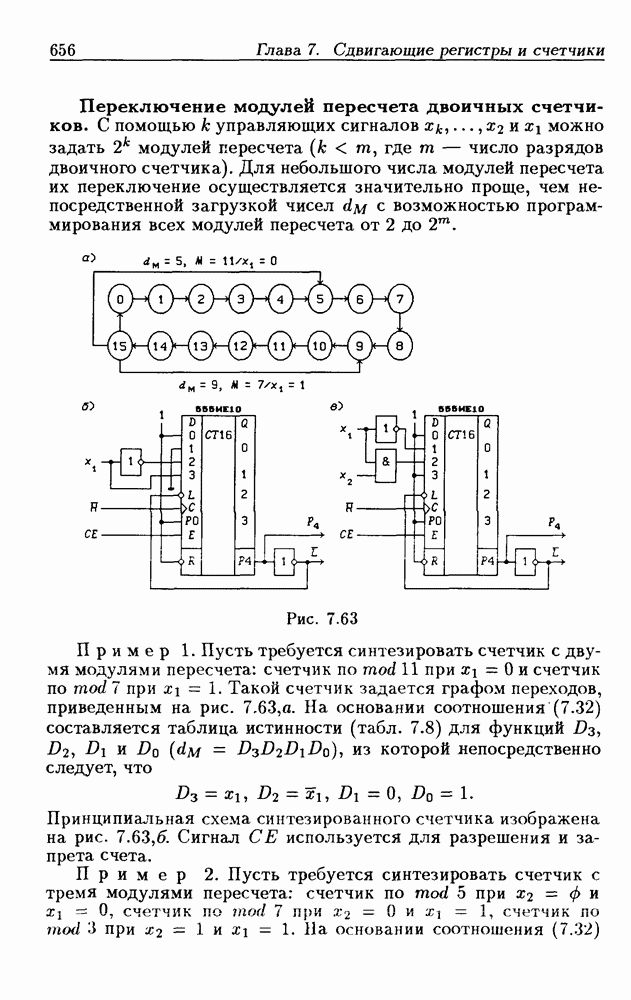
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
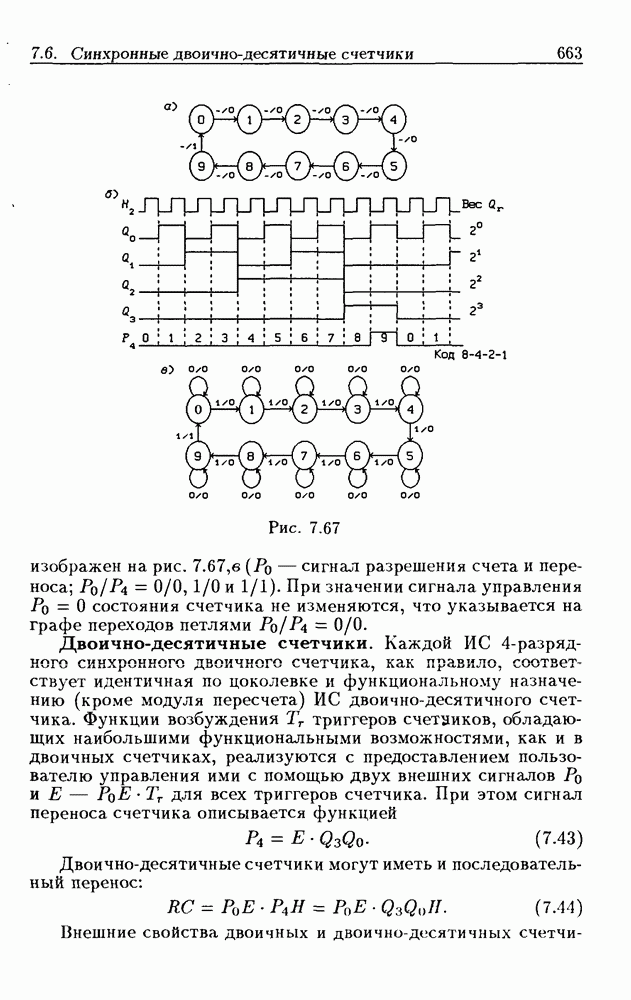
- 7.6. Синхронные двоично-десятичные счетчики
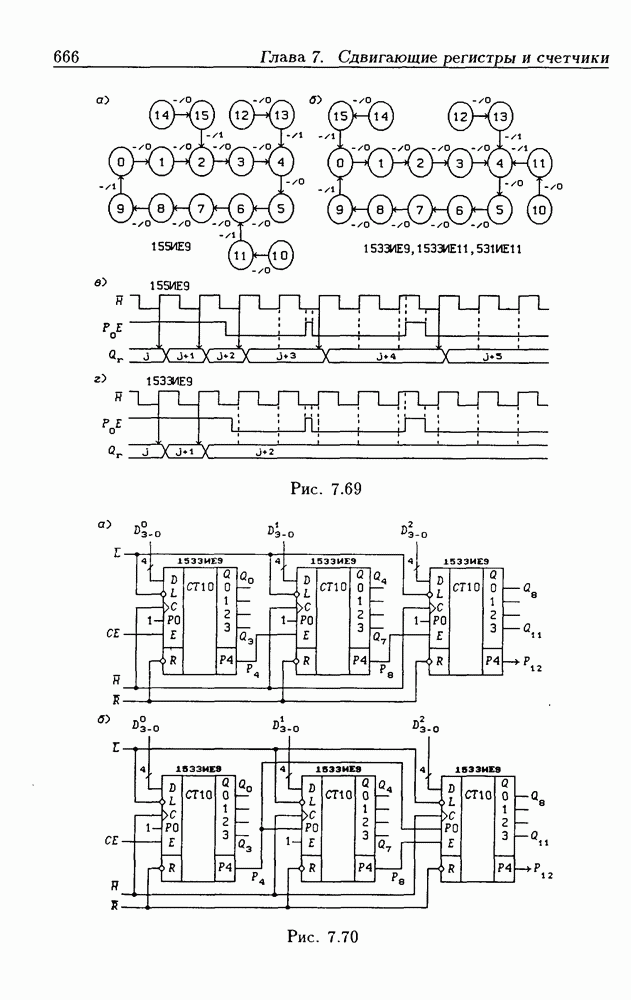
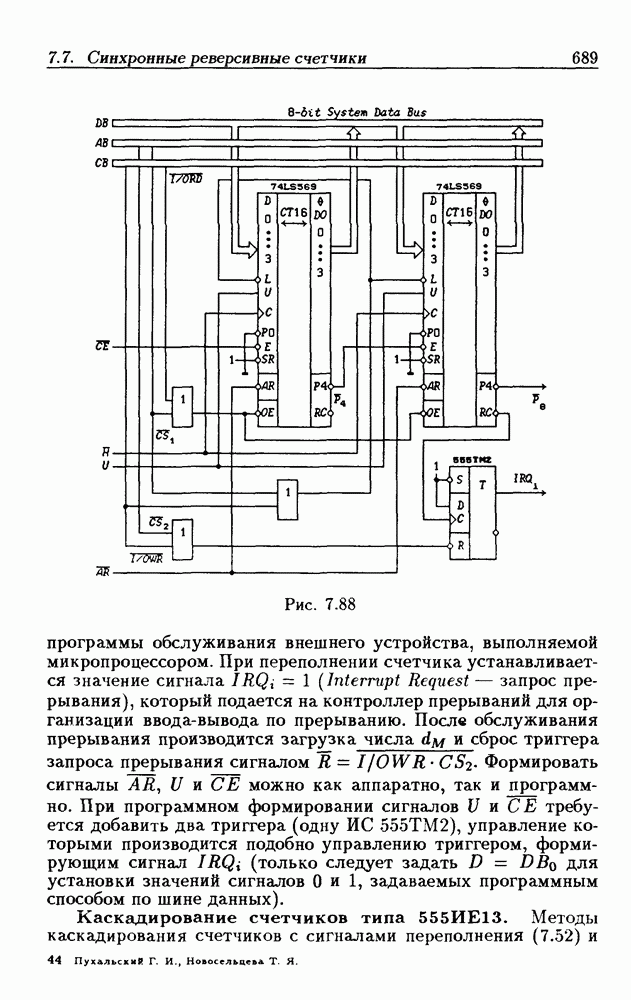
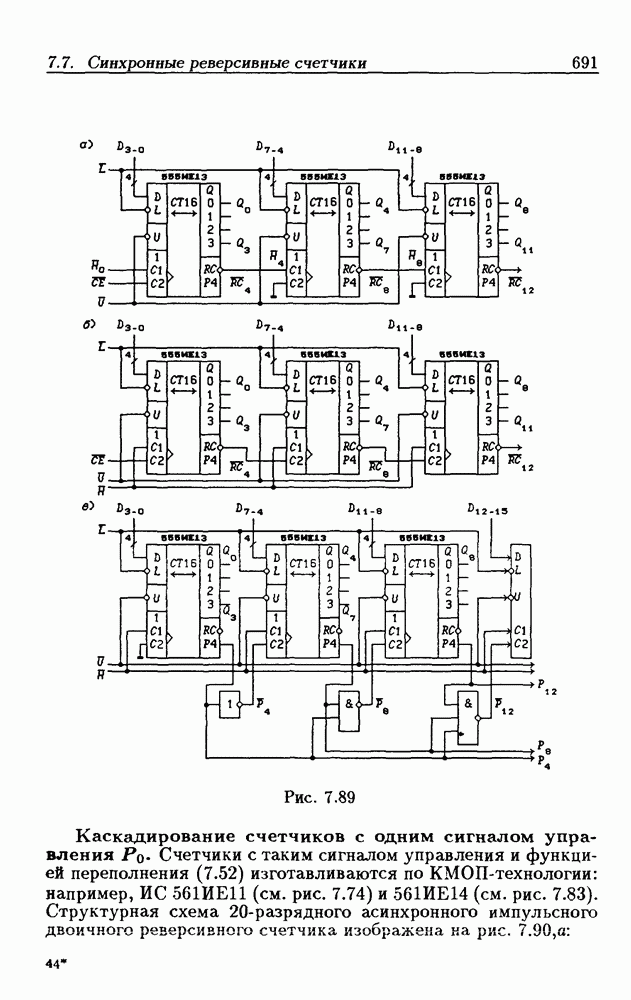
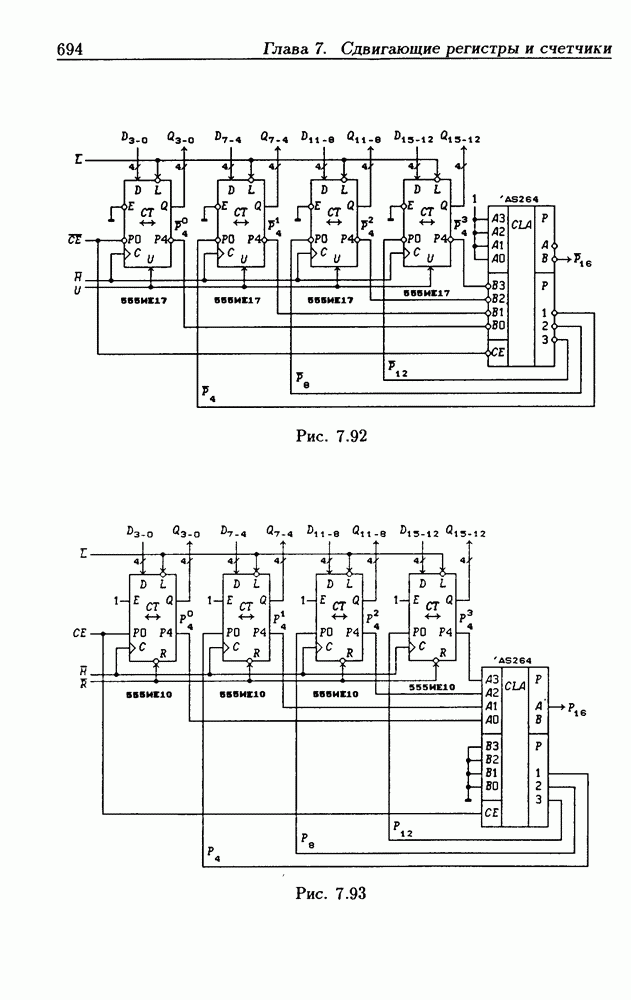
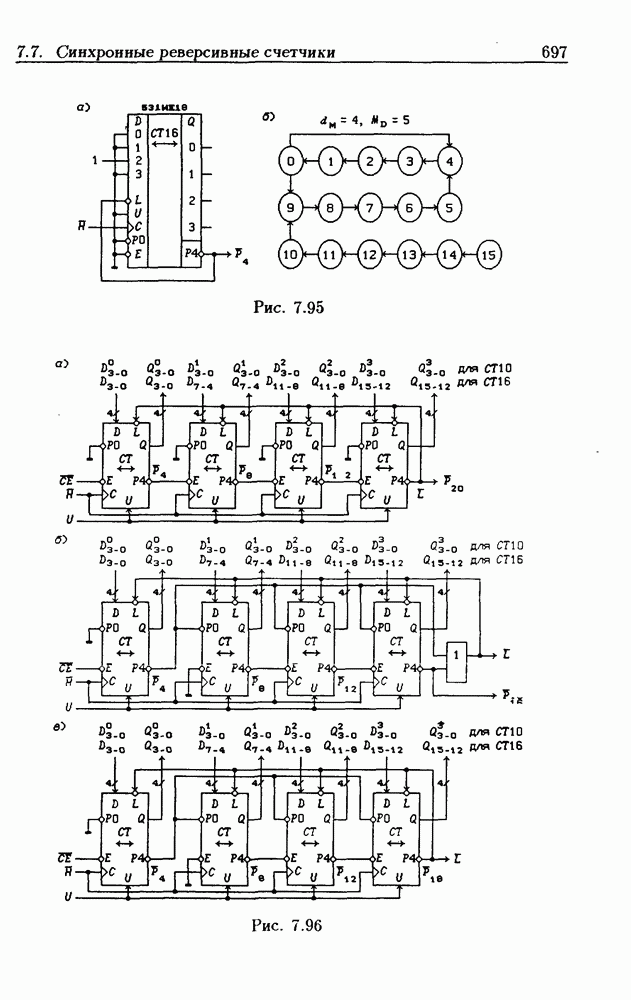
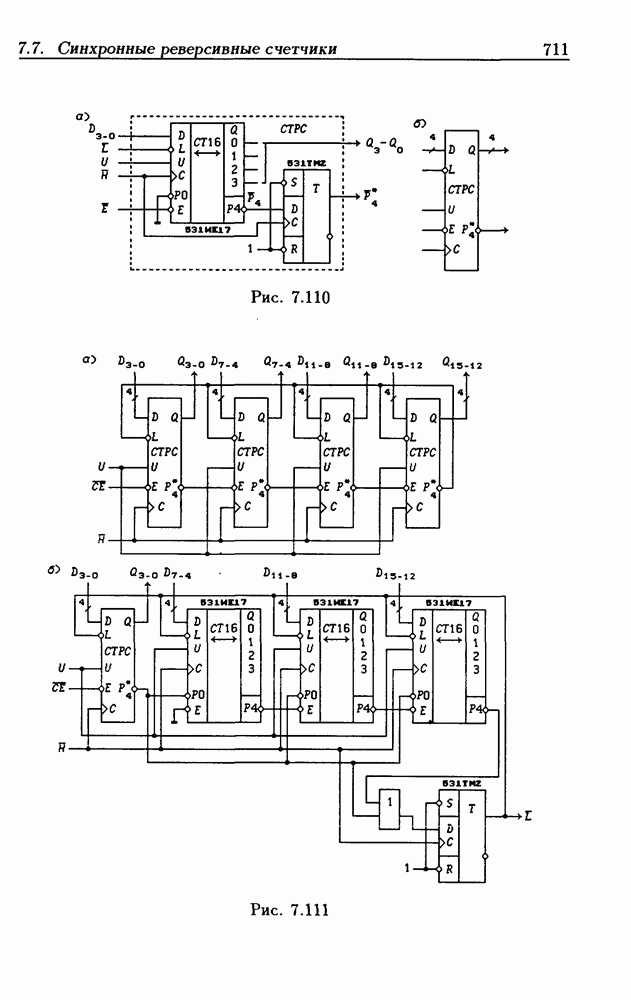
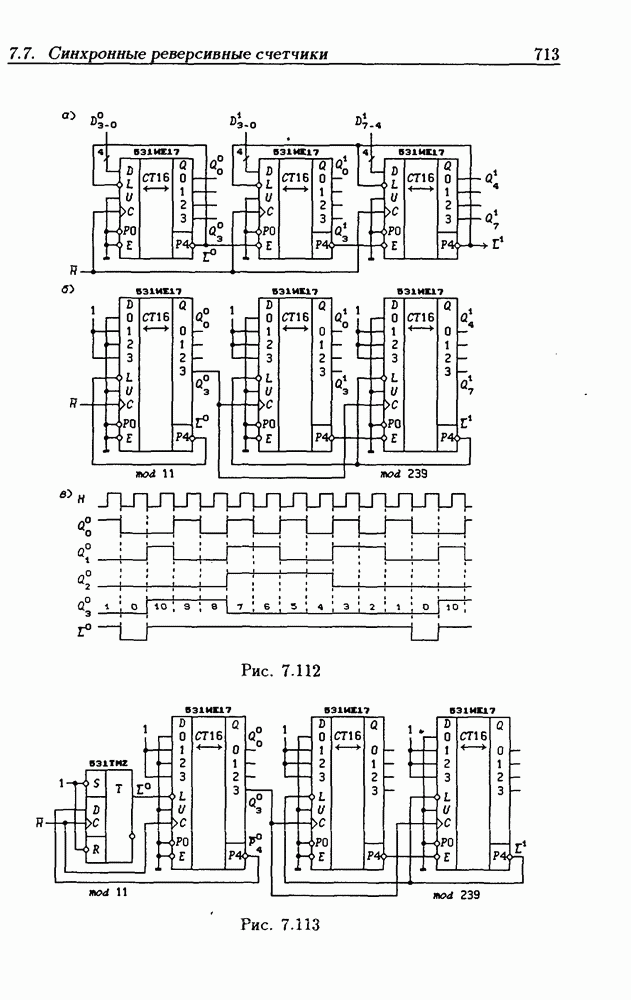
- 7.7. Синхронные реверсивные счетчики
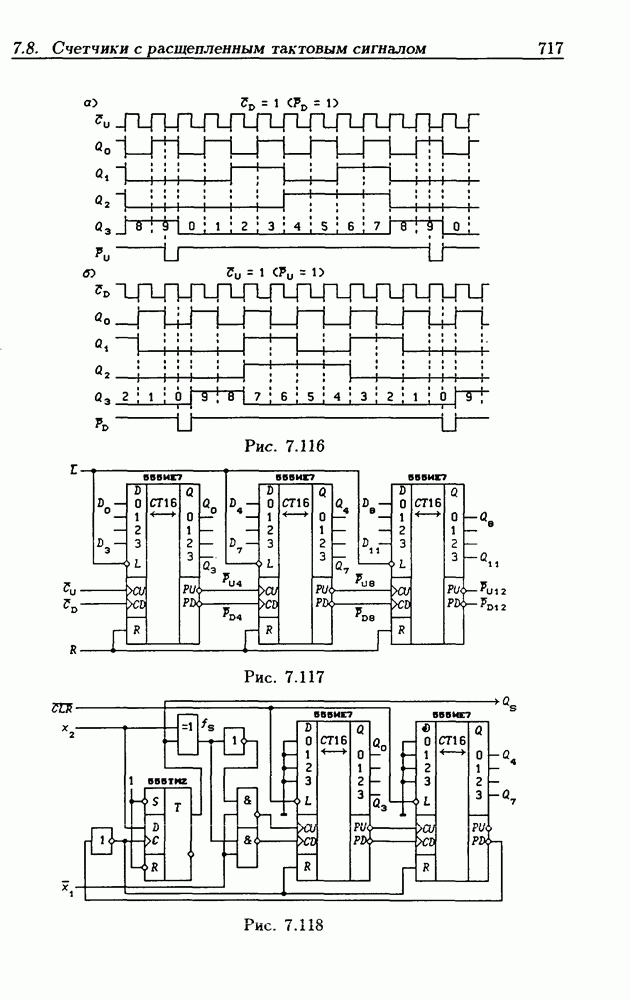
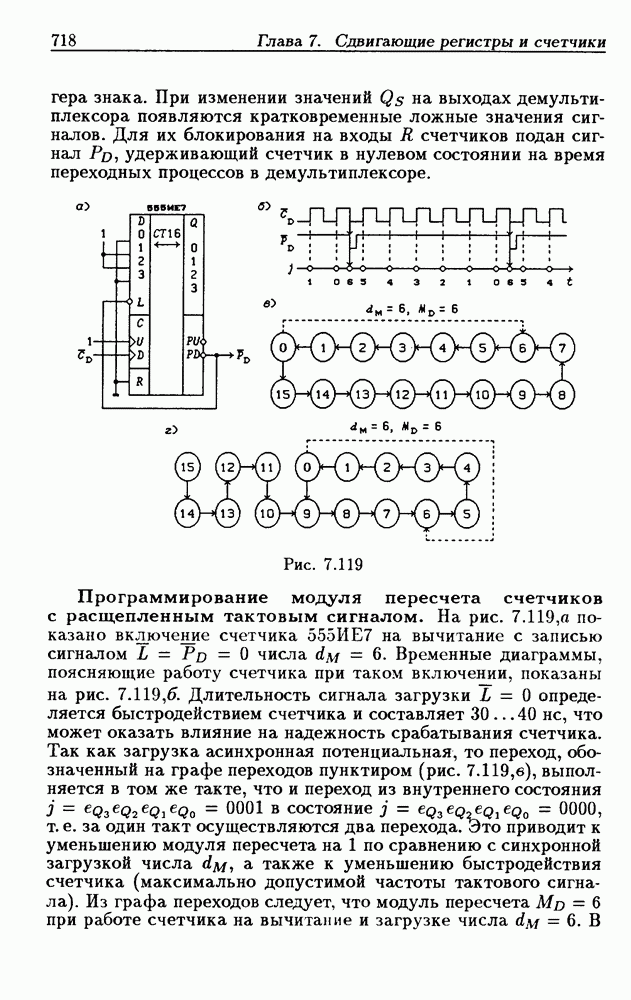
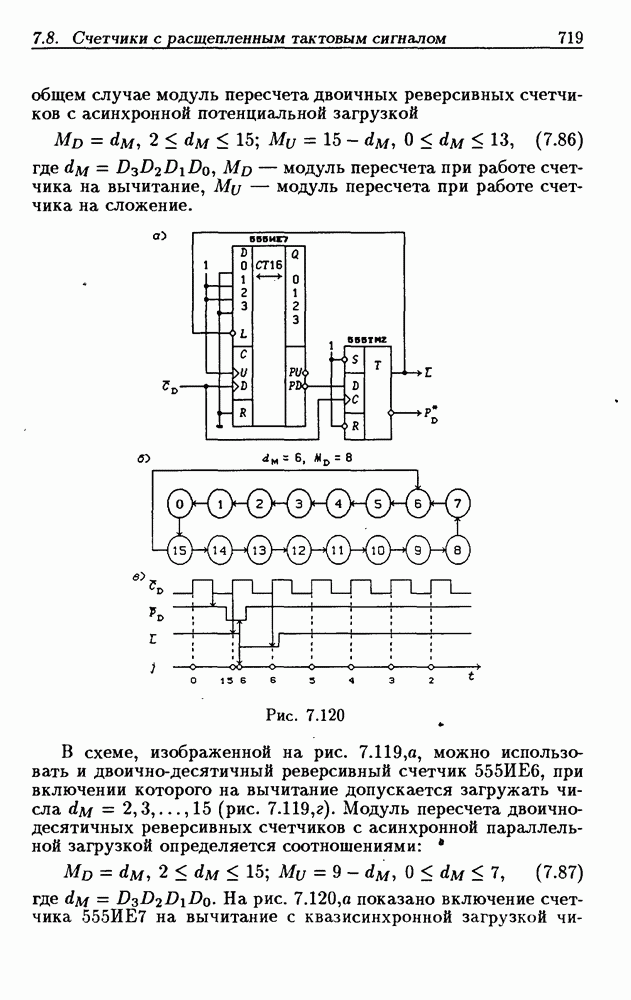
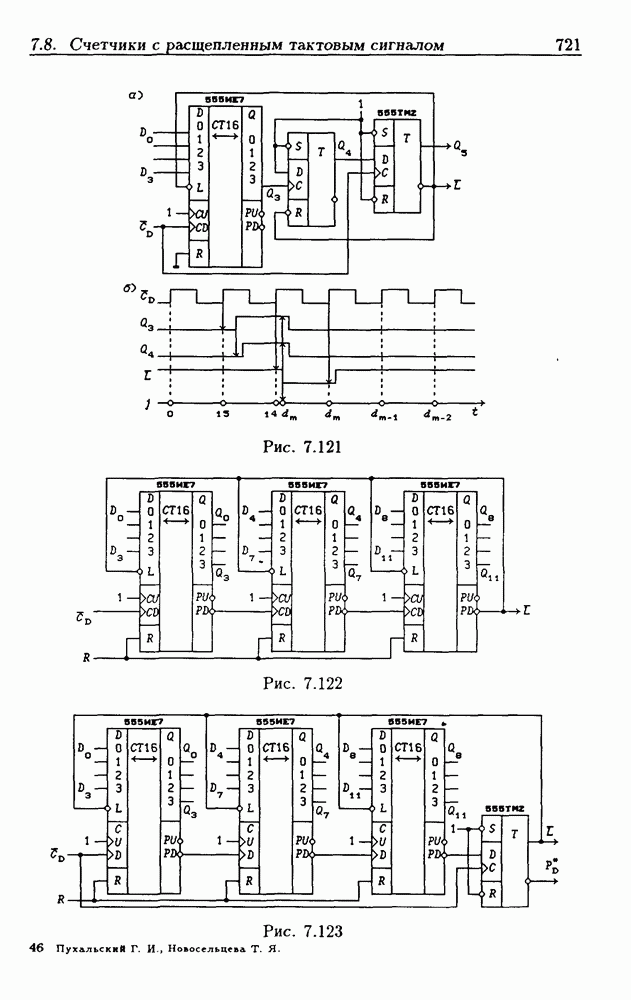
- 7.8. Счетчики с расщепленным тактовым сигналом
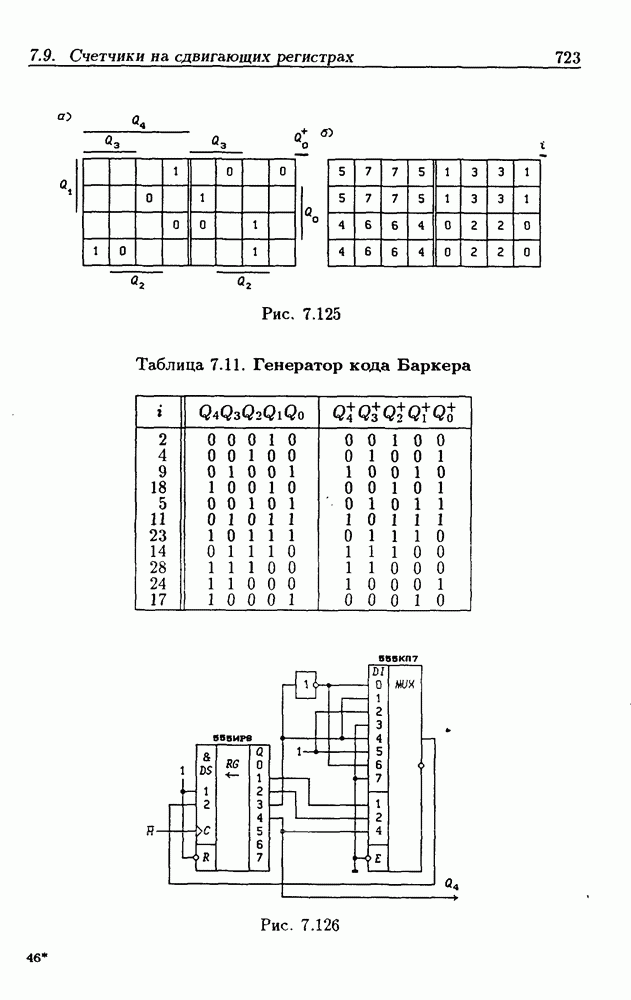
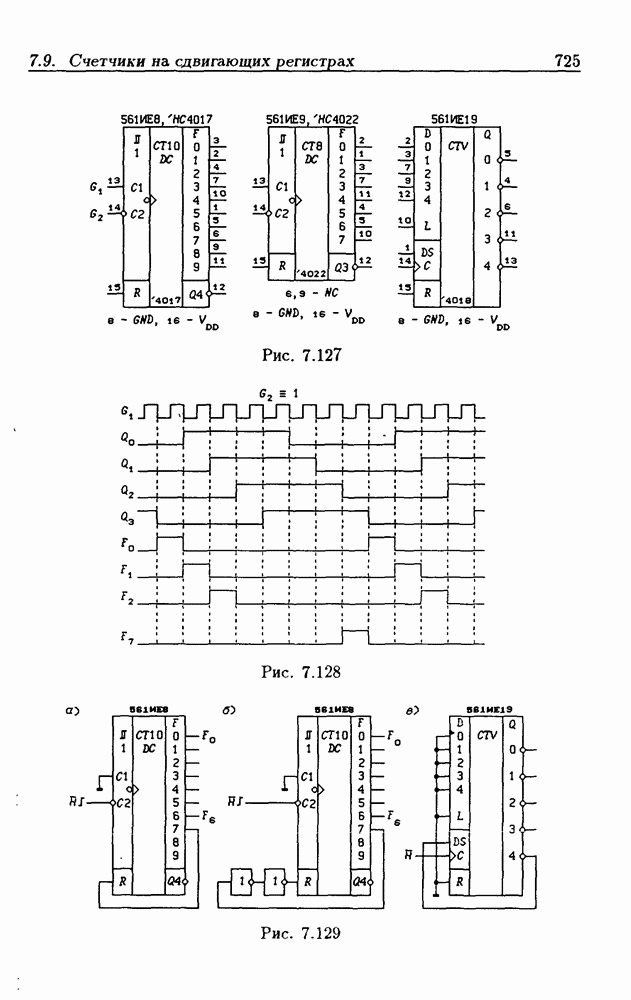
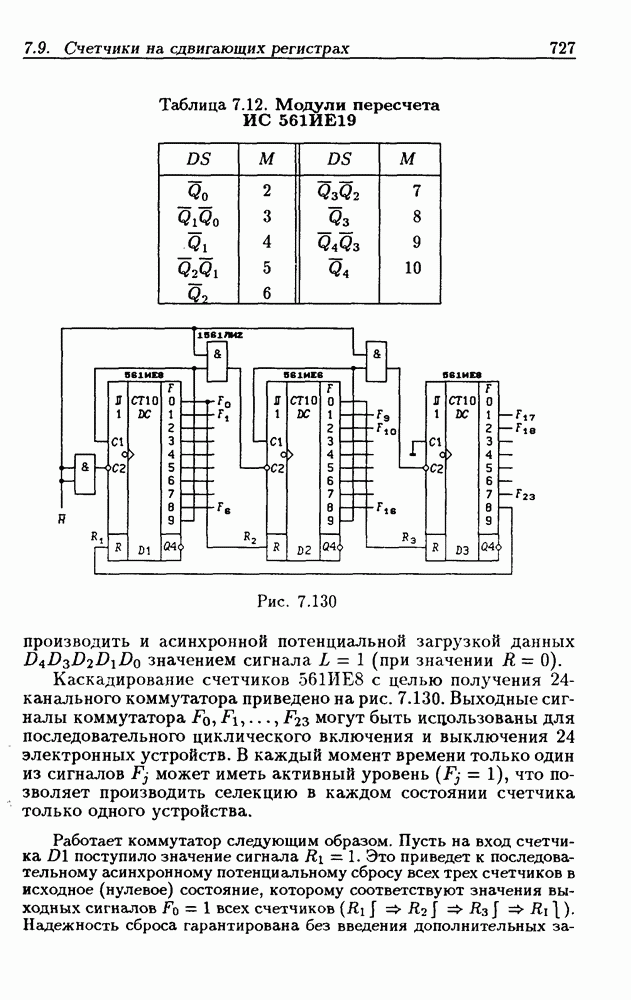
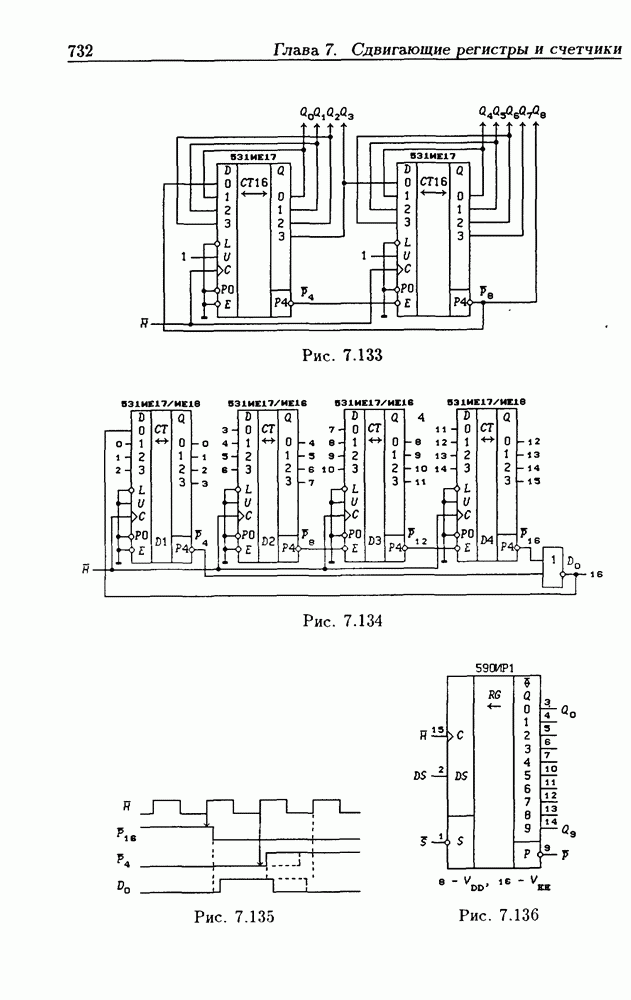
- 7.9. Счетчики на сдвигающих регистрах
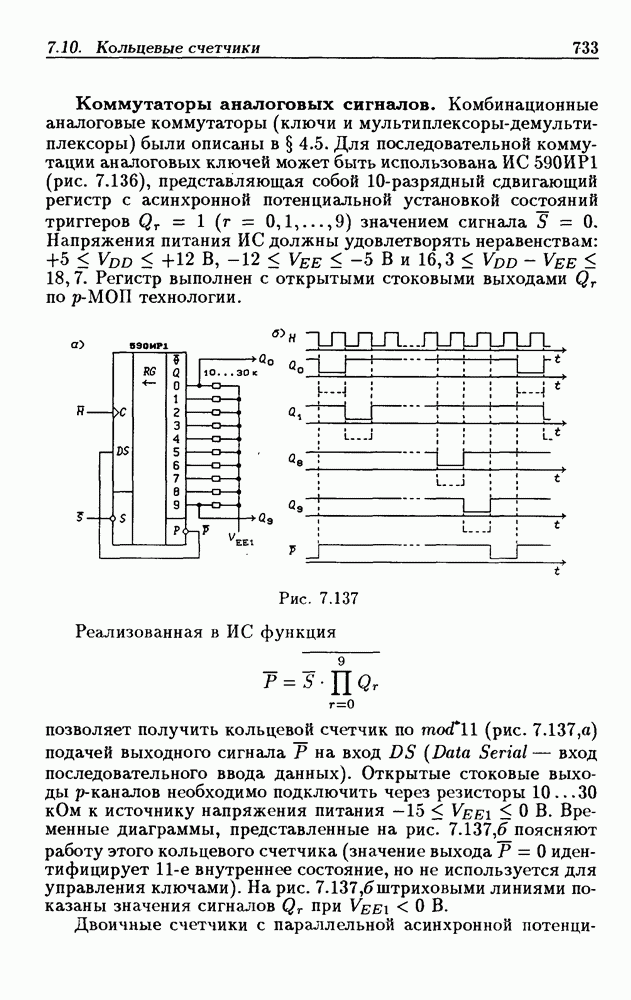
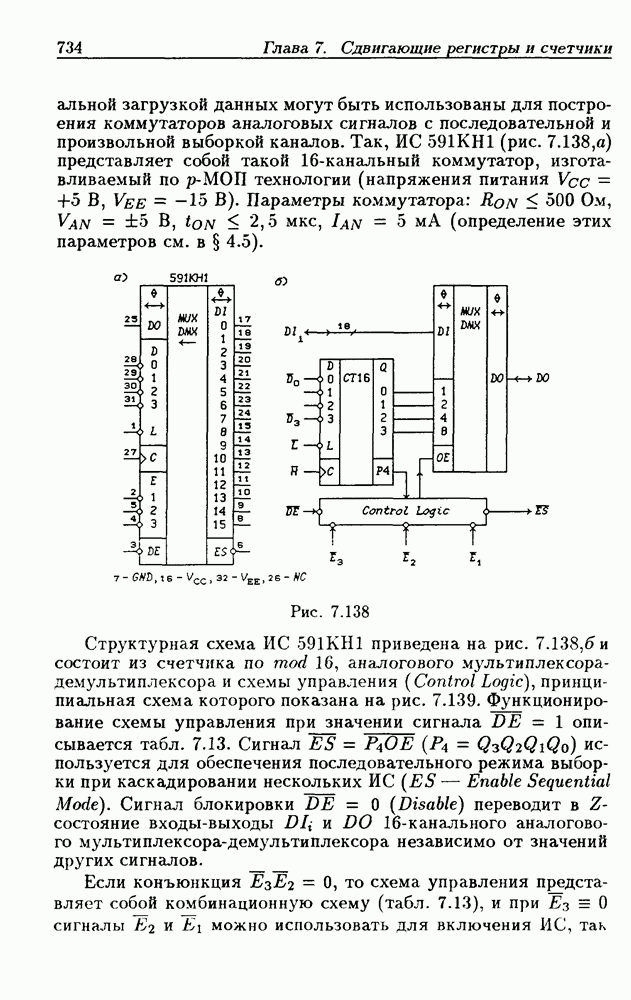
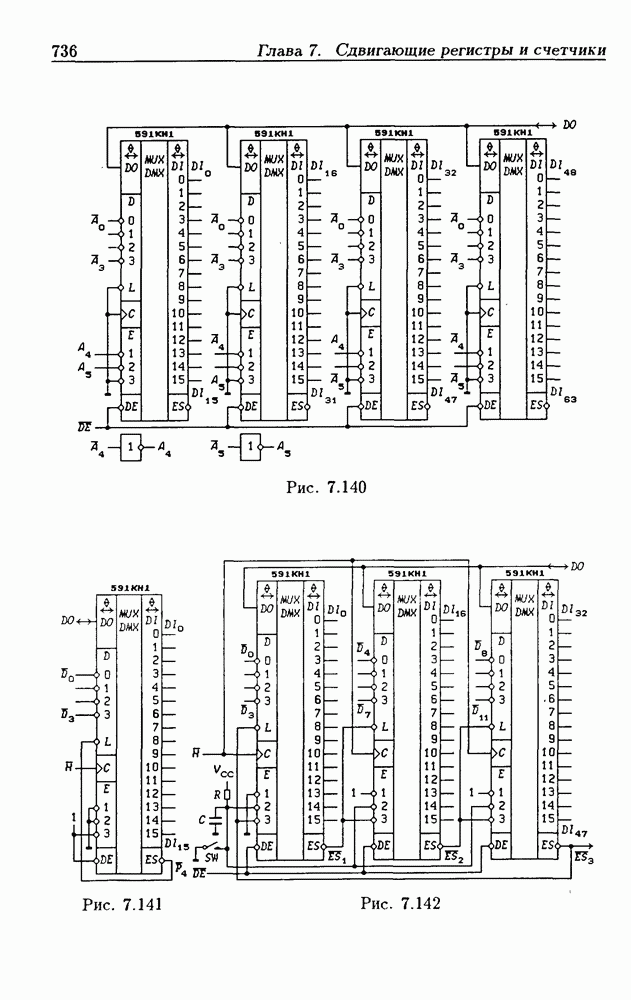
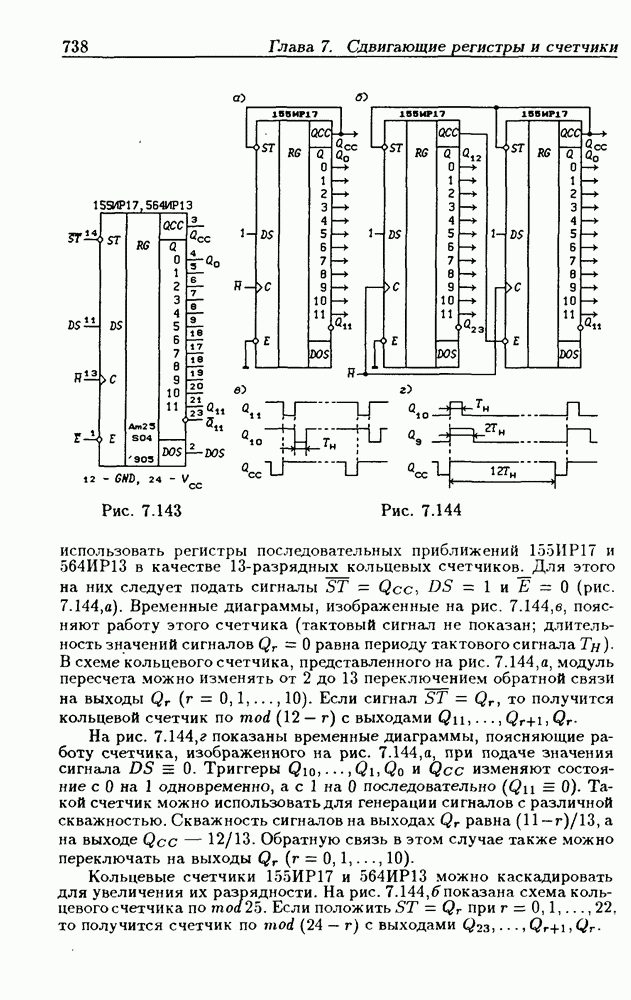
- 7.10. Кольцевые счетчики
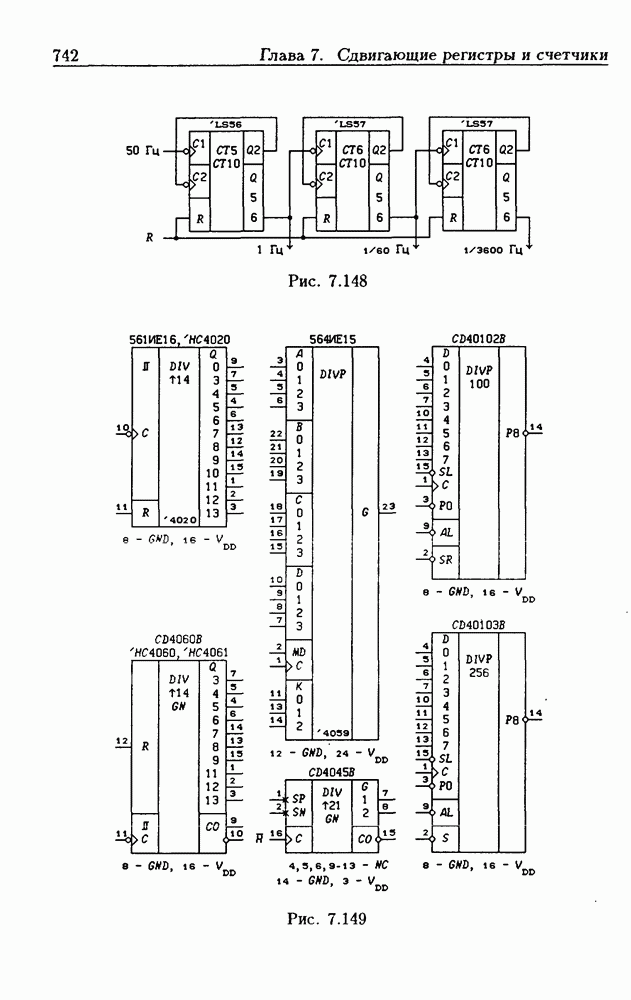
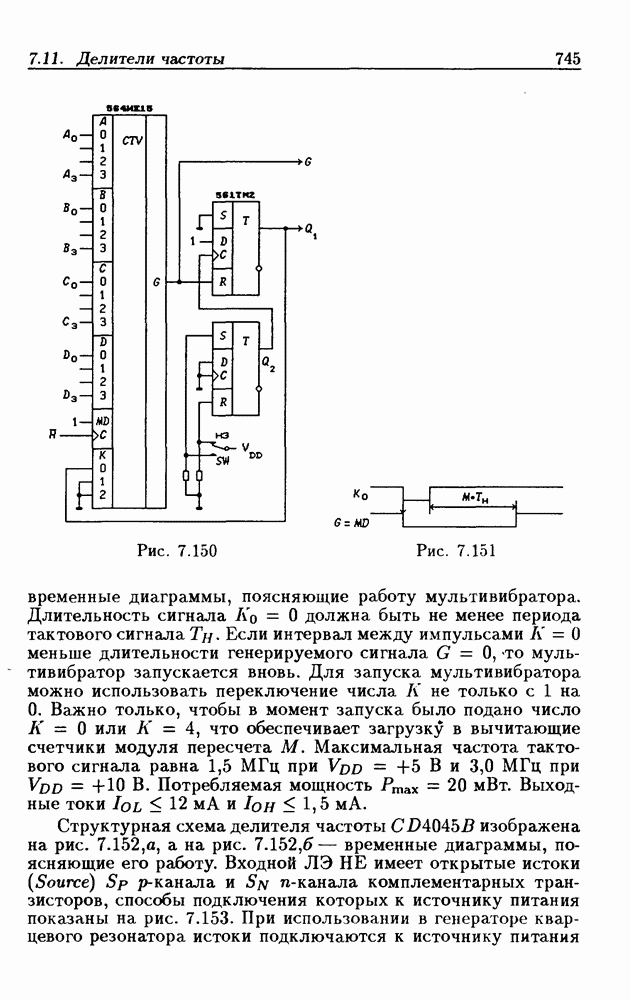
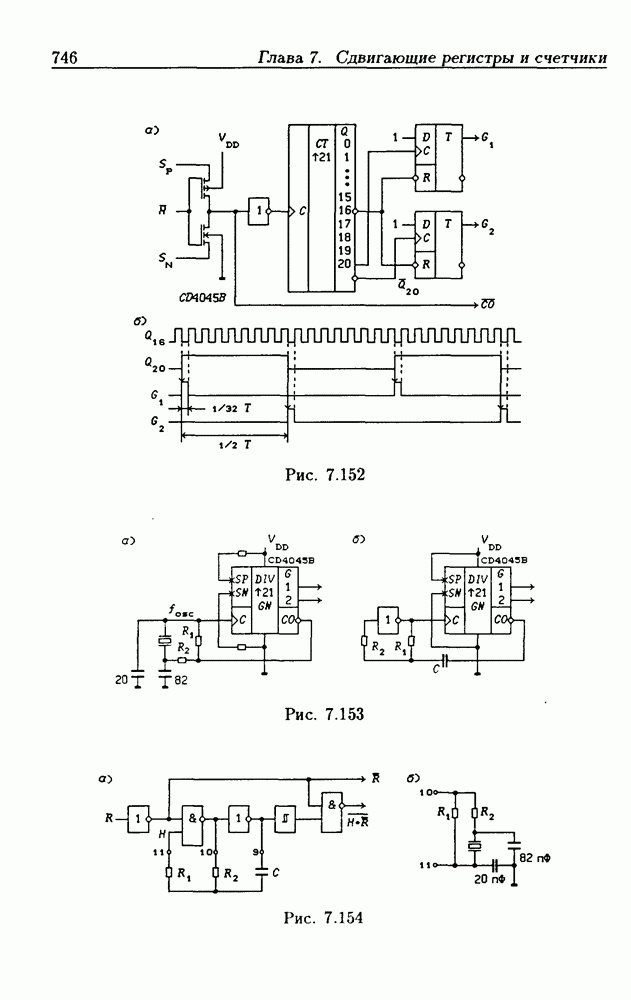
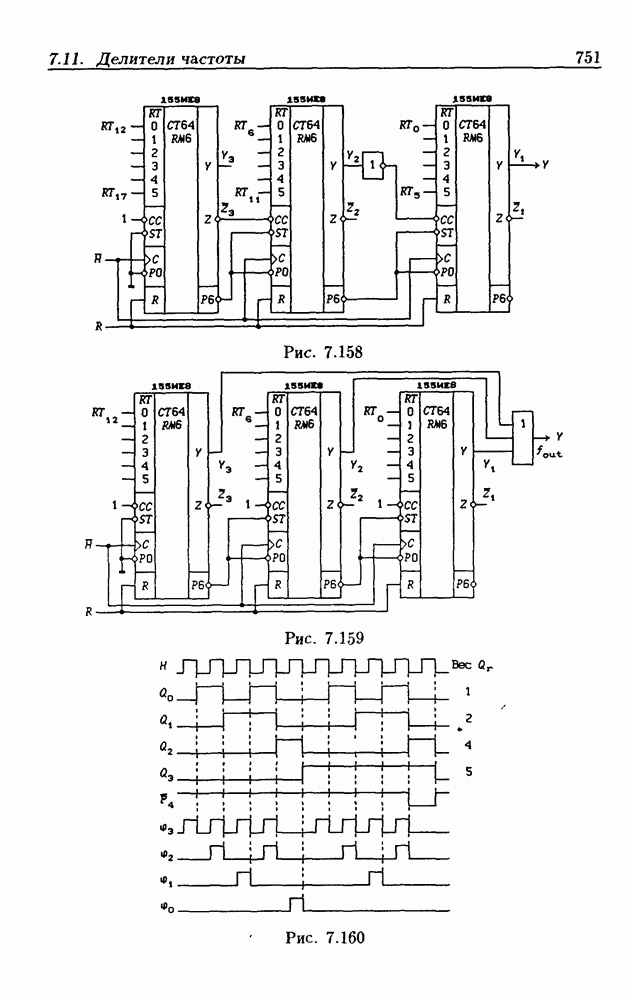
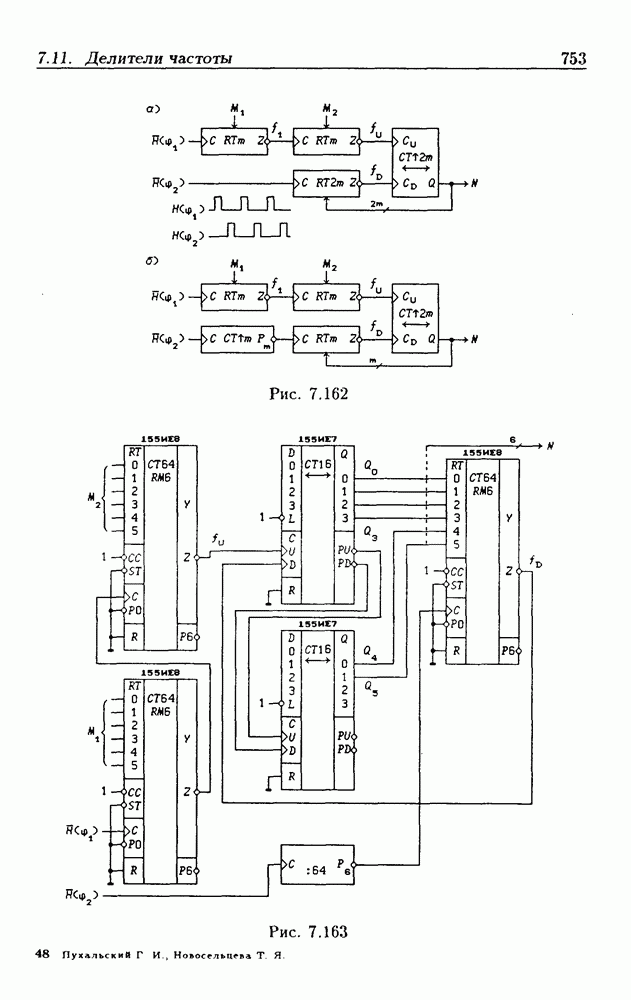
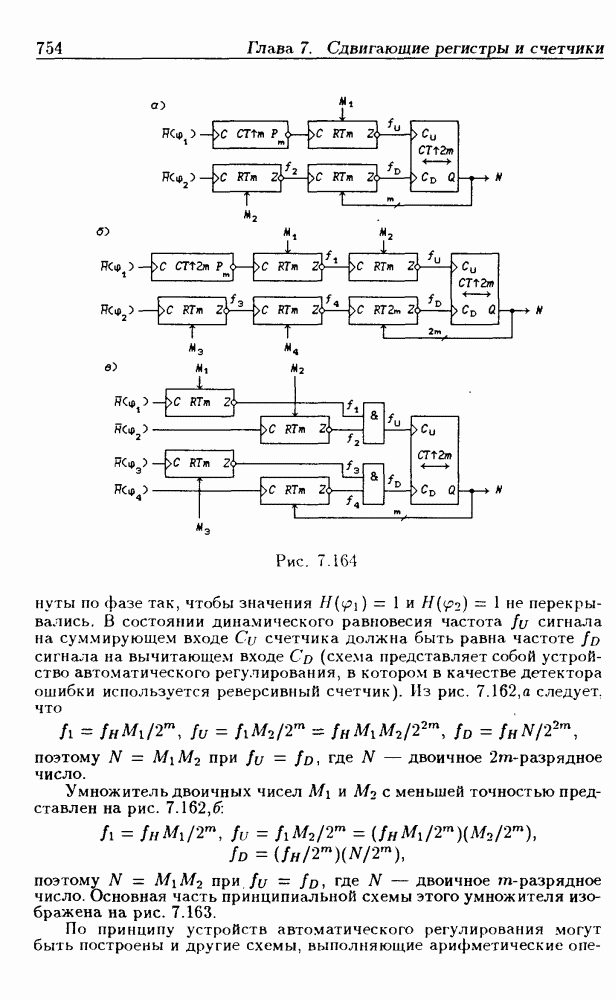
- 7.11. Делители частоты
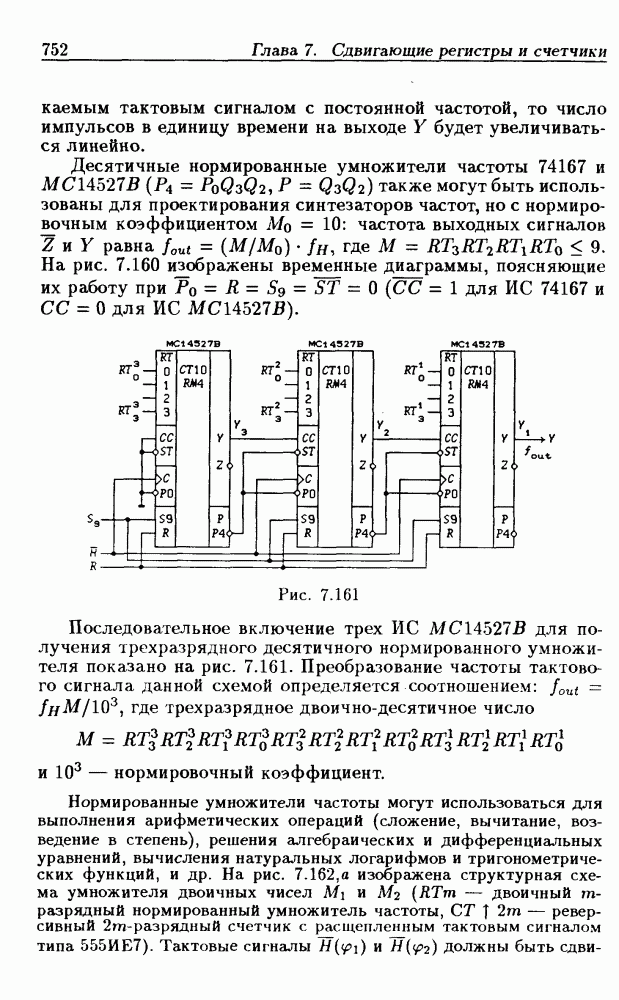
- Нормированные умножители частоты.
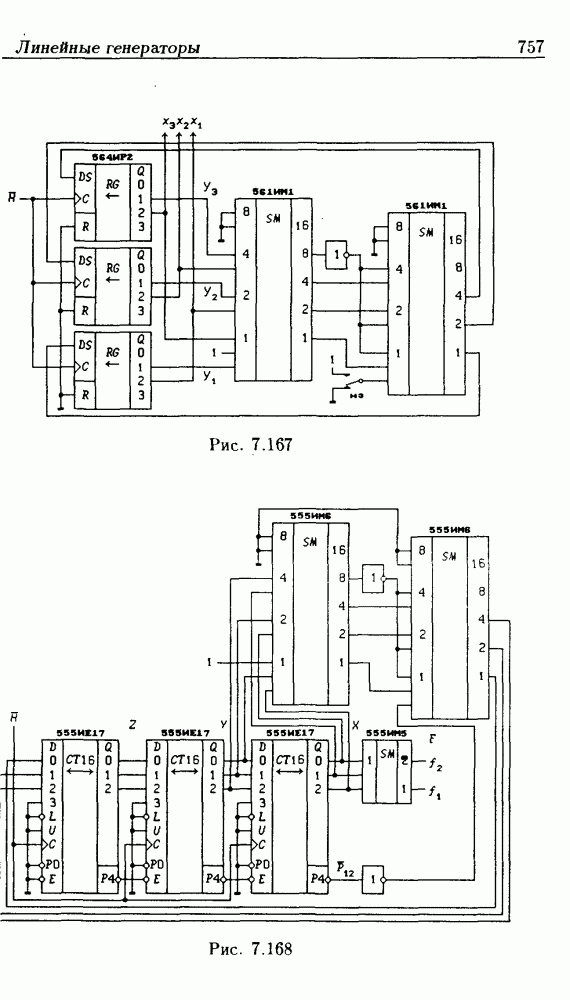
- 7.12. Линейные генераторы
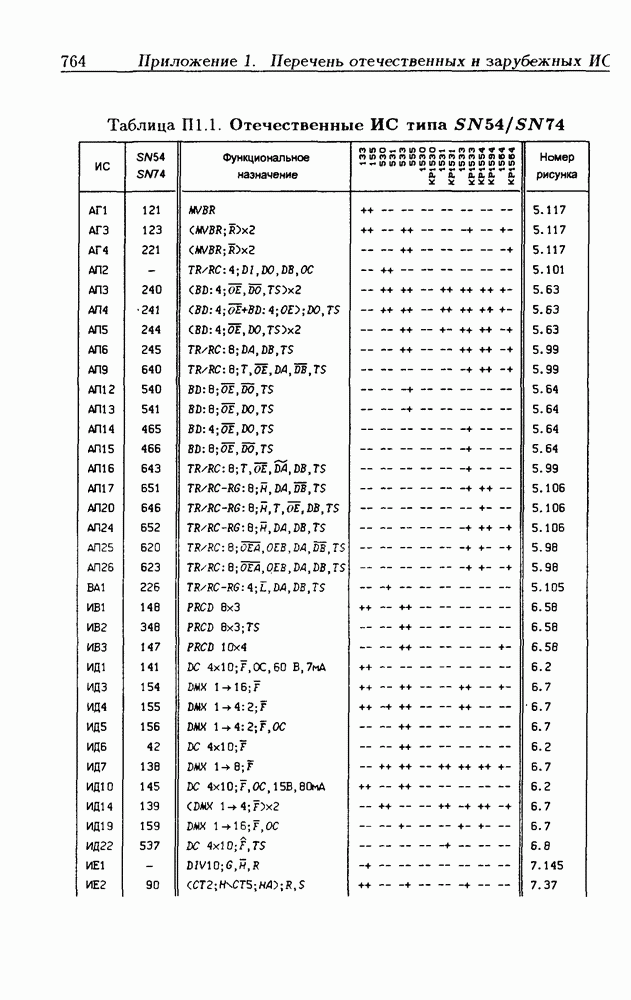
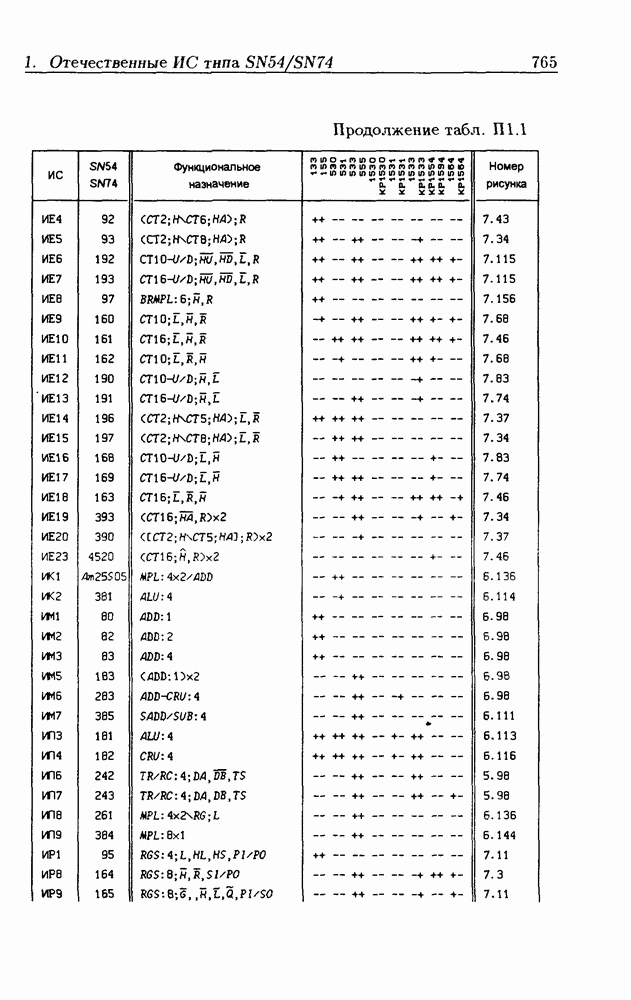
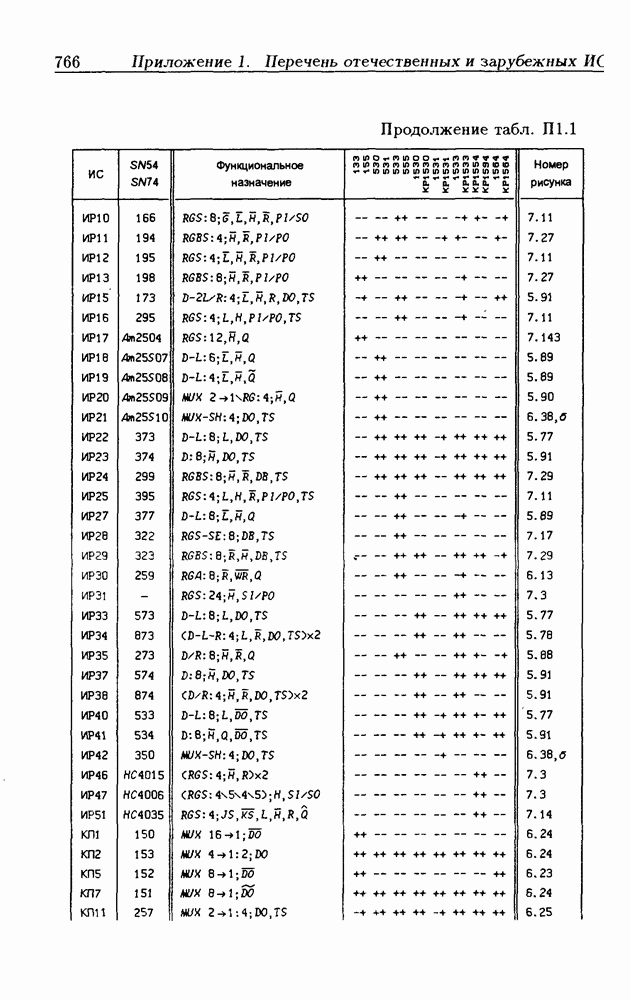
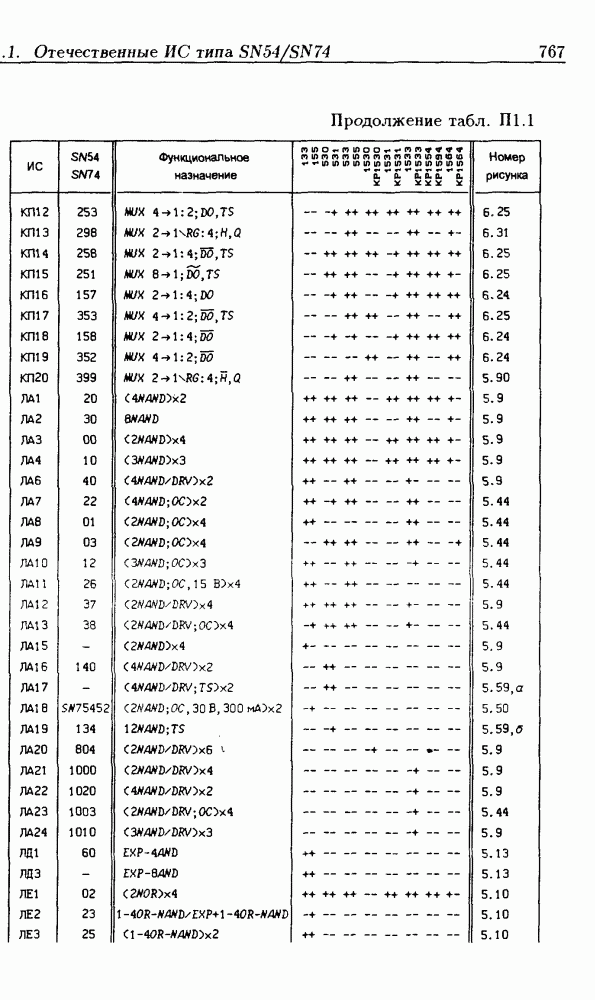
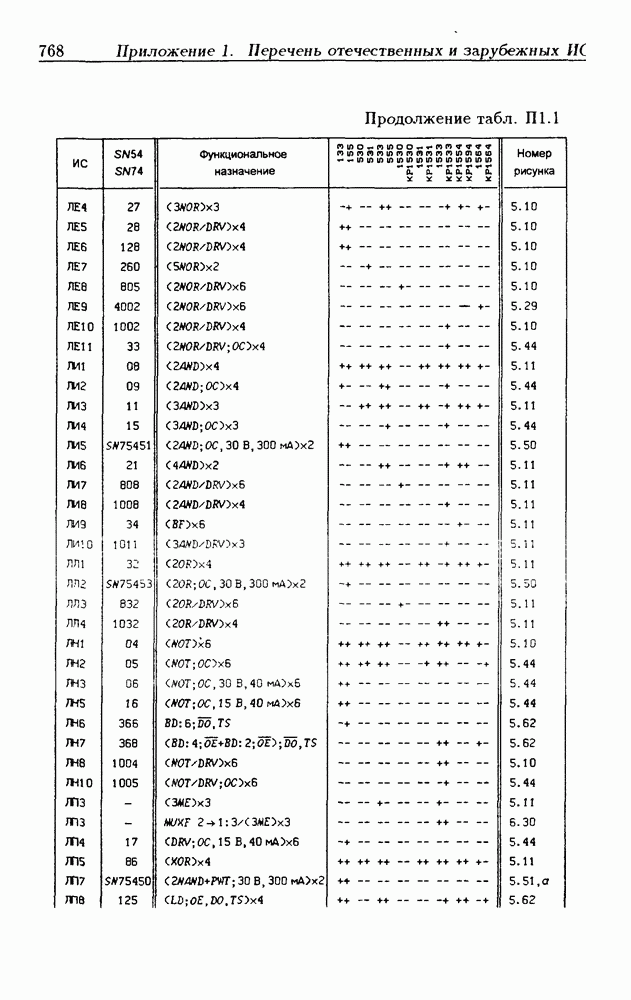
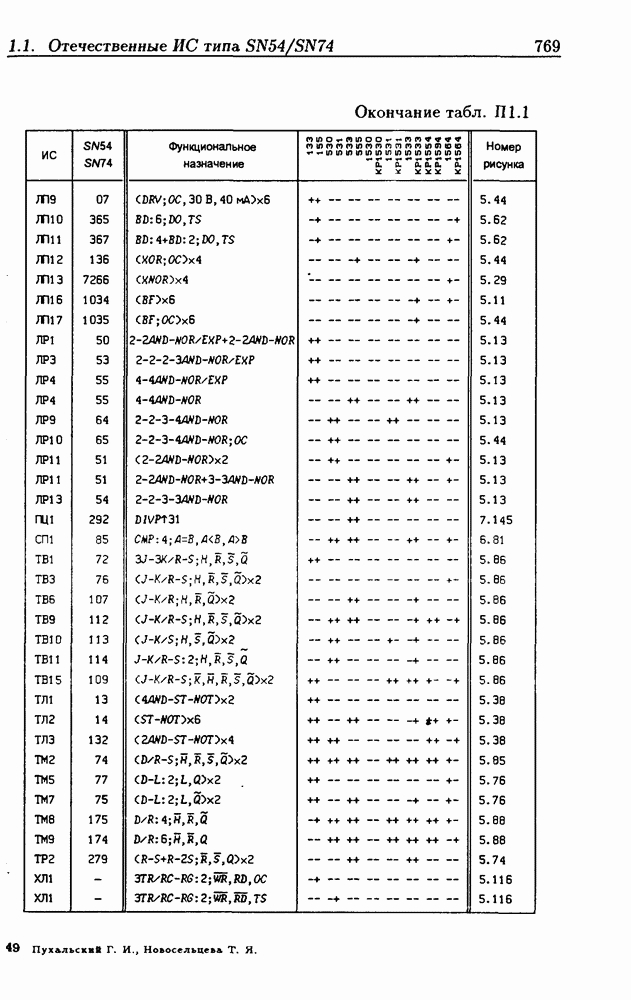
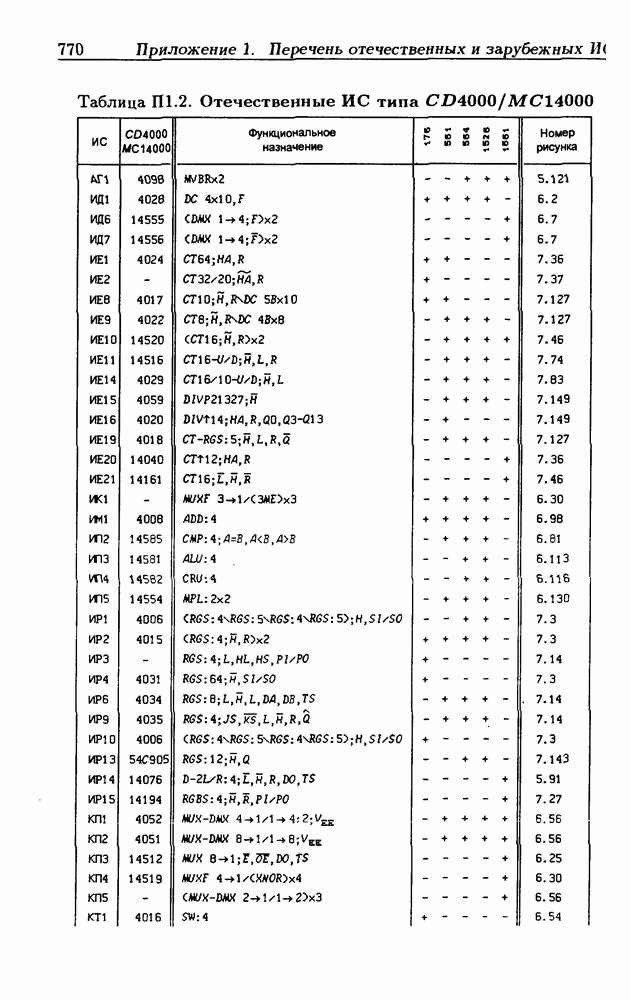
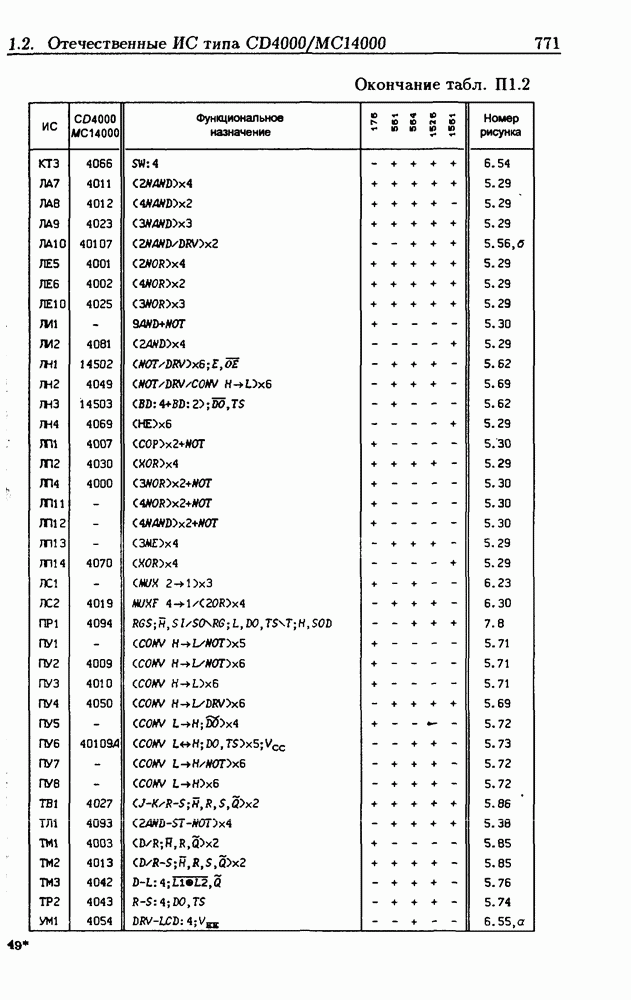
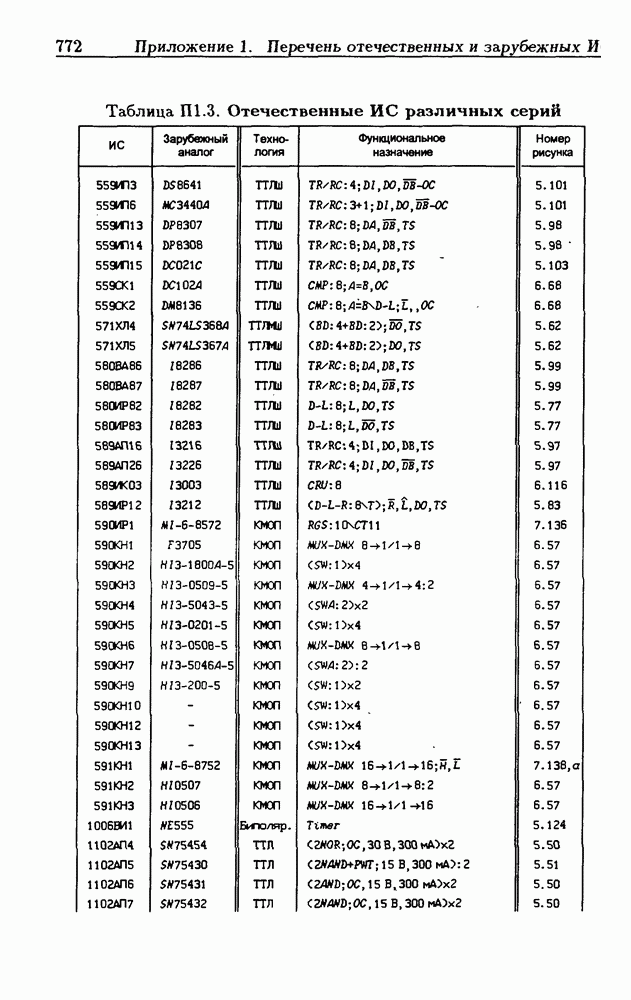
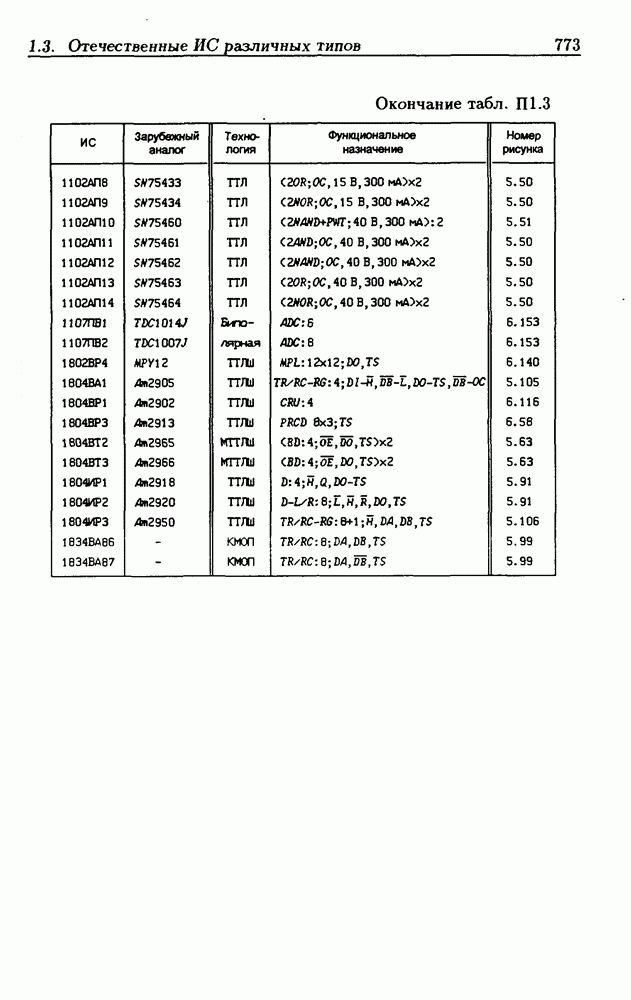
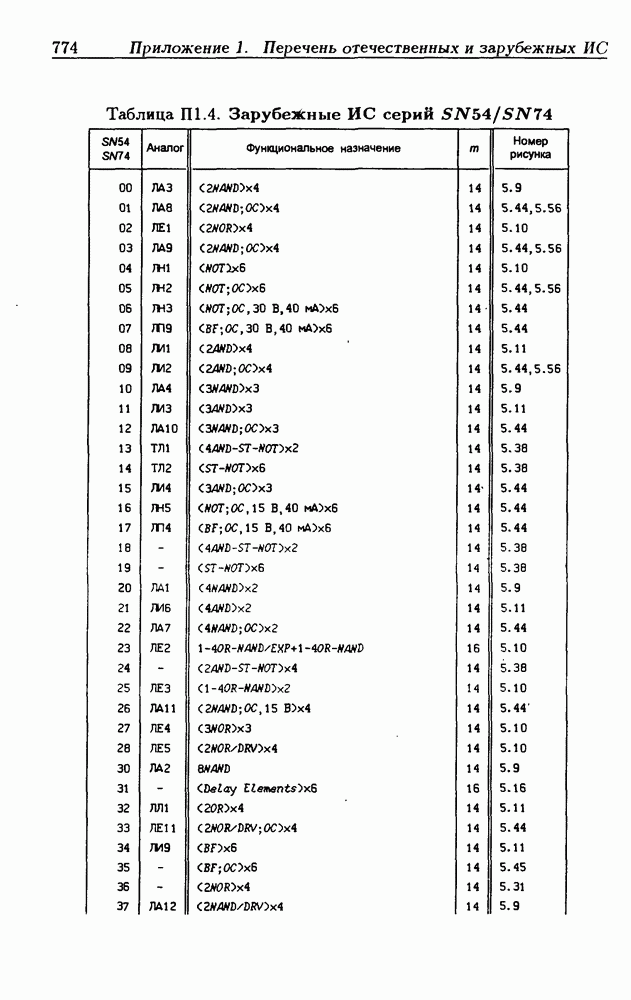
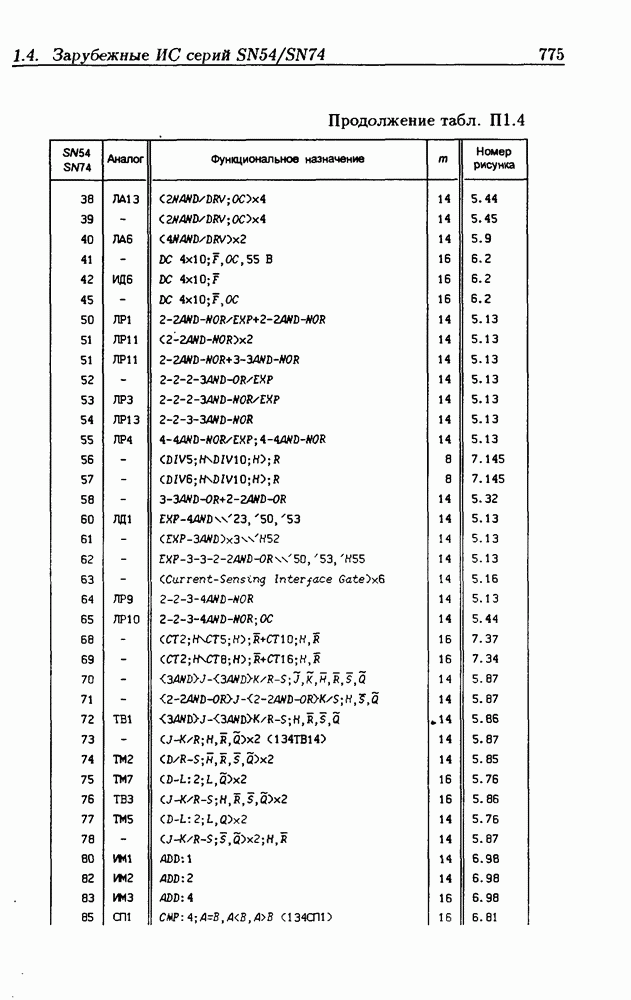
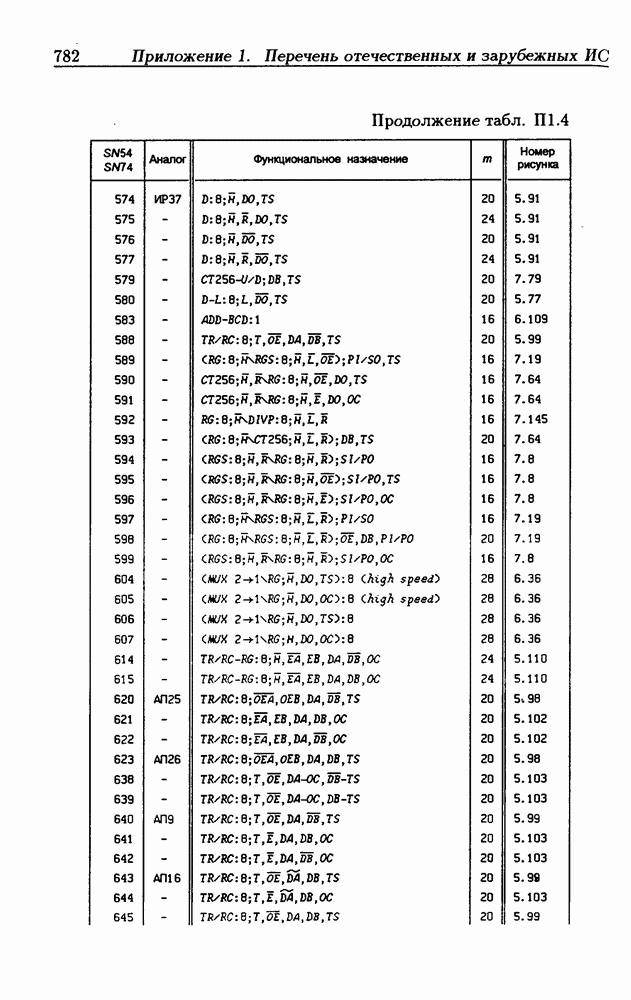
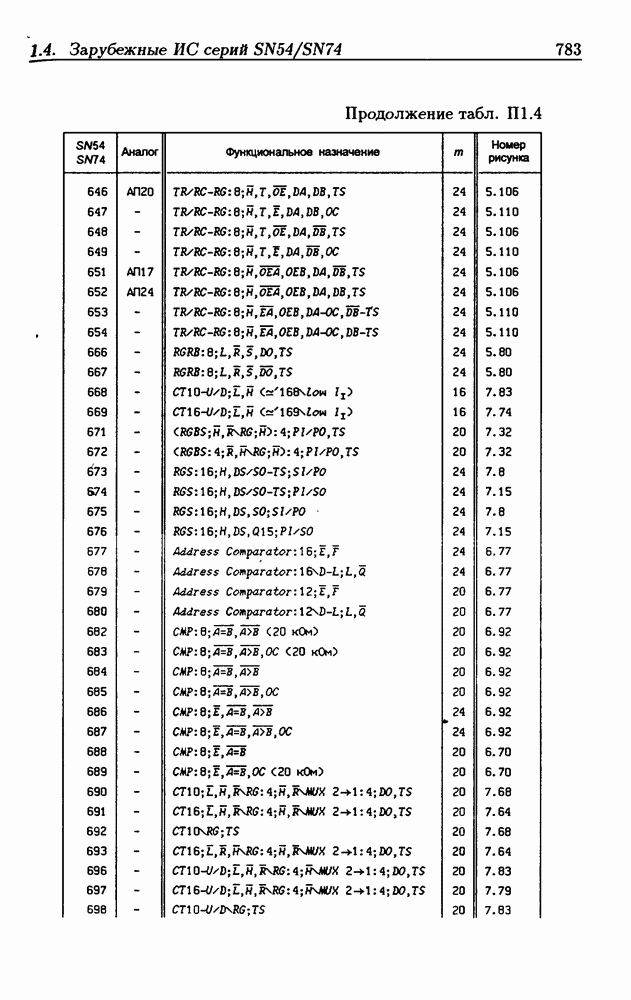
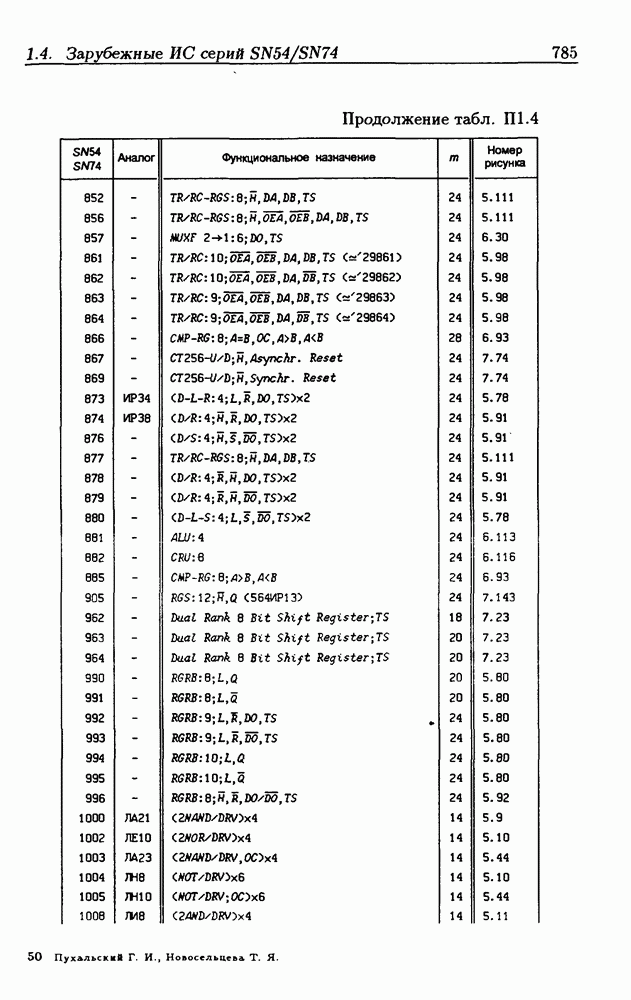
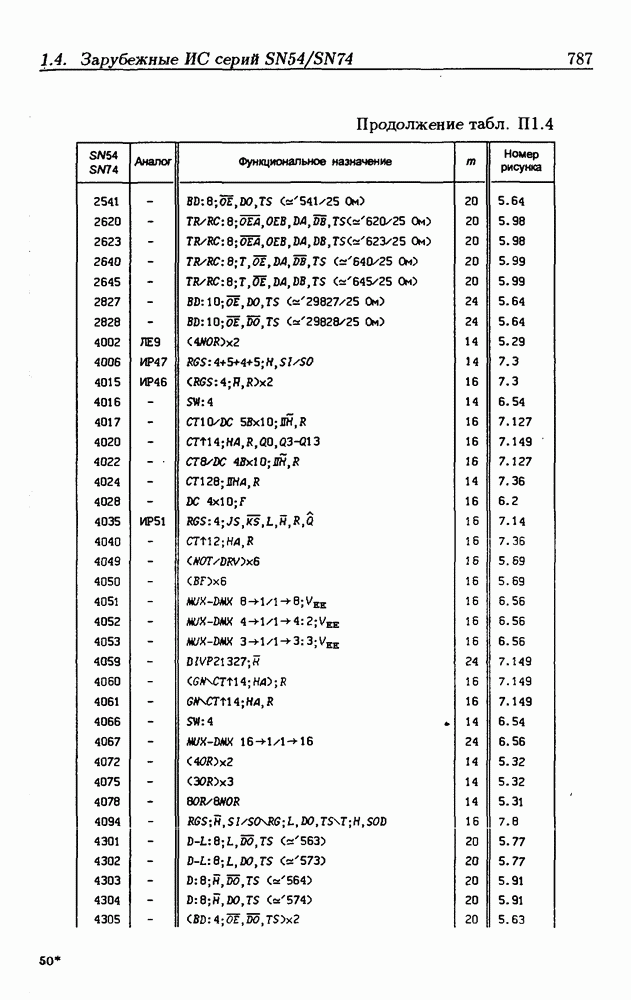
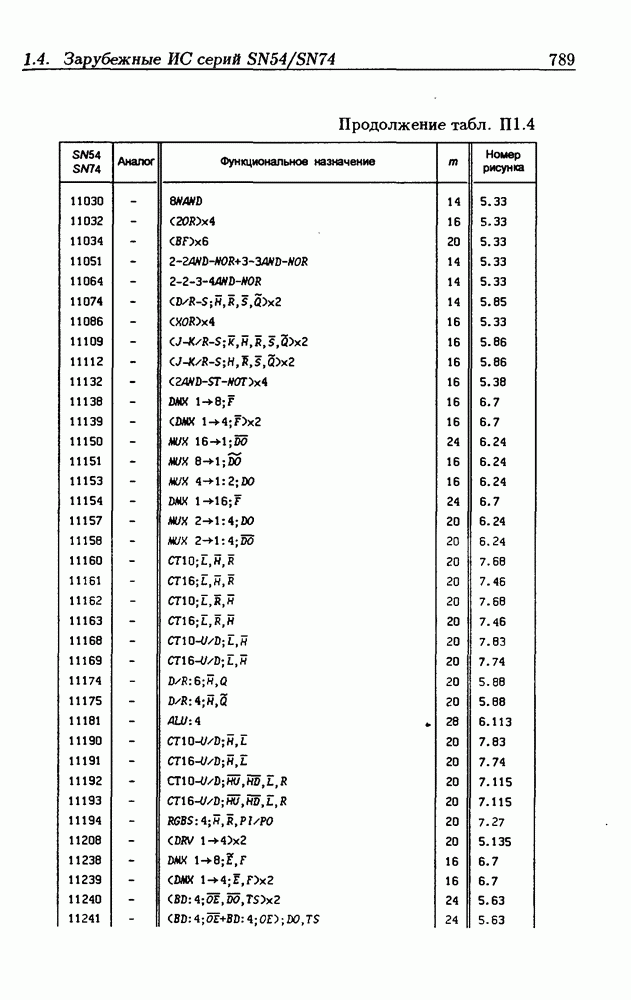
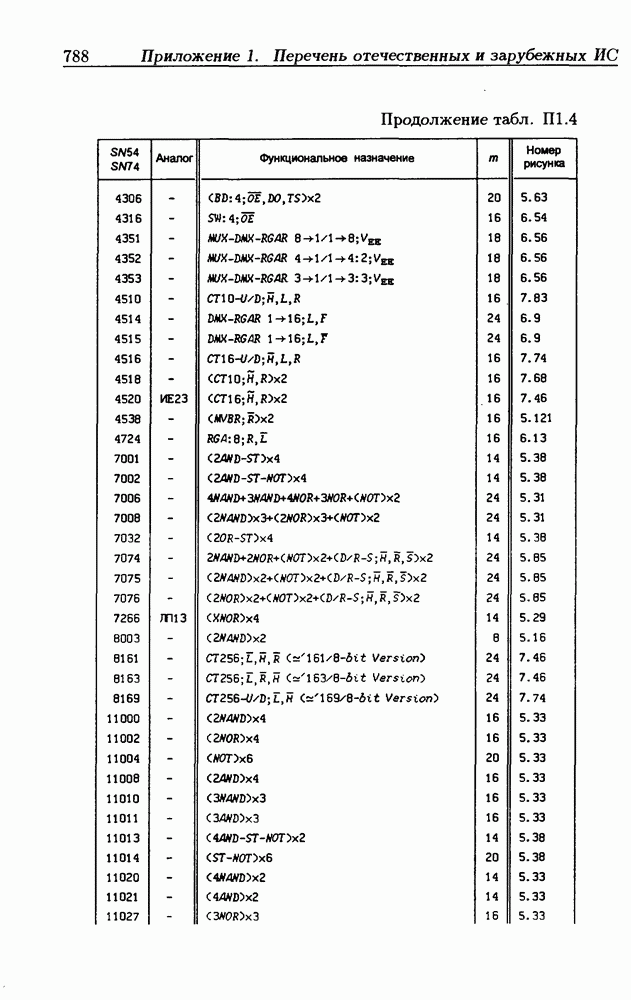
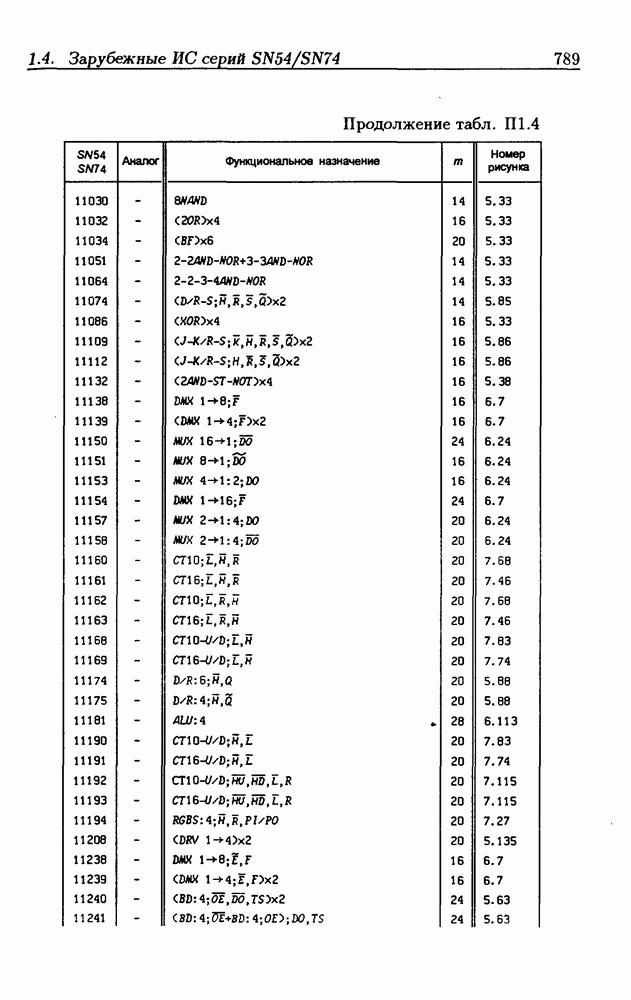
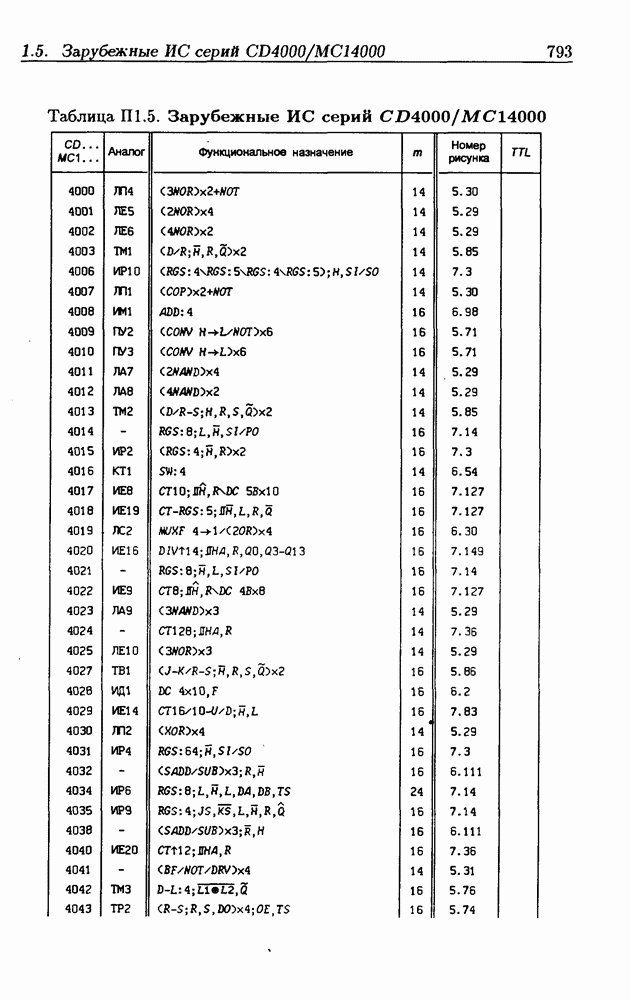
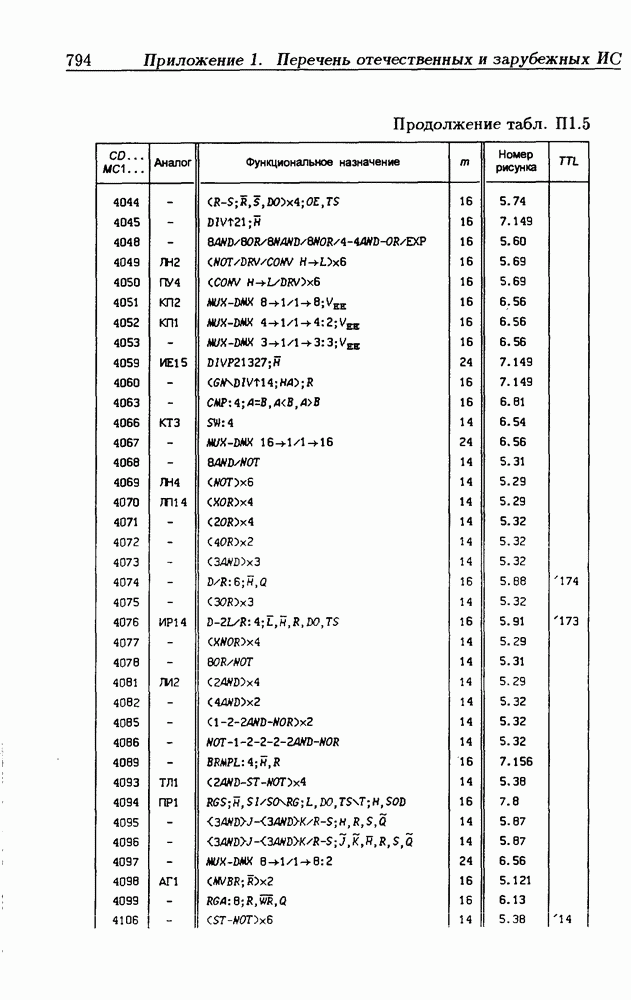
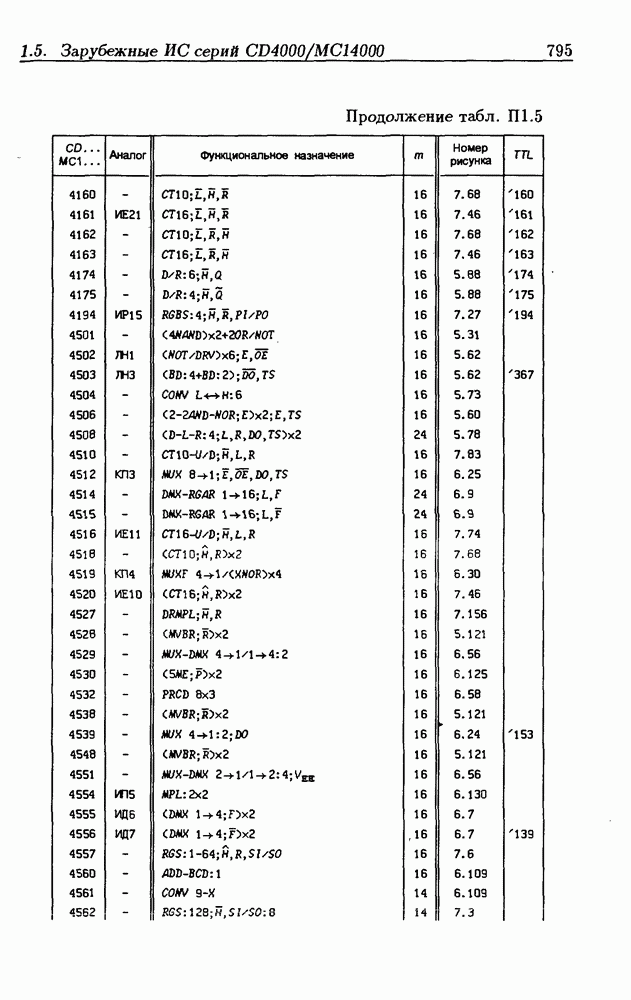
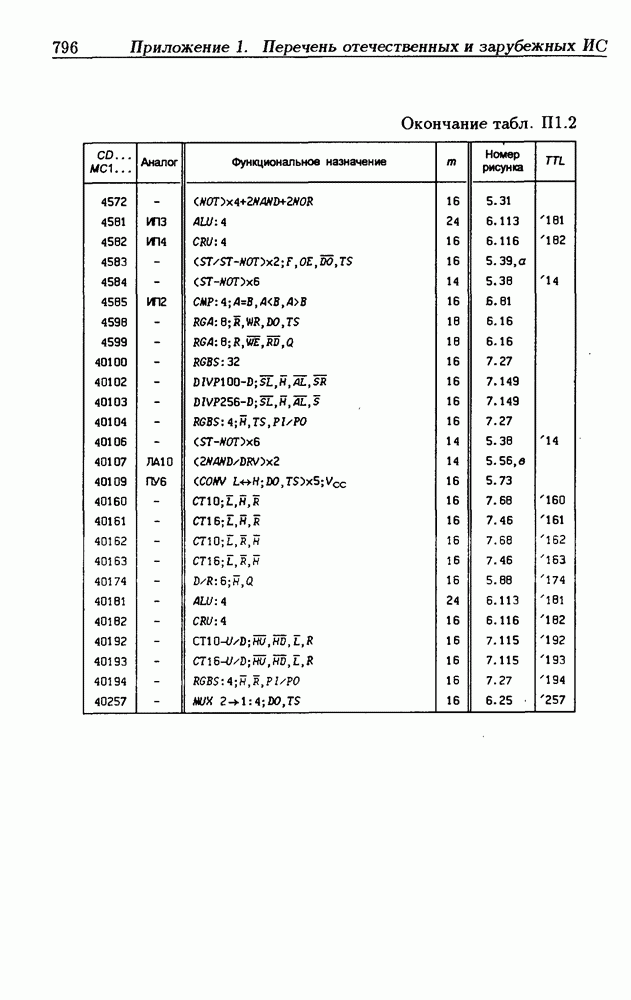
- Приложение 1. Перечень отечественных и зарубежных ИС
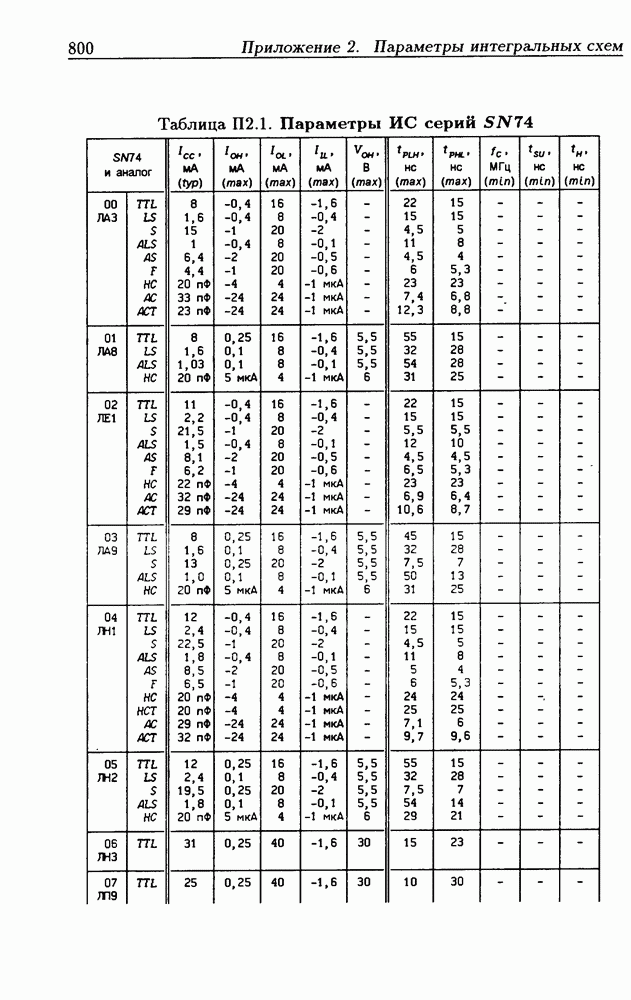
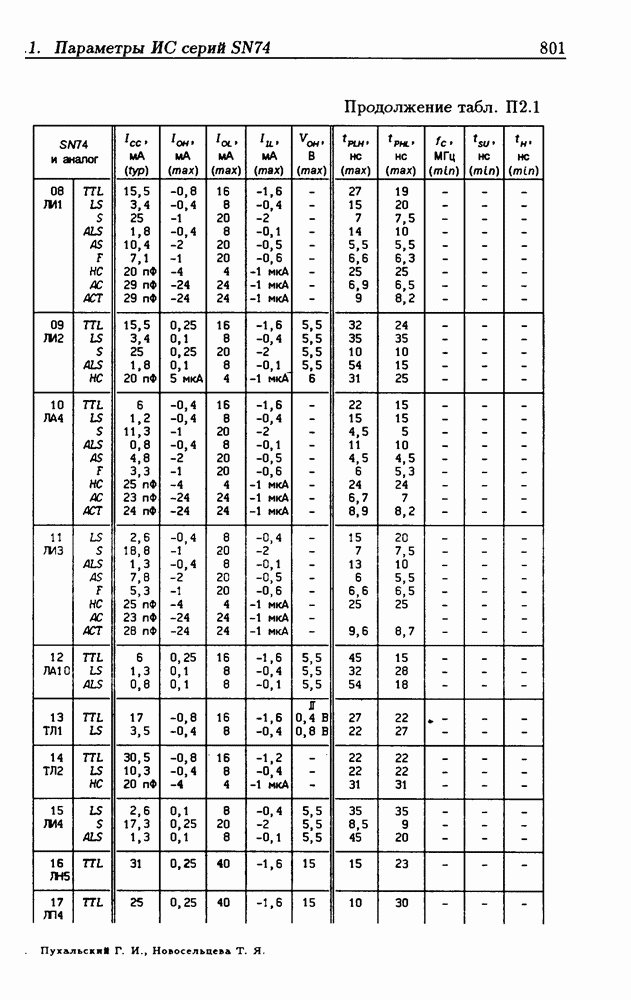
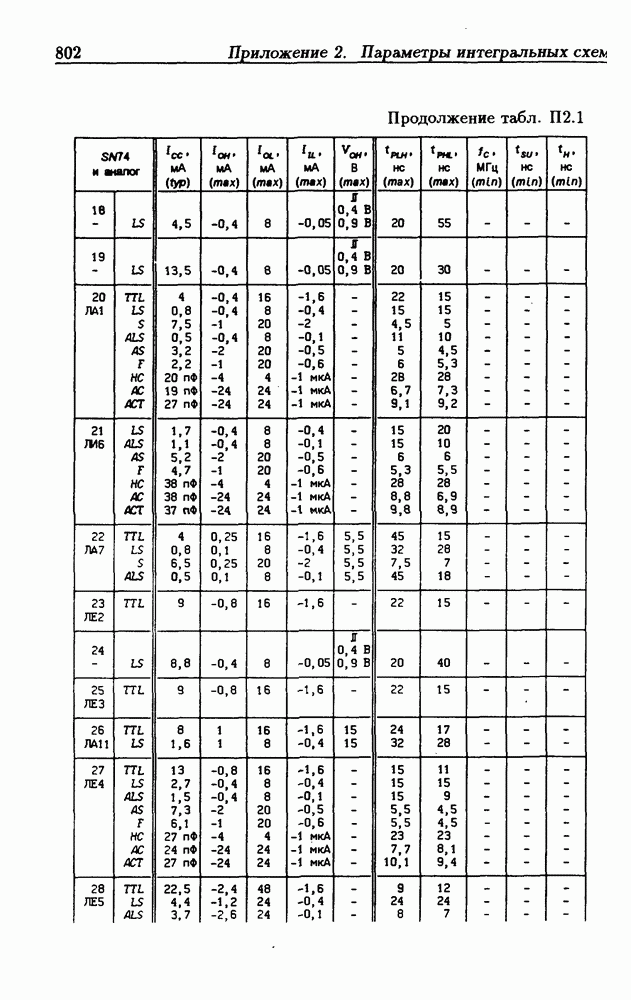
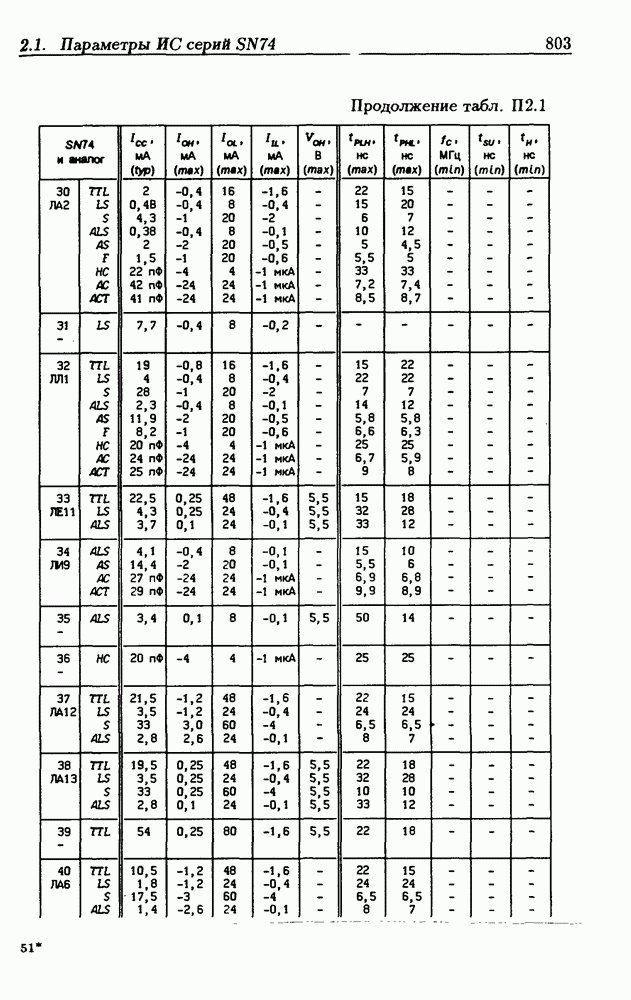
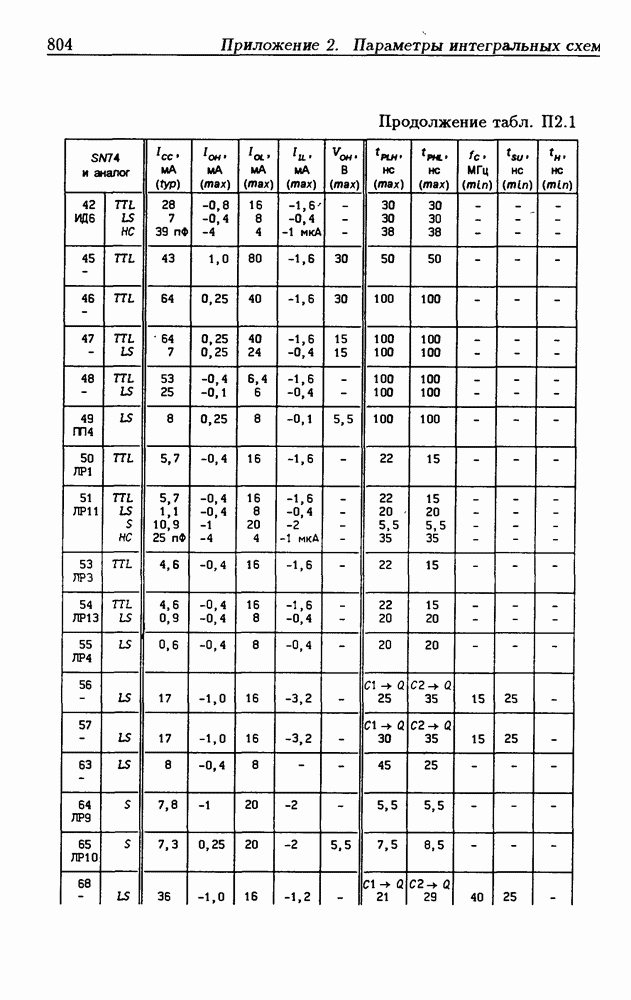
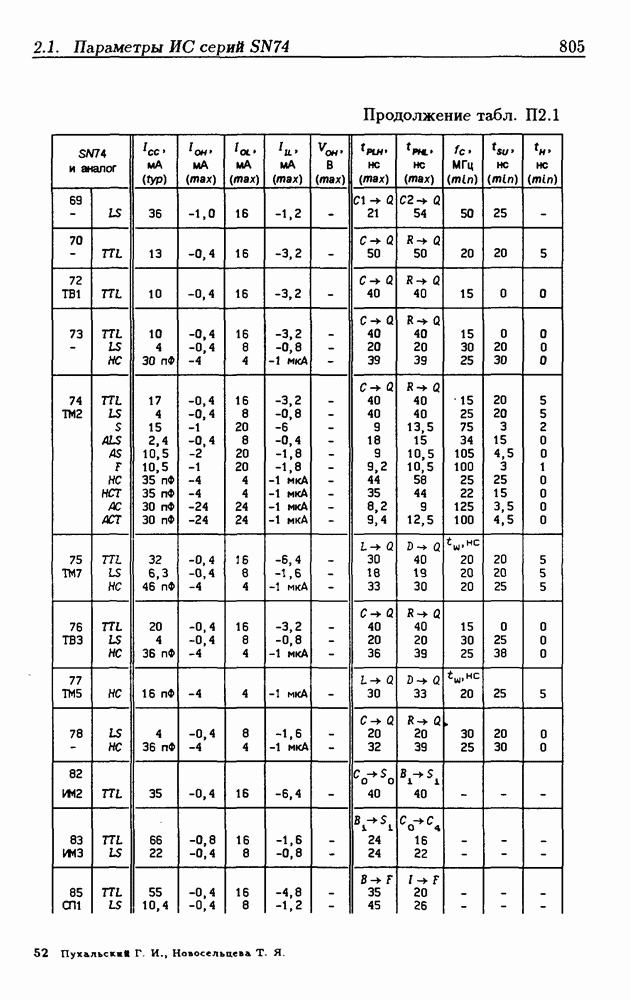
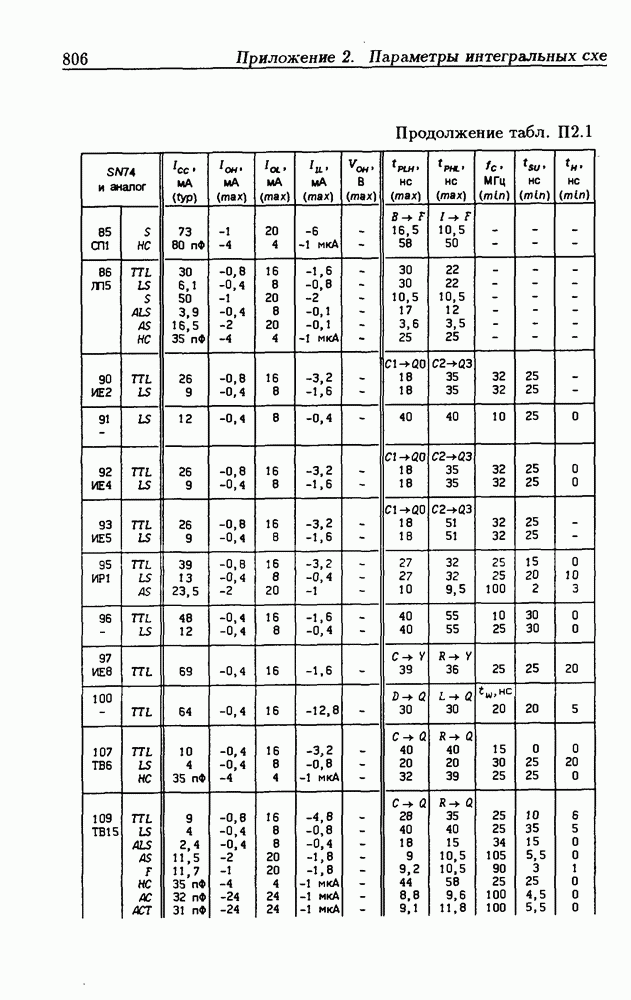
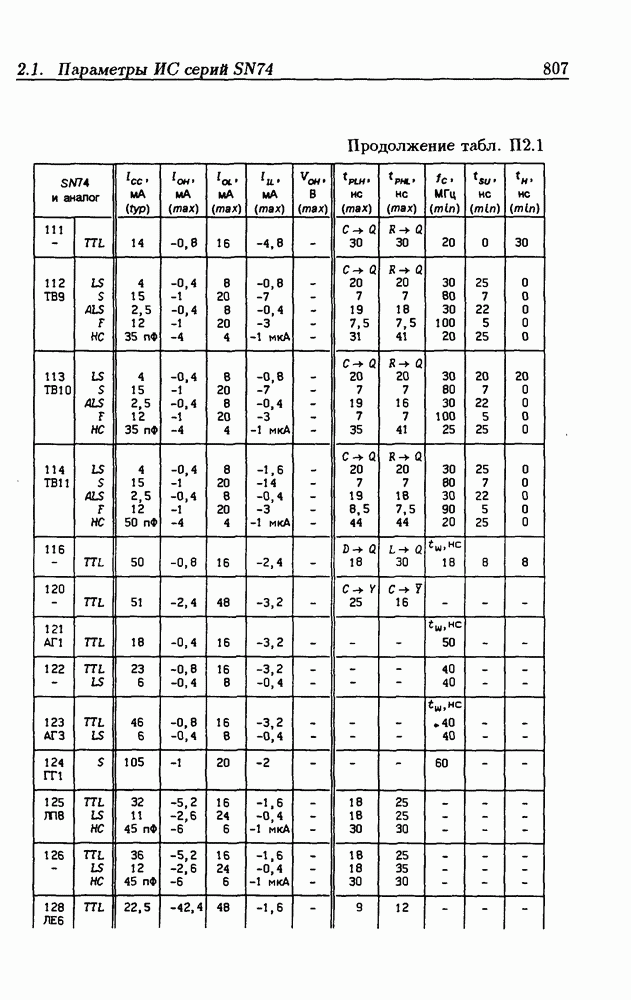
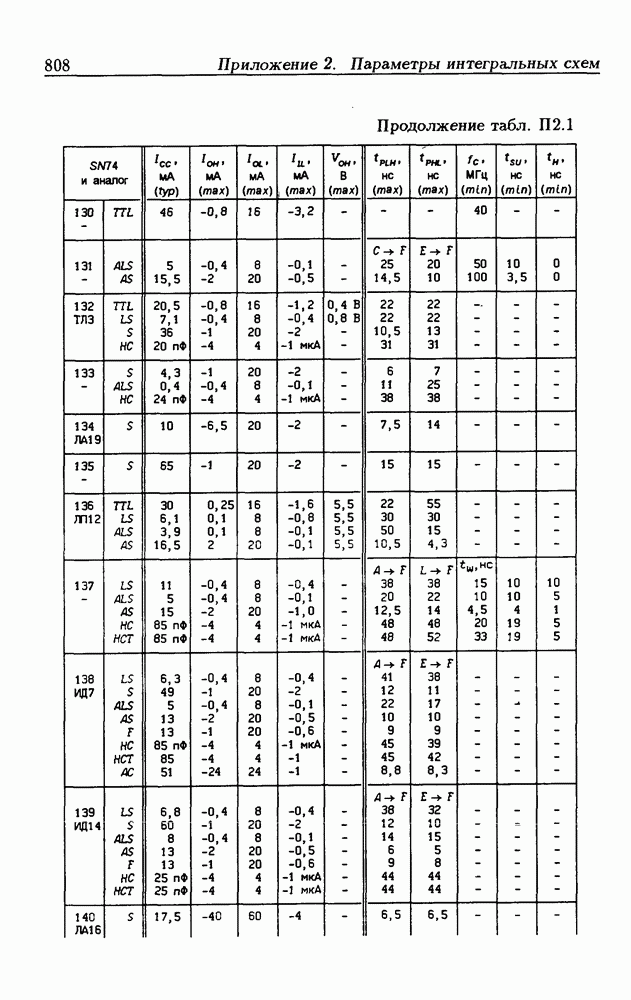
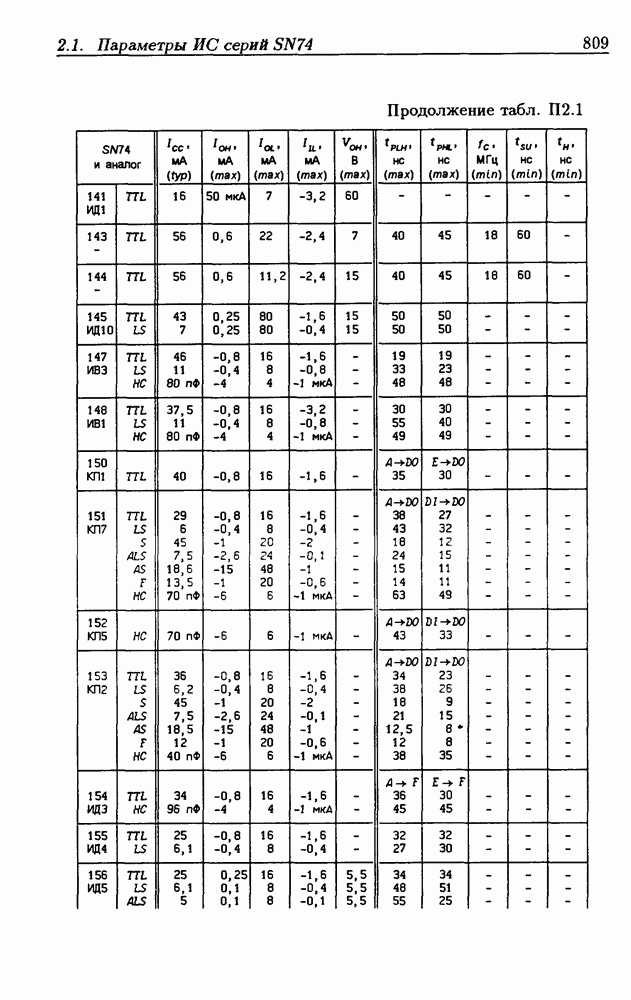
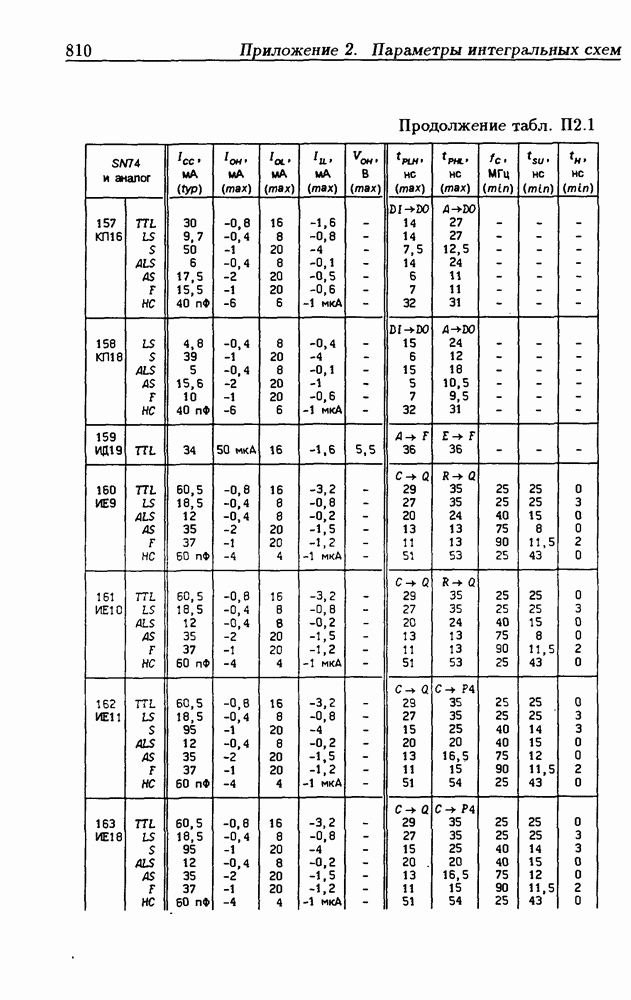
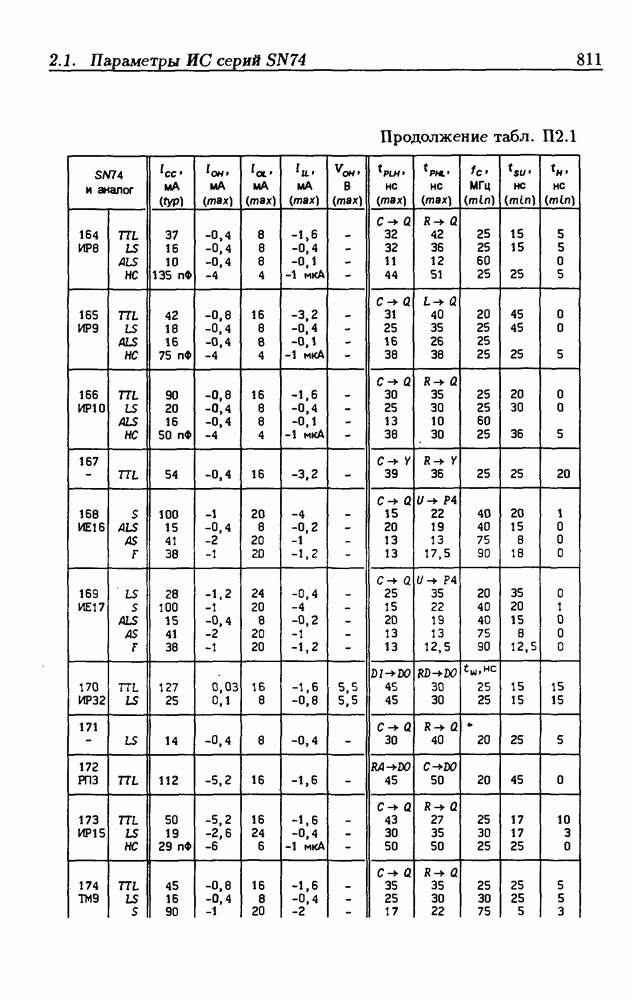
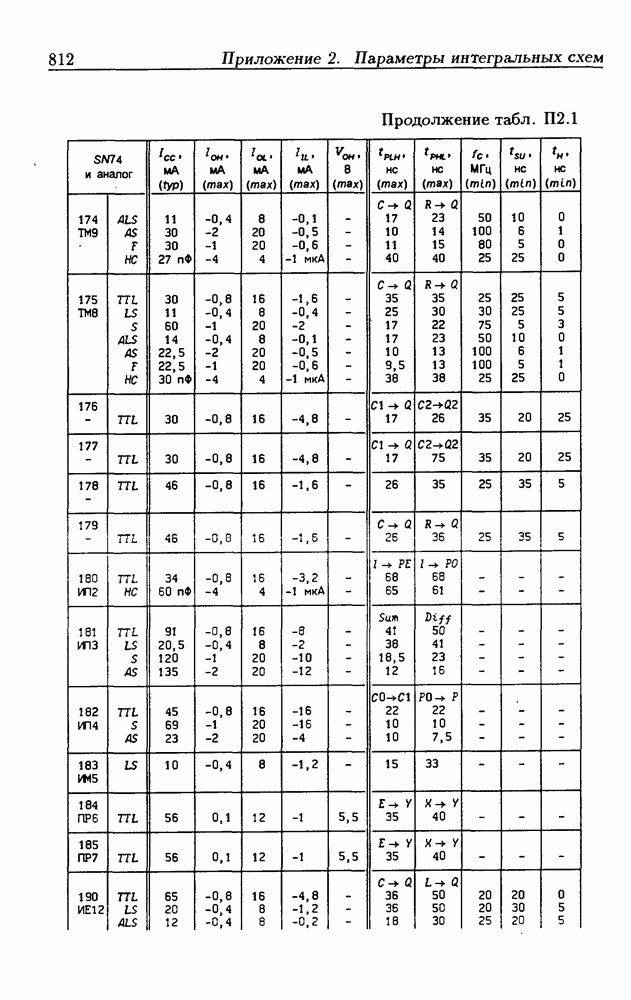
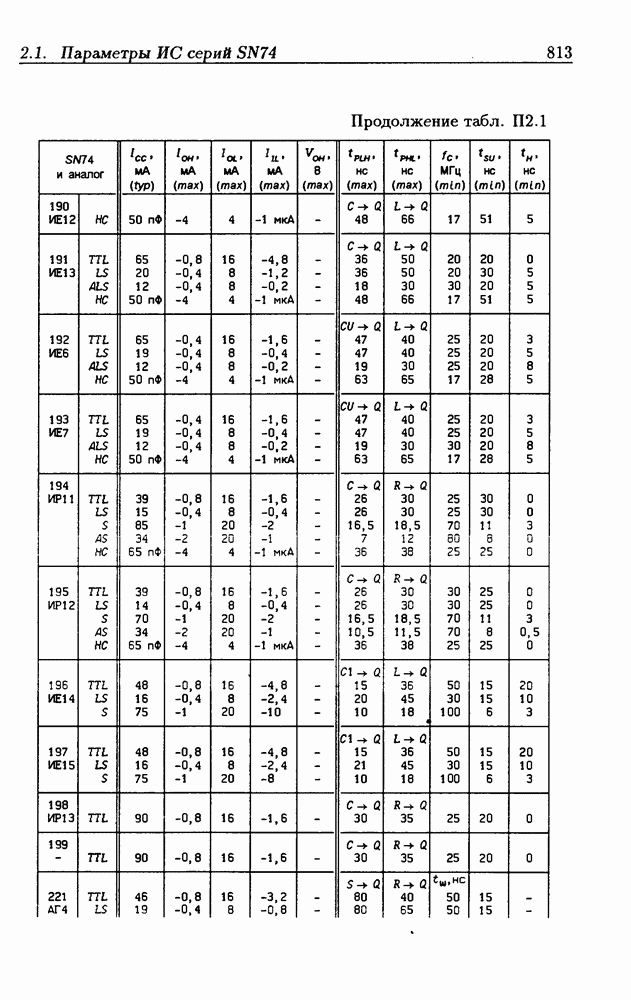
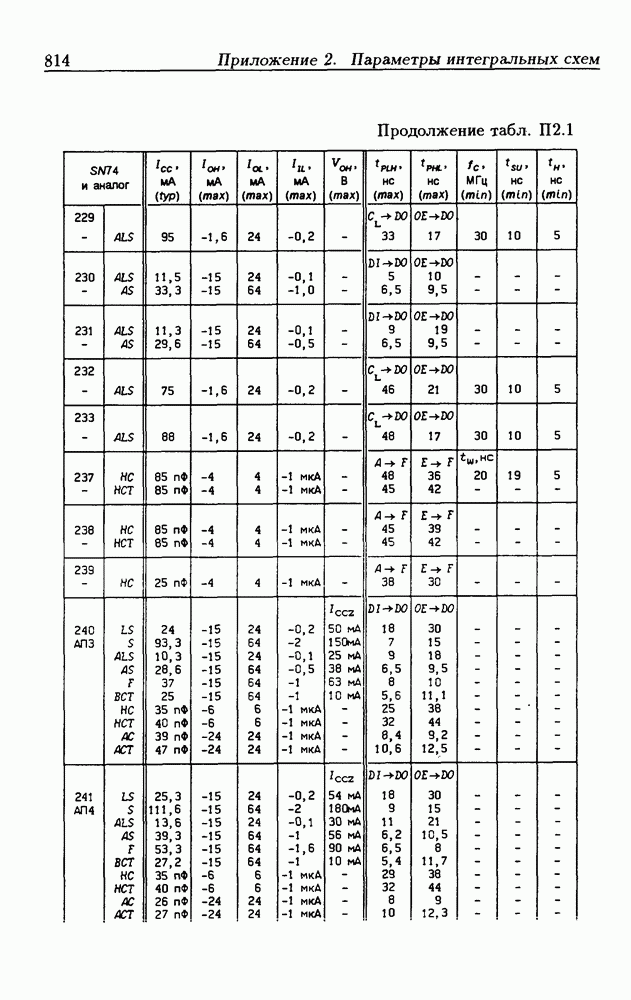
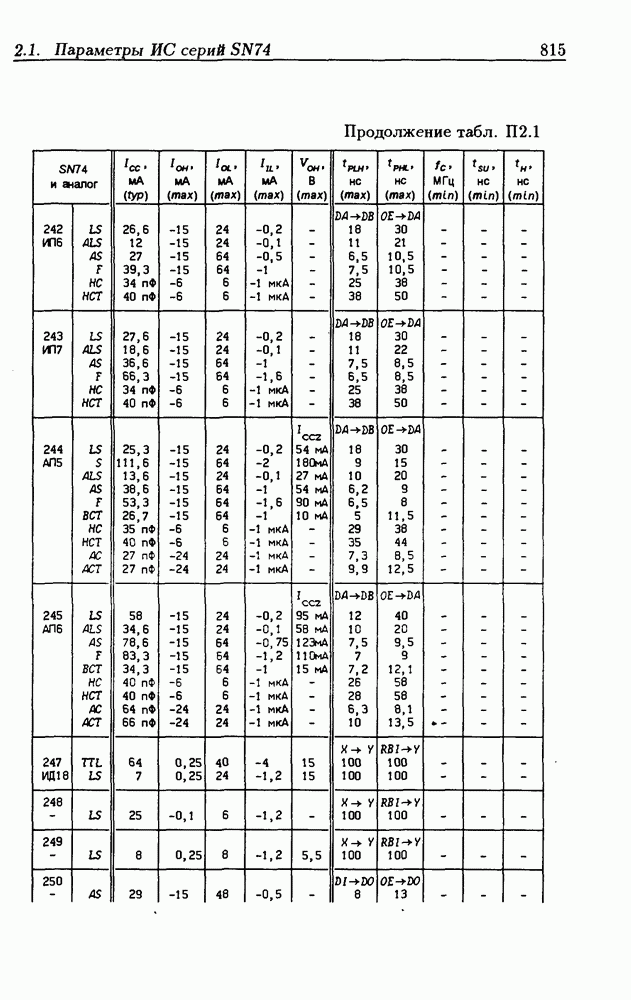
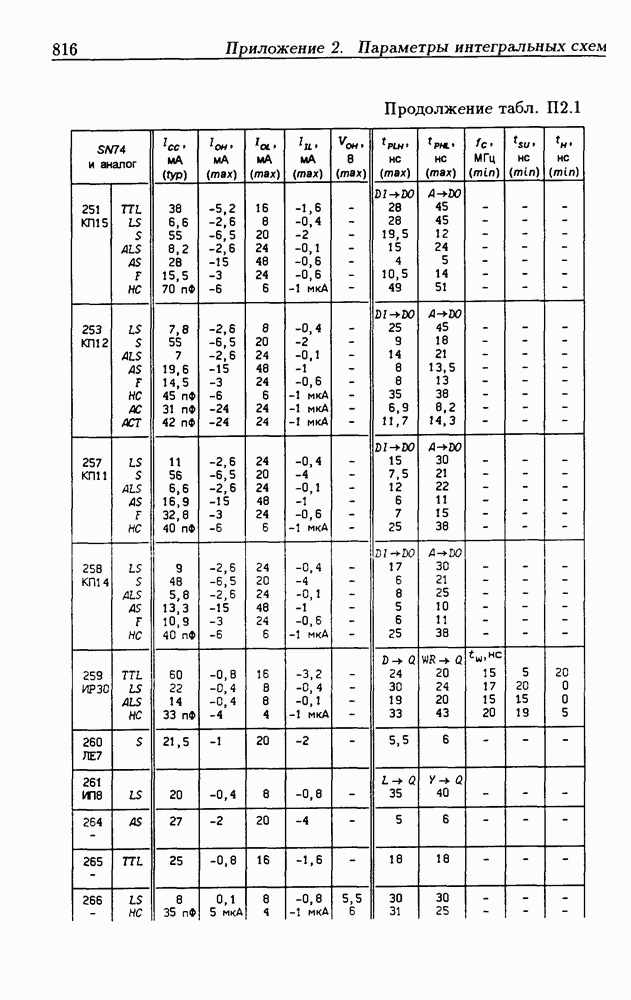
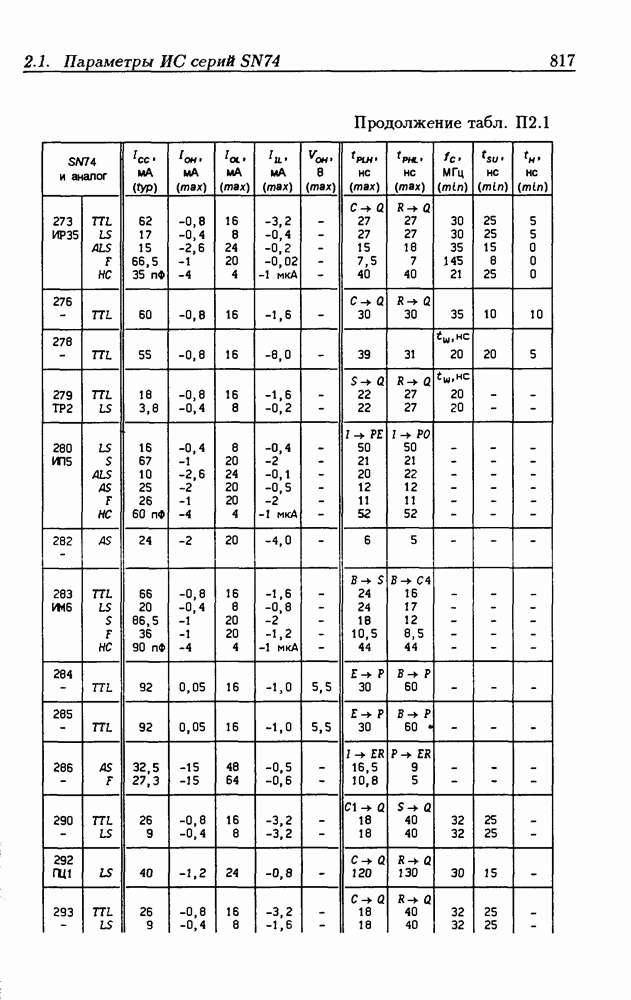
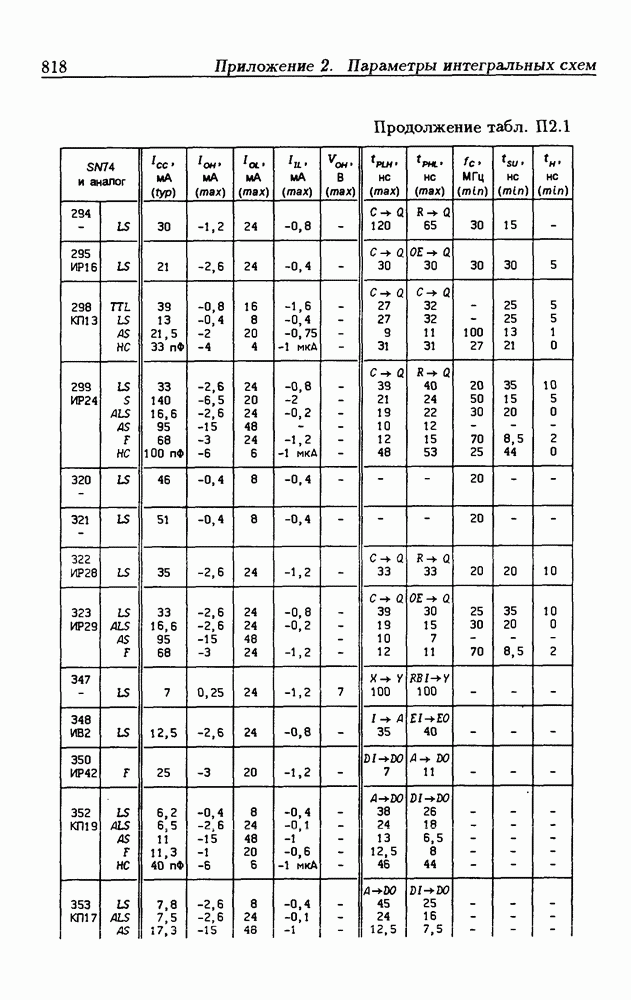
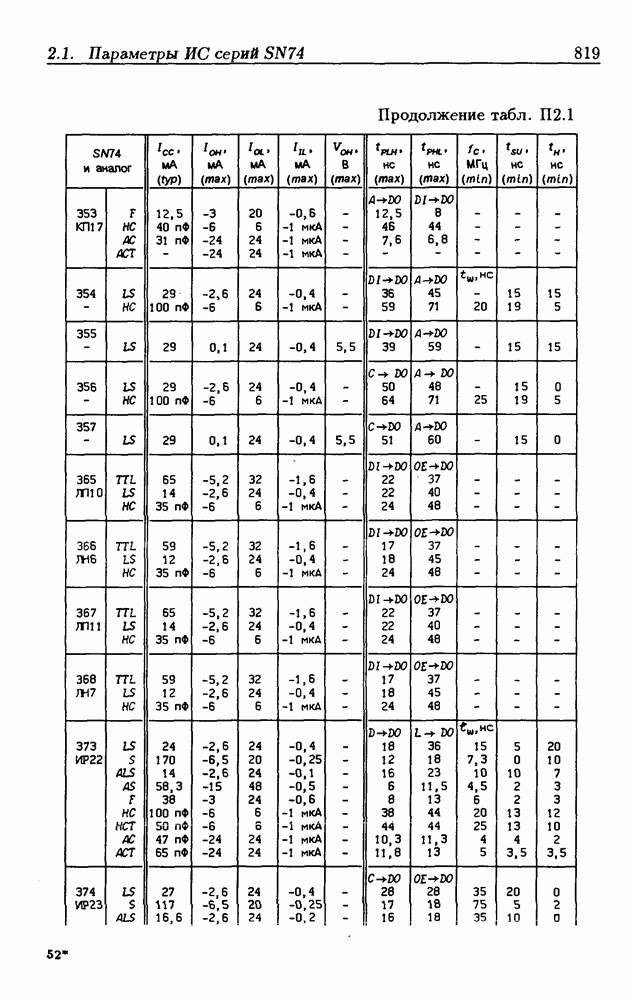
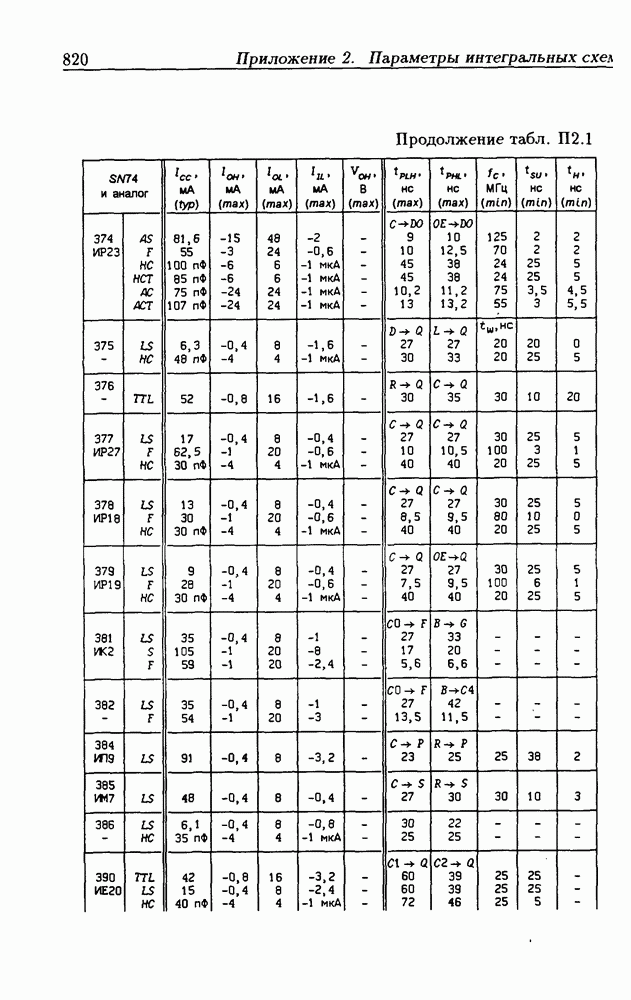
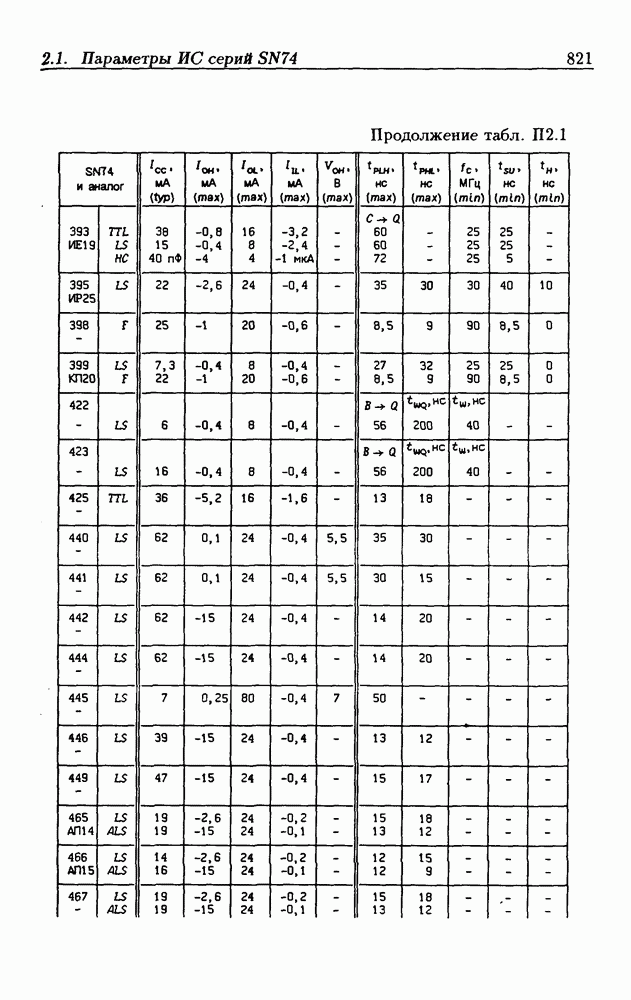
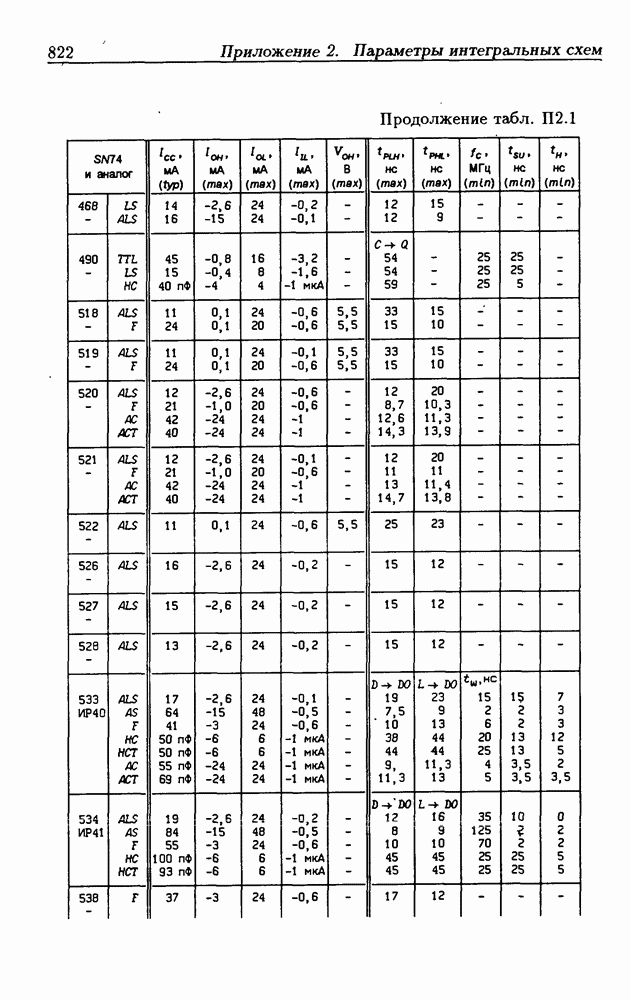
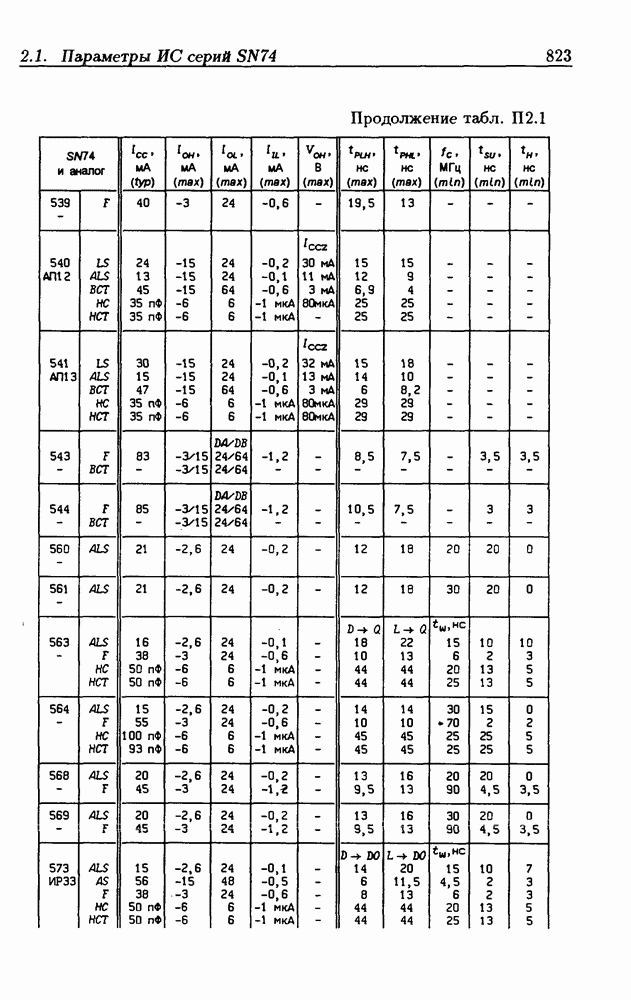
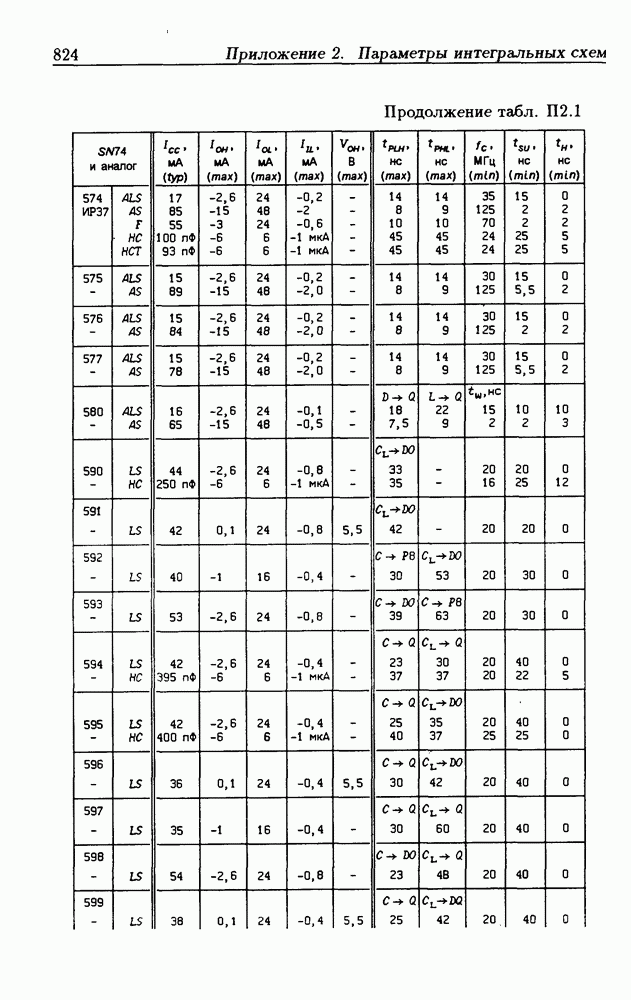
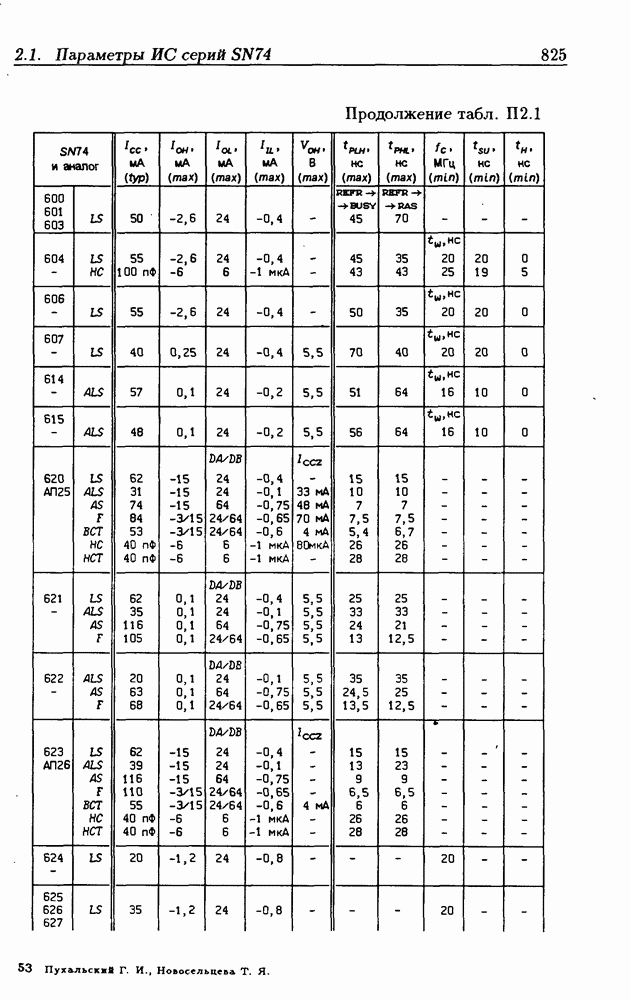
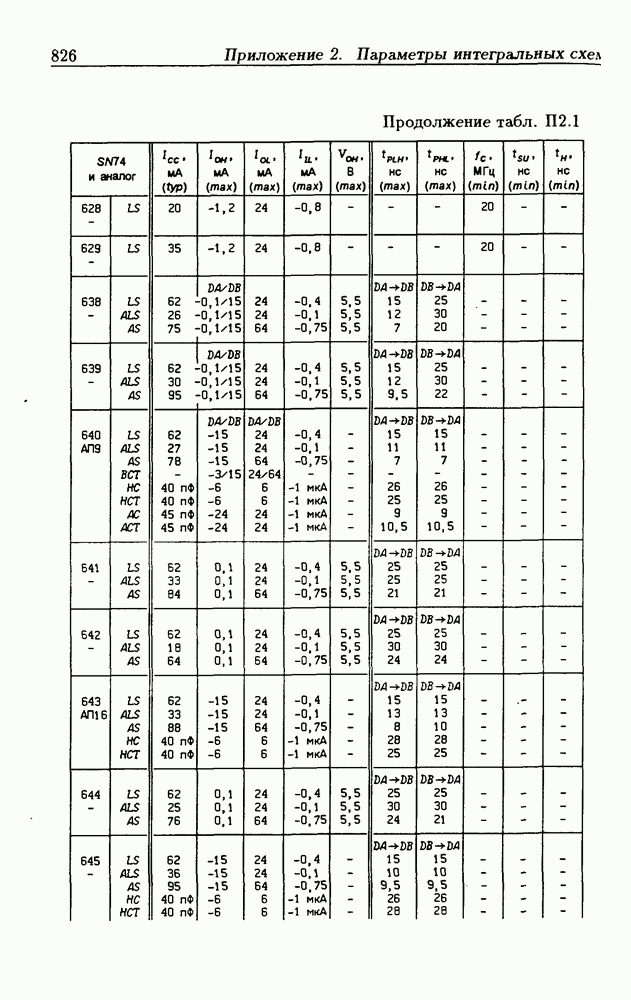
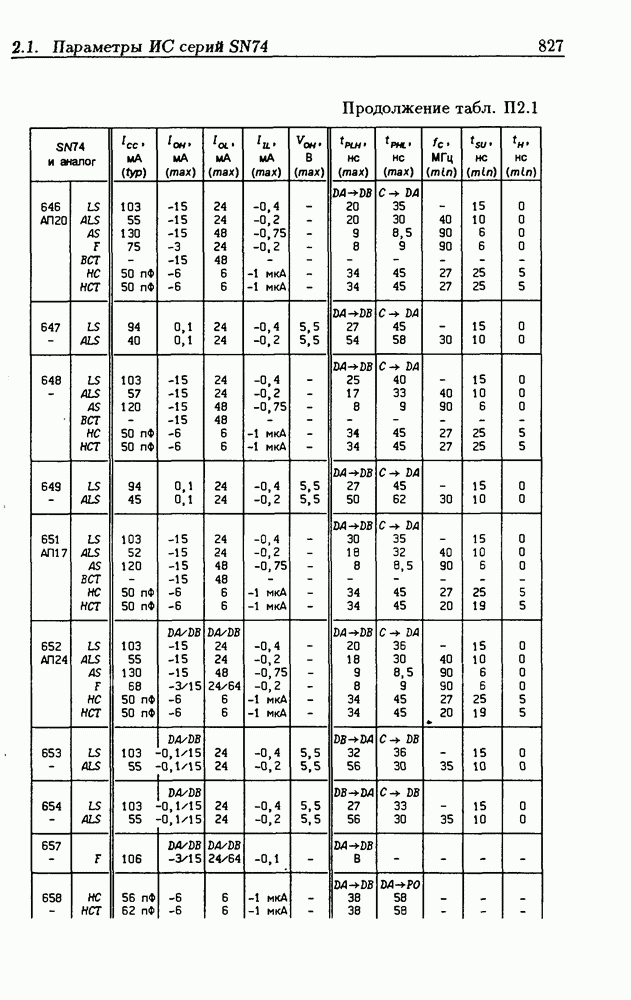
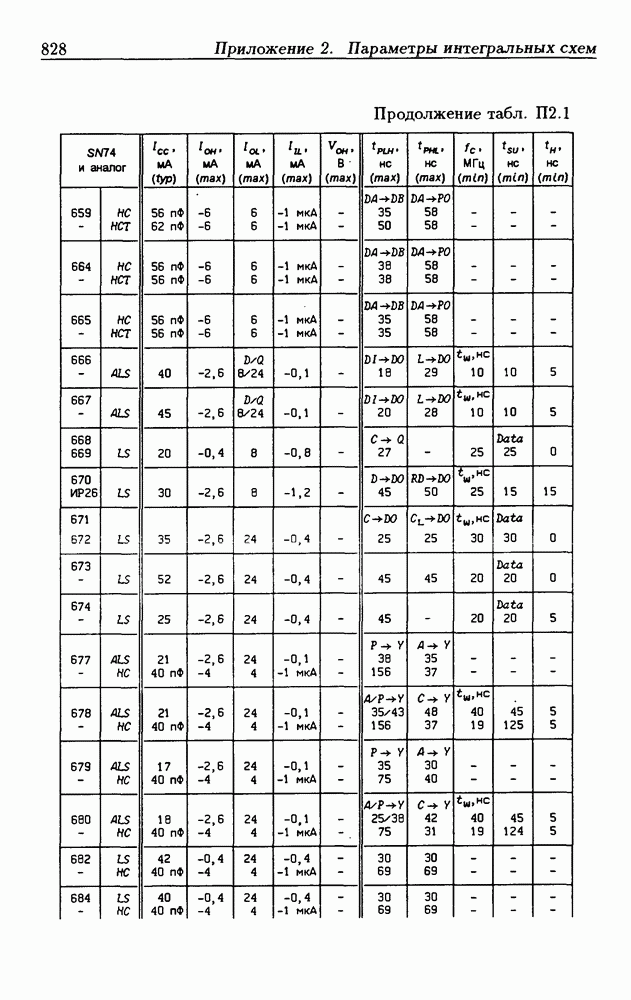
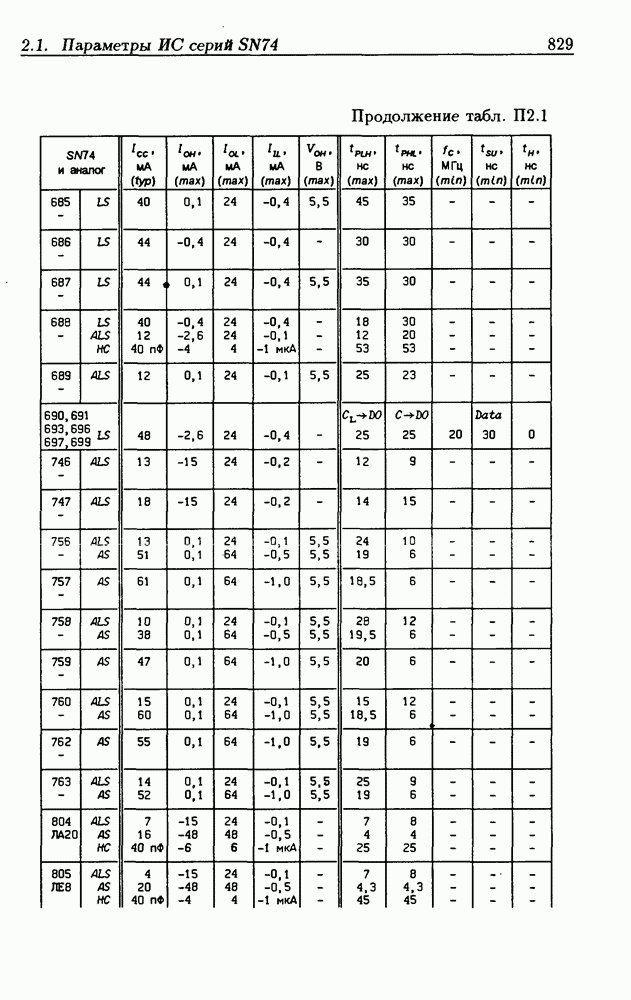
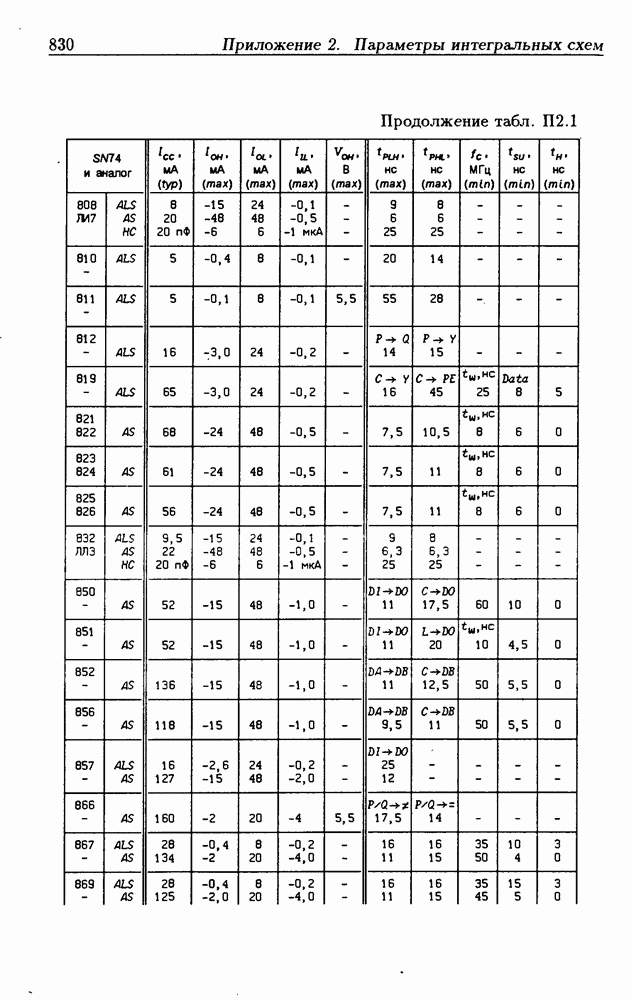
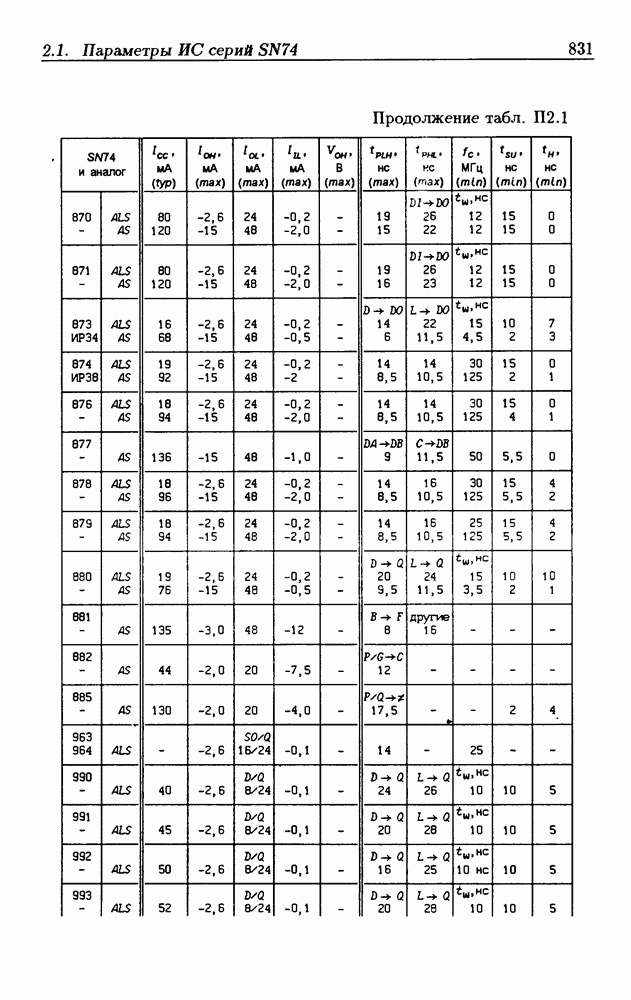
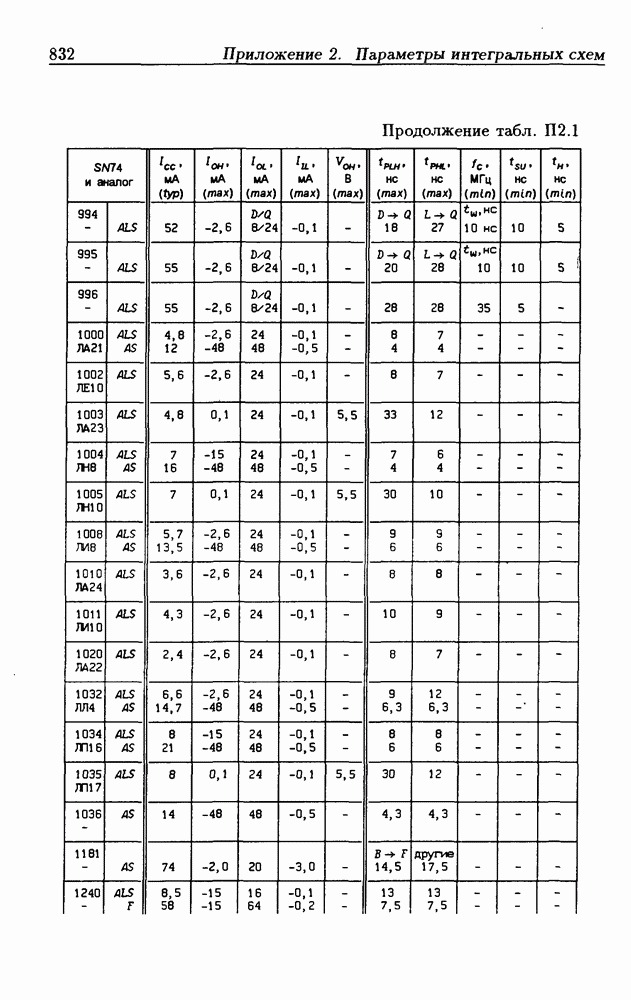
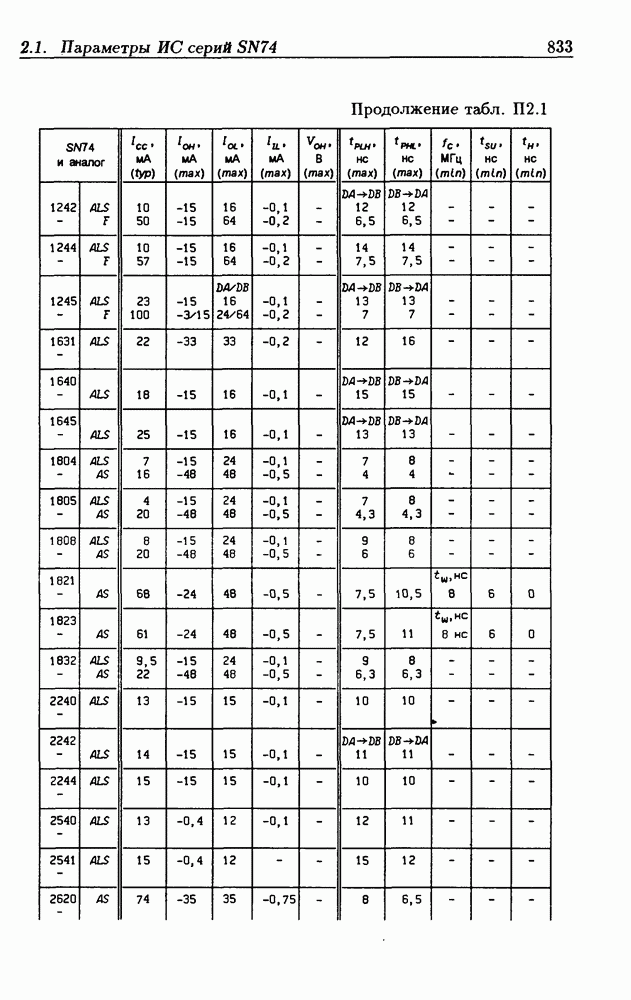
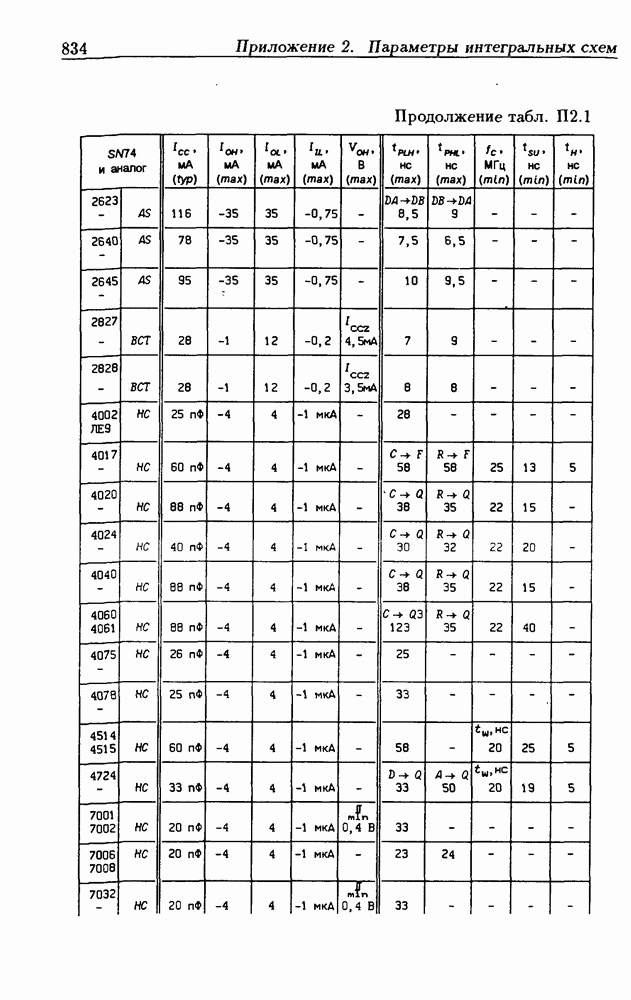
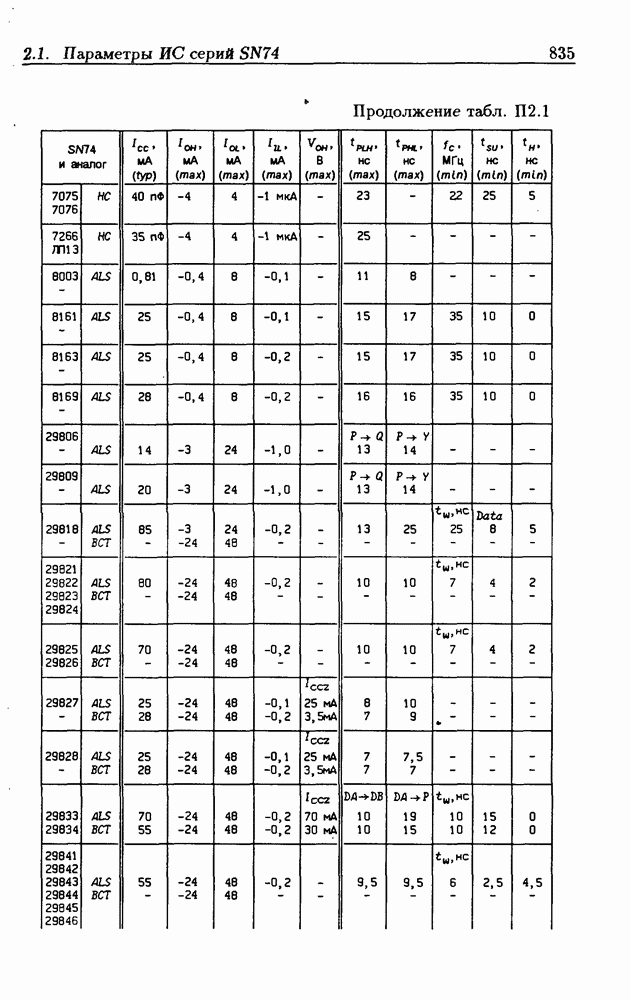
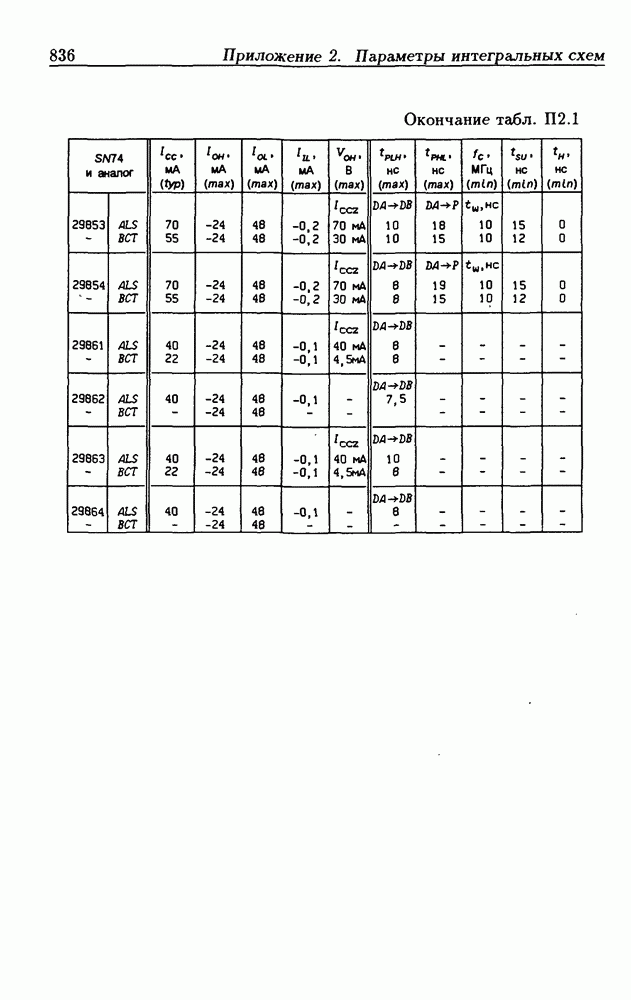
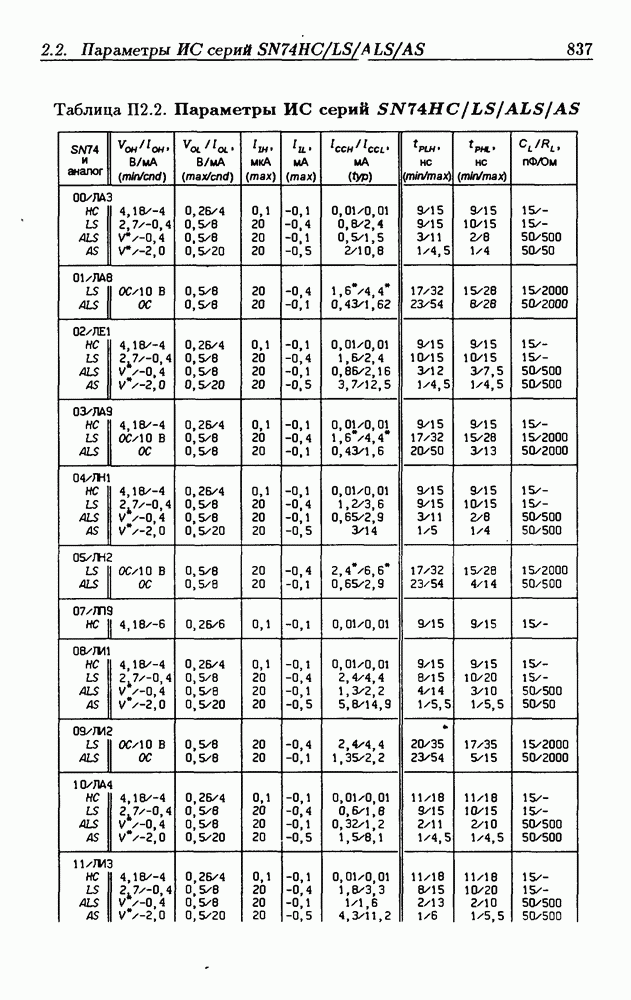
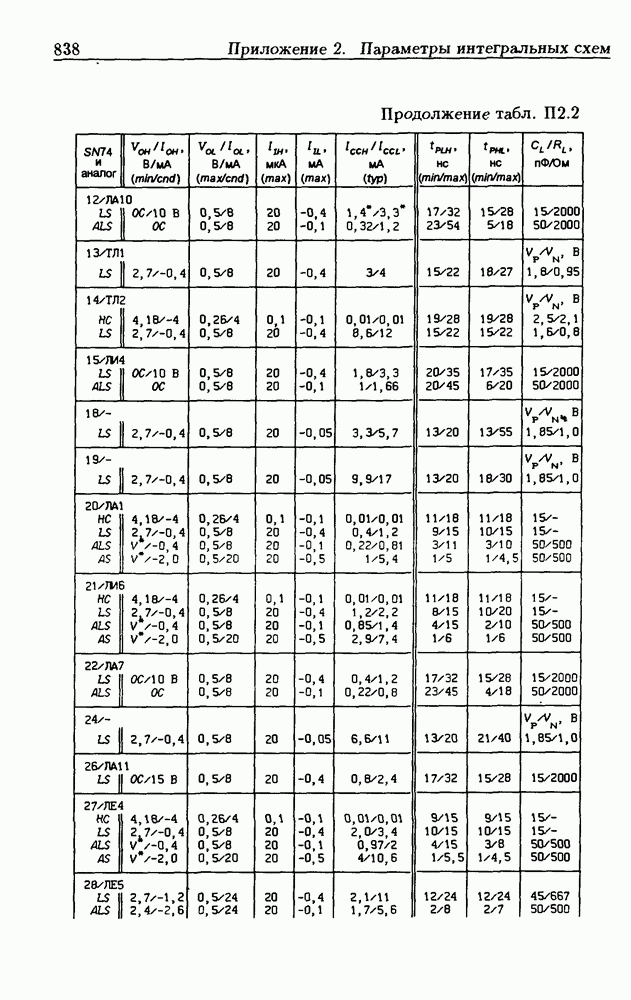
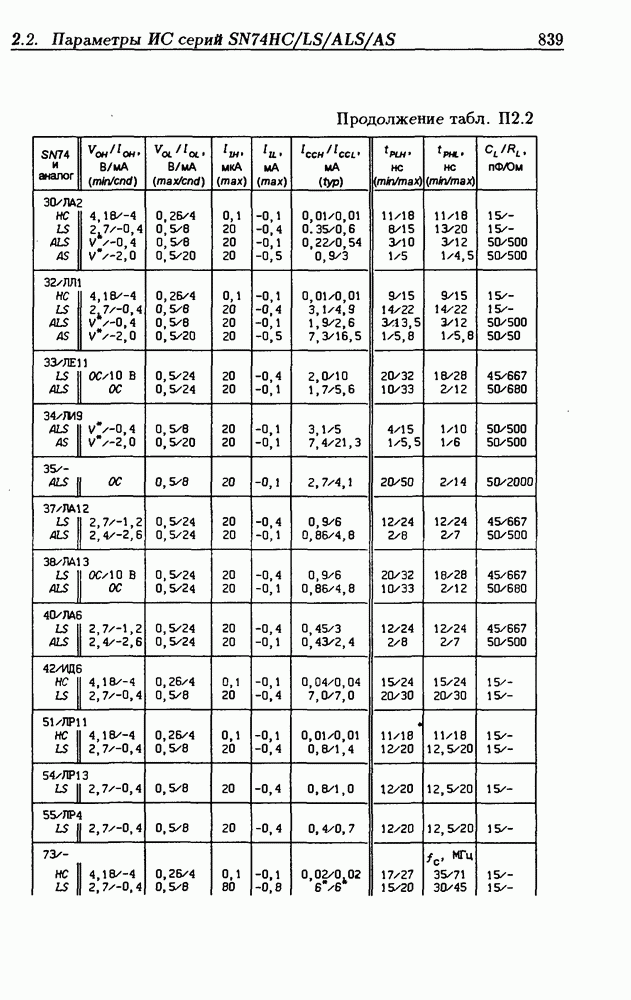
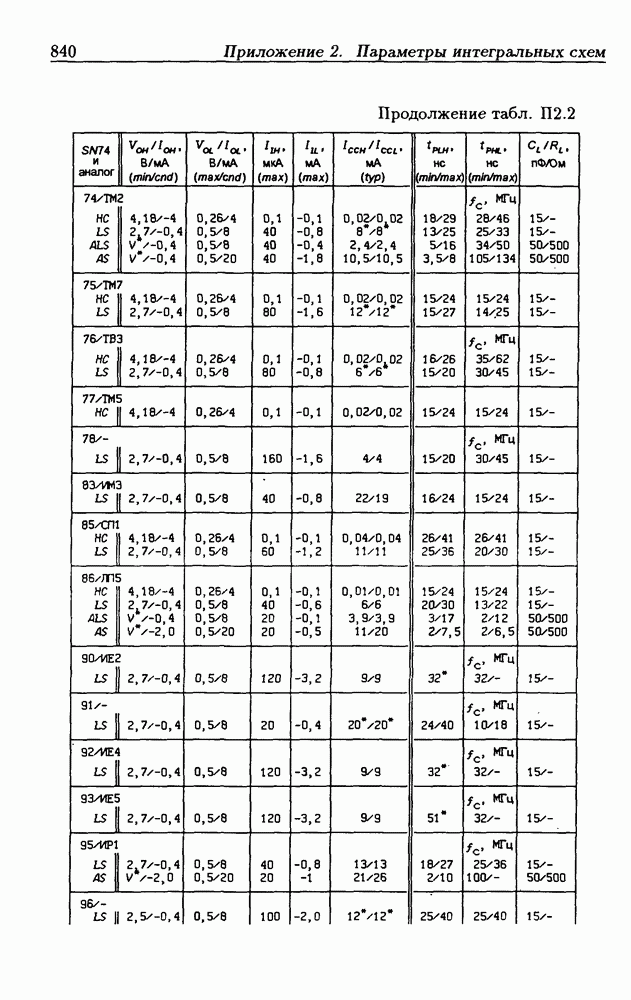
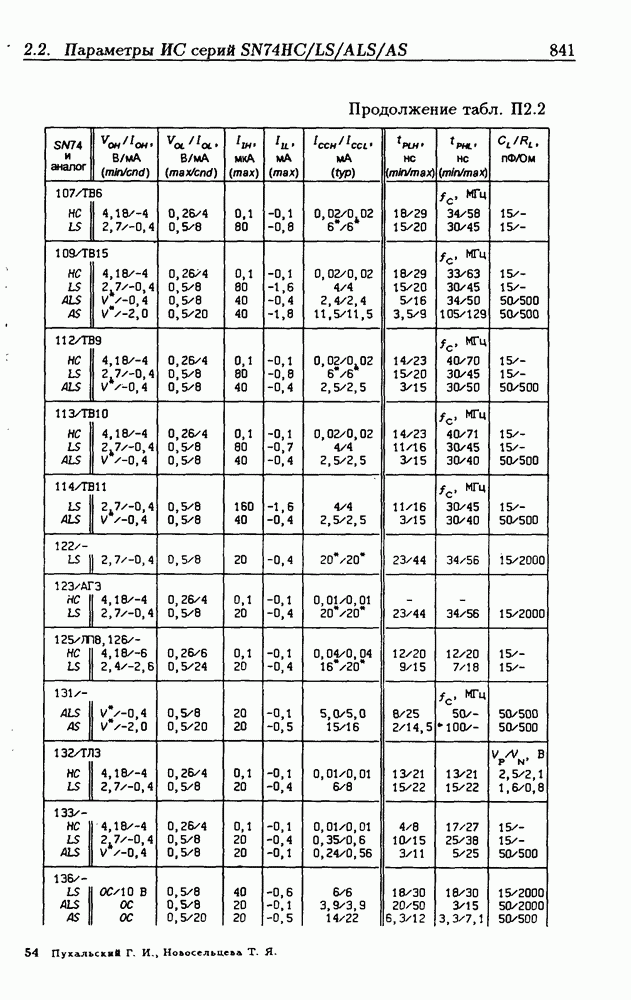
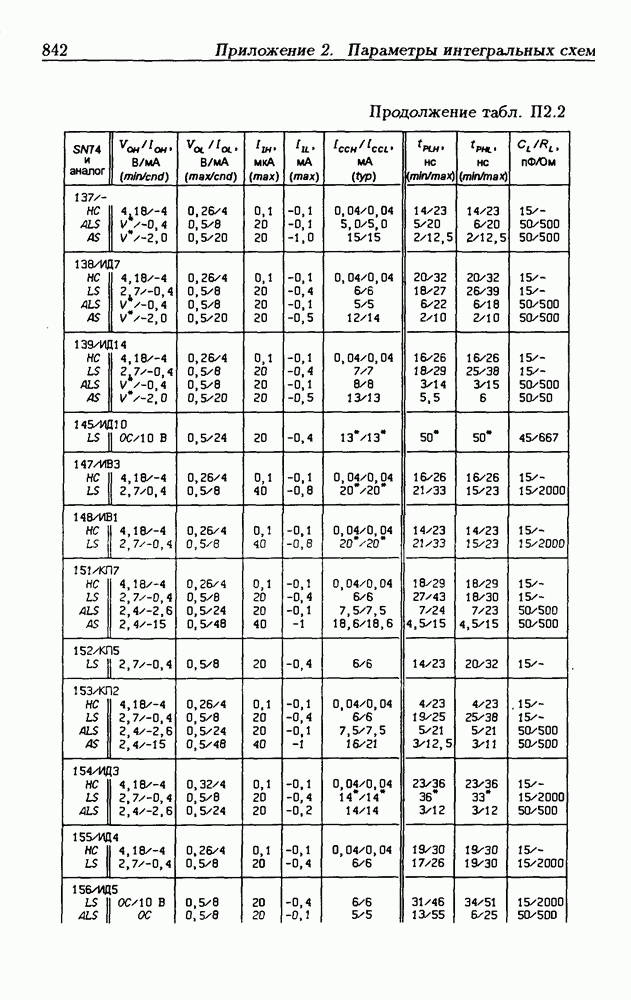
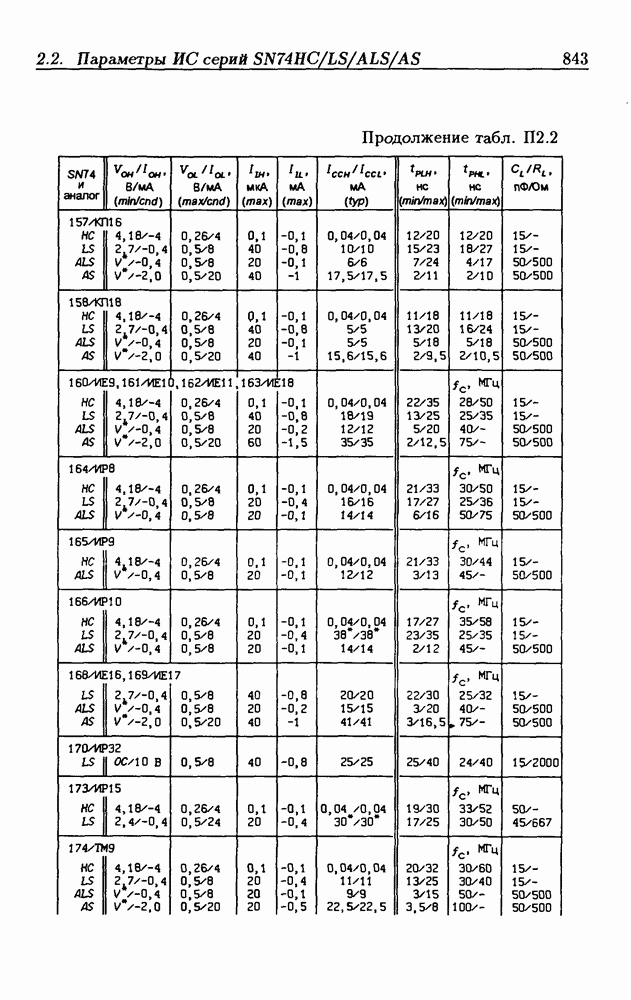
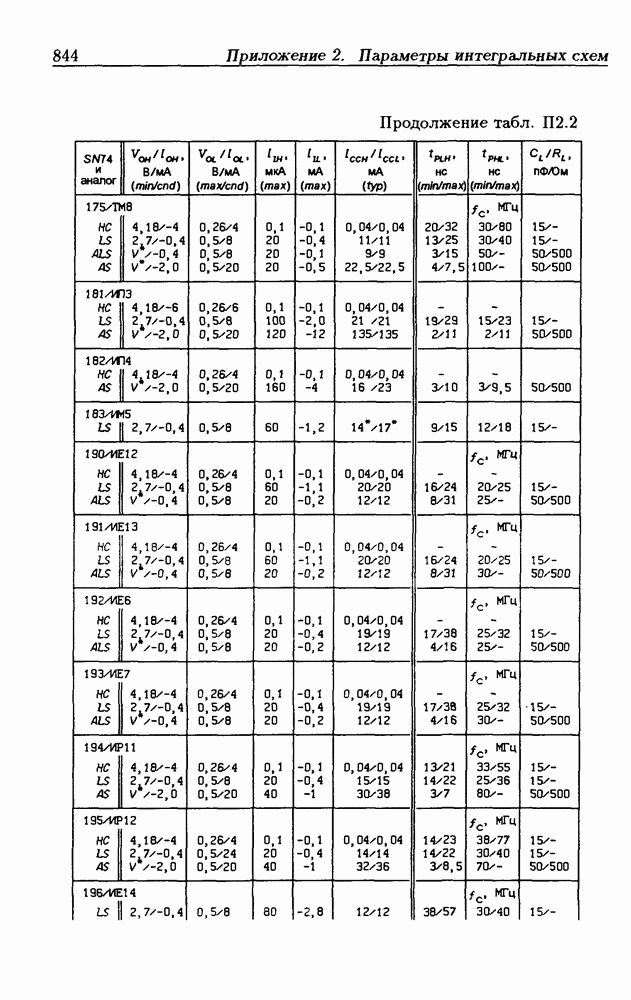
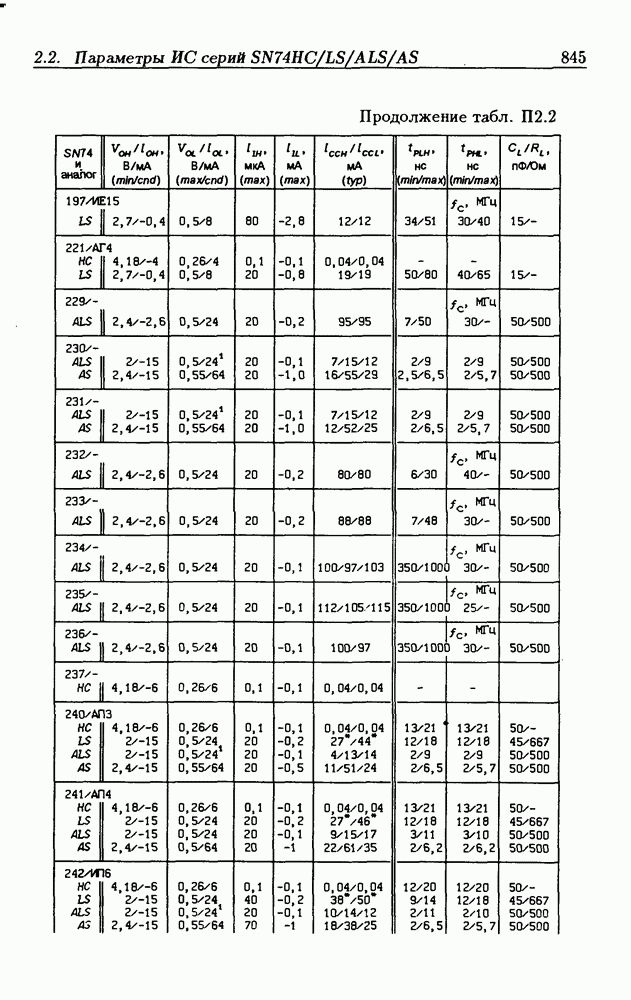
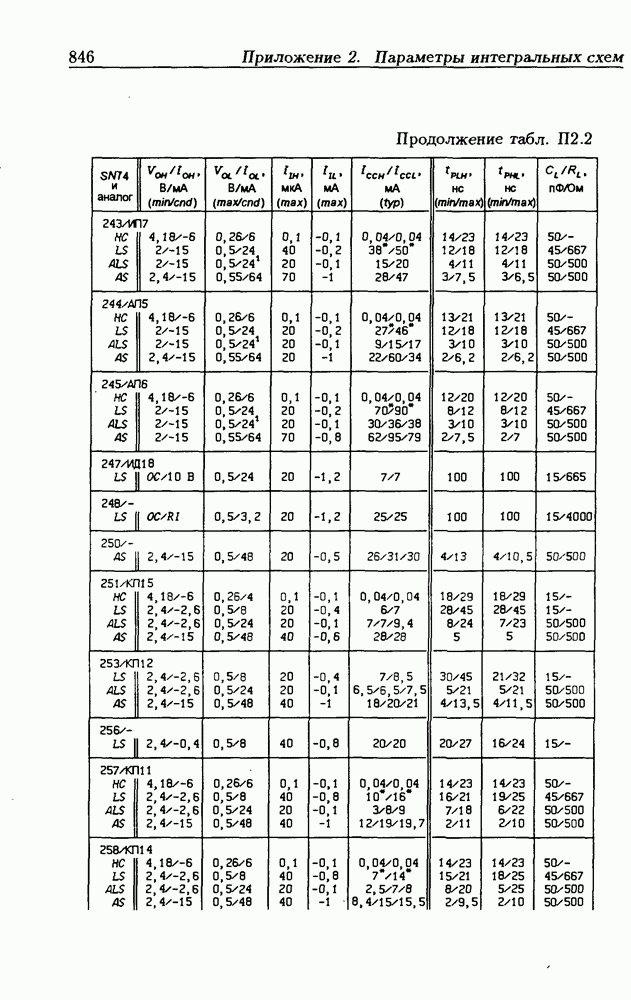
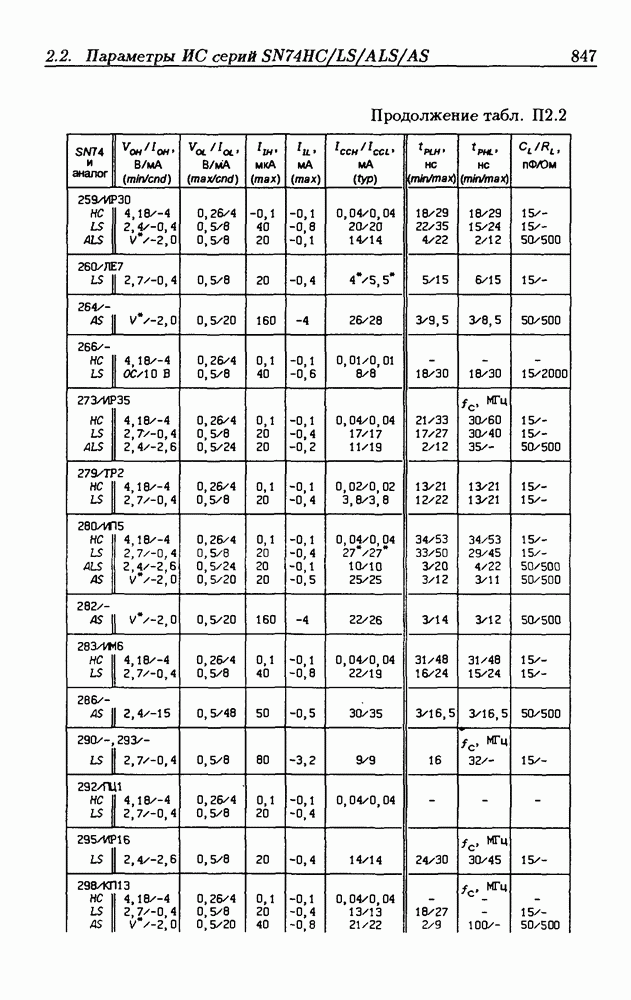
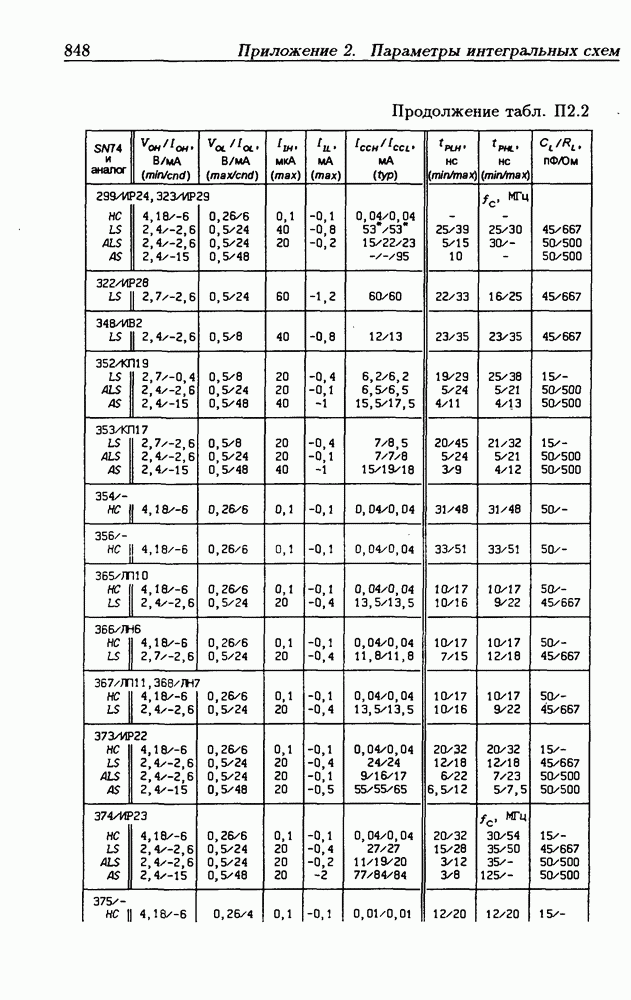
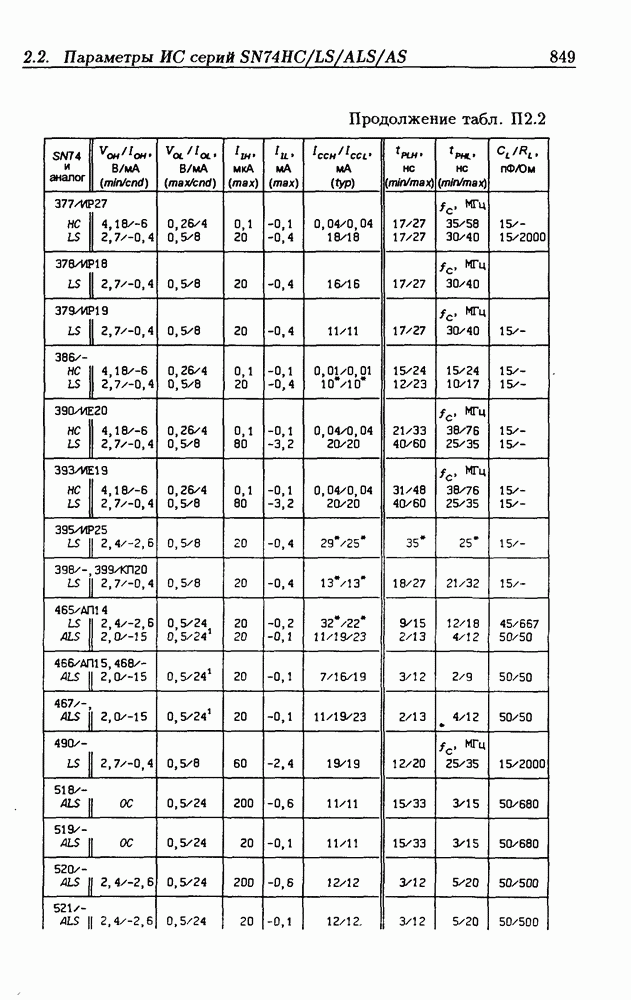
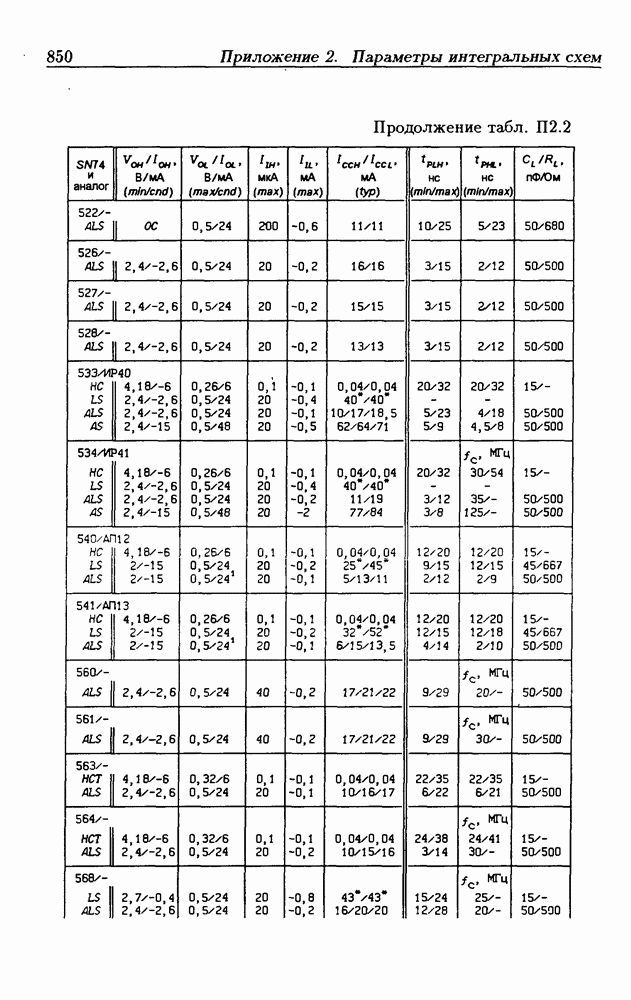
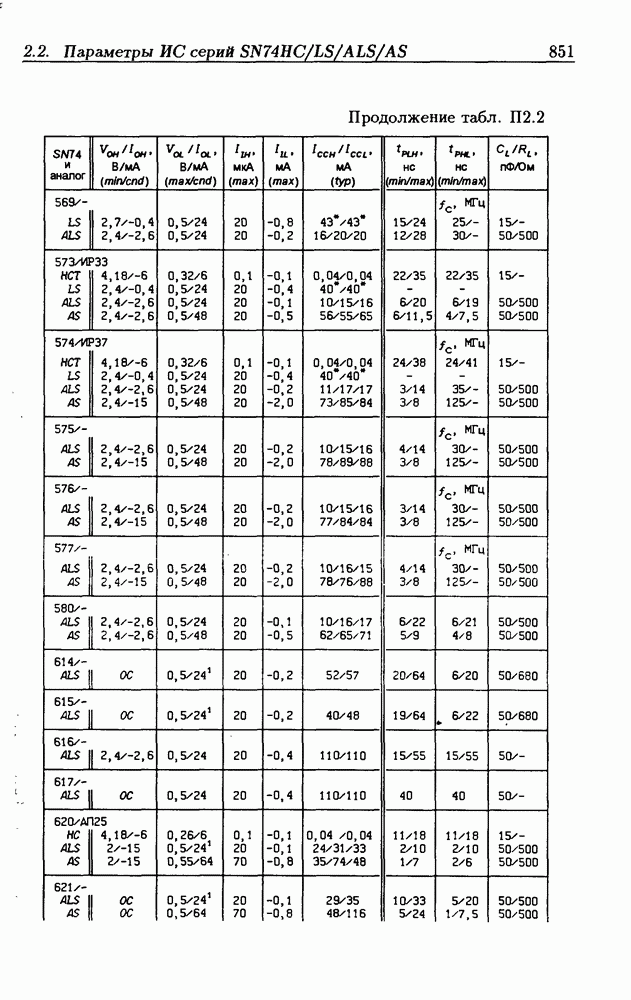
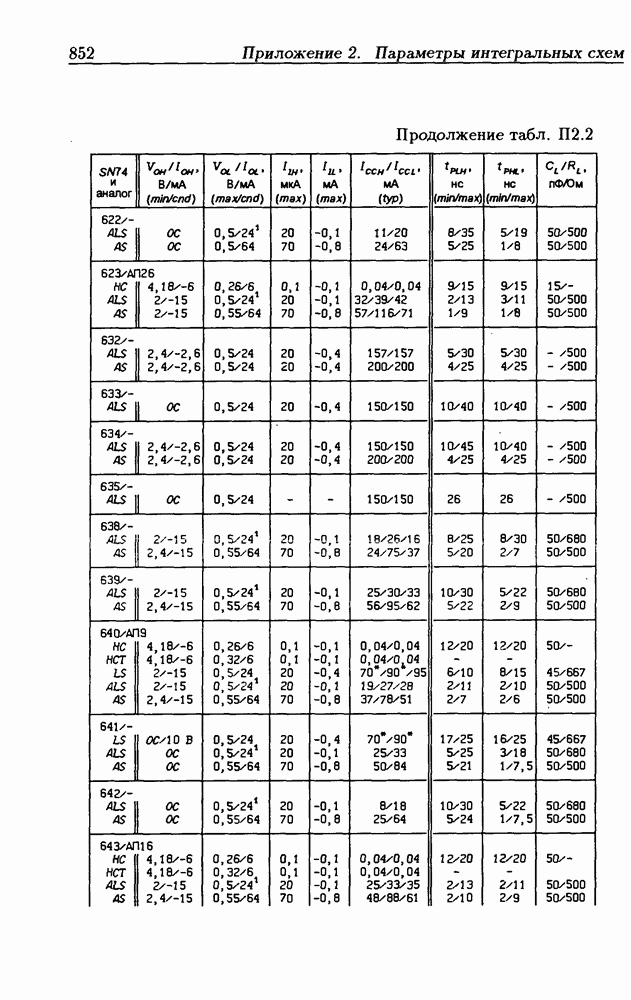
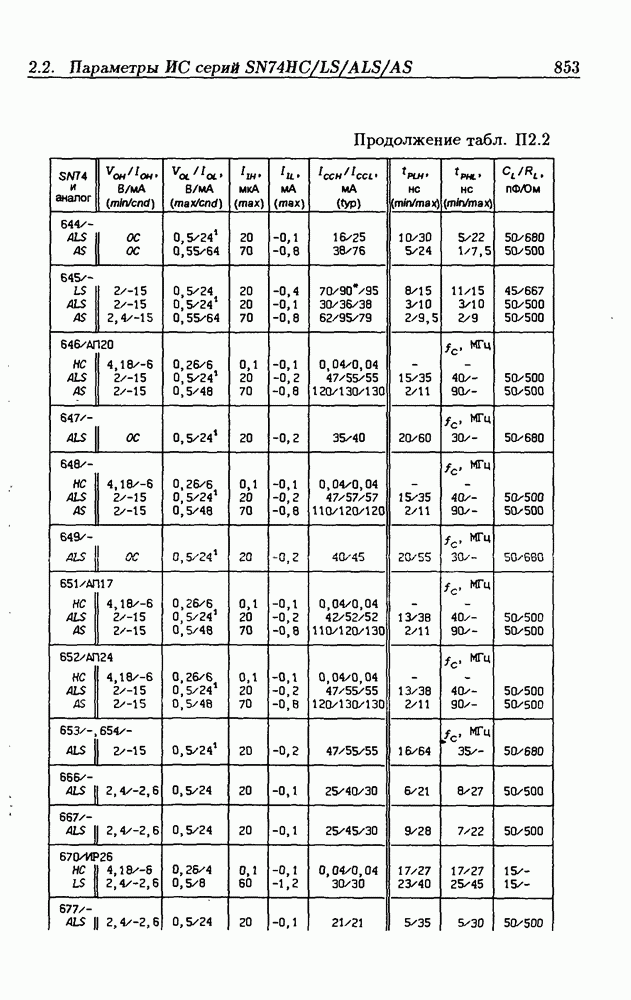
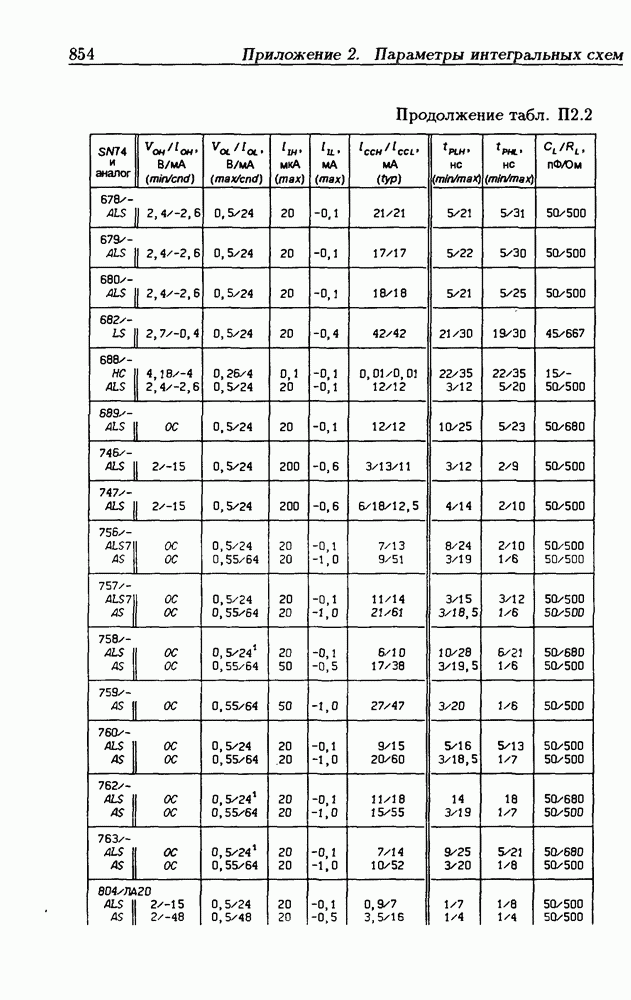
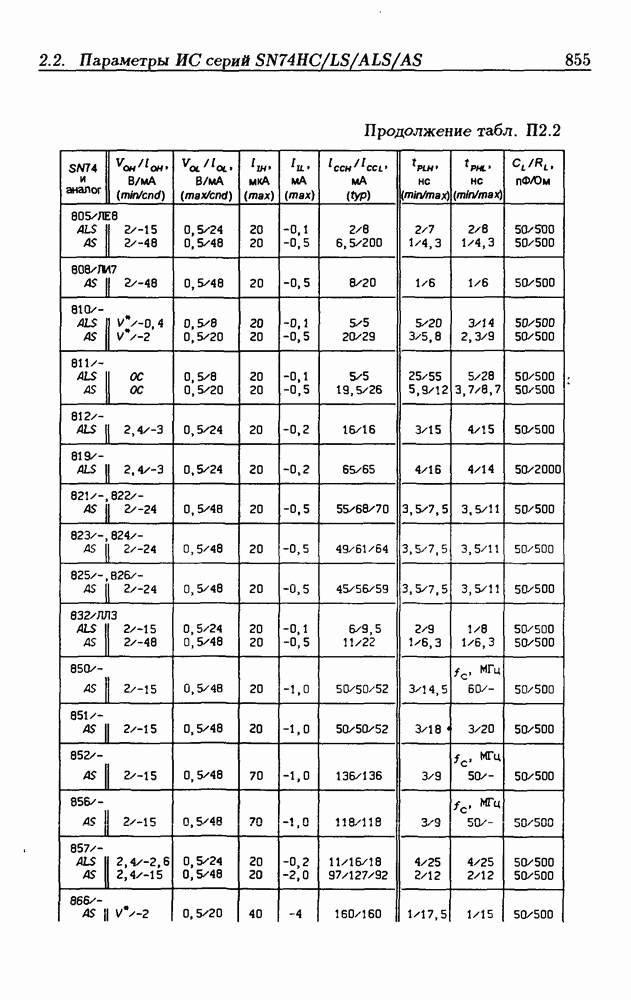
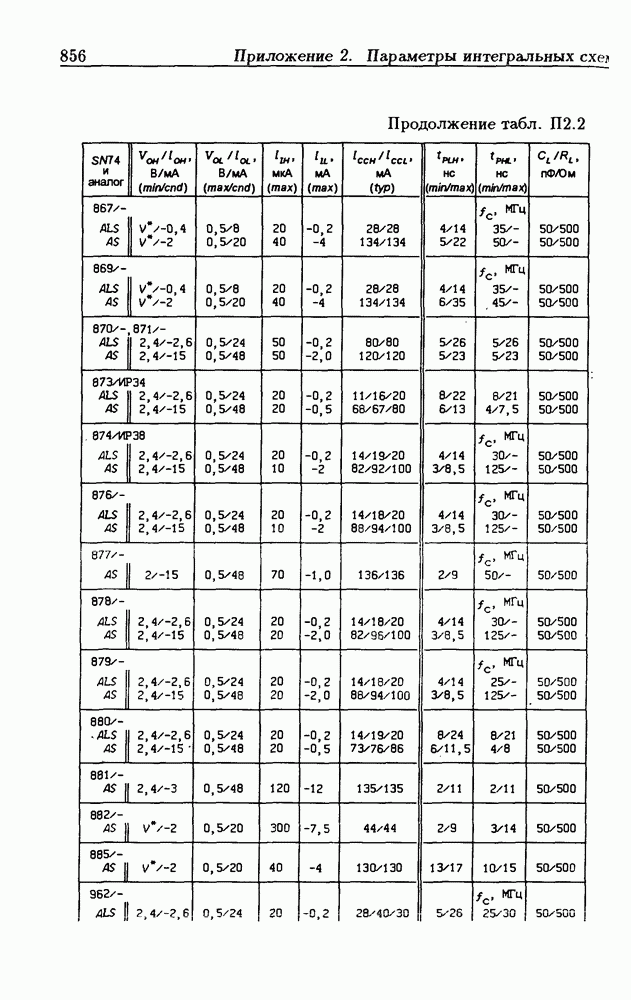
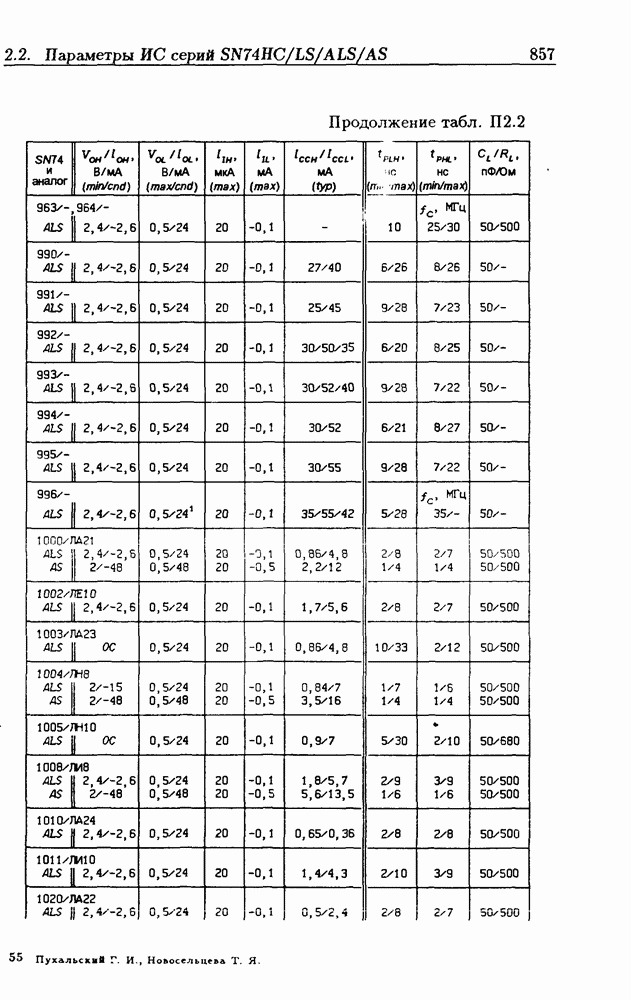
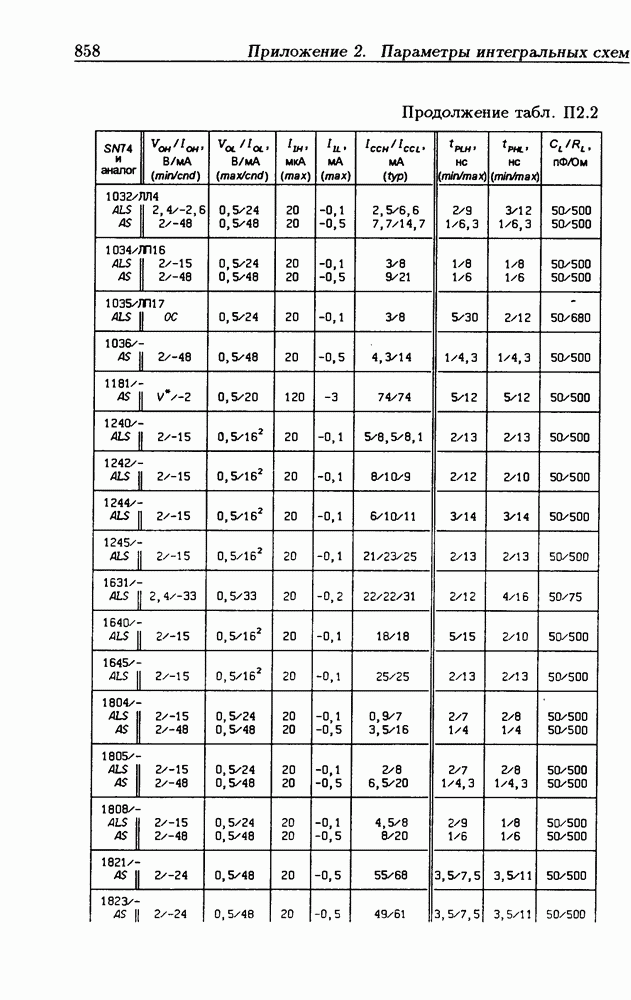
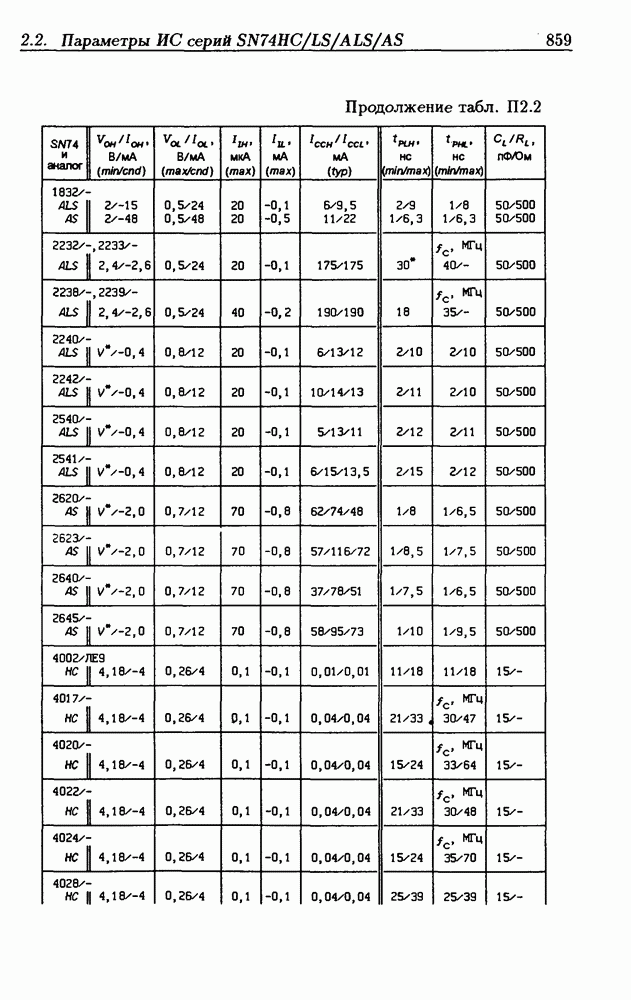
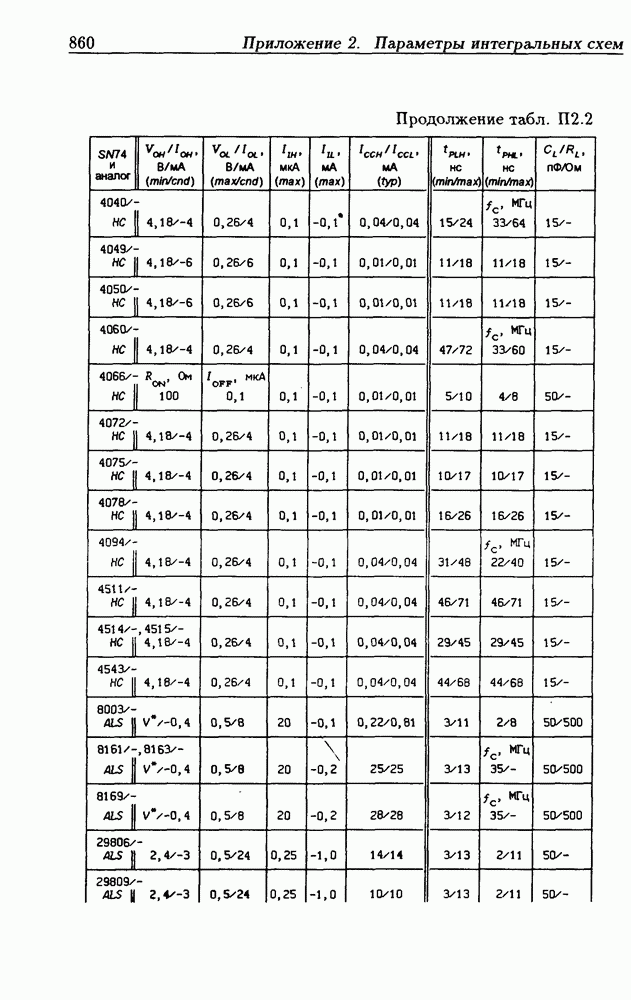
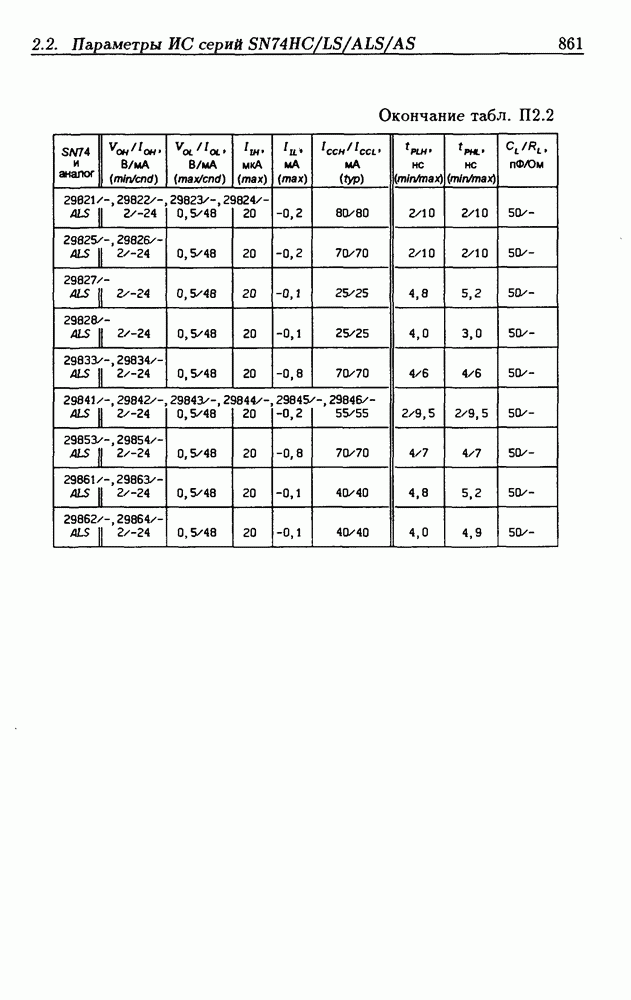
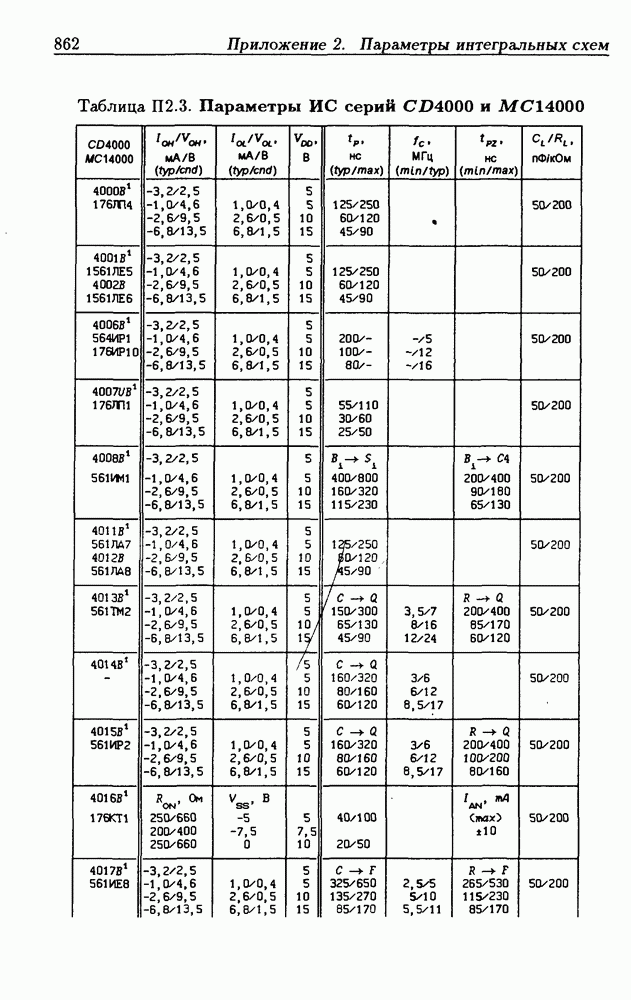
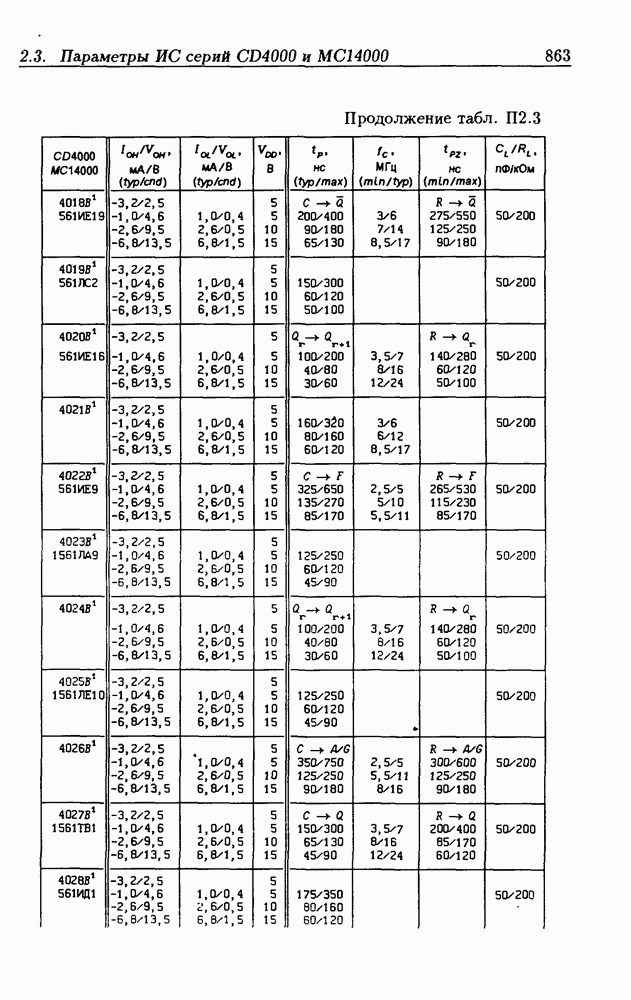
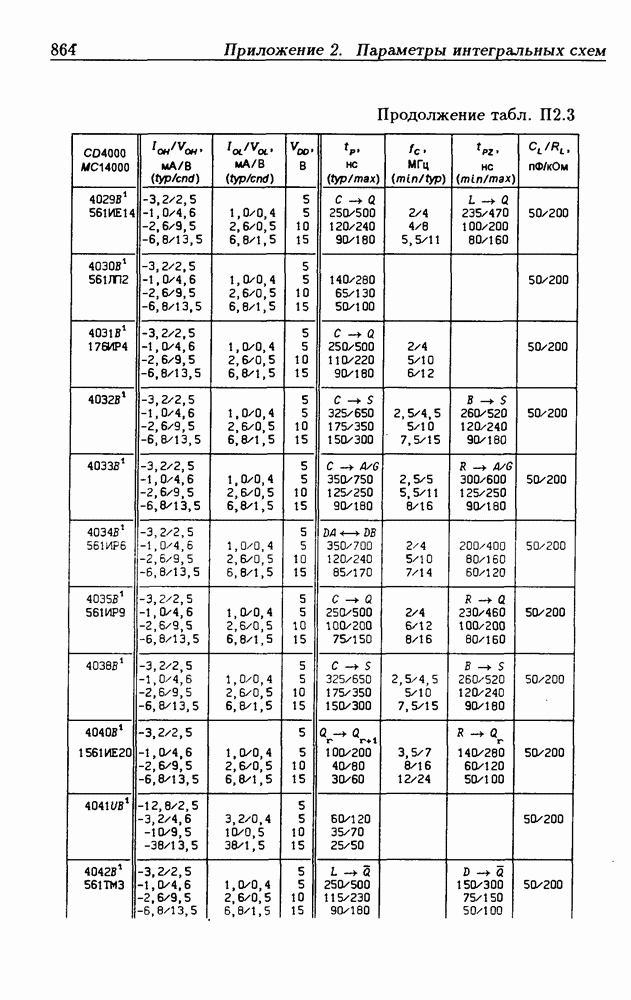
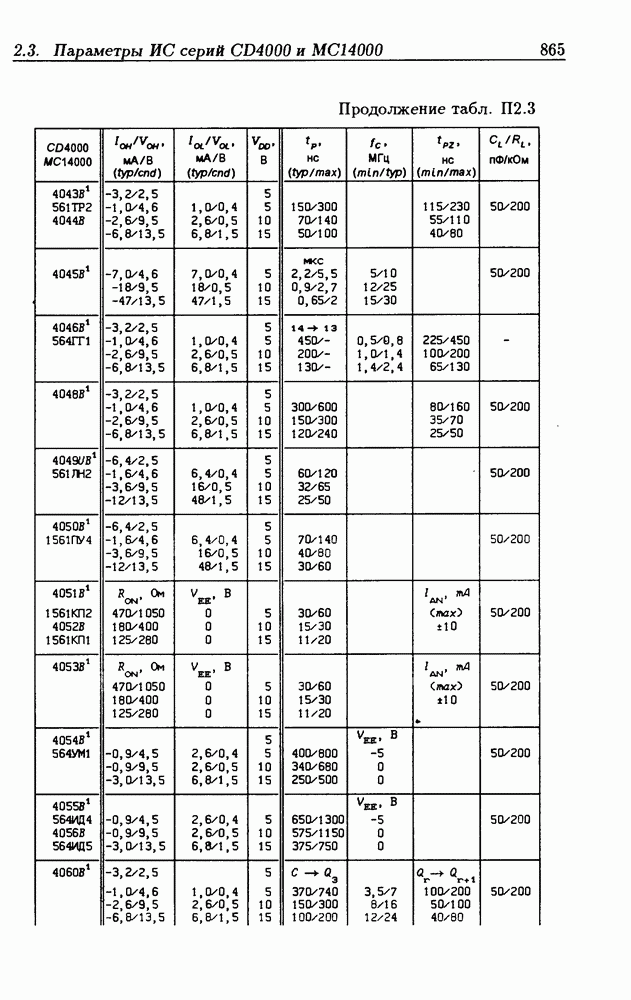
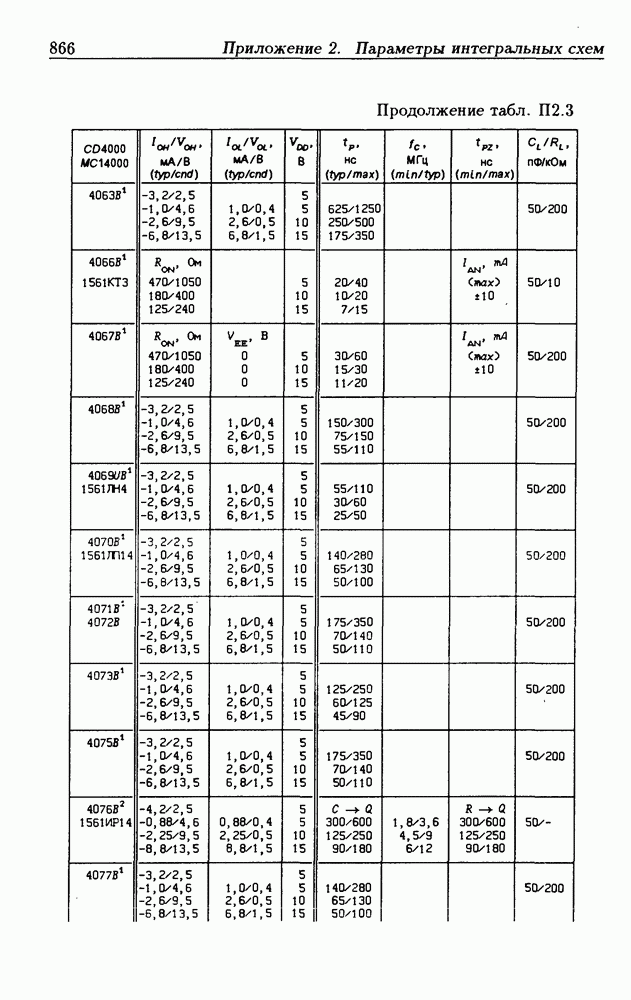
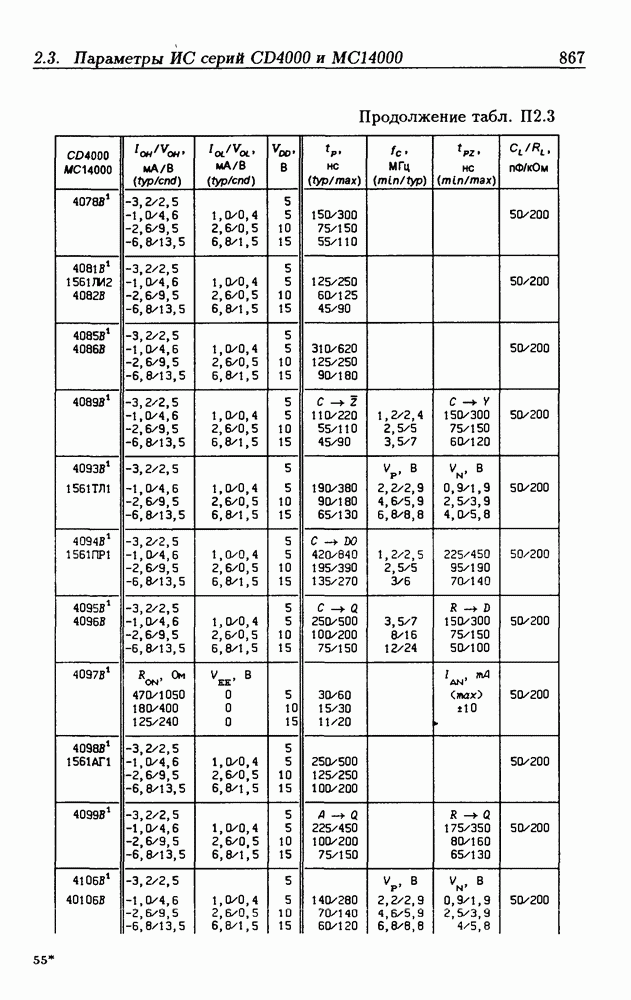
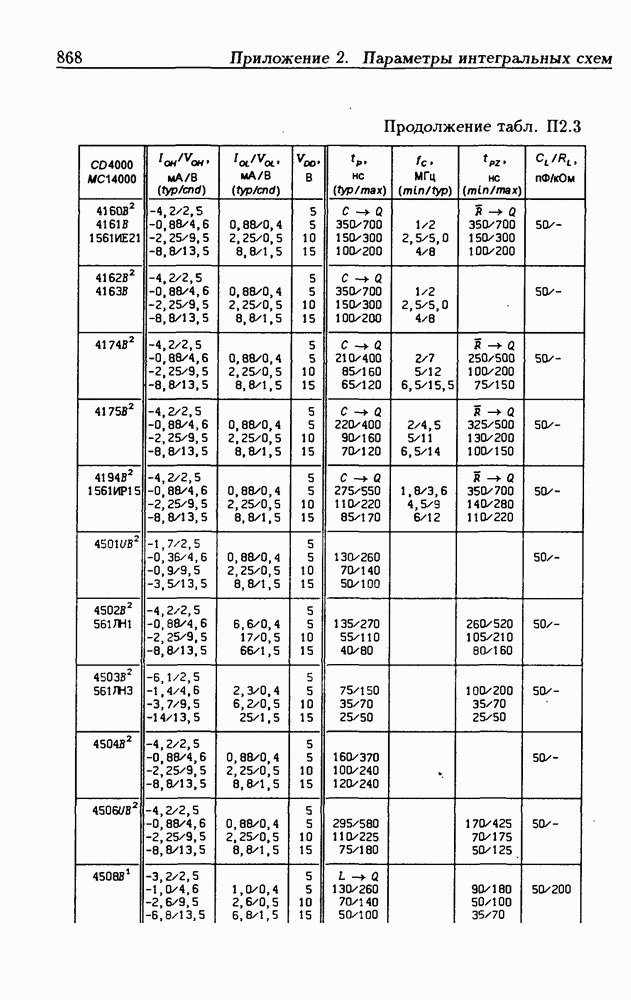
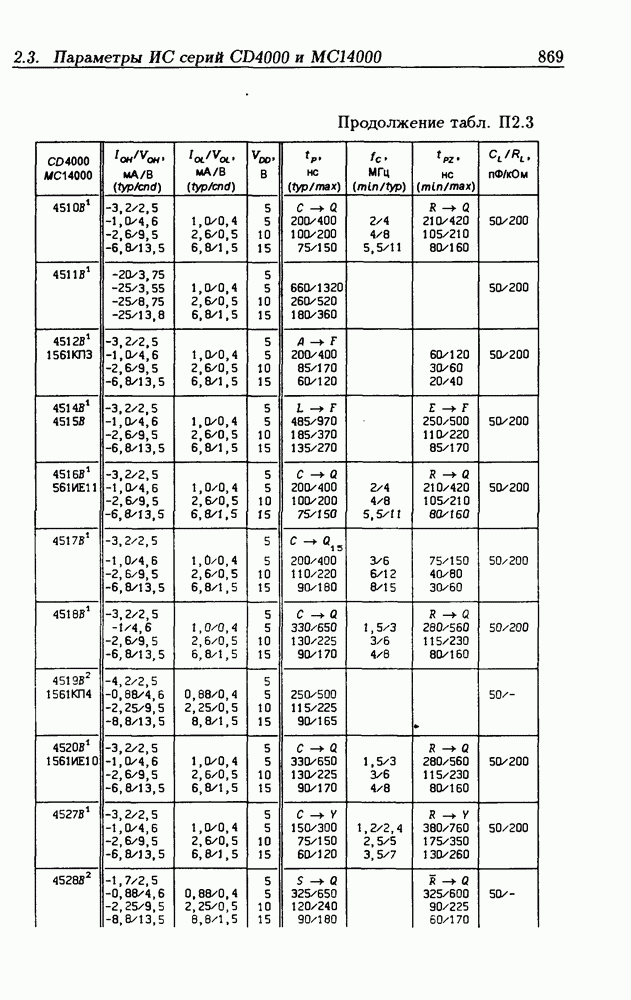
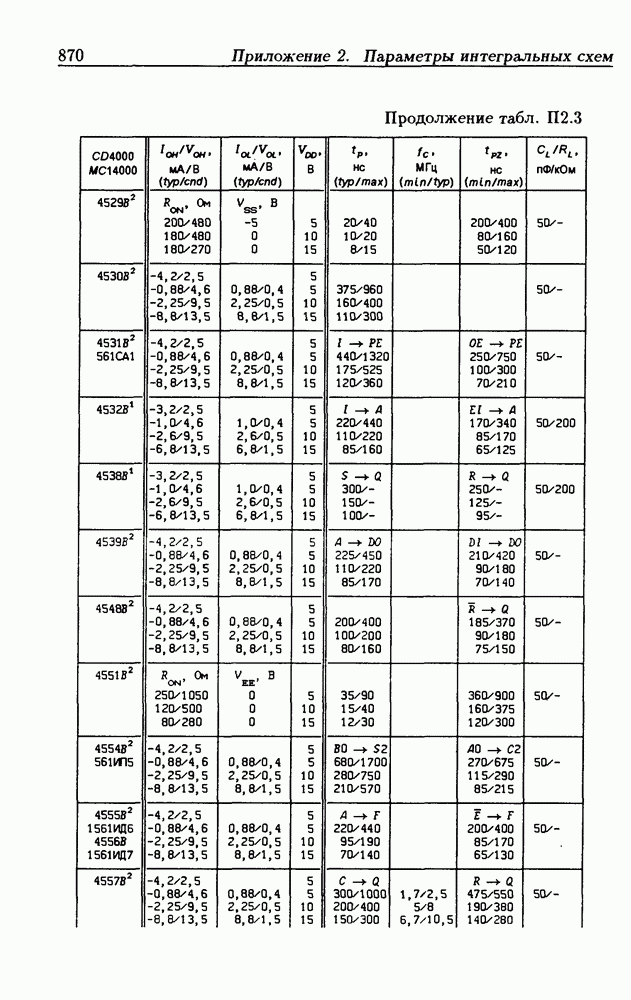
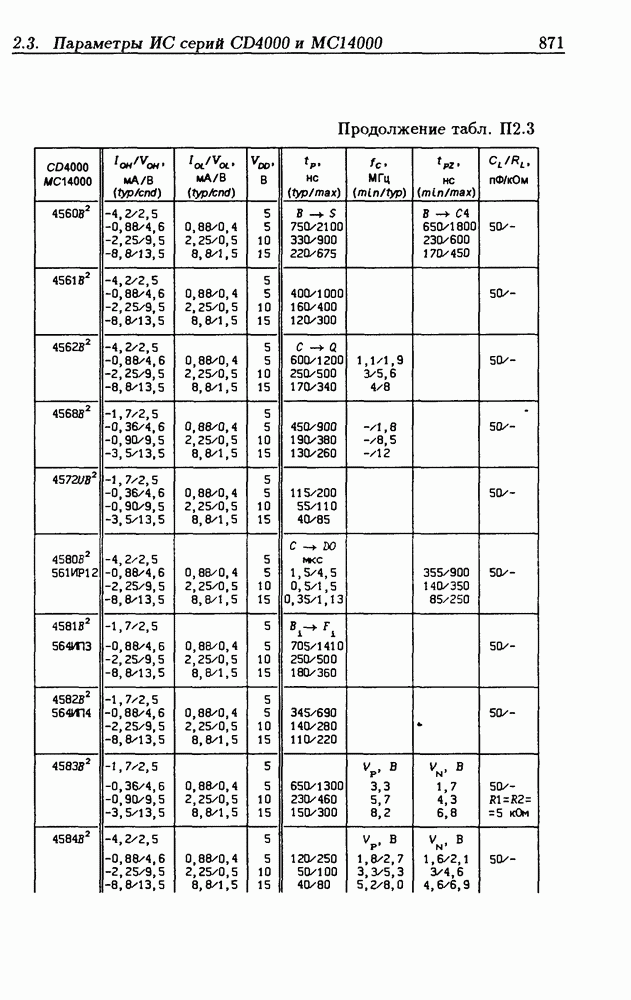
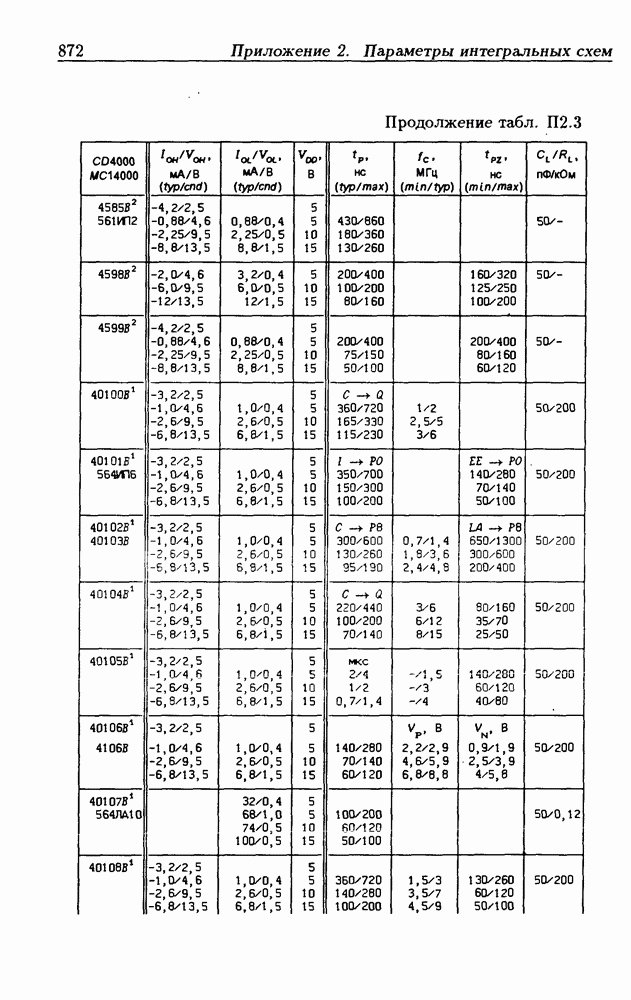
- Приложение 2. Параметры интегральных схем