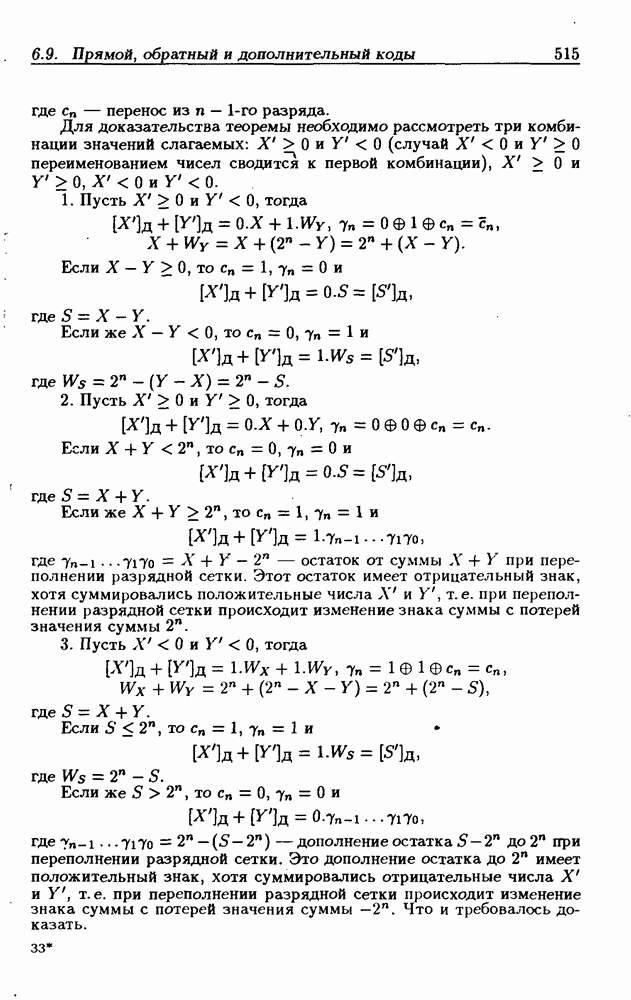| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Триггеры типа dJ-dK.
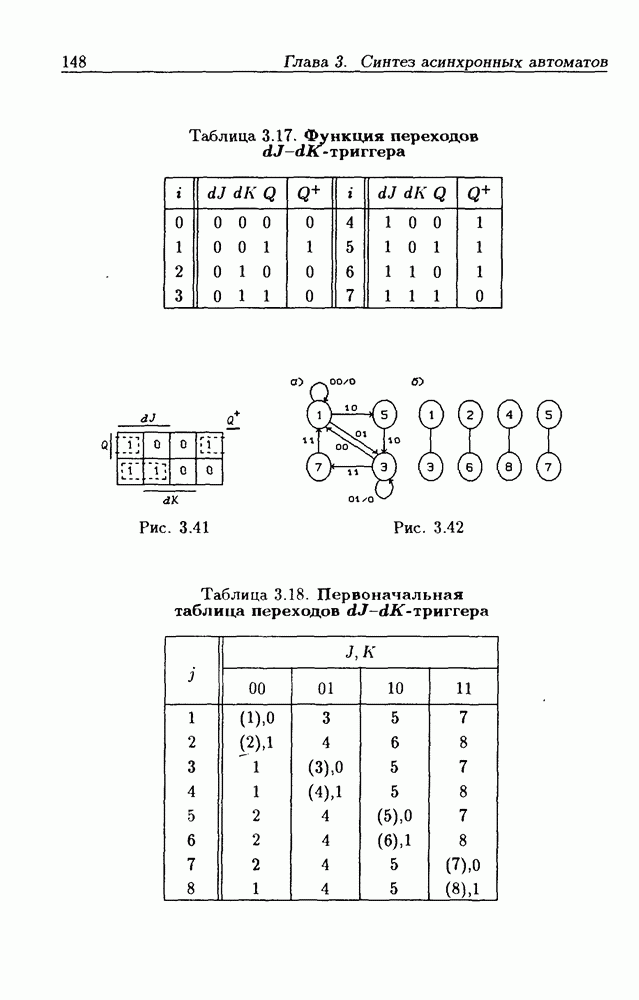
Синтезируем асинхронный импульсный  -триггер (J - Jerk, К - Kill), функция переходов которого задается табл. 3.17. Данный триггер имеет два информационных входа:
-триггер (J - Jerk, К - Kill), функция переходов которого задается табл. 3.17. Данный триггер имеет два информационных входа:  вход установки состояния
вход установки состояния  и А — вход установки состояния
и А — вход установки состояния  При одновременном изменении обоих сигналов с 1 на
При одновременном изменении обоих сигналов с 1 на  триггер изменяет свое состояние на инверсное
триггер изменяет свое состояние на инверсное  Из диаграммы Вейча (рис. 3.41), построенной по табл. 3.17, следует, что функция переходов триггера
Из диаграммы Вейча (рис. 3.41), построенной по табл. 3.17, следует, что функция переходов триггера

Если сигналы  не изменяются, то
не изменяются, то  поэтому в устойчивых состояниях выполняется соотношение
поэтому в устойчивых состояниях выполняется соотношение  Из этого следует, что первоначальная таблица переходов должна иметь в каждом столбце по два устойчивых состояния, отличающихся значением функции выхода
Из этого следует, что первоначальная таблица переходов должна иметь в каждом столбце по два устойчивых состояния, отличающихся значением функции выхода  и 1 (табл. 3.18). Неустойчивые состояния определяются точно так же, как и для
и 1 (табл. 3.18). Неустойчивые состояния определяются точно так же, как и для  -триггера. Например, пусть исходным является состояние входа
-триггера. Например, пусть исходным является состояние входа  которому соответствуют устойчивые состояния
которому соответствуют устойчивые состояния  затем оно изменяется на состояние входа
затем оно изменяется на состояние входа  Так как в этом случае
Так как в этом случае  то автомат должен перейти в то внутреннее состояние, которому соответствует состояние выхода, определяемое функцией переходов (3.55):
то автомат должен перейти в то внутреннее состояние, которому соответствует состояние выхода, определяемое функцией переходов (3.55):  т. е. автомат независимо от исходного устойчивого состояния
т. е. автомат независимо от исходного устойчивого состояния  или
или  должен перейти в устойчивое состояние
должен перейти в устойчивое состояние  (табл. 3.18).
(табл. 3.18).

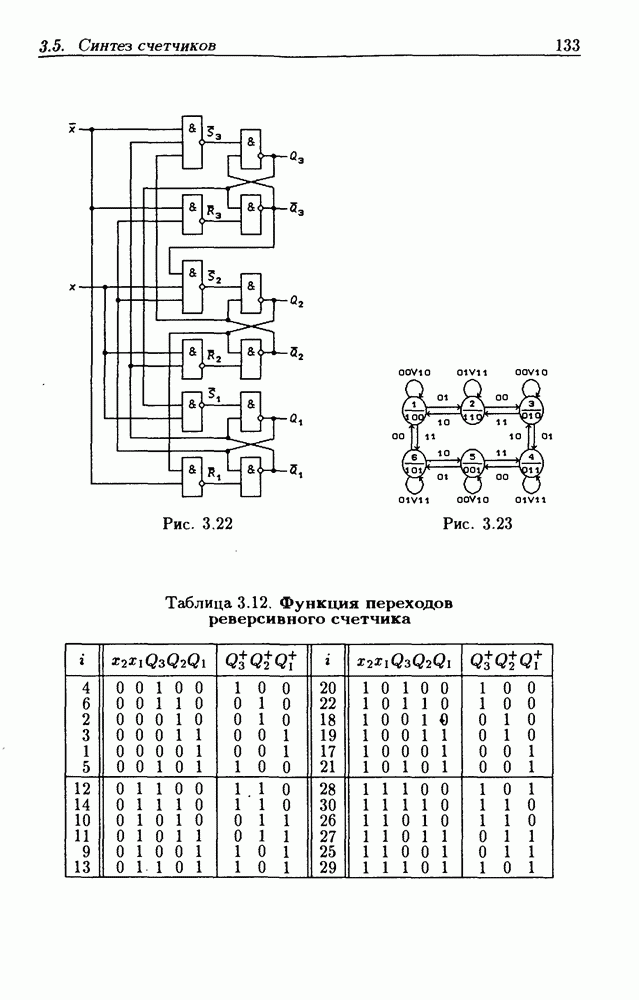
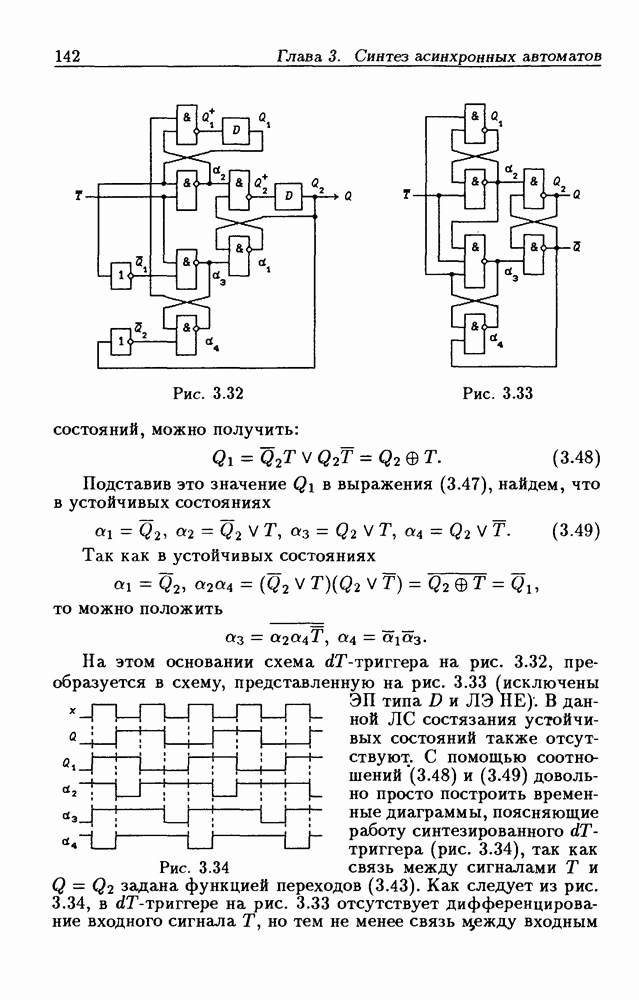
Рис. 3.40
Первоначальная таблица переходов может содержать избыточное число устойчивых внутренних состояний, так как при ее построении требовалось заносить в каждую строку таблицы точно по одному
(см. скан)
устойчивому состоянию. Поэтому возникает задача минимизации числа внутренних состояний. Чтобы пояснить идею минимизации, составим на основании табл. 3.18 подграф переходов, в который включим переходы только из двух устойчивых состояний  (рис. 3.42,а). Из подграфа переходов следует, что два внутренних состояния
(рис. 3.42,а). Из подграфа переходов следует, что два внутренних состояния  можно заменить одним состоянием (например,
можно заменить одним состоянием (например,  ) без изменения закона функционирования автомата, так как между этими состояниями есть взаимный переход, а состояния входа — (1,0) и
) без изменения закона функционирования автомата, так как между этими состояниями есть взаимный переход, а состояния входа — (1,0) и  переводят автомат из состояний
переводят автомат из состояний  в одни и те же состояния
в одни и те же состояния 
Внутренние состояния, обладающие рассмотренными свойствами, называются совместимыми и их можно объединять, заменяя одним внутренним состоянием, которое будет устойчивым уже при двух различных состояниях входа. Если не все переходы между устойчивыми состояниями заданы (недоопределенный автомат), то в соответствующей клетке таблицы переходов ставится прочерк. Недоопределенные автоматы можно доопределять произвольным способом с целью получения максимального числа совместимых состояний.
Совместимые состояния легко отыскиваются непосредственно по таблице переходов. Действительно, если в табл. 3.18 взять две строки  которым, как было показано выше, соответствуют совместимые состояния
которым, как было показано выше, соответствуют совместимые состояния  то легко заметить, что в каждом столбце стоят одинаковые цифры, характеризующие внутреннее состояние автомата. Из этого следует, что совместимыми внутренними состояниями являются такие два внутренних состояния
то легко заметить, что в каждом столбце стоят одинаковые цифры, характеризующие внутреннее состояние автомата. Из этого следует, что совместимыми внутренними состояниями являются такие два внутренних состояния  которым в таблице переходов соответствуют строки с непротиворечивым размещением цифр, т. е. такие строки, в одном и том же столбце которых стоят одинаковые цифры или в одной строке цифра, а в другой — прочерк (для недоопределенного автомата).
которым в таблице переходов соответствуют строки с непротиворечивым размещением цифр, т. е. такие строки, в одном и том же столбце которых стоят одинаковые цифры или в одной строке цифра, а в другой — прочерк (для недоопределенного автомата).
Множество внутренних состояний  является совместимым, если все внутренние состояния из
является совместимым, если все внутренние состояния из  попарно совместимы. Такое множество можно заменить одним внутренним состоянием, присвоив ему, например, наименьший из номеров внутренних состояний, входящих в множество
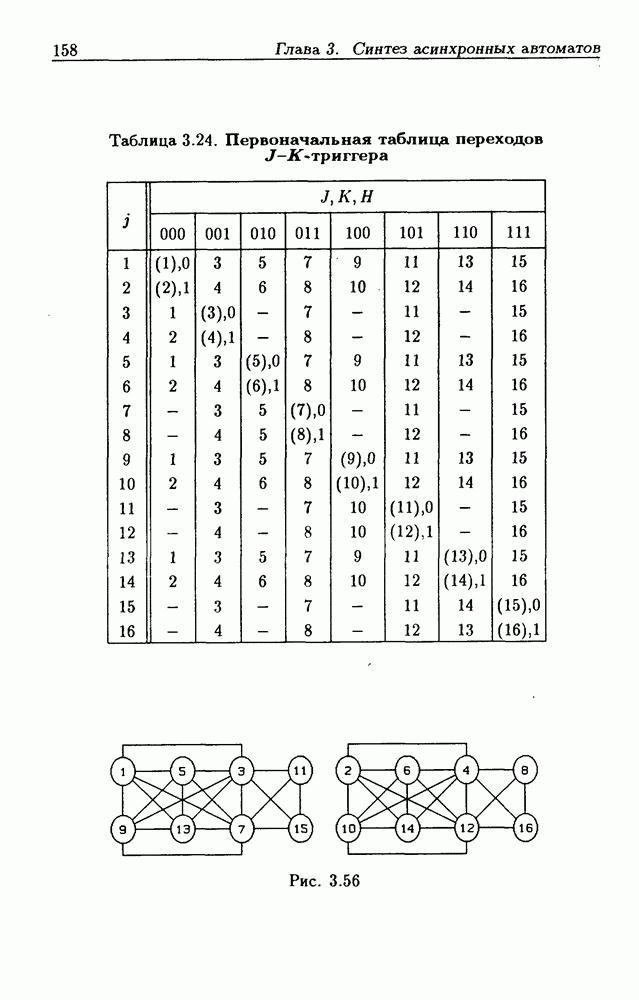
попарно совместимы. Такое множество можно заменить одним внутренним состоянием, присвоив ему, например, наименьший из номеров внутренних состояний, входящих в множество  Удобным средством отыскания всех вариантов совместимости внутренних состояний является диаграмма совместимых состояний. Такая диаграмма состоит из узлов, обозначающих внутренние состояния автомата, каждая пара которых соединена ненаправленными линиями, если узлам, входящим в пары, соответствуют совместимые внутренние состояния.
Удобным средством отыскания всех вариантов совместимости внутренних состояний является диаграмма совместимых состояний. Такая диаграмма состоит из узлов, обозначающих внутренние состояния автомата, каждая пара которых соединена ненаправленными линиями, если узлам, входящим в пары, соответствуют совместимые внутренние состояния.
На рис. 3.42, б показана диаграмма совместимых состояний, из которой видно, что первоначальная таблица переходов (табл. 3.18) имеет четыре пары совместимых внутренних состояний. Объединив эти внутренние состояния, получим табл. 3.19, в которой символами  и
и  обозначены введенные переходные состояния и
обозначены введенные переходные состояния и  так как граф переходов (рис. 3.43,а) без переходных состояний содержит контуры нечетной длины, что не позволяет осуществить соседнее кодирование внутренних состояний (например, символ
так как граф переходов (рис. 3.43,а) без переходных состояний содержит контуры нечетной длины, что не позволяет осуществить соседнее кодирование внутренних состояний (например, символ  означает, что исходное внутреннее состояние
означает, что исходное внутреннее состояние  необходимо заменить на состояние
необходимо заменить на состояние  Преобразованной таблице переходов соответствует граф
Преобразованной таблице переходов соответствует граф
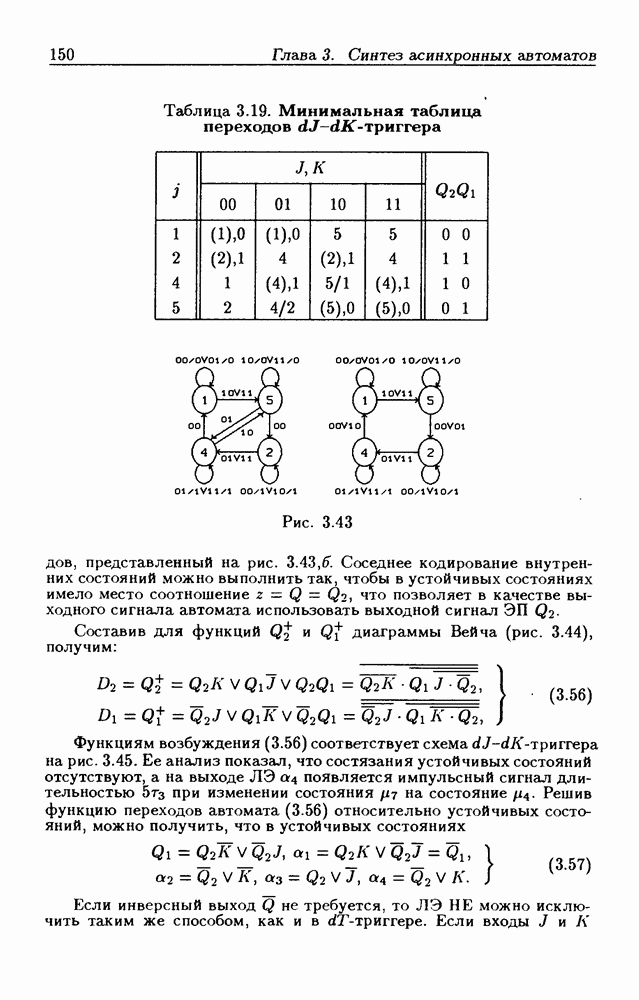
Таблица 3.19. (см. скан) Минимальная таблица переходов  -триггера
-триггера

Рис. 3.43
переходов, представленный на рис.  Соседнее кодирование внутренних состояний можно выполнить так, чтобы в устойчивых состояниях имело место соотношение
Соседнее кодирование внутренних состояний можно выполнить так, чтобы в устойчивых состояниях имело место соотношение  что позволяет в качестве выходного сигнала автомата использовать выходной сигнал
что позволяет в качестве выходного сигнала автомата использовать выходной сигнал 
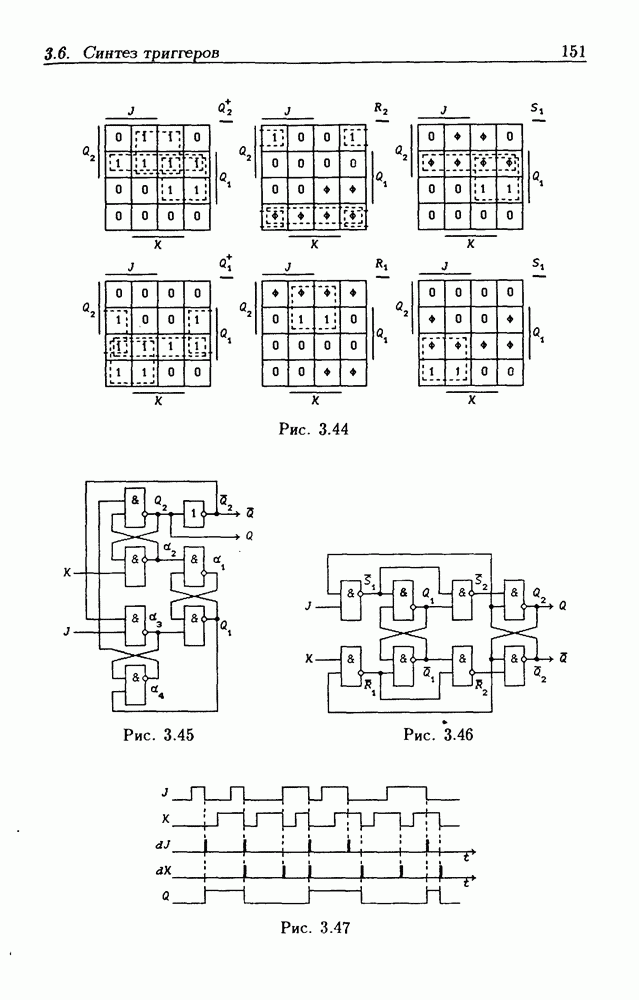
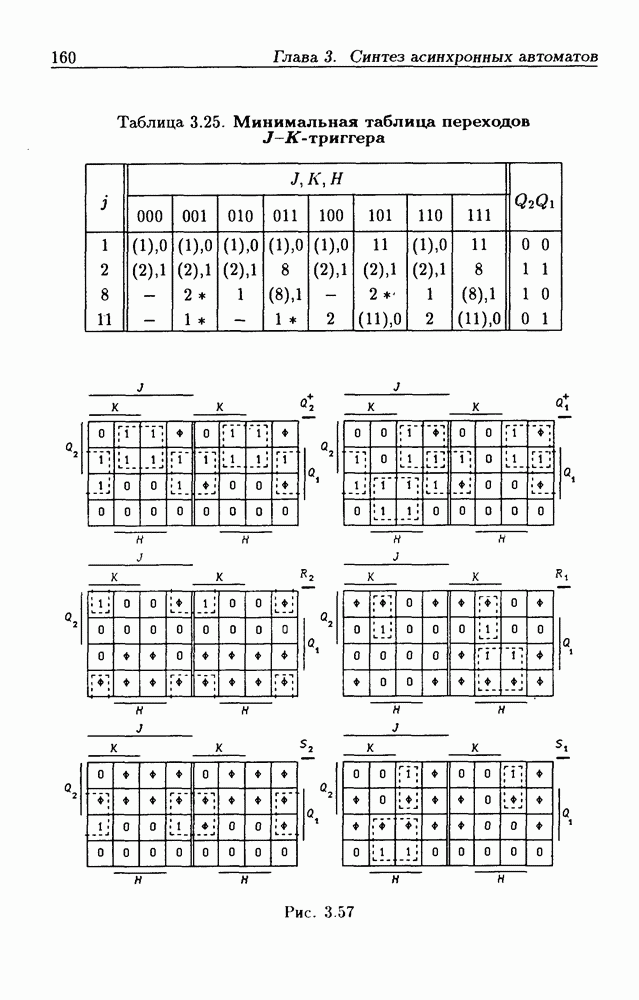
Составив для функций  диаграммы Вейча (рис. 3.44), получим:
диаграммы Вейча (рис. 3.44), получим:

Функциям возбуждения (3.56) соответствует схема  -триггера на рис. 3.45. Ее анализ показал, что состязания устойчивых состояний отсутствуют, а на выходе
-триггера на рис. 3.45. Ее анализ показал, что состязания устойчивых состояний отсутствуют, а на выходе  появляется импульсный сигнал длительностью
появляется импульсный сигнал длительностью  при изменении состояния
при изменении состояния  на состояние
на состояние  Решив функцию переходов автомата (3.56) относительно устойчивых состояний, можно получить, что в устойчивых состояниях
Решив функцию переходов автомата (3.56) относительно устойчивых состояний, можно получить, что в устойчивых состояниях

Если инверсный выход  не требуется, то ЛЭ НЕ можно исключить таким же способом, как и в
не требуется, то ЛЭ НЕ можно исключить таким же способом, как и в  -триггере. Если входы
-триггере. Если входы  и К
и К

(кликните для просмотра скана)
поменять местами, то прямой и инверсный выходы триггера тоже поменяются местами.
Синтез  -триггера можно сделать и на
-триггера можно сделать и на  -триггерах, получив из диаграмм Вейча (см. рис. 3.44) функции возбуждения:
-триггерах, получив из диаграмм Вейча (см. рис. 3.44) функции возбуждения:

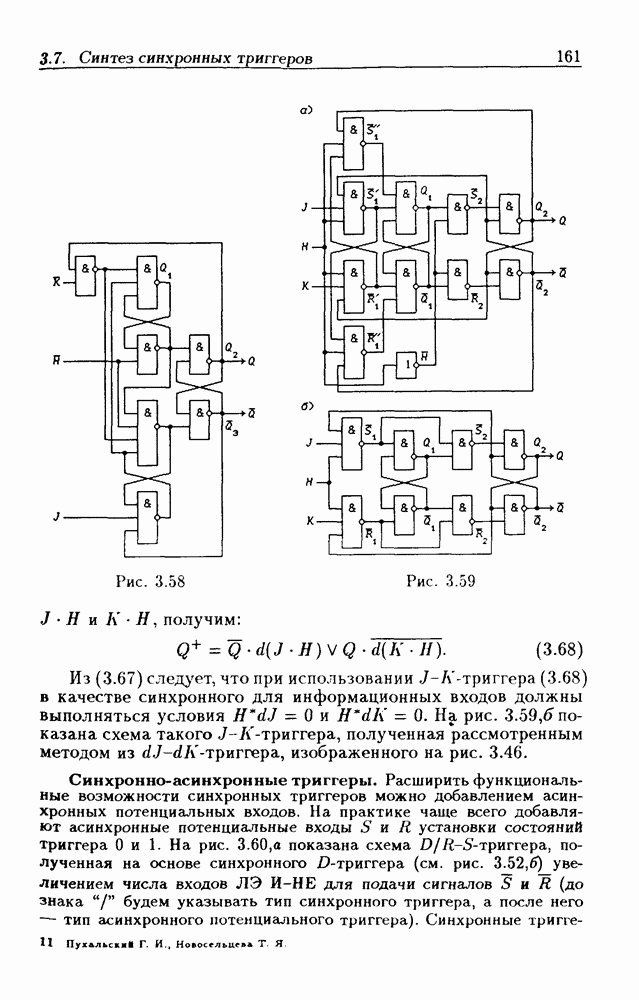
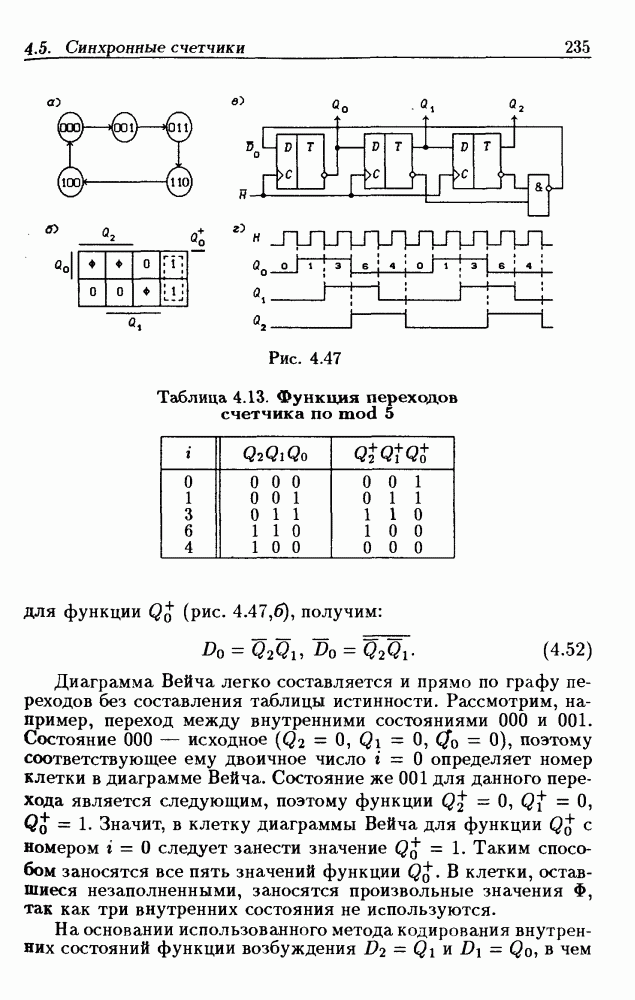
Этим функциям возбуждения соответствует схема  -триггера на рис. 3.46. Временные диаграммы, поясняющие его работу, показаны на рис. 3.47. Условные графические обозначения асинхронных импульсных триггеров типов dT и dJ-dK приведены на рис. 3.48 (у импульсных входов указаны перепады сигналов, вызывающие изменение их состояний).
-триггера на рис. 3.46. Временные диаграммы, поясняющие его работу, показаны на рис. 3.47. Условные графические обозначения асинхронных импульсных триггеров типов dT и dJ-dK приведены на рис. 3.48 (у импульсных входов указаны перепады сигналов, вызывающие изменение их состояний).

Рис. 3.48
Если в функцию переходов (3.55)  -триггера подставить значения
-триггера подставить значения  то получится функция переходов
то получится функция переходов  -триггера. Из этого следует, что если в dJ-dК-триггере входы
-триггера. Из этого следует, что если в dJ-dК-триггере входы  соединить, то получится
соединить, то получится  -триггер. Это подтверждается также сравнением полученных схем триггеров типов
-триггер. Это подтверждается также сравнением полученных схем триггеров типов  показанных на рис. 3.35, б и 3.46.
показанных на рис. 3.35, б и 3.46.
Импульсные триггеры используются в качестве строительных элементов при логическом проектировании асинхронных импульсных автоматов. Как было показано выше, внутреннее устройство импульсных триггеров может быть самым различным, но тем не менее законы их функционирования могут быть одинаковыми. В этой связи важно понять, что для логического проектирования автоматов нужно знать только логические свойства триггеров, определяемые функциями переходов, а не их внутреннее устройство, так же как при синтезе КС необходимо знать только функции, выполняемые ЛЭ, а не их внутреннюю структуру. Выше на примере триггеров со счетным входом было показано, что все известные и неизвестные в настоящее время схемы  -триггеров, которые могут быть построены по принципу логического дифференцирования сигналов, задаются одной и той же первоначальной таблицей переходов. По этой причине нет никакого принципиального различия между этими схемами.
-триггеров, которые могут быть построены по принципу логического дифференцирования сигналов, задаются одной и той же первоначальной таблицей переходов. По этой причине нет никакого принципиального различия между этими схемами.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
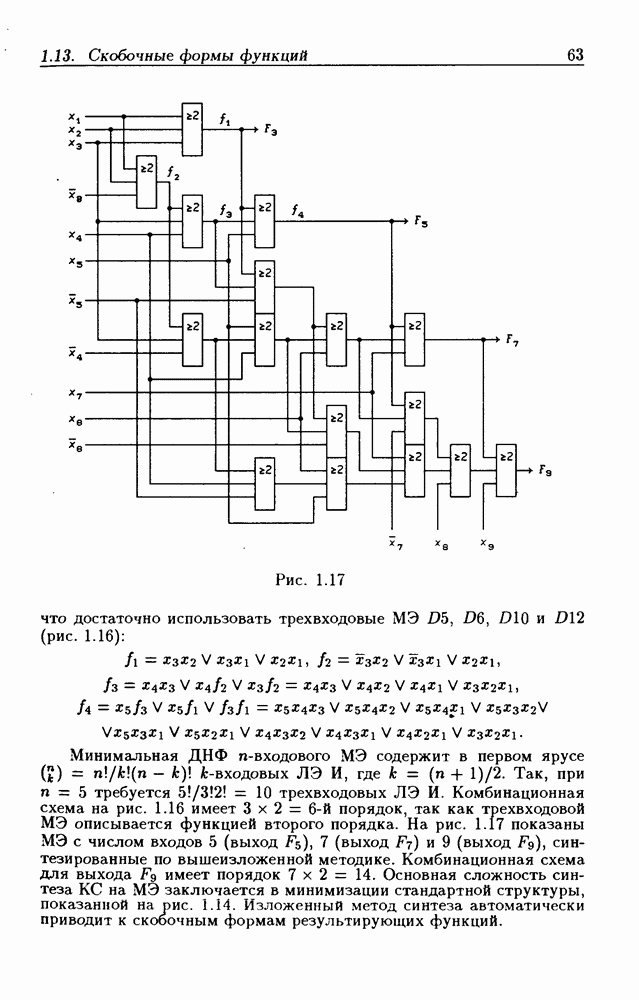
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
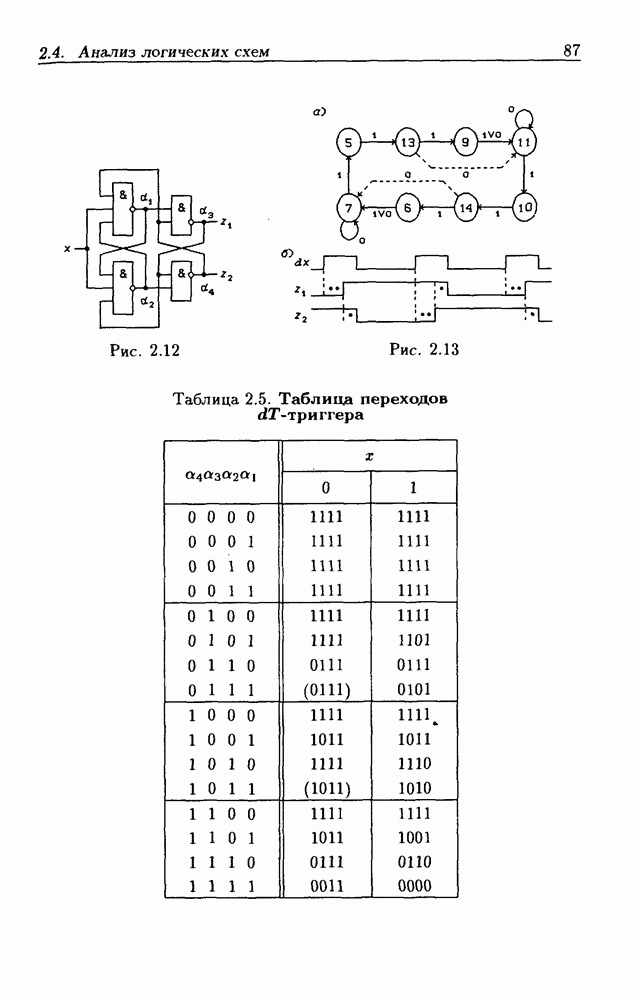
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
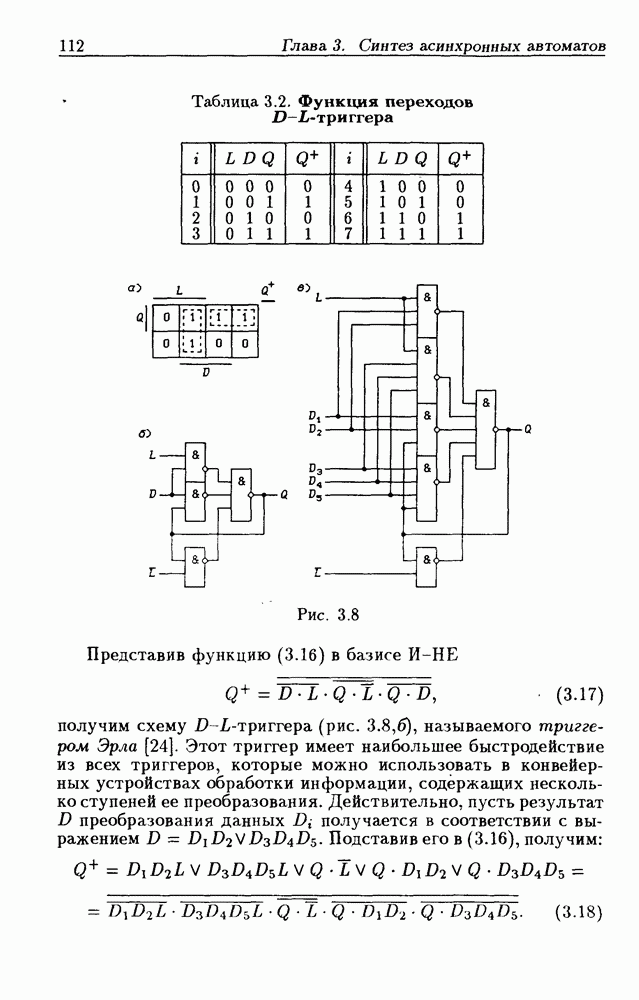
- Триггеры типа D-L
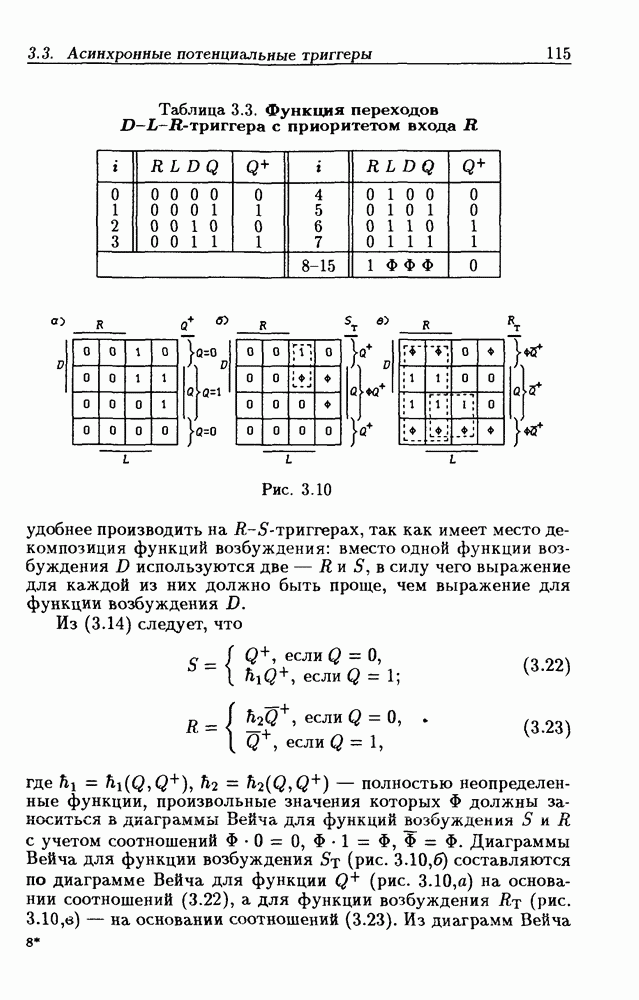
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
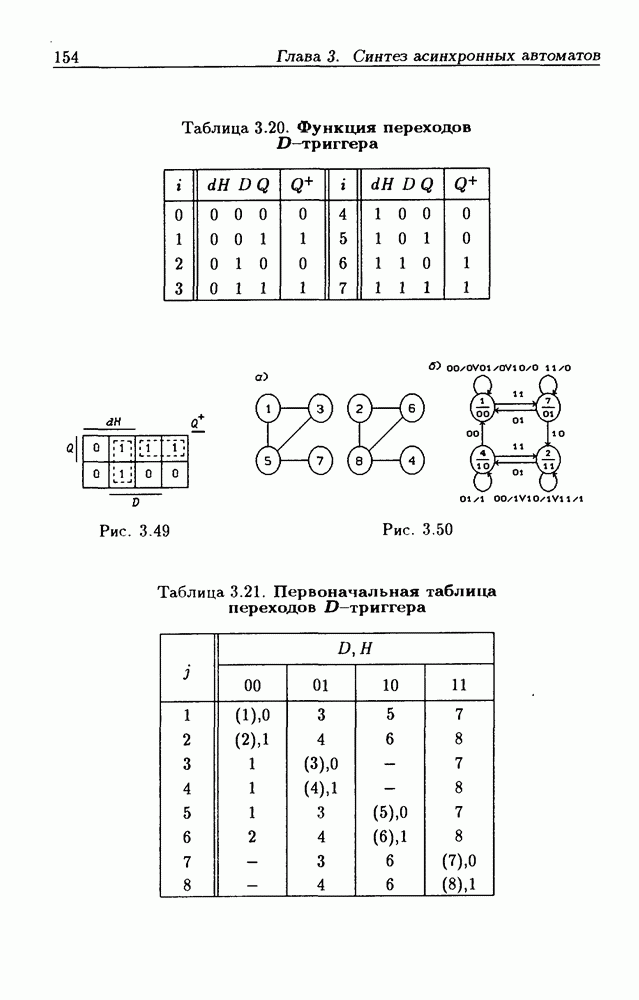
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
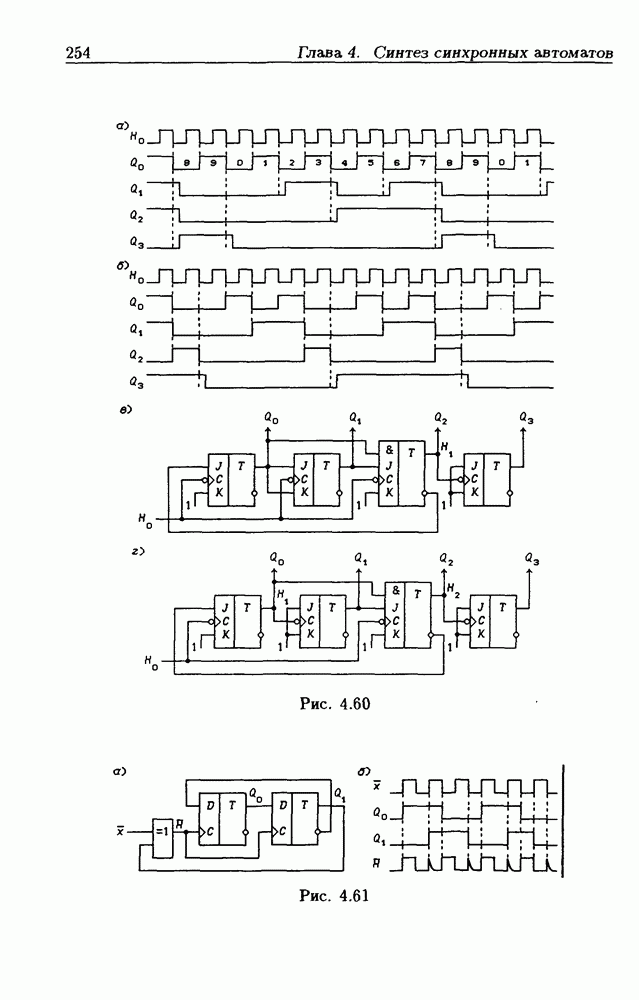
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
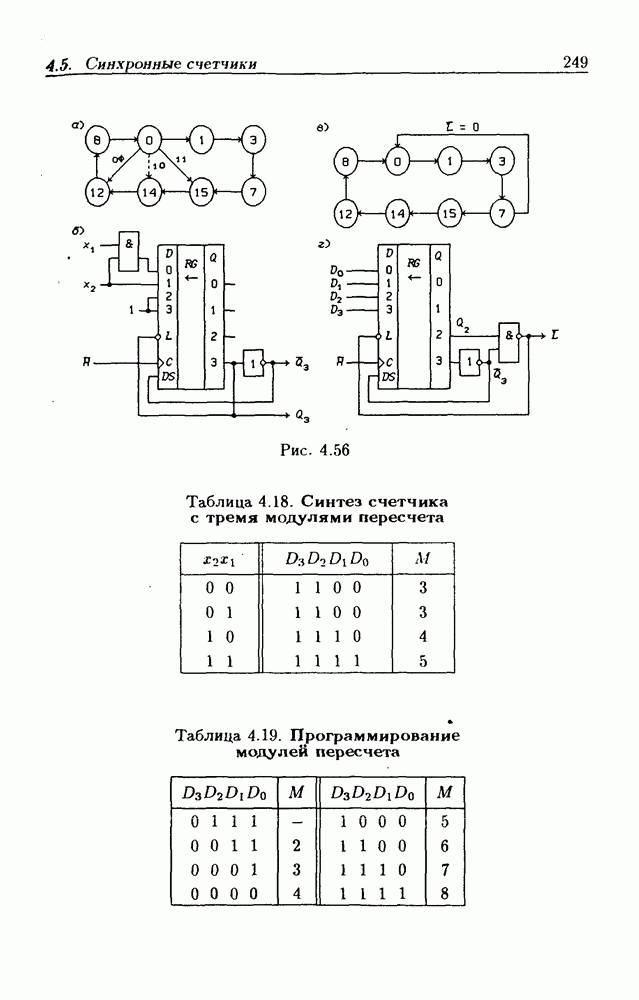
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
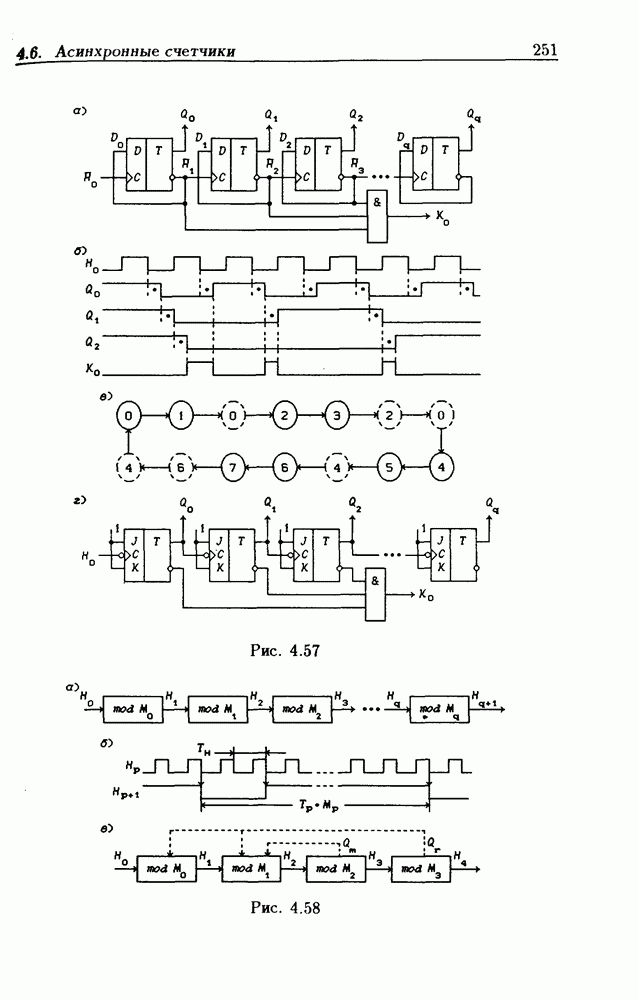
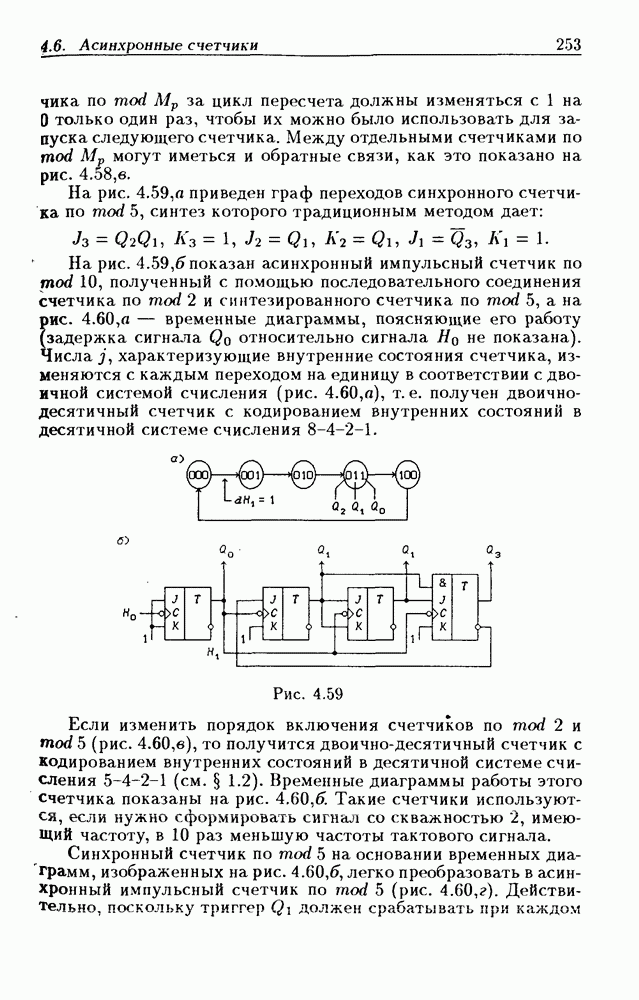
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
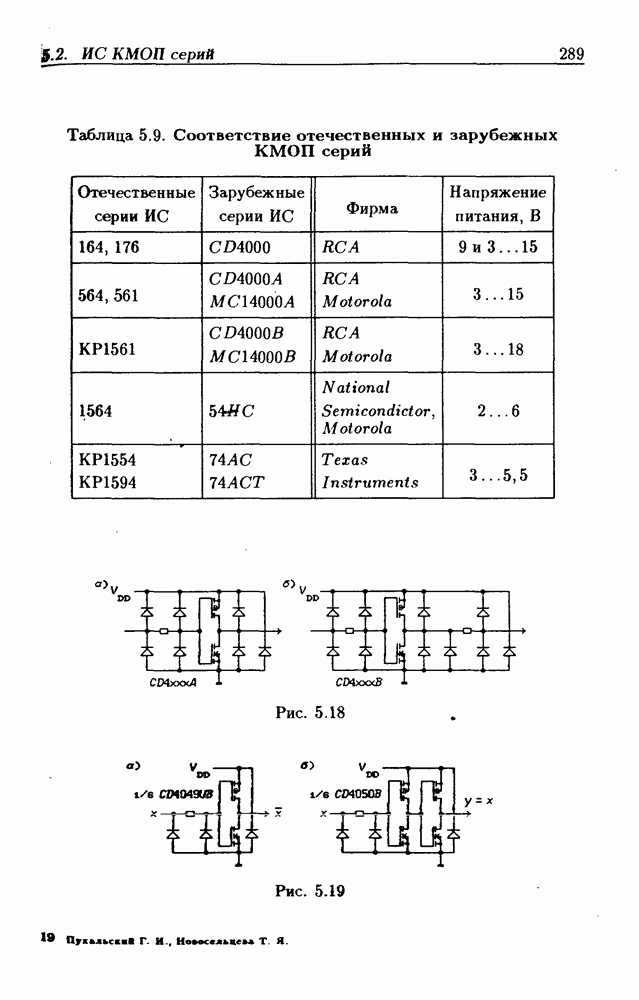
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
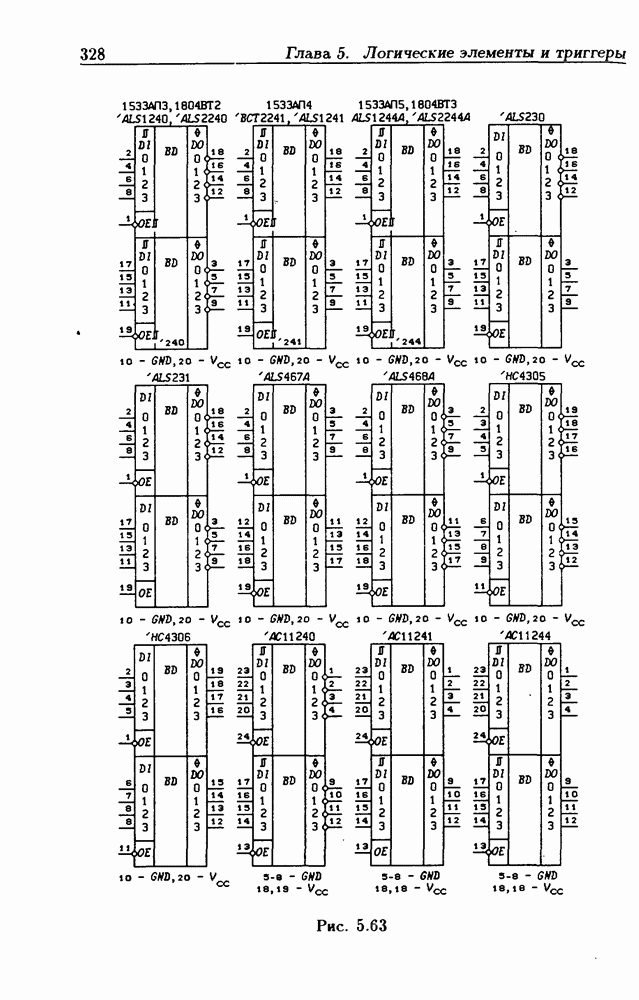
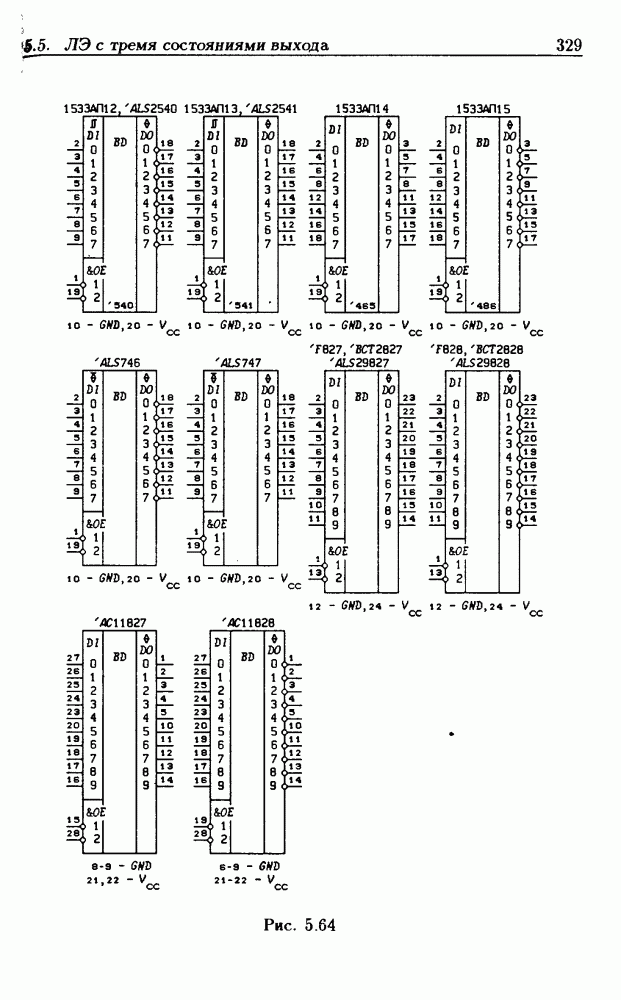
- Типовые цоколевки ИС.
- 5.5. Логические элементы с тремя состояниями выхода
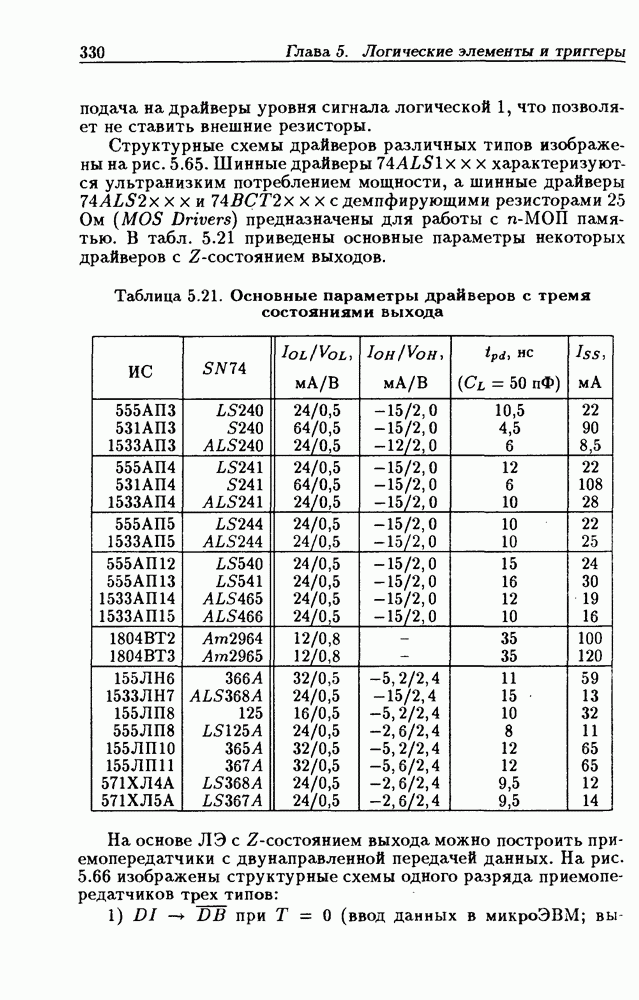
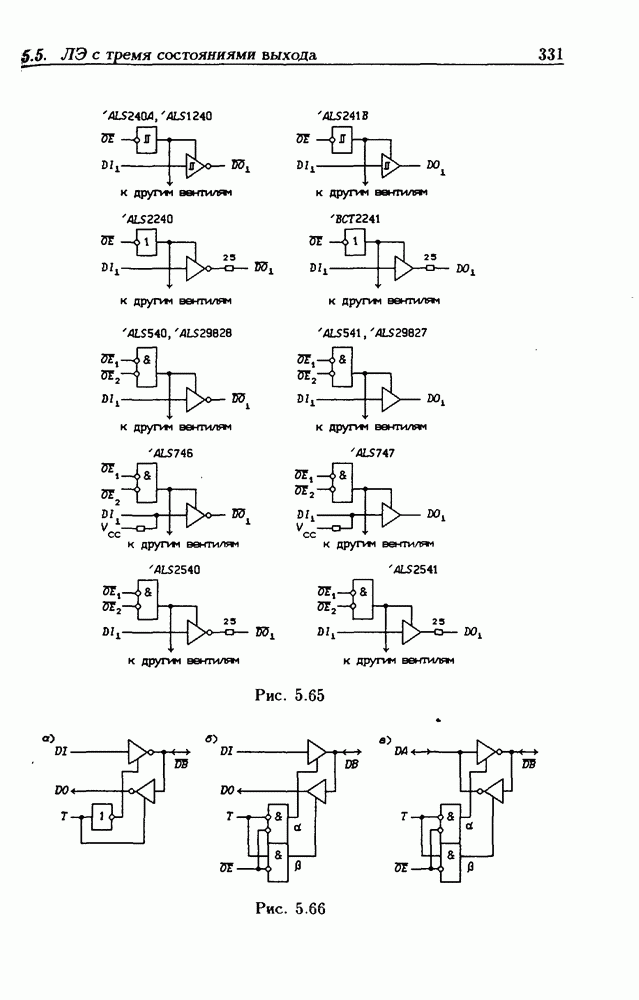
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
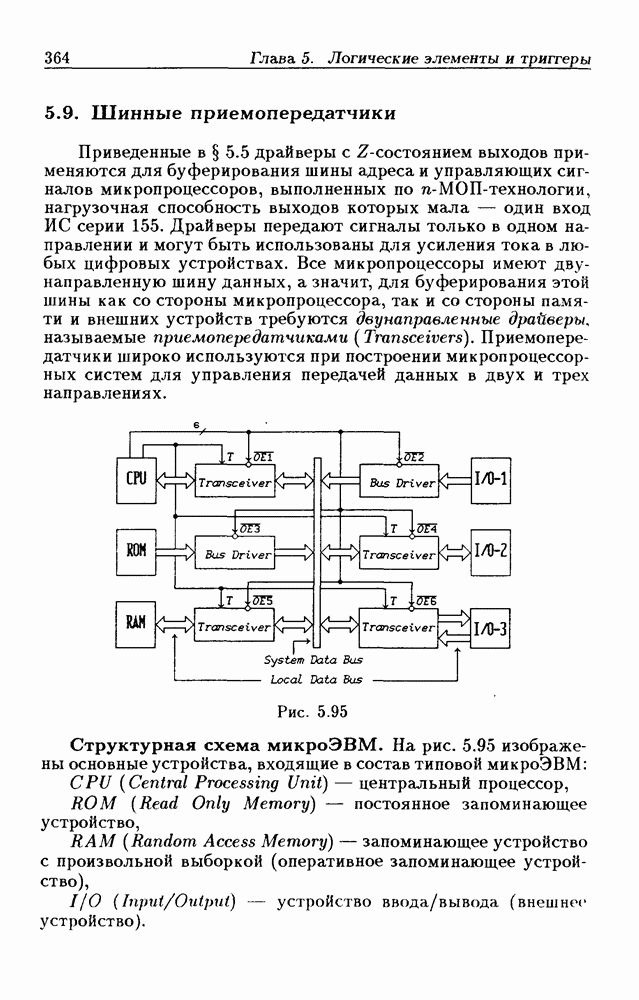
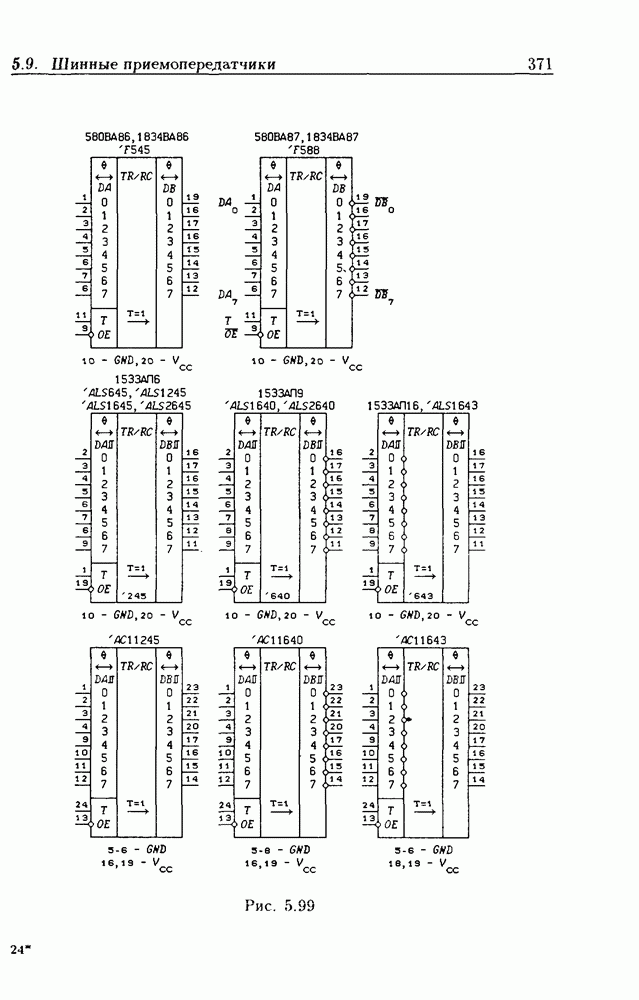
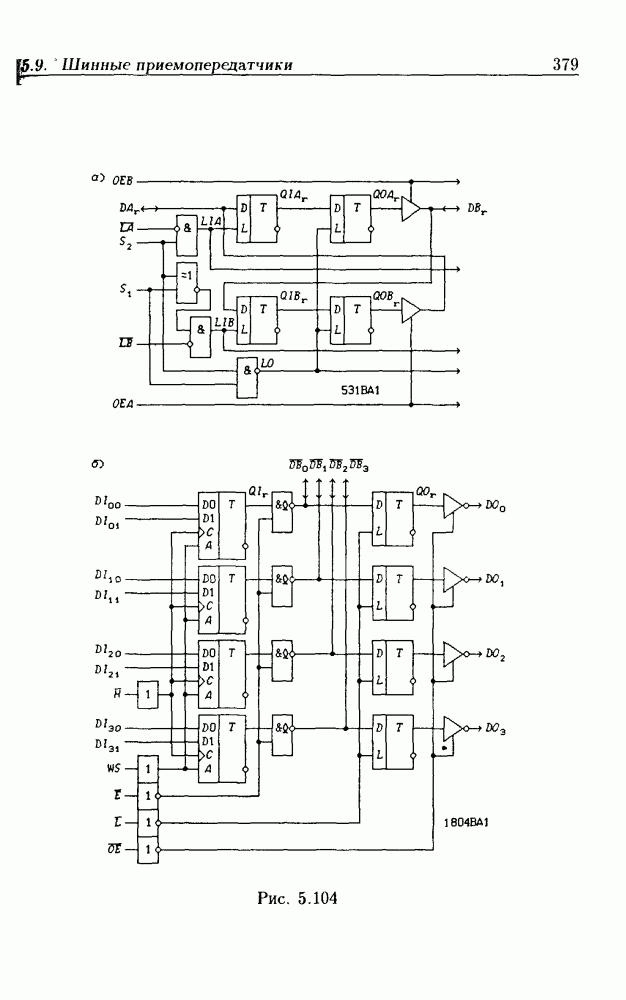
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
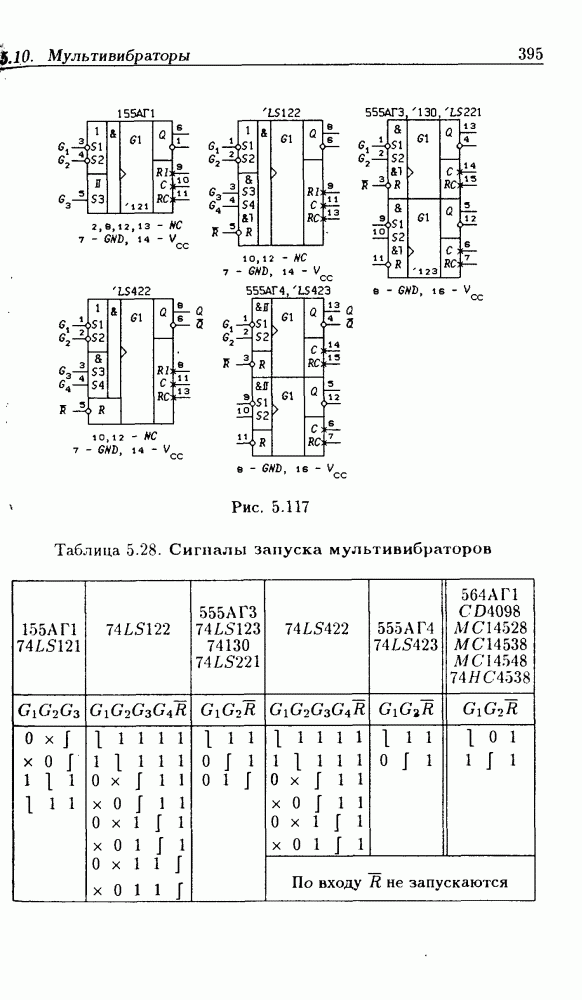
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения «дребезга» механических контактов.
- Автогенераторы периодических сигналов.
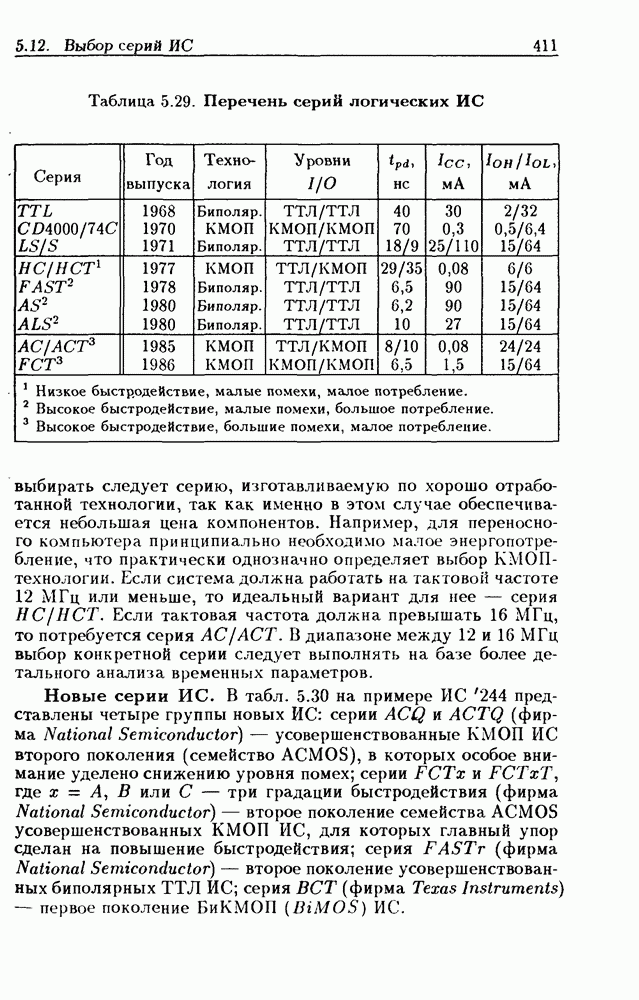
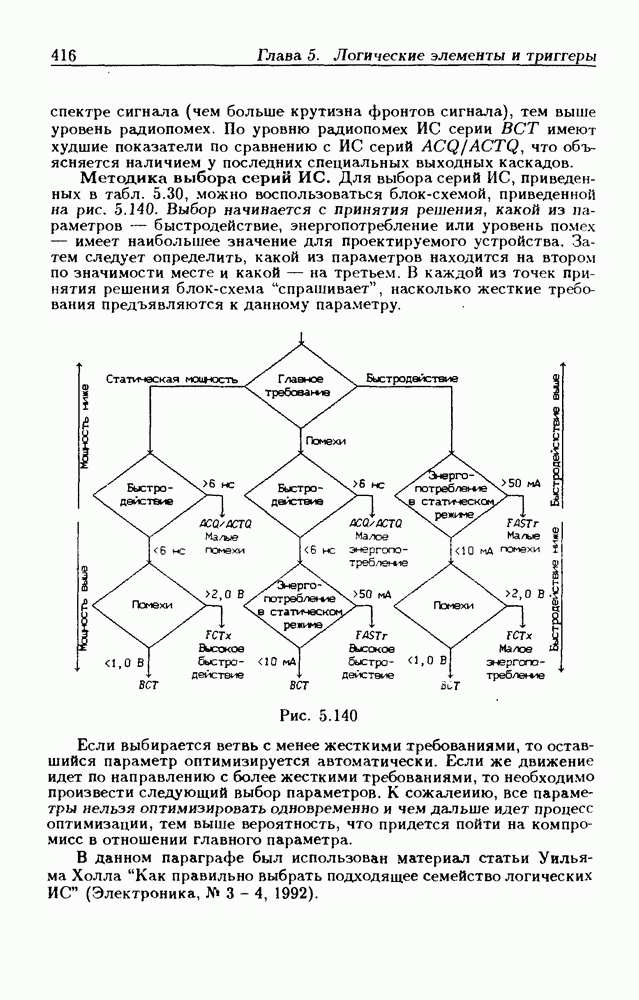
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
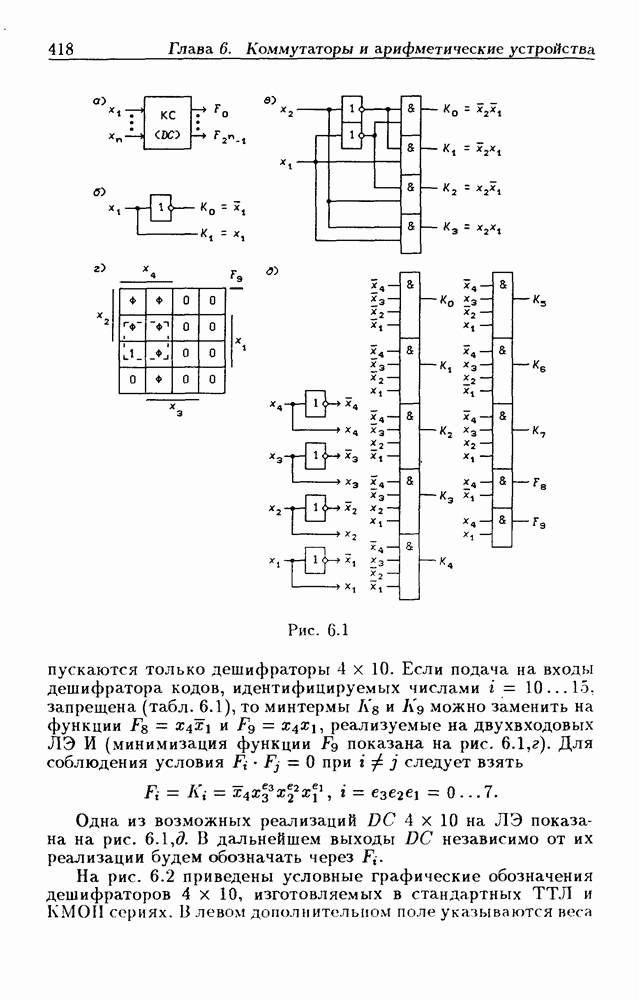
- 6.1. Дешифраторы
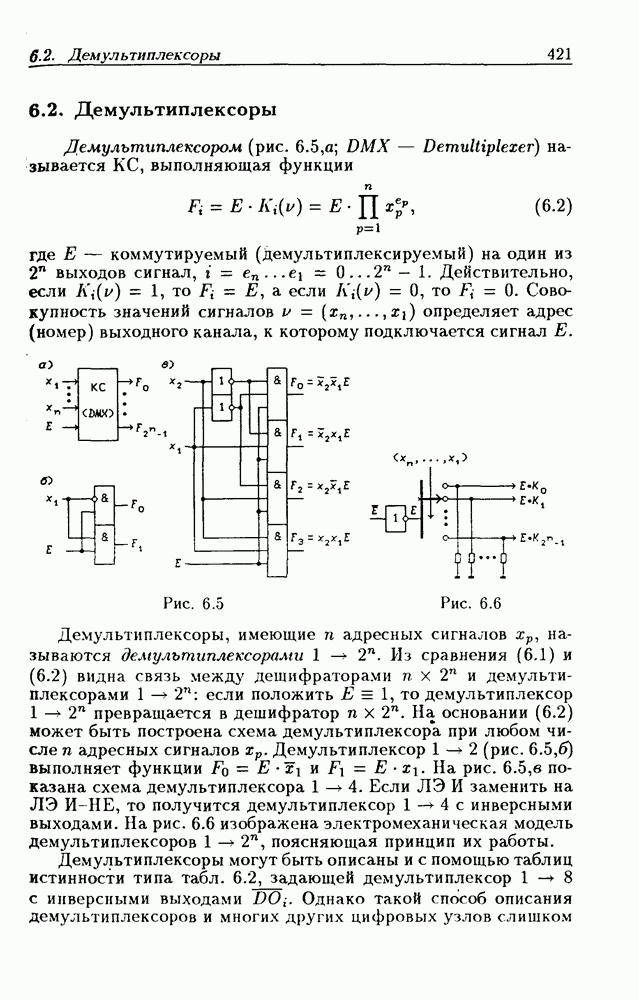
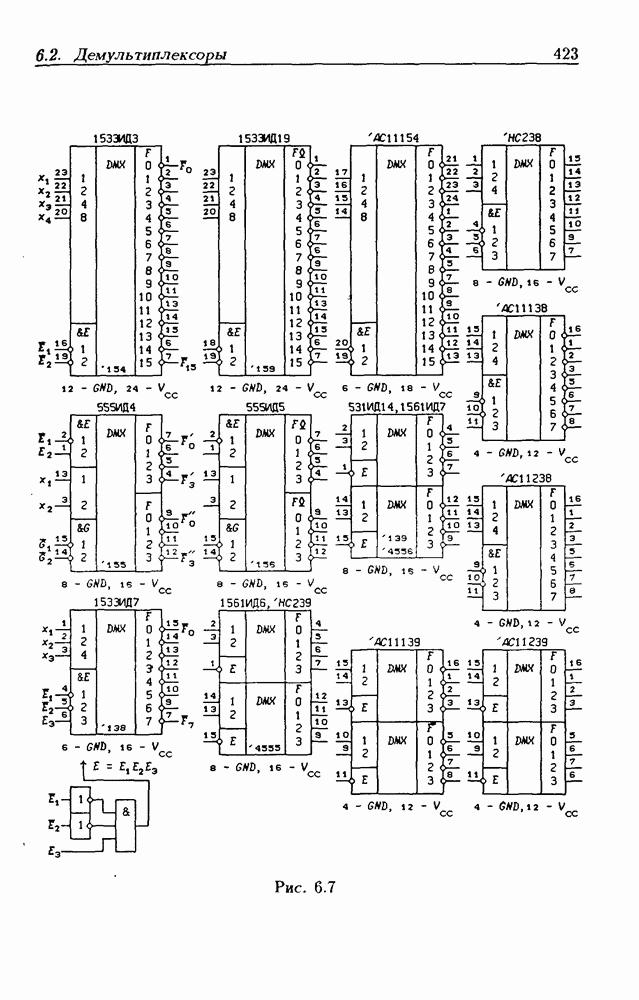
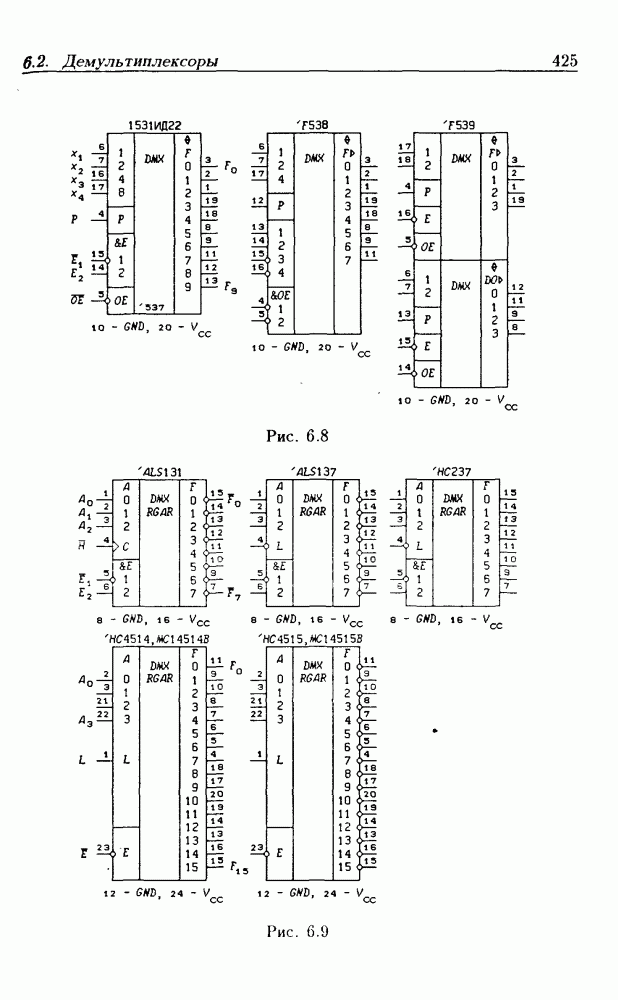
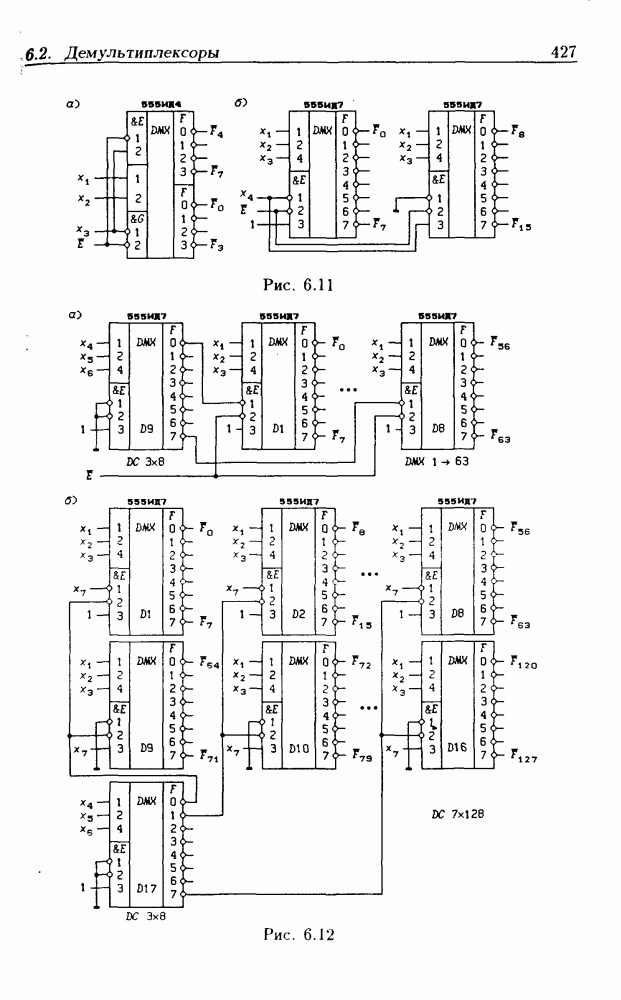
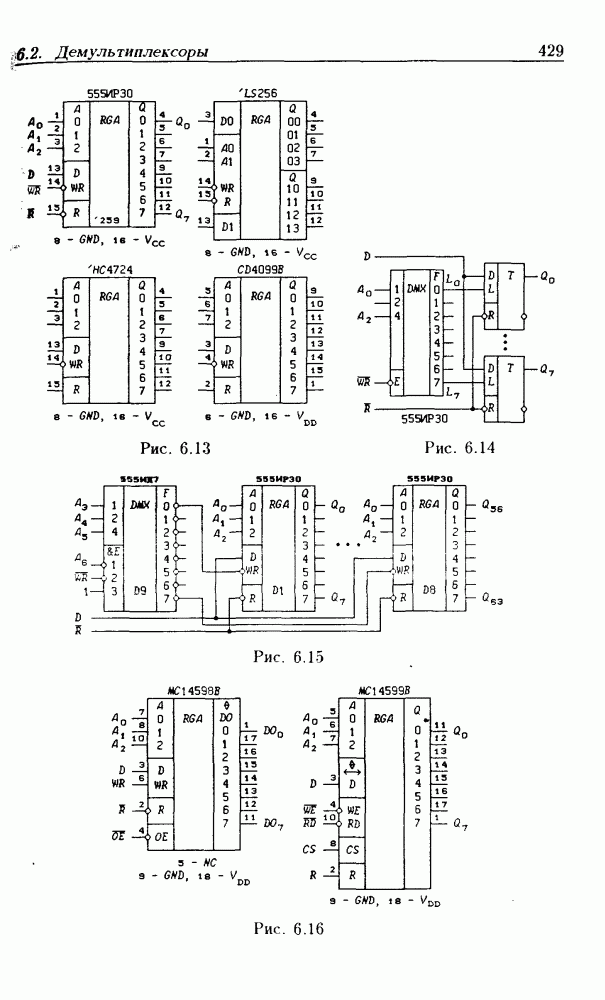
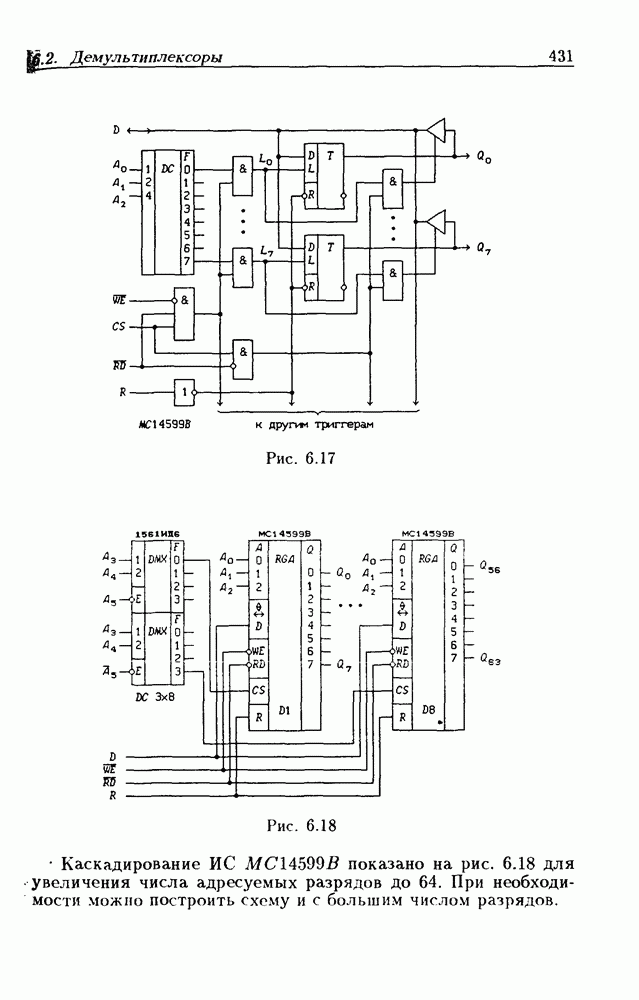
- 6.2. Демультиплексоры
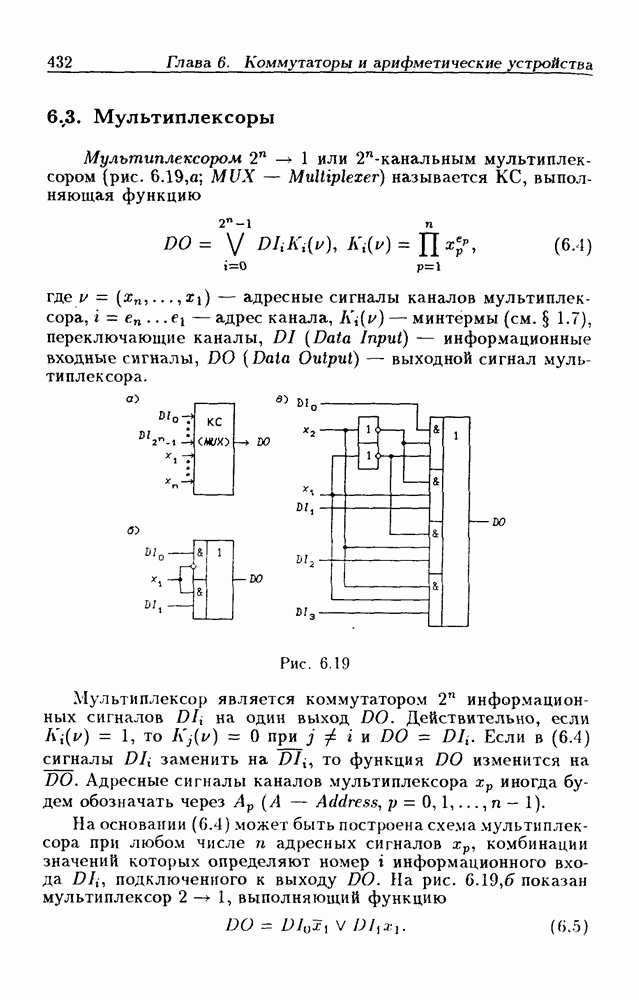
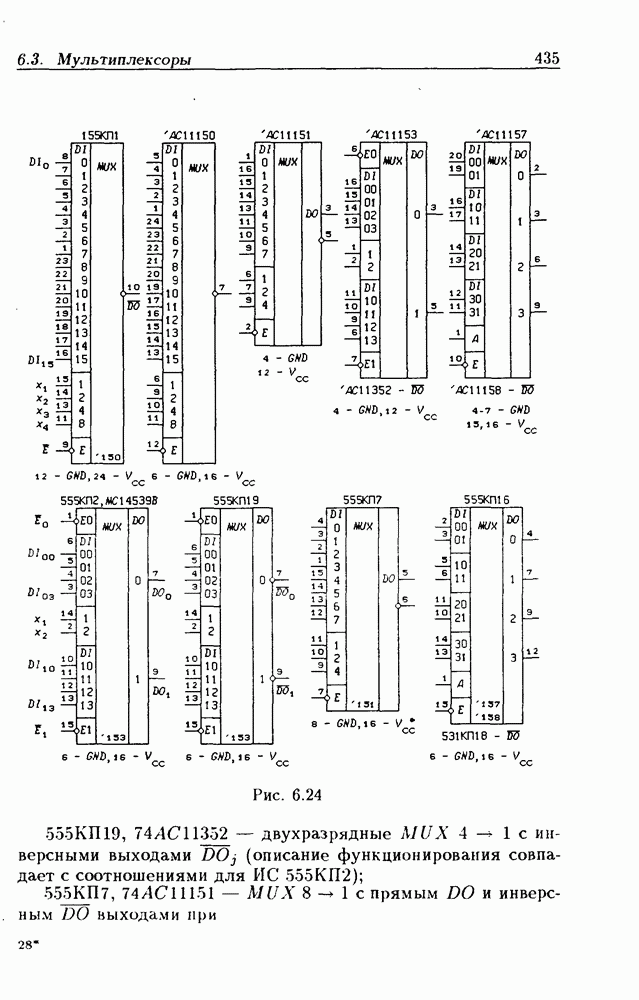
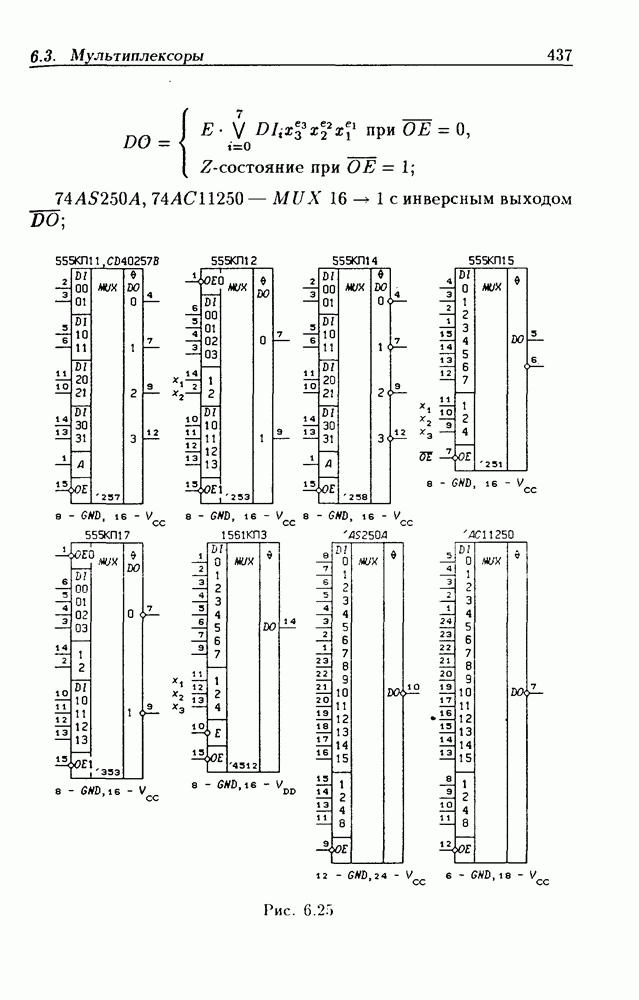
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
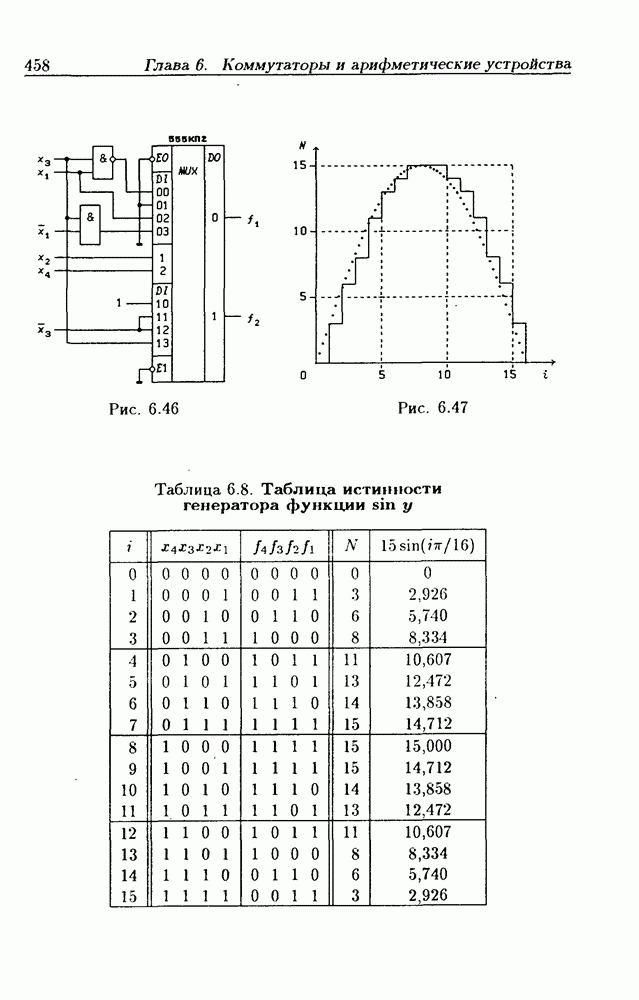
- Синтез генератора синусоидальной функции на мультиплексорах.
- Синтез триггеров на мультиплексорах.
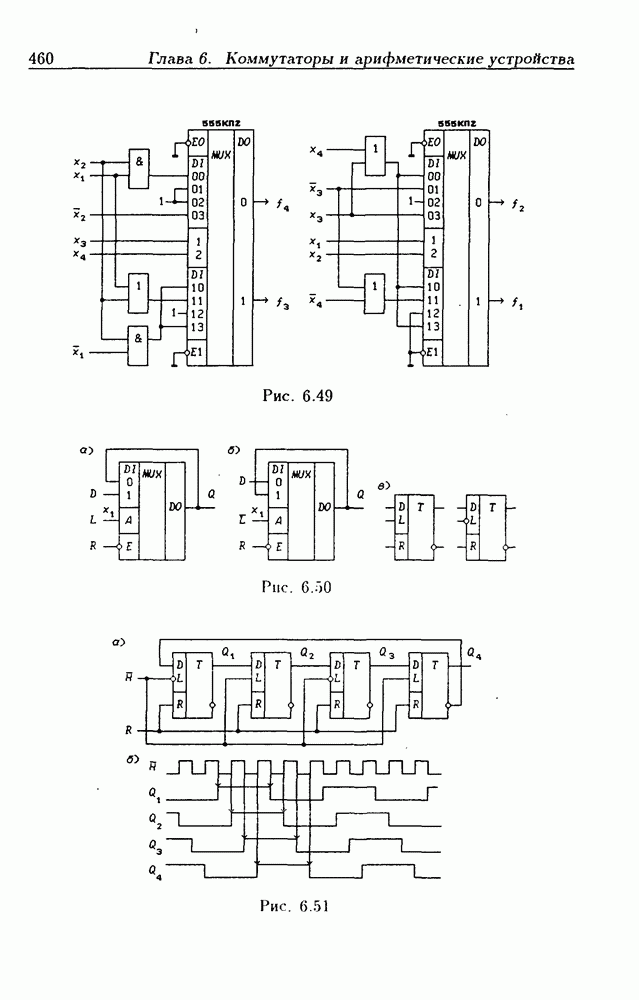
- Синтез счетчиков на мультиплексорах.
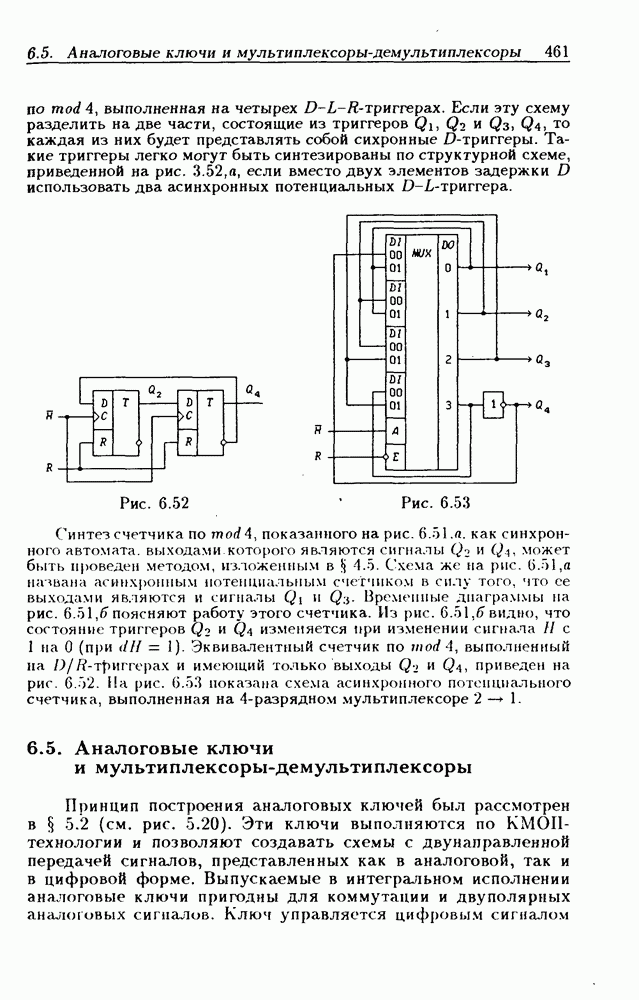
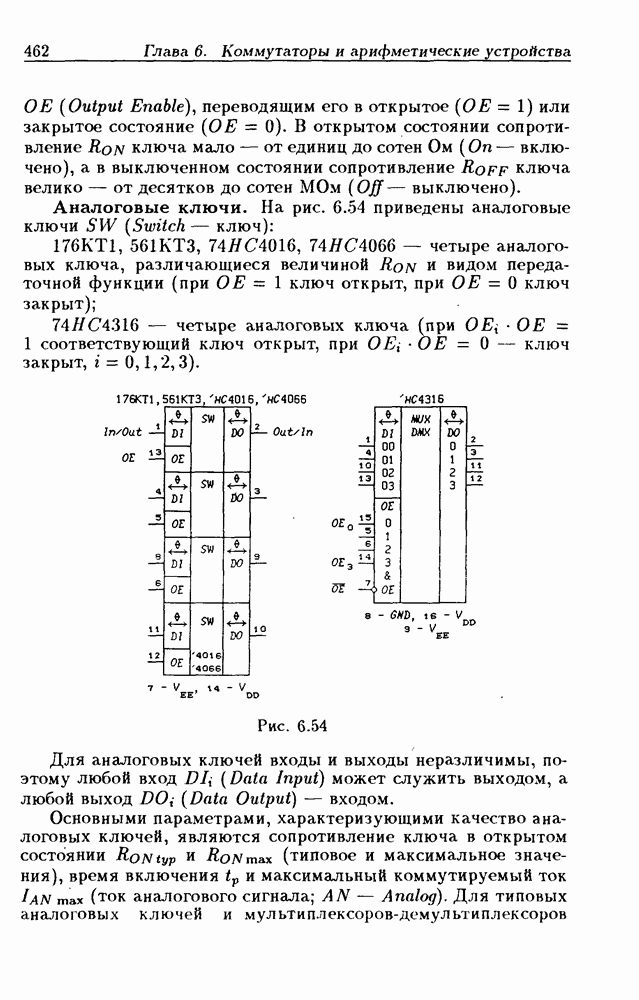
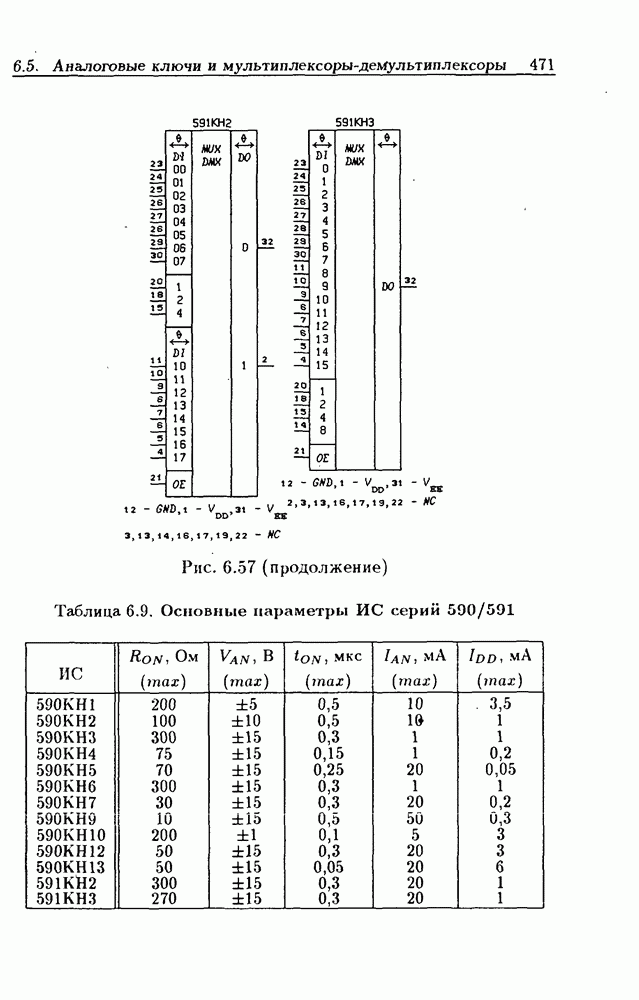
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
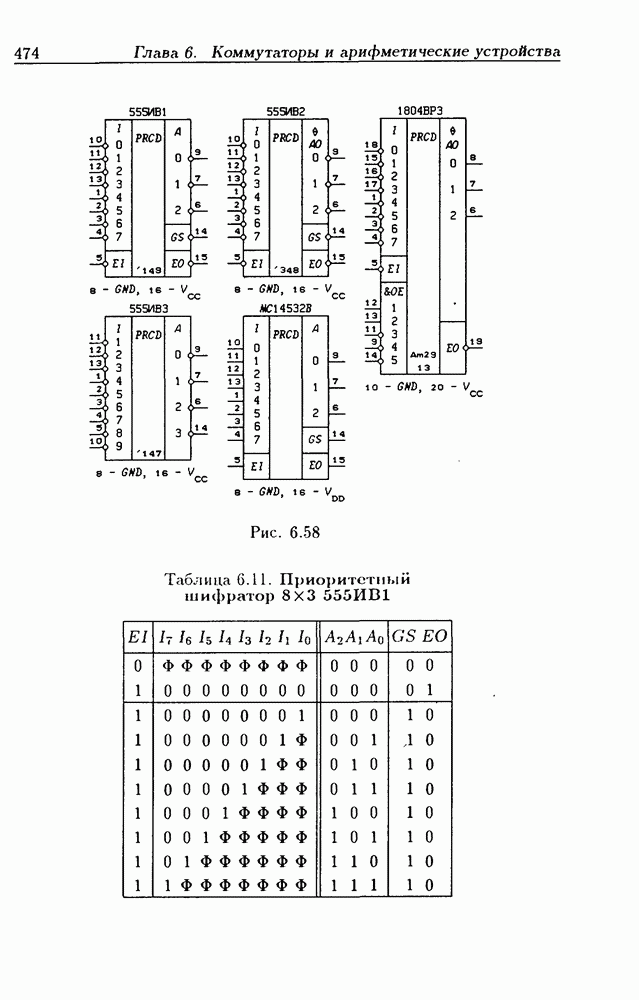
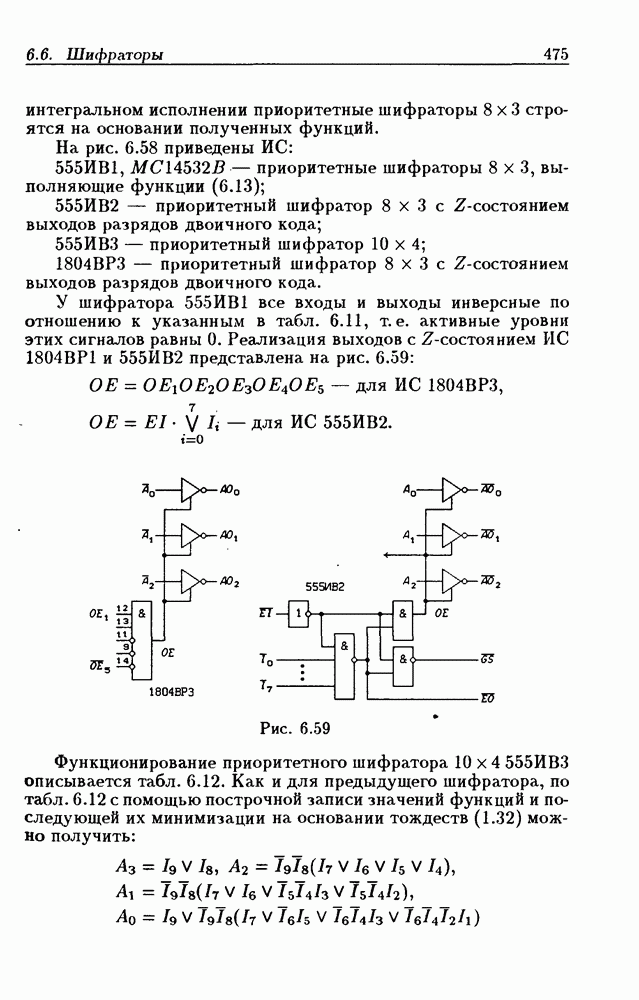
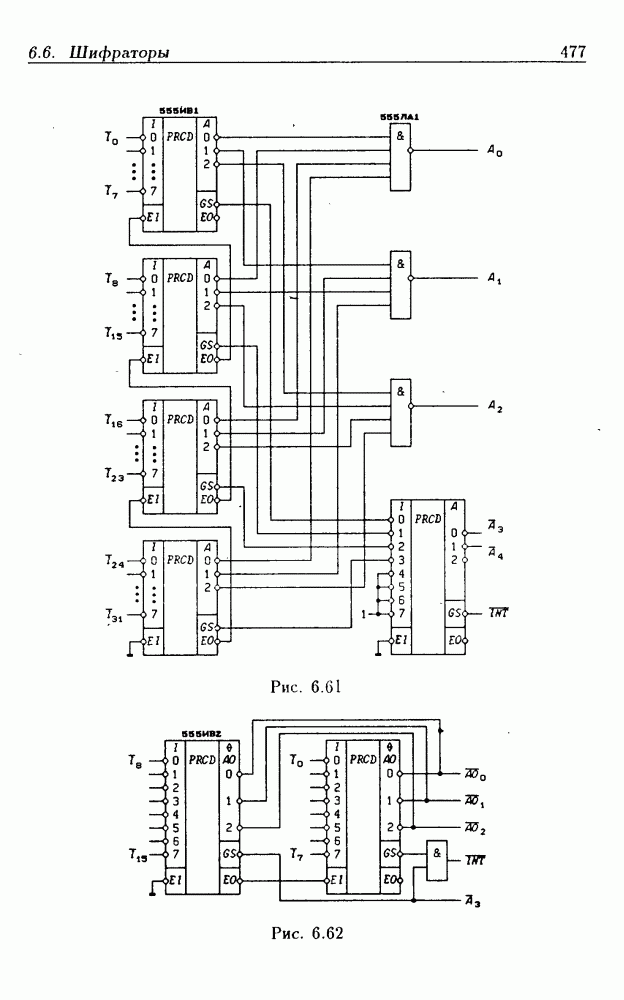
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
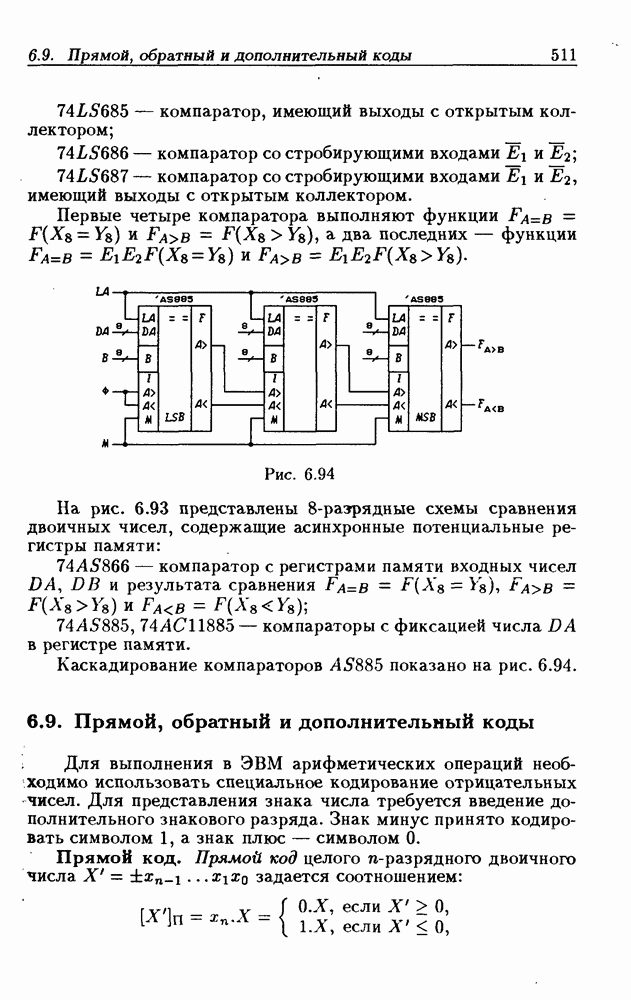
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
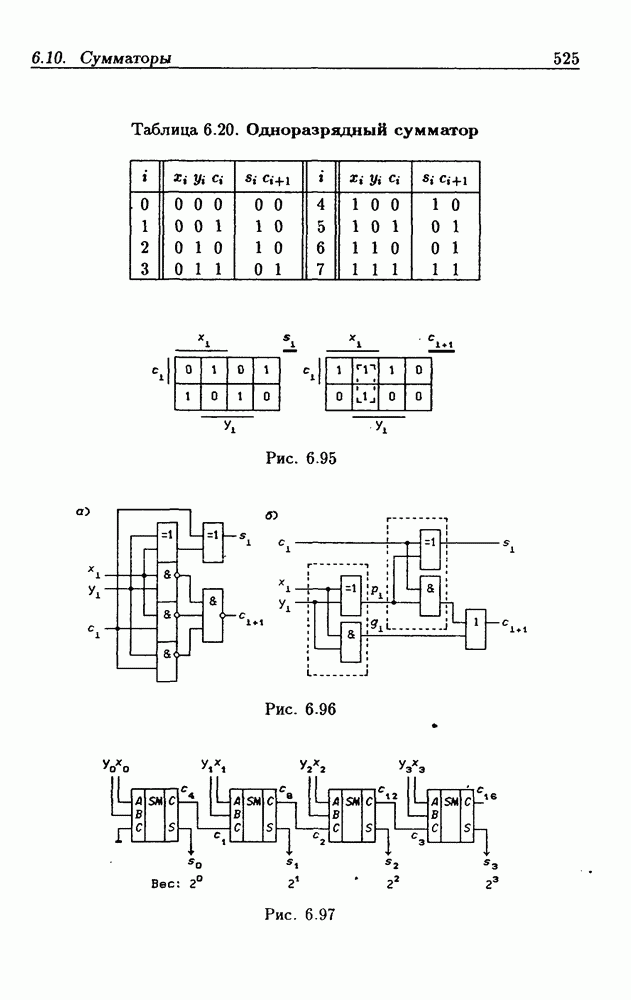
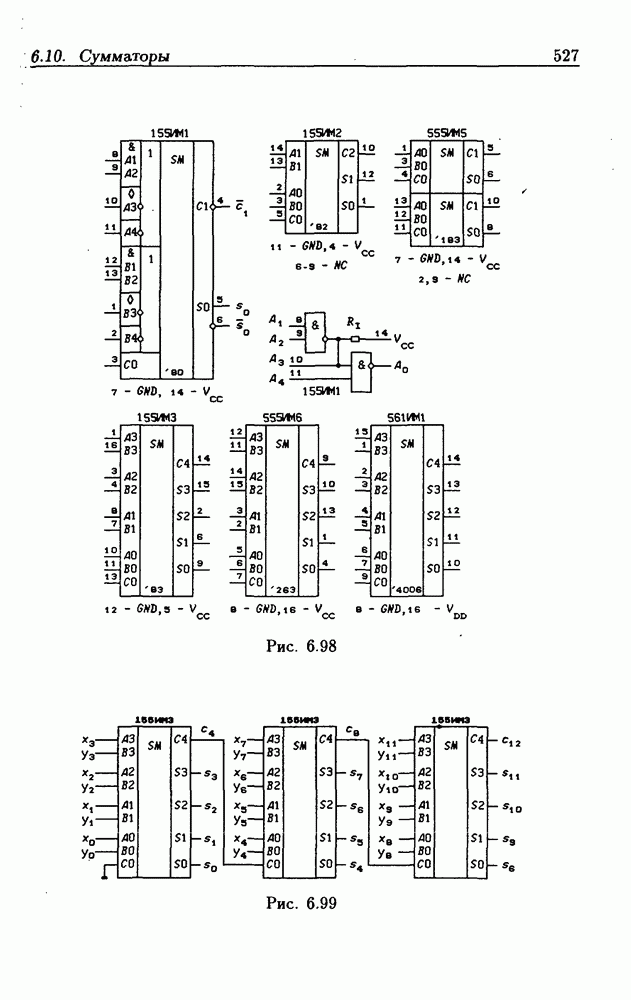
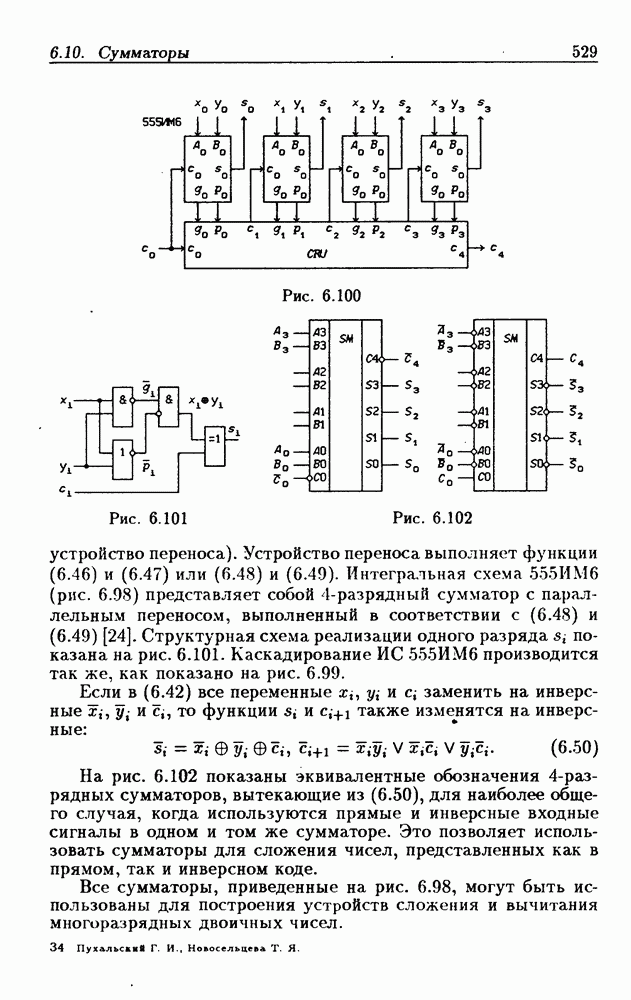
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
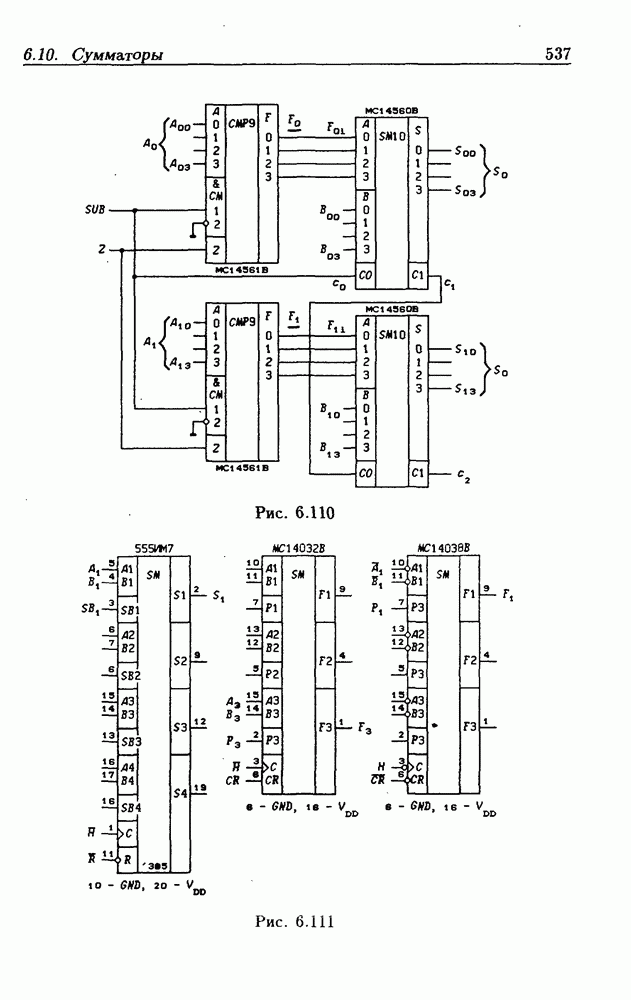
- Применения сумматоров.
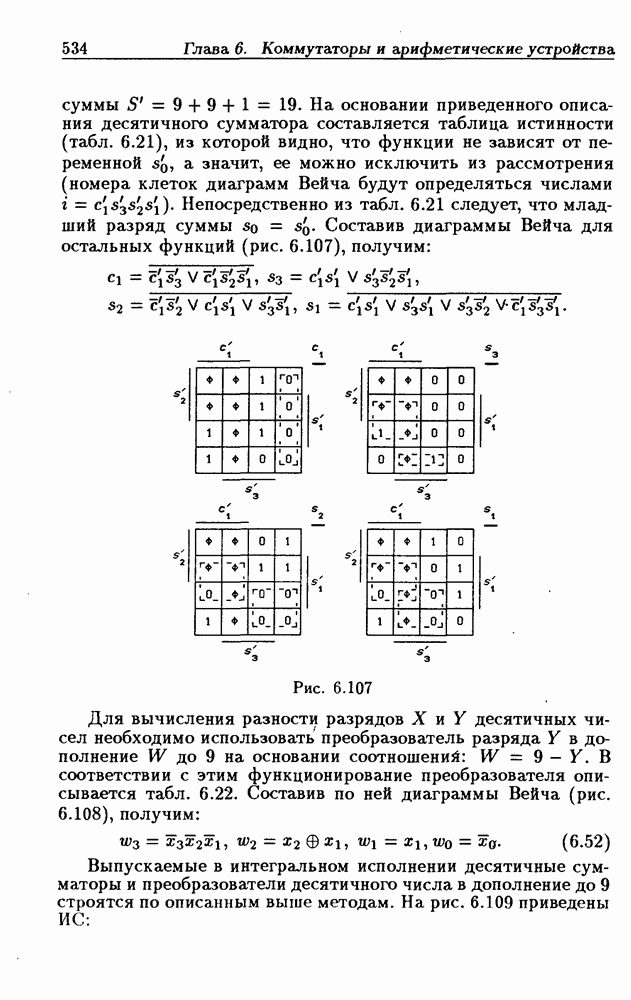
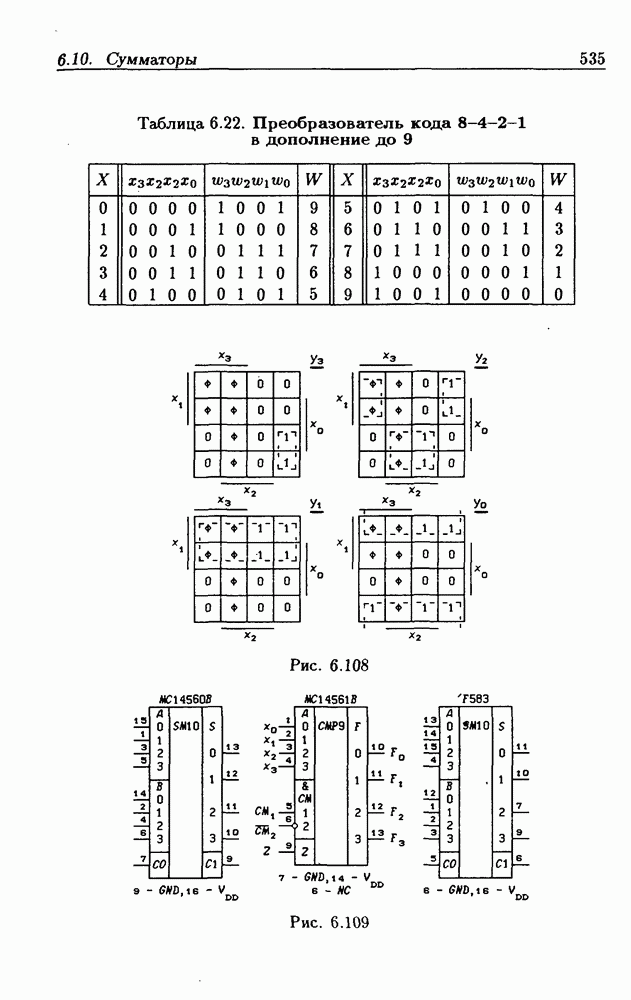
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
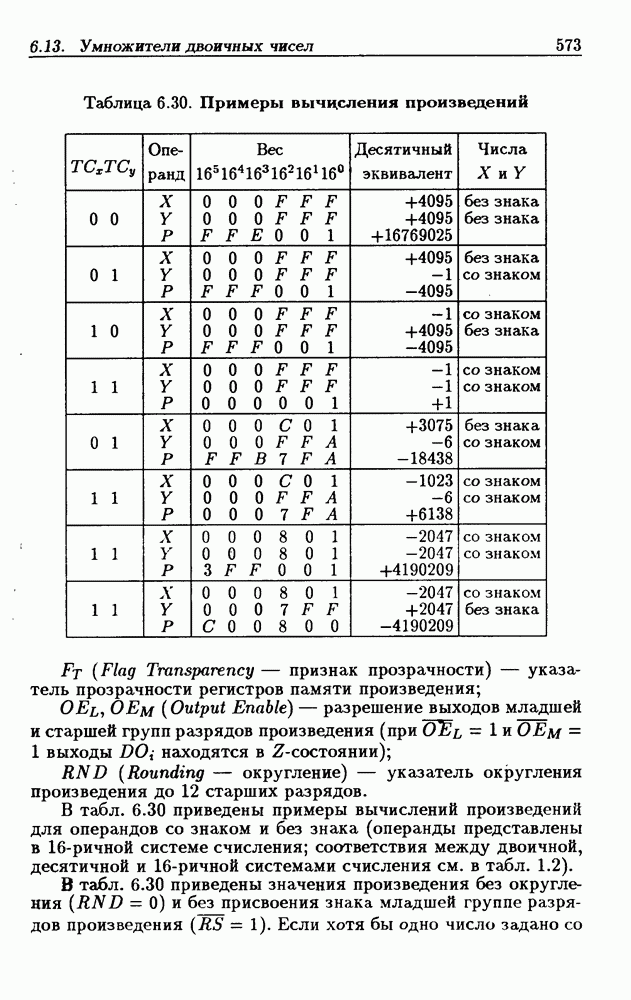
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
- БИС умножителя 12×12 разрядов 1802ВР4.
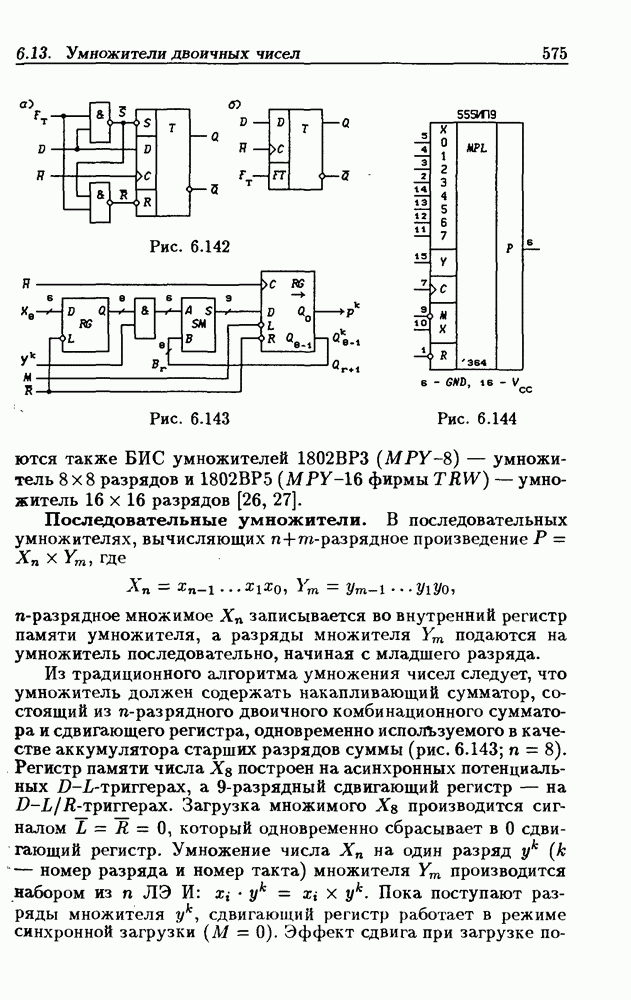
- Последовательные умножители.
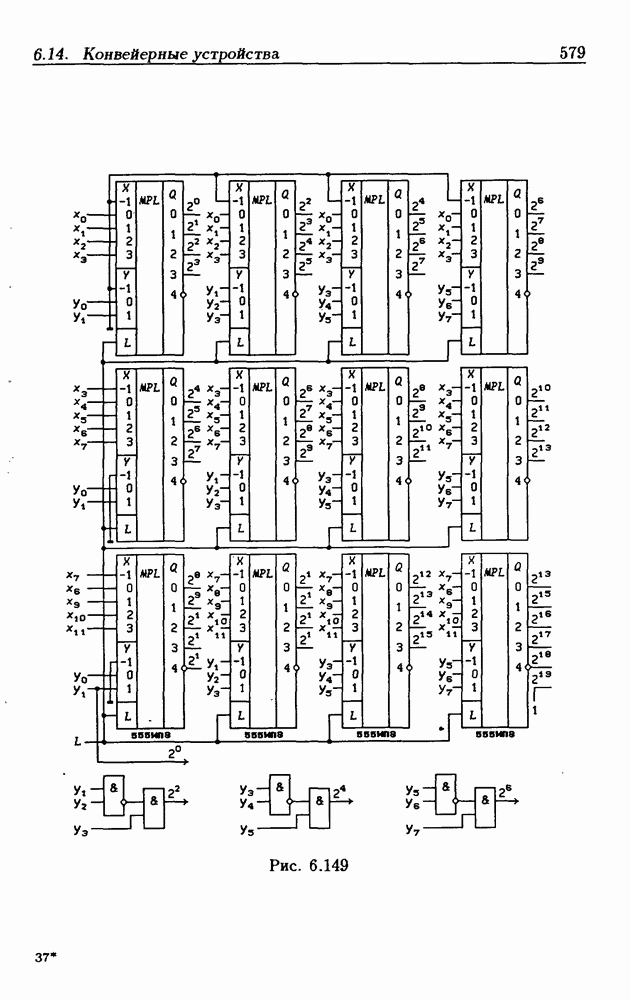
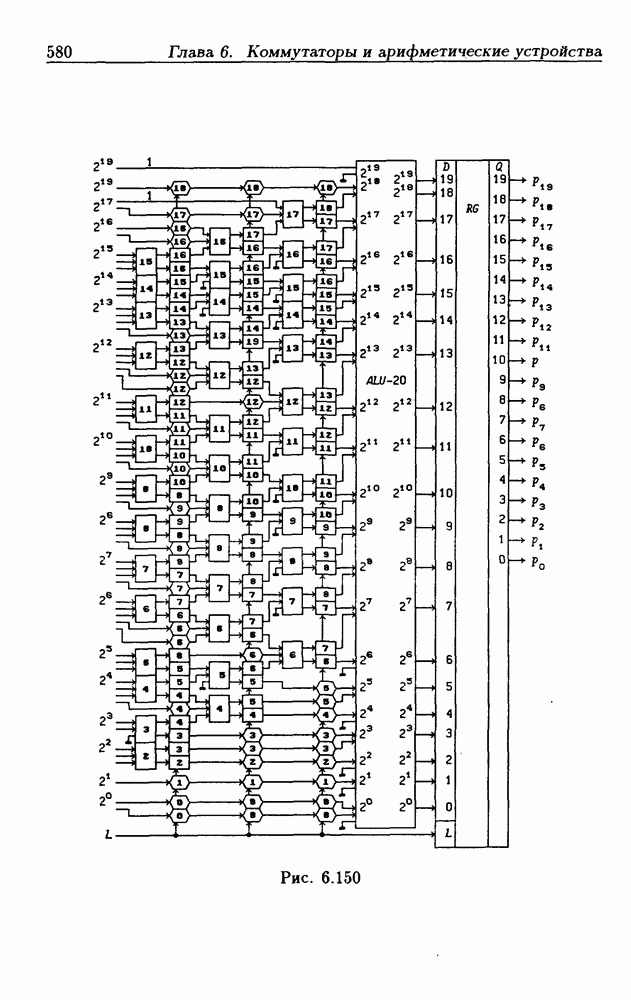
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
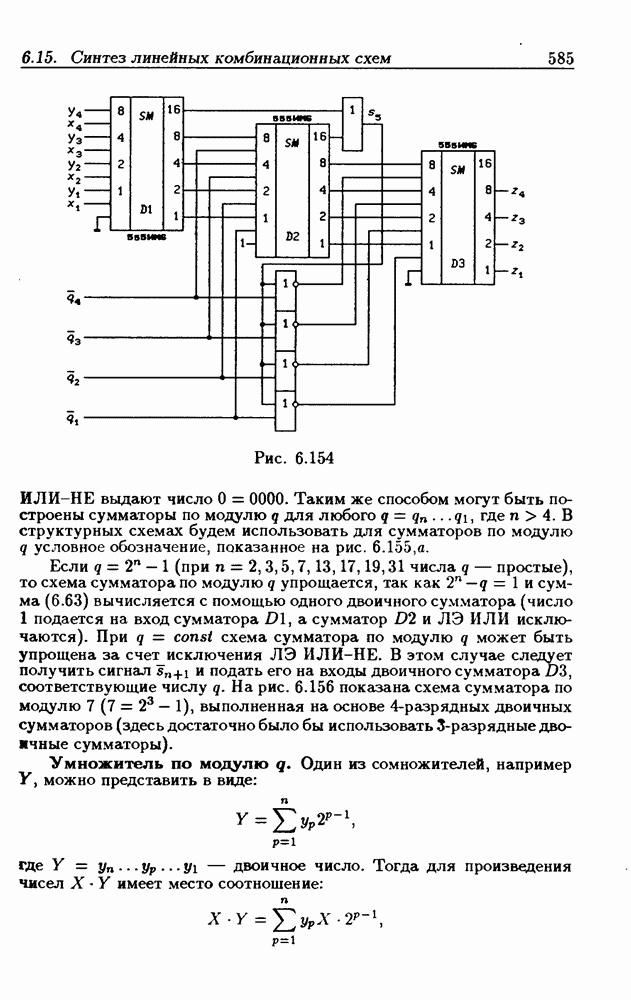
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
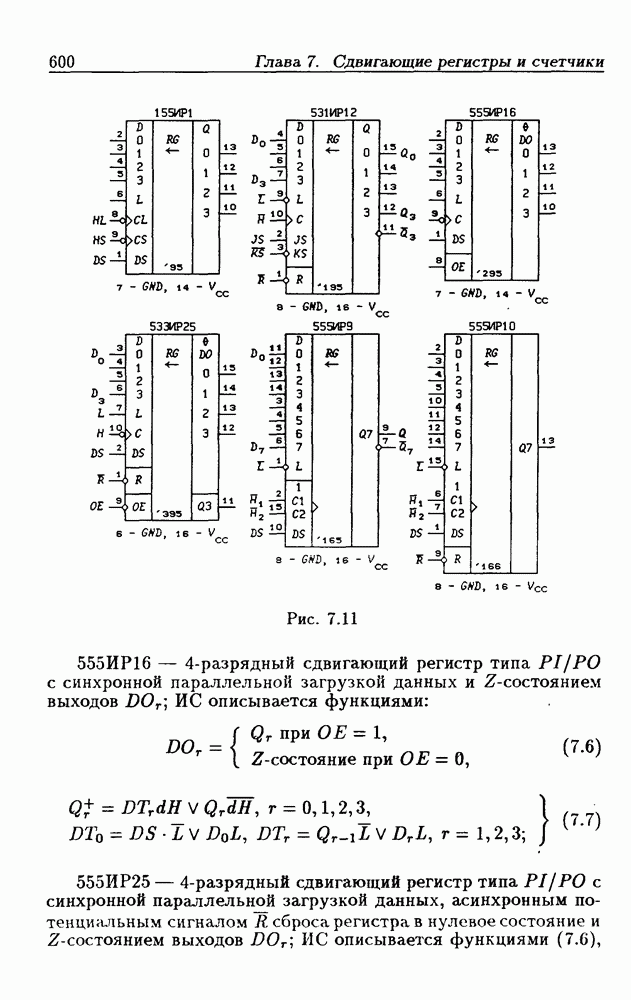
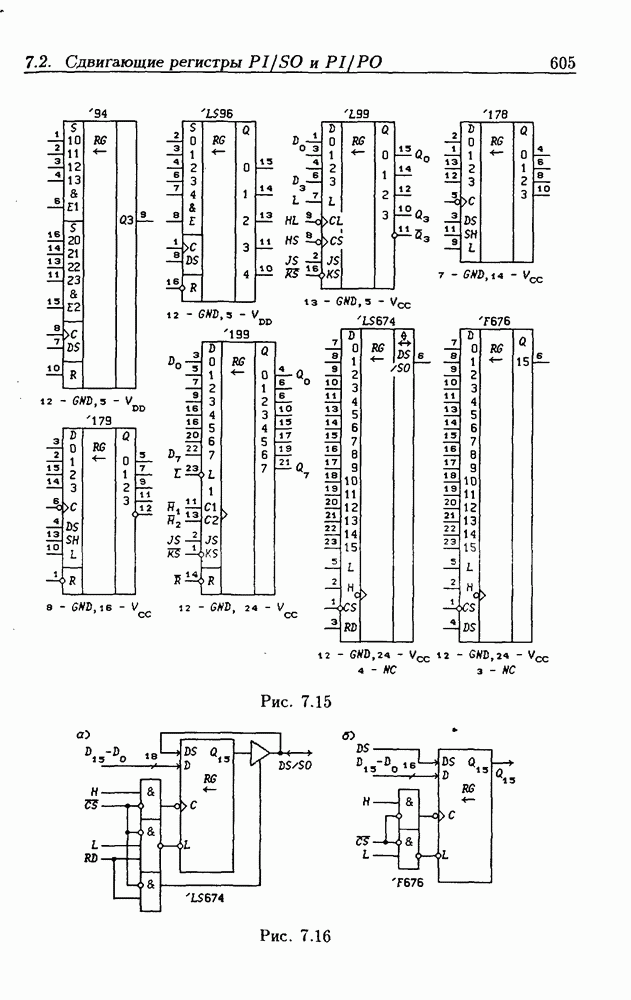
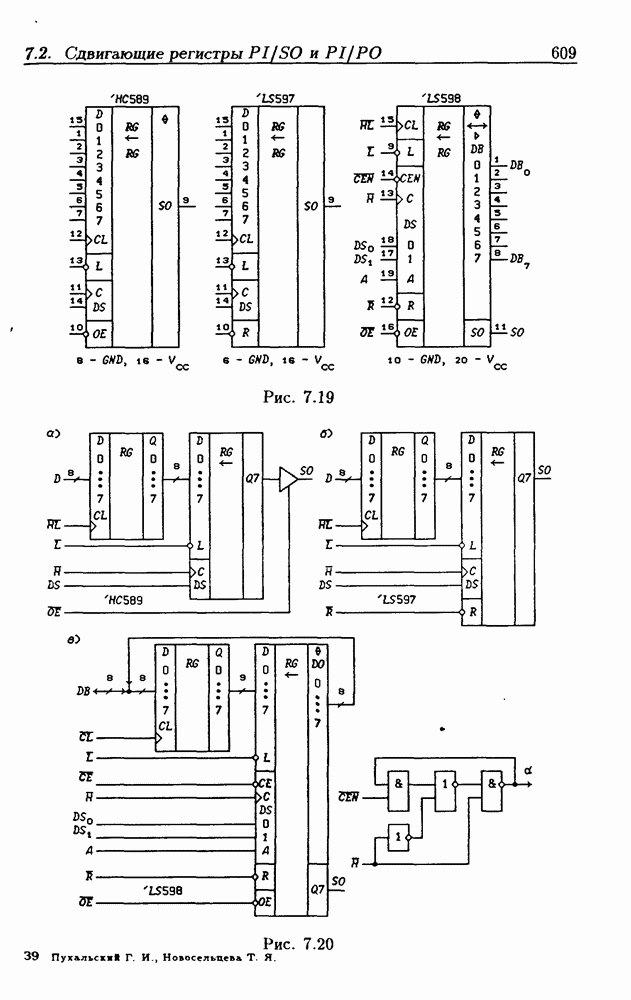
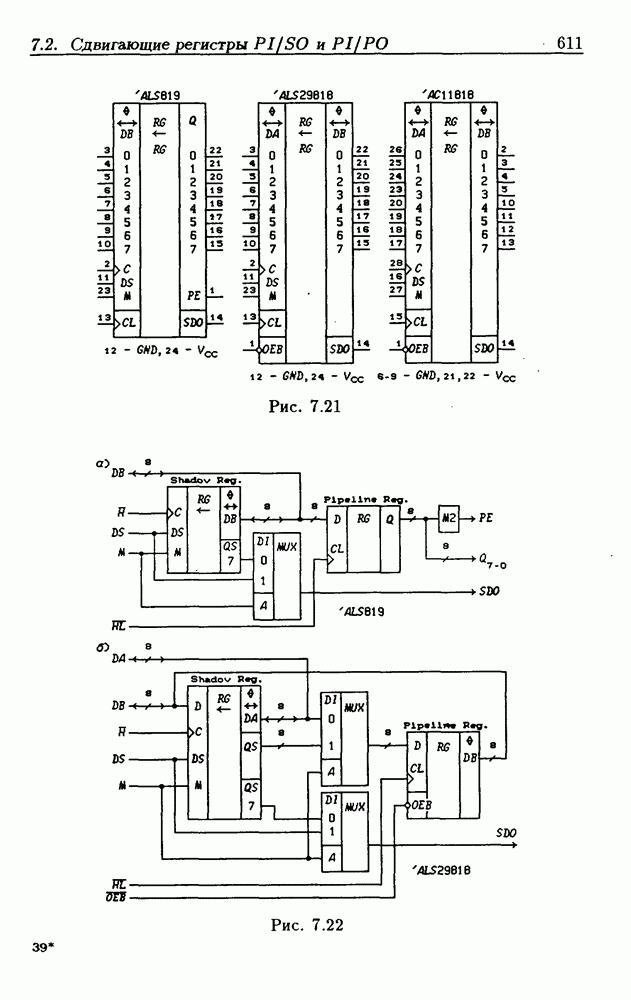
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
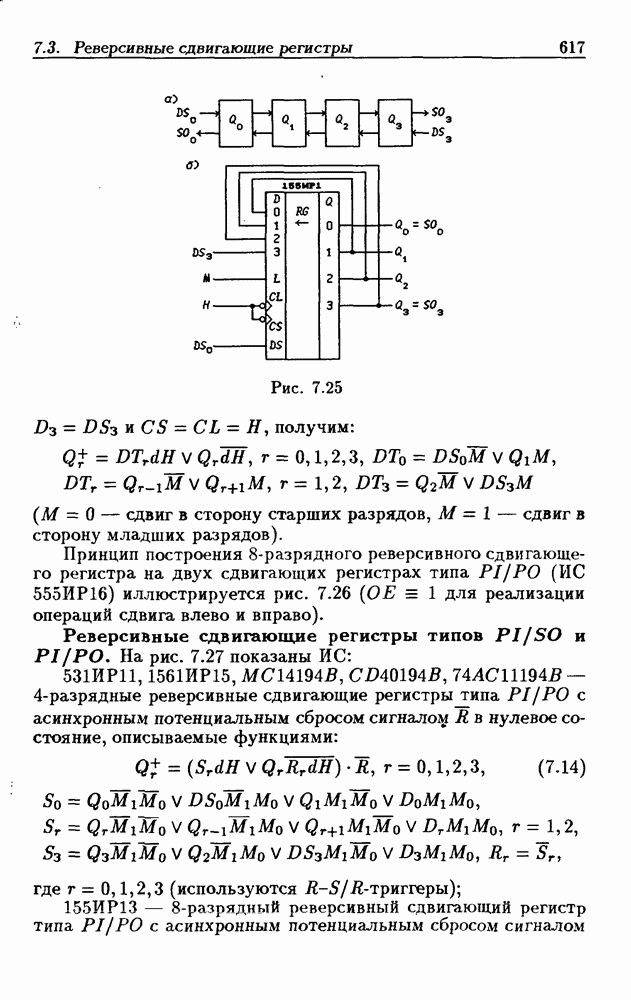
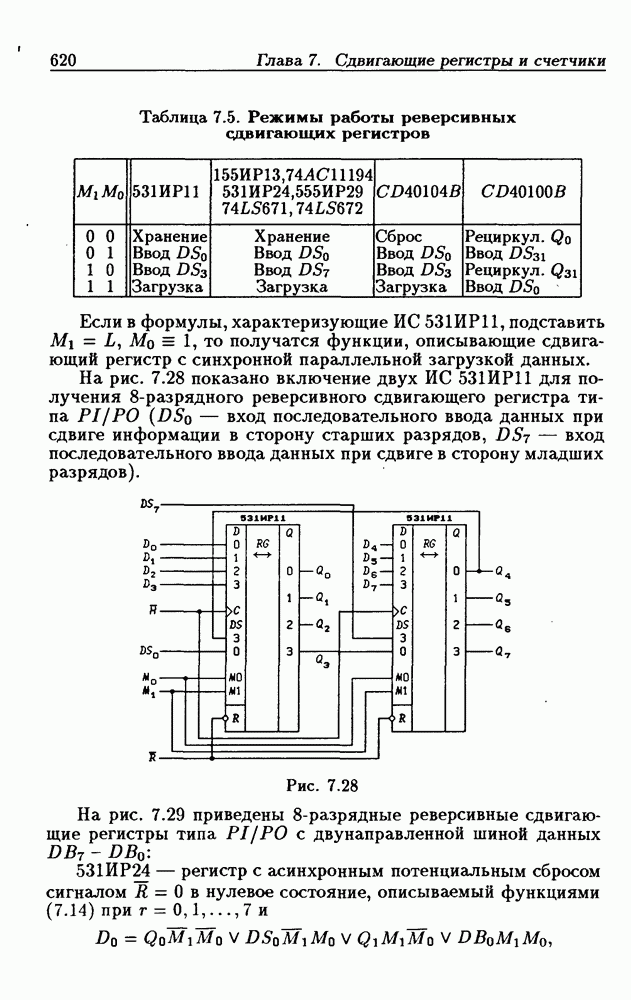
- 7.3. Реверсивные сдвигающие регистры
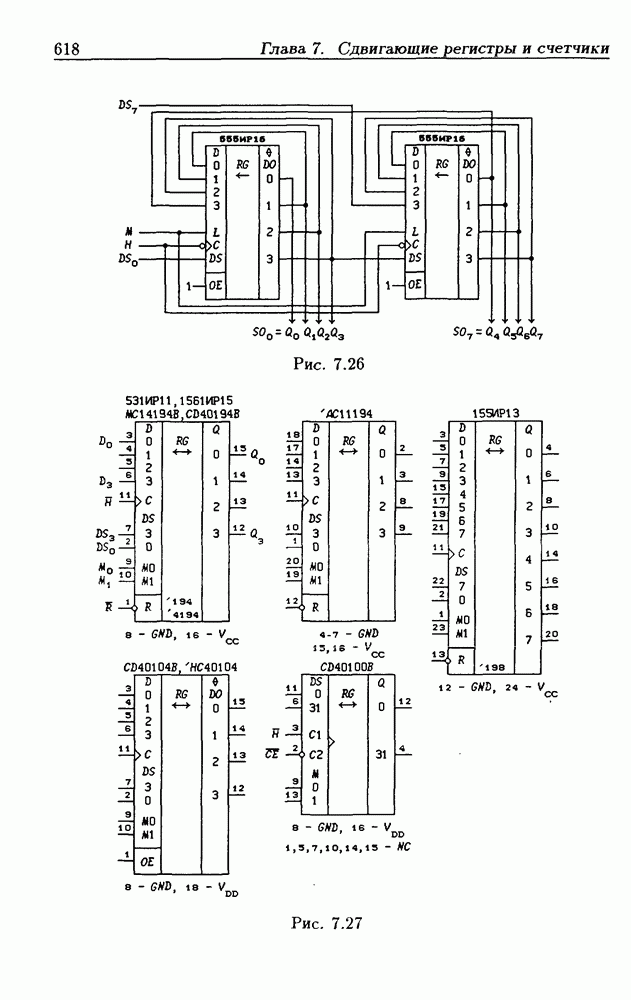
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
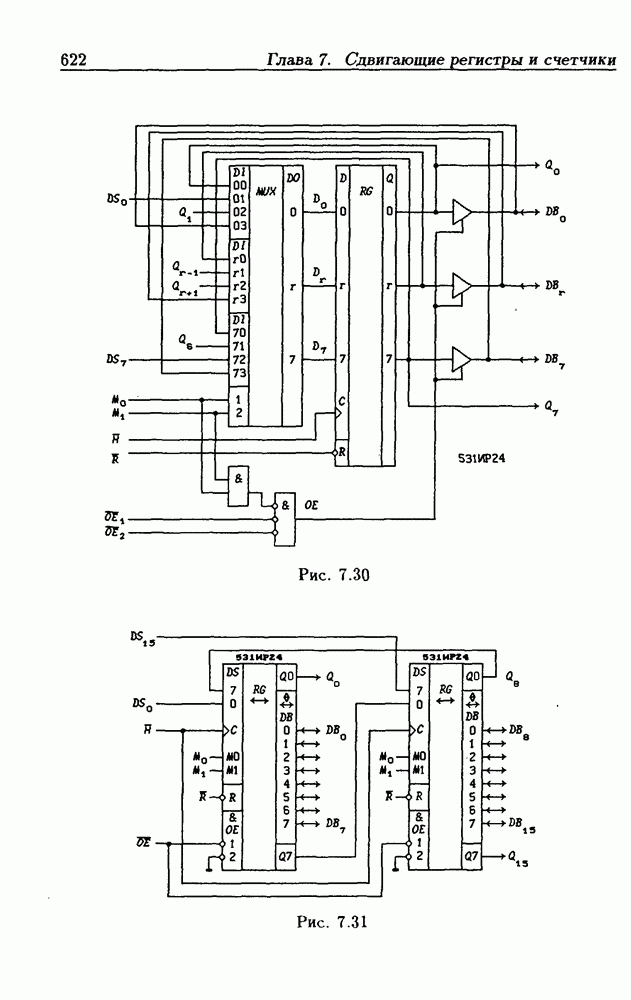
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
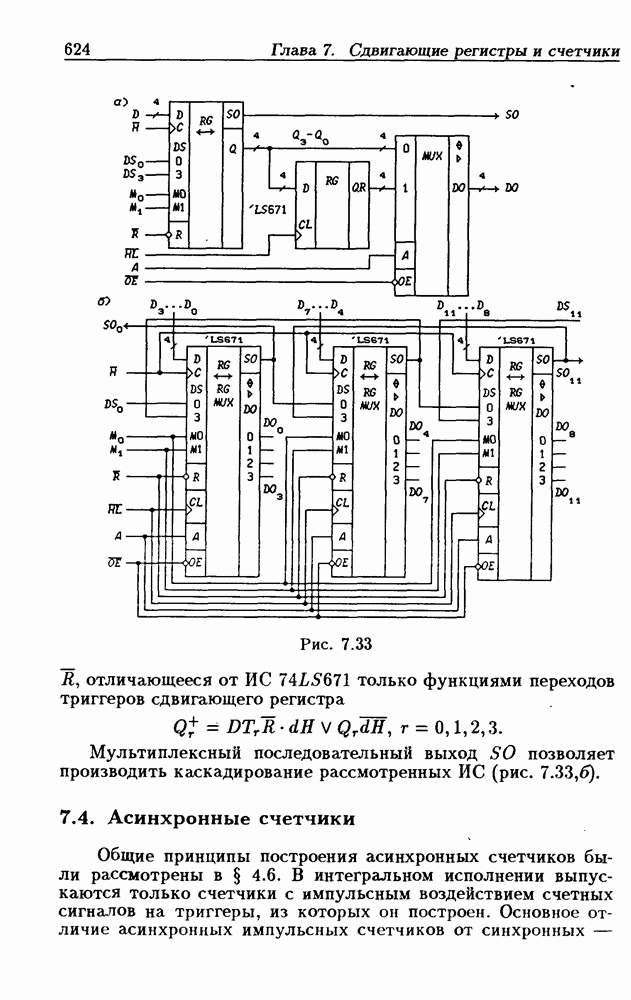
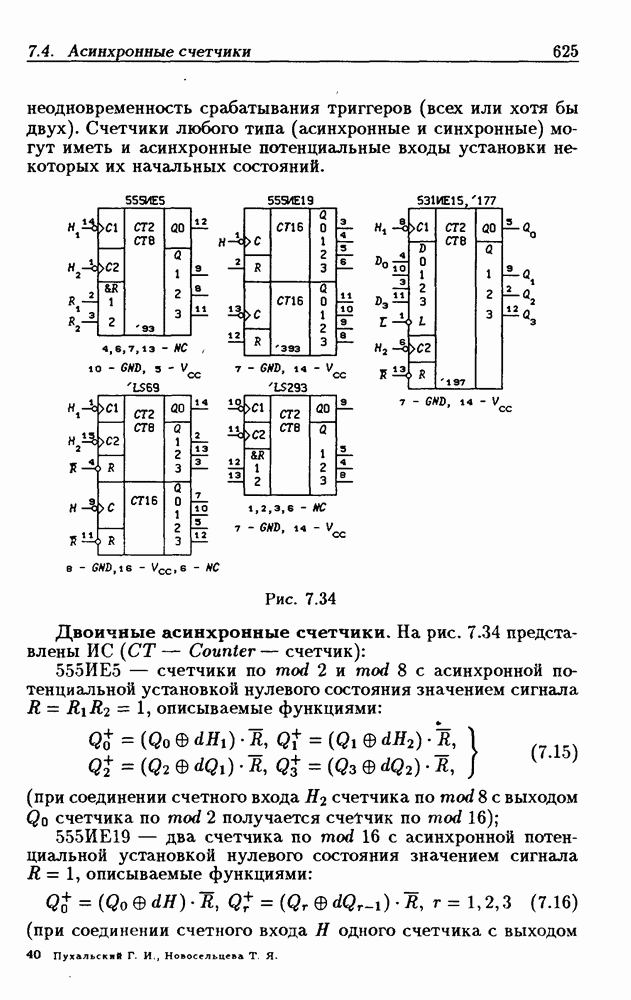
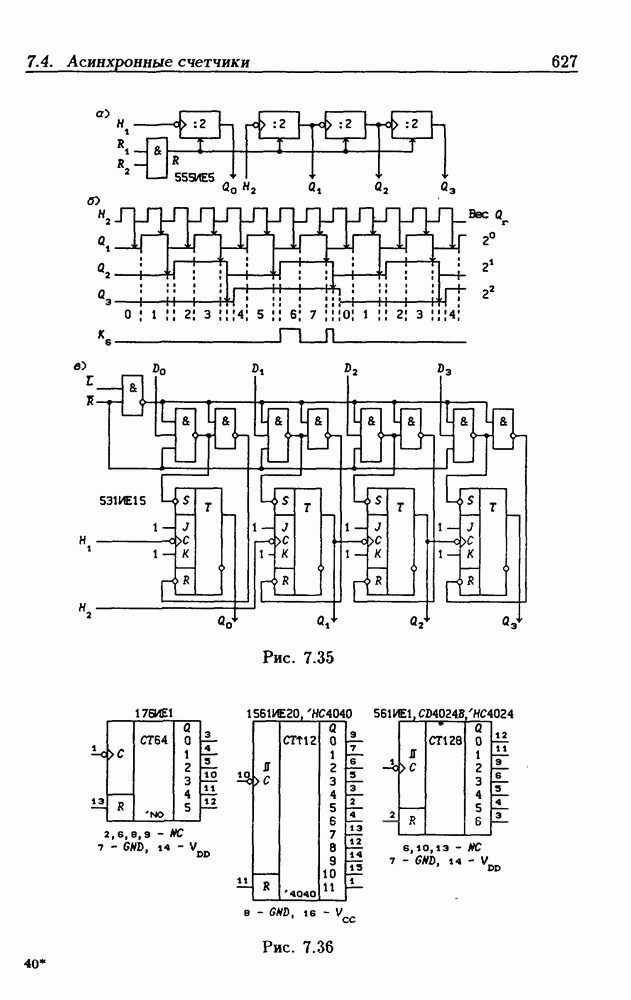
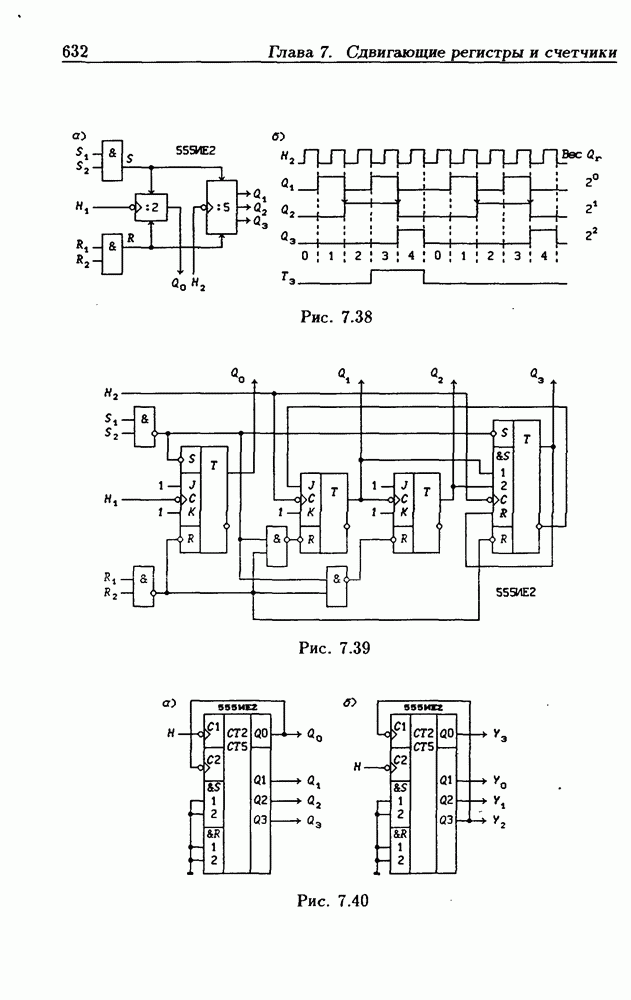
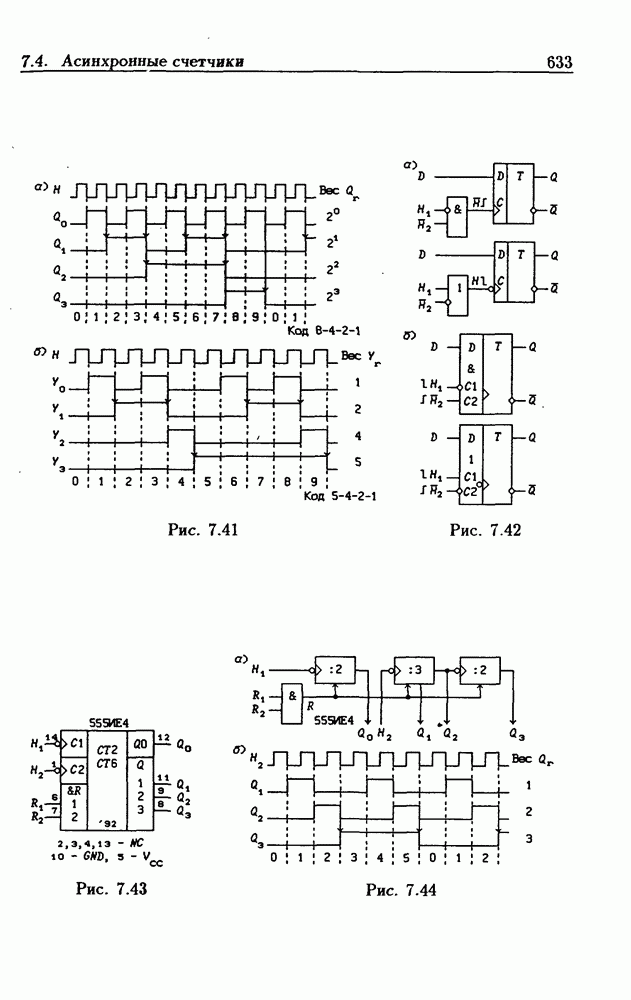
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
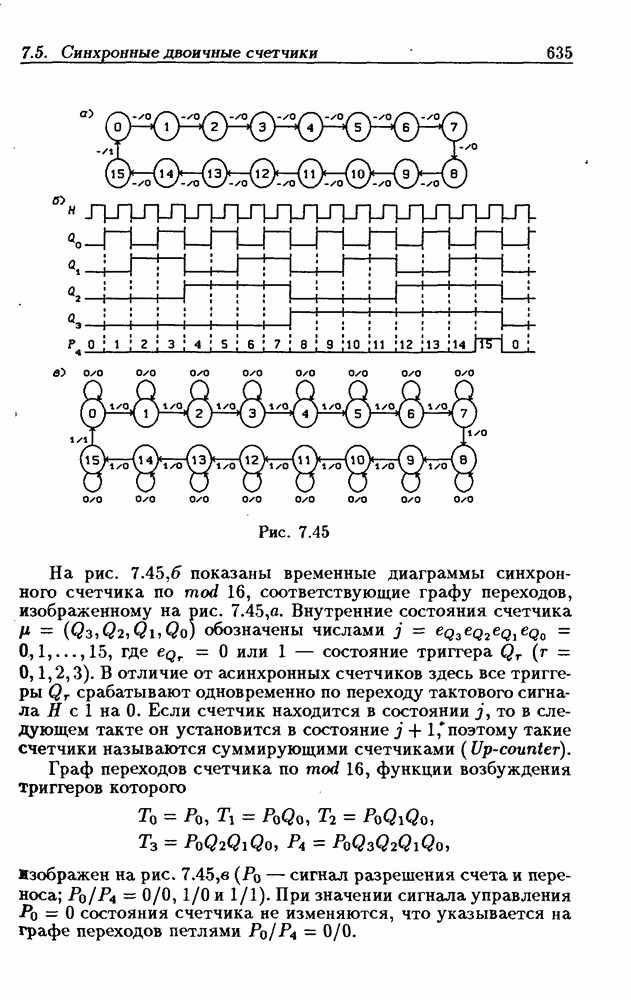
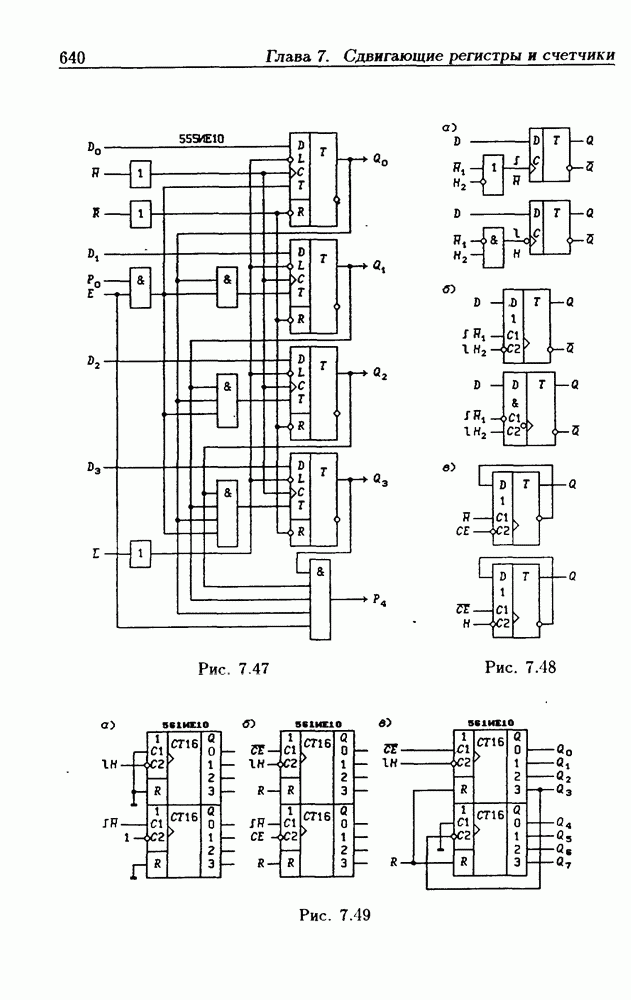
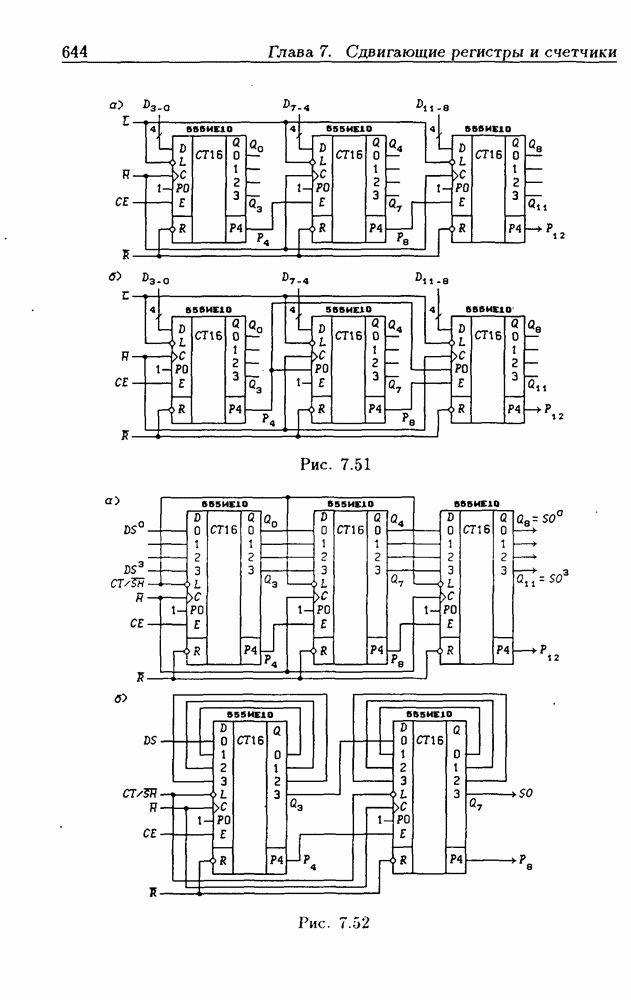
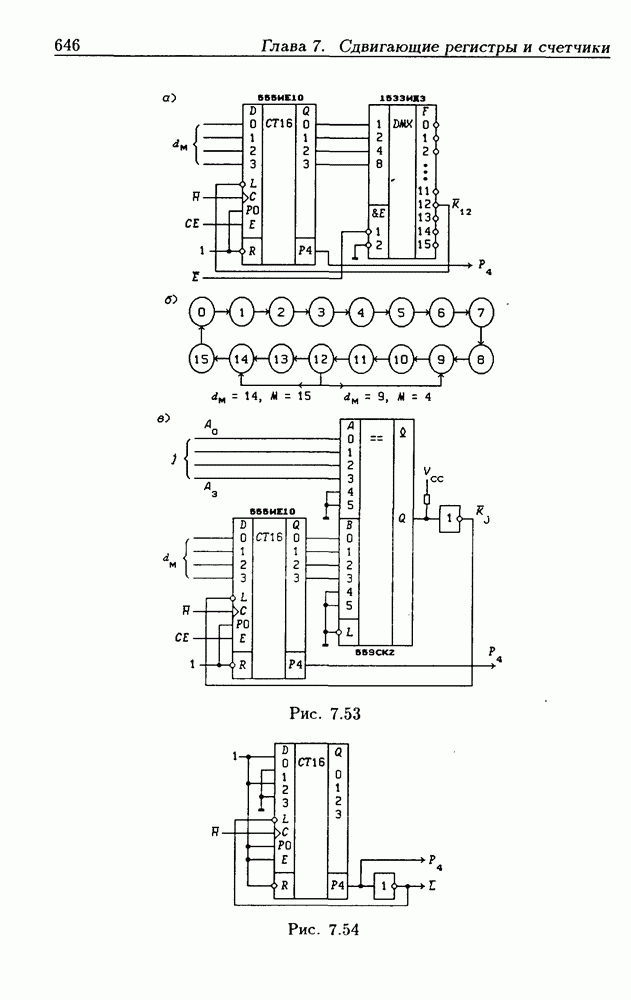
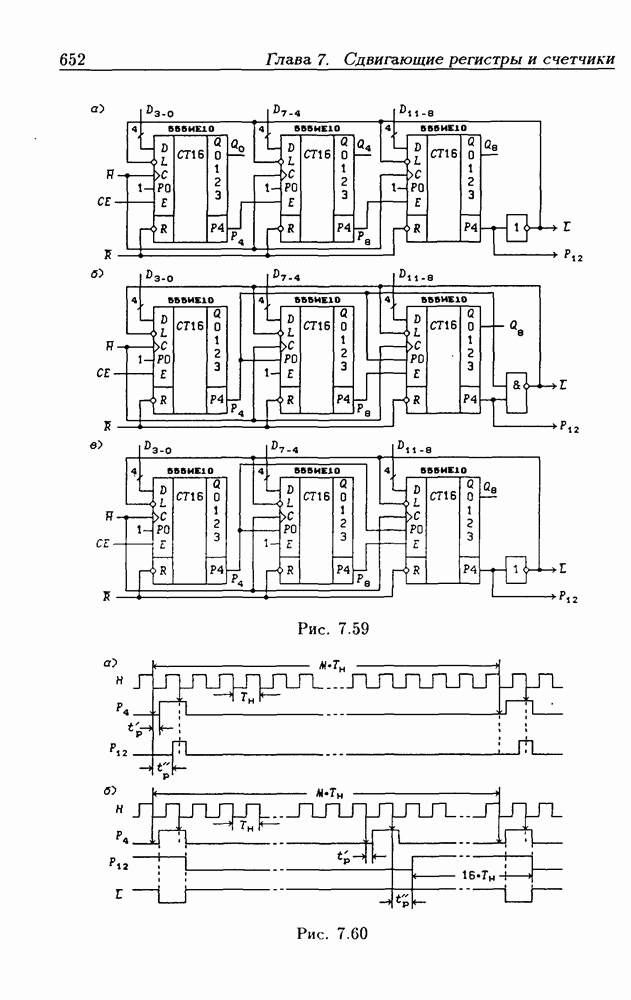
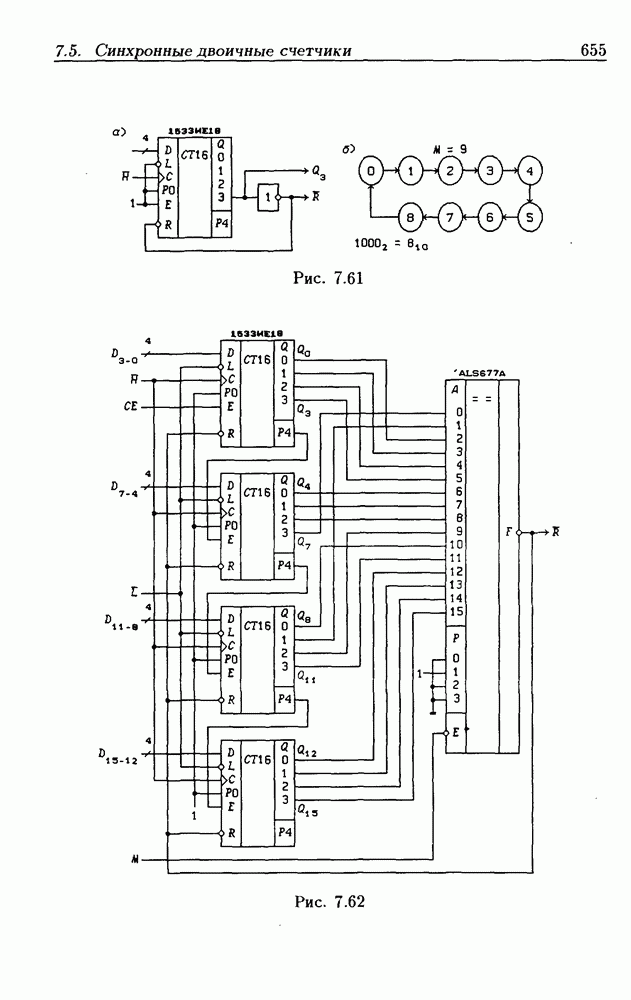
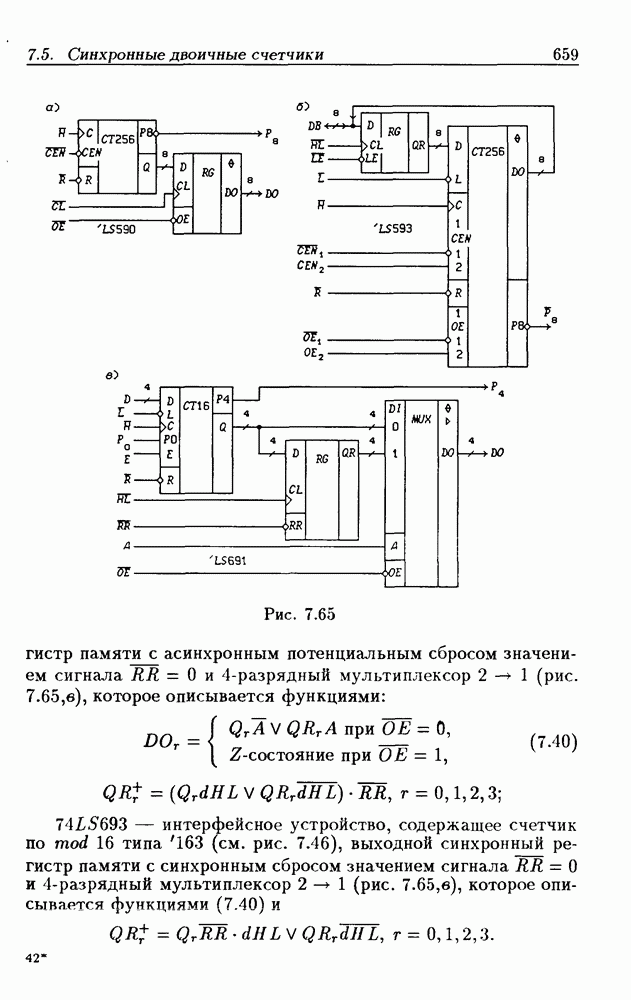
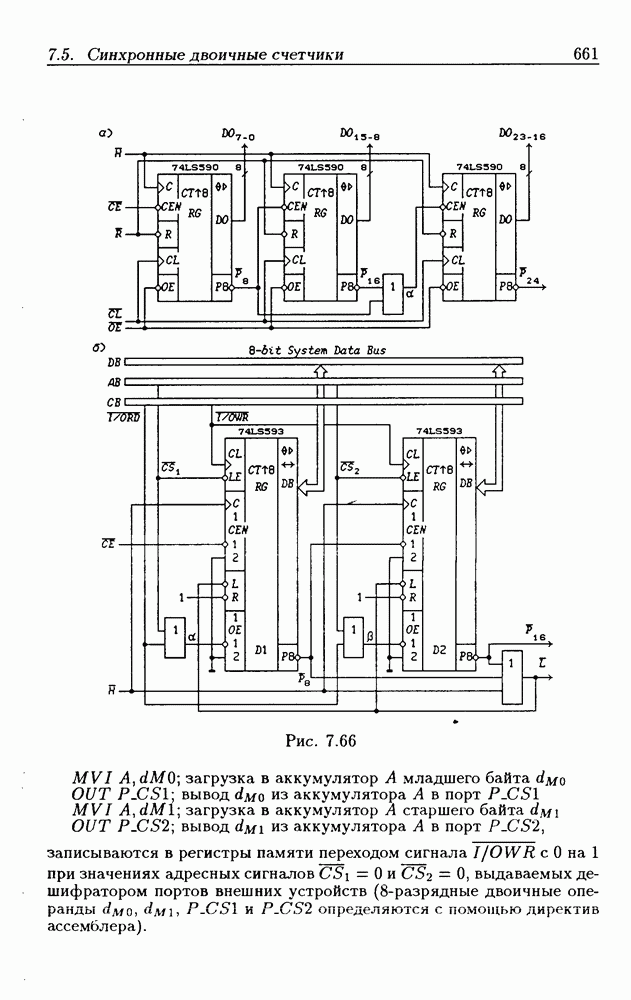
- 7.5. Синхронные двоичные счетчики
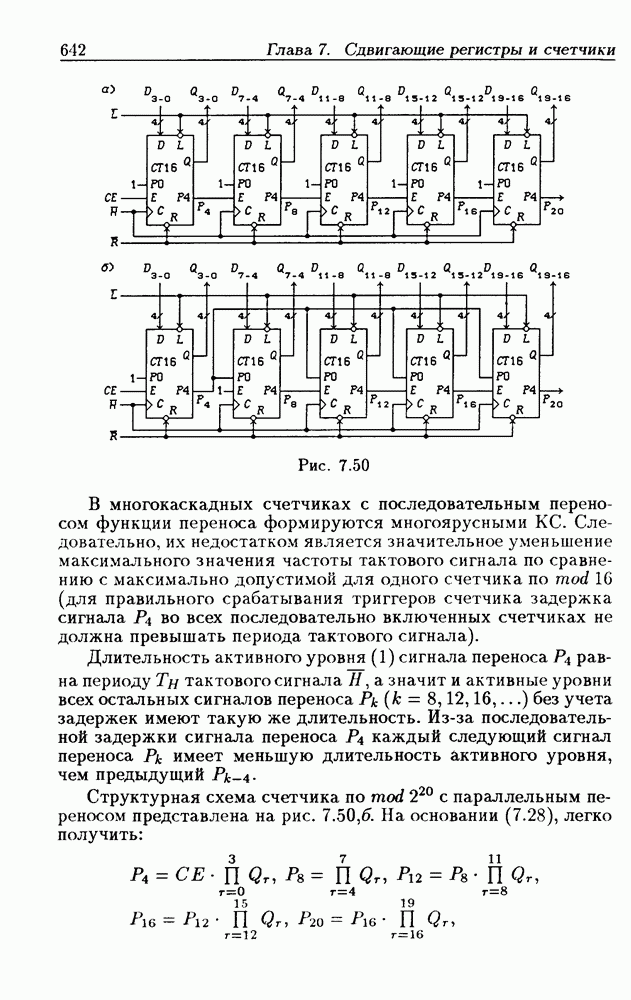
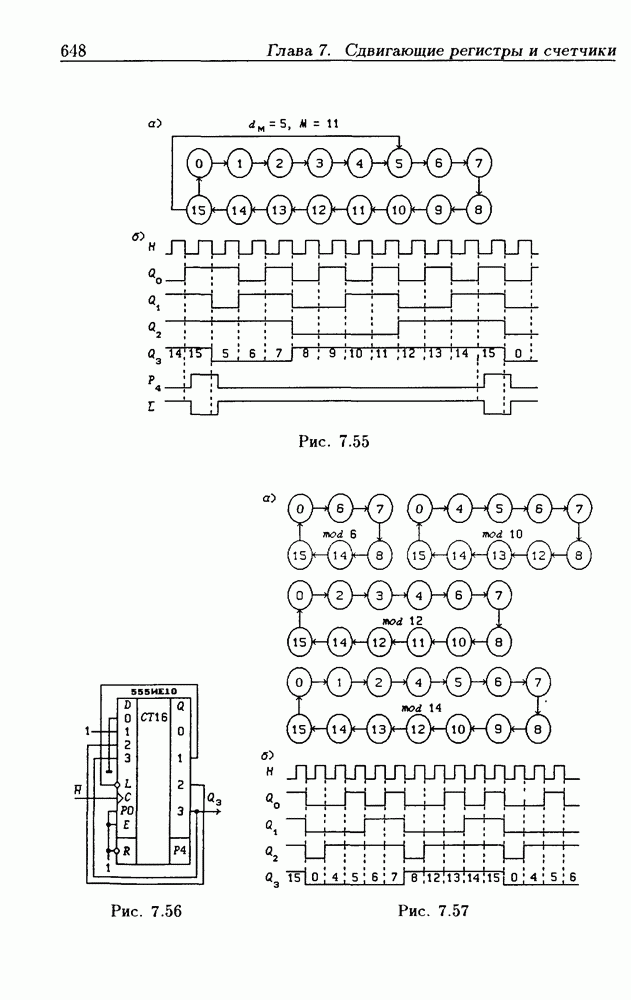
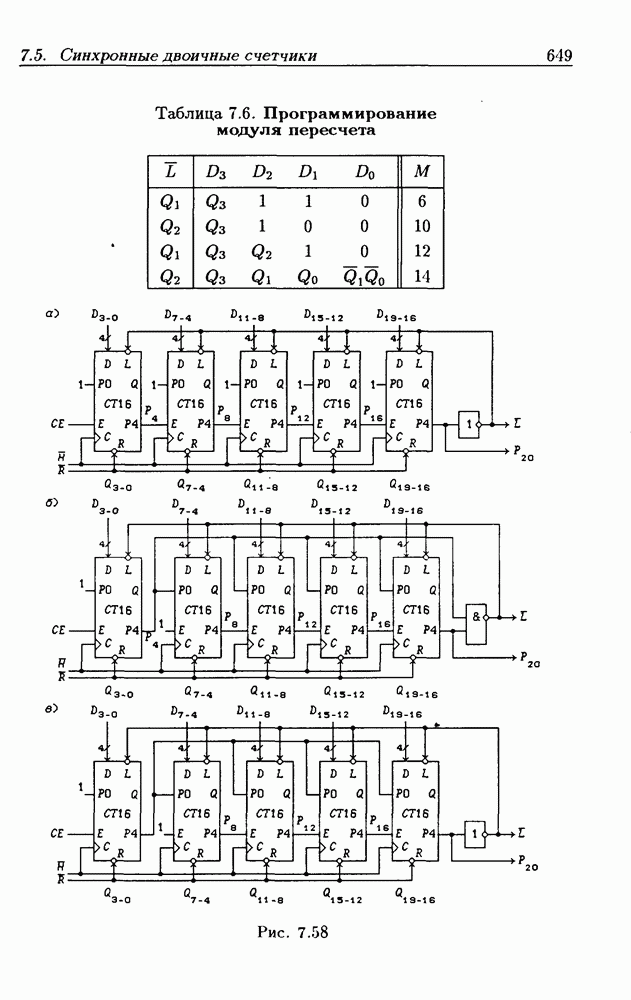
- Программирование модуля пересчета двоичных счетчиков.
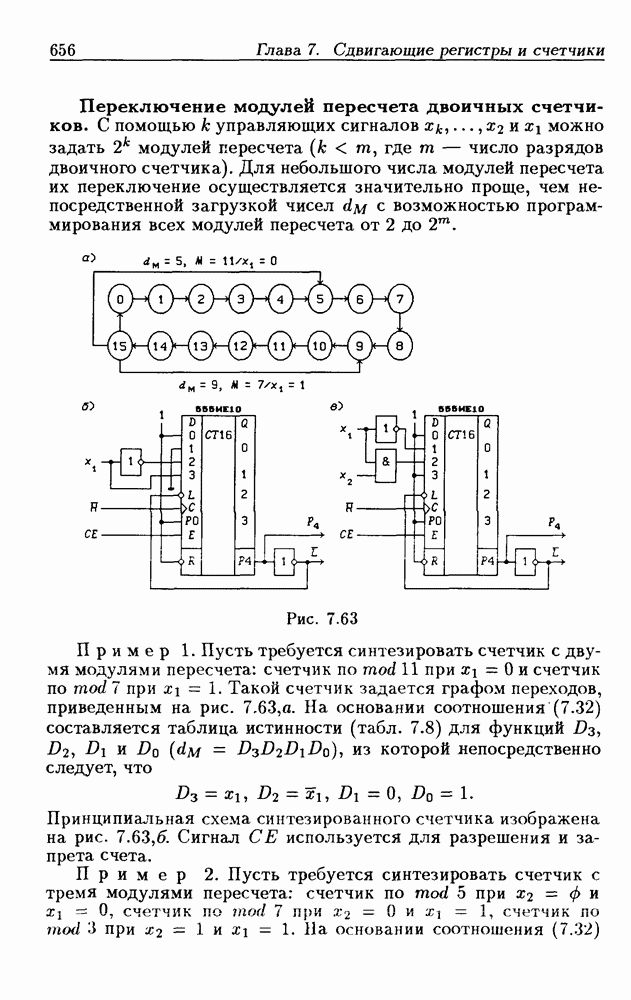
- Переключение модулей пересчета двоичных счетчиков.
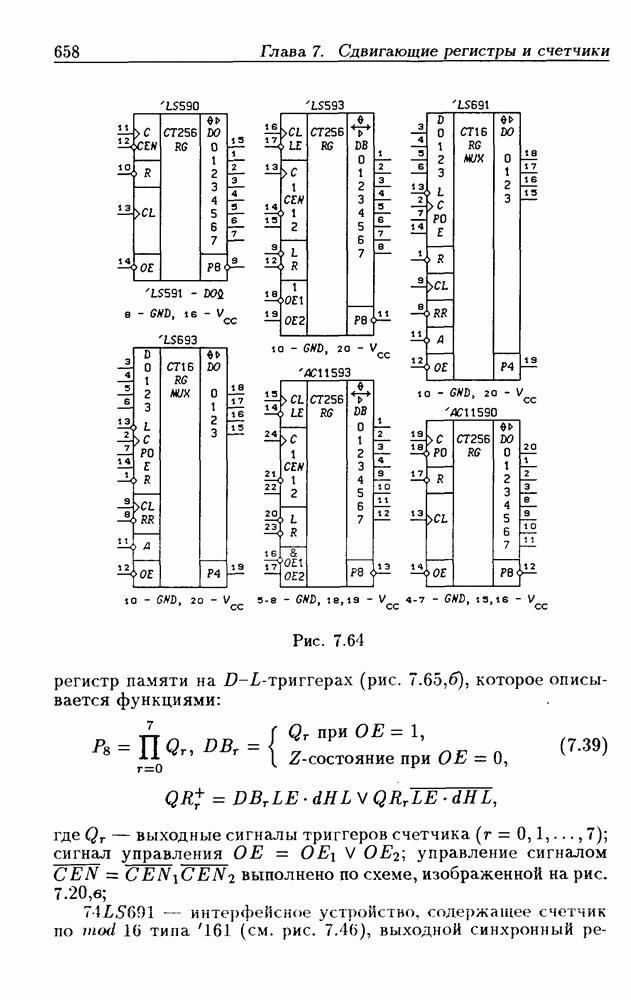
- Функциональные устройства на основе двоичных счетчиков.
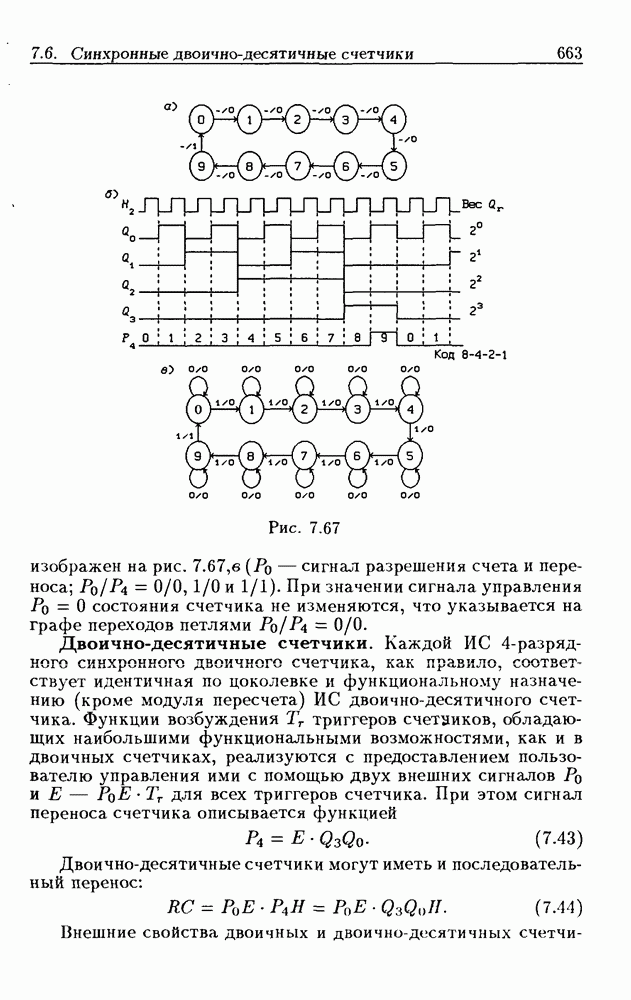
- 7.6. Синхронные двоично-десятичные счетчики
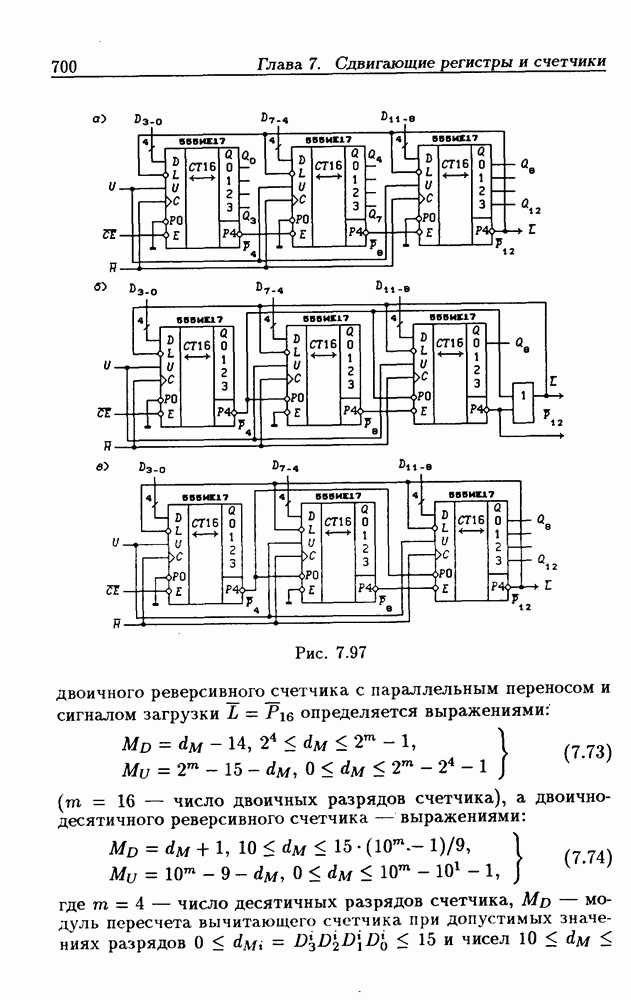
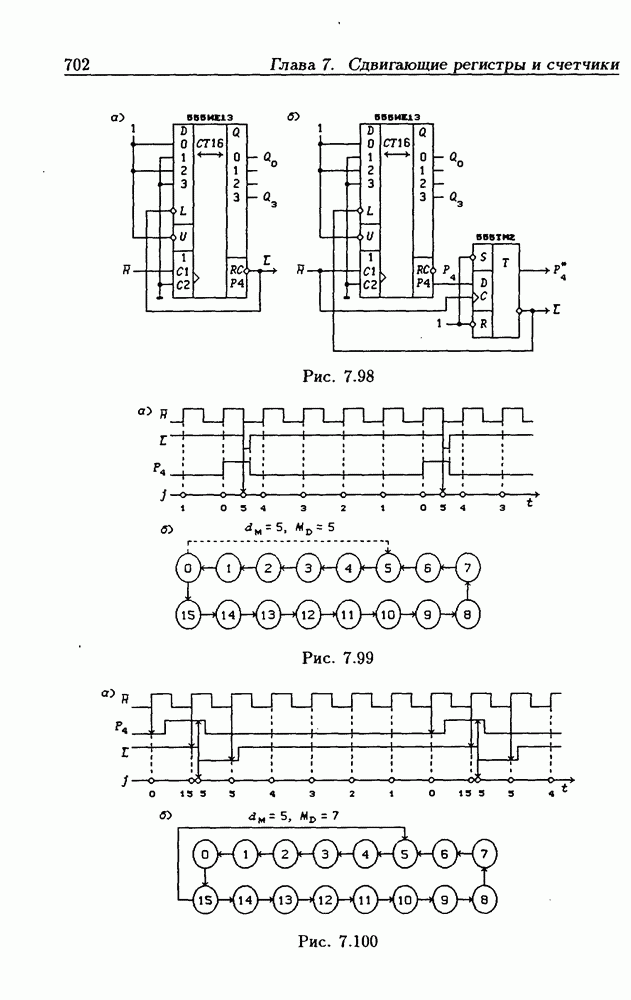
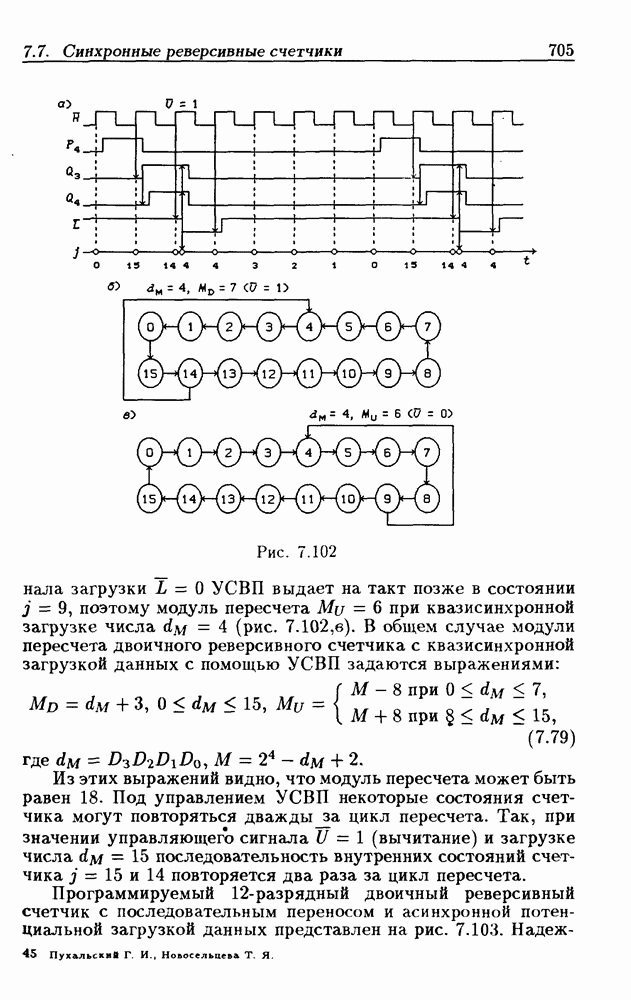
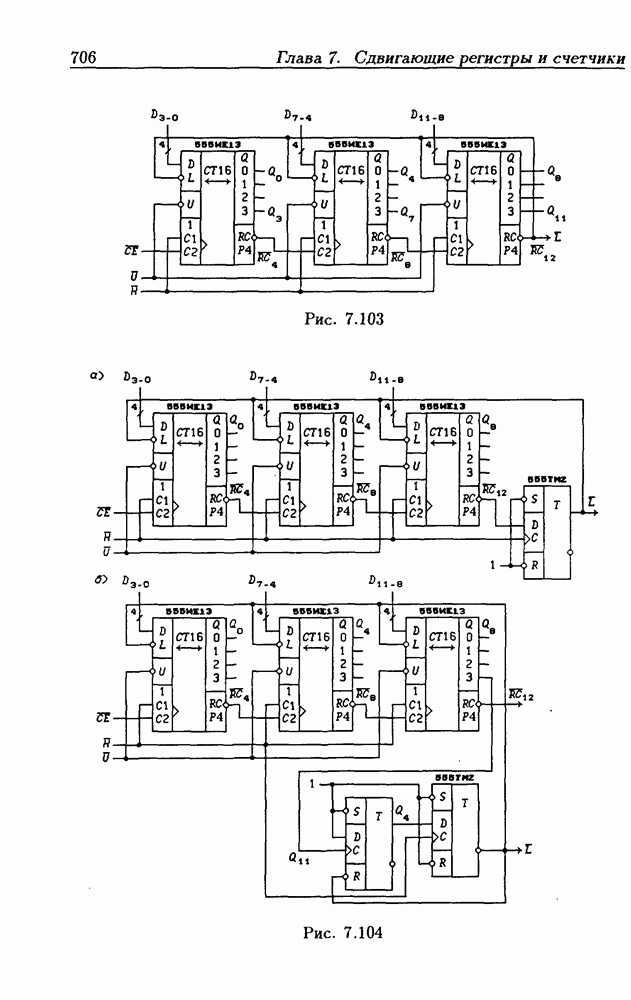
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
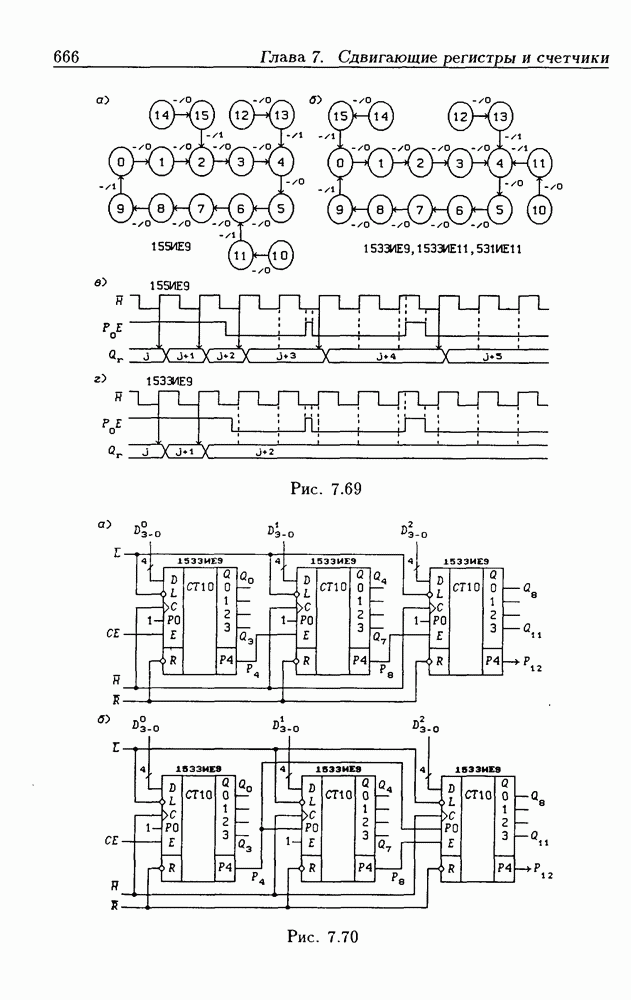
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
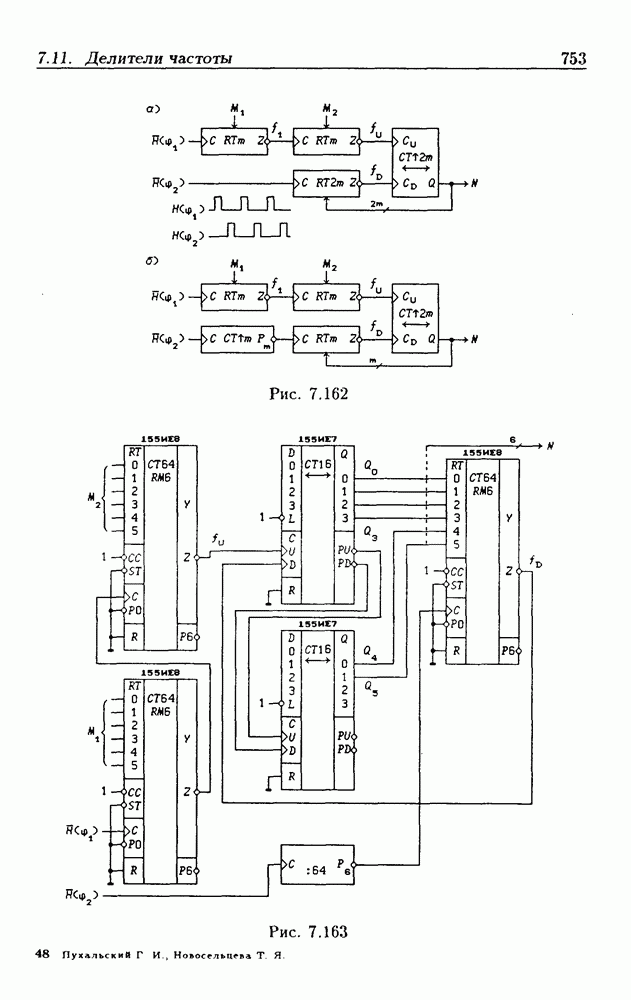
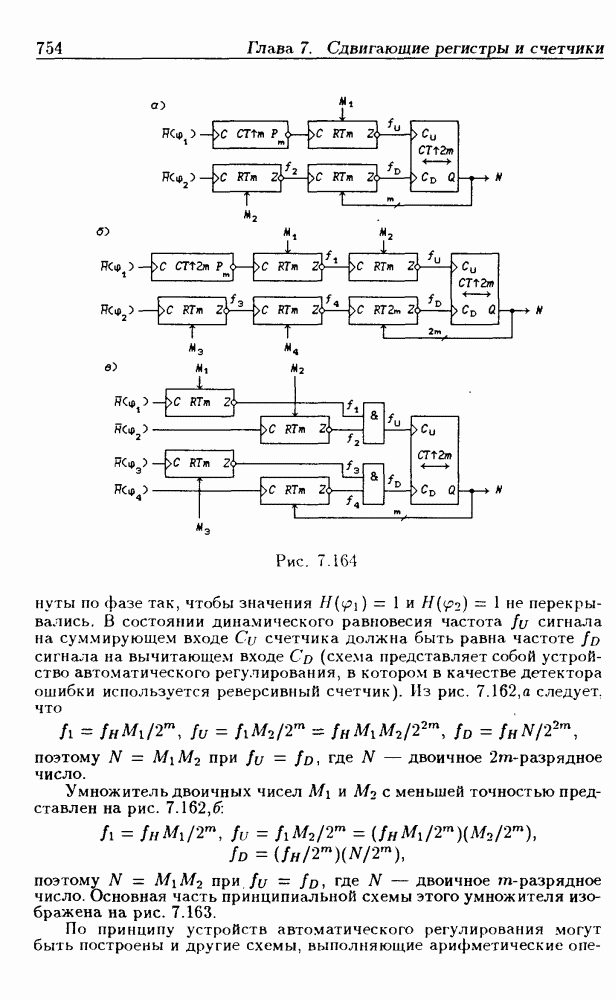
- 7.11. Делители частоты
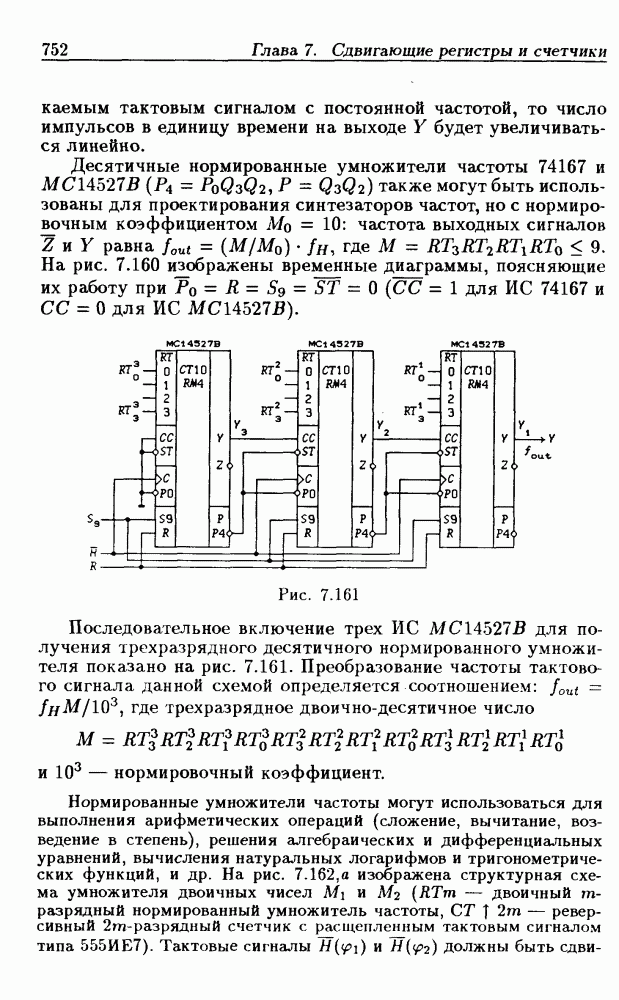
- Нормированные умножители частоты.
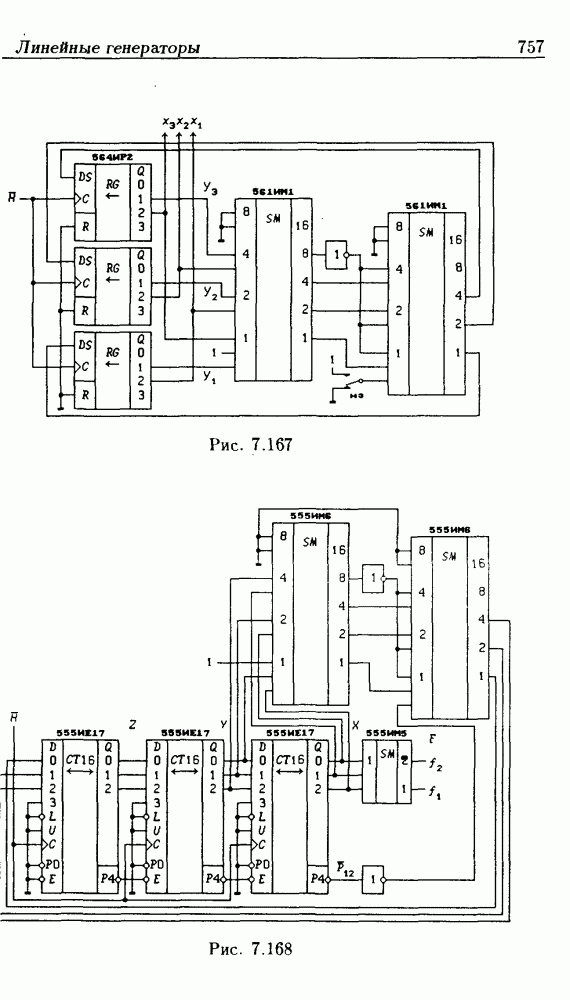
- 7.12. Линейные генераторы
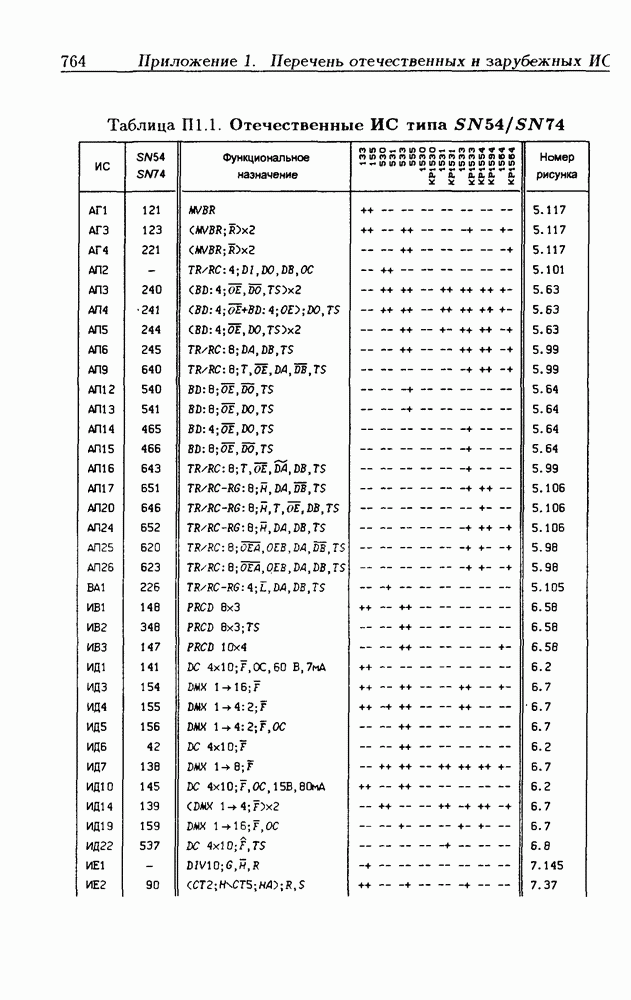
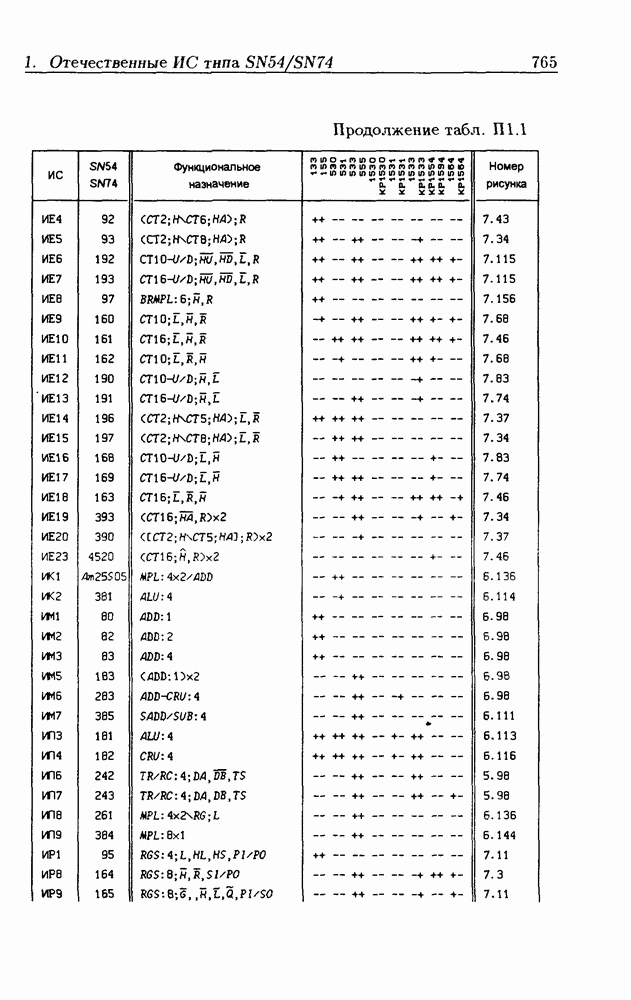
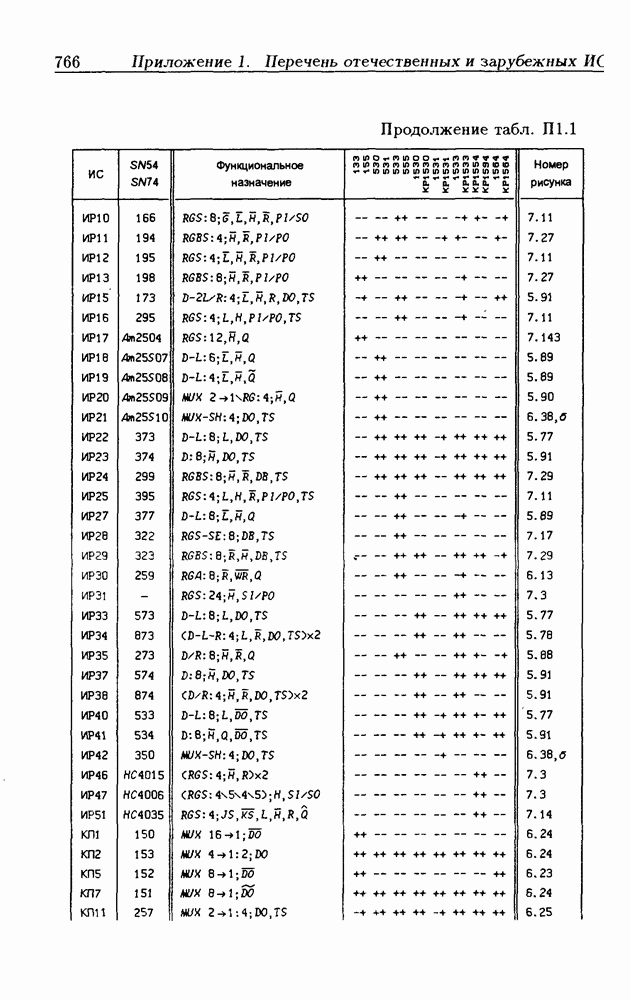
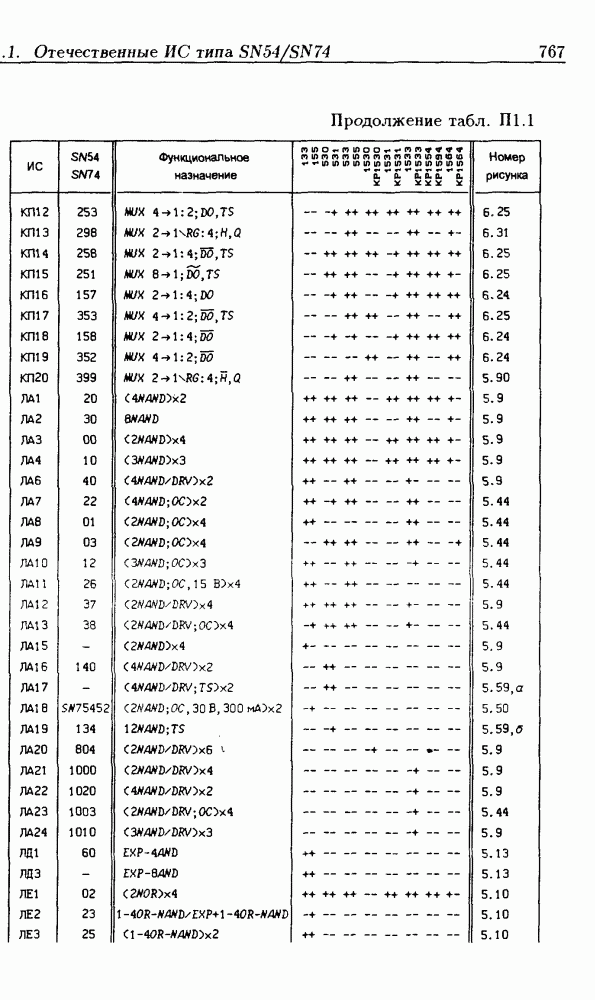
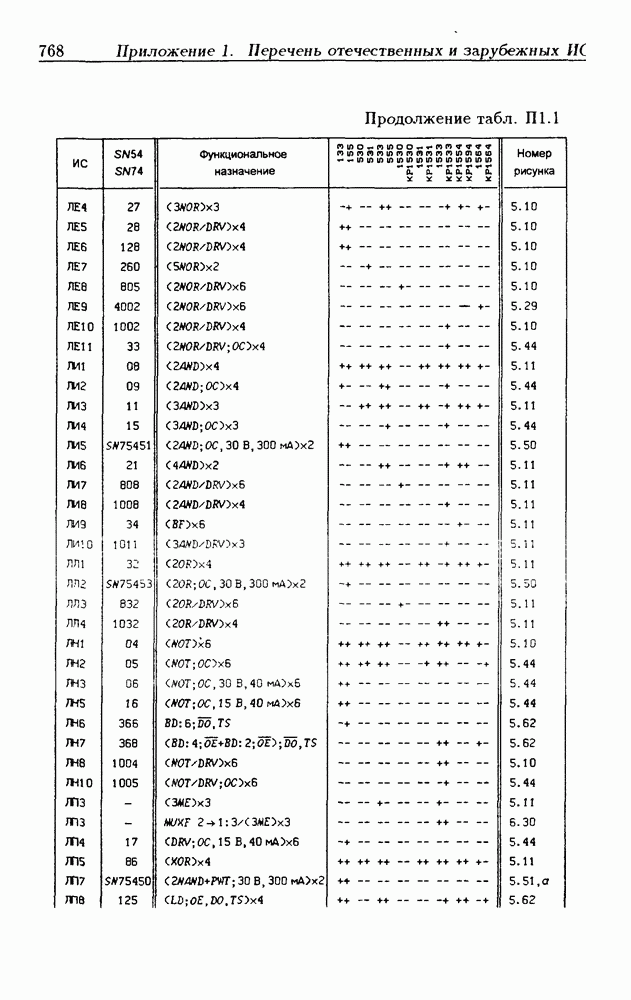
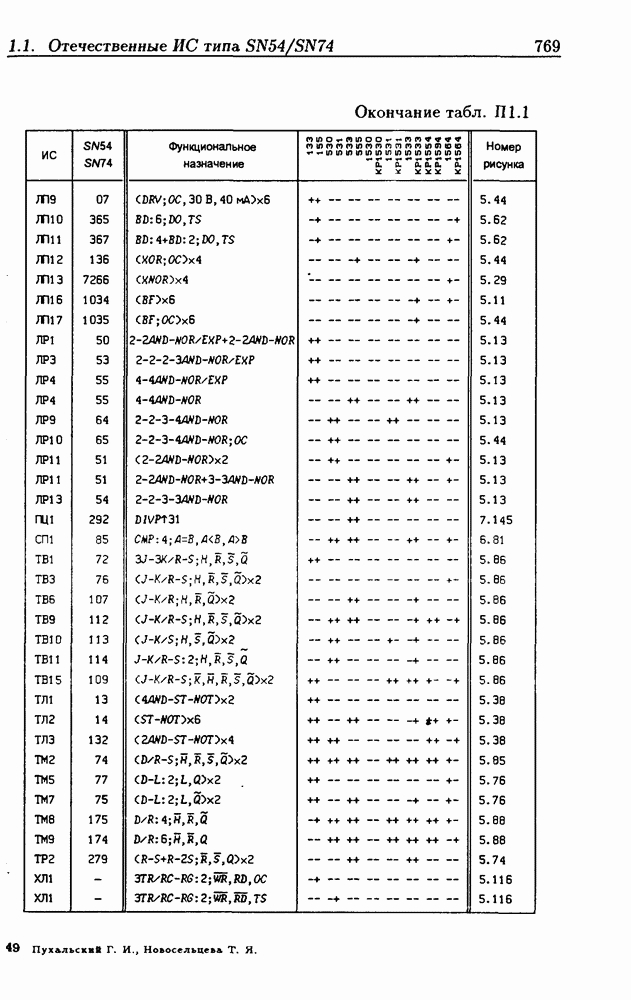
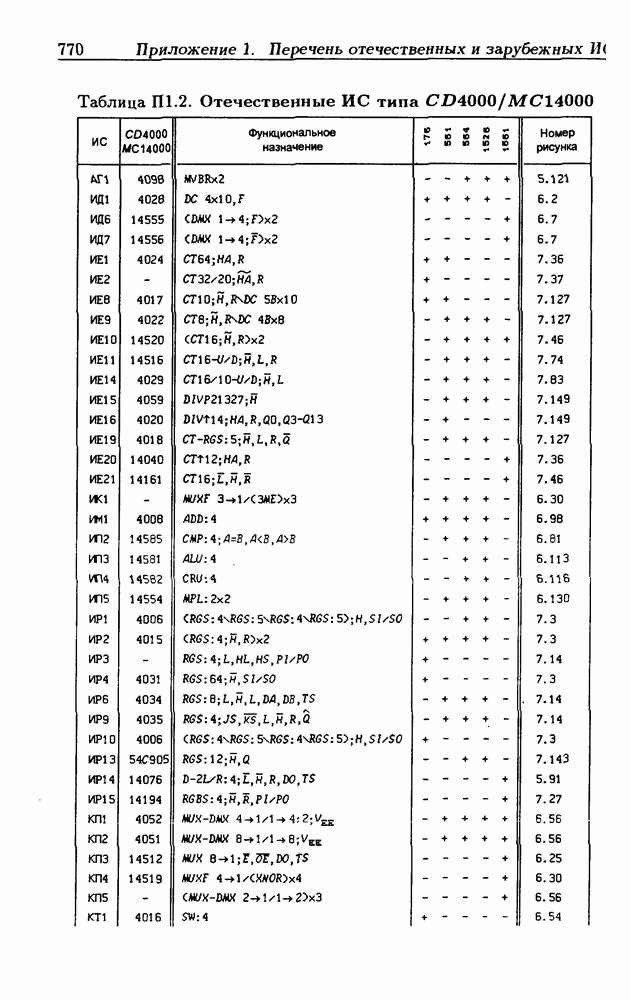
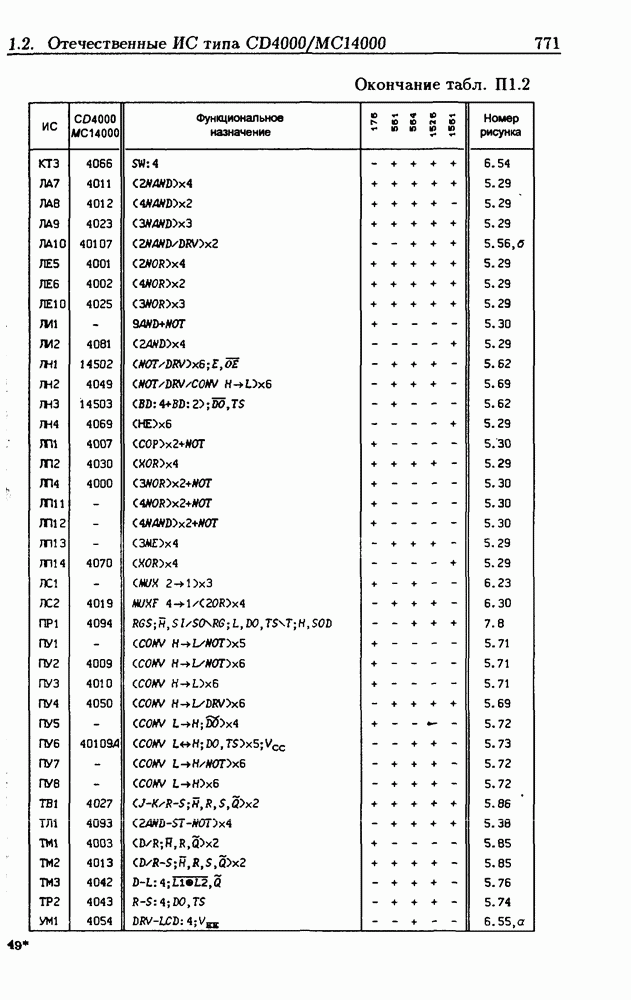
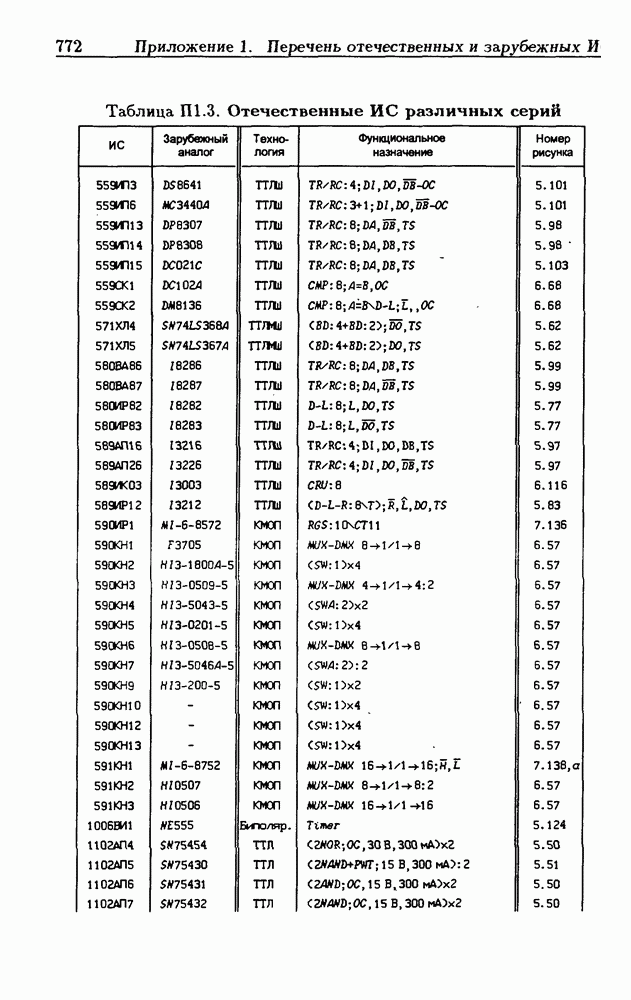
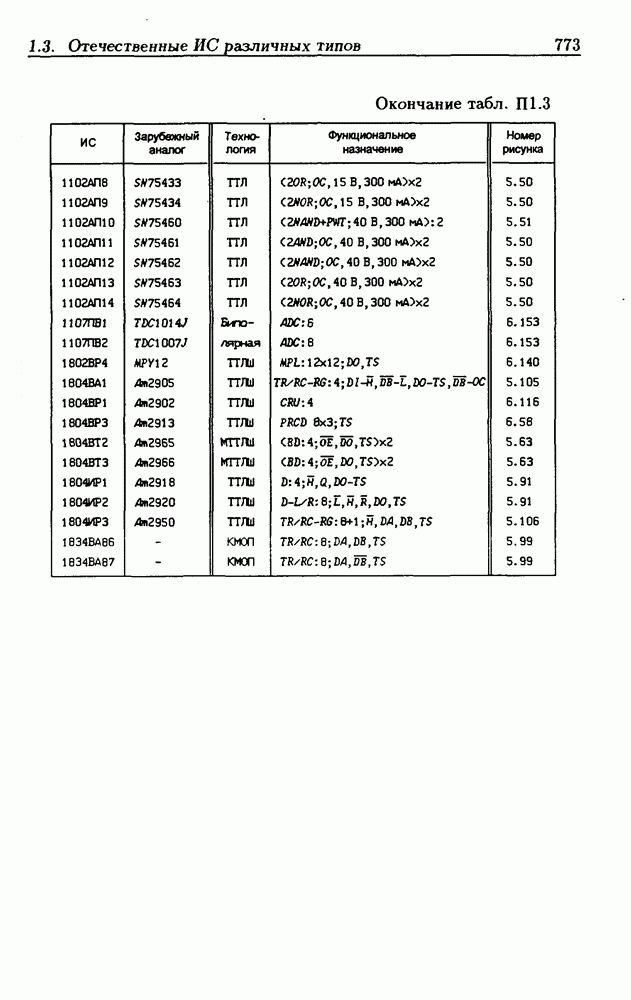
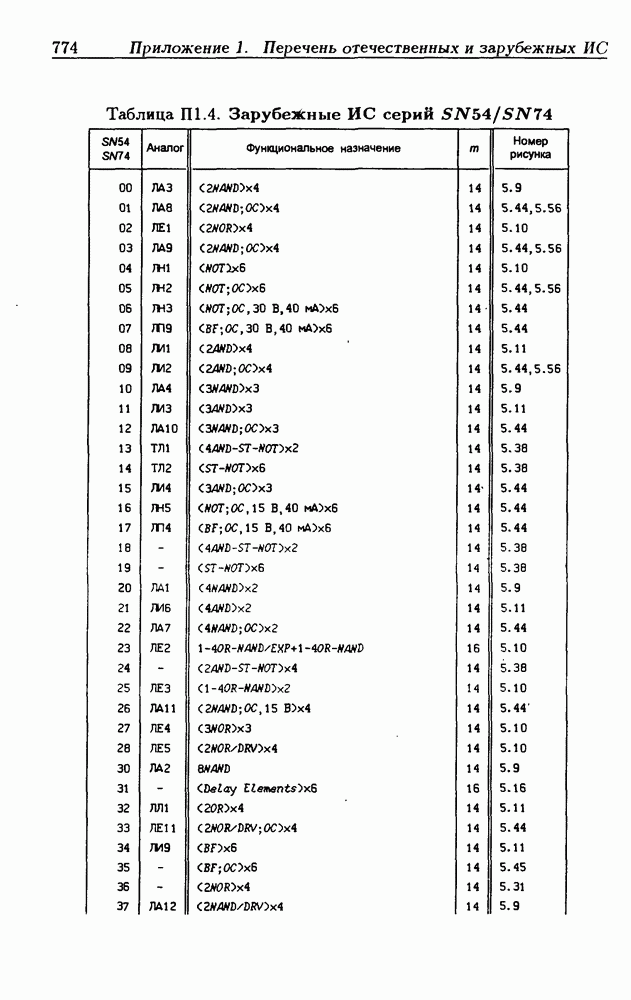
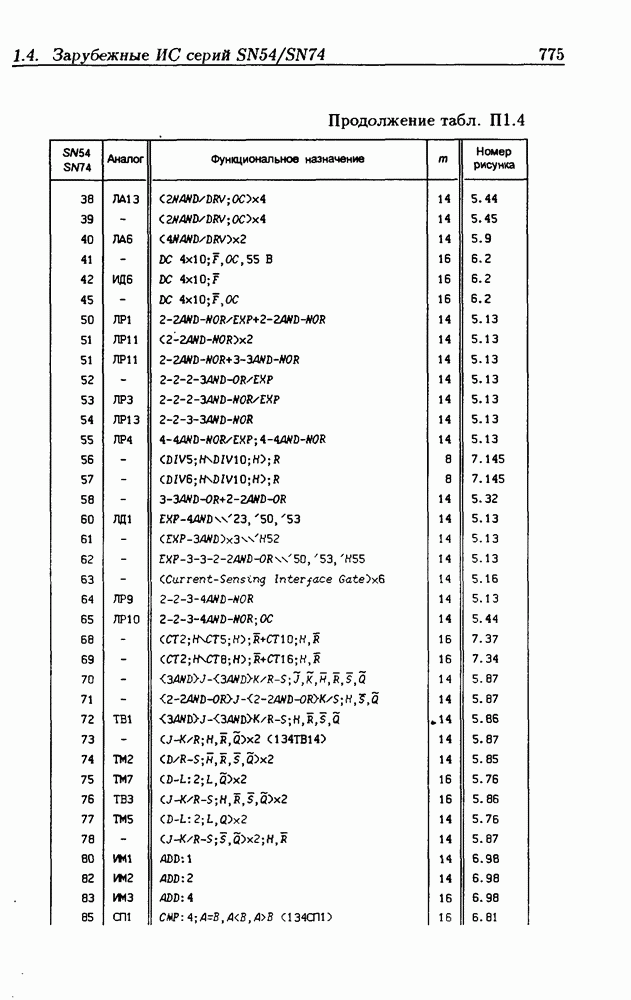
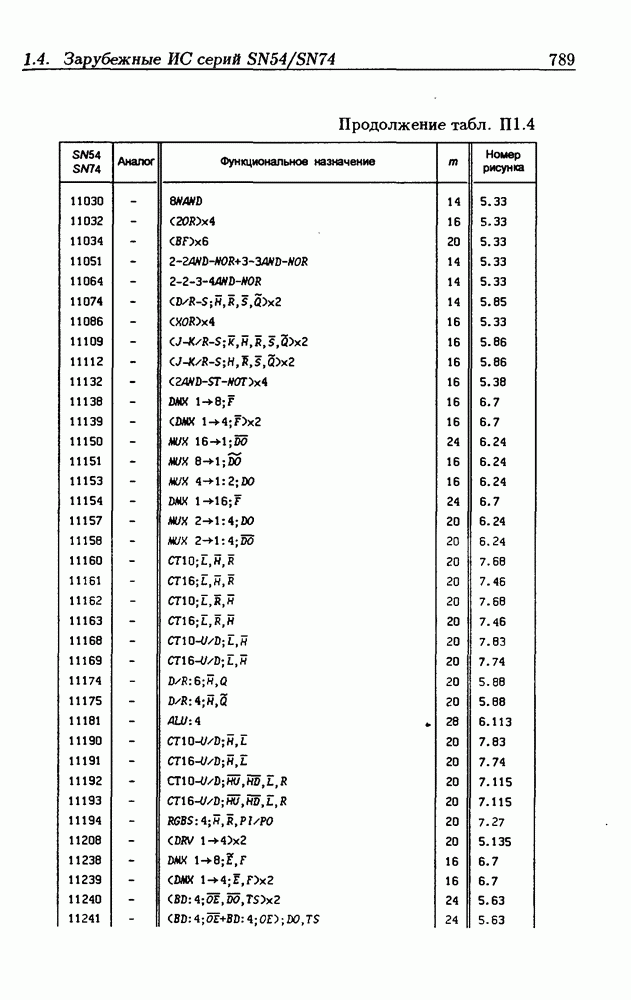
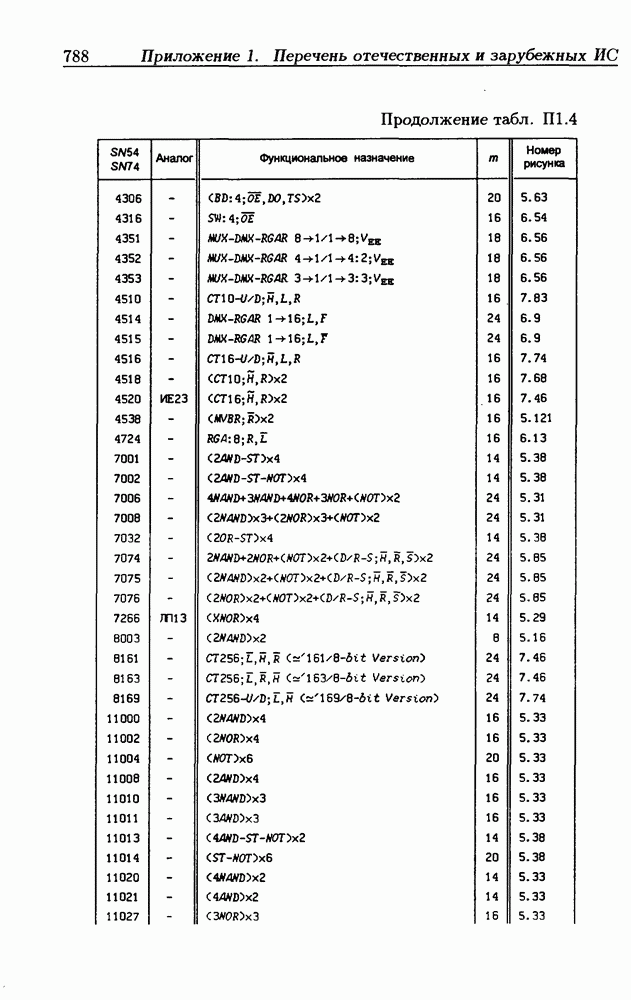
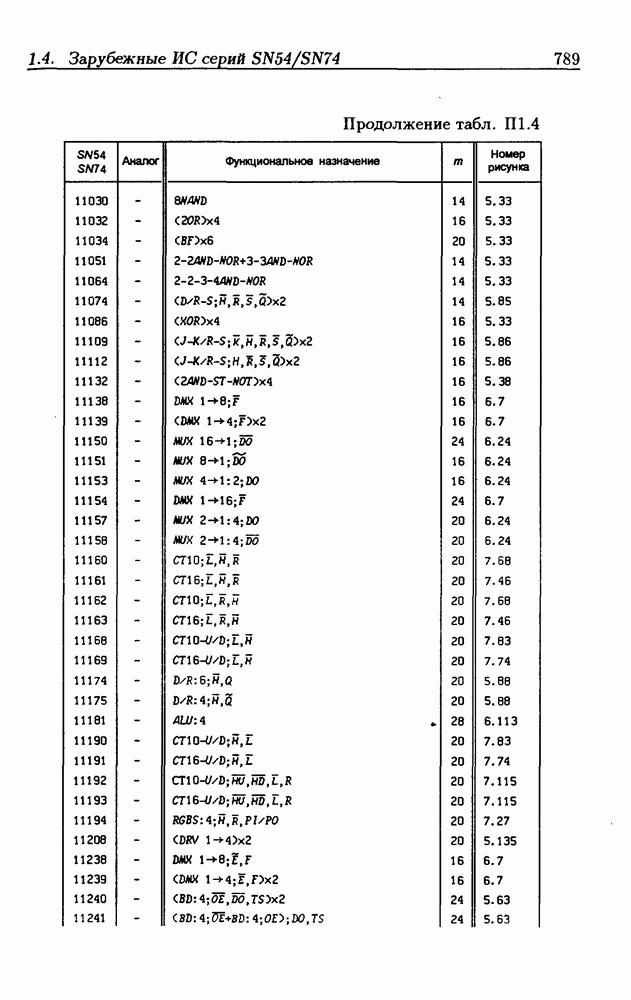
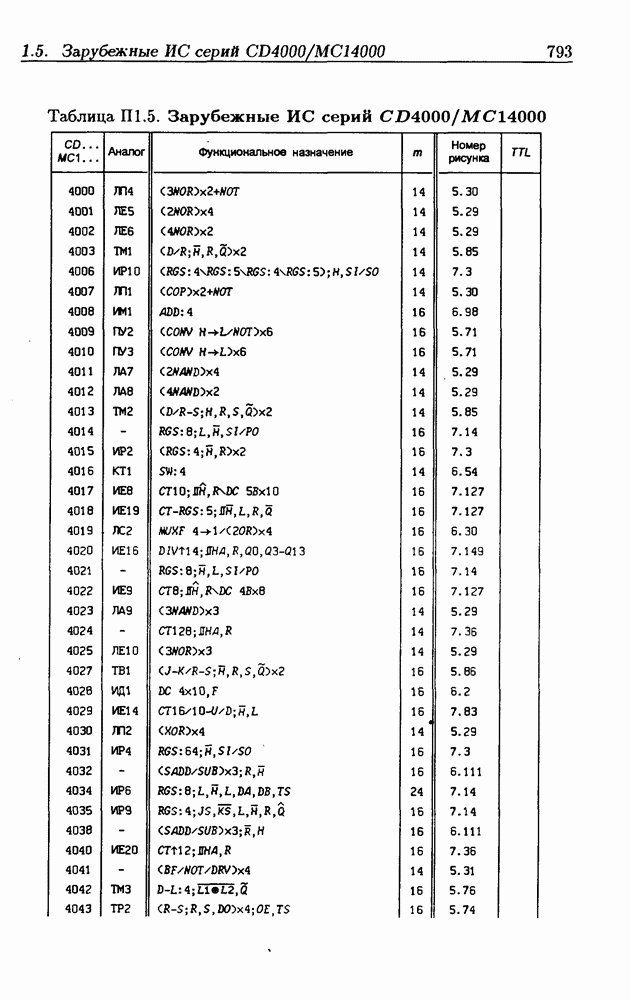
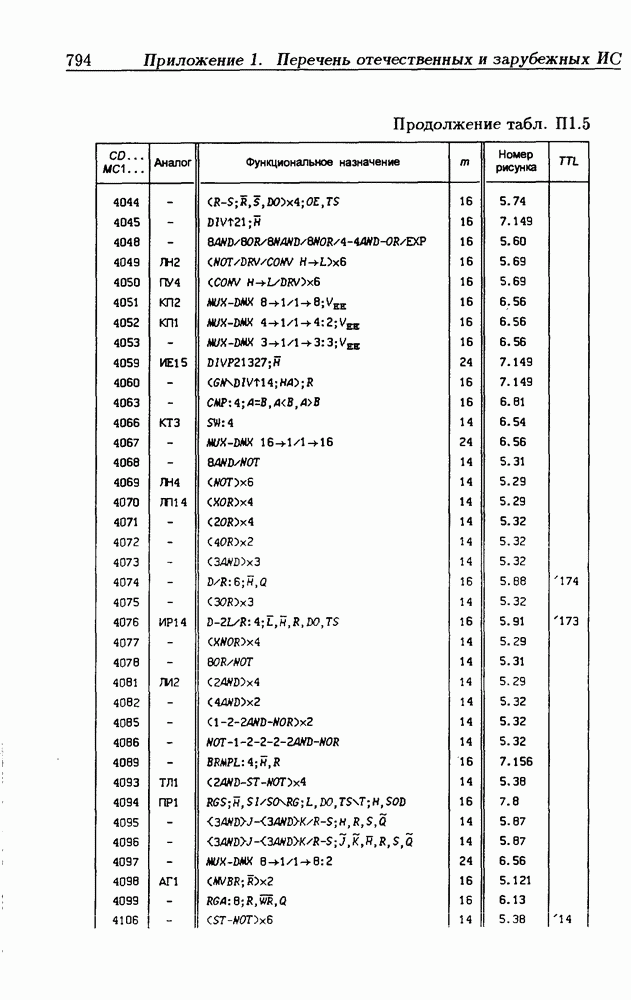
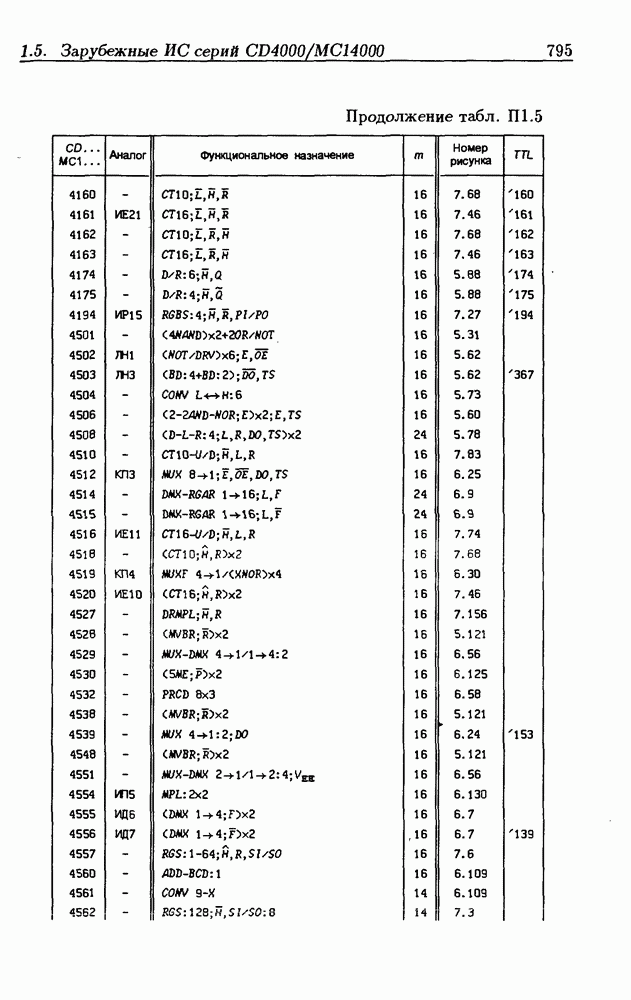
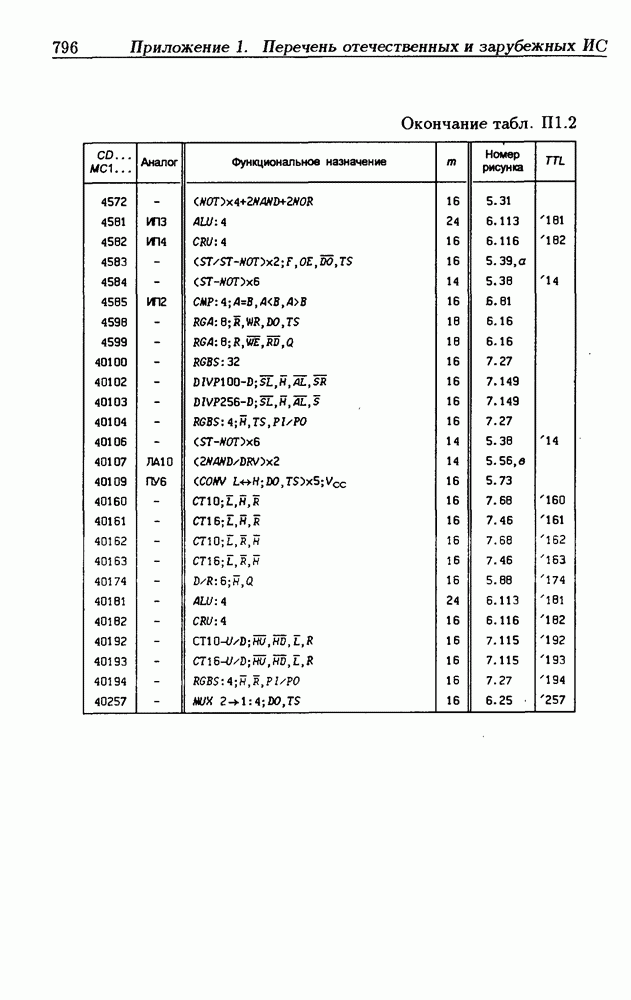
- Приложение 1. Перечень отечественных и зарубежных ИС
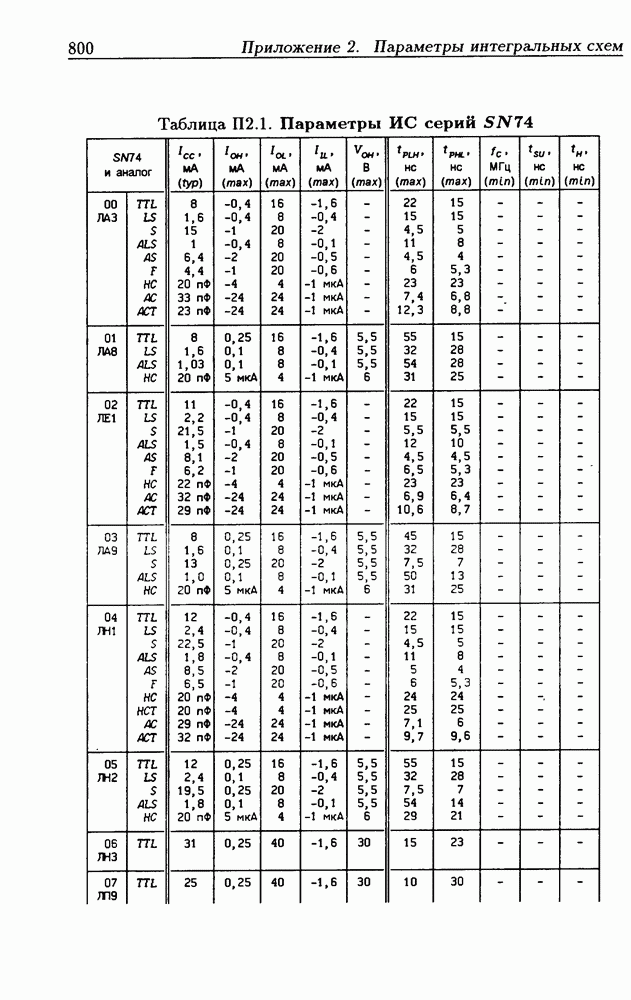
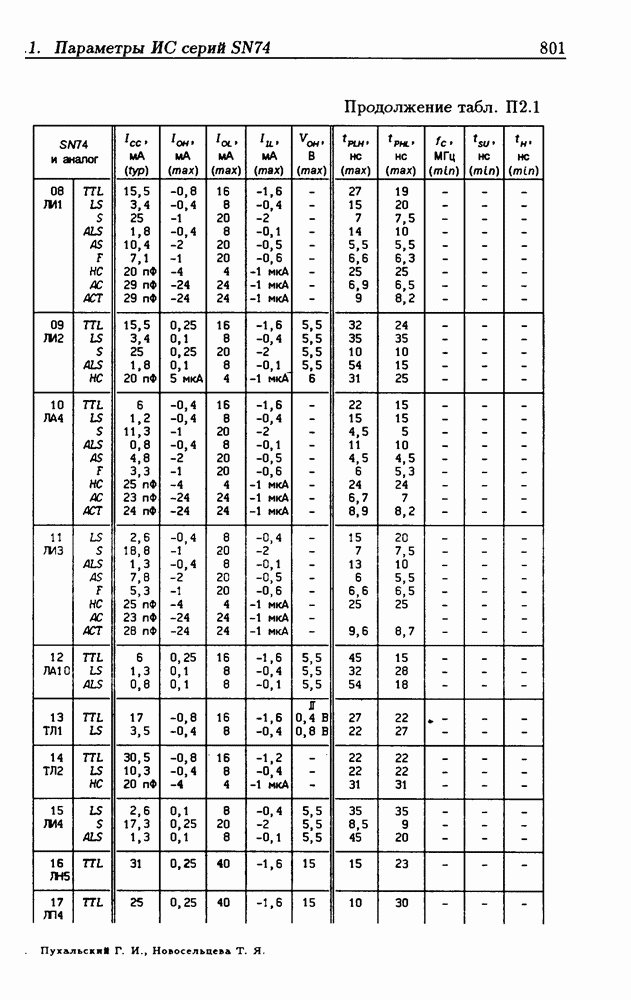
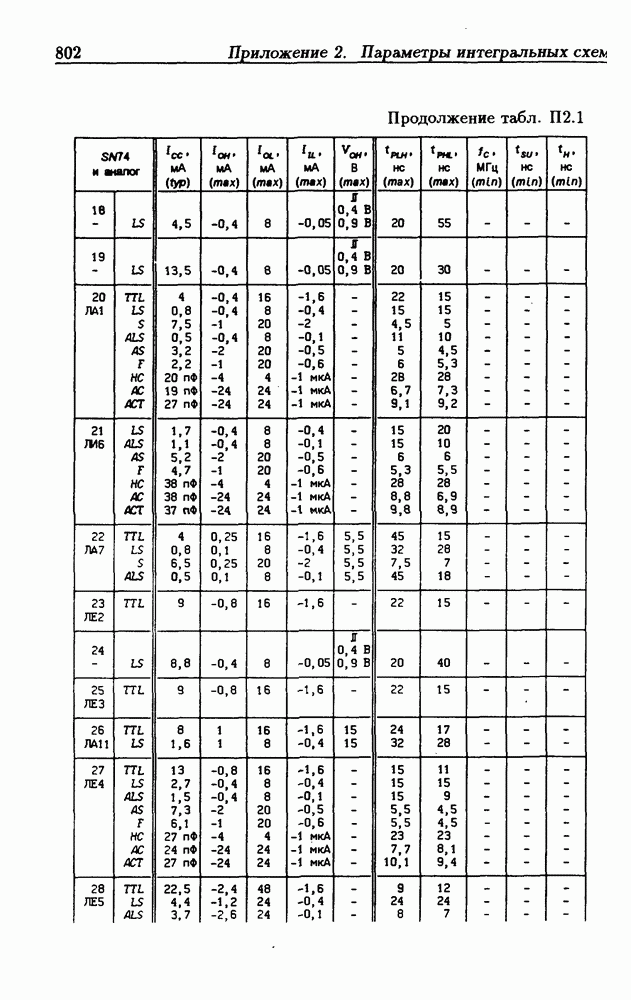
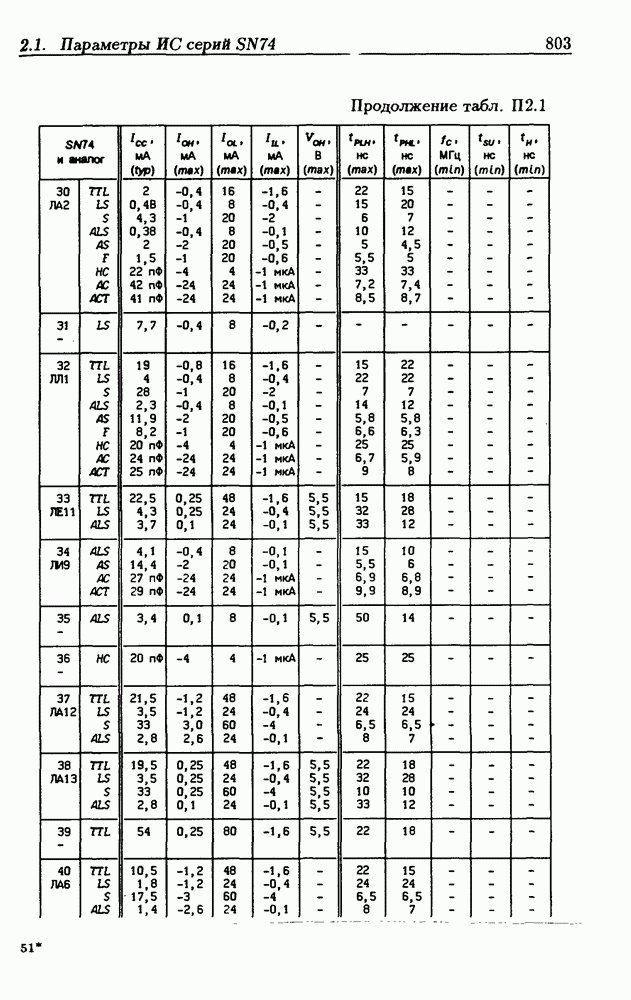
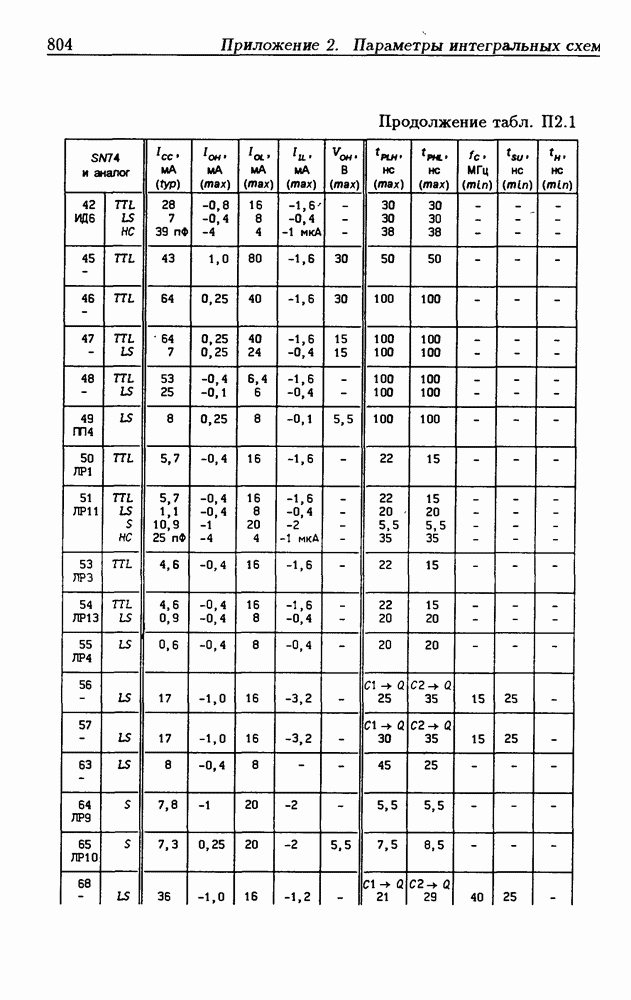
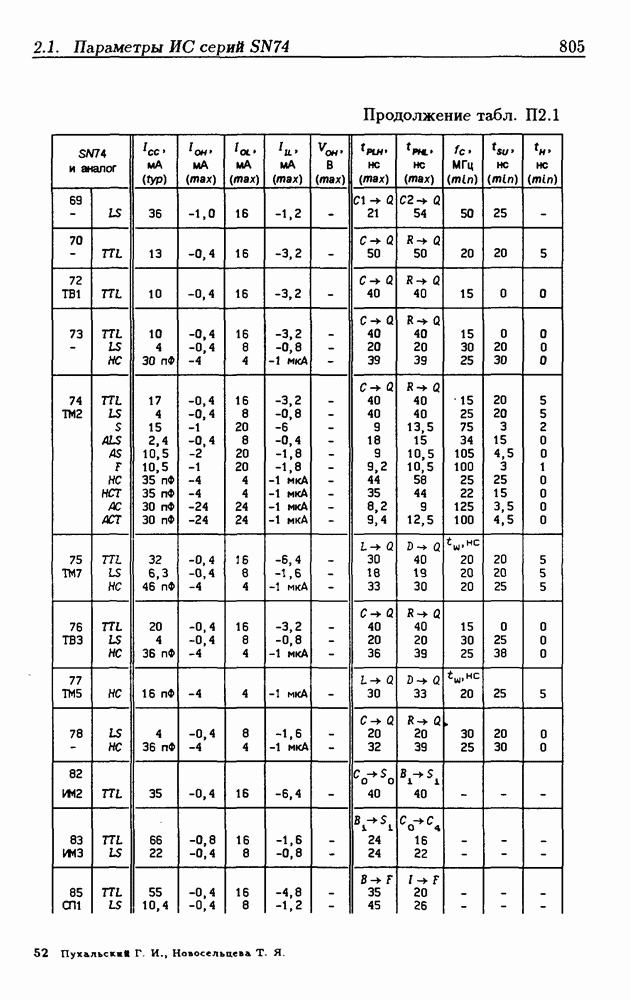
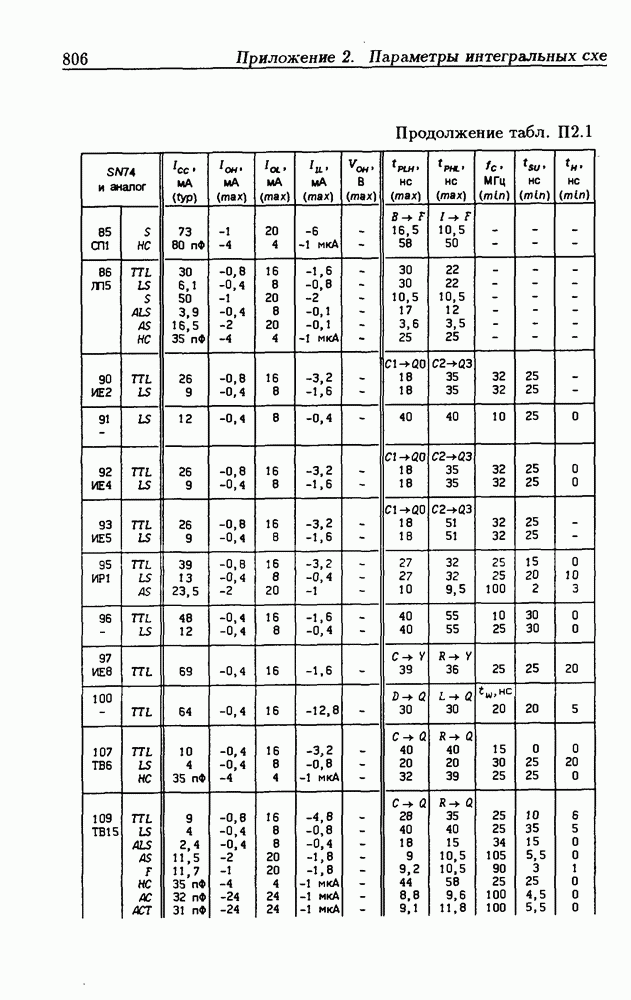
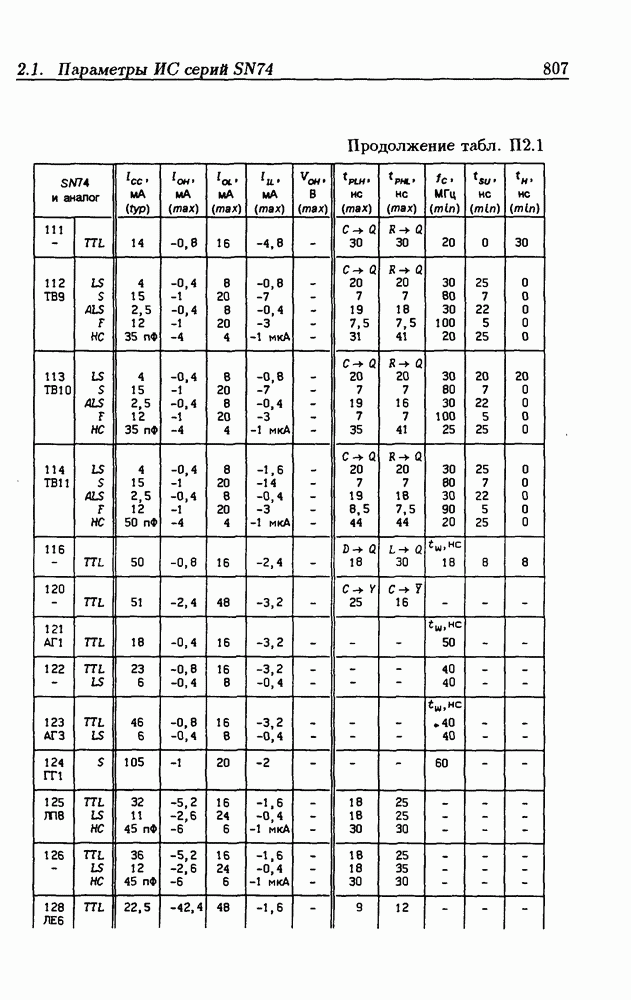
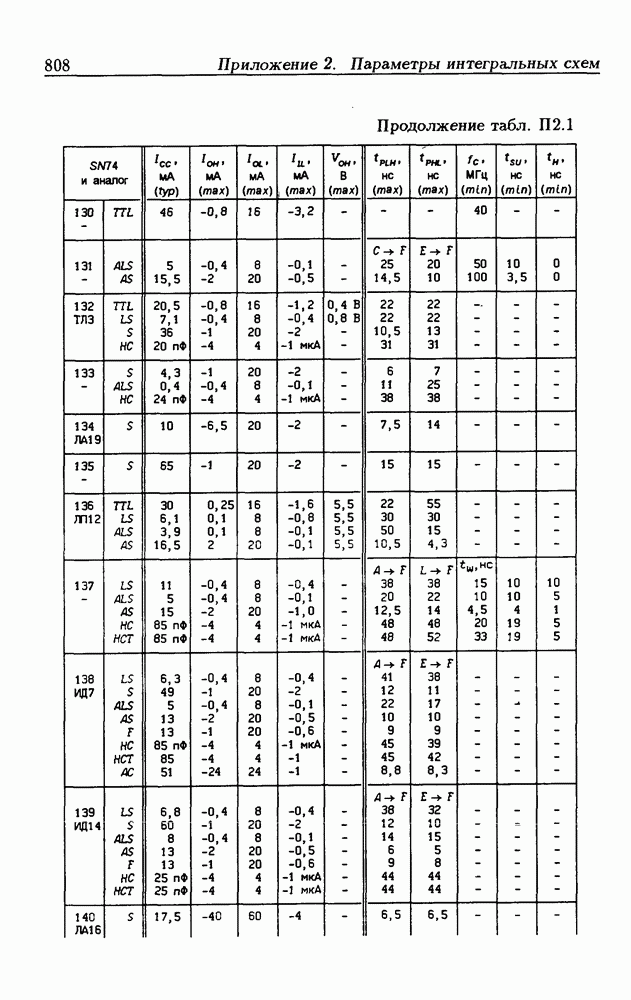
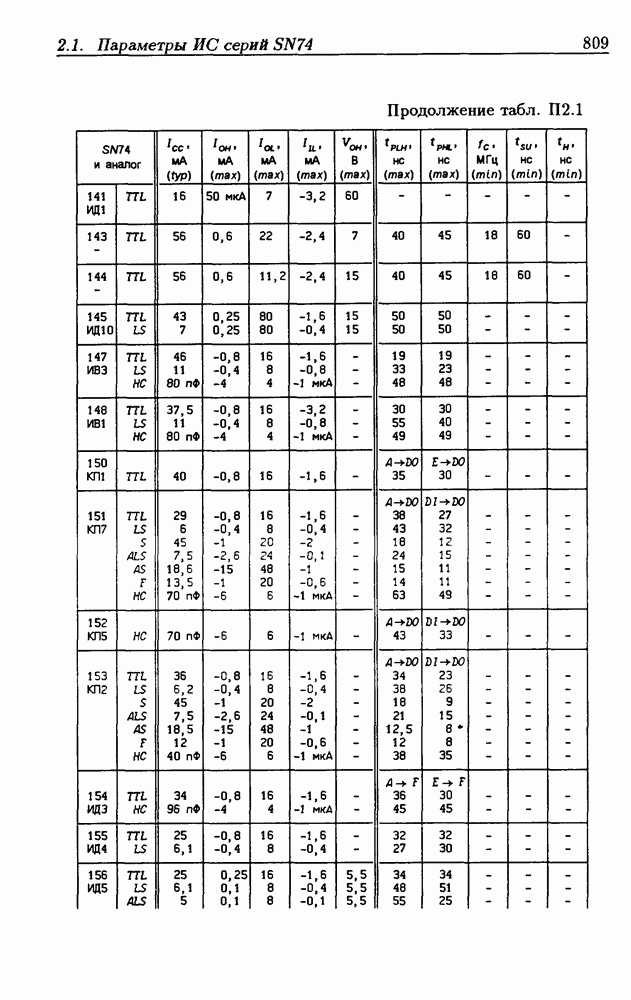
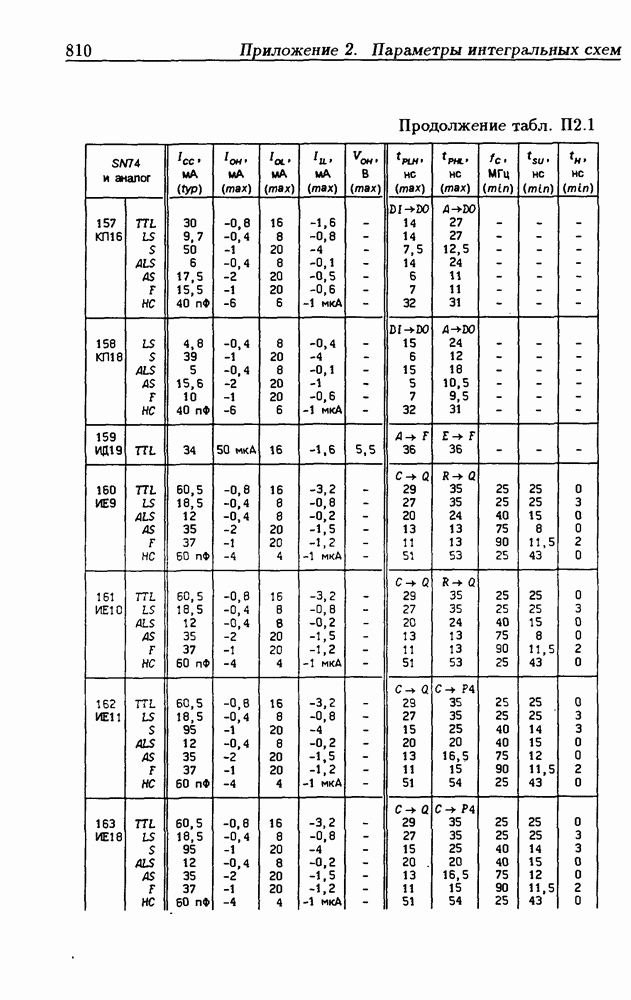
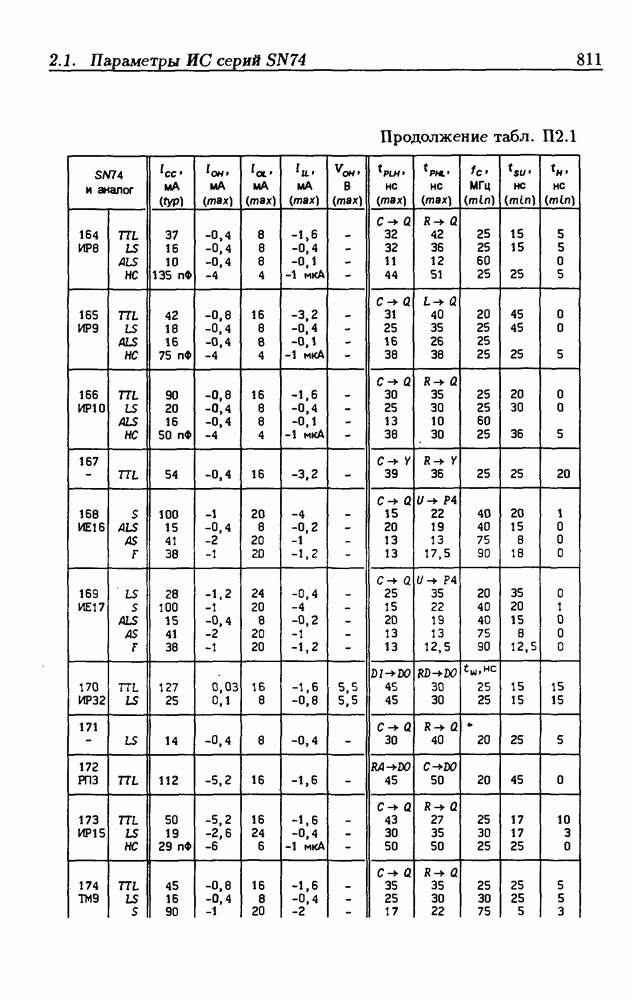
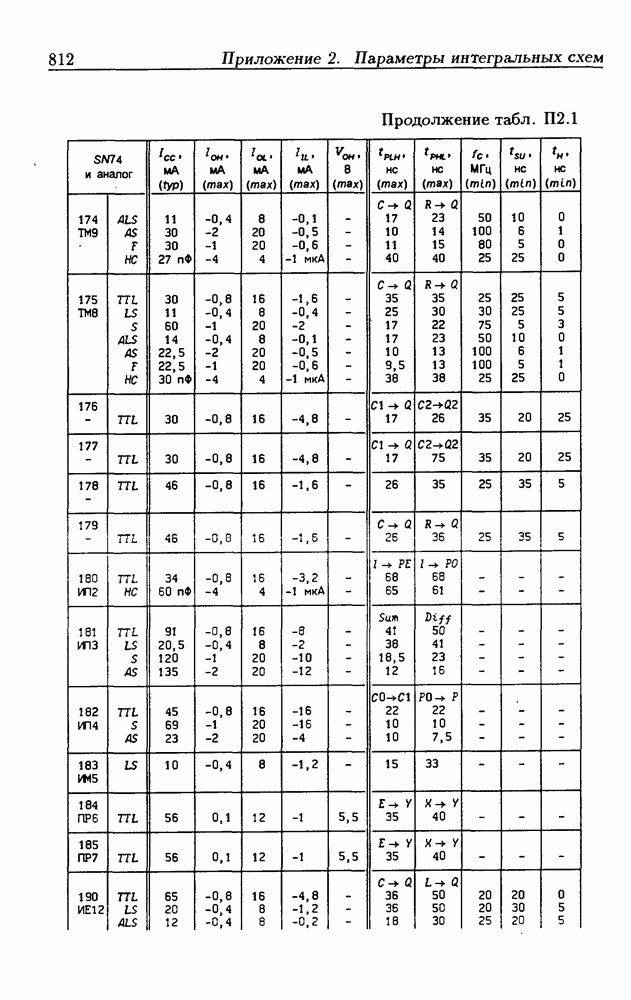
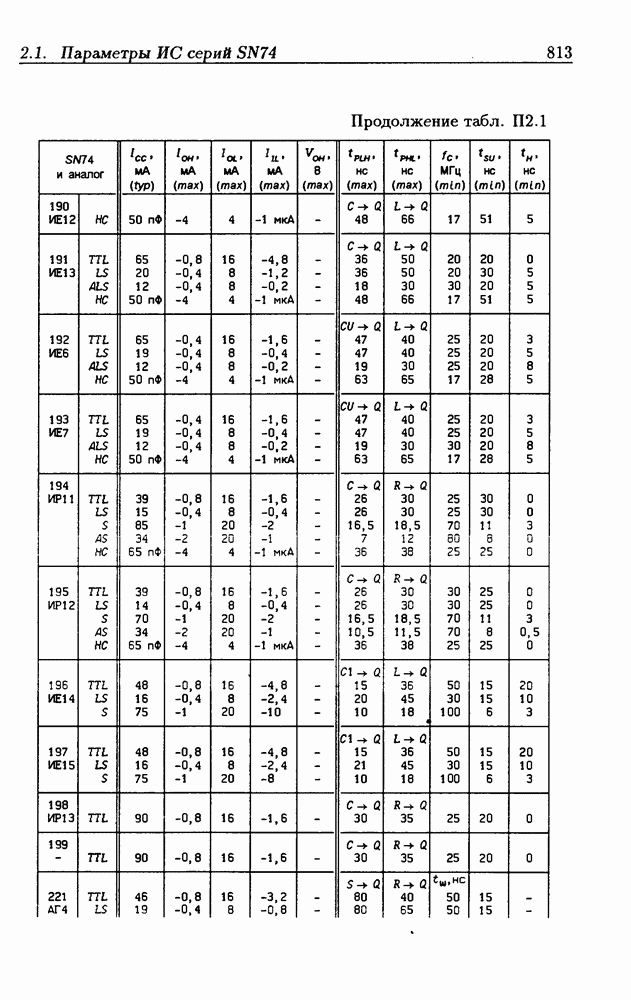
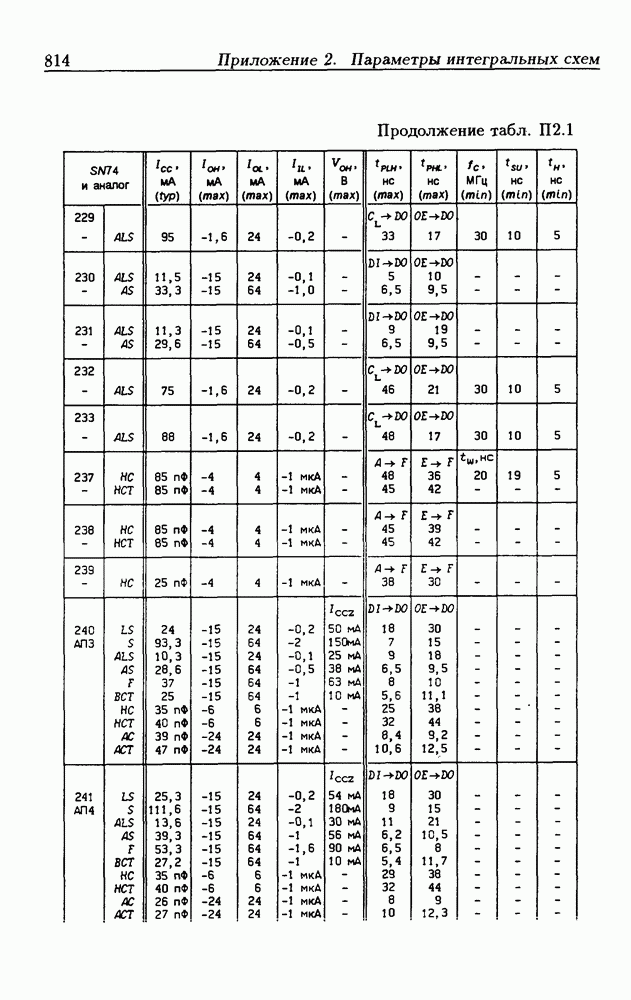
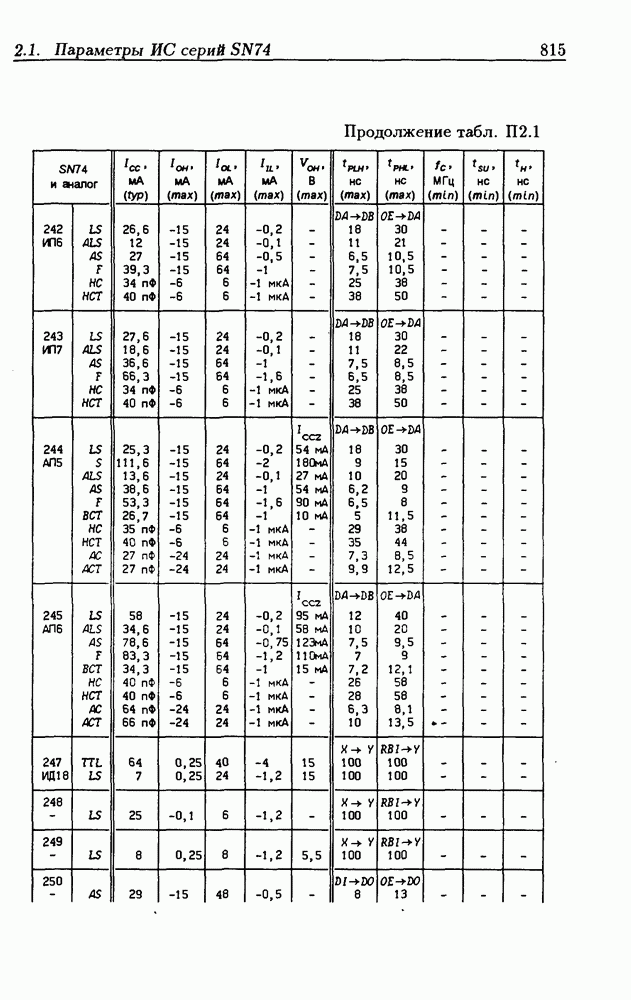
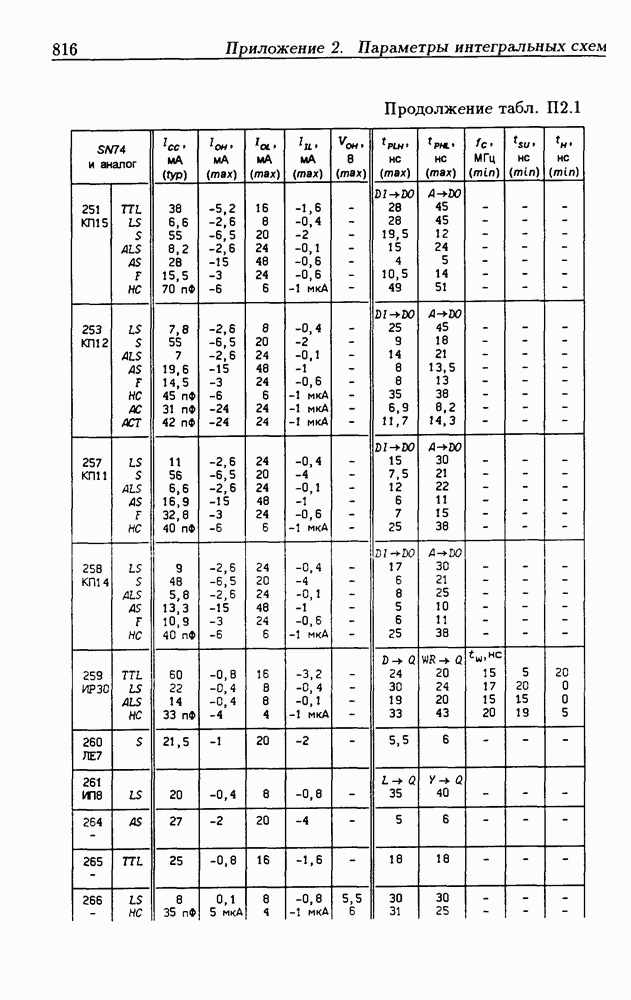
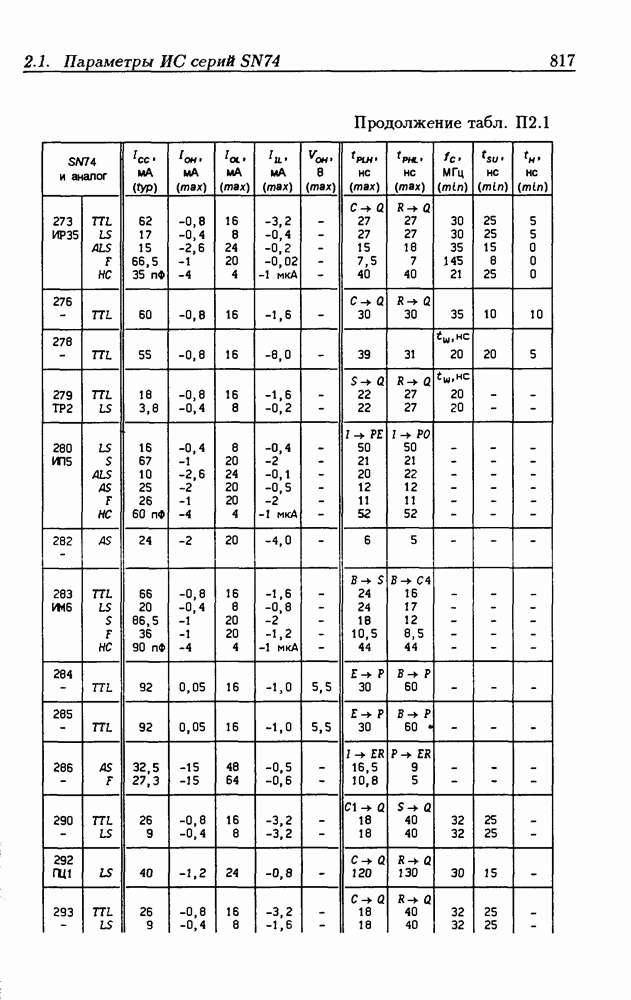
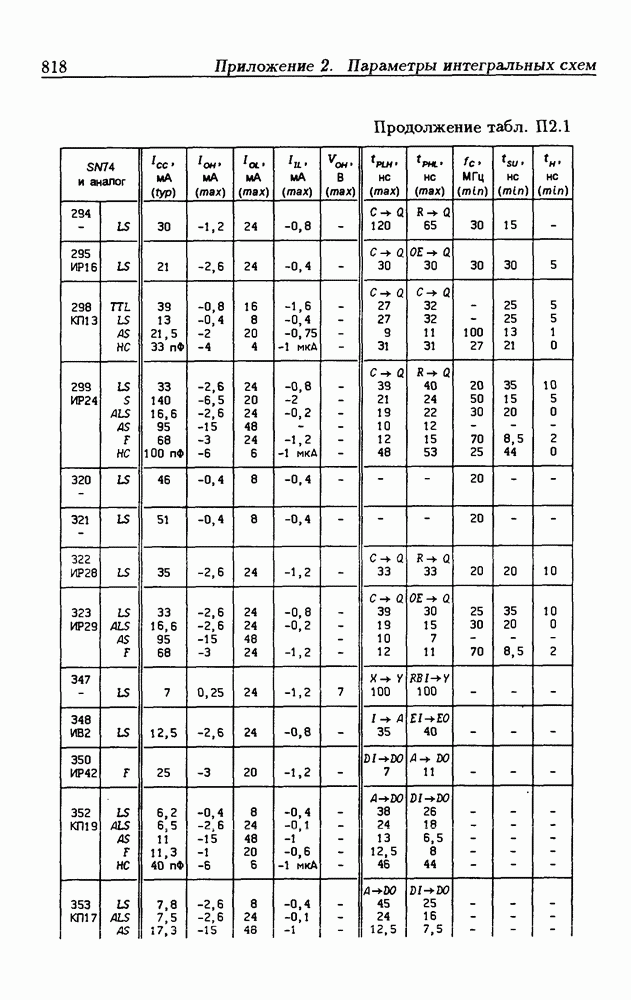
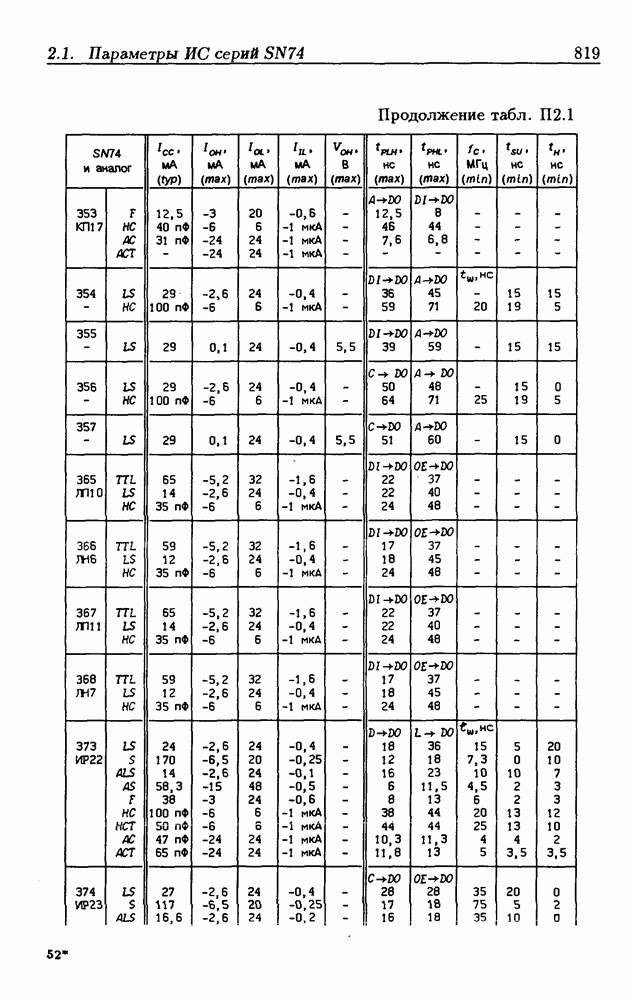
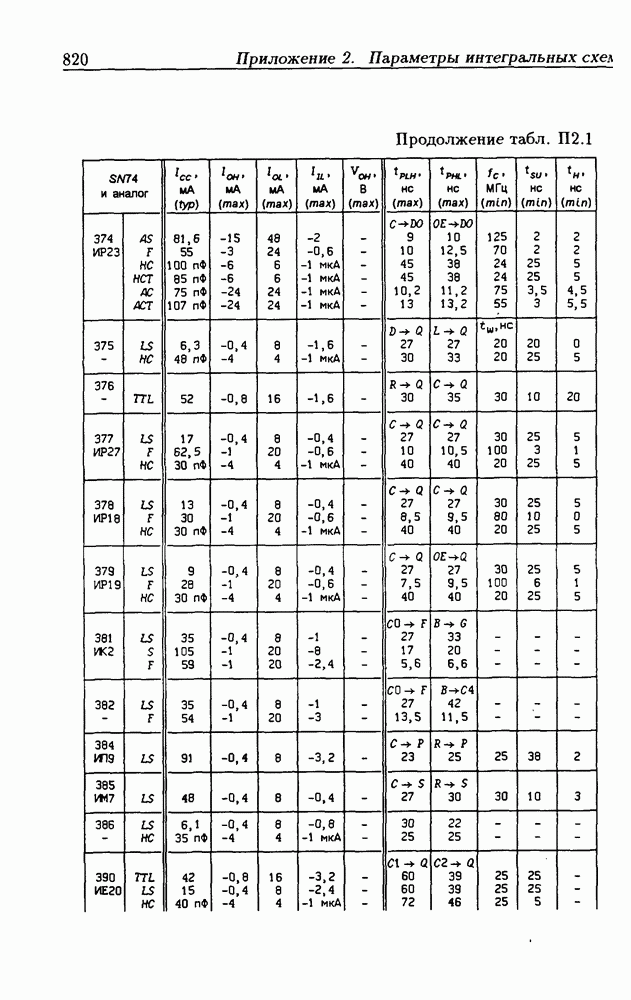
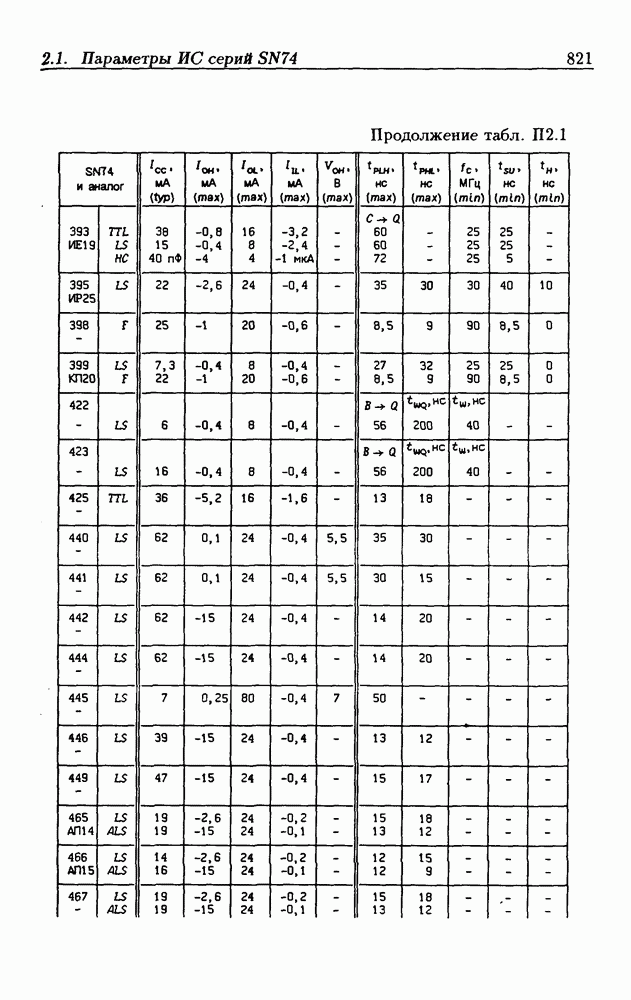
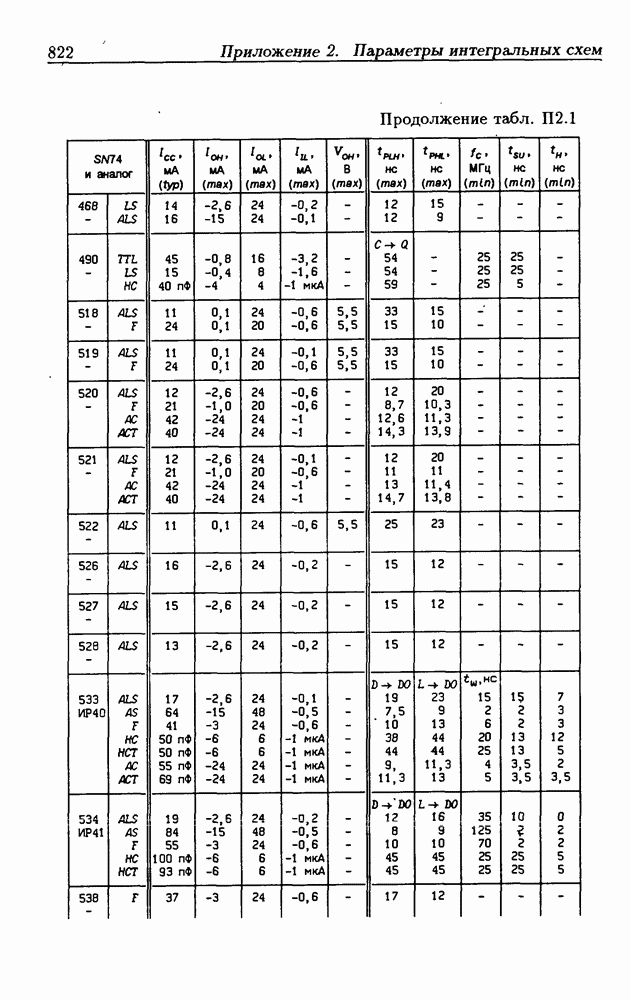
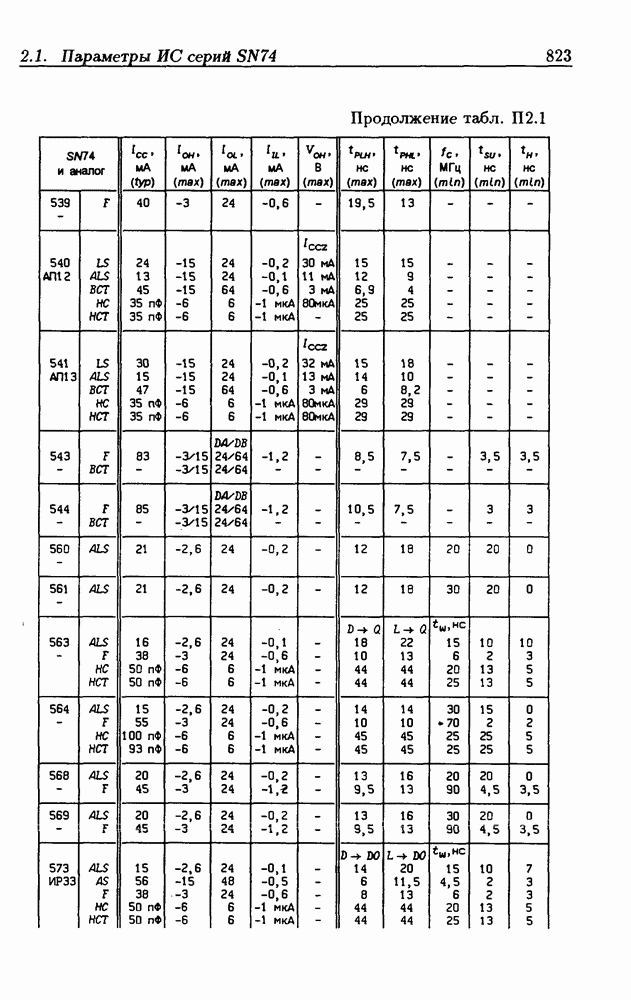
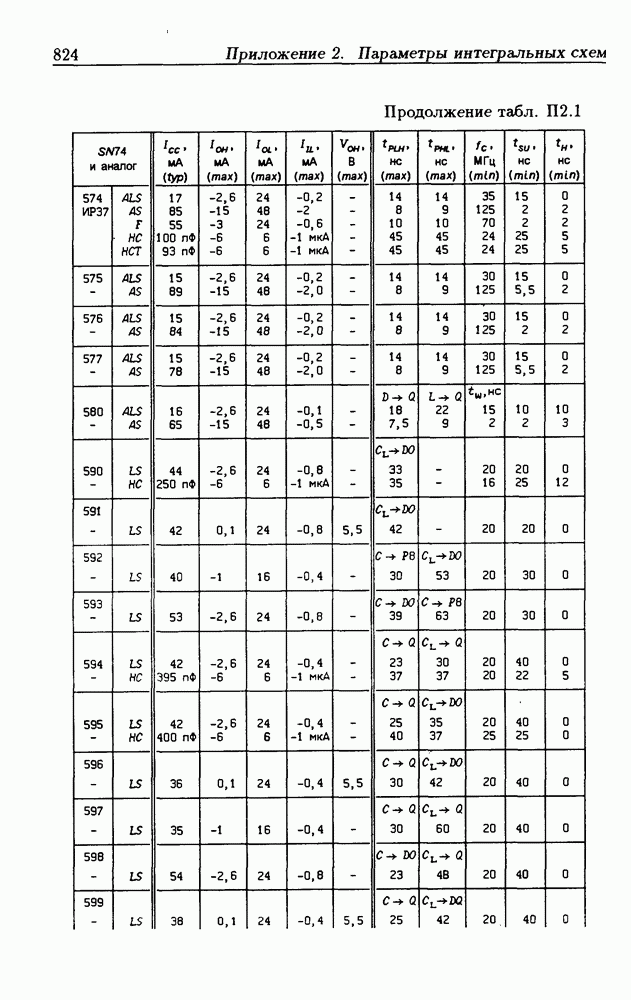
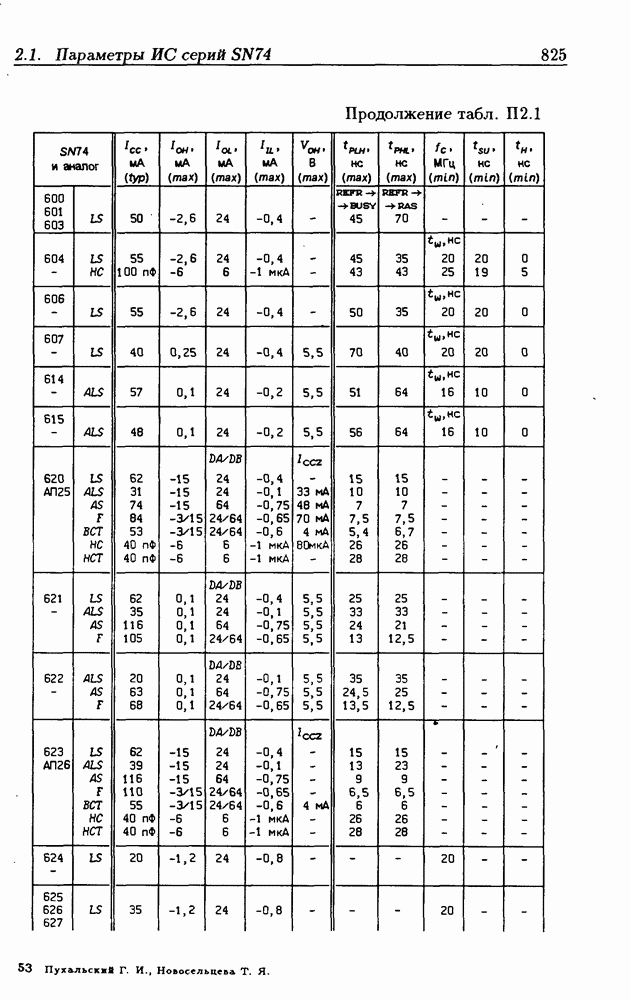
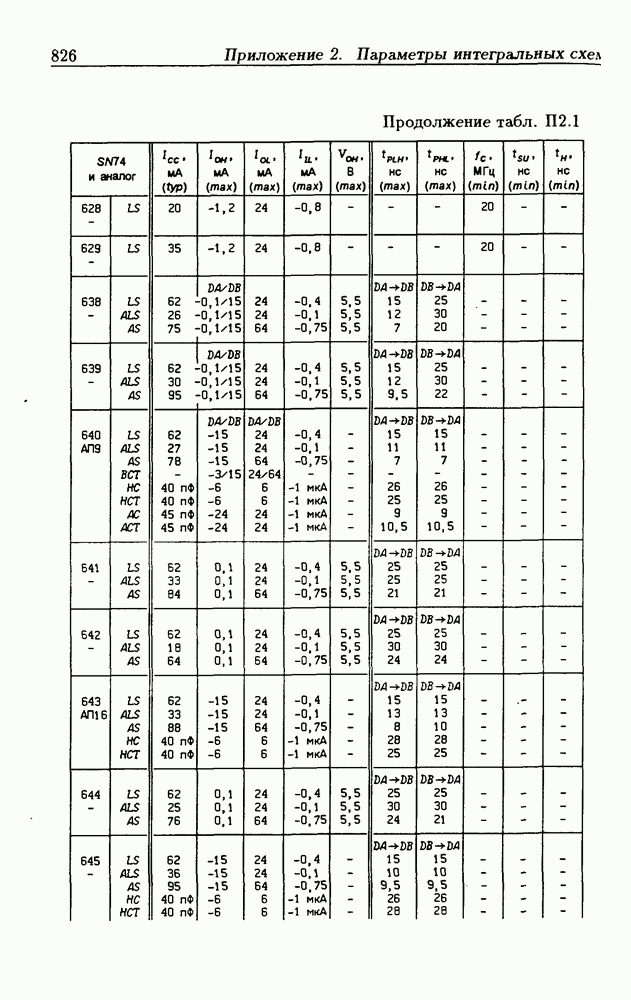
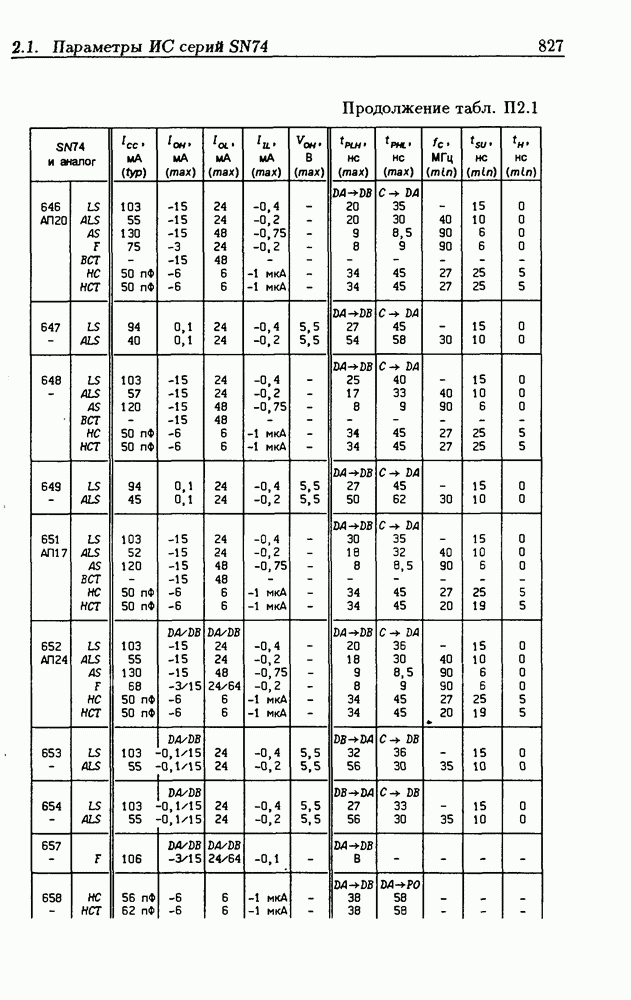
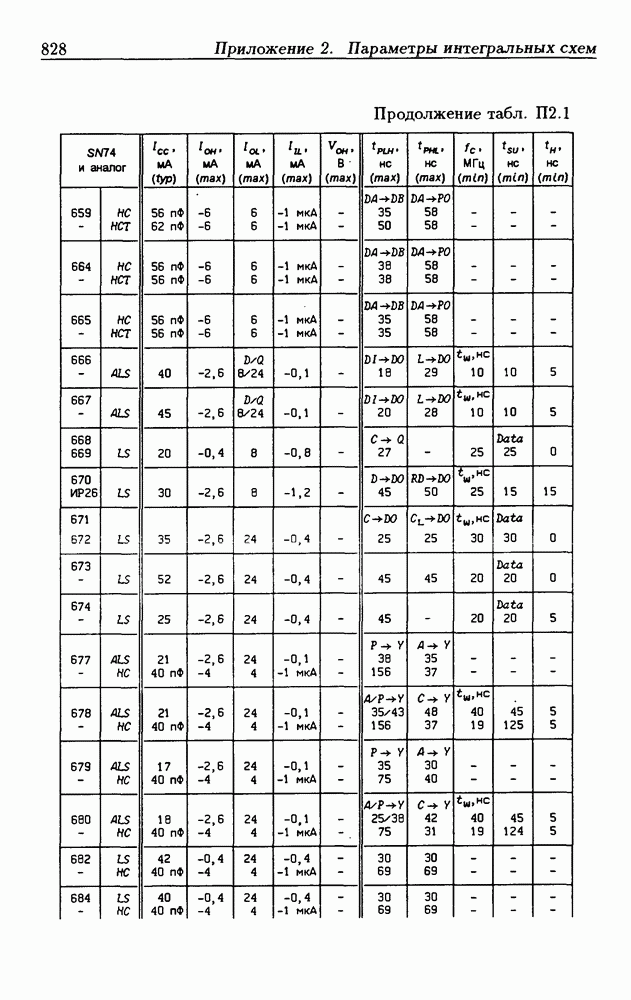
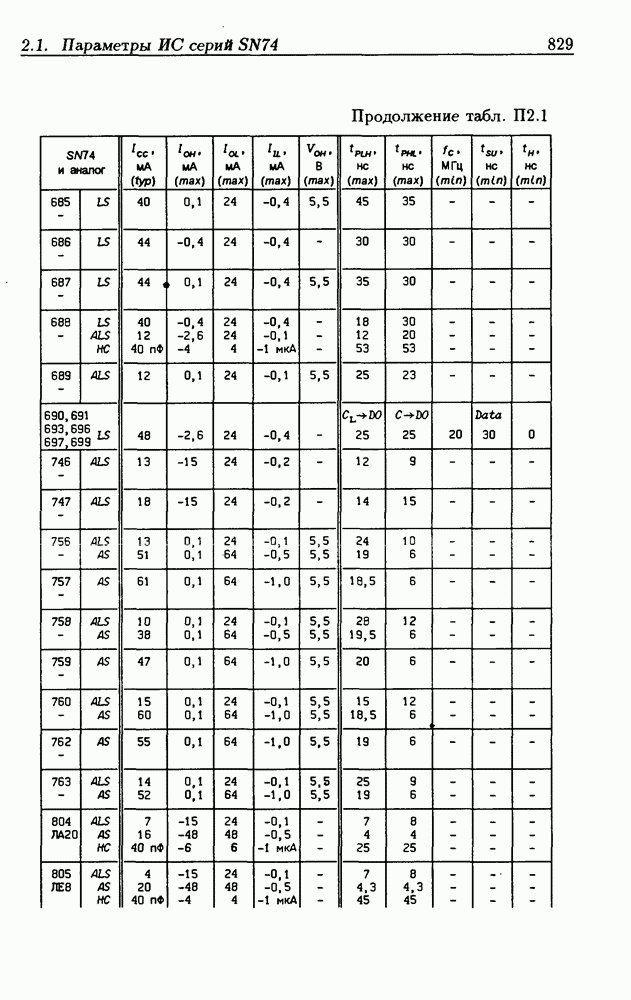
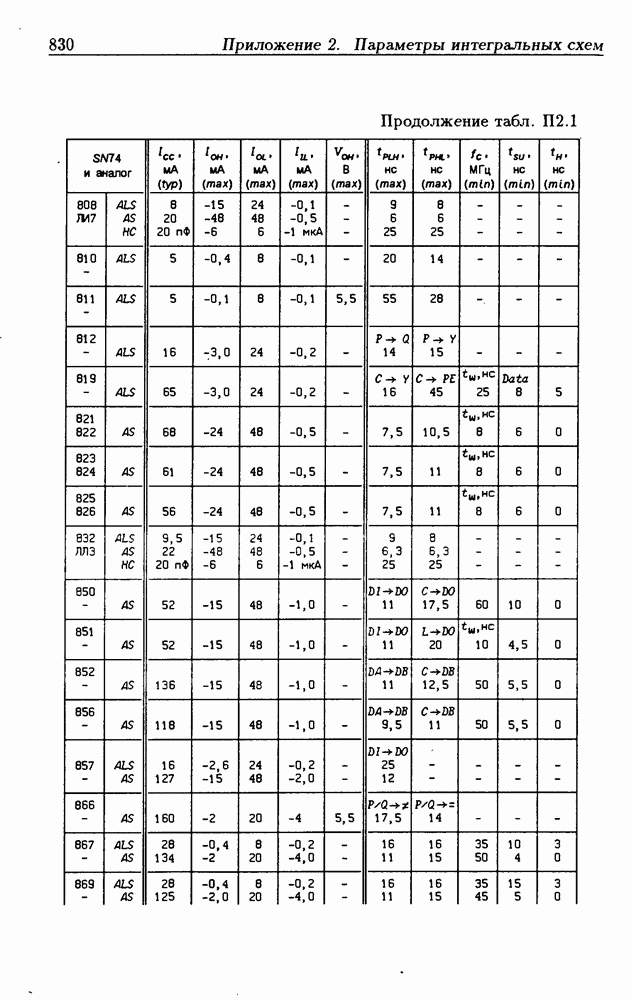
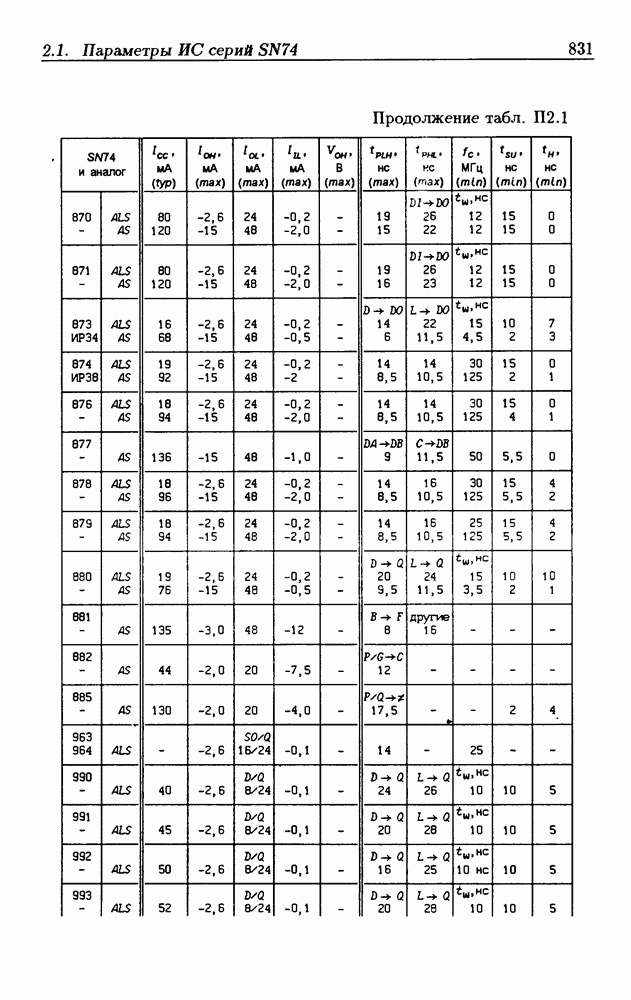
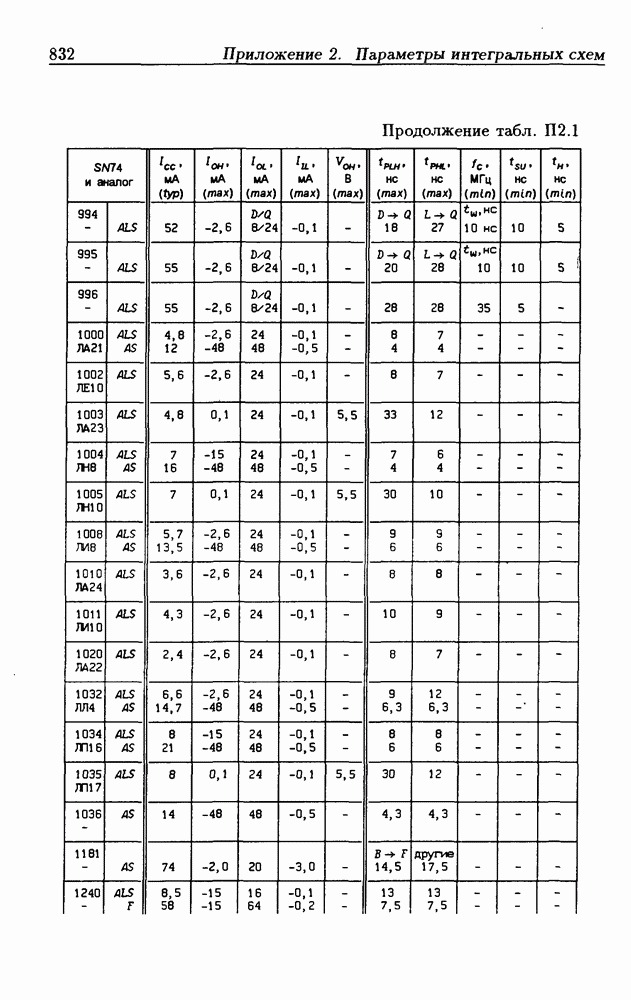
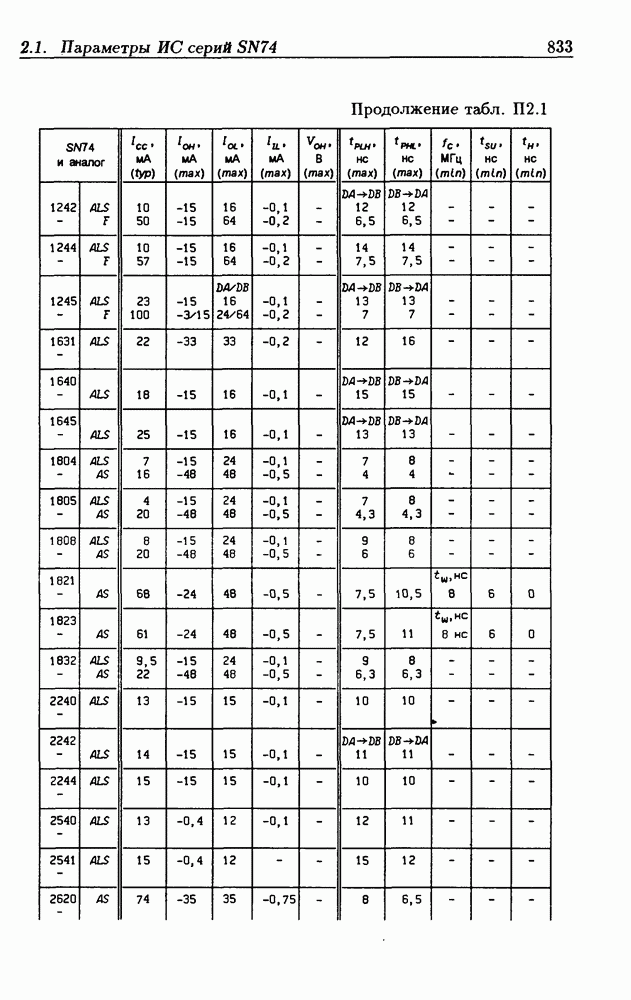
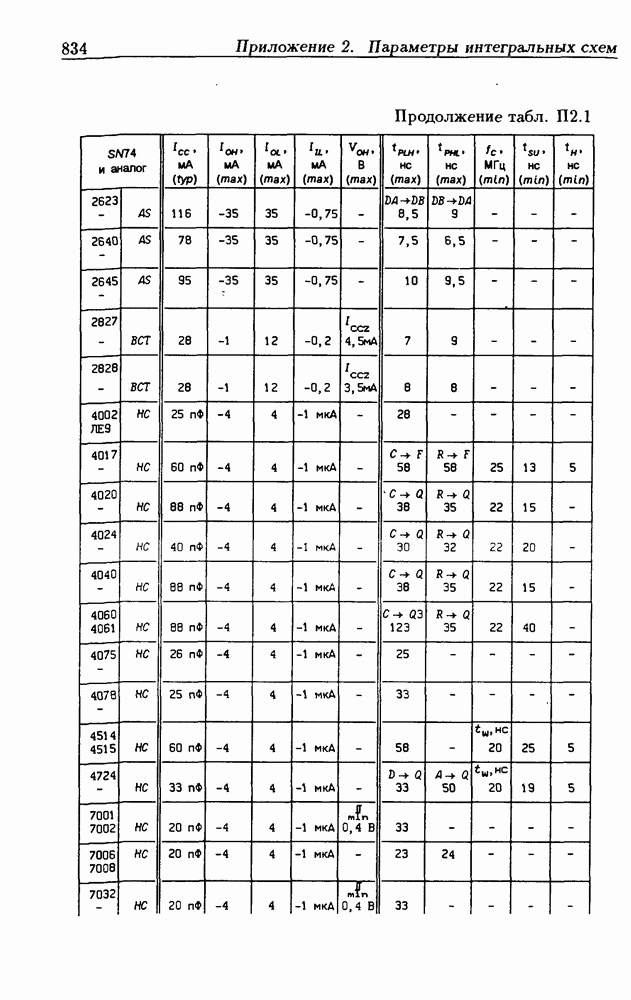
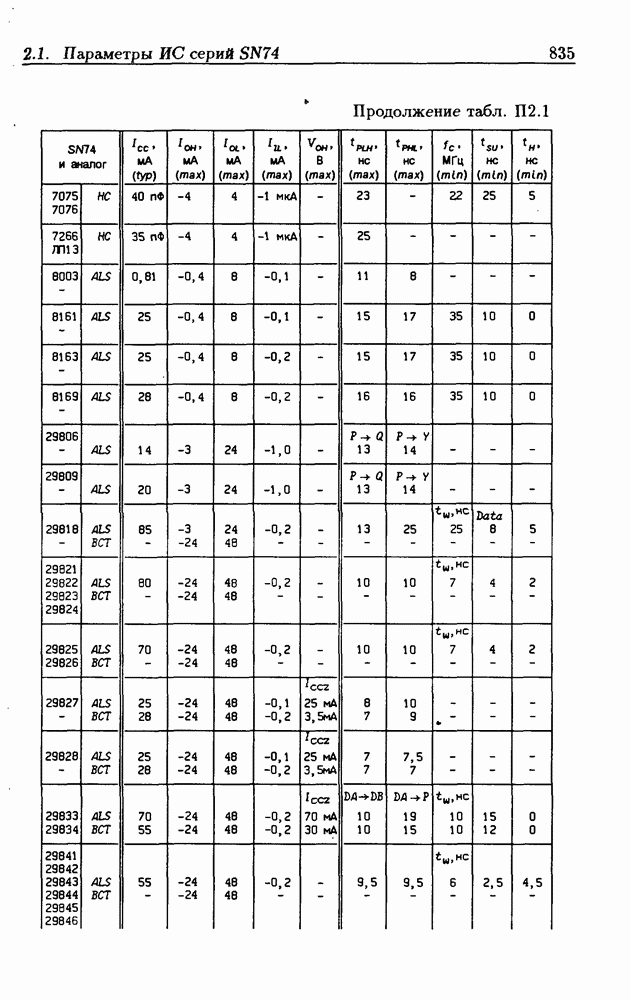
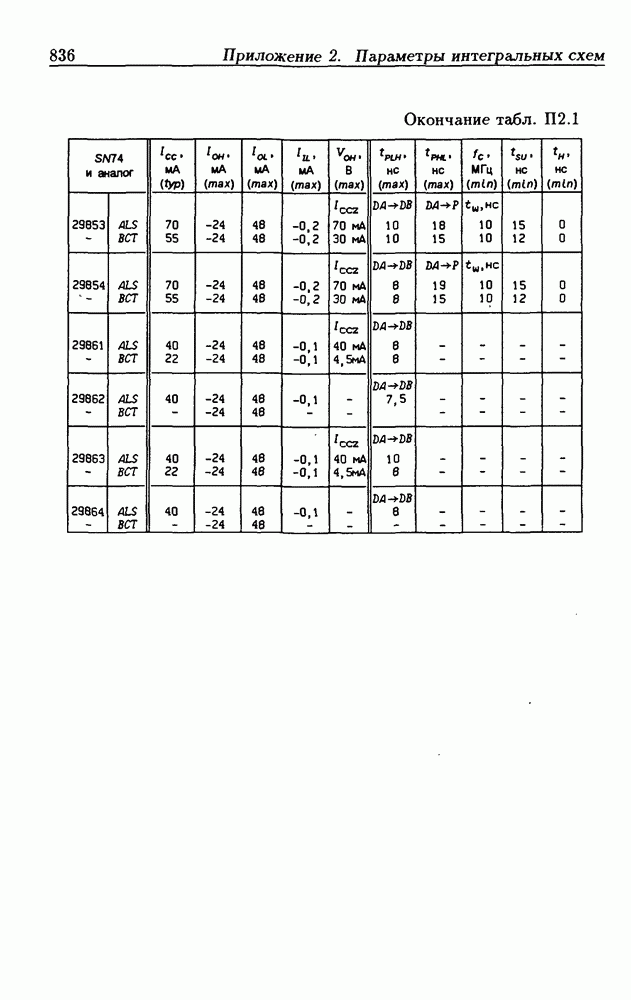
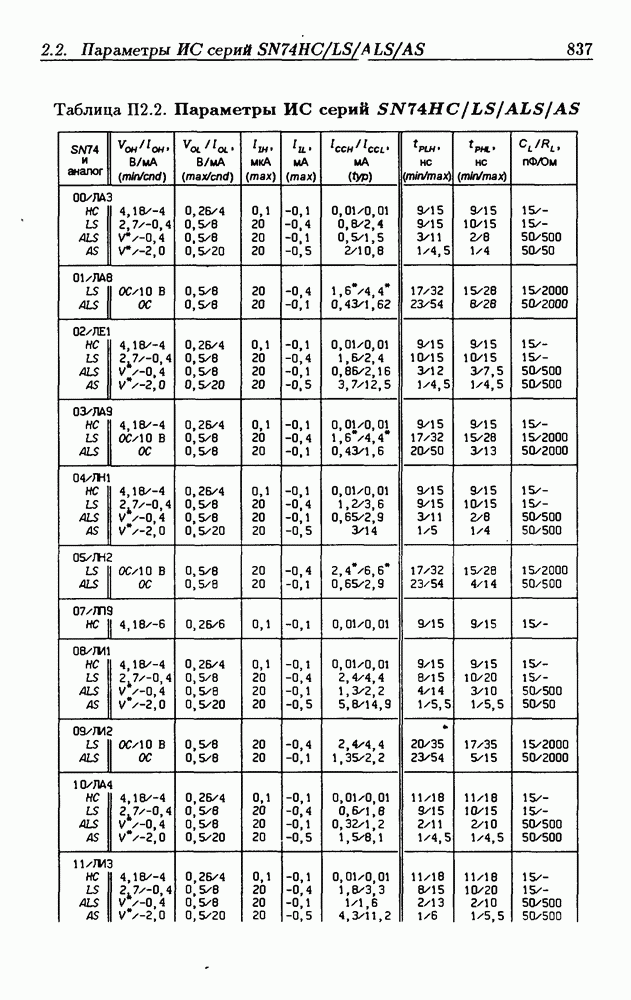
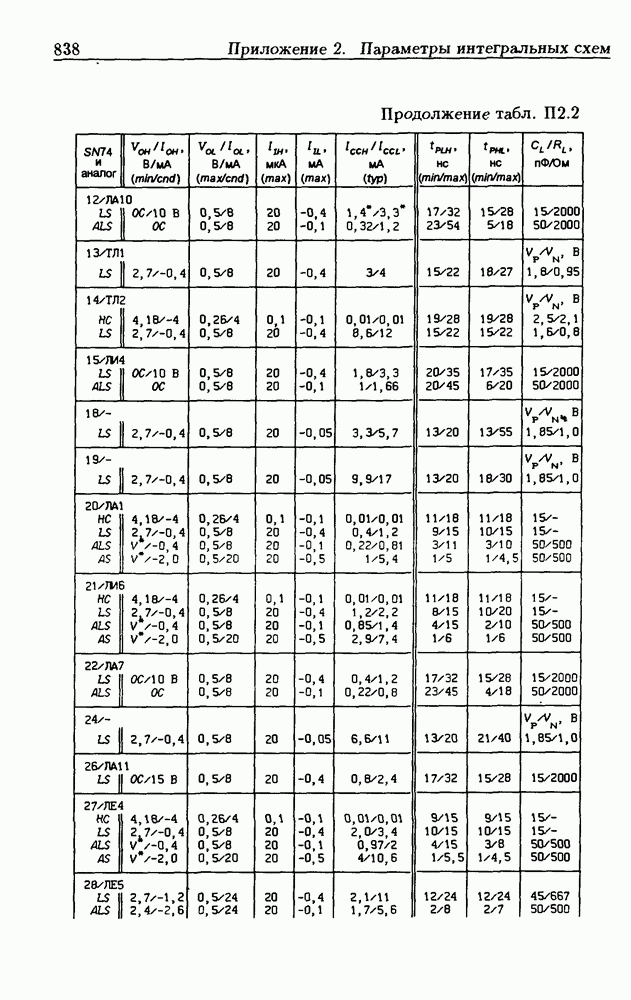
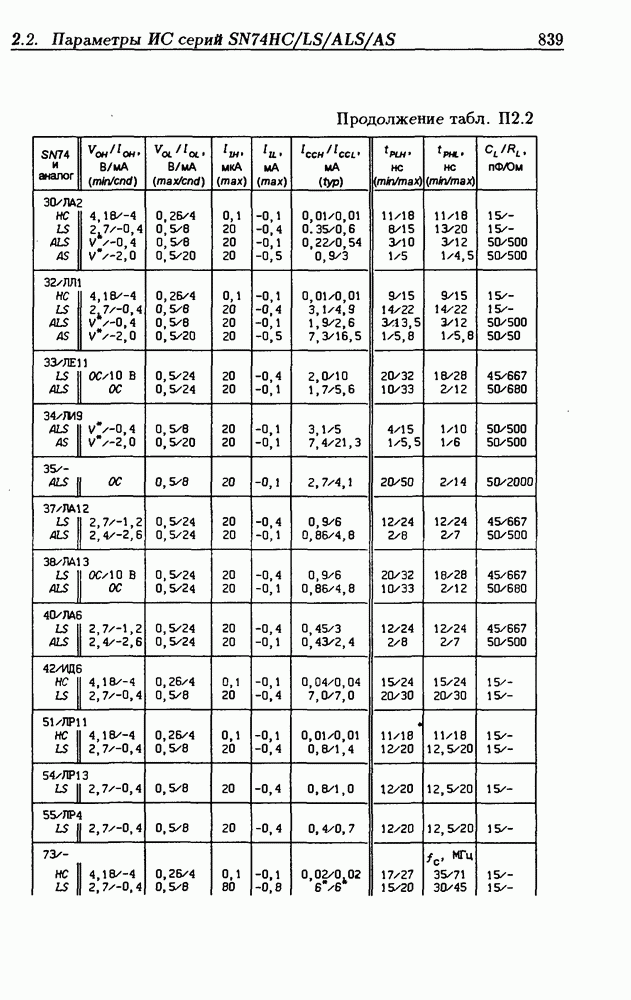
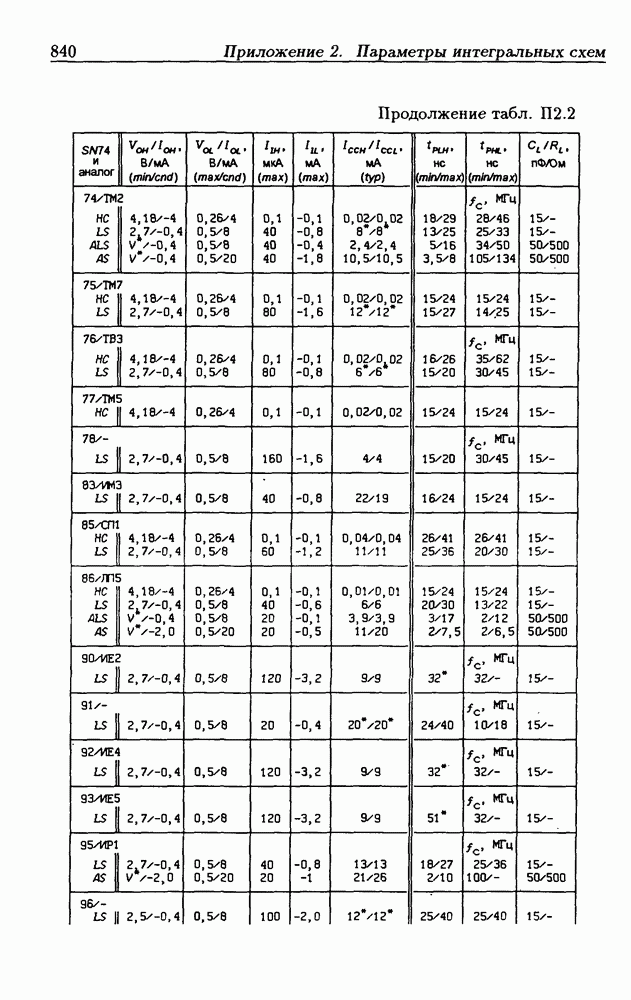
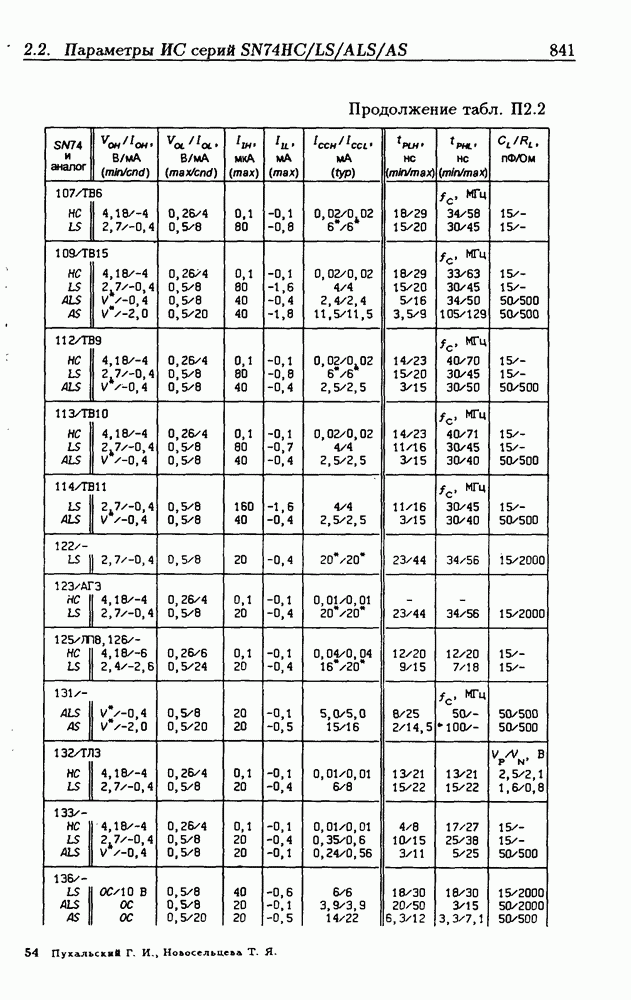
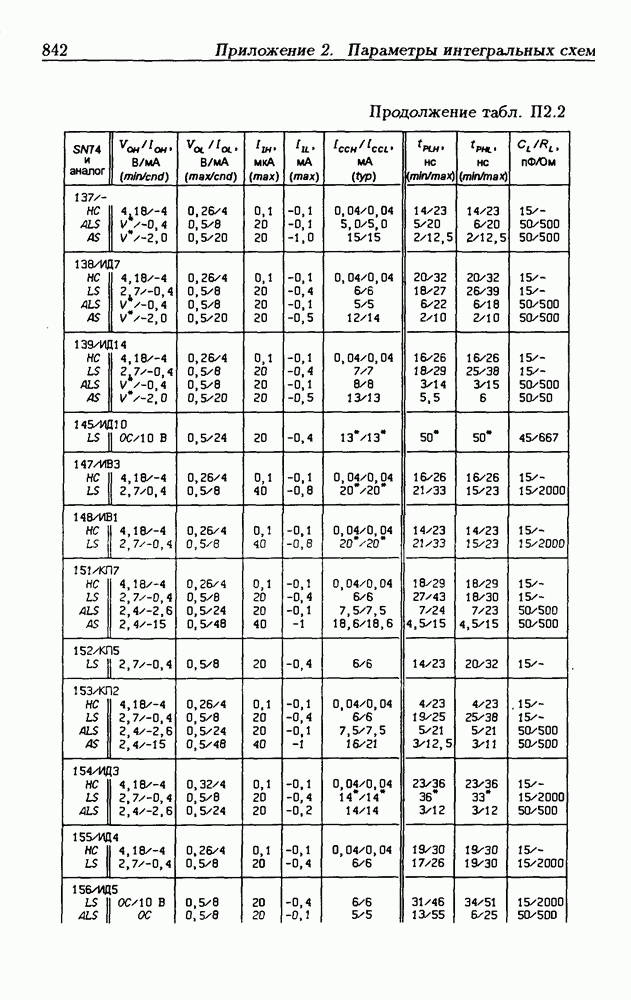
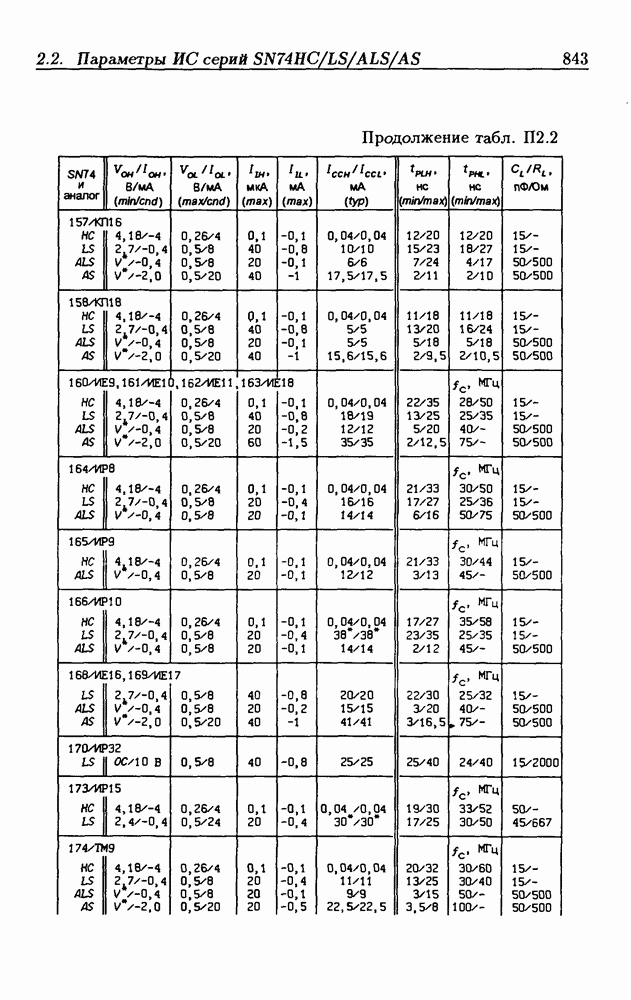
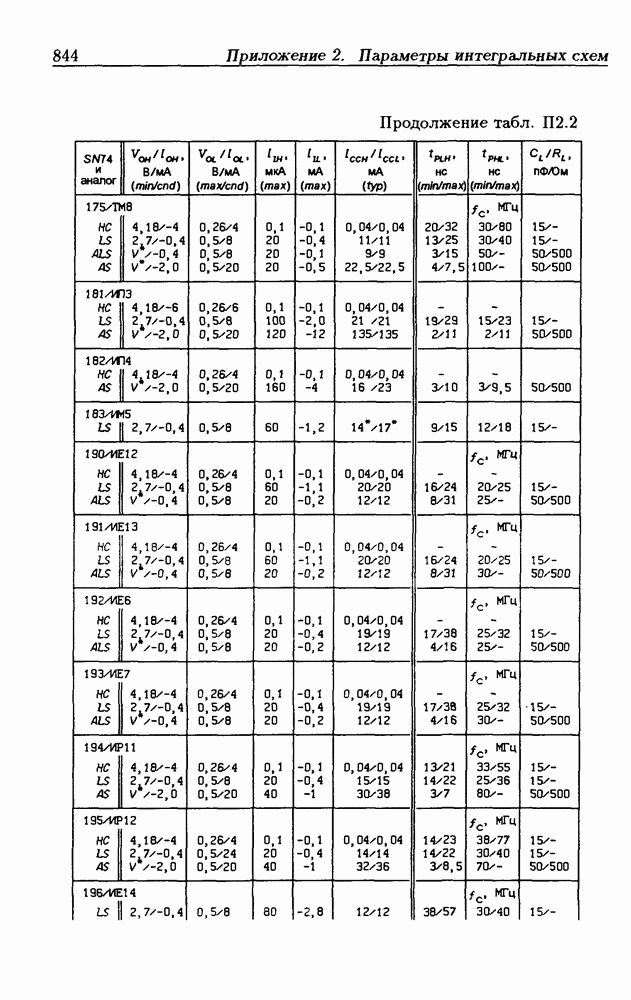
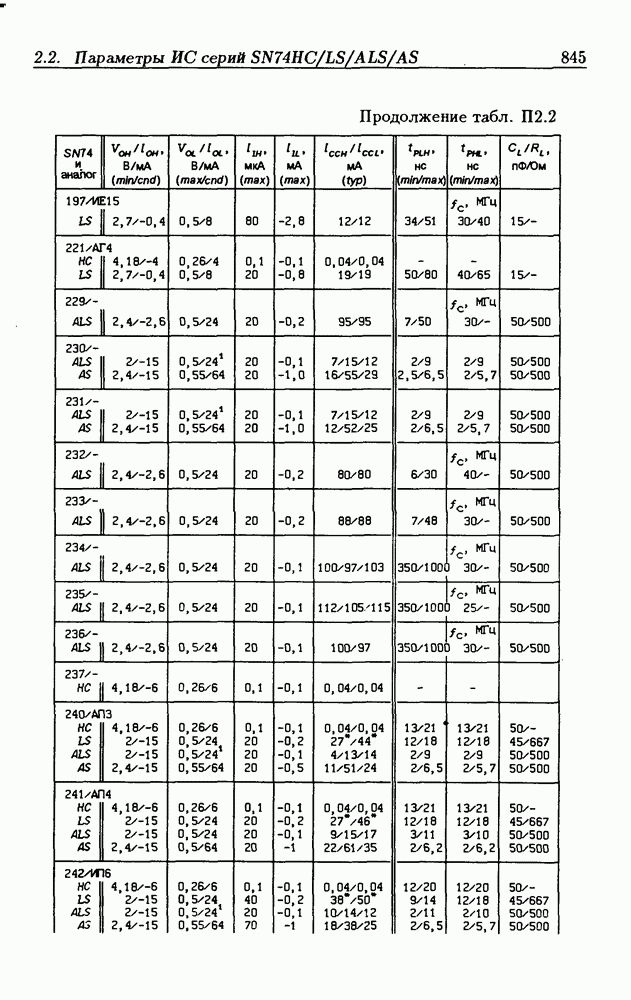
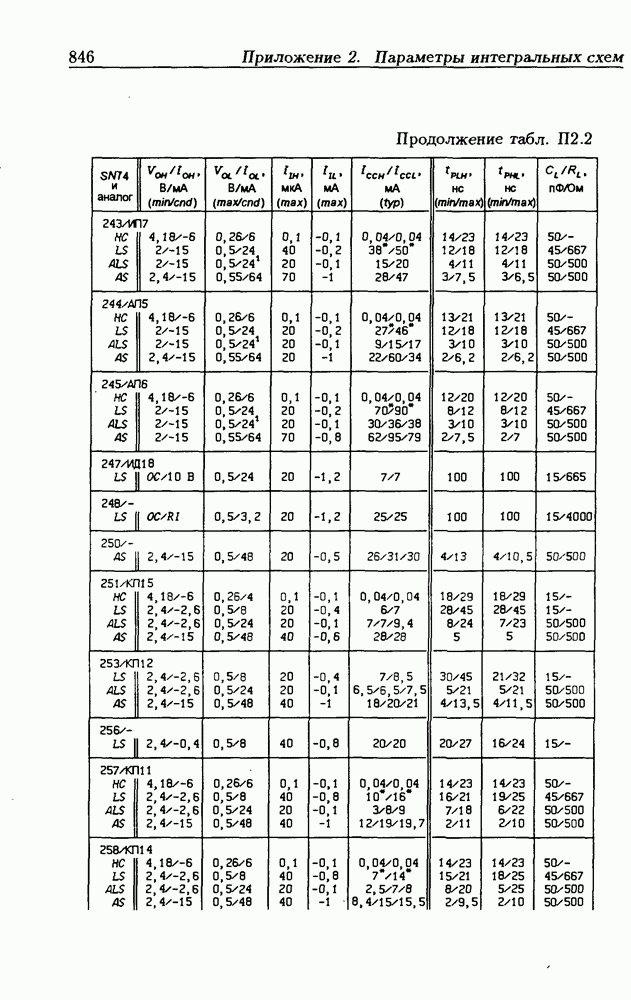
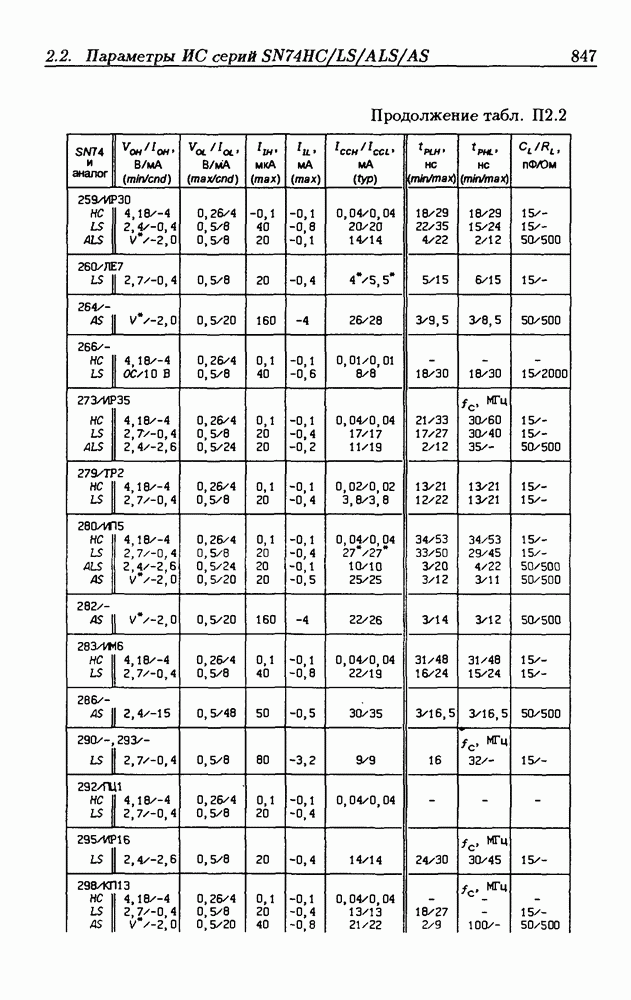
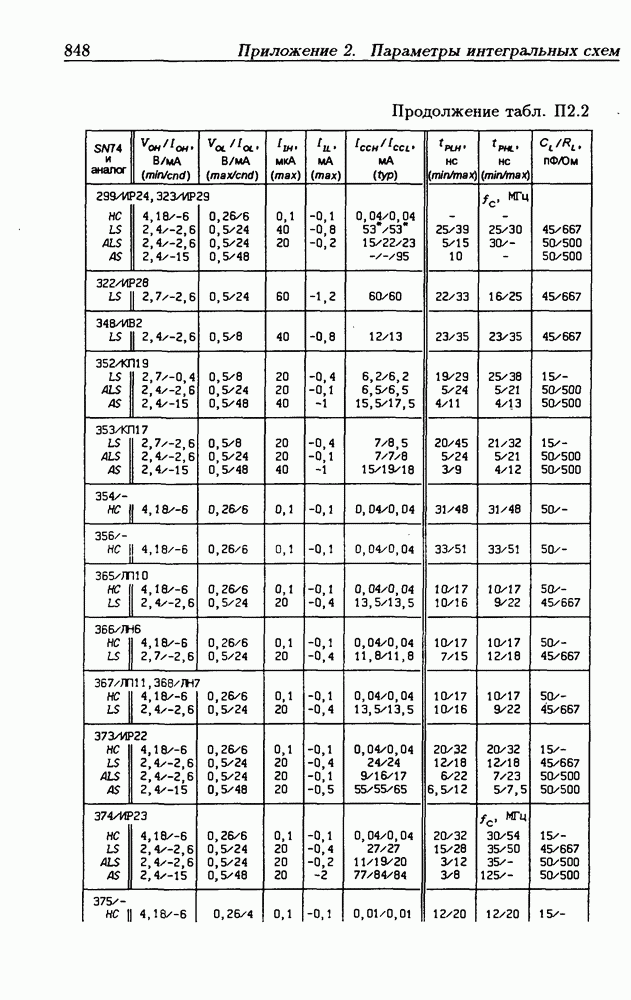
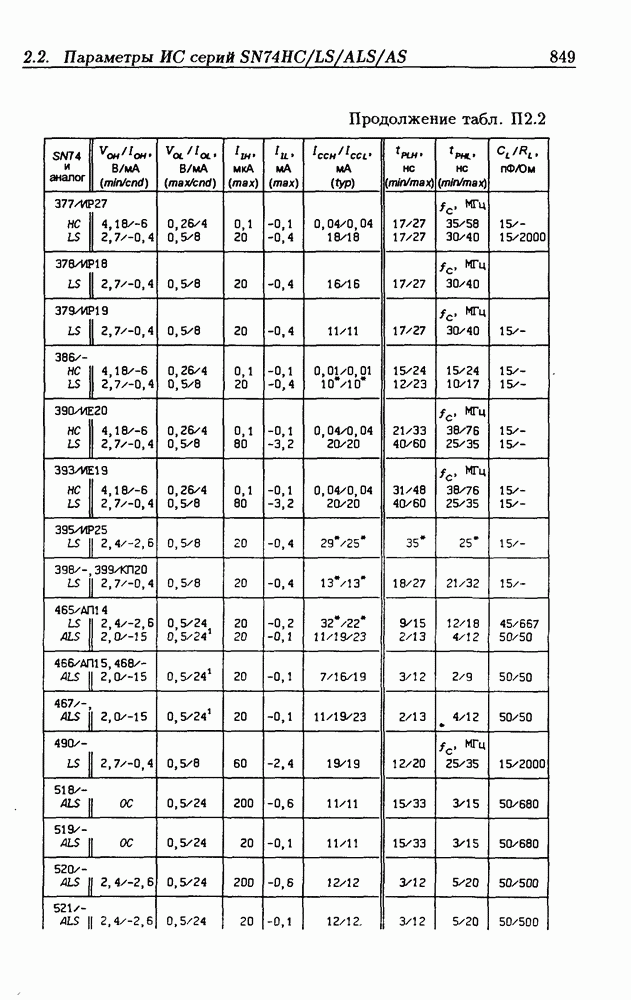
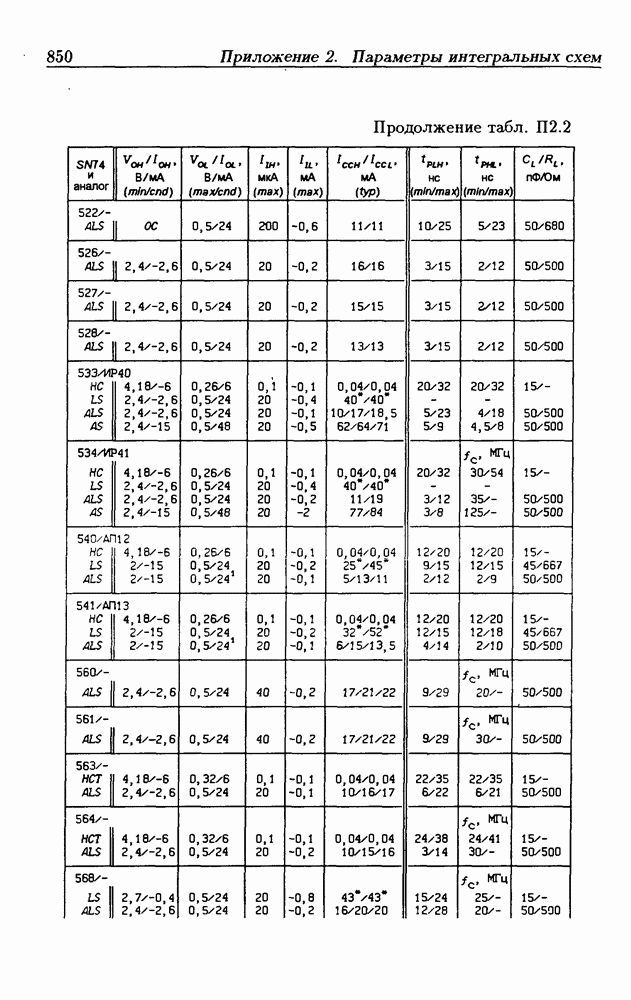
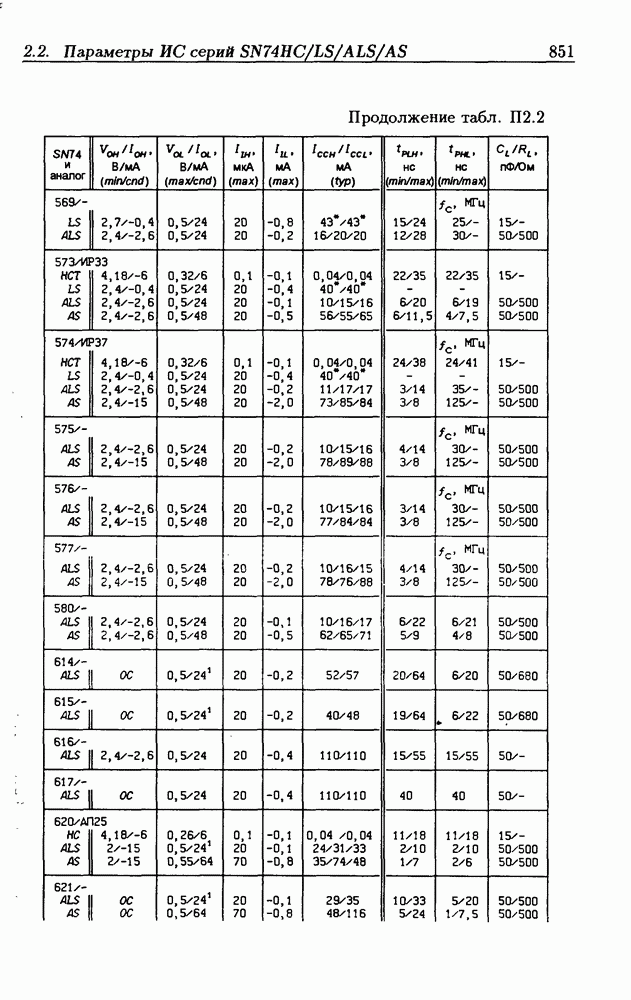
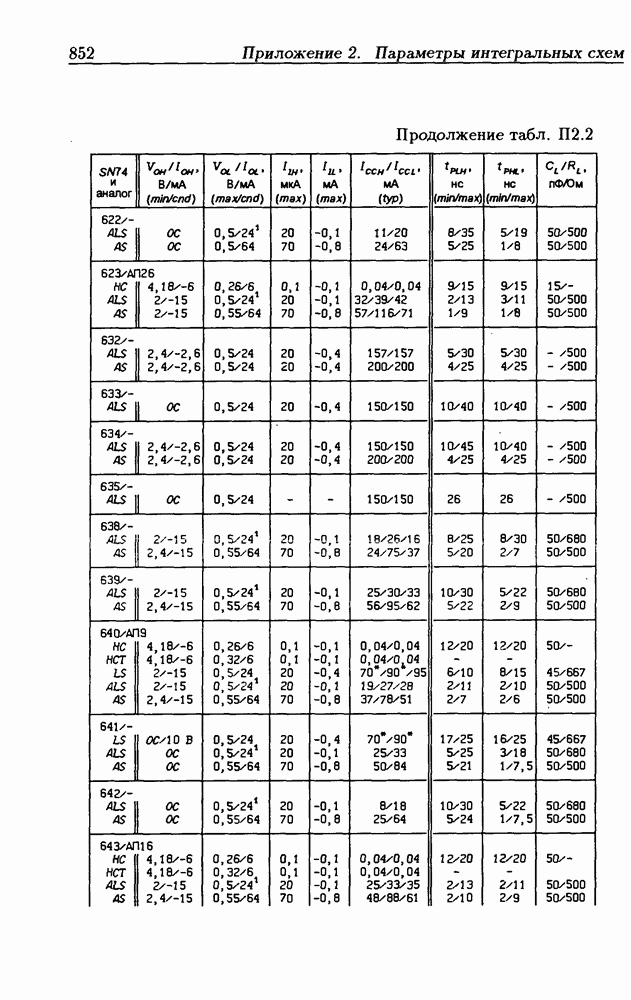
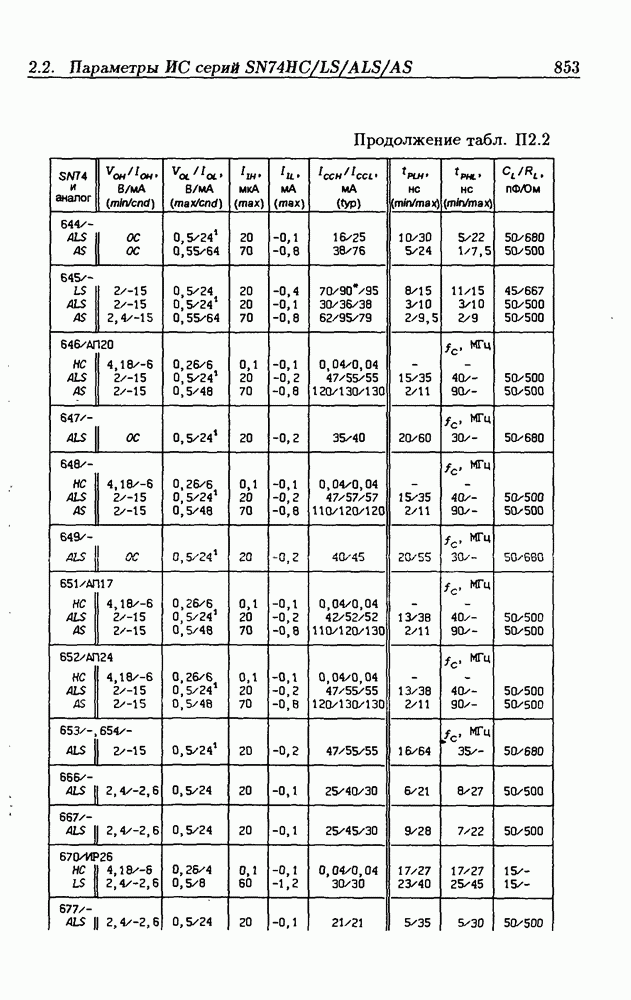
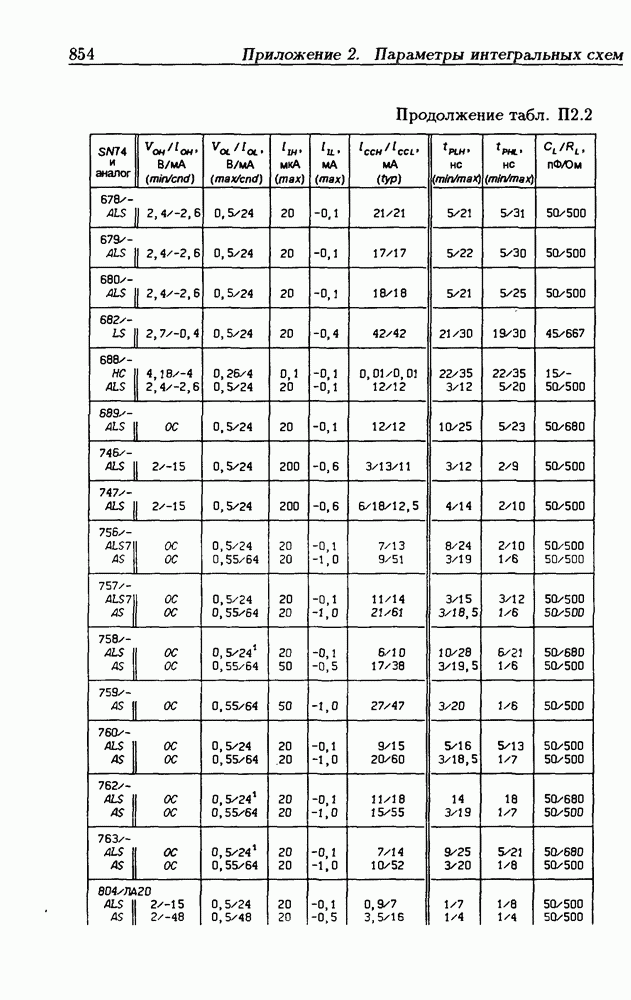
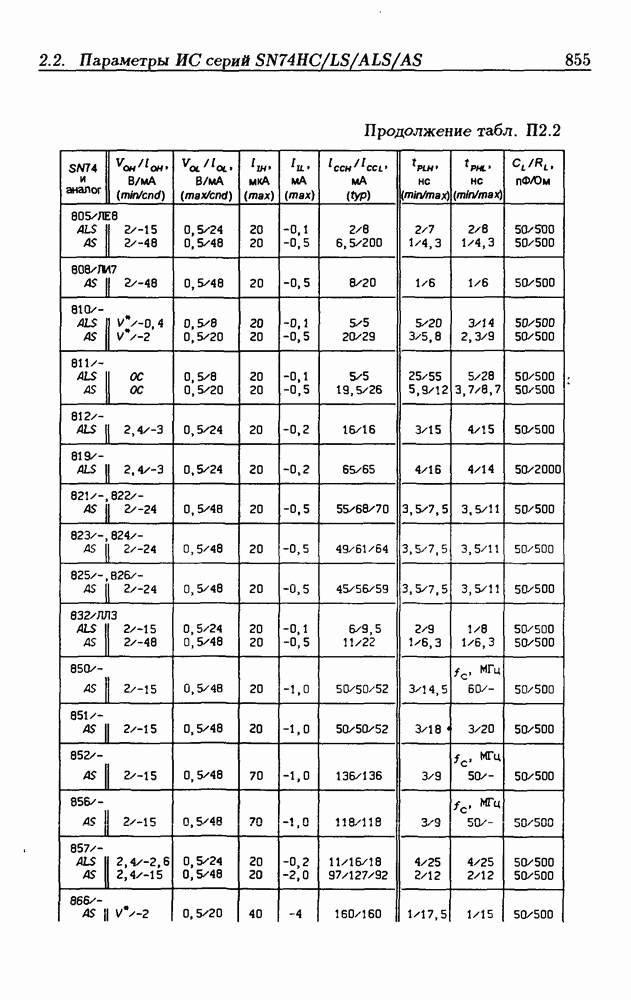
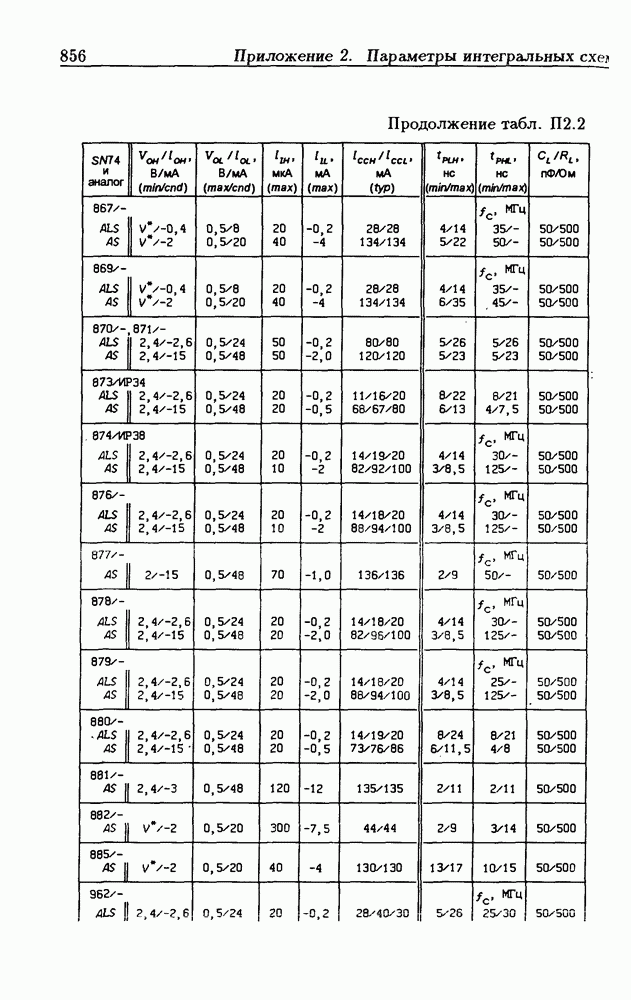
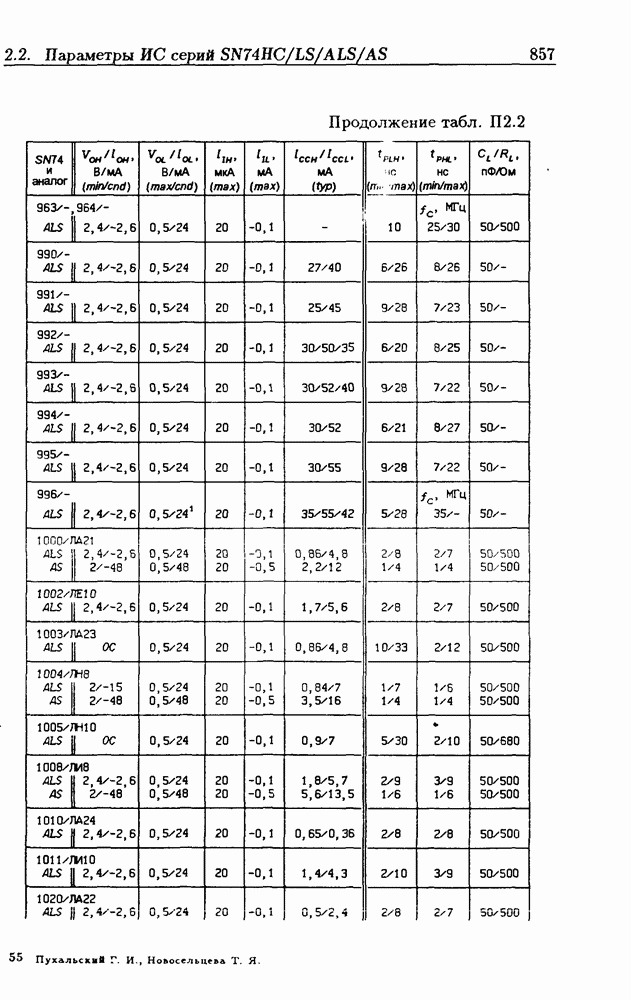
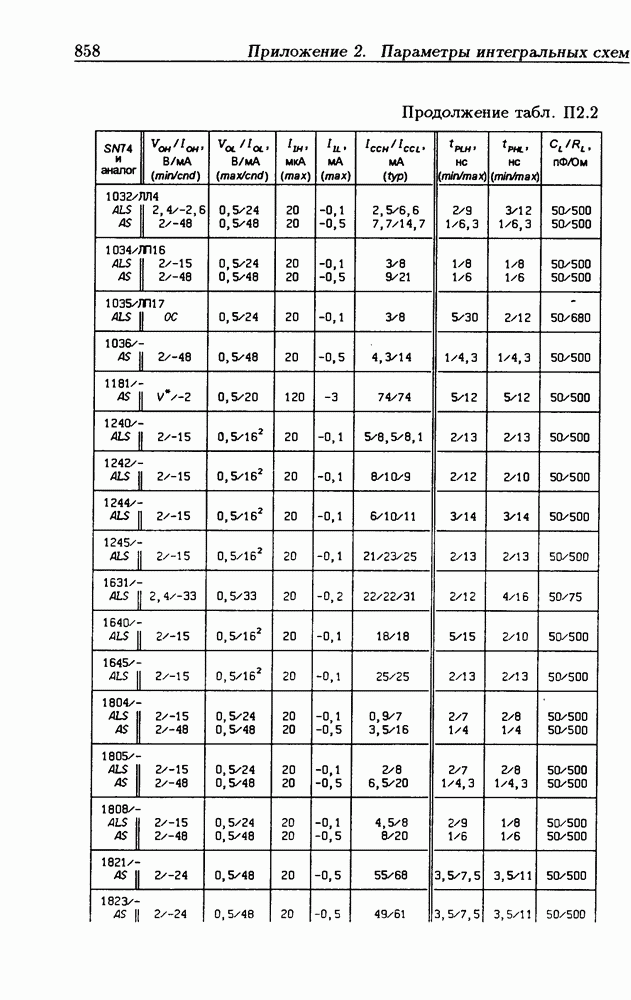
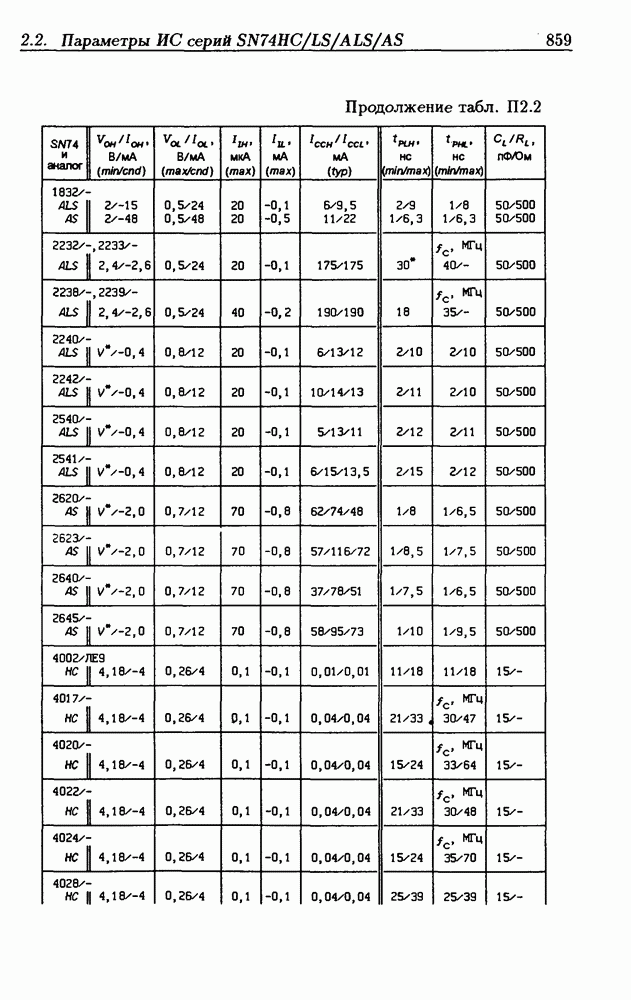
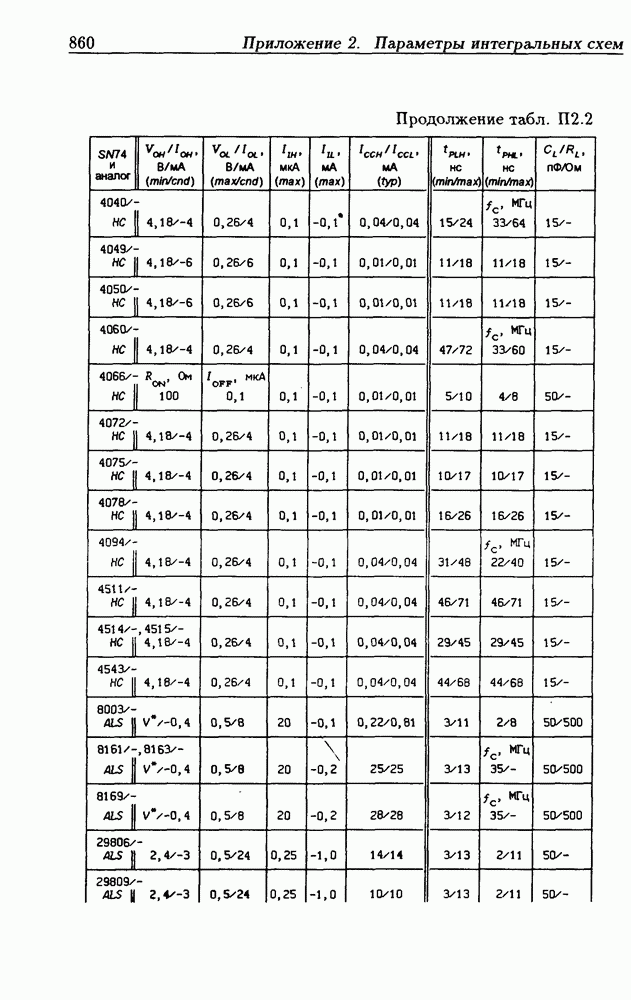
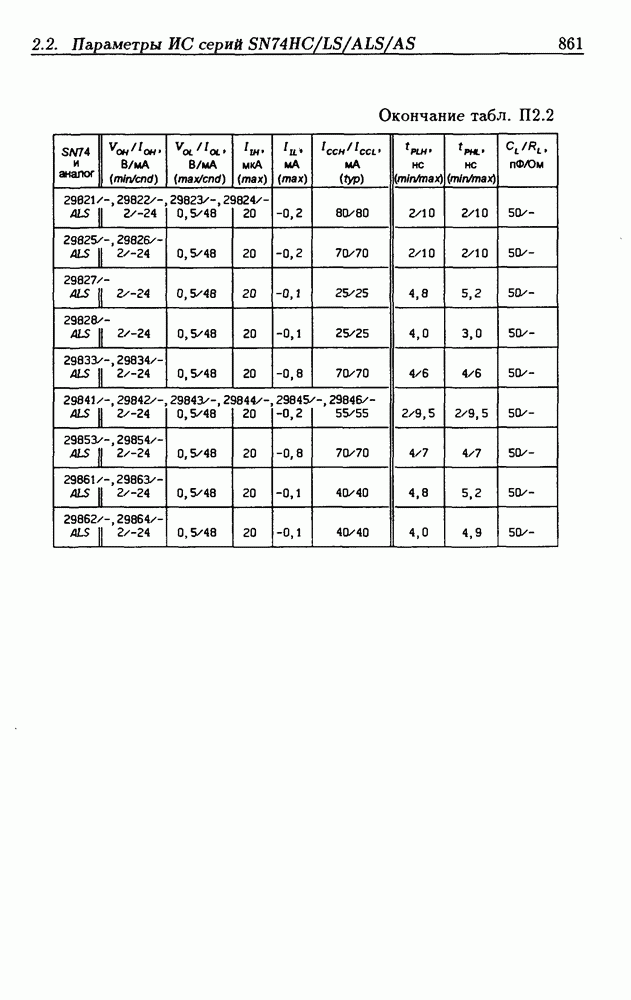
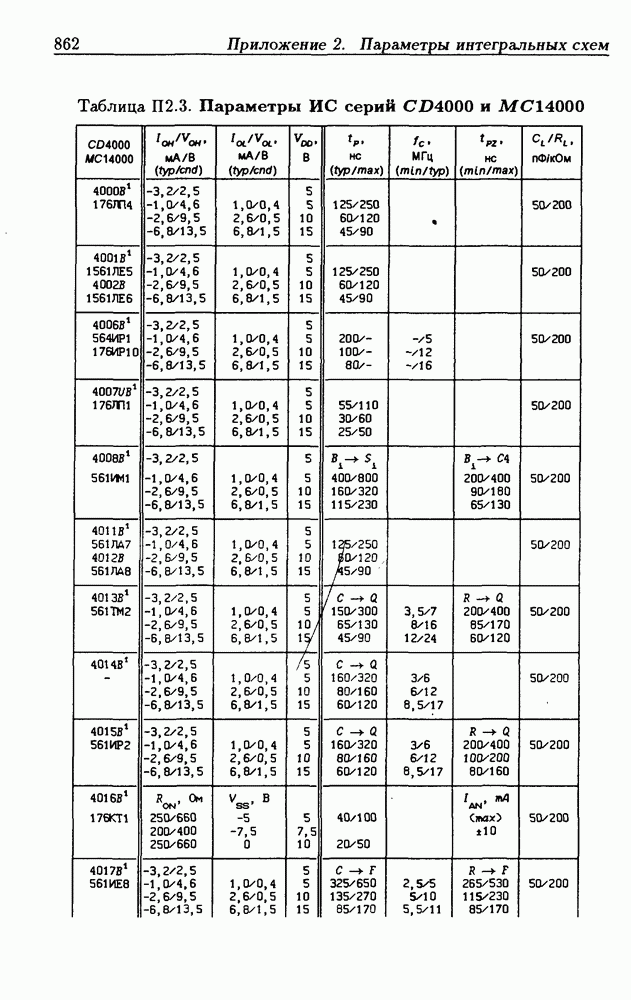
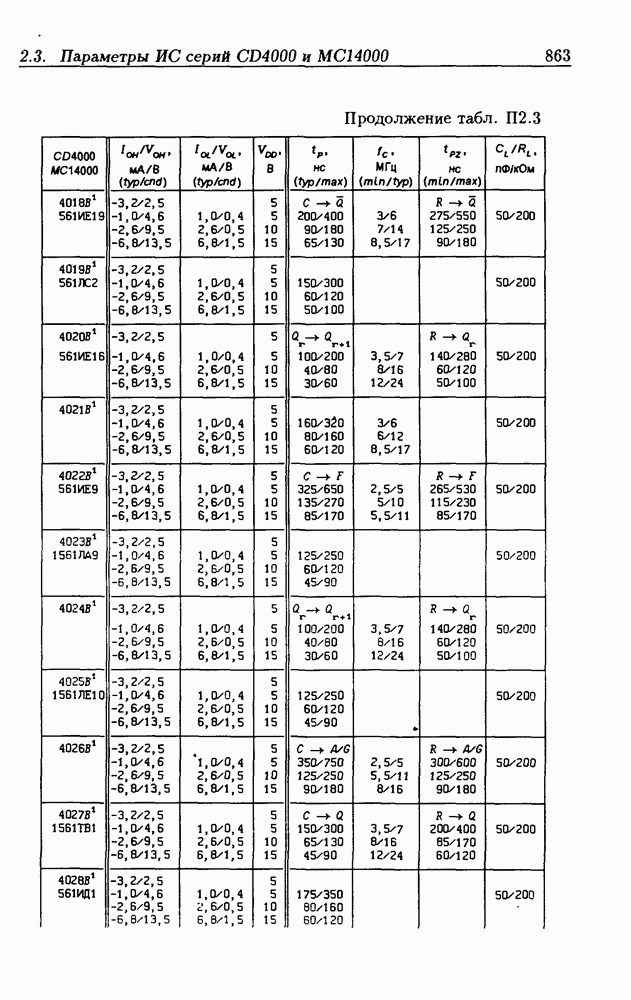
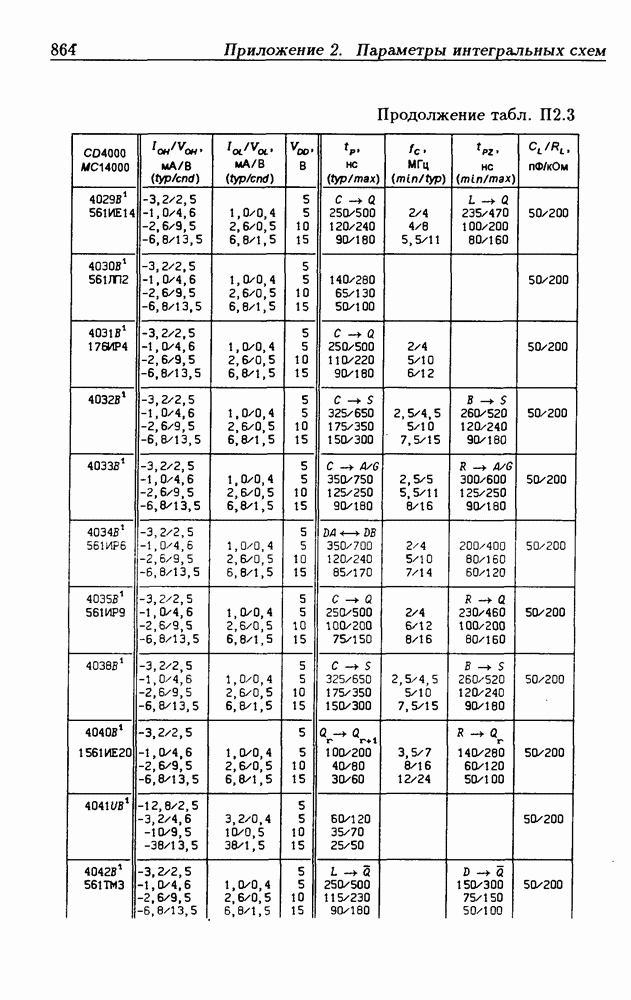
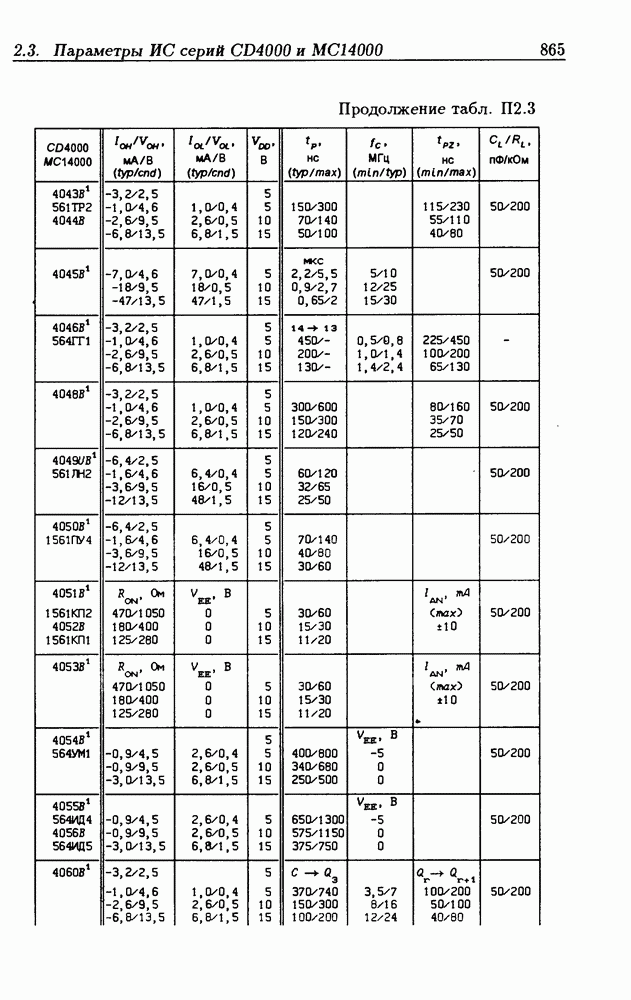
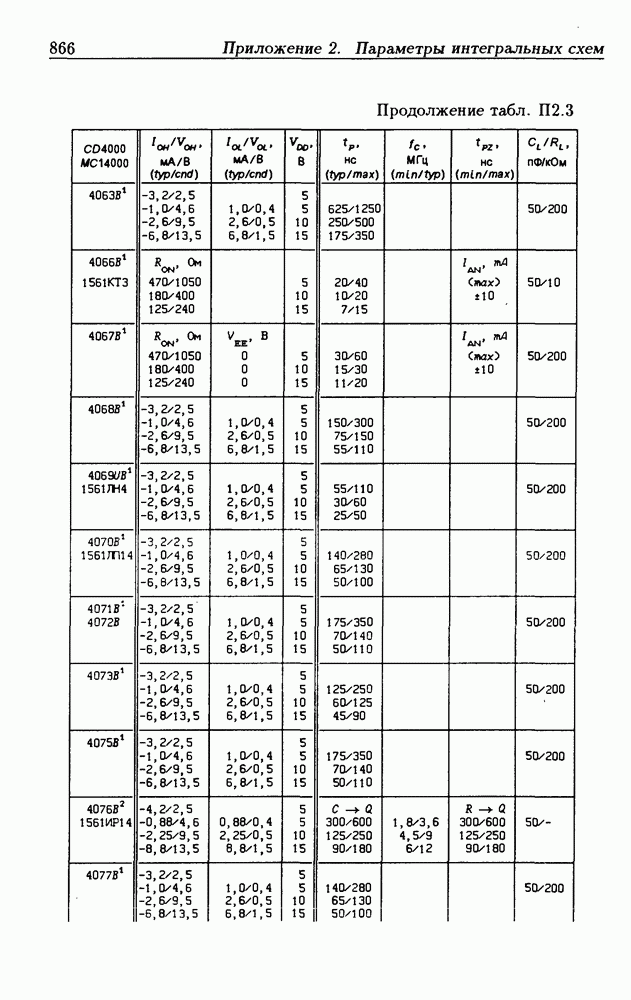
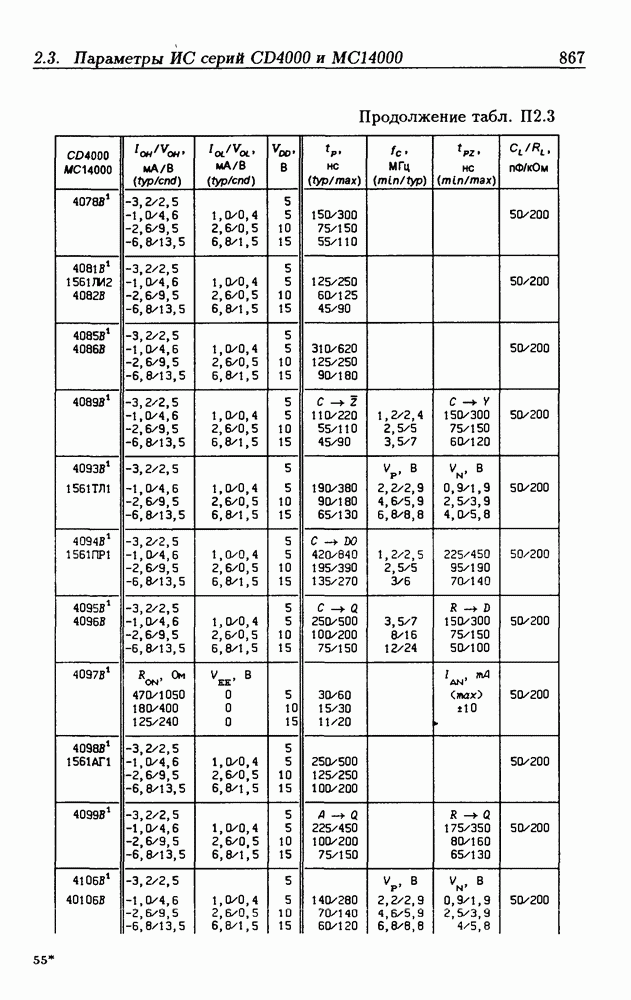
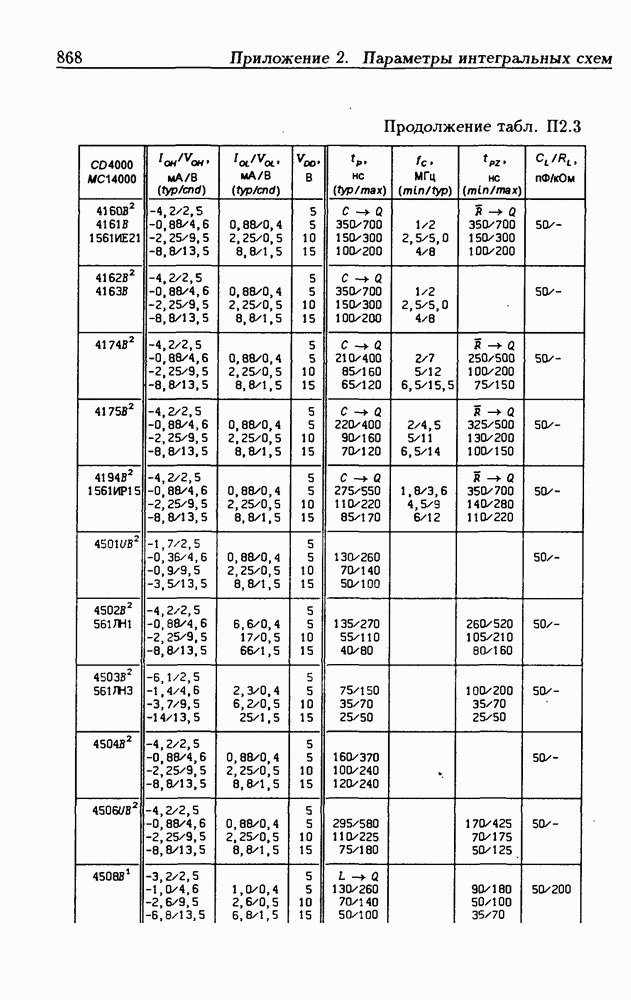
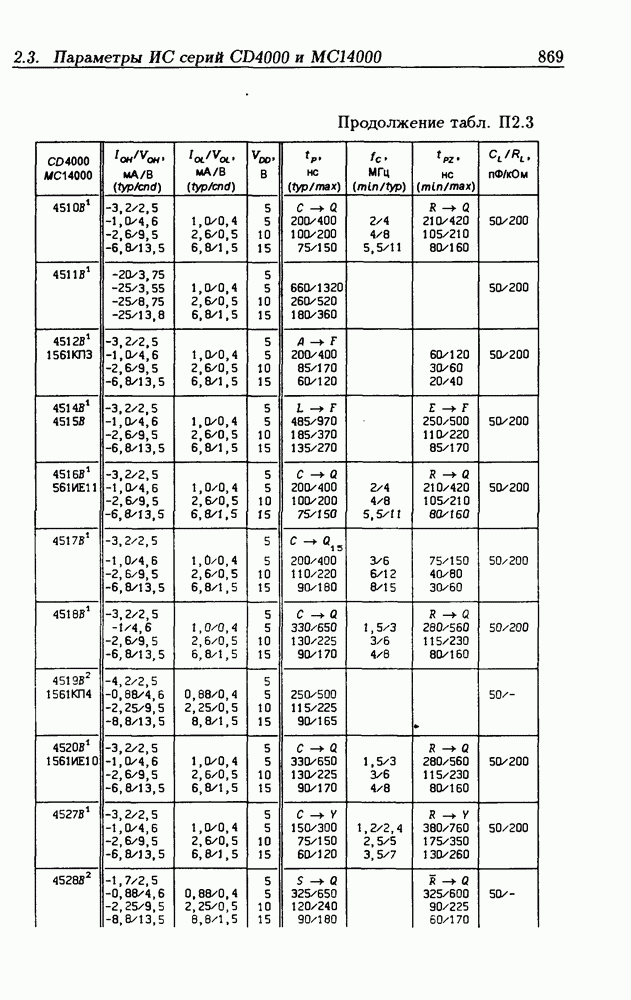
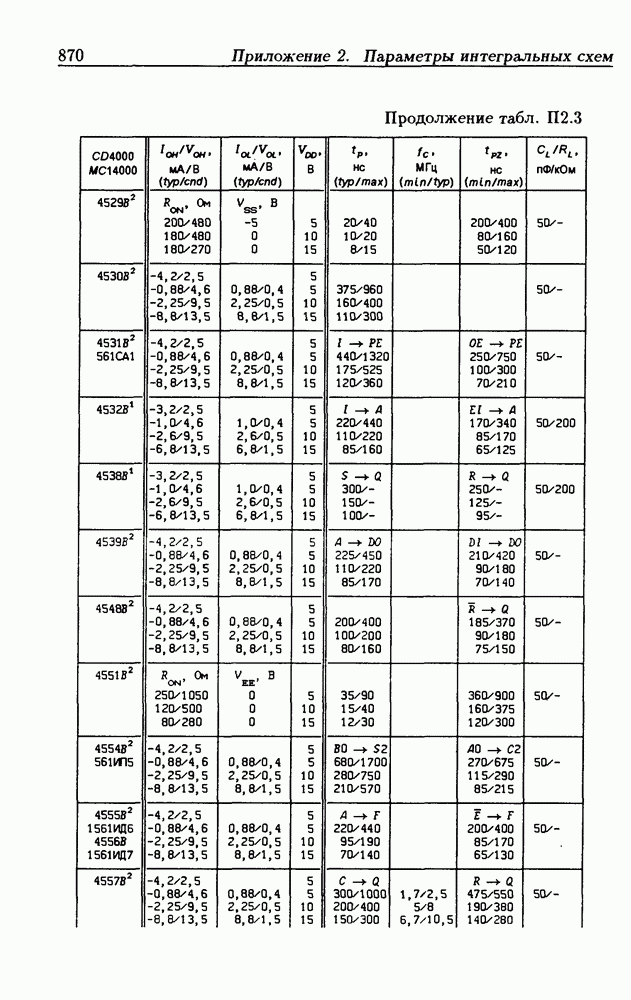
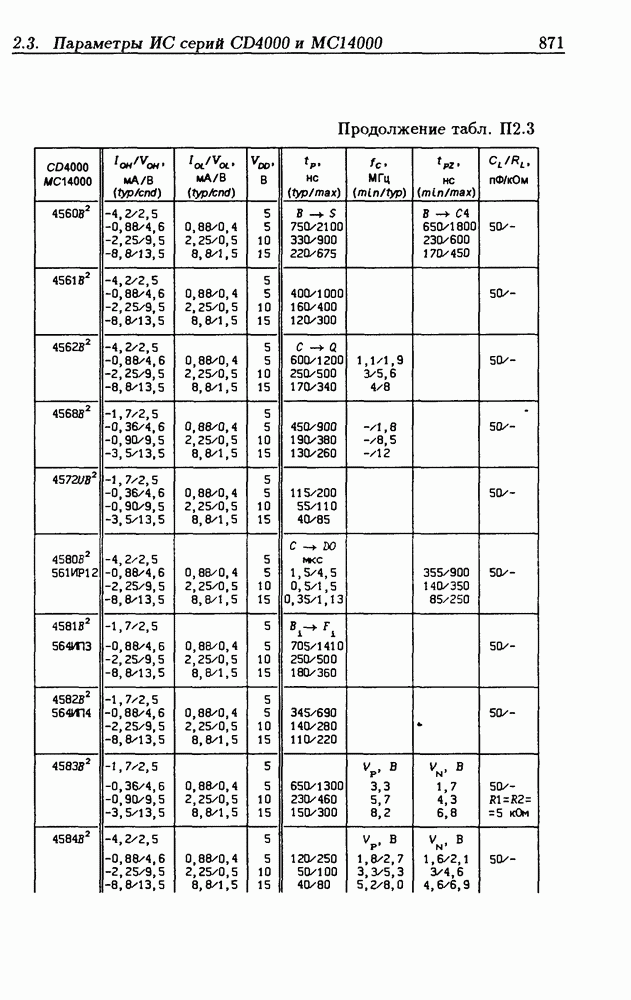
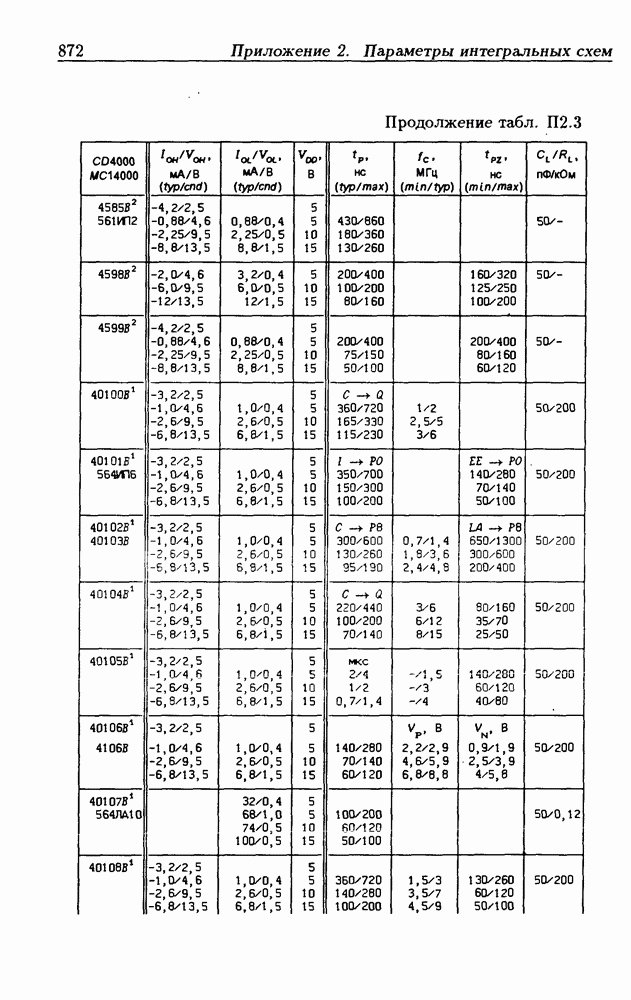
- Приложение 2. Параметры интегральных схем