| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
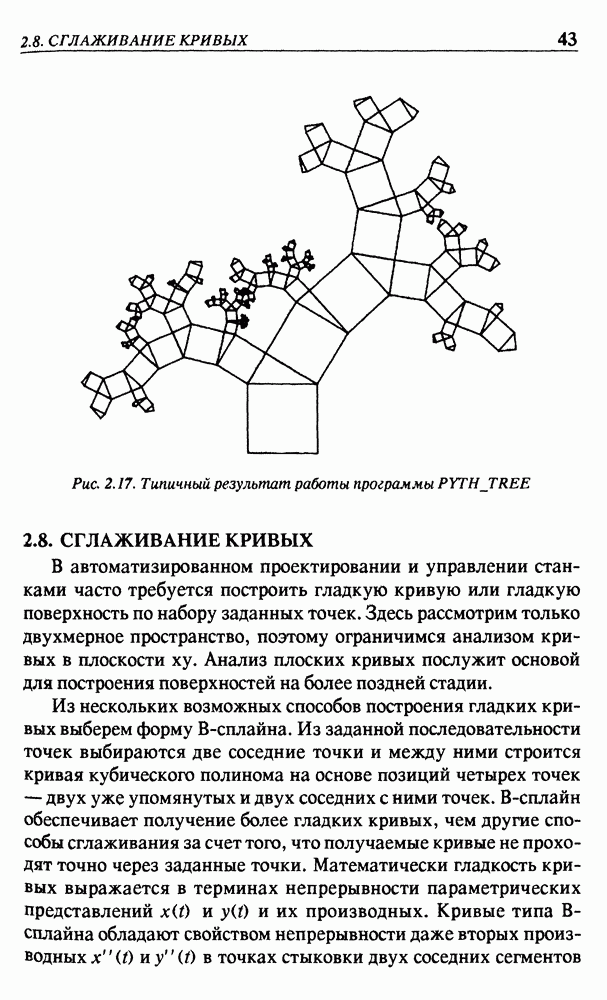
2.8. СГЛАЖИВАНИЕ КРИВЫХ
В автоматизированном проектировании и управлении станками часто требуется построить гладкую кривую или гладкую поверхность по набору заданных точек. Здесь рассмотрим только двухмерное пространство, поэтому ограничимся анализом кривых в плоскости  Анализ плоских кривых послужит основой для построения поверхностей на более поздней стадии.
Анализ плоских кривых послужит основой для построения поверхностей на более поздней стадии.
Из нескольких возможных способов построения гладких кривых выберем форму В-сплайна. Из заданной последовательности точек выбираются две соседние точки и между ними строится кривая кубического полинома на основе позиций четырех точек
— двух уже упомянутых и двух соседних с ними точек. В-сплайн обеспечивает получение более гладких кривых, чем другие способы сглаживания за счет того, что получаемые кривые не проходят точно через заданные точки Математически гладкость кривых выражается в терминах непрерывности параметрических представлений  и их производных. Кривые типа В-сплайна обладают свойством непрерывности даже вторых производных
и их производных. Кривые типа В-сплайна обладают свойством непрерывности даже вторых производных  и
и  в точках стыковки двух соседних сегментов
в точках стыковки двух соседних сегментов

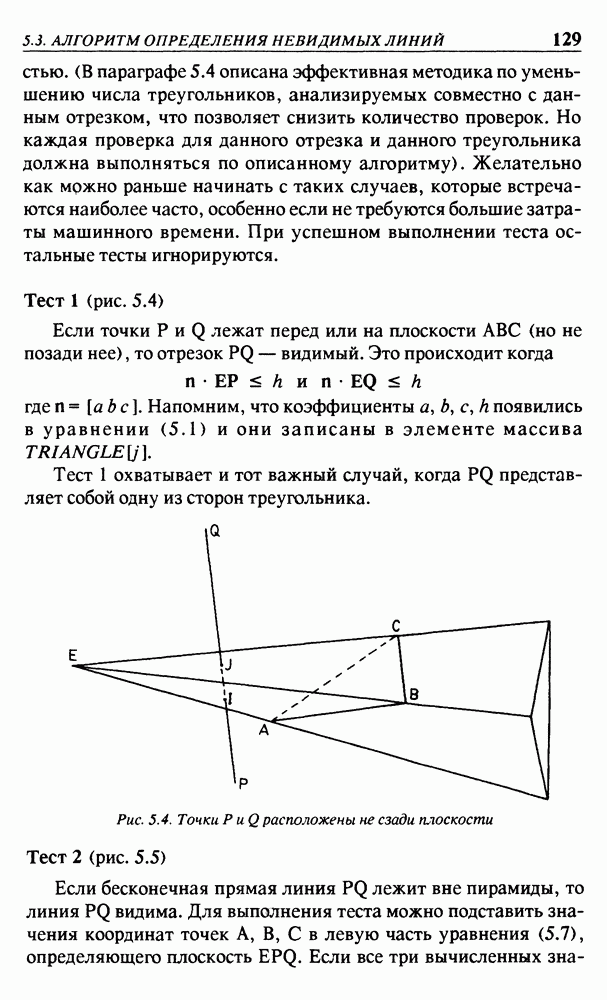
Рис. 2.18. (а) - нулевая производная разрывна; (б) - первая производная не непрерывна; (в) - вторая производная не непрерывна
кривой. Из рис. 2.18 можно видеть, как выглядят кривые, если их нулевая, первая и вторая производные не непрерывны в некоторой точке. Кривая на рис.  может считаться гладкой, но она не удовлетворяет строгим требованиям, которые выполняются в способе В-сплайна.
может считаться гладкой, но она не удовлетворяет строгим требованиям, которые выполняются в способе В-сплайна.
После такого краткого обсуждения рассмотрим этот метод в работе. Будем использовать параметрическое представление кривых. Любая точка части кривой между двумя заданными последовательными точками  будет иметь координаты
будет иметь координаты  где
где  увеличивается от 0 до 1, если отслеживается часть кривой от точки Р до точки
увеличивается от 0 до 1, если отслеживается часть кривой от точки Р до точки  Можно считать, что
Можно считать, что  это время. Если имеются заданные точки
это время. Если имеются заданные точки

то часть кривой В-сплайна между двумя последовательными точками  получается путем вычисления функций
получается путем вычисления функций  для изменения
для изменения  от 0 до 1
от 0 до 1

Эти уравнения содержат следующие коэффициенты:

а коэффициенты  вычисляются по значениям
вычисляются по значениям  аналогичным образом. Вышеприведенные формулы пригодны для эффективных вычислений. Вычисление значений
аналогичным образом. Вышеприведенные формулы пригодны для эффективных вычислений. Вычисление значений  производится быстрее по правилу Горнера, чем по обычному полиномиальному выражению. Коэффициенты
производится быстрее по правилу Горнера, чем по обычному полиномиальному выражению. Коэффициенты  вычисляются только однажды для каждого сегмента кривой, что очень важно, поскольку на каждом сегменте кривой может вычисляться большое число промежуточных точек
вычисляются только однажды для каждого сегмента кривой, что очень важно, поскольку на каждом сегменте кривой может вычисляться большое число промежуточных точек 
Для получения некоторого представления о свойствах кривой в точках стыковки двух сегментов рассмотрим функцию  и ее первую и вторую производные для значений
и ее первую и вторую производные для значений  (функция
(функция  будет обладать аналогичными свойствами)
будет обладать аналогичными свойствами)

Используя уравнение (2.13), после упрощения получаем

Можно видеть, что значение  не равно в точности х-координате
не равно в точности х-координате  точки
точки  : оно зависит от позиций точек
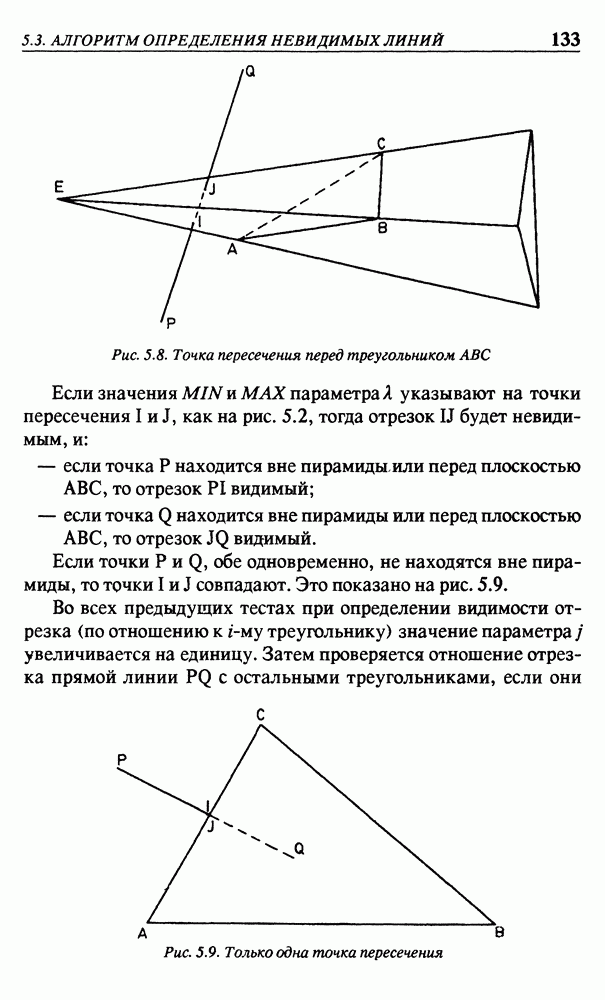
: оно зависит от позиций точек  Из рис. 2.19 видно, что точка В является точкой сегмента
Из рис. 2.19 видно, что точка В является точкой сегмента  но одновременно и начальной точкой сегмента
но одновременно и начальной точкой сегмента 

Рис. 2.19. Три последовательные точки
Для первого сегмента имеем

где через  обозначено вычисленное значение координаты х для точки В. Рассматривая эту же точку как принадлежащую сегменту
обозначено вычисленное значение координаты х для точки В. Рассматривая эту же точку как принадлежащую сегменту  получим
получим

Отсюда видно, что оба способа вычисления значения х дают одинаковый результат, что означает непрерывность функции  в точке В. Продифференцировав
в точке В. Продифференцировав  дважды, найдем производные
дважды, найдем производные  Подставляя в них значения
Подставляя в них значения  как это было сделано для
как это было сделано для  можно будет убедиться, что производные непрерывны в точке В. Поскольку функция
можно будет убедиться, что производные непрерывны в точке В. Поскольку функция  и ее первые две производные тоже непрерывны, то становится ясно, что кривая В-сплайна очень гладкая.
и ее первые две производные тоже непрерывны, то становится ясно, что кривая В-сплайна очень гладкая.
Для расчета любого сегмента кривой между точками Р и  используются также точки
используются также точки  Из этого следует, что первый сегмент кривой будет располагаться между точками
Из этого следует, что первый сегмент кривой будет располагаться между точками  а последний — между точками
а последний — между точками  что начальная и конечная точки всей кривой будут располагаться вблизи и
что начальная и конечная точки всей кривой будут располагаться вблизи и  но не вблизи
но не вблизи  Приведенная ниже программа считывает числа
Приведенная ниже программа считывает числа

из файла  При выводе каждая из
При выводе каждая из  точек обозначается маркером в виде креста. Затем вычерчивается кривая В-сплайна.
точек обозначается маркером в виде креста. Затем вычерчивается кривая В-сплайна.
(см. скан)
(см. скан)
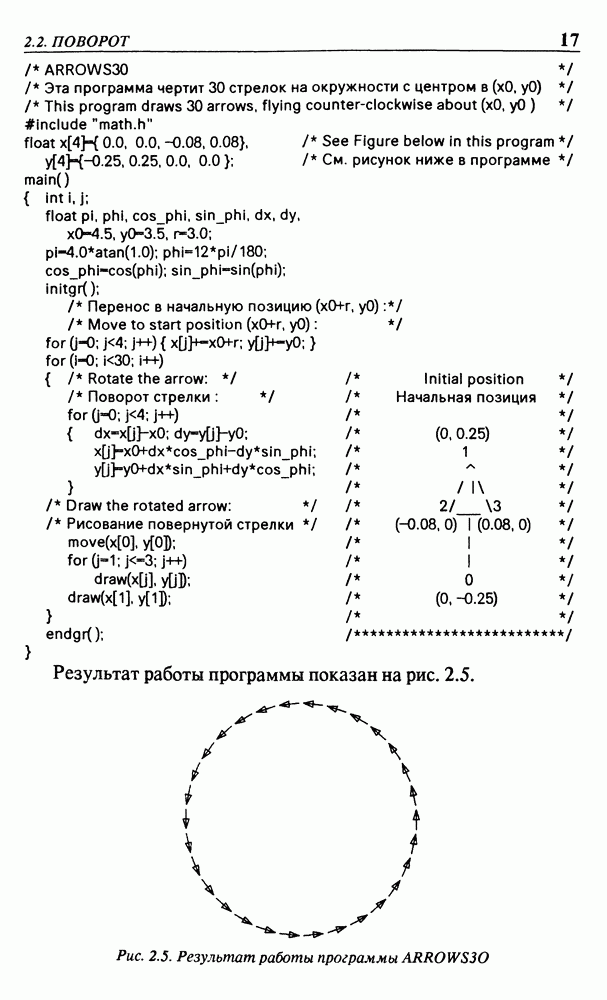
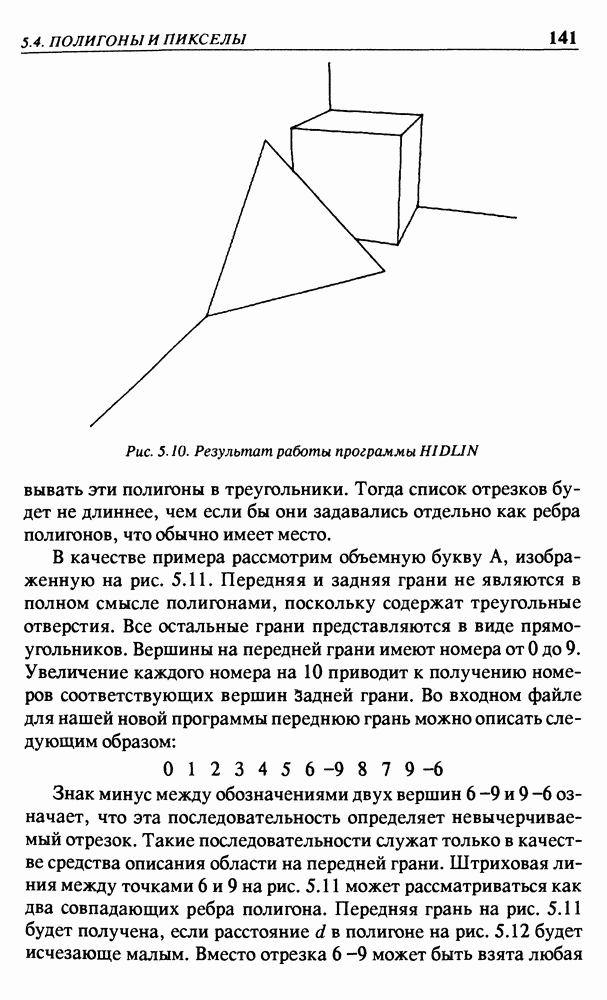
то в результате работы программы получим изображение, показанное на рис. 2.20.

Рис. 2.20. Результат работы программы 
УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
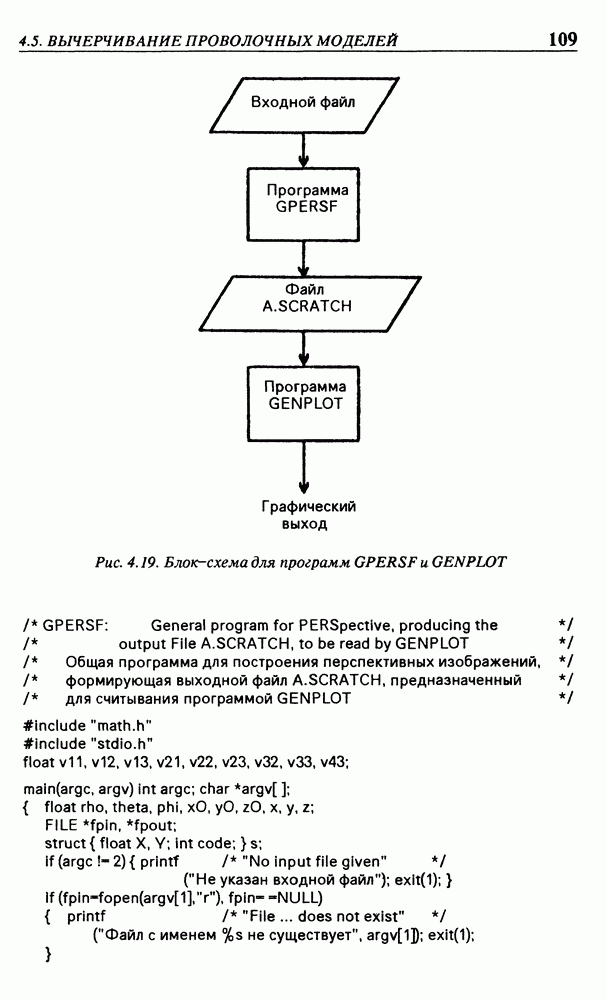
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
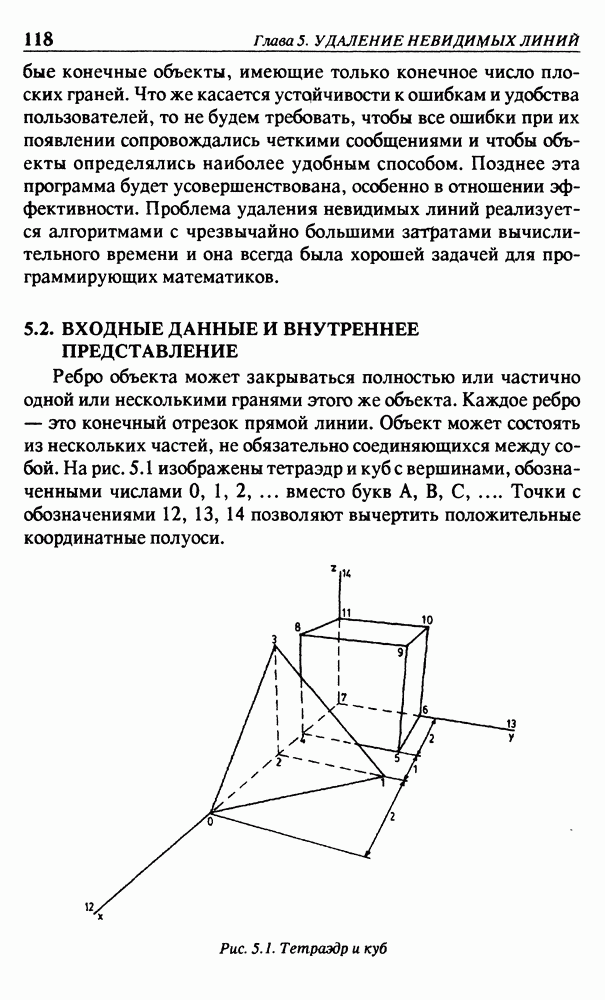
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
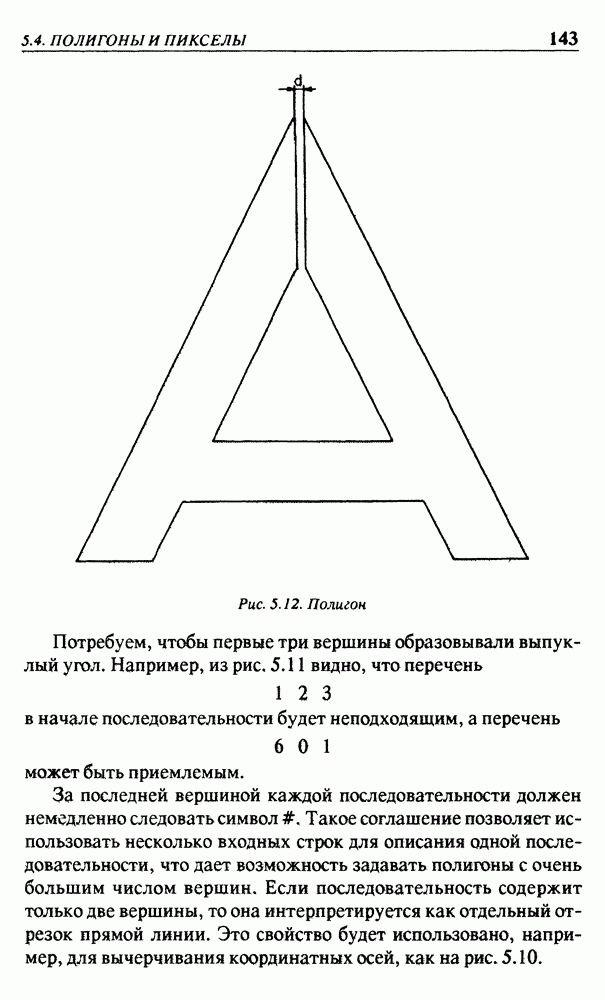
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
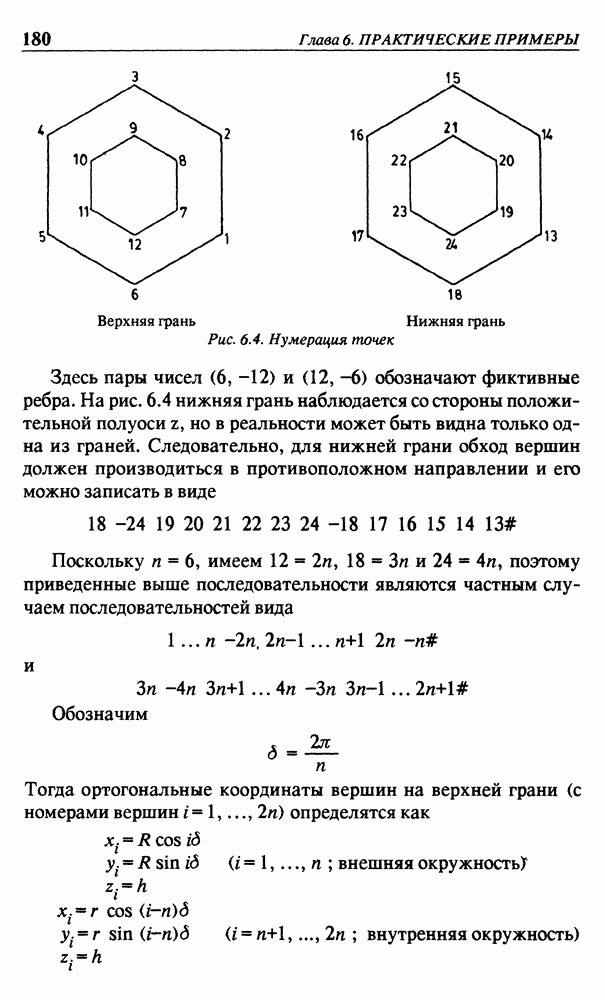
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
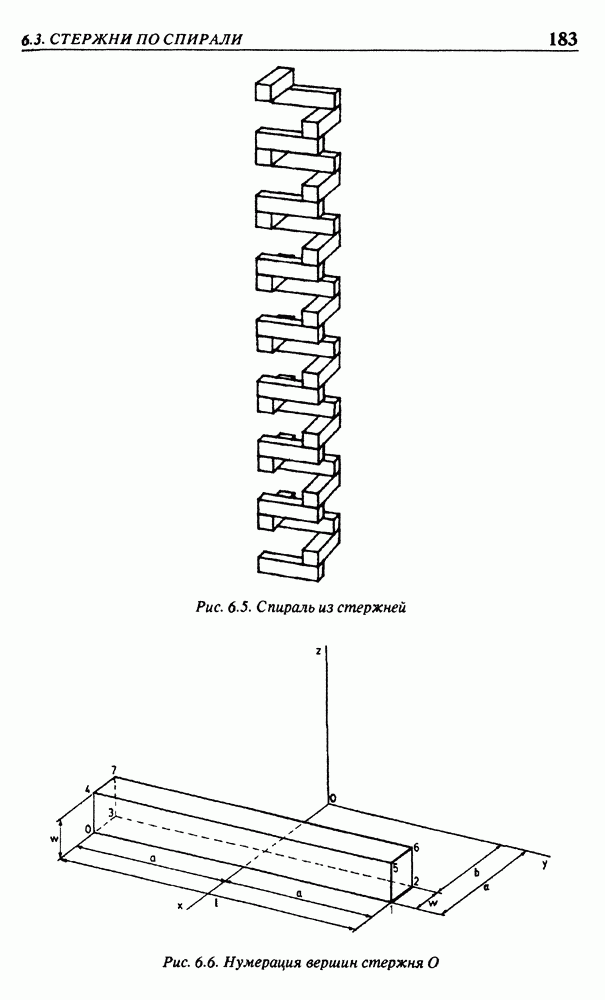
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
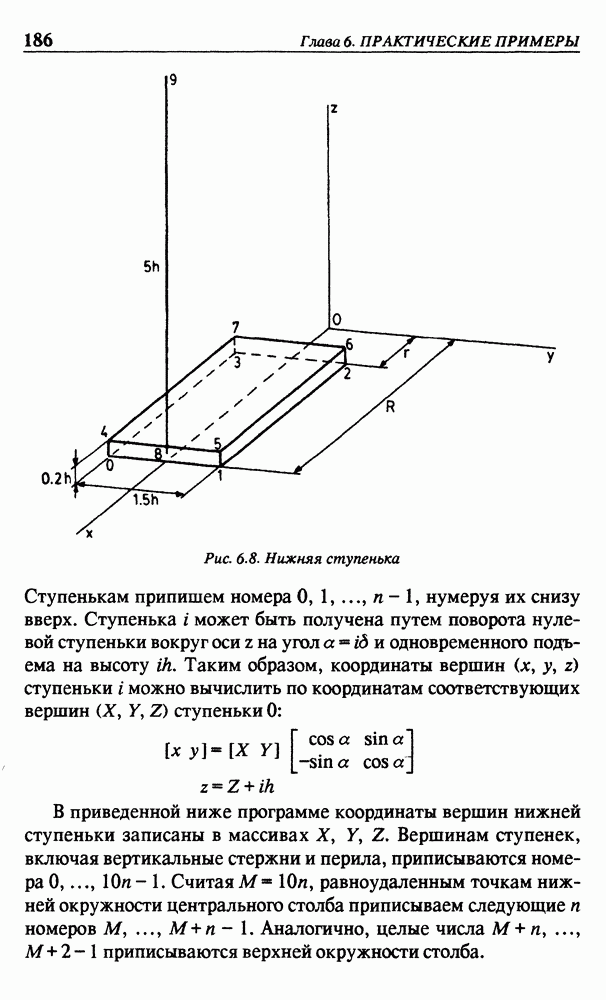
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
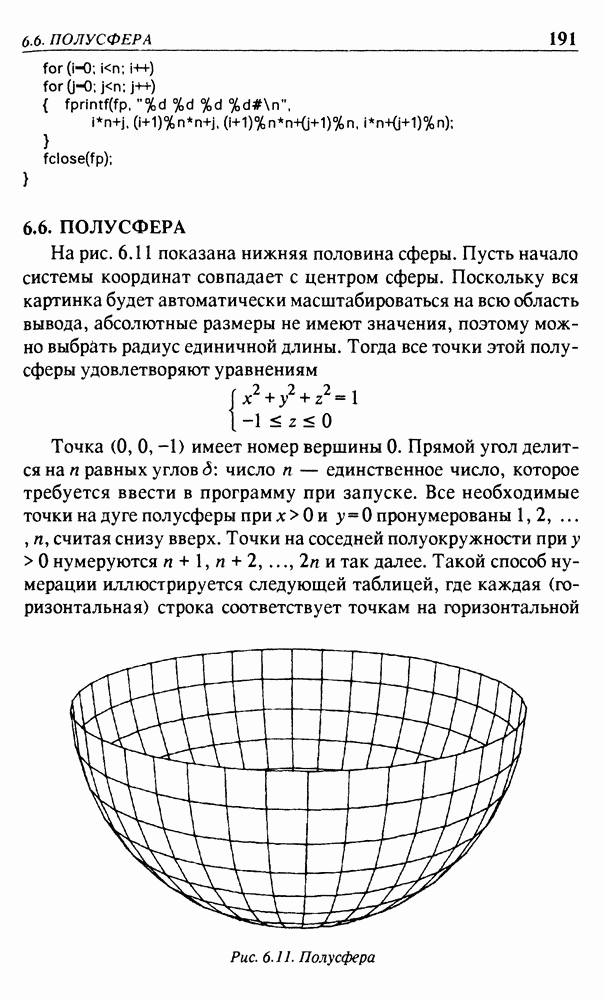
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА