| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Если каждая точка  отображается на точку
отображается на точку  в соответствии с уравнениями
в соответствии с уравнениями

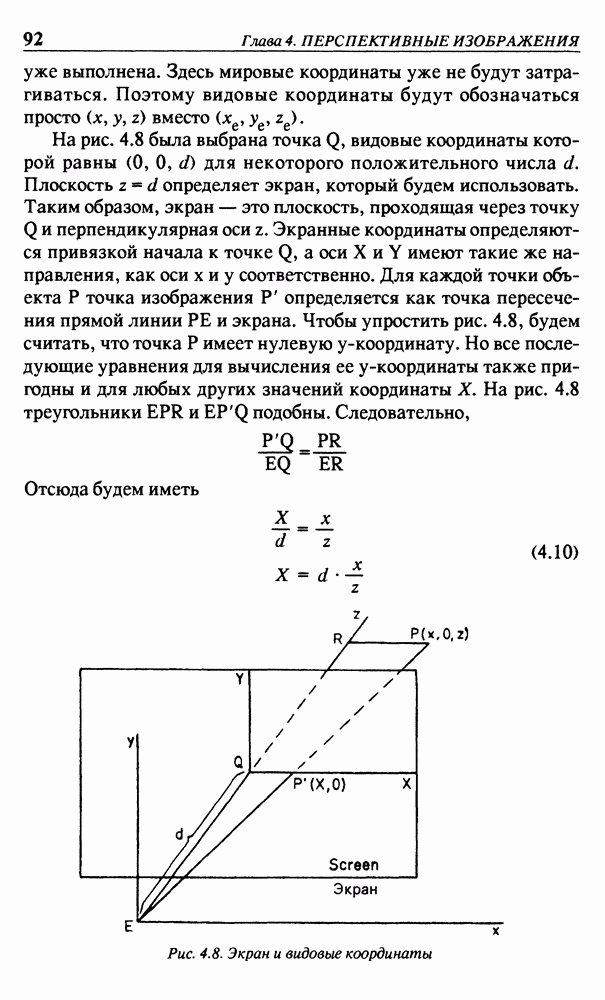
где  константы, то этот процесс называется переносом в трехмерном пространстве. Такой перенос может быть записан в матричной форме
константы, то этот процесс называется переносом в трехмерном пространстве. Такой перенос может быть записан в матричной форме

Читатель, ознакомившийся с параграфом 3.6, может легко распознать, что первая, вторая и третья строки матрицы Т соответствуют отображениям бесконечно удаленных точек на координатных осях, а четвертая строка — отображению точки  Последнее означает, что в однородных координатах точка
Последнее означает, что в однородных координатах точка  является отображением точки начала координат О. Поворот вокруг координатных осей может быть описан матрицей без использования однородных координат. Ради краткости так и будем поступать, обращаясь к однородным координатам только в тех случаях, когда они действительно необходимы. Будем использовать правую координатную систему, считая вращение вокруг оси положительным, если оно соответствует
является отображением точки начала координат О. Поворот вокруг координатных осей может быть описан матрицей без использования однородных координат. Ради краткости так и будем поступать, обращаясь к однородным координатам только в тех случаях, когда они действительно необходимы. Будем использовать правую координатную систему, считая вращение вокруг оси положительным, если оно соответствует

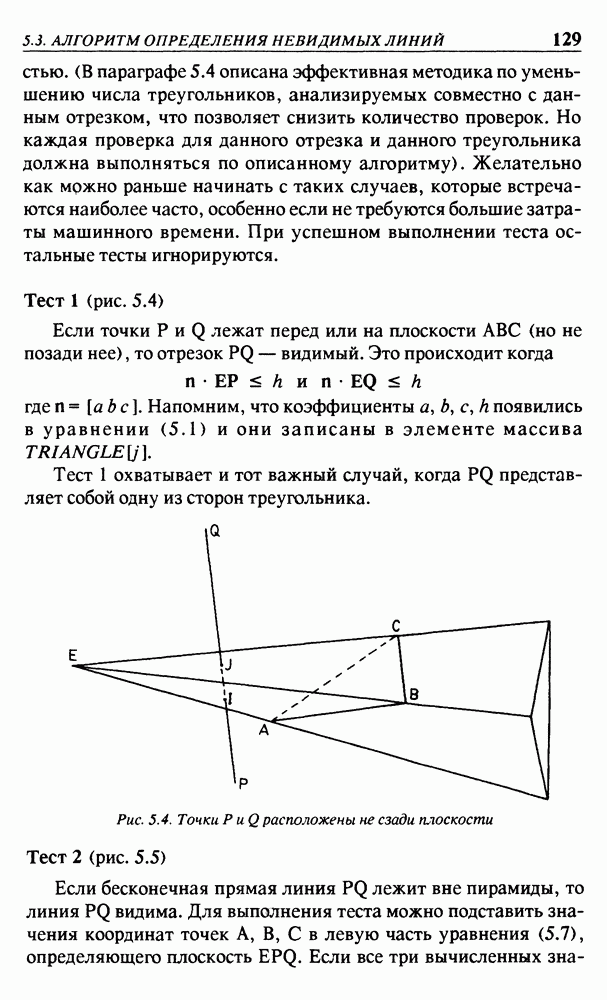
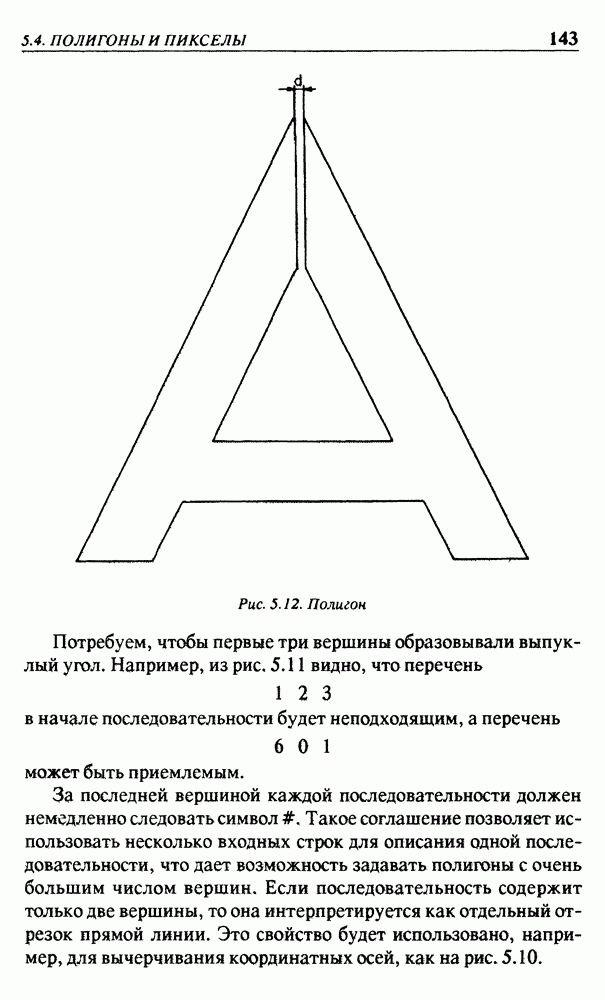
Рис. 3.18. Вращение в положительном направлении вокруг координатных осей
положительному направлению этой оси по правилу винта с правой резьбой. Это показано на рис. 3.18.
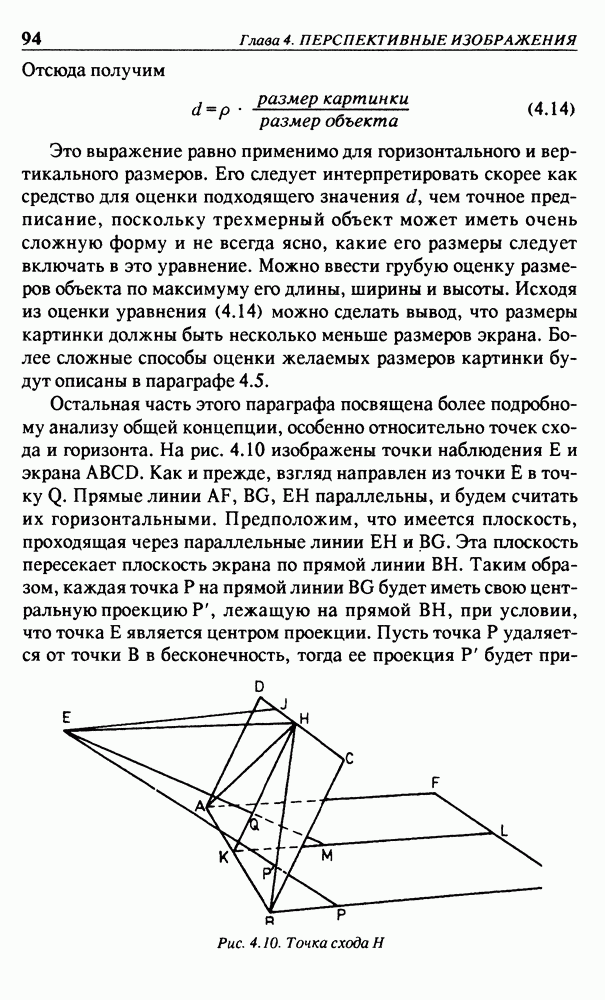
Рассмотрим поворот вокруг оси z на угол а и для сокращения обозначим  Тогда можно записать
Тогда можно записать

что непосредственно следует из уравнений (2.4) в параграфе 2.3.
Матрицу  можно использовать для получения матриц
можно использовать для получения матриц  определяющих поворот вокруг соответствующих осей, чисто формальным образом, то есть без применения картинки. Это делается путем циклических перестановок, получаемых заменой каждой из букв х, у, z на последующую, считая, что за буквой z следует буква х.
определяющих поворот вокруг соответствующих осей, чисто формальным образом, то есть без применения картинки. Это делается путем циклических перестановок, получаемых заменой каждой из букв х, у, z на последующую, считая, что за буквой z следует буква х.
Матрица  превратится в матрицу
превратится в матрицу  циклическим переносом каждой строки на одну позицию и затем выполнением аналогичной операции для столбцов:
циклическим переносом каждой строки на одну позицию и затем выполнением аналогичной операции для столбцов:

Так же матрица  преобразуется в “последующую” матрицу У:
преобразуется в “последующую” матрицу У:

Суммируя сказанное, получим следующие матрицы:

Для поворота точки вокруг оси х на угол а матрица  используется следующим образом:
используется следующим образом:

Матрицы  применяются аналогично.
применяются аналогично.
Как объяснялось в параграфе  уравнения для преобразований могут интерпретироваться как изменения координат. Перенос точки на определенное расстояние вправо описывается теми же уравнениями, как перенос системы координат на такое же расстояние влево. На практике удобнее перемещать координатную систему вместо точки, но для этого требуется инвертирование матрицы. К счастью, инверсия матриц
уравнения для преобразований могут интерпретироваться как изменения координат. Перенос точки на определенное расстояние вправо описывается теми же уравнениями, как перенос системы координат на такое же расстояние влево. На практике удобнее перемещать координатную систему вместо точки, но для этого требуется инвертирование матрицы. К счастью, инверсия матриц  (уравнения (3.12)-(3.15)) может быть записана немедленно:
(уравнения (3.12)-(3.15)) может быть записана немедленно:


Теперь можно найти матрицу  для поворота вокруг любой прямой линии, проходящей через точку начала координат О. Для определенности будем полагать, что поворот осуществляется вокруг вектора
для поворота вокруг любой прямой линии, проходящей через точку начала координат О. Для определенности будем полагать, что поворот осуществляется вокруг вектора  начало которого расположено в точке О. Тогда положительное направление вращения соответствует направлению вектора по правилу винта с правой резьбой. Как и ранее, поворот будем производить на угол а.
начало которого расположено в точке О. Тогда положительное направление вращения соответствует направлению вектора по правилу винта с правой резьбой. Как и ранее, поворот будем производить на угол а.
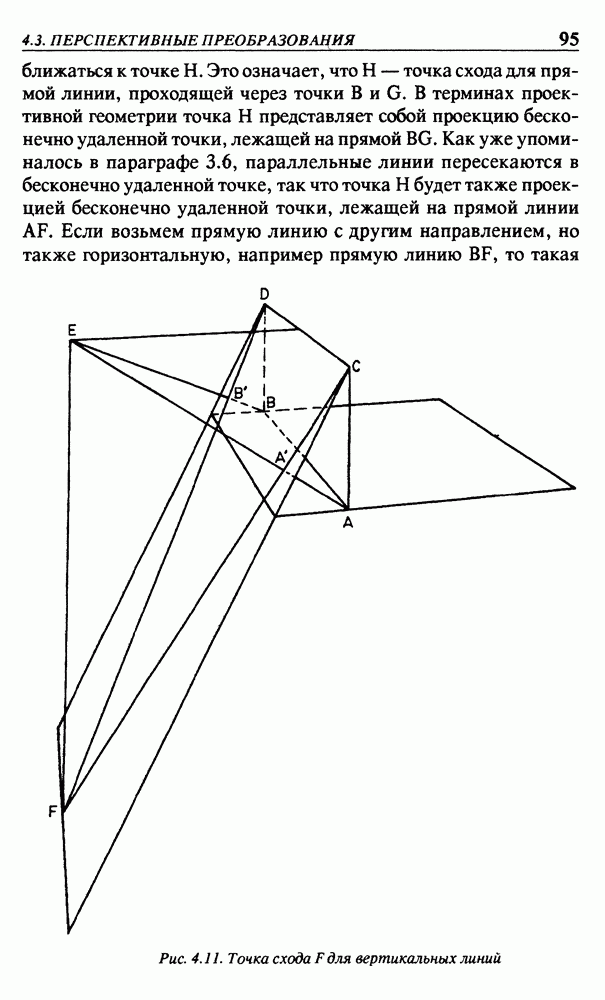
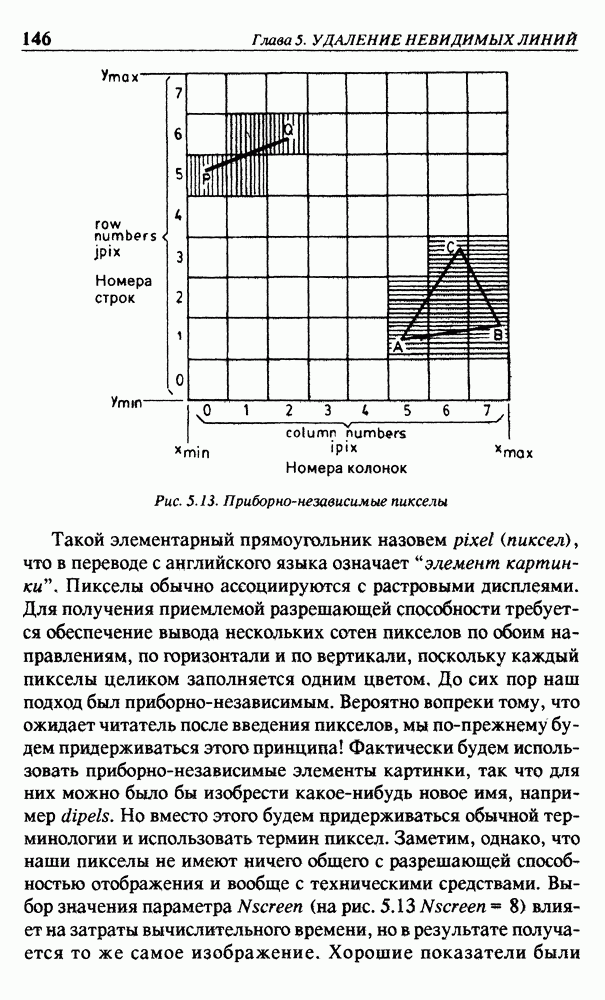
Если концевая точка вектора  задана в ортогональных координатах, то сначала вычислим его сферические координаты
задана в ортогональных координатах, то сначала вычислим его сферические координаты  (см. рис. 3.19)
(см. рис. 3.19)

Если  то будем считать, что
то будем считать, что  В противном случае
В противном случае  если
если 

Читателю, возможно, известно обратное вычисление

Теперь стратегия заключается в таком изменении системы координат, чтобы вектор  (ось вращения) совпадал с новым направлением положительной полуоси z. Начнем с поворота осей х и у вокруг оси z на угол
(ось вращения) совпадал с новым направлением положительной полуоси z. Начнем с поворота осей х и у вокруг оси z на угол  В соответствии с уравнением (3.19)
В соответствии с уравнением (3.19)

Ось х имеет положительное направление вектора  Теперь повернем оси
Теперь повернем оси  вокруг оси у на угол
вокруг оси у на угол  до совпадения оси
до совпадения оси  с вектором
с вектором  рис. 3.19).
рис. 3.19).
Обращаясь к уравнению (3.18), это условие запишем как

Фактический поворот вокруг вектора  на угол а теперь можно выполнить как поворот вокруг осиг". Из уравнения (3.15) получим
на угол а теперь можно выполнить как поворот вокруг осиг". Из уравнения (3.15) получим

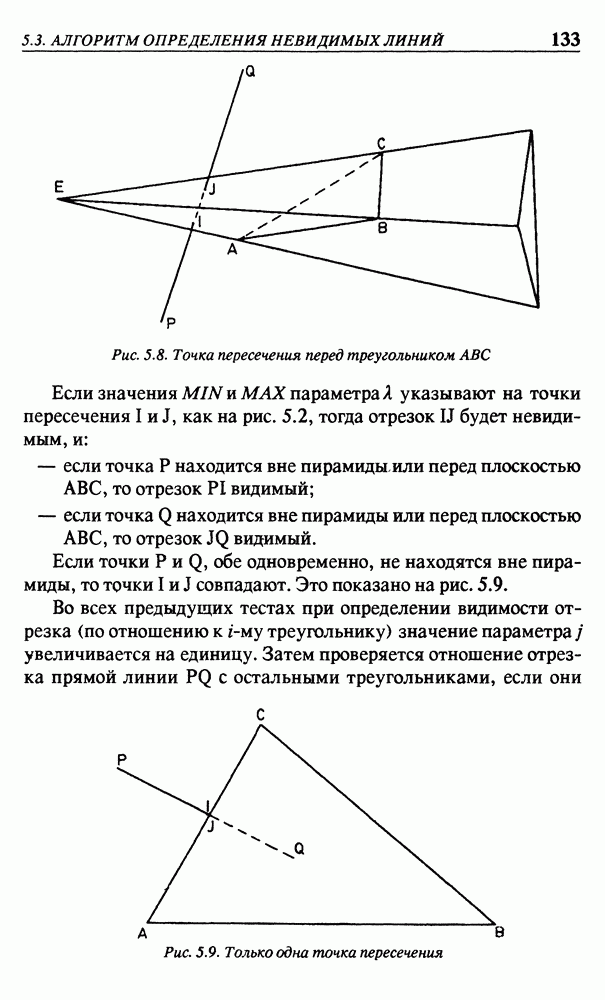
К этому моменту достигнуто выполнение соотношения


Рис. 3.19. Сферические координаты
К сожалению, координаты  относятся к самой последней системе координат, тоща как их необходимо выразить в исходной системе. Обозначим эти координаты в исходной системе через
относятся к самой последней системе координат, тоща как их необходимо выразить в исходной системе. Обозначим эти координаты в исходной системе через  Переход к исходной системе инвертированных матриц
Переход к исходной системе инвертированных матриц  (которые будут совпадать с матрицами
(которые будут совпадать с матрицами  и
и  в обратном порядке для преобразования точки
в обратном порядке для преобразования точки 

Это означает, что полный поворот вокруг вектора  на угол а вычисляется по следующей формуле:
на угол а вычисляется по следующей формуле:

где

Для последующего применения запишем

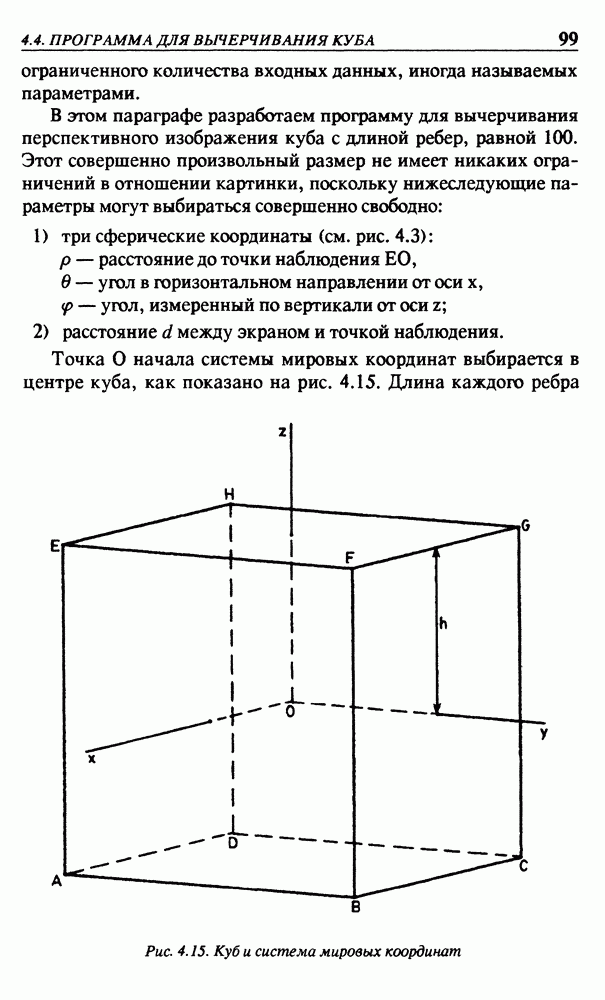
До сих пор обсуждалось решение задачи о повороте относительно вектора, привязанного к точке начала системы координат О. Теперь нужно устранить это последнее ограничение и поставить задачу определения поворота относительно вектора, начало которого расположено в любой произвольной точке 
Для этого будем использовать вектор  для вычисления матрицы
для вычисления матрицы  в уравнении (3.20) таким же образом, как и ранее. Затем нужно выполнить три следующих шага:
в уравнении (3.20) таким же образом, как и ранее. Затем нужно выполнить три следующих шага:
1. Обращаясь к уравнению (3.16), выполним перенос из заданной точки в точку начала координат О, используя однородные координаты и следующую матрицу:

2. Теперь можем осуществить поворот относительно оси, проходящей через О, как и ранее, но матрицу  из уравнения (3.20) необходимо расширить тривиальным образом, чтобы можно было использовать однородные координаты
из уравнения (3.20) необходимо расширить тривиальным образом, чтобы можно было использовать однородные координаты

3. Применить преобразование, обратное шагу 1, используя матрицу

После этого матрица обобщенного поворота вычисляется как

и ее можно использовать следующим образом:

УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
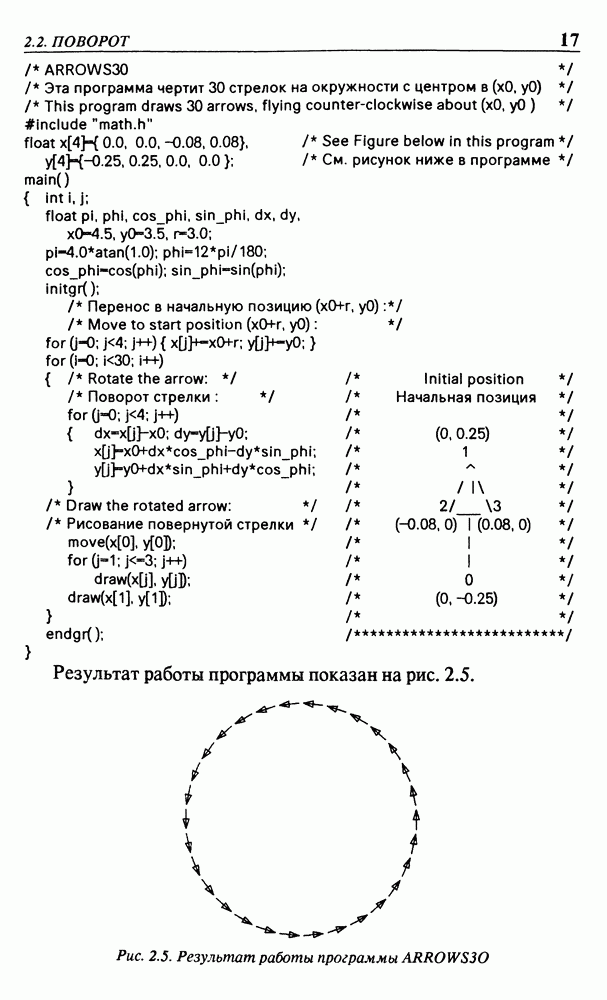
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
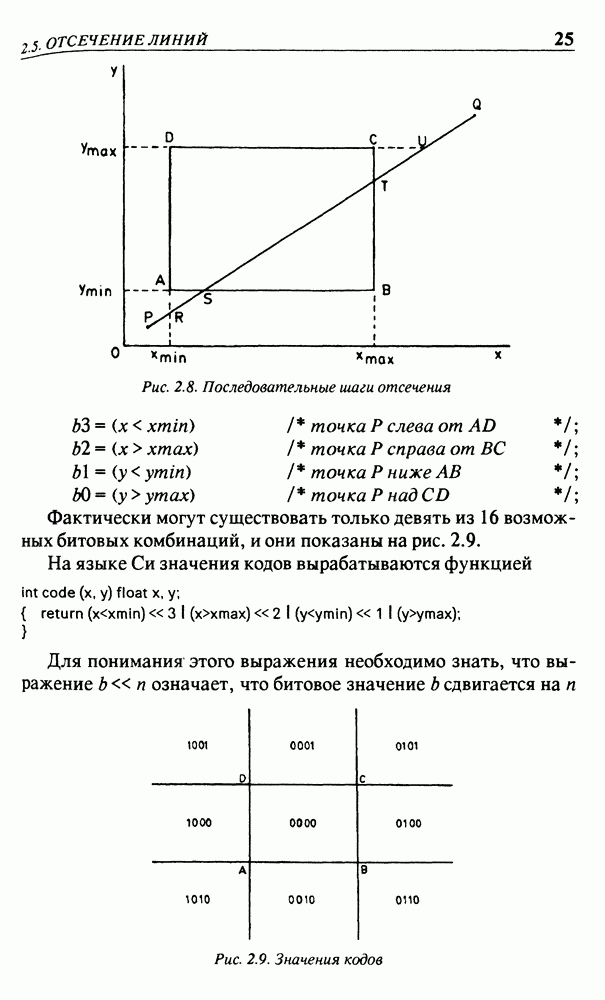
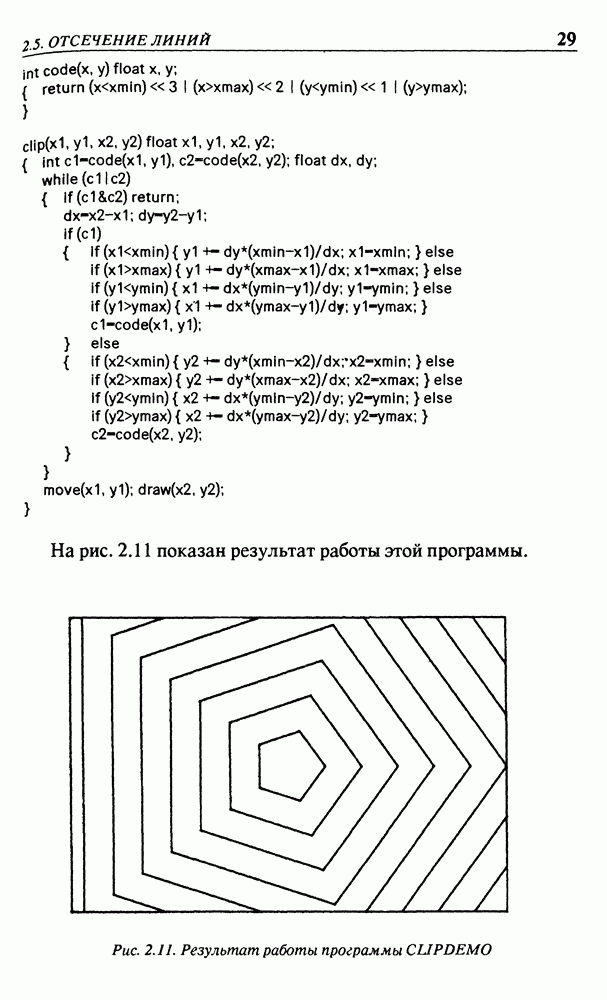
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
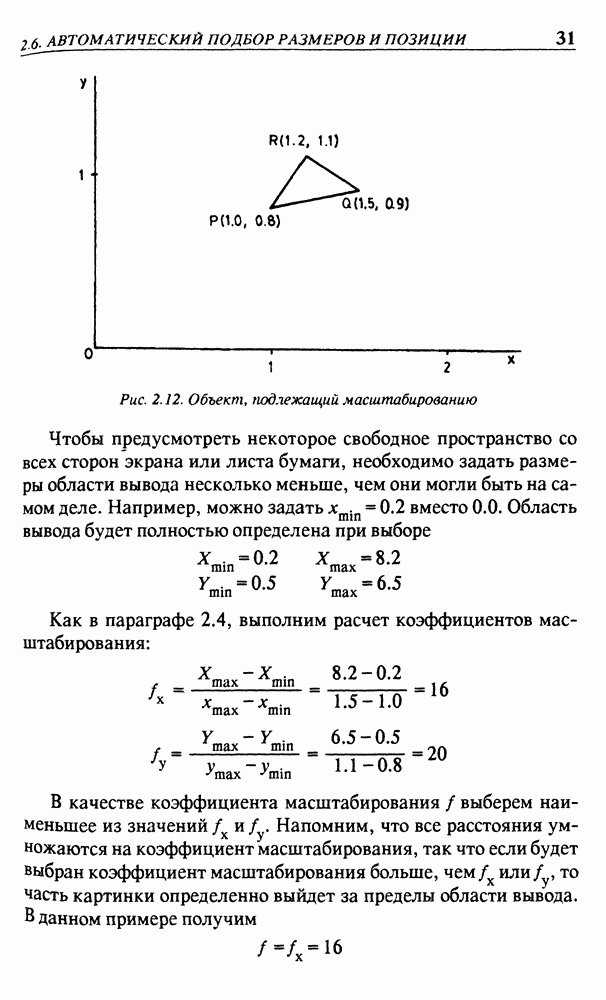
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
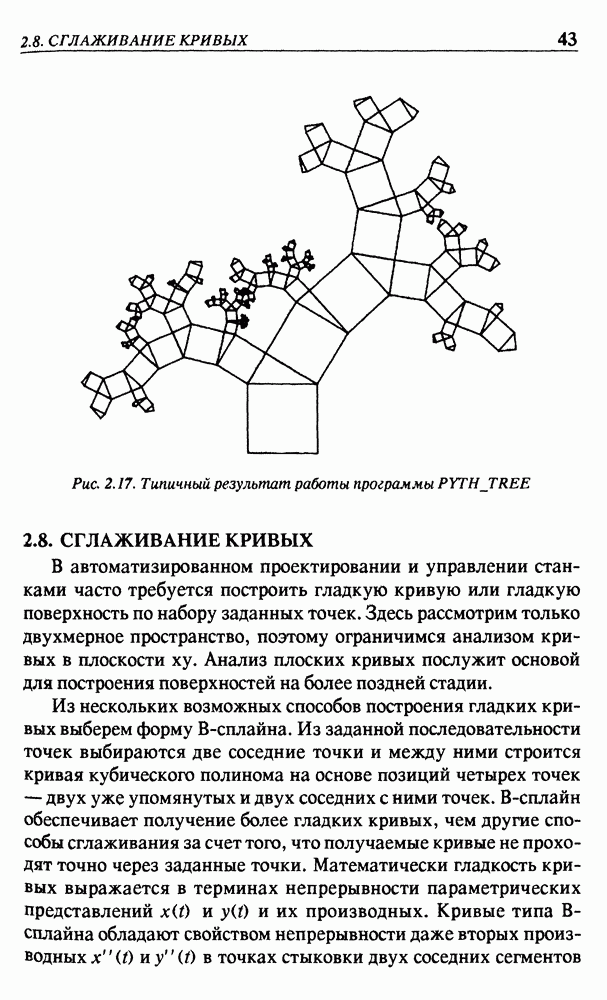
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
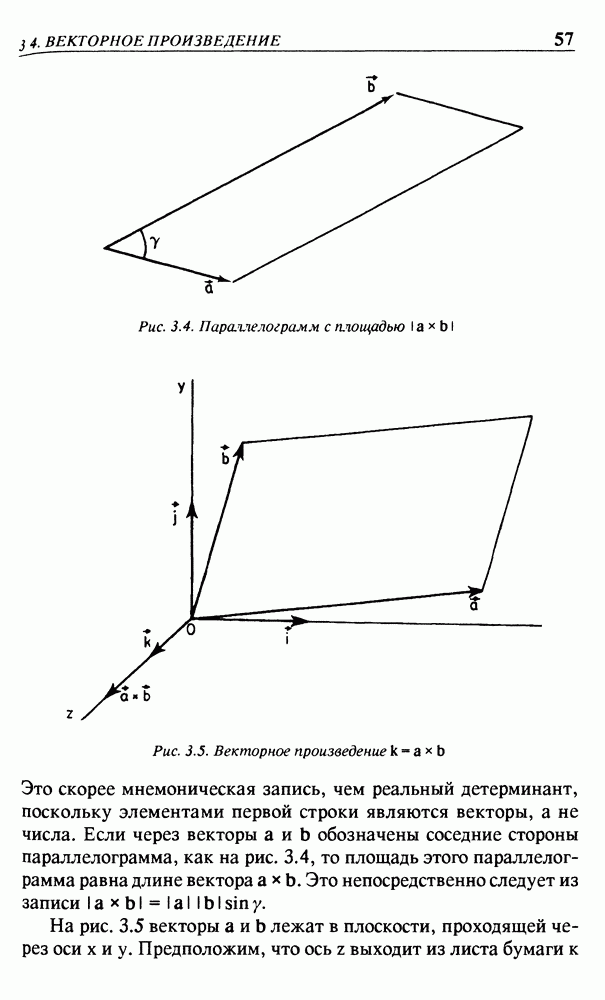
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
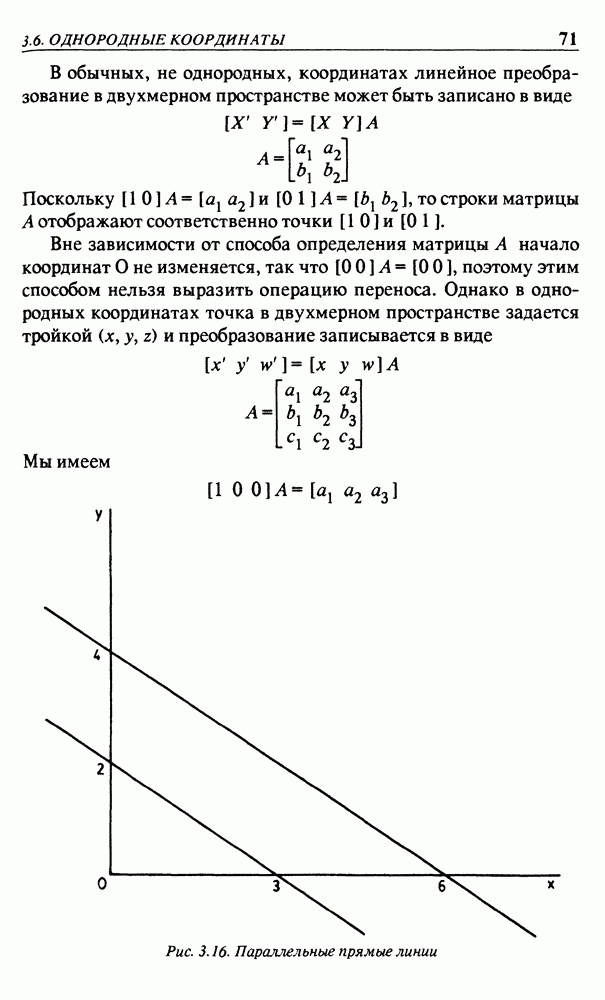
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
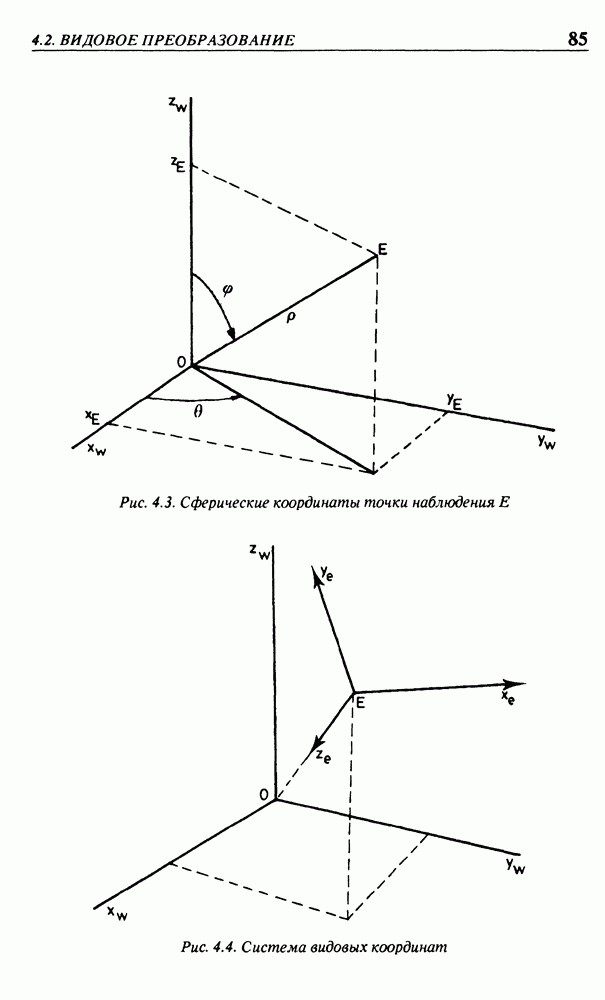
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
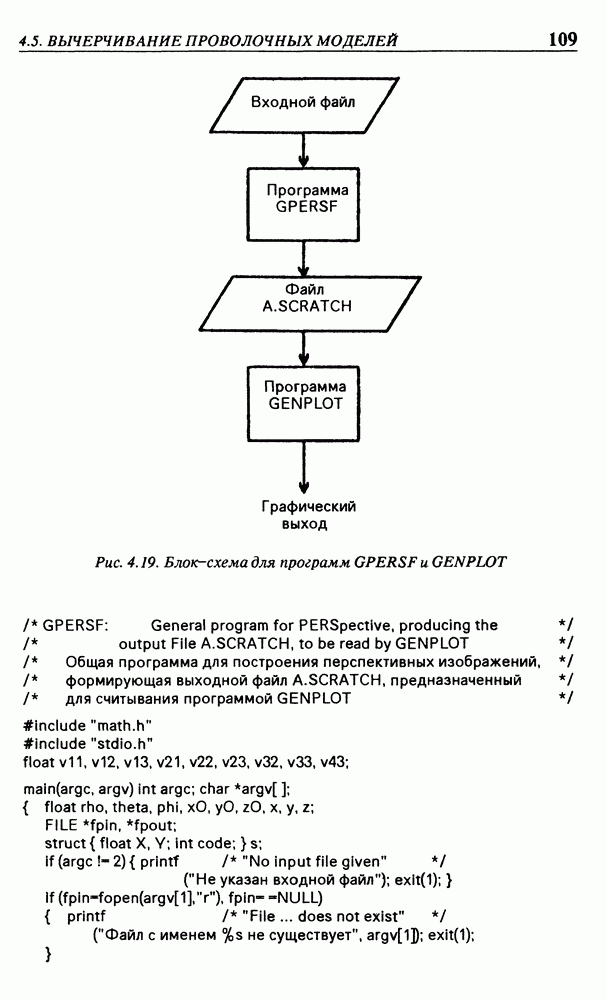
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
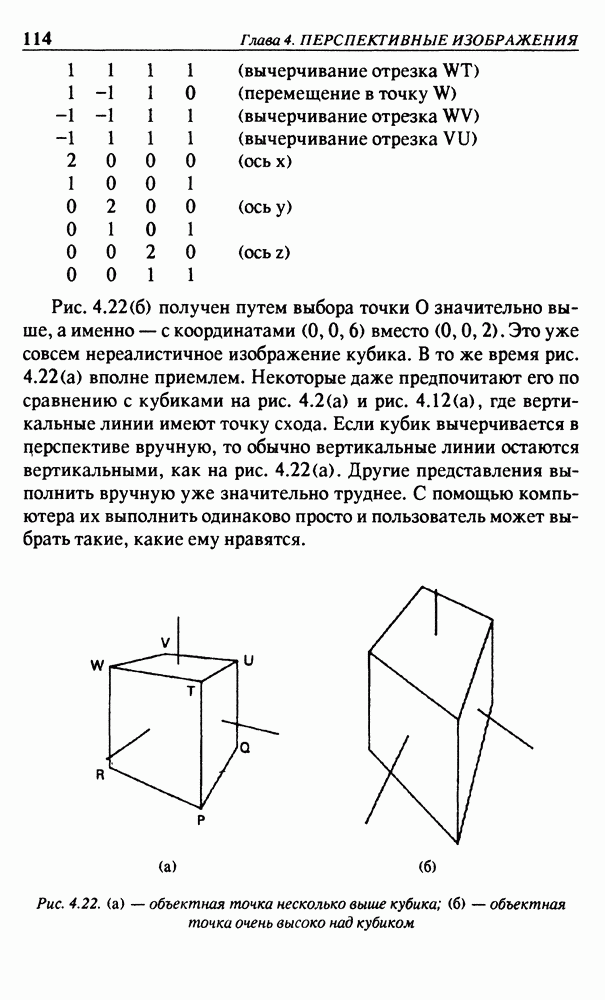
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
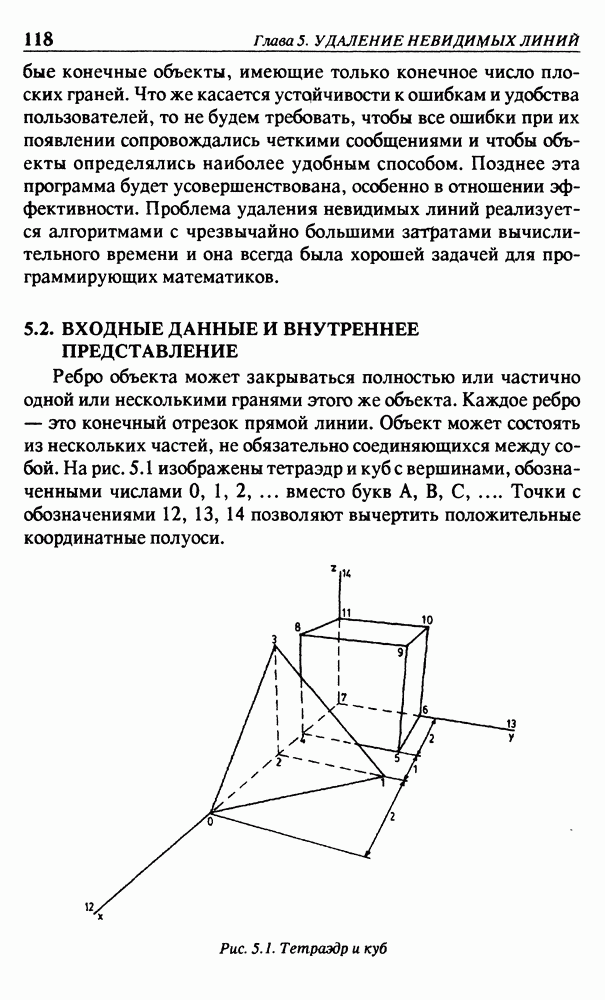
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
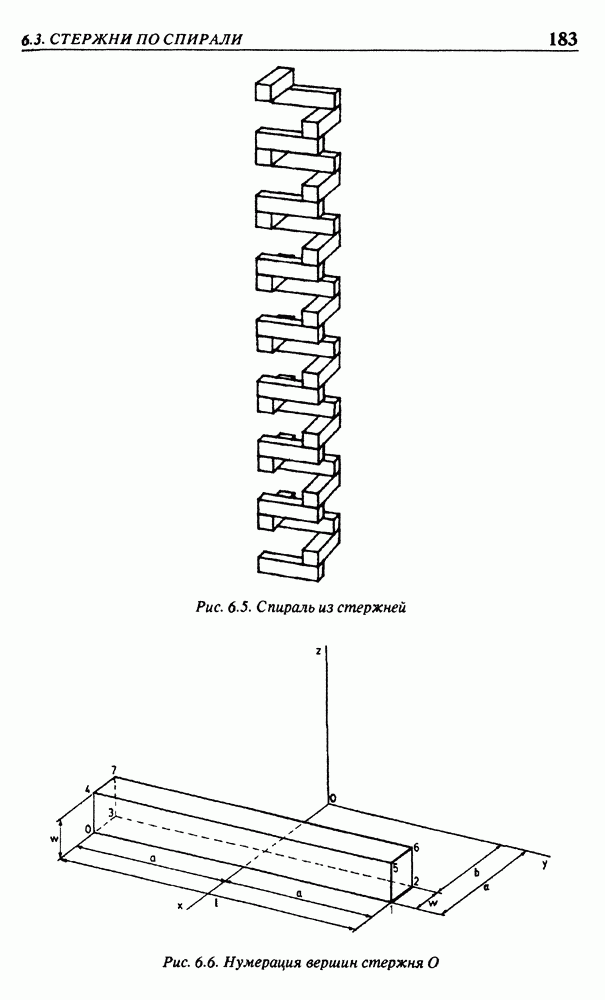
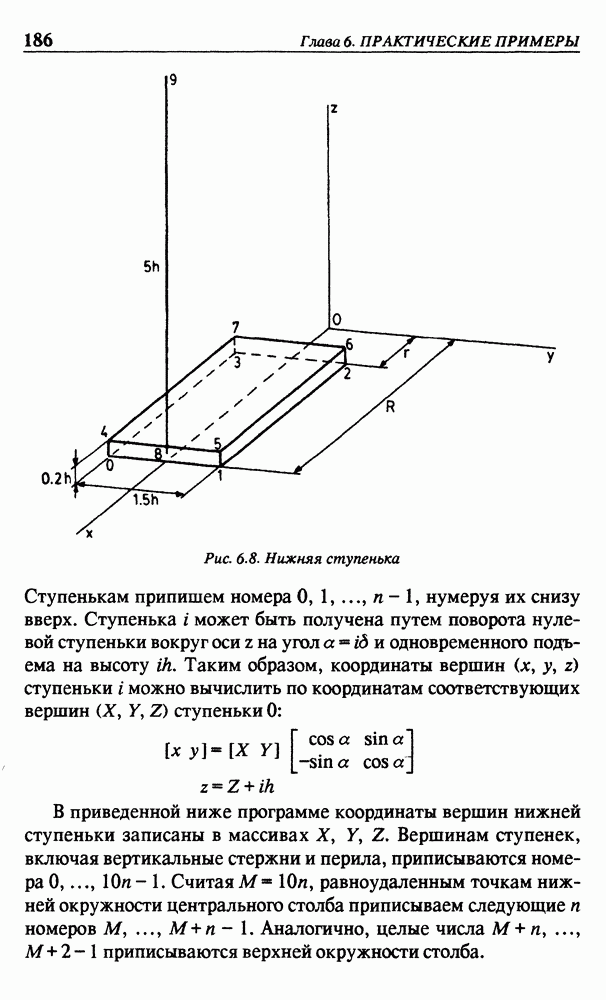
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
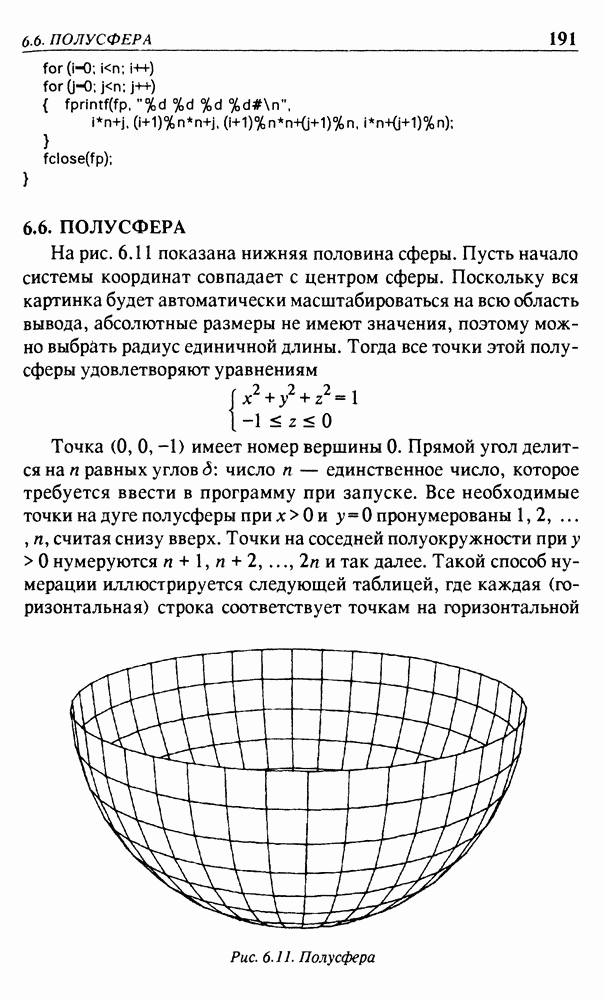
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА