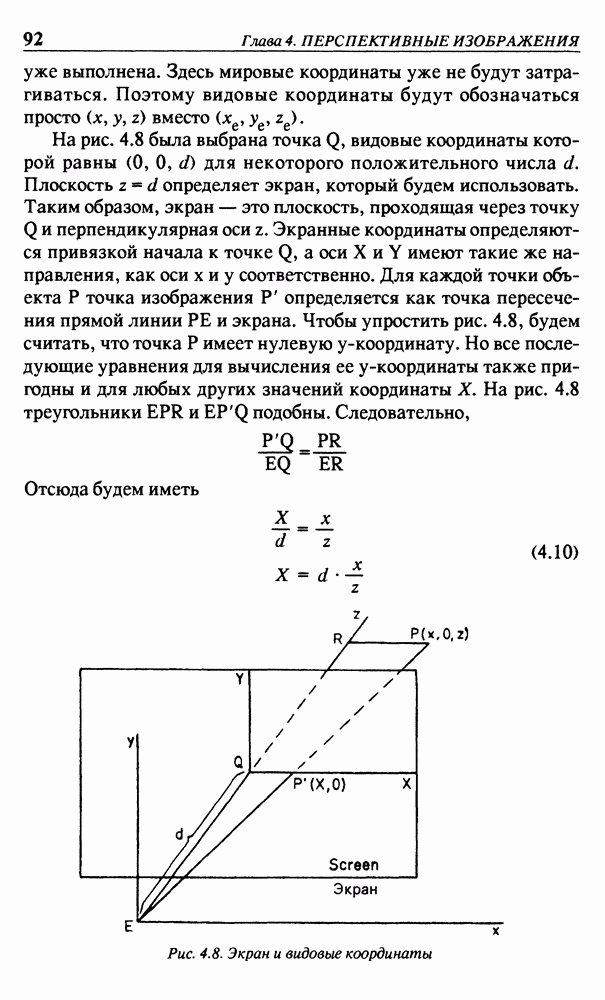
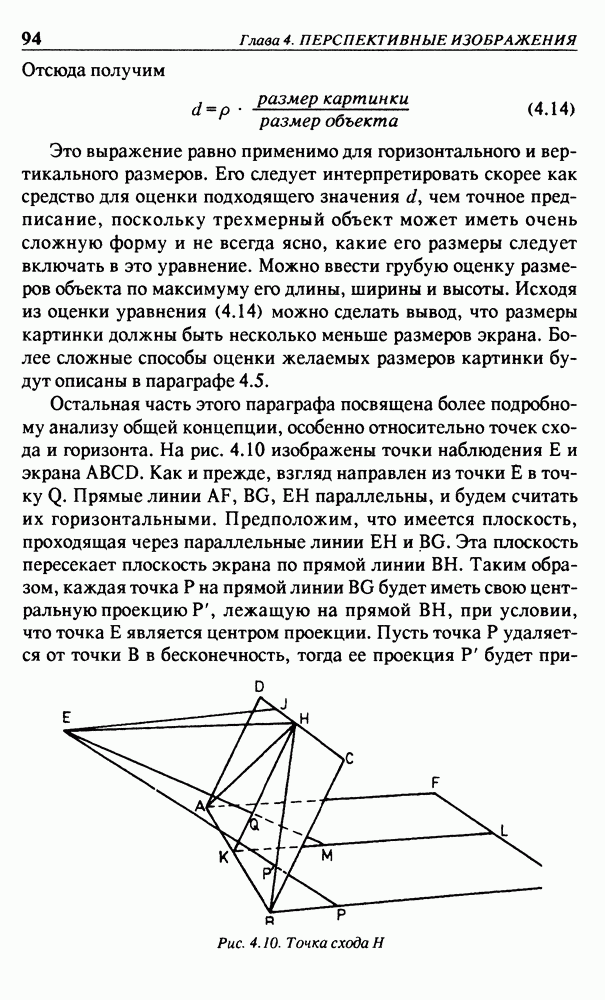
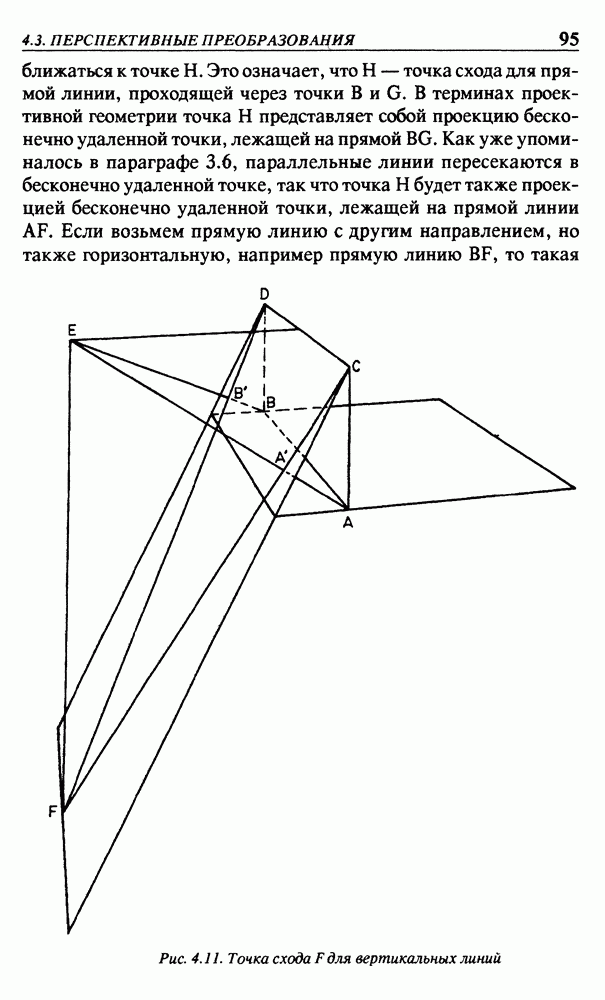
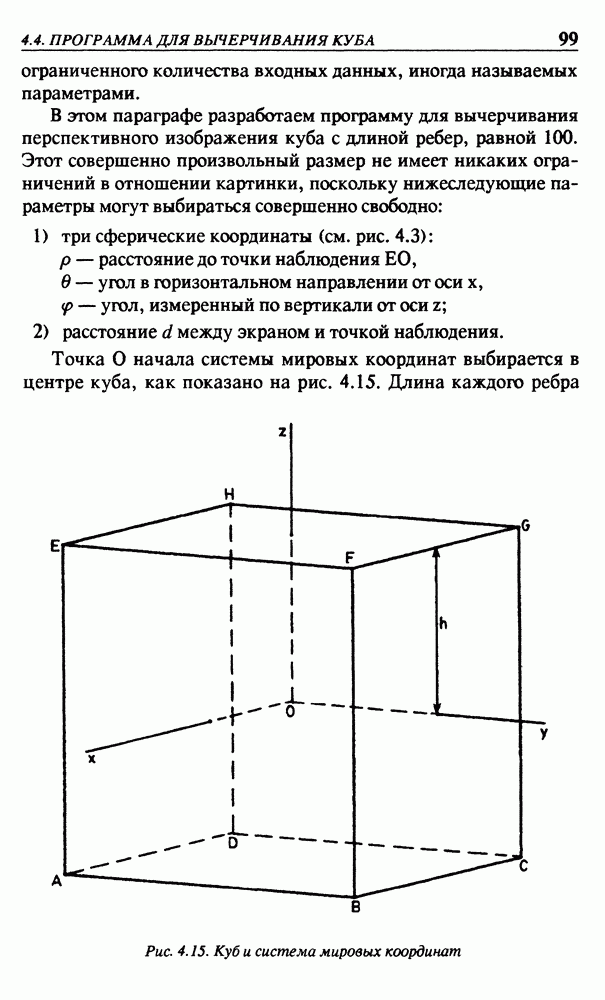
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
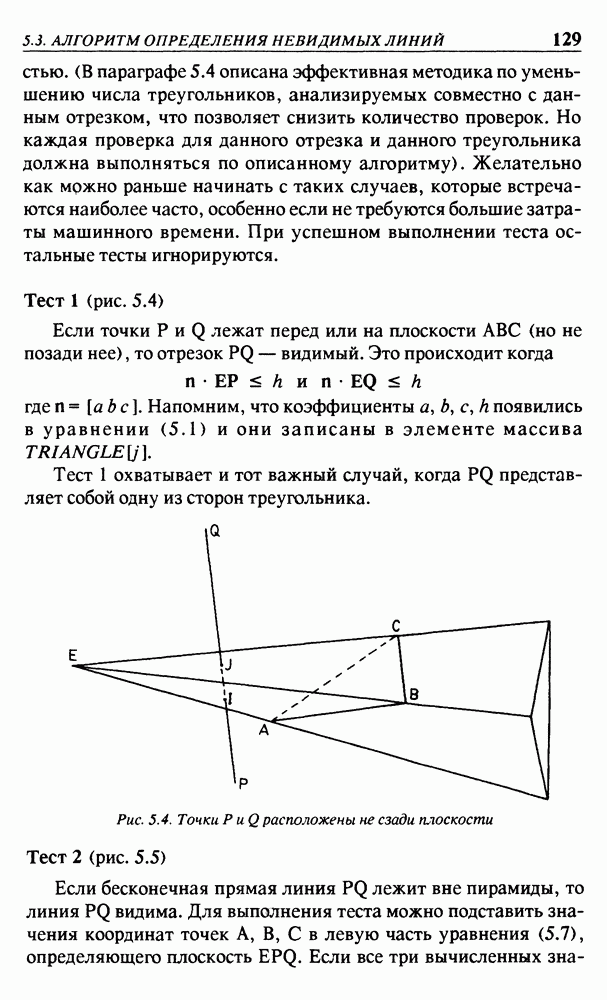
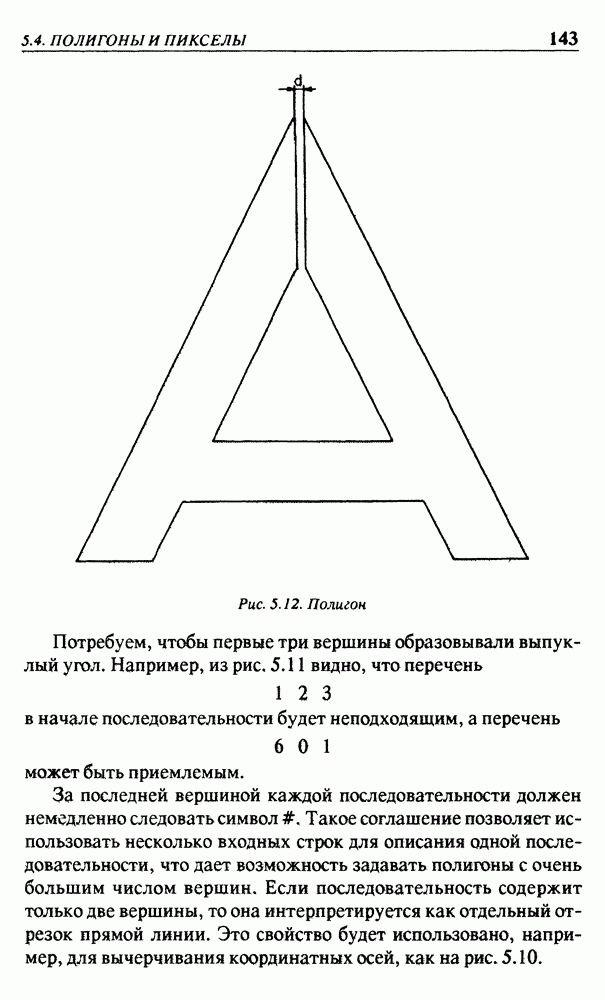
В главах 4 и 5 будут формироваться изображения трехмерных объектов, границы поверхностей которых могут быть полигонами. Это не очень серьезное ограничение, поскольку кривые по верхности могут аппроксимироваться большим числом полигонов, точно так же, как линии аппроксимируются последовательностью отрезков прямых линий. Обработка произвольных полигонов может привести к очень сложным ситуациям, особенно если нужно различать видимые и невидимые части отрезков прямых. На рис. 3.7 показан пример такой ситуации.
Если внутренние углы при всех вершинах полигона меньше 180°, то такой полигон называется выпуклым. На рис. 3.8(б) внутренний угол при вершине Р больше 180°. Такую вершину будем называть невыпуклой. Все другие вершины на рис. 3.8 — выпуклые. Если полигон имеет хотя бы одну невыпуклую вершину, то весь такой полигон будем называть невыпуклым.
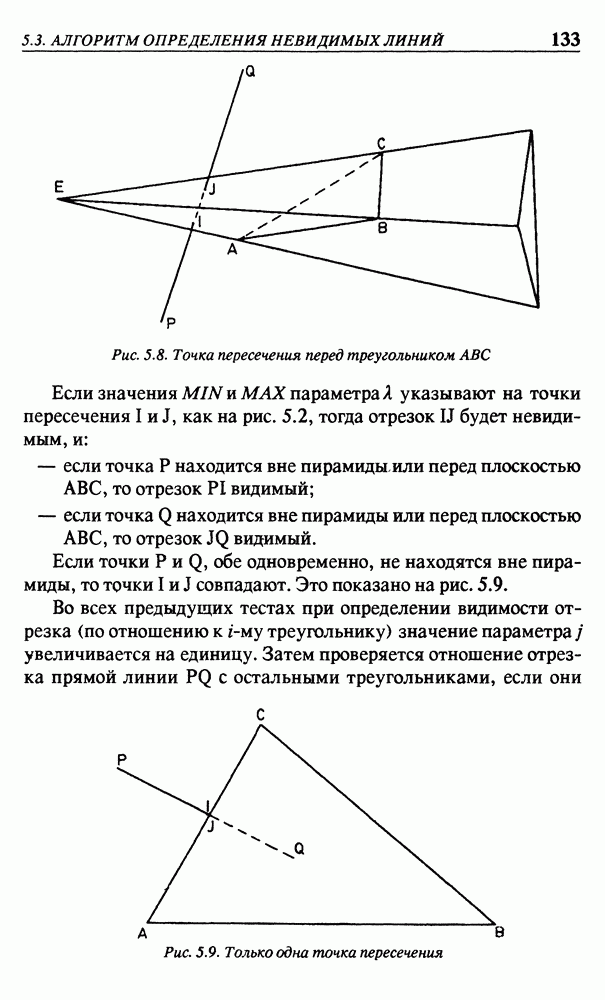
Если  две точки на границе выпуклого полигона, то и весь отрезок
две точки на границе выпуклого полигона, то и весь отрезок  будет принадлежать полигону. Для невыпуклых
будет принадлежать полигону. Для невыпуклых

Рис. 3.7. Два полигона частично перекрывают друг друга

Рис. 3.8. (а) - выпуклый полигон; (б) - невыпуклый полигон
полигонов это условие может не соблюдаться. Невыпуклость полигонов является источником сложностей, это же касается и переменного числа вершин полигонов. По этой причине уделим большое внимание треугольникам. Вполне очевидно, что треугольники всегда имеют фиксированное число вершин и они обязательно выпуклые. Особый интерес к ним выявляется в связи с рассмотрением произвольных полигонов, поскольку любой полигон может быть разбит на конечное число треугольников. Это и будет предметом рассмотрения данного параграфа.
Операция разбивки выпуклого полигона на треугольники чрезвычайно проста, как это видно из рис. 3.9. Если вершины полигона пронумеровать последовательно  а затем вычертить диагонали
а затем вычертить диагонали  то этого будет
то этого будет

Рис. 3.9. (а) - диагонали внутри полигона; (б) - диагональ  использовать нельзя
использовать нельзя
достаточно. В невыпуклом полигоне, как на рис. 3.9(6), этот простой способ работать не будет, поскольку некоторые из диагоналей  выходить за пределы полигона.
выходить за пределы полигона.
Составим теперь программу, которая будет считывать координаты вершин полигона и выполнит разбиение полигона на треугольники. Требуется, чтобы вершины были указаны обязательно в порядке обхода против часовой стрелки. Например, у полигона на рис. 3.9(б) верной окажется последовательность  а последовательность
а последовательность  будет непригодной. Для полигона с
будет непригодной. Для полигона с  вершинами сначала указывается количество вершин
вершинами сначала указывается количество вершин  затем последовательно перечисляются
затем последовательно перечисляются  пар координат всех вершин в порядке обхода полигона против часовой стрелки. В результате будет получен чертеж полигона с вычерченными диагоналями, полностью разбивающими весь полигон на треугольники. Перед вычерчиванием диагоналей необходимо удостовериться, что все диагонали лежат полностью внутри полигона.
пар координат всех вершин в порядке обхода полигона против часовой стрелки. В результате будет получен чертеж полигона с вычерченными диагоналями, полностью разбивающими весь полигон на треугольники. Перед вычерчиванием диагоналей необходимо удостовериться, что все диагонали лежат полностью внутри полигона.
Предположим, что  обозначают три соседние вершины, причем будем считать, что
обозначают три соседние вершины, причем будем считать, что  чтобы можно было рассматривать случаи, когда
чтобы можно было рассматривать случаи, когда  Напомним, что вершины должны быть перечислены в порядке обхода против часовой стрелки. В этом случае Р. будет выпуклой вершиной тогда, и только тогда, когда три вершины
Напомним, что вершины должны быть перечислены в порядке обхода против часовой стрелки. В этом случае Р. будет выпуклой вершиной тогда, и только тогда, когда три вершины  именно в этом порядке будут обходиться в направлении против
именно в этом порядке будут обходиться в направлении против

Рис. 3.10. Диагональ  вне полигона
вне полигона
часовой стрелки. В качестве контрпримера рассмотрим рис. 3.10, в котором обход тройки  выполняется по часовой стрелке. Вершина
выполняется по часовой стрелке. Вершина  является невыпуклой, и диагональ
является невыпуклой, и диагональ  лежит вне полигона. Таким образом, диагональ
лежит вне полигона. Таким образом, диагональ  может быть только кандидатом для наших целей, если три вершины
может быть только кандидатом для наших целей, если три вершины  именно в этом порядке, обходятся в направлении против часовой стрелки, то есть если
именно в этом порядке, обходятся в направлении против часовой стрелки, то есть если

Это условие является необходимым, но, к сожалению, недостаточным, как это показано на рис. 3.11. Здесь точки  обходятся именно в таком порядке, в направлении против часе
обходятся именно в таком порядке, в направлении против часе

Рис. 3.11. Диагональ Р Р частично находится вне полигона
вой стрелки, но отрезок  нельзя использовать для деления полигона на треугольники. Такой ситуации можно избежать, если принимать во внимание также длину диагоналей Будем выбирать наикратчайшую диагональ
нельзя использовать для деления полигона на треугольники. Такой ситуации можно избежать, если принимать во внимание также длину диагоналей Будем выбирать наикратчайшую диагональ  которую может иметь выпуклая вершина
которую может иметь выпуклая вершина  между точками
между точками  . Эта диагональ используется для отсечения треугольника
. Эта диагональ используется для отсечения треугольника  Затем таким же образом проверяется оставшийся полигон
Затем таким же образом проверяется оставшийся полигон

и так далее. Технически это реализуется введением целочисленного массива  содержащего номера вершин оставшегося полигона. Вначале задаем
содержащего номера вершин оставшегося полигона. Вначале задаем  Каждый раз при отсечении треугольника число
Каждый раз при отсечении треугольника число  уменьшается на единицу. Если подобная программа предназначается для практического применения, то желательно выполнить некоторое число испытаний на допустимость входных данных. Программа, которая надежно отвергает любой непригодный набор данных, может быть названа устойчивой. В нашей ситуации необходимо провести испытание, действительно ли заданный набор координат точек
уменьшается на единицу. Если подобная программа предназначается для практического применения, то желательно выполнить некоторое число испытаний на допустимость входных данных. Программа, которая надежно отвергает любой непригодный набор данных, может быть названа устойчивой. В нашей ситуации необходимо провести испытание, действительно ли заданный набор координат точек

вообще описывает полигон. Например, совершенно непригодна последовательность

поскольку обход точек в заданном порядке приведет к ситуации, показанной на рис. 3.12, но в качестве полигона такую фигуру принять нельзя.

Рис. 3.12. Результат недопустимой последовательности
Из других проверок следует обратить внимание на:
- максимальное количество точек  , например,
, например,  ;
;
- минимальное и максимальное значения координат;
- ориентацию обхода точек в направлении против часовой стрелки.
Несмотря на их очевидную важность, большинство проверок здесь опущено и они оставлены для упражнений читателя. С другой стороны, в программу включены некоторые специальные средства, которые, вообще говоря, можно опустить. Это относится к представлению диагоналей в виде штриховых линий вместо сплошных. Пусть все штрихи должны иметь одинаковую длину. Штриховая линия не должна начинаться или кончаться пробелом, в начале и в конце штрихи должны быть полной длины, как это показано для отрезка PQ на рис. 3.13.

Рис. 3.13. Штриховая линия
Читателю предлагается самостоятельно решить эту проблему и сравнить свое решение с функцией  из следующей программы:
из следующей программы:
(см. скан)
(см. скан)

Рис. 3.14. Результат работы программы  приведет к выводу изображения, показанного на рис. 3.14.
приведет к выводу изображения, показанного на рис. 3.14.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
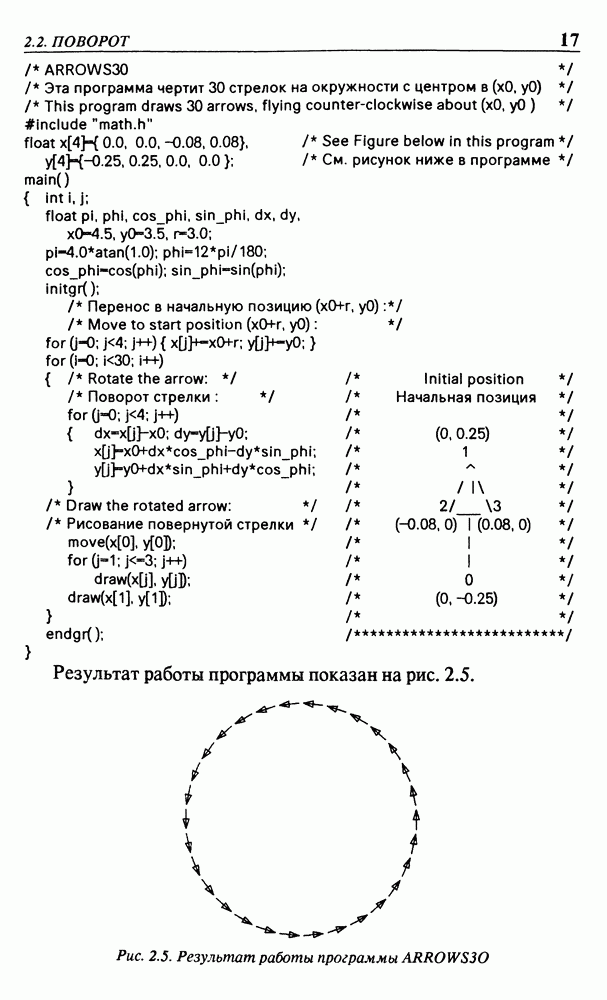
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
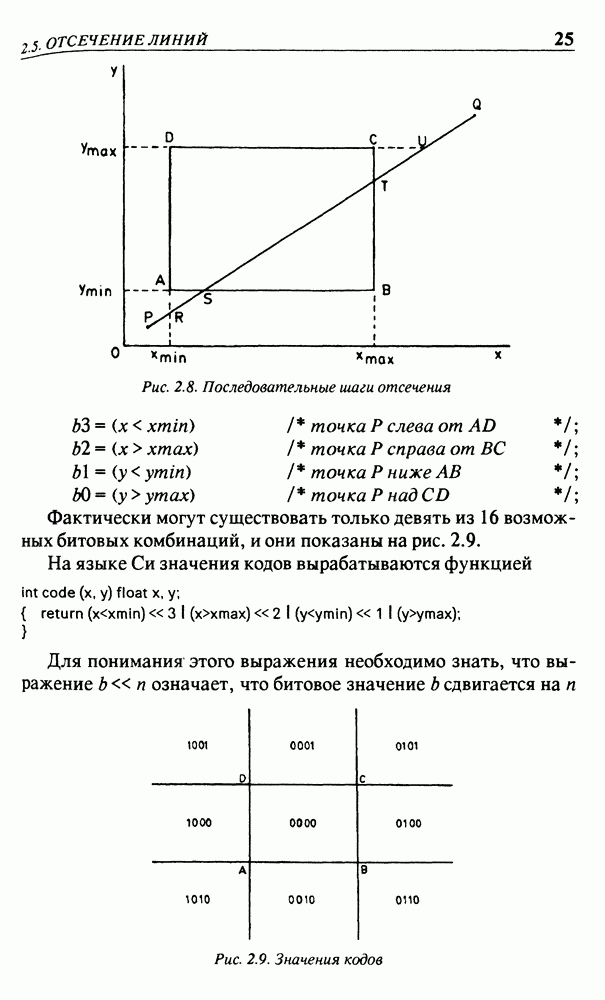
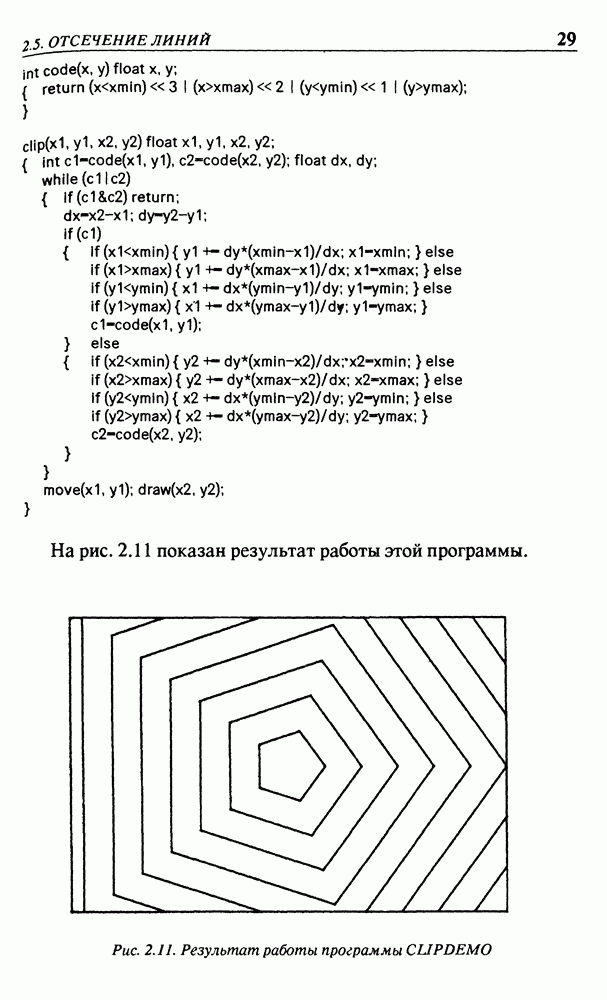
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
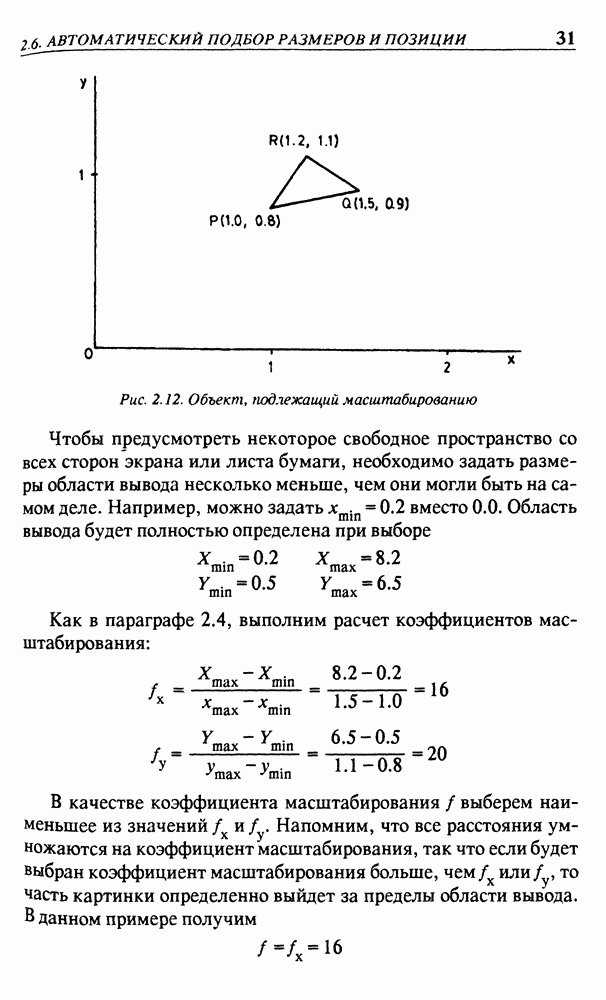
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
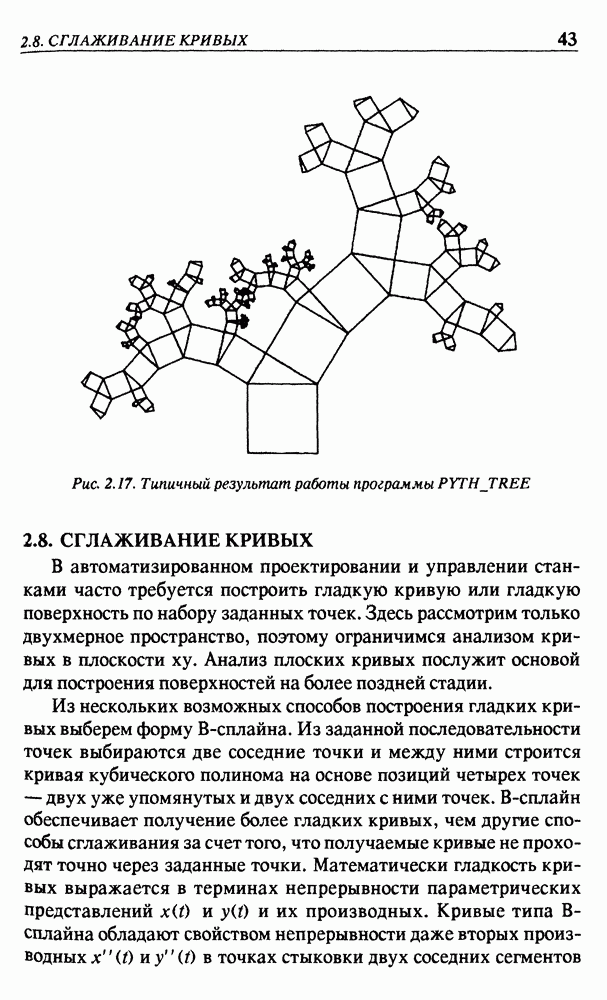
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
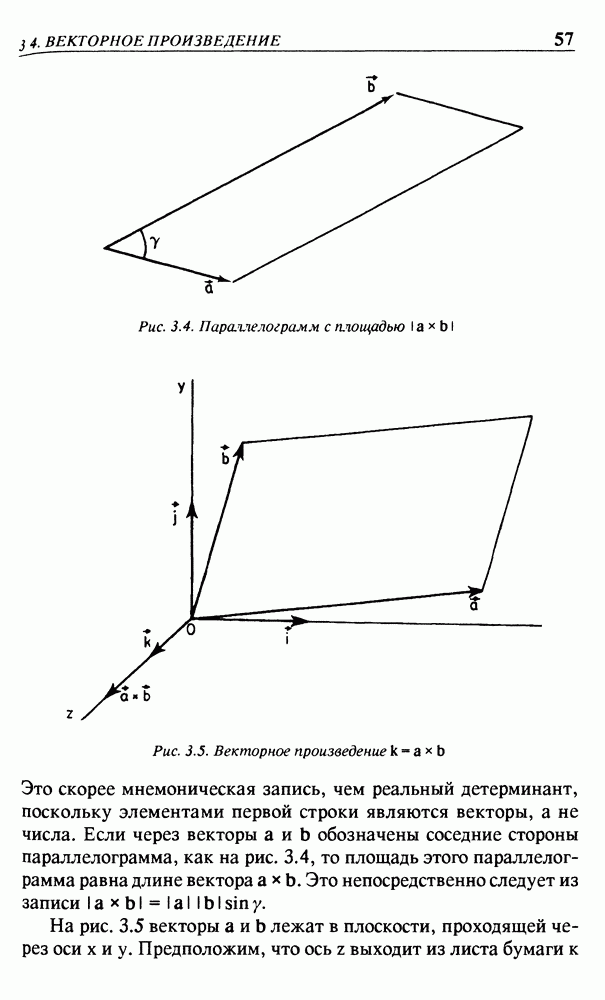
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
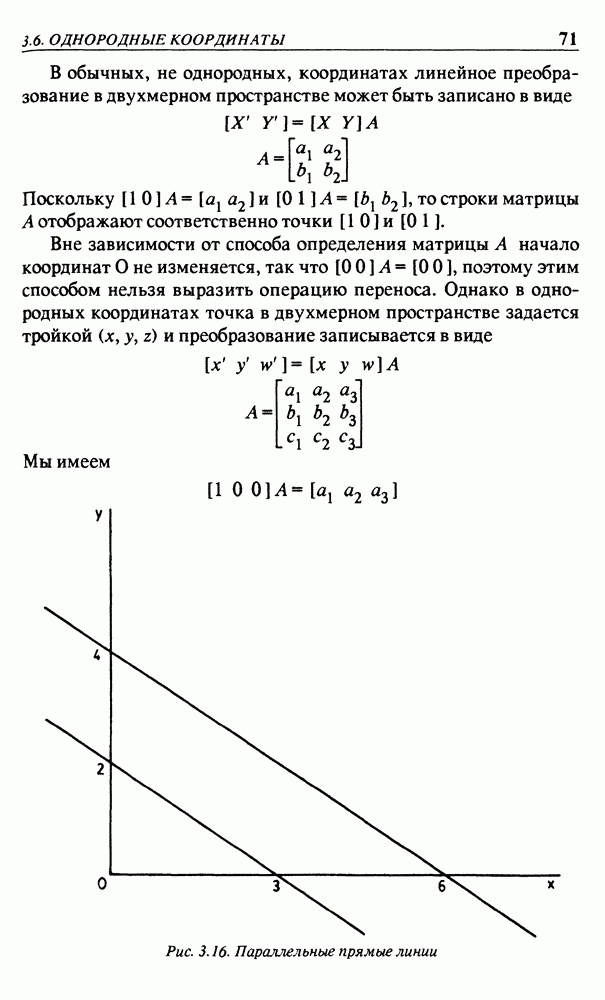
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
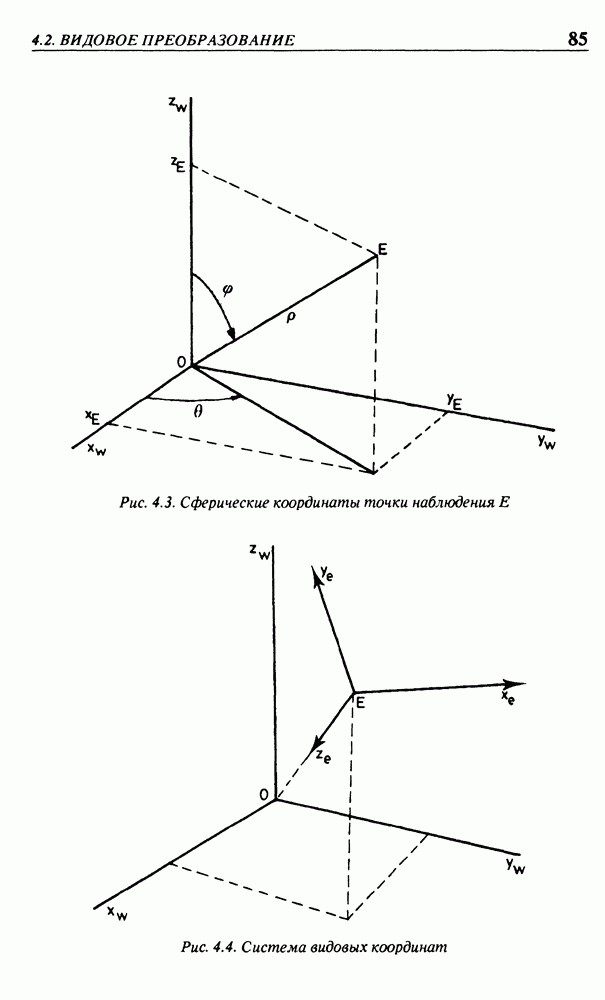
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
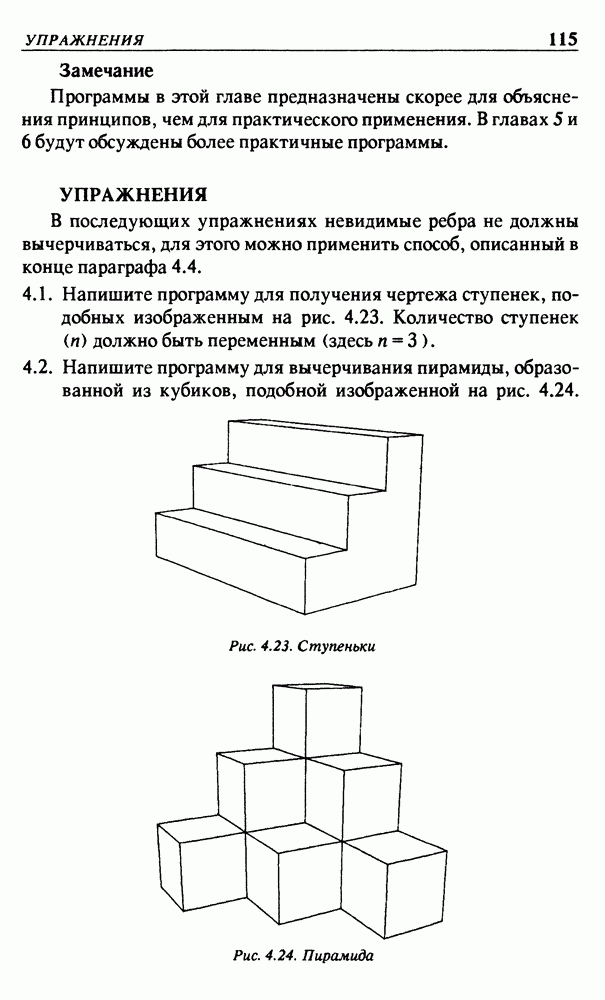
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
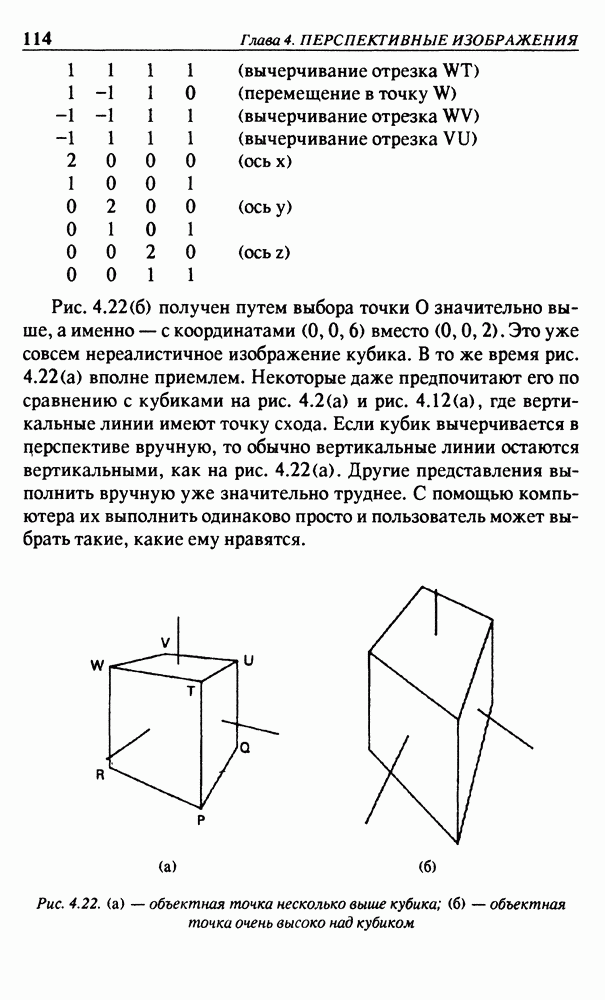
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
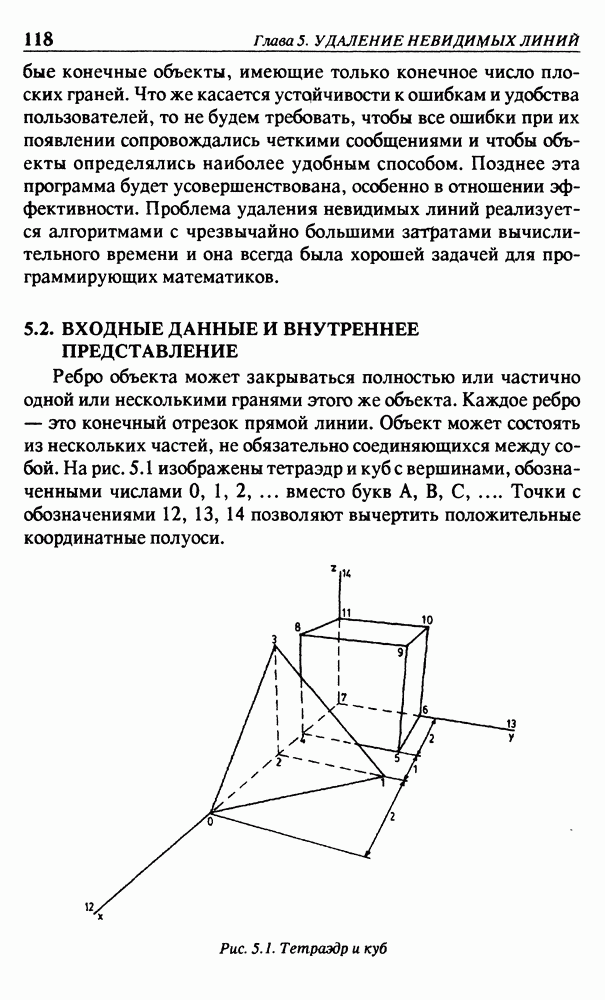
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
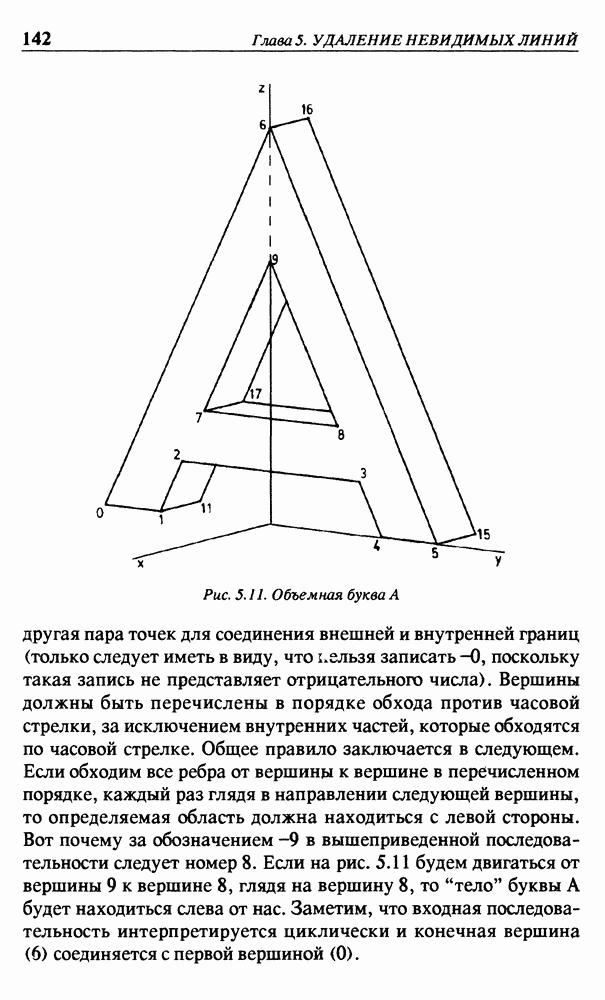
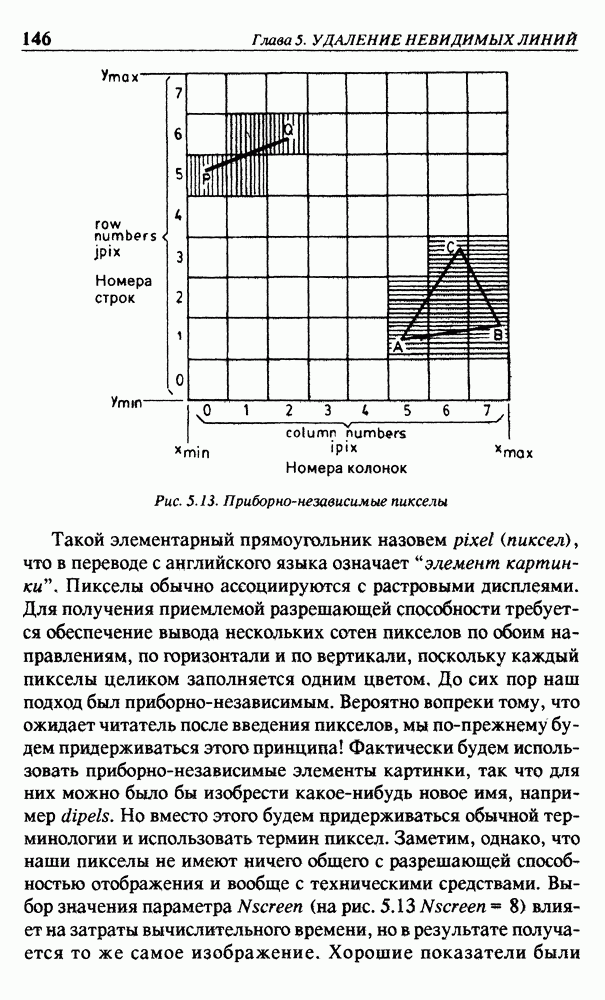
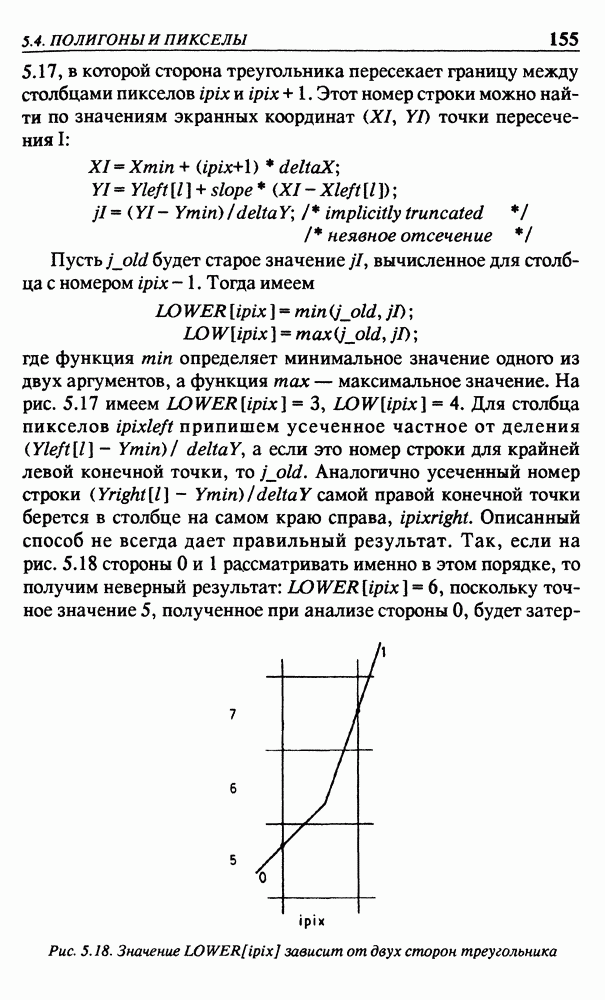
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
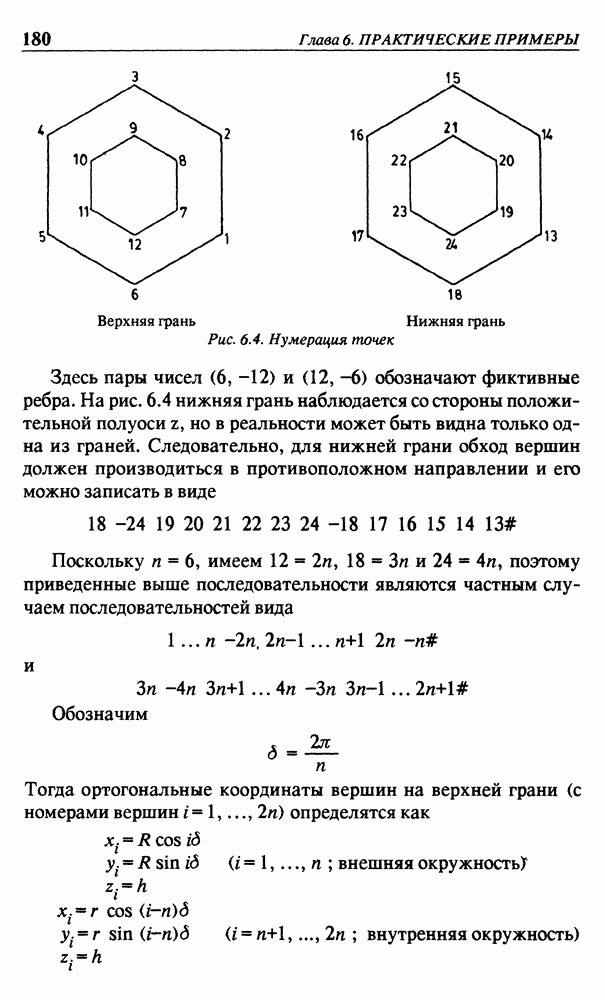
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
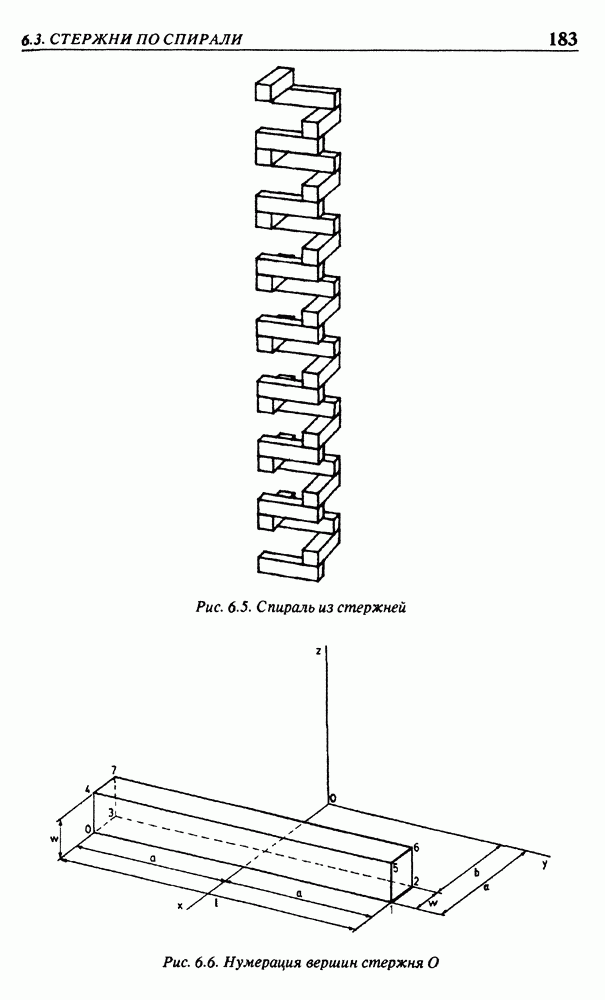
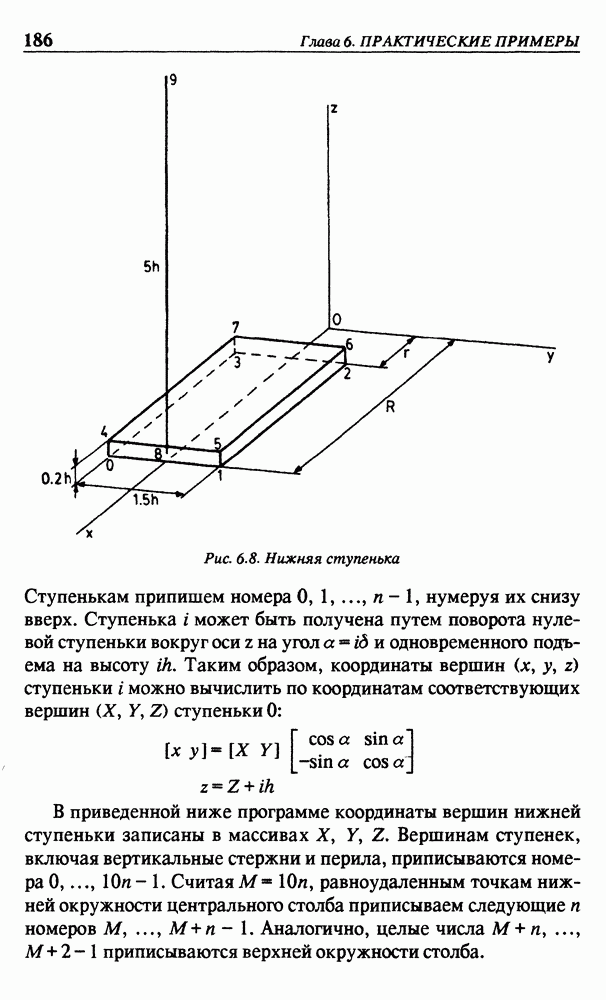
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
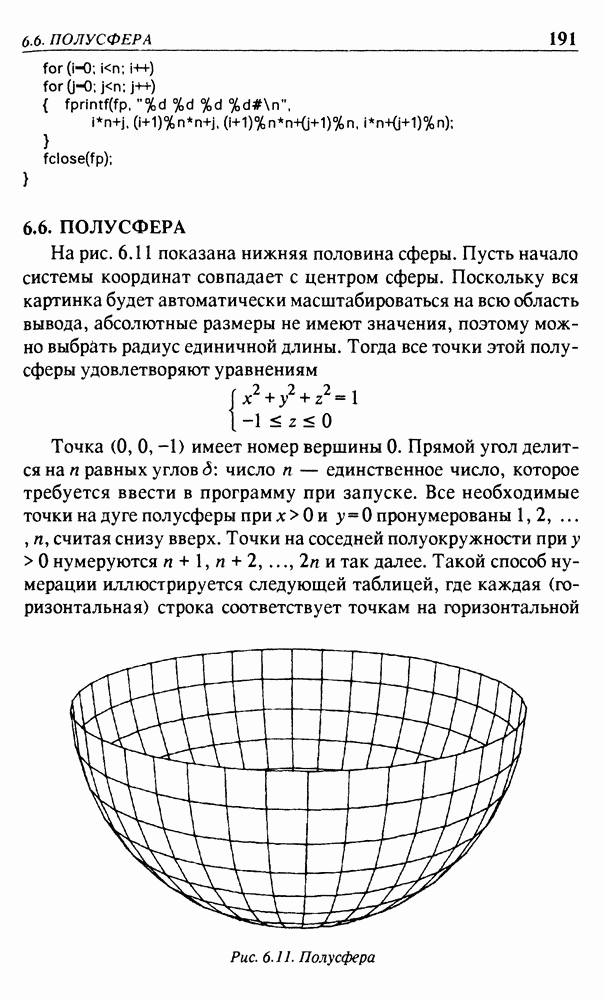
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА