| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
Разработаем теперь очень важный алгоритм, задача которого заключается в вычерчивании только видимых частей отрезка
 Для краткости часто будем записывать
Для краткости часто будем записывать  для обозначения “отрезка прямой линии
для обозначения “отрезка прямой линии  являющегося частью бесконечной прямой, проходящей через точки
являющегося частью бесконечной прямой, проходящей через точки  Для каждого треугольника ABC из списка, записанного в массив
Для каждого треугольника ABC из списка, записанного в массив  необходимо выполнить проверку — не будет ли он закрывать PQ (или его часть). Как и ранее, Е — точка наблюдения. Будем говорить, что треугольник ABC закрывает точку
необходимо выполнить проверку — не будет ли он закрывать PQ (или его часть). Как и ранее, Е — точка наблюдения. Будем говорить, что треугольник ABC закрывает точку  если отрезок
если отрезок  пересекает треугольник ABC в точке, внутренней как по отношению к отрезку, так и по отношению к треугольнику. Стороны треугольника не относятся к внутренним точкам, а концевые точки отрезка не являются внутренними для отрезка. Таким образом, точка
пересекает треугольник ABC в точке, внутренней как по отношению к отрезку, так и по отношению к треугольнику. Стороны треугольника не относятся к внутренним точкам, а концевые точки отрезка не являются внутренними для отрезка. Таким образом, точка  не закрывается треугольником ABC ни в том случае, когда точка
не закрывается треугольником ABC ни в том случае, когда точка  принадлежит внутренней части треугольника, ни в том случае, когда она принадлежит стороне треугольника, закрытой другим треугольником. Если треугольник ABC не закрывает точку
принадлежит внутренней части треугольника, ни в том случае, когда она принадлежит стороне треугольника, закрытой другим треугольником. Если треугольник ABC не закрывает точку  то будем говорить, что точка
то будем говорить, что точка  видима по отношению к треугольнику
видима по отношению к треугольнику  Если только конечное число точек отрезка PQ видимо по отношению к треугольнику
Если только конечное число точек отрезка PQ видимо по отношению к треугольнику  все равно будем говорить, что ABC закрывает
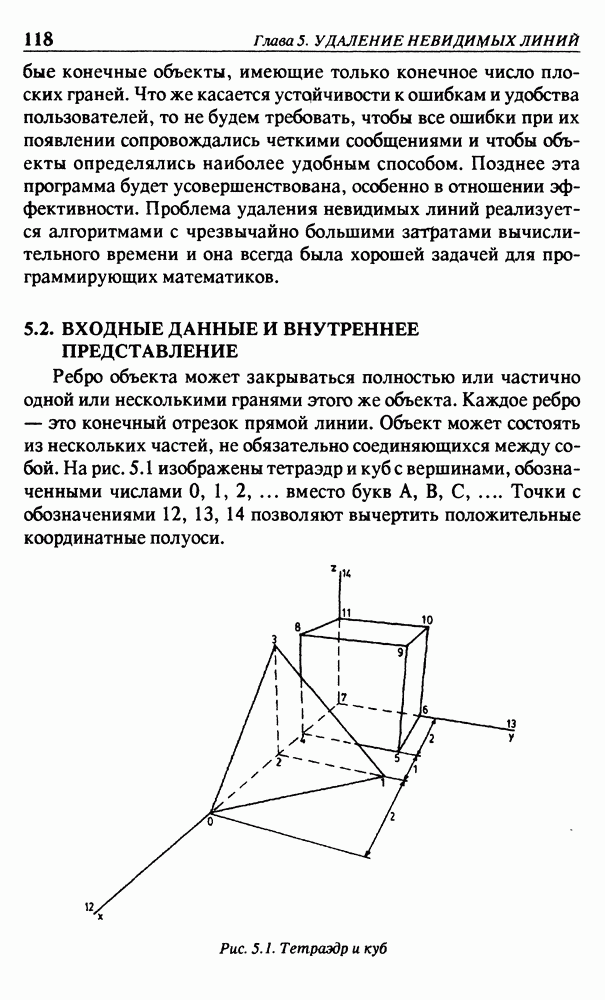
все равно будем говорить, что ABC закрывает  Например, на рис. 5.1 треугольник 130 закрывает отрезок 12, хотя этот треугольник не закрывает точку 1. Если треугольник не закрывает
Например, на рис. 5.1 треугольник 130 закрывает отрезок 12, хотя этот треугольник не закрывает точку 1. Если треугольник не закрывает  нельзя сделать заключение, что все точки PQ видимы по отношению к этому треугольнику, поскольку треугольник может закрыть PQ частично. Треугольник частично закрывает
нельзя сделать заключение, что все точки PQ видимы по отношению к этому треугольнику, поскольку треугольник может закрыть PQ частично. Треугольник частично закрывает  если он закрывает бесконечно много точек отрезка PQ и в то же время бесконечно много точек этого отрезка остаются видимыми по отношению к этому треугольнику.
если он закрывает бесконечно много точек отрезка PQ и в то же время бесконечно много точек этого отрезка остаются видимыми по отношению к этому треугольнику.
Если некоторый треугольник закрывает  то нет необходимости учитывать оставшиеся треугольники в списке, но можно немедленно прийти к заключению, что PQ закрыт и не должен вычерчиваться.
то нет необходимости учитывать оставшиеся треугольники в списке, но можно немедленно прийти к заключению, что PQ закрыт и не должен вычерчиваться.
Обсудим видимость отрезка прямой линии PQ по отношению к треугольнику ABC в алгоритмическом смысле. Пусть заданы видовые координаты  и так далее для пяти точек
и так далее для пяти точек  и коэффициенты
и коэффициенты  уравнения
уравнения  Вся информация о треугольнике ABC сохраняется в элементе массива
Вся информация о треугольнике ABC сохраняется в элементе массива  Ключевым фактором в нашем анализе будет бесконечная пирамида, вершина которой находится в точке Е, а боковые грани проходят через стороны треугольника
Ключевым фактором в нашем анализе будет бесконечная пирамида, вершина которой находится в точке Е, а боковые грани проходят через стороны треугольника 

Рис. 5.2. Пирамида
 Эту пирамиду для краткости назовем одним словом “пирамида”, а треугольник
Эту пирамиду для краткости назовем одним словом “пирамида”, а треугольник  термином “треугольник”.
термином “треугольник”.
Все внутри пирамиды позади треугольника будет невидимым, а все точки впереди или вне пирамиды — видимыми (относительно данного треугольника). На рис. 5.2 отрезок прямой линии PQ пересекает пирамиду в двух точках —  Часть
Часть  отрезка PQ будет невидимой, а части
отрезка PQ будет невидимой, а части  и
и  видимыми. (Ради краткости вместо фразы “видимый по отношению к треугольнику ABC” будем применять термин “видимый”.)
видимыми. (Ради краткости вместо фразы “видимый по отношению к треугольнику ABC” будем применять термин “видимый”.)
Сложность нашей задачи заключается в очень большом количестве случаев, которые предстоит рассмотреть. В ситуации, показанной на рис. 5.2, можем вычислить положение точки I следующим образом. Векторное представление прямой линии PQ записывается в виде

где  , откуда
, откуда

точка  принадлежит прямой линии
принадлежит прямой линии  если
если

Для значений А между 0 и 1 точка лежит между точками  Уравнение плоскости
Уравнение плоскости  может быть записано как
может быть записано как

поскольку эта плоскость проходит через точки  Уравнение можно переписать в виде
Уравнение можно переписать в виде

где

Подставляя правые части уравнений (5.3) в уравнение (5.4), находим

Используя значение  в уравнении (5.3), получаем координаты точки
в уравнении (5.3), получаем координаты точки  Изображенная на рис. 5.2 ситуация возникает только тогда, когда значение А находится в пределах от 0 до 1. Для других значений
Изображенная на рис. 5.2 ситуация возникает только тогда, когда значение А находится в пределах от 0 до 1. Для других значений  точка I лежит не на отрезке
точка I лежит не на отрезке  а на одном из его продолжений. Нельзя утверждать, что при значении
а на одном из его продолжений. Нельзя утверждать, что при значении  от 0 до 1 отрезок PQ пересекает пирамиду, верно лишь обратное утверждение. На рис. 5.3 показана ситуация, видимая из точки Е, когда значение
от 0 до 1 отрезок PQ пересекает пирамиду, верно лишь обратное утверждение. На рис. 5.3 показана ситуация, видимая из точки Е, когда значение  лежит в пределах от 0 до 1, хотя отрезок PQ не пересекает пирамиду.
лежит в пределах от 0 до 1, хотя отрезок PQ не пересекает пирамиду.
Возвращаясь к трехмерному пространству (рис. 5.2), можно представить плоскость, проходящую через прямую линию PQ и точку наблюдения Е. Теперь мы хотим узнать, не будет ли эта плоскость проходить через точки, принадлежащие отрезку 

Рис. 5.3. Отрезок PQ вне пирамиды
Здесь необходимо выполнить вычисления, аналогичные проводимым при определении значения  . Запишем векторное представление прямой линии
. Запишем векторное представление прямой линии 

Тогда точка (х, у, z) принадлежит прямой линии  если
если

Для значений  от 0 до 1 точка лежит между
от 0 до 1 точка лежит между 
Уравнение плоскости 

Перепишем это уравнение в виде

где

Совмещая уравнения (5.6) и (5.7), получаем

Отрезок прямой линии PQ и плоскость пирамиды  имеют общую точку, если, и только если
имеют общую точку, если, и только если

До сих пор мы рассматривали пересечение прямой PQ только с одной из плоскостей пирамиды, а именно с  Необходимо также рассмотреть плоскости
Необходимо также рассмотреть плоскости  и
и  Отрезок PQ может не иметь либо иметь одно или два пересечения с пирамидой. Соответственно
Отрезок PQ может не иметь либо иметь одно или два пересечения с пирамидой. Соответственно  точки
точки  могут лежать внутри, вне или на пирамиде, то есть располагаться впереди, позади или на плоскости
могут лежать внутри, вне или на пирамиде, то есть располагаться впереди, позади или на плоскости  Для проверки каждой пары из одного отрезка и одного треугольника может потребоваться большой объем работы. Обычно имеется очень много отрезков прямых, и каждый из них необходимо проверять относительно большого количества треугольников. Такие проверки нужно выполнять с большой
Для проверки каждой пары из одного отрезка и одного треугольника может потребоваться большой объем работы. Обычно имеется очень много отрезков прямых, и каждый из них необходимо проверять относительно большого количества треугольников. Такие проверки нужно выполнять с большой
эффективностью. (В параграфе 5.4 описана эффективная методика по уменьшению числа треугольников, анализируемых совместно с данным отрезком, что позволяет снизить количество проверок. Но каждая проверка для данного отрезка и данного треугольника должна выполняться по описанному алгоритму). Желательно как мржно раньше начинать с таких случаев, которые встречаются наиболее часто, особенно если не требуются большие затраты машинного времени. При успешном выполнении теста остальные тесты игнорируются.
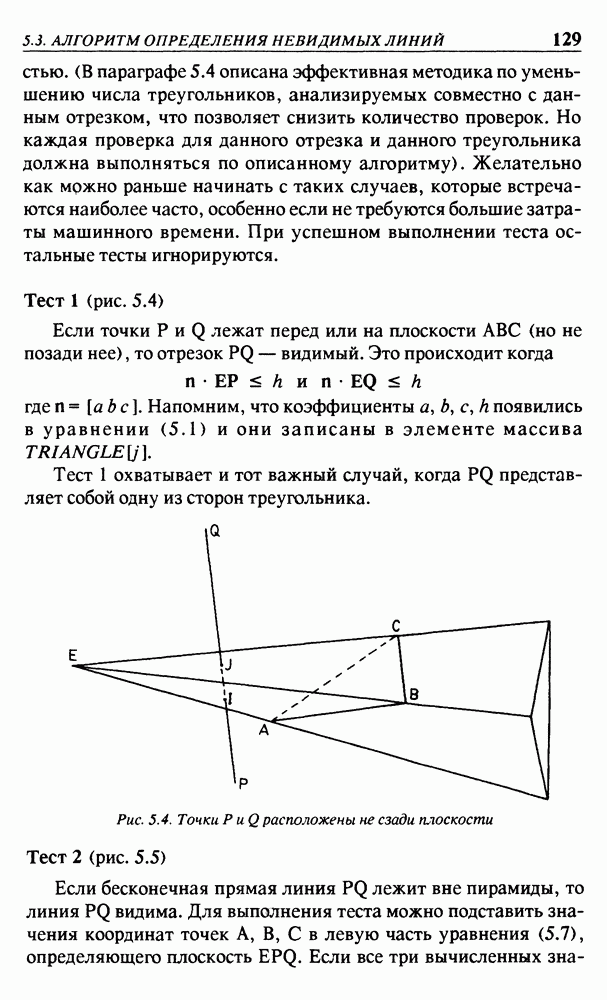
Тест 1 (рис. 5.4)
Если точки  лежат перед или на плоскости ABC (но не позади нее), то отрезок
лежат перед или на плоскости ABC (но не позади нее), то отрезок  видимый. Это происходит когда
видимый. Это происходит когда

где  Напомним, что коэффициенты
Напомним, что коэффициенты  появились в уравнении (5.1) и они записаны в элементе массива
появились в уравнении (5.1) и они записаны в элементе массива 
Тест 1 охватывает и тот важный случай, когда PQ представляет собой одну из сторон треугольника.

Рис. 5.4. Точки  расположены не сзади плоскости
расположены не сзади плоскости
Тест 2 (рис. 5.5)
Если бесконечная прямая линия PQ лежит вне пирамиды, то линия PQ видима. Для выполнения теста можно подставить значения координат точек А, В, С в левую часть уравнения (5.7), определяющего плоскость  Если все три вычисленных
Если все три вычисленных

Рис. 5.5. (а) - модуль суммы знаков  модуль суммы знаков - 2
модуль суммы знаков - 2
значения (для точек  имеют одинаковые знаки (все положительные или все отрицательные), то все точки А, В, С лежат по одну сторону от плоскости
имеют одинаковые знаки (все положительные или все отрицательные), то все точки А, В, С лежат по одну сторону от плоскости  Следовательно, линия PQ расположена вне пирамиды и является видимой. Несколько ослабим это знаковое условие в том смысле, что один из знаков может быть равен нулю. Предположим, что каждый из знаков обозначается одним из чисел -1,0, 1, и проверим, не будет ли сумма знаков для точек А, В, С равна одному из чисел -3, -2, 2,3. Заметим, что на рис.
Следовательно, линия PQ расположена вне пирамиды и является видимой. Несколько ослабим это знаковое условие в том смысле, что один из знаков может быть равен нулю. Предположим, что каждый из знаков обозначается одним из чисел -1,0, 1, и проверим, не будет ли сумма знаков для точек А, В, С равна одному из чисел -3, -2, 2,3. Заметим, что на рис.  может произойти и такой случай, когда точка Р совпадает с точкой А. Это тоже очень важный специальный случай.
может произойти и такой случай, когда точка Р совпадает с точкой А. Это тоже очень важный специальный случай.
Тест 3
Теперь найдем точку пересечения прямой линии PQ с плоскостями  и
и  Вычислим значения параметров А для точки пересечения прямой линии PQ с плоскостью
Вычислим значения параметров А для точки пересечения прямой линии PQ с плоскостью  по уравнению (5.5) и
по уравнению (5.5) и  для точки пересечения прямой
для точки пересечения прямой  с плоскостью
с плоскостью  по уравнению (5.8). (В обоих случаях прямая линия может оказаться параллельной плоскости, поэтому параметрам
по уравнению (5.8). (В обоих случаях прямая линия может оказаться параллельной плоскости, поэтому параметрам  будут присвоены очень большие числа.) Уравнение (5.4) описывает плоскость
будут присвоены очень большие числа.) Уравнение (5.4) описывает плоскость  Если левая часть этого уравнения при подстановке координат точек
Если левая часть этого уравнения при подстановке координат точек  принимает разные знаки, то это означает, что точки
принимает разные знаки, то это означает, что точки  лежат по разные стороны от прямой
лежат по разные стороны от прямой  Тогда можно сказать, что точка Р лежит за прямой
Тогда можно сказать, что точка Р лежит за прямой  Если точка лежит за одной из сторон треугольника, то она расположена вне этого треугольника. Запомним эту
Если точка лежит за одной из сторон треугольника, то она расположена вне этого треугольника. Запомним эту

Рис. 5.6. (а) - точки  за АВ; (б) - точка Р за
за АВ; (б) - точка Р за  точка
точка 
информацию в логической переменной Poutside (“точка Р вне”). Аналогично для точки  введена переменная Qoutside (“точка Q вне”). Эти переменные будут проверяться в тестах 4 и 6. Если точки
введена переменная Qoutside (“точка Q вне”). Эти переменные будут проверяться в тестах 4 и 6. Если точки  лежат за одной и той же стороной треугольника или одна точка находится за стороной, а другая — точно на этой стороне, то будем говорить, что отрезок PQ лежит вне этого треугольника. Тогда отрезок
лежат за одной и той же стороной треугольника или одна точка находится за стороной, а другая — точно на этой стороне, то будем говорить, что отрезок PQ лежит вне этого треугольника. Тогда отрезок  видимый. Обе ситуации показаны на рис. 5.6. Важный специальный случай возникает при небольшой модификации рис.
видимый. Обе ситуации показаны на рис. 5.6. Важный специальный случай возникает при небольшой модификации рис.  когда точка
когда точка  совпадает с точкой А. Заметим, что в отличие от рис.
совпадает с точкой А. Заметим, что в отличие от рис.  бесконечная прямая линия PQ на рис.
бесконечная прямая линия PQ на рис.  может пересекать отрезок
может пересекать отрезок  между точками
между точками  так, что тест 3 будет выполнен в том случае, когда тест 2 оказался невыполненным.
так, что тест 3 будет выполнен в том случае, когда тест 2 оказался невыполненным.
Большая часть работы должна быть выполнена трижды, а именно: для каждой из плоскостей  и
и  следовательно, будем иметь три пары значений
следовательно, будем иметь три пары значений  . Затем найдем минимальное и максимальное из значений А, удовлетворяющие условиям
. Затем найдем минимальное и максимальное из значений А, удовлетворяющие условиям

и эти значения обозначим  и
и  соответственно. Они являются побочным продуктом этого теста и определяются только тогда, когда отрезок PQ пересекает треугольник, то есть если тесты 3 и 4 (см. ниже) не выполнены.
соответственно. Они являются побочным продуктом этого теста и определяются только тогда, когда отрезок PQ пересекает треугольник, то есть если тесты 3 и 4 (см. ниже) не выполнены.
Тест 4 (рис. 5.7)
Если и точка Р, и точка  находятся внутри пирамиды, а предыдущий тест не удовлетворен, то отрезок PQ лежит позади треугольника и, следовательно, невидим.
находятся внутри пирамиды, а предыдущий тест не удовлетворен, то отрезок PQ лежит позади треугольника и, следовательно, невидим.
При выполнении этого теста также может встретиться весьма хитрая ситуация. Предположим, например, что отрезок PQ лежит на пирамиде позади отрезка  Поскольку отрезок PQ не находится ни снаружи, ни внутри пирамиды, то кажется сомнительным, можем ли мы сказать, что треугольник закрывает отрезок
Поскольку отрезок PQ не находится ни снаружи, ни внутри пирамиды, то кажется сомнительным, можем ли мы сказать, что треугольник закрывает отрезок  Однако отрезок
Однако отрезок  может быть не ребром, а диагональю грани. Тогда эта грань определенно закрывает отрезок и он не должен вычерчиваться. С другой стороны, если бы отрезок
может быть не ребром, а диагональю грани. Тогда эта грань определенно закрывает отрезок и он не должен вычерчиваться. С другой стороны, если бы отрезок  был ребром объекта, то и тогда отрезок PQ вычерчивать было бы не нужно, поскольку изображение отрезка PQ совпадало бы с ребром
был ребром объекта, то и тогда отрезок PQ вычерчивать было бы не нужно, поскольку изображение отрезка PQ совпадало бы с ребром  а чертить совпадающие отрезки линий нет никакого смысла.
а чертить совпадающие отрезки линий нет никакого смысла.

Рис. 5.7. Отрезок PQ позади треугольника ABC
Тест 5 (рис. 5.8)
Если точка I, в которой прямая линия PQ пересекает пирамиду, лежит впереди треугольника, то прямая PQ видима. Этот тест основан на том факте, что объект является сплошным телом, поэтому прямая PQ не может проходить через внутренние точки треугольника. Для нахождения такой точки I используем значения  и
и  параметра Я, вычисленные при выполнении теста 3. Затем можно просто проверить, не будет ли скалярное произведение векторов
параметра Я, вычисленные при выполнении теста 3. Затем можно просто проверить, не будет ли скалярное произведение векторов  и
и  меньше, чем
меньше, чем 
Тест 6
Этот тест выполняется только в том случае, если все предыдущие тесты не дали положительного результата, то есть когда прямая PQ пересекает пирамиду позади треугольника.

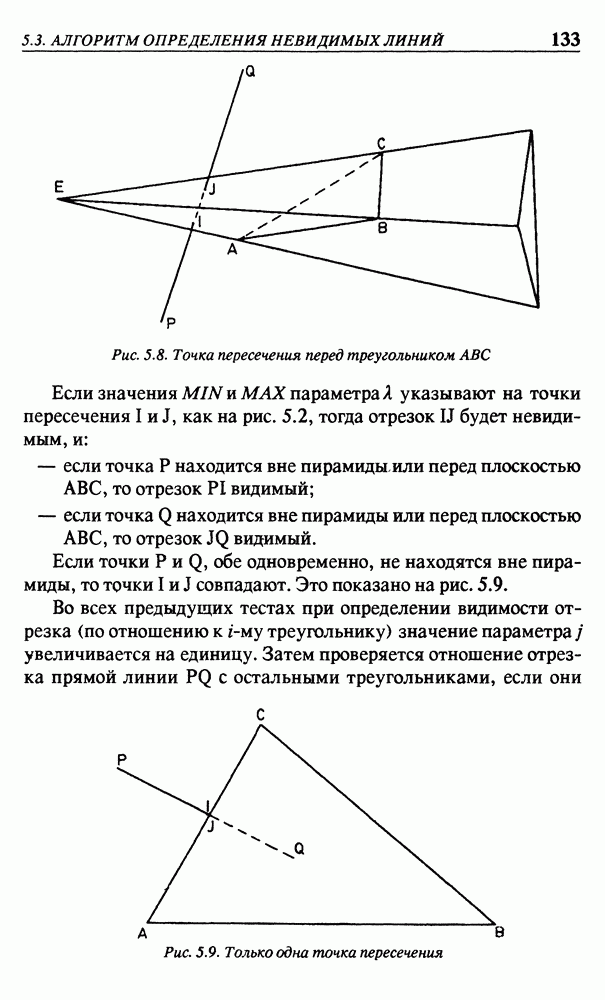
Рис. 5.8. Точка пересечения перед треугольником ABC
Если значения  и
и  параметра X указывают на точки пересечения
параметра X указывают на точки пересечения  как на рис. 5.2, тогда отрезок
как на рис. 5.2, тогда отрезок  будет невидимым, и:
будет невидимым, и:
— если точка Р находится вне пирамиды, или перед плоскостью  то отрезок
то отрезок  видимый;
видимый;
— если точка  находится вне пирамиды или перед плоскостью
находится вне пирамиды или перед плоскостью  то отрезок
то отрезок  видимый.
видимый.
Если точки  обе одновременно, не находятся вне пирамиды, то точки
обе одновременно, не находятся вне пирамиды, то точки  совпадают. Это показано на рис. 5.9.
совпадают. Это показано на рис. 5.9.
Во всех предыдущих тестах при определении видимости отрезка (по отношению к  треугольнику) значение параметра
треугольнику) значение параметра  увеличивается на единицу. Затем проверяется отношение отрезка прямой линии PQ с остальными треугольниками, если они
увеличивается на единицу. Затем проверяется отношение отрезка прямой линии PQ с остальными треугольниками, если они

Рис. 5.9. Только одна точка пересечения
еще есть, или отрезок вычерчивается, если треугольников больше нет. Но в этом тесте могут появиться два новых отрезка  и
и  которые должны быть проверены на отношение с оставшимися треугольниками. Здесь можно будет рекурсивно дважды обратиться к этому же алгоритму. Для каждого рекурсивного обращения будем задавать концевые точки отрезка прямой линии и номер
которые должны быть проверены на отношение с оставшимися треугольниками. Здесь можно будет рекурсивно дважды обратиться к этому же алгоритму. Для каждого рекурсивного обращения будем задавать концевые точки отрезка прямой линии и номер  треугольника, с которого должна начаться проверка.
треугольника, с которого должна начаться проверка.
Замечания о точности представления чисел
Для сложных вычислений целесообразно использовать тип double вместо float. Поскольку тип double означает «двойная точность с плавающей точкой», то неформально можно говорить о вычислениях с “плавающей точкой”, хотя в действительности при этом имеется в виду двойная точность  Но даже при использовании типа double вещественные числа представляются с конечной точностью. Если в результате некоторых сложных вычислений были получены два числа, например 5.843216 и 5.843217, отличающихся только последней цифрой, то их вполне можно считать равными. Если хотим, чтобы так же действовал и компьютер, то это правило необходимо сформулировать более определенно. Для чисел с плавающей точкой оно может оказаться совсем не простым. Обычно задается небольшая положительная величина (например,
Но даже при использовании типа double вещественные числа представляются с конечной точностью. Если в результате некоторых сложных вычислений были получены два числа, например 5.843216 и 5.843217, отличающихся только последней цифрой, то их вполне можно считать равными. Если хотим, чтобы так же действовал и компьютер, то это правило необходимо сформулировать более определенно. Для чисел с плавающей точкой оно может оказаться совсем не простым. Обычно задается небольшая положительная величина (например,  и вместо условного оператора
и вместо условного оператора  а (для числа с плавающей точкой х и константы а) записывают один из условных операторов:
а (для числа с плавающей точкой х и константы а) записывают один из условных операторов:

В первом условии параметр epsilon равен абсолютной ошибке, которая допускается при вычислениях. При такой проверке могут возникнуть проблемы для больших значений  если в этих случаях не задавать несколько большие значения epsilon. Поскольку абсолютная величина х и а обычно заранее не известна, то предпочтительнее иметь фиксированное значение для epsilon, но заменить первую проверку на вторую, где через epsilon обозначена максимальная относительная ошибка. Однако если величина а будет равна (почти) нулю, то правая часть неравенства будет также (почти) нуль, что совсем не то, чего бы
если в этих случаях не задавать несколько большие значения epsilon. Поскольку абсолютная величина х и а обычно заранее не известна, то предпочтительнее иметь фиксированное значение для epsilon, но заменить первую проверку на вторую, где через epsilon обозначена максимальная относительная ошибка. Однако если величина а будет равна (почти) нулю, то правая часть неравенства будет также (почти) нуль, что совсем не то, чего бы
нам хотелось. Поэтому будем использовать третью проверку, где абсолютная и относительная ошибки соймещены. Очевидно, что она сводится к первой при 
На основании сказанного, проверка значений вещественных переменных  выполняется в соответствии со следующей таблицей, где введено обозначение
выполняется в соответствии со следующей таблицей, где введено обозначение 
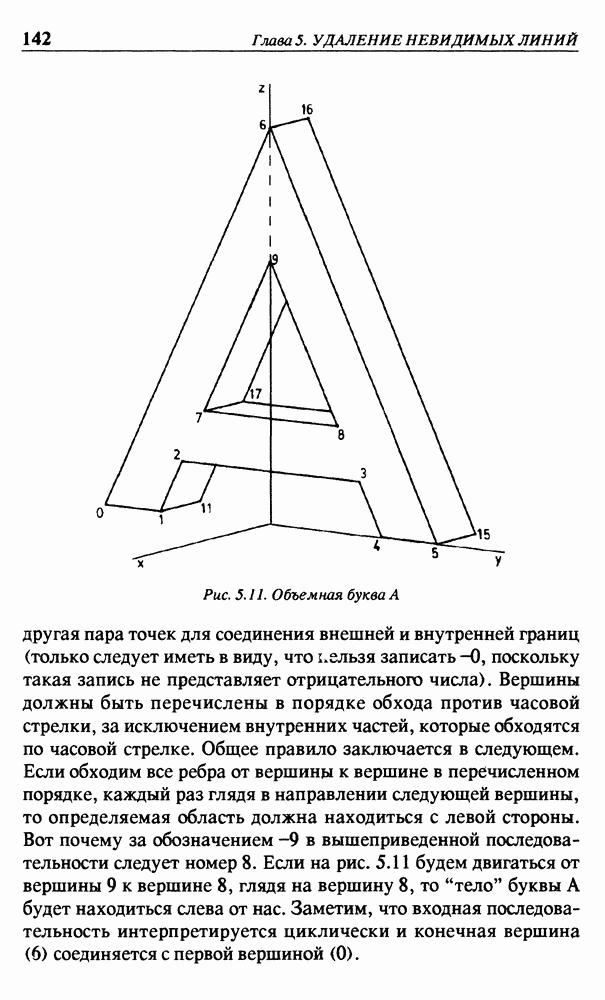
(см. скан)
Заметим, что вторая часть этой таблицы может быть выведена из первой. Эти тесты будут использованы в программе  приведенной ниже.
приведенной ниже.
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
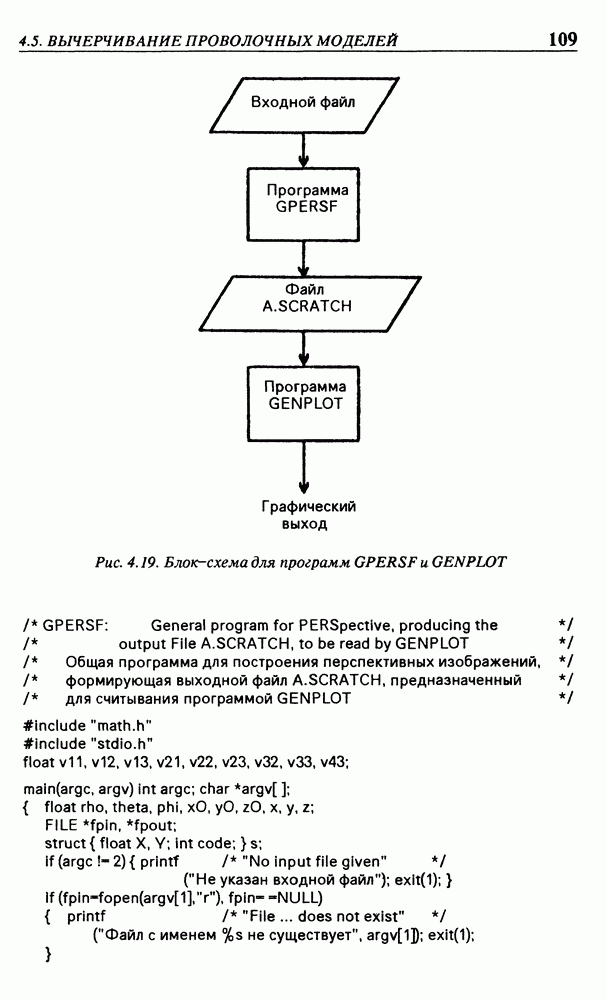
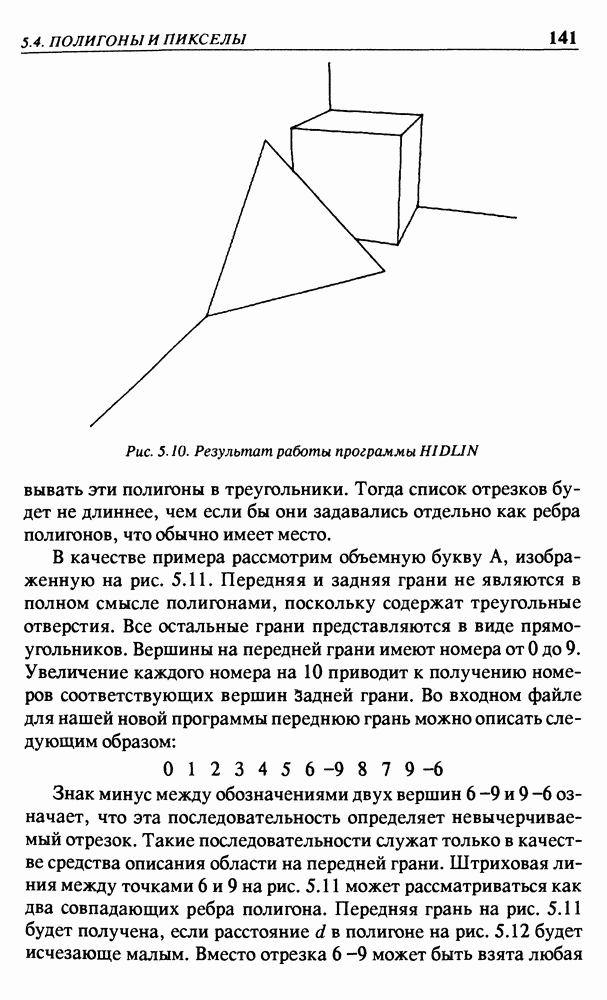
Этой программой были считаны входные данные, приведенные в параграфе 5.2; результат ее работы записан в файл A SCRATCH и считан программой GENPLOT, которая выдала изображение, показанное на рис. 5.10.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
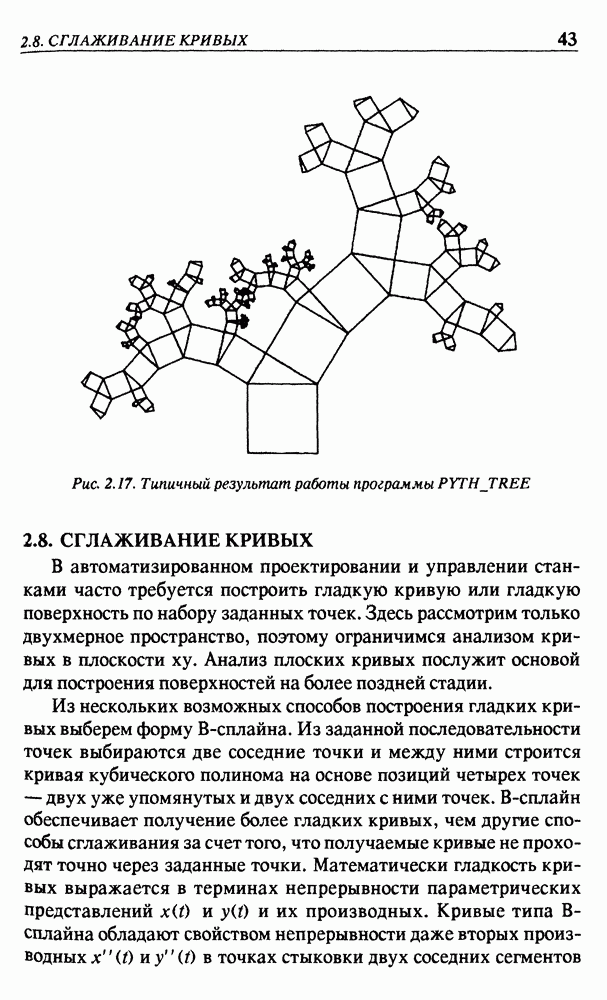
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
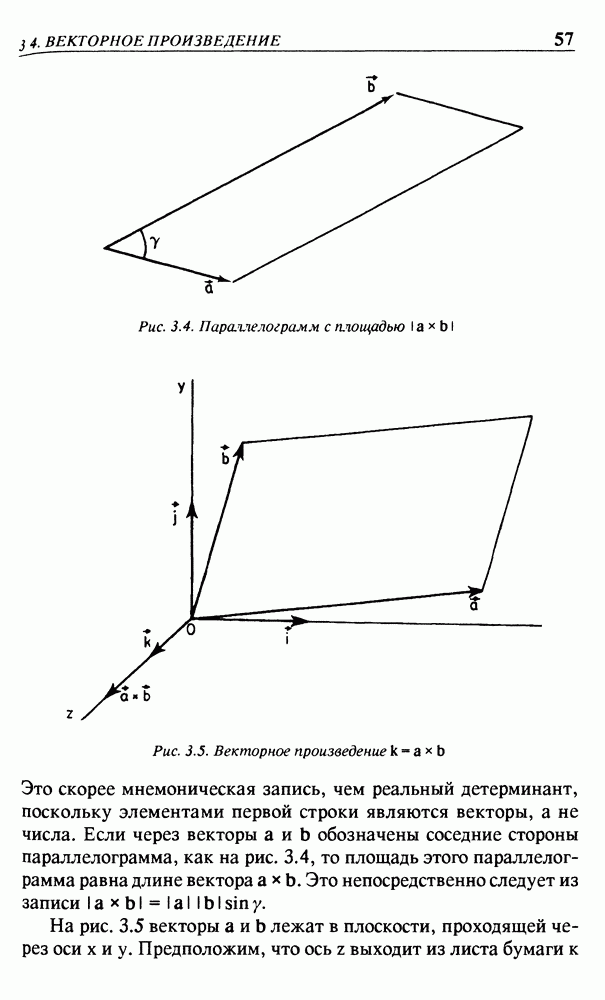
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
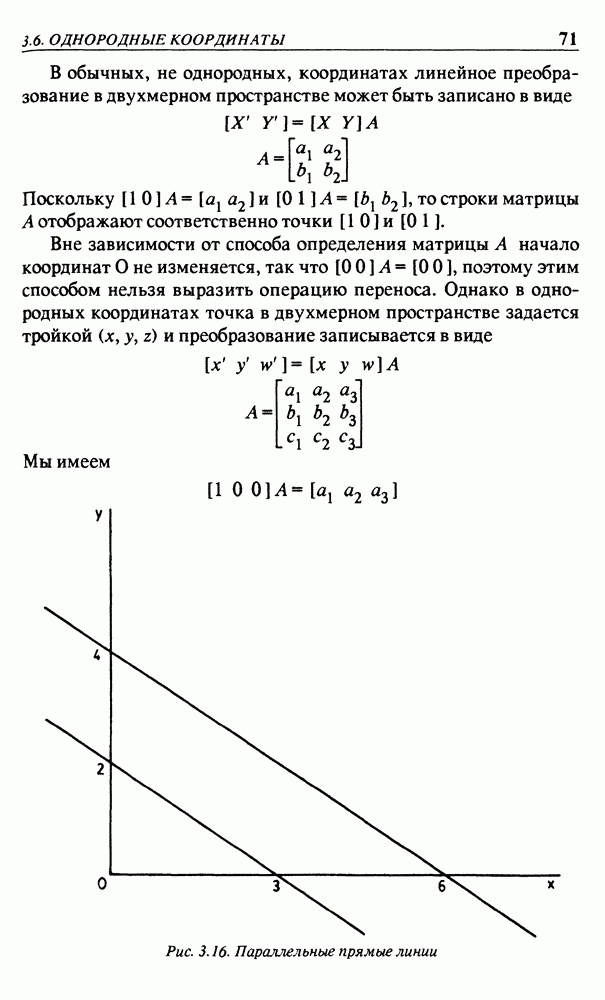
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
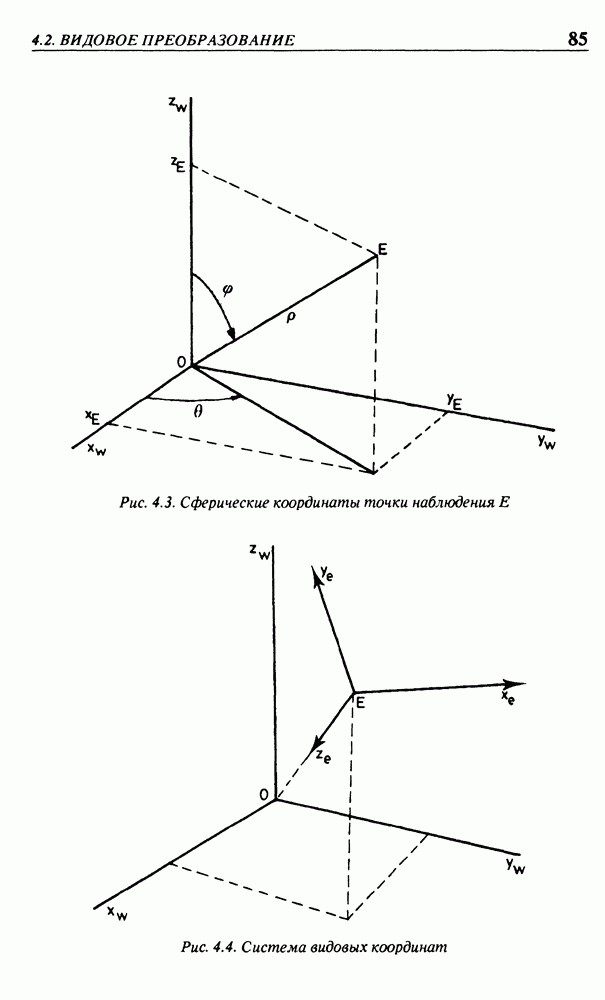
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
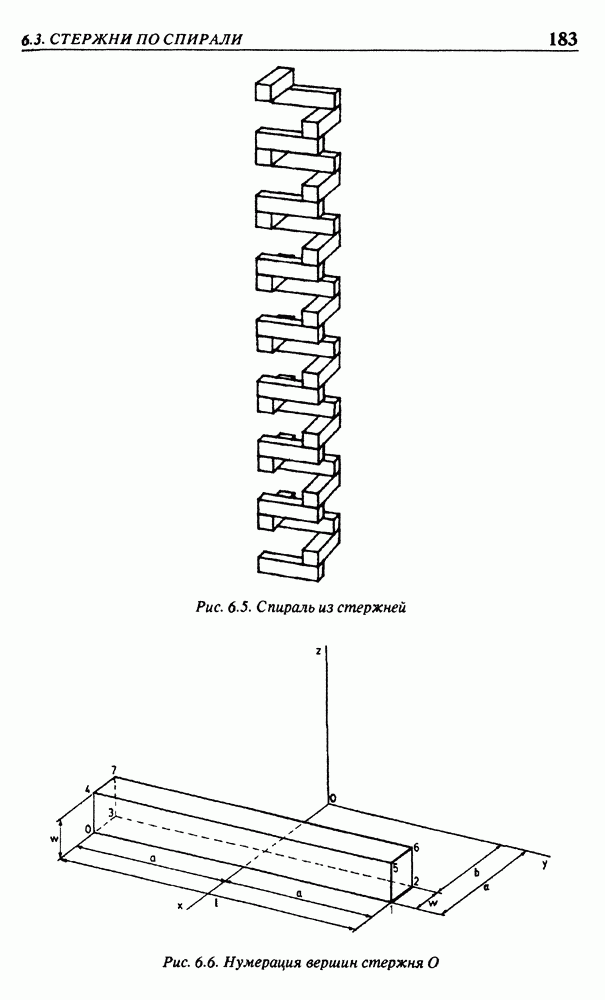
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА