| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
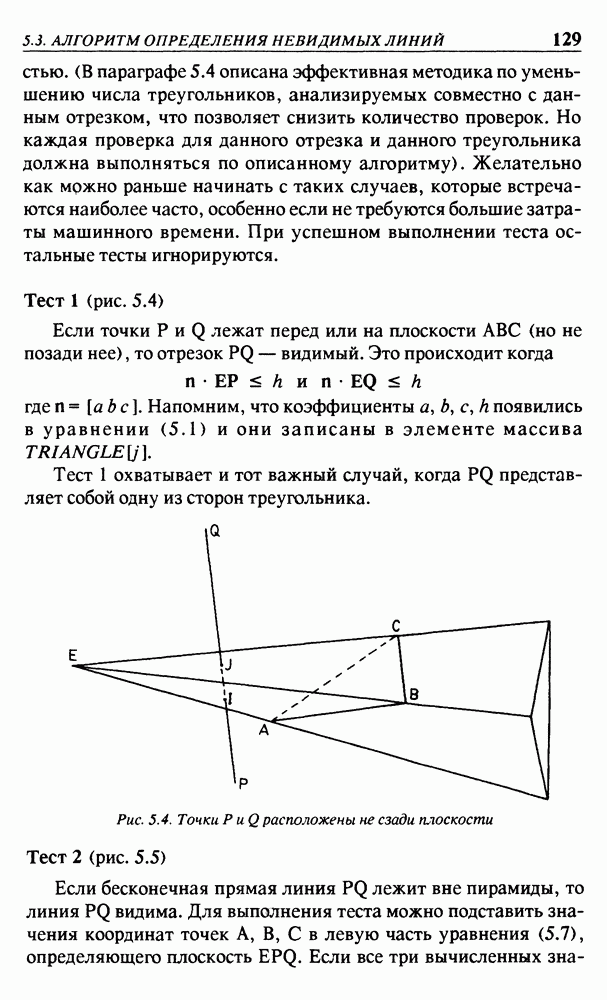
4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
Используем программу GPERSF для обсуждения некоторых новых интересных аспектов. Предположим, что объект очень длинный в направлении оси х, как, например, балка на рис. 4.20, размеры которой  Интересным аспектом этого примера является задание точки О, которую мы должны указать для определения направления наблюдения
Интересным аспектом этого примера является задание точки О, которую мы должны указать для определения направления наблюдения  До сих пор точка О выбиралась в центре объекта. Однако фактически нужна такая точка О, изображение которой будет располагаться в центре картинки. Часто это не существенно, но иногда очень сильно влияет на изображение. Например, на рис. 4.21 точка О оказывается по средине отрезка
До сих пор точка О выбиралась в центре объекта. Однако фактически нужна такая точка О, изображение которой будет располагаться в центре картинки. Часто это не существенно, но иногда очень сильно влияет на изображение. Например, на рис. 4.21 точка О оказывается по средине отрезка  хотя соответствующая ей точка О выбрана не на середине исходного отрезка
хотя соответствующая ей точка О выбрана не на середине исходного отрезка  Если бы для нее была задана середина отрезка
Если бы для нее была задана середина отрезка  то направление наблюдения получилось бы совершенно иным.
то направление наблюдения получилось бы совершенно иным.
Вернемся к балке, изображенной на рис. 4.20. Очевидно, что точку О следует выбирать не в середине балки, а значительно ближе к глазу. Это возможно осуществить потому, что в нашей программе объектная точка задается пользователем, а не вычисляется как центр объекта. Реальные бесконечные линии при изображении ландшафта на картинке получаются в виде отрезков

Рис. 4.20. Длинная балка

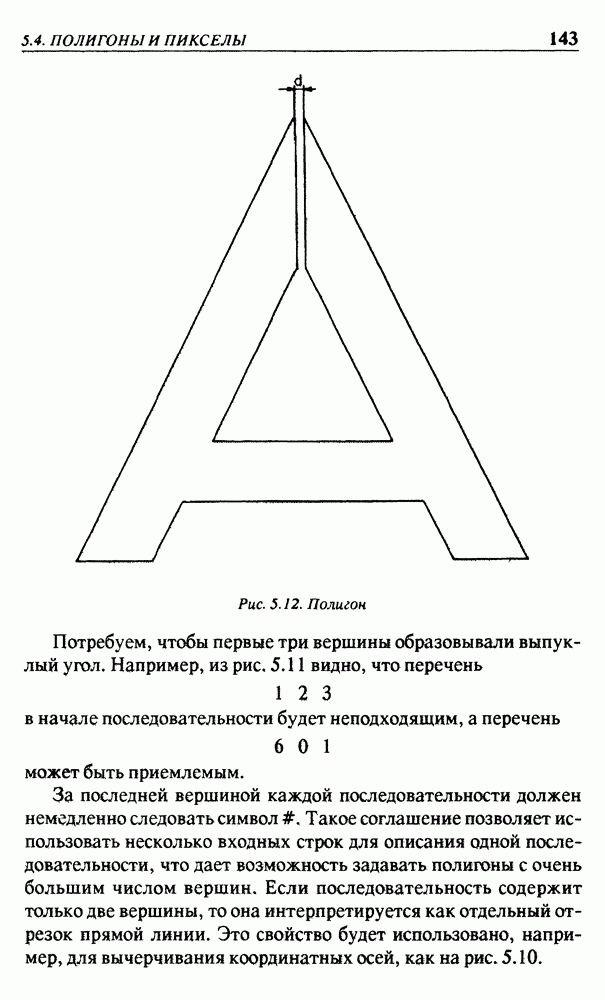
Рис. 4.21. Объектная тонка не в центре объекта
прямых конечной длины. Для бесконечных объектов нет никакого смысла говорить о центре, хотя направление наблюдения  существует. Поэтому и требуется определить положение “центральной” точки О объекта. Балка на рис. 4.20, конечно, не является ландшафтом в точном смысле, но ее длина предполагает существование бесконечности; если это не совсем ясно, то для определения ее длины можно задать число значительно больше 200. Для данной балки выберем точку
существует. Поэтому и требуется определить положение “центральной” точки О объекта. Балка на рис. 4.20, конечно, не является ландшафтом в точном смысле, но ее длина предполагает существование бесконечности; если это не совсем ясно, то для определения ее длины можно задать число значительно больше 200. Для данной балки выберем точку  . За исключением букв
. За исключением букв  вся эта картинка была вычерчена с помощью программ
вся эта картинка была вычерчена с помощью программ  и
и  Пересечение балки с плоскостью
Пересечение балки с плоскостью  обозначено буквами
обозначено буквами  а пересечение с плоскостью
а пересечение с плоскостью  Следовательно, точка О лежит в плоскости
Следовательно, точка О лежит в плоскости  а плоскость
а плоскость  расположена по центру балки. Полный набор входных данных для получения рис. 4.20 определяется списком:
расположена по центру балки. Полный набор входных данных для получения рис. 4.20 определяется списком:


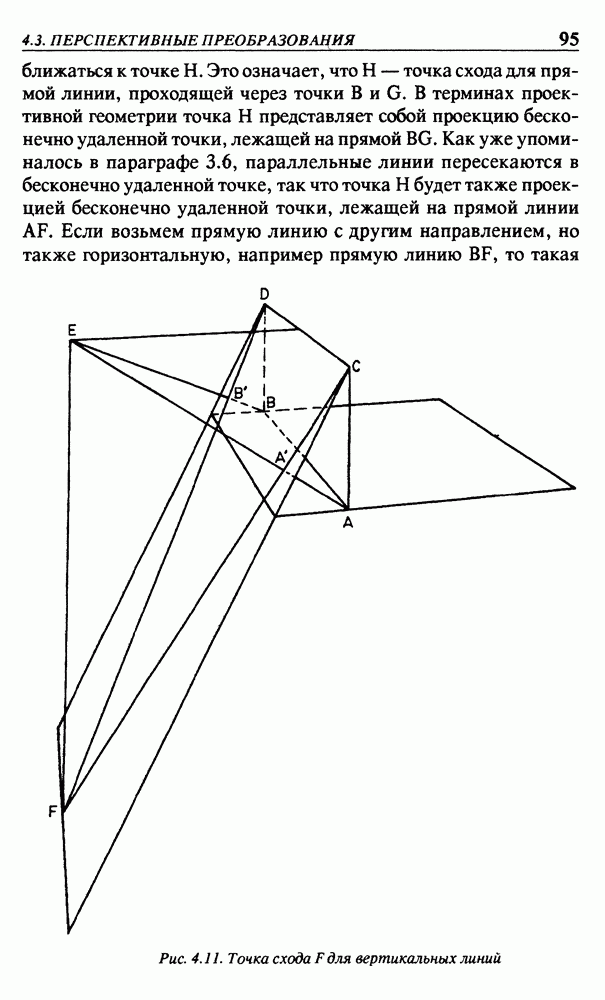
Другой аспект, требующий специального рассмотрения, — это представление вертикальных линий, кратко упомянутое в параграфе 4.3. На рис. 4.11 мы видели, что спроецированные вертикальные линии встречаются в точке схода  Мы также сравнивали представления кубиков на рис. 4.12. Если точка О расположена в центре кубика, то наша программа не сможет сформировать изображение рис. 4.12(б). Но точку О можно поместить над кубиком так, чтобы направление наблюдения
Мы также сравнивали представления кубиков на рис. 4.12. Если точка О расположена в центре кубика, то наша программа не сможет сформировать изображение рис. 4.12(б). Но точку О можно поместить над кубиком так, чтобы направление наблюдения  было горизонтальным. Тогда экран будет занимать вертикальное положение, поскольку он перпендикулярен направлению наблюдения. Это означает, что вертикальные ребра кубика будут параллельны экрану. Следовательно, их проекции на картинке также будут точно вертикальными. Курьезным здесь является то, что, хотя линия наблюдения горизонтальная, мы будем видеть верхнюю грань кубика как бы сверху.
было горизонтальным. Тогда экран будет занимать вертикальное положение, поскольку он перпендикулярен направлению наблюдения. Это означает, что вертикальные ребра кубика будут параллельны экрану. Следовательно, их проекции на картинке также будут точно вертикальными. Курьезным здесь является то, что, хотя линия наблюдения горизонтальная, мы будем видеть верхнюю грань кубика как бы сверху.
Получаемая картинка выглядит совершенно натурально, пока мы не преувеличим и не выберем точку наблюдения слишком высоко. На рис. 4.22 показаны оба таких случая.
Линии на рис. 4.22(a) были вычерчены программами GPERSF и GENPLOT на основе следующего списка входных данных:


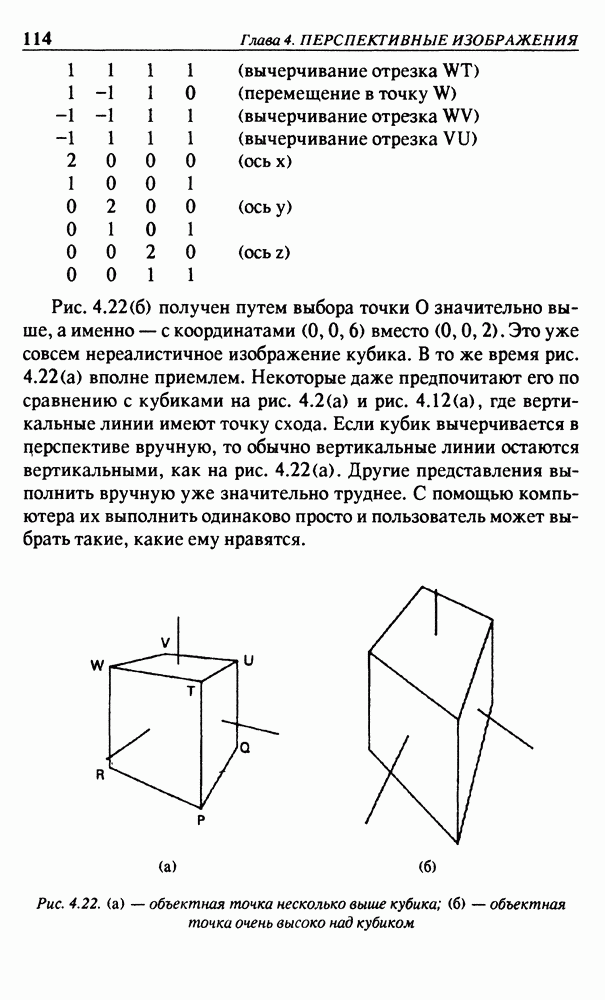
Рис. 4.22(б) получен путем выбора точки О значительно выше, а именно — с координатами (0,0,6) вместо (0,0,2). Это уже совсем нереалистичное изображение кубика. В то же время рис. 4.22(a) вполне приемлем. Некоторые даже предпочитают его по сравнению с кубиками на рис. 4.2(a) и рис. 4.12(a), где вертикальные линии имеют точку схода. Если кубик вычерчивается в перспективе вручную, то обычно вертикальные линии остаются вертикальными, как на рис. 4.22(a). Другие представления выполнить вручную уже значительно труднее. С помощью компьютера их выполнить одинаково просто и пользователь может выбрать такие, какие ему нравятся.

Рис. 4.22. (а) - объектная тонка несколько выше кубика; (б) - объектная точка очень высоко над кубиком
Замечание
Программы в этой главе предназначены скорее для объяснения принципов, чем для практического применения. В главах 5 и
6 будут обсуждены более практичные программы.
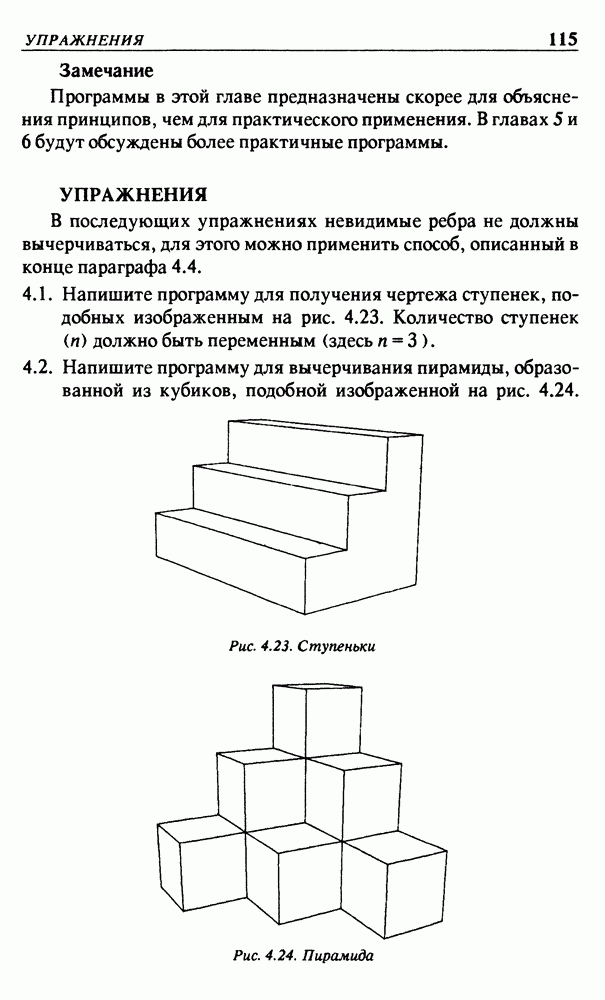
УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
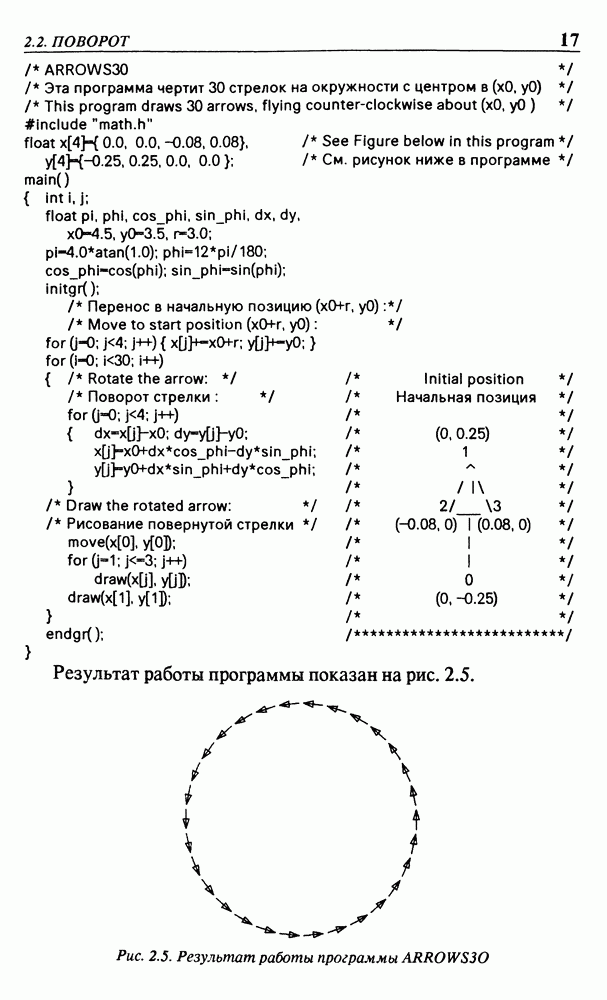
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
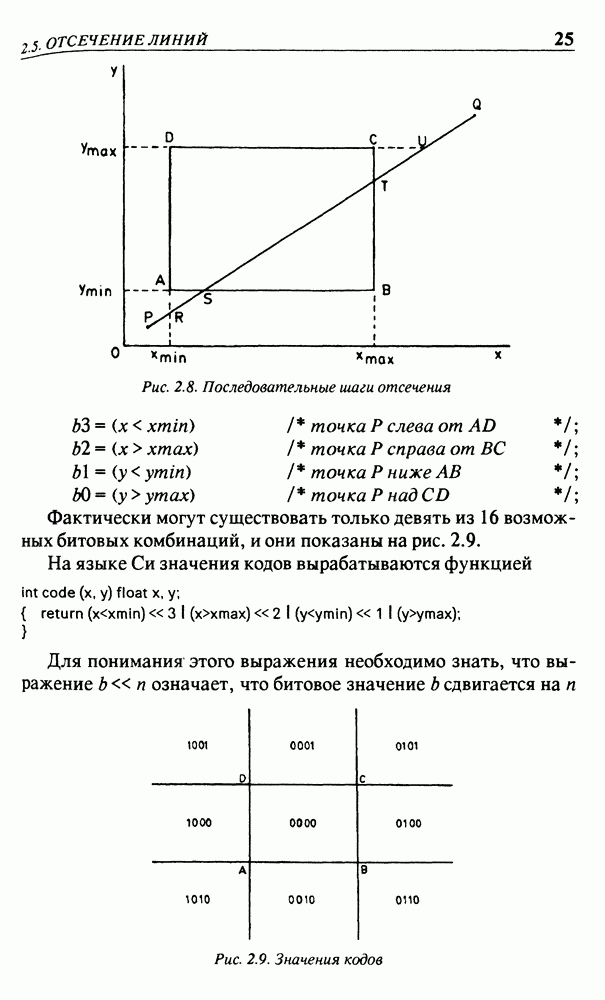
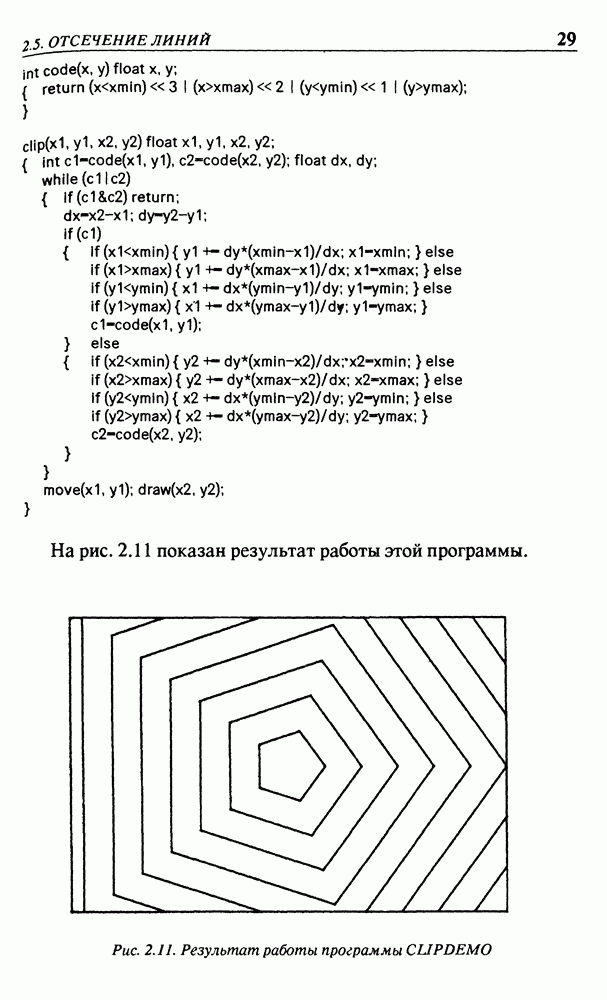
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
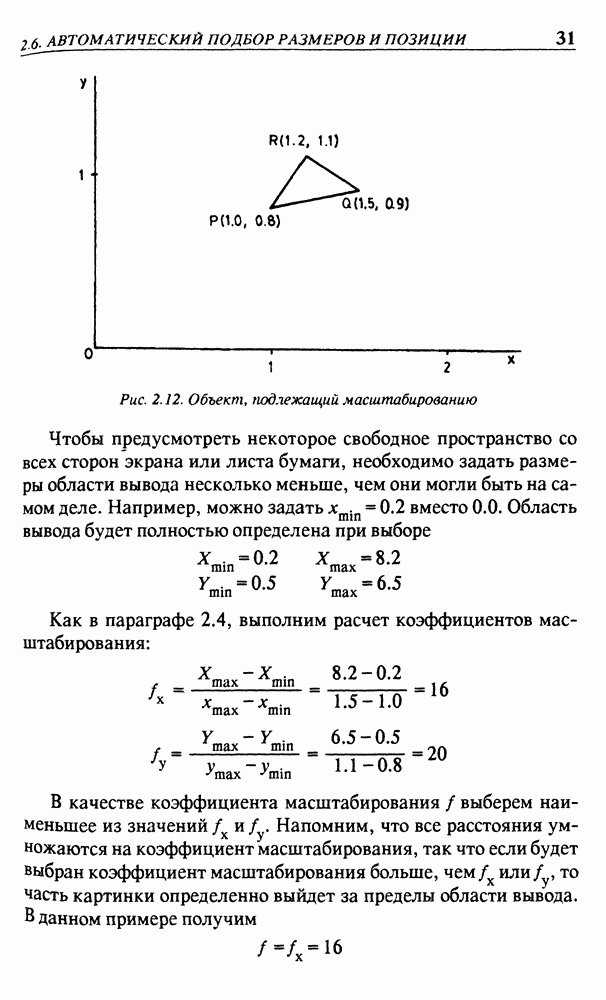
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
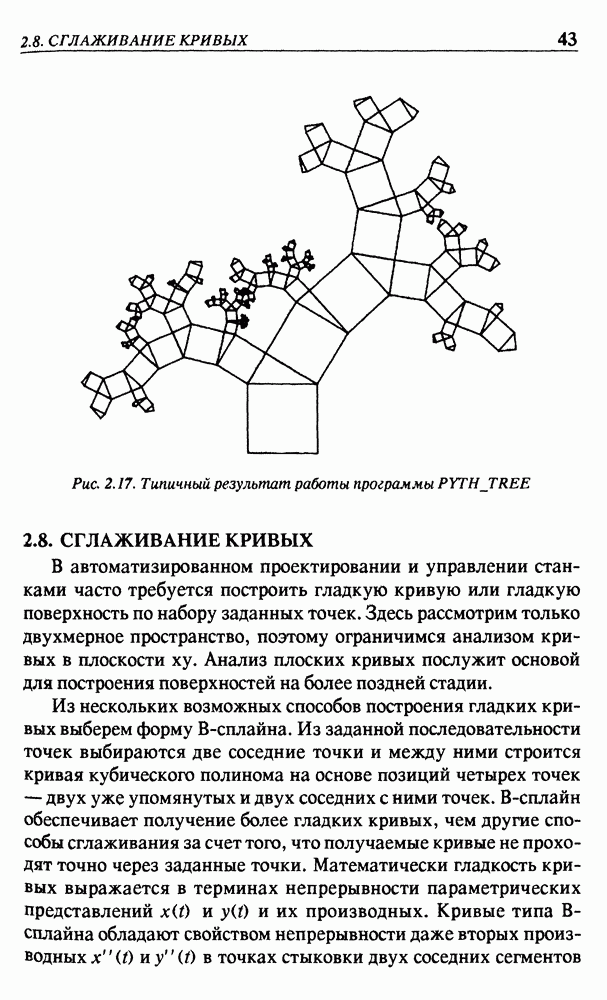
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
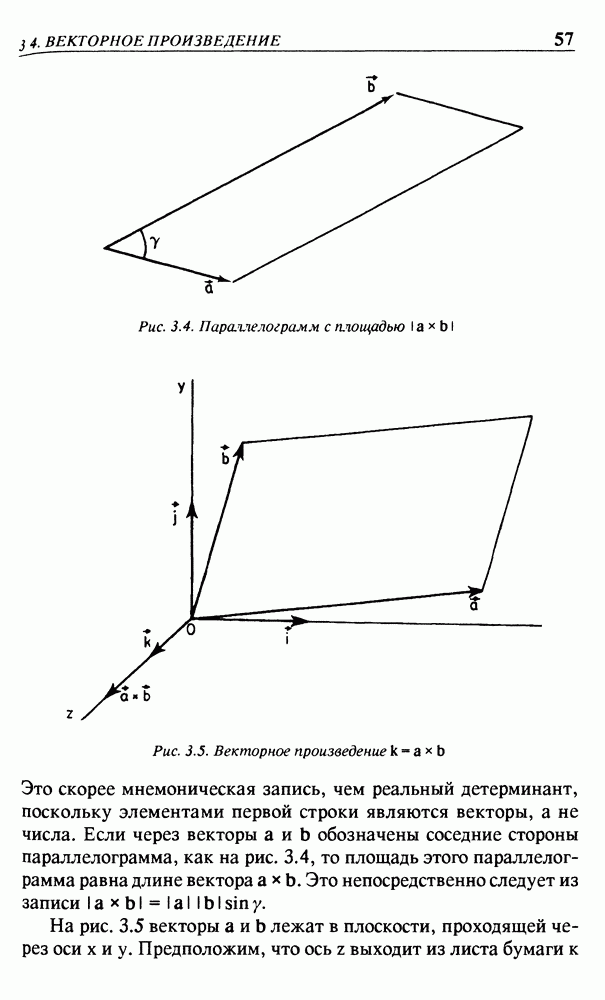
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
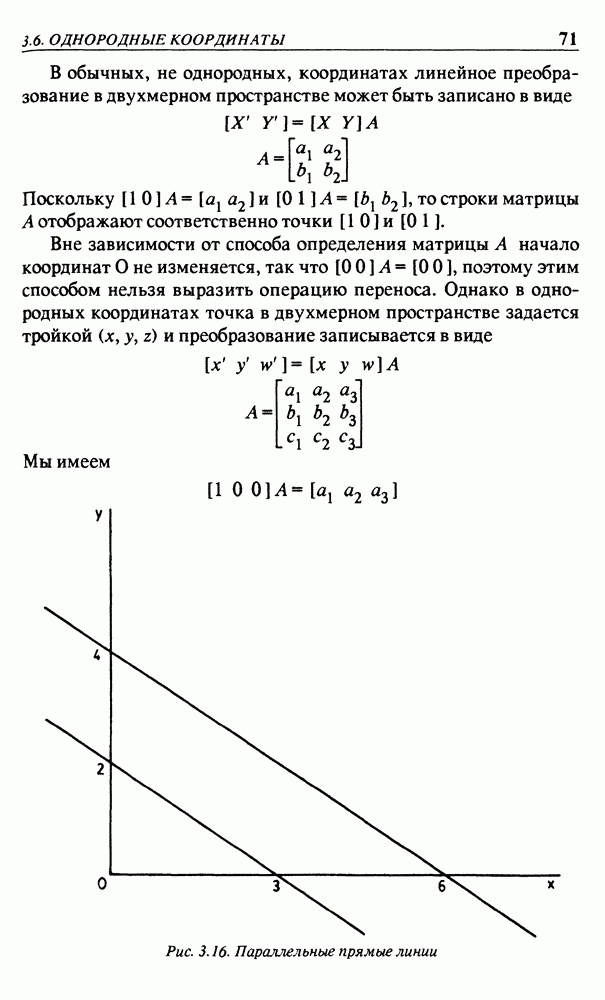
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
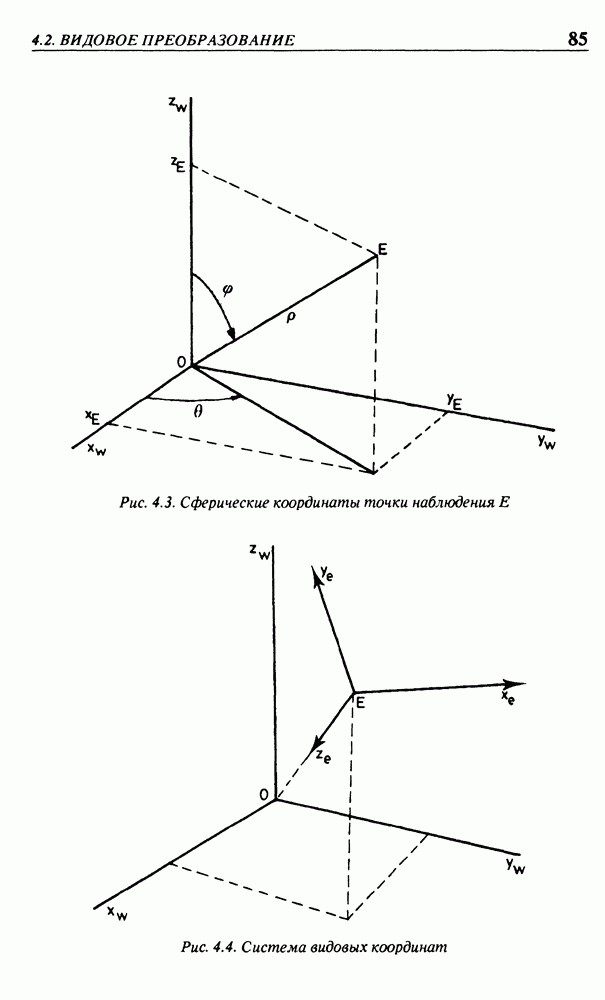
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
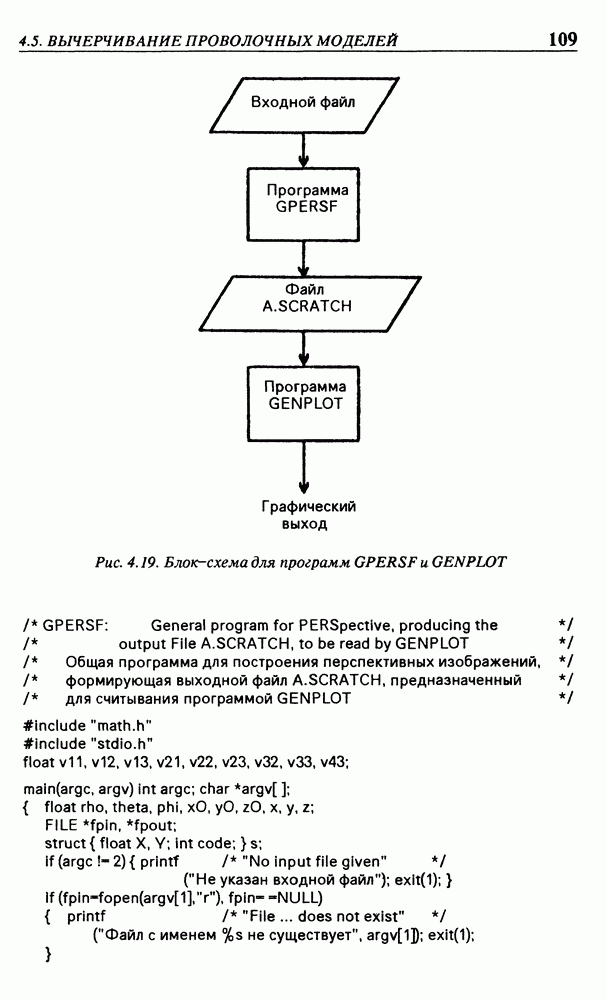
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
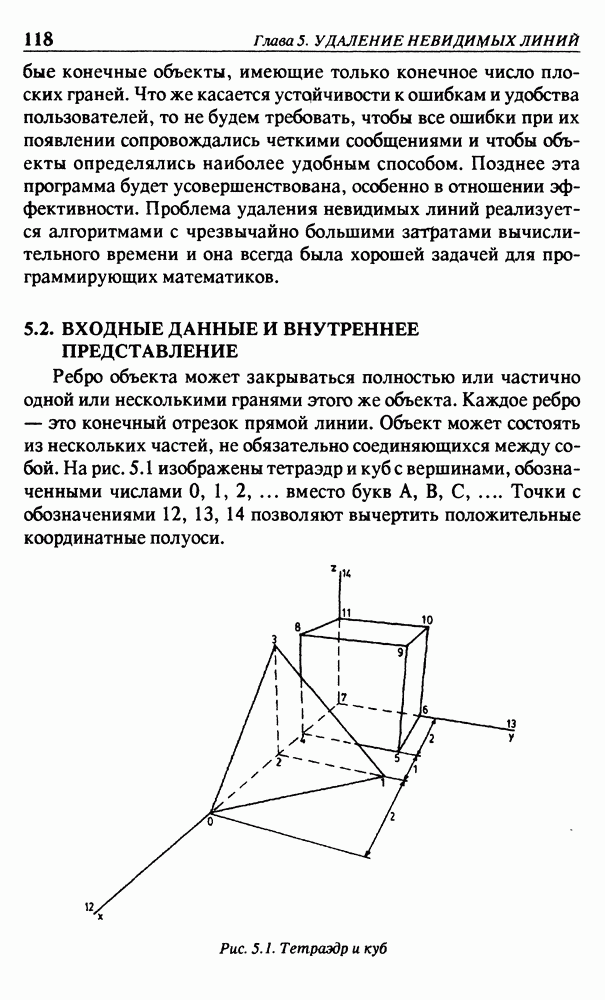
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
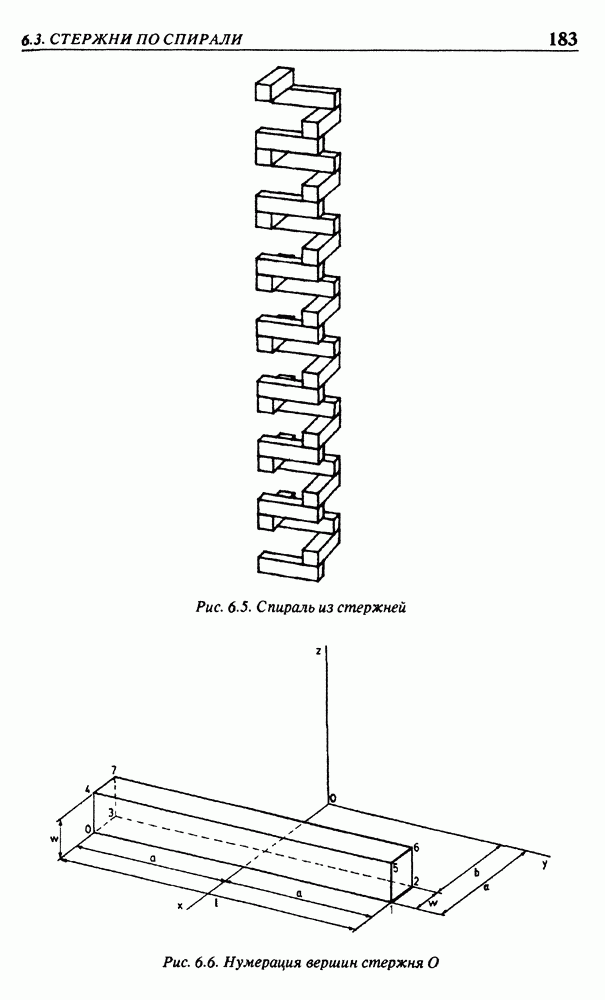
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
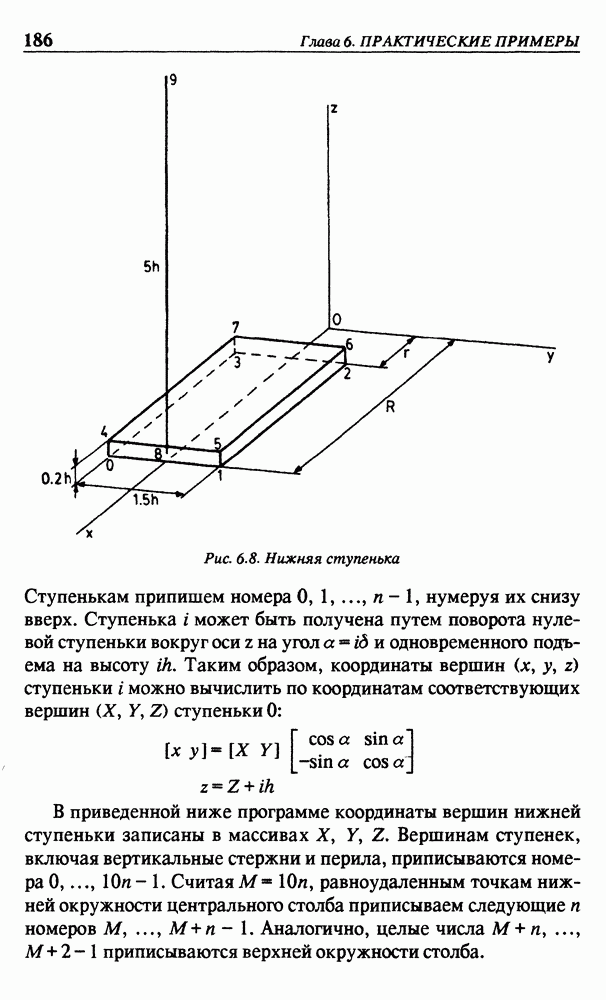
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
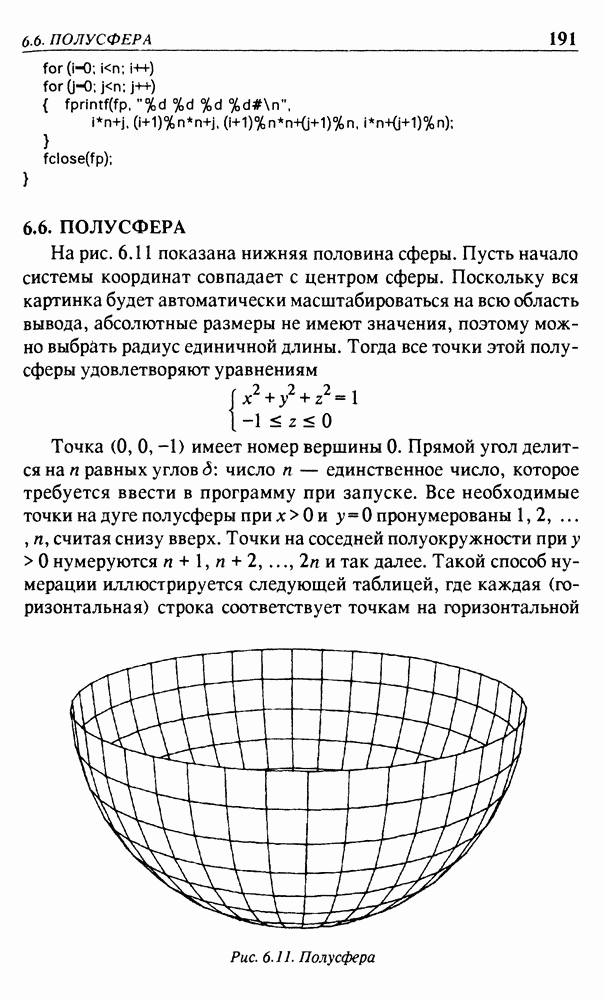
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА