| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
2.1. ПРЕОБРАЗОВАНИЕ И НОВЫЕ КООРДИНАТЫ
Рассмотрим следующую систему уравнений:

Эти уравнения можно интерпретировать двояким образом:
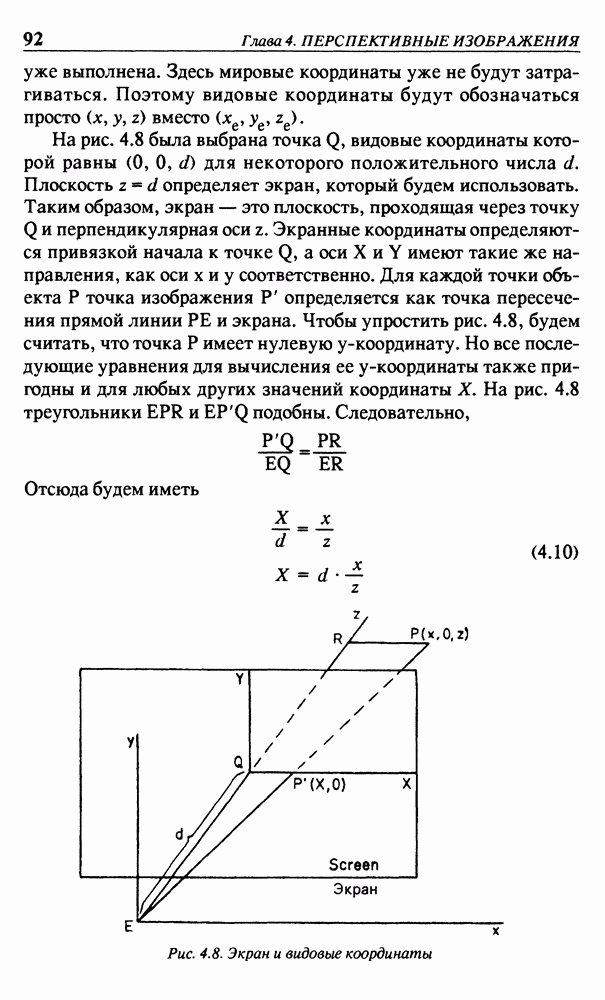
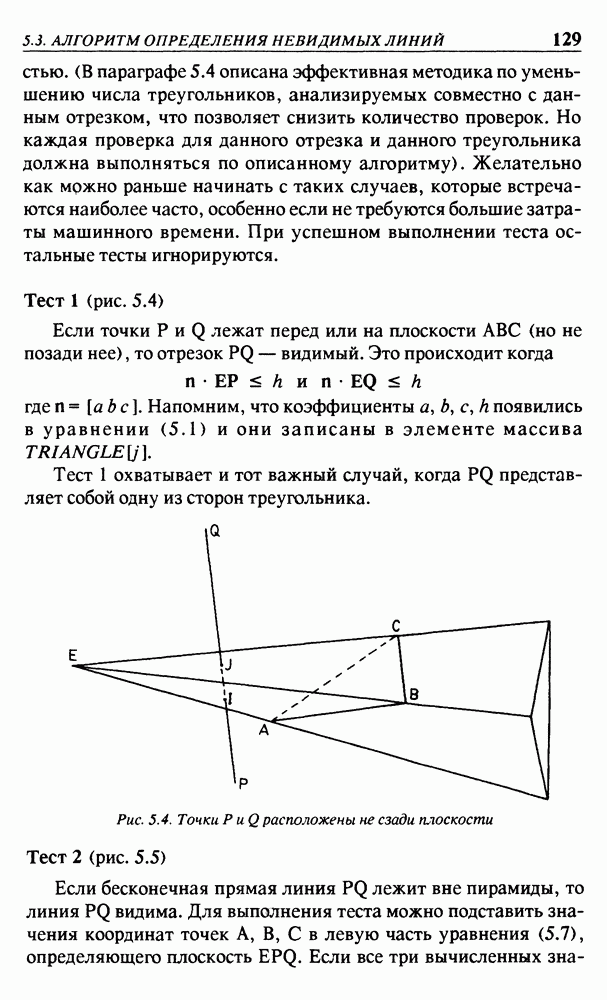
1. Все точки на плоскости  перемещаются вправо на расстояние а — см. рис. 2.1 (а);
перемещаются вправо на расстояние а — см. рис. 2.1 (а);
2. Координатные оси х и у перемещаются влево на расстояние а — см. рис. 2.1(б).

Рис. 2.1. (а) - перенос; (б) - изменение координат
Этот простой пример иллюстрирует принцип, применимый и в более сложных ситуациях. Мы и далее будем рассматривать системы уравнений, обычно записываемых в виде произведений матриц, интерпретируя их как преобразования всех точек в фиксированной системе координат. Однако та же самая система уравнений может интерпретироваться и как изменение системы координат.
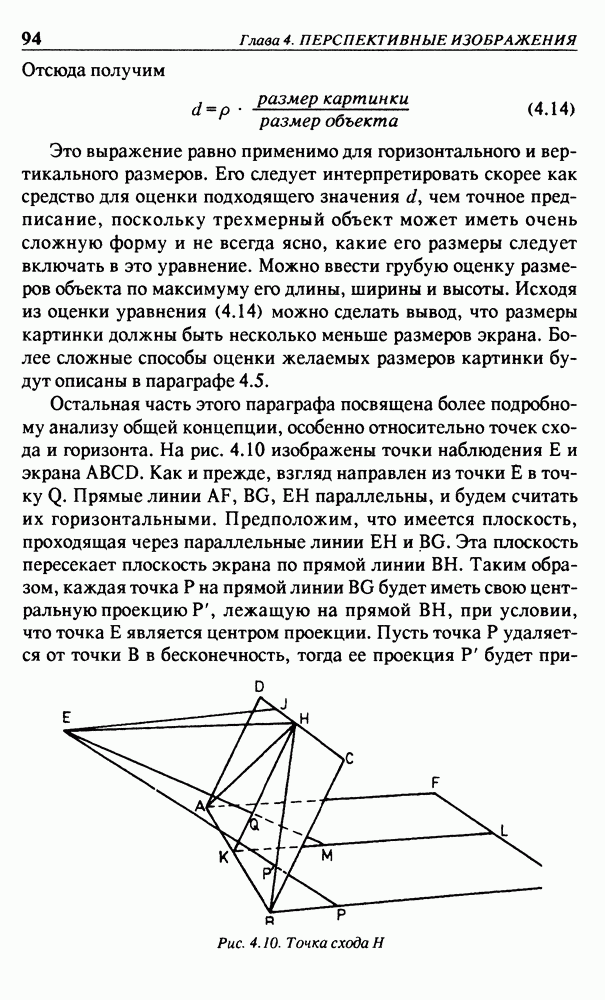
Пусть необходимо повернуть точку  вокруг начала координат О на угол
вокруг начала координат О на угол  Изображение новой точки на рис. 2.2 обозначим через
Изображение новой точки на рис. 2.2 обозначим через  Существуют четыре числа
Существуют четыре числа  такие,
такие,

Рис. 2.2. Поворот вокруг точки О на угол 
что новые координатах  могут быть вычислены по значениям старых координат х и у из следующих уравнений:
могут быть вычислены по значениям старых координат х и у из следующих уравнений:

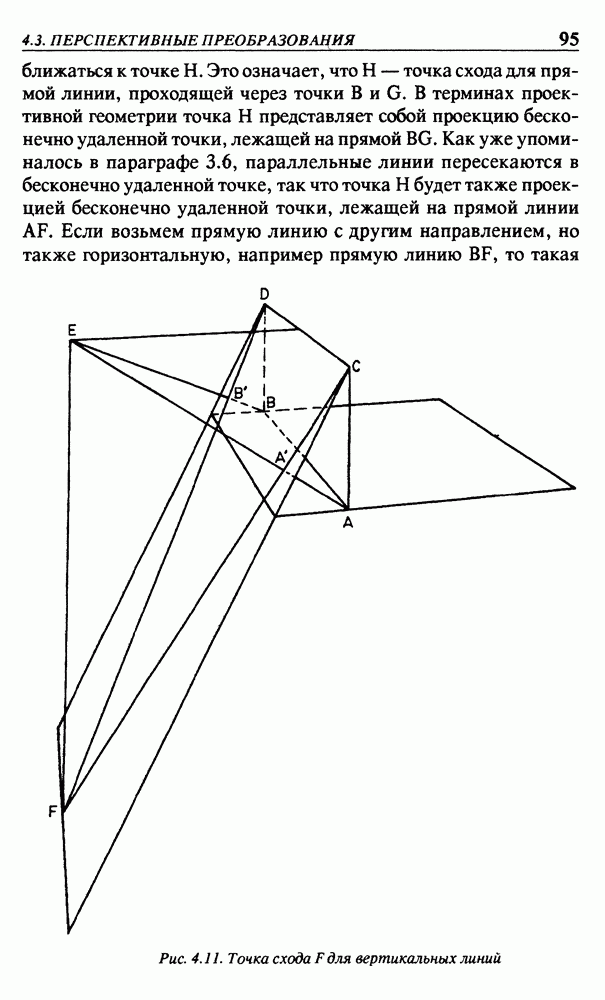
Для получения значений  рассмотрим вначале точку (х, у) = (1,0). Полагая
рассмотрим вначале точку (х, у) = (1,0). Полагая  в уравнении (2.1), получим
в уравнении (2.1), получим

Но в этом простом случае, как это видно из рис.  значения х и у равны соответственно
значения х и у равны соответственно  Тогда будем иметь
Тогда будем иметь

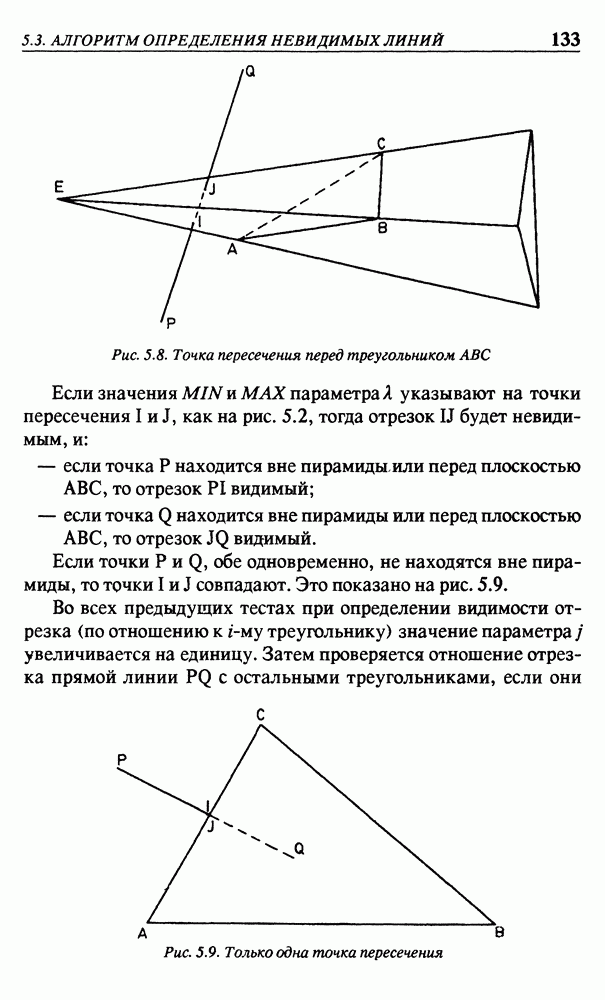
Аналогичным образом из рис. 2.3(б) следует

Тогда вместо системы уравнений (2.1) можем записать


Рис. 2.5. (а) - отображение точки (1,0); (б) - отображение точки (0,1)
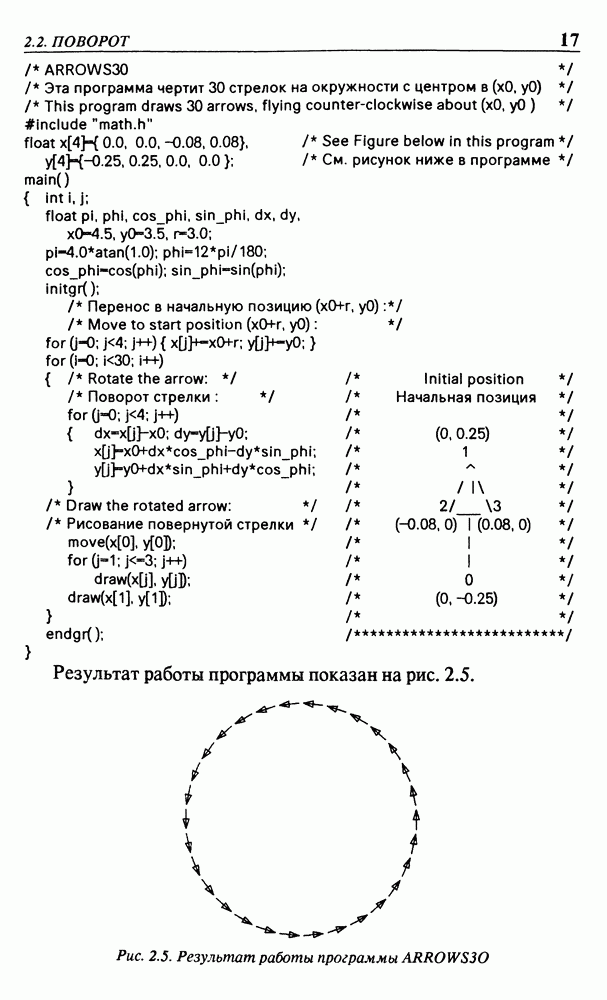
В приведенной ниже программе изображение стрелки вычерчивается после предварительного поворота вокруг точки О на 6°.
(см. скан)
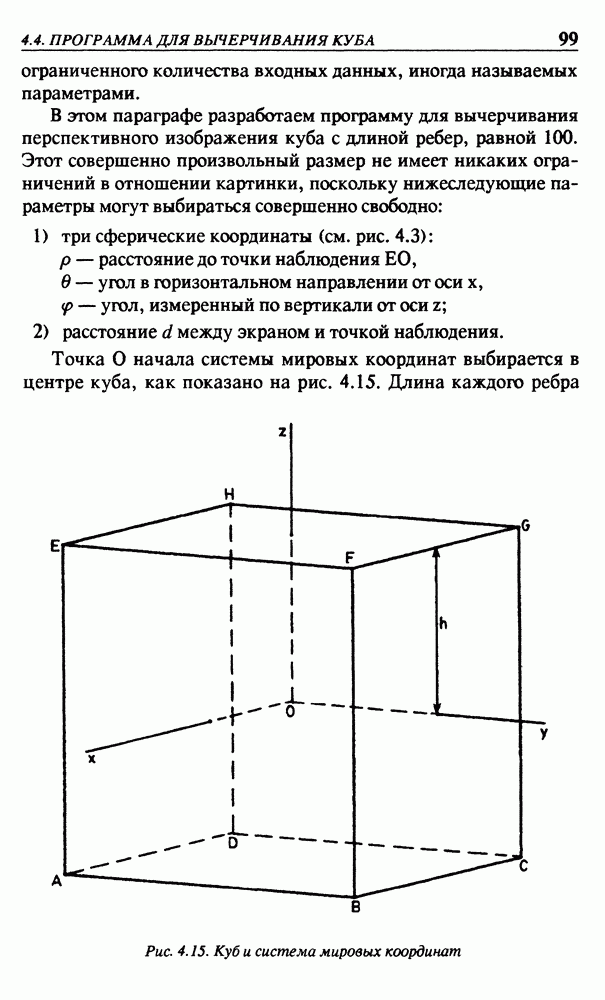
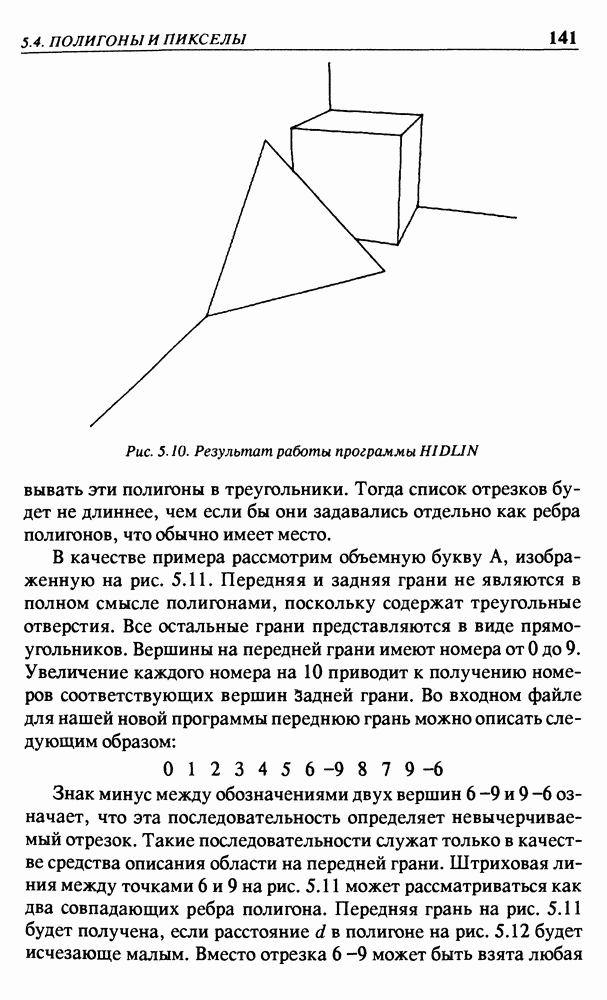
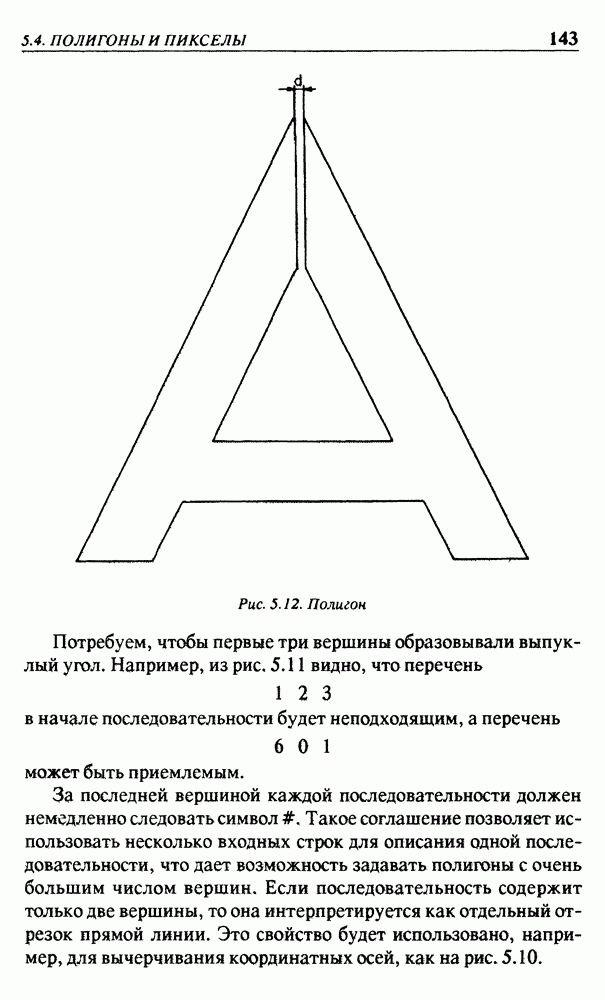
В геометрии точки объекта обычно обозначаются прописными буквами  Здесь будем обозначать их цифрами
Здесь будем обозначать их цифрами  В начальной позиции стрелка указывает вверх, ее центр расположен в точке
В начальной позиции стрелка указывает вверх, ее центр расположен в точке  В комментариях в правой части программы сделана попытка (правда, не очень успешная) показать стрелку в исходной позиции. Значения координат х и у для вершин ломаной линии, изображающей стрелку, записаны в элементах массивов
В комментариях в правой части программы сделана попытка (правда, не очень успешная) показать стрелку в исходной позиции. Значения координат х и у для вершин ломаной линии, изображающей стрелку, записаны в элементах массивов  . Эти массивы — внешние: они определены вне функции
. Эти массивы — внешние: они определены вне функции  Внешние массивы обладают очень полезным свойством — значения элементов массива можно
Внешние массивы обладают очень полезным свойством — значения элементов массива можно
инициализировать. Нумерация индексов элементов массива начинается с 0, в описании массива необходимо задать количество элементов массива. Таким образом, описание массива (которое также называется “декларацией” или “объявлением”)

вводит четыре элемента массива с начальными значениями

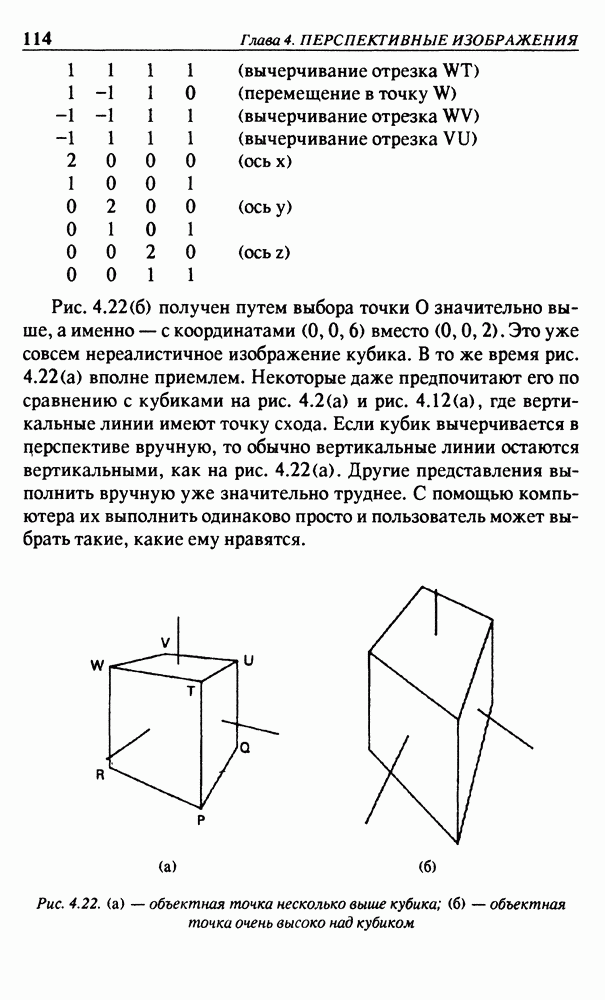
То обстоятельство, что начальное значение  задано отрицательным, а все координаты для вычерчивания должны быть положительными, не вызывает сложностей, поскольку перед вычерчиванием стрелка подвергается повороту, который переносит ее в область над осью х. На рис. 2.4 показан результат работы этой программы.
задано отрицательным, а все координаты для вычерчивания должны быть положительными, не вызывает сложностей, поскольку перед вычерчиванием стрелка подвергается повороту, который переносит ее в область над осью х. На рис. 2.4 показан результат работы этой программы.

Рис. 2.4. Результат работы программы 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
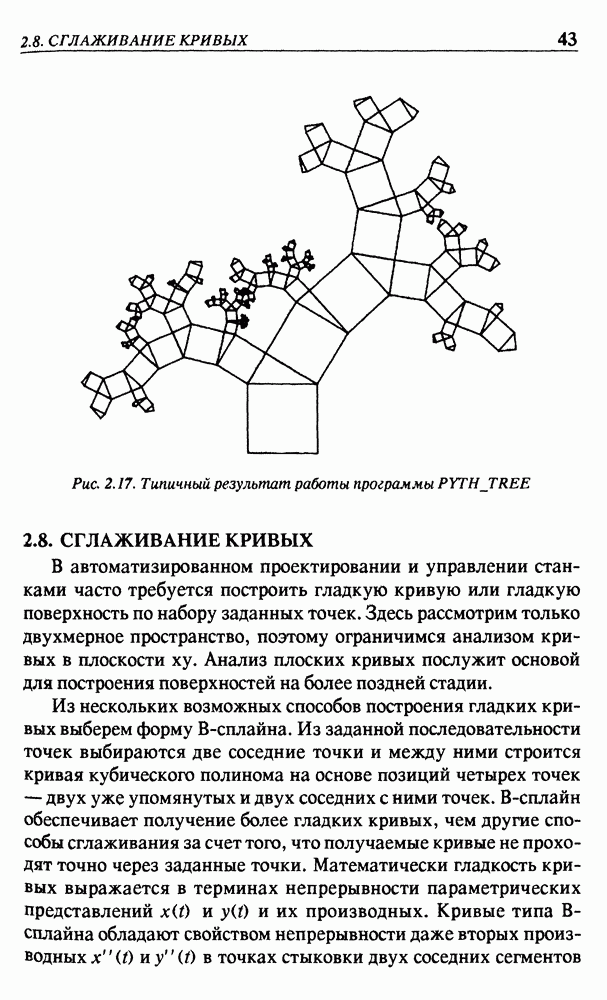
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
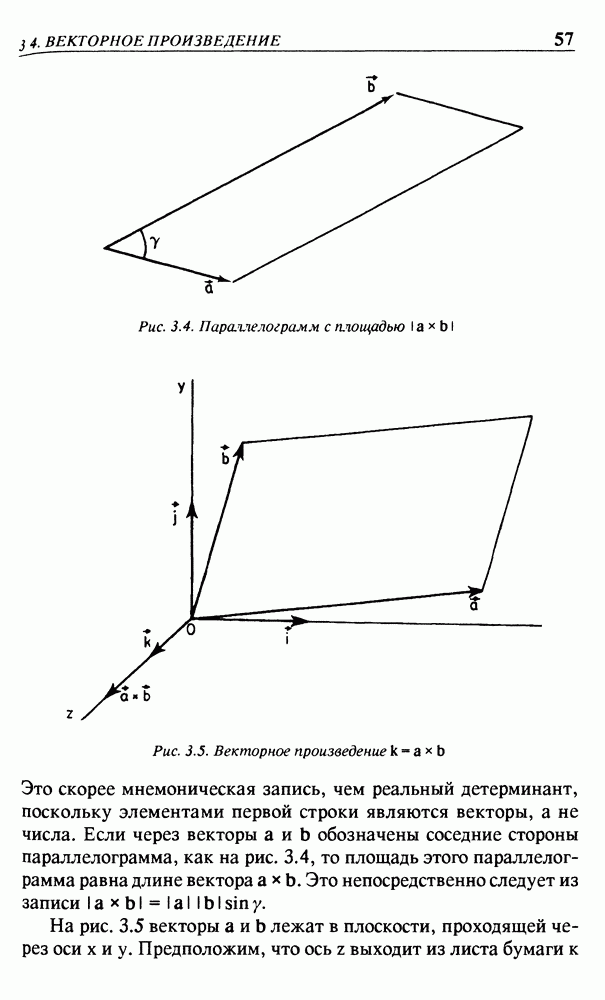
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
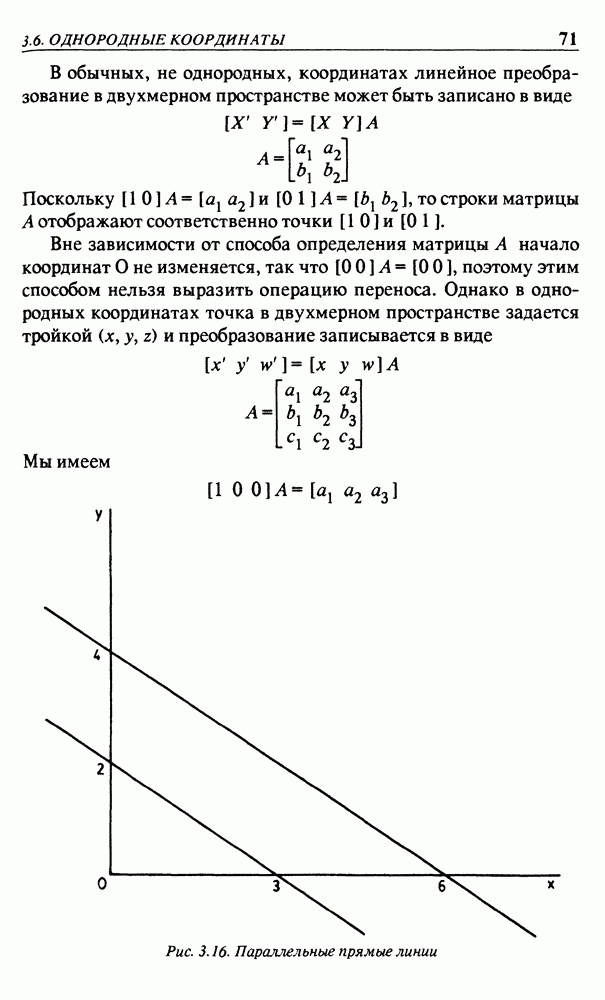
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
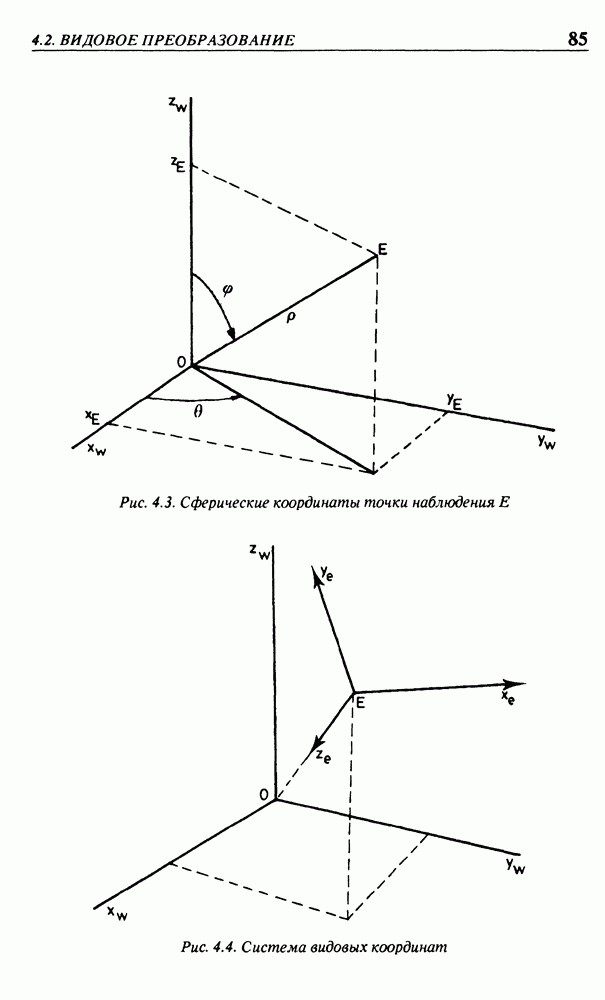
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
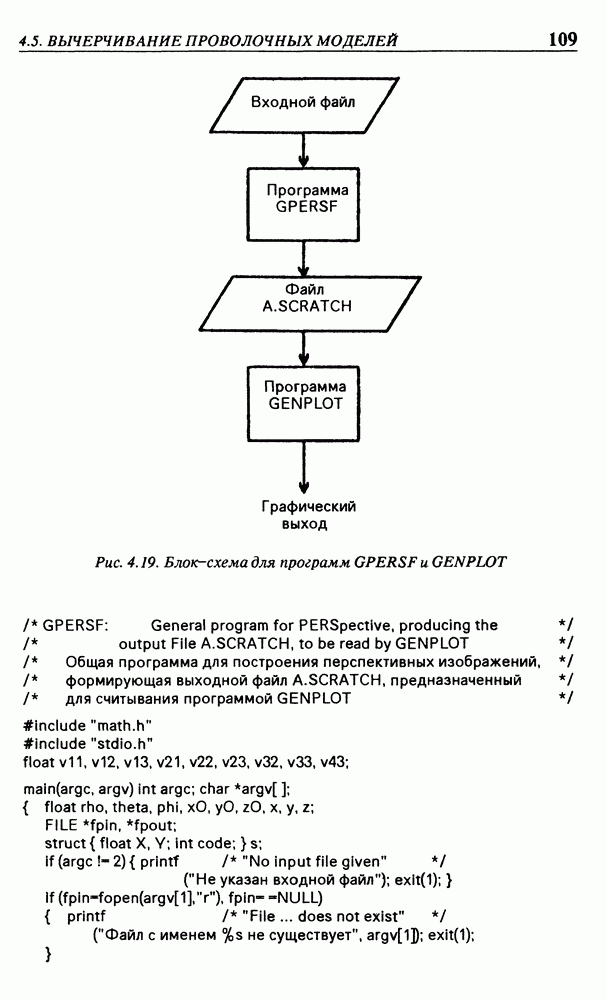
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
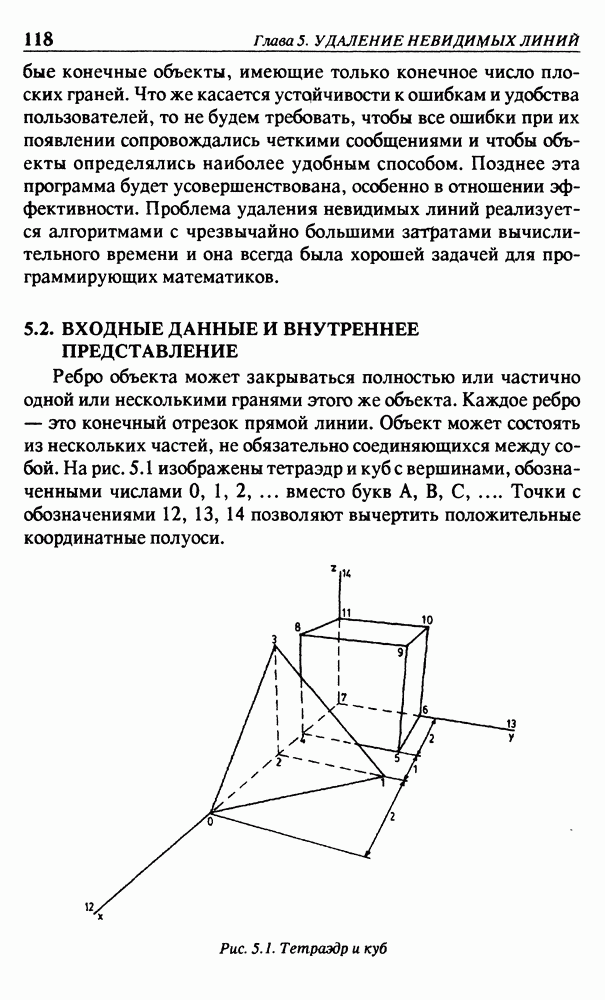
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
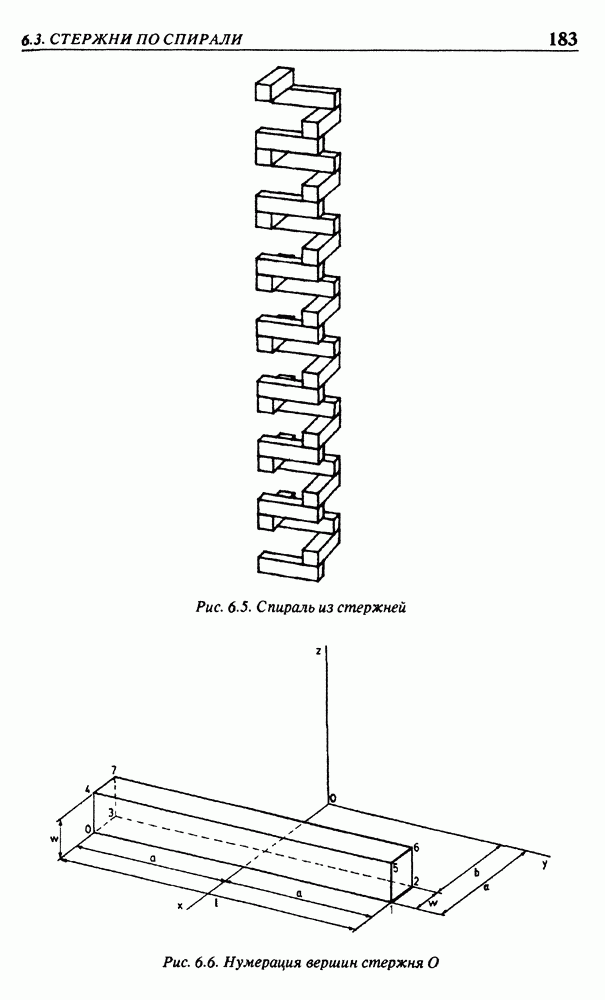
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
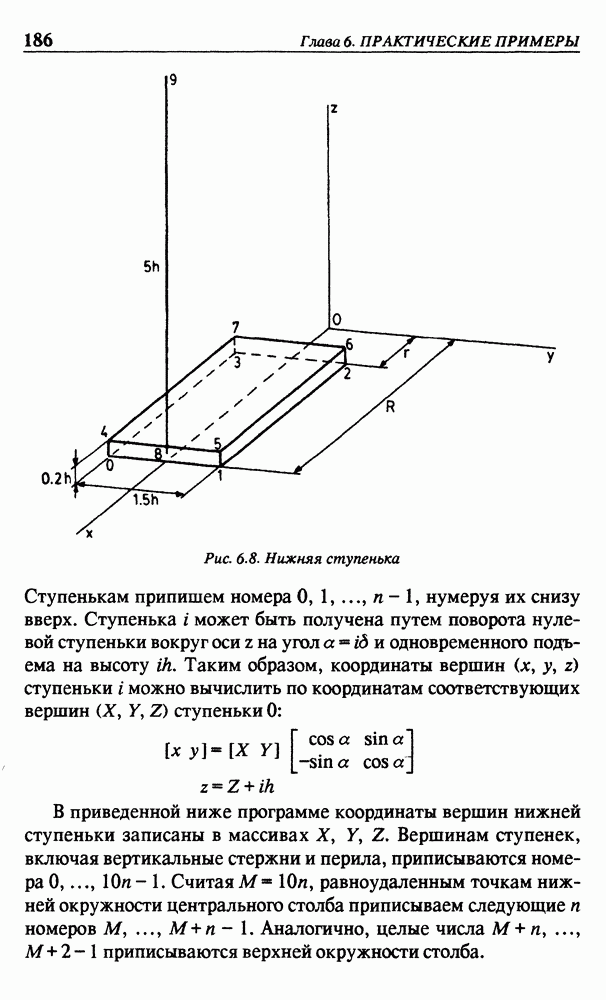
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
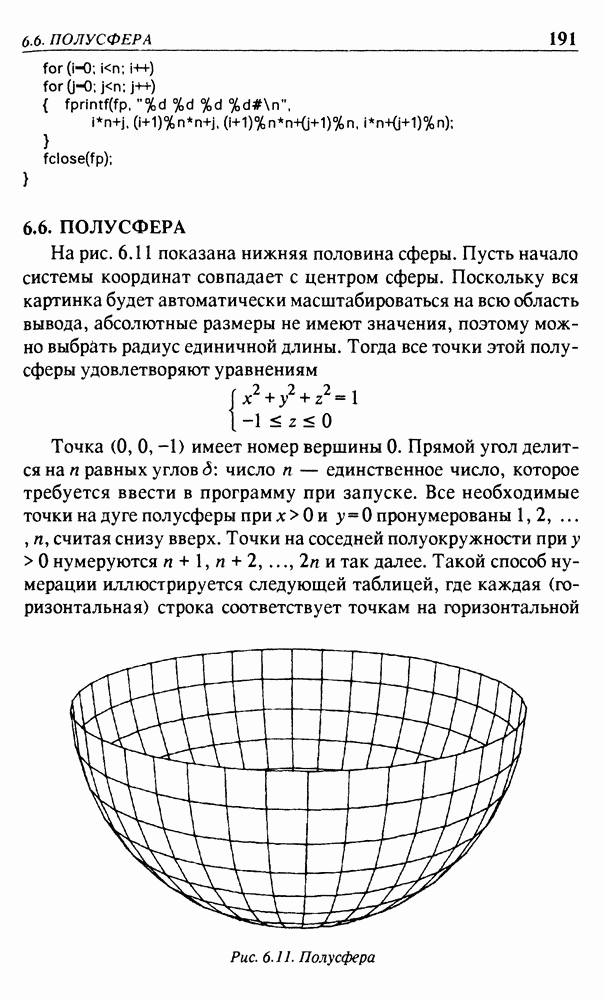
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА