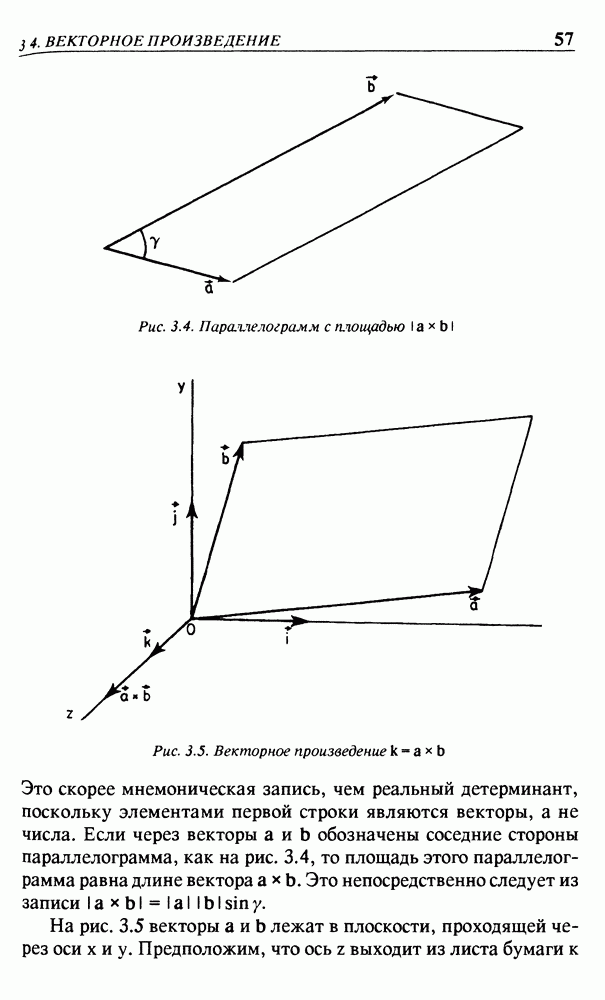
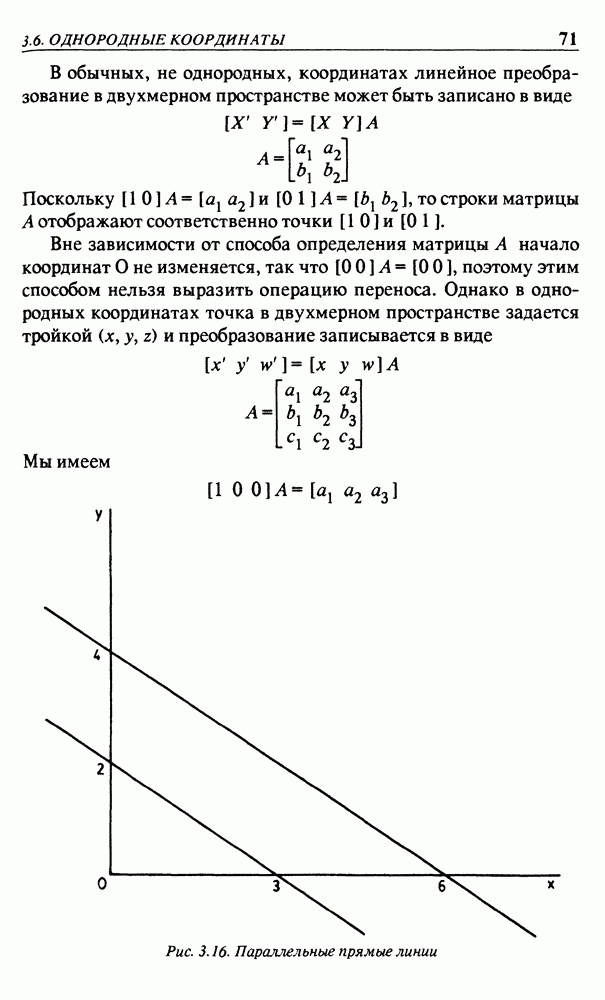
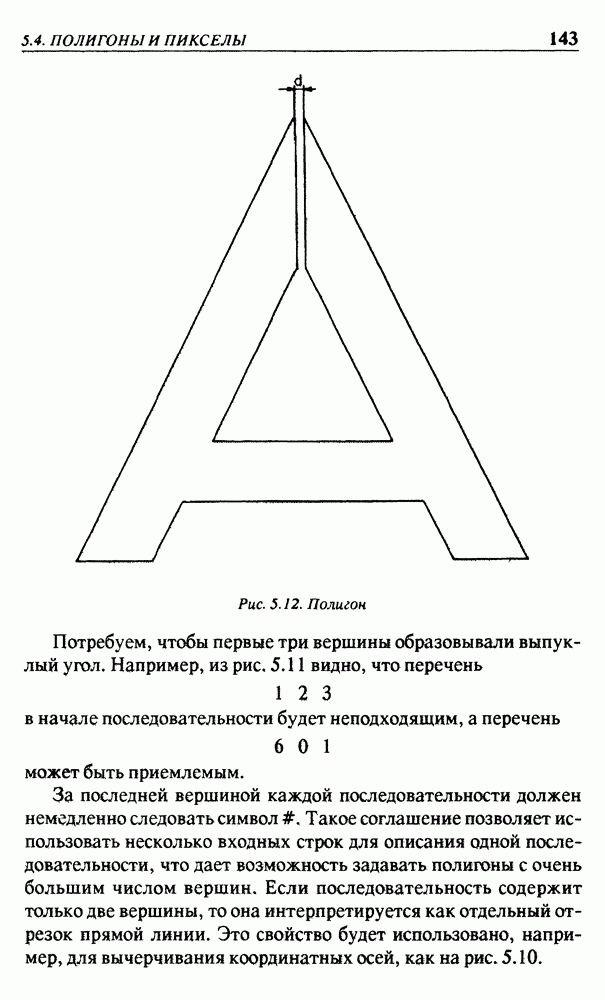
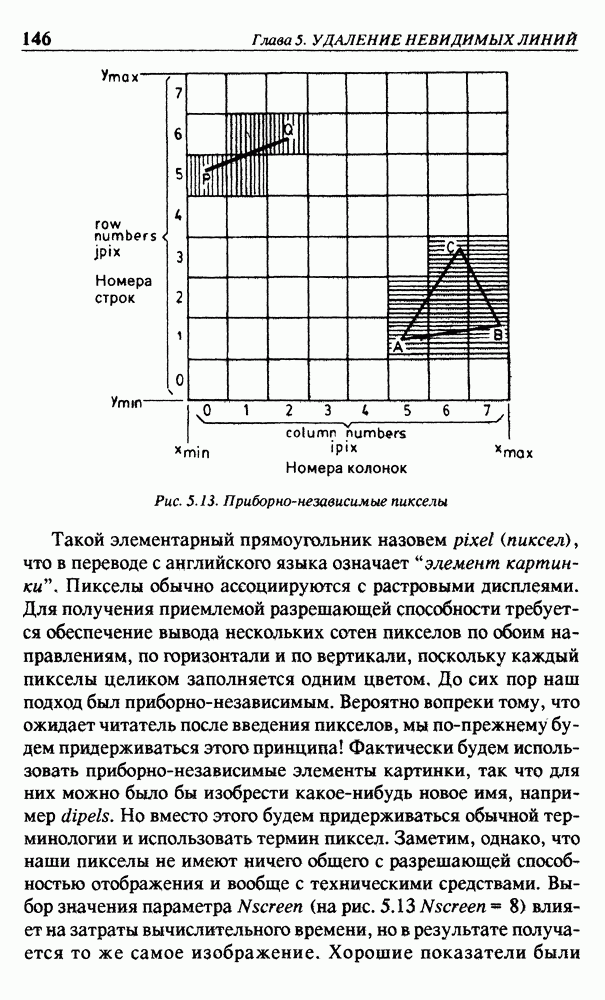
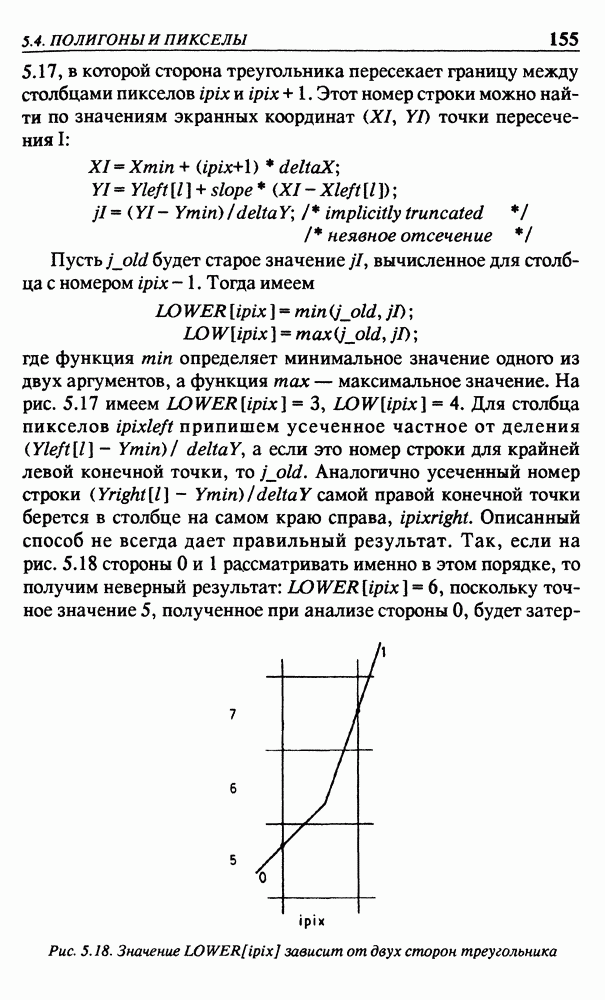
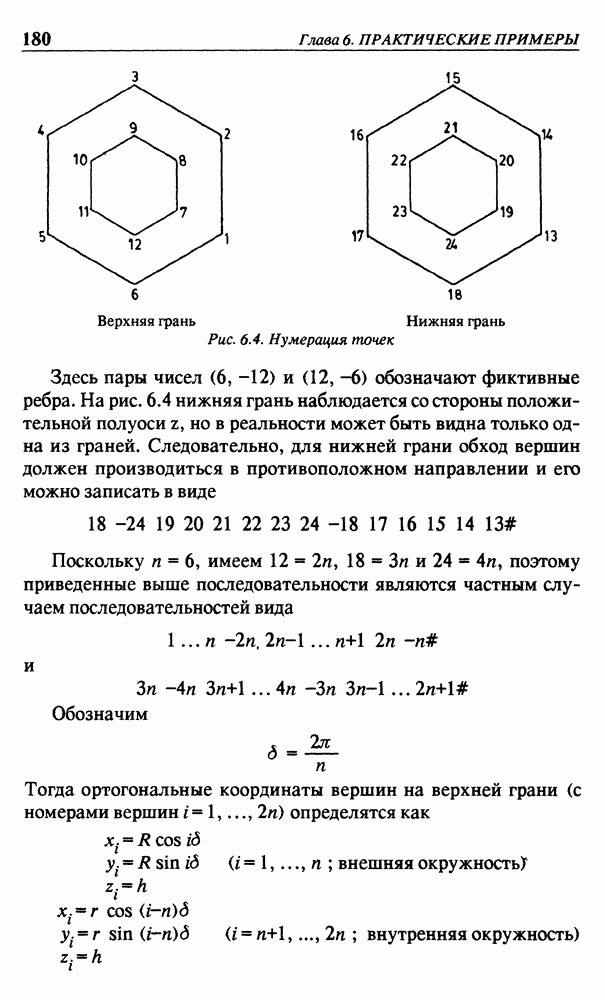
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
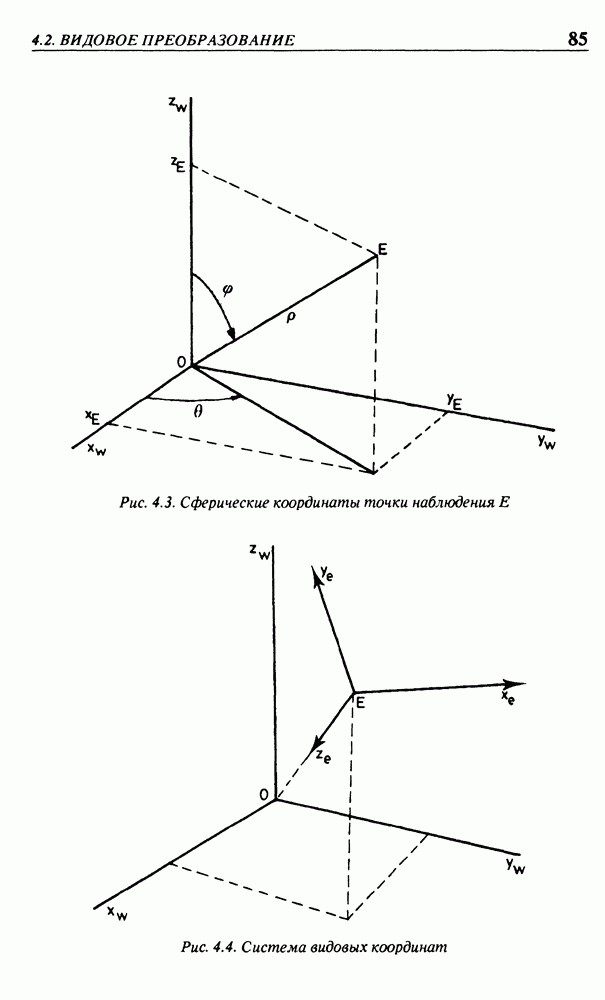
Для выполнения видовых преобразований должны быть заданы точка наблюдения, совпадающая с глазом, и объект. Желательно, чтобы система мировых координат была правой. Будет удобно, если начало ее координат располагается где-то вблизи центра объекта, поскольку объект наблюдается в направлении от Е к О. Предположим, что это условие выполняется. На практике это означает, что, возможно, потребуется некоторое преобразование координат, заключающееся в вычитании из исходных значений координат положения центральной точки объекта. Это очень простое преобразование будет включено в программу, но без записи в математической форме. Пусть точка наблюдения Е будет задана в сферических координатах  по отношению к мировым координатам. То есть мировые координаты могут быть вычислены по формулам:
по отношению к мировым координатам. То есть мировые координаты могут быть вычислены по формулам:

Обозначения сферических координат схематически изображены на рис. 4.3. Говорят, что вектор направления  (равный
(равный  ) определяет направление наблюдения. Из точки наблюдения Е можно видеть точки объекта только внутри некоторого конуса, ось которого совпадает с линией
) определяет направление наблюдения. Из точки наблюдения Е можно видеть точки объекта только внутри некоторого конуса, ось которого совпадает с линией  а вершина — с точкой Е.
а вершина — с точкой Е.  ли заданы ортогональные координаты
ли заданы ортогональные координаты  точки Е, то
точки Е, то

(кликните для просмотра скана)
можно вычислить ее сферические координаты по методике, изложенной в параграфе 3.7.
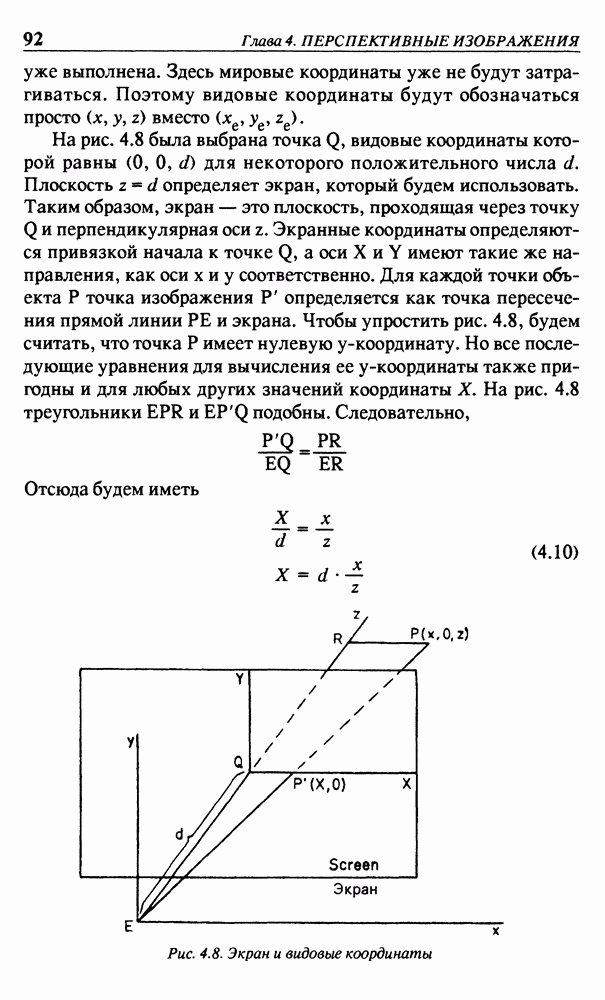
Нашей конечной задачей будет вычисление экранных координат  для которых оси
для которых оси  лежат в плоскости экрана, расположенной между точками
лежат в плоскости экрана, расположенной между точками  и перпендикулярной направлению наблюдения
и перпендикулярной направлению наблюдения  Начало системы видовых координат располагается в точке наблюдения Е (рис. 4.4). При направлении взгляда из
Начало системы видовых координат располагается в точке наблюдения Е (рис. 4.4). При направлении взгляда из  положительная полуось
положительная полуось  направлена вправо, а положительная полуось
направлена вправо, а положительная полуось  вверх. Такое направление осей позволит нам впоследствии определить экранные оси в тех же направлениях. Направление оси
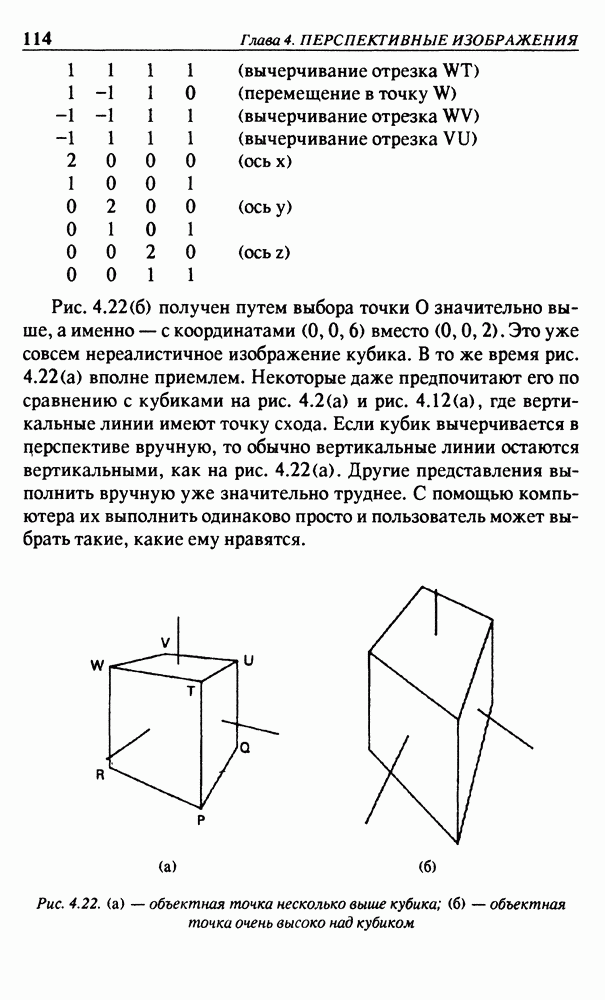
вверх. Такое направление осей позволит нам впоследствии определить экранные оси в тех же направлениях. Направление оси  выбирается таким образом, что значения координат увеличиваются по мере удаления от точки наблюдения. Такие определения осей логичны и удобны, но их взаимное соответствие таково, что система видовых координат является левосторонней. Хотя такой вывод может показаться несуразным, но это совершенно обычная ситуация в машинной графике и не вызовет появления каких-либо проблем. (Заметим, что система мировых координат всегда выбирается как правосторонняя.)
выбирается таким образом, что значения координат увеличиваются по мере удаления от точки наблюдения. Такие определения осей логичны и удобны, но их взаимное соответствие таково, что система видовых координат является левосторонней. Хотя такой вывод может показаться несуразным, но это совершенно обычная ситуация в машинной графике и не вызовет появления каких-либо проблем. (Заметим, что система мировых координат всегда выбирается как правосторонняя.)
Видовое преобразование может быть записано в форме

где V - матрица видового преобразования размерами  Для нахождения матрицы V предположим, что преобразования отображения могут быть составлены из четырех элементарных преобразований, для которых легко написать свои матрицы преобразований. Матрица V получается путем перемножения этих четырех матриц. Фактически каждое из четырех преобразований изменяет координаты и, следовательно, определяется матрицей, обратной матрице, соответствующей преобразованию точки.
Для нахождения матрицы V предположим, что преобразования отображения могут быть составлены из четырех элементарных преобразований, для которых легко написать свои матрицы преобразований. Матрица V получается путем перемножения этих четырех матриц. Фактически каждое из четырех преобразований изменяет координаты и, следовательно, определяется матрицей, обратной матрице, соответствующей преобразованию точки.
Перенос начала из O в E
Выполним такой перенос системы координат, при котором точка Е становится новым началом координат. Матрица для такого изменения координат выгладит так:


Рис. 4.5. Новые оси после переноса
Новая система координат показана на рис. 4.5.
Поворот координатной системы вокруг оси z
Обращаясь к рис. 4.5, повернем систему координат вокруг оси z на угол  в в отрицательном направлении. В результате ось у совпадет по направлению с горизонтальной составляющей отрезка
в в отрицательном направлении. В результате ось у совпадет по направлению с горизонтальной составляющей отрезка  а ось х будет расположена перпендикулярно отрезку
а ось х будет расположена перпендикулярно отрезку  Матрица для такого изменения координат будет совпадать с матрицей для поворота точки на такой же угол в положительном направлении. Матрица
Матрица для такого изменения координат будет совпадать с матрицей для поворота точки на такой же угол в положительном направлении. Матрица  для этого поворота равна
для этого поворота равна

Новое положение осей показано на рис. 4.6.
Поворот системы координат вокруг оси х
Поскольку новая ось z должна совпадать по направлению с отрезком  повернем систему координат вокруг оси х на угол
повернем систему координат вокруг оси х на угол

Рис. 4.6. Новые оси после поворота вокруг оси z
 в положительном направлении, что соответствует повороту точки на угол
в положительном направлении, что соответствует повороту точки на угол  Из уравнения (3.13), получаем матрицу:
Из уравнения (3.13), получаем матрицу:

Новые оси показаны на рис. 4.7.
Изменение направления оси х
На рис. 4.7 оси  имеют правильную ориентацию, а ось х должна быть направлена в противоположную сторону. Поэтому необходима матрица для выполнения преобразования
имеют правильную ориентацию, а ось х должна быть направлена в противоположную сторону. Поэтому необходима матрица для выполнения преобразования  то есть
то есть

После этого завершающего преобразования получим систему видовых координат, уже показанную на рис. 4.4.

Рис. 4.7. Новые оси после поворота вокруг оси х
Вычислим матрицу отображения V как матричное произведение

где обозначение  использовано для матрицы
использовано для матрицы  полученной путем расширения матрицы
полученной путем расширения матрицы  имеющей размерность
имеющей размерность  добавлением четвертой строки и четвертого столбца, содержащих числа
добавлением четвертой строки и четвертого столбца, содержащих числа  именно в этом порядке. Матричное произведение не коммутативно (то есть в общем случае
именно в этом порядке. Матричное произведение не коммутативно (то есть в общем случае  , но ассоциативно, поэтому уравнение (4.7) можно переписать в виде
, но ассоциативно, поэтому уравнение (4.7) можно переписать в виде

Таким образом можно работать с матрицами  до тех пор, пока это возможно. Дальнейшая проработка задачи умножения матриц связана с использованием обозначений
до тех пор, пока это возможно. Дальнейшая проработка задачи умножения матриц связана с использованием обозначений

откуда следует, что 
На основе уравнения (4.1), перепишем уравнение (4.3) в виде

а уравнения (4.4) и (4.5) как

Следовательно,

Умножив эту матрицу справа на матрицу Мух из уравнения (4.6), получим

Затем искомую матрицу отображения V найдем как произведение двух матриц

и

откуда

где


Таким образом, мы нашли

Здесь мы получили важный результат. Если были заданы сферические координаты  для точки наблюдения Е, то положение точки в системе видовых координат можно вычислить по значениям ее мировых координат, используя только уравнения (4.2) и (4.9).
для точки наблюдения Е, то положение точки в системе видовых координат можно вычислить по значениям ее мировых координат, используя только уравнения (4.2) и (4.9).
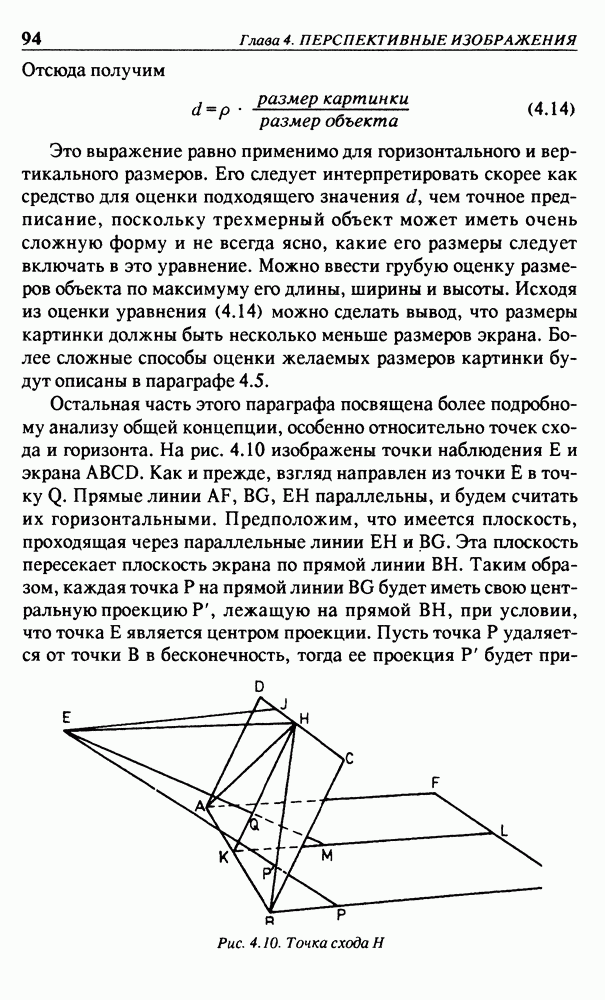
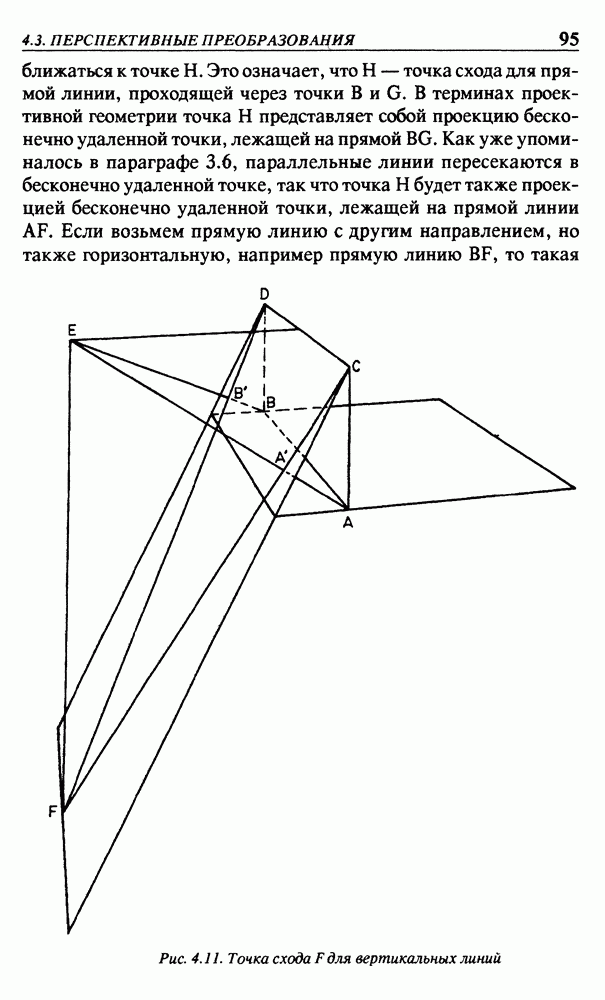
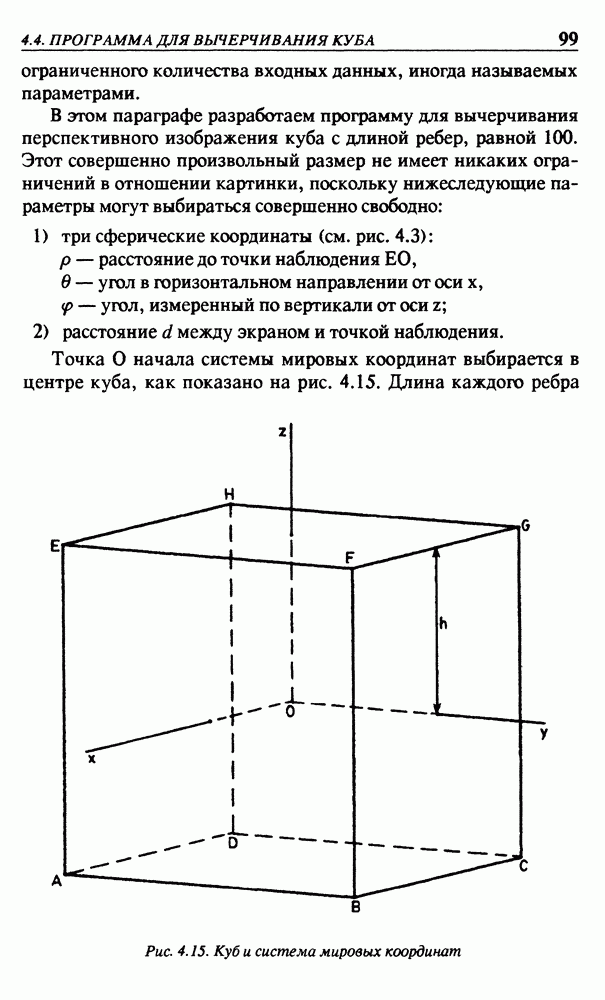
После только что выполненного преобразования отображения необходимо определить перспективные преобразования, и это будет сделано в следующем параграфе. Но уже сейчас можно использовать видовые координаты  просто игнорируя координату
просто игнорируя координату  . В этом случае будет получена так называемая ортогональная проекция. Каждая точка Р объекта проецируется в точку Р проведением прямой линии из точки Р перпендикулярно плоскости, определяемой осями х и у. Эту проекцию можно также считать перспективной картинкой, которая была бы получена при удалении точки наблюдения в бесконечность. Примером такой картинки может служить изображение куба на рис. 4.2(б). Параллельные линии остаются параллельными и на картинке, полученной при ортогональном проецировании. На практике такие проекции применяются очень часто.
. В этом случае будет получена так называемая ортогональная проекция. Каждая точка Р объекта проецируется в точку Р проведением прямой линии из точки Р перпендикулярно плоскости, определяемой осями х и у. Эту проекцию можно также считать перспективной картинкой, которая была бы получена при удалении точки наблюдения в бесконечность. Примером такой картинки может служить изображение куба на рис. 4.2(б). Параллельные линии остаются параллельными и на картинке, полученной при ортогональном проецировании. На практике такие проекции применяются очень часто.
С другой стороны, внесение некоторого эффекта перспективы делает картинку более реалистичной. Поэтому после преобразования отображения необходимо выполнить перспективные преобразования, которые, к удивлению, потребуют очень незначительных дополнительных вычислений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
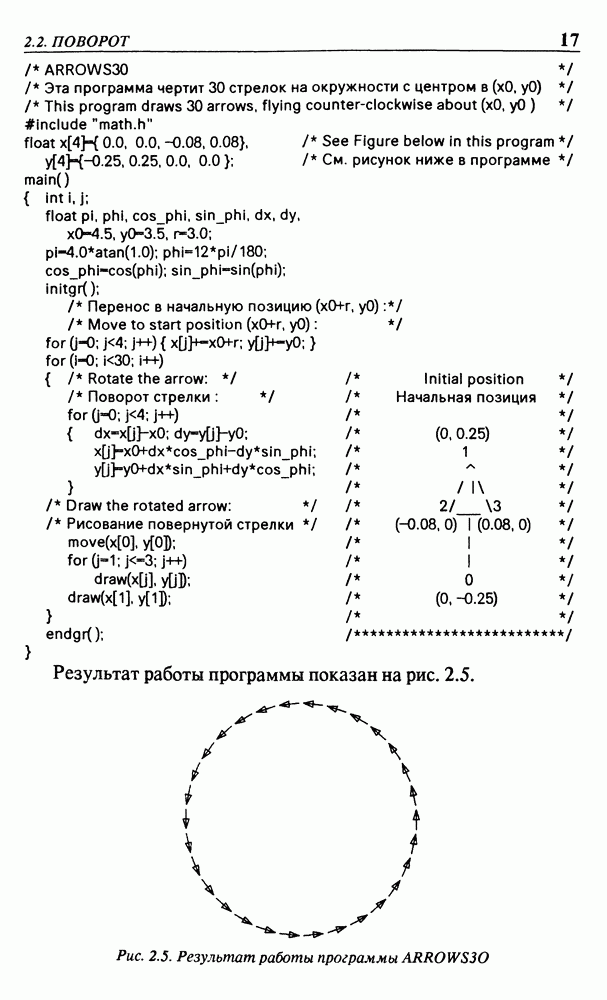
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
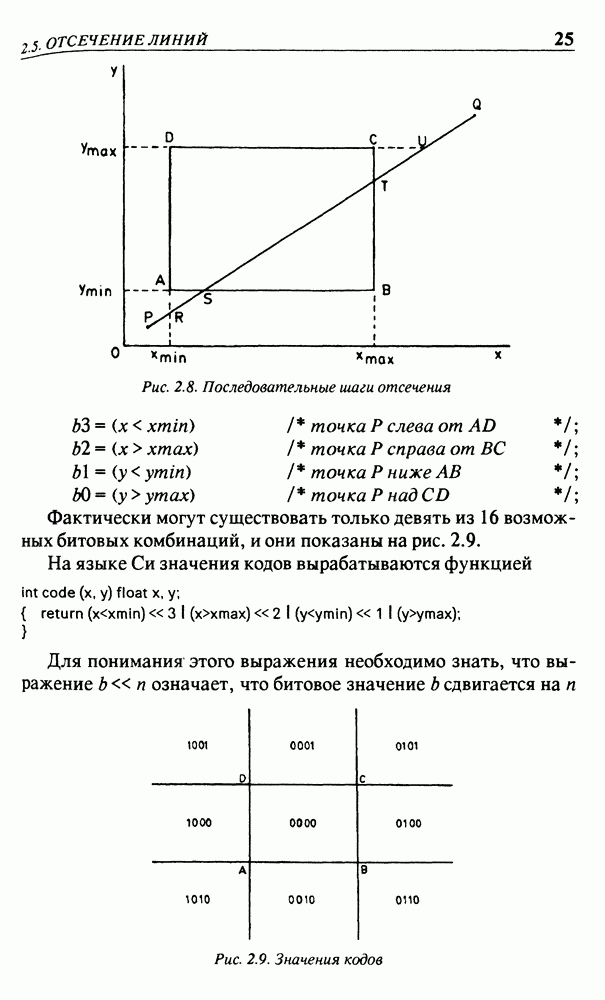
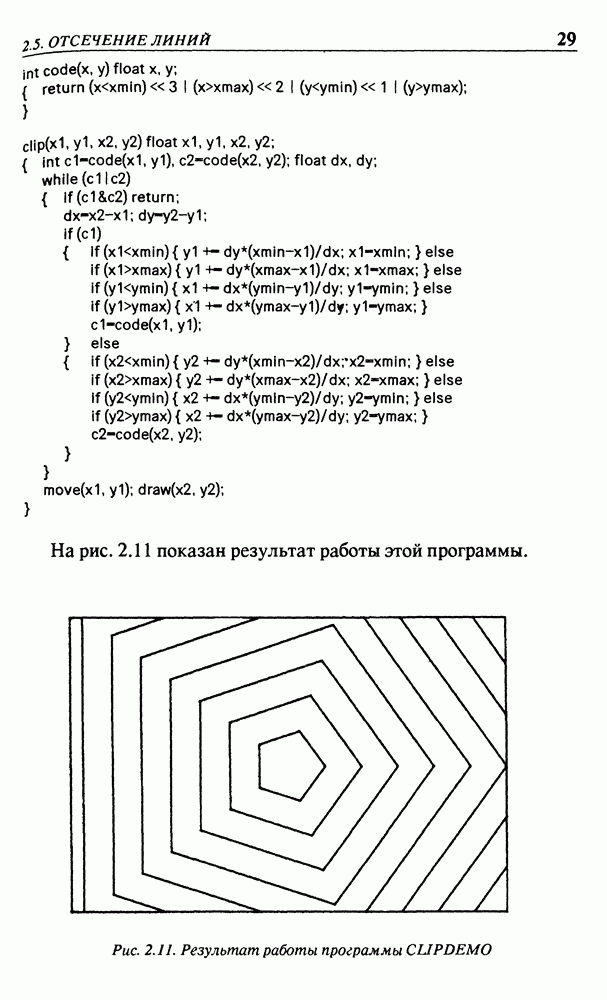
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
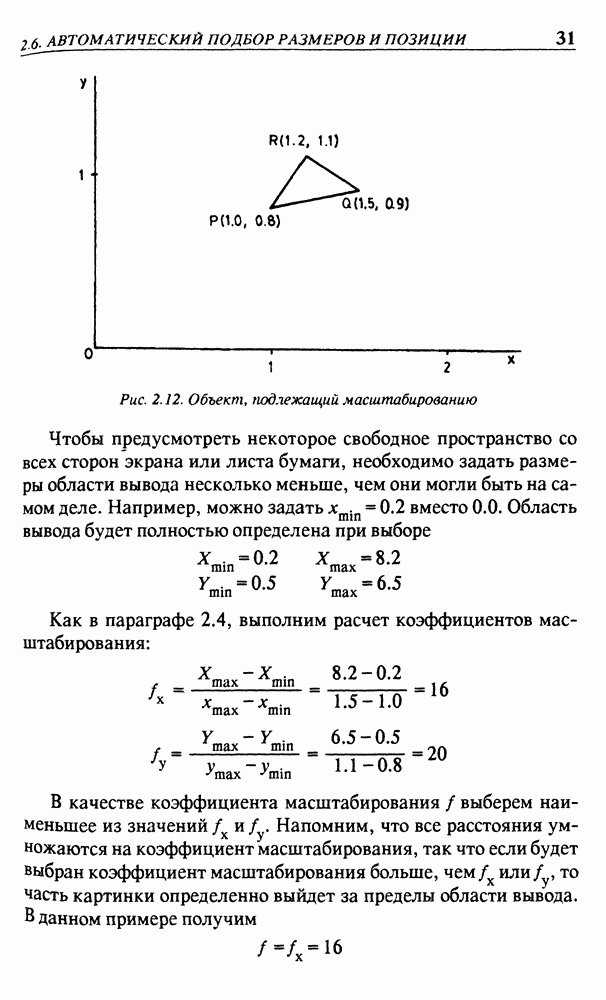
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
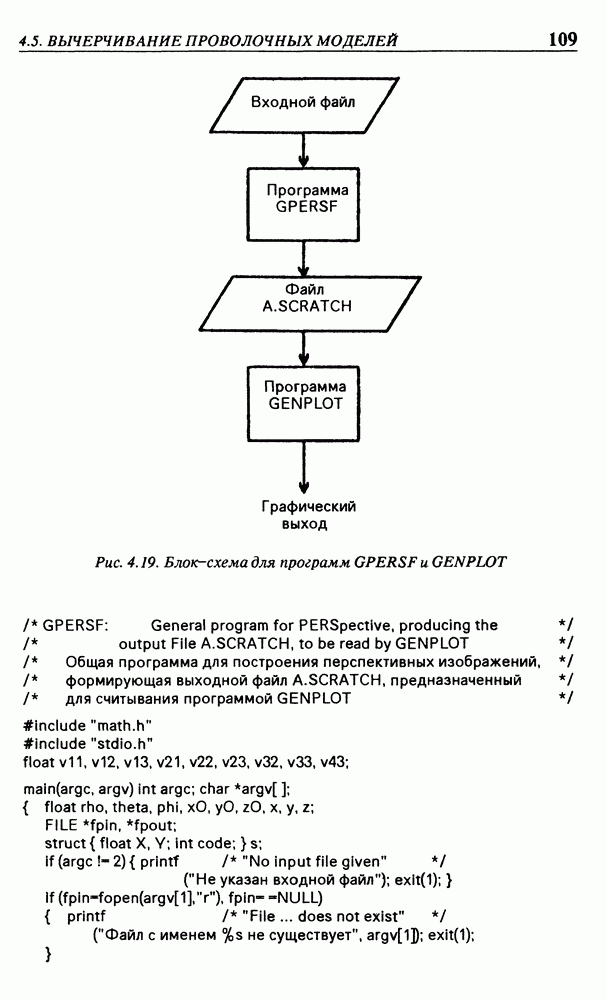
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
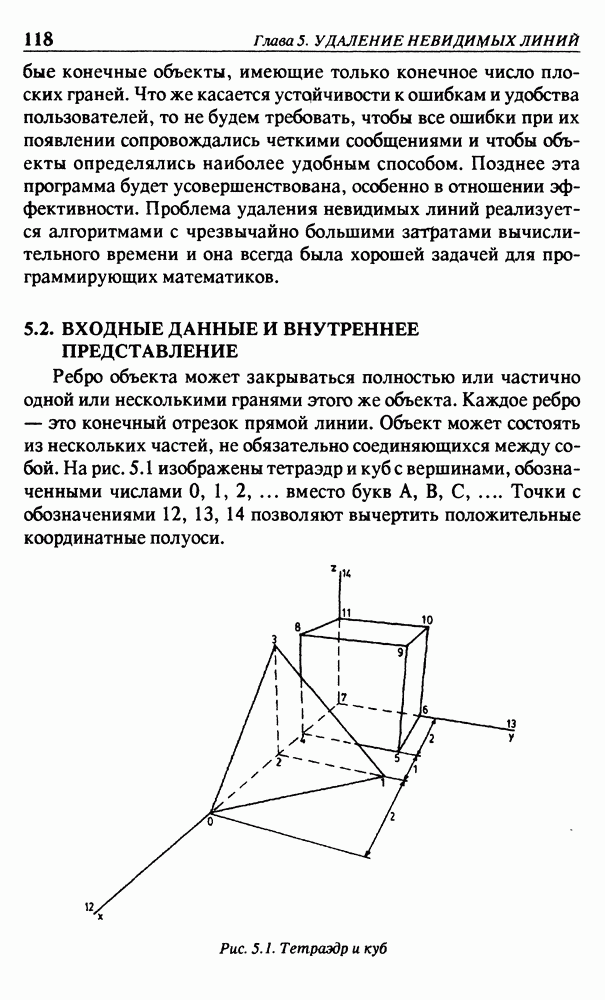
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
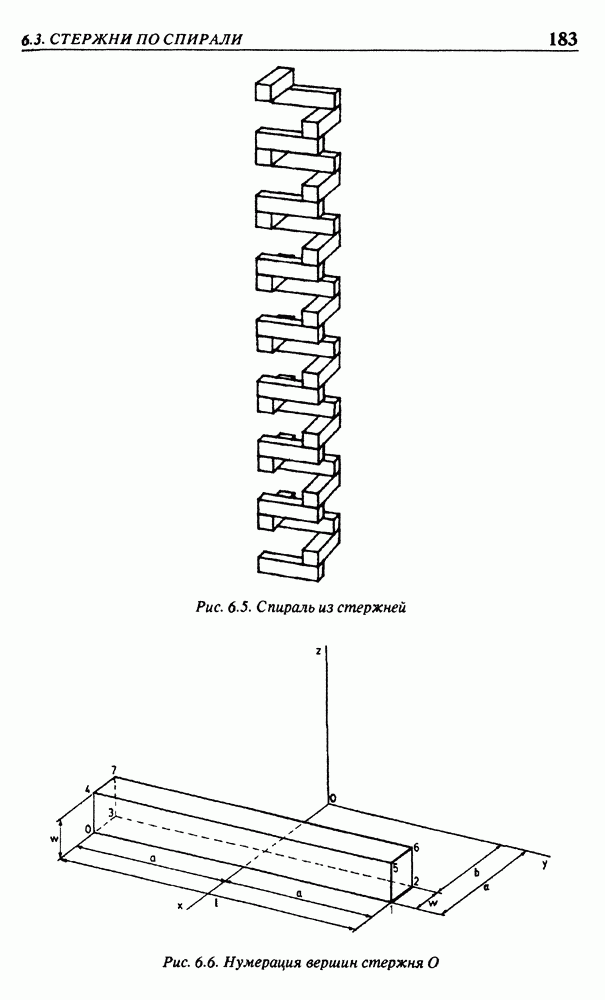
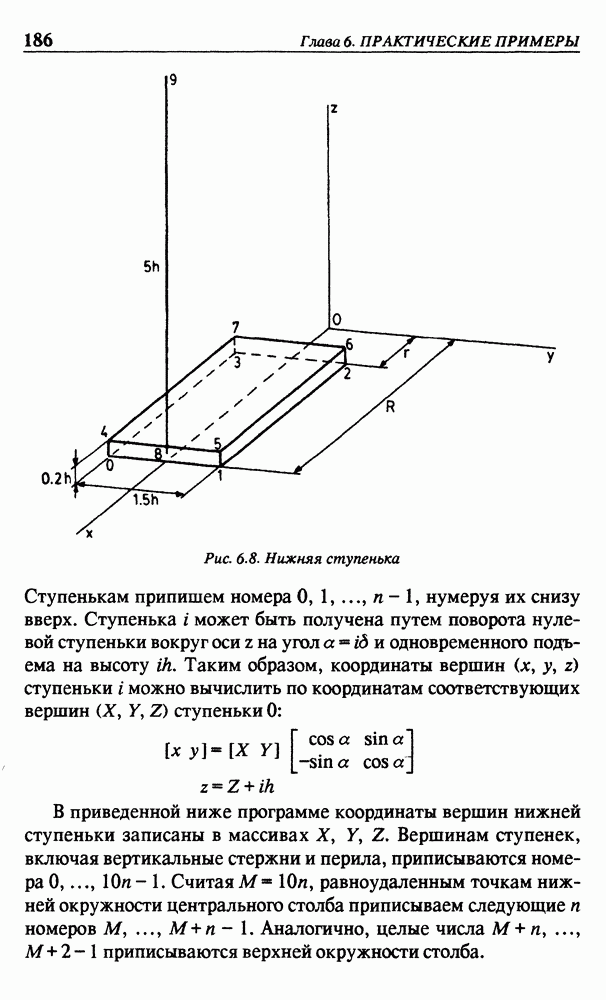
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
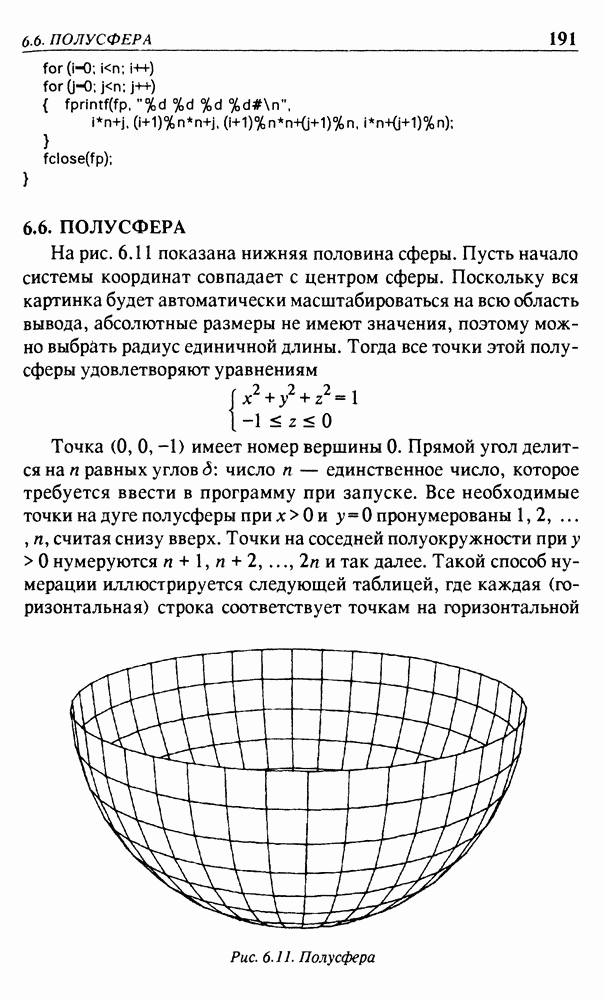
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА