| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. МАТРИЧНАЯ ЗАПИСЬ
Система уравнений (2.2) может быть записана в виде одного матричного уравнения

или с использованием вектора-столбца

В книгах по машинной графике запись с вектором-строкой (2.4) встречается чаще, чем с вектором-столбцом (2.5). Здесь также будет применяться запись типа (2.4). В такой записи  строка квадратной матрицы всегда является отображением
строка квадратной матрицы всегда является отображением  единичного вектора (здесь
единичного вектора (здесь  Вполне возможно записать в матричной форме систему уравнений (2.3)
Вполне возможно записать в матричной форме систему уравнений (2.3)

Однако первая часть этого уравнения не является чисто матричным произведением. В более сложных ситуациях, когда поворот совмещается с другими преобразованиями, было бы более удобно иметь единое матричное произведение для каждого элементарного преобразования. На первый взгляд это кажется невозможным, если преобразование включает операцию переноса. Но, как мы увидим ниже, с помощью матрицы преобразования размером  это вполне реально. Начнем с простого переноса. Пусть точка
это вполне реально. Начнем с простого переноса. Пусть точка  переносится в точку
переносится в точку  где
где

Эти уравнения можно переписать в виде

Но с учетом будущих потребностей это уравнение лучше переписать в следующей форме

Легко проверить, что уравнения (2.7) и (2.8) эквивалентны.
Такую запись принято называть записью в системе “однородных координат”. Однородные координаты более подробно обсуждаются в параграфе 3.6. Запись каждого преобразования в форме произведения матриц позволяет совмещать несколько преобразований в одном. Чтобы показать такое совмещение преобразований, объединим поворот с двумя переносами. Поворот на угол  вокруг начала координат О был описан уравнением (2.4).
вокруг начала координат О был описан уравнением (2.4).
Заменим это уравнение следующим:

Теперь выведем новую версию уравнений (2.6) для описания поворота на угол  вокруг точки
вокруг точки  это уравнение может быть выражено формулой
это уравнение может быть выражено формулой

где через  обозначена матрица размером
обозначена матрица размером  Для нахождения этой матрицы
Для нахождения этой матрицы  будем считать, что преобразование состоит из трех шагов с промежуточными точками
будем считать, что преобразование состоит из трех шагов с промежуточными точками 
1. Преобразование для переноса точки ( в начало координат О
в начало координат О

где

2. Поворот на угол  относительно точки начала координат О
относительно точки начала координат О

где

3. Перенос из начала координат в точку 

где

Возможность комбинации этих шагов основана на свойстве ассоциативности матричного умножения, то есть

для любых трех матриц  имеющих размерности, допускающие такое умножение. Для любой части этого уравнения мы можем просто записать
имеющих размерности, допускающие такое умножение. Для любой части этого уравнения мы можем просто записать 
Теперь найдем

где

Это и будет искомая матрица, которая после выполнения двух матричных умножений дает

где введены обозначения

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. МОТИВАЦИЯ НЕОБХОДИМОСТИ ГРАФИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 1.2. ПРОГРАММИРОВАНИЕ ГРАФИКИ НА ЯЗЫКЕ СИ
- Глава 2. ДВУХМЕРНЫЕ АЛГОРИТМЫ
- 2.2. ПОВОРОТ
- 2.3. МАТРИЧНАЯ ЗАПИСЬ
- 2.4. ОКНА И ОБЛАСТИ ВЫВОДА
- 2.5. ОТСЕЧЕНИЕ ЛИНИЙ
- 2.6. АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИИ
- 2.7. ПРИМЕНЕНИЕ РЕКУРСИЙ
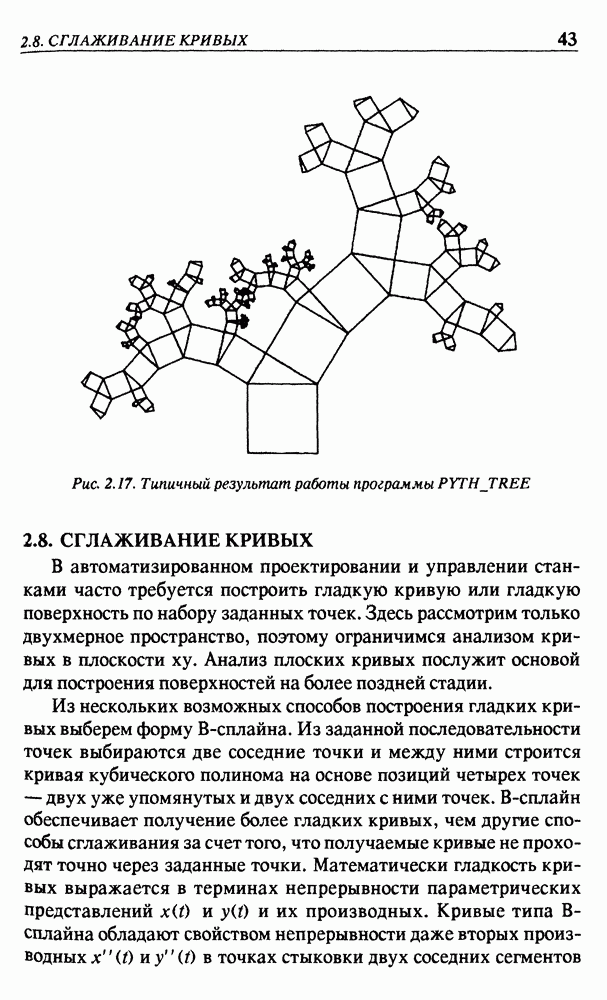
- 2.8. СГЛАЖИВАНИЕ КРИВЫХ
- Глава 3. ГЕОМЕТРИЧЕСКИЙ ИНСТРУМЕНТ ДЛЯ АЛГОРИТМОВ ТРЕХМЕРНОЙ ГРАФИКИ
- 3.2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
- 3.3. ДЕТЕРМИНАНТЫ
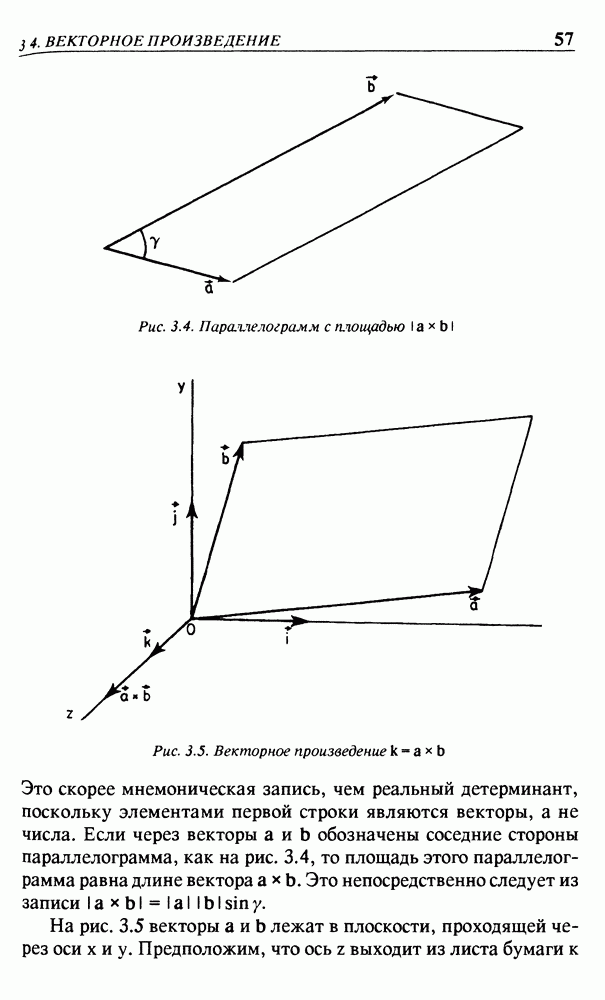
- 3.4. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 3.5. ДЕКОМПОЗИЦИЯ ПОЛИГОНОВ НА ТРЕУГОЛЬНИКИ
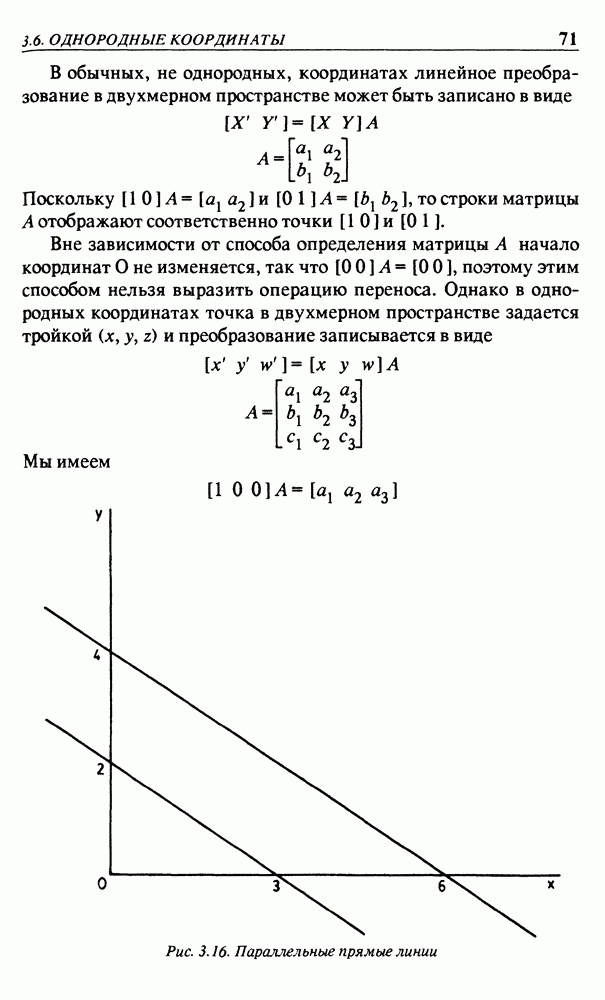
- 3.6. ОДНОРОДНЫЕ КООРДИНАТЫ
- 3.7. ПЕРЕНОС И ПОВОРОТЫ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
- Глава 4. ПЕРСПЕКТИВНЫЕ ИЗОБРАЖЕНИЯ
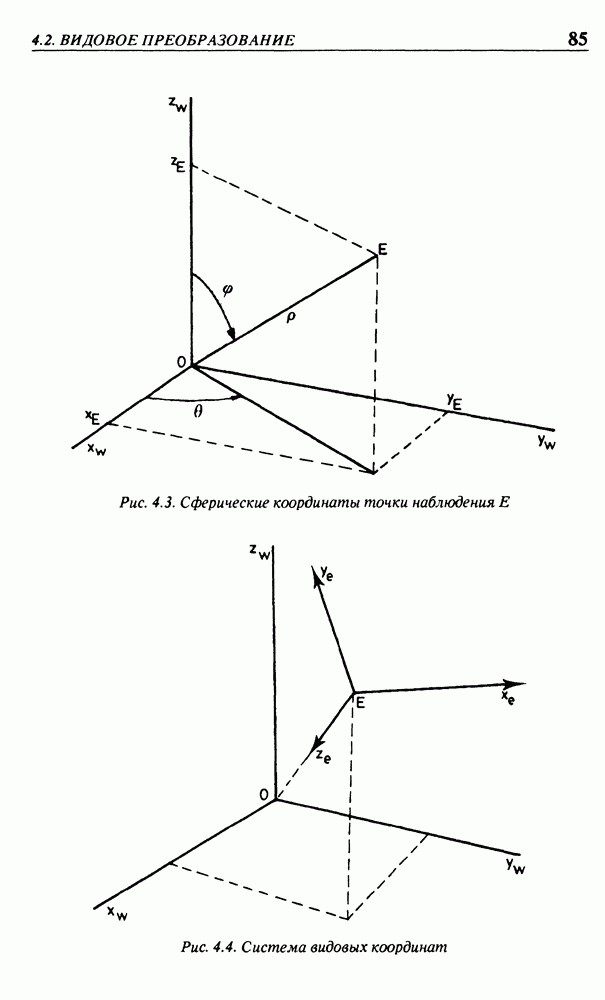
- 4.2. ВИДОВОЕ ПРЕОБРАЗОВАНИЕ
- 4.3. ПЕРСПЕКТИВНЫЕ ПРЕОБРАЗОВАНИЯ
- 4.4. ПРОГРАММА ДЛЯ ВЫЧЕРЧИВАНИЯ КУБА
- 4.5. ВЫЧЕРЧИВАНИЕ ПРОВОЛОЧНЫХ МОДЕЛЕЙ
- 4.6. НАПРАВЛЕНИЕ НАБЛЮДЕНИЯ, БЕСКОНЕЧНОСТЬ, ВЕРТИКАЛЬНЫЕ ЛИНИИ
- Глава 5. УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ
- 5.2. ВХОДНЫЕ ДАННЫЕ И ВНУТРЕННЕЕ ПРЕДСТАВЛЕНИЕ
- 5.3. АЛГОРИТМ ОПРЕДЕЛЕНИЯ НЕВИДИМЫХ ЛИНИЙ
- 5.4. ПОЛИГОНЫ И ПИКСЕЛЫ
- 5.5. УЛУЧШЕННАЯ ПРОГРАММА
- Глава 6. ПРАКТИЧЕСКИЕ ПРИМЕРЫ
- 6.2. ПОЛЫЙ ЦИЛИНДР
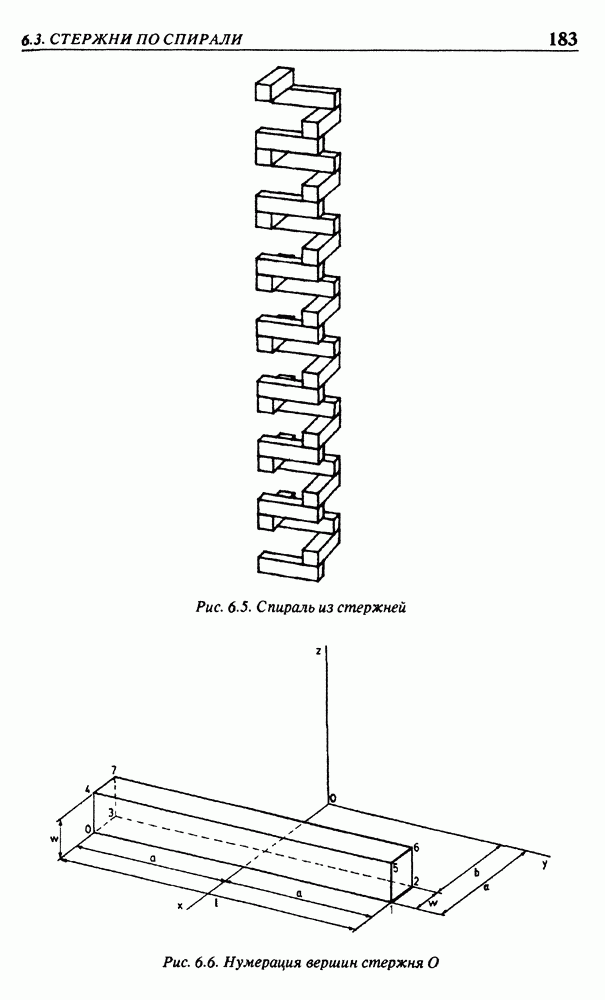
- 6.3. СТЕРЖНИ ПО СПИРАЛИ
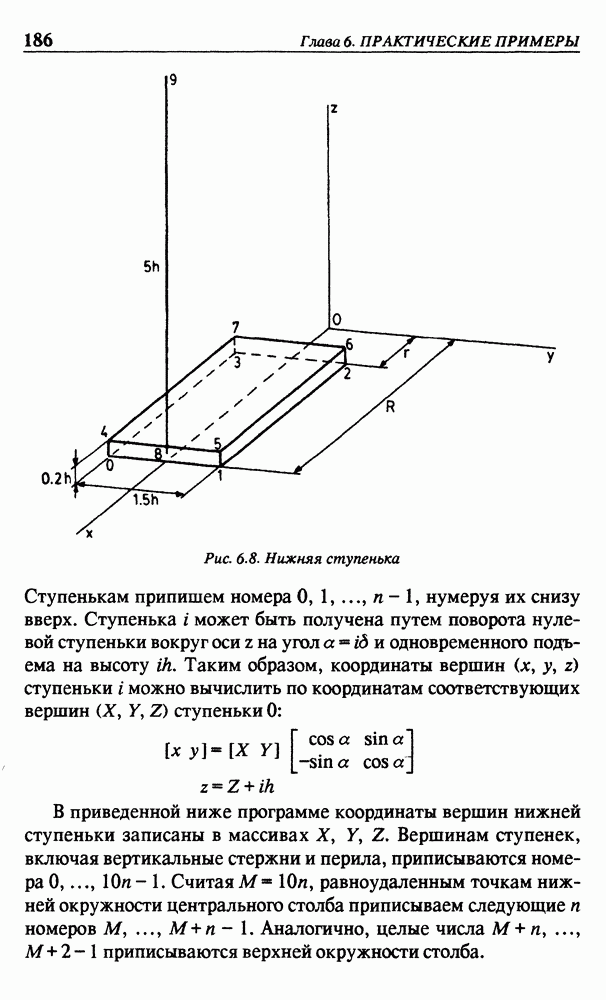
- 6.4. ВИНТОВАЯ ЛЕСТНИЦА
- 6.5. ТОР
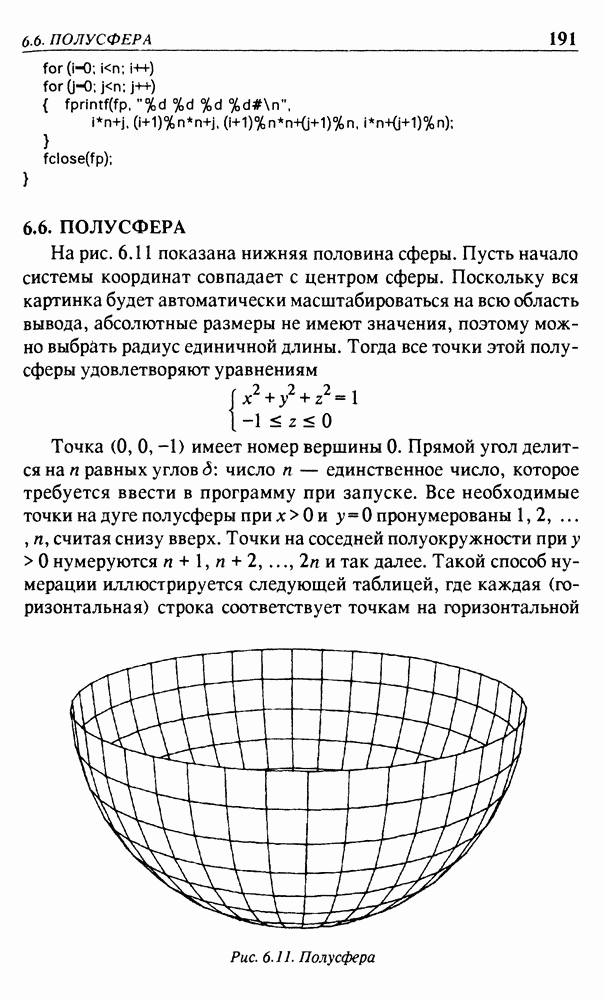
- 6.6. ПОЛУСФЕРА
- 6.7. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ
- Приложение. КРАТКОЕ ВВЕДЕНИЕ В ЯЗЫК СИ
- ЛИТЕРАТУРА