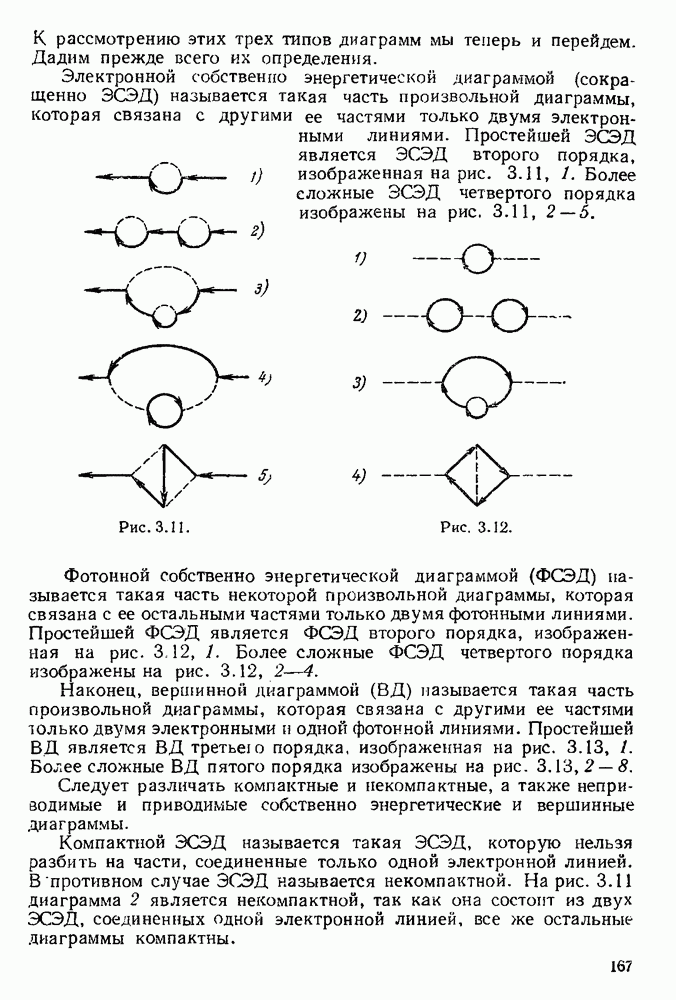
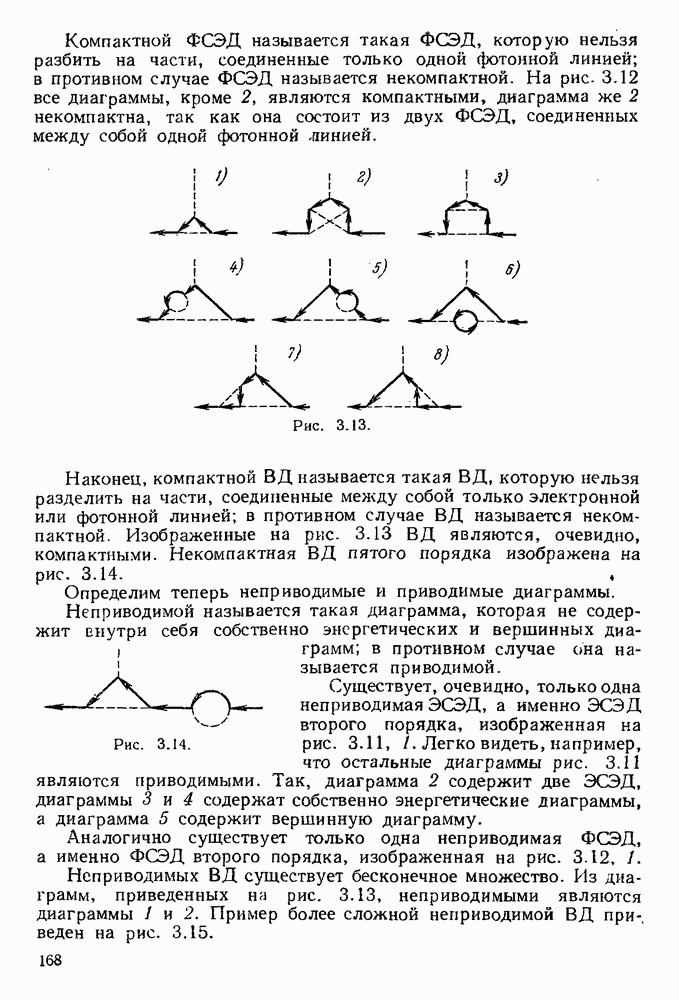
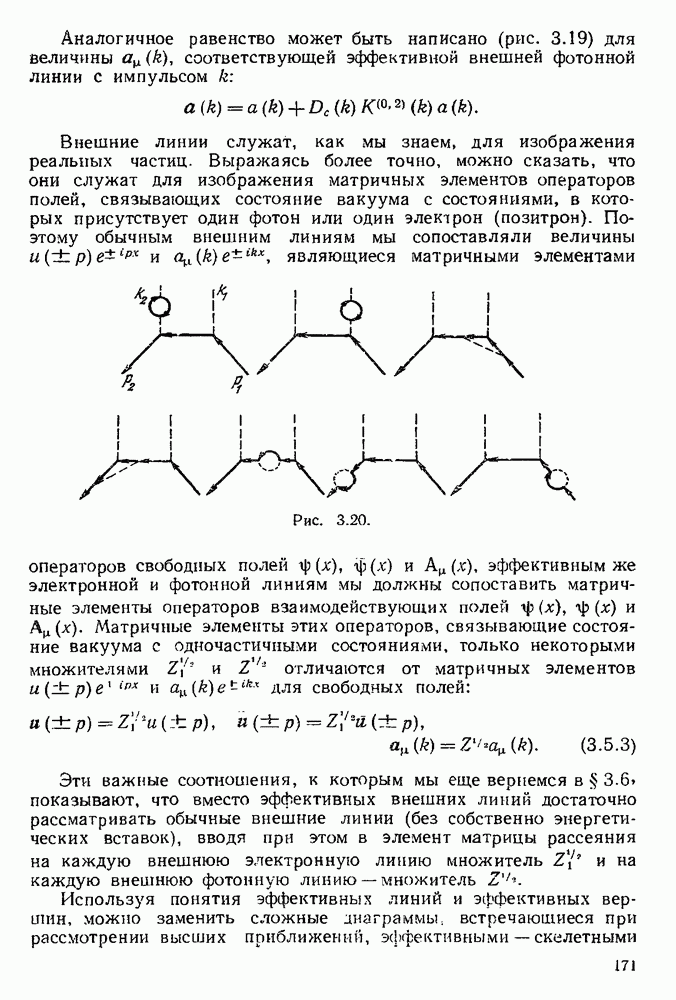
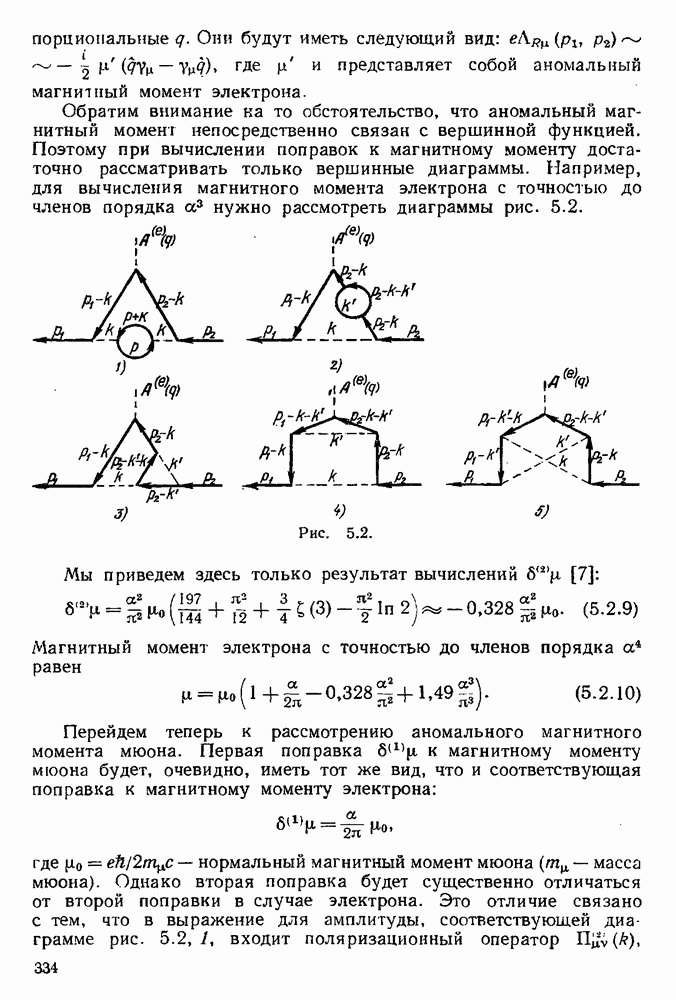
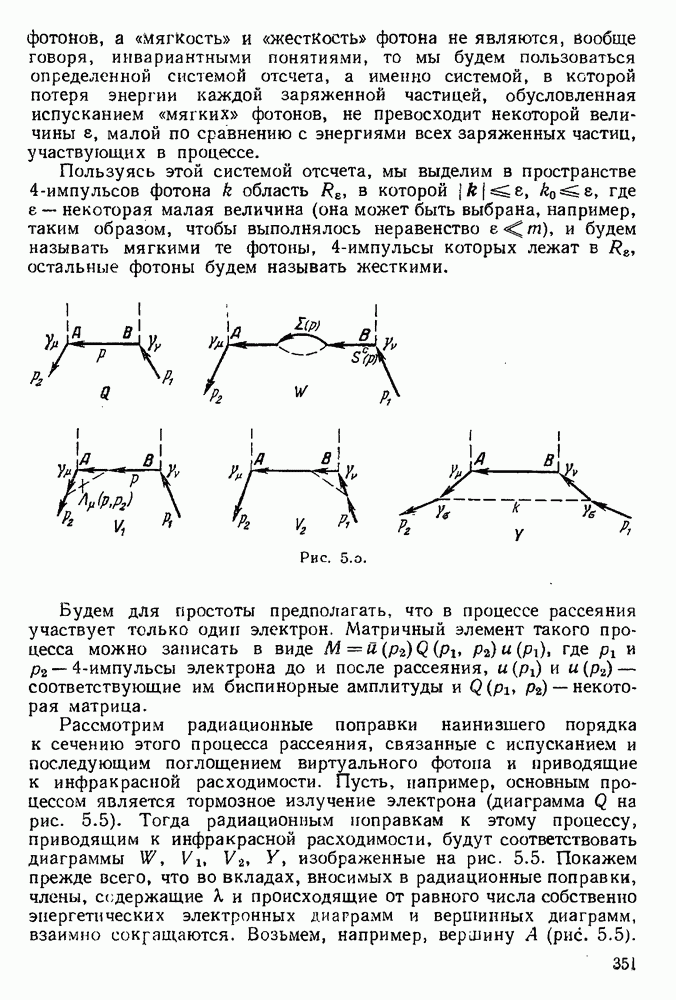
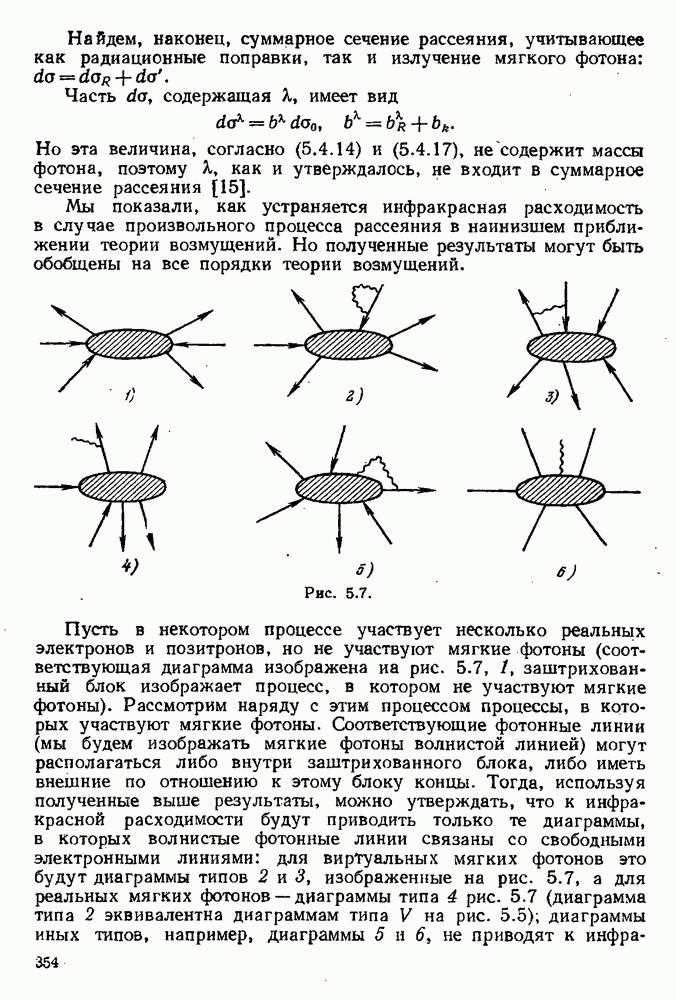
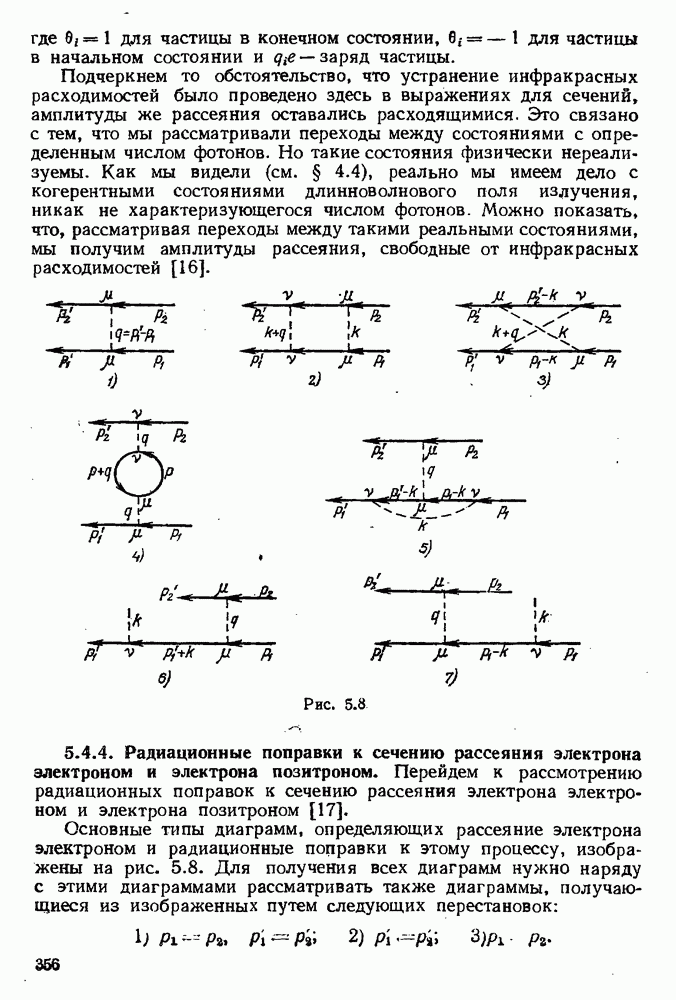
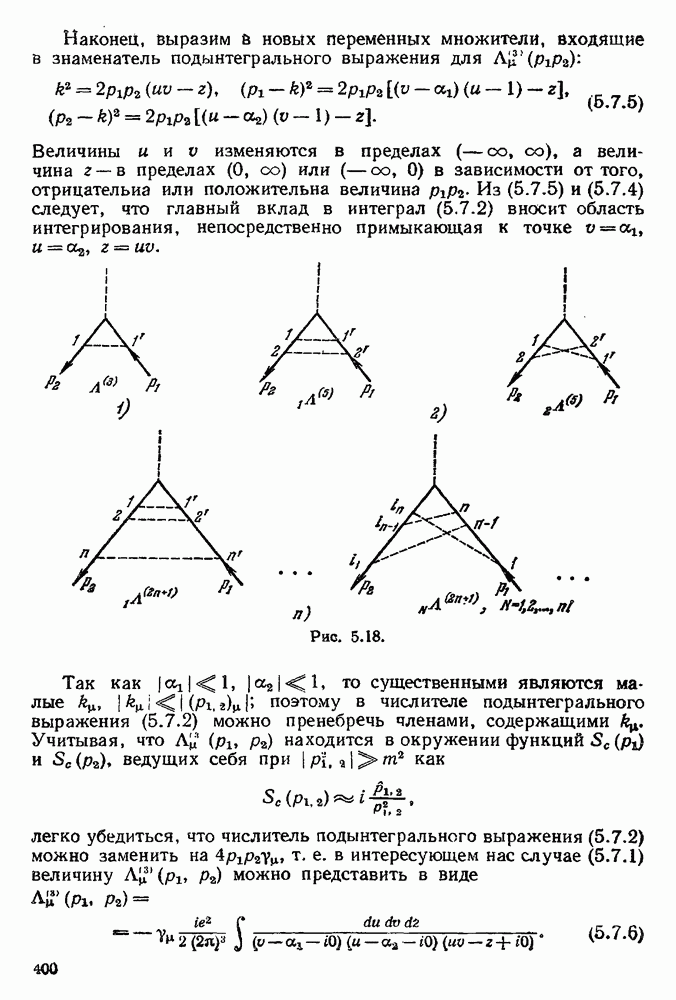
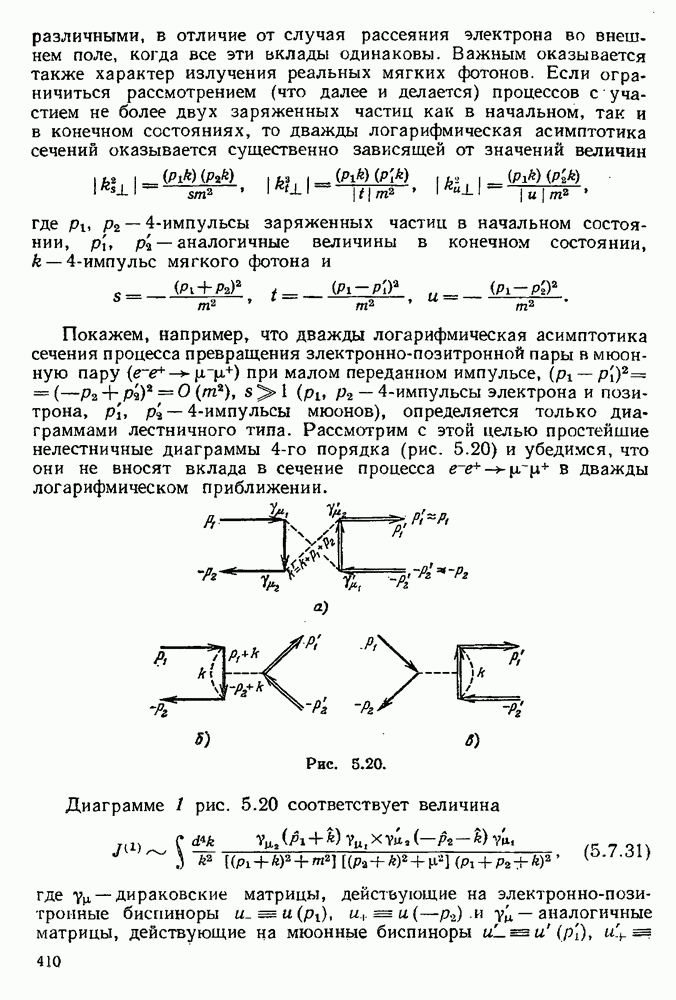
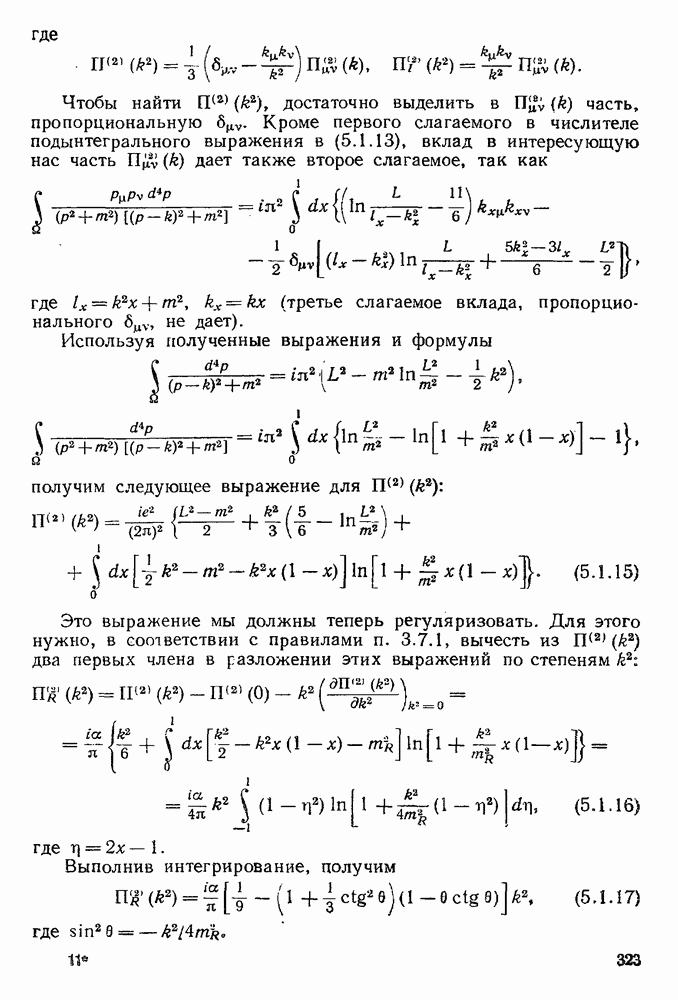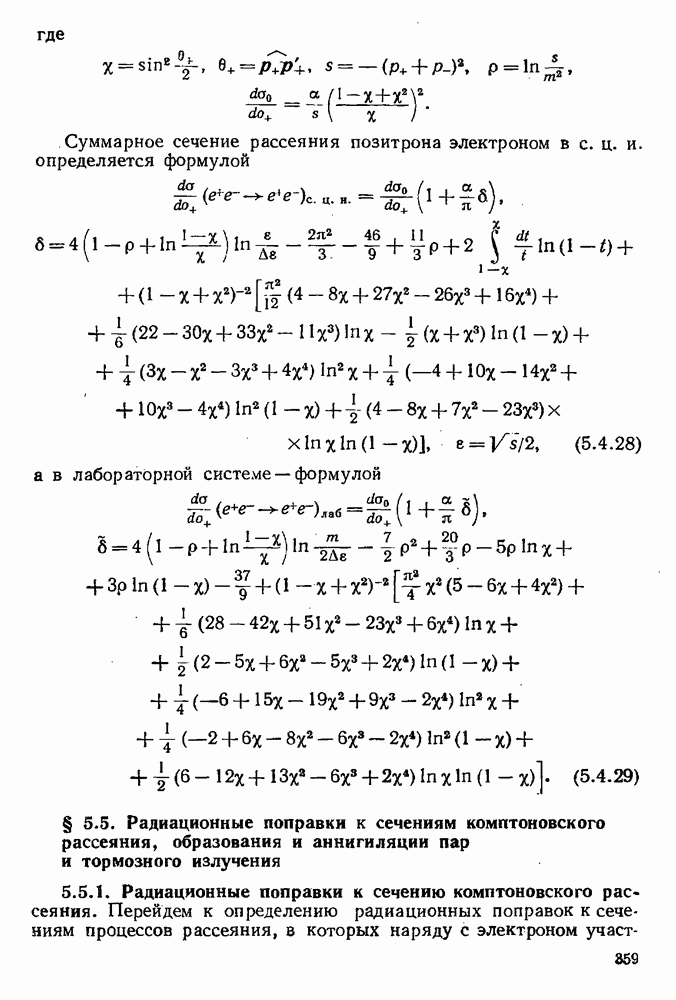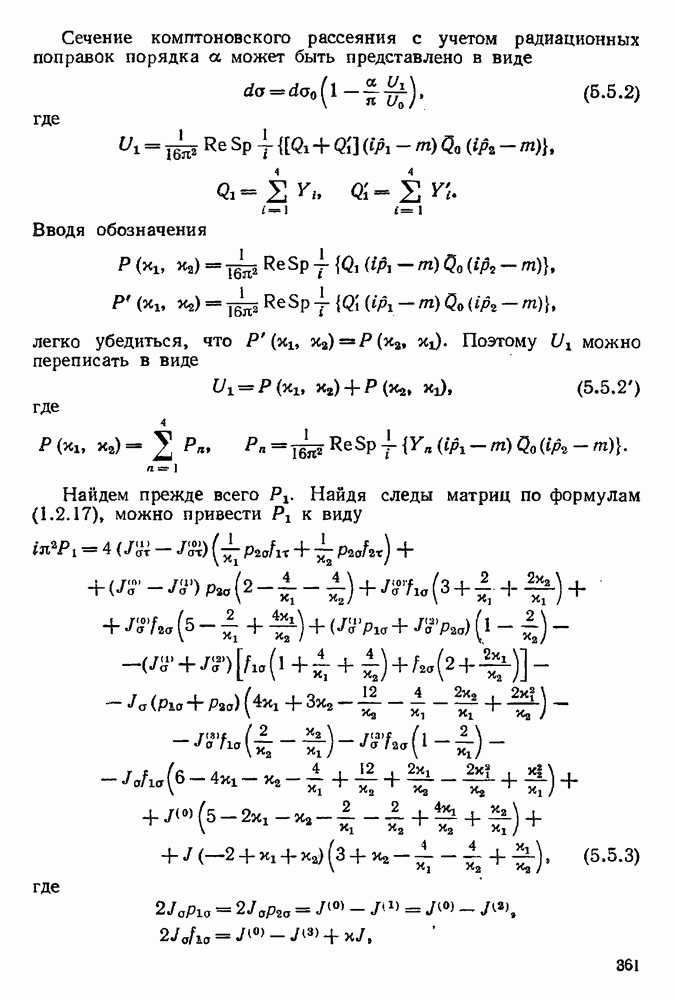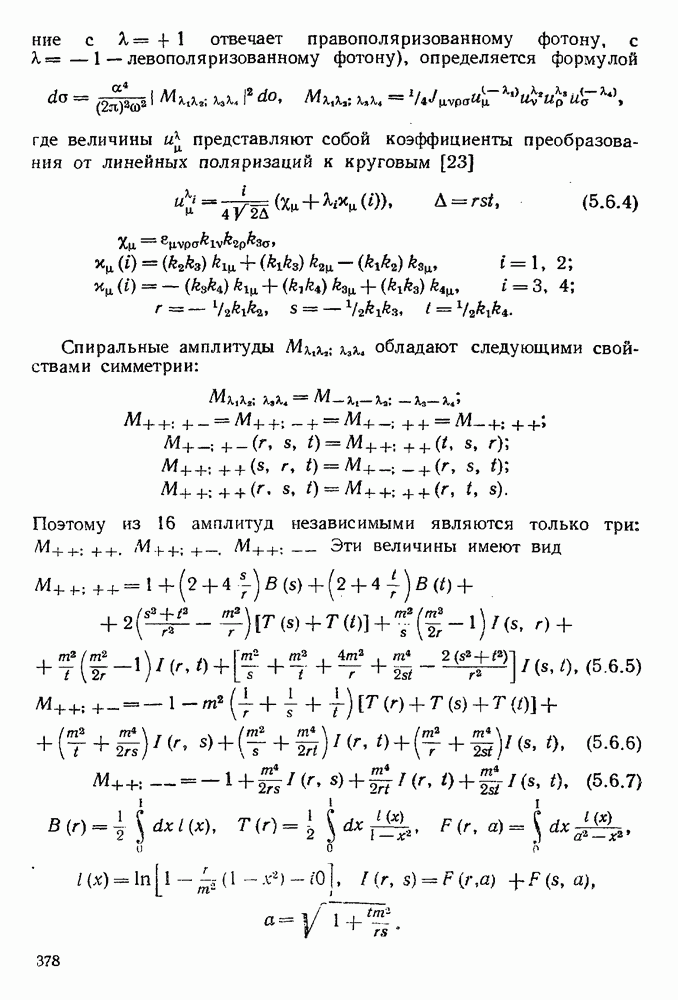| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3.3. Графическое представление элементов матрицы рассеяния
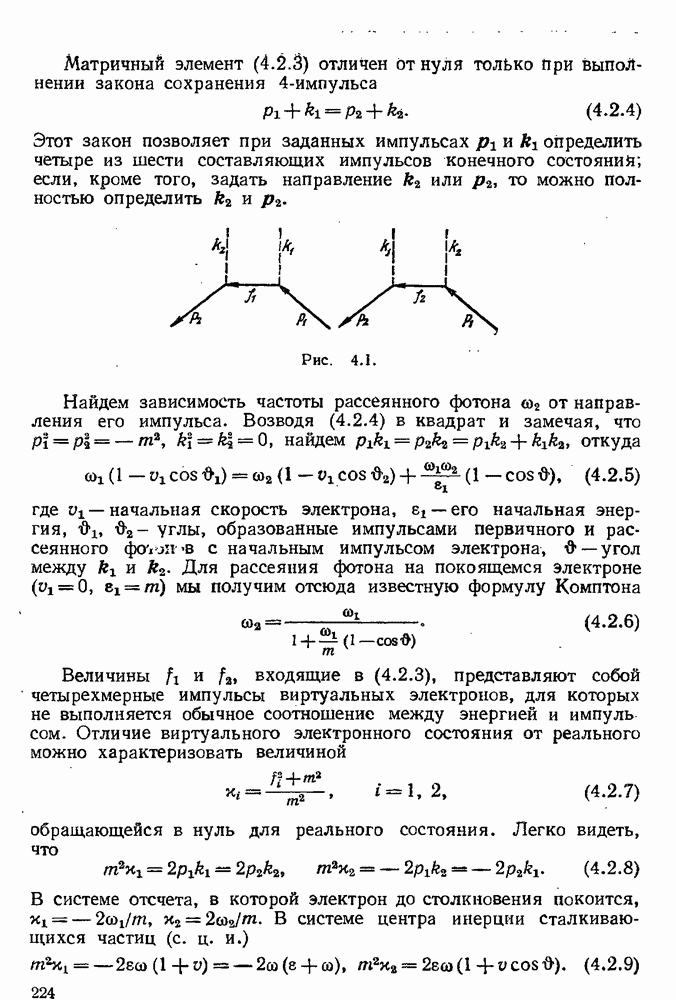
3.3.1. Графическое представление нормальных произведений.
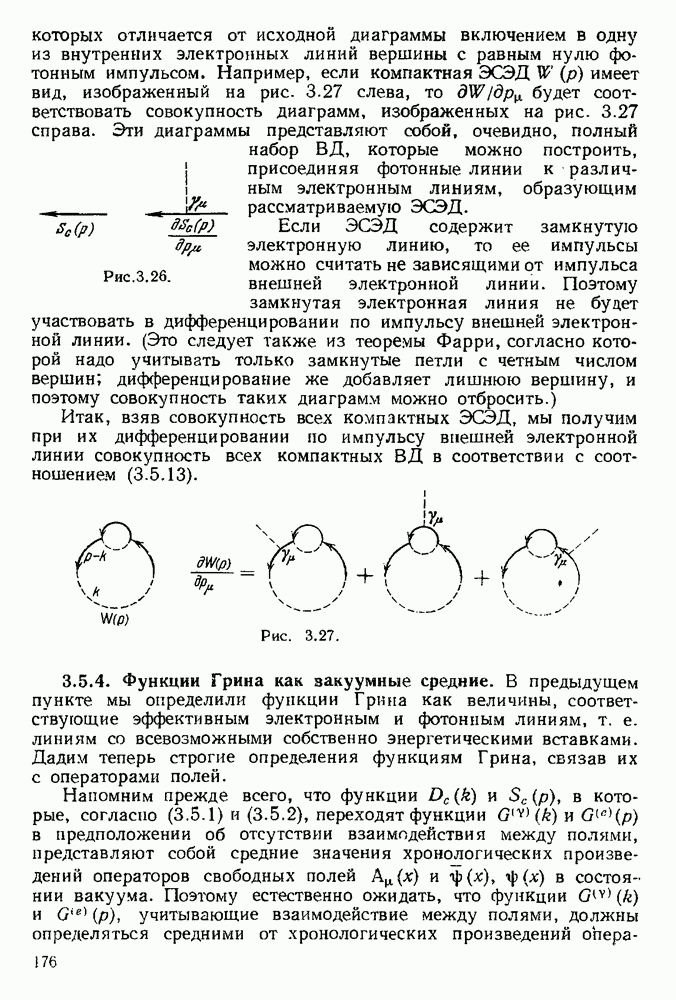
В п. 3.2.3 было показано, что матрицу рассеяния можно представить в виде суммы нормальных произведений операторов полей, соответствующих различным процессам рассеяния частиц. Каждое такое нормальное произведение, а следовательно, и любой процесс рассеяния, можно изображать графически [6], если условиться сопоставлять  -векторам
-векторам  по которым производится интегрирование в матрице
по которым производится интегрирование в матрице  точки диаграммы, а операторам полей — линии, проходящие через эти точки, называемые вершинами диаграммы. Оператор
точки диаграммы, а операторам полей — линии, проходящие через эти точки, называемые вершинами диаграммы. Оператор  мы будем изображать пунктирным лучом без определенного направления с началом в вершине
мы будем изображать пунктирным лучом без определенного направления с началом в вершине  оператор
оператор  — направленным сплошным лучом, идущим к вершине
— направленным сплошным лучом, идущим к вершине  и оператор
и оператор  — направленным сплошным лучом, идущим из вершины
— направленным сплошным лучом, идущим из вершины  Все эти лучи, которые называются внешними линиями, предполагаются уходящими за пределы диаграммы.
Все эти лучи, которые называются внешними линиями, предполагаются уходящими за пределы диаграммы.
Так как  представляет собой сумму операторов поглощения и испускания фотонов, то пунктирной внешней линией будет изображаться фотон, испущенный или поглощенный в результате процесса рассеяния; кроме того, пунктирной внешней линией мы будем изображать также внешнее электромагнитное поле. Аналогичным образом, поскольку
представляет собой сумму операторов поглощения и испускания фотонов, то пунктирной внешней линией будет изображаться фотон, испущенный или поглощенный в результате процесса рассеяния; кроме того, пунктирной внешней линией мы будем изображать также внешнее электромагнитное поле. Аналогичным образом, поскольку  представляет собой сумму операторов уничтожения электронов и рождения позитронов, то сплошная внешняя линия, направленная к вершине, будет служить для изображения электрона, существовавшего до процесса рассеяния, или позитрона, образовавшегося в результате процесса рассеяния. Наконец, так как
представляет собой сумму операторов уничтожения электронов и рождения позитронов, то сплошная внешняя линия, направленная к вершине, будет служить для изображения электрона, существовавшего до процесса рассеяния, или позитрона, образовавшегося в результате процесса рассеяния. Наконец, так как  представляет собой сумму операторов рождения электронов и уничтожения позитронов, то сплошная внешняя линия, направленная от вершины, будет служить для изображения позитрона, существовавшего до процесса рассеяния, или электрона, образовавшегося в результате процесса рассеяния.
представляет собой сумму операторов рождения электронов и уничтожения позитронов, то сплошная внешняя линия, направленная от вершины, будет служить для изображения позитрона, существовавшего до процесса рассеяния, или электрона, образовавшегося в результате процесса рассеяния.
Кроме операторов полей мы должны графически изображать также связи между операторами. Условимся сопоставлять связям между операторами внутренние линии диаграммы, соединяющие ее вершины, а именно будем изображать связь между фотонными
операторами  пунктирной линией (не имеющей определенного направления), соединяющей вершины х и у, и связь между электронными операторами
пунктирной линией (не имеющей определенного направления), соединяющей вершины х и у, и связь между электронными операторами  сплошной линией, соединяющей вершины х и у и имеющей направление от вершины х к вершине у.
сплошной линией, соединяющей вершины х и у и имеющей направление от вершины х к вершине у.
Так как в выражении для  каждая точка
каждая точка  является аргументом трех операторов — одного фотонного и двух электронных, то через каждую вершину диаграммы проходит одна фотонная и две электронные линии.
является аргументом трех операторов — одного фотонного и двух электронных, то через каждую вершину диаграммы проходит одна фотонная и две электронные линии.
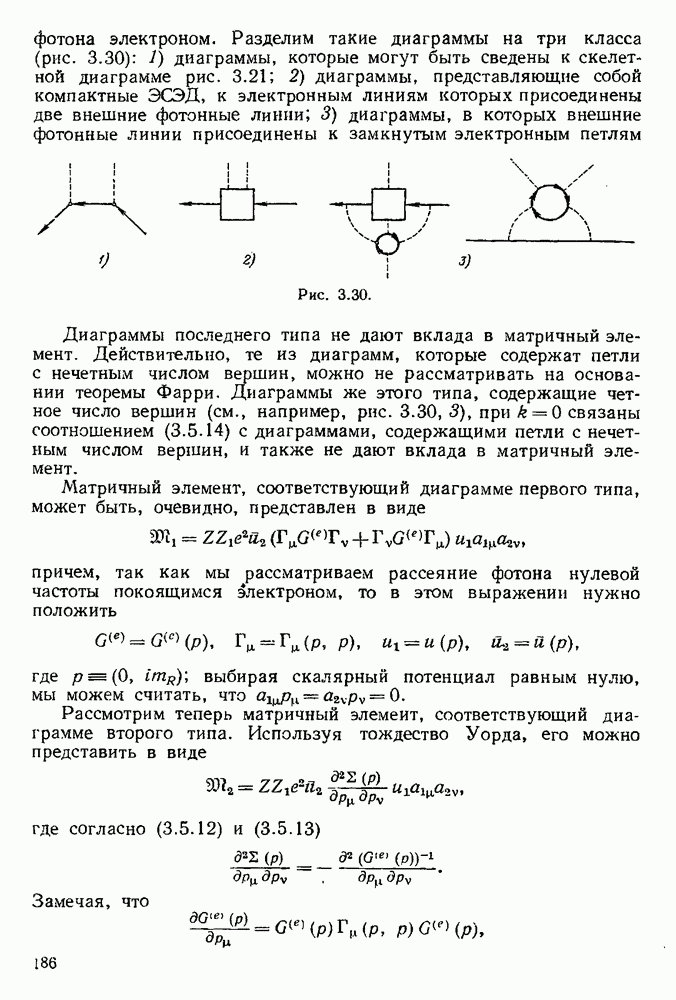
Диаграммы, изображающие отдельные нормальные произведения, входящие в матрицу  содержат
содержат  вершин. Мы будем называть их диаграммами
вершин. Мы будем называть их диаграммами  порядка.
порядка.
Они могут служить для изображения эффектов  приближения теории возмущений.
приближения теории возмущений.
Приведем несколько примеров.
Начнем с эффектов первого порядка.
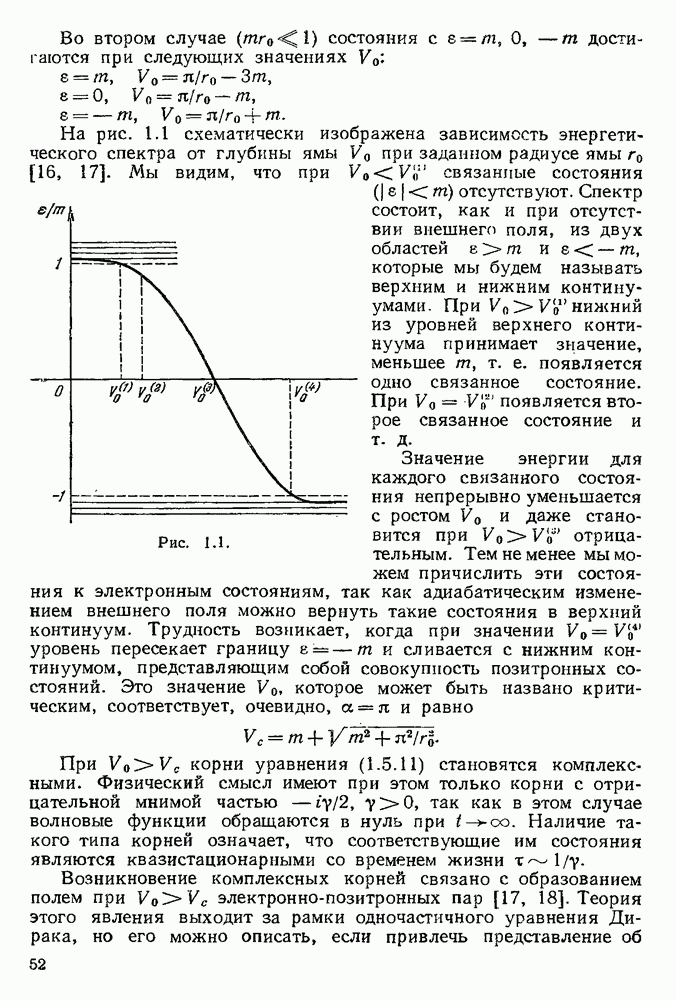
В этом случае имеется, очевидно, только одна диаграмма, представленная на рис. 3.2.

Рис. 3.2.
Она изображает рассеяние электрона  позитрона во внешнем поле, излучение или поглощение фотона электроном (позитроном), а также образование или поглощение электронно-позитронной пары. (Справа от диаграммы символически указано подынтегральное выражение матричного элемента
позитрона во внешнем поле, излучение или поглощение фотона электроном (позитроном), а также образование или поглощение электронно-позитронной пары. (Справа от диаграммы символически указано подынтегральное выражение матричного элемента  ) без знака нормального произведения.)
) без знака нормального произведения.)

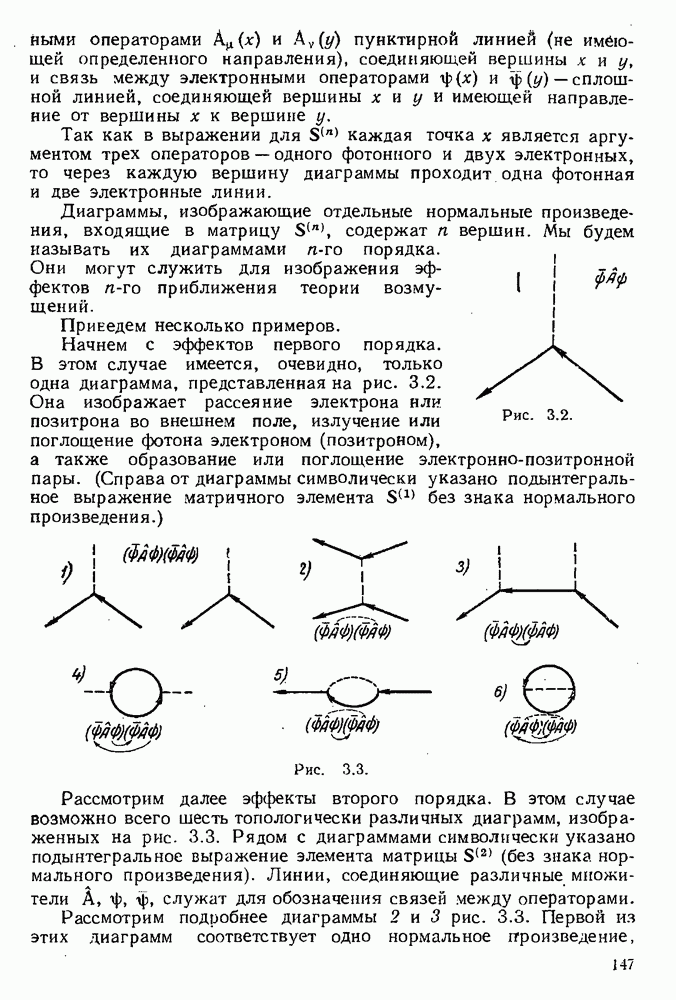
Рис. 3.3.
Рассмотрим далее эффекты второго порядка. В этом случае возможно всего шесть топологически различных диаграмм, изображенных на рис. 3.3. Рядом с диаграммами символически указано подынтегральное выражение элемента матрицы  (без знака нормального произведения). Линии, соединяющие различные множители
(без знака нормального произведения). Линии, соединяющие различные множители  служат для обозначения связей между операторами.
служат для обозначения связей между операторами.
Рассмотрим подробнее диаграммы 2 и 3 рис. 3.3. Первой из этих диаграмм соответствует одно нормальное произведение,
 второй диаграмме — два нормальных произведения
второй диаграмме — два нормальных произведения  . Оба последних
. Оба последних  -произведения, отличающихся местом наложения одной связи между электронными операторами, после интегрирования по
-произведения, отличающихся местом наложения одной связи между электронными операторами, после интегрирования по  вносят, как легко убедиться, одинакозый вклад в элемент матрицы
вносят, как легко убедиться, одинакозый вклад в элемент матрицы  соответствующий диаграмме 3. Поэтому достаточно рассматривать только одно из этих нормальных произведений и вносимый им вклад в элемент матрицы
соответствующий диаграмме 3. Поэтому достаточно рассматривать только одно из этих нормальных произведений и вносимый им вклад в элемент матрицы  умножить на 2.
умножить на 2.
Аналогичная ситуация имеет место и для других диаграмм. Каждой из них может соответствовать несколько нормальных произведений, отличающихся только местами наложения связей между операторами полей и вносящих одинаковый вклад в элемент матрицы рассеяния. Они называются эквивалентными нормальными произведениями.
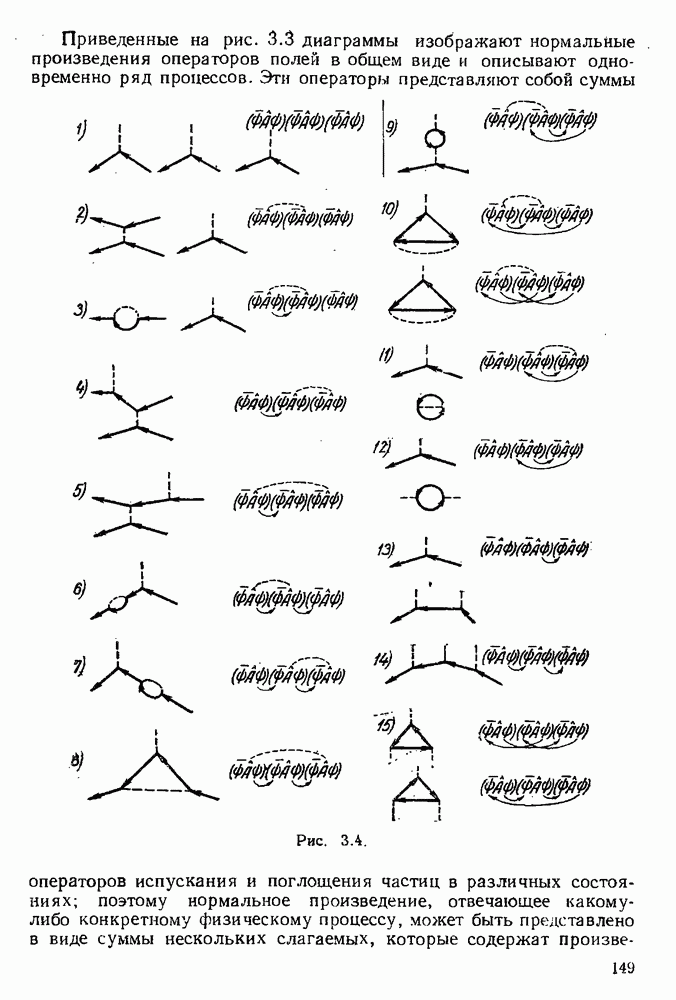
Перейдем к перечислению диаграмм третьего порядка. Легко убедиться, что всего существует 15 топологически различных диаграмм, соответствующих различным эффектам третьего порядка 
Например, диаграмме 8 рис. 3.4 соответствует шесть эквивалентных  -произведений:
-произведений:

Учитывая, что в  -произведении можно менять местами электронные операторы, умножая при этом
-произведении можно менять местами электронные операторы, умножая при этом  -произведение на четность произведенной перестановки и используя (2.3.24) и (2.5.25), легко убедиться, что все шесть
-произведение на четность произведенной перестановки и используя (2.3.24) и (2.5.25), легко убедиться, что все шесть  -произведений вносят одинаковый вклад в элемент матрицы
-произведений вносят одинаковый вклад в элемент матрицы  соответствующий изображенному на диаграмме 8 процессу рассеяния.
соответствующий изображенному на диаграмме 8 процессу рассеяния.
Заметим, что число эквивалентных N-произведений, соответствующих данной диаграмме, можно определять следующим простым способом. Нужно, перенумеровав вершины диаграммы числами  , определить число перестановок этих чисел, не меняющих вида диаграммы. Если это число равно
, определить число перестановок этих чисел, не меняющих вида диаграммы. Если это число равно  для диаграммы 2 рис. 3.3 и
для диаграммы 2 рис. 3.3 и  для диаграммы 3 рис. 3.3), то число эквивалентных
для диаграммы 3 рис. 3.3), то число эквивалентных  -произведений будет
-произведений будет 
Приведенные на рис. 3.3 диаграммы изображают нормальные произведения операторов полей в общем виде и описывают одновременно ряд процессов.
(см. скан)
Рис. 3.4
Эти операторы представляют собой суммы операторов испускания и поглощения частиц в различных состояниях; поэтому нормальное произведение, отвечающее какому-либо конкретному физическому процессу, может быть представлено в виде суммы нескольких слагаемых, которые содержат произведения
операторов испускания и поглощения частиц, участвующих в рассматриваемом процессе, и отличаются друг от друга только порядком расположения операторов. Эти слагаемые можно изображать диаграммами, которые топологически эквивалентны и отличаются друг от друга только порядком расположения электронных и фотонных линий.
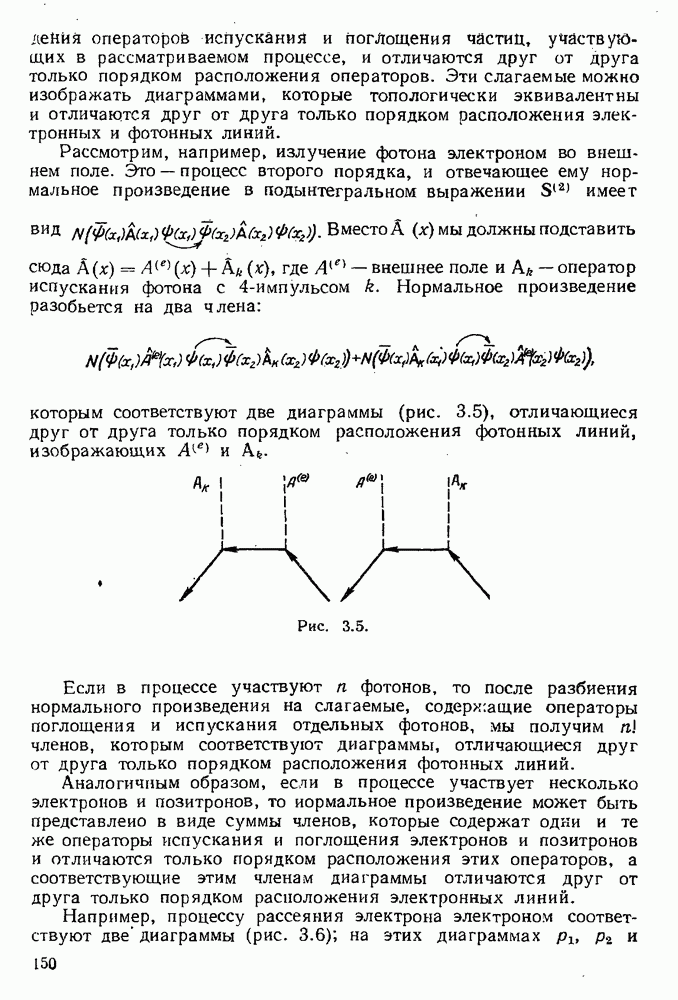
Рассмотрим, например, излучение фотона электроном во внешнем поле. Это — процесс второго порядка, и отвечающее ему нормальное произведение в подынтегральном выражении  имеет вид
имеет вид  . Вместо
. Вместо  мы должны подставить сюда
мы должны подставить сюда  , где
, где  — внешнее поле и А — оператор испускания фотона с 4-импульсом k. Нормальное произведение разобьется на два члена:
— внешнее поле и А — оператор испускания фотона с 4-импульсом k. Нормальное произведение разобьется на два члена:

которым соответствуют две диаграммы (рис. 3.5), отличающиеся друг от друга только порядком расположения фотонных линий, изображающих 

Рис. 3.5.
Если в процессе участвуют  фотонов, то после разбиения нормального произведения на слагаемые, содержащие операторы поглощения и испускания отдельных фотонов, мы получим
фотонов, то после разбиения нормального произведения на слагаемые, содержащие операторы поглощения и испускания отдельных фотонов, мы получим  членов, которым соответствуют диаграммы, отличающиеся друг от друга только порядком расположения фотонных линий.
членов, которым соответствуют диаграммы, отличающиеся друг от друга только порядком расположения фотонных линий.
Аналогичным образом, если в процессе участвует несколько электронов и позитронов, то нормальное произведение может быть представлено в виде суммы членов, которые содержат одни и те же операторы испускания и поглощения электронов и позитронов и отличаются только порядком расположения этих операторов, а соответствующие этим членам диаграммы отличаются друг от друга только порядком расположения электронных линий.
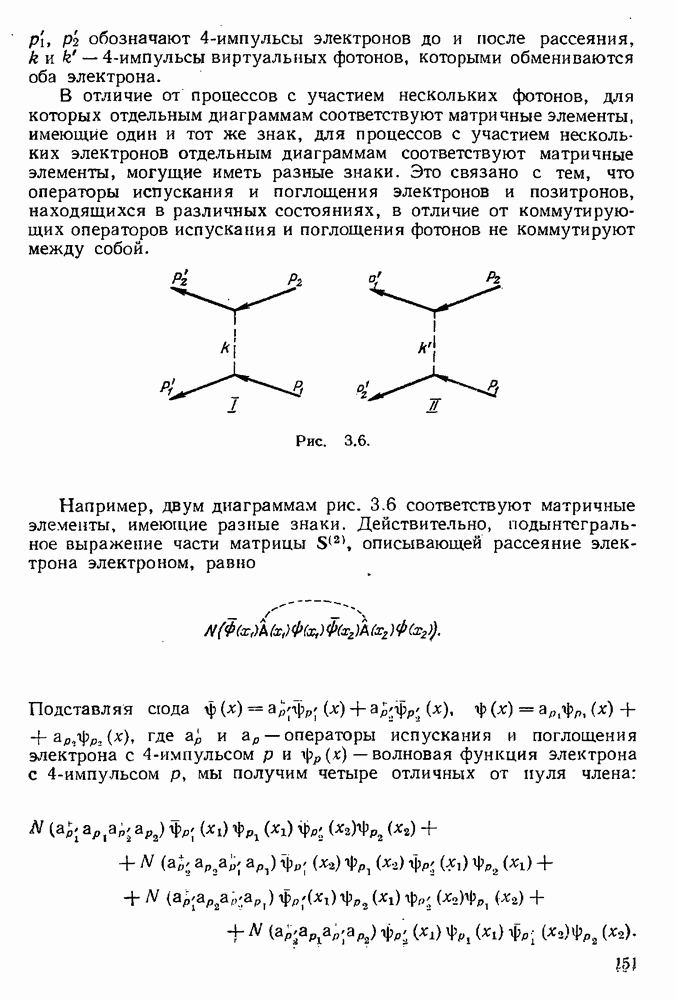
Например, процессу рассеяния электрона электроном соответствуют две диаграммы (рис. 3.6); на этих диаграммах  и
и
 обозначают
обозначают  -импульсы электронов до и после рассеяния,
-импульсы электронов до и после рассеяния,  — 4-импульсы виртуальных фотонов, которыми обмениваются оба электрона.
— 4-импульсы виртуальных фотонов, которыми обмениваются оба электрона.
В отличие от процессов с участием нескольких фотонов, для которых отдельным диаграммам соответствуют матричные элементы, имеющие один и тот же знак, для процессов с участием нескольких электронов отдельным диаграммам соответствуют матричные элементы, могущие иметь разные знаки. Это связано с тем, что операторы испускания и поглощения электронов и позитронов, находящихся в различных состояниях, в отличие от коммутирующих операторов испускания и поглощения фотонов не коммутируют между собой.

Рис. 3.6.
Например, двум диаграммам рис. 3.6 соответствуют матричные элементы, имеющие разные знаки. Действительно, подынтегральное выражение части матрицы  описывающей рассеяние электрона электроном, равно
описывающей рассеяние электрона электроном, равно

Подставляя сюда  , где
, где  — операторы испускания и поглощения электрона с 4-импульсом
— операторы испускания и поглощения электрона с 4-импульсом  — волновая функция электрона с 4-импульсом
— волновая функция электрона с 4-импульсом  , мы получим четыре отличных от нуля члена:
, мы получим четыре отличных от нуля члена:

Первые два члена представляют собой два эквивалентных нор мальных произведения, соответствующих первой диаграмме рис. 3.6, а вторые два члена — два эквивалентных нормальных произведения, соответствующих второй диаграмме.
Переставляя в третьем члене операторы а и  легко убедиться, что
легко убедиться, что  поэтому, как и утверждалось, матричные элементы, соответствующие обеим диаграммам, имеют разные знаки.
поэтому, как и утверждалось, матричные элементы, соответствующие обеим диаграммам, имеют разные знаки.
Этот результат может быть обобщен следующим образом. Пусть в процессе участвует z электронов, импульсы которых до и после рассеяния равны соответственно  тогда процессу будут соответствовать
тогда процессу будут соответствовать  диаграмм, которые отличаются обозначениями электронных линий после рассеяния. Если на двух диаграммах электронные линии после рассеяния (являющиеся продолжением электронных линий до рассеяния) обозначены соответственно через
диаграмм, которые отличаются обозначениями электронных линий после рассеяния. Если на двух диаграммах электронные линии после рассеяния (являющиеся продолжением электронных линий до рассеяния) обозначены соответственно через  то относительный знак матричных элементов, отвечающих обеим диаграммам, будет определяться четностью перестановки
то относительный знак матричных элементов, отвечающих обеим диаграммам, будет определяться четностью перестановки 
Таким образом, матричный элемент, соответствующий какому-либо физическому процессу, всегда можно после разбиения нормального произведения представить в виде
 (3.3.1)
(3.3.1)
где отдельные слагаемые  отличаются друг от друга порядком расположения операторов поглощения и испускания частиц, участвующих в процессе; диаграммы, изображающие эти слагаемые, топологически эквивалентны и отличаются только порядком расположения электронных и фотонных линий.
отличаются друг от друга порядком расположения операторов поглощения и испускания частиц, участвующих в процессе; диаграммы, изображающие эти слагаемые, топологически эквивалентны и отличаются только порядком расположения электронных и фотонных линий.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА ЭЛЕКТРОНА
- 1.1.2. Симметричная форма уравнения Дирака.
- 1.1.3. Решения с положительными и отрицательными частотами.
- 1.1.4. Плоские волны.
- 1.1.5. Поляризационные состояния электрона.
- 1.1.6. Поляризационная матрица плотности электрона.
- 1.1.7. Поляризационные состояния электрона в ультрарелятизистском пределе.
- § 1.2. Уравнение Дирака для электрона в электромагнитном поле и свойства инвариантности уравнения Дирака
- 1.2.1. Уравнение Дирака для электрона во внешнем электромагнитном поле.
- 1.2.2. Уравнение непрерывности.
- 1.2.3. Различные представления уравнения Дирака.
- 1.2.4. Алгебра матриц Дирака.
- 1.2.5. Релятивистская инвариантность уравнения Дирака.
- 1.2.6. Пространственное отражение, обращение времени и зарядовое сопряжение.
- 1.2.7. Ковариантные билинейные формы.
- 1.2.8. Использование обозначений, соответствующих псевдоевклидовой метрике.
- § 1.3. Предельные переходы к нерелятивистской квантовой механике и релятивистской классической механике
- 1.3.2. Второе приближение.
- 1.3.3. Переход к релятивистской классической механике.
- 1.3.4. Высокоэнергетическое приближение.
- 1.3.5. Борновское приближение.
- § 1.4. Момент импульса электрона
- 1.4.2. Волновая функция свободного электрона с определенным моментом.
- 1.4.3. Четность состояния.
- 1.4.4. Разложение по сферическим волнам.
- § 1.5. Движение электрона в центральном поле
- 1.5.2. Сферически-симметричная потенциальная яма.
- 1.5.3. Движение электрона в кулоновском поле ядра.
- 1.5.4. Волновые функции непрерывного спектра в кулоновском поле ядра.
- 1.5.5. Критический заряд ядра.
- § 1.6. Движение в однородных полях
- 1.6.2. Электрон в постоянном и однородном магнитном поле.
- 1.6.3. Электрон в постоянном и однородном электрическом поле.
- 1.6.4. Парадокс Клейна.
- § 1.7. Рассеяние электронов
- 1.7.2. Амплитуда и сечение рассеяния.
- 1.7.3. Поляризация и азимутальная асимметрия.
- 1.7.4. Упругое рассеяние в борцовском приближении.
- 1.7.5. Упругое рассеяние в эйкональном приближении.
- 1.7.6. Рассеяние в кулоновском поле ядра.
- ГЛАВА 2. КВАНТОВАНИЕ ПОЛЕЙ
- § 2.1. Квантовая механика фотона
- 2.1.2. Волновая функция фотона.
- 2.1.3. Плоские волны.
- § 2.2. Момент импульса фотона
- 2.2.2. Собственные функции оператора момента фотона.
- 2.2.3. Продольный и поперечные шаровые векторы.
- 2.2.4. Четность состоянии фотона.
- 2.2.5. Сферические электромагнитные волны.
- § 2.3. Квантование электромагнитного поля
- 2.3.2. Перестановочные соотношения для потенциалов электромагнитного поля.
- 2.3.3. Хронологическое и нормальное произведения операторов электромагнитных потенциалов.
- § 2.4. Корреляционные функции электромагнитного поля
- 2.4.2. Когерентные состояния.
- 2.4.3. Корреляционные функции и когерентность высших порядков.
- 2.4.4. Поляризационная матрица плотности.
- § 2.5. Квантование электронно-позитронного поля
- 2.5.2. Операторы испускания и поглощения электронов и позитронов.
- 2.5.3. Антикоммутаторы электронного поля.
- 2.5.4. Хронологическое и нормальное произведения операторов электронного поля.
- ГЛАВА 3. ЭЛЕКТРОМАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ
- § 3.1. Основные уравнения квантовой электродинамики
- 3.1.2. Лагранжиан и гамильтониан взаимодействующих полей.
- 3.1.3. Представление взаимодействия.
- § 3.2. Матрица рассеяния
- 3.2.2. Инвариантная теория возмущений.
- 3.2.3. Представление матрицы рассеяния в виде суммы нормальных произведений.
- 3.2.4. Функциональная форма представления матрицы рассеяния в виде N-упорядоченного оператора.
- § 3.3. Графическое представление элементов матрицы рассеяния
- 3.3.2. Импульсное представление.
- 3.3.3. Правила Фейнмана.
- § 3.4. Вероятность и эффективное сечение
- 3.4.2. Суммирование по состояниям поляризации электронов и фотонов.
- 3.4.3. Эффективное сечение.
- 3.4.4. Вероятность процессов рассеяния поляризованных частиц.
- § 3.5. Структура диаграмм матрицы рассеяния
- 3.5.2. Эффективные линии.
- 3.5.3. Уравнения Дайсона для функций Грина и графическое уравнение для вершинной функции.
- 3.5.4. Функции Грина как вакуумные средние.
- § 3.6. Перенормировка массы и заряда электрона
- 3.6.2. Физический заряд электрона.
- 3.6.3. Перенормировка функций Грина и вершинной функции.
- 3.6.4. Перенормировка элементов матрицы рассеяния.
- § 3.7. Расходимости в матрице рассеяния и их устранение
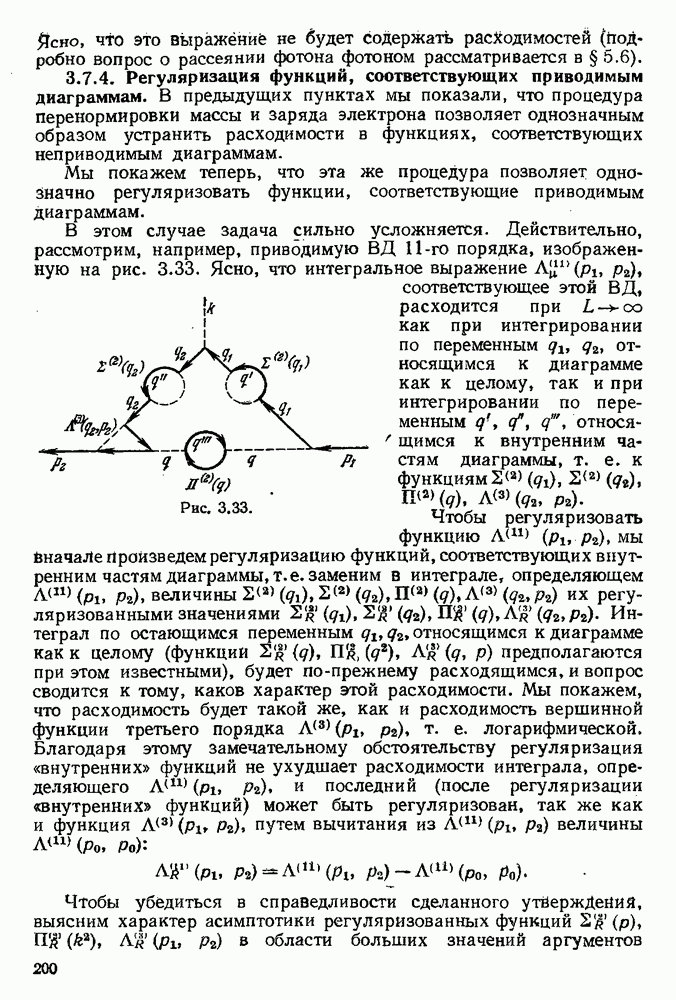
- 3.7.2. Введение граничного импульса.
- 3.7.3. Регуляризация функций, соответствующих неприводимым диаграммам.
- 3.7.4. Регуляризация функций, соответствующих приводимым диаграммам.
- § 3.8. Асимптотические свойства функций Грина
- 3.8.2. Асимптотические выражения для функций Грина.
- 3.8.3. Асимптотический характер регулярнзованных разложений матрицы рассеяния и проблема замкнутости квантовой электродинамики.
- ГЛАВА 4. ОСНОВНЫЕ ЭЛЕКТРОДИНАМИЧЕСКИЕ ЯВЛЕНИЯ
- § 4.1. Излучение фотона
- 4.1.2. Излучение электрического и магнитного мультиполей.
- 4.1.3. Излучение ядер. Правила отбора.
- 4.1.4. Фотоэффект.
- § 4.2. Рассеяние фотона электроном
- 4.2.2. Дифференциальное сечение рассеяния неполяризованных частиц.
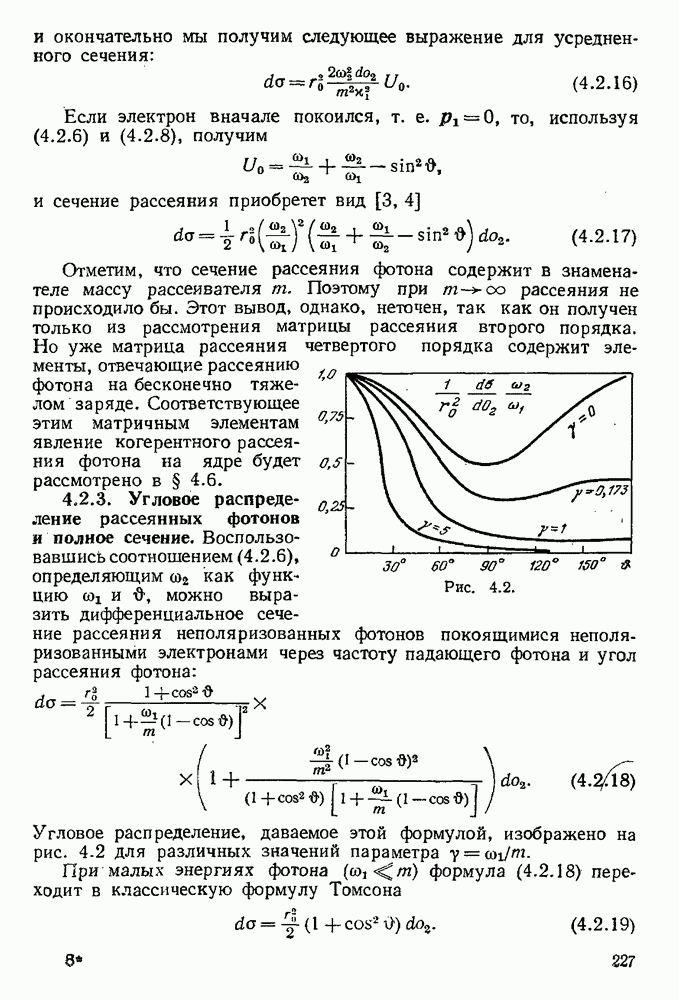
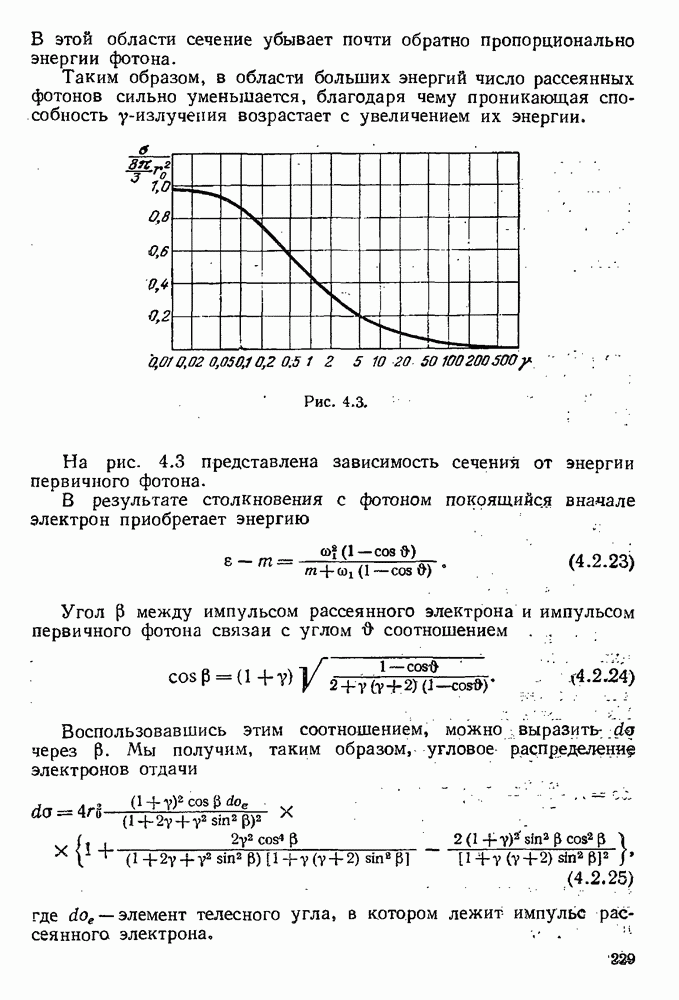
- 4.2.3. Угловое распределение рассеянных фотонов и полное сечение.
- 4.2.4. Поляризационные эффекты.
- 4.2.5. Рассеяние поляризованных фотонов неполяризованными электронами.
- 4.2.6. Дисперсионная формула.
- § 4.3. Тормозное излучение
- 4.3.2. Тормозное излучение в высокоэнергетическом приближении.
- 4.3.3. Сечение тормозного излучения в кулоновском поле ядра в борновском приближении.
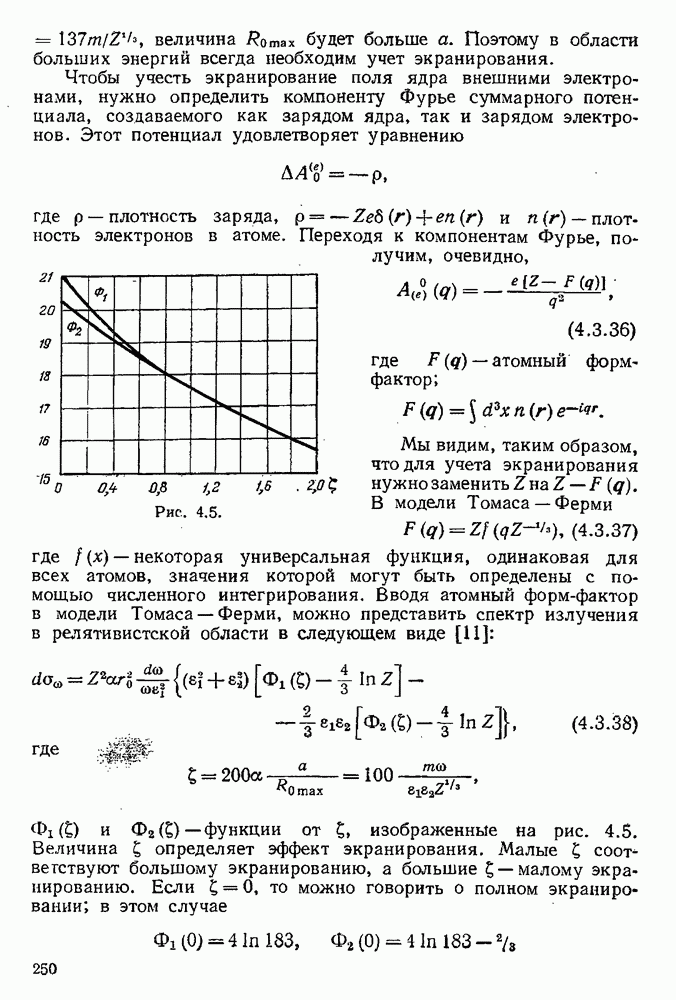
- 4.3.4. Экранирование.
- 4.3.5. Потеря энергии на излучение.
- 4.3.6. Тормозное излучение в кулоновском поле ядра в высокоэнергетическом приближении.
- 4.3.7. Точная теория тормозного излучения в нерелятивистской области.
- § 4.4. Излучение длинноволновых фотонов
- 4.4.2. Сечение рассеяния электрона с излучением мягкого фотона.
- 4.4.3. Исследование расходимости в области малых частот.
- 4.4.4. Излучение мягких фотонов при произвольных столкновениях.
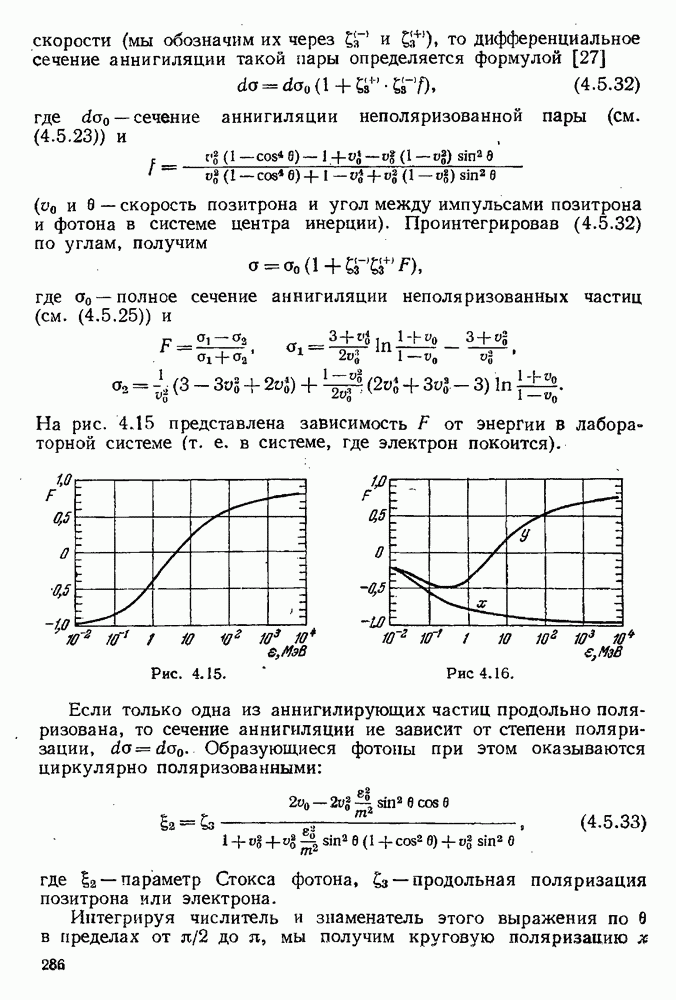
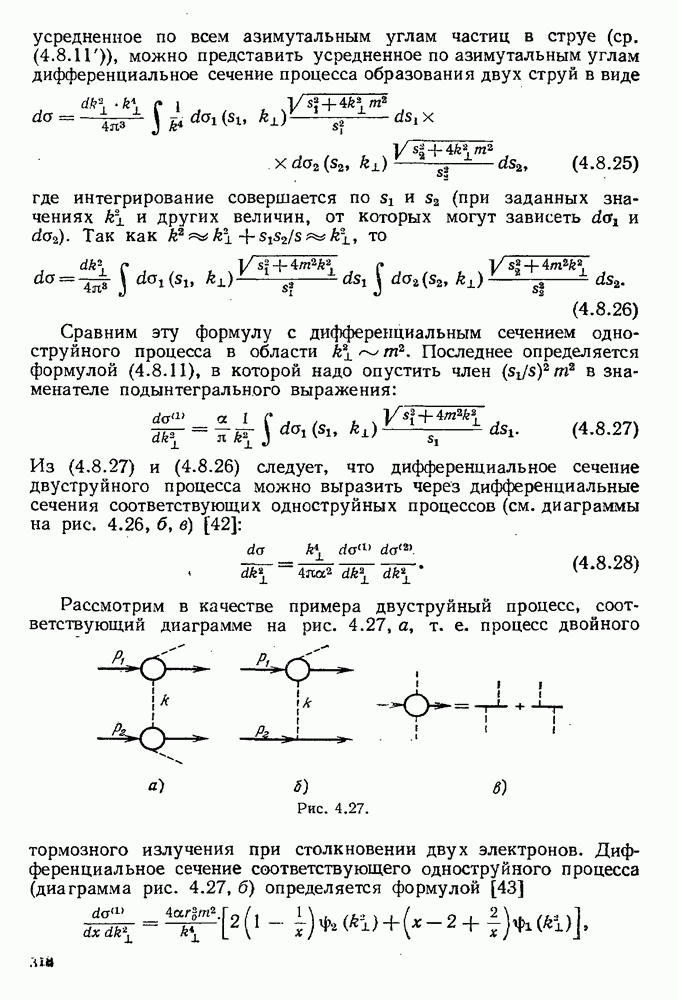
- § 4.5. Образование и аннигиляция электронно-позитронных пар
- 4.5.2. Точная теория образования пары фотоном в поле ядра вблизи порога.
- 4.5.3. Образование пары двзмя фотонами.
- 4.5.4. Аннигиляция пары в два и три фотона.
- 4.5.5. Поляризационные эффекты при двухфотонной аннигиляции пар.
- 4.5.6. Распад позитрония.
- 4.5.7. Превращение пары в один фотон.
- § 4.6. Рассеяние электрона и позитрона электроном
- 4.6.2. Сечение рассеяния позитрона электроном.
- 4.6.3. Рассеяние поляризованных электронов.
- 4.6.4. Рассеяние мюона электроном.
- 4.6.5. Излучение фотона при рассеянии электрона электроном и электрона позитроном и при превращении …
- § 4.7. Запаздывающее взаимодействие зарядов
- 4.7.3. Взаимодействие электрона с позитроном и позитроний.
- § 4.8. Метод эквивалентных фотонов
- 4.8.2. Тормозное излучение в процессах рассеяния электрона ядром и электрона электроном.
- 4.8.3. Образование пар фотоном в поле ядра и при столкно вении двух быстрых заряженных частиц.
- 4.8.4. Сечение двуструйного процесса.
- ГЛАВА 5. КВАНТОВОЭЛЕКТРОДИНАМИЧЕСКИЕ ЭФФЕКТЫ В ВЫСШИХ ПРИБЛИЖЕНИЯХ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 5.1. Радиационные поправки к электродинамическим функциям Грина
- 5.1.2. Поляризационный оператор второго порядка.
- 5.1.3. Вершинная функция третьего порядка.
- § 5.2. Модификация закона Кулона. Аномальный магнитный момент электрона
- 5.2.2. Аномальный магнитный момент электрона и мюона.
- § 5.3. Радиационное смещение атомных уровней
- 5.3.2. Радиационное смещение и естественная ширина атомных уровней.
- 5.3.3. Радиационное смещение уровней атома водорода.
- 5.3.4. Рассеяние фотона вблизи резонанса.
- § 5.4. Радиационные поправки к сечениям рассеяния электрона во внешнем поле и рассеяния электрона электроном
- 5.4.2. Исключение «массы» фотона из сечения рассеяния.
- 5.4.3. Устранение инфракрасной расходимости в случае произвольного процесса рассеяния.
- 5.4.4. Радиационные поправки к сечению рассеяния электрона электроном и электрона позитроном.
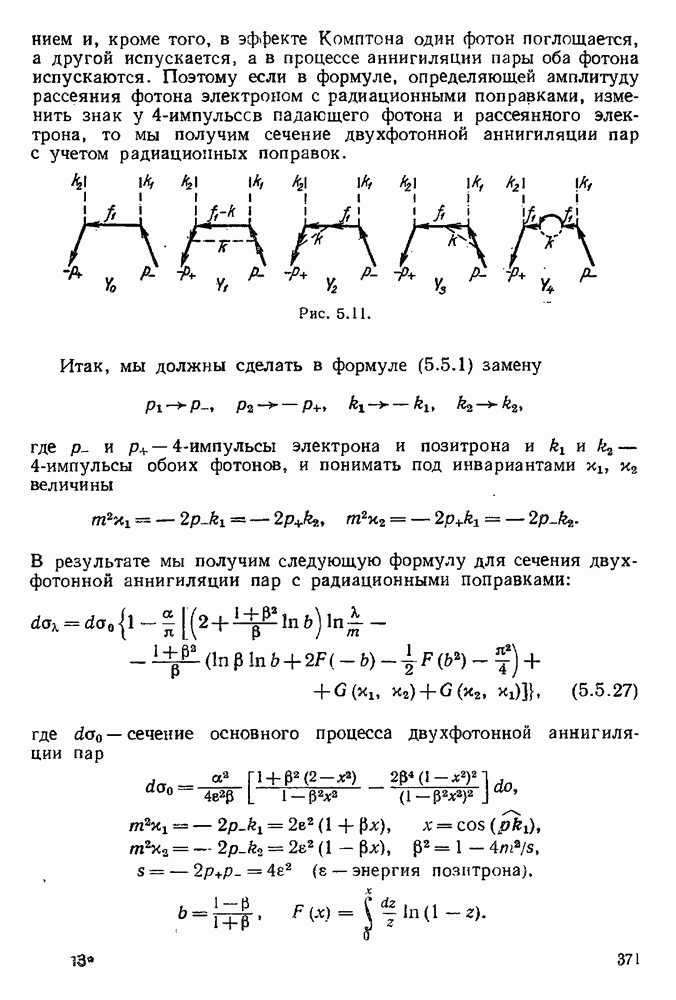
- § 5.5. Радиационные поправки к сечениям комптоновского рассеяния, образования и аннигиляции пар и тормозного излучения
- 5.5.1. Радиационные поправки к сечению комптоновского рассеяния.
- 5.5.2. Рассеяние электроном фотонов малой частоты.
- 5.5.3. Радиационные поправки к сечению двухфотонной аннигиляции пар.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.4. Радиационные поправки к сечению тормозного излучения.
- 5.5.5. Радиационные поправки к сечению превращения электронно-позитронной пары в мюонную пару.
- § 5.6. Нелинейная электродинамика вакуума
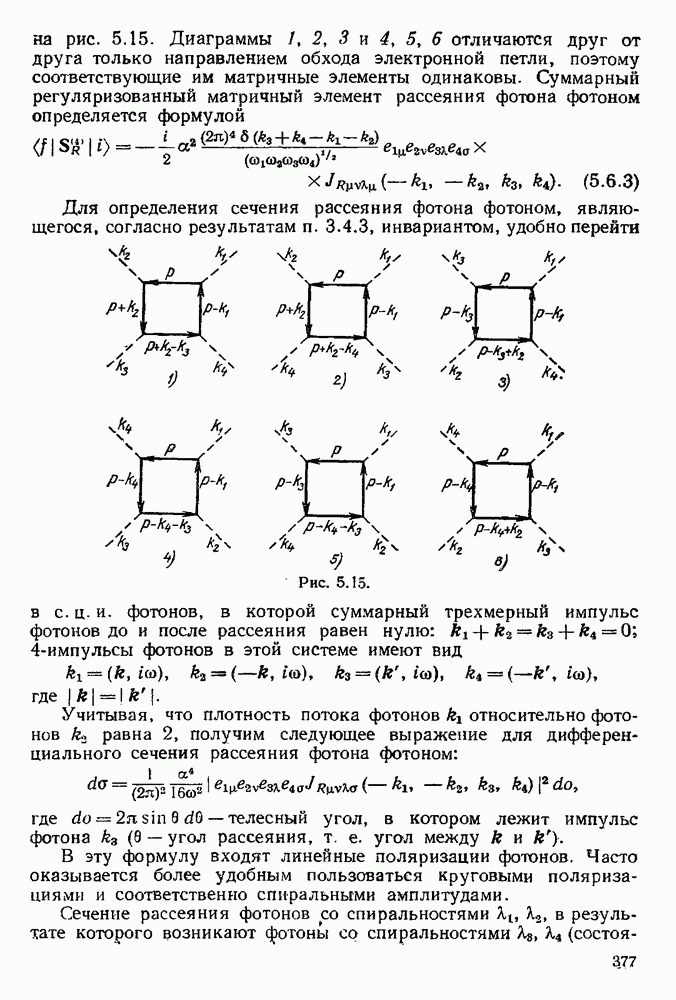
- 5.6.1. Тензор рассеяния фотона фотоном четвертого ранга.
- 5.6.2. Сечение рассеяния фотона фотоном.
- 5.6.3. Радиационные поправки к функции Лагранжа электромагнитного поля в вакууме.
- 5.6.4. Точное выражение для лагранжиана произвольного медленно меняющегося электромагнитного поля.
- 5.6.5. Сечение рассеяния фэтэна в постоянном электромагнитном поле.
- 5.6.6. Связь между амплитудой рассеяния фотона на нулевой угол и сечением образования пар.
- 5.6.7. Импульсное и угловое распределения ядер отдачи при образовании пар фотоном в поле ядра.
- § 5.7. Дважды логарифмическая асимптотика сечений квантовоэлектродинамических процессов
- 5.7.2. Дважды логарифмическая асимптотика сечения рассеяния электрона во внешнем поле.
- 5.7.3. Дважды логарифмическая асимптотика сечения процесса …
- 5.7.4. Сводка формул для сечений квантовоэлектродинамических процессов в дважды логарифмическом приближении.
- ПРИЛОЖЕНИЕ
- А.1. Вычисление интегралов по инвариантному объему в 4-импульсном пространстве.
- A.2. Метод размерной регуляризации.
- ЛИТЕРАТУРА