1. Разложение сигналов по базисным функциям

Для того чтобы иметь возможность представить вектор в пространстве  измерений необходимо задать систему координат. Оси системы координат определяются векторами. В качестве простого примера рассмотрим ортогональную систему координат двух измерений, называемую декартовой. Базисные вектора описываются выражениями

, .

Графически такую систему координат можно представить следующим образом:

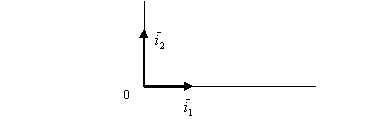
Рис. 1. Графическое представление базисных векторов

Увеличим размерность пространства на единицу и добавим к уже существующим базисным векторам  и  вектор . Соответствующая система координат примет вид:

.

Из полученных выражений базисных векторов двух и трех измерений следует, что такое определении базиса представляет собой единичную матрицу, в которой строки или столбцы определяют координаты базисных векторов. Таким образом, для любого  - мерного пространства легко определить определить базис как единичную матрицу размерности  элементов.

Данное определение базиса в  - мерном пространстве не является единственным. В общем случае в качестве векторов  можно выбрать другой набор векторов .  Причем их ориентация будет всегда определяться относительно базиса . При этом набор векторов  будет образовывать базис в  - мерном пространстве только тогда, когда проекции любого -мерного вектора на данные вектора будут уникальны. Это условие обеспечивается в том случае, когда вектора  линейно независимы.

Определим математически данное условие. Пусть вектор  задан в базисе векторов , ,…, . Тогда его координаты в новом базисе  вычисляются как скалярные произведения вектора  с векторами :

, ,

Или в матричной форме

.

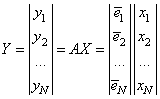Матрица  размерностью  элементов, составленная из базисных векторов , называется матрицей преобразования.

Из условия единственности представления вектора  следует, что вычисленные координаты , должны уникальным образом описывать вектор  в базисе векторов . Следовательно, существует обратное преобразование из  в , которое можно записать следующим образом:

.

Данное выражения справедливо, т.к. произведение матрицы на соответствующую обратную матрицу дает единичную, а произведение вектора  на единичную матрицу даст тот же вектор . Таким образом, необходимым и достаточным условием того, что векторы  образуют базис в  - мерном пространстве является существование обратной матрицы составленной из данных векторов.

Представленное разложение векторов можно обобщить на двумерный случай. Пусть задана матрица  размерностью  элементов. Ее проекции  в базисе векторов  вычисляются как

.

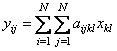Данное выражение показывает, что для преобразования двумерных сигналов, в общем случае, необходимо задавать четырехмерную матрицу преобразования .

Рассмотрим частный случай двумерного преобразования. Пусть проекции ,  вычисляются как

,

, .                              (1)

Анализ данного выражения показывает, что сначала вычисляется преобразование по столбцам матрицы  и результат записывается в . Затем выполняется преобразование по строкам матрицы , . Преобразование вида (1) называют разделимым, которое в матричном виде записывается как

.                                                                   (2)

Обратное преобразование имеет вид

.                                                        (3)

Из формул (2) и (3) видно, что основная доля вычислений приходится на нахождение обратной матрицы. Сократить объем вычислений можно, если воспользоваться ортогональными базисными векторами, которые удовлетворяют условию

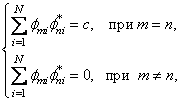                                        (4)

где  - базисные вектора, соответствующие обратной матрице . Из выражения (4) следует, что . Тогда обратное преобразование (1) можно записать в виде

.

В этом случае матрица  называется матрицей ортогонального преобразования, а само преобразование унитарным.