| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. Основы вейвлет-преобразования
Известно, что произвольный сигнал ![]() , для которого
выполняется условие
, для которого
выполняется условие 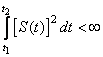 может
быть представлен ортогональной системой функций
может
быть представлен ортогональной системой функций ![]() :
:
![]() , (18)
, (18)
коэффициенты определяются из соотношения
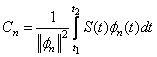 ,
,
где 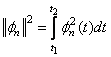 -
квадрат нормы или энергия базисной функции
-
квадрат нормы или энергия базисной функции ![]() . Ряд (18) называется обобщенным рядом
Фурье. При этом произведения вида
. Ряд (18) называется обобщенным рядом
Фурье. При этом произведения вида ![]() , входящие в ряд (18), представляют собой
спектральную плотность сигнала
, входящие в ряд (18), представляют собой
спектральную плотность сигнала ![]() , а коэффициенты
, а коэффициенты ![]() - спектр сигнала. Суть
спектрального анализа сигнала
- спектр сигнала. Суть
спектрального анализа сигнала ![]() состоит в определении коэффициентов
состоит в определении коэффициентов ![]() . Зная эти коэффициенты
возможен синтез (аппроксимация) сигналов при фиксированном числе
. Зная эти коэффициенты
возможен синтез (аппроксимация) сигналов при фиксированном числе ![]() ряда:
ряда:
![]() .
.
Обобщенный ряд Фурье
при заданной системе базисных функций ![]() и числе слагаемых
и числе слагаемых ![]() он обеспечивает наилучший синтез
по критерию минимума среднеквадратической ошибки
он обеспечивает наилучший синтез
по критерию минимума среднеквадратической ошибки ![]() , под которой понимается величина
, под которой понимается величина
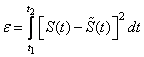 .
.
Известные преобразования (Адамара, Карунена-Лоэва, Фурье) «плохо» представляют нестационарный сигнал в коэффициентах разложения. Покажем это на следующем примере. Пусть дана нестационарная функция
![]() (19)
(19)
и ее преобразование Фурье (рис. 9).
Анализ рис. 9
показывает, что нестационарность временного сигнала ![]() представляется большим числом
высокочастотных коэффициентов отличных от нуля. При этом возникают следующие
проблемы:
представляется большим числом
высокочастотных коэффициентов отличных от нуля. При этом возникают следующие
проблемы:
- сложно провести анализ временного сигнала по его Фурье образу;
- приемлемая аппроксимация временного сигнала возможна при учете большого числа высокочастотных коэффициентов;
- плохое визуальное качество реальных изображений восстановленных по низкочастотным коэффициентам; и т.п.
Существующие проблемы обусловили необходимость разработки математического аппарата преобразования нестационарных сигналов. Одним из возможных путей анализа таких сигналов стало вейвлет-преобразование (ВП).
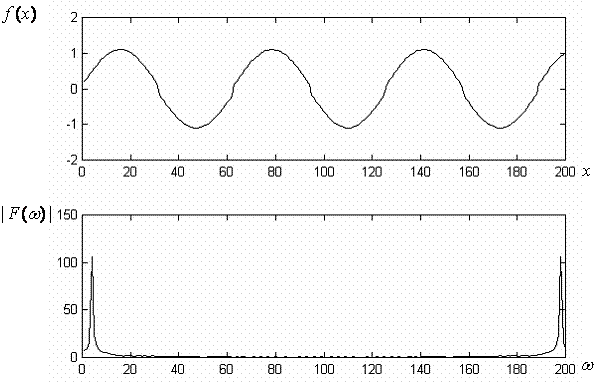
Рис. 9. Преобразование Фурье синусоидального сигнала с небольшими ступеньками при переходе через нуль
ВП одномерного сигнала – это его представление в виде обобщенного ряда Фурье или интеграла Фурье по системе базисных функций локализованных как в пространственной, так и в частотной областях. Примером такой базисной функции может служить вейвлет Хаара, который определяется выражением
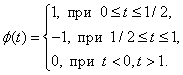 (20)
(20)
Графически вейвлет Хаара представляется следующим образом:
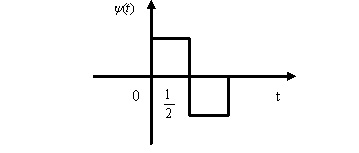
Рис. 10. Базисная функция вейвлета Хаара
Рассмотрим процесс
разложения сигнала ![]() в
системе базисных функций Хаара. Первая базисная функция, в отличие от всех
последующих, представляет собой прямую линию. В случае нормированного базиса
в
системе базисных функций Хаара. Первая базисная функция, в отличие от всех
последующих, представляет собой прямую линию. В случае нормированного базиса ![]() , свертка первой базисной
функции с исходным сигналом будет определять его среднее значение. Пусть дан
дискретный сигнал
, свертка первой базисной
функции с исходным сигналом будет определять его среднее значение. Пусть дан
дискретный сигнал ![]() длиной
длиной
![]() отсчетов.
Нормированная базисная функция на интервале
отсчетов.
Нормированная базисная функция на интервале ![]() описывается выражением
описывается выражением ![]() . Тогда свертка данной функции с
сигналом
. Тогда свертка данной функции с
сигналом ![]() приводит
к выражению
приводит
к выражению
![]() .
.
Если выполнить
синтез сигнала ![]() по
коэффициенту
по
коэффициенту ![]() с
помощью синтезирующей функции
с
помощью синтезирующей функции ![]() , получим постоянную составляющую,
соответствующую среднему значению сигнала. Для того чтобы иметь возможность
более детально описать сигнал, вычислим второй коэффициент с помощью базисной
функции, представленной выражением (20):
, получим постоянную составляющую,
соответствующую среднему значению сигнала. Для того чтобы иметь возможность
более детально описать сигнал, вычислим второй коэффициент с помощью базисной
функции, представленной выражением (20):

Анализ данного выражения показывает,
что коэффициент ![]() характеризует
разности средних значений половинок сигнала
характеризует
разности средних значений половинок сигнала ![]() . Если теперь выполнить синтез по двум
коэффициентам с синтезирующей базисной функцией для второго коэффициента
. Если теперь выполнить синтез по двум
коэффициентам с синтезирующей базисной функцией для второго коэффициента
![]()
получим следующую аппроксимацию:
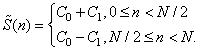
Дальнейшая операция анализа, т.е
вычисления коэффициентов ![]() и синтеза аналогична рассмотренной, с той
разницей, что все действия повторяются для половинок сигнала, затем для
четверти, и т.д. На самой последней итерации анализ осуществляется для пар
случайных величин (рис 11).
и синтеза аналогична рассмотренной, с той
разницей, что все действия повторяются для половинок сигнала, затем для
четверти, и т.д. На самой последней итерации анализ осуществляется для пар
случайных величин (рис 11).
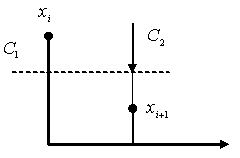
Рис. 11. Преобразование пар случайных величин
В результате исходный сигнал точно описывается коэффициентами вейвлет-преобразования Хаара. Вейвлет-коэффициенты сигнала (19) показаны на рис. 10.
Из приведенного рисунка видно, что нестационарности сигнала (резкие перепады) локализуются в малом числе вейвлет-коэффициентов. Это приводит к возможности лучшего восстановления нестационарного сигнала по неполным данным.
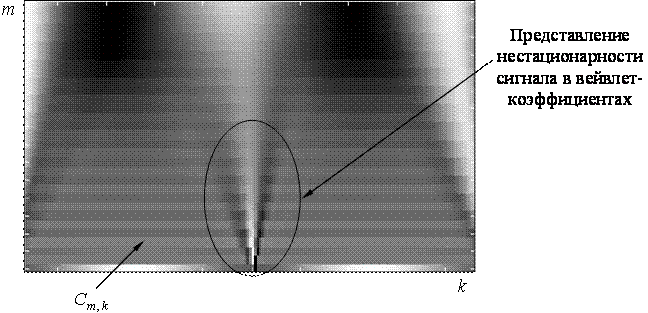
Рис. 12. Вейвлет-коэффициенты одного периода функции (19)
При вычислении
вейвлет-коэффициентов ![]() базисные
функции покрывали анализируемый сигнал следующим образом (рис. 12). Из
рис. 12 видно, что система базисных функций Хаара в дискретном
пространстве должна задаваться двумя параметрами: сдвига и частоты (масштаба):
базисные
функции покрывали анализируемый сигнал следующим образом (рис. 12). Из
рис. 12 видно, что система базисных функций Хаара в дискретном
пространстве должна задаваться двумя параметрами: сдвига и частоты (масштаба):
![]() ,
,
где ![]() -
масштаб базисной функции;
-
масштаб базисной функции; ![]() - сдвиг. В дискретном случае параметр
масштаба
- сдвиг. В дискретном случае параметр
масштаба ![]() , где
, где ![]() - любое целое
положительное число, параметр сдвига
- любое целое
положительное число, параметр сдвига ![]() . Таким образом, все множество базисных
функций можно записать как
. Таким образом, все множество базисных
функций можно записать как
![]() .
.
Прямое и обратное дискретные ВП вычисляются по формулам
![]() ,
,
![]() .
.
Следует отметить, что если число отсчетов
![]() , то
максимальное значение
, то
максимальное значение ![]() равно
равно
![]() . Наибольшее
значение
. Наибольшее
значение ![]() для
текущего
для
текущего ![]() равно
равно
![]() .
.
Для непрерывных сигналов будут справедливы следующие интегральные выражения:
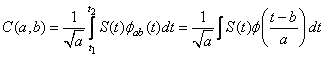 ,
,
![]() .
.
Таким образом, задавая вейвлет-функции, можно выполнять разложение сигнала по вейвлет-базису непрерывных или дискретных сигналов.
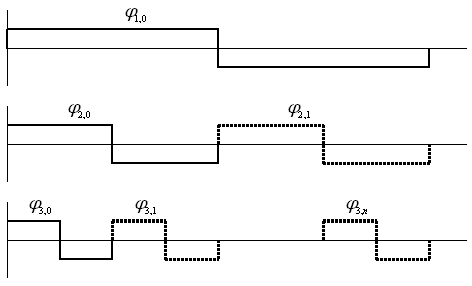
Рис. 13. Распределение базисных функций Хаара при анализе сигнала
Функция ![]() может образовывать
вейвлет-базис, если она удовлетворяет следующим условиям:
может образовывать
вейвлет-базис, если она удовлетворяет следующим условиям:
1. Ограниченность нормы:
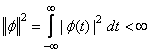 .
.
2. Вейвлет-функция должна быть ограничена и по времени и по частоте:
![]() и
и ![]() , при
, при ![]() .
.
Контрпример: дельта-функция и гармоническая функция не удовлетворяют данному условию.
3. Нулевое среднее:
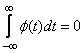 .
.
Если обобщить данное
условие, то можно получить формулу 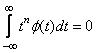 , которая определяет степень гладкости
функции
, которая определяет степень гладкости
функции ![]() . Считается,
что чем выше степень гладкости базисной функции, тем лучше ее аппроксимационные
свойства.
. Считается,
что чем выше степень гладкости базисной функции, тем лучше ее аппроксимационные
свойства.
В качестве примера приведем следующие известные вейвлет-функции:
![]() ,
, ![]() .
.
Для ВП, также как и
для ДПФ существует алгоритм быстрого преобразования. Рассмотрим снова ВП Хаара.
Из рис. 13 видно, что функции с малым масштабным коэффициентом ![]() используют те же отсчеты
сигнала для вычисления коэффициентов, что и функции с большим масштабным
коэффициентом. При этом операция суммирования одних и тех же отсчетов
повторяется неоднократно. Следовательно, для уменьшения объема вычислений целесообразно
вычислять ВП с самого малого масштабного коэффициента. В результате получаем вейвлет-коэффициенты,
представляющие собой средние значения
используют те же отсчеты
сигнала для вычисления коэффициентов, что и функции с большим масштабным
коэффициентом. При этом операция суммирования одних и тех же отсчетов
повторяется неоднократно. Следовательно, для уменьшения объема вычислений целесообразно
вычислять ВП с самого малого масштабного коэффициента. В результате получаем вейвлет-коэффициенты,
представляющие собой средние значения ![]() и разности
и разности ![]() . Для коэффициентов
. Для коэффициентов ![]() повторяем данную процедуру. При
этом усреднение коэффициентов
повторяем данную процедуру. При
этом усреднение коэффициентов ![]() будет соответствовать усреднению четырех отсчетов
сигнала, но при этом расходуется одна операция умножения и одна операция
сложения. Процесс разложения повторяется до тех пор, пока не будут вычислены
все коэффициенты спектра
будет соответствовать усреднению четырех отсчетов
сигнала, но при этом расходуется одна операция умножения и одна операция
сложения. Процесс разложения повторяется до тех пор, пока не будут вычислены
все коэффициенты спектра ![]() .
.
Запишем алгоритм
быстрого вейвлет-преобразования Хаара в матричном виде. Пусть дан вектор ![]() размером 8 элементов. Матрица
преобразования Хаара запишется в виде
размером 8 элементов. Матрица
преобразования Хаара запишется в виде
 ,
,
В приведенных обозначениях один шаг быстрого ВП запишется как
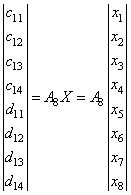 . (21)
. (21)
Повторяем операцию преобразования
для коэффициентов ![]() :
:
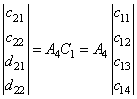 , (22)
, (22)
для
коэффициентов ![]()
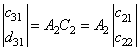 . (23)
. (23)
В результате
получается набор вейвлет-коэффициентов ![]() , по которым можно точно восстановить
исходный сигнал. Для этого необходимо задать матрицу синтеза
, по которым можно точно восстановить
исходный сигнал. Для этого необходимо задать матрицу синтеза ![]()
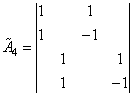 ,
, ![]() .
.
Восстановленный сигнал запишется в виде
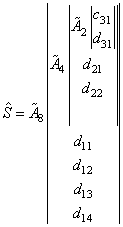 . (24)
. (24)
В общем случае вместо
коэффициентов ![]() могут
быть любые другие, которые описывают соответствующее ВП. При этом элементы в
матрицах
могут
быть любые другие, которые описывают соответствующее ВП. При этом элементы в
матрицах ![]() можно
характеризовать как коэффициенты низко- и высокочастотных фильтров анализа и
синтеза соответственно:
можно
характеризовать как коэффициенты низко- и высокочастотных фильтров анализа и
синтеза соответственно:
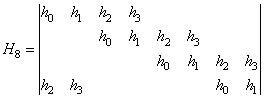 ,
,
 ,
,
где
![]() - матрица
выделения низкочастотных составляющих;
- матрица
выделения низкочастотных составляющих; ![]() - матрица выделения высокочастотных
составляющих. При этом преобразование сигнала можно представить через свертку
КИХ-фильтров (рис. 14).
- матрица выделения высокочастотных
составляющих. При этом преобразование сигнала можно представить через свертку
КИХ-фильтров (рис. 14).
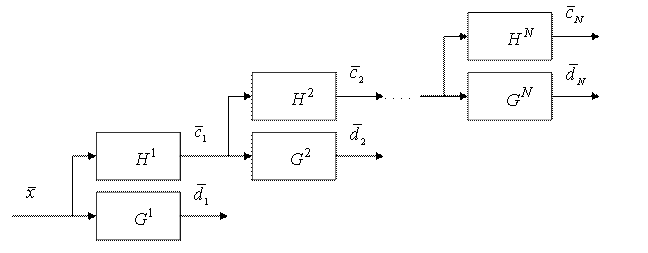
Рис. 14. Представление ВП через набор низко- и высокочастотных фильтров
Обобщение ВП на двумерный случай приводит к разделимому преобразованию:
![]() ,
,
где
![]() -
низкочастотная составляющая;
-
низкочастотная составляющая; ![]() ,
, ![]() ,
, ![]() - высокочастотные составляющие. Таким
образом, при двумерном ВП изображение разбивается на четыре компоненты: три
высокочастотные, представляющие мелкие детали, и одна низкочастотная,
представляющая собой уменьшенную и сглаженную копию исходного изображения. В
соответствии с алгоритмом БВП второй шаг ВП запишется в виде
- высокочастотные составляющие. Таким
образом, при двумерном ВП изображение разбивается на четыре компоненты: три
высокочастотные, представляющие мелкие детали, и одна низкочастотная,
представляющая собой уменьшенную и сглаженную копию исходного изображения. В
соответствии с алгоритмом БВП второй шаг ВП запишется в виде
![]()
В
результате получаем представление изображения на разных уровнях масштаба ![]() ,
, ![]() , и т.д. Операции преобразования
сигнала можно рекуррентно выполнять, пока низкочастотная составляющая не будет
представлена одним отсчетом.
, и т.д. Операции преобразования
сигнала можно рекуррентно выполнять, пока низкочастотная составляющая не будет
представлена одним отсчетом.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Разложение сигналов по базисным функциям
- 1. Разложение сигналов по базисным функциям
- 2. Преобразование Адамара
- 2. Преобразование Адамара
- 3. Преобразование Карунена-Лоэва
- 3. Преобразование Карунена-Лоэва
- 4. Преобразование Фурье
- 4. Преобразование Фурье
- 5. Алгоритмы быстрых вычислений
- 5. Алгоритмы быстрых вычислений
- 6. Сжатие изображений с использованием унитарных преобразований
- 6. Сжатие изображений с использованием унитарных преобразований
- 7. Основы вейвлет-преобразования
- 7. Основы вейвлет-преобразования
- 8. Расчет ортогональных вейвлет-фильтров
- 8. Расчет ортогональных вейвлет-фильтров
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 10. Применение ВП. Низкочастотная фильтрация
- 10. Применение ВП. Низкочастотная фильтрация
- 11. Применение ВП. Подчеркивание границ
- 11. Применение ВП. Подчеркивание границ
- 12. Сжатие изображений на основе лифтинговой схемы
- 12. Сжатие изображений на основе лифтинговой схемы
- 13. Восстановление изображений по отдельным отсчетам
- 13. Восстановление изображений по отдельным отсчетам
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 15. Восстановление сигналов по преобразованным данным
- 15. Восстановление сигналов по преобразованным данным
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 18. Введение во фракталы
- 18. Введение во фракталы
- 19. Системы итерируемых функций
- 19. Системы итерируемых функций
- 20. Примеры систем итерируемых функций
- 20. Примеры систем итерируемых функций
- 21. Сжатие изображений с использованием СИФ
- 21. Сжатие изображений с использованием СИФ
- 22. Фильтрация изображений с помощью ДПФ
- 22. Фильтрация изображений с помощью ДПФ
- 23. Линейные системы
- 23. Линейные системы
