| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13. Восстановление изображений по отдельным отсчетам
При восстановлении изображений
необходимо выбрать некоторый критерий качества, в соответствии с которым можно
говорить о лучших и худших результатах восстановления. При этом обычно выбирают
величину ![]() ,
где
,
где ![]() -
восстановленное значение
-
восстановленное значение ![]() -ого элемента. Для данного критерия
известен алгоритм оптимального оценивания.
-ого элемента. Для данного критерия
известен алгоритм оптимального оценивания.
Пусть дан вектор ![]() пораженный белым гауссовским
шумом
пораженный белым гауссовским
шумом ![]() с
с ![]() и
и ![]() :
:
![]() ,
,
где ![]() - исходный вектор. Выполним синтез
оптимального фильтра по критерию минимума дисперсии ошибок оценивания:
- исходный вектор. Выполним синтез
оптимального фильтра по критерию минимума дисперсии ошибок оценивания:
![]() , (40)
, (40)
где ![]() -
вектор коэффициентов фильтра для восстановления
-
вектор коэффициентов фильтра для восстановления ![]() -ого элемента. Целью синтеза является
определение вектора
-ого элемента. Целью синтеза является
определение вектора ![]() ,
обеспечивающего минимум
,
обеспечивающего минимум ![]() . Для этого продифференцируем выражение (40)
по
. Для этого продифференцируем выражение (40)
по ![]() и
приравняем результат нулю:
и
приравняем результат нулю:
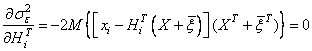 .
.
Вычислим оптимальные коэффициенты, учитывая, что шум
наблюдения ![]() не
коррелирован с элементами вектора
не
коррелирован с элементами вектора ![]() :
:
![]() , (41)
, (41)
где ![]() -
взаимная корреляция вектора элемента
-
взаимная корреляция вектора элемента ![]() с вектором
с вектором ![]() ;
; ![]() - корреляционная матрица вектора
- корреляционная матрица вектора ![]() ;
; ![]() - диагональная матрица дисперсий
шума наблюдений.
- диагональная матрица дисперсий
шума наблюдений.
Таким образом, при построении
оптимальной линейной оценки необходимо знать корреляционную матрицу случайного
процесса или случайного поля (изображения). Рассмотрим задачу восстановления
элементов вектора ![]() по
наблюдениям
по
наблюдениям ![]() ,
, ![]() ,
, ![]() , которые в дальнейшем будем
называть множеством неполных наблюдений. При этом выражения (40) и (41) перепишутся
в виде:
, которые в дальнейшем будем
называть множеством неполных наблюдений. При этом выражения (40) и (41) перепишутся
в виде:
![]() ,
,
![]() , (42)
, (42)
где ![]() -
-
![]() - матрица
выделения множества неполных наблюдений:
- матрица
выделения множества неполных наблюдений: ![]() ,
, ![]() . Например, для выделения нечетных
элементов вектора
. Например, для выделения нечетных
элементов вектора ![]() ,
матрица
,
матрица ![]() имеет
вид:
имеет
вид:

Вектор весовых коэффициентов ![]() размером
размером ![]() элементов, вычисленный
по формуле (42), позволяет строить оптимальный прогноз неизвестных элементов вектора
элементов, вычисленный
по формуле (42), позволяет строить оптимальный прогноз неизвестных элементов вектора
![]() в виде
линейной комбинации
в виде
линейной комбинации
![]() .
.
Обобщим приведенные выражения
восстановления последовательности по множеству неполных наблюдений на двумерный
случай для восстановления изображений. Пусть дано случайное поле ![]() размером
размером ![]() отсчетов и известна его
корреляционная матрица
отсчетов и известна его
корреляционная матрица ![]() . Рассмотрим алгоритм построения
оптимального линейного прогноза неизвестных элементов по известным наблюдениям
. Рассмотрим алгоритм построения
оптимального линейного прогноза неизвестных элементов по известным наблюдениям ![]() ,
, ![]() ,
, ![]() . Не теряя общности, наблюдаемый двумерный
сигнал
. Не теряя общности, наблюдаемый двумерный
сигнал ![]() можно представить
в виде одномерного
можно представить
в виде одномерного ![]() ,
где
,
где ![]() -
- ![]() -й вектор столбец матрицы
-й вектор столбец матрицы
![]() .
Корреляционную функцию такого одномерного сигнала можно записать в виде
.
Корреляционную функцию такого одномерного сигнала можно записать в виде

В приведенных обозначениях выражение (42) можно переписать в виде
![]() , (43)
, (43)
где ![]() - взаимная корреляция элемента
- взаимная корреляция элемента ![]() с вектором
с вектором ![]() ;
;
![]() -
- ![]() матрица выделения
элементов наблюдений вектора
матрица выделения
элементов наблюдений вектора ![]() . Вектор коэффициентов
. Вектор коэффициентов ![]() позволяет строить прогноз
элемента
позволяет строить прогноз
элемента ![]() изображения
изображения
![]() :
:
![]() , при
, при ![]() ,
, ![]() , (44)
, (44)
где ![]() -
оператор отбрасывания дробной части.
-
оператор отбрасывания дробной части.
Подставляя вычисленные коэффициенты ![]() в выражение (40) можно
найти дисперсию ошибок оценивания неизвестных элементов. После возведения в
квадрат и вычисления математического ожидания получаем
в выражение (40) можно
найти дисперсию ошибок оценивания неизвестных элементов. После возведения в
квадрат и вычисления математического ожидания получаем
![]() . (45)
. (45)
Таким образом, выражения (43)-(45)
позволяют восстанавливать изображения по множеству неполных наблюдений ![]() ,
, ![]() ,
, ![]() и вычислять дисперсию ошибок оценивания.
Рассмотрим пример восстановления изображения
и вычислять дисперсию ошибок оценивания.
Рассмотрим пример восстановления изображения ![]() размером 3х3 отсчета по наблюдениям,
расположение которых представлено на рис. 19, с корреляционной функцией
размером 3х3 отсчета по наблюдениям,
расположение которых представлено на рис. 19, с корреляционной функцией ![]() .
.
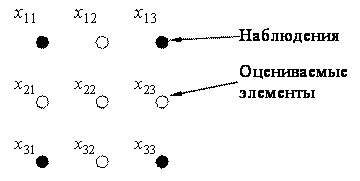
Рис. 19. Расположение наблюдений и оцениваемых элементов
Корреляционная функция ![]() случайного процесса
случайного процесса ![]() имеет вид
имеет вид
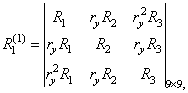
где 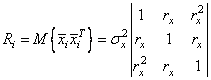 - 3х3 - корреляционная матрица строк
вектора
- 3х3 - корреляционная матрица строк
вектора ![]() .
Матрица выделения наблюдений
.
Матрица выделения наблюдений
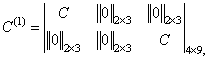
где ![]() - матрица выделения наблюдений для первой
и третьей строк изображения. Вектор
- матрица выделения наблюдений для первой
и третьей строк изображения. Вектор ![]() оптимальных коэффициентов для построения
прогноза
оптимальных коэффициентов для построения
прогноза ![]() -го
отсчета находится по формуле (43). Например, при
-го
отсчета находится по формуле (43). Например, при ![]() получаем вектор
получаем вектор ![]() . Тогда прогноз элемента
. Тогда прогноз элемента ![]() в соответствии с
выражением (44) имеет вид
в соответствии с
выражением (44) имеет вид
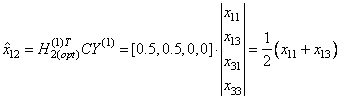 .
.
Таким образом, при разделимой
экспоненциальной корреляционной функции и коэффициентах корреляции близких к
единице, оптимальный линейный прогноз строится как среднее арифметическое двух
ближайших наблюдений от оцениваемого элемента. При других корреляционных
матрицах и коэффициентах корреляции будут получаться другие коэффициенты
оптимального фильтра ![]() и
другие значения оценок неизвестных элементов.
и
другие значения оценок неизвестных элементов.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Разложение сигналов по базисным функциям
- 1. Разложение сигналов по базисным функциям
- 2. Преобразование Адамара
- 2. Преобразование Адамара
- 3. Преобразование Карунена-Лоэва
- 3. Преобразование Карунена-Лоэва
- 4. Преобразование Фурье
- 4. Преобразование Фурье
- 5. Алгоритмы быстрых вычислений
- 5. Алгоритмы быстрых вычислений
- 6. Сжатие изображений с использованием унитарных преобразований
- 6. Сжатие изображений с использованием унитарных преобразований
- 7. Основы вейвлет-преобразования
- 7. Основы вейвлет-преобразования
- 8. Расчет ортогональных вейвлет-фильтров
- 8. Расчет ортогональных вейвлет-фильтров
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 10. Применение ВП. Низкочастотная фильтрация
- 10. Применение ВП. Низкочастотная фильтрация
- 11. Применение ВП. Подчеркивание границ
- 11. Применение ВП. Подчеркивание границ
- 12. Сжатие изображений на основе лифтинговой схемы
- 12. Сжатие изображений на основе лифтинговой схемы
- 13. Восстановление изображений по отдельным отсчетам
- 13. Восстановление изображений по отдельным отсчетам
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 15. Восстановление сигналов по преобразованным данным
- 15. Восстановление сигналов по преобразованным данным
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 18. Введение во фракталы
- 18. Введение во фракталы
- 19. Системы итерируемых функций
- 19. Системы итерируемых функций
- 20. Примеры систем итерируемых функций
- 20. Примеры систем итерируемых функций
- 21. Сжатие изображений с использованием СИФ
- 21. Сжатие изображений с использованием СИФ
- 22. Фильтрация изображений с помощью ДПФ
- 22. Фильтрация изображений с помощью ДПФ
- 23. Линейные системы
- 23. Линейные системы
