| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8. Расчет ортогональных вейвлет-фильтров
Рассмотрим матричный способ расчета вейвлет-фильтров для преобразования сигнала. Допустим, что низко- и высокочастотные коэффициенты фильтров ортогональны друг другу. В этом случае можно записать
![]() ,
, ![]() . (25)
. (25)
где
![]() – коэффициенты
низкочастотного фильтра;
– коэффициенты
низкочастотного фильтра; ![]() – высокочастотного. Запишем матрицу
преобразования
– высокочастотного. Запишем матрицу
преобразования ![]() размером
8х8 элементов, при длине вейвлет-фильтров
размером
8х8 элементов, при длине вейвлет-фильтров ![]() :
:
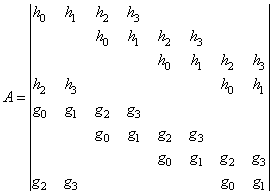 .
.
В соответствии с третьим условием базисных вейвлет-функций потребуем наличия 2-х нулевых моментов:
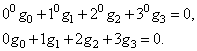
Для
того чтобы преобразование было обратимым, необходимо выполнение условия ![]() , где
, где ![]() – единичная матрица. В результате
получаем еще два уравнения:
– единичная матрица. В результате
получаем еще два уравнения:
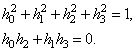
Решение полученной системы уравнений даст коэффициенты низкочастотного фильтра:
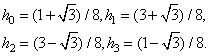
Коэффициенты высокочастотного фильтра находятся из уравнения (25).
Вычисленные ортогональные вейвлеты получили название вейвлетов Добеши. Другим видом ВП является биортогональное преобразование. В этом случае базисные функции анализа не ортогональны друг другу. При этом удается получить вейвлет-фильтры с большим числом нулевых моментов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- 1. Разложение сигналов по базисным функциям
- 1. Разложение сигналов по базисным функциям
- 2. Преобразование Адамара
- 2. Преобразование Адамара
- 3. Преобразование Карунена-Лоэва
- 3. Преобразование Карунена-Лоэва
- 4. Преобразование Фурье
- 4. Преобразование Фурье
- 5. Алгоритмы быстрых вычислений
- 5. Алгоритмы быстрых вычислений
- 6. Сжатие изображений с использованием унитарных преобразований
- 6. Сжатие изображений с использованием унитарных преобразований
- 7. Основы вейвлет-преобразования
- 7. Основы вейвлет-преобразования
- 8. Расчет ортогональных вейвлет-фильтров
- 8. Расчет ортогональных вейвлет-фильтров
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 10. Применение ВП. Низкочастотная фильтрация
- 10. Применение ВП. Низкочастотная фильтрация
- 11. Применение ВП. Подчеркивание границ
- 11. Применение ВП. Подчеркивание границ
- 12. Сжатие изображений на основе лифтинговой схемы
- 12. Сжатие изображений на основе лифтинговой схемы
- 13. Восстановление изображений по отдельным отсчетам
- 13. Восстановление изображений по отдельным отсчетам
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 15. Восстановление сигналов по преобразованным данным
- 15. Восстановление сигналов по преобразованным данным
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 18. Введение во фракталы
- 18. Введение во фракталы
- 19. Системы итерируемых функций
- 19. Системы итерируемых функций
- 20. Примеры систем итерируемых функций
- 20. Примеры систем итерируемых функций
- 21. Сжатие изображений с использованием СИФ
- 21. Сжатие изображений с использованием СИФ
- 22. Фильтрация изображений с помощью ДПФ
- 22. Фильтрация изображений с помощью ДПФ
- 23. Линейные системы
- 23. Линейные системы
