6. Сжатие изображений с использованием унитарных преобразований

Пусть кодируемое изображение  представлено матрицей размером  отсчетов. Применим к данному изображению одно из рассмотренных унитарных преобразований Адамара, Карунена-Лоэва, Фурье, получим

,

где  - матрица ортогонального преобразования, размером  отсчетов. Типичный спектр имеет вид (рис. 3)

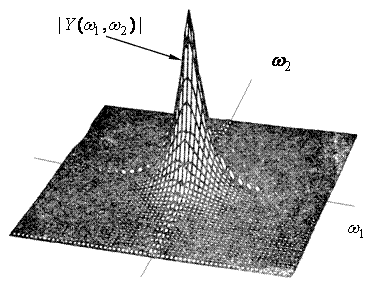
Рис. 3. Типичный спектр изображения

Анализ рис. 3 показывает, что большая часть информации сосредоточена в низких частотах, меньше, - в высоких. Следовательно, из всего множества значений  можно запомнить лишь , . При восстановлении отброшенные значения принимаются равными нулю. Тогда реконструированное изображение определяется как

,

где  - восстановленный амплитудный спектр с добавленными нулевыми отсчетами. При этом возникают ошибки восстановления, которые часто определяются по формуле

,

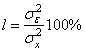где  - дисперсия изображения;  - дисперсия ошибок восстановления.

Так как при восстановлении отбрасываются высокочастотные коэффициенты, то изображение  будет выглядеть сглаженным относительно оригинала. В свою очередь, низкочастотные коэффициенты носят вещественный характер и для их хранения необходимо большое число бит. Сократить объем информации можно путем квантования, т.е. представления вещественных величин целыми числами:

,

где  - шаг квантования;  - оператор округления до ближайшего целого. Процедура квантования подробно рассмотрена ниже. Здесь отметим, что чем больше шаг , тем меньше бит требуется для представления вещественных величин и тем больше потери при восстановлении изображения. Например, при  имеем простое округление вещественных величин. Полученные целые числа можно записать в бинарный файл, который и будет определять сжатое изображение. Однако часто преобразованные и квантованные данные  сжимают алгоритмами сжатия без потерь, например Шеннона-Фэно, Хаффмена, арифметическим кодером, или архиваторами rar, arj, zip, и т.п. Данная процедура, как правило, позволяет еще больше сжать изображение при сохранении качества восстановления.

В рассматриваемом методе сжатия мы полагали, что унитарное преобразование применяется ко всему изображению. Однако при достаточно больших значениях  объем вычислений может быть очень большим. В связи с этим, в известных алгоритмах сжатия изображение разбивают на отдельные не пересекающиеся блоки , к которым, затем применяют унитарное преобразование. Например, в стандарте сжатия JPEG размер этих блоков составляет  отсчетов, а в качестве унитарного преобразования используется ДКП. Таким образом, преобразованные данные записываются как

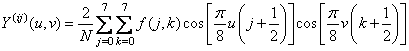, при .

Блоки , называемые трансформантами, квантуются в соответствии с матрицей квантования  по формуле

, при .

Матрица  задается так, чтобы низкочастотные коэффициенты квантовались с малым шагом, а высокочастотные с большим. В результате упорядоченная цепочка по схеме рис. 4 целых чисел будет иметь множество нулевых элементов, которые эффективно сжимаются по алгоритму Хаффмена.

Рис. 4. Зигзаг-сканирование элементов спектра

Полученные выходные данные записываются в выходной файл, который  представляет сжатое изображение.