| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Преобразование Карунена-Лоэва
В случае
ортогонального преобразования с набором ![]() базисных векторов
базисных векторов ![]() преобразование из
преобразование из ![]() в
в ![]() можно записать как
можно записать как
![]() ,
,
где
![]() -
- ![]() матрица ортогонального
преобразования.
матрица ортогонального
преобразования.
Из всего множества
значений ![]() запоминаются
первые
запоминаются
первые ![]() , причем
, причем
![]() . После
восстановления получаем оценку вектора
. После
восстановления получаем оценку вектора ![]() :
:
![]() ,
,
где
![]() - некоторое
константное значение отброшенных коэффициентов разложения
- некоторое
константное значение отброшенных коэффициентов разложения ![]() . Ошибка при отбрасывании
. Ошибка при отбрасывании ![]() коэффициентов
определяется как
коэффициентов
определяется как
![]() ,
,
а дисперсия этой ошибки
 . (9)
. (9)
Анализ выражения (9)
показывает, что для минимизации дисперсии ошибки необходимо подобрать
соответствующие значения ![]() и векторы
и векторы ![]() . Очевидно, значения
. Очевидно, значения ![]() или, для центрированных случайных
величин
или, для центрированных случайных
величин ![]() ,
, ![]() .
.
Для нахождения
оптимальных векторов ![]() ,
перепишем выражение (9) с учетом
,
перепишем выражение (9) с учетом ![]() и
и ![]() , при
, при ![]() ; в виде
; в виде
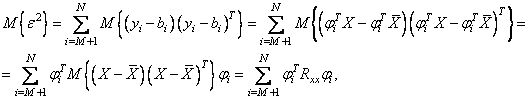 (10)
(10)
где
![]() представляет
собой ковариационную матрицу. Для минимизации (10) применяется метод множителей
Лагранжа. В результате получаем
представляет
собой ковариационную матрицу. Для минимизации (10) применяется метод множителей
Лагранжа. В результате получаем
![]() (11)
(11)
Выражение (11) определяет векторы ![]() и значения
и значения ![]() как собственные векторы
и собственные значения корреляционной матрицы
как собственные векторы
и собственные значения корреляционной матрицы ![]() . Таким образом, матрица преобразования
. Таким образом, матрица преобразования ![]() , составленная из
собственных векторов корреляционной матрицы
, составленная из
собственных векторов корреляционной матрицы ![]() , позволяет выполнять преобразование
Карунена-Лоэва, которое минимизирует среднюю дисперсию ошибки при
восстановлении сигнала по неполным данным.
, позволяет выполнять преобразование
Карунена-Лоэва, которое минимизирует среднюю дисперсию ошибки при
восстановлении сигнала по неполным данным.
Недостатком описанного метода
является необходимость априорных сведений о корреляционной матрице ![]() исходного сигнала
исходного сигнала ![]() , а также относительно высокая
вычислительная сложность. Так, в случае применения разделимого преобразования
Карунена-Лоэва, для вычисления всех коэффициентов преобразования требуется
, а также относительно высокая
вычислительная сложность. Так, в случае применения разделимого преобразования
Карунена-Лоэва, для вычисления всех коэффициентов преобразования требуется ![]() арифметических операций, где
арифметических операций, где ![]() количество отсчетов
исходного сигнала
количество отсчетов
исходного сигнала ![]() .
.
Таким образом, рассмотренный метод
может быть применен в задачах, в которых априори известна корреляционная
матрица ![]() , а
также нет больших ограничений на вычислительные ресурсы.
, а
также нет больших ограничений на вычислительные ресурсы.
В связи с этим возникает проблема поиска преобразования, которое обладало бы малой вычислительной сложностью и давало результаты преобразования близкие к преобразованию Карунена-Лоэва. Этим условиям удовлетворяет преобразование Фурье.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Разложение сигналов по базисным функциям
- 1. Разложение сигналов по базисным функциям
- 2. Преобразование Адамара
- 2. Преобразование Адамара
- 3. Преобразование Карунена-Лоэва
- 3. Преобразование Карунена-Лоэва
- 4. Преобразование Фурье
- 4. Преобразование Фурье
- 5. Алгоритмы быстрых вычислений
- 5. Алгоритмы быстрых вычислений
- 6. Сжатие изображений с использованием унитарных преобразований
- 6. Сжатие изображений с использованием унитарных преобразований
- 7. Основы вейвлет-преобразования
- 7. Основы вейвлет-преобразования
- 8. Расчет ортогональных вейвлет-фильтров
- 8. Расчет ортогональных вейвлет-фильтров
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 10. Применение ВП. Низкочастотная фильтрация
- 10. Применение ВП. Низкочастотная фильтрация
- 11. Применение ВП. Подчеркивание границ
- 11. Применение ВП. Подчеркивание границ
- 12. Сжатие изображений на основе лифтинговой схемы
- 12. Сжатие изображений на основе лифтинговой схемы
- 13. Восстановление изображений по отдельным отсчетам
- 13. Восстановление изображений по отдельным отсчетам
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 15. Восстановление сигналов по преобразованным данным
- 15. Восстановление сигналов по преобразованным данным
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 18. Введение во фракталы
- 18. Введение во фракталы
- 19. Системы итерируемых функций
- 19. Системы итерируемых функций
- 20. Примеры систем итерируемых функций
- 20. Примеры систем итерируемых функций
- 21. Сжатие изображений с использованием СИФ
- 21. Сжатие изображений с использованием СИФ
- 22. Фильтрация изображений с помощью ДПФ
- 22. Фильтрация изображений с помощью ДПФ
- 23. Линейные системы
- 23. Линейные системы
