| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23. Линейные системы
Допустим, на вход некоторой линейной
системы ![]() подается
входной сигнал
подается
входной сигнал ![]() .
При этом на выходе этой системы наблюдается сигнал
.
При этом на выходе этой системы наблюдается сигнал ![]() . Спрашивается, как смоделировать
работу «черного ящика»
. Спрашивается, как смоделировать
работу «черного ящика» ![]() , зная входной и наблюдая выходной сигналы?
Так как имеется возможность выбирать любые входные сигналы, то подадим на вход
дельта-импульс
, зная входной и наблюдая выходной сигналы?
Так как имеется возможность выбирать любые входные сигналы, то подадим на вход
дельта-импульс
![]()
На выходе получим некоторую последовательность ![]() , которая называется
откликом на единичное входное воздействие, или импульсным откликом. В силу
линейности системы изменение масштаба дельта-импульса приведет к аналогичному
изменению выходной последовательности
, которая называется
откликом на единичное входное воздействие, или импульсным откликом. В силу
линейности системы изменение масштаба дельта-импульса приведет к аналогичному
изменению выходной последовательности ![]() , т.е.
, т.е. ![]() . При этом любые дискретные сигналы можно
рассматривать как последовательности дельта-импульсов с разными масштабами:
. При этом любые дискретные сигналы можно
рассматривать как последовательности дельта-импульсов с разными масштабами: ![]() . Подадим на вход
линейной системы последовательность дельта-импульсов:
. Подадим на вход
линейной системы последовательность дельта-импульсов: ![]() . Каждый входной отсчет сигнала
. Каждый входной отсчет сигнала ![]() будет генерировать
смещенную последовательность
будет генерировать
смещенную последовательность ![]() (рис. 5).
(рис. 5).
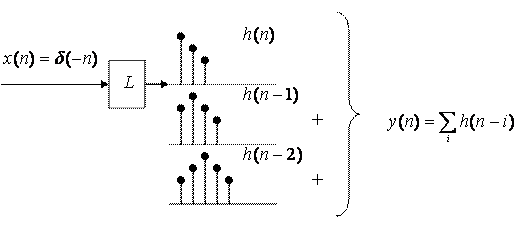
Рис. 5. Формирование выходного сигнала в линейных системах с постоянными параметрами
Следовательно, при произвольном входном сигнале линейной системы с постоянными параметрами, выходной будет определяться выражением
![]() . (13)
. (13)
Таким образом, работа линейной
системы полностью определяется импульсным откликом ![]() этой системы.
этой системы.
Рассмотрим реакцию линейной системы
на входное воздействие ![]() , которое описывает комплексную синусоиду с
частотой
, которое описывает комплексную синусоиду с
частотой ![]() .
После подстановки в выражение (13) данного выражения, получим
.
После подстановки в выражение (13) данного выражения, получим
![]() , (14)
, (14)
где ![]() -
частотная характеристика системы. Таким образом, пропуская комплексную
синусоиду через линейную системы, получаем ту же самую синусоиду, но с
измененными амплитудой и фазой
-
частотная характеристика системы. Таким образом, пропуская комплексную
синусоиду через линейную системы, получаем ту же самую синусоиду, но с
измененными амплитудой и фазой ![]() . Представление частотной характеристики на
комплексной плоскости показано на рис. 6.
. Представление частотной характеристики на
комплексной плоскости показано на рис. 6.

Рис. 6. Представление частотной характеристики на комплексной плоскости
Из рис. 6 видно, что частотную характеристику можно записать в следующем виде:
![]() ,
,
где ![]() -
начальная фаза;
-
начальная фаза; ![]() .
Начальную фазу можно выразить через отношения мнимой и действительной частей
частотной характеристики:
.
Начальную фазу можно выразить через отношения мнимой и действительной частей
частотной характеристики:
![]() .
.
Так как частотная характеристика ![]() связана с импульсным
откликом
связана с импульсным
откликом ![]() через
преобразование Фурье, то
через
преобразование Фурье, то
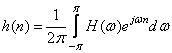 . (15)
. (15)
Если ![]() , то комплексные синусоиды данной частоты
проходят через линейную систему без искажений. Соответственно, если
, то комплексные синусоиды данной частоты
проходят через линейную систему без искажений. Соответственно, если ![]() , то комплексные
синусоиды данной частоты не пропускаются. Используя это свойство частотной
характеристики можно выполнять фильтрацию сигналов. Например, при идеальной
низкочастотной фильтрации можно положить
, то комплексные
синусоиды данной частоты не пропускаются. Используя это свойство частотной
характеристики можно выполнять фильтрацию сигналов. Например, при идеальной
низкочастотной фильтрации можно положить
![]()
Из выражения (15) импульсная характеристика такого фильтра ![]() и определена на
интервале
и определена на
интервале ![]() .
Поэтому в общем случае реализовать на практике идеальный фильтр низких частот
невозможно. Аналогичное выражение импульсной характеристики можно получить для
фильтра высоких частот, который также является нереализуемым.
.
Поэтому в общем случае реализовать на практике идеальный фильтр низких частот
невозможно. Аналогичное выражение импульсной характеристики можно получить для
фильтра высоких частот, который также является нереализуемым.
Вычисление свертки (13) можно выполнить
в частотной области. Известно, что сигнал ![]() связан со своим образом в частотной
области преобразованием Фурье:
связан со своим образом в частотной
области преобразованием Фурье:
![]() ,
,
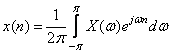 .
.
При этом если на вход линейной системы подать
последовательность ![]() ,
то по аналогии с выражением (14) получим отклик
,
то по аналогии с выражением (14) получим отклик ![]() . С помощью обратного преобразования Фурье
получаем
. С помощью обратного преобразования Фурье
получаем
 ,
,
или в частотной области
![]() . (16)
. (16)
Таким образом, свертка в частотной
области представляет собой умножение сигнала ![]() на частотную характеристику фильтра
на частотную характеристику фильтра ![]() .
.
Приведенные выражения преобразования сигнала можно обобщить на двумерный случай. При этом получим следующие выражения:
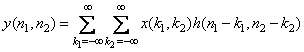 ,
,
![]() .
.
Допустим, что двумерный импульсный
отклик ![]() .
Тогда выходной сигнал можно записать в виде
.
Тогда выходной сигнал можно записать в виде
 (17)
(17)
Выражение (17) описывает разделимое
преобразование входного сигнала ![]() в линейной системе. При этом для
вычисления одного отсчета требуется
в линейной системе. При этом для
вычисления одного отсчета требуется ![]() арифметических операций, тогда как для
неразделимых
арифметических операций, тогда как для
неразделимых ![]() .
Следует отметить, что на практике не всегда удается построить фильтр, который
можно представить в разделимом виде. В таких случаях пытаются аппроксимировать
неразделимый импульсный отклик разделимым, либо уменьшить область весового
суммирования
.
Следует отметить, что на практике не всегда удается построить фильтр, который
можно представить в разделимом виде. В таких случаях пытаются аппроксимировать
неразделимый импульсный отклик разделимым, либо уменьшить область весового
суммирования ![]() .
.
Несколько линейных систем можно
соединить последовательно и параллельно. Пусть имеются импульсные отклики двух
линейных систем ![]() и
и
![]() . Рассмотрим
последовательное соединение этих систем (рис. 7)
. Рассмотрим
последовательное соединение этих систем (рис. 7)
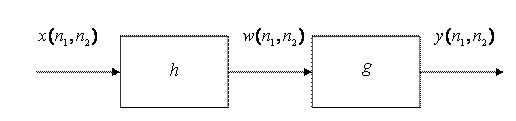
Рис. 7. Последовательное соединение линейных систем
Выходной сигнал
![]() ,
,
где знак ** обозначает двумерную свертку. Таким образом, две последовательно соединенные линейные системы можно заменить одной с эквивалентным импульсным откликом
![]() .
.
При параллельном соединении линейных систем (рис. 8) выходной сигнал определяется выражением
![]()
Следовательно, две параллельно соединенные линейные системы можно заменить одной с эквивалентным импульсным откликом
![]() .
.
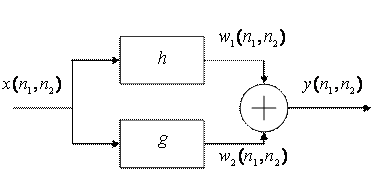
Рис. 8. Параллельное соединение линейных систем
На практике
представляют интерес лишь устойчивые системы, т.е. когда при ограниченной
входной последовательности выходная последовательность также ограничена. Для
таких систем при ![]() должно
существовать такое
должно
существовать такое ![]() ,
что
,
что ![]() для всех
для всех ![]() . Необходимым и
достаточным условием принадлежности линейной системы к классу устойчивых систем
является абсолютная суммируемость ее импульсного отклика
. Необходимым и
достаточным условием принадлежности линейной системы к классу устойчивых систем
является абсолютная суммируемость ее импульсного отклика
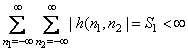 .
.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Разложение сигналов по базисным функциям
- 1. Разложение сигналов по базисным функциям
- 2. Преобразование Адамара
- 2. Преобразование Адамара
- 3. Преобразование Карунена-Лоэва
- 3. Преобразование Карунена-Лоэва
- 4. Преобразование Фурье
- 4. Преобразование Фурье
- 5. Алгоритмы быстрых вычислений
- 5. Алгоритмы быстрых вычислений
- 6. Сжатие изображений с использованием унитарных преобразований
- 6. Сжатие изображений с использованием унитарных преобразований
- 7. Основы вейвлет-преобразования
- 7. Основы вейвлет-преобразования
- 8. Расчет ортогональных вейвлет-фильтров
- 8. Расчет ортогональных вейвлет-фильтров
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 9. Выполнение вейвлет-преобразования на основе лифтинговой схемы
- 10. Применение ВП. Низкочастотная фильтрация
- 10. Применение ВП. Низкочастотная фильтрация
- 11. Применение ВП. Подчеркивание границ
- 11. Применение ВП. Подчеркивание границ
- 12. Сжатие изображений на основе лифтинговой схемы
- 12. Сжатие изображений на основе лифтинговой схемы
- 13. Восстановление изображений по отдельным отсчетам
- 13. Восстановление изображений по отдельным отсчетам
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 14. Алгоритм сжатия изображений на основе оценивания элементов
- 15. Восстановление сигналов по преобразованным данным
- 15. Восстановление сигналов по преобразованным данным
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 16. Восстановление стационарных сигналов по неточным коэффициентам разложения
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 17. Восстановление нестационарных случайных последовательностей по неточным вейвлет-коэффициентам
- 18. Введение во фракталы
- 18. Введение во фракталы
- 19. Системы итерируемых функций
- 19. Системы итерируемых функций
- 20. Примеры систем итерируемых функций
- 20. Примеры систем итерируемых функций
- 21. Сжатие изображений с использованием СИФ
- 21. Сжатие изображений с использованием СИФ
- 22. Фильтрация изображений с помощью ДПФ
- 22. Фильтрация изображений с помощью ДПФ
- 23. Линейные системы
- 23. Линейные системы
