| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
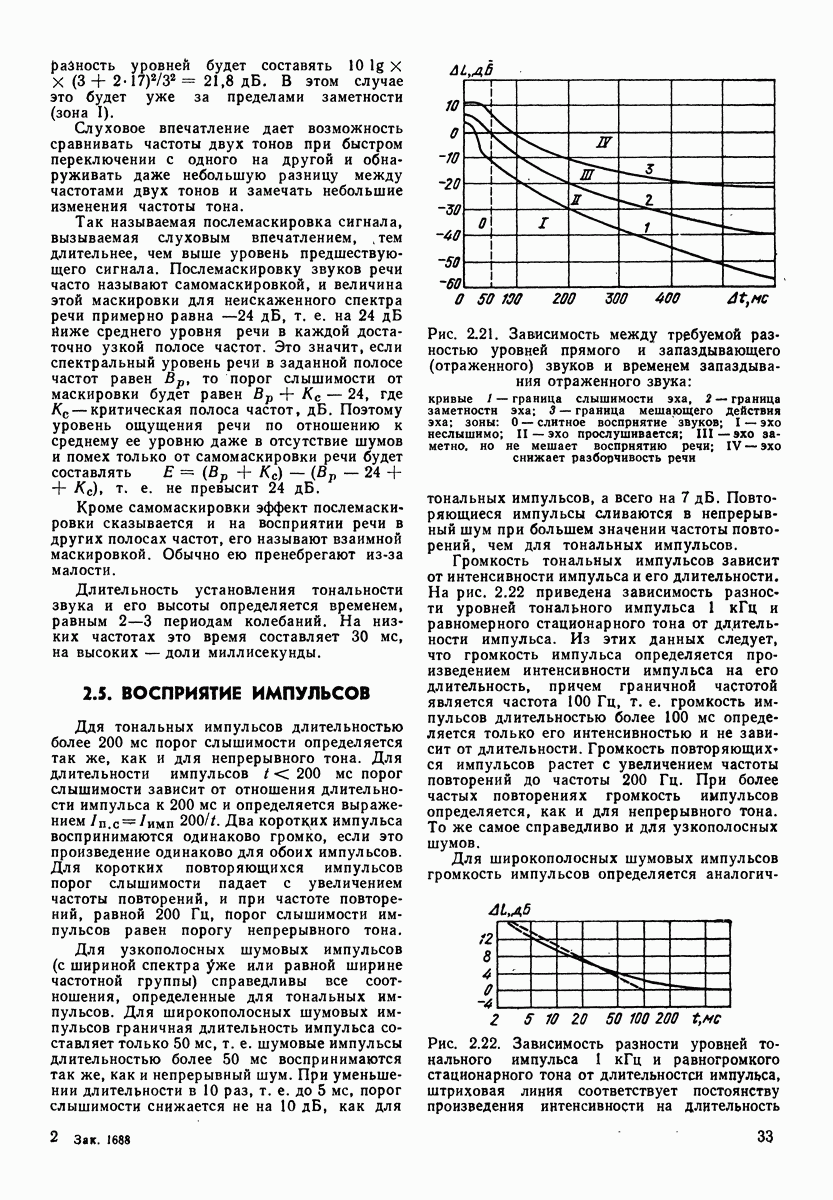
3.3. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
Акустический сигнал от каждого из первичных источников звука, используемых в системе вещания, связи, телевидения и т. п., как правило, имеет непрерывно изменяющиеся форму и состав спектра. Эти спектры могут быть дискретными, сплошными и смешанными, высокочастотными и низкочастотными. Дискретные спектры могут быть гармоническими, т. е. представляющими спектр сложного тона, и тональными, т. е. представляющими суммарный спектр ряда сложных тонов, некратных по частоте. Сигнал с гармоническим спектром может быть представлен в виде ряда Фурье

где  период колебаний;
период колебаний;  угловая частота колебаний первой гармоники; к — целые числа от
угловая частота колебаний первой гармоники; к — целые числа от  до
до  комплексная амплитуда;
комплексная амплитуда;  амплитуда гармоники;
амплитуда гармоники;  начальная фаза ее.
начальная фаза ее.
Комплексная амплитуда 

В вещественной форме ряд Фурье имеет вид

где  коэффициенты Фурье: 77 2
коэффициенты Фурье: 77 2

Отсюда 

Спектр тонального сигнала с некратными частотами со  имеет вид
имеет вид

где  частоты, амплитуды и фазы составляющих:
частоты, амплитуды и фазы составляющих:

Для сплошного спектра его плотность (по амплитуде)

а сигнал имеет вид

Для процессов, ограниченных во времени, введено понятие текущего спектра

и мгновенного 

где  весовая функция или окно, предствляющее импульсный отклик прототипа полосового фильтра.
весовая функция или окно, предствляющее импульсный отклик прототипа полосового фильтра.

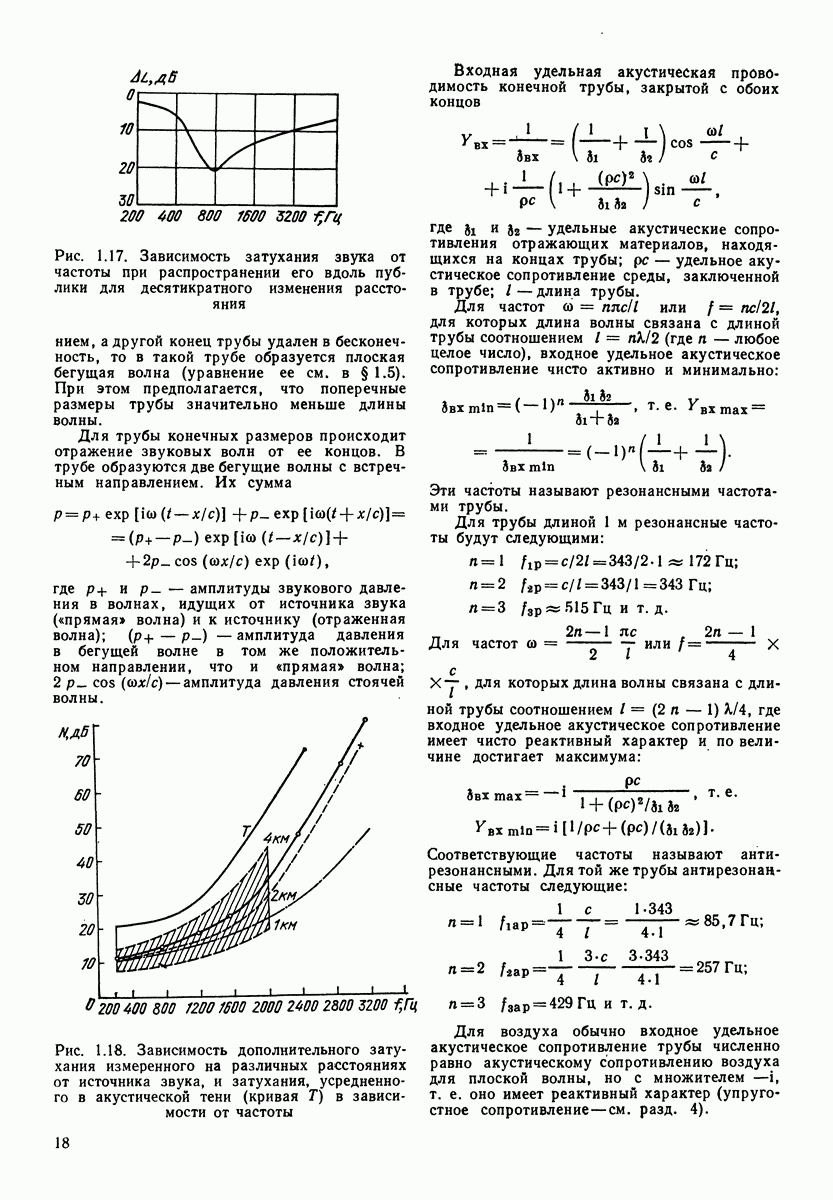
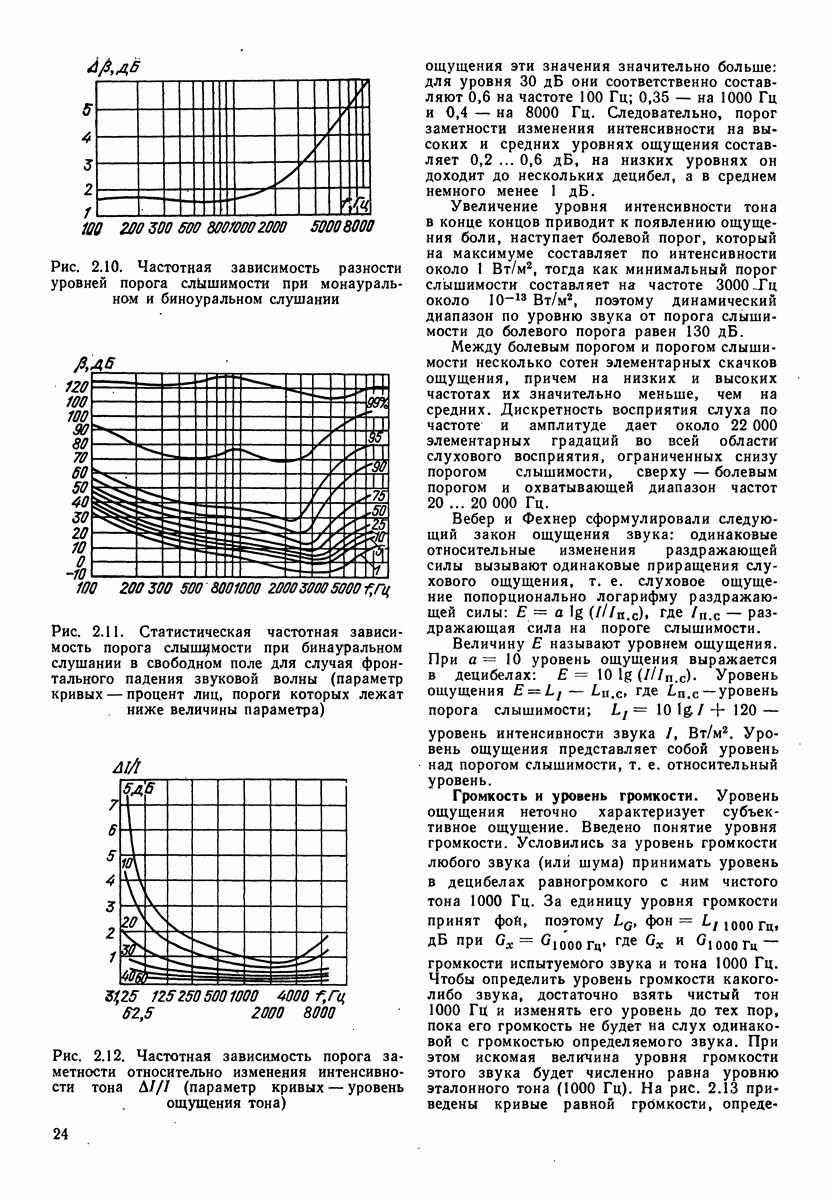
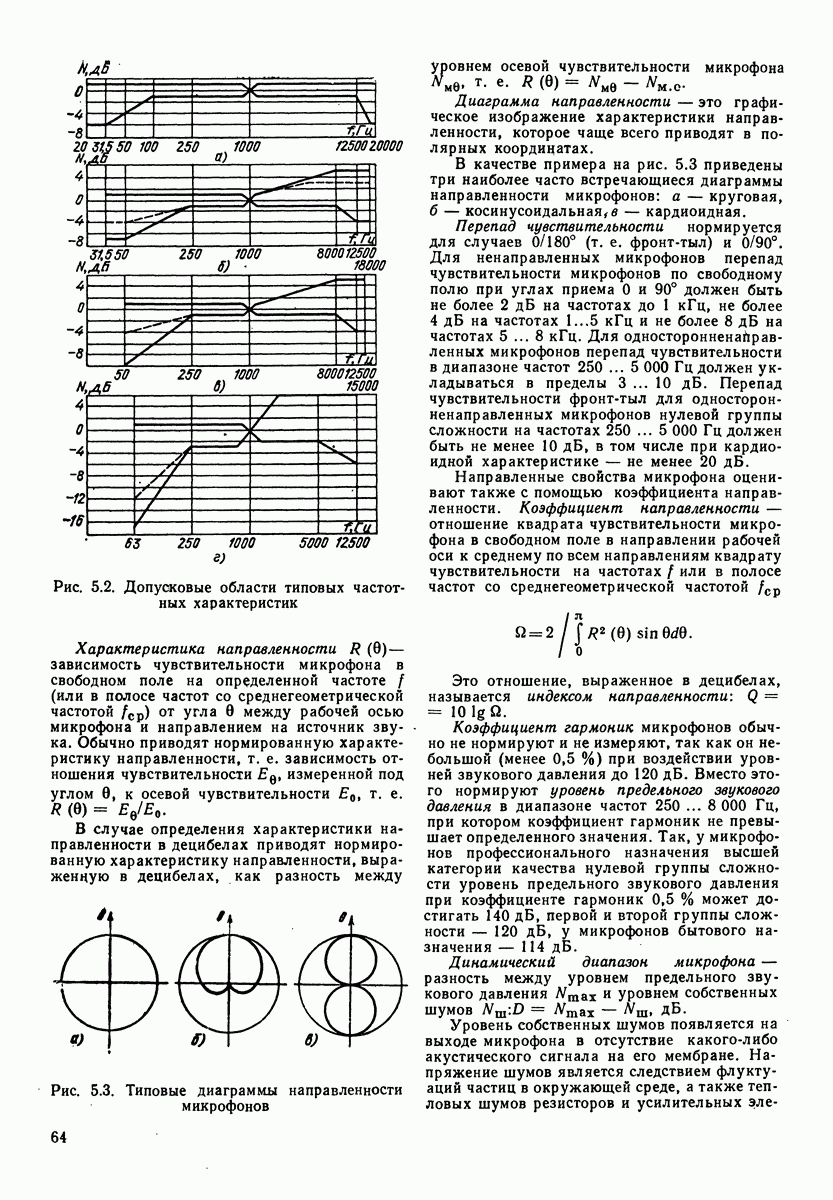
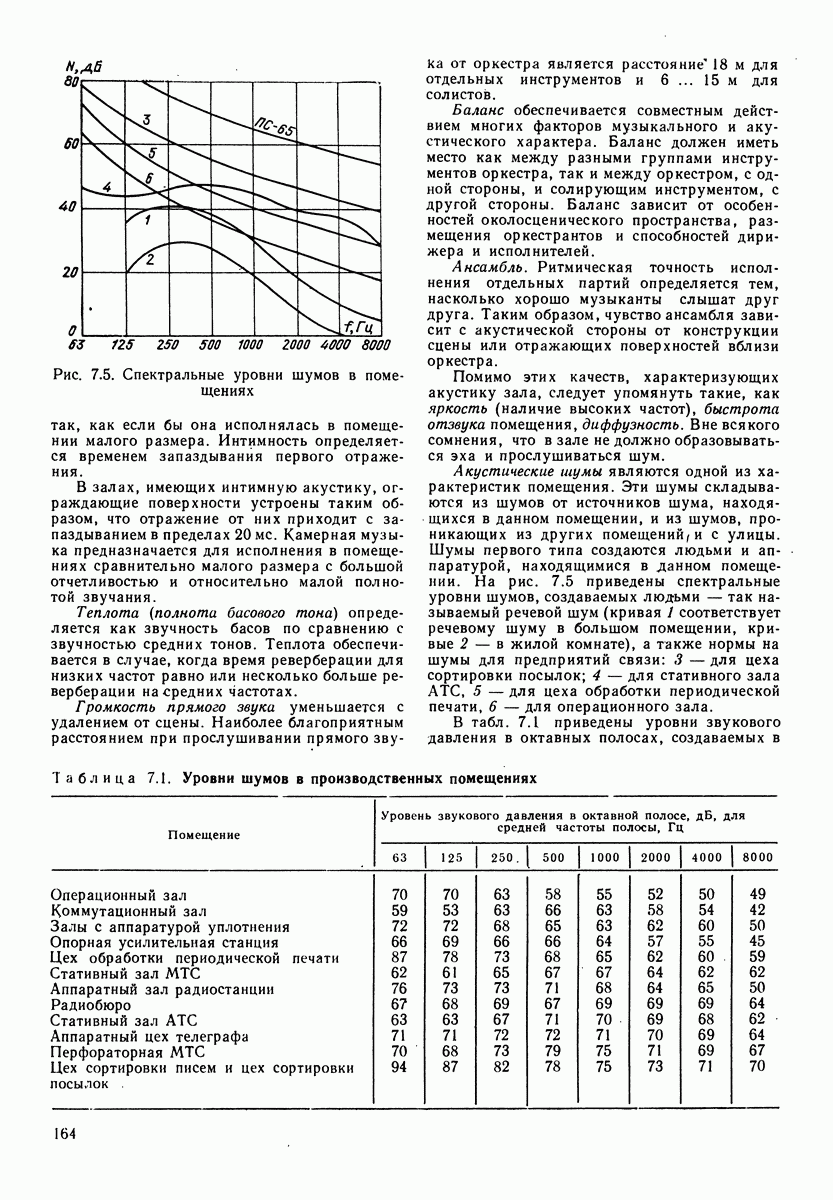
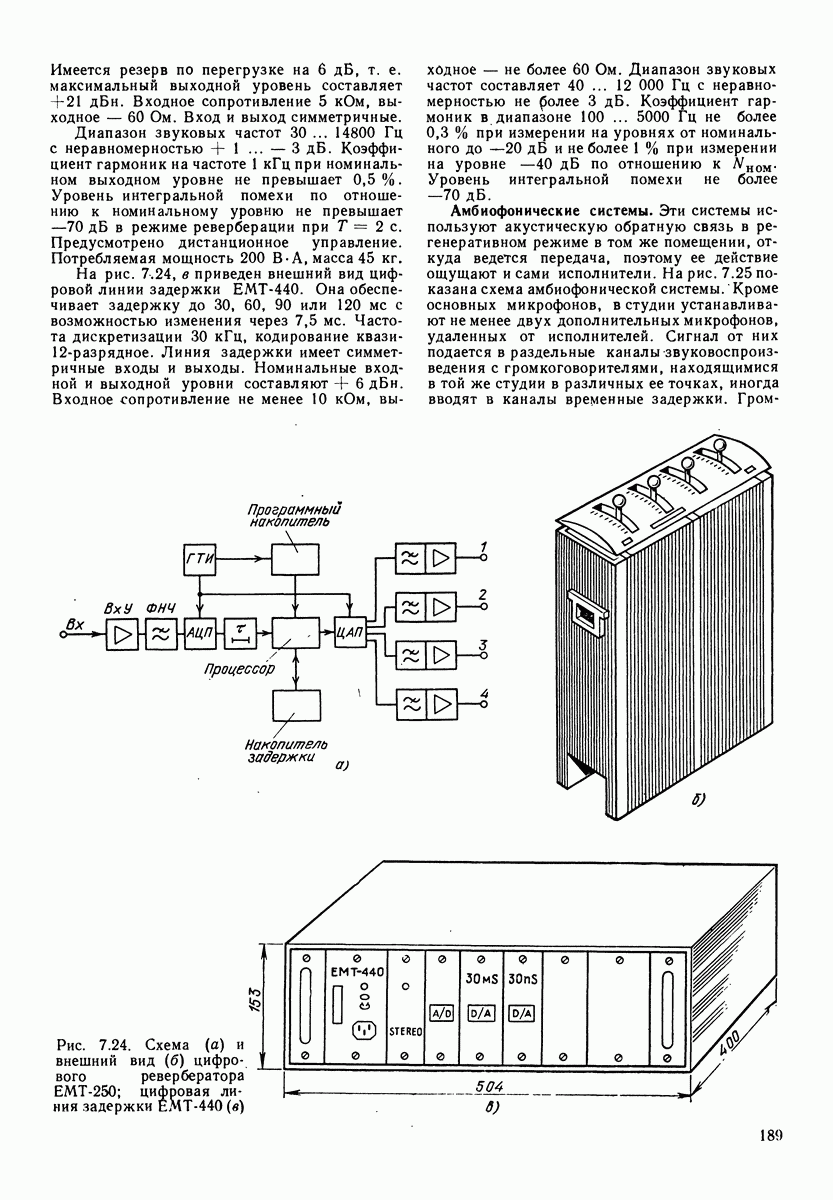
Рис. 3.4. Огибающая спектрального уровня В и третьоктавных уровней  речевого шума
речевого шума
Для резонансного контура  для фильтра с
для фильтра с  -образной характеристикой
-образной характеристикой  где
где  полоса пропускания фильтра на уровне —
полоса пропускания фильтра на уровне — 
В практике часто приходится иметь дело с энергетическим спектром сигнала. Под ним подразумевается огибающая квадратичных значений амплитуд частотных составляющих сигнала (для дискретных спектров) или плотности спектра квадрата амплитуд  (для сплошных спектров). Последняя будет представлять собой спектральную плотность по интенсивности
(для сплошных спектров). Последняя будет представлять собой спектральную плотность по интенсивности  т. е. спектральной плотностью называют интенсивность звука в полосе частот шириной в единицу частоты. В акустике эту полоску берут равой 1 Гц, т. е. спектральная плотность I — где
т. е. спектральной плотностью называют интенсивность звука в полосе частот шириной в единицу частоты. В акустике эту полоску берут равой 1 Гц, т. е. спектральная плотность I — где  интенсивность, измеренная в узкой полоске частот
интенсивность, измеренная в узкой полоске частот  Измерения для этой дели приводят с помощью узкополосных фильтров (обычно третьоктавных). Единица спектральной плотности
Измерения для этой дели приводят с помощью узкополосных фильтров (обычно третьоктавных). Единица спектральной плотности  метр на герц).
метр на герц).
Для удобства введена логарифмическая мера оценки плотности спектра аналогично оценке по уровню интенсивности. Эта мера называется уровнем спектральной плотности или спектральным уровнем. Спектральный уровень  где
где  т. е. то же условное (нормированное) значение, что и для оценки уровня интенсивности, поэтому размерность
т. е. то же условное (нормированное) значение, что и для оценки уровня интенсивности, поэтому размерность  выражается в единице на герц
выражается в единице на герц 
Очень часто для представления спектра вместо спектральной плотности пользуются интенсивностью или звуковым давлением, измеренными в октавной, полуоктавной или третьоктавной полосе частот, и соответственно определяют уровни в этих полосах. В этом случае спектральный уровень  , а уровень в октавной полосе
, а уровень в октавной полосе  где
где  ширина соответствующей октавной полосы. Вычитая первое из второго, имеем
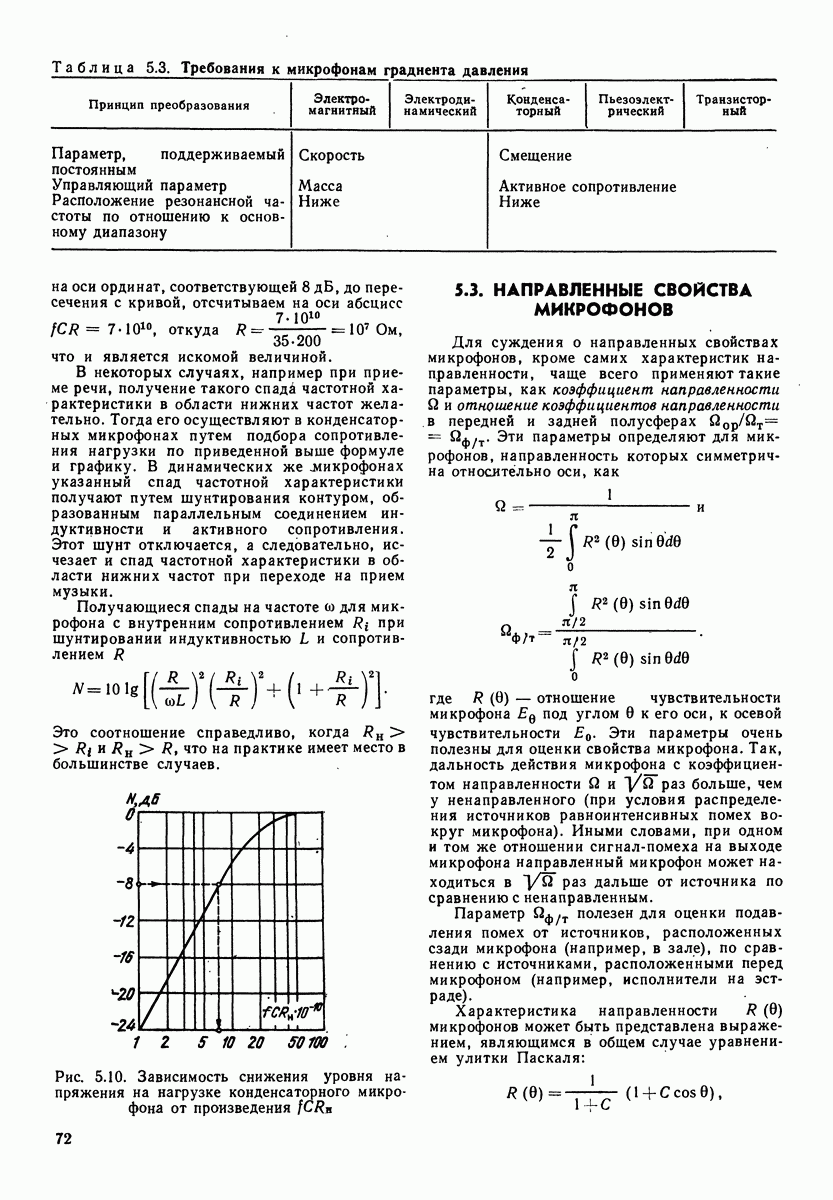
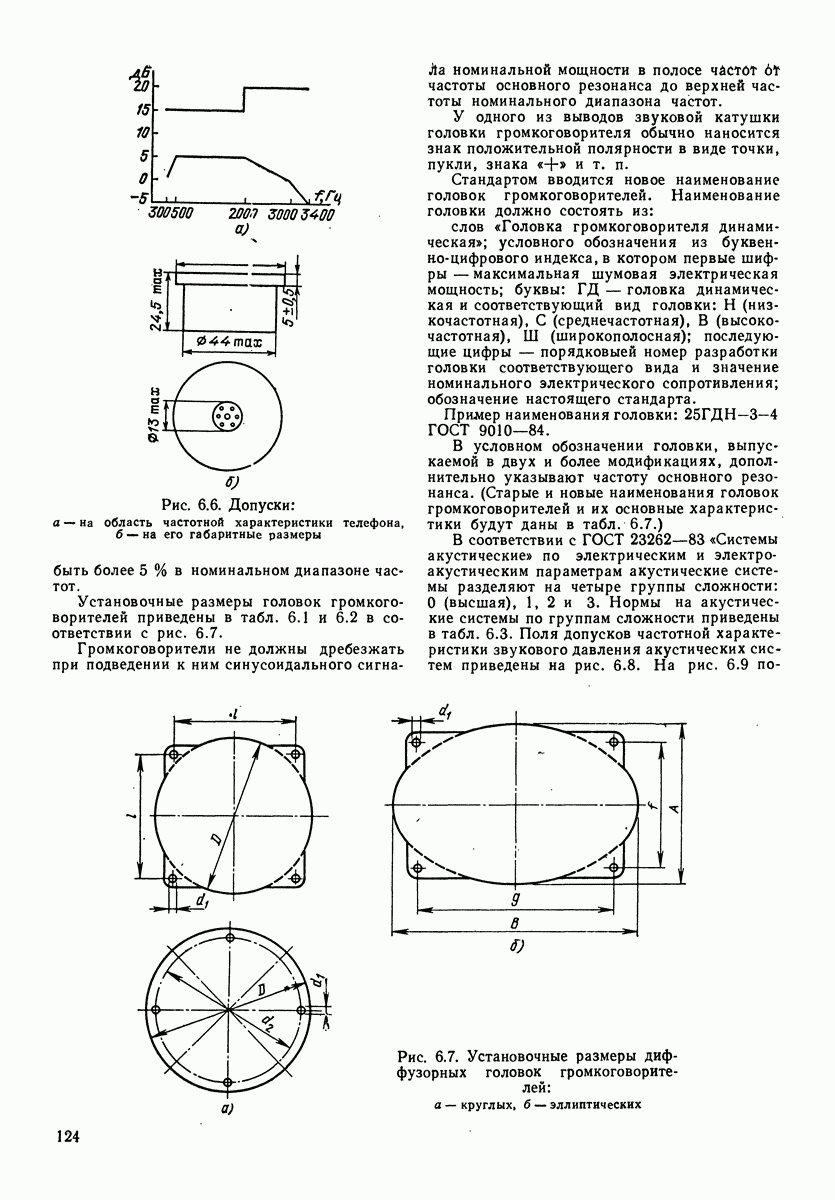
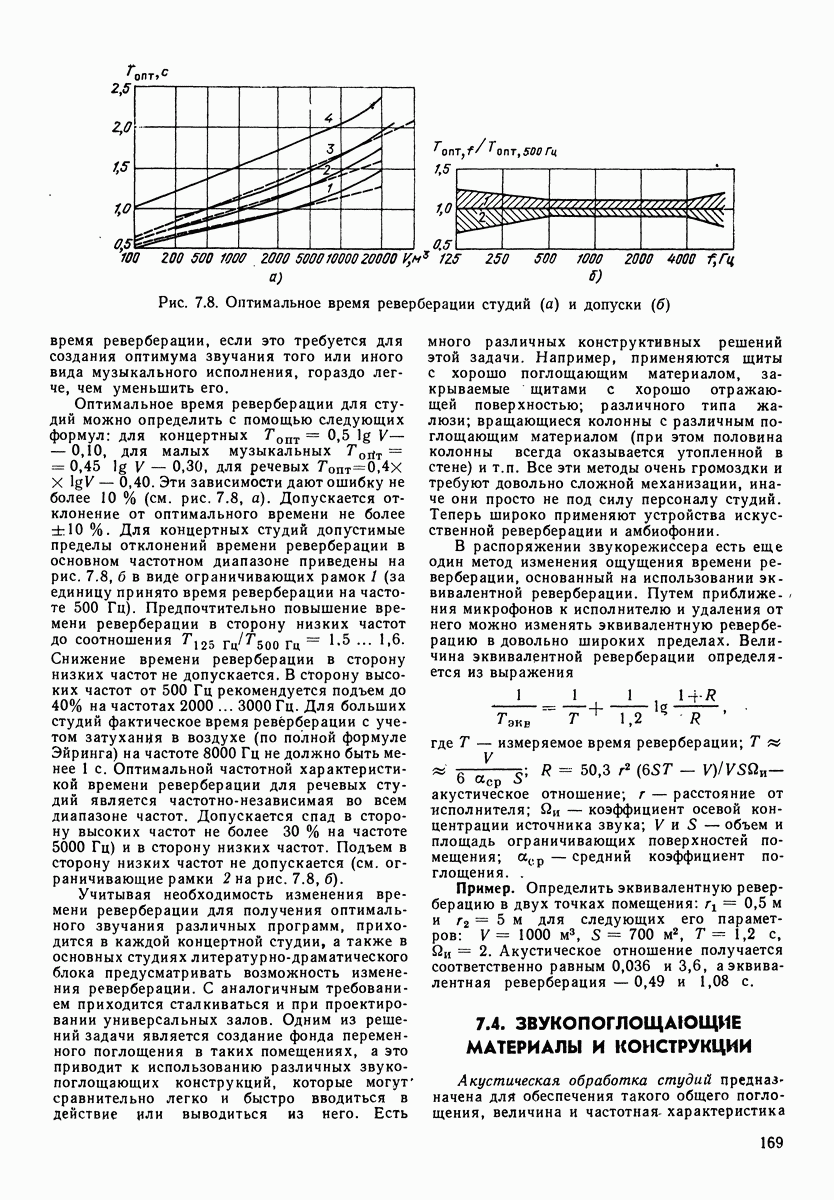
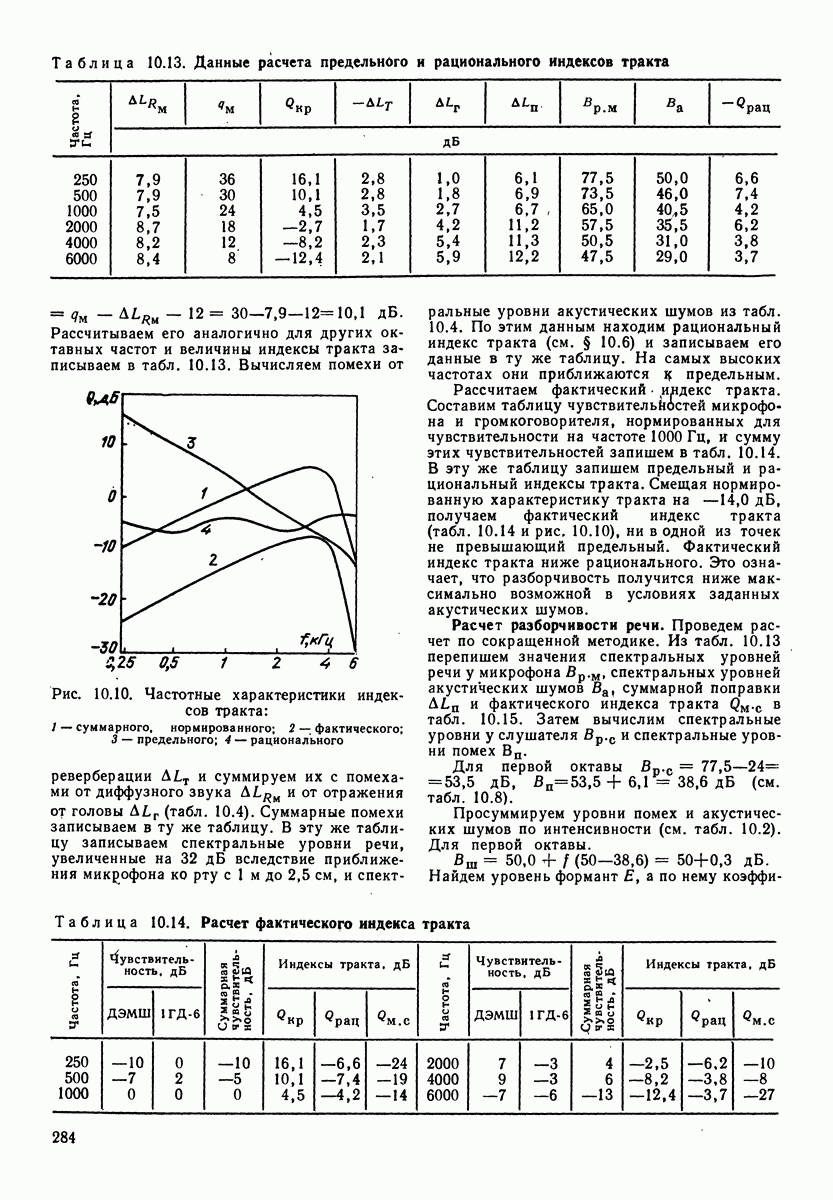
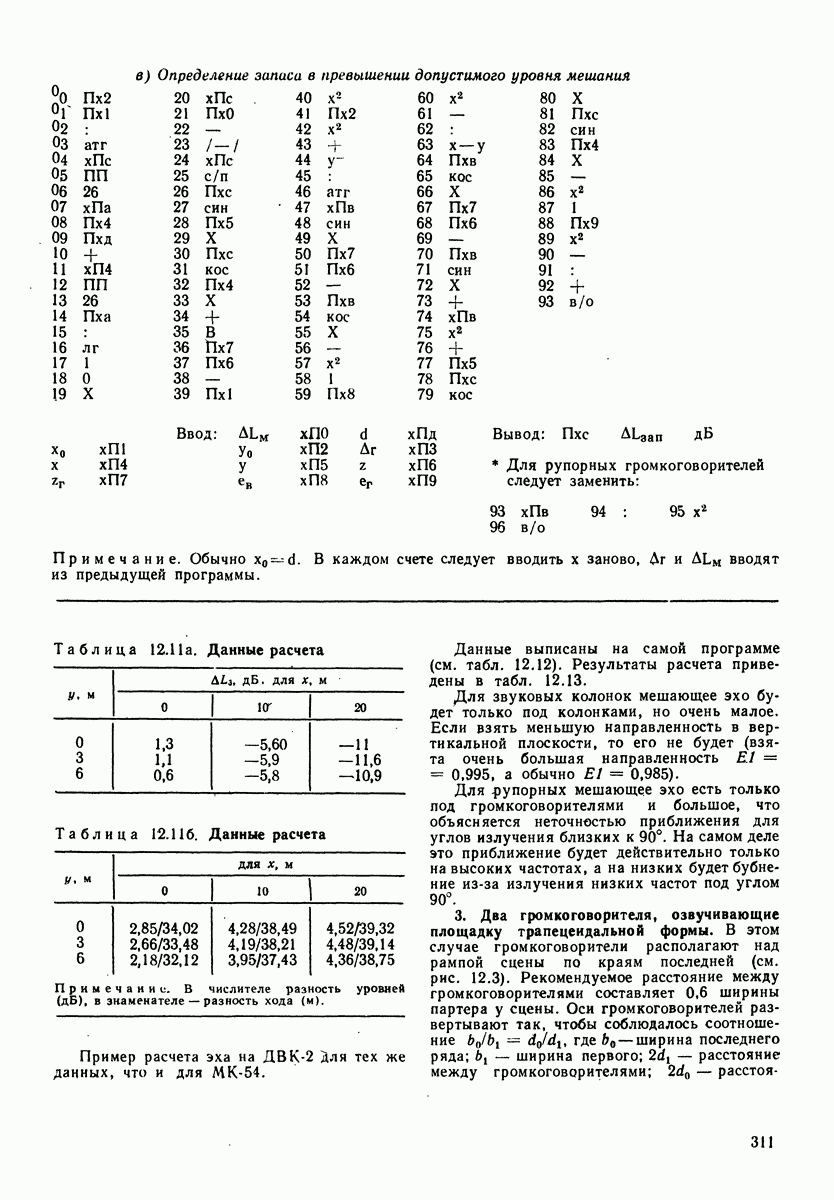
ширина соответствующей октавной полосы. Вычитая первое из второго, имеем  рис. 3.4 приведены огибающие для спектрального уровня и третьоктавных уровней речевого шума.
рис. 3.4 приведены огибающие для спектрального уровня и третьоктавных уровней речевого шума.
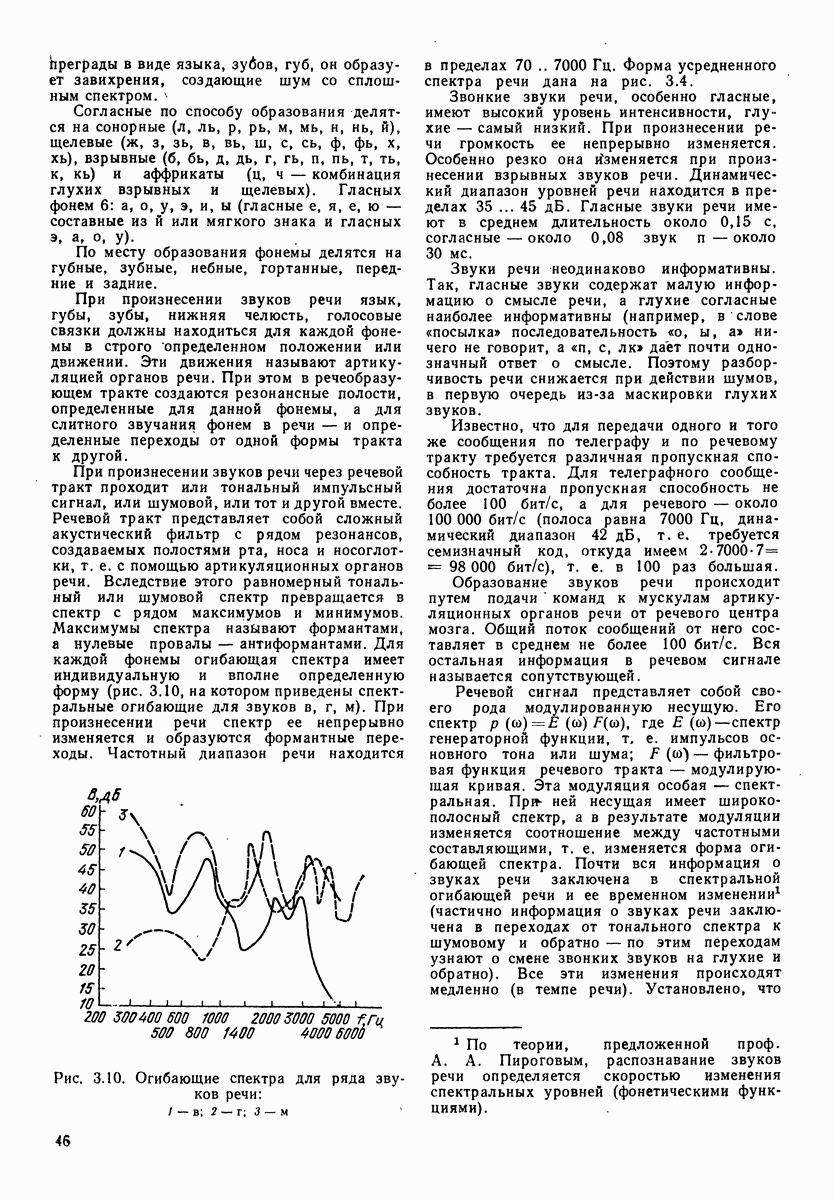
У каждого источника звука, даже того же самого типа, спектры имеют индивидуальные черты, что придает звучанию этих источников, как говорят, характерную окраску. Эта окраска называется тембром. Существуют понятия тембра скрипки, тромбона, органа и т. п., а также спектра голоса: звонкий, когда подчеркнуты высокочастотные составляющие; глухой, когда они подавлены по отношению к среднему голосу. Чаще всего необходимо знать средний спектр для однородных источников звука и усредненный спектр за длительный интервал времени (15 с для информационных сигналов и 1 мин — для
музыкальных). Усредненный спектр можёг быть только сплошным и достаточно сглаженным по форме. Такие сплошные спектры хорошо характеризуются зависимостью спектральной плотности от частоты и вероятностью появления уровня в октавной полосе.
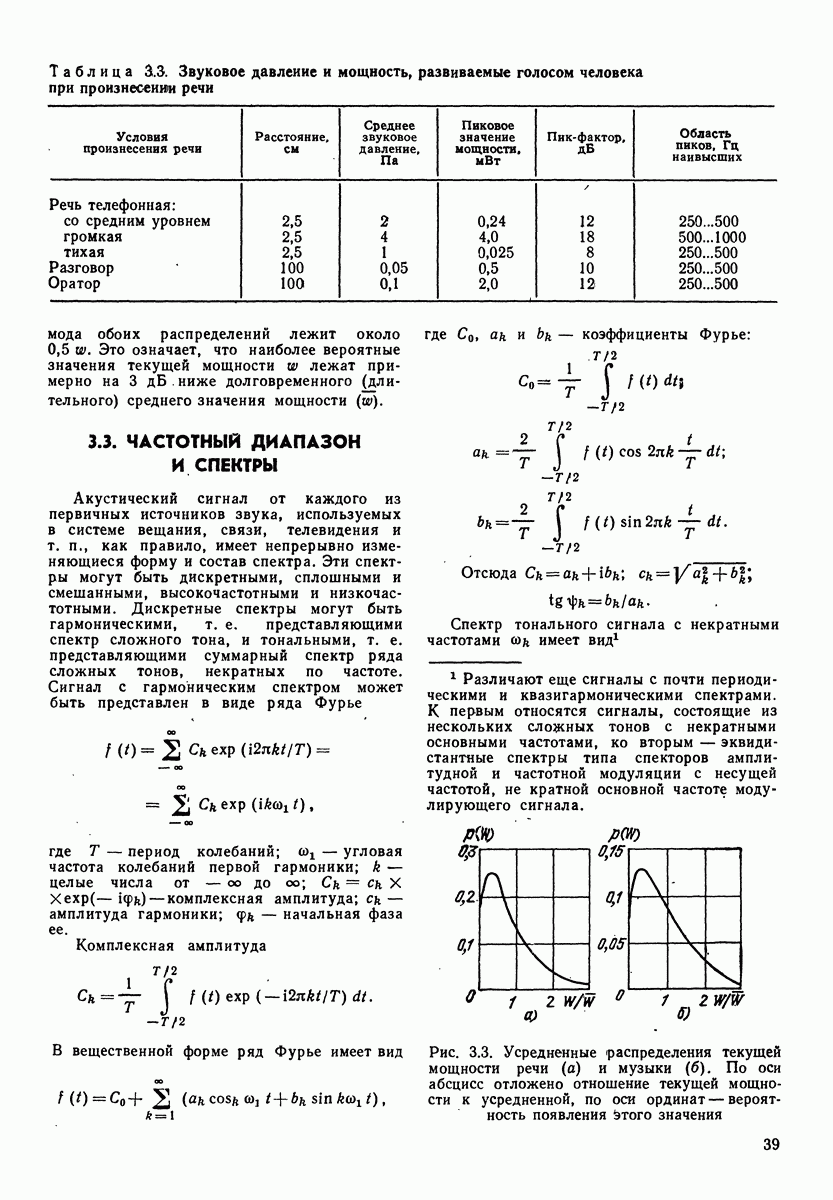
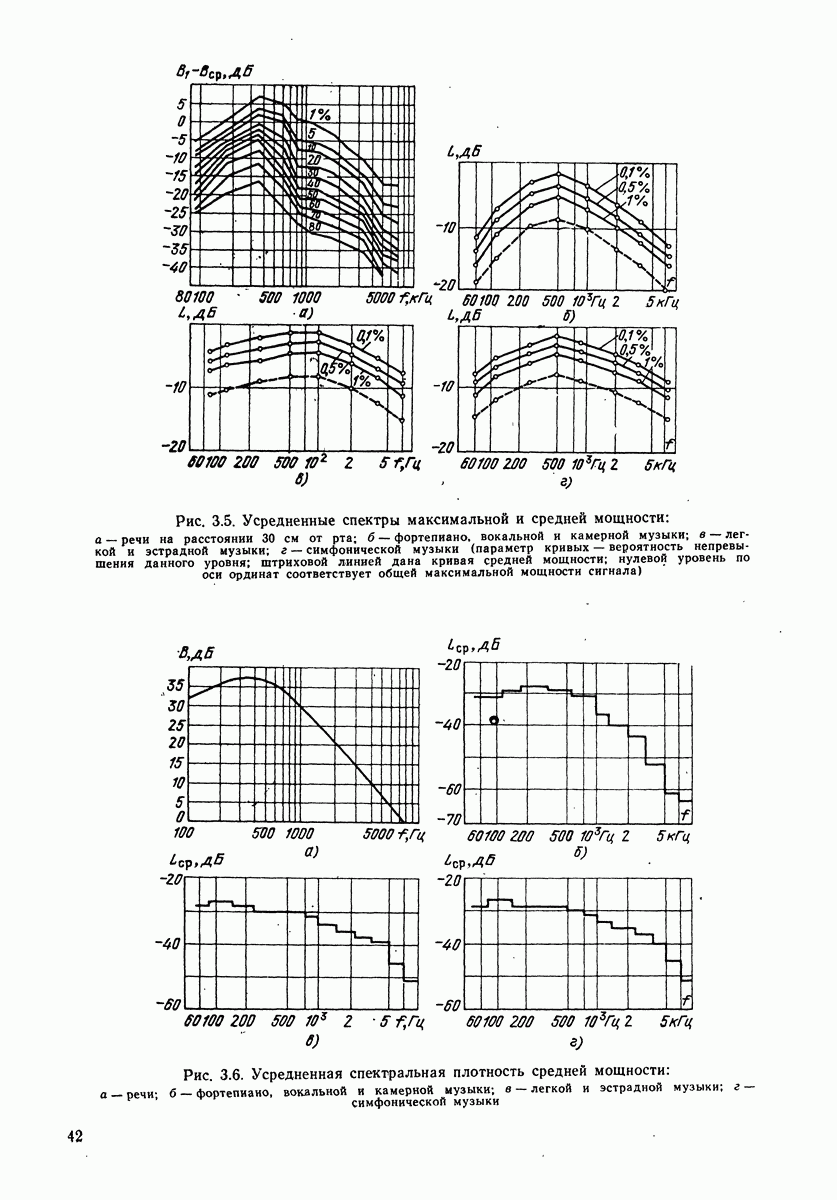
На рис. 3.5 приведены усредненные спектры максимальной мощности для различных значений вероятности появления заданных уровней в октавных полосах, там же приведены средние спектры. Эти спектры даны для речи и различных музыкальных звучаний. На рис. 3.6 приведены усредненные частотные распределения (спектральные плотности) средней мощности для речи и ряда музыкальных звучаний.
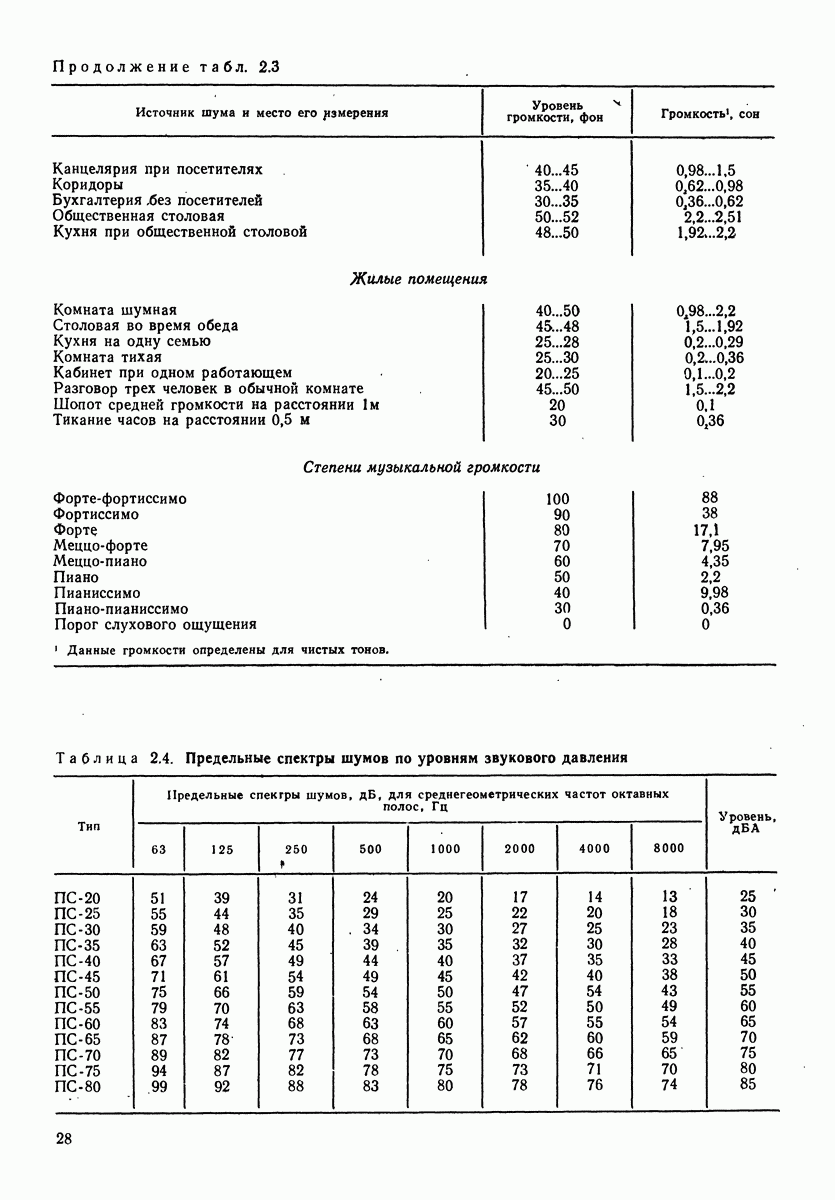
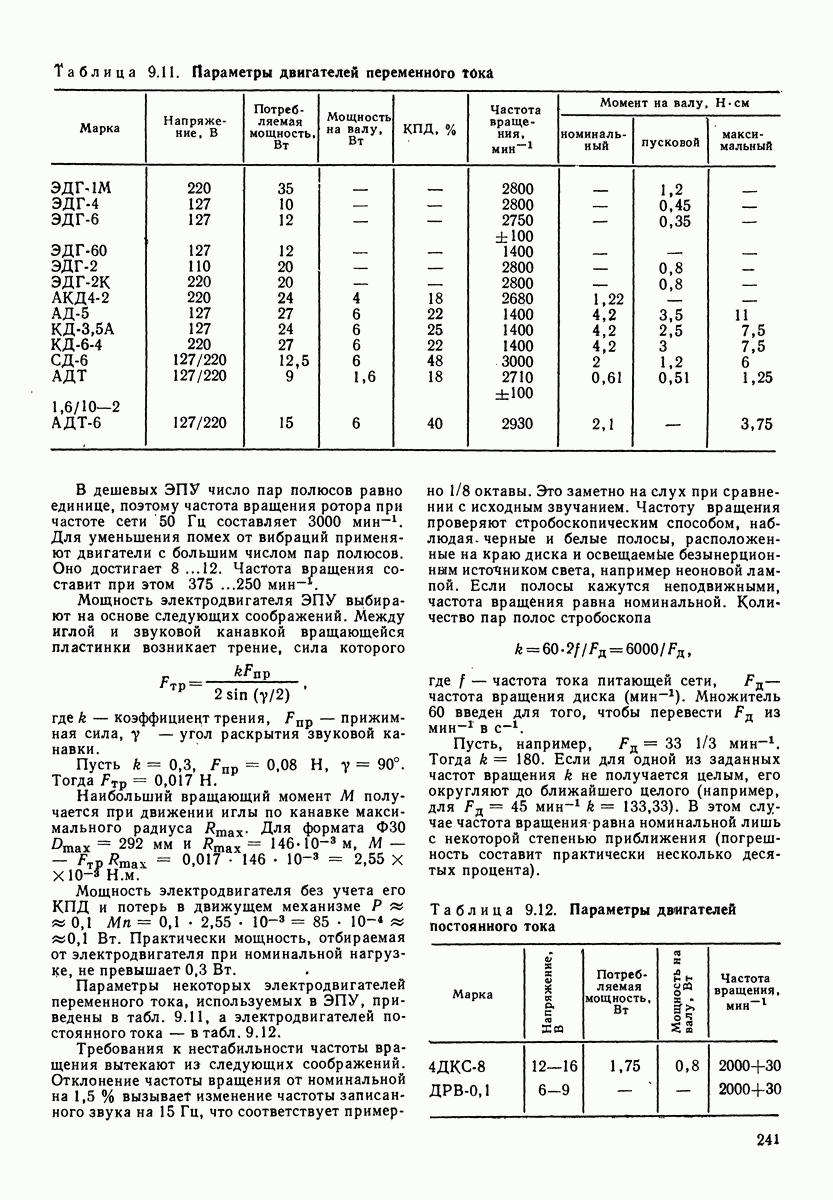
В табл. 3.2 и 3.3 даны акустические мощности в пределах полосы с максимальным уровнем.
Пример. Определить, какова вероятность появления уровня речи на  ниже пикового на расстоянии 30 см от рта в полуоктавной полосе частот около 1000 Гц. Из рис. 3.5, а для частоты 1000 Гц и уровня
ниже пикового на расстоянии 30 см от рта в полуоктавной полосе частот около 1000 Гц. Из рис. 3.5, а для частоты 1000 Гц и уровня  находим точку, лежащую около кривой
находим точку, лежащую около кривой  Следовательно, вероятность появления уровней выше
Следовательно, вероятность появления уровней выше  в этой полосе составляет
в этой полосе составляет 
Когда спектры имеют спад в ту или иную сторону, то их оценивают тенденцией т. е. средним наклоном спектральной кривой в сторону низких или высоких частот.. Так, речевой спектр в диапазоне выше 500 Гц оценивают тенденцией спектра в  (спад в сторону высоких частот).
(спад в сторону высоких частот).
Если известны спектральные или октавные уровни сигнала, то можно оцределить его суммарный уровень. Если спектр задан в форме уровней в октавных (третьоктавных или полуоктавных) полосах, то достаточно перевести эти уровни (в каждой из полос) в относительные интенсивности  и затем просуммировать все эти интенсивности, а по суммарной интенсивности для всего спектра найти суммарный уровень
и затем просуммировать все эти интенсивности, а по суммарной интенсивности для всего спектра найти суммарный уровень 
Пример. Заданы уровни в октавных полосах, найти суммарный уровень.

Суммарный уровень  Этот уровень можно найти с помощью программируемого микрокалькулятора, как показано в 1.4.
Этот уровень можно найти с помощью программируемого микрокалькулятора, как показано в 1.4.
Если заданы спектральные уровни сплошного спектра, то точное значение суммарного уровня для всего спектра определится интегралом

где  верхняя и нижняя границы частотного диапазона.
верхняя и нижняя границы частотного диапазона.
Пример. Задан равномерный спектр, соответствующий рис. 3.8. Спектральный уровень равен  Гц. Соответственно имеем
Гц. Соответственно имеем

в то время как для составляющей около 100 Гц уровень в частотной группе (см. рис. 2.3) равен  а в самой верхней группе (12 000 —15 500 Гц) он составляет (см. рис. 2.3)
а в самой верхней группе (12 000 —15 500 Гц) он составляет (см. рис. 2.3)  Суммарный уровень можно приближенно найти путем деления частотного диапазона на
Суммарный уровень можно приближенно найти путем деления частотного диапазона на  полосок
полосок  в пределах каждой из которых спектральный уровень
в пределах каждой из которых спектральный уровень  примерно постоянен. Суммарный уровень
примерно постоянен. Суммарный уровень

Пример. В табл. 3.4 приведены спектральные уровни для речевого сигнала на средних частотах третьоктавных полос, там же дана ширина третьоктавных полос в  (см. табл. 2.2). Складывая спектральные уровни с шириной полосы, получаем уровни в треть-» октавных полосах (графа 3 в табл. 3.4) Переводя их в интенсивности, получаем интенсивности в относительных единицах для каждой полосы частот (графа 4 в табл. 3.4). Например, для пятой строки имеем: спектральный уровень
(см. табл. 2.2). Складывая спектральные уровни с шириной полосы, получаем уровни в треть-» октавных полосах (графа 3 в табл. 3.4) Переводя их в интенсивности, получаем интенсивности в относительных единицах для каждой полосы частот (графа 4 в табл. 3.4). Например, для пятой строки имеем: спектральный уровень  ширина полосы
ширина полосы  на
на  уровень в третьоктавной полосе
уровень в третьоктавной полосе  откуда интенсивность в этой полосе
откуда интенсивность в этой полосе  отн.
отн.  Проделывая эти расчеты для всех полос, суммируем интенсивности в полосах, получаем общую интенсивность
Проделывая эти расчеты для всех полос, суммируем интенсивности в полосах, получаем общую интенсивность  Следовательно, общий уровень будет
Следовательно, общий уровень будет 
Частотный диапазон акустического сигнала определяют из кривой спектральных уровней. Но так как нет четких определений границы частотного диапазона, то  определение можно сделать только приближенно на слух. Считают такими границам» заметность ограничения диапазона для
определение можно сделать только приближенно на слух. Считают такими границам» заметность ограничения диапазона для  слушателей На рис. 3,7 показаны частотные
слушателей На рис. 3,7 показаны частотные

(кликните для просмотра скана)

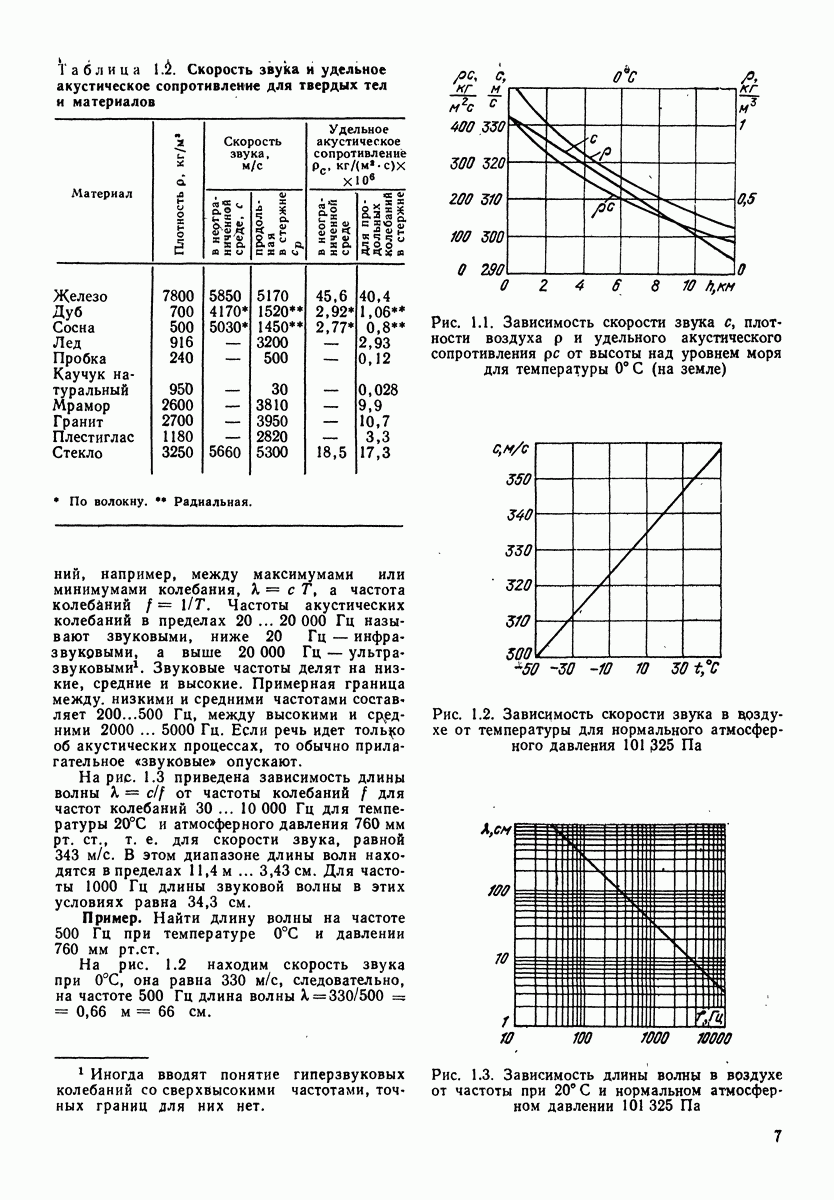
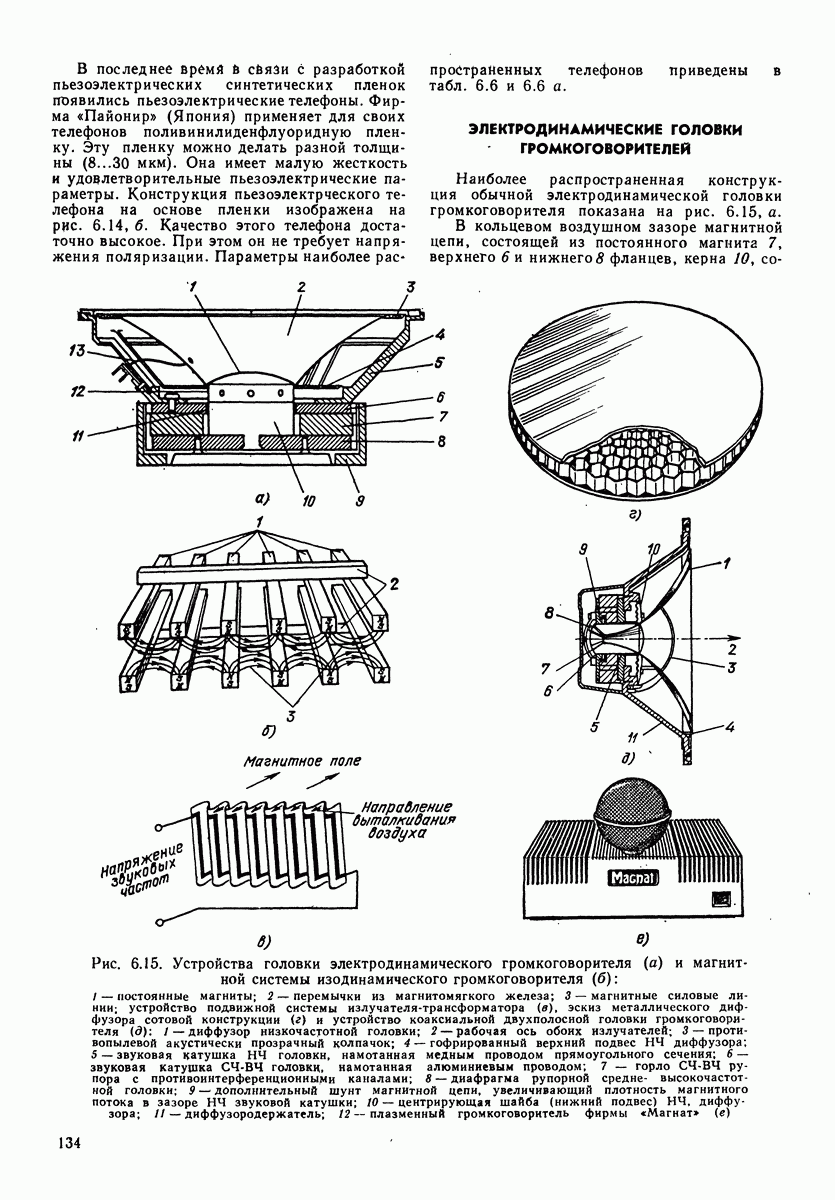
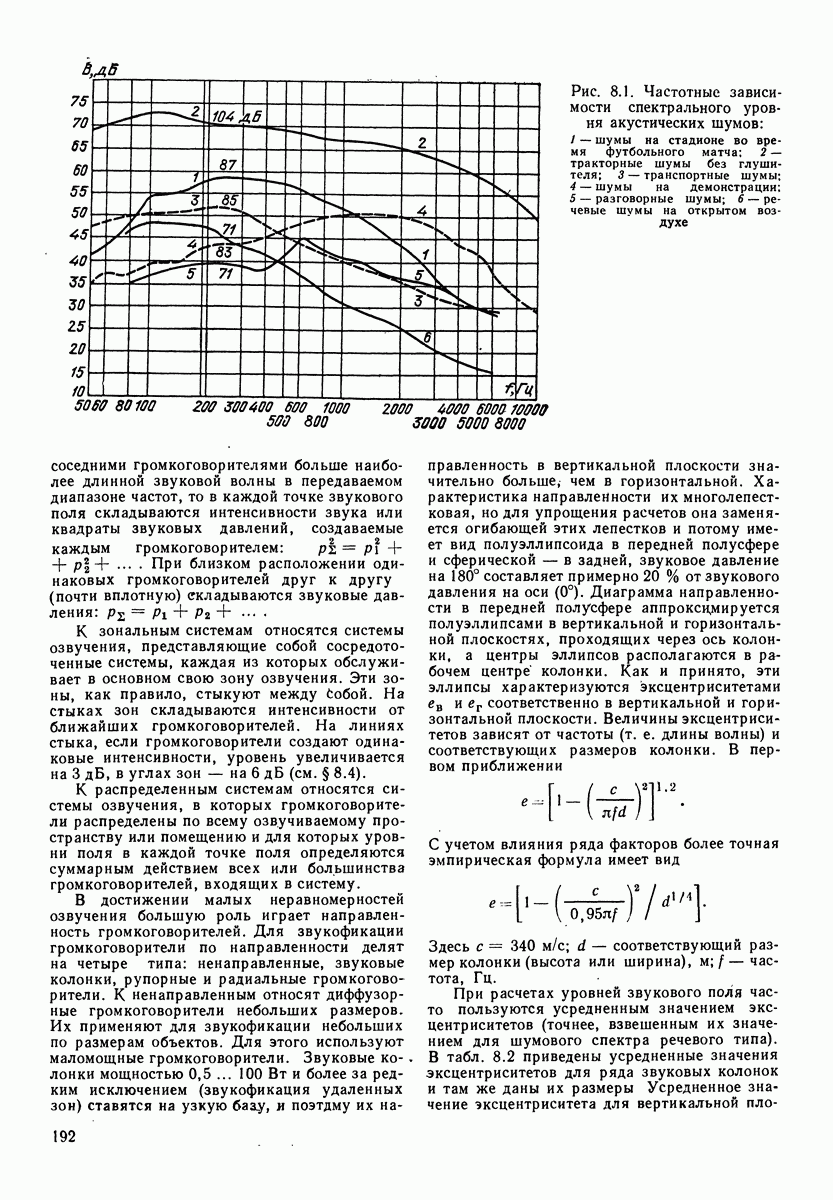
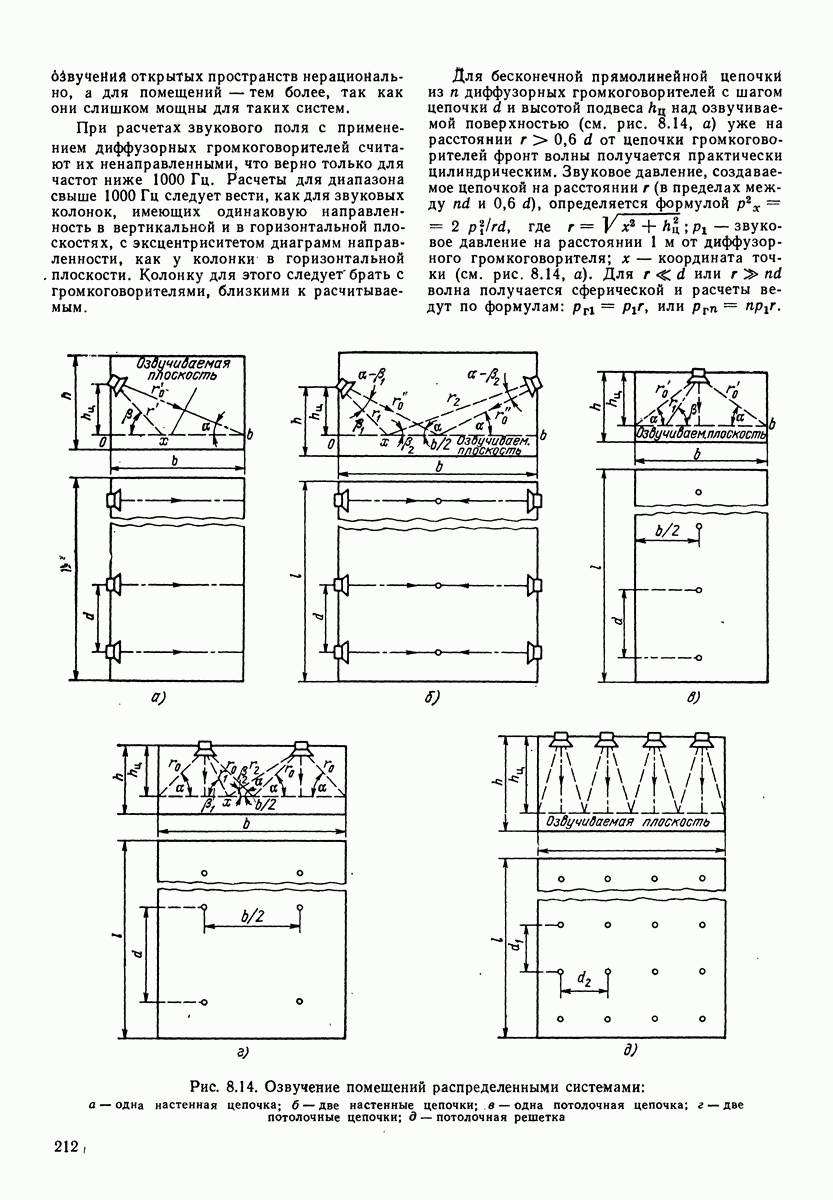
Рис. 3.7. Частотные диапазоны первичных источников звука
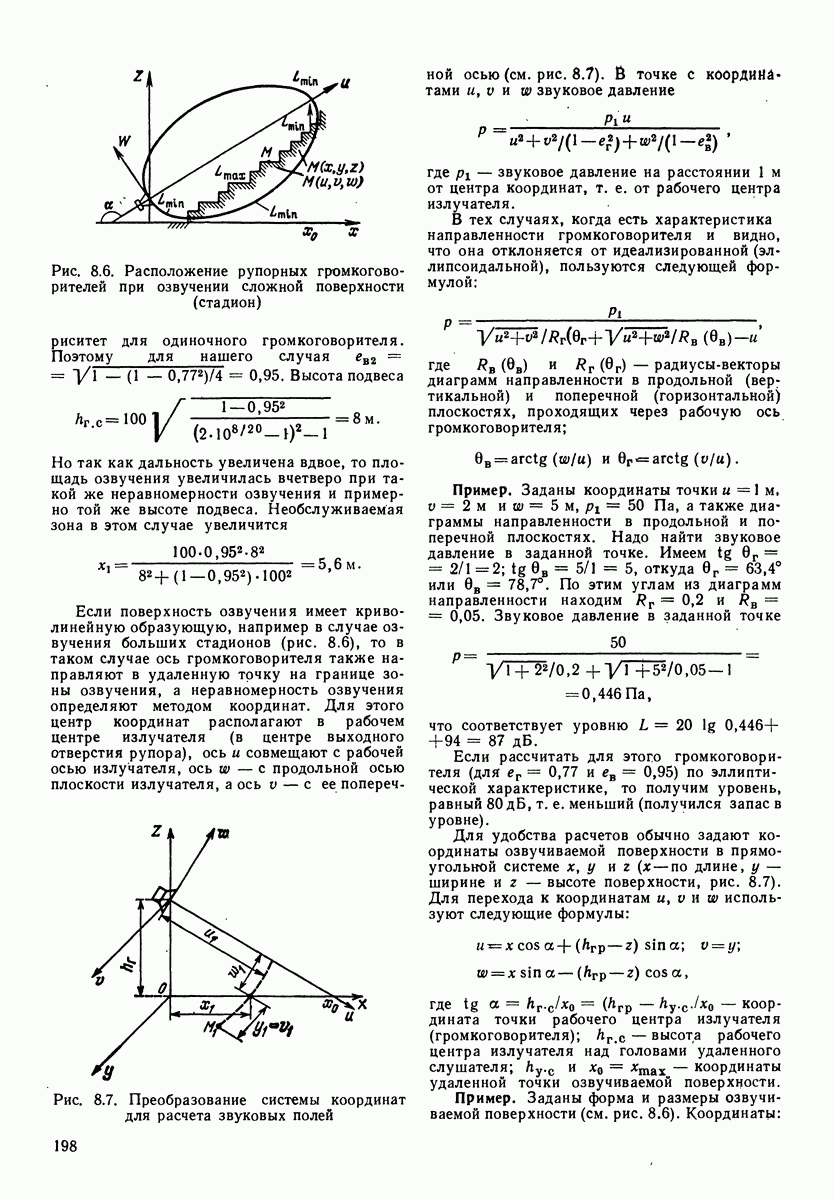
Таблица 3.4. (см. скан) Данные примера расчета суммарного уровня

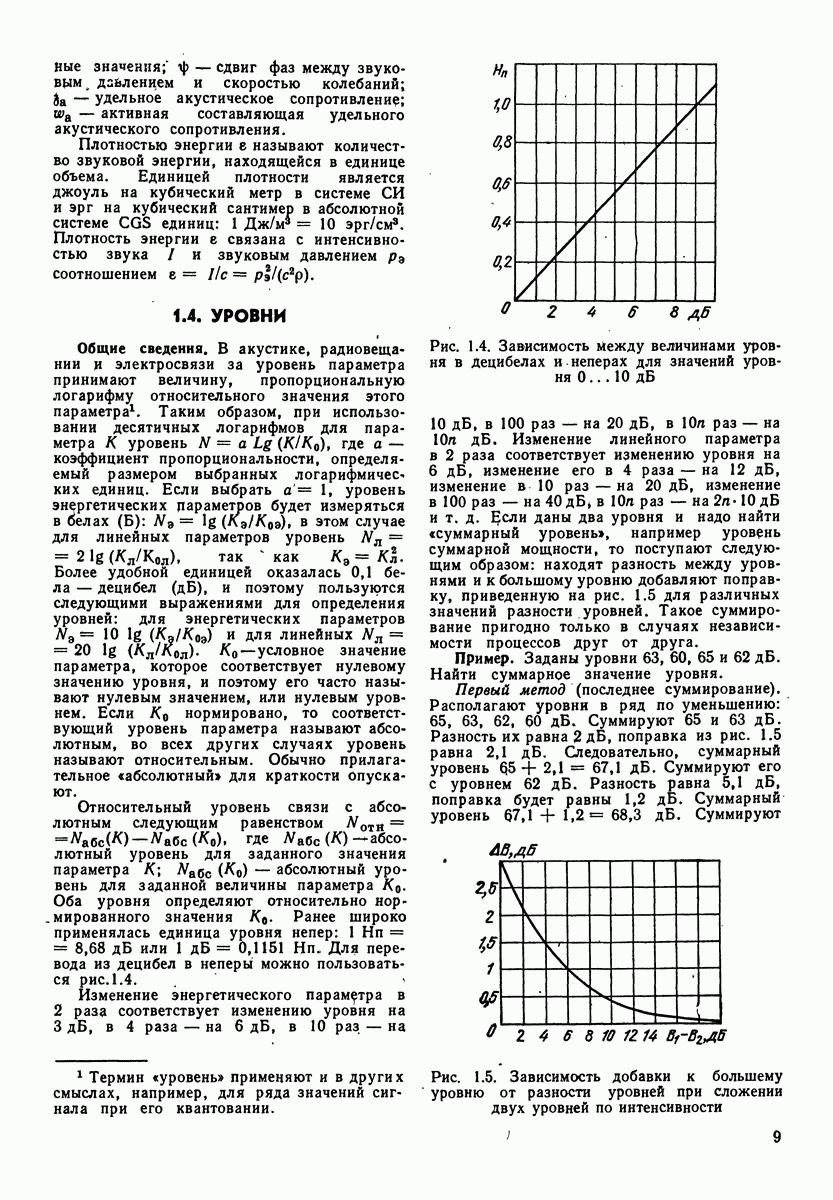
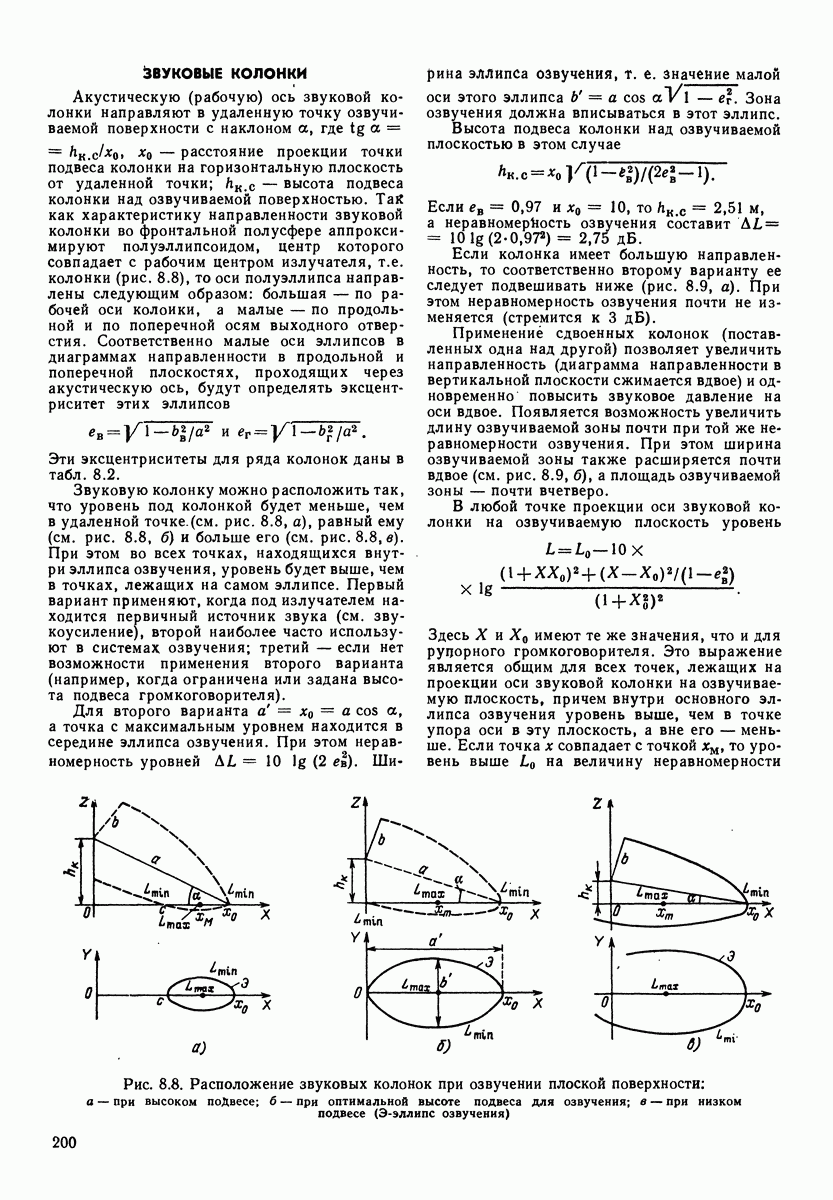
Рис. 3.8. Спектральные уровни некоторых шумов: 1 — белого; 2 — розового; 3 — речевого. На графике показан суммарный уровень для каждого типа шума
диапазоны для ряда первичных источников звука, в том числе и для речи.
Как видим, весь оркестр имеет широкополосный спектр, Флейта-пикколо и труба имеют соответственно высокочастотный и низкочастотный спектры.
Акустические шумы могут рассматриваться и как акустические сигналы, и как помехи. На рис. 3.8 приведены три типа шумов: белые, розовые и речевые. Термин «белые» относится к шумам, имеющим одинаковую спектральную плотность во всем частотном диапазоне. Термин «розовые» относится к шумам, имеющим тенденцию спйда на  в сторону высоких частот. Речевые шумы — шумы, создаваемые одновременным разговором нескольких человек.
в сторону высоких частот. Речевые шумы — шумы, создаваемые одновременным разговором нескольких человек.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ 1. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- 1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ ЗВУКОВОГО ПОЛЯ
- 1.3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВУКОВОГО ПОЛЯ
- 1.4. УРОВНИ
- 1.5. ПЛОСКАЯ ВОЛНА
- 1.6. СФЕРИЧЕСКАЯ ВОЛНА
- 1.7. ЦИЛИНДРИЧЕСКАЯ ВОЛНА
- 1.8. ИНТЕРФЕРЕНЦИЯ ВОЛН
- 1.9. ОТРАЖЕНИЕ ЗВУКА
- 1.10. ПРЕЛОМЛЕНИЕ ЗВУКА
- 1.11. ДИФРАКЦИЯ ВОЛН
- 1.12. ЗАТУХАНИЕ ВОЛН
- 1.13. РАСПРОСТРАНЕНИЕ ЗВУКА В ТРУБАХ
- Раздел 2. ОСНОВНЫЕ СВОЙСТВА СЛУХА
- 2.2. ВОСПРИЯТИЕ ПО ЧАСТОТЕ
- 2.3. ВОСПРИЯТИЕ ПО АМПЛИТУДЕ
- 2.4. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЛУХА
- 2.5. ВОСПРИЯТИЕ ИМПУЛЬСОВ
- 2.6. НЕЛИНЕЙНЫЕ СВОЙСТВА СЛУХА
- 2.7. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- РАЗДЕЛ 3. ПЕРВИЧНЫЕ АКУСТИЧЕСКИЕ СИГНАЛЫ И ИХ ИСТОЧНИКИ
- 3.2. ДИНАМИЧЕСКИЙ ДИАПАЗОН И УРОВНИ
- 3.3. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
- 3.4. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ АКУСТИЧЕСКОГО СИГНАЛА
- 3.5. ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ РЕЧИ ВОКРУГ ГОЛОВЫ
- 3.6. ПЕРВИЧНЫЙ РЕЧЕВОЙ СИГНАЛ
- 3.7. ГОРТАНЬ КАК ИСТОЧНИК ЗВУКОВЫХ КОЛЕБАНИЙ
- РАЗДЕЛ 4. ЭЛЕКТРОАКУСТИЧЕСКИЕ ЭЛЕМЕНТЫ И СИСТЕМЫ
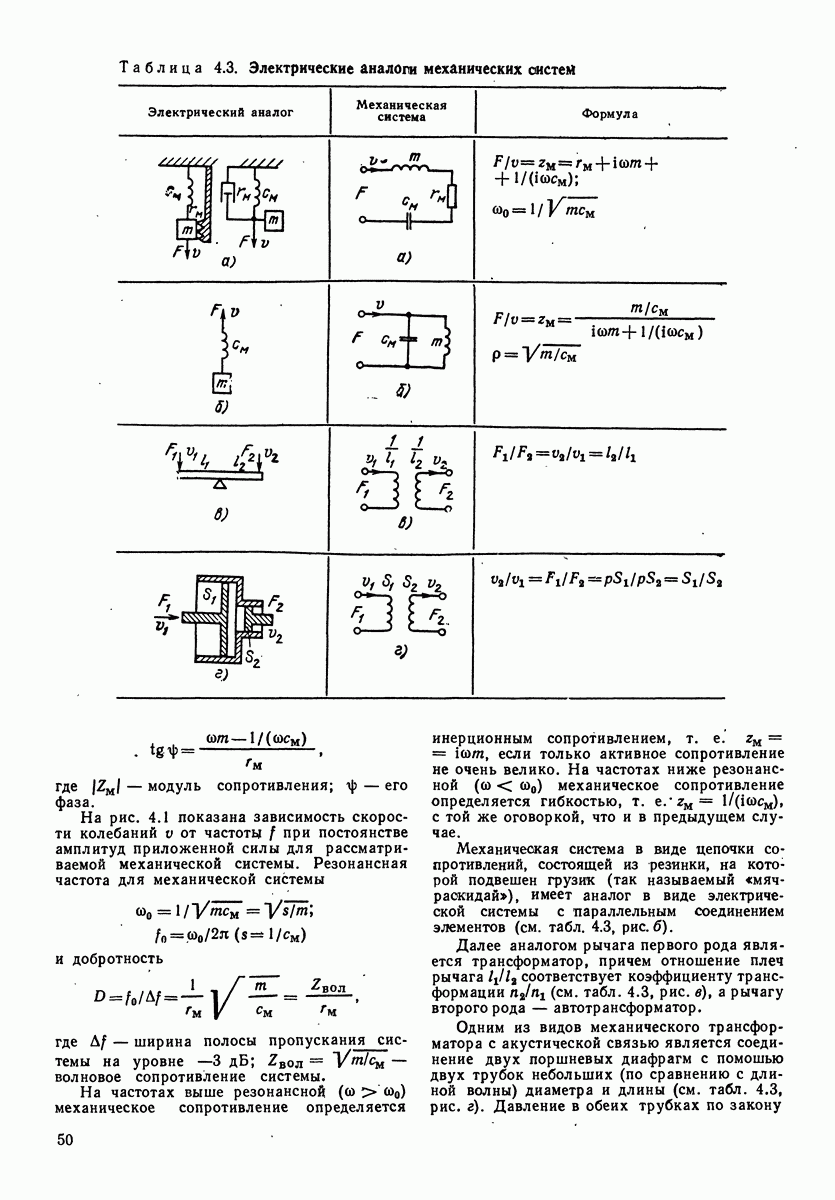
- 4.2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИ
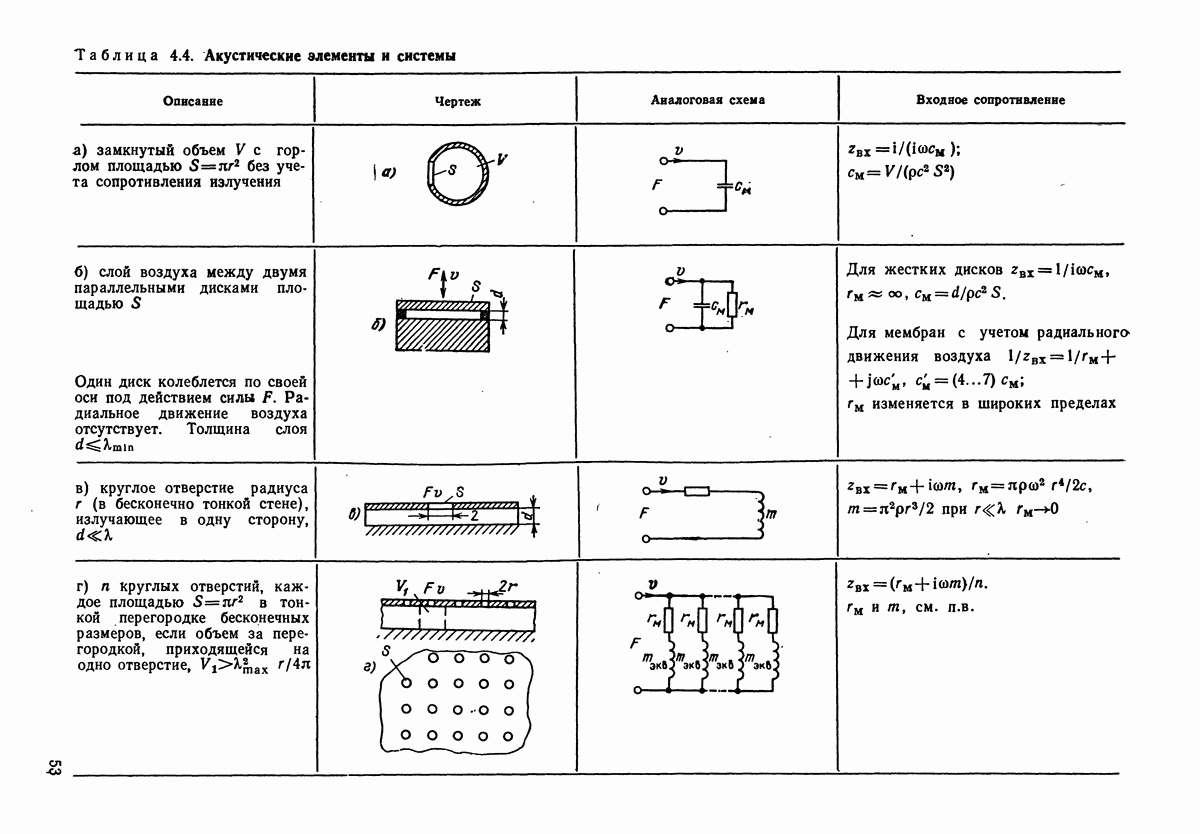
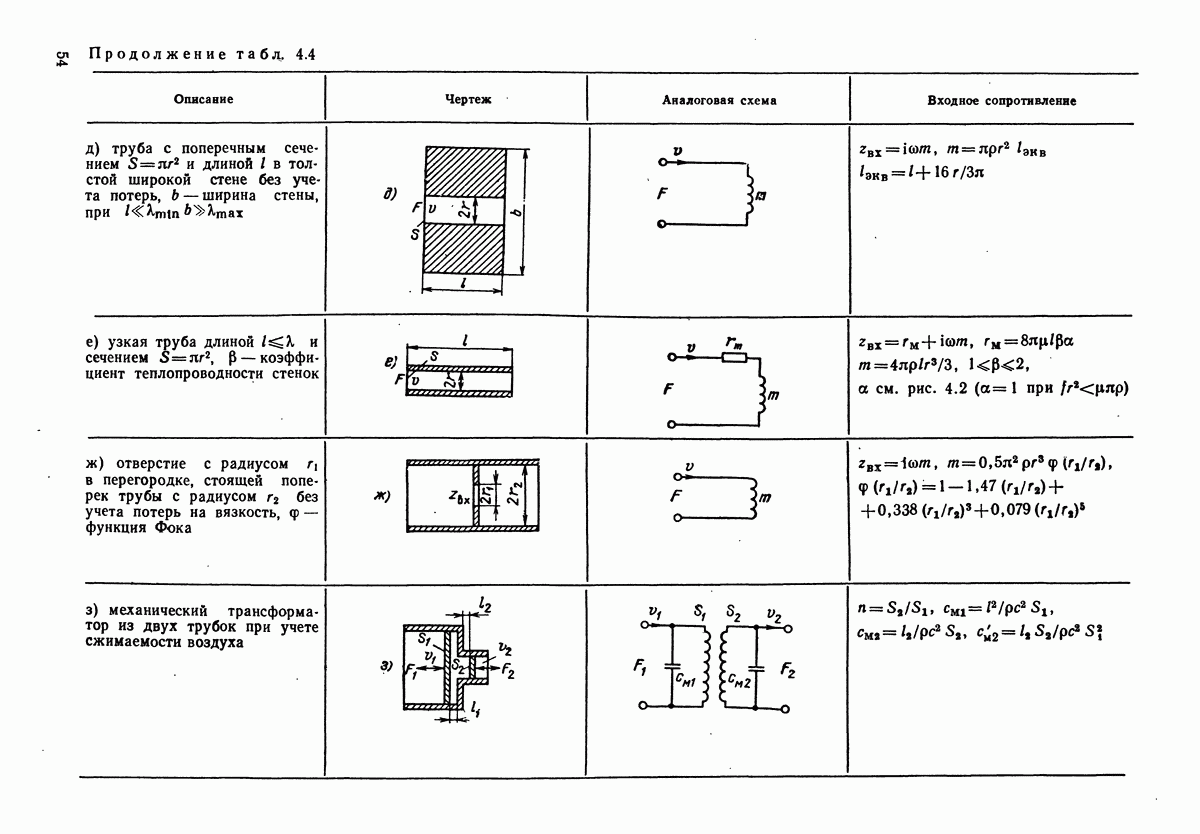
- 4.3. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 4.4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4.5. МЕТОДЫ СОСТАВЛЕНИЯ АНАЛОГОВЫХ СХЕМ
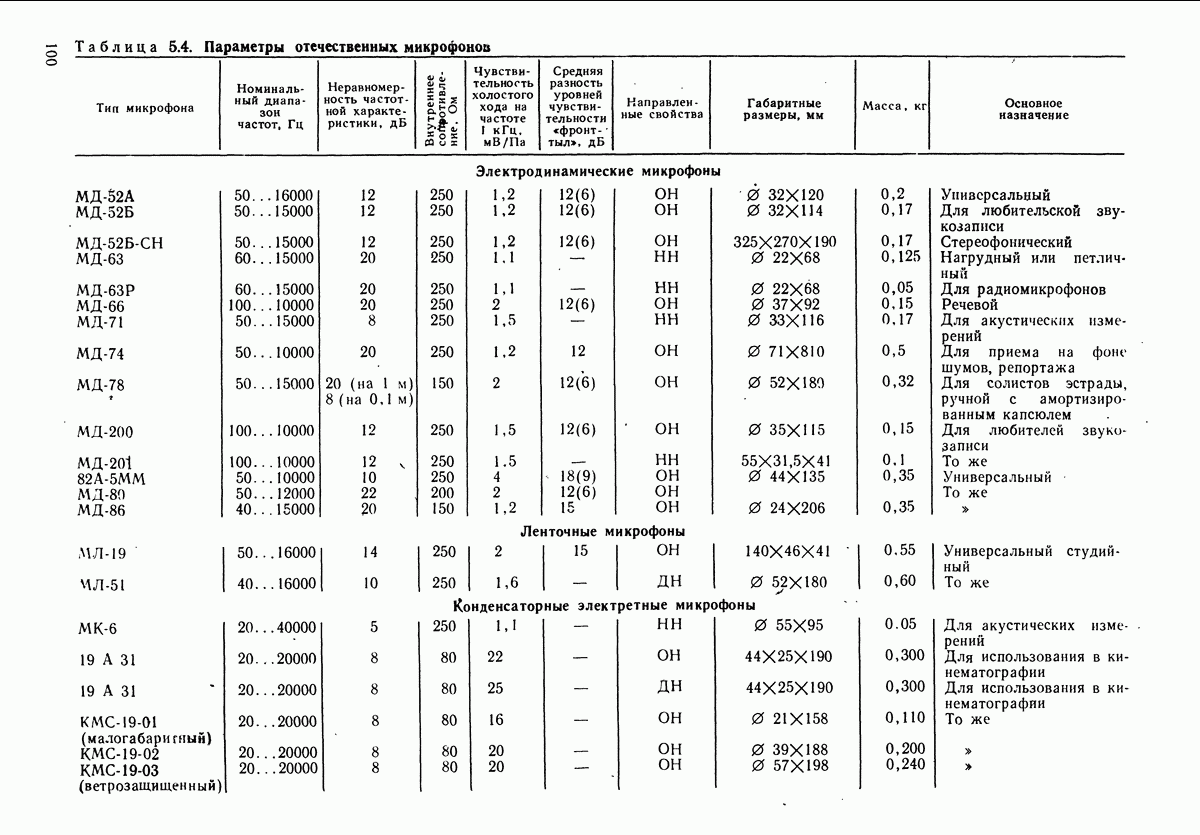
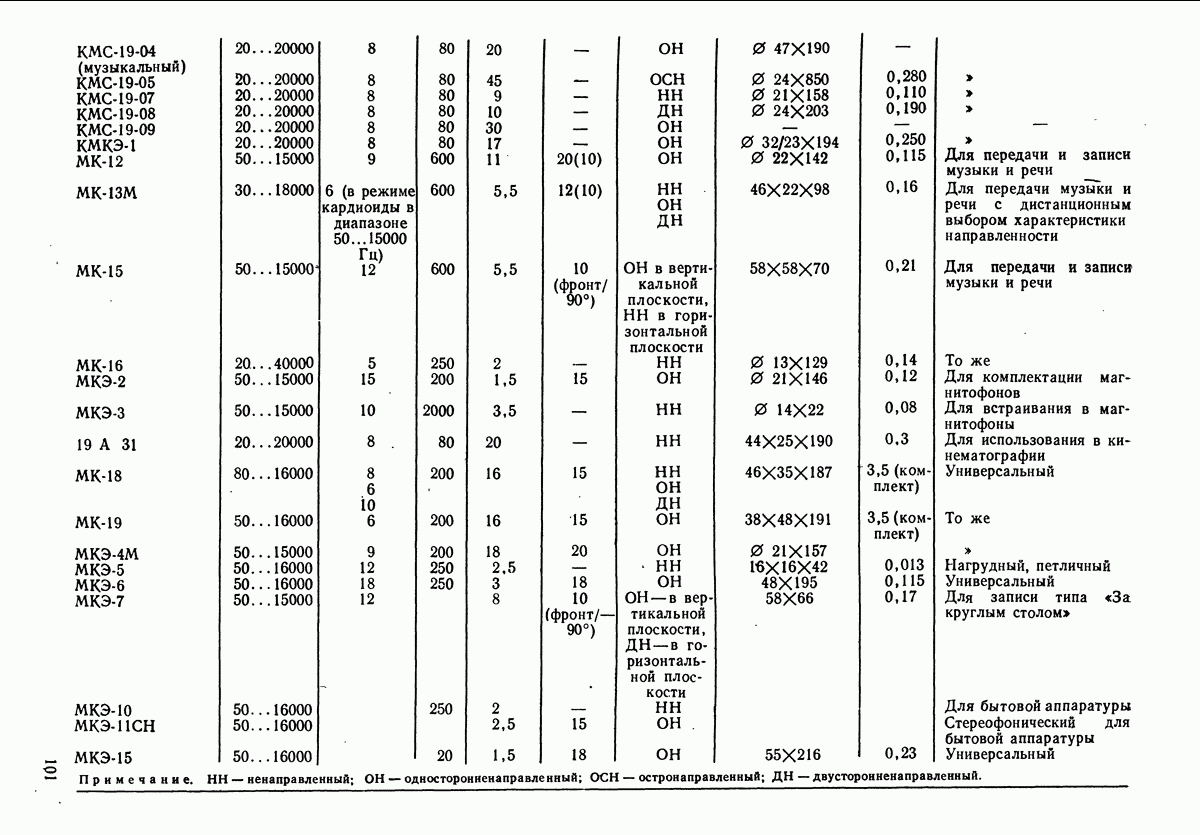
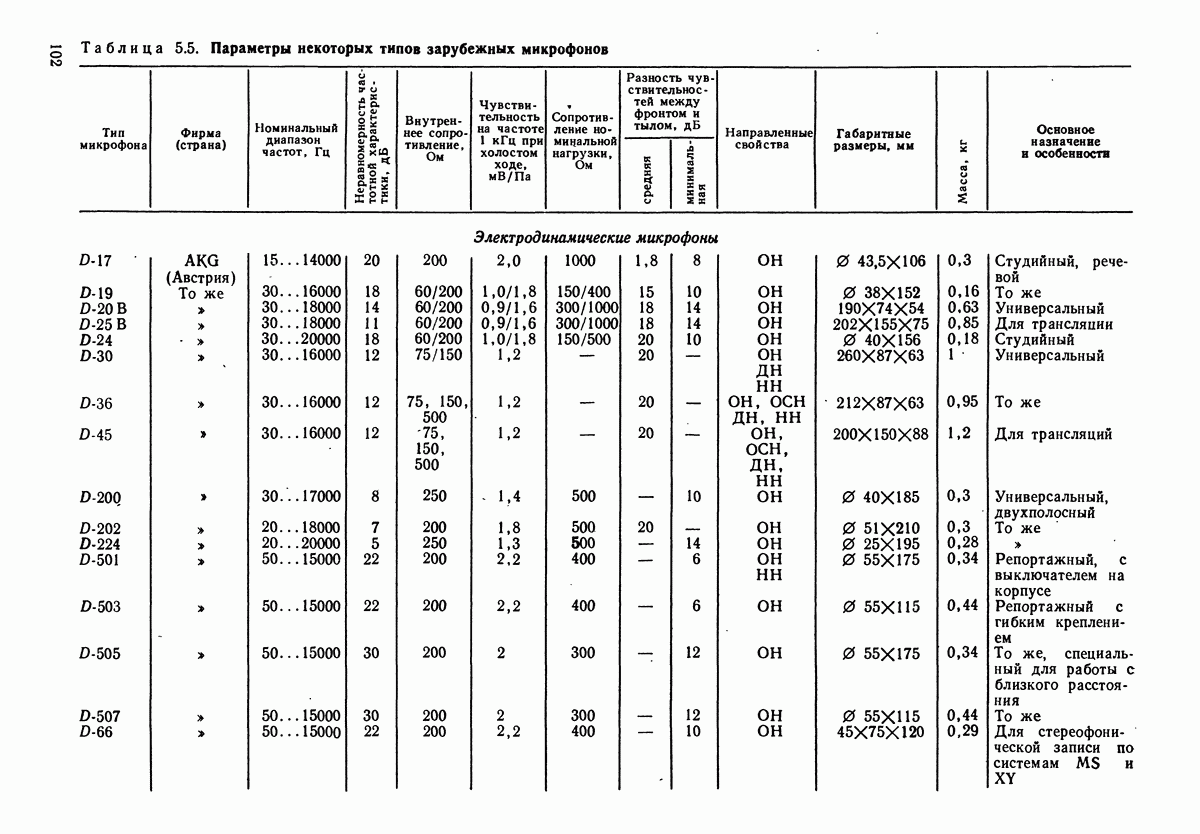
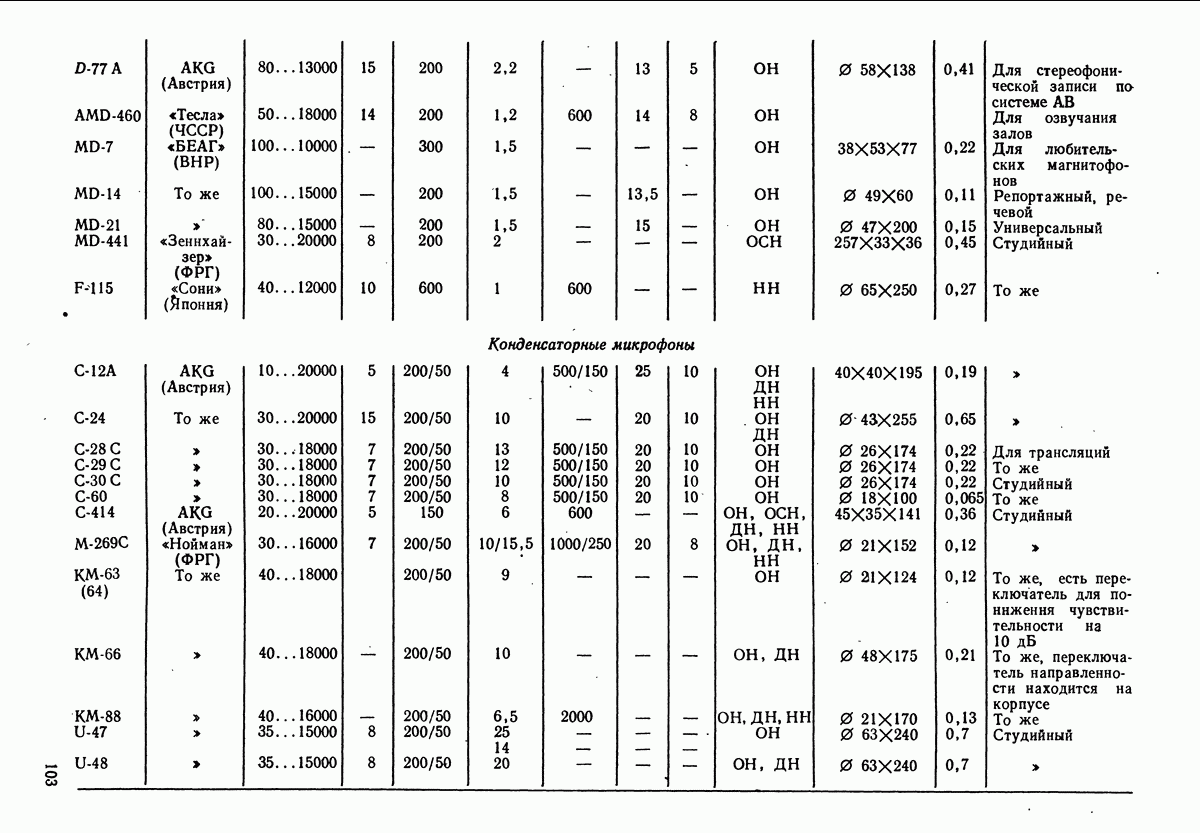
- РАЗДЕЛ 5. МИКРОФОНЫ И ЛАРИНГОФОНЫ
- 5.2. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ МИКРОФОНОВ
- 5.3. НАПРАВЛЕННЫЕ СВОЙСТВА МИКРОФОНОВ
- 5.4. ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- 5.5. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- 5.6. НЕКОТОРЫЕ ДРУГИЕ ТИПЫ МИКРОФОНОВ
- 5.7. ТЕХНИЧЕСКАЯ ЭКСПЛУАТАЦИЯ МИКРОФОНОВ
- РАЗДЕЛ 6. ГРОМКОГОВОРИТЕЛИ И ТЕЛЕФОНЫ
- 6.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ТЕЛЕФОНОВ И ГРОМКОГОВОРИТЕЛЕЙ
- 6.3. ТРЕБОВАНИЯ К ГРОМКОГОВОРИТЕЛЯМ И ТЕЛЕФОНАМ
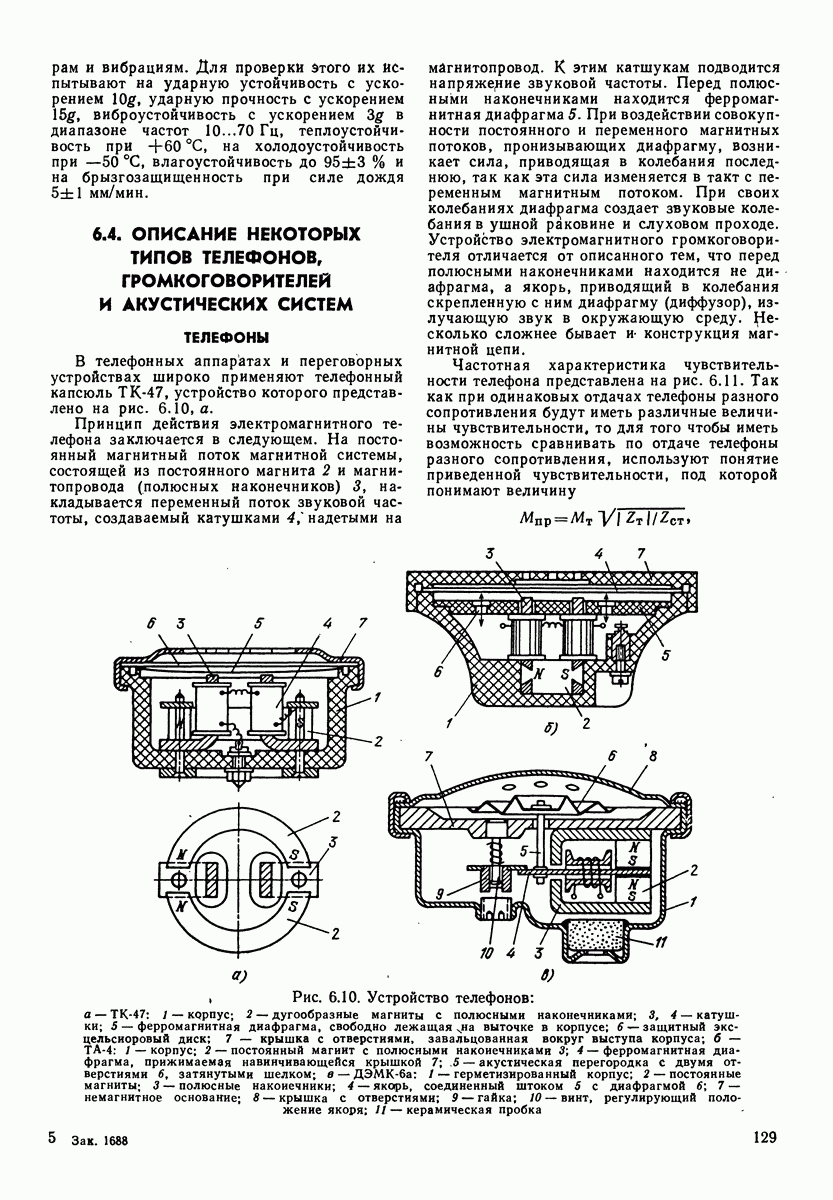
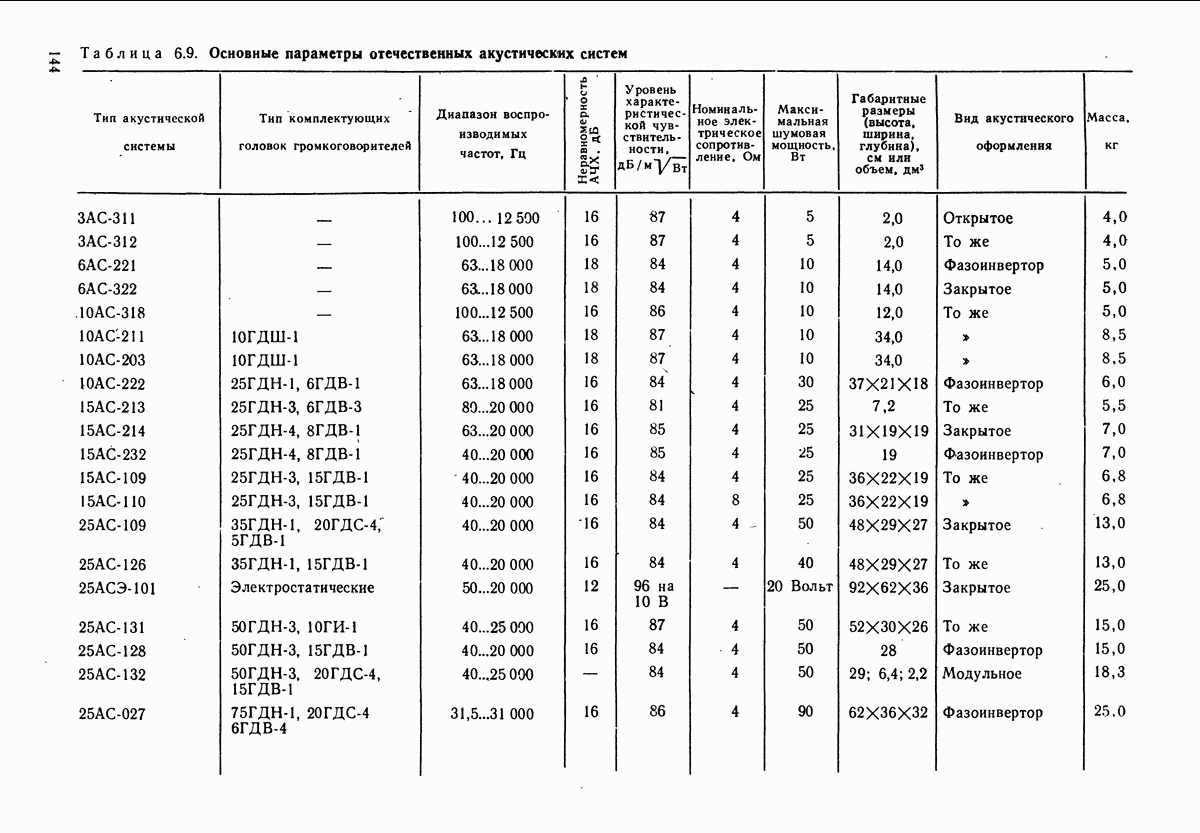
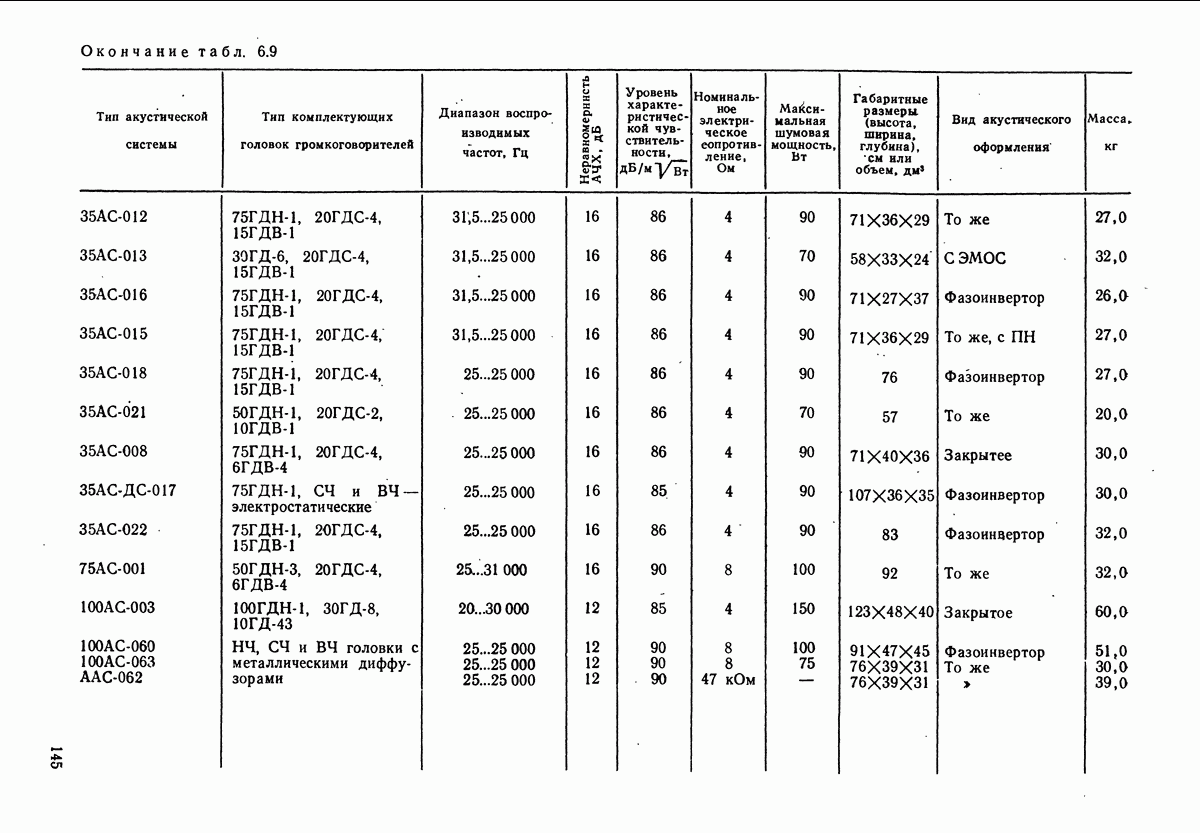
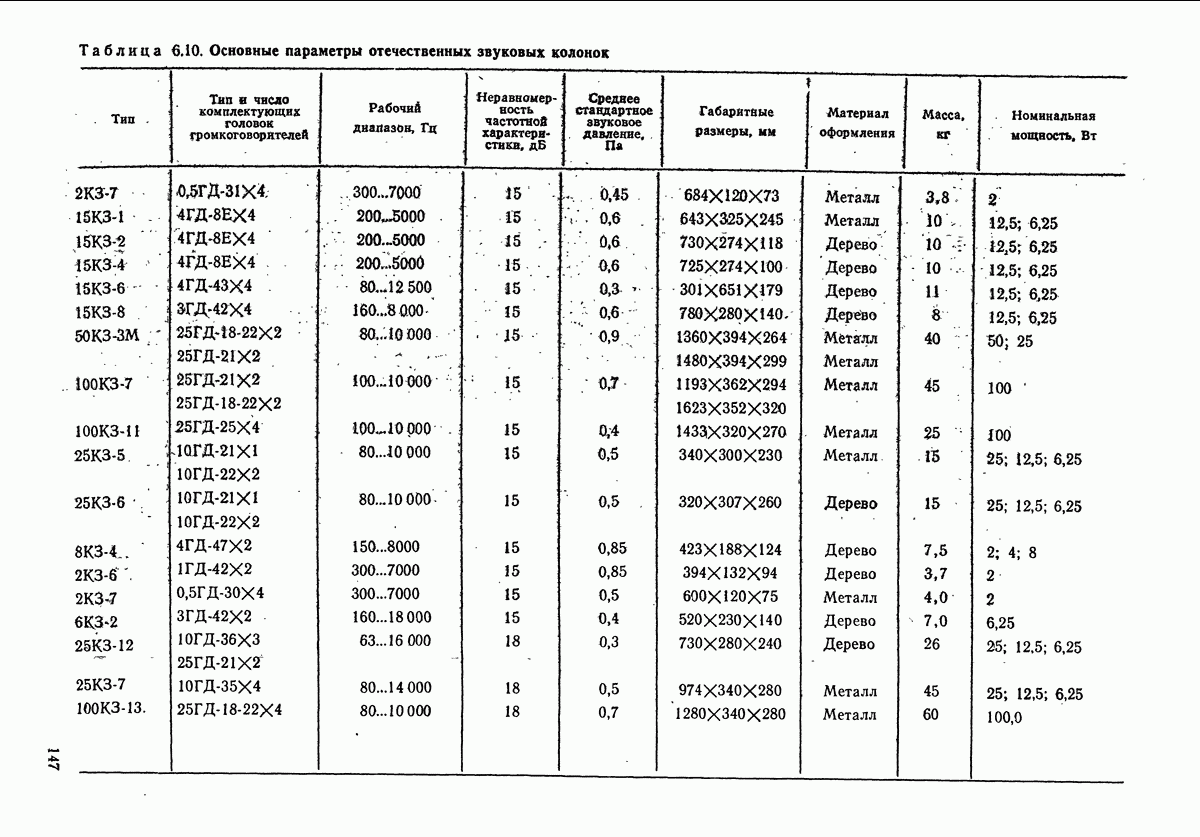
- 6.4. ОПИСАНИЕ НЕКОТОРЫХ ТИПОВ ТЕЛЕФОНОВ, ГРОМКОГОВОРИТЕЛЕЙ И АКУСТИЧЕСКИХ СИСТЕМ ТЕЛЕФОНЫ
- 6.5. КОНСТРУКЦИИ АКУСТИЧЕСКИХ ОФОРМЛЕНИЙ ПЛОСКИЙ ЭКРАН
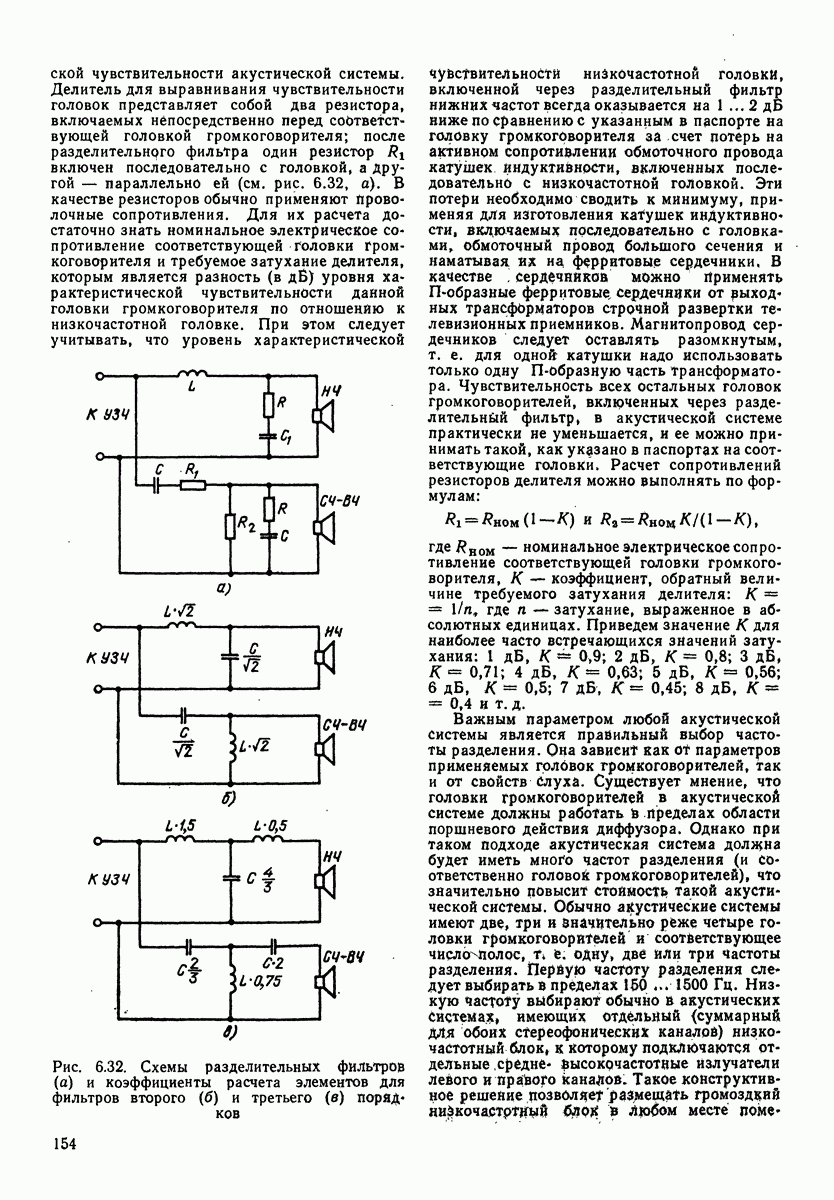
- 6.6. ВКЛЮЧЕНИЕ ГОЛОВОК ГРОМКОГОВОРИТЕЛЕЙ В АКУСТИЧЕСКИЕ СИСТЕМЫ
- 6.7. РАЗМЕЩЕНИЕ АКУСТИЧЕСКИХ СИСТЕМ
- РАЗДЕЛ 7. АКУСТИКА СТУДИЙ И ДРУГИХ ПОМЕЩЕНИЙ
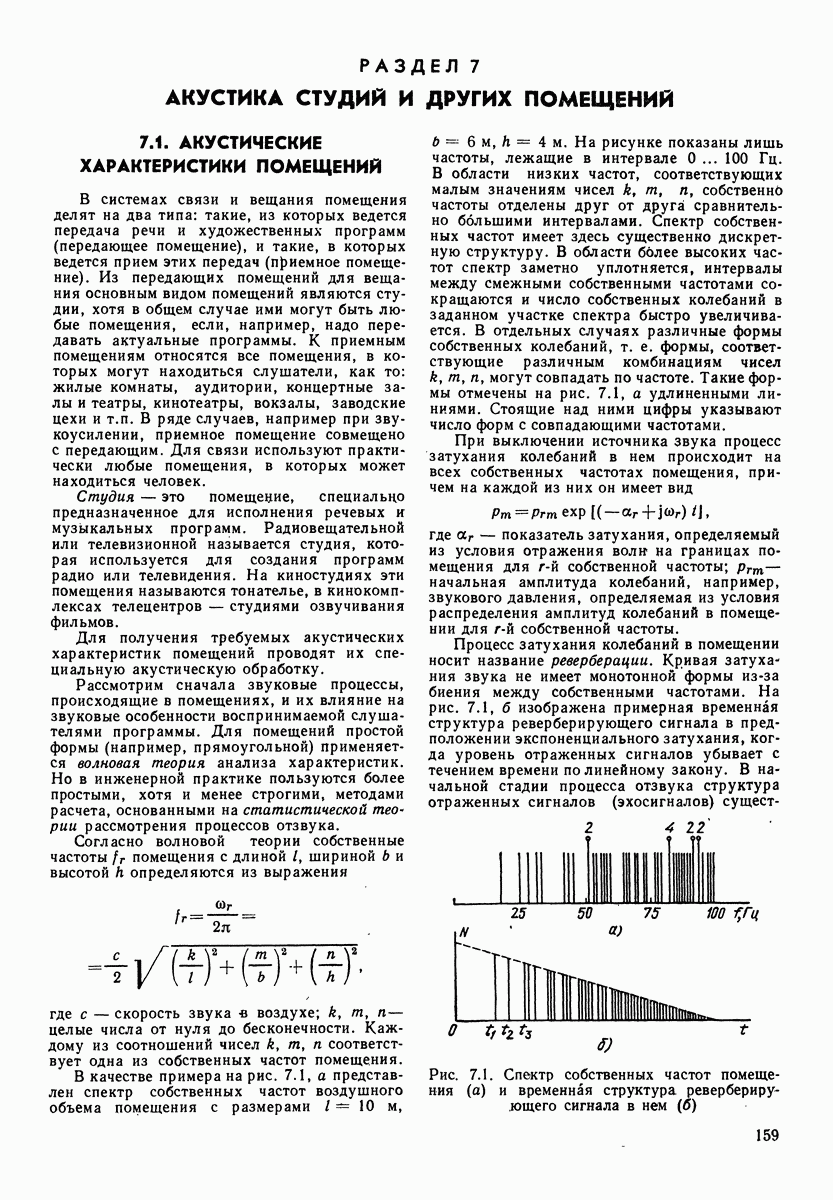
- 7.1. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОМЕЩЕНИЙ
- 7.2. КЛАССИФИКАЦИЯ РАДИОВЕЩАТЕЛЬНЫХ И ТЕЛЕВИЗИОННЫХ СТУДИЙ
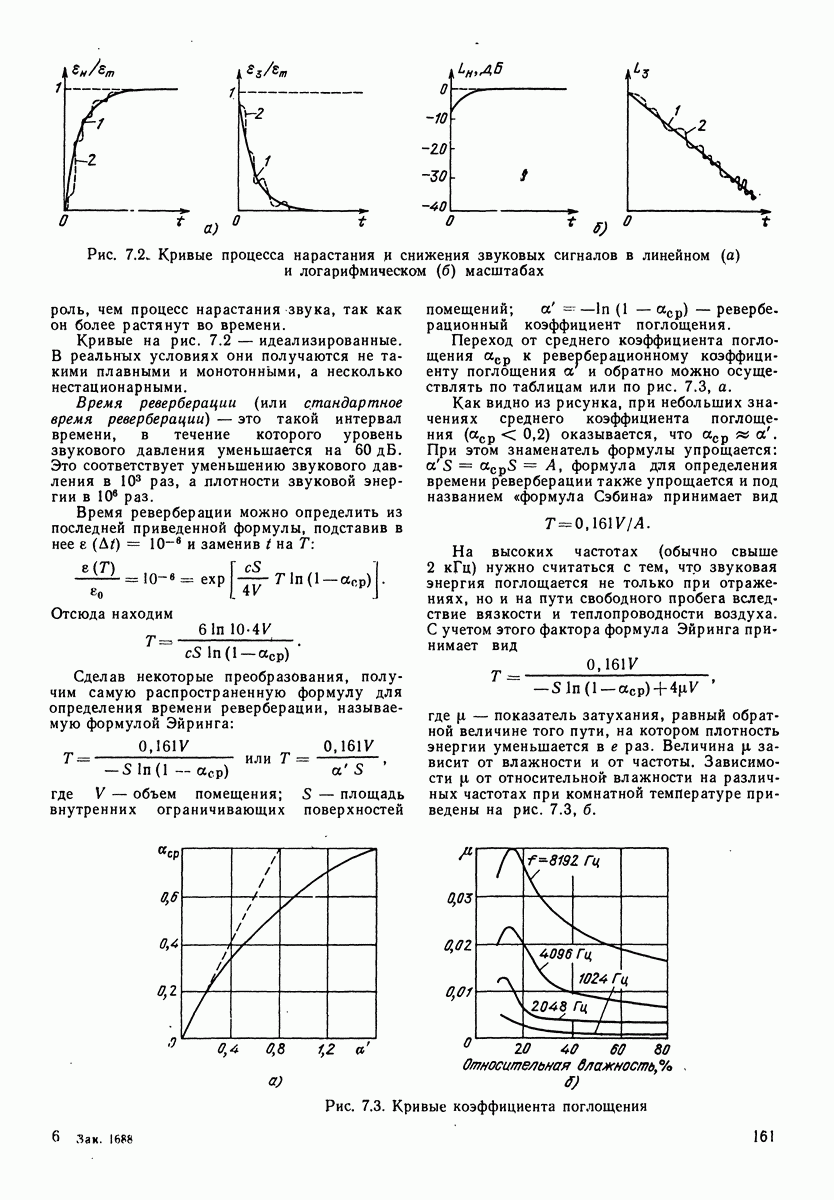
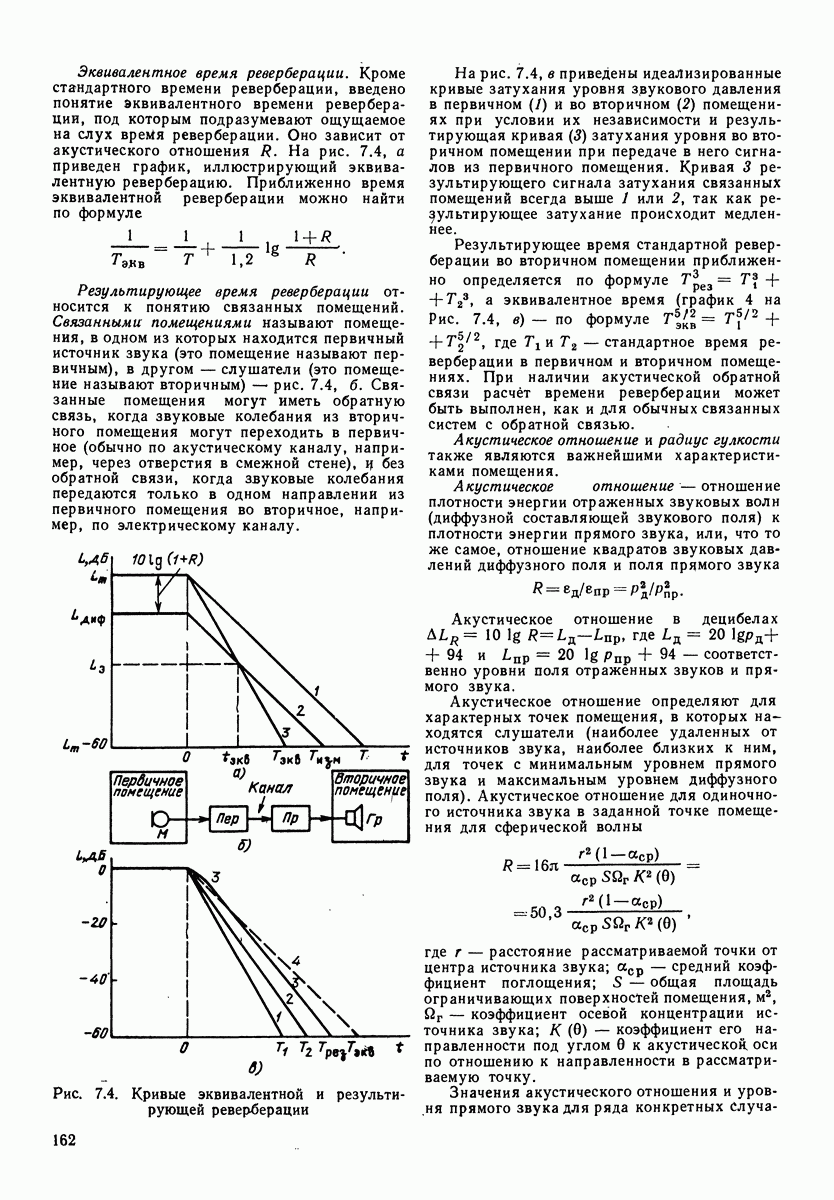
- 7.3. ОПТИМАЛЬНАЯ РЕВЕРБЕРАЦИЯ В СТУДИЯХ И ПРИЕМНЫХ ПОМЕЩЕНИЯХ
- 7.4. ЗВУКОПОГЛОЩАЮЩИЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ
- 7.5. ЗВУКОИЗОЛЯЦИЯ СТУДИЙ
- 7.6. ЭЛЕКТРОАКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ СТУДИЙ И АППАРАТНЫХ
- РАЗДЕЛ 8. ОЗВУЧЕНИЕ И ЗВУКОУСИЛЕНИЕ
- 8.2. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ОТКРЫТЫХ ПРОСТРАНСТВ
- 8.3. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.4. ЗОНАЛЬНЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.5. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 8.6. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 8.7. РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.8. ЗВУКОУСИЛЕНИЕ
- 8.9. ГРОМКОГОВОРЯЩАЯ СВЯЗЬ
- РАЗДЕЛ 9. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- 9.1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ ЗАПИСИ ЗВУКА
- 9.2. МЕХАНИЧЕСКАЯ ЗВУКОЗАПИСЬ
- 9.3. ФОТОГРАФИЧЕСКАЯ ЗВУКОЗАПИСЬ
- 9.4. МАГНИТНАЯ ЗВУКОЗАПИСЬ
- 9.5. МАГНИТНЫЕ ГОЛОВКИ
- 9.6. МАГНИТНЫЕ НОСИТЕЛИ ЗАПИСИ
- 9.7. МАГНИТОФОНЫ
- 9.8. ЛАЗЕРНАЯ ЗВУКОЗАПИСЬ НА КОМПАКТ-ДИСК
- РАЗДЕЛ 10. ПЕРЕДАЧА АКУСТИЧЕСКИХ СИГНАЛОВ
- 10.2. ИСКАЖЕНИЯ СИГНАЛОВ
- 10.3. ШУМЫ И ПОМЕХИ В ТРАКТАХ И КАНАЛАХ СВЯЗИ И ВЕЩАНИЯ
- 10.4. ДОПУСТИМЫЕ ИСКАЖЕНИЯ ВЕЩАТЕЛЬНЫХ СИГНАЛОВ
- 10.5. ПОНЯТНОСТЬ И РАЗБОРЧИВОСТЬ РЕЧИ
- 10.6. ИНДЕКСЫ ТРАКТА
- 10.7. РАСЧЕТ РАЗБОРЧИВОСТИ РЕЧИ
- 10.8. РАСЧЕТ ОБЩЕГО УРОВНЯ ЗВУКОВОГО ПОЛЯ ПРИ ПЕРЕДАЧЕ РЕЧИ И ВЫБОР АППАРАТУРЫ ЗВУКОУСИЛЕНИЯ
- 10.9. ПРИМЕРЫ РАСЧЕТА ИНДЕКСОВ ТРАКТА, РАЗБОРЧИВОСТИ РЕЧИ И ОБЩЕГО УРОВНЯ ПЕРЕДАЧИ
- 10.10. ОПРЕДЕЛЕНИЕ РАЗБОРЧИВОСТИ РЕЧИ ДЛЯ ТРАКТОВ РАДИОТЕЛЕФОННОЙ СВЯЗИ
- 10.11. МЕТОДЫ ПОВЫШЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- 10.12. ВОКОДЕРНАЯ СВЯЗЬ
- РАЗДЕЛ 11. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ
- 11.2. МЕТОДЫ ИЗМЕРЕНИЙ ОСНОВНЫХ ХАРАКТЕРИСТИК ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЫ И ПОМЕЩЕНИЙ
- 11.3. ЭКСПЕРТИЗА МУЗЫКАЛЬНЫХ ПЕРЕДАЧ
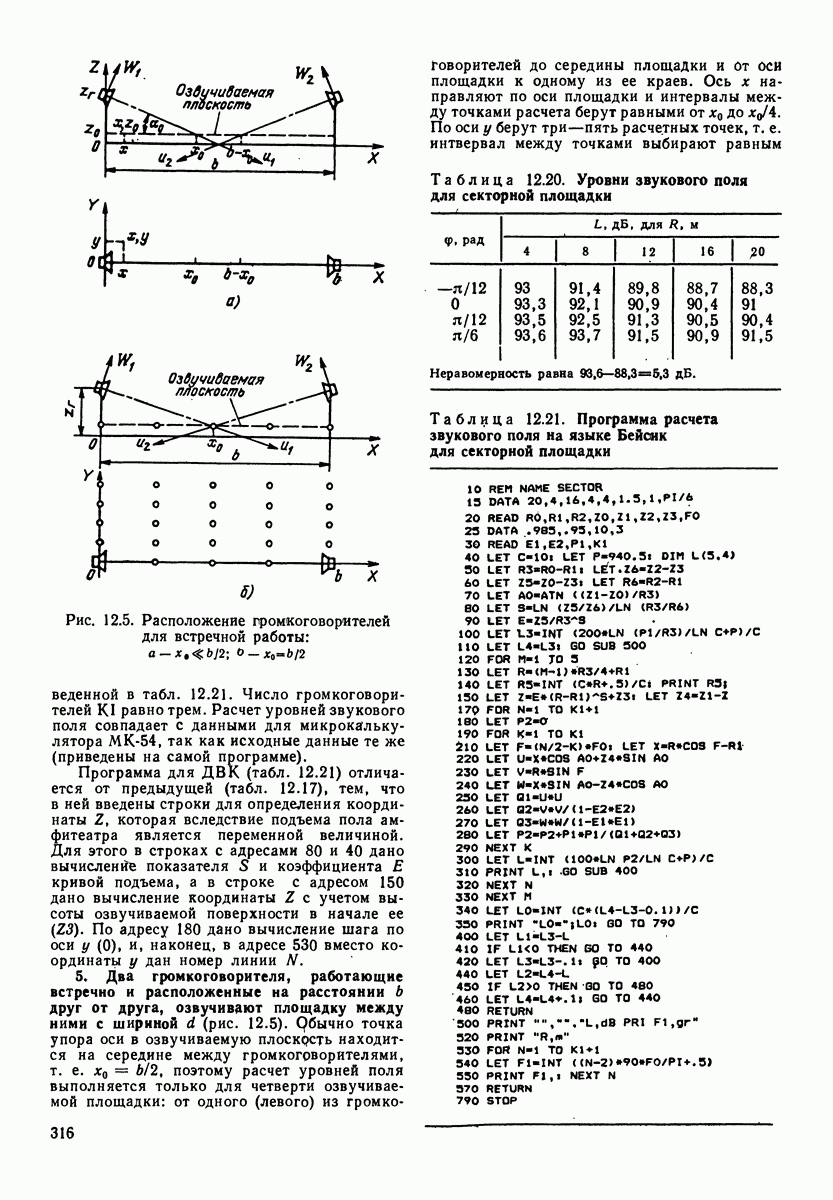
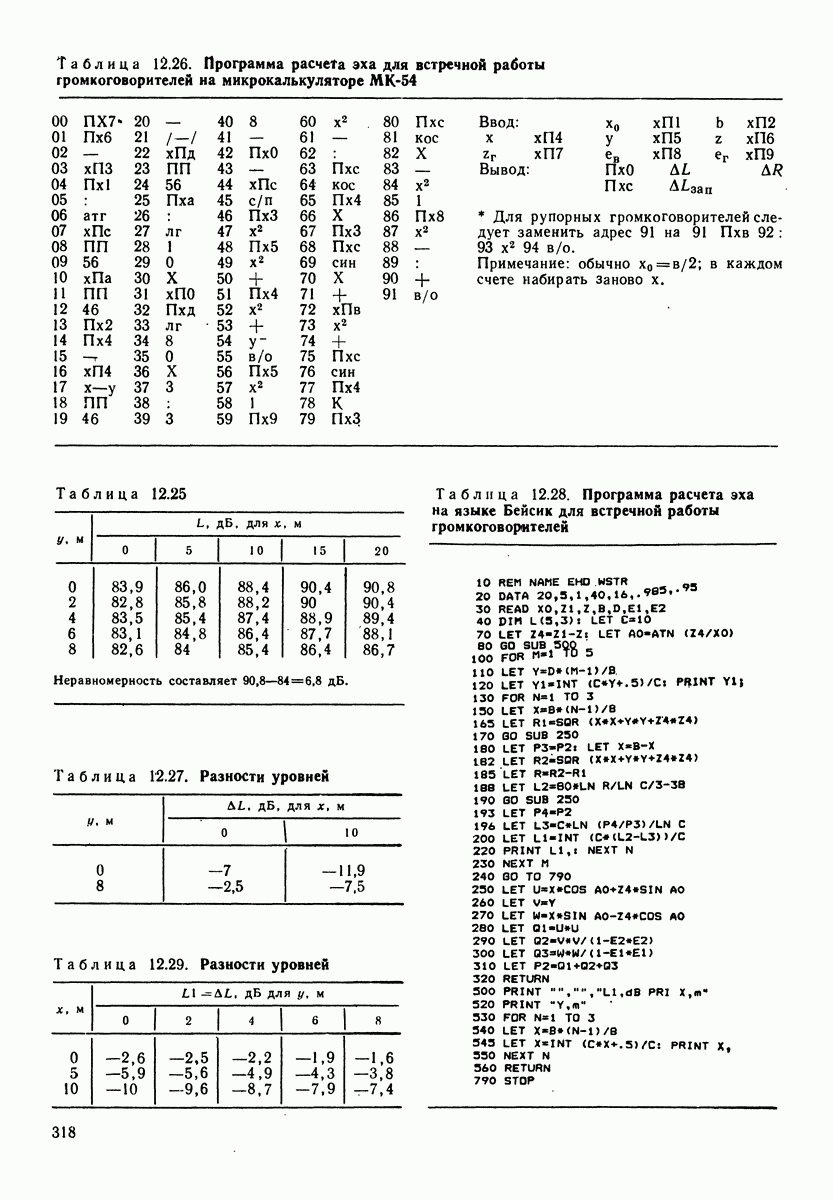
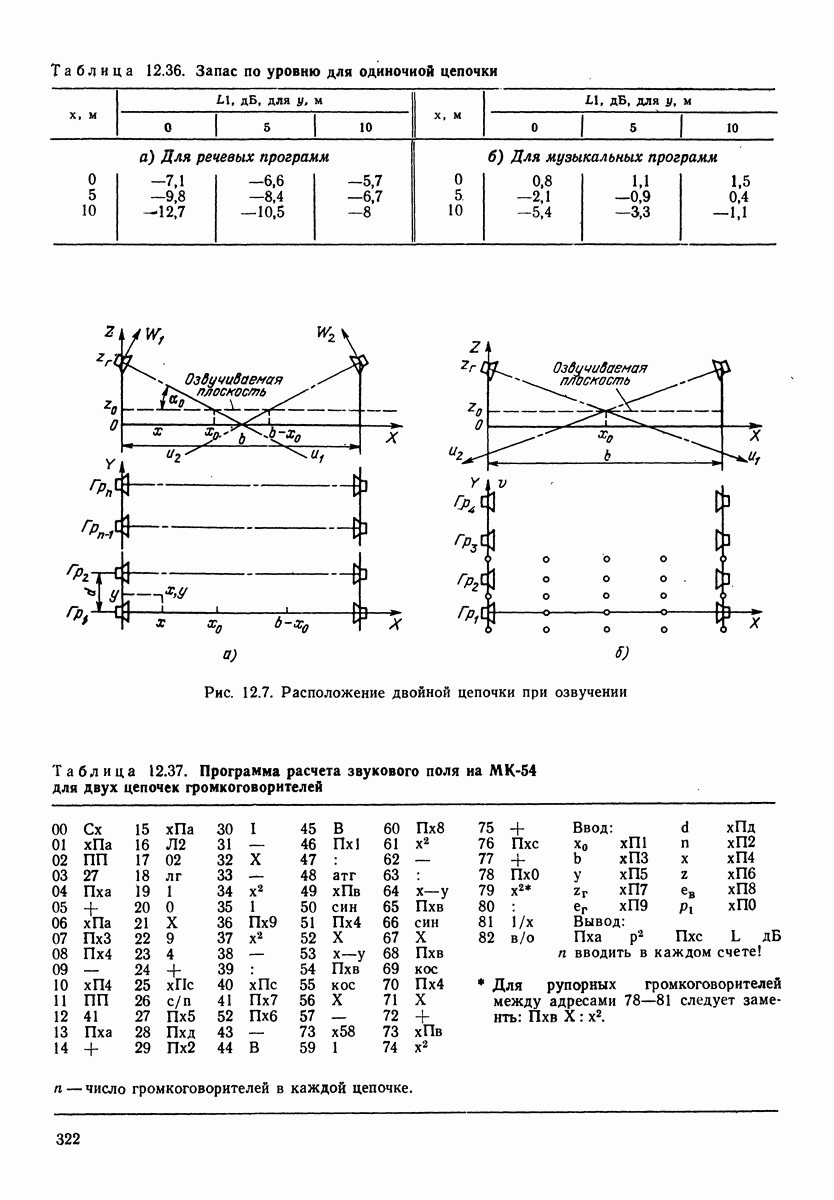
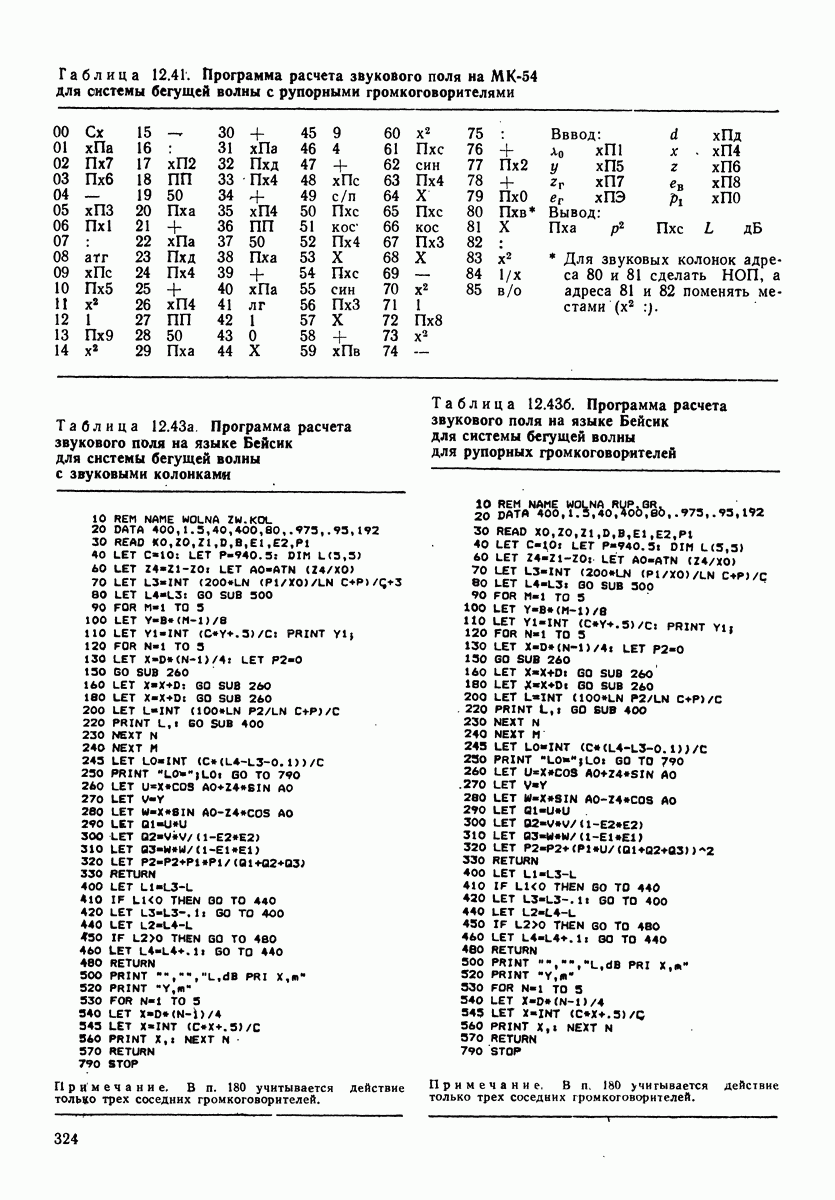
- РАЗДЕЛ 12. ПРОГРАММЫ ДЛЯ МИКРОКАЛЬКУЛЯТОРОВ И ЭВМ ТИПА ДВК
- 12.1. КОМПЛЕКС ПРОГРАММ ПО РАСЧЕТУ ЗВУКОВОГО ПОЛЯ И ЭХА ПРИ ЗВУКОФИКАЦИИ
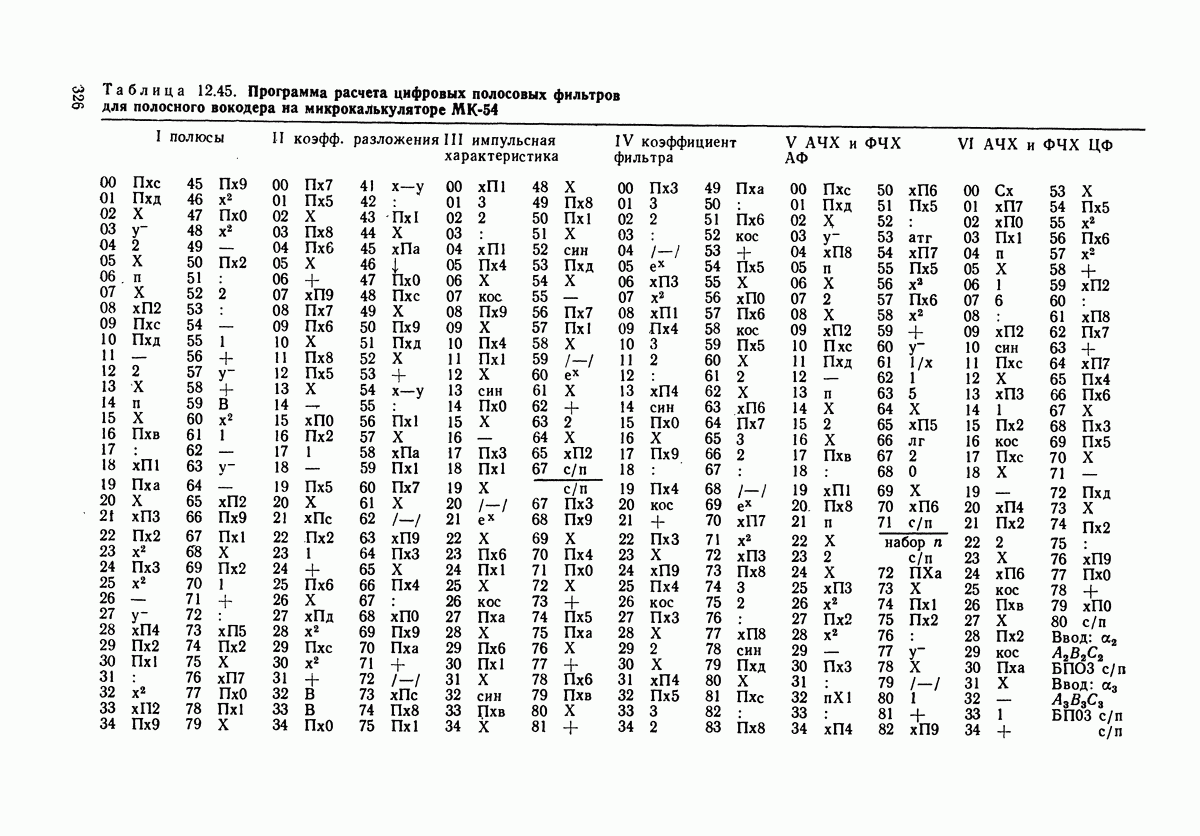
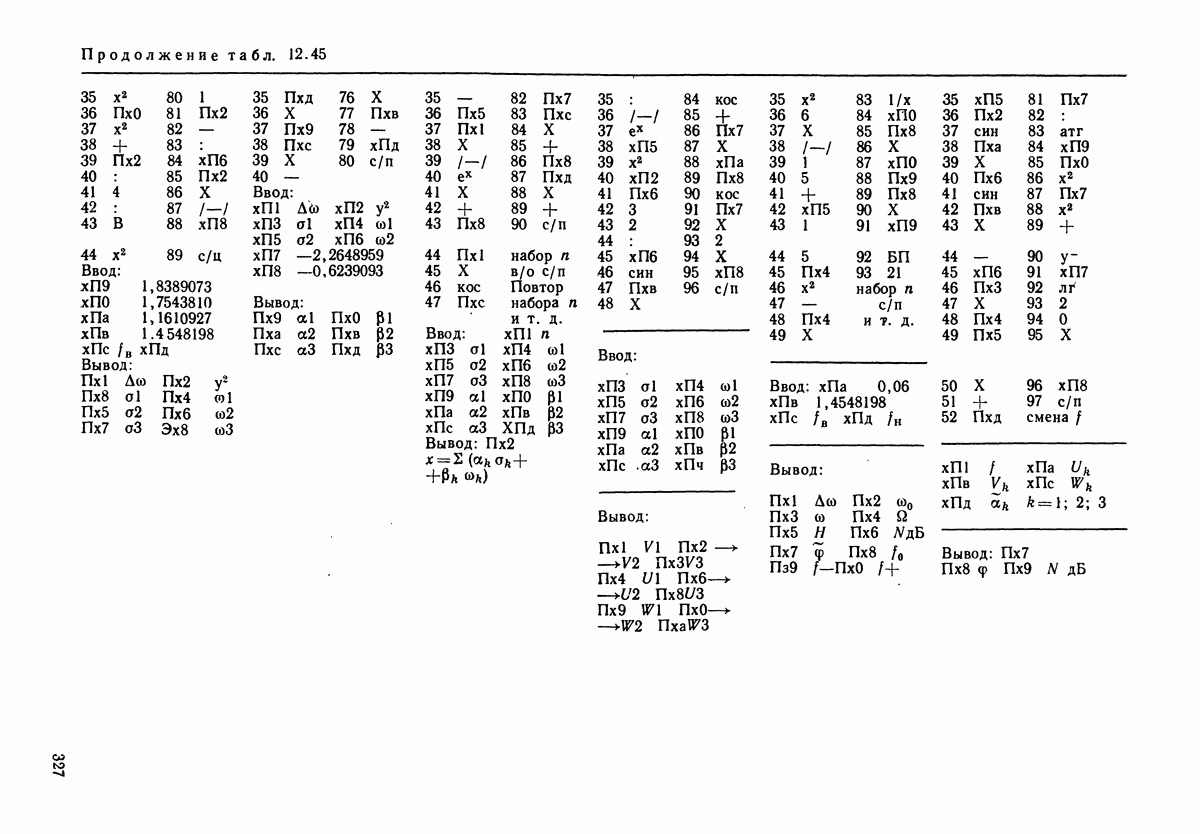
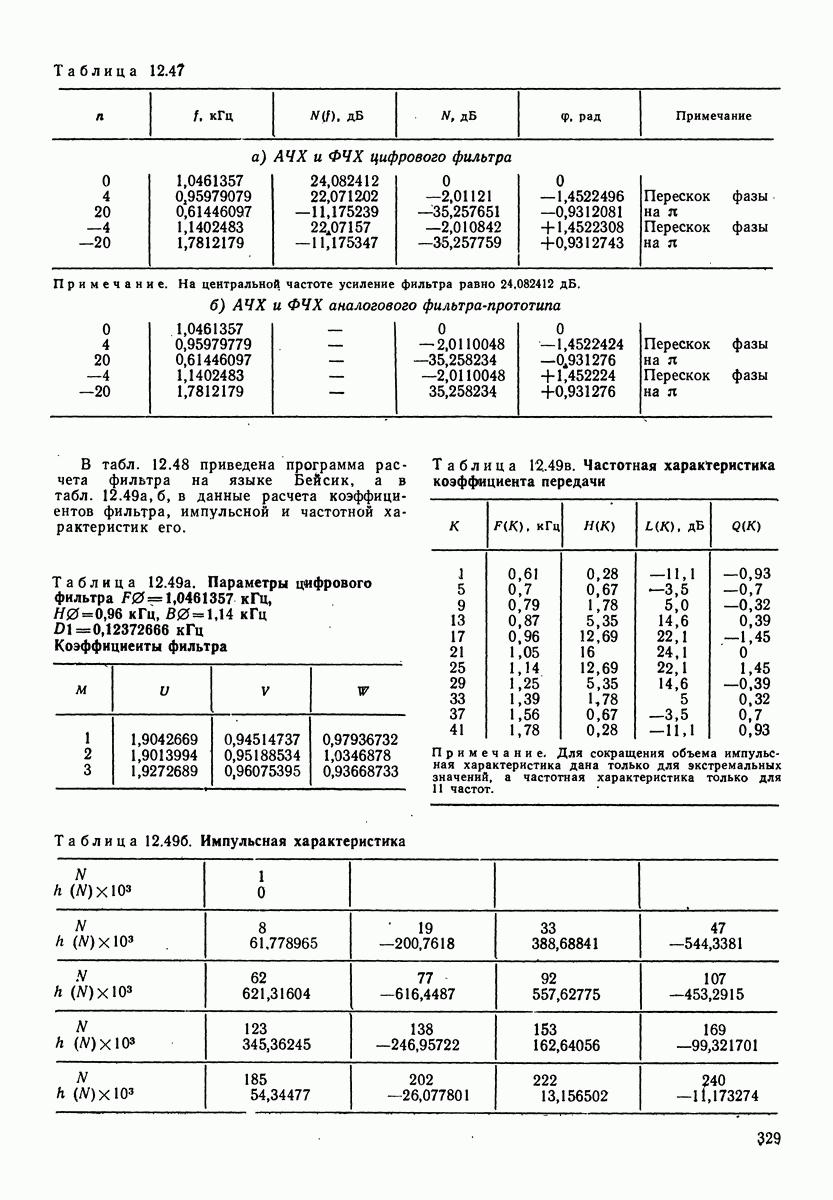
- 12.2. ПРОГРАММЫ РАСЧЕТА ДЛЯ ВОКОДЕРНЫХ ФИЛЬТРОВ (В ЦИФРОВОМ ИСПОЛНЕНИИ)
- 12.3. ПРОГРАММЫ ДЛЯ РАСЧЕТА РАЗБОРЧИВОСТИ РЕЧИ И ОБЩЕГО УРОВНЯ ПЕРЕДАЧИ РЕЧИ