| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИ
Почти вся электроакустическая аппаратура имеет в своем составе механическую систему как посредник между электрической и акустической системами. Для возможности использования хорошо разработанного аппарата в виде теории электрических
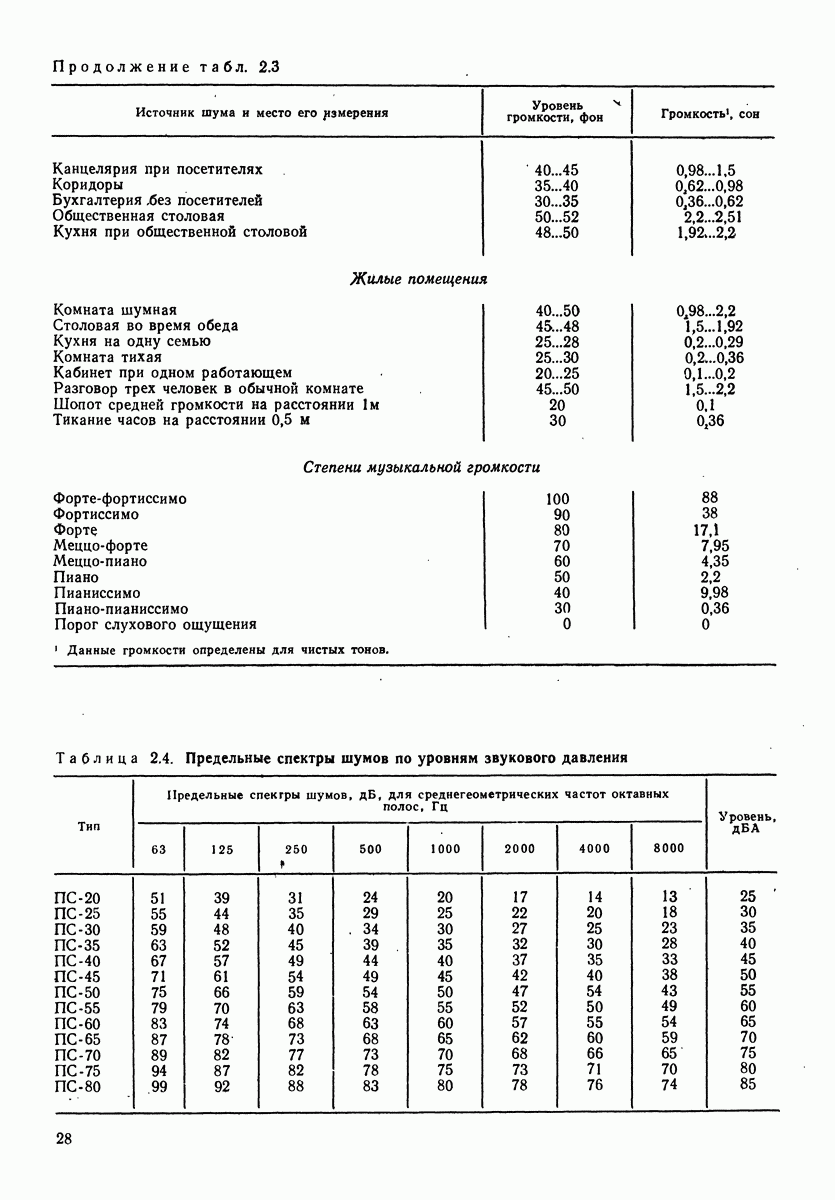
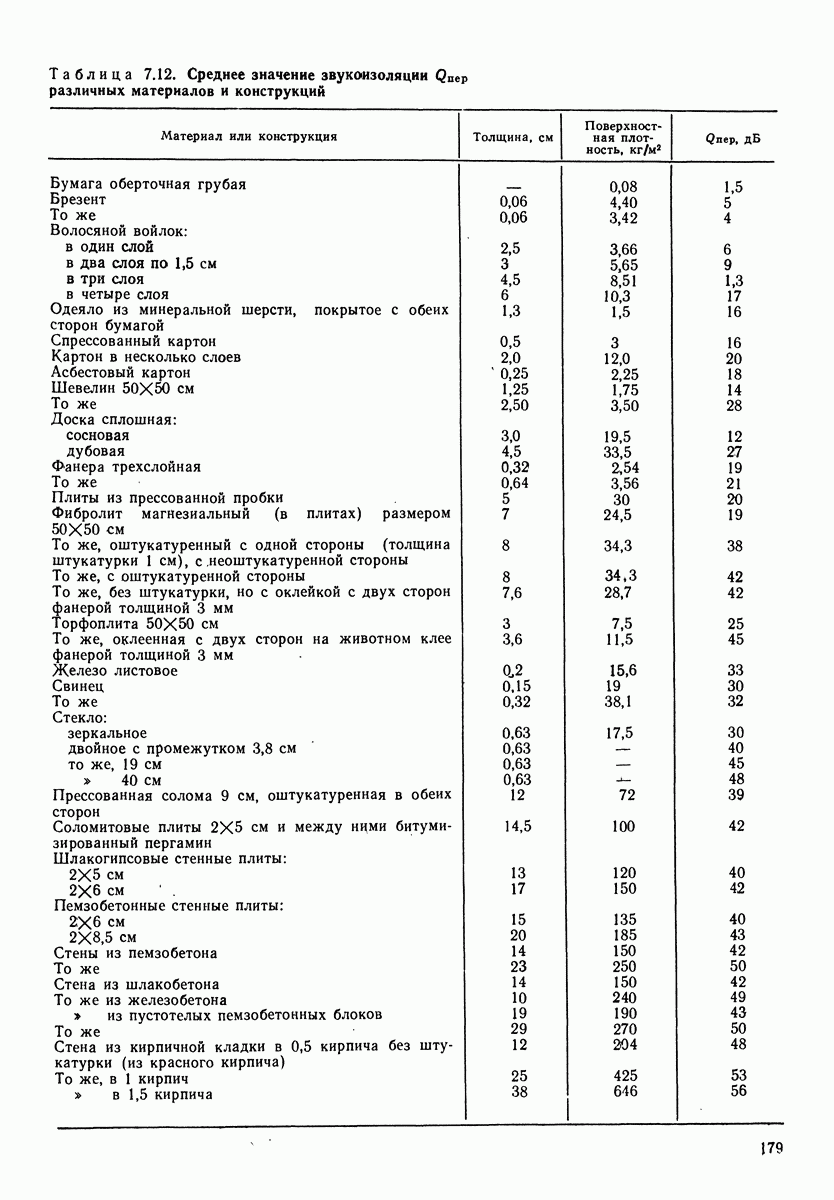
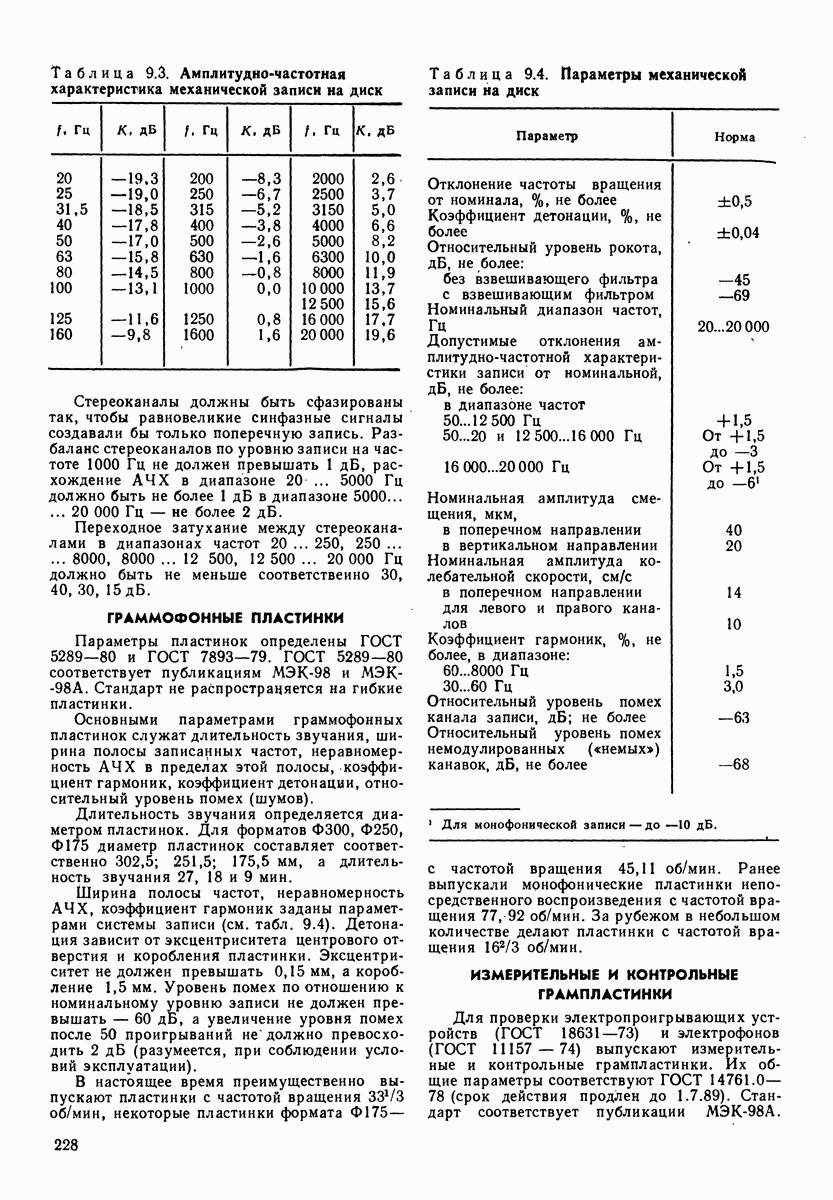
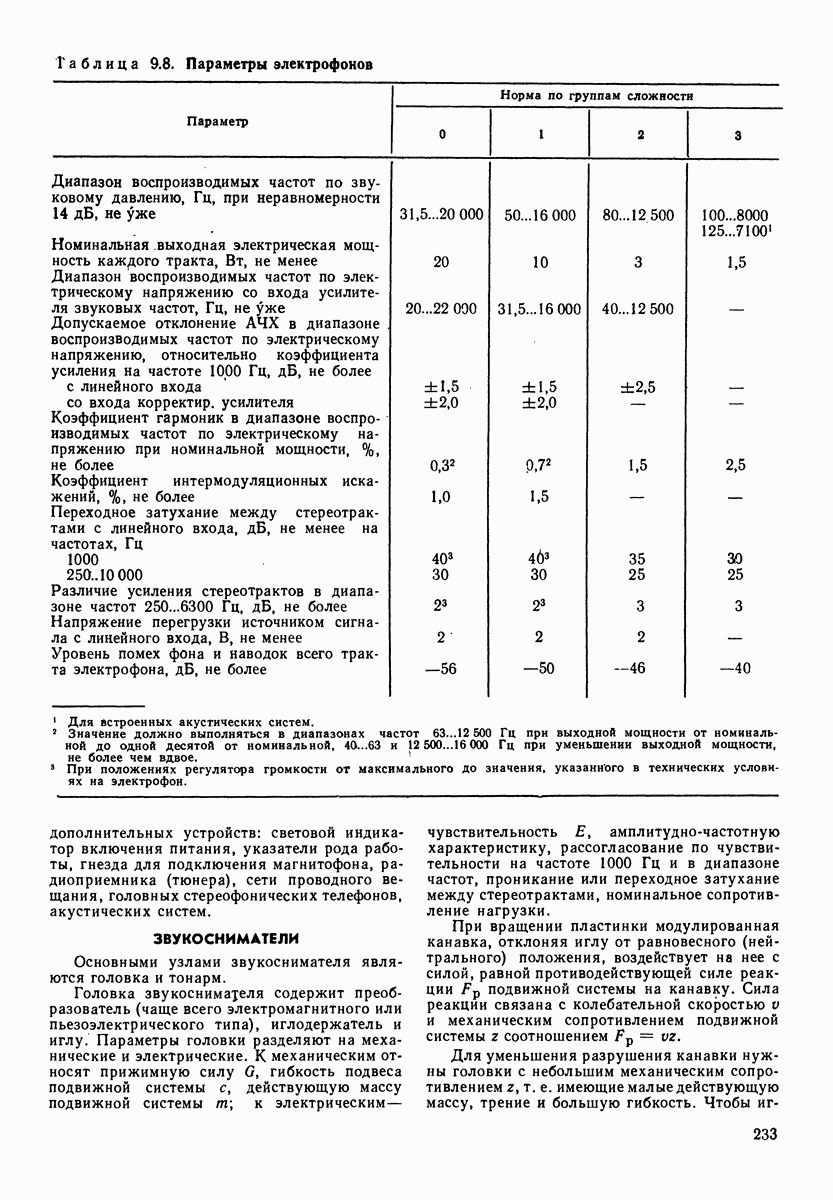
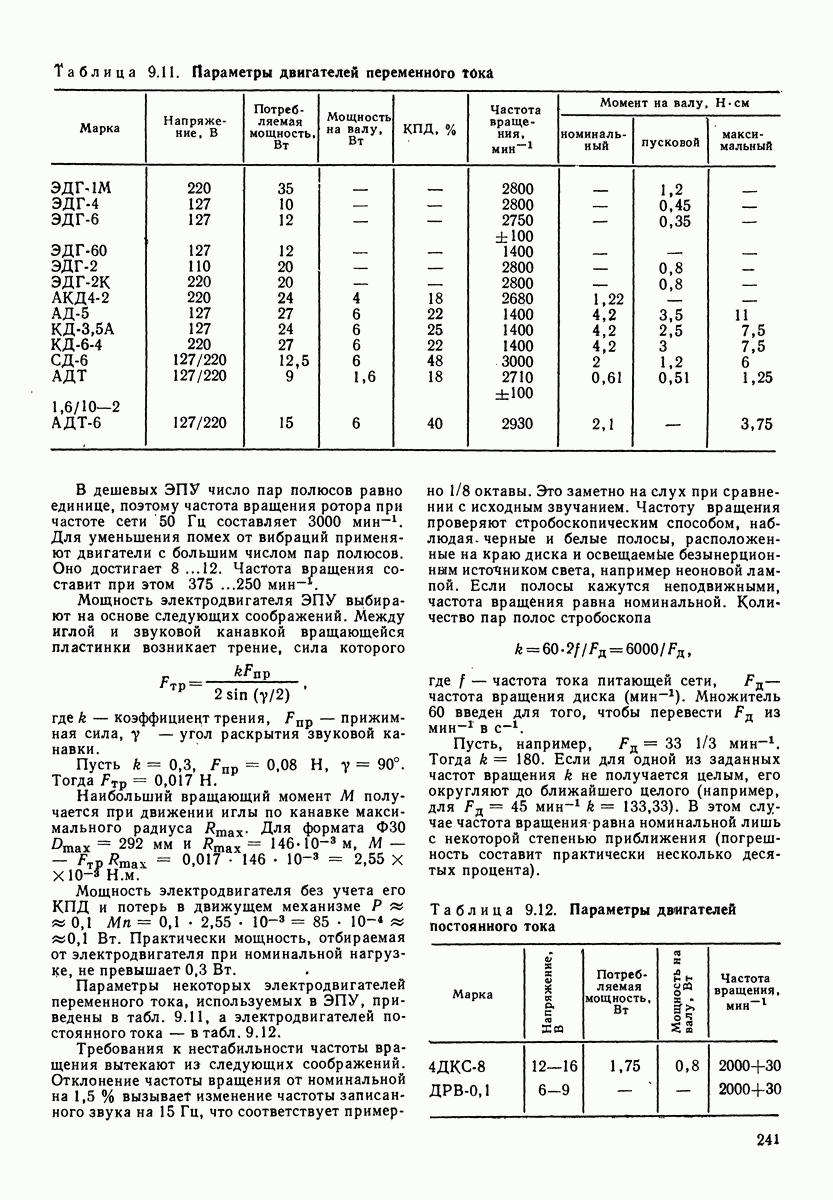
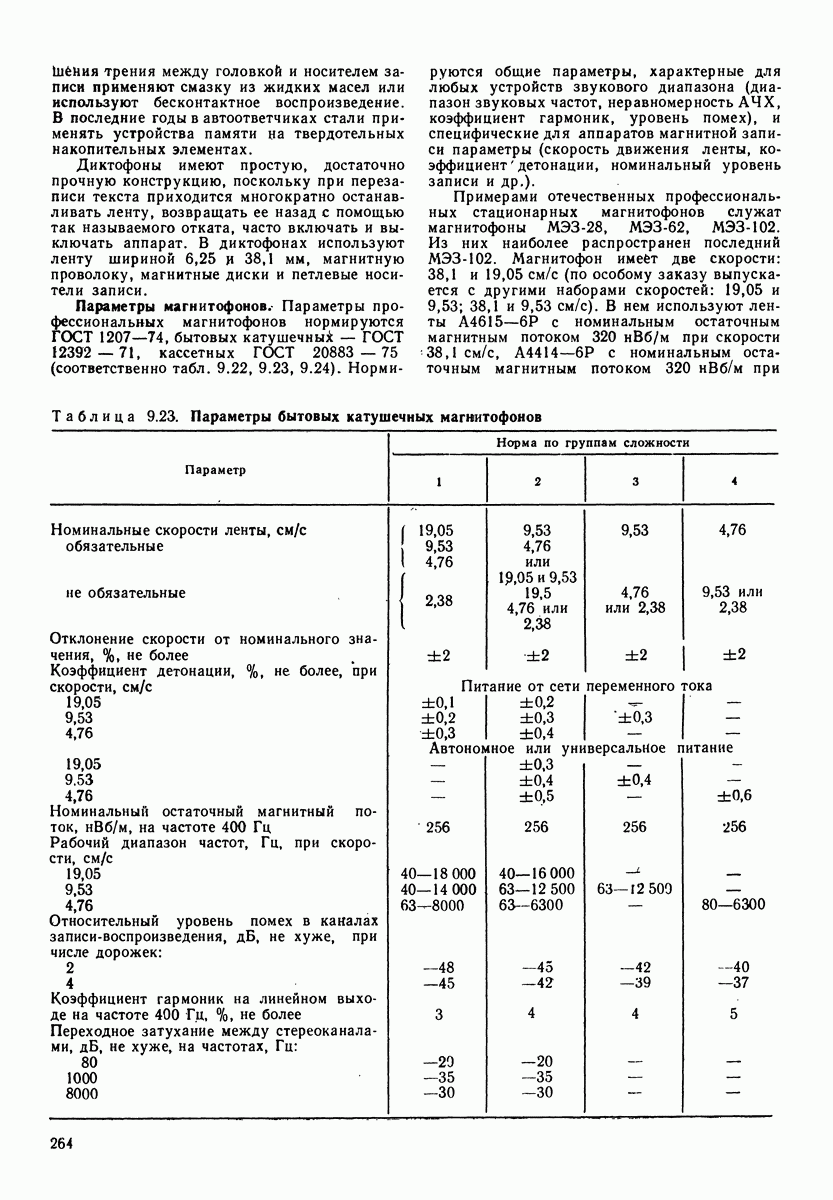
Таблица 4.1. (см. скан) Электромеханические аналоги
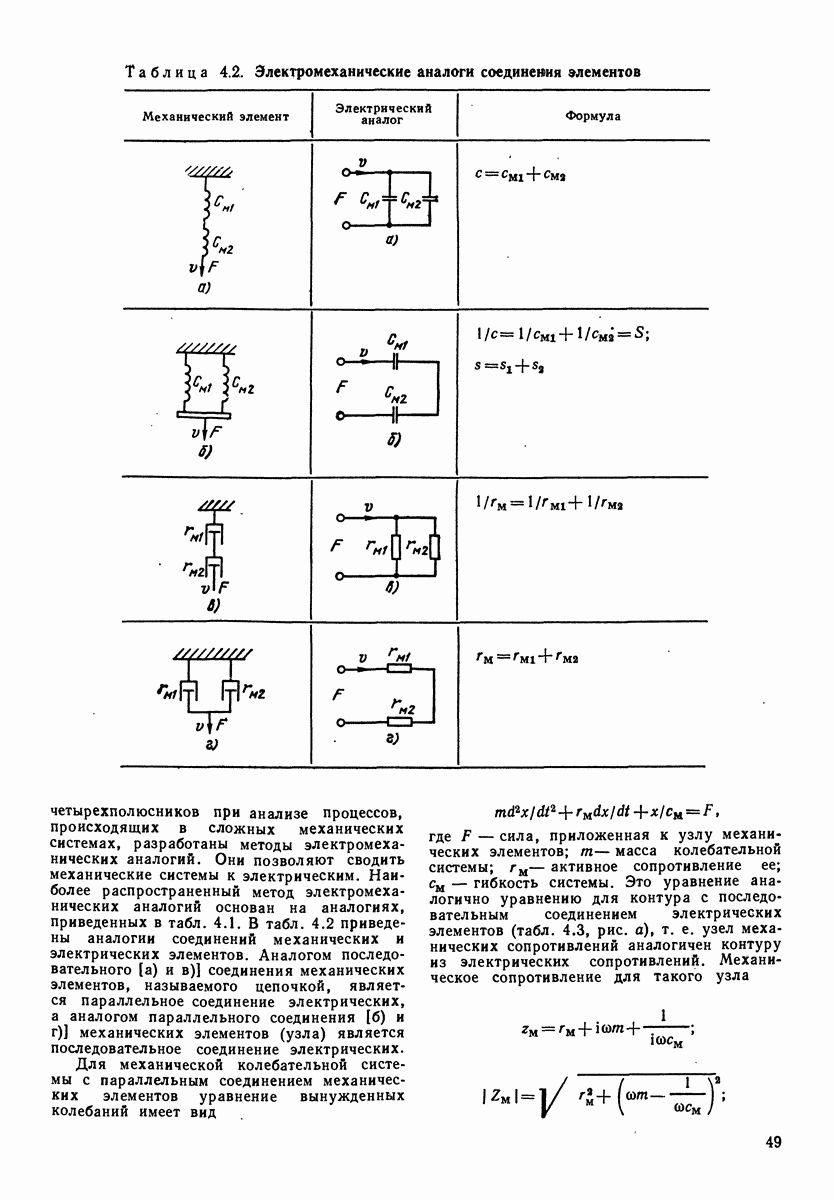
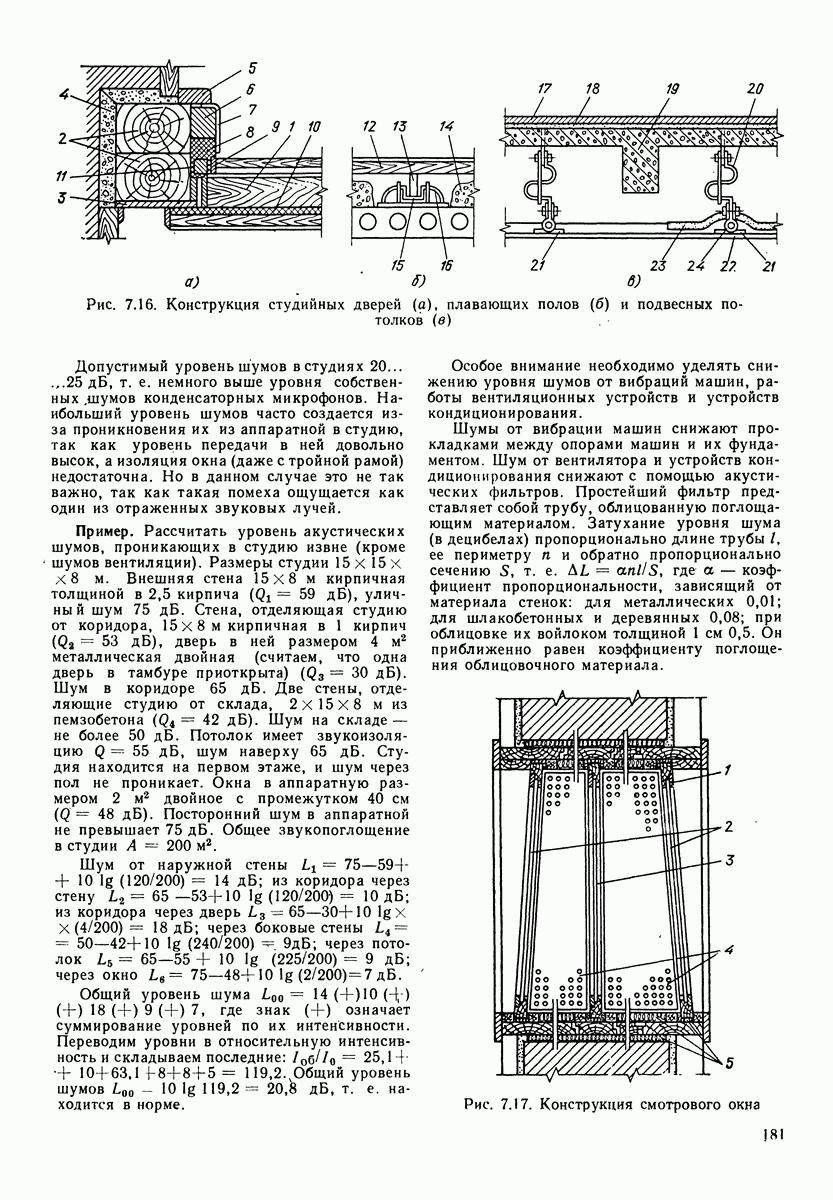
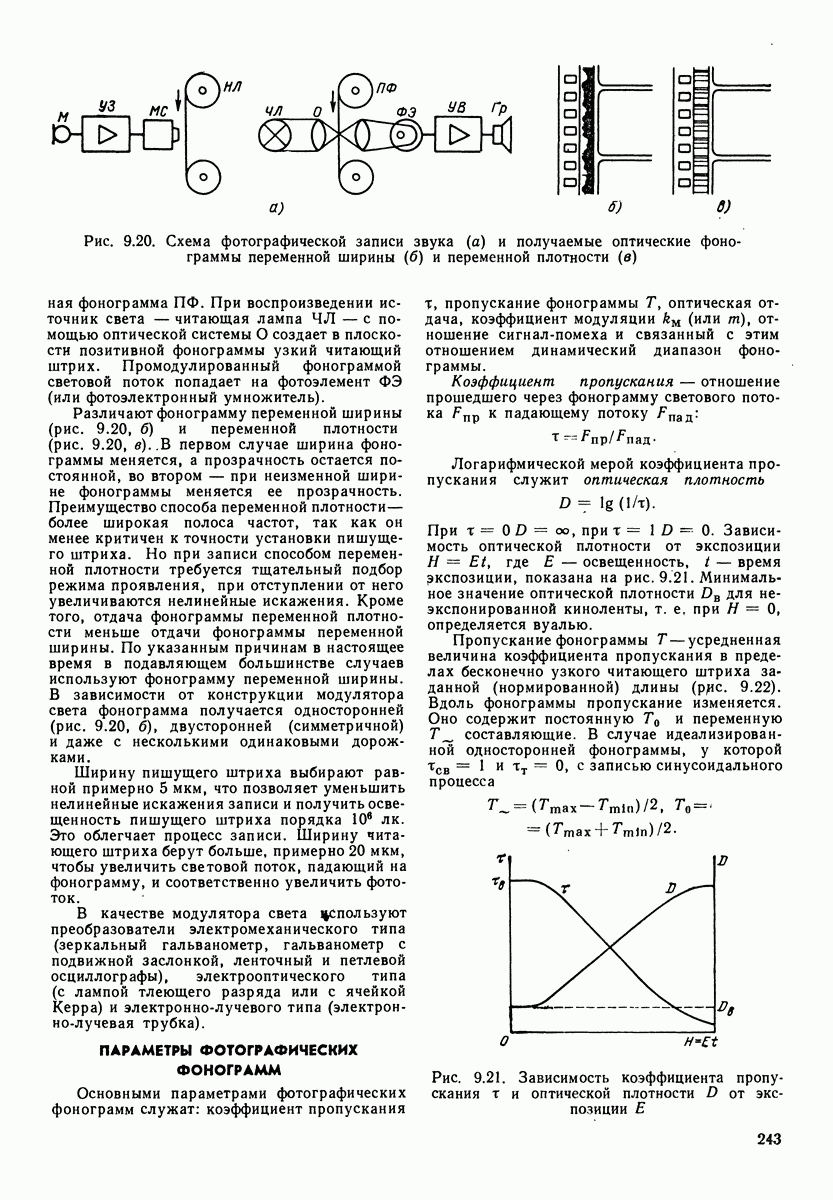
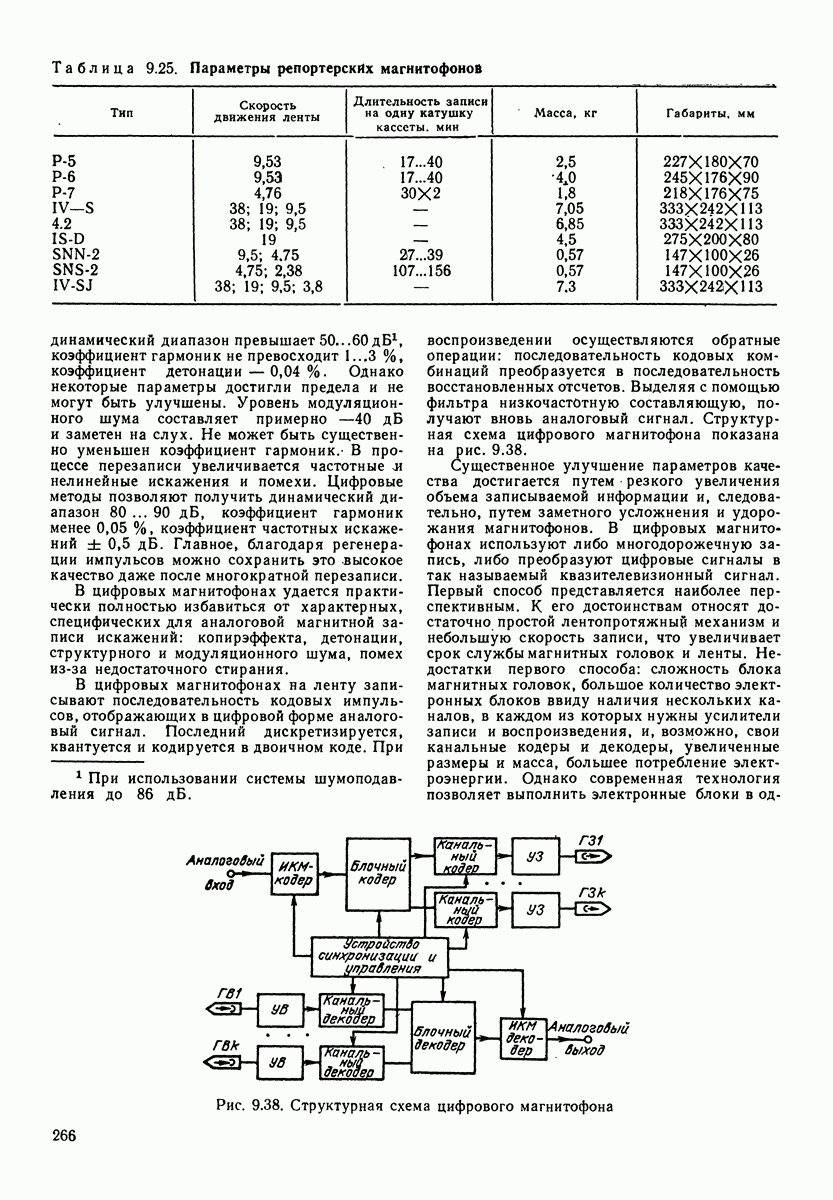
Таблица 4.2. (см. скан) Электромеханические аналоги соединения элементов
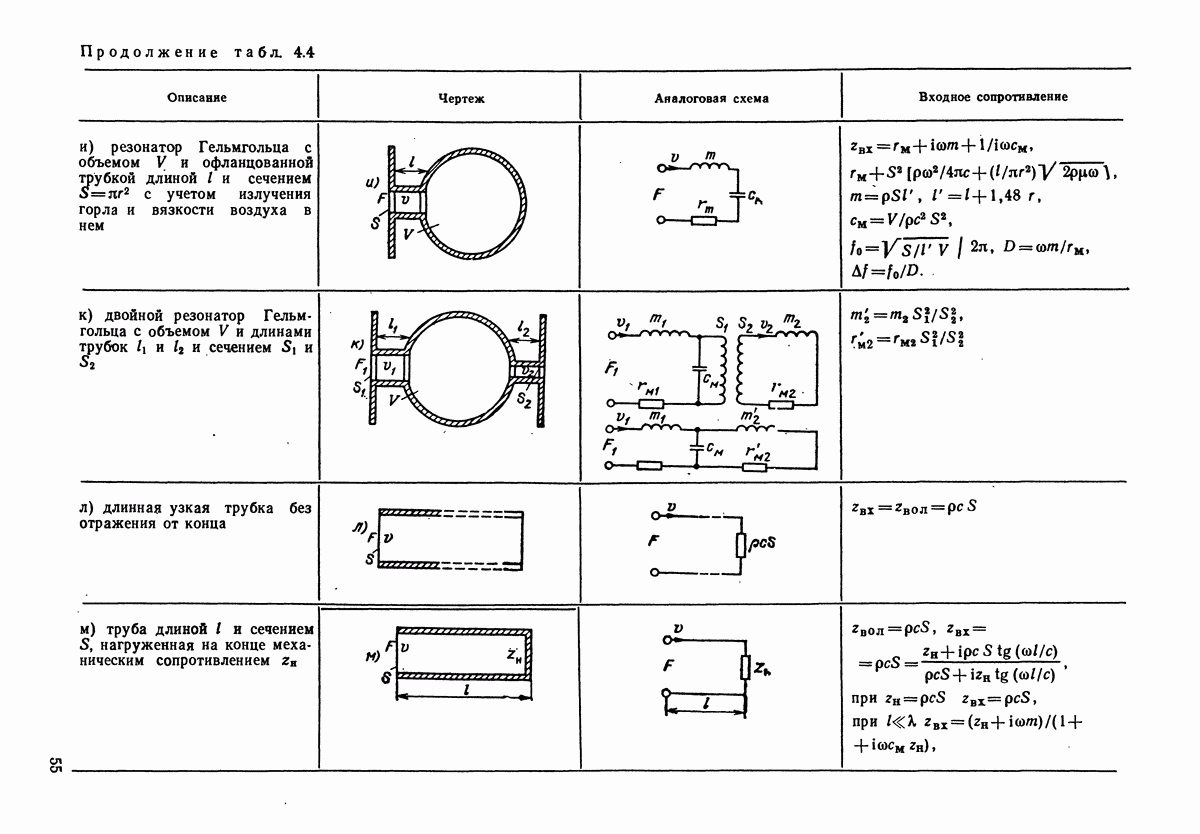
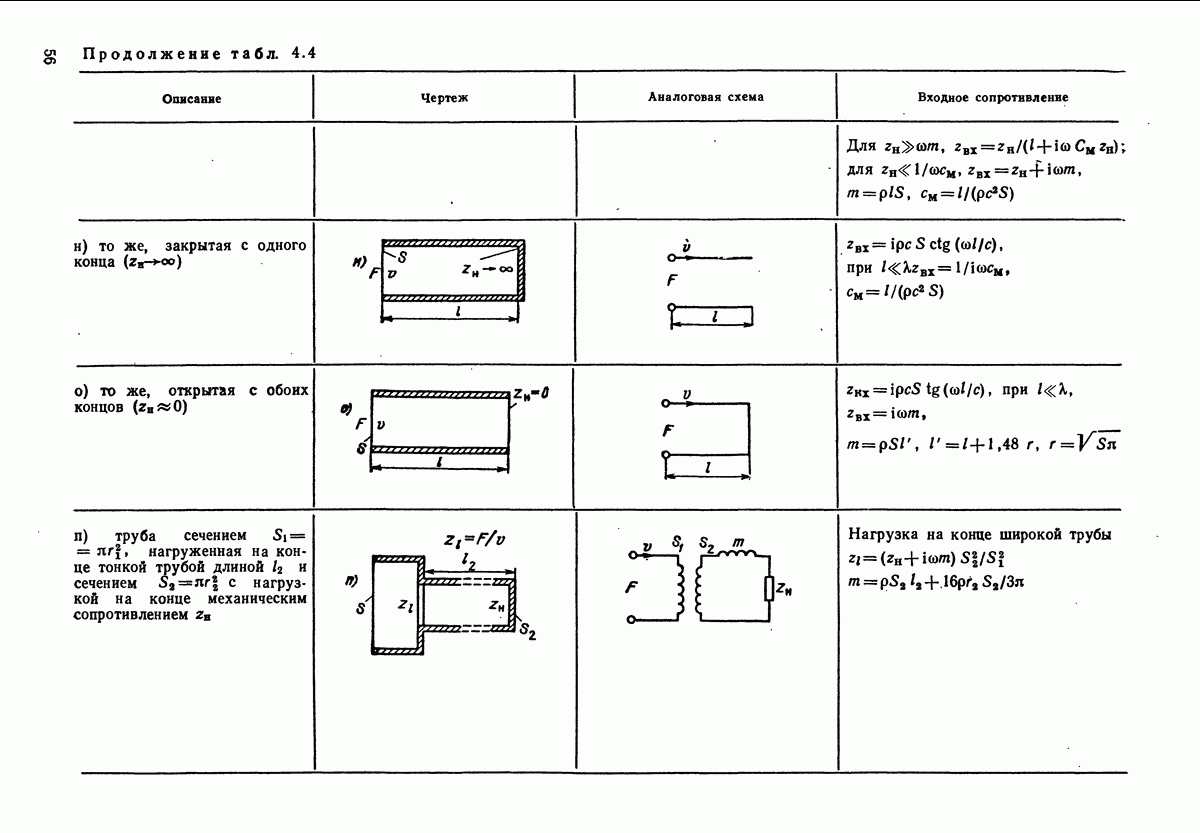
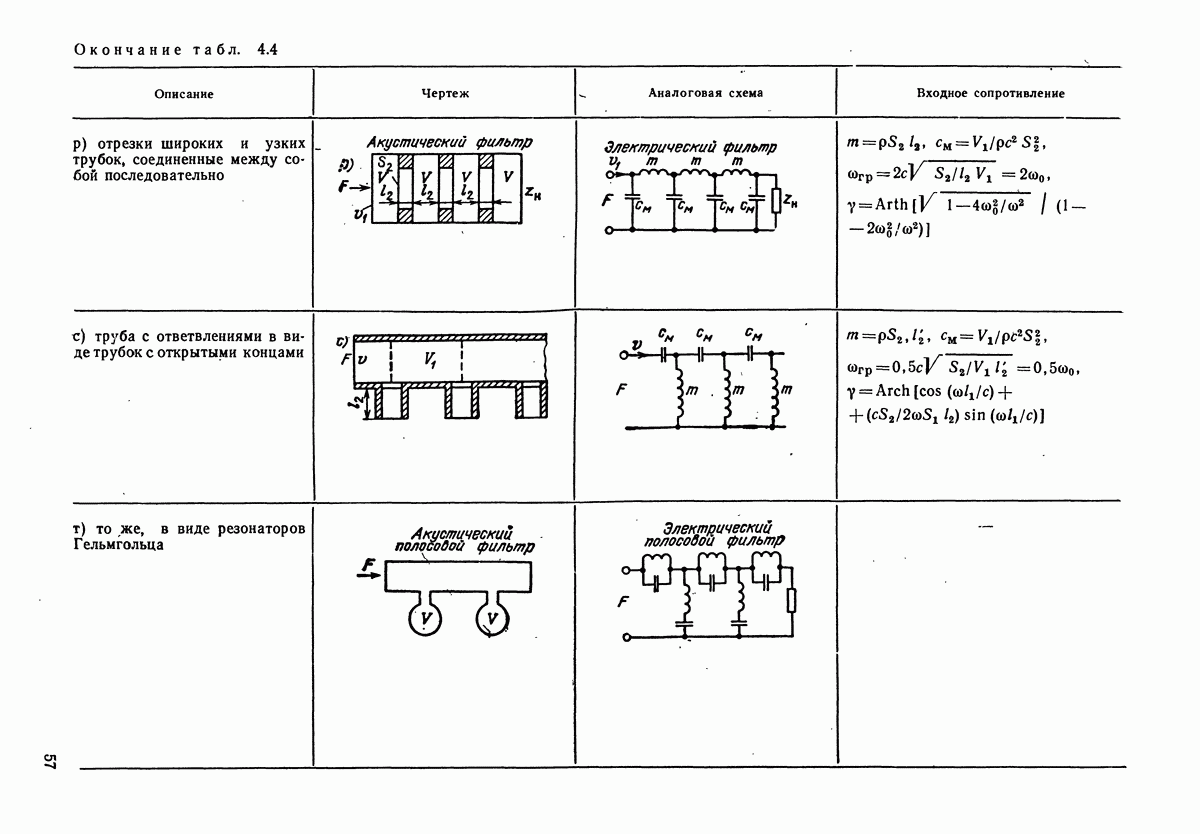
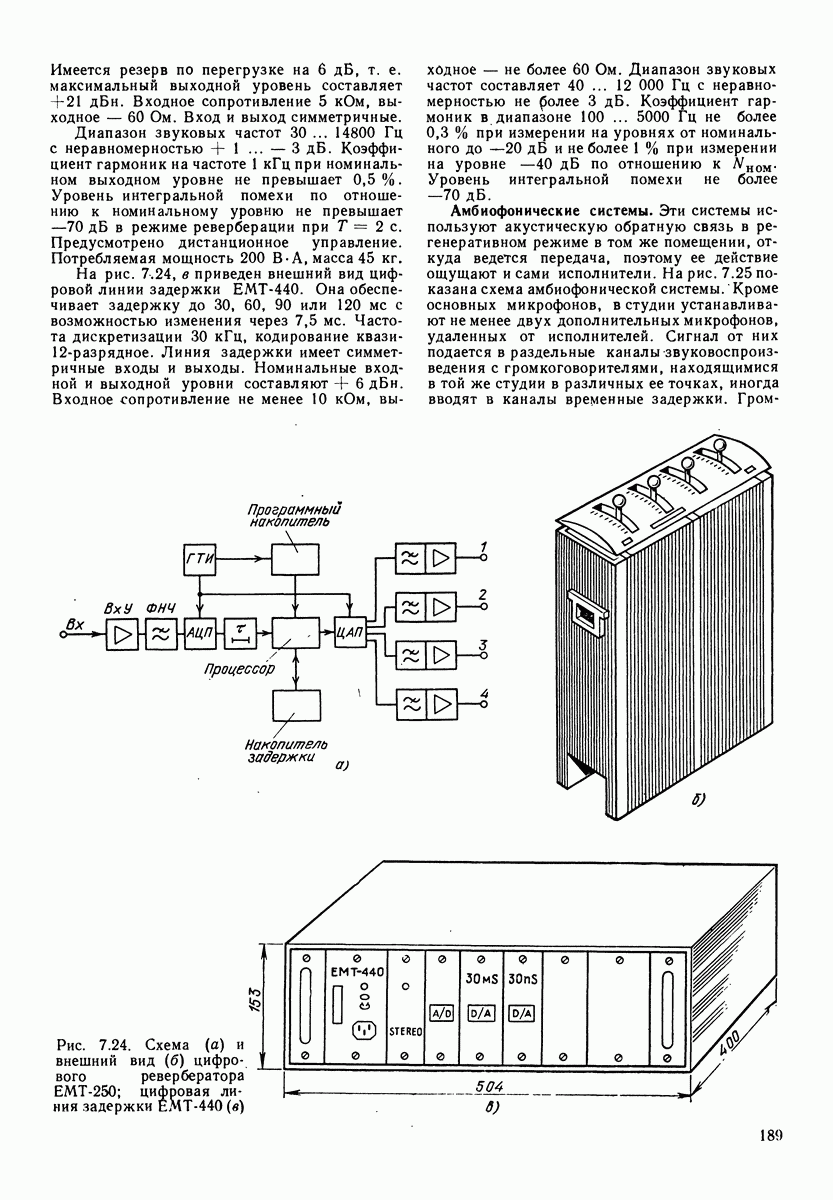
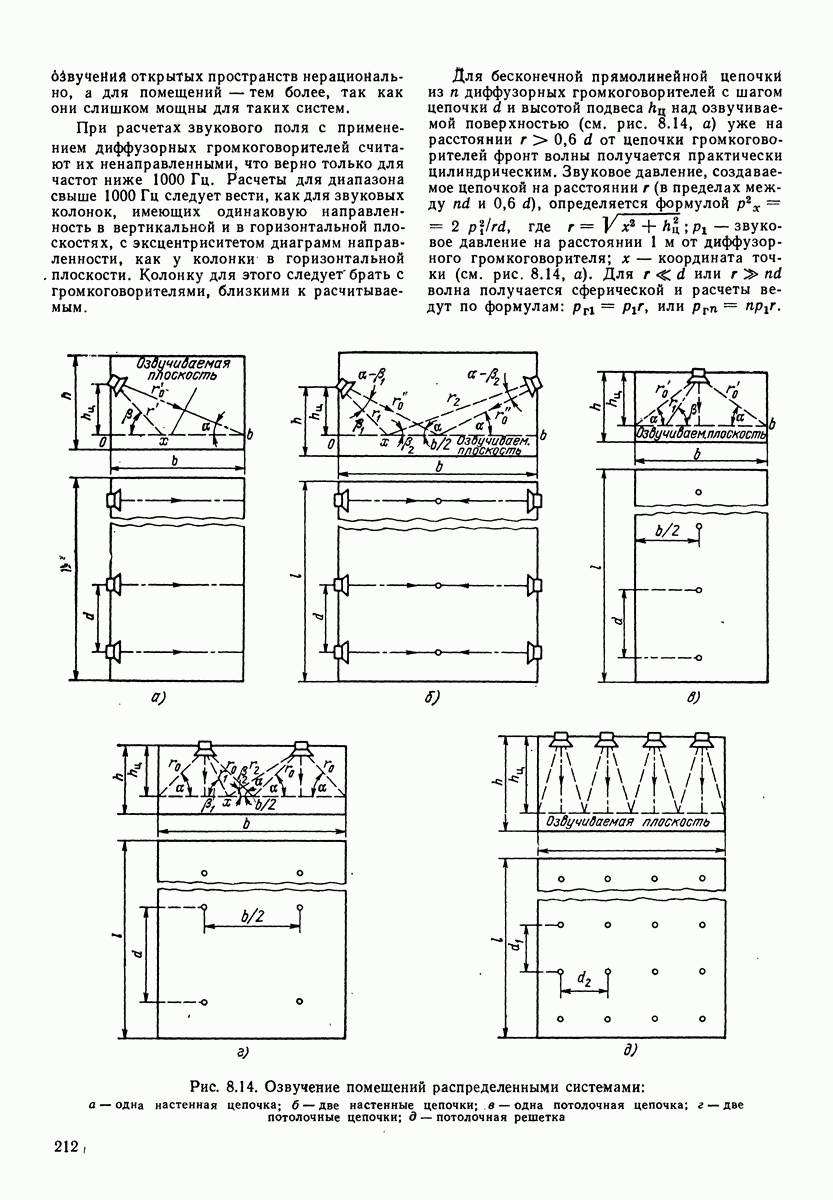
четырехполюсников при анализе процессов, происходящих в сложных механических системах, разработаны методы электромеханических аналогий. Они позволяют сводить механические системы к электрическим. Наиболее распространенный метод электромеханических аналогий основан на аналогиях, приведенных в табл. 4.1. В табл. 4.2 приведены аналогии соединений механических и электрических элементов. Аналогом последовательного (а) и (в)] соединения механических элементов, называемого цепочкой, является параллельное соединение электрических, а аналогом параллельного соединения (б) и г)] механических элементов (узла) является последовательное соединение электрических.
Для механической колебательной системы с параллельным соединением механических элементов уравнение вынужденных колебаний имеет вид

где  сила, приложенная к узлу механических элементов;
сила, приложенная к узлу механических элементов;  масса колебательной системы;
масса колебательной системы;  активное сопротивление ее;
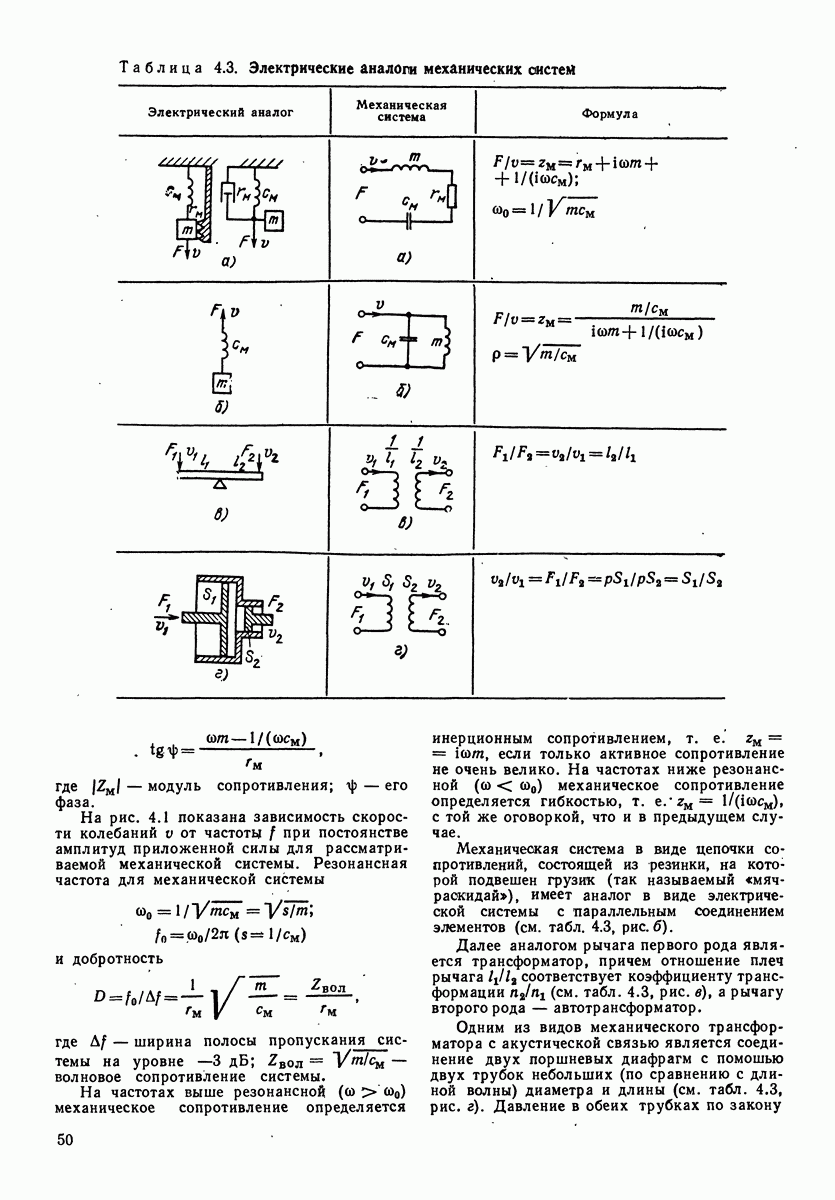
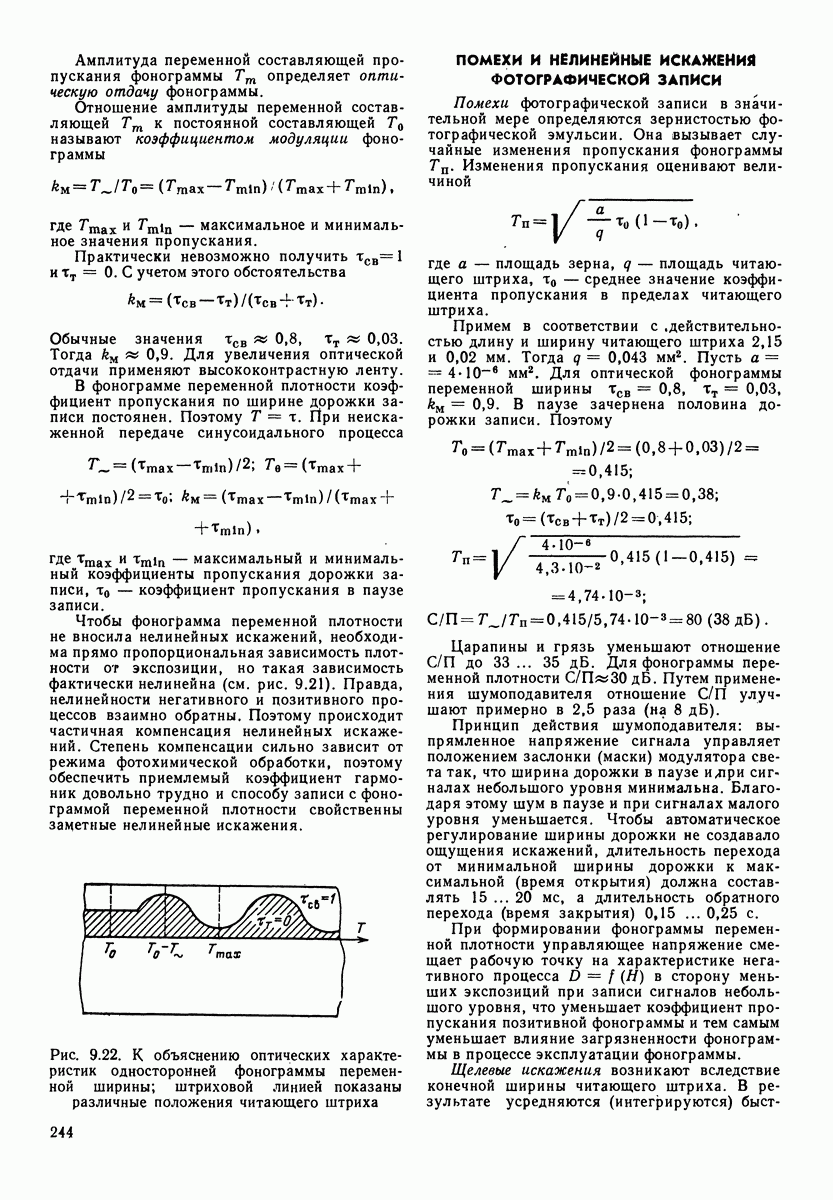
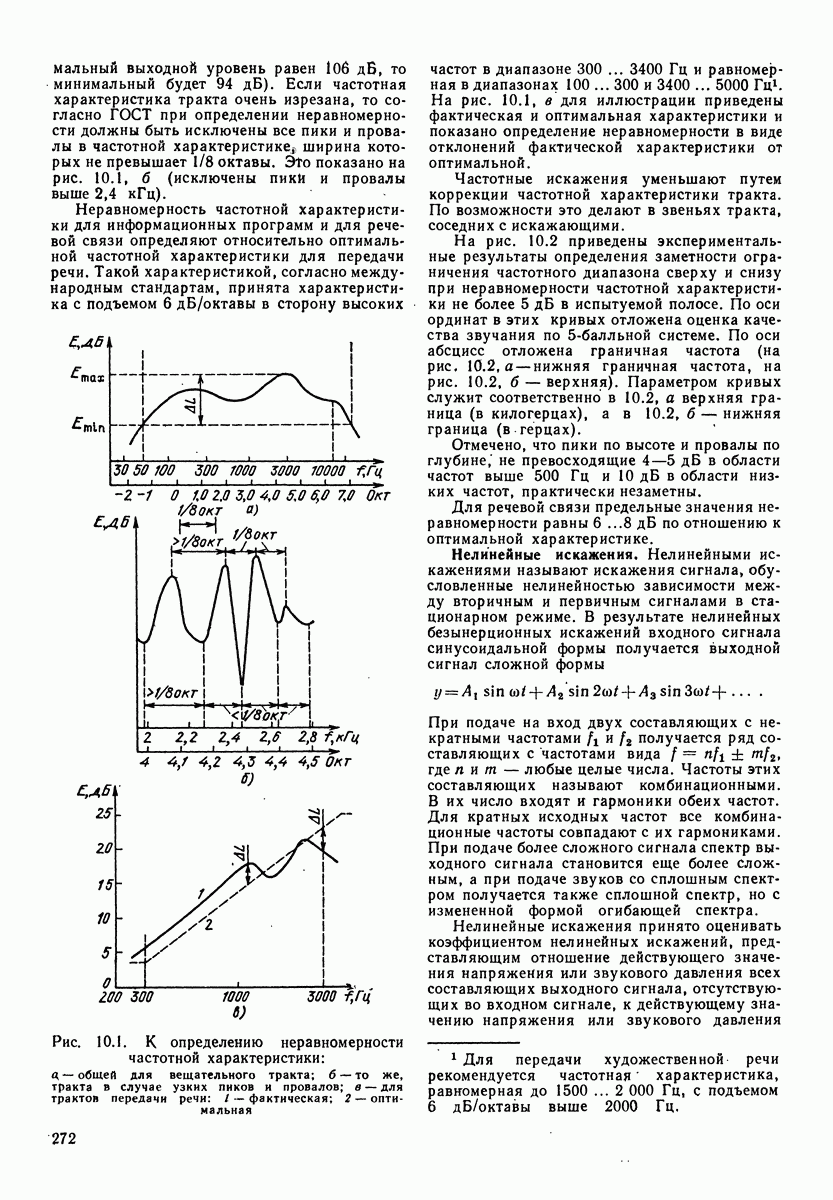
активное сопротивление ее;  — гибкость системы. Это уравнение аналогично уравнению для контура с последовательным соединением электрических элементов (табл. 4.3, рис. а), т. е. узел механических сопротивлений аналогичен контуру из электрических сопротивлений. Механическое сопротивление для такого узла
— гибкость системы. Это уравнение аналогично уравнению для контура с последовательным соединением электрических элементов (табл. 4.3, рис. а), т. е. узел механических сопротивлений аналогичен контуру из электрических сопротивлений. Механическое сопротивление для такого узла

Таблица 4.3. (см. скан) Электрические аналога механических систем

где  модуль сопротивления;
модуль сопротивления;  его фаза.
его фаза.
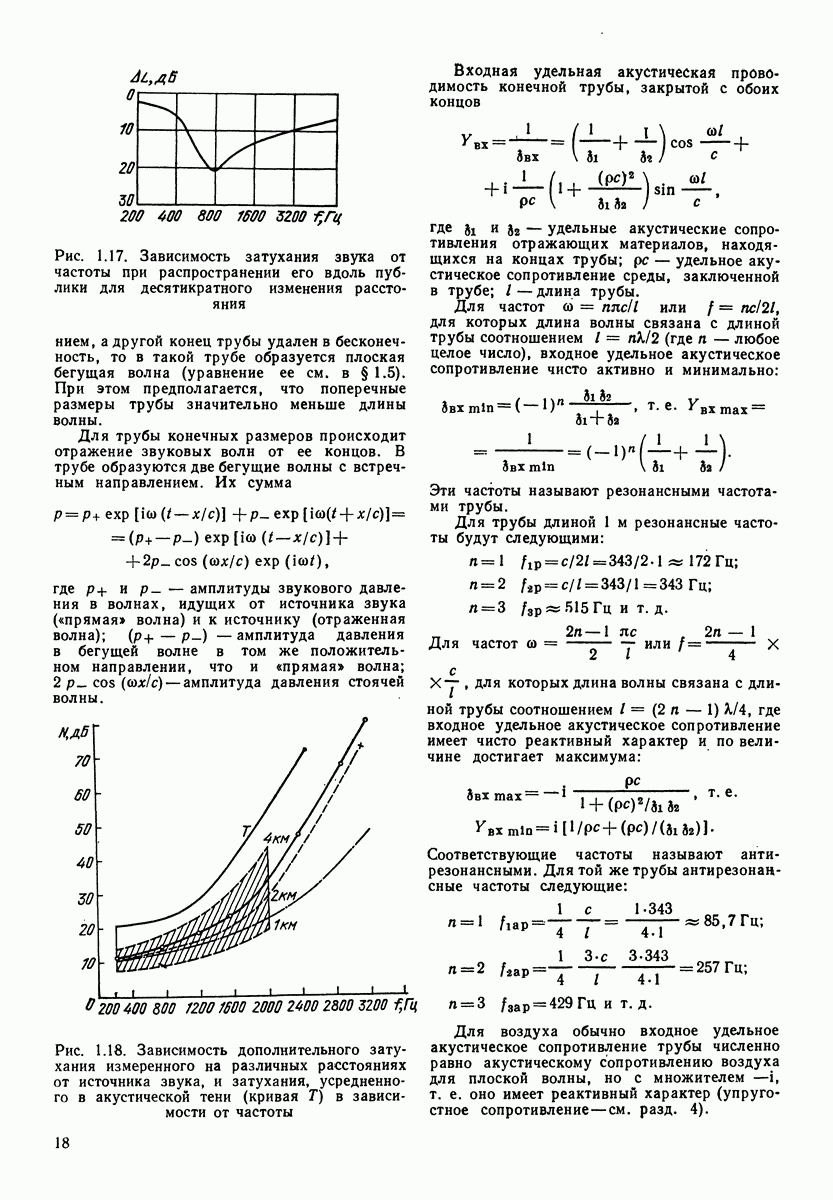
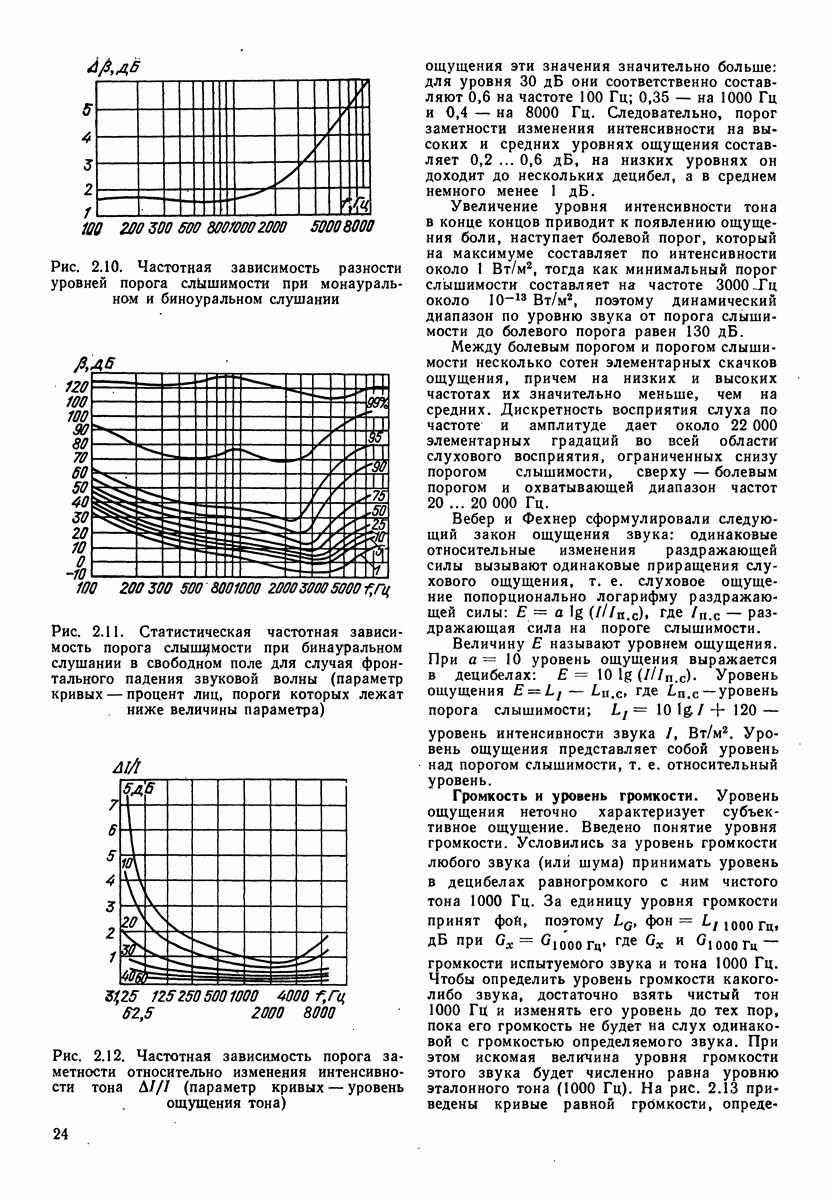
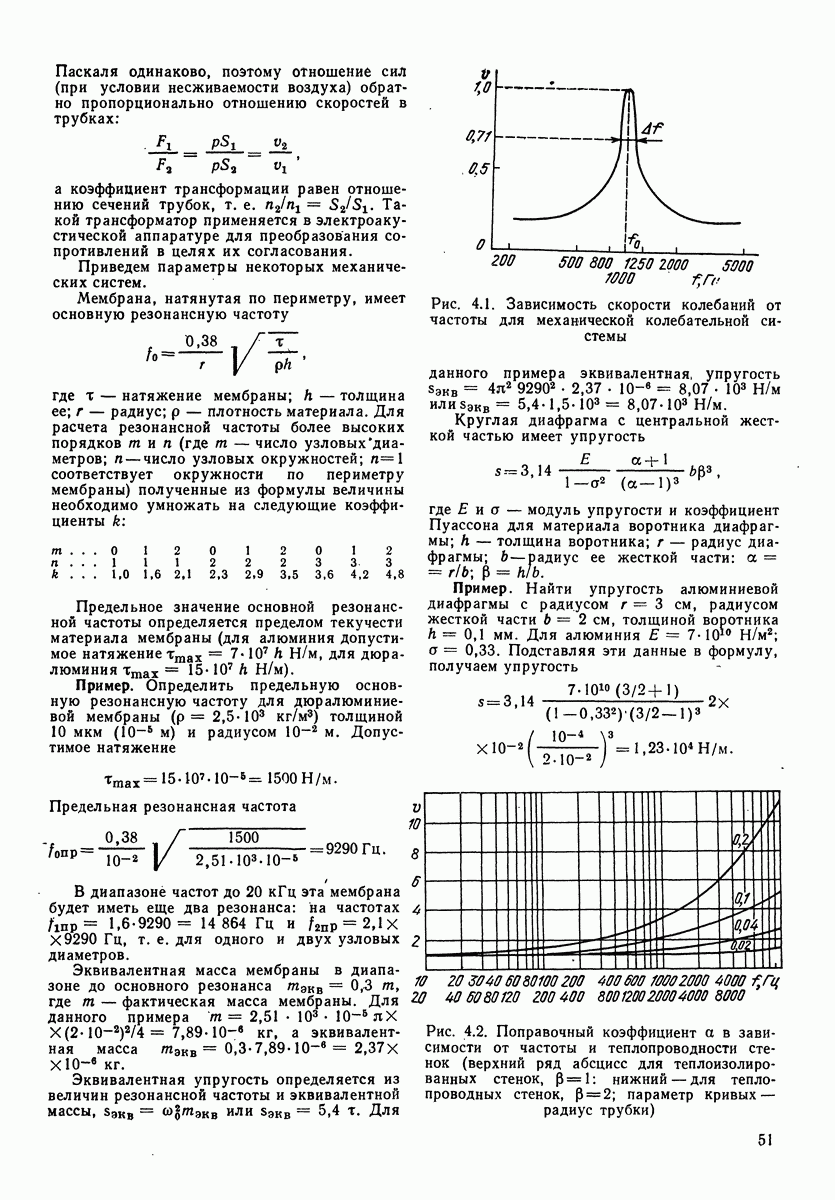
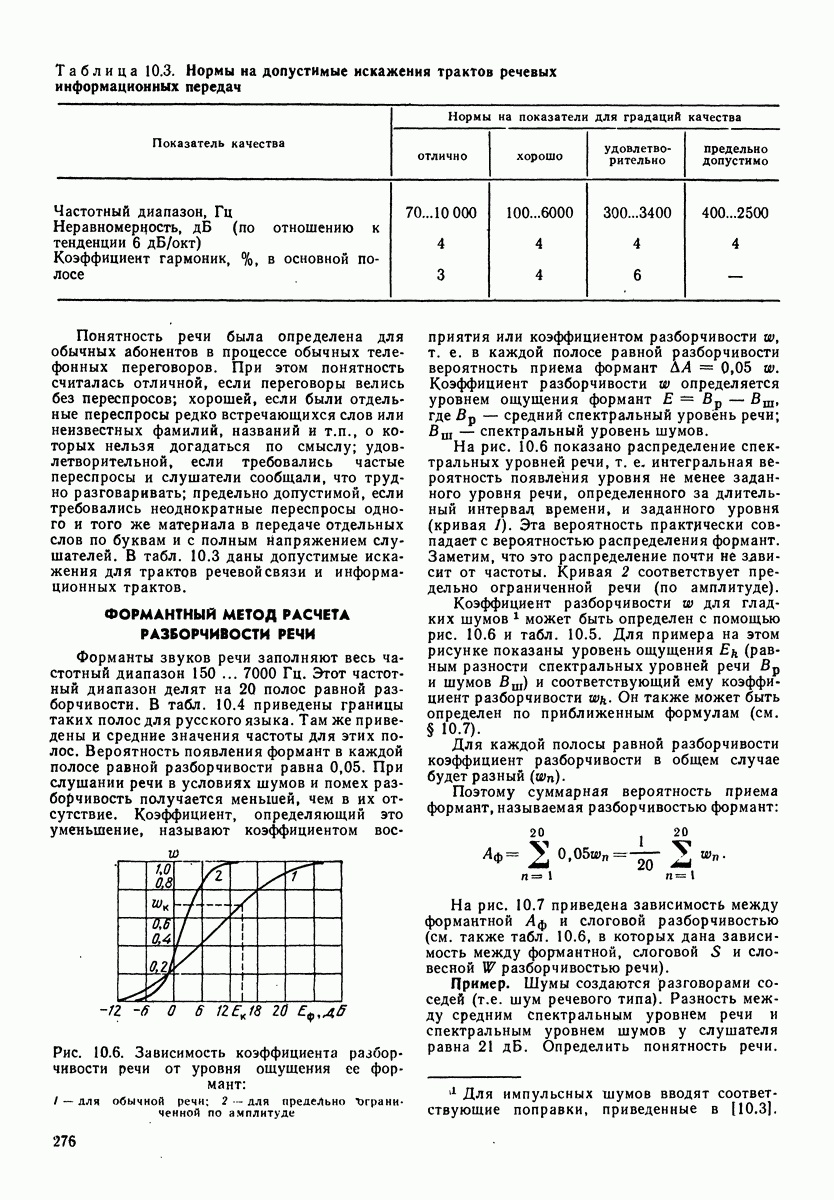
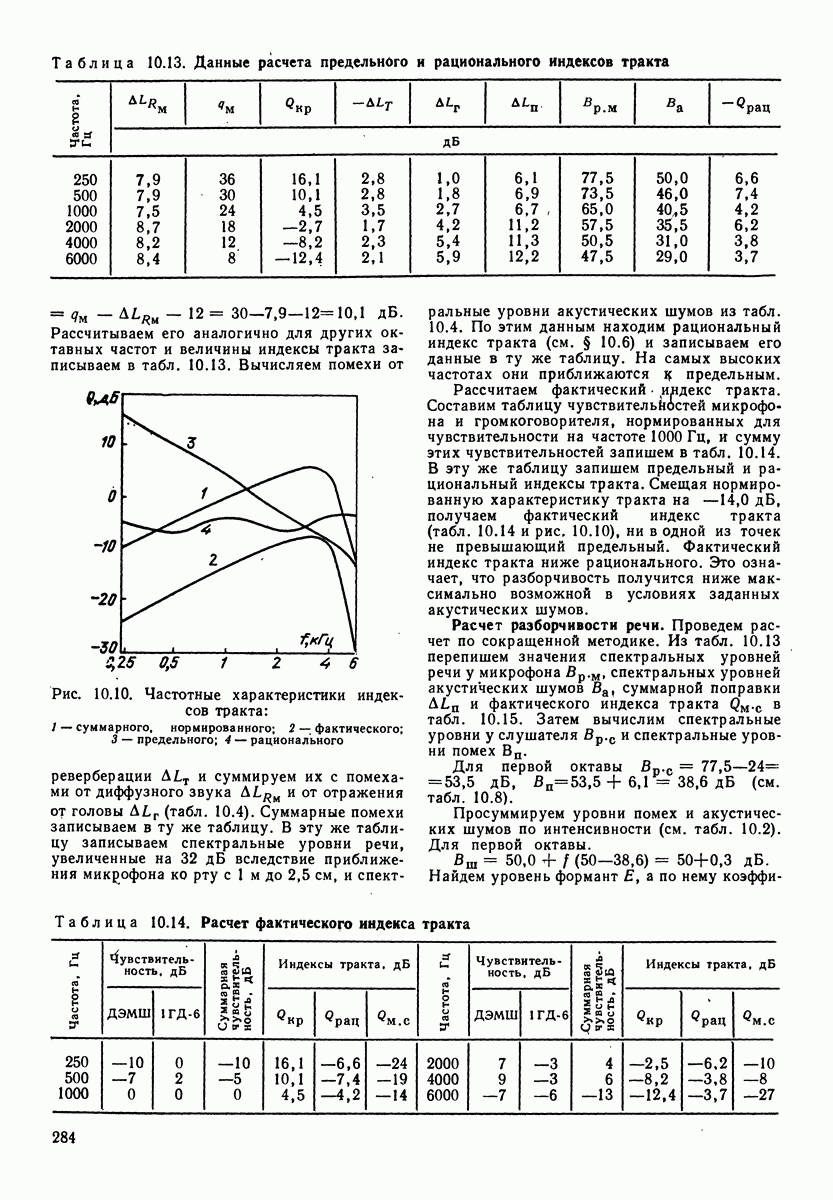
На рис. 4.1 показана зависимость скорости колебаний  от частоты
от частоты  при постоянстве амплитуд приложенной силы для рассматриваемой механической системы. Резонансная частота для механической системы
при постоянстве амплитуд приложенной силы для рассматриваемой механической системы. Резонансная частота для механической системы

и добротность

где  ширина полосы пропускания системы на уровне
ширина полосы пропускания системы на уровне  волновое сопротивление системы.
волновое сопротивление системы.
На частотах выше резонансной  механическое сопротивление определяется инерционным сопротивлением, т. е.
механическое сопротивление определяется инерционным сопротивлением, т. е.  если только активное сопротивление не очень велико. На частотах ниже резонансной
если только активное сопротивление не очень велико. На частотах ниже резонансной  механическое сопротивление определяется гибкостью,
механическое сопротивление определяется гибкостью,  с той же оговоркой, что и в предыдущем случае.
с той же оговоркой, что и в предыдущем случае.
Механическая система в виде цепочки сопротивлений, состоящей из резинки, на которой подвешен грузик (так называемый «мяч-раекидай»), имеет аналог в виде электрической системы с параллельным соединением элементов (см. табл. 4.3, рис. б).
Далее аналогом рычага первого рода является трансформатор, причем отношение плеч рычага  соответствует коэффициенту трансформации
соответствует коэффициенту трансформации  (см. табл. 4.3, рис. в), а рычагу второго рода — автотрансформатор.
(см. табл. 4.3, рис. в), а рычагу второго рода — автотрансформатор.
Одним из видов механического трансформатора с акустической связью является соединение двух поршневых диафрагм с помошью двух трубок небольших (по сравнению с длиной волны) диаметра и длины (см. табл. 4.3, рис. г). Давление в обеих трубках по закону
Паскаля одинаково, поэтому отношение сил (при условии несживаемости воздуха) обратно пропорционально отношению скоростей в трубках:

а коэффициент трансформации равен отношению сечений трубок, т. е.  Такой трансформатор применяется в электроакустической аппаратуре для преобразования сопротивлений в целях их согласования.
Такой трансформатор применяется в электроакустической аппаратуре для преобразования сопротивлений в целях их согласования.
Приведем параметры некоторых механических систем.
Мембрана, натянутая по периметру, имеет основную резонансную частоту

где  натяжение мембраны;
натяжение мембраны;  толщина ее;
толщина ее;  радиус;
радиус;  Плотность материала. Для расчета резонансной частоты более высоких порядков тип (где
Плотность материала. Для расчета резонансной частоты более высоких порядков тип (где  число узловыхдиаметров;
число узловыхдиаметров;  число узловых окружностей;
число узловых окружностей;  соответствует окружности по периметру мембраны) полученные из формулы величины необходимо умножать на следующие коэффициенты к:
соответствует окружности по периметру мембраны) полученные из формулы величины необходимо умножать на следующие коэффициенты к:

Предельное значение основной резонансной частоты определяется пределом текучести материала мембраны (для алюминия допустимое натяжение ттах  для дюралюминия ттах
для дюралюминия ттах 
Пример. Определить предельную основную резонансную частоту для дюралюминиевой мембраны  толщиной
толщиной  и радиусом
и радиусом  Допустимое натяжение
Допустимое натяжение

Предельная резонансная частота

В диапазоне частот до  эта мембрана будет иметь еще два резонанса: на частотах
эта мембрана будет иметь еще два резонанса: на частотах  Гц и
Гц и  Гц, т. е. для одного и двух узловых диаметров.
Гц, т. е. для одного и двух узловых диаметров.
Эквивалентная масса мембраны в диапазоне до основного резонанса  где
где  фактическая масса мембраны. Для данного примера
фактическая масса мембраны. Для данного примера  а эквивалентная масса тэкв
а эквивалентная масса тэкв 
Эквивалентная упругость определяется из величин резонансной частоты и эквивалентной массы,  или
или 

Рис. 4.1. Зависимость скорости колебаний от частоты для механической колебательной системы
Для данного примера эквивалентная, упругость  илиээкв
илиээкв 
Круглая диафрагма с центральной жесткой частью имеет упругость

где  — модуль упругости и коэффициент Пуассона для материала воротника диафрагмы;
— модуль упругости и коэффициент Пуассона для материала воротника диафрагмы;  толщина воротника;
толщина воротника;  радиус диафрагмы;
радиус диафрагмы;  -радиус ее жесткой части:
-радиус ее жесткой части: 
Пример. Найти упругость алюминиевой диафрагмы с радиусом  см, радиусом жесткой части
см, радиусом жесткой части  см, толщиной воротника
см, толщиной воротника  Для алюминия
Для алюминия  . Подставляя эти данные в формулу, получаем упругость
. Подставляя эти данные в формулу, получаем упругость


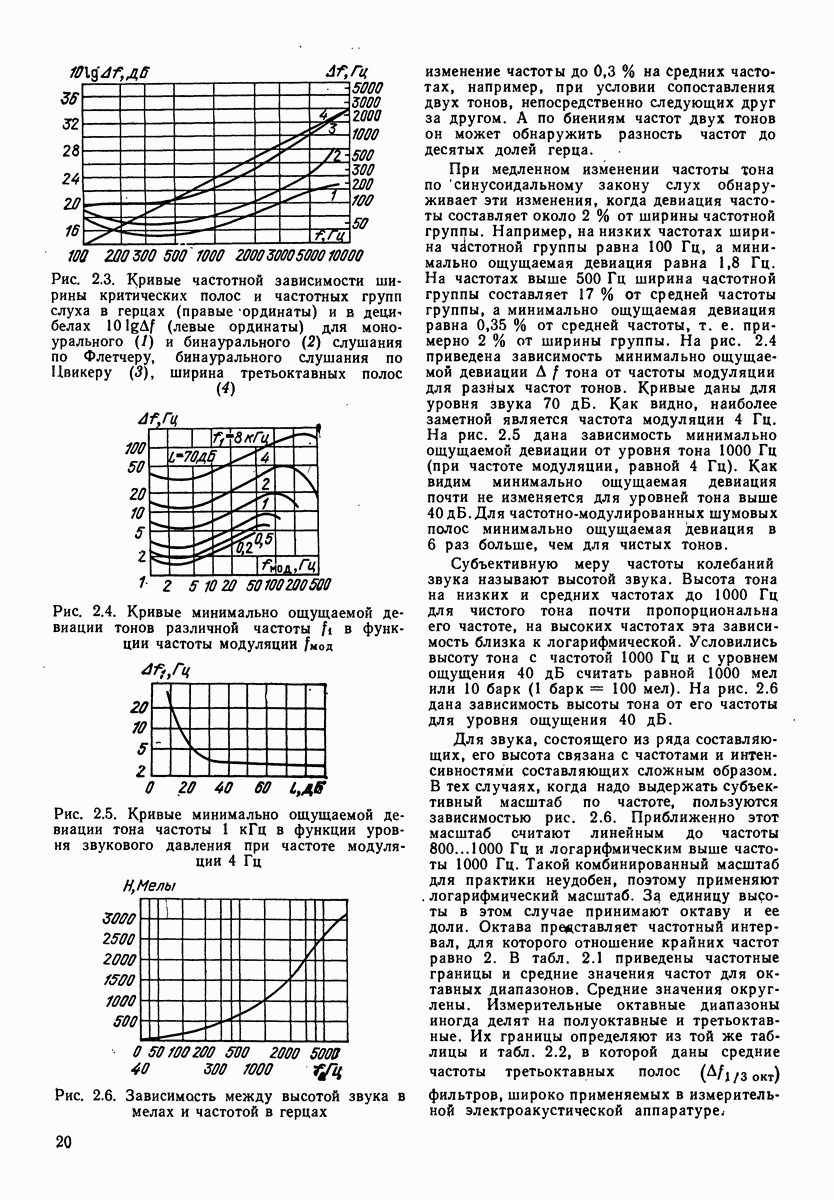
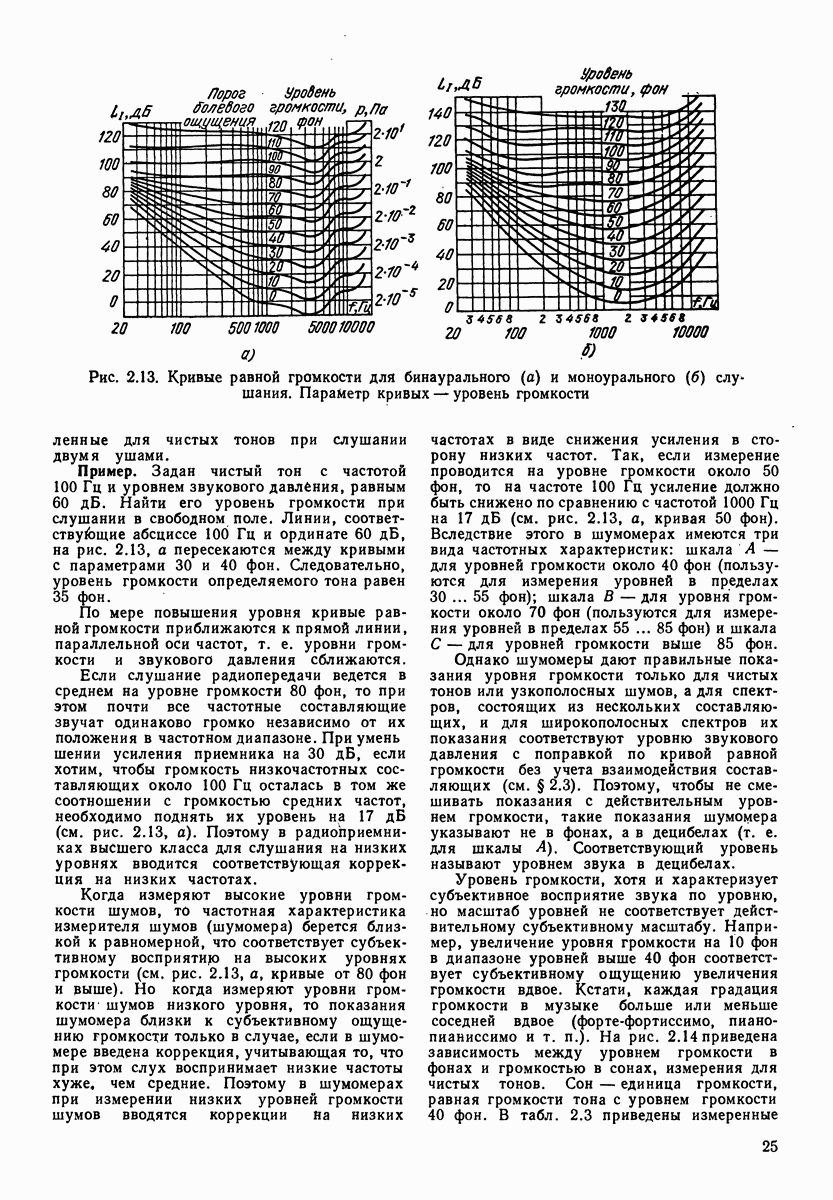
Рис. 4.2. Поправочный коэффициент а в зависимости от частоты и теплопроводности стенок (верхний ряд абсцисс для теплоизолированных стенок,  нижний — для теплопроводных стенок,
нижний — для теплопроводных стенок,  параметр кривых — радиус трубки)
параметр кривых — радиус трубки)
Следовательно, гибкость 
Эквивалентная масса такой диафрагмы  где
где  массы жесткой части и воротника диафрагмы.
массы жесткой части и воротника диафрагмы.
Если жесткая часть имеет толщину  то ее масса
то ее масса

Эквивалентная масса воротника и диафрагмы соответственно  Резонансная частота диафрагмы
Резонансная частота диафрагмы

Для рассматриваемого случая

Круглая, зажатая по периметру, пластинка имеет упругость и основную резонансную частоту соответственно:

где  — модуль упругости и коэффициент Пуассона для материала пластинки;
— модуль упругости и коэффициент Пуассона для материала пластинки;  толщина пластинки
толщина пластинки  радиус ее;
радиус ее;  плотность материала.
плотность материала.
Эквивалентная масса пластинки  где
где  фактическая масса пластинки.
фактическая масса пластинки.
Для определения первых четырех резонансных частот сложного колебания полученные значения основной частоты необходимо умножить на следующие коэффициенты: 1, 6, 15, 28 соответственно числу узловых окружностей; 1, 2, 3, 4.
Пример. Найти основную резонансную частоту, упругость и эквивалентную массу стальной пластинки радиусом 2 см и толщиной  Для стали модуль
Для стали модуль  коэффициент Пуассона
коэффициент Пуассона  и плотность
и плотность 
Основная резонансная частота

Упругость

Эквивалентная масса 
Круглая, запертая по периметру, пластиика имеет упругость и резонансную частоту соответственно:

Эквивалентная масса тэкв 
Для пластинки из предыдущего примера упругость будет меньше в  раза, а резонансная частота в
раза, а резонансная частота в  раз меньше, т. е.
раз меньше, т. е.  Эквивалентная масса
Эквивалентная масса  т.е. в 1,85 раза больше, чем для зажатой пластинки.
т.е. в 1,85 раза больше, чем для зажатой пластинки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ 1. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- 1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ ЗВУКОВОГО ПОЛЯ
- 1.3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВУКОВОГО ПОЛЯ
- 1.4. УРОВНИ
- 1.5. ПЛОСКАЯ ВОЛНА
- 1.6. СФЕРИЧЕСКАЯ ВОЛНА
- 1.7. ЦИЛИНДРИЧЕСКАЯ ВОЛНА
- 1.8. ИНТЕРФЕРЕНЦИЯ ВОЛН
- 1.9. ОТРАЖЕНИЕ ЗВУКА
- 1.10. ПРЕЛОМЛЕНИЕ ЗВУКА
- 1.11. ДИФРАКЦИЯ ВОЛН
- 1.12. ЗАТУХАНИЕ ВОЛН
- 1.13. РАСПРОСТРАНЕНИЕ ЗВУКА В ТРУБАХ
- Раздел 2. ОСНОВНЫЕ СВОЙСТВА СЛУХА
- 2.2. ВОСПРИЯТИЕ ПО ЧАСТОТЕ
- 2.3. ВОСПРИЯТИЕ ПО АМПЛИТУДЕ
- 2.4. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЛУХА
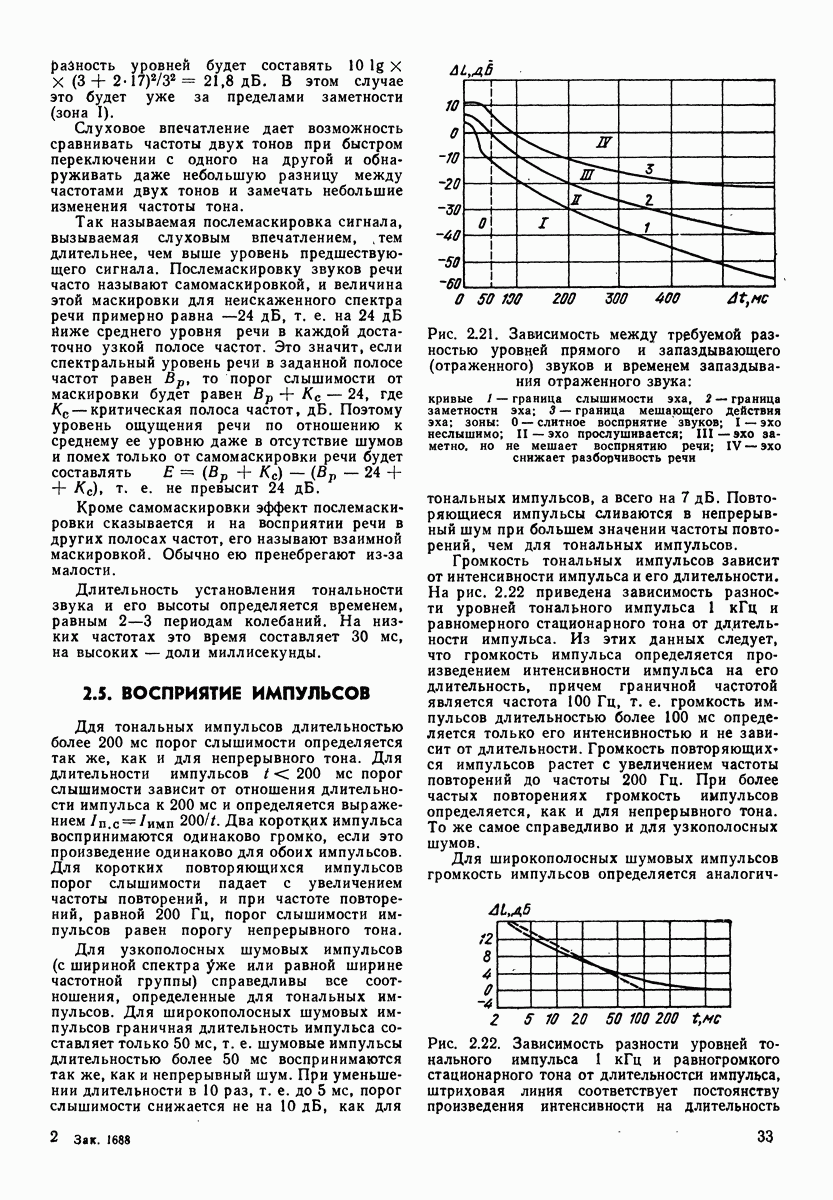
- 2.5. ВОСПРИЯТИЕ ИМПУЛЬСОВ
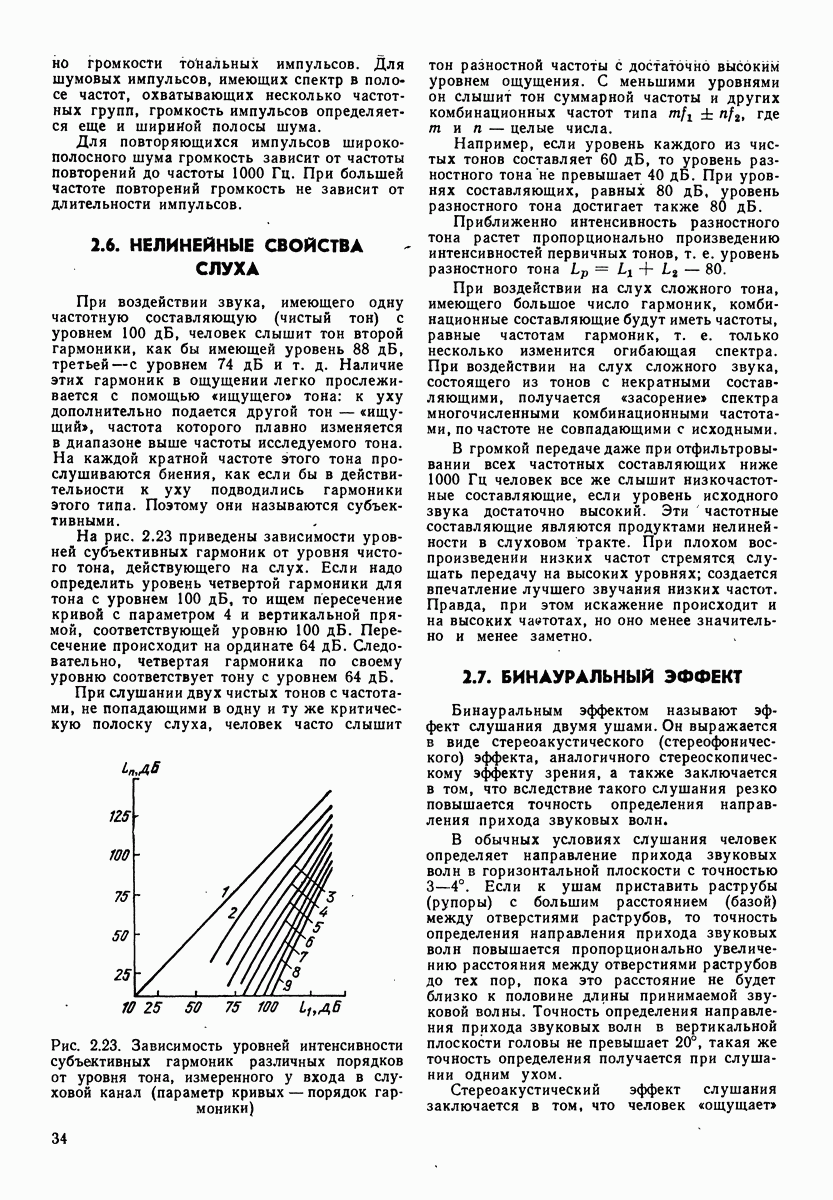
- 2.6. НЕЛИНЕЙНЫЕ СВОЙСТВА СЛУХА
- 2.7. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- РАЗДЕЛ 3. ПЕРВИЧНЫЕ АКУСТИЧЕСКИЕ СИГНАЛЫ И ИХ ИСТОЧНИКИ
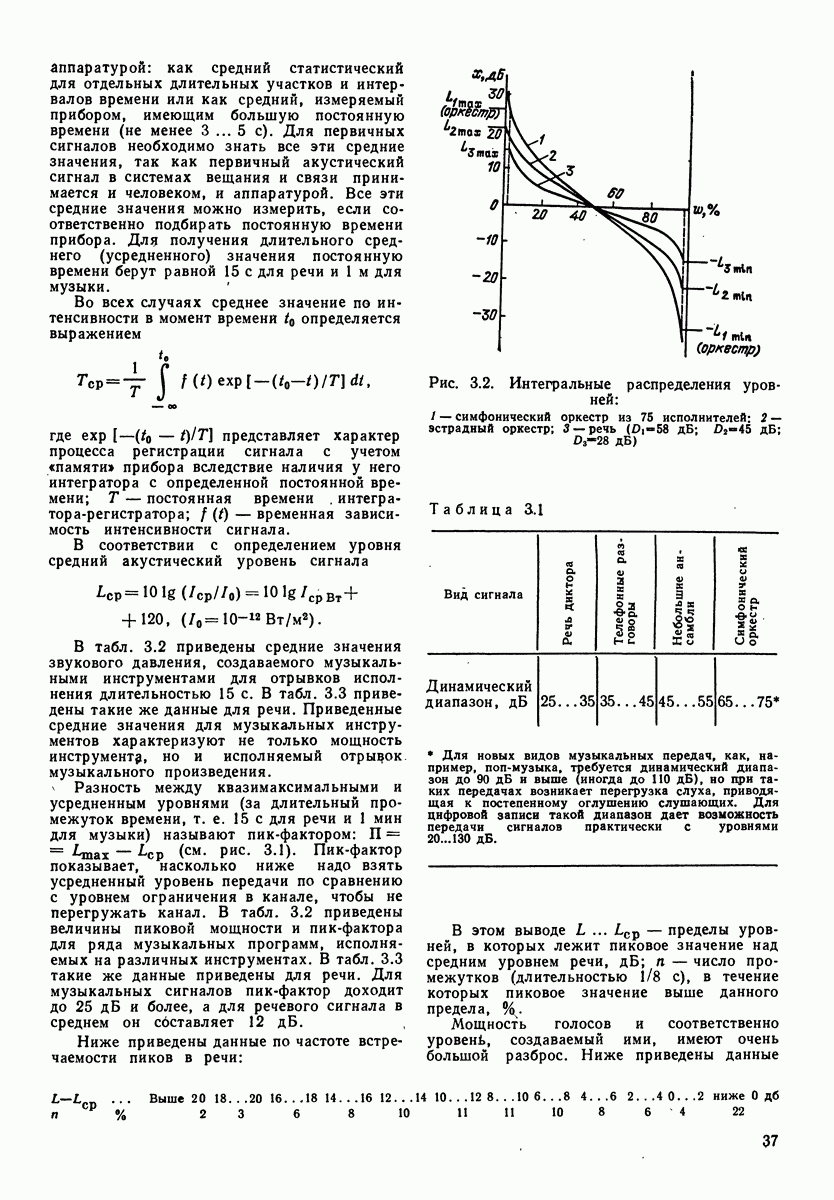
- 3.2. ДИНАМИЧЕСКИЙ ДИАПАЗОН И УРОВНИ
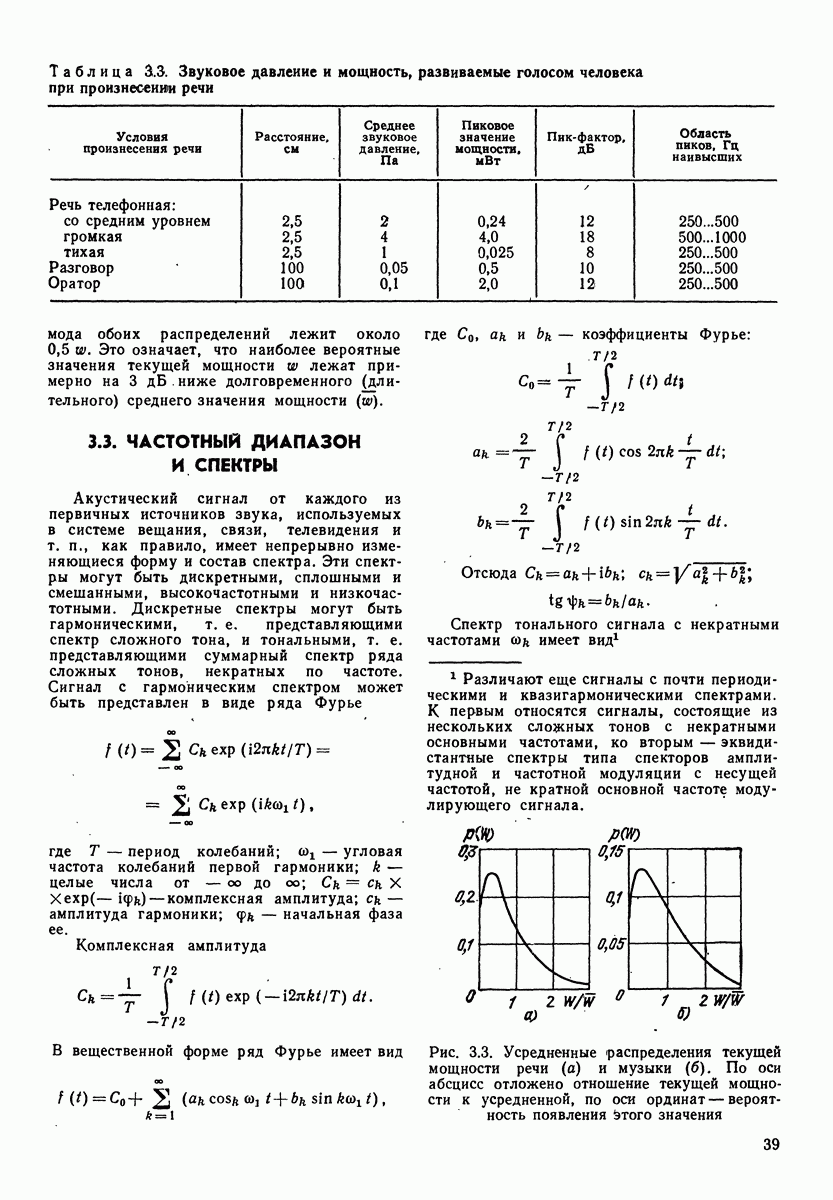
- 3.3. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
- 3.4. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ АКУСТИЧЕСКОГО СИГНАЛА
- 3.5. ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ РЕЧИ ВОКРУГ ГОЛОВЫ
- 3.6. ПЕРВИЧНЫЙ РЕЧЕВОЙ СИГНАЛ
- 3.7. ГОРТАНЬ КАК ИСТОЧНИК ЗВУКОВЫХ КОЛЕБАНИЙ
- РАЗДЕЛ 4. ЭЛЕКТРОАКУСТИЧЕСКИЕ ЭЛЕМЕНТЫ И СИСТЕМЫ
- 4.2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИ
- 4.3. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
- 4.4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4.5. МЕТОДЫ СОСТАВЛЕНИЯ АНАЛОГОВЫХ СХЕМ
- РАЗДЕЛ 5. МИКРОФОНЫ И ЛАРИНГОФОНЫ
- 5.2. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ МИКРОФОНОВ
- 5.3. НАПРАВЛЕННЫЕ СВОЙСТВА МИКРОФОНОВ
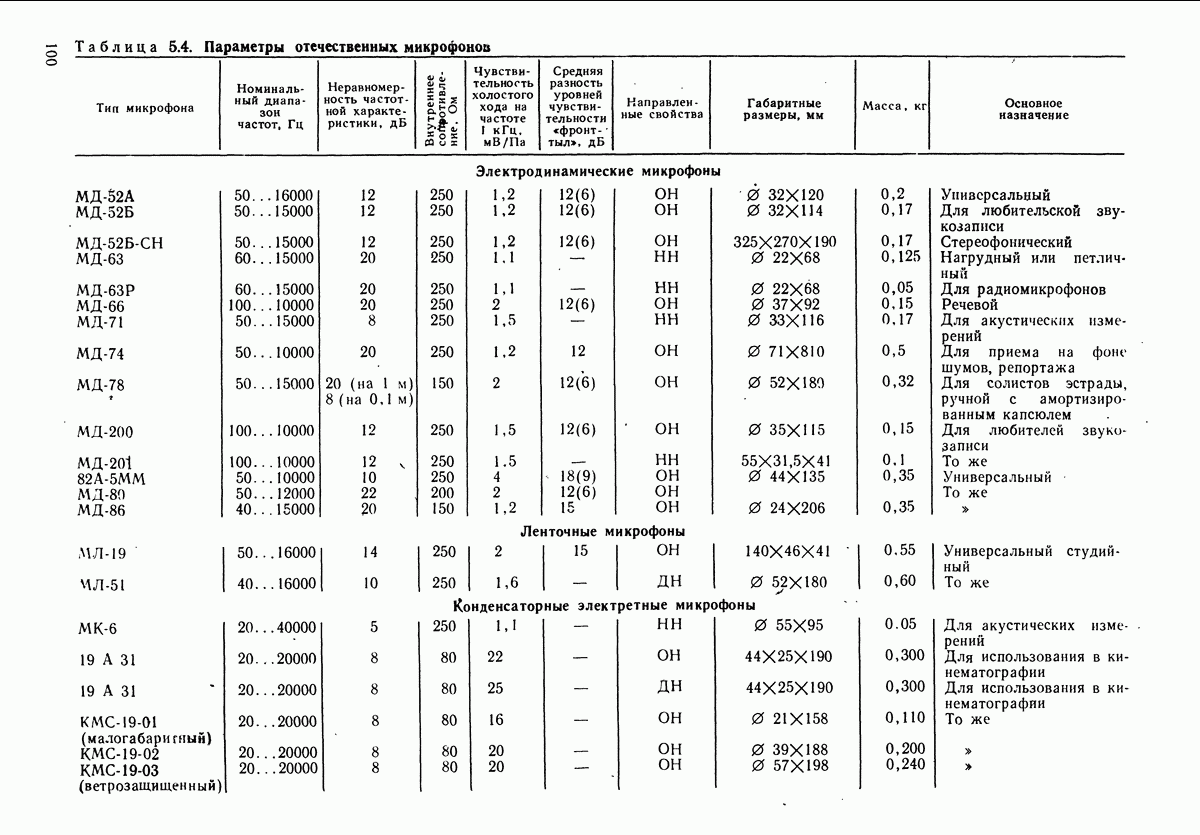
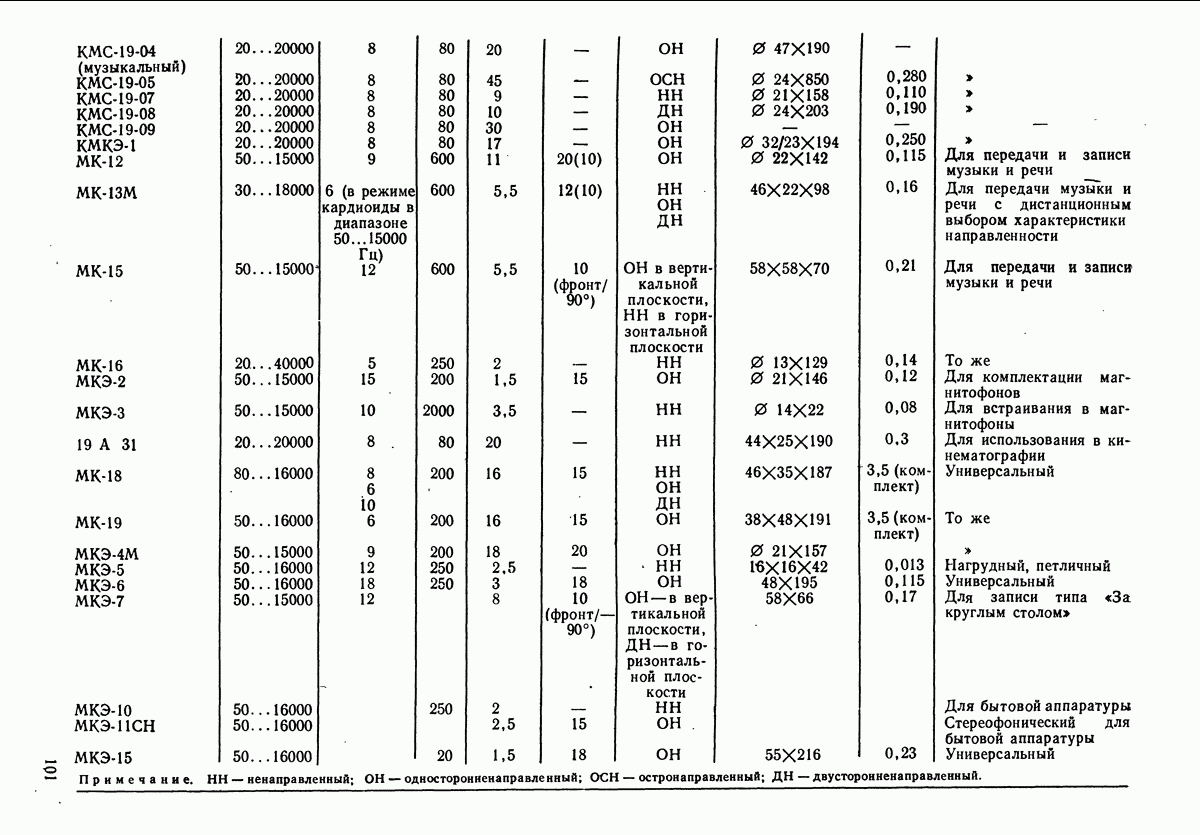
- 5.4. ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
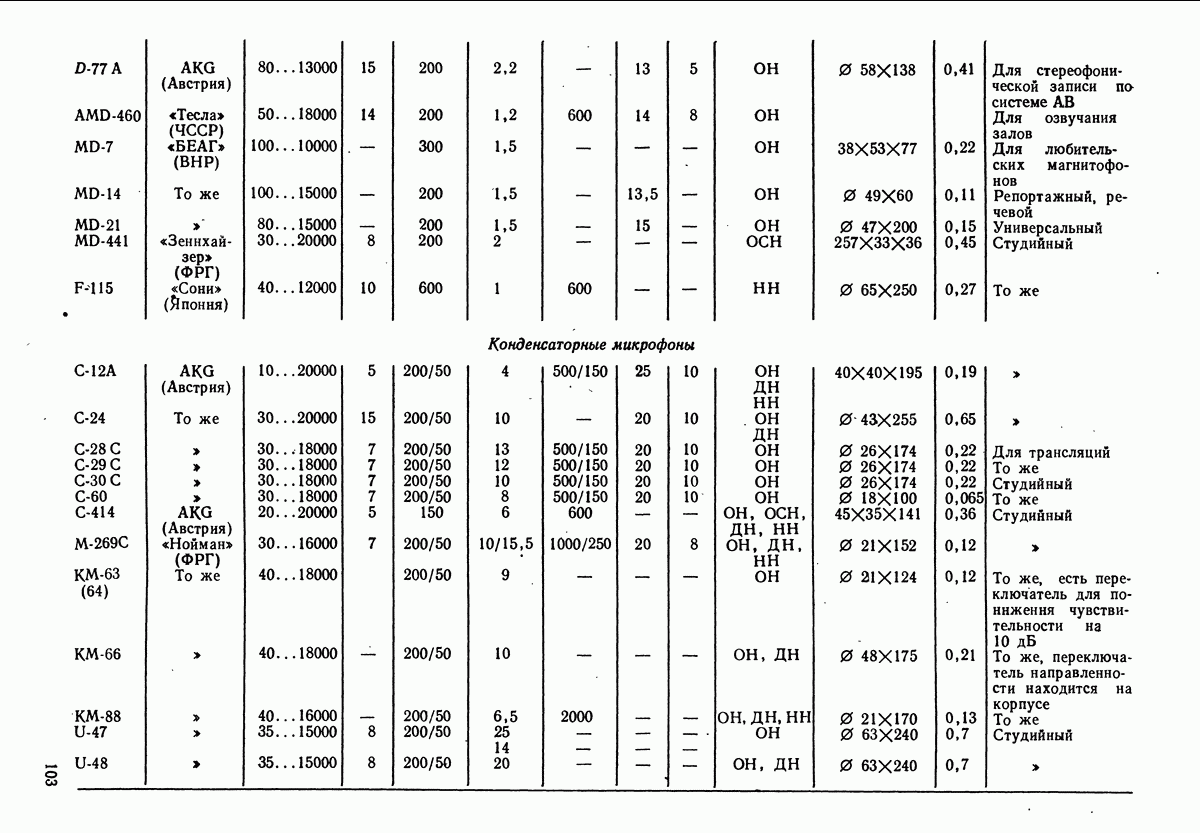
- 5.5. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
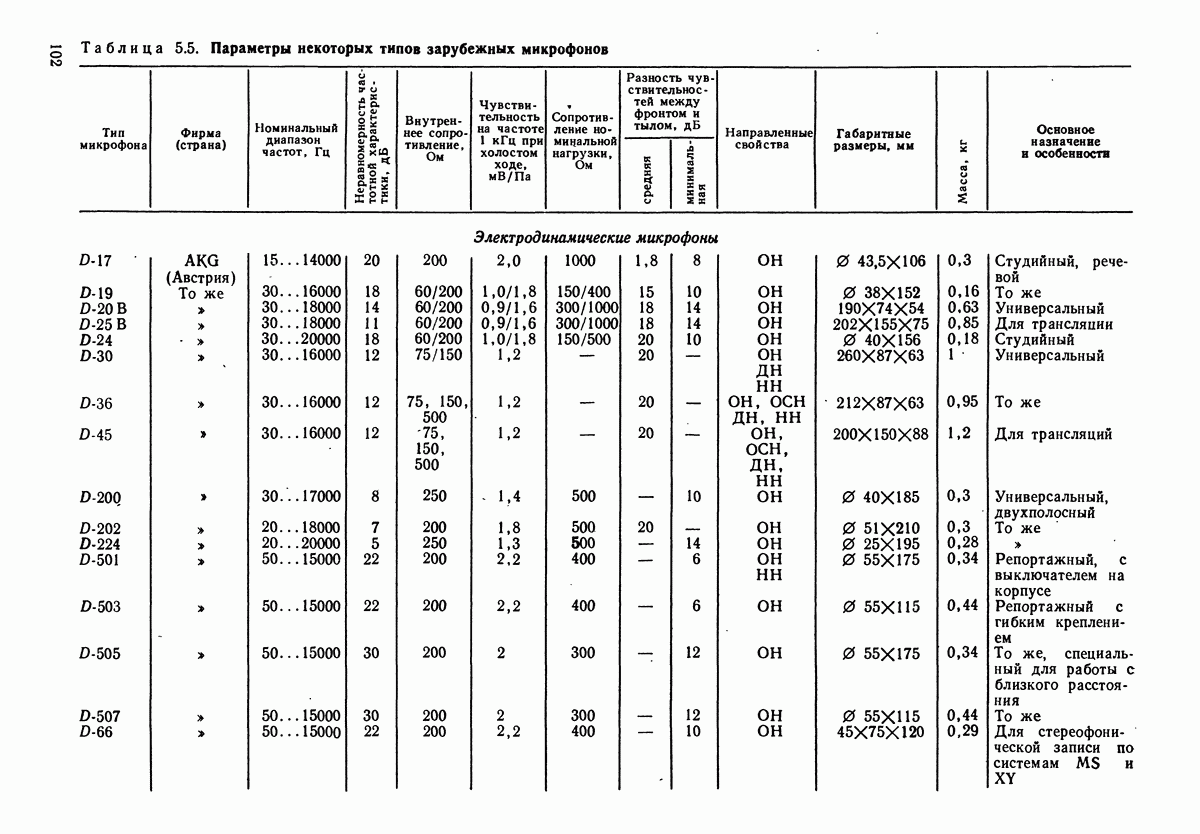
- 5.6. НЕКОТОРЫЕ ДРУГИЕ ТИПЫ МИКРОФОНОВ
- 5.7. ТЕХНИЧЕСКАЯ ЭКСПЛУАТАЦИЯ МИКРОФОНОВ
- РАЗДЕЛ 6. ГРОМКОГОВОРИТЕЛИ И ТЕЛЕФОНЫ
- 6.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ТЕЛЕФОНОВ И ГРОМКОГОВОРИТЕЛЕЙ
- 6.3. ТРЕБОВАНИЯ К ГРОМКОГОВОРИТЕЛЯМ И ТЕЛЕФОНАМ
- 6.4. ОПИСАНИЕ НЕКОТОРЫХ ТИПОВ ТЕЛЕФОНОВ, ГРОМКОГОВОРИТЕЛЕЙ И АКУСТИЧЕСКИХ СИСТЕМ ТЕЛЕФОНЫ
- 6.5. КОНСТРУКЦИИ АКУСТИЧЕСКИХ ОФОРМЛЕНИЙ ПЛОСКИЙ ЭКРАН
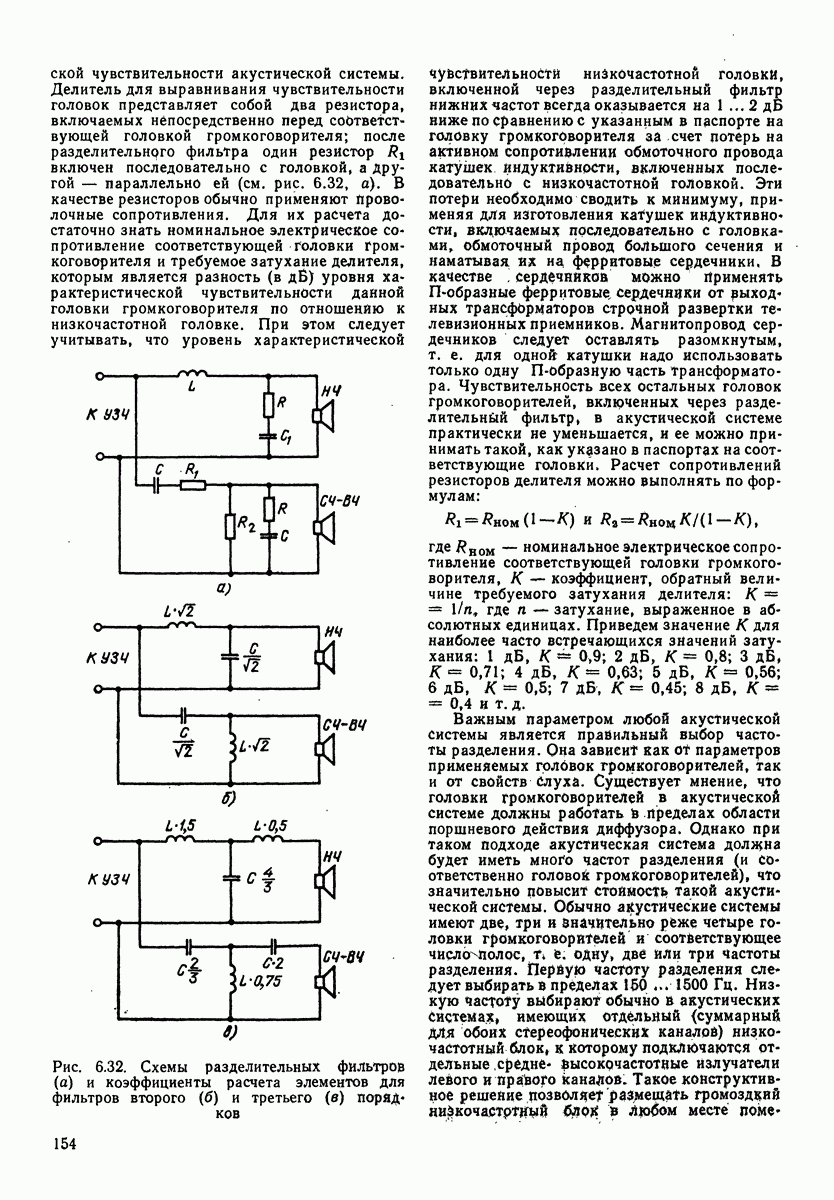
- 6.6. ВКЛЮЧЕНИЕ ГОЛОВОК ГРОМКОГОВОРИТЕЛЕЙ В АКУСТИЧЕСКИЕ СИСТЕМЫ
- 6.7. РАЗМЕЩЕНИЕ АКУСТИЧЕСКИХ СИСТЕМ
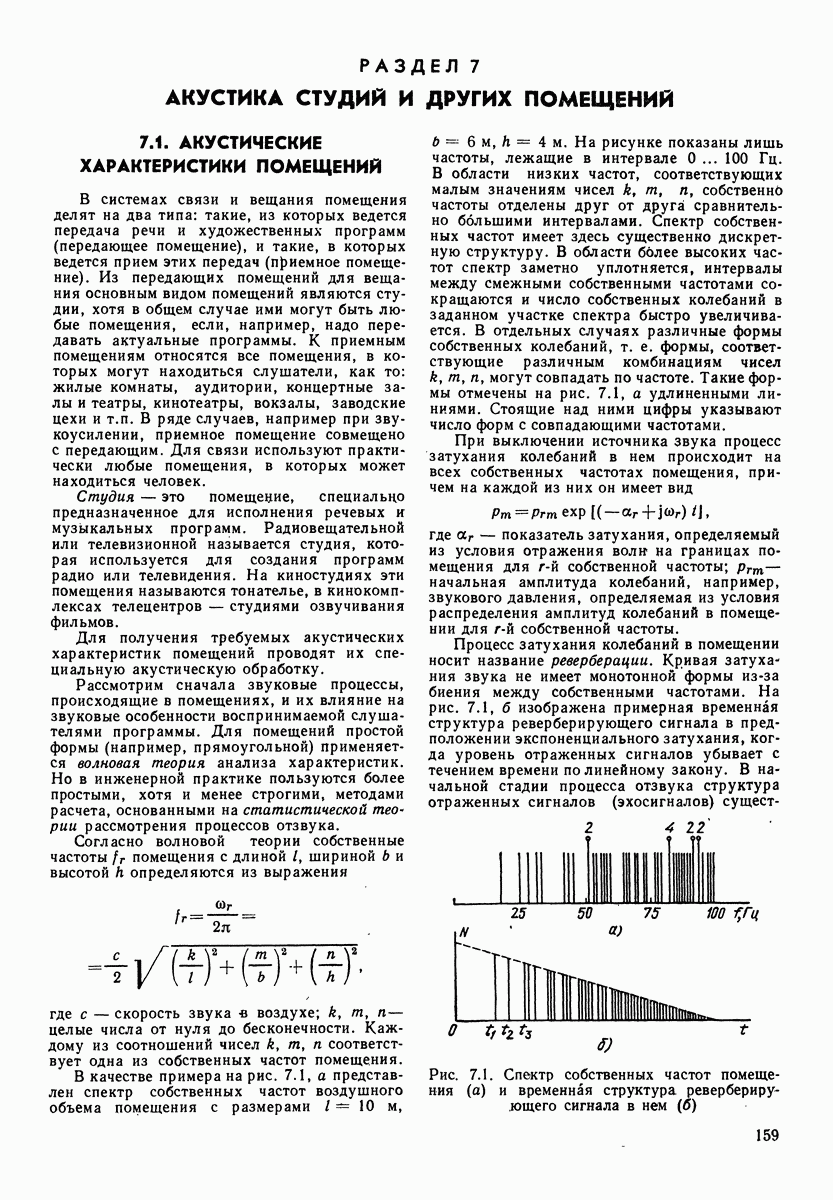
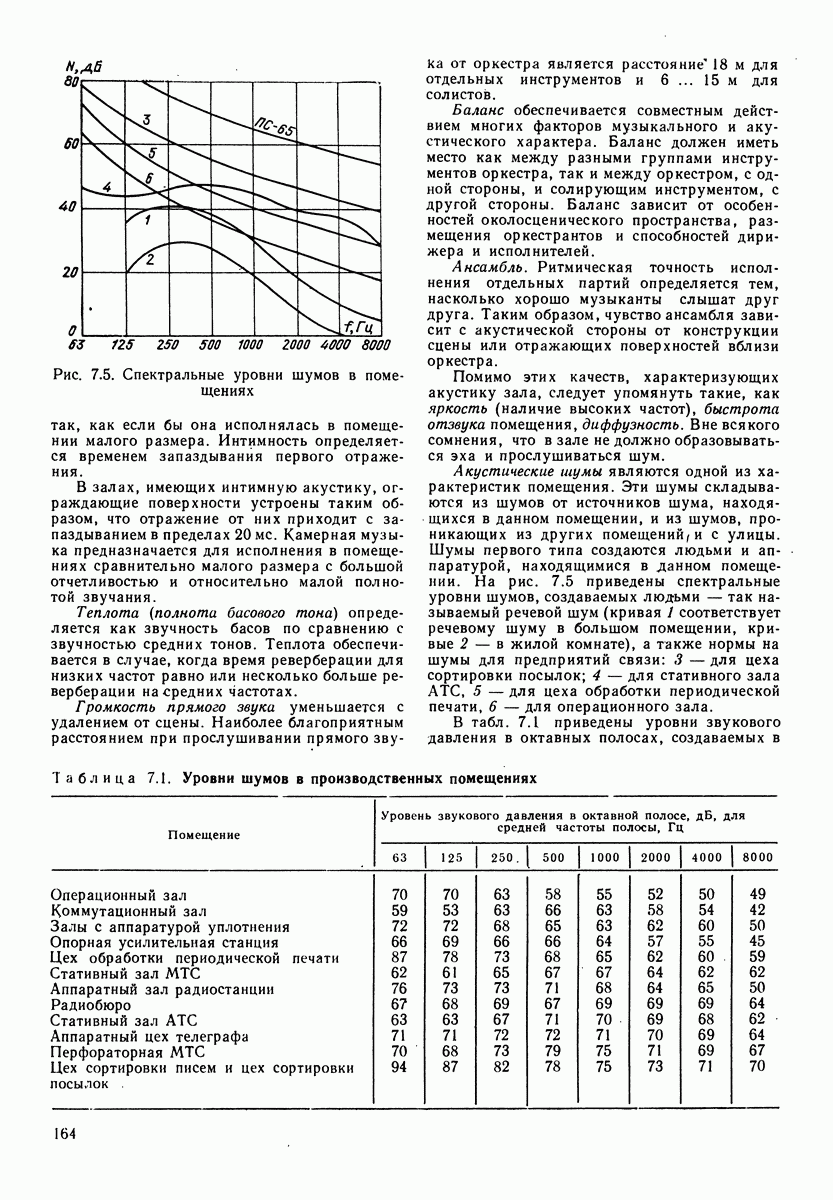
- РАЗДЕЛ 7. АКУСТИКА СТУДИЙ И ДРУГИХ ПОМЕЩЕНИЙ
- 7.1. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОМЕЩЕНИЙ
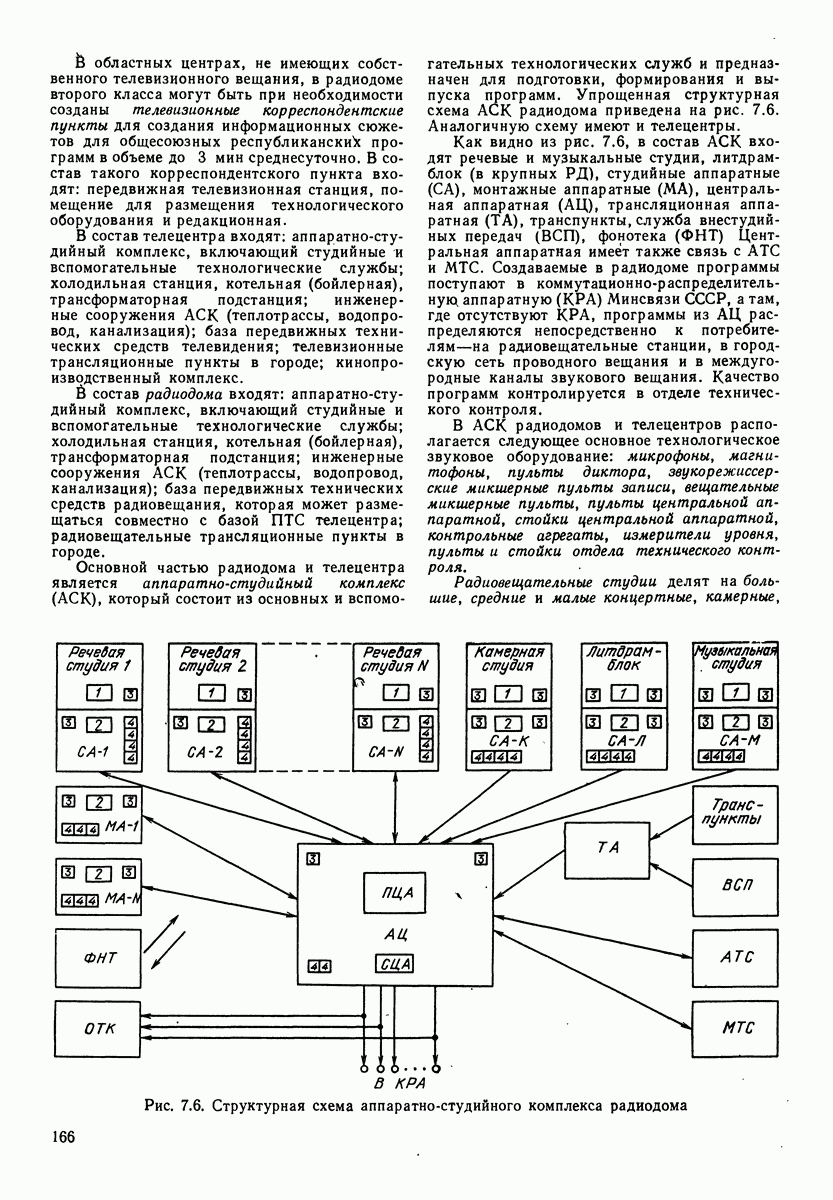
- 7.2. КЛАССИФИКАЦИЯ РАДИОВЕЩАТЕЛЬНЫХ И ТЕЛЕВИЗИОННЫХ СТУДИЙ
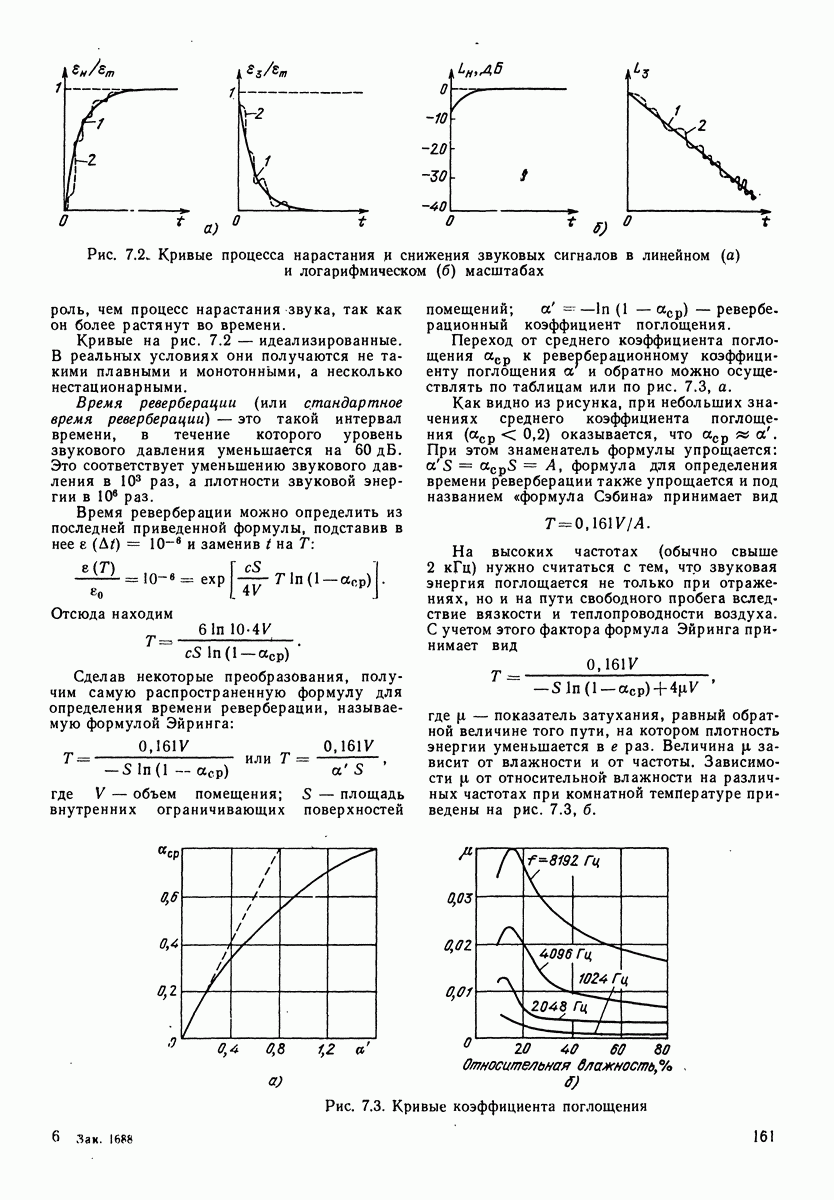
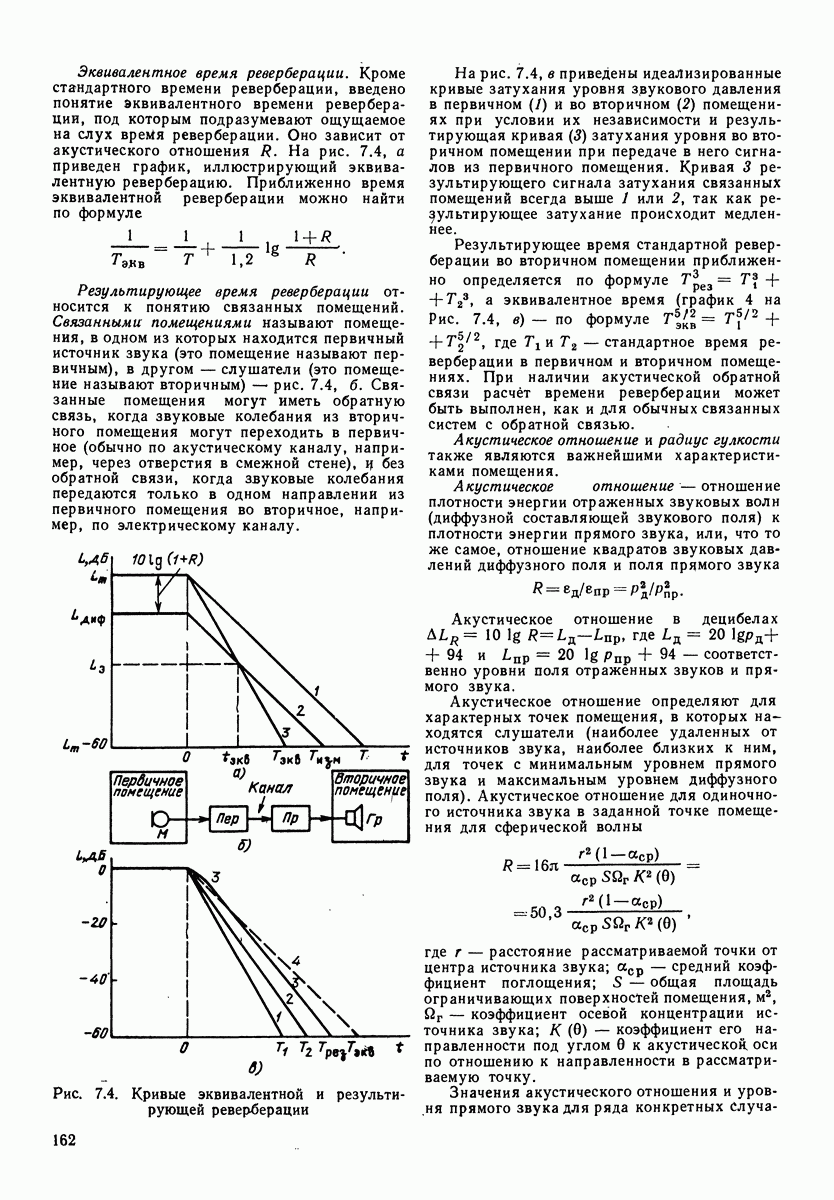
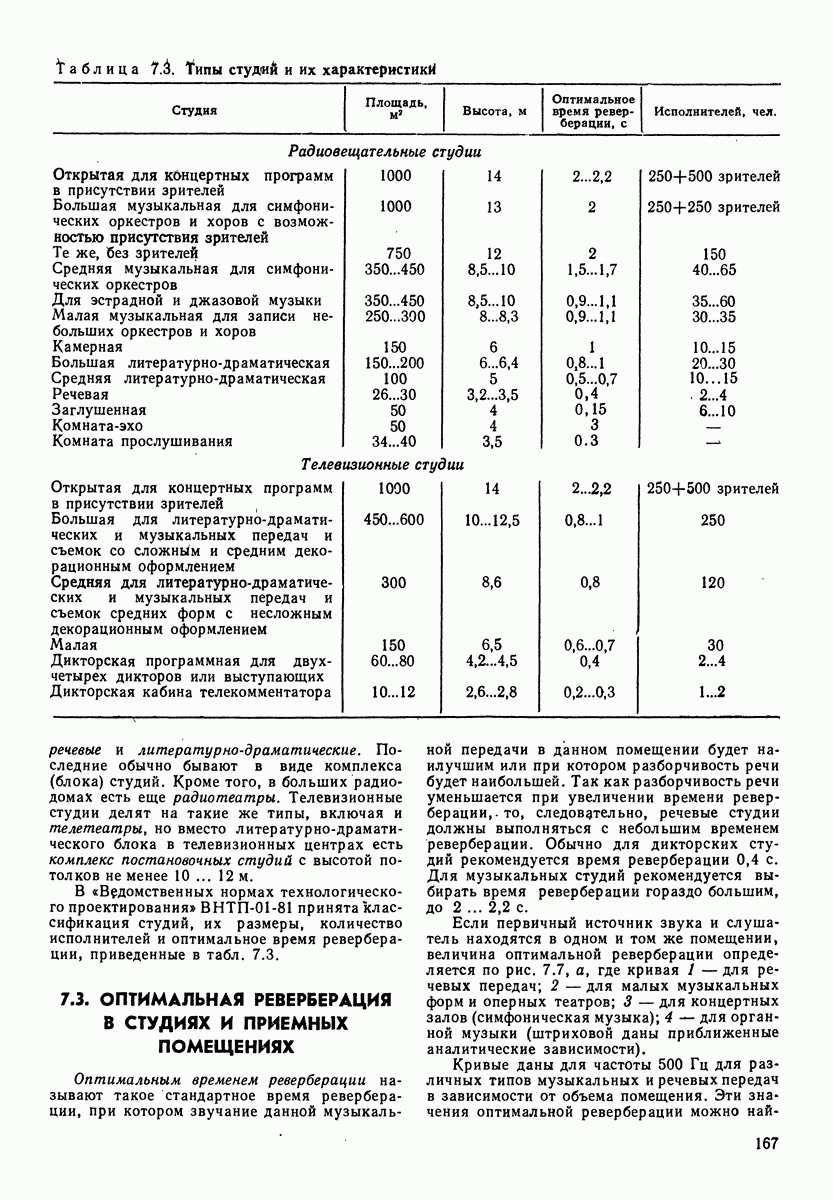
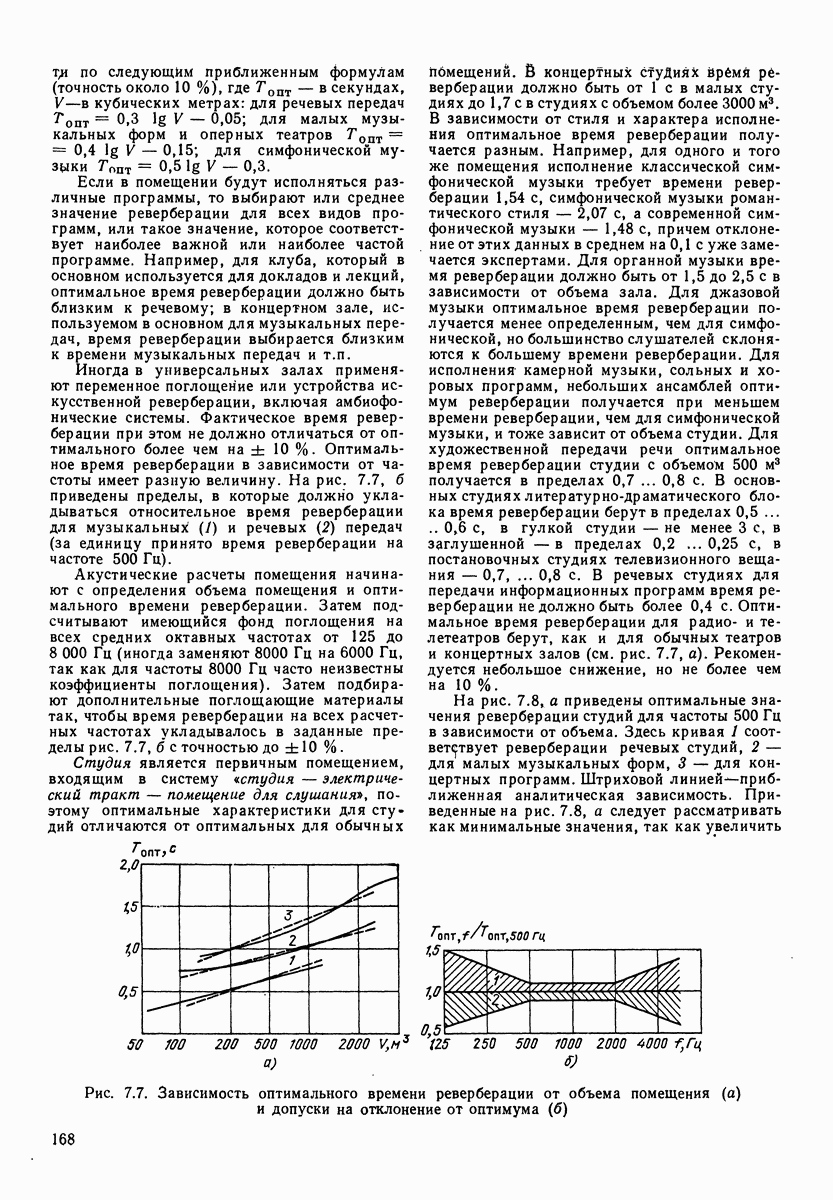
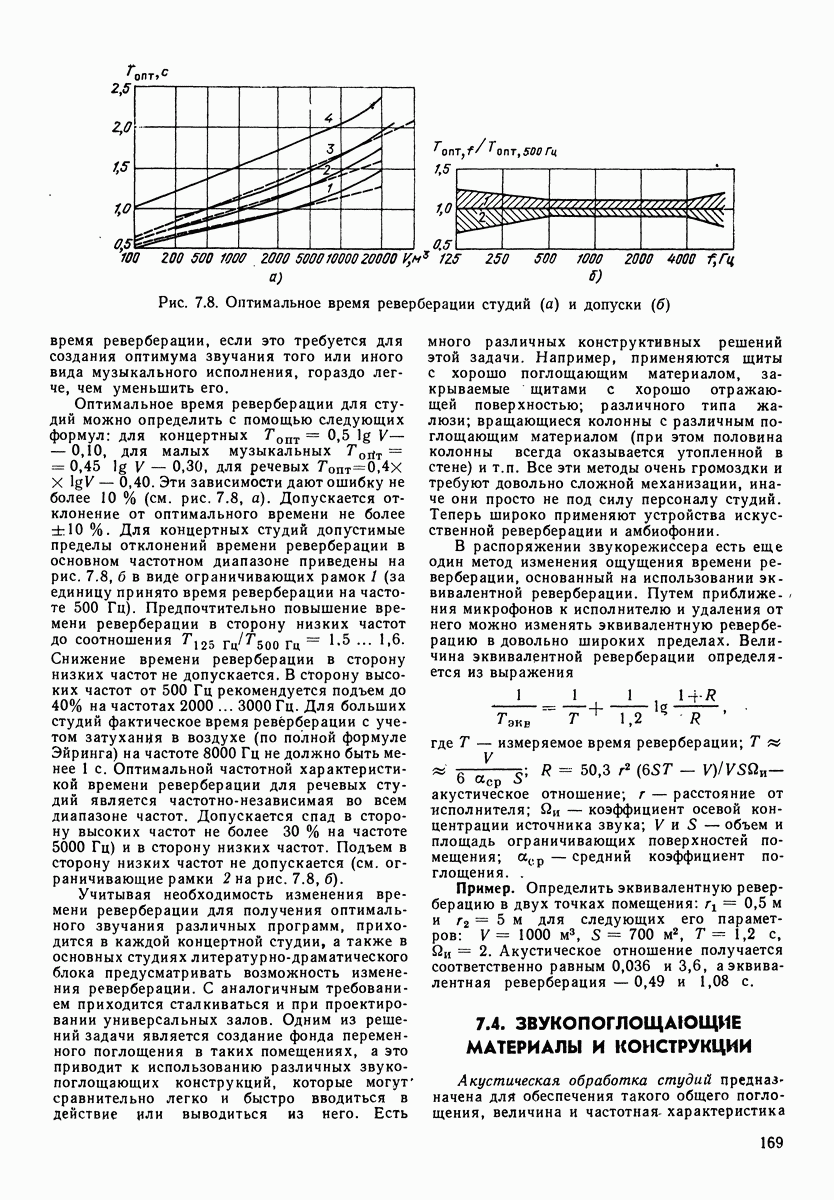
- 7.3. ОПТИМАЛЬНАЯ РЕВЕРБЕРАЦИЯ В СТУДИЯХ И ПРИЕМНЫХ ПОМЕЩЕНИЯХ
- 7.4. ЗВУКОПОГЛОЩАЮЩИЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ
- 7.5. ЗВУКОИЗОЛЯЦИЯ СТУДИЙ
- 7.6. ЭЛЕКТРОАКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ СТУДИЙ И АППАРАТНЫХ
- РАЗДЕЛ 8. ОЗВУЧЕНИЕ И ЗВУКОУСИЛЕНИЕ
- 8.2. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ОТКРЫТЫХ ПРОСТРАНСТВ
- 8.3. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.4. ЗОНАЛЬНЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.5. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 8.6. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 8.7. РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.8. ЗВУКОУСИЛЕНИЕ
- 8.9. ГРОМКОГОВОРЯЩАЯ СВЯЗЬ
- РАЗДЕЛ 9. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- 9.1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ ЗАПИСИ ЗВУКА
- 9.2. МЕХАНИЧЕСКАЯ ЗВУКОЗАПИСЬ
- 9.3. ФОТОГРАФИЧЕСКАЯ ЗВУКОЗАПИСЬ
- 9.4. МАГНИТНАЯ ЗВУКОЗАПИСЬ
- 9.5. МАГНИТНЫЕ ГОЛОВКИ
- 9.6. МАГНИТНЫЕ НОСИТЕЛИ ЗАПИСИ
- 9.7. МАГНИТОФОНЫ
- 9.8. ЛАЗЕРНАЯ ЗВУКОЗАПИСЬ НА КОМПАКТ-ДИСК
- РАЗДЕЛ 10. ПЕРЕДАЧА АКУСТИЧЕСКИХ СИГНАЛОВ
- 10.2. ИСКАЖЕНИЯ СИГНАЛОВ
- 10.3. ШУМЫ И ПОМЕХИ В ТРАКТАХ И КАНАЛАХ СВЯЗИ И ВЕЩАНИЯ
- 10.4. ДОПУСТИМЫЕ ИСКАЖЕНИЯ ВЕЩАТЕЛЬНЫХ СИГНАЛОВ
- 10.5. ПОНЯТНОСТЬ И РАЗБОРЧИВОСТЬ РЕЧИ
- 10.6. ИНДЕКСЫ ТРАКТА
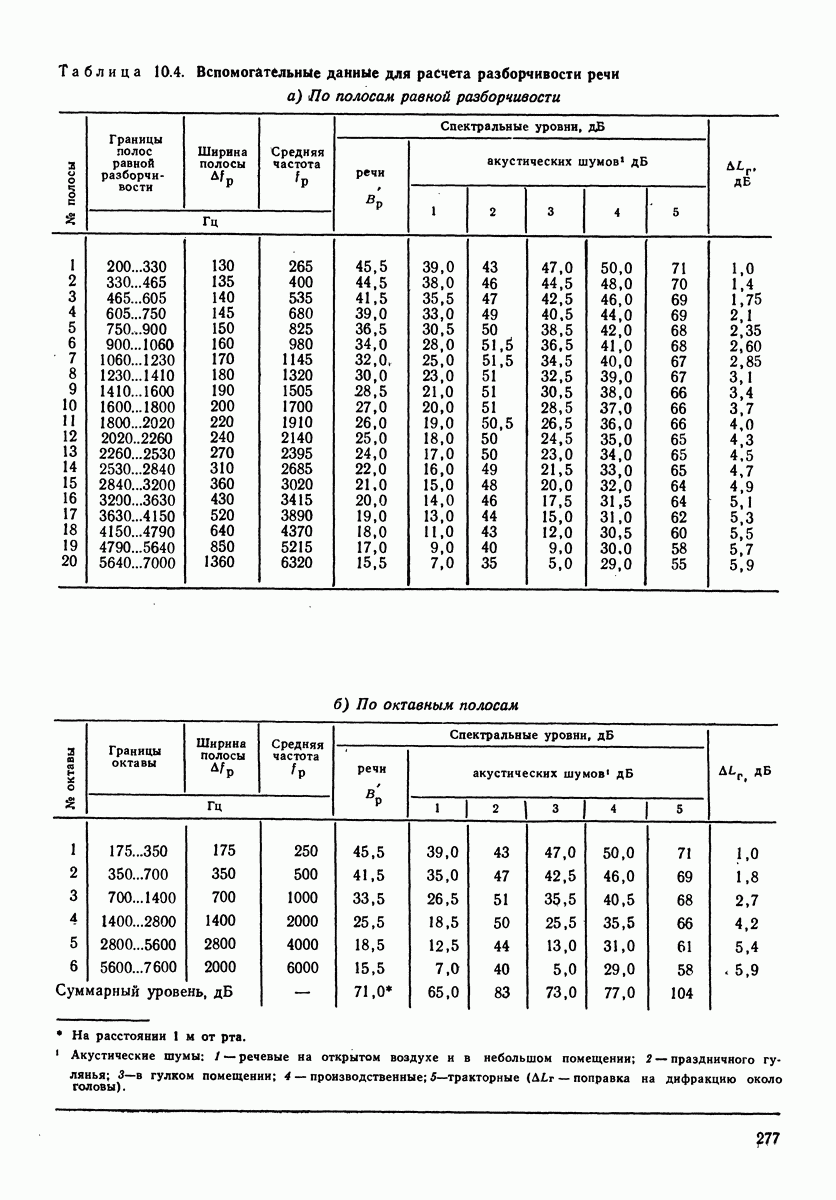
- 10.7. РАСЧЕТ РАЗБОРЧИВОСТИ РЕЧИ
- 10.8. РАСЧЕТ ОБЩЕГО УРОВНЯ ЗВУКОВОГО ПОЛЯ ПРИ ПЕРЕДАЧЕ РЕЧИ И ВЫБОР АППАРАТУРЫ ЗВУКОУСИЛЕНИЯ
- 10.9. ПРИМЕРЫ РАСЧЕТА ИНДЕКСОВ ТРАКТА, РАЗБОРЧИВОСТИ РЕЧИ И ОБЩЕГО УРОВНЯ ПЕРЕДАЧИ
- 10.10. ОПРЕДЕЛЕНИЕ РАЗБОРЧИВОСТИ РЕЧИ ДЛЯ ТРАКТОВ РАДИОТЕЛЕФОННОЙ СВЯЗИ
- 10.11. МЕТОДЫ ПОВЫШЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- 10.12. ВОКОДЕРНАЯ СВЯЗЬ
- РАЗДЕЛ 11. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ
- 11.2. МЕТОДЫ ИЗМЕРЕНИЙ ОСНОВНЫХ ХАРАКТЕРИСТИК ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЫ И ПОМЕЩЕНИЙ
- 11.3. ЭКСПЕРТИЗА МУЗЫКАЛЬНЫХ ПЕРЕДАЧ
- РАЗДЕЛ 12. ПРОГРАММЫ ДЛЯ МИКРОКАЛЬКУЛЯТОРОВ И ЭВМ ТИПА ДВК
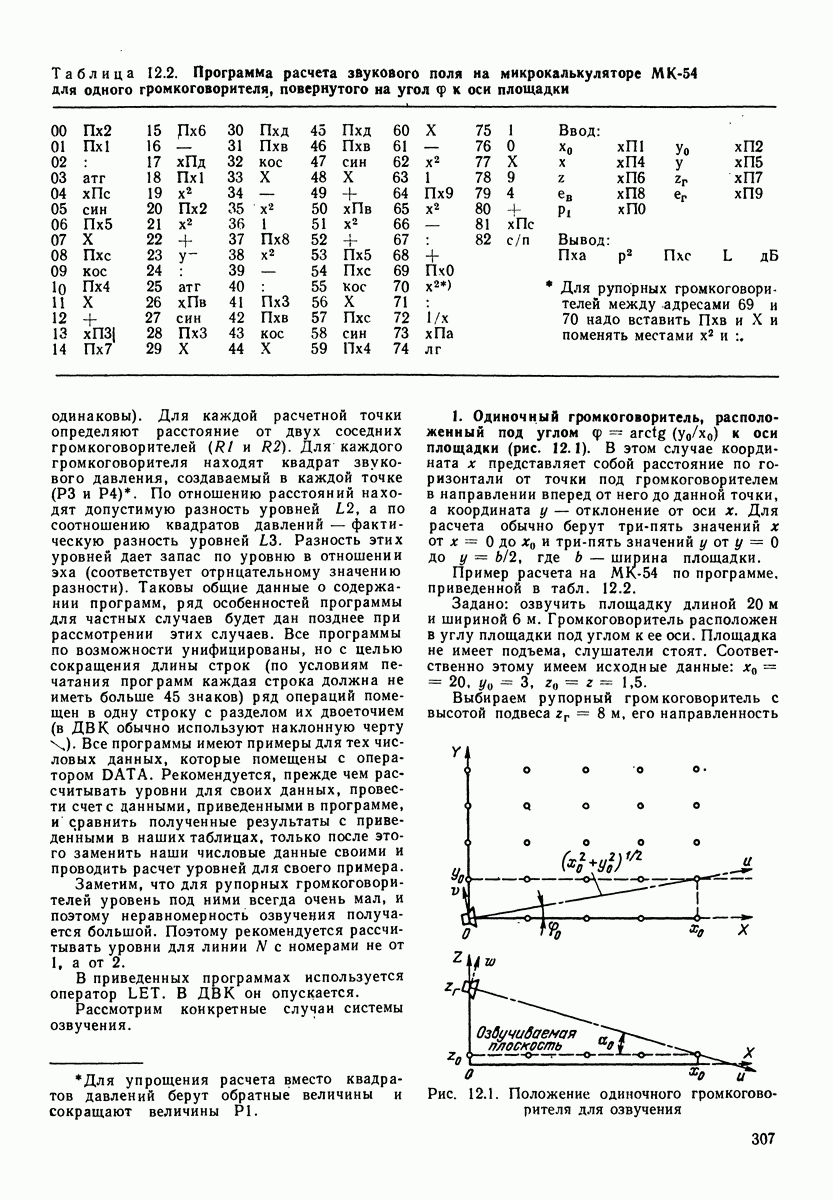
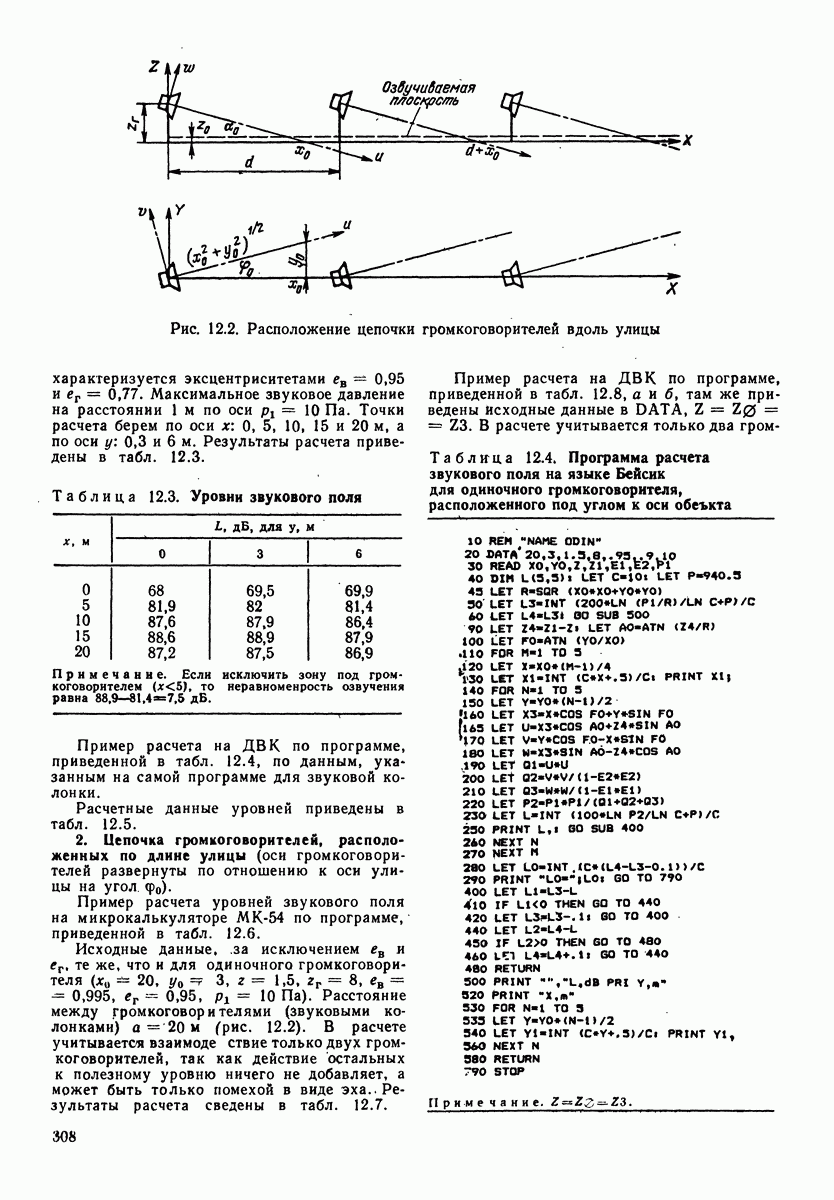
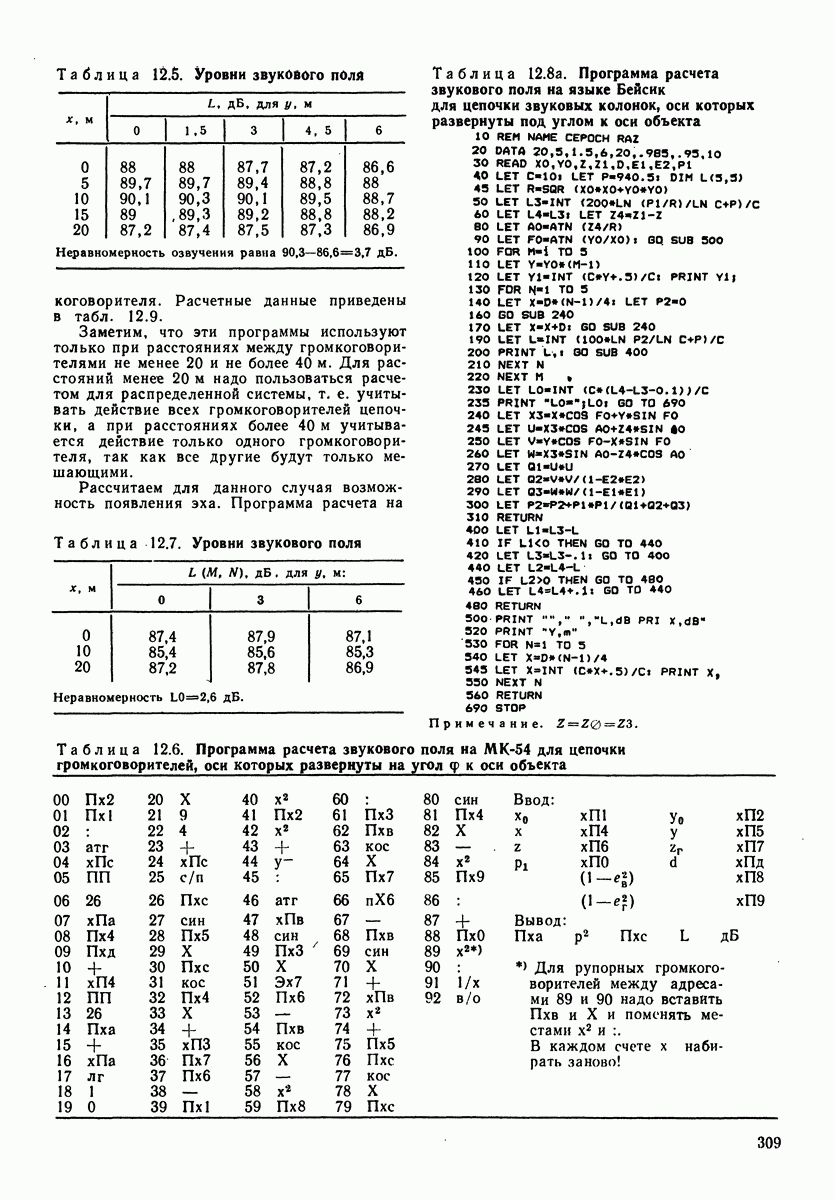
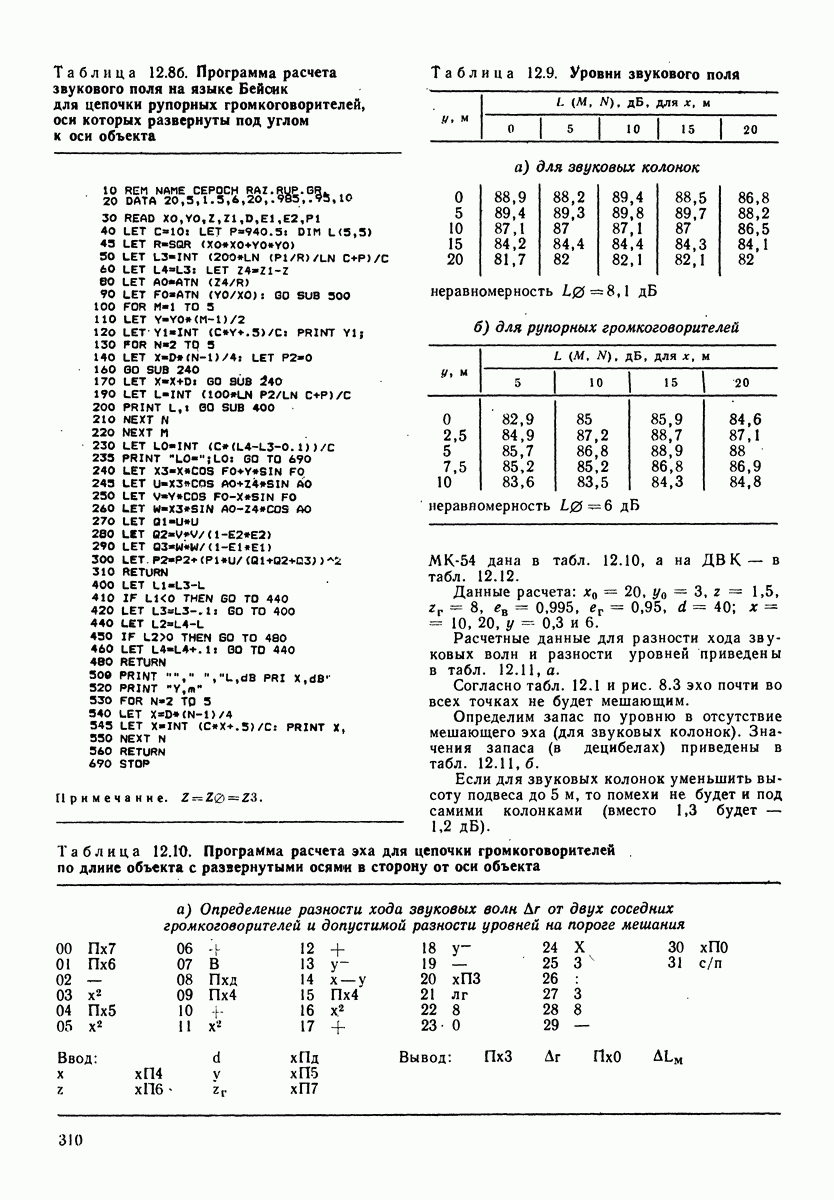
- 12.1. КОМПЛЕКС ПРОГРАММ ПО РАСЧЕТУ ЗВУКОВОГО ПОЛЯ И ЭХА ПРИ ЗВУКОФИКАЦИИ
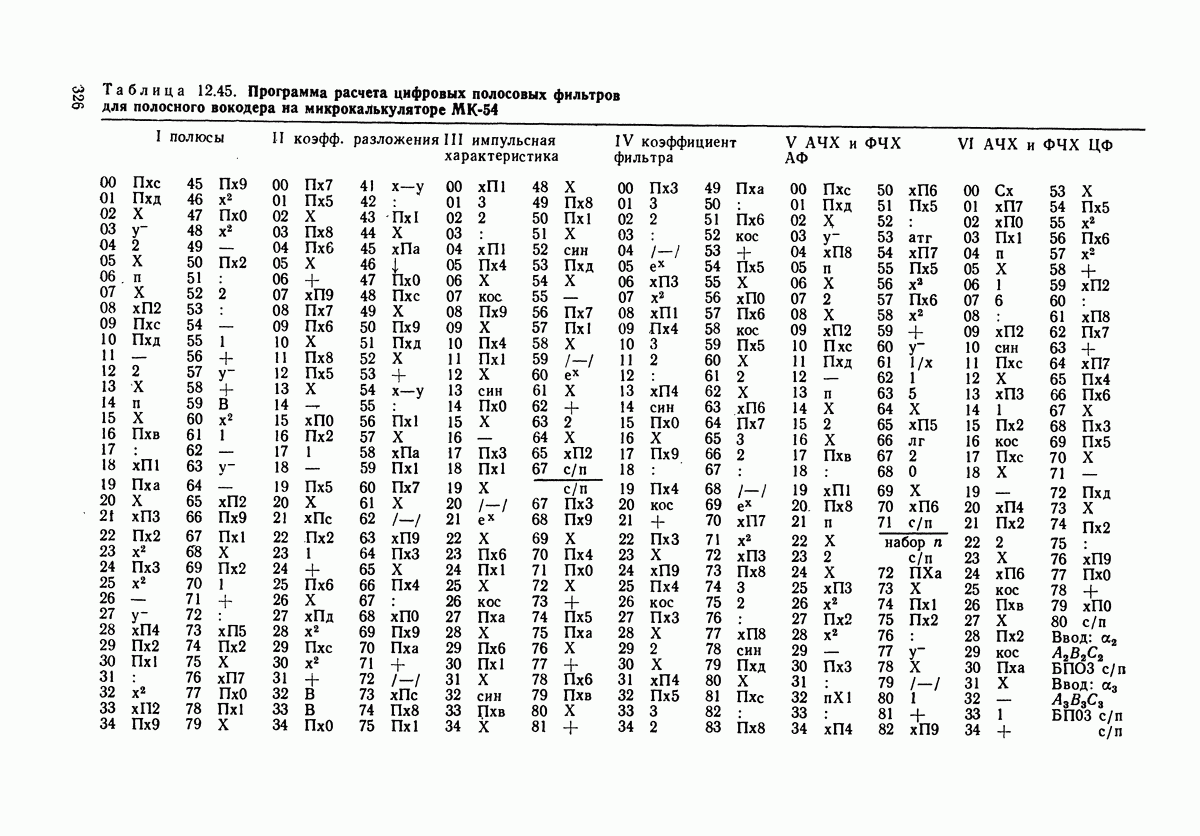
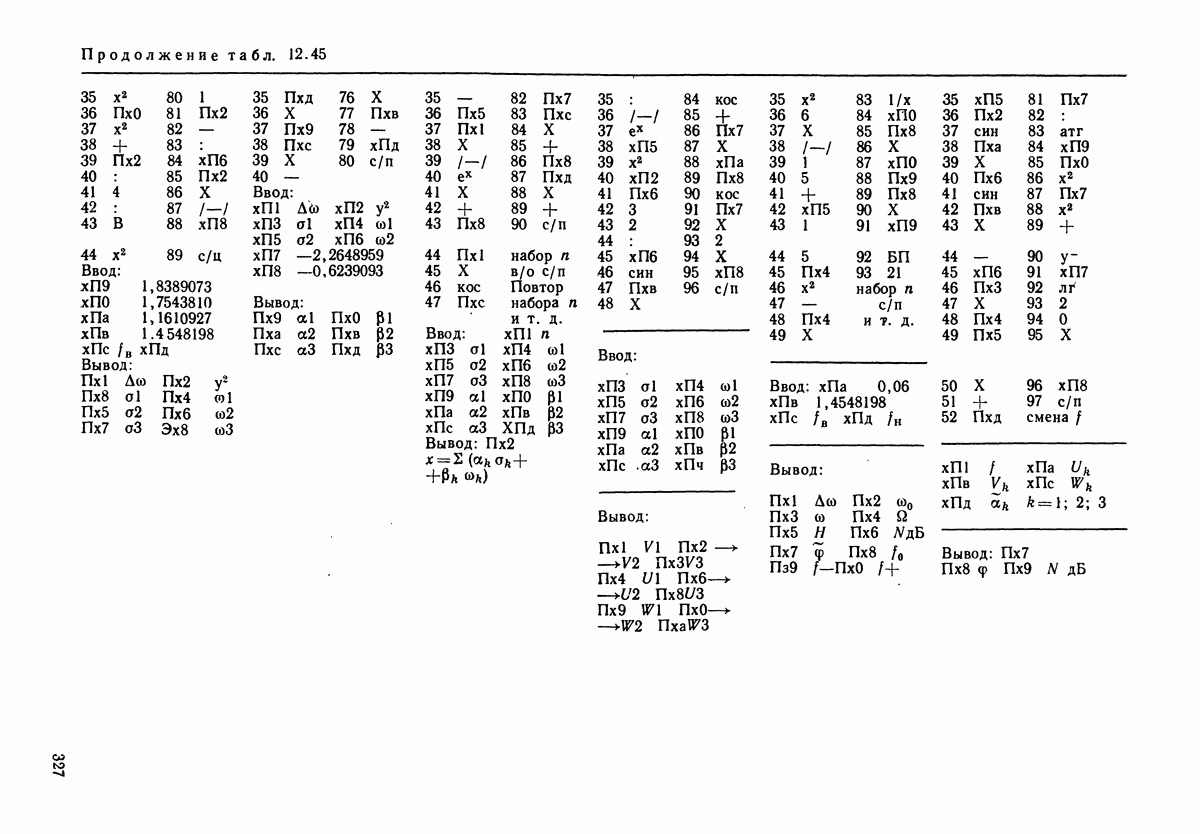
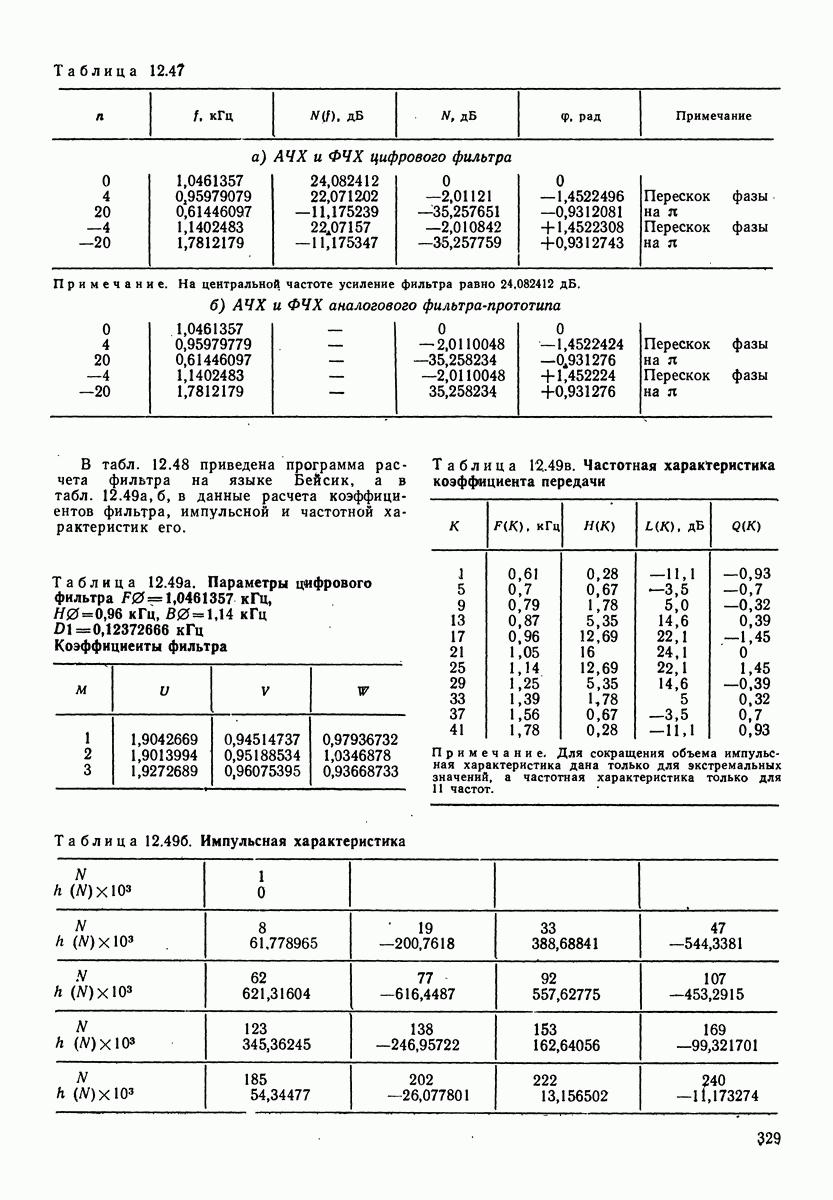
- 12.2. ПРОГРАММЫ РАСЧЕТА ДЛЯ ВОКОДЕРНЫХ ФИЛЬТРОВ (В ЦИФРОВОМ ИСПОЛНЕНИИ)
- 12.3. ПРОГРАММЫ ДЛЯ РАСЧЕТА РАЗБОРЧИВОСТИ РЕЧИ И ОБЩЕГО УРОВНЯ ПЕРЕДАЧИ РЕЧИ