| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.6. СФЕРИЧЕСКАЯ ВОЛНА
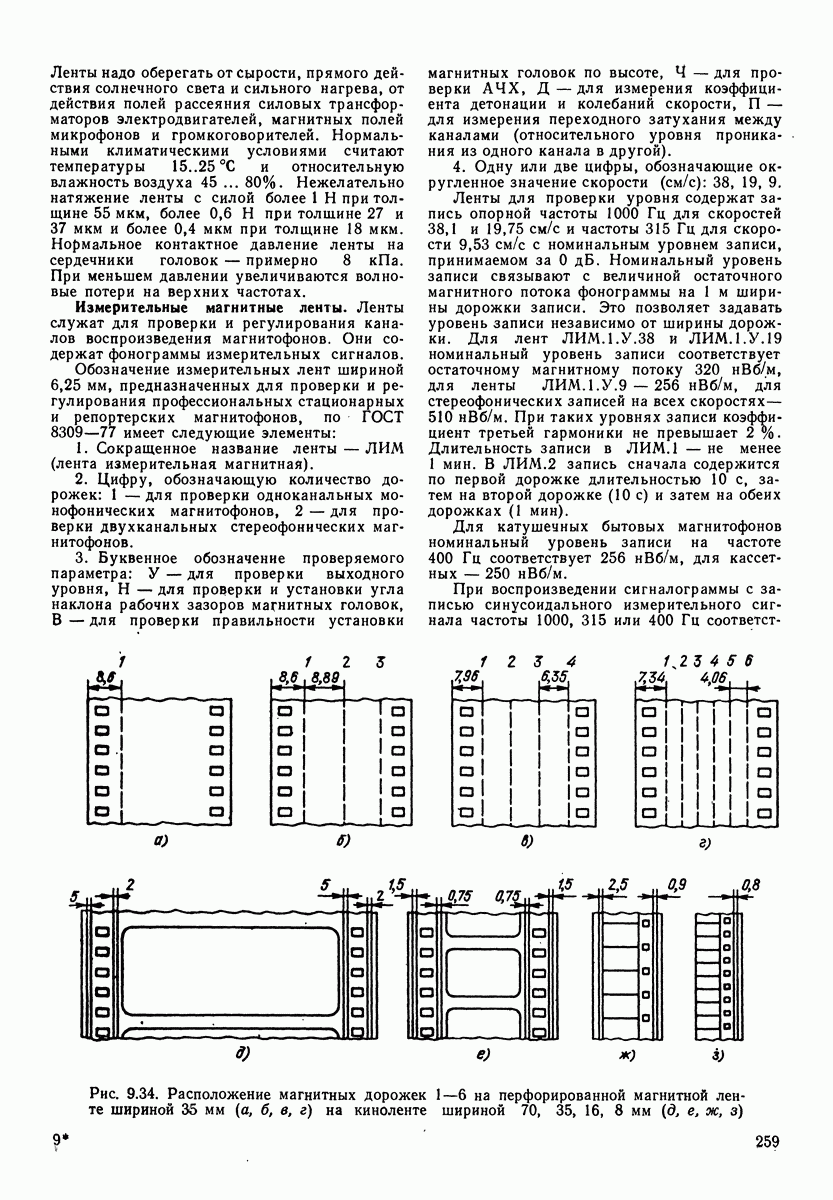
Фронт сферической волны представляет собой сферу, в центре которой находится источник колебаний, а звуковые лучи совпадают с радиусами сферы.
Полная мощность звука, исходящая из источника звука и расходящаяся по всем направлениям, не изменяется по величине с удалением от источника звука, если пренебречь потерями на вязкость среды и молекулярное рассеяние, т. е.  Интенсивность звука с удалением от источника звука уменьшается по квадратичному закону
Интенсивность звука с удалением от источника звука уменьшается по квадратичному закону  где — интенсивность звука на расстоянии единицы длины от центра источника звука;
где — интенсивность звука на расстоянии единицы длины от центра источника звука;  расстояние фронта волны от этого центра. Звуковое давление для сферической волны с расстоянием уменьшается по гиперболическому закону
расстояние фронта волны от этого центра. Звуковое давление для сферической волны с расстоянием уменьшается по гиперболическому закону  где
где  звуковое давление на расстоянии единицы длины от центра источника звука.
звуковое давление на расстоянии единицы длины от центра источника звука.
Волновое уравнение для трехмерного пространства


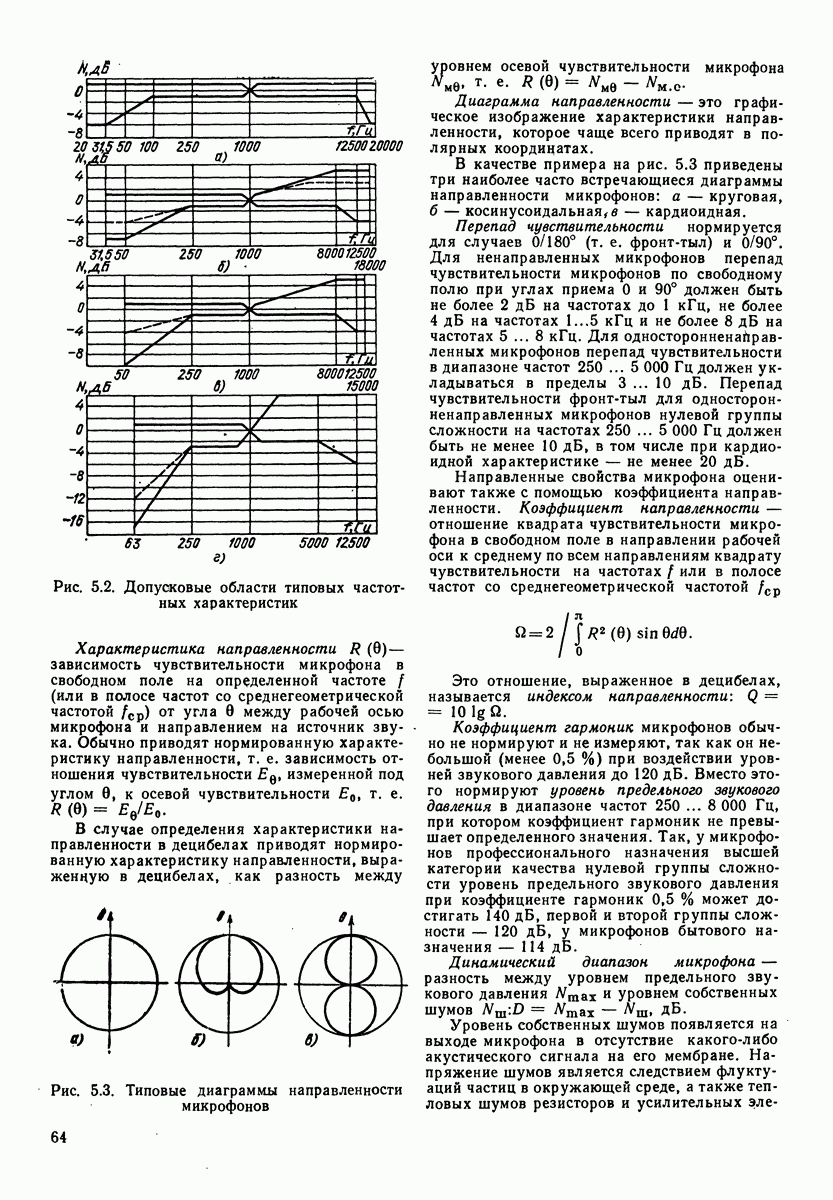
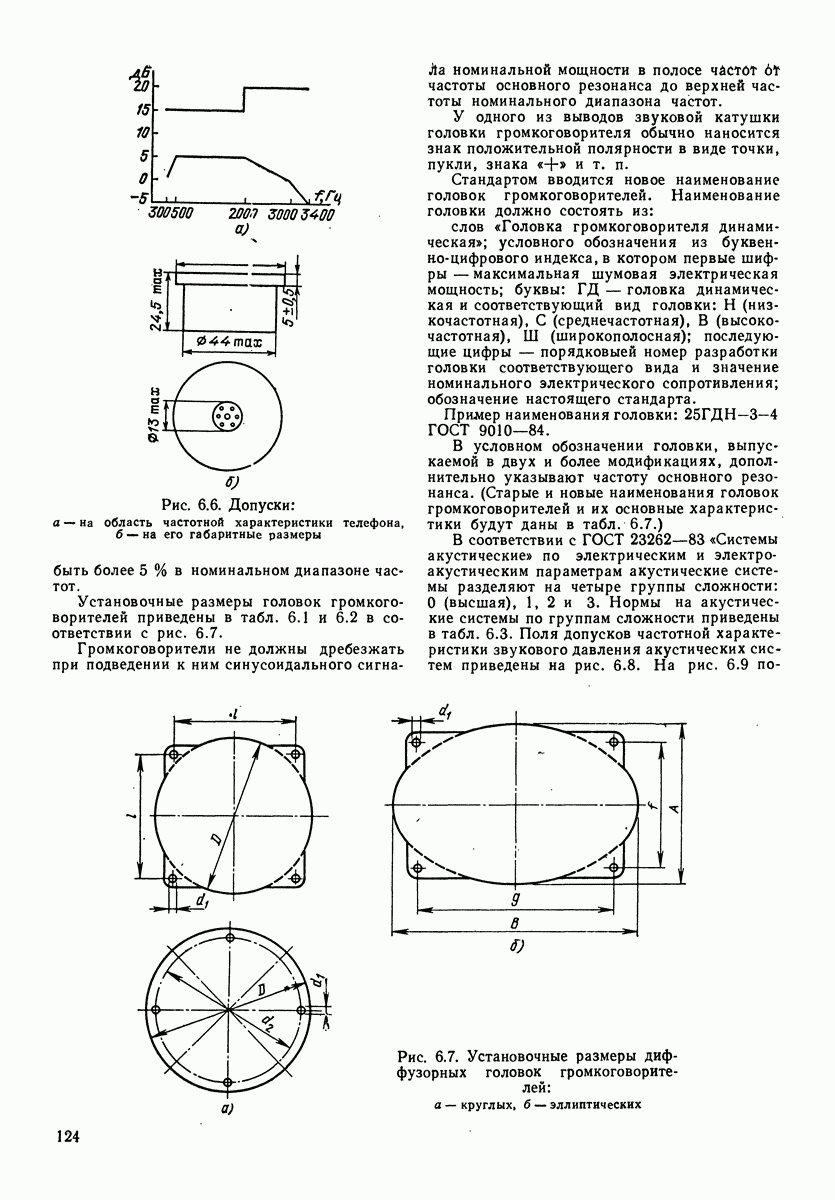
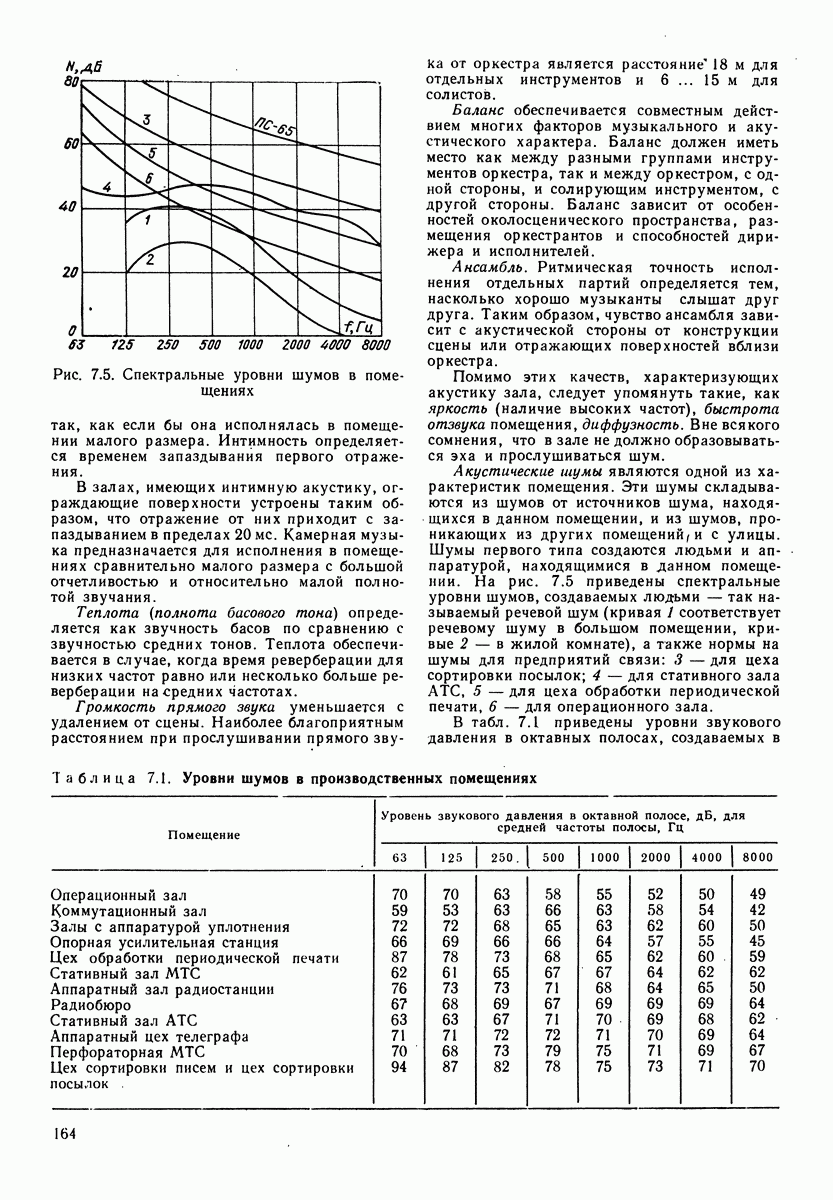
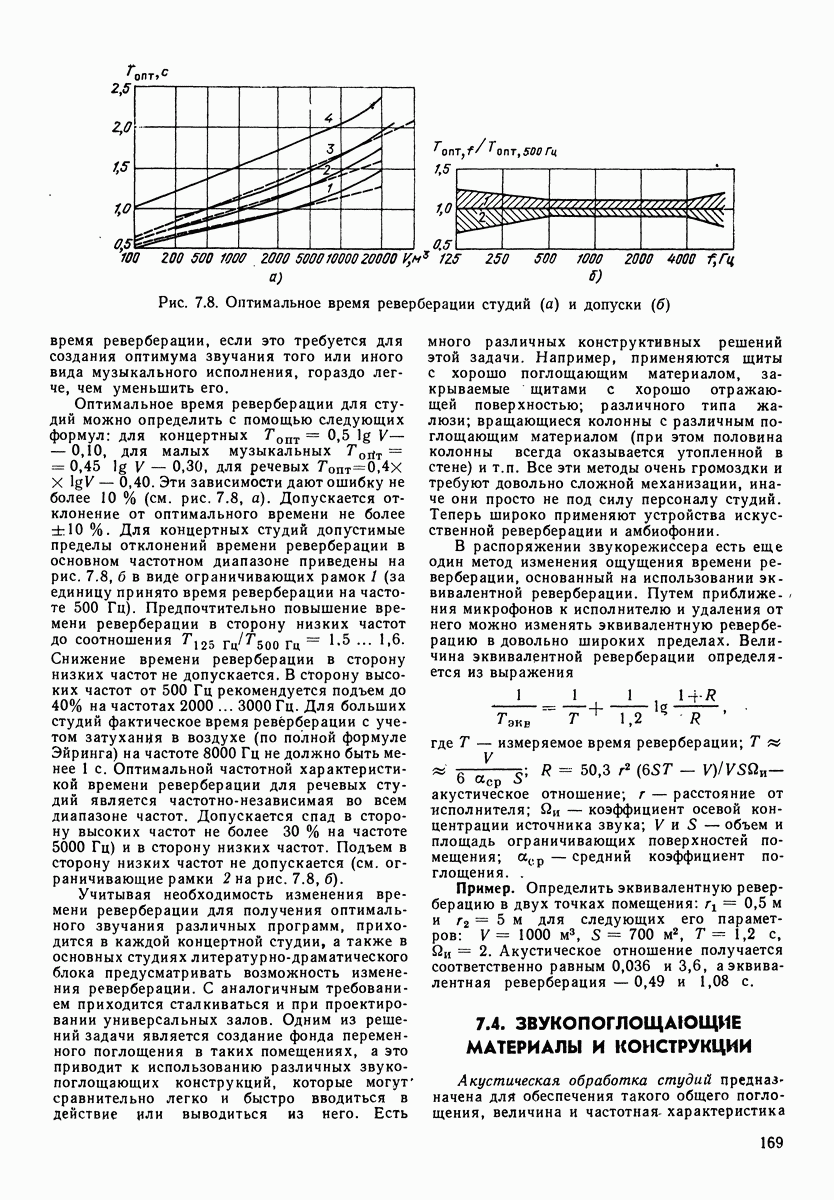
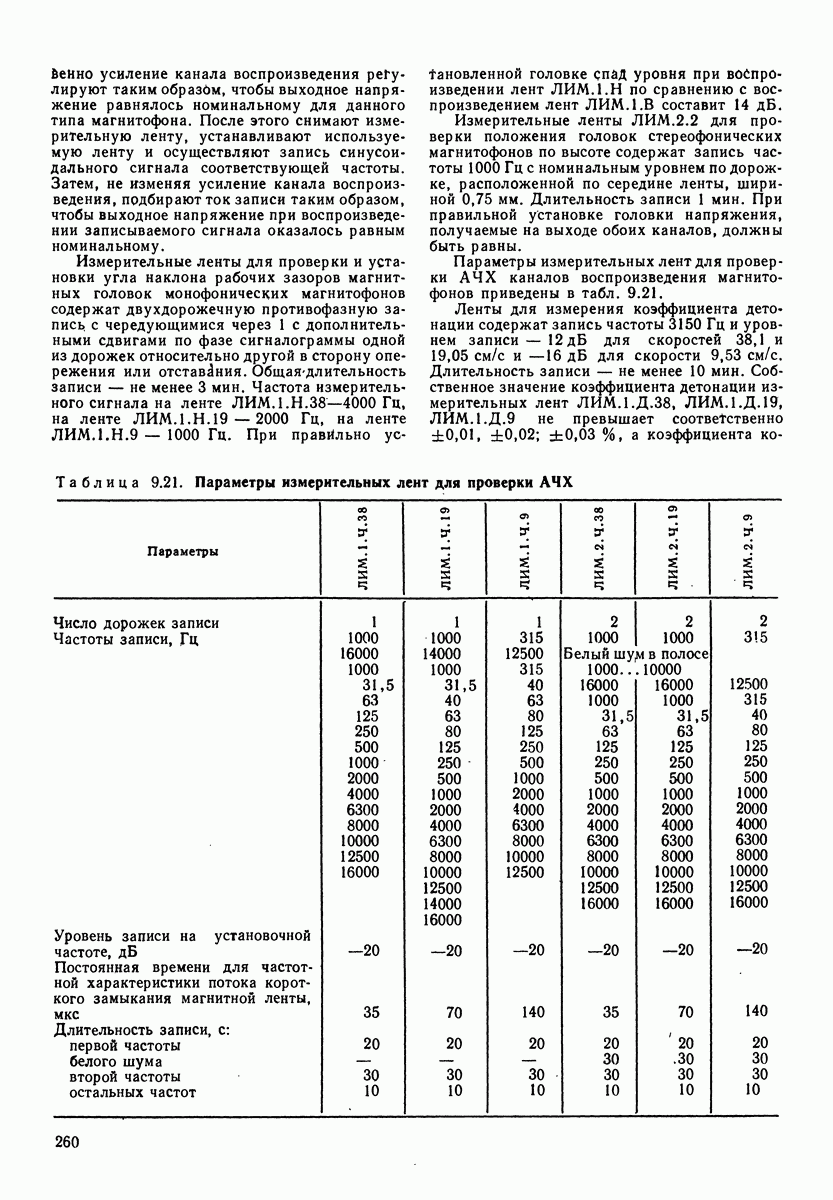
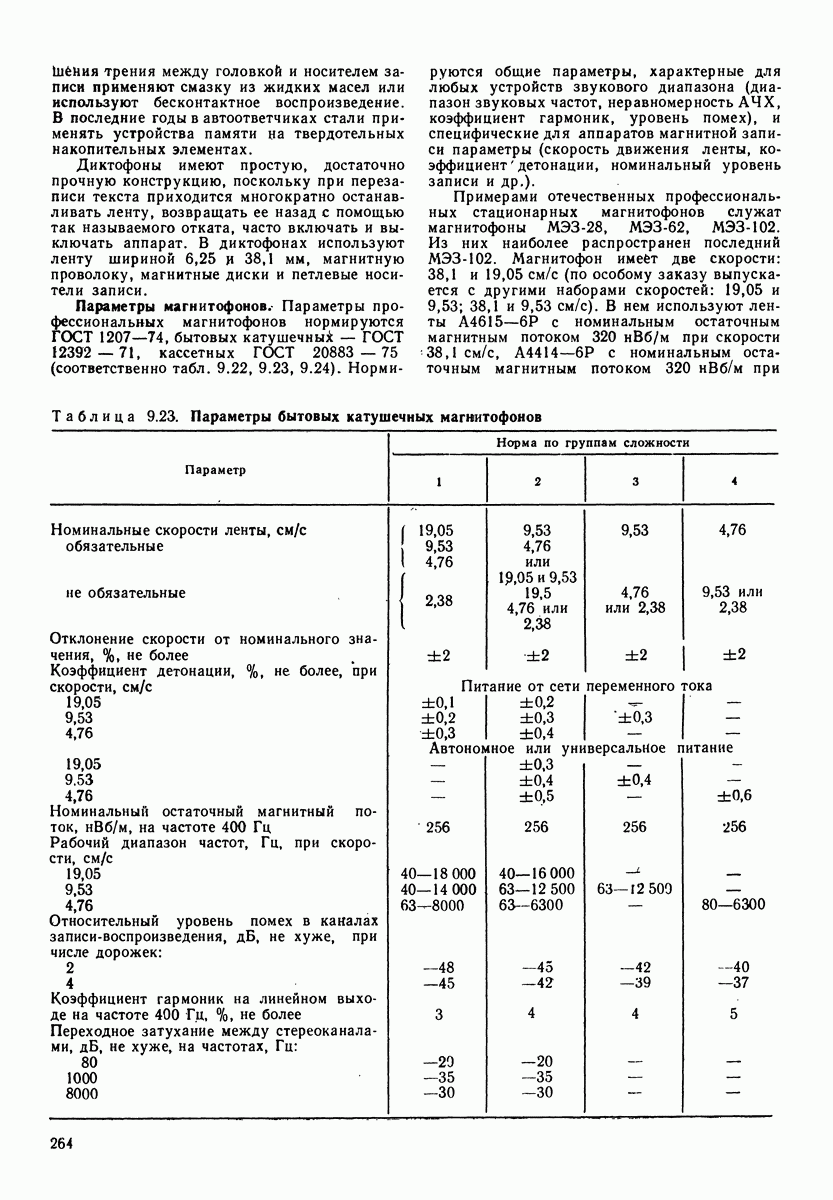
Рис. 1.6. Зависимость фазового угла между звуковым давлением и скоростью колебания в сферической волне от отношения радиуса волны к длине волны
При преобразовании координат из прямоугольных в сферические волновое уравнение имеет вид

Общий вид решения волнового уравнения для сферической волны

где первый член соответствует волне, распространяющейся в положительном направлении от источника звука, а второй — в отрицательном (к источнику звука).

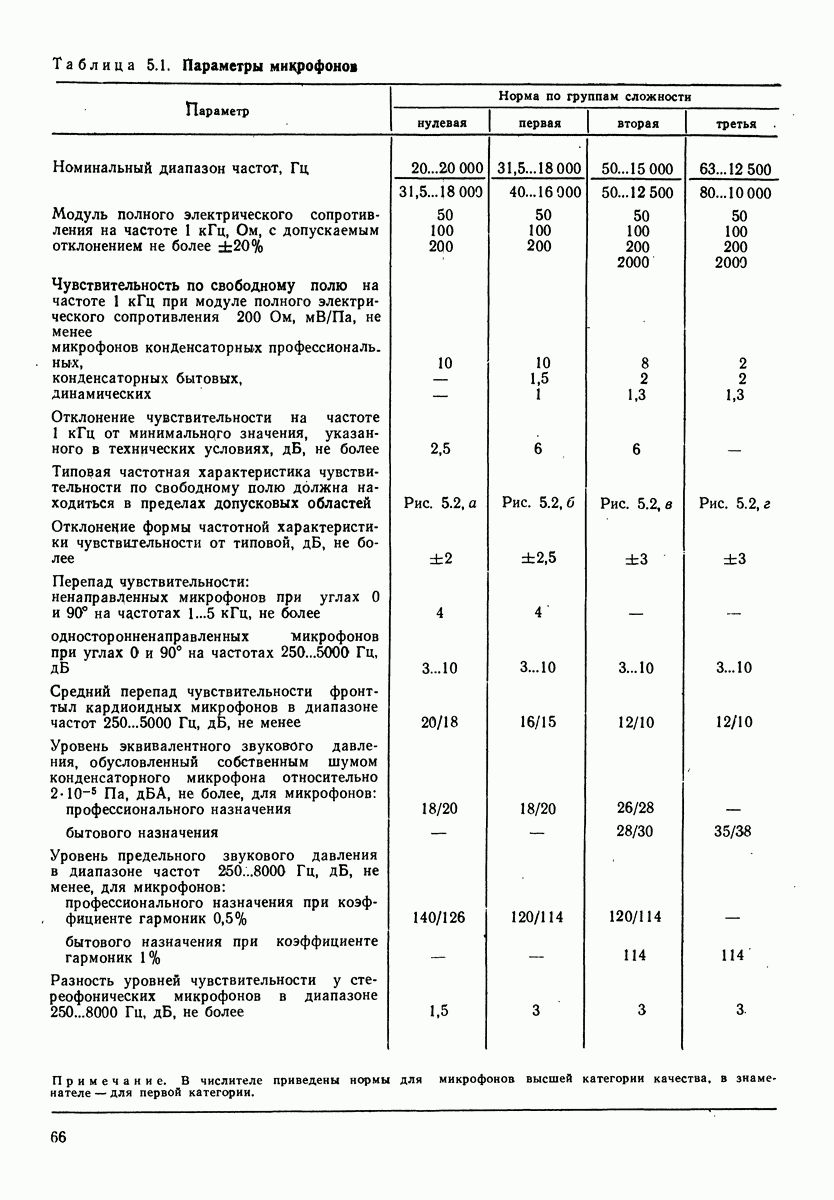
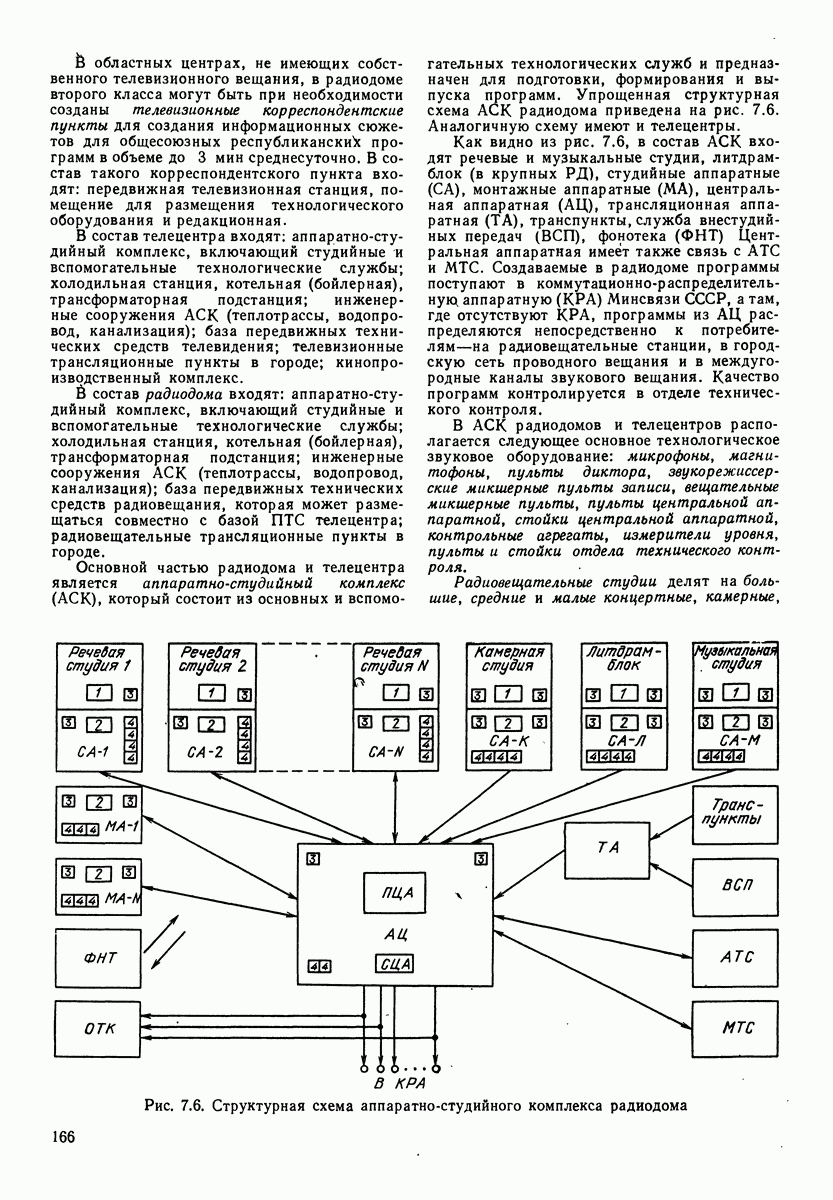
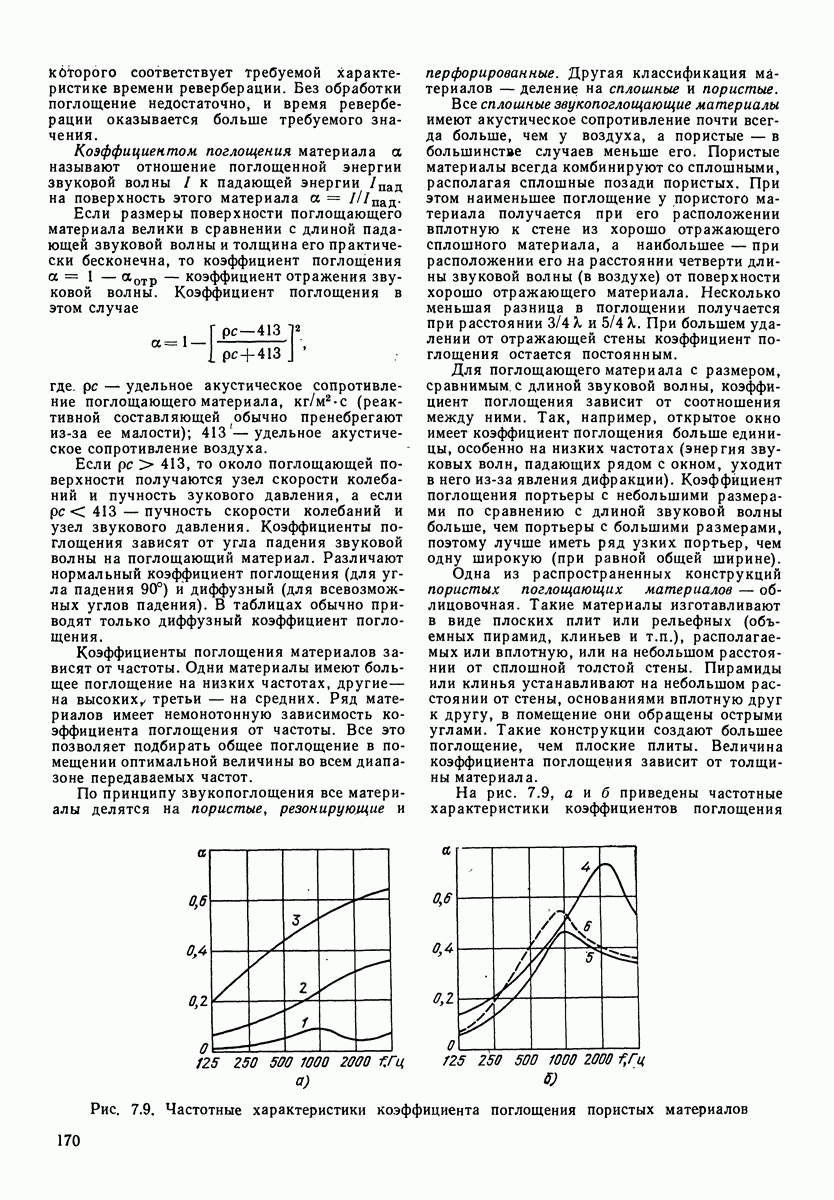
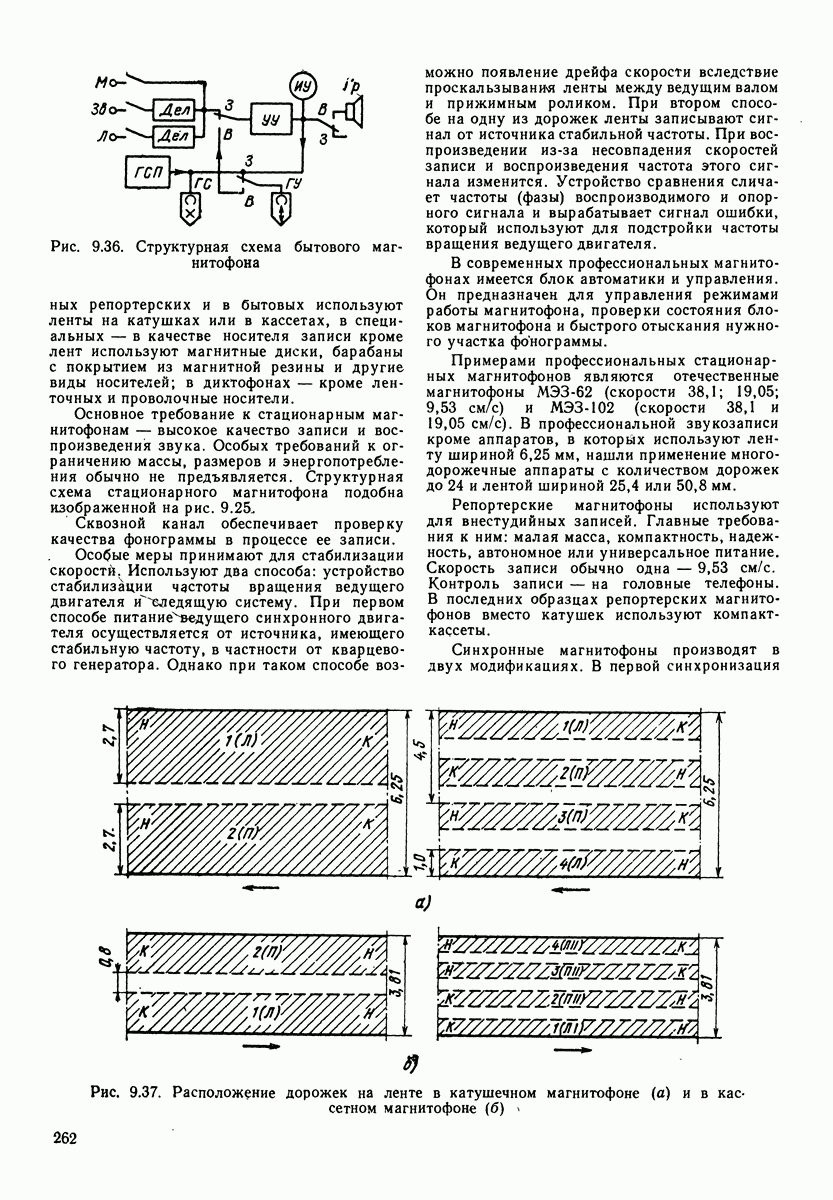
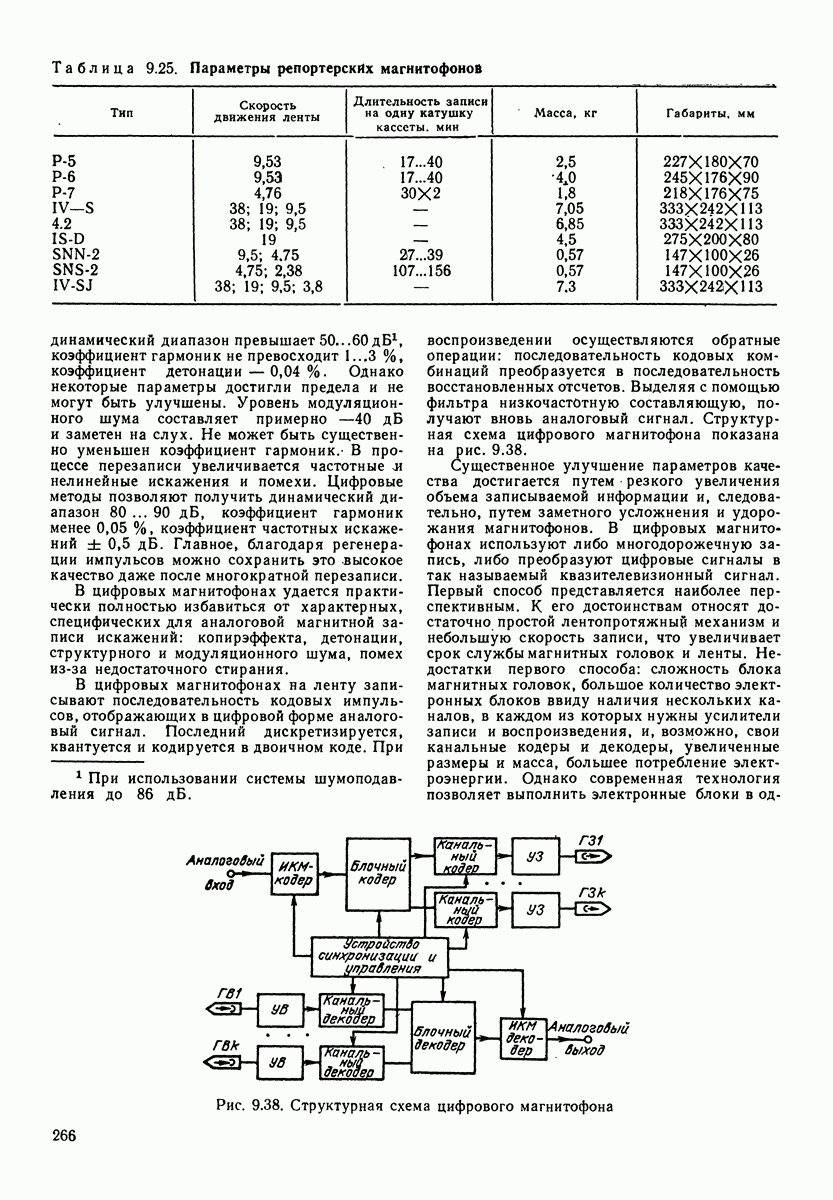
Рис. 1.7, Зависимость удельного акустического сопротивления для сферической волны от отношения удвоенного расстояния до центра источника звука к длине волны  -активная составляющая;
-активная составляющая;  реактивная составляющая)
реактивная составляющая)
Типовое частное решение для волны, распространяющейся в положительном направлении:

где  расстояние от центра источника звука (радиус волны); со — угловая частота колебаний;
расстояние от центра источника звука (радиус волны); со — угловая частота колебаний;  амплитуда звукового давления на расстоянии единицы длины от центра источника звука;
амплитуда звукового давления на расстоянии единицы длины от центра источника звука;  волновое число. Скорость колебаний в сферической волне
волновое число. Скорость колебаний в сферической волне 

где  амплитуда скорости колебаний на расстоянии единицы длины от центра источника звука:
амплитуда скорости колебаний на расстоянии единицы длины от центра источника звука:

 сдвиг фаз между звуковым давлением и скоростью колебаний;
сдвиг фаз между звуковым давлением и скоростью колебаний; 
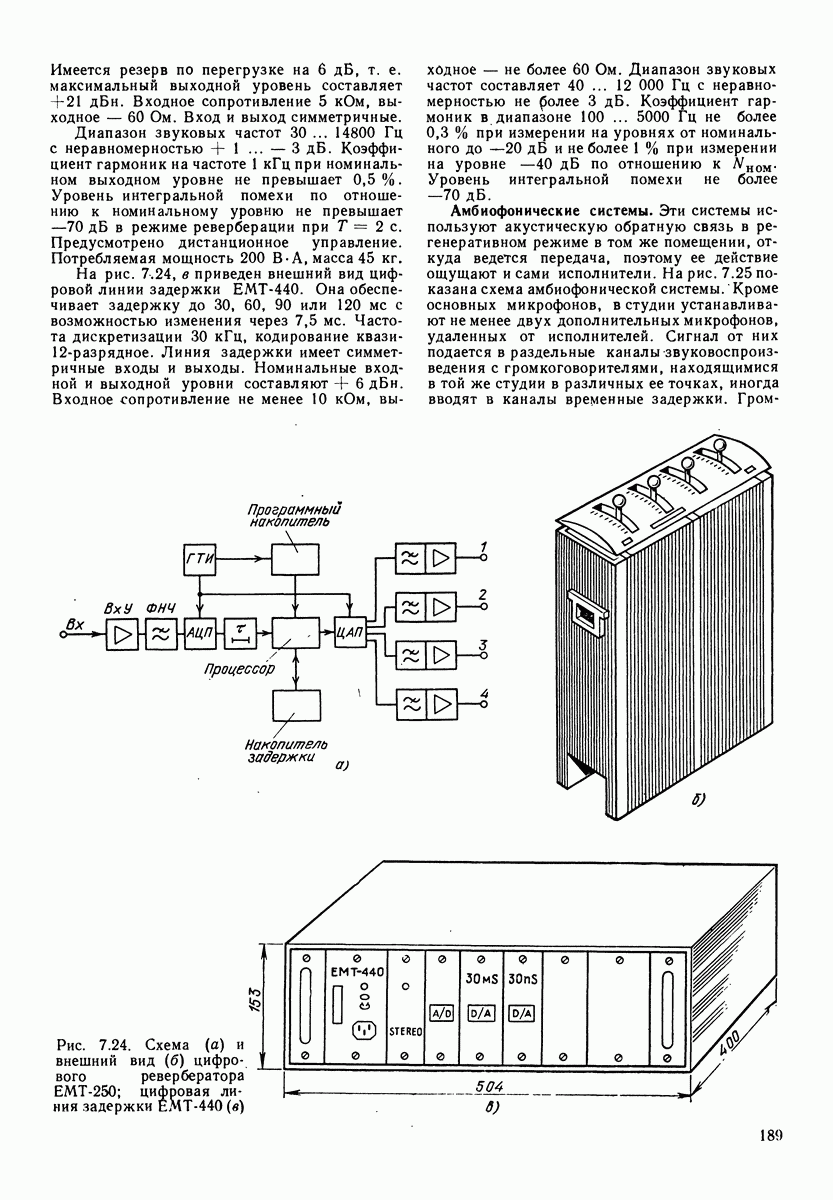
На рис. 1.6 приведена зависимость сдвига фаз в сферической волне от Соотношения между расстоянием фронта от источника звука (от центра сферы) и длиной волны. Чем меньше отношение длины волны к радиусу волны (расстоянию от центра источника звука) тем меньше сдвиг фаз между звуковым давлением и скоростью колебаний. Определим угол сдвига фаз на расстоянии  от центра источника звука для частоты 100 Гц
от центра источника звука для частоты 100 Гц 

что соответствует углу  Для расстояния
Для расстояния  на частоте 1000 Гц
на частоте 1000 Гц  этот сдвиг фаз составляет
этот сдвиг фаз составляет

что соответствует углу 3°.
На средних частотах для расстояний больше  можно не считаться со сдвигом фаз.
можно не считаться со сдвигом фаз.
Удельное акустическое сопротивление в сферической волне

Активная составляющая акустического сопротивления

Реактивная составляющая

Модуль сопротивления

т. е. акустическое сопротивление в сферической волне по величине не превышает акустического сопротивления в плоской волне.
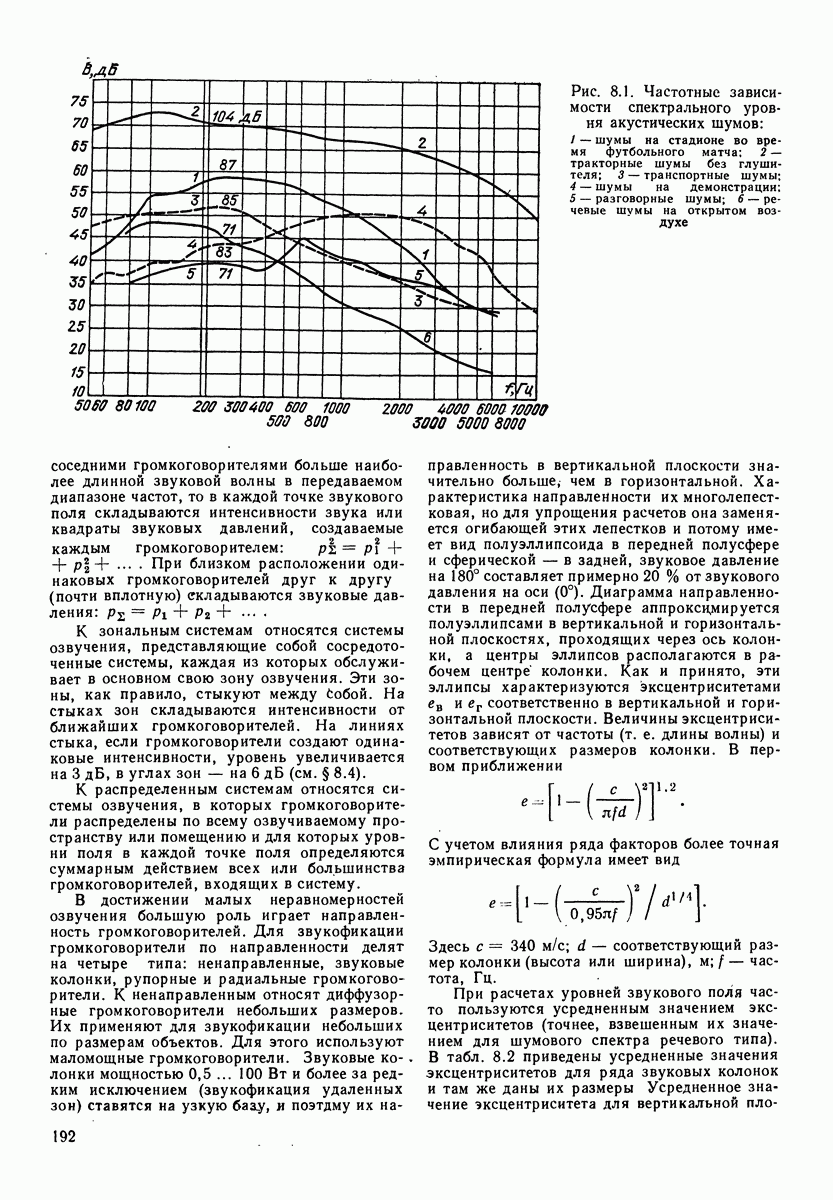
На рис. 1.7 приведены активная и реактивная составляющие удельного акустического сопротивления для сферической волны. Реактивное сопротивление имеет характер инерционного сопротивления (см. разд. 4), т. е. сопротивления массы, называемой «соко-леблющейся». Соколеблющаяся масса для всей сферы

где  плотность среды;
плотность среды;  расстояние от центра сферы.
расстояние от центра сферы.
При  соколеблющаяся масса
соколеблющаяся масса  где
где  объем сферы с радиусом
объем сферы с радиусом 
Пример. Найти активную составляющую акустического сопротивления сферической волны и соколеблющуюся массу для следующих условий:  . Активная составляющая
. Активная составляющая

и

Соколеблющаяся масса

и

при 
Интенсивность звука в сферической волне связана со звуковым давлением следующим соотношением:  где
где  эффективное значение звукбвого давления!
эффективное значение звукбвого давления!  амплитудное значение звукового давления.
амплитудное значение звукового давления.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ 1. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- 1.2. ЛИНЕЙНЫЕ ХАРАКТЕРИСТИКИ ЗВУКОВОГО ПОЛЯ
- 1.3. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗВУКОВОГО ПОЛЯ
- 1.4. УРОВНИ
- 1.5. ПЛОСКАЯ ВОЛНА
- 1.6. СФЕРИЧЕСКАЯ ВОЛНА
- 1.7. ЦИЛИНДРИЧЕСКАЯ ВОЛНА
- 1.8. ИНТЕРФЕРЕНЦИЯ ВОЛН
- 1.9. ОТРАЖЕНИЕ ЗВУКА
- 1.10. ПРЕЛОМЛЕНИЕ ЗВУКА
- 1.11. ДИФРАКЦИЯ ВОЛН
- 1.12. ЗАТУХАНИЕ ВОЛН
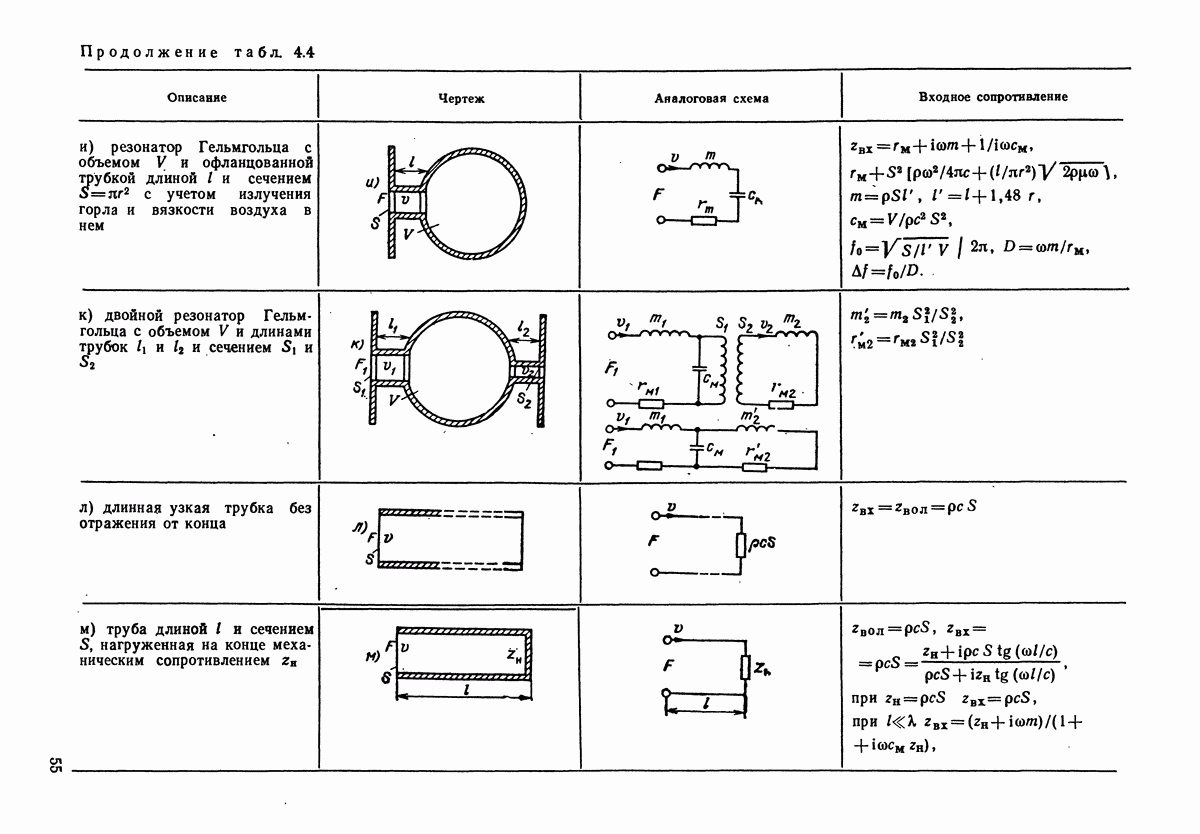
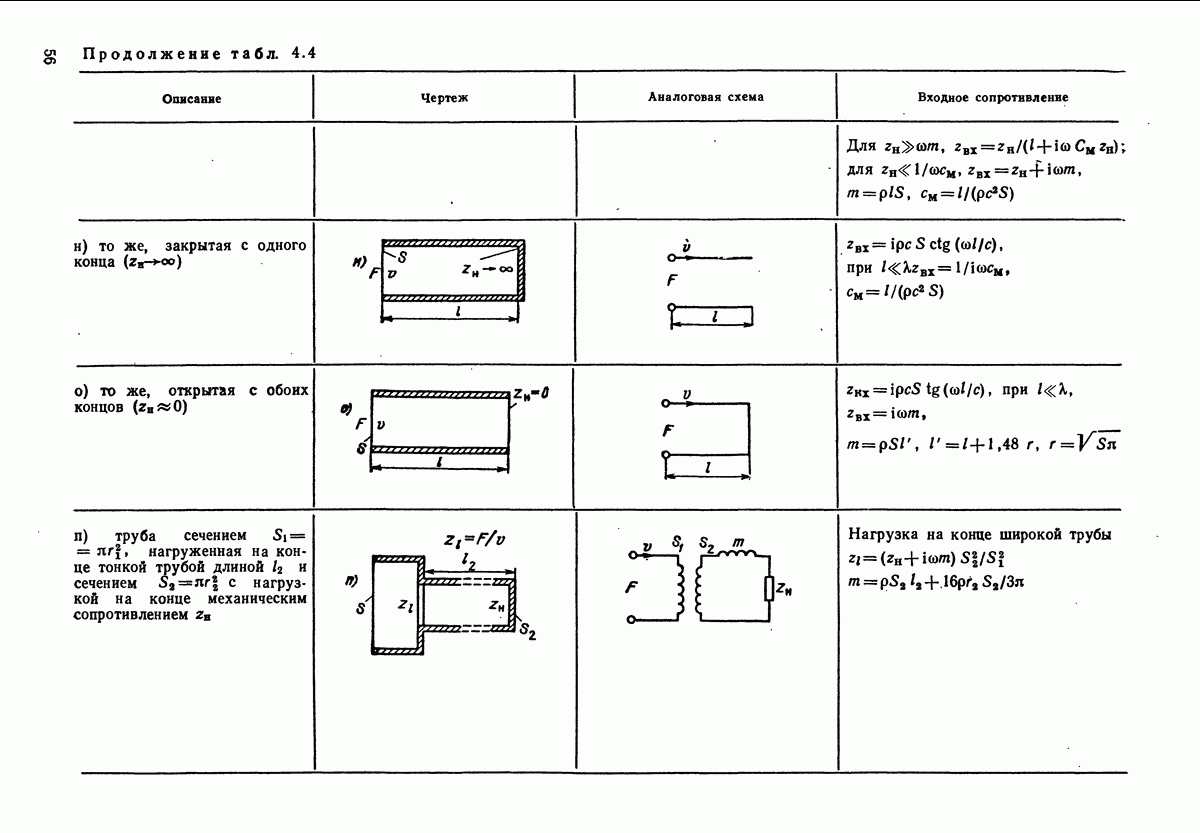
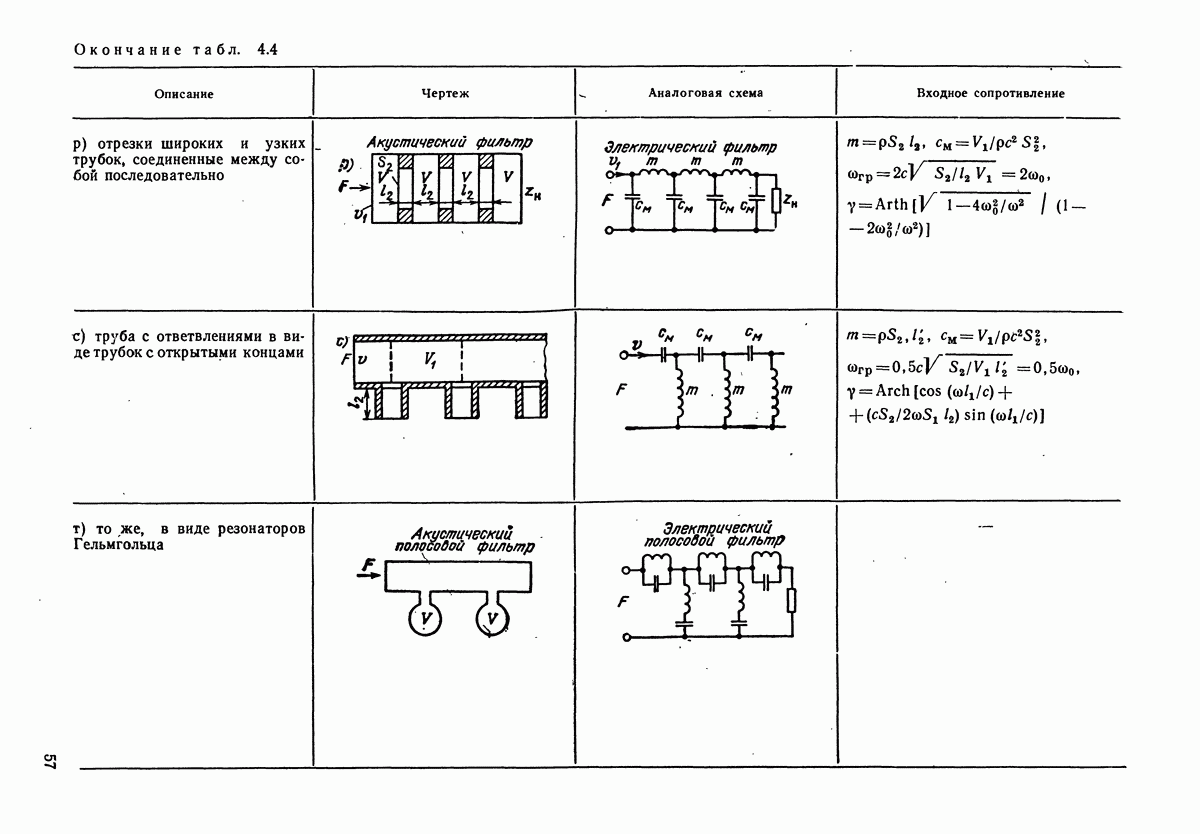
- 1.13. РАСПРОСТРАНЕНИЕ ЗВУКА В ТРУБАХ
- Раздел 2. ОСНОВНЫЕ СВОЙСТВА СЛУХА
- 2.2. ВОСПРИЯТИЕ ПО ЧАСТОТЕ
- 2.3. ВОСПРИЯТИЕ ПО АМПЛИТУДЕ
- 2.4. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СЛУХА
- 2.5. ВОСПРИЯТИЕ ИМПУЛЬСОВ
- 2.6. НЕЛИНЕЙНЫЕ СВОЙСТВА СЛУХА
- 2.7. БИНАУРАЛЬНЫЙ ЭФФЕКТ
- РАЗДЕЛ 3. ПЕРВИЧНЫЕ АКУСТИЧЕСКИЕ СИГНАЛЫ И ИХ ИСТОЧНИКИ
- 3.2. ДИНАМИЧЕСКИЙ ДИАПАЗОН И УРОВНИ
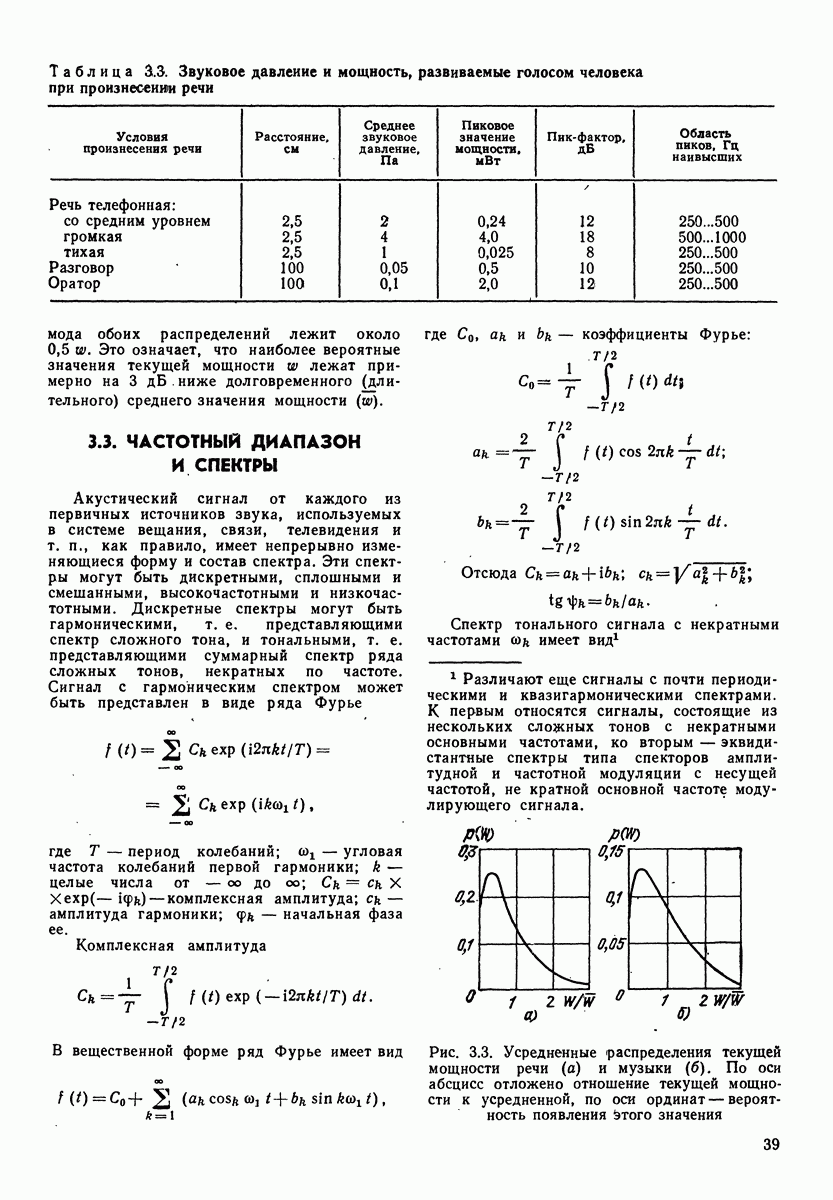
- 3.3. ЧАСТОТНЫЙ ДИАПАЗОН И СПЕКТРЫ
- 3.4. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ АКУСТИЧЕСКОГО СИГНАЛА
- 3.5. ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ РЕЧИ ВОКРУГ ГОЛОВЫ
- 3.6. ПЕРВИЧНЫЙ РЕЧЕВОЙ СИГНАЛ
- 3.7. ГОРТАНЬ КАК ИСТОЧНИК ЗВУКОВЫХ КОЛЕБАНИЙ
- РАЗДЕЛ 4. ЭЛЕКТРОАКУСТИЧЕСКИЕ ЭЛЕМЕНТЫ И СИСТЕМЫ
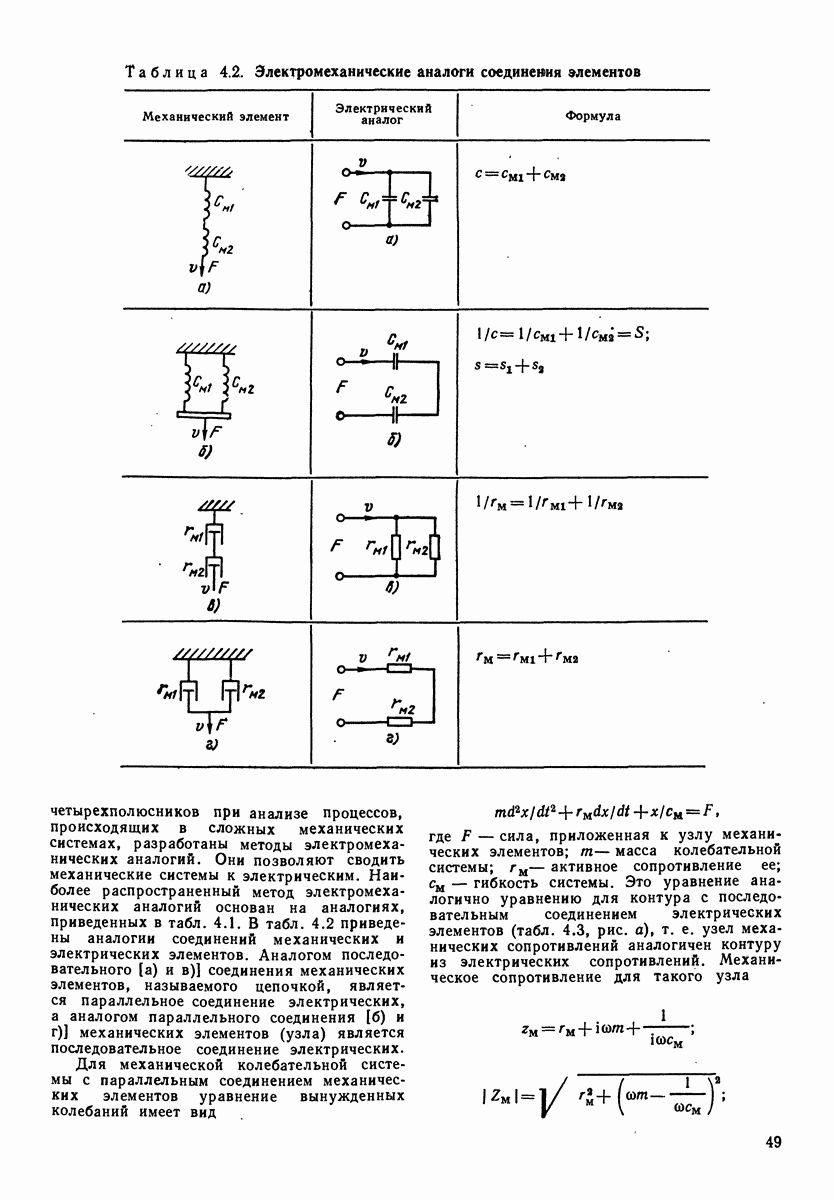
- 4.2. ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИ
- 4.3. ЭЛЕКТРОАКУСТИЧЕСКИЕ АНАЛОГИИ
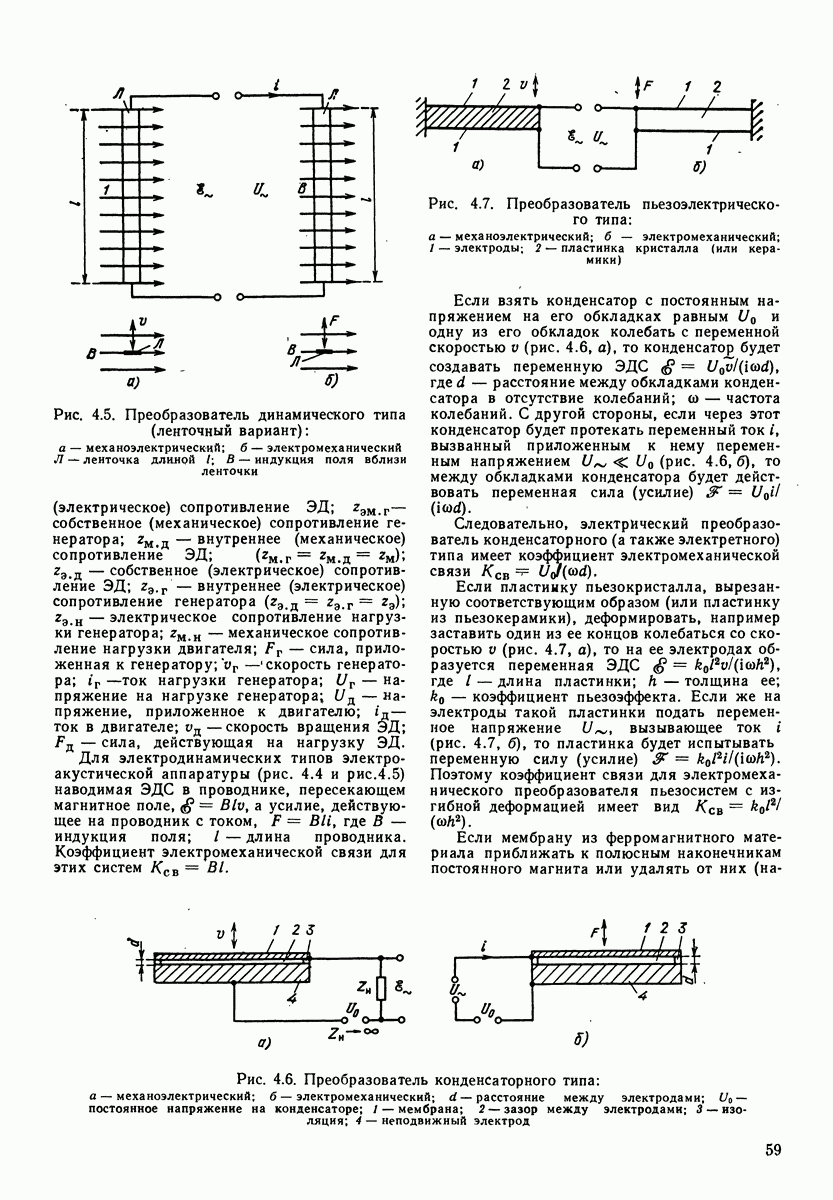
- 4.4. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4.5. МЕТОДЫ СОСТАВЛЕНИЯ АНАЛОГОВЫХ СХЕМ
- РАЗДЕЛ 5. МИКРОФОНЫ И ЛАРИНГОФОНЫ
- 5.2. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ МИКРОФОНОВ
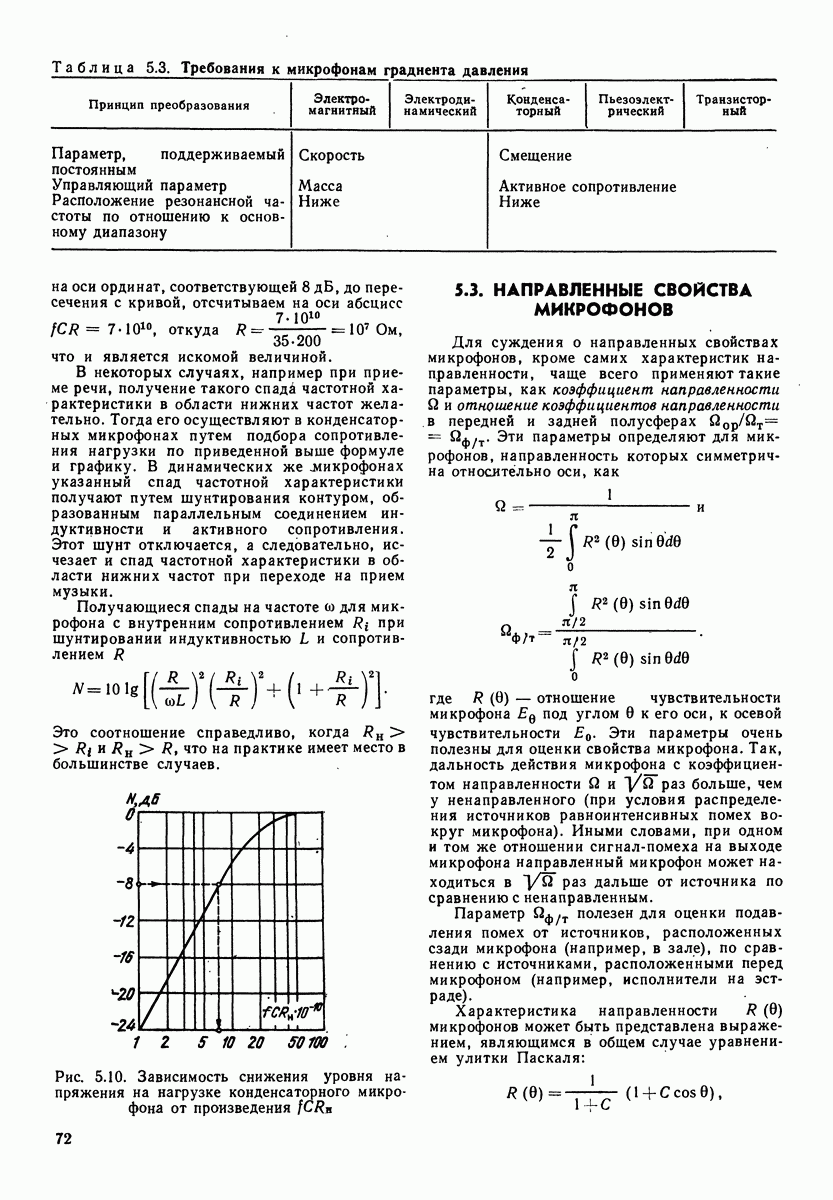
- 5.3. НАПРАВЛЕННЫЕ СВОЙСТВА МИКРОФОНОВ
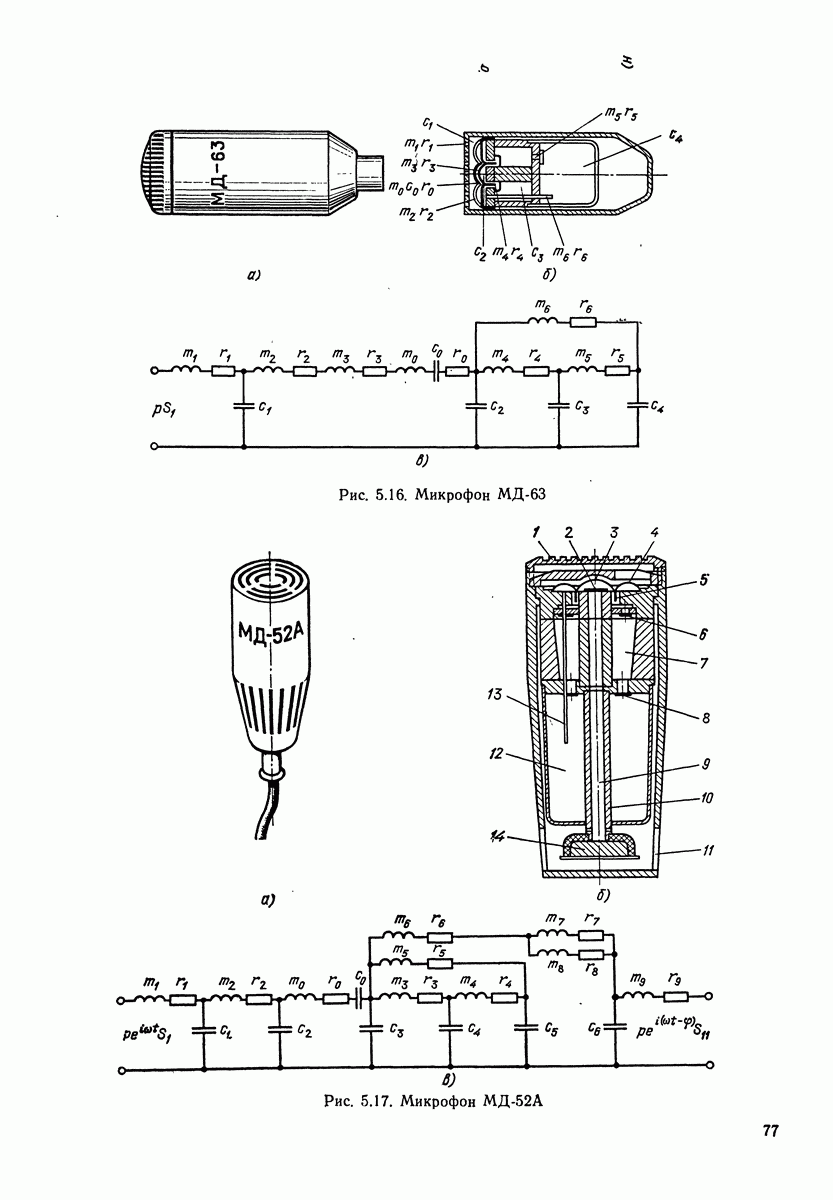
- 5.4. ЭЛЕКТРОДИНАМИЧЕСКИЕ МИКРОФОНЫ
- 5.5. КОНДЕНСАТОРНЫЕ МИКРОФОНЫ
- 5.6. НЕКОТОРЫЕ ДРУГИЕ ТИПЫ МИКРОФОНОВ
- 5.7. ТЕХНИЧЕСКАЯ ЭКСПЛУАТАЦИЯ МИКРОФОНОВ
- РАЗДЕЛ 6. ГРОМКОГОВОРИТЕЛИ И ТЕЛЕФОНЫ
- 6.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ТЕЛЕФОНОВ И ГРОМКОГОВОРИТЕЛЕЙ
- 6.3. ТРЕБОВАНИЯ К ГРОМКОГОВОРИТЕЛЯМ И ТЕЛЕФОНАМ
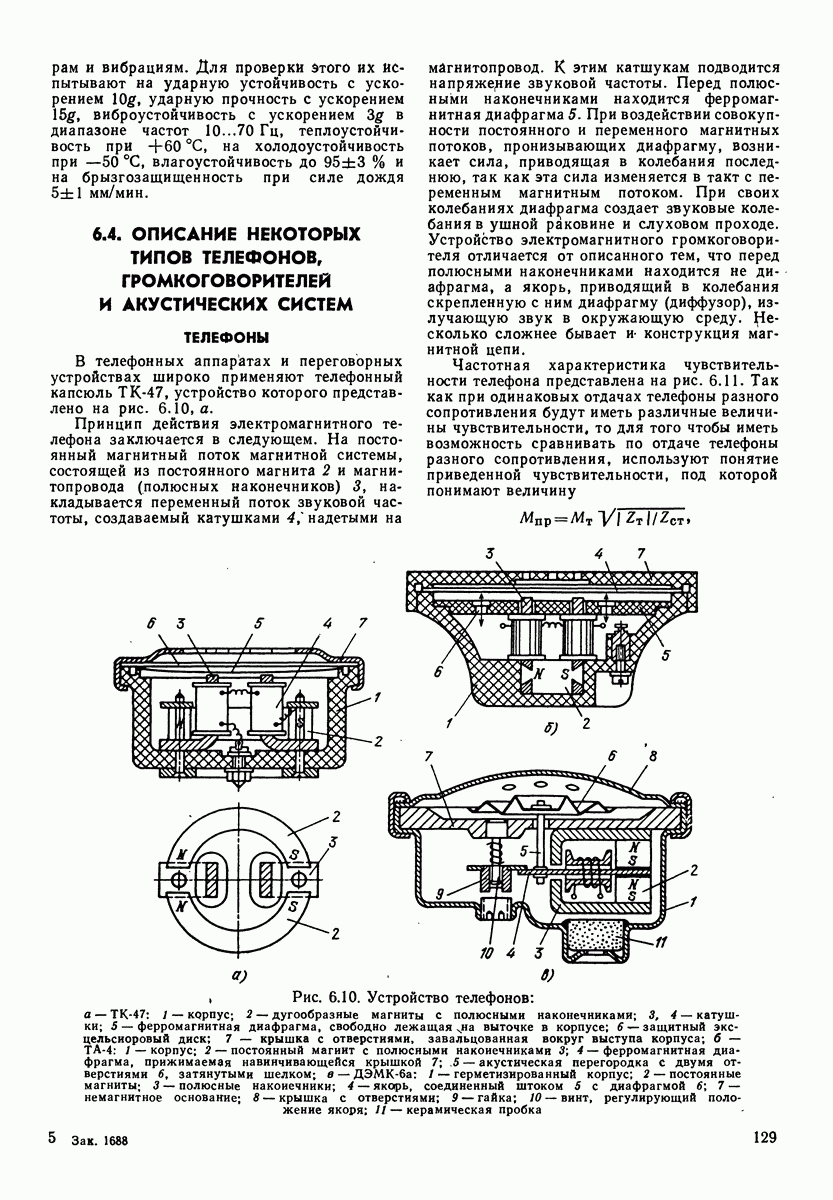
- 6.4. ОПИСАНИЕ НЕКОТОРЫХ ТИПОВ ТЕЛЕФОНОВ, ГРОМКОГОВОРИТЕЛЕЙ И АКУСТИЧЕСКИХ СИСТЕМ ТЕЛЕФОНЫ
- 6.5. КОНСТРУКЦИИ АКУСТИЧЕСКИХ ОФОРМЛЕНИЙ ПЛОСКИЙ ЭКРАН
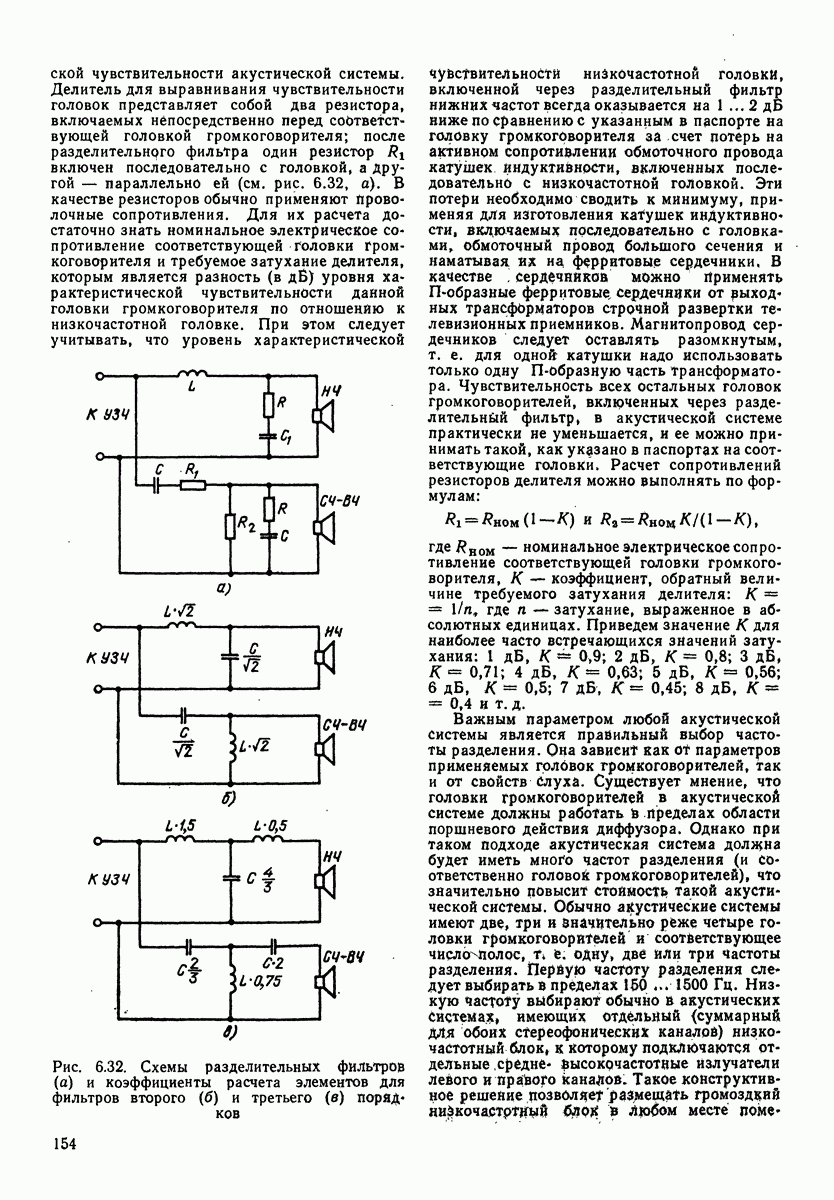
- 6.6. ВКЛЮЧЕНИЕ ГОЛОВОК ГРОМКОГОВОРИТЕЛЕЙ В АКУСТИЧЕСКИЕ СИСТЕМЫ
- 6.7. РАЗМЕЩЕНИЕ АКУСТИЧЕСКИХ СИСТЕМ
- РАЗДЕЛ 7. АКУСТИКА СТУДИЙ И ДРУГИХ ПОМЕЩЕНИЙ
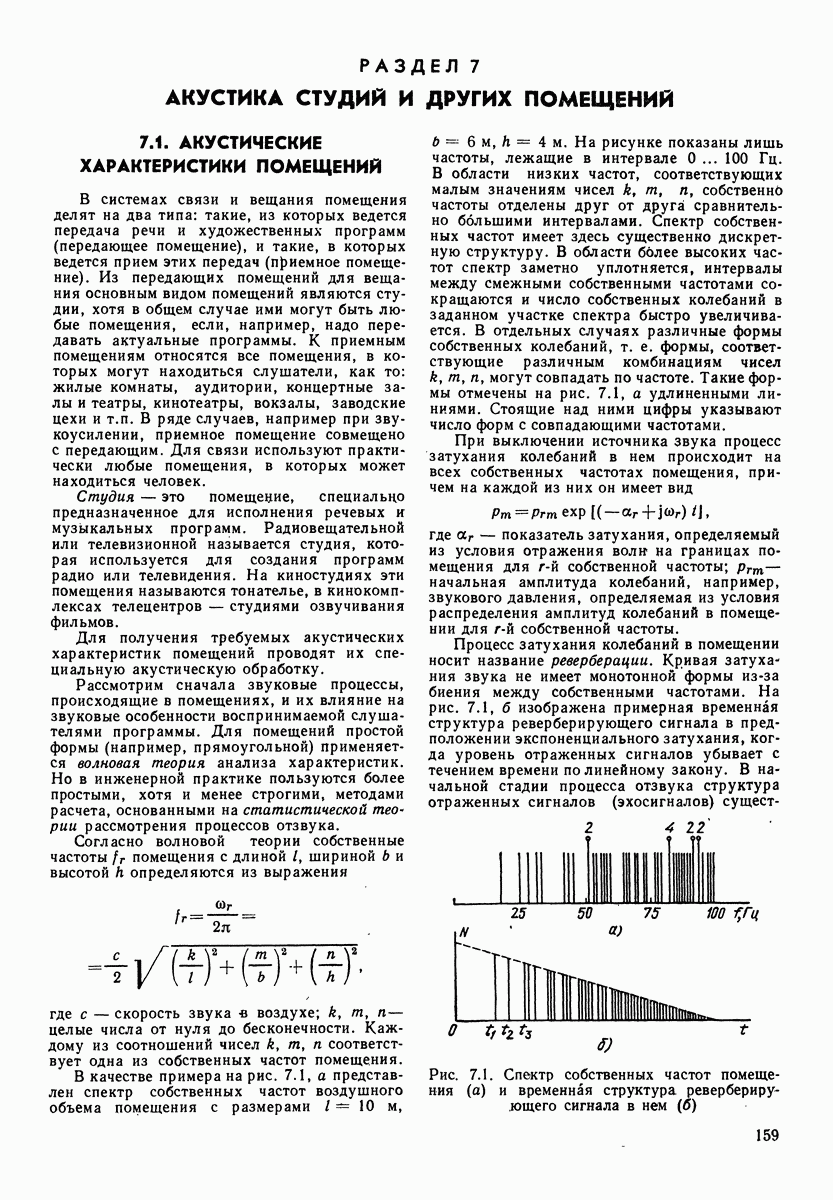
- 7.1. АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОМЕЩЕНИЙ
- 7.2. КЛАССИФИКАЦИЯ РАДИОВЕЩАТЕЛЬНЫХ И ТЕЛЕВИЗИОННЫХ СТУДИЙ
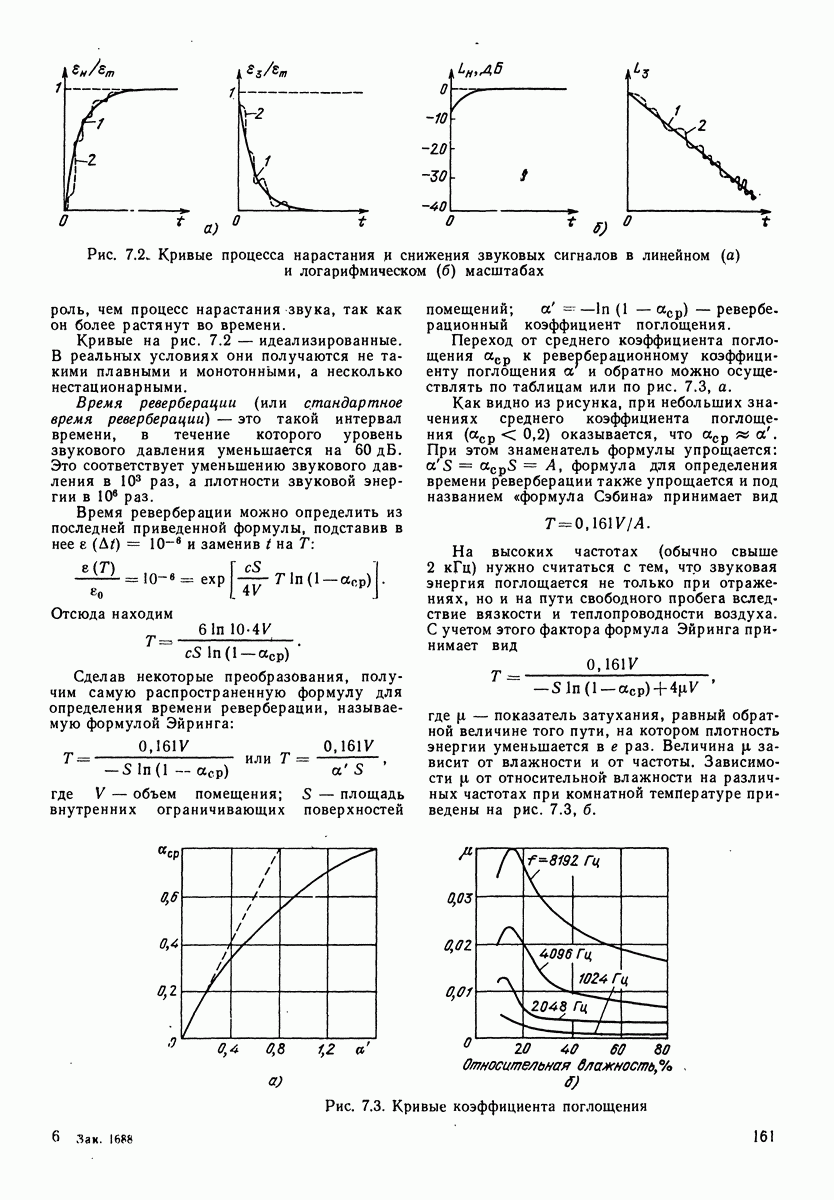
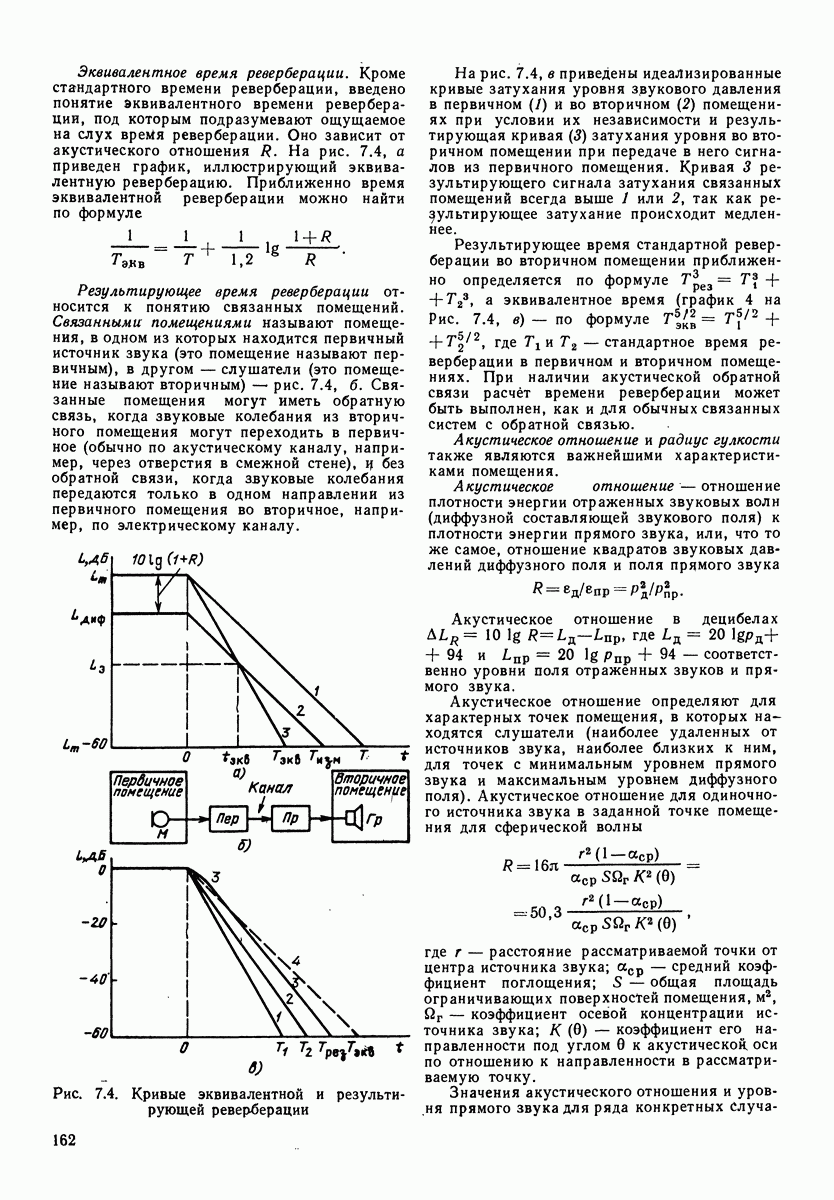
- 7.3. ОПТИМАЛЬНАЯ РЕВЕРБЕРАЦИЯ В СТУДИЯХ И ПРИЕМНЫХ ПОМЕЩЕНИЯХ
- 7.4. ЗВУКОПОГЛОЩАЮЩИЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ
- 7.5. ЗВУКОИЗОЛЯЦИЯ СТУДИЙ
- 7.6. ЭЛЕКТРОАКУСТИЧЕСКОЕ ОБОРУДОВАНИЕ СТУДИЙ И АППАРАТНЫХ
- РАЗДЕЛ 8. ОЗВУЧЕНИЕ И ЗВУКОУСИЛЕНИЕ
- 8.2. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ОТКРЫТЫХ ПРОСТРАНСТВ
- 8.3. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.4. ЗОНАЛЬНЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.5. ОСОБЕННОСТИ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
- 8.6. СОСРЕДОТОЧЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ ПОМЕЩЕНИЙ
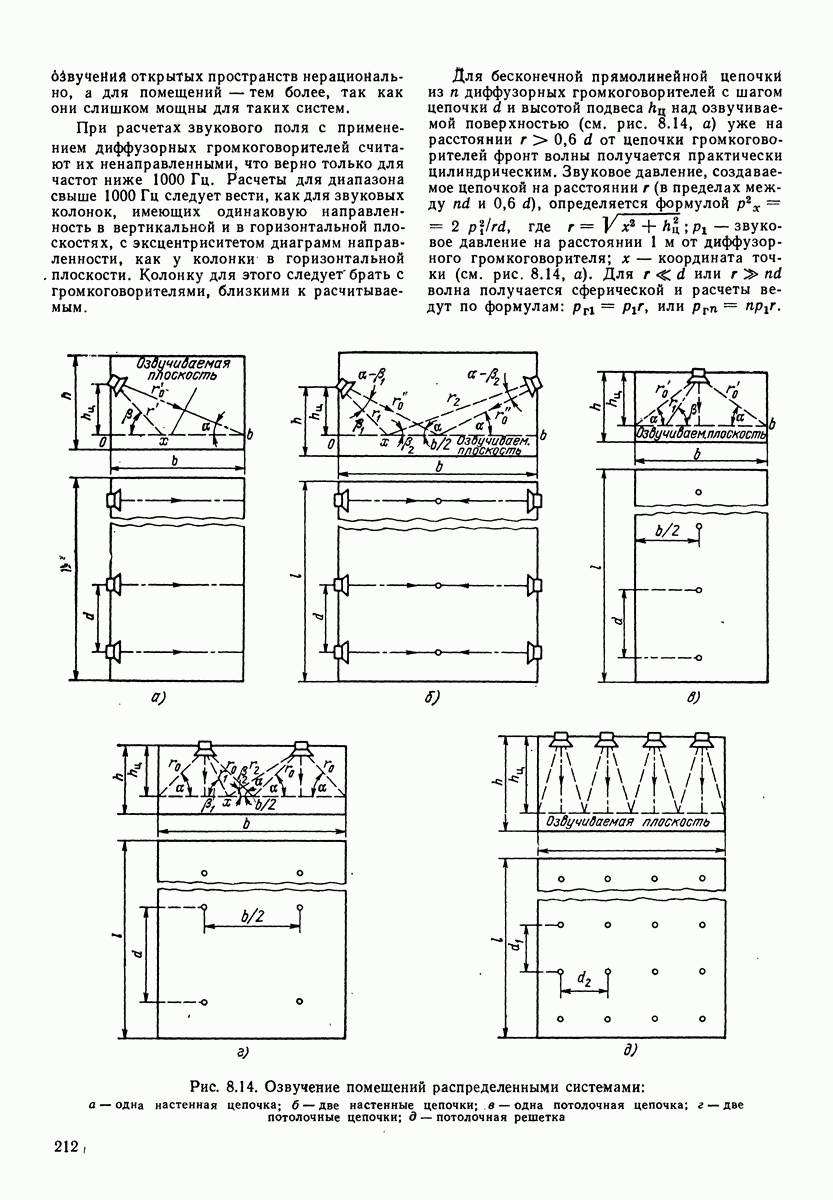
- 8.7. РАСПРЕДЕЛЕННЫЕ СИСТЕМЫ ОЗВУЧЕНИЯ
- 8.8. ЗВУКОУСИЛЕНИЕ
- 8.9. ГРОМКОГОВОРЯЩАЯ СВЯЗЬ
- РАЗДЕЛ 9. ЗАПИСЬ И ВОСПРОИЗВЕДЕНИЕ ЗВУКА
- 9.1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ ЗАПИСИ ЗВУКА
- 9.2. МЕХАНИЧЕСКАЯ ЗВУКОЗАПИСЬ
- 9.3. ФОТОГРАФИЧЕСКАЯ ЗВУКОЗАПИСЬ
- 9.4. МАГНИТНАЯ ЗВУКОЗАПИСЬ
- 9.5. МАГНИТНЫЕ ГОЛОВКИ
- 9.6. МАГНИТНЫЕ НОСИТЕЛИ ЗАПИСИ
- 9.7. МАГНИТОФОНЫ
- 9.8. ЛАЗЕРНАЯ ЗВУКОЗАПИСЬ НА КОМПАКТ-ДИСК
- РАЗДЕЛ 10. ПЕРЕДАЧА АКУСТИЧЕСКИХ СИГНАЛОВ
- 10.2. ИСКАЖЕНИЯ СИГНАЛОВ
- 10.3. ШУМЫ И ПОМЕХИ В ТРАКТАХ И КАНАЛАХ СВЯЗИ И ВЕЩАНИЯ
- 10.4. ДОПУСТИМЫЕ ИСКАЖЕНИЯ ВЕЩАТЕЛЬНЫХ СИГНАЛОВ
- 10.5. ПОНЯТНОСТЬ И РАЗБОРЧИВОСТЬ РЕЧИ
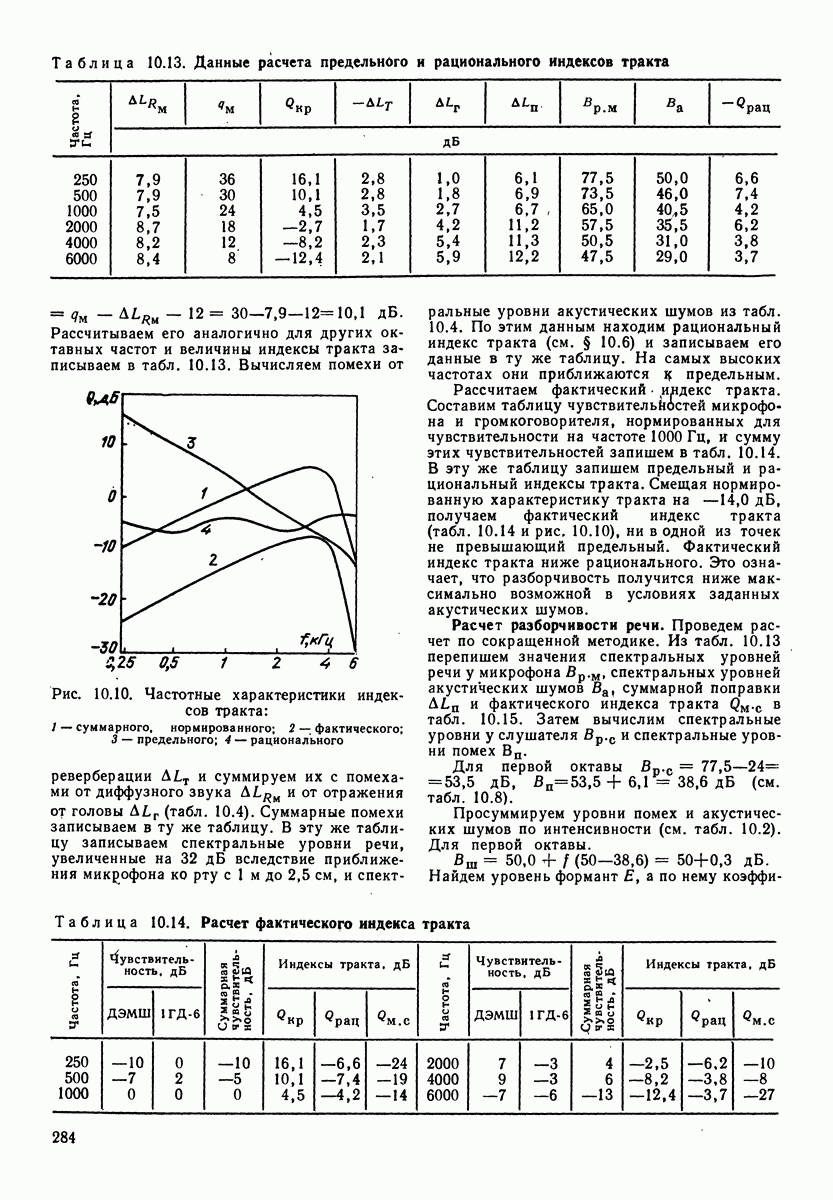
- 10.6. ИНДЕКСЫ ТРАКТА
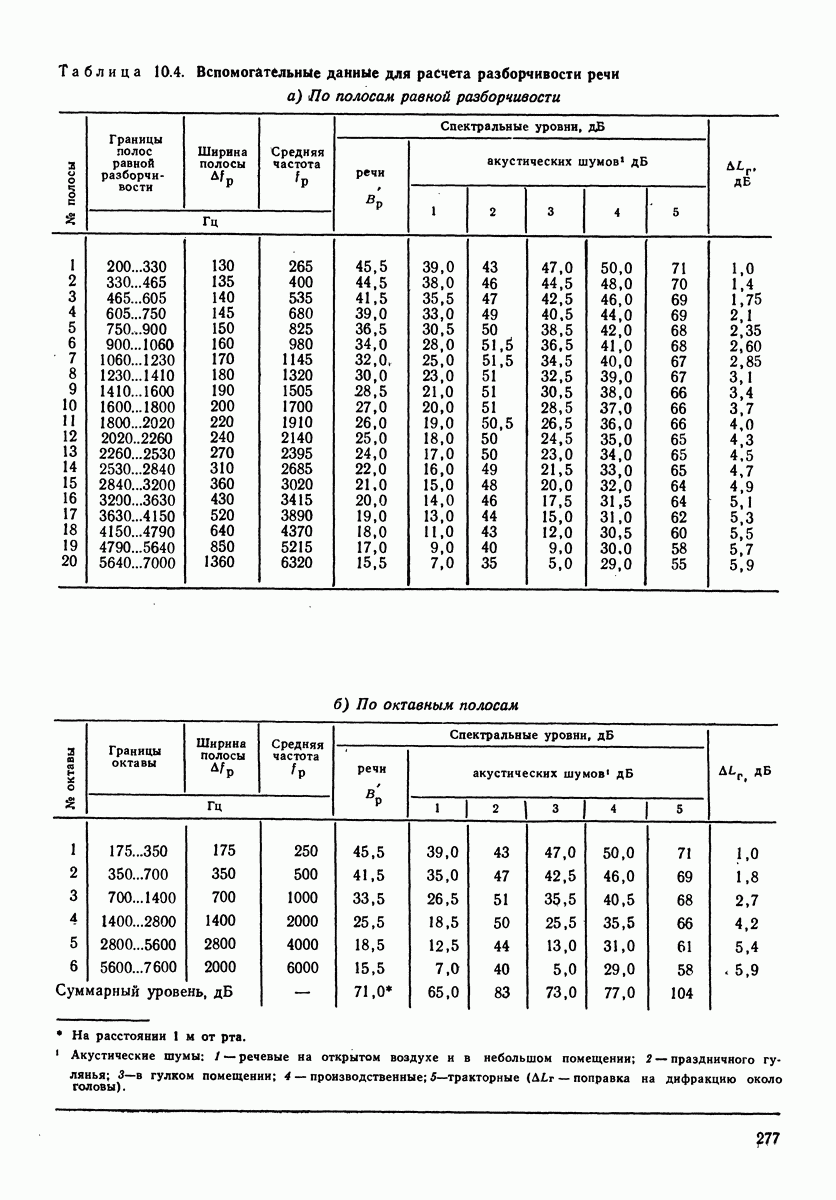
- 10.7. РАСЧЕТ РАЗБОРЧИВОСТИ РЕЧИ
- 10.8. РАСЧЕТ ОБЩЕГО УРОВНЯ ЗВУКОВОГО ПОЛЯ ПРИ ПЕРЕДАЧЕ РЕЧИ И ВЫБОР АППАРАТУРЫ ЗВУКОУСИЛЕНИЯ
- 10.9. ПРИМЕРЫ РАСЧЕТА ИНДЕКСОВ ТРАКТА, РАЗБОРЧИВОСТИ РЕЧИ И ОБЩЕГО УРОВНЯ ПЕРЕДАЧИ
- 10.10. ОПРЕДЕЛЕНИЕ РАЗБОРЧИВОСТИ РЕЧИ ДЛЯ ТРАКТОВ РАДИОТЕЛЕФОННОЙ СВЯЗИ
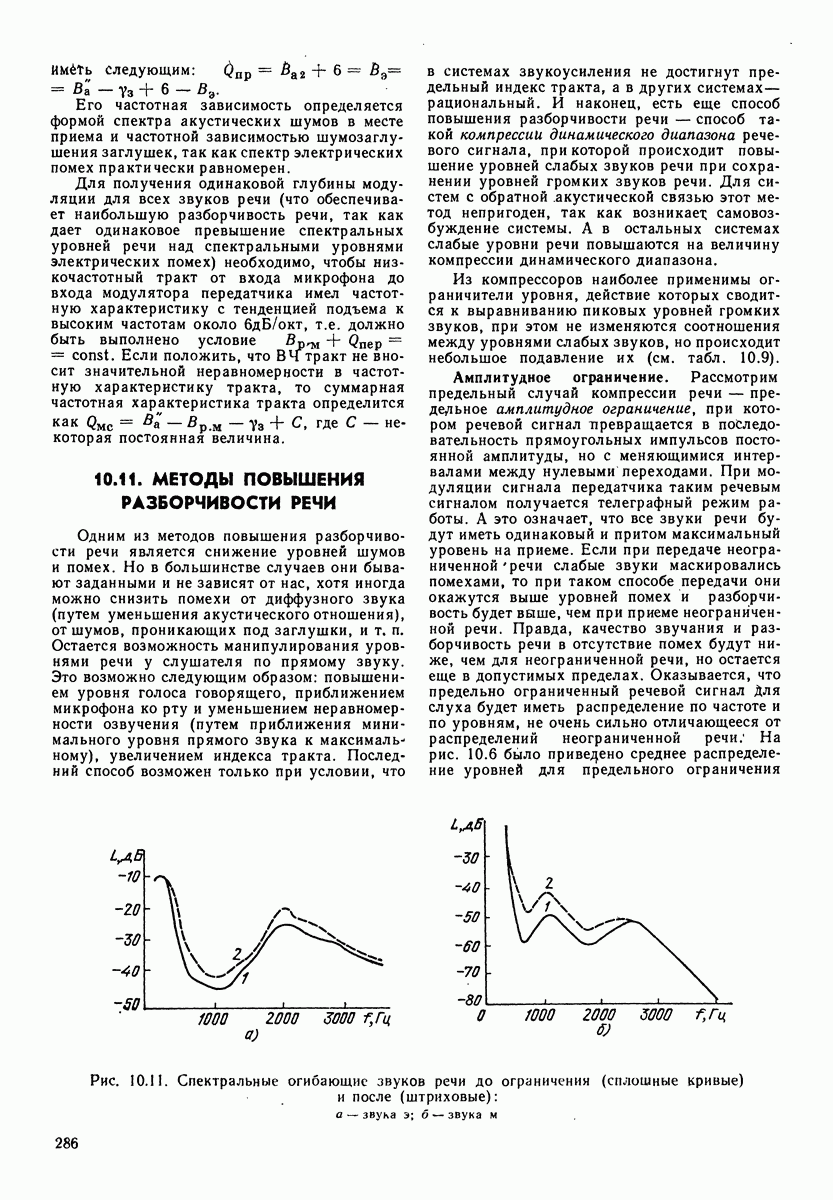
- 10.11. МЕТОДЫ ПОВЫШЕНИЯ РАЗБОРЧИВОСТИ РЕЧИ
- 10.12. ВОКОДЕРНАЯ СВЯЗЬ
- РАЗДЕЛ 11. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ
- 11.2. МЕТОДЫ ИЗМЕРЕНИЙ ОСНОВНЫХ ХАРАКТЕРИСТИК ЭЛЕКТРОАКУСТИЧЕСКОЙ АППАРАТУРЫ И ПОМЕЩЕНИЙ
- 11.3. ЭКСПЕРТИЗА МУЗЫКАЛЬНЫХ ПЕРЕДАЧ
- РАЗДЕЛ 12. ПРОГРАММЫ ДЛЯ МИКРОКАЛЬКУЛЯТОРОВ И ЭВМ ТИПА ДВК
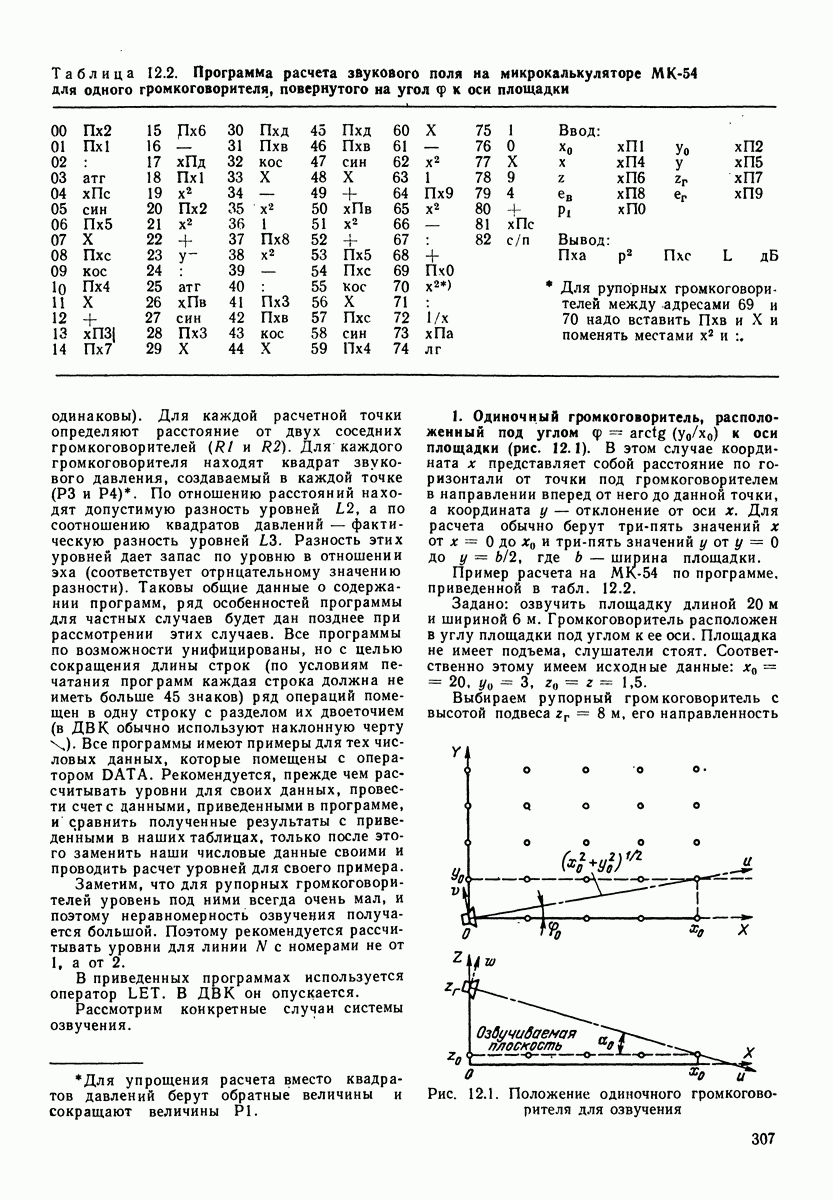
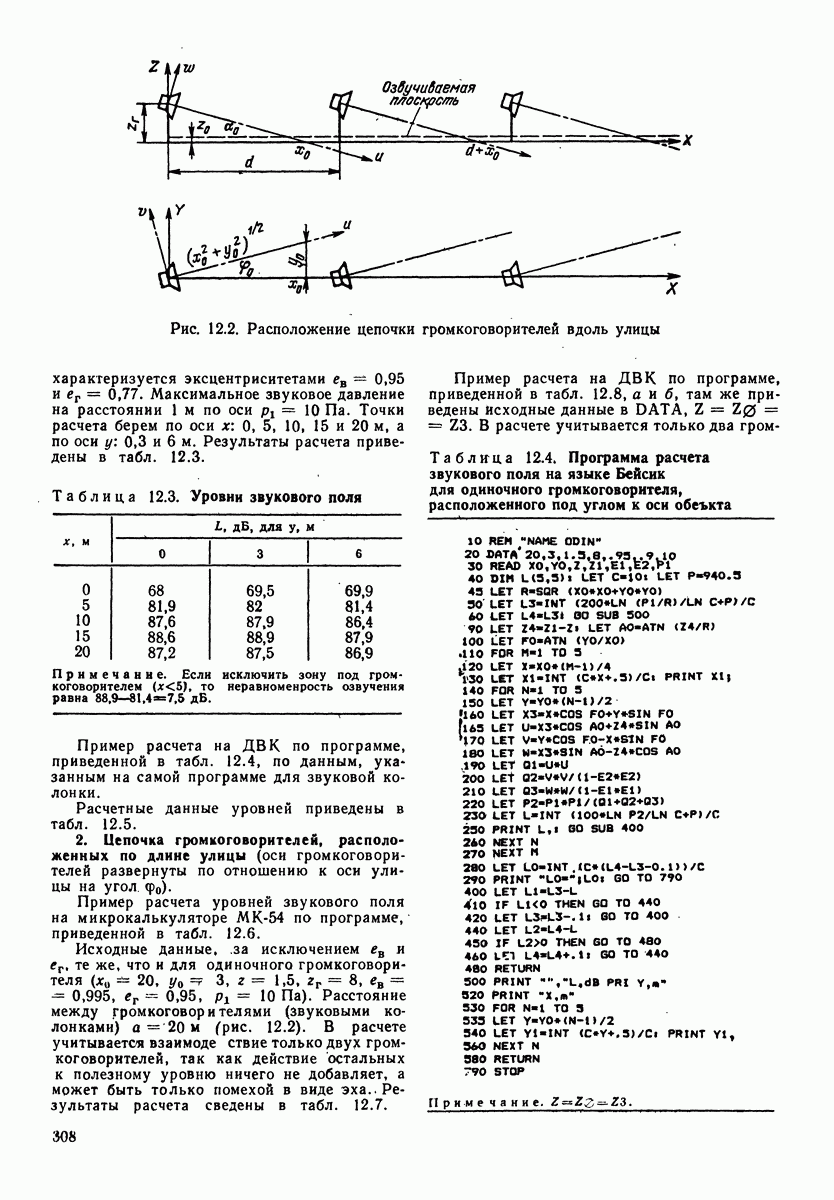
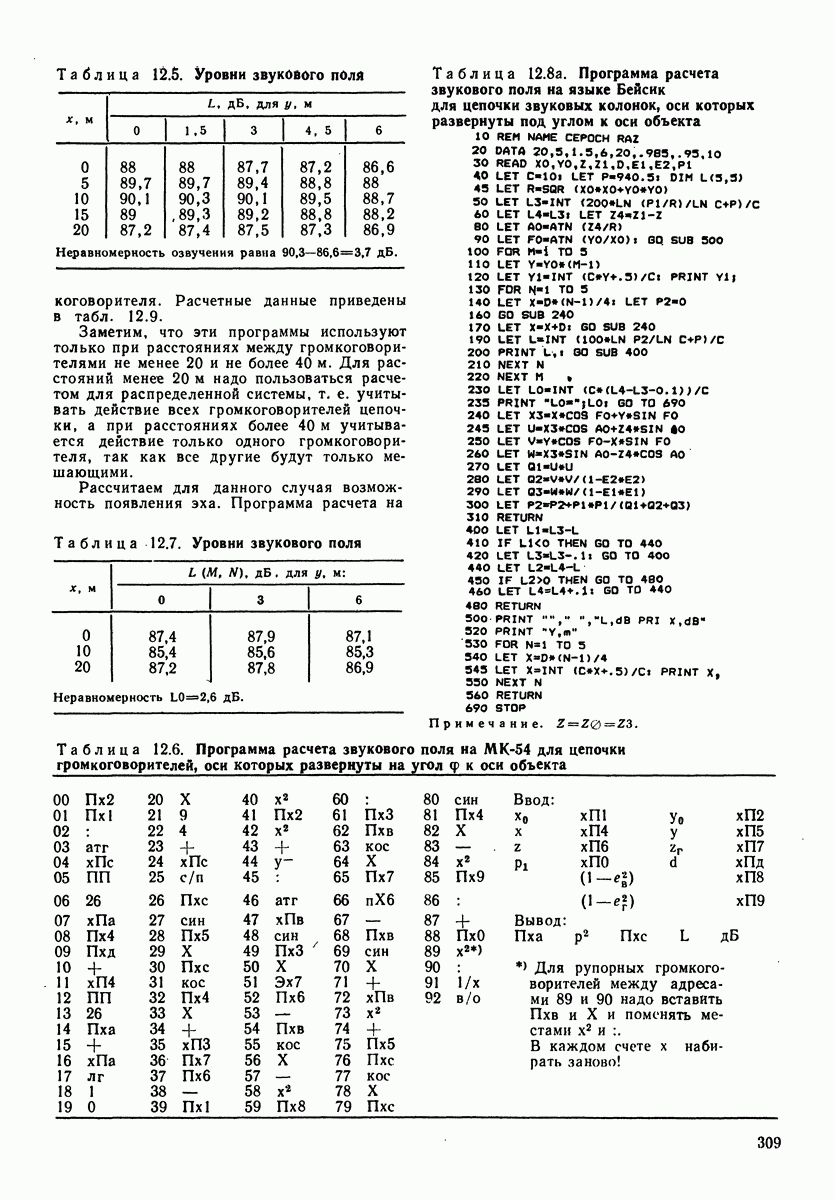
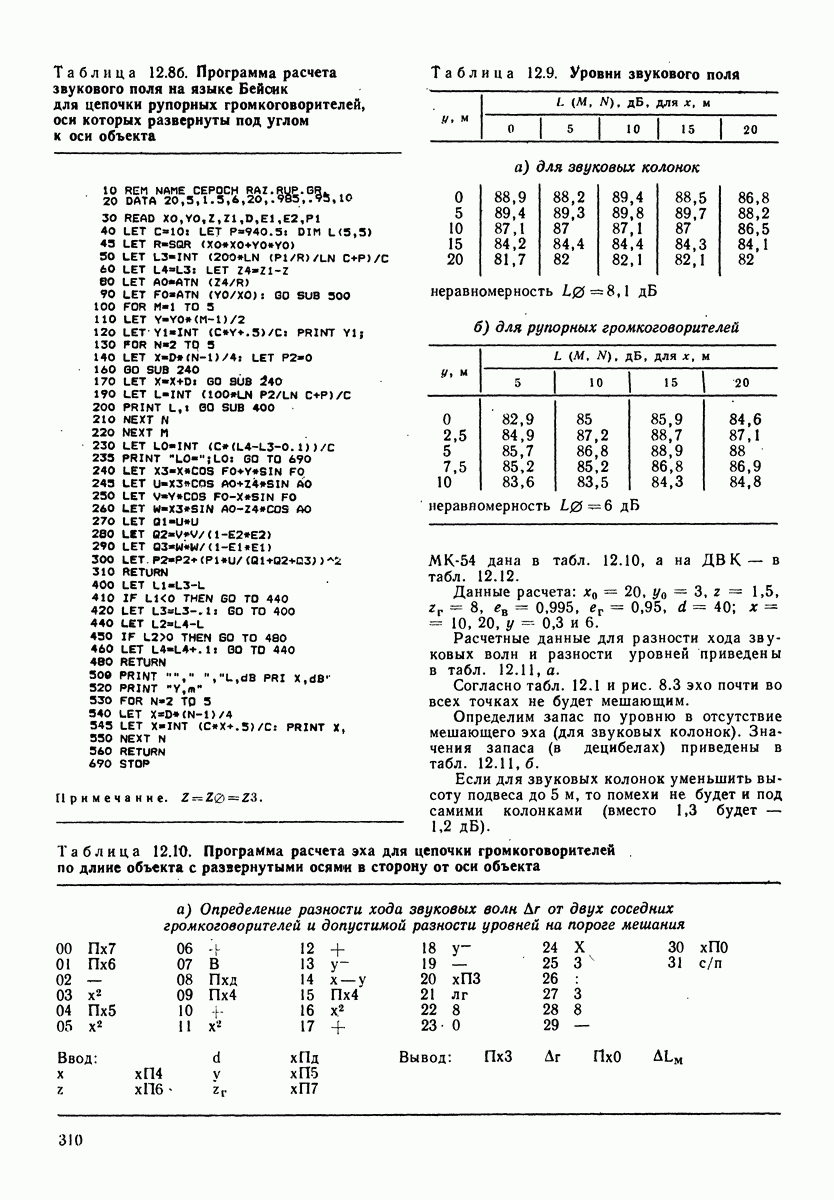
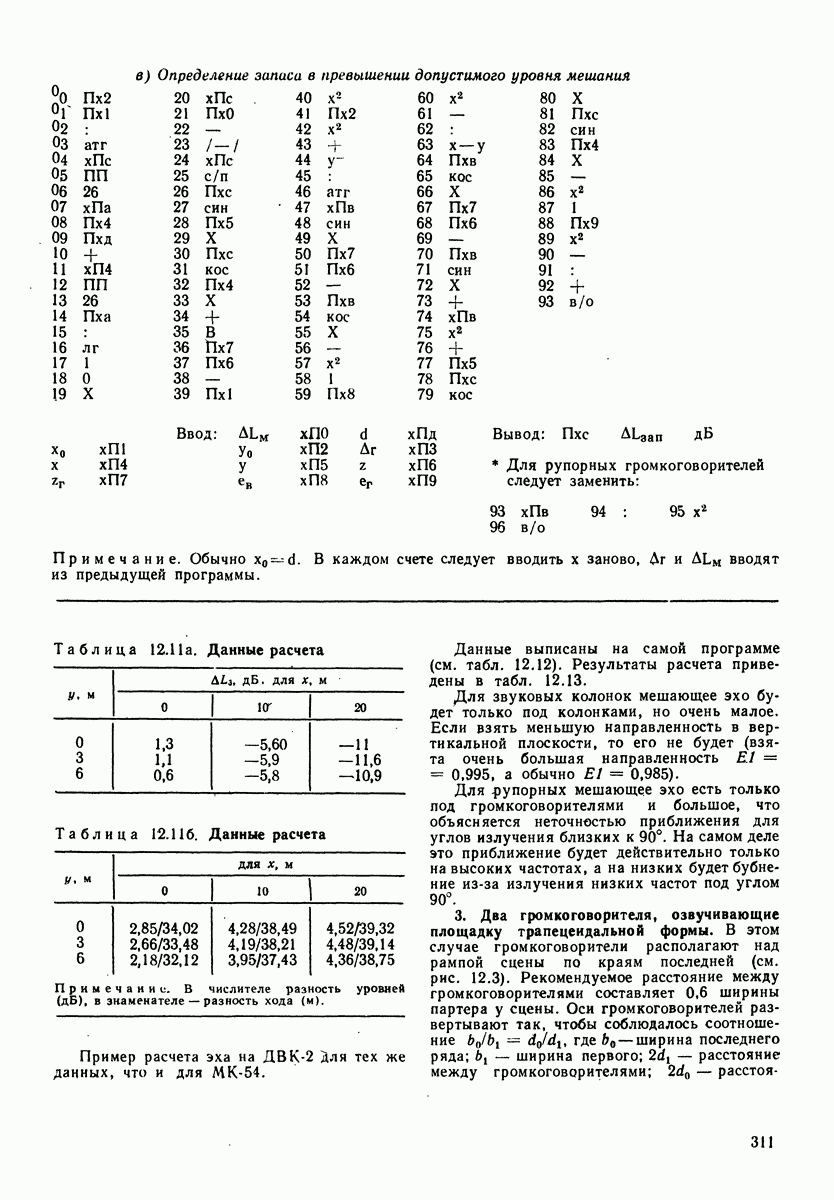
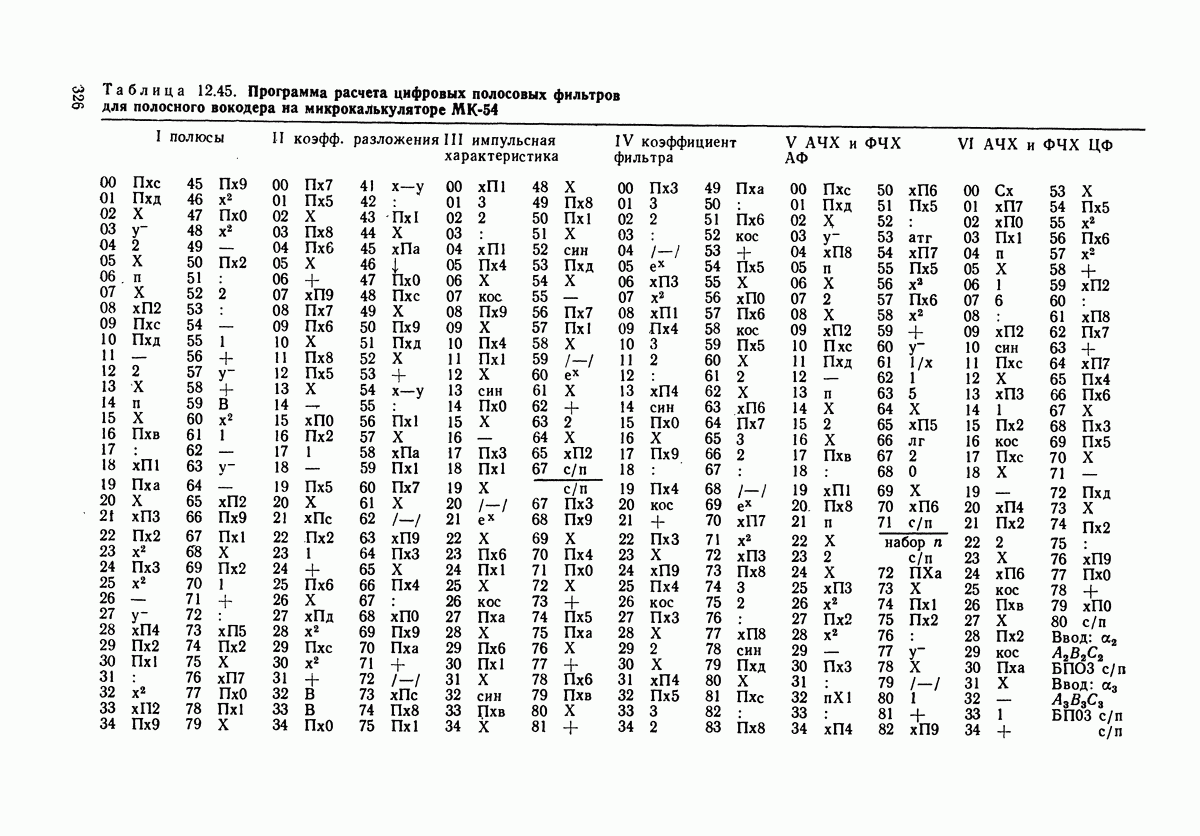
- 12.1. КОМПЛЕКС ПРОГРАММ ПО РАСЧЕТУ ЗВУКОВОГО ПОЛЯ И ЭХА ПРИ ЗВУКОФИКАЦИИ
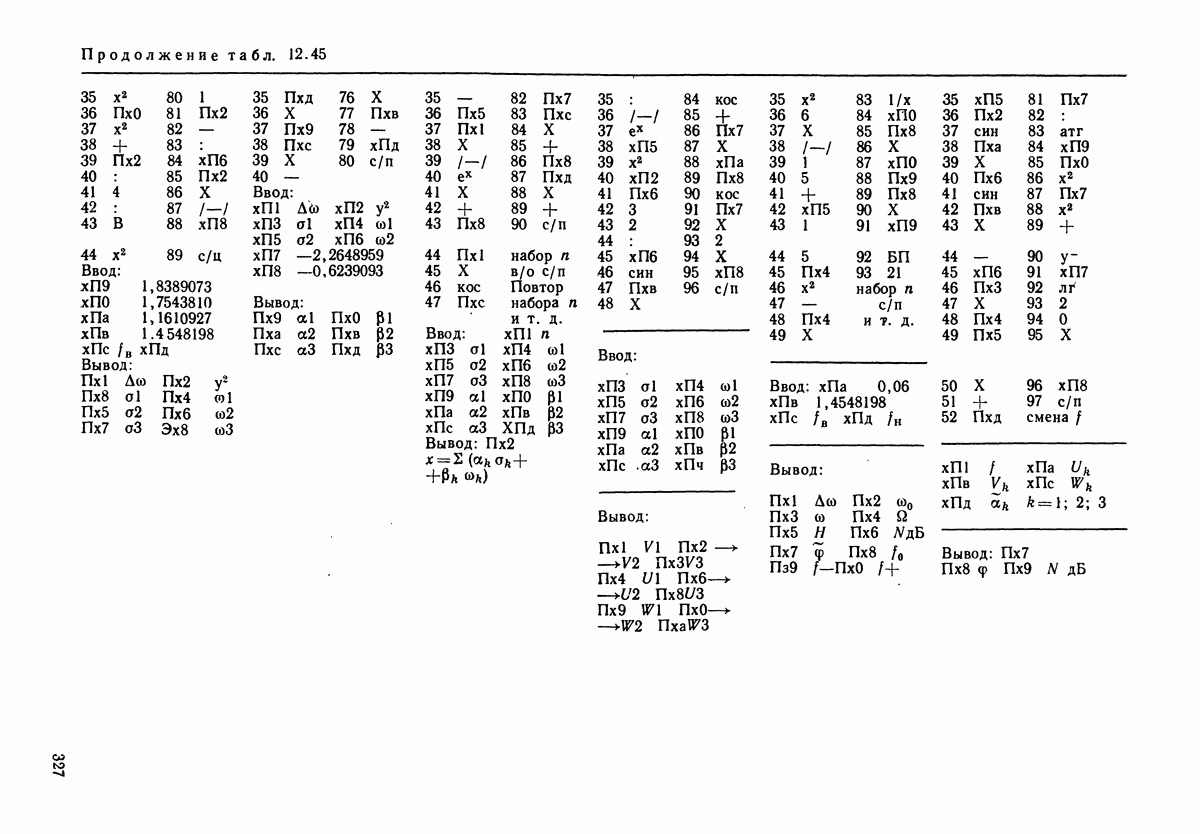
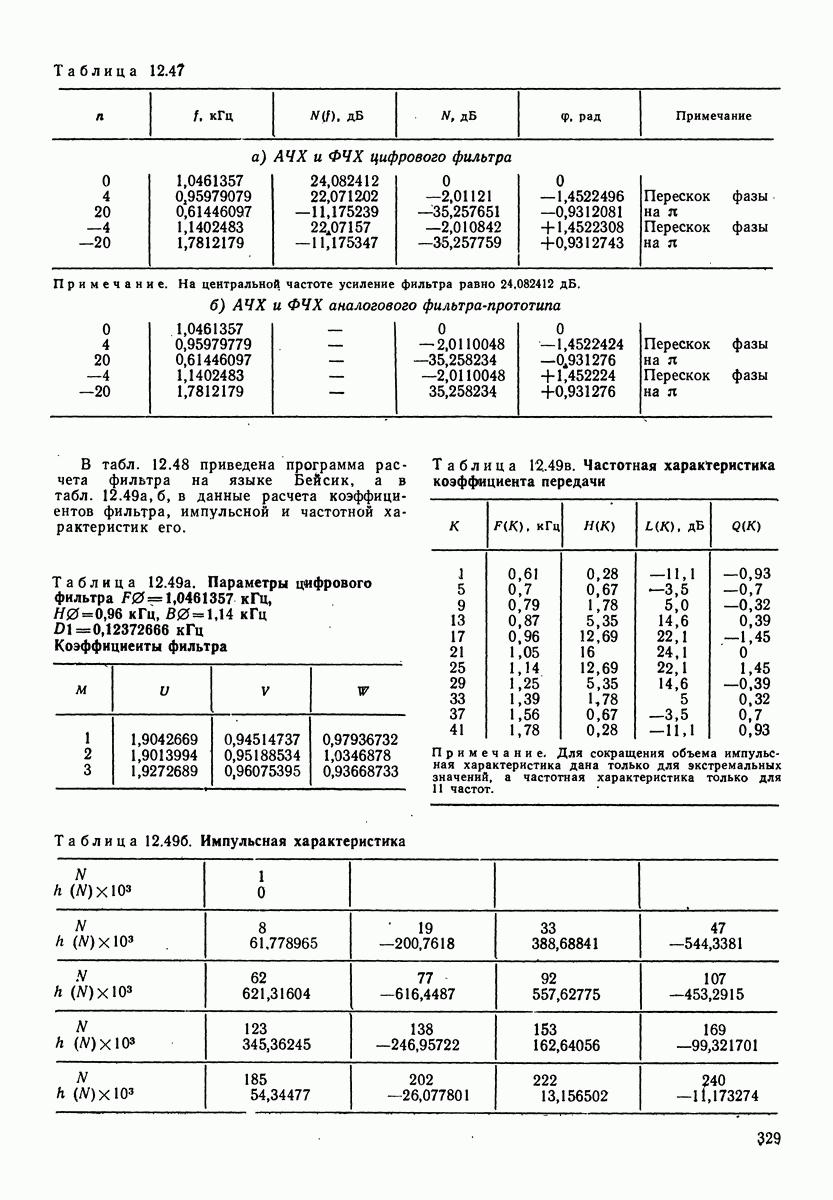
- 12.2. ПРОГРАММЫ РАСЧЕТА ДЛЯ ВОКОДЕРНЫХ ФИЛЬТРОВ (В ЦИФРОВОМ ИСПОЛНЕНИИ)
- 12.3. ПРОГРАММЫ ДЛЯ РАСЧЕТА РАЗБОРЧИВОСТИ РЕЧИ И ОБЩЕГО УРОВНЯ ПЕРЕДАЧИ РЕЧИ