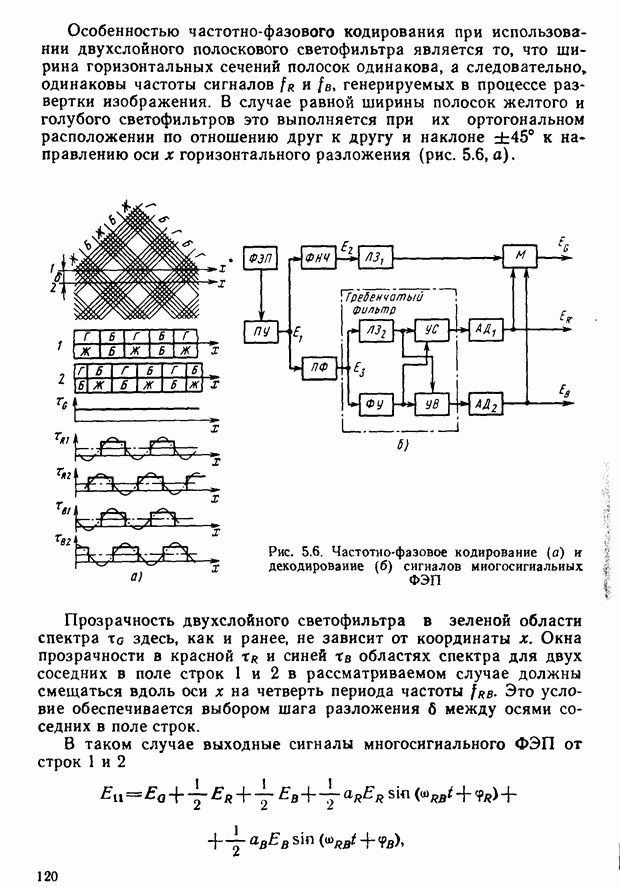
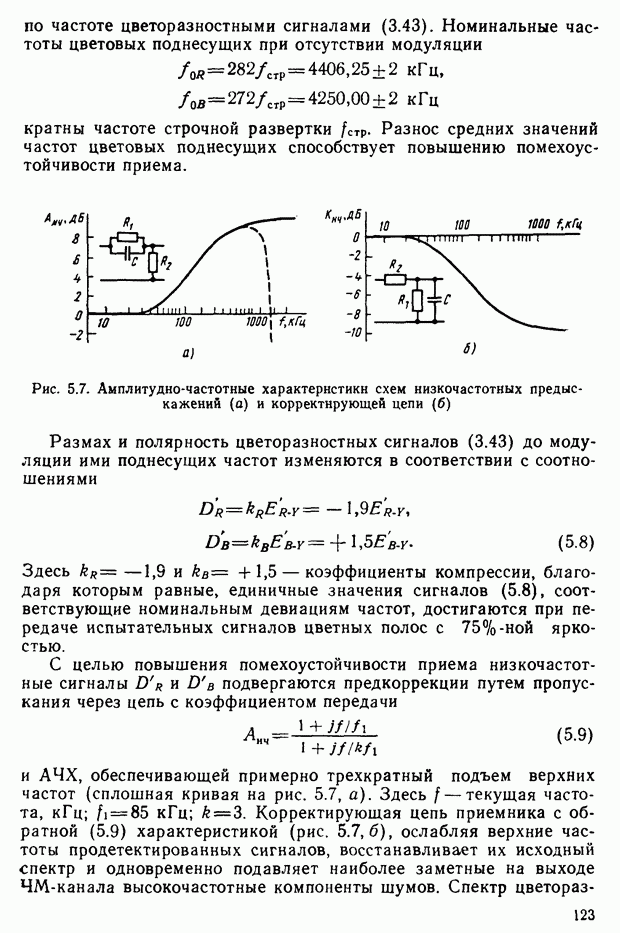
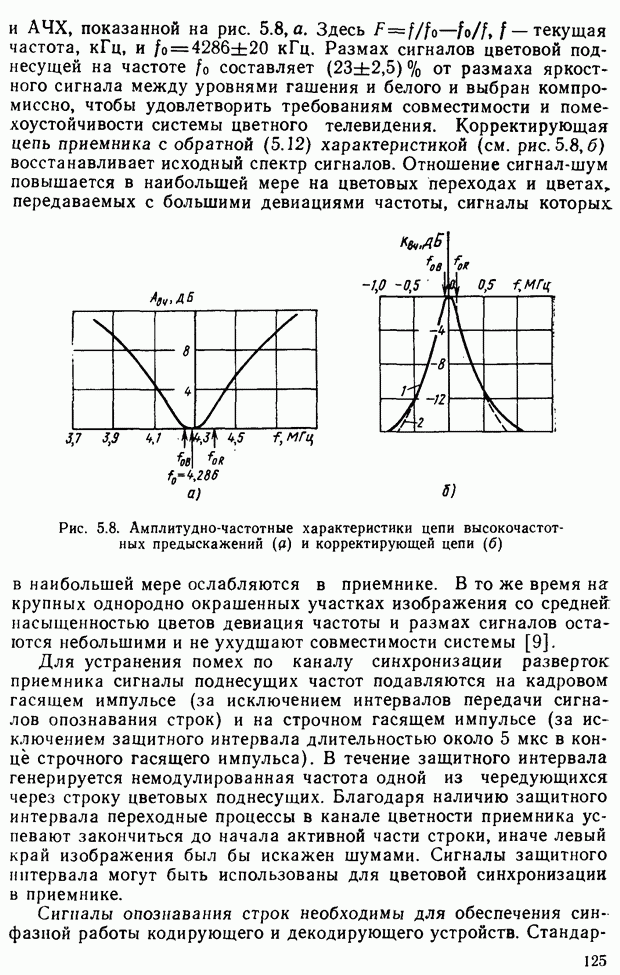
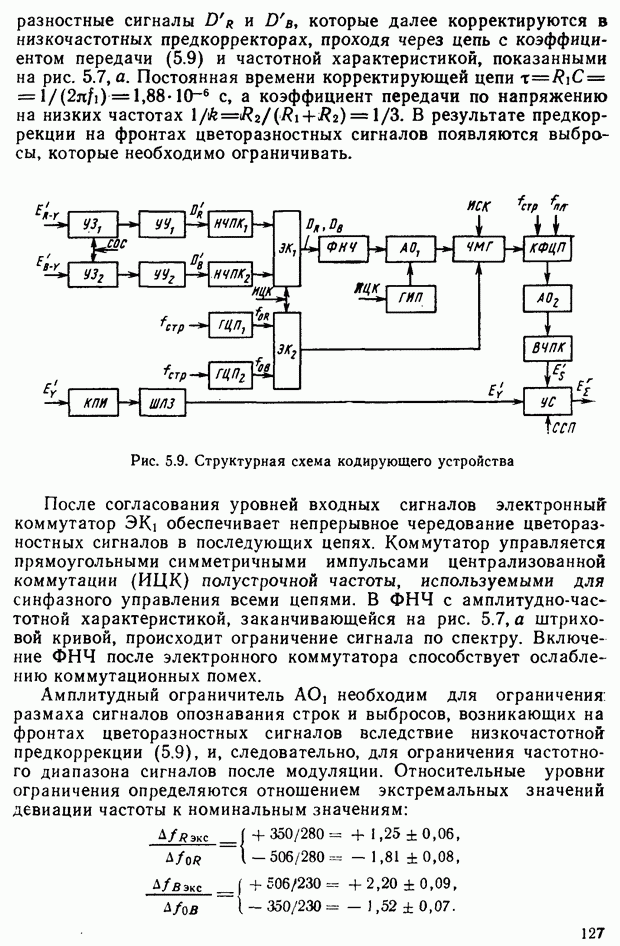
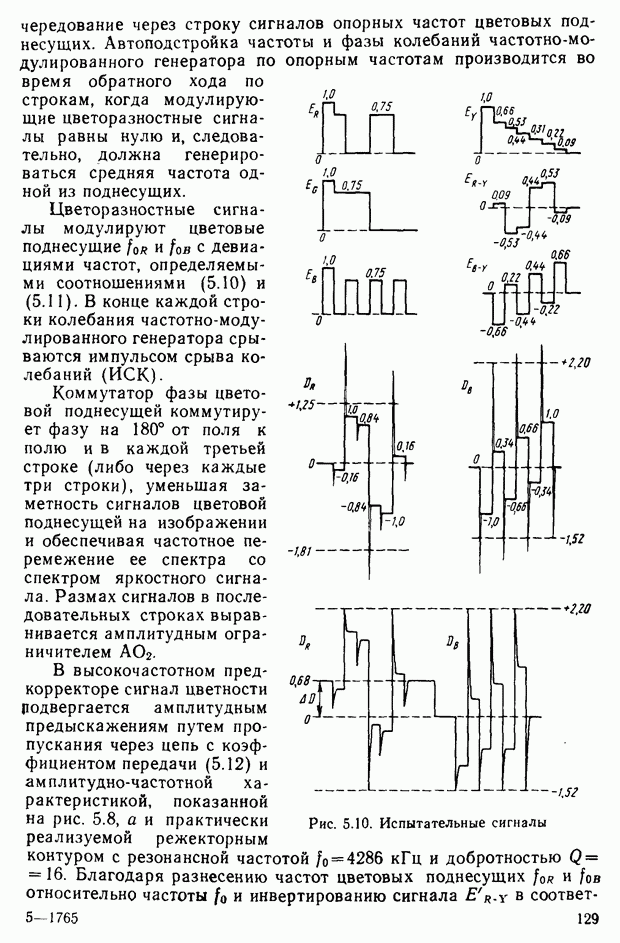
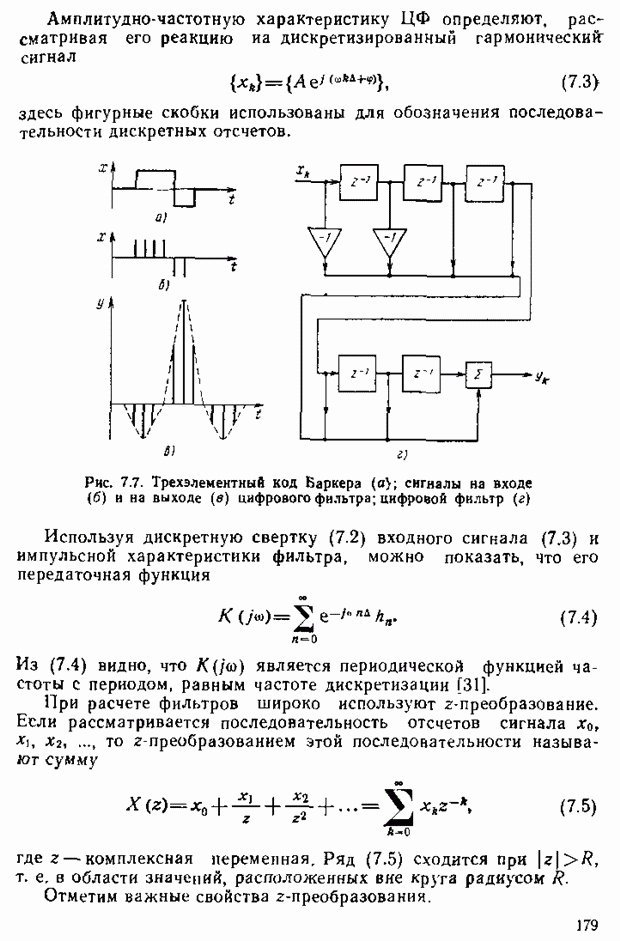
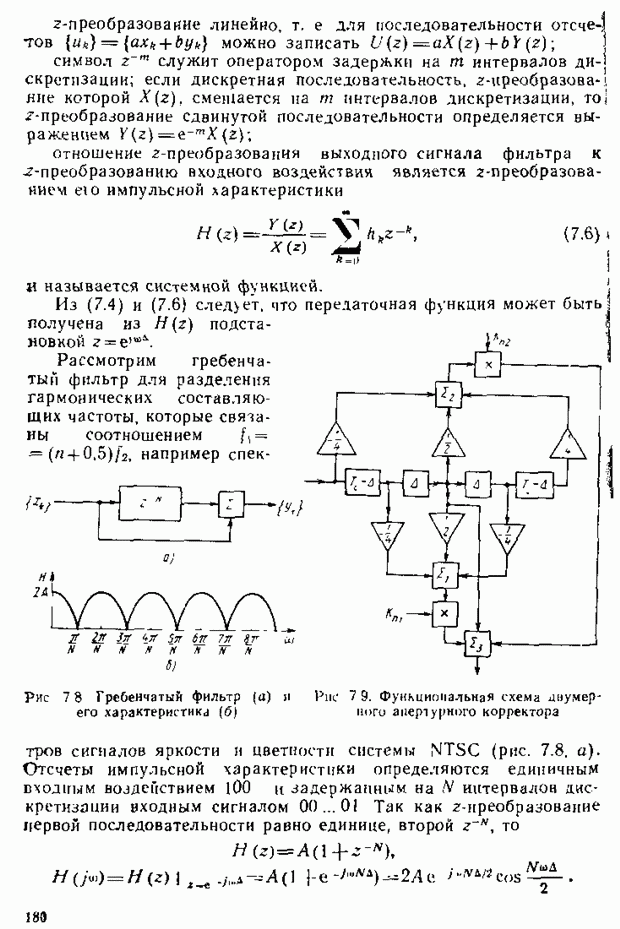
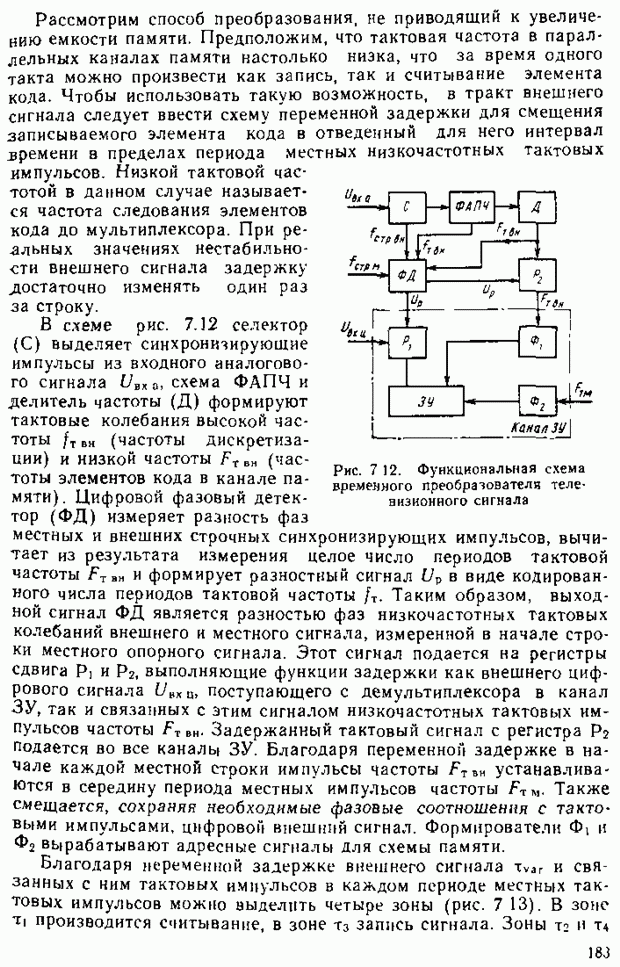
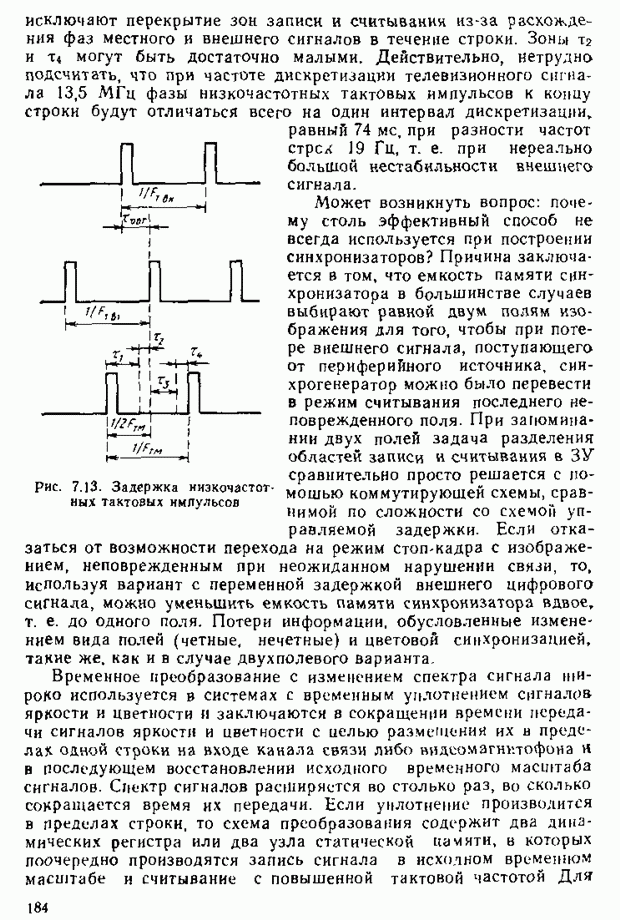
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
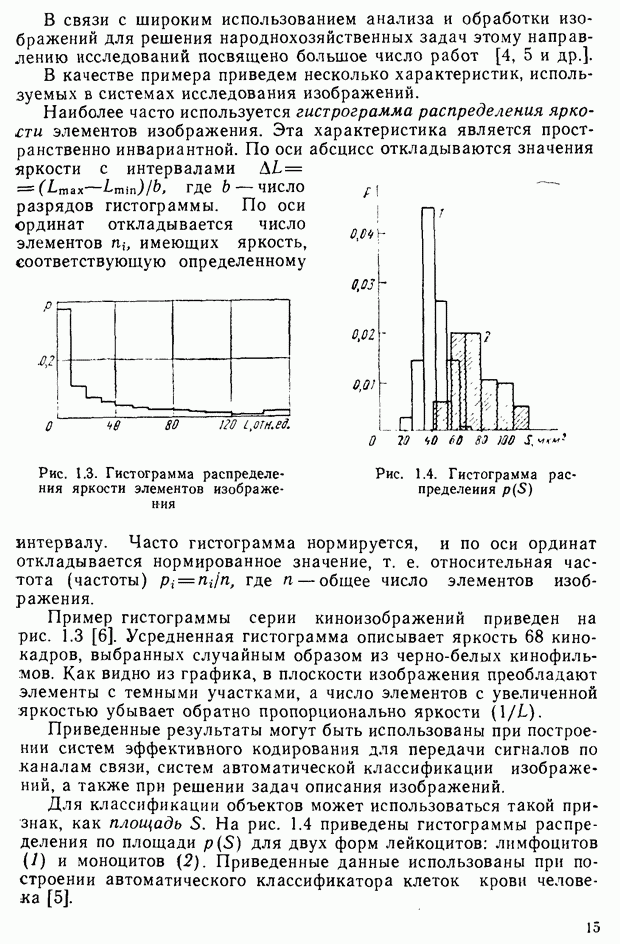
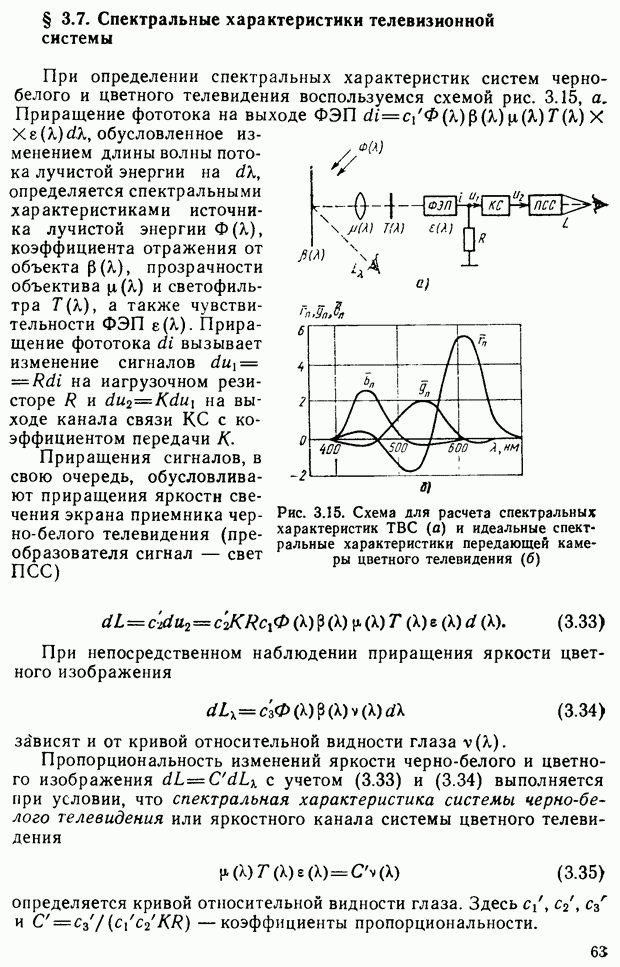
§ 2.7. Цветовые измерения и расчеты
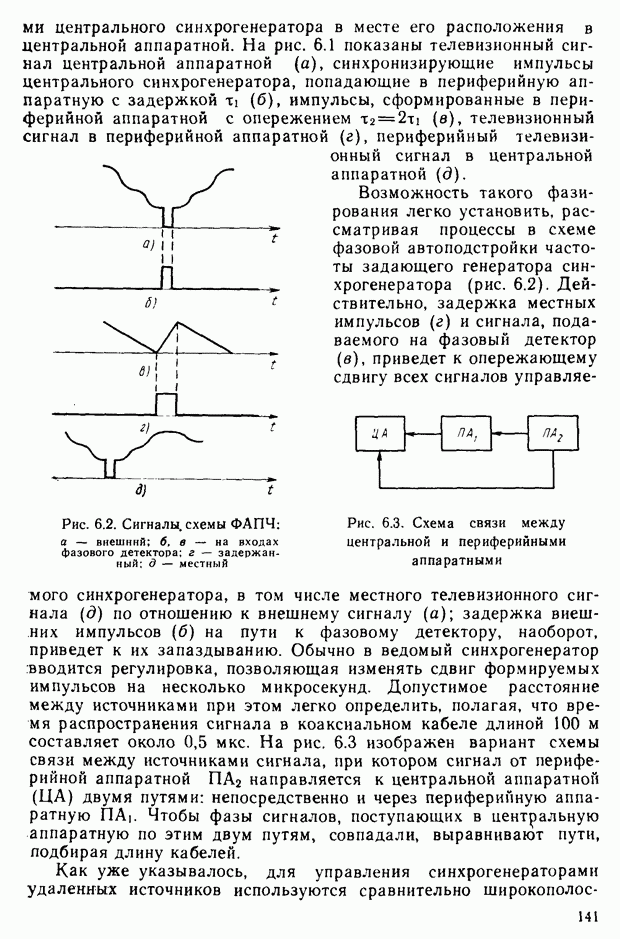
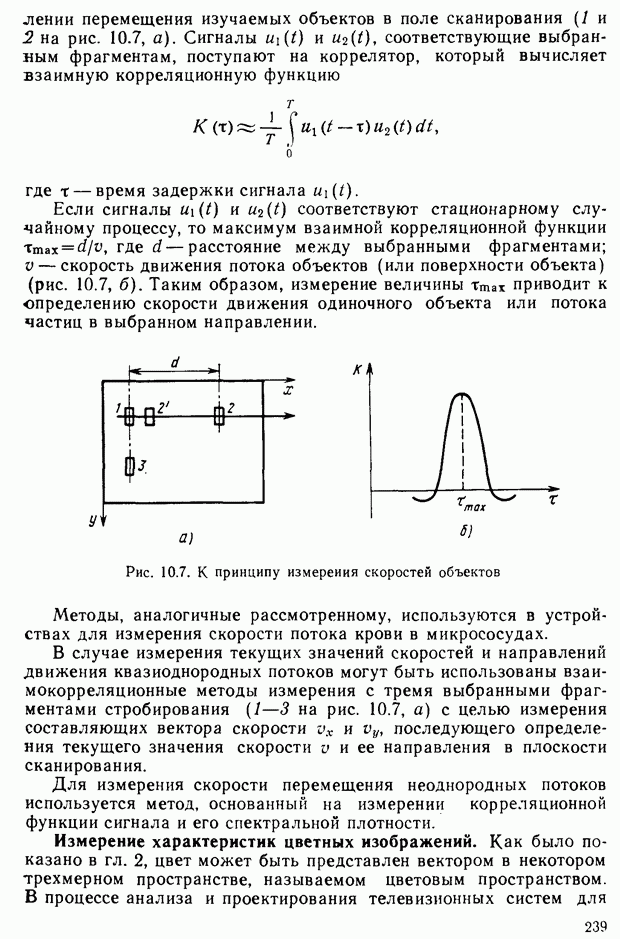
Цветовое уравнение. Практически произвести сравнение ощущений от исследуемого и эталонного излучений можно путем витального сопоставления их на расположенных в непосредственной близости поверхностях. Возьмем гипсовую призму и осветим ее различными световыми потоками, обозначенными на рис. 2.14 через  и
и  Для конкретизации рассматриваемого эксперимента предположим, например, что
Для конкретизации рассматриваемого эксперимента предположим, например, что  — цвет монохроматического излучения с длиной волны 550 нм, а
— цвет монохроматического излучения с длиной волны 550 нм, а  — с длиной волны 650 нм. Наблюдатель фиксирует цветовое различие между видимыми гранями призмы, которое никакими регулировками интенсивностей световых потоков, например, с помощью нейтральных светофильтров
— с длиной волны 650 нм. Наблюдатель фиксирует цветовое различие между видимыми гранями призмы, которое никакими регулировками интенсивностей световых потоков, например, с помощью нейтральных светофильтров  ликвидировать не удастся.
ликвидировать не удастся.
Добавим к цвету  цвет
цвет  (монохроматическое излучение с длиной волны, например, 500 нм). Если наблюдателю предоставить возможность изменять цвета
(монохроматическое излучение с длиной волны, например, 500 нм). Если наблюдателю предоставить возможность изменять цвета  и
и  (изменяя прозрачность нейтральных светофильтров), то он сможет добиться исчезновения цветового различия. Условимся цветовое равенство обозначать знаком равенства, а пропорции, в которых смешиваются световые потоки, множителями. На основании результатов эксперимента запишем уравнение
(изменяя прозрачность нейтральных светофильтров), то он сможет добиться исчезновения цветового различия. Условимся цветовое равенство обозначать знаком равенства, а пропорции, в которых смешиваются световые потоки, множителями. На основании результатов эксперимента запишем уравнение

где  — обозначение выбранных монохроматических излучений — основных цветов;
— обозначение выбранных монохроматических излучений — основных цветов;  множители — модули цветов;
множители — модули цветов;  — обозначение цвета смеси. Уравнение (2.14) будем называть цветовым уравнением. Следует подчеркнуть, что это уравнение описывает цветовые ощущения и имеет смысл только для глаза или его моделей
— обозначение цвета смеси. Уравнение (2.14) будем называть цветовым уравнением. Следует подчеркнуть, что это уравнение описывает цветовые ощущения и имеет смысл только для глаза или его моделей
В рассматриваемом эксперименте оказалось достаточным двух цветов  и
и  для получения цветового равенства с третьим
для получения цветового равенства с третьим  но не всякие три цвета находятся в такой зависимости. Для получения цветового равенства в некоторых случаях приходится
но не всякие три цвета находятся в такой зависимости. Для получения цветового равенства в некоторых случаях приходится

Рис. 2.14. К определению цветового уравнения
добавлять третий цвет  выбранный определенным образом. Следовательно, можно записать
выбранный определенным образом. Следовательно, можно записать

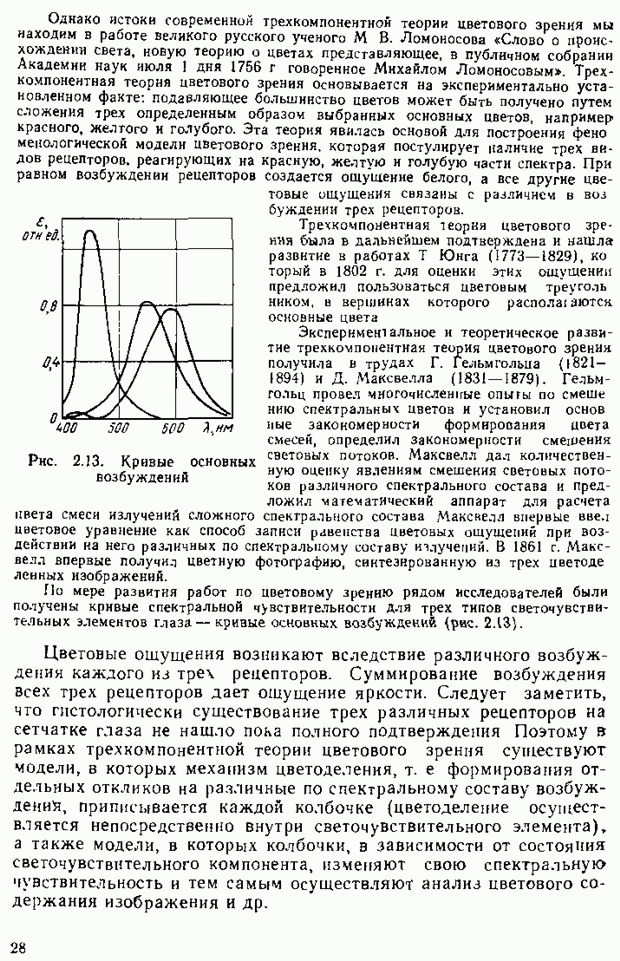
Основные цвета введены для удобства выражения результатов цветовых измерений и классификации цветов.
Построим характеристики, показывающие, в каких пропорциях необходимо смешивать цвета для получения ощущения, соответствующего заданному монохроматическому излучению. Для этого необходимо провести эксперименты, подобные рассмотренным, для каждого монохроматического излучения и построить соответствующие кривые для всего видимого диапазона длин волн электромагнитного излучения.
Опыты показали, что не всякий цвет монохроматического излучения может быть получен путем сложения трех основных цветов. Для получения цветового равенства в этом случае можно монохроматический цвет  «разбавить» одним из основных цветов. Если он «разбавляется» красным и этим достигается равенство цветовых ощущений от левой и правой граней призмы (см. рис. 2.15), то можно записать
«разбавить» одним из основных цветов. Если он «разбавляется» красным и этим достигается равенство цветовых ощущений от левой и правой граней призмы (см. рис. 2.15), то можно записать  Следовательно
Следовательно  откуда видно, что некоторые модули цветов цветового уравнения (2.15) могут быть отрицательными (здесь это
откуда видно, что некоторые модули цветов цветового уравнения (2.15) могут быть отрицательными (здесь это 
В качестве основных  стремятся выбрать такие цвета, чтобы каждый из них действовал преимущественно на один из рецепторов модели зрительного восприятия. Кроме того, учитывают необходимость достаточно простого получения этих излучений. Международной Комиссией по освещению
стремятся выбрать такие цвета, чтобы каждый из них действовал преимущественно на один из рецепторов модели зрительного восприятия. Кроме того, учитывают необходимость достаточно простого получения этих излучений. Международной Комиссией по освещению  в качестве основных цветов рекомендованы монохроматические излучения с длинами волн;
в качестве основных цветов рекомендованы монохроматические излучения с длинами волн;  нм;
нм;  нм. Последние два являются линиями в спектре излучения паров ртути и легко выделяются путем селекции из спектра с помощью фильтров.
нм. Последние два являются линиями в спектре излучения паров ртути и легко выделяются путем селекции из спектра с помощью фильтров.
При выборе основных цветов необходимо установить и их яркости. Удобно яркости основных цветов взять такими, чтобы белый цвет создавался от смешанных в равных количествах, т. е. модули цветов при этом должны быть одинаковы:  Путем статистических исследований установлено, что эти условия выполняются в случае, когда яркости эталонов находятся в соотношении
Путем статистических исследований установлено, что эти условия выполняются в случае, когда яркости эталонов находятся в соотношении  . Если в качестве красного
. Если в качестве красного  взять источник яркостью
взять источник яркостью  то яркости источников двух других основных цветов должны составлять:
то яркости источников двух других основных цветов должны составлять:  При смещении
При смещении  получим белый цвет
получим белый цвет  яркостью
яркостью 
Если смешать выбранные основные цвета равной яркости, то получится не белый цвет, а синий. Если яркость одного из основных цветов принимается за единицу (например,  то относительные яркости основных цветов
то относительные яркости основных цветов  при смешении которых в
при смешении которых в
равных количествах получают белый, называют яркостными коэффициентами.
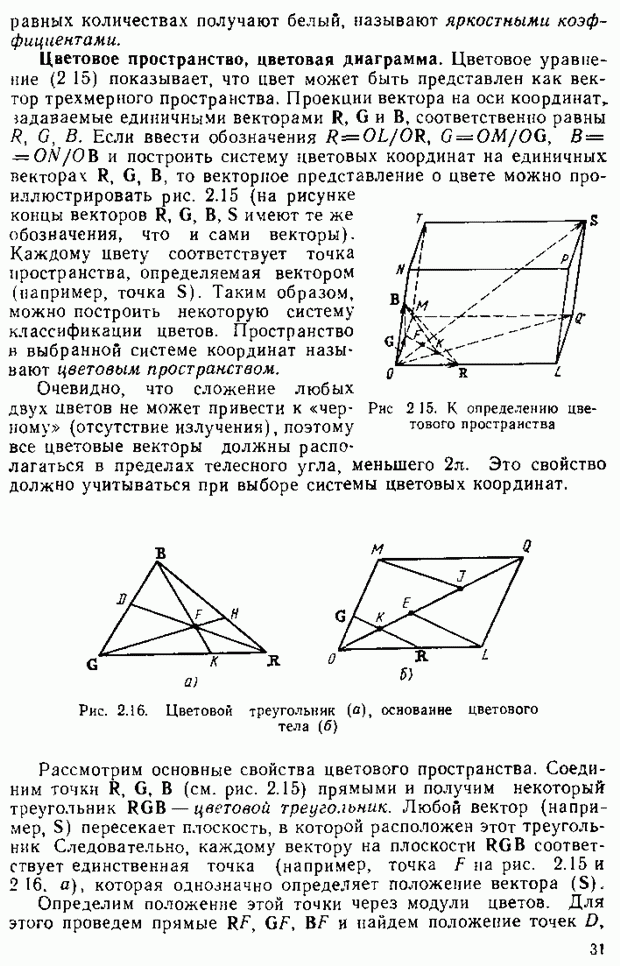
Цветовое пространство, цветовая диаграмма. Цветовое уравнение (2 15) показывает, что цвет может быть представлен как вектор трехмерного пространства. Проекции вектора на оси координат, задаваемые единичными векторами  и В. соответственно равны
и В. соответственно равны  Если ввести обозначения
Если ввести обозначения  и построить систему цветовых координат на единичных векторах
и построить систему цветовых координат на единичных векторах  , то векторное представление о цвете можно проиллюстрировать рис. 2.15 (на рисунке концы векторов
, то векторное представление о цвете можно проиллюстрировать рис. 2.15 (на рисунке концы векторов  имеют те же обозначения, что и сами векторы).
имеют те же обозначения, что и сами векторы).
Каждому цвету соответствует точка пространства, определяемая вектором (папример, точка  Таким образом, можно построить некоторую систему классификации цветов. Пространство в выбранной системе координат называют цветовым пространством.
Таким образом, можно построить некоторую систему классификации цветов. Пространство в выбранной системе координат называют цветовым пространством.
Очевидно, что сложение любых двух цветов не может привести к «черному» (отсутствие излучения), поэтому все цветовые векторы должны располагаться в пределах телесного угла, меньшего  Это свойство должно учитываться при выборе системы цветовых координат.
Это свойство должно учитываться при выборе системы цветовых координат.

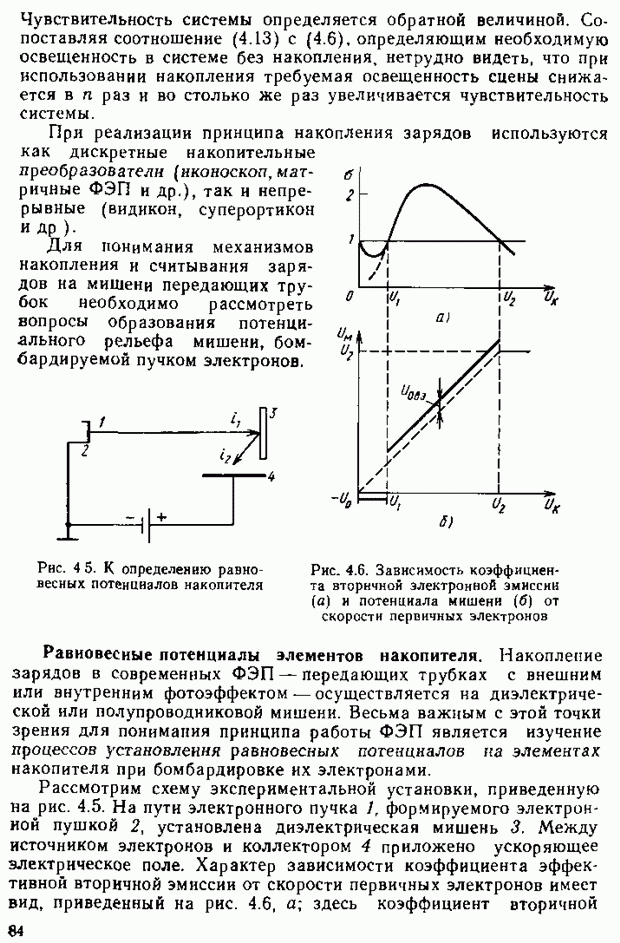
Рис. 2.15. К определению цветового пространства

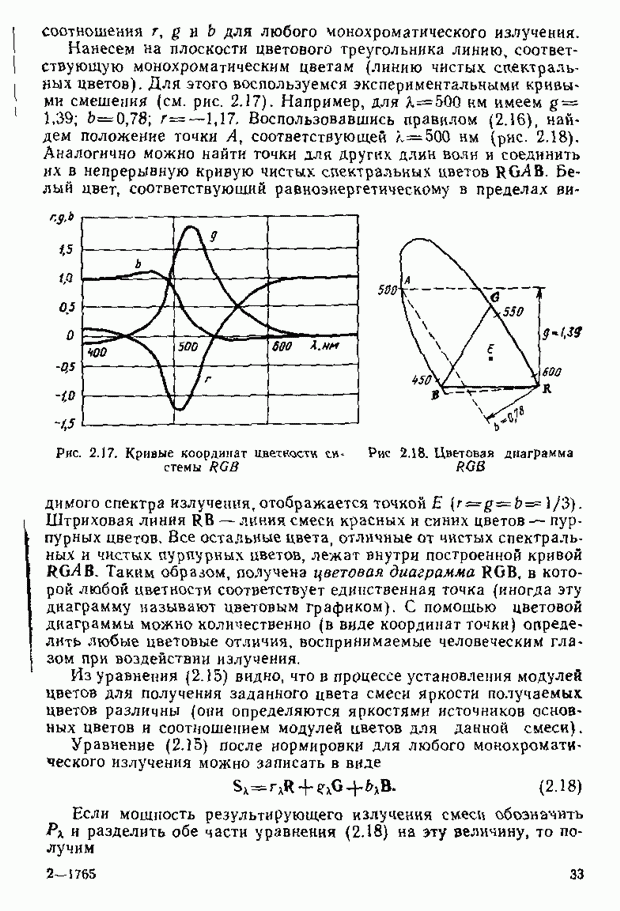
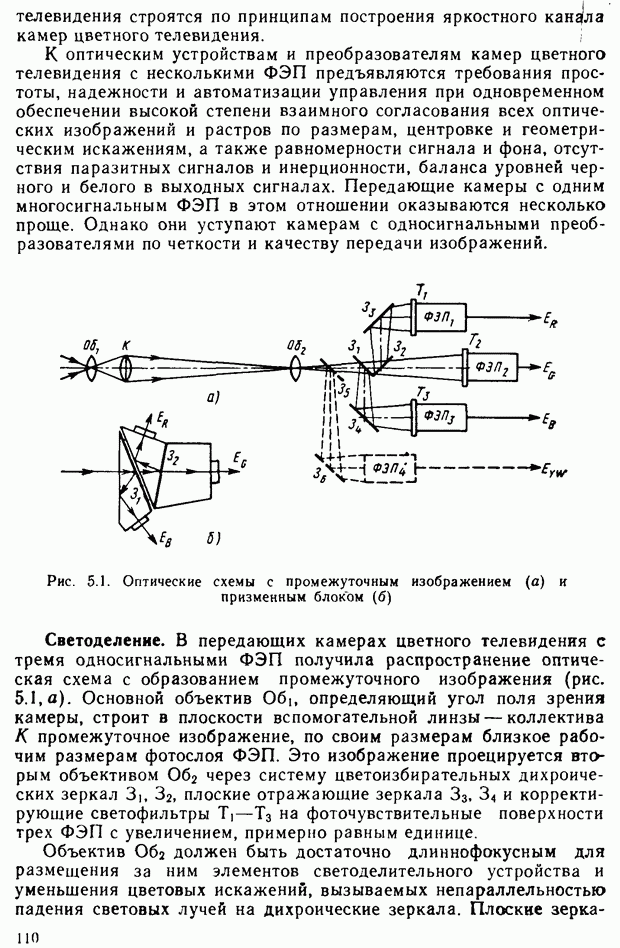
Рис. 2.16. Цветовой треугольник  основание цветового тела (б)
основание цветового тела (б)
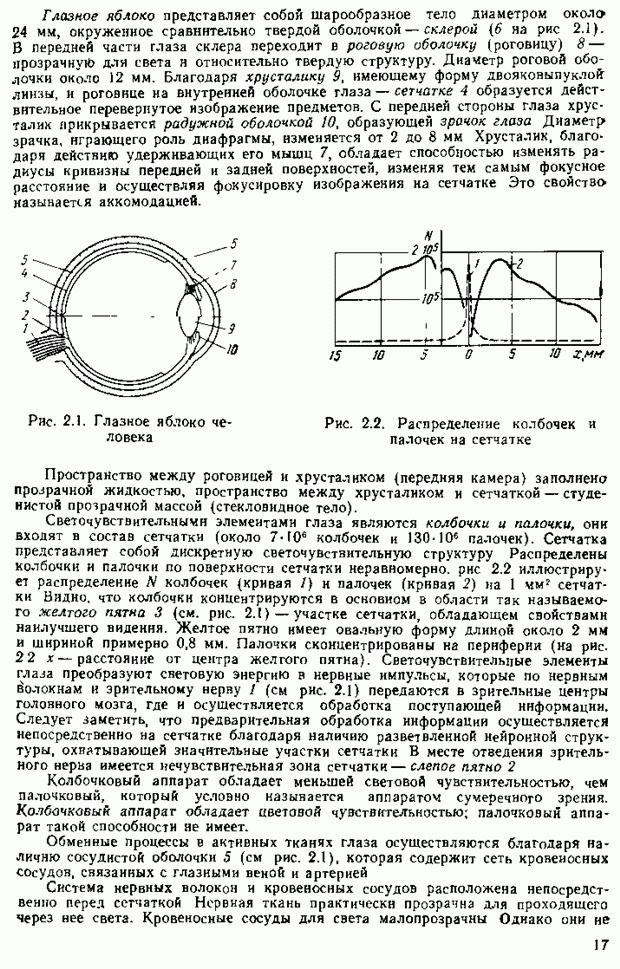
Рассмотрим основные свойства цветового пространства. Соединим точки  (см. рис. 2.15) прямыми и получим некоторый треугольник RGB — цветовой треугольник. Любой вектор (например,
(см. рис. 2.15) прямыми и получим некоторый треугольник RGB — цветовой треугольник. Любой вектор (например,  пересекает плоскость, в которой расположен этот треугольник Следовательно, каждому вектору на плоскости RGB соответствует единственная точка (например, точка
пересекает плоскость, в которой расположен этот треугольник Следовательно, каждому вектору на плоскости RGB соответствует единственная точка (например, точка  на рис. 2.15 и 2 16. а), которая однозначно определяет положение вектора
на рис. 2.15 и 2 16. а), которая однозначно определяет положение вектора 
Определим положение этой точки через модули цветов. Для этого проведем прямые  и найдем положение точек
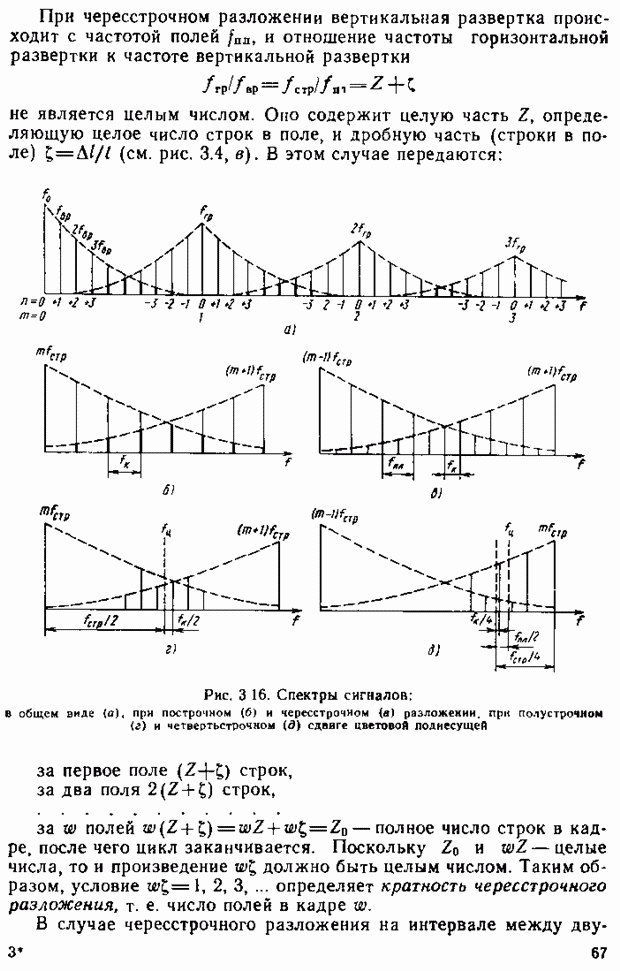
и найдем положение точек 
H и K пересечения этих прямых со сторонами треугольника RGB. На рис. 2.16, б изображено основание фигуры, приведенной на рис. 2.15  . Тогда
. Тогда  Следовательно,
Следовательно,  Учитывая, что
Учитывая, что  имеем
имеем

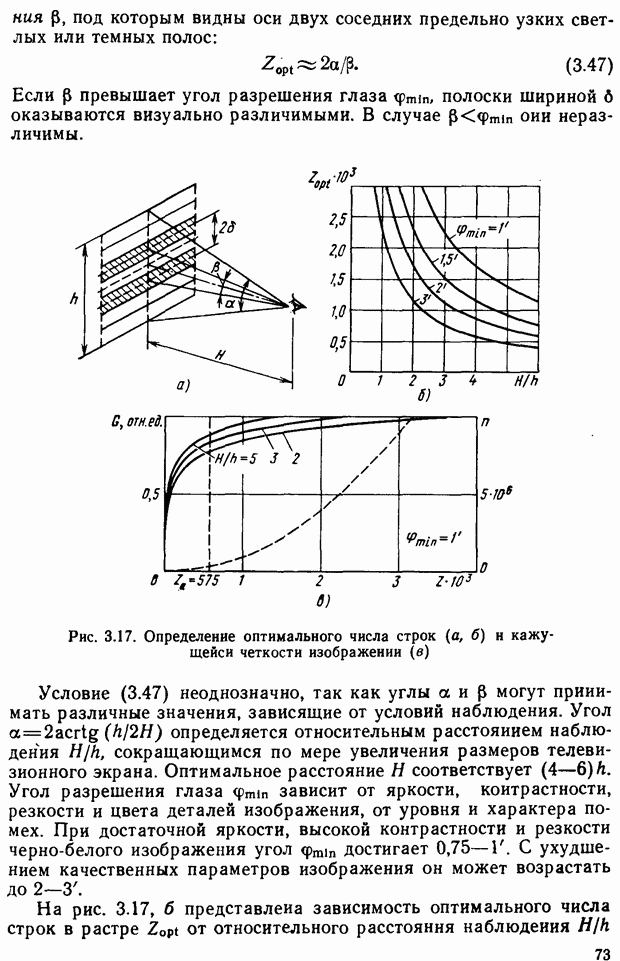
Аналогично можно показать, что

Соотношения (2,16) определяют положение точек Н, К и  через модули цветое Нетрудно видеть, что полученное правило (2.16) соответствует правилу отыскания центра тяжести треугольника с грузами, сосредоточенными а его вершинах и равными
через модули цветое Нетрудно видеть, что полученное правило (2.16) соответствует правилу отыскания центра тяжести треугольника с грузами, сосредоточенными а его вершинах и равными  и В соответственно.
и В соответственно.
Произведем нормировку по компонентам смешиваемых цветов:

Видно, что 
Нормированные компоненты  определяют соотношения количеств трех основных цветов, при которых они воспроизводят данный цвет. Они не содержат информации о модуле цветового вектора, но в них полностью сохранена информация о его направлении. Точку пересечения вектора цвета с плоскостью треугольника RGB называют точкой цветности (точка
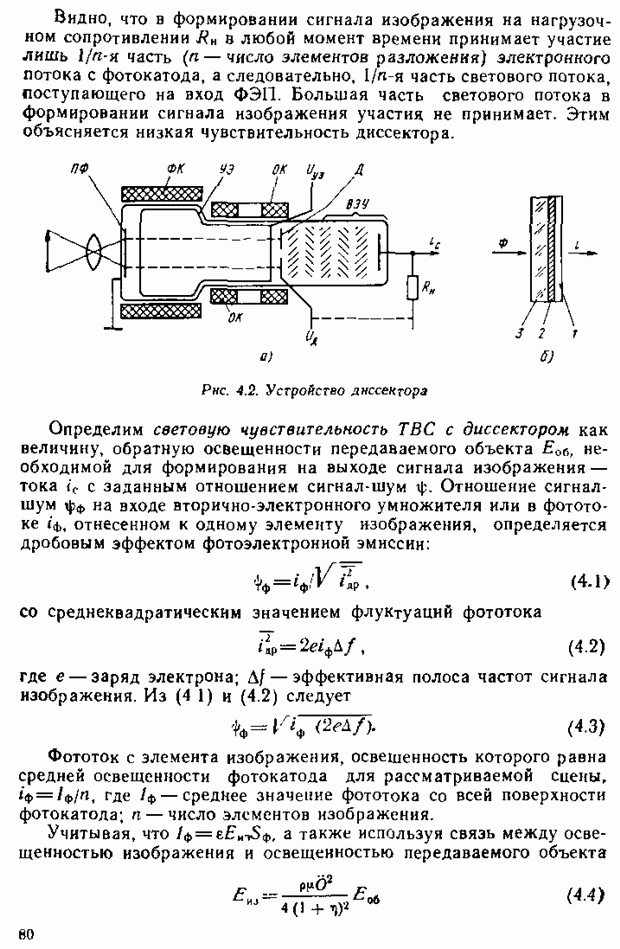
определяют соотношения количеств трех основных цветов, при которых они воспроизводят данный цвет. Они не содержат информации о модуле цветового вектора, но в них полностью сохранена информация о его направлении. Точку пересечения вектора цвета с плоскостью треугольника RGB называют точкой цветности (точка  на рис. 2.15 и 2.16, а) или просто цветностью. Отличия цветности, фиксируемые в экспериментах с гипсовой призмой, отражают различия в цветовых ощущениях наблюдателя, т. е. термин «цветность» предполагает корреляцию с ощущением цветовых различий (ощущением цветности).
на рис. 2.15 и 2.16, а) или просто цветностью. Отличия цветности, фиксируемые в экспериментах с гипсовой призмой, отражают различия в цветовых ощущениях наблюдателя, т. е. термин «цветность» предполагает корреляцию с ощущением цветовых различий (ощущением цветности).
Компоненты r, g, b, которые полностью определяют цветность, называются трехцветными коэффициентами или координатами цветности. Задавая две из них, как видно из соотношения (2.17), можно однозначно определить цветность.
Таким образом, любой цвет в выбранной системе координат выражается тремя числами — модулями цветов, цветность же определяется любыми двумя числами из трех: r, g, b.
Эксперименты по уравнению цветов измеряемого и эталонного источников, описываемые уравнением (2.15), могут быть повторены для всех монохроматических излучений видимого спектра.
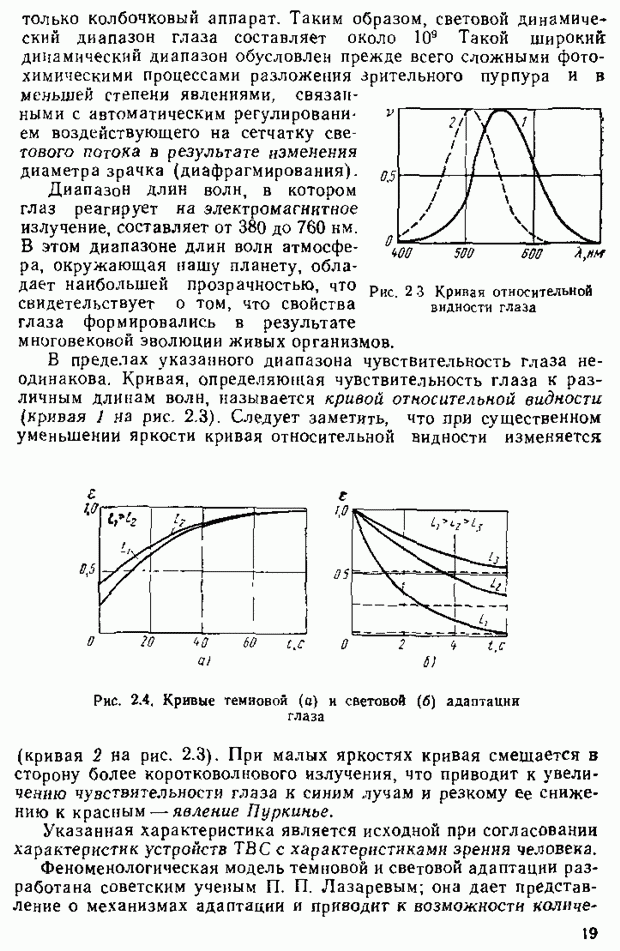
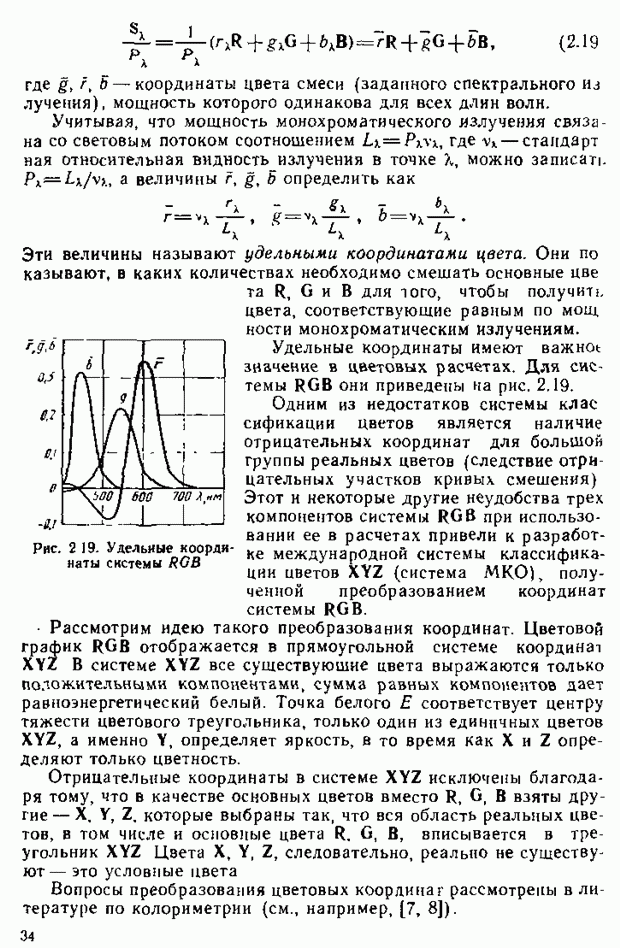
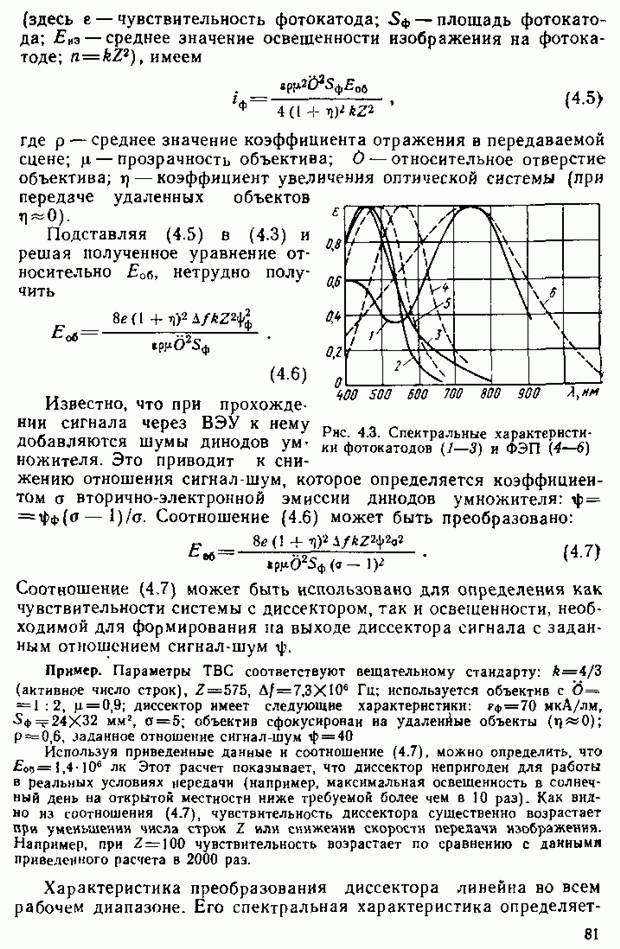
Результаты статистических исследований подобных характеристик цветового зрения человека приводят к зависимостям  (рис 2.17). Из них видно, например, что для получения ощущения эквивалентного вызываемому монохроматическим излучением с длиной волны
(рис 2.17). Из них видно, например, что для получения ощущения эквивалентного вызываемому монохроматическим излучением с длиной волны  , необходимо смешать выбранные основные цвета в соотношении
, необходимо смешать выбранные основные цвета в соотношении  . Аналогично с помощью кривых смешения могут быть определены необходимые
. Аналогично с помощью кривых смешения могут быть определены необходимые
соотношения  и
и  для любого монохроматического излучеиия.
для любого монохроматического излучеиия.
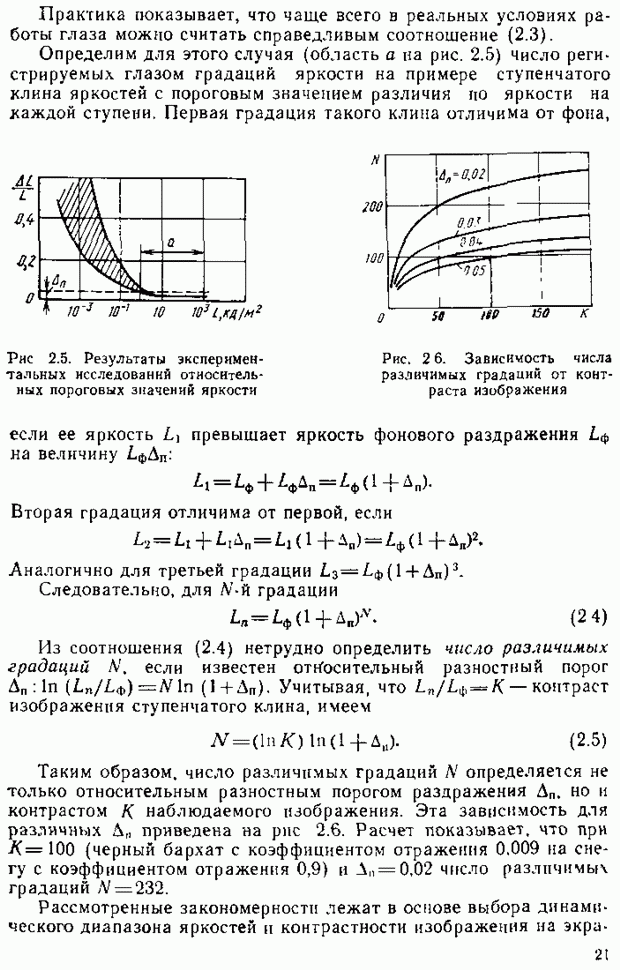
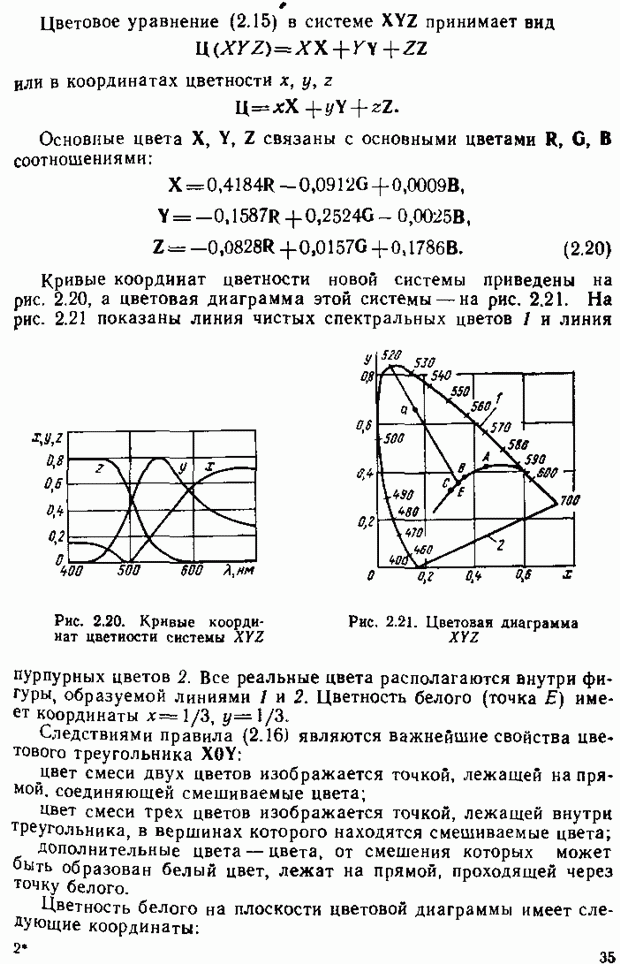
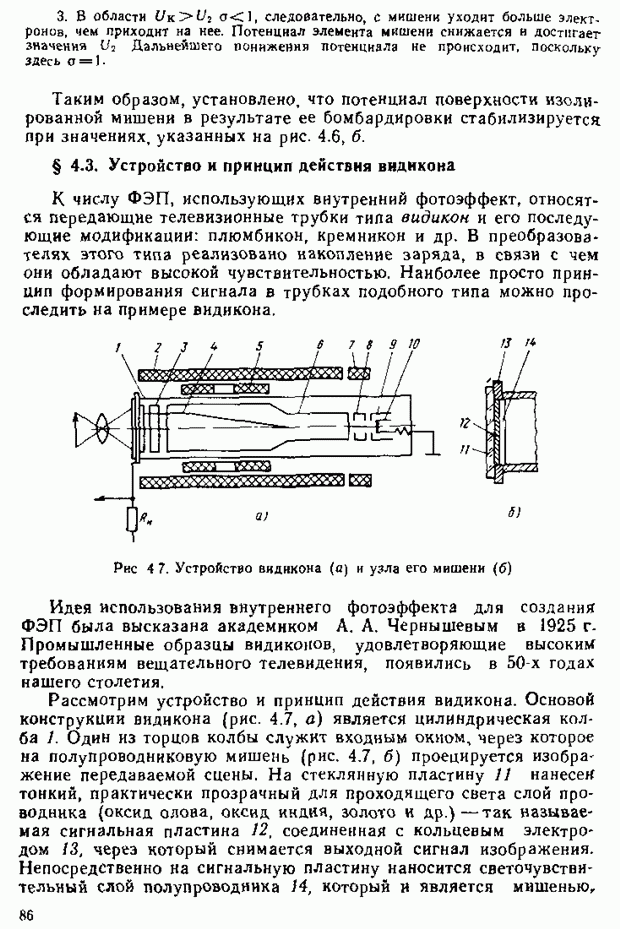
Нанесем на плоскости цветового треугольника линию, соответствующую монохроматическим цветам (линию чистых, спектральных цветов). Для этого воспользуемся экспериментальными кривыми смешения (см. рис. 2.17). Например, для  нм имеем
нм имеем  Воспользовавшись правилом (2.16), найдем положение точки А, соответствующей
Воспользовавшись правилом (2.16), найдем положение точки А, соответствующей  нм (рис. 2.18). Аналогично можно найти точки для других длин волн и соединить их в непрерывную кривую чистых спектральных цветов
нм (рис. 2.18). Аналогично можно найти точки для других длин волн и соединить их в непрерывную кривую чистых спектральных цветов  Белый цвет, соответствующий равноэиергетическому в пределах видимого спектра излучения, отображается точкой
Белый цвет, соответствующий равноэиергетическому в пределах видимого спектра излучения, отображается точкой  Штриховая линия
Штриховая линия  — линия смеси красных и синих цветов — пурпурных цветов. Все остальные цвета, отличные от чистых спектральных и чистых пурпурных цветов, лежат внутри построенной кривой
— линия смеси красных и синих цветов — пурпурных цветов. Все остальные цвета, отличные от чистых спектральных и чистых пурпурных цветов, лежат внутри построенной кривой  Таким образом, получена цветовая диаграмма
Таким образом, получена цветовая диаграмма  в которой любой цветности соответствует единственная точка (иногда эту диаграмму называют цветовым графиком). С помощью цветовой диаграммы можно количественно (в виде координат точки) определить любые цветовые отличия, воспринимаемые человеческим глазом при воздействии излучения.
в которой любой цветности соответствует единственная точка (иногда эту диаграмму называют цветовым графиком). С помощью цветовой диаграммы можно количественно (в виде координат точки) определить любые цветовые отличия, воспринимаемые человеческим глазом при воздействии излучения.

рис. 2.17. Кривые координат цветности системы RGB

Рис 2.18. Цветовая диаграмма 
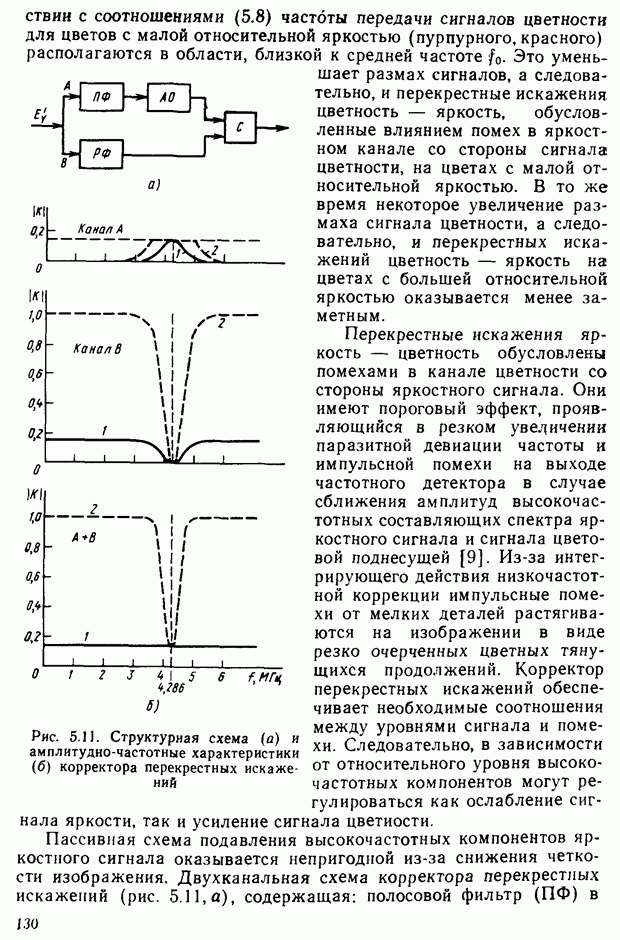
Из уравнения (2.15) видно, что в процессе установления модулей цветов для получения заданного цвета смеси яркости получаемых цветов различны (они определяются яркостями источников основных цветов и соотношением модулей цветов для данной смеси).
Уравнение (2.15) после нормировки для любого монохроматического излучения можно записать в виде

Если мощность результирующего излучения смеси обозначить  и разделить обе части уравнения (2.18) на эту величину, то получим
и разделить обе части уравнения (2.18) на эту величину, то получим

где  - координаты цвета смеси (заданного спектрального из лучения), мощность которого одинакова для всех длин волн.
- координаты цвета смеси (заданного спектрального из лучения), мощность которого одинакова для всех длин волн.
Учитывая, что мощность монохроматического излучения связана со световым потоком соотношением  где
где  — стандарт
— стандарт  относительная видность излучения в точке можно записать
относительная видность излучения в точке можно записать  а величины
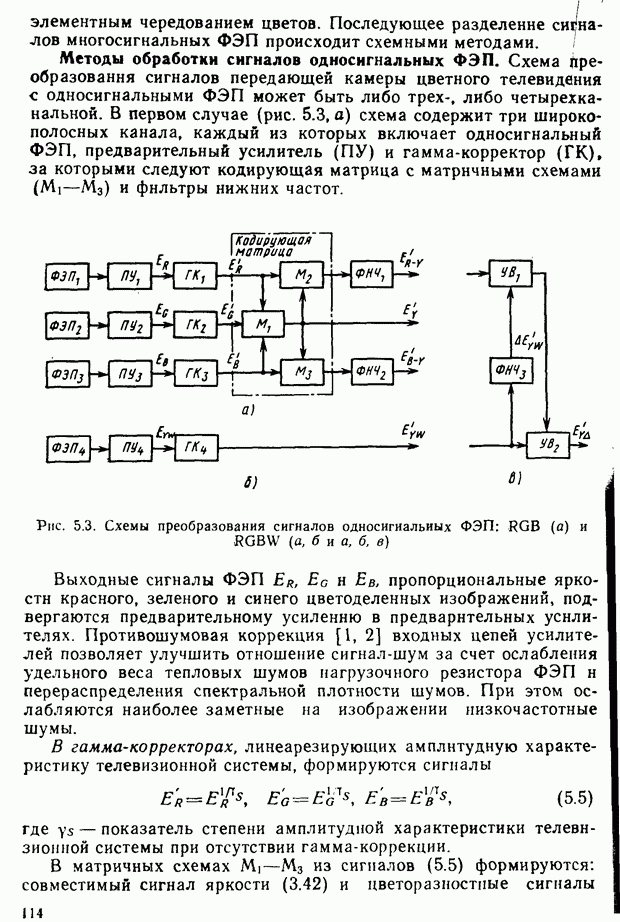
а величины  определить как
определить как

Эти величины называют удельными координатами цвета. Они по называют, в каких количествах необходимо смешать основные цвета R, G и В для того, чтобы получить цвета, соответствующие равным по мощности монохроматическим излучениям.
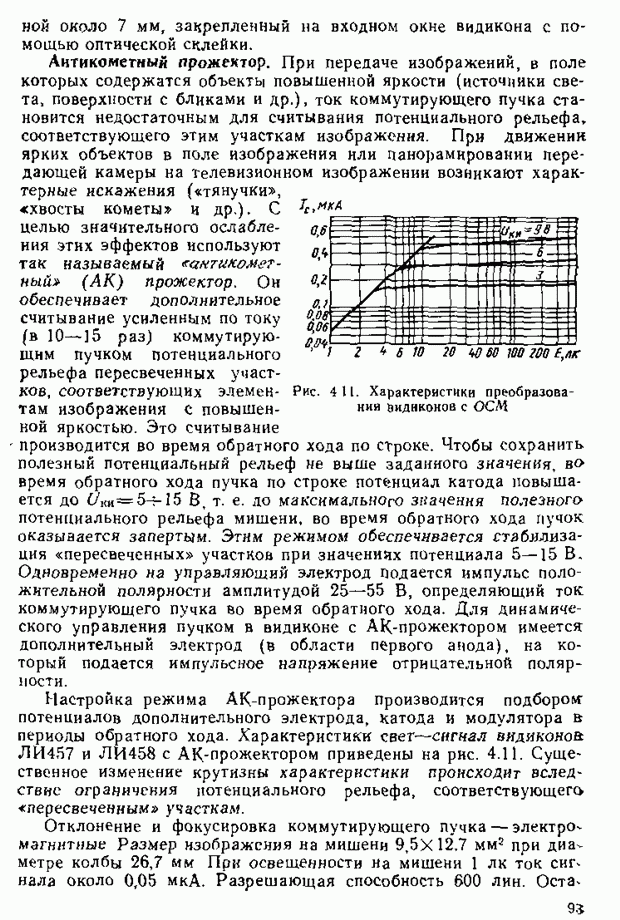
Удельные координаты имеют  значение в цветовых расчетах. Для системы RGB они приведены на рис. 2.19.
значение в цветовых расчетах. Для системы RGB они приведены на рис. 2.19.

Рис. 2.19. Удельные координаты системы 
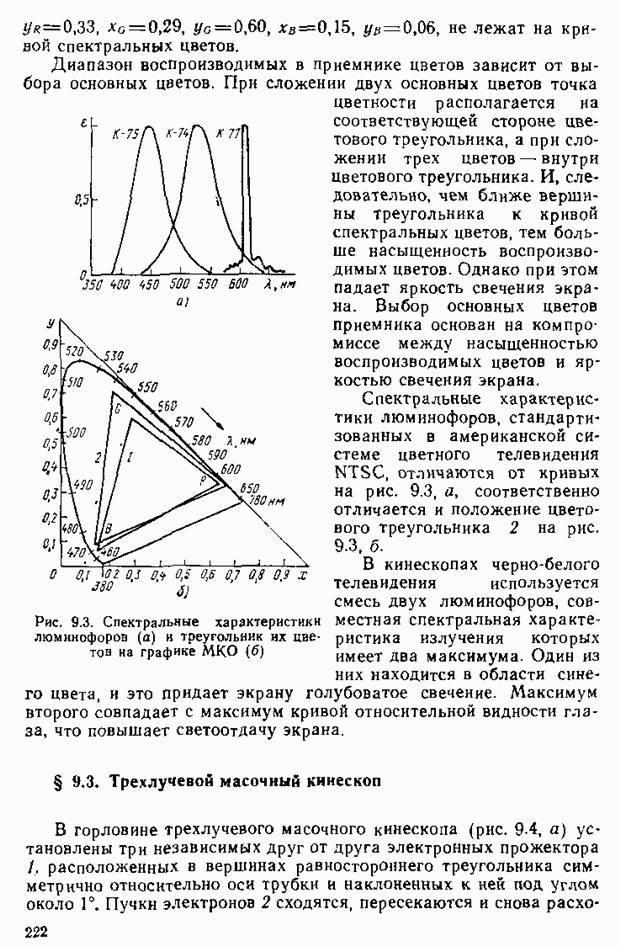
Одним из недостатков системы классификации цветов является наличие отрицательных координат для большой группы реальных цветов (следствие отрицательных участков кривых смешения) Этот и некоторые другие неудобства трех компонентов системы RGB при использовании ее в расчетах привели к разработке международной системы классификации цветов  (система
(система  полученной преобразованием координат системы
полученной преобразованием координат системы 
Рассмотрим идею такого преобразования координат. Цветовой график  отображается в прямоугольной системе координат
отображается в прямоугольной системе координат  . В системе
. В системе  все существующие цвета выражаются только положительными компонентами, сумма равных компонентов дает равноэнергетический белый. Точка белого Е соответствует центру тяжести цветового треугольника, только один из единичных цветов
все существующие цвета выражаются только положительными компонентами, сумма равных компонентов дает равноэнергетический белый. Точка белого Е соответствует центру тяжести цветового треугольника, только один из единичных цветов  а именно
а именно  определяет яркость, в то время как X и
определяет яркость, в то время как X и  определяют только цветность.
определяют только цветность.
Отрицательные координаты в системе XYZ исключены благодаря тому, что в качестве основных цветов вместо  взяты другие — X, Y, Z. которые выбраны так, что вся область реальных цветов, в том числе и основные цвета
взяты другие — X, Y, Z. которые выбраны так, что вся область реальных цветов, в том числе и основные цвета  , вписывается в треугольник
, вписывается в треугольник  Цвета X, Y, Z, следовательно, реально не существуют — это условные цвета
Цвета X, Y, Z, следовательно, реально не существуют — это условные цвета
Вопросы преобразования цветовых координат рассмотрены в литературе по колориметрии (см., например, [7, 8]).
Цветовое уравнение (2.15) в системе  принимает вид
принимает вид

или в координатах цветности 

Основные цвета X, Y, Z связаны с основными цветами  соотношениями:
соотношениями:

Кривые координат цветности новой системы приведены на рис. 2.20, а цветовая диаграмма этой системы — на рис. 2.21. На рис. 2.21 показаны линия чистых спектральных цветов  и линия пурпурных цветов 2. Все реальные цвета располагаются внутри фигуры, образуемой линиями
и линия пурпурных цветов 2. Все реальные цвета располагаются внутри фигуры, образуемой линиями  и 2. Цветность белого (точка Е) имеет координаты
и 2. Цветность белого (точка Е) имеет координаты 

Рис. 2.20. Кривые координат цветности системы 

Рис. 2.21. Цветовая диаграмма 
Следствиями правила (2.16) являются важнейшие свойства цветового треугольника 
цвет смеси двух цветов изображается точкой, лежащей на прямой. соединяющей смешиваемые цвета;
Цвет смеси трех цветов изображается точкой, лежащей внутри треугольника, в вершинах которого находятся смешиваемые цвета;
дополнительные цвета — цвета, от смешения которых может быть образован белый цвет, лежат на прямой, проходящей через точку белого.
Цветность белого на плоскости цветовой диаграммы имеет следующие координаты:
белый, образованный равноэнергетическим излучением, соответствующий точке  , лежит в центре тяжести треугольника
, лежит в центре тяжести треугольника  и его цветность определяется координатами
и его цветность определяется координатами  источник типа А (вольфрамовая нить с температурой 2854 К):
источник типа А (вольфрамовая нить с температурой 2854 К):  ;
;
источник типа В (естественное освещение в облачный день): 
источник типа С (естественное освещение в солнечный день): 
Координаты точки на плоскости цветовой диаграммы могут быть выражены в полярной системе координат с центром в точке белого. Такой прием используется для построения системы оценки цветности «цветовой тон — чистота цвета».
Цветовой тон для любой цветности, например а (см. рис. 2.21), определяется длиной волны, соответствующей пересечению прямой, проведенной через начало координат полярной системы (точка Е) и точку, определяющую данную цветность (точка а), с линией чистых спектральных цветов (в рассматриваемом примере цветовой тон  нм).
нм).
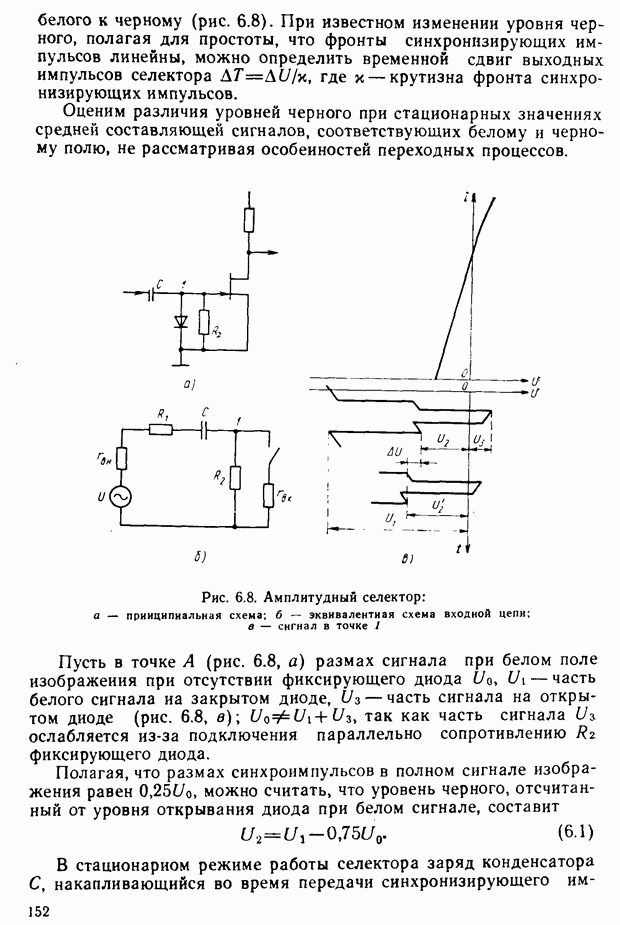
Чистота цвета  определяет степень «разбавления» монохроматического излучения
определяет степень «разбавления» монохроматического излучения  белым Фе. Нетрудно видеть, что для монохроматических цветов
белым Фе. Нетрудно видеть, что для монохроматических цветов  а для белого
а для белого 
На цветовую диаграмму (см. рис. 2.21) часто наносят сетку равных значений 
Рассмотрим, как выражается яркость в системе  Зная яркостные коэффициенты системы RGB и связь между X, Y, Z и
Зная яркостные коэффициенты системы RGB и связь между X, Y, Z и  можно определить яркостные коэффициенты системы
можно определить яркостные коэффициенты системы  Подставив в уравнение (2.20) значения яркостных коэффициентов соответствующих цветов
Подставив в уравнение (2.20) значения яркостных коэффициентов соответствующих цветов  , получим следующие соотношения яркостных коэффициентов системы
, получим следующие соотношения яркостных коэффициентов системы  причем яркость
причем яркость  Это естественно, так как цвета X и
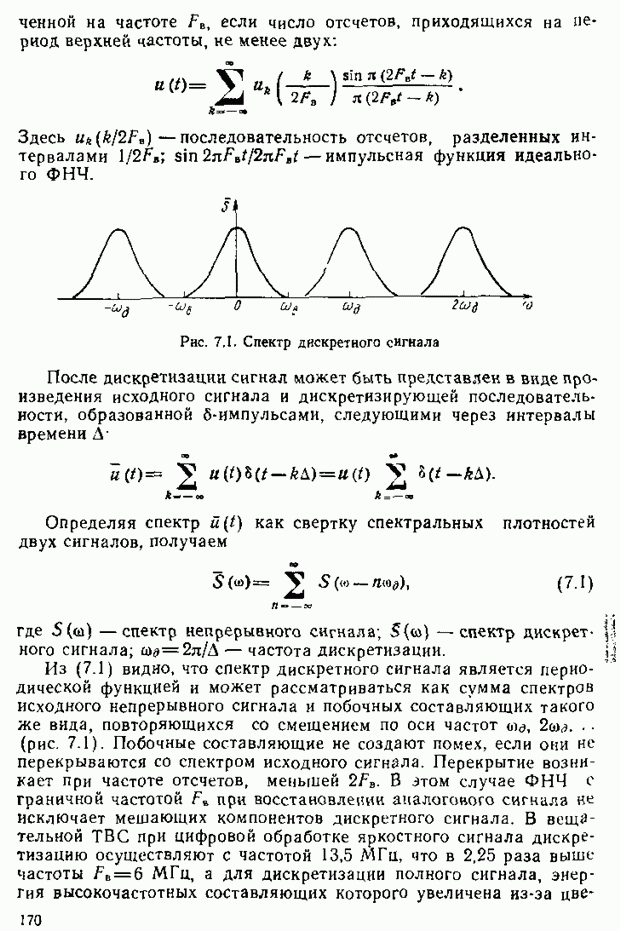
Это естественно, так как цвета X и  реально не существуют (без
реально не существуют (без  Цвет
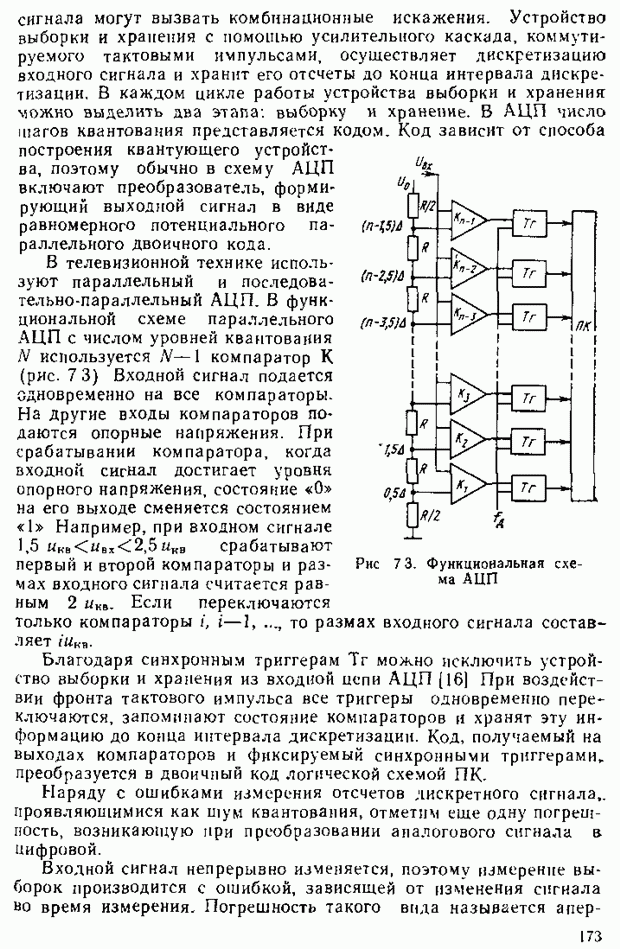
Цвет  может быть реален при
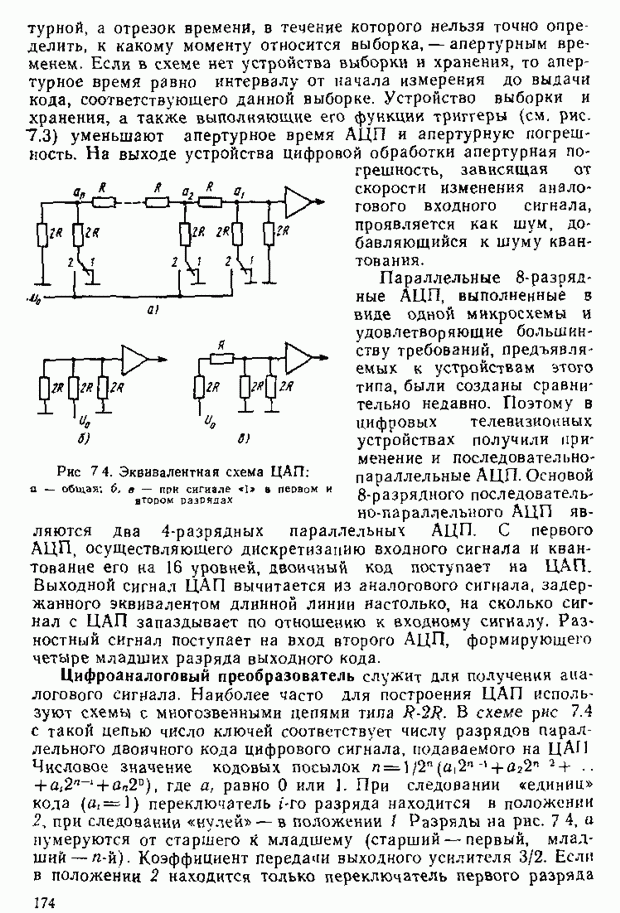
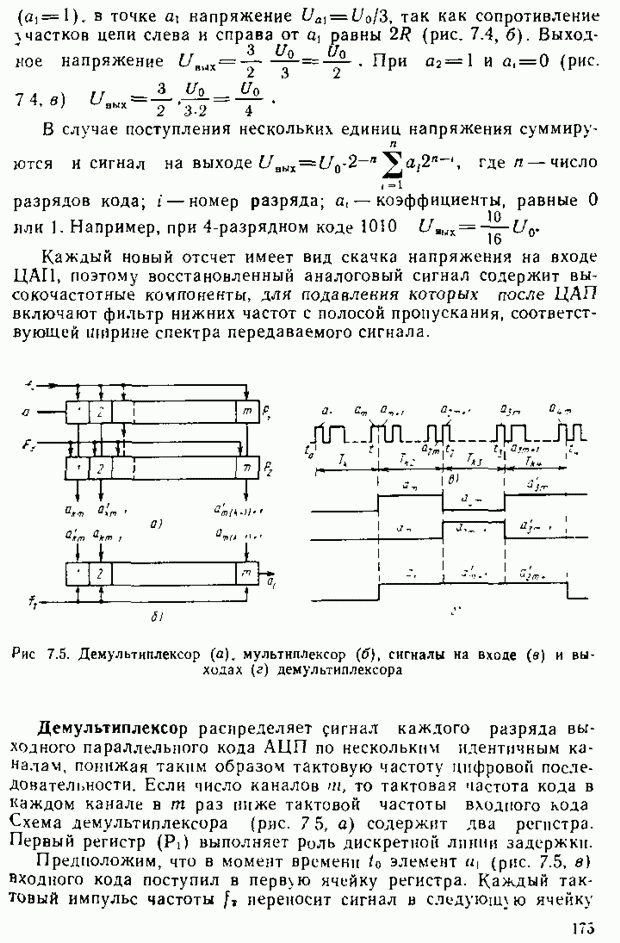
может быть реален при 
Теперь можно дать оценку яркости любого цвета в системе  Произвольный цвет может быть записан в виде
Произвольный цвет может быть записан в виде

Яркость этого цвета  . В частном случае единичного цвета его яркость определяется трехцветиым коэффициентом у.
. В частном случае единичного цвета его яркость определяется трехцветиым коэффициентом у.
Поскольку  где
где  — цветовой модуль,
— цветовой модуль,  откуда
откуда  Выражая и другие количественные компоненты уравнения (2.21) через
Выражая и другие количественные компоненты уравнения (2.21) через  получаем
получаем

Соотношение (2.21) можно переписать в виде

Выразив яркость монохроматического излучения с длиной волны  через мощность
через мощность  — стандартная относительная видность излучения в точке
— стандартная относительная видность излучения в точке  , получим
, получим

Разделив обе части этого уравнения на  получим соответствующее выражение для
получим соответствующее выражение для  энергия излучения
энергия излучения

Введем новые обозначения

Тогда выражение (2.23) можно записать в виде

Коэффициенты  являются удельными координатами системы
являются удельными координатами системы  и показывают, в каких соотношениях нужно смешать основные цвета
и показывают, в каких соотношениях нужно смешать основные цвета  чтобы воспроизвести цвета равных по мощности монохроматических излучений с заданной длиной волны
чтобы воспроизвести цвета равных по мощности монохроматических излучений с заданной длиной волны  .
.

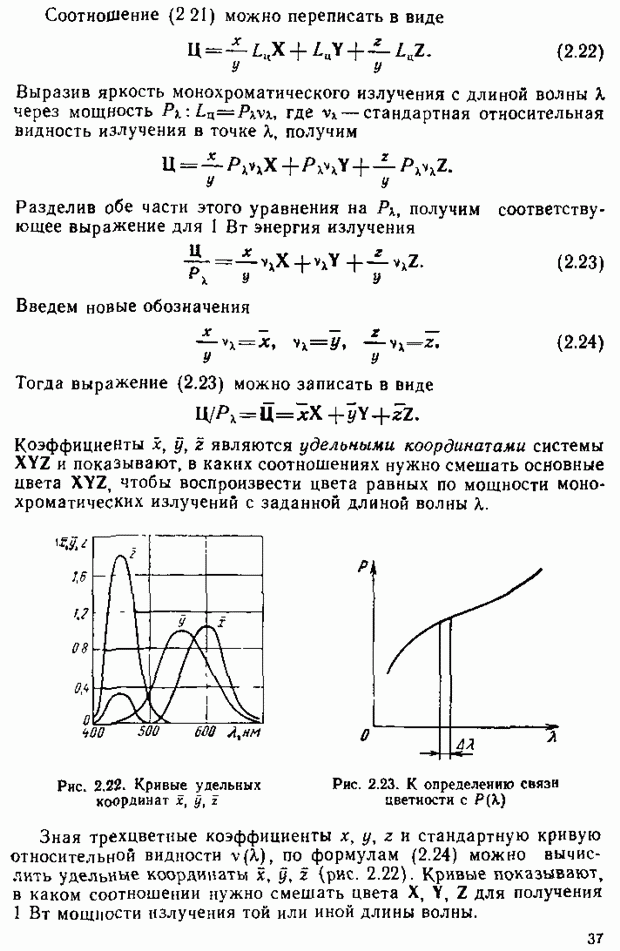
Рис. 2.22. Кривые удельных координат 

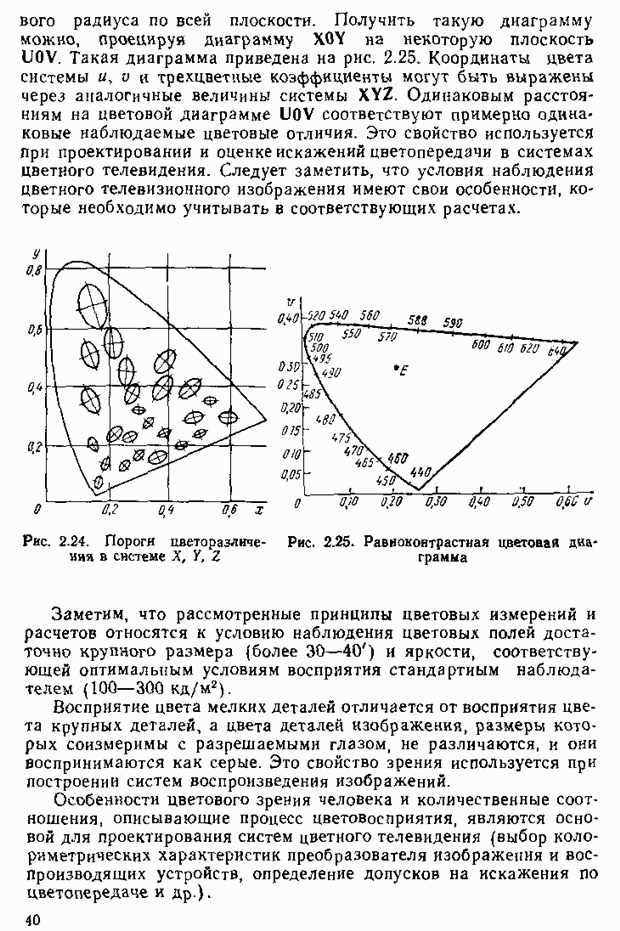
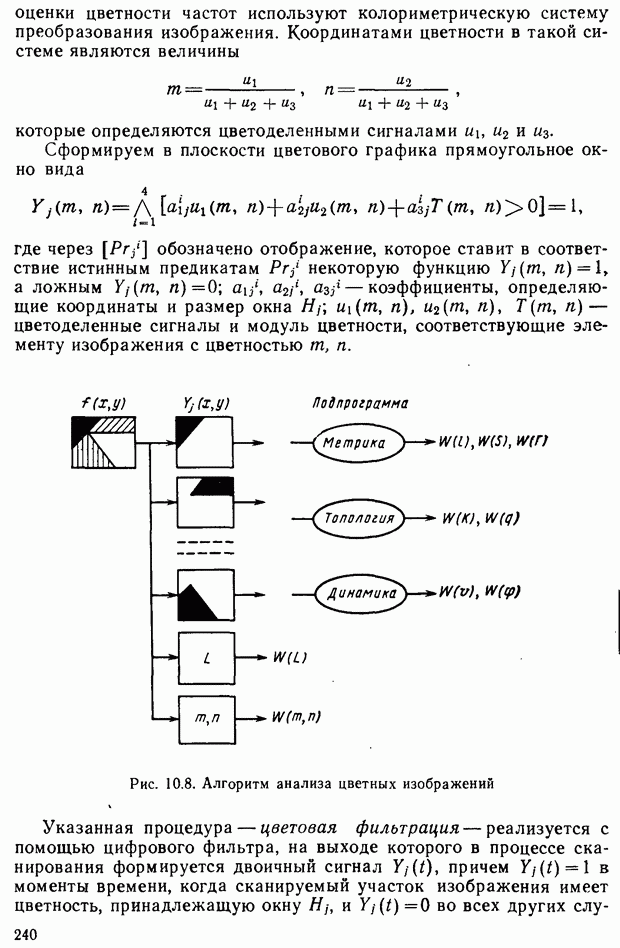
Рис. 2.23. К определению связи цветности с 
Зная трехцветные коэффициенты х,  и стандартную кривую относительной видности по формулам (2,24) можно вычислить удельные координаты
и стандартную кривую относительной видности по формулам (2,24) можно вычислить удельные координаты  (рис. 2.22). Кривые показывают, в каком соотношении нужно смешать цвета X, Y, Z для получения 1 Вт мощности излучения той или иной длины волны.
(рис. 2.22). Кривые показывают, в каком соотношении нужно смешать цвета X, Y, Z для получения 1 Вт мощности излучения той или иной длины волны.
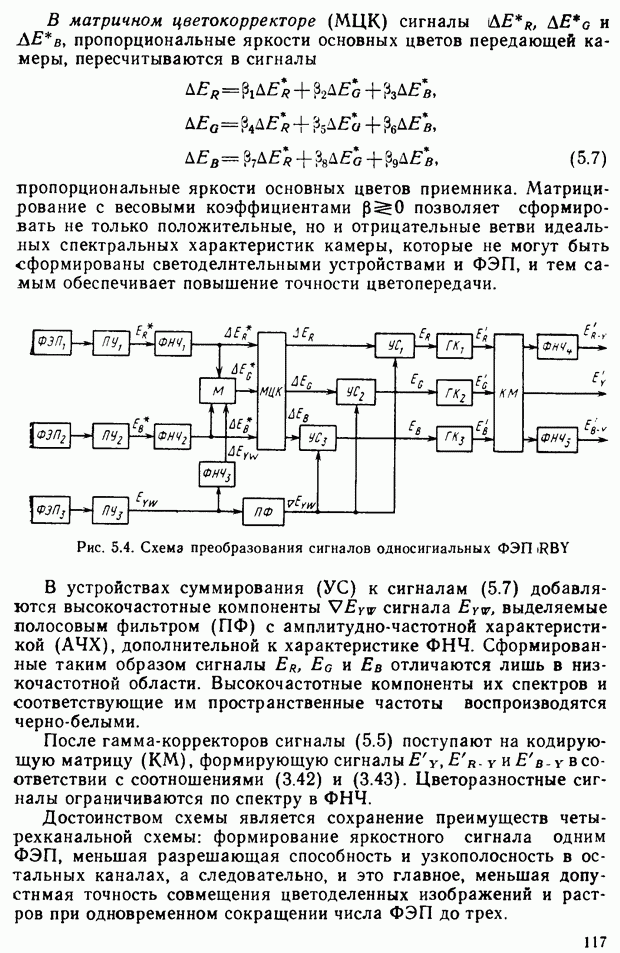
Связь между спектральными характеристиками и цветом. Введя понятия яркостных коэффициентов и удельных координат, можно установить связь между спектральными характеристиками и цветом, т. е. определить цвет излучения по известному спектральному составу.
Любое излучение, имеющее заданное спектральное распределение мощности  можно рассматривать как смесь большого числа монохроматических излучений. Возьмем спектральную составляющую
можно рассматривать как смесь большого числа монохроматических излучений. Возьмем спектральную составляющую  в интервале
в интервале  (рис. 2.23). Цвет этой составляющей определяется уравнением
(рис. 2.23). Цвет этой составляющей определяется уравнением  Цвет смеси
Цвет смеси  спектральных составляющих, т. е. цвет всего излучения, получим, суммируя цвета составляющих:
спектральных составляющих, т. е. цвет всего излучения, получим, суммируя цвета составляющих:

— координаты цвета сложного излучения. Если излучение имеет сплошной спектр, то суммирование следует заменить интегрированием:

где  — диапазон видимого спектра.
— диапазон видимого спектра.
Таким образом, зная спектральное распределение мощности излучения и удельные координаты, можно определить величины X, Y, Z и координаты цветности:

В качестве примера рассмотрим, как произвести определение цветности по заданной спектральной характеристике излучения  Значения
Значения  известны, следовательно, воспользовавшись соотношениями (2.25), можно определить X, Y, Z, а из соотношений (2.26) — значения
известны, следовательно, воспользовавшись соотношениями (2.25), можно определить X, Y, Z, а из соотношений (2.26) — значения  Если определяется цветность отражающей поверхности, то нетрудно заметить, что при определении значений
Если определяется цветность отражающей поверхности, то нетрудно заметить, что при определении значений  используется спектральный коэффициент
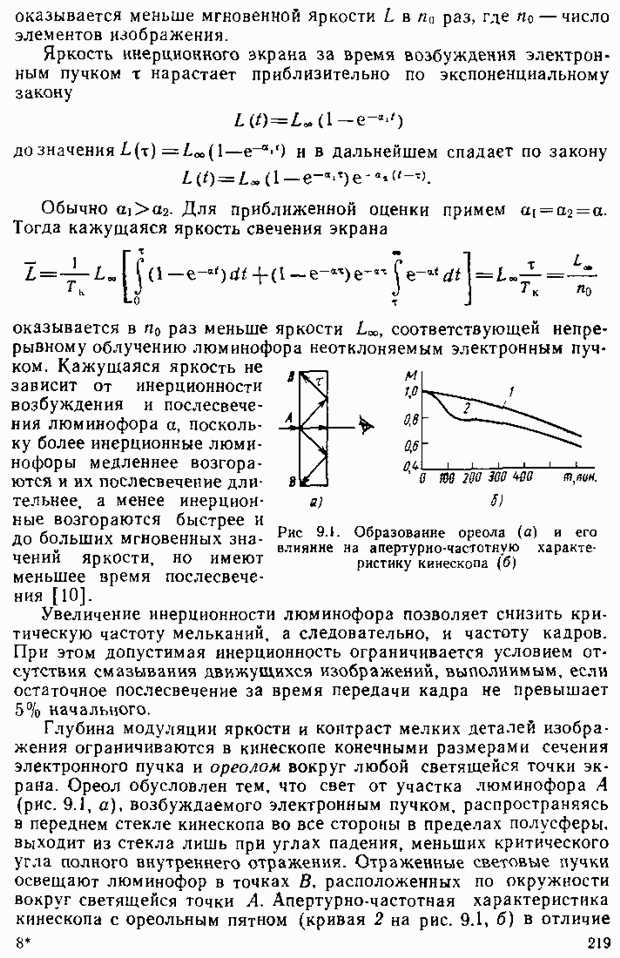
используется спектральный коэффициент
отражения  и спектральный состав освещающего излучения
и спектральный состав освещающего излучения

При определении цвета просвечиваемого объекта (транспарант)  приобретает смысл спектрального коэффициента пропускания рассматриваемого участка. Значения цветности х, у определяются из соотношений (2.26).
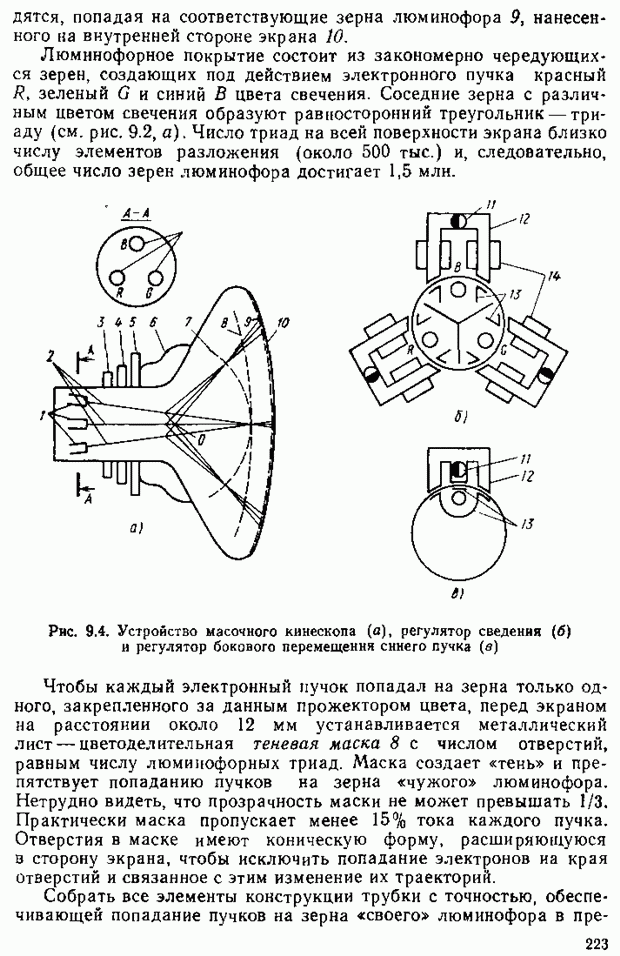
приобретает смысл спектрального коэффициента пропускания рассматриваемого участка. Значения цветности х, у определяются из соотношений (2.26).
Равноконтрастная цветовая диаграмма. Мерой различия цветностей, отображаемых двумя точками на плоскости цветовой Диаграммы, может служить расстояние между ними. Психофизиологические эксперименты показывают, что одинаковым ощущениям цветовых отличий в разных участках цветовой диаграммы  или RGB соответствуют неодинаковые расстояния между точками, отображающими сравниваемые цветности. Однако путем преобразования координат можно построить цветовую диаграмму, на которой одинаковым расстояниям между точками двух цветностей соответствуют одинаковые цветовые различия, оцениваемые по зрительному восприятию. Такая цветовая диаграмма называется равноконтрастной.
или RGB соответствуют неодинаковые расстояния между точками, отображающими сравниваемые цветности. Однако путем преобразования координат можно построить цветовую диаграмму, на которой одинаковым расстояниям между точками двух цветностей соответствуют одинаковые цветовые различия, оцениваемые по зрительному восприятию. Такая цветовая диаграмма называется равноконтрастной.
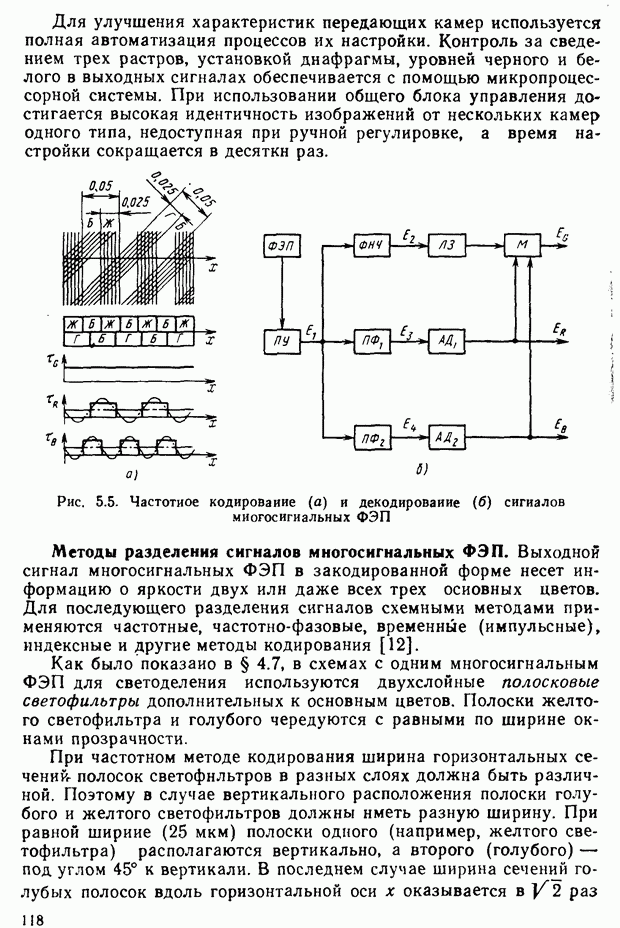
Для построения равноконтрастной цветовой диаграммы необходимо определить пороги цветоразличения, т. е. те минимальные цветовые отличия, которые лежат на грани цветоразличения в выбранных условиях наблюдения. Вокруг любой точки цветовой диаграммы на основе экспериментов можно построить окрестность, в пределах которой испытуемый не воспринимает изменения цвета. Используя статистическую обработку результатов измерений, можно построить эллипсы, представляющие в статистическом смысле геометрическое место точек одинаково воспринимаемых цветностей. Полуоси эллипсов равны среднеквадратическим ошибкам установки цветовых равенств по оценке испытуемых. Эти значения и принимают за пороги цветоразличения. На рис. 2.24 указаны пороги цветоразличения для выборочных точек цветовой диаграммы (для наглядности они увеличены в 10 раз). Видно, что пороги цветоразличения на разных участках цветовой диаграммы различны. Нетрудно представить, что по порогам цветоразличения можно определить число цветностей, различимых глазом.
Очевидно, что цветовая диаграмма была бы равноконтрастной, если бы пороги цветоразличения имели вид окружностей одинакового
радиуса по всей плоскости. Получить такую диаграмму можно, проецируя диаграмму  на некоторую плоскость
на некоторую плоскость  Такая диаграмма приведена на рис. 2.25. Координаты цвета системы
Такая диаграмма приведена на рис. 2.25. Координаты цвета системы  и трехцветные коэффициенты могут быть выражены через аналогичные величины системы
и трехцветные коэффициенты могут быть выражены через аналогичные величины системы  Одинаковым расстояниям на цветовой диаграмме
Одинаковым расстояниям на цветовой диаграмме  соответствуют примерно одинаковые наблюдаемые цветовые отличия. Это свойство используется при проектировании и оценке искажений цветопередачи в системах цветного телевидения. Следует заметить, что условия наблюдения цветного телевизионного изображения имеют свои особенности, которые необходимо учитывать в соответствующих расчетах.
соответствуют примерно одинаковые наблюдаемые цветовые отличия. Это свойство используется при проектировании и оценке искажений цветопередачи в системах цветного телевидения. Следует заметить, что условия наблюдения цветного телевизионного изображения имеют свои особенности, которые необходимо учитывать в соответствующих расчетах.

Рис. 2.24. Пороги цветоразличения в системе X, Y, Z

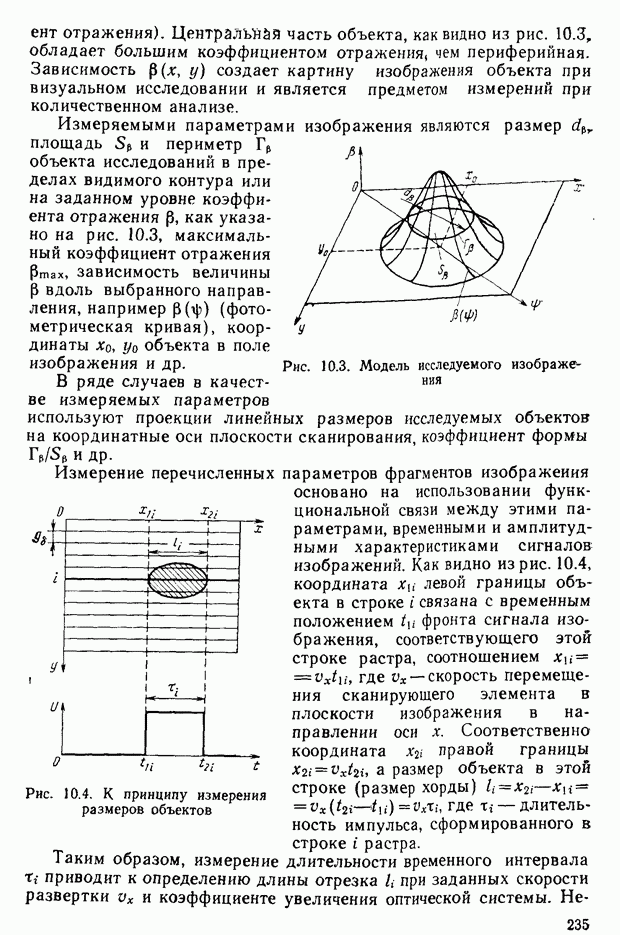
Рис. 2.25. Равноконтрастная цветовая диаграмма
Заметим, что рассмотренные принципы цветовых измерений и расчетов относятся к условию наблюдения цветовых полей достаточно крупного размера (более 30—40) и яркости, соответствующей оптимальным условиям восприятия стандартным наблюдателем 
Восприятие цвета мелких деталей отличается от восприятия цвета крупных деталей, а цвета деталей изображения, размеры которых соизмеримы с разрешаемыми глазом, не различаются, и они воспринимаются как серые. Это свойство зрения используется при построении систем воспроизведения изображений.
Особенности цветового зрения человека и количественные соотношения, описывающие процесс цветовосприятия, являются основой для проектирования систем цветного телевидения (выбор колориметрических характеристик преобразователя изображения и воспроизводящих устройств, определение допусков на искажения по цветопередаче и др.).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ИЗОБРАЖЕНИЕ
- § 1.1. Электромагнитное излучение как переносчик информации
- § 1.2. Классификация изображений
- § 1.3. Телевизионное изображение
- § 1.4. Изображение — объект исследования
- ГЛАВА 2. ЗРИТЕЛЬНОЕ ВОСПРИЯТИЕ
- § 2.2. Световая чувствительность глаза
- § 2.3. Восприятие яркости и число различимых градаций
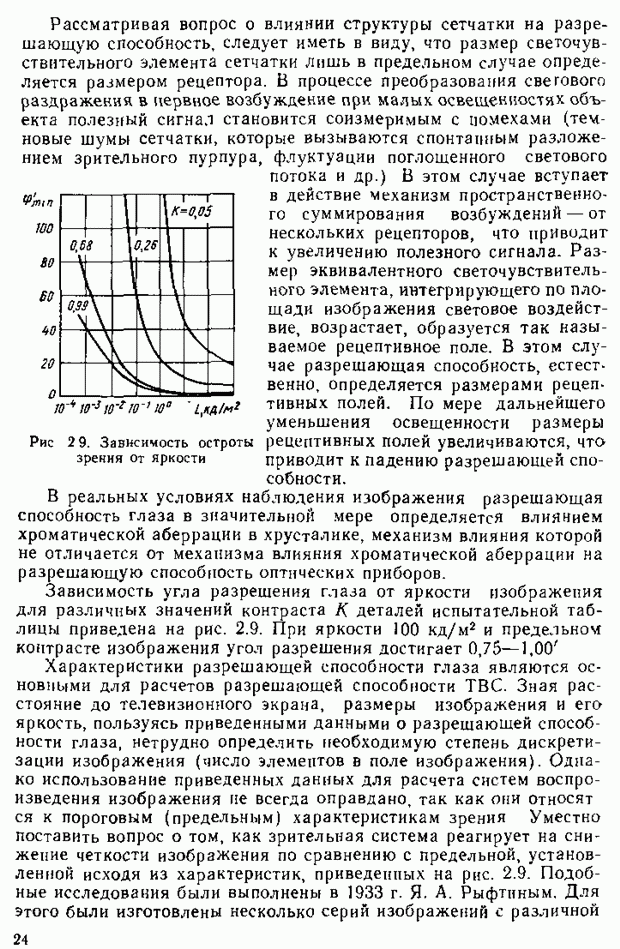
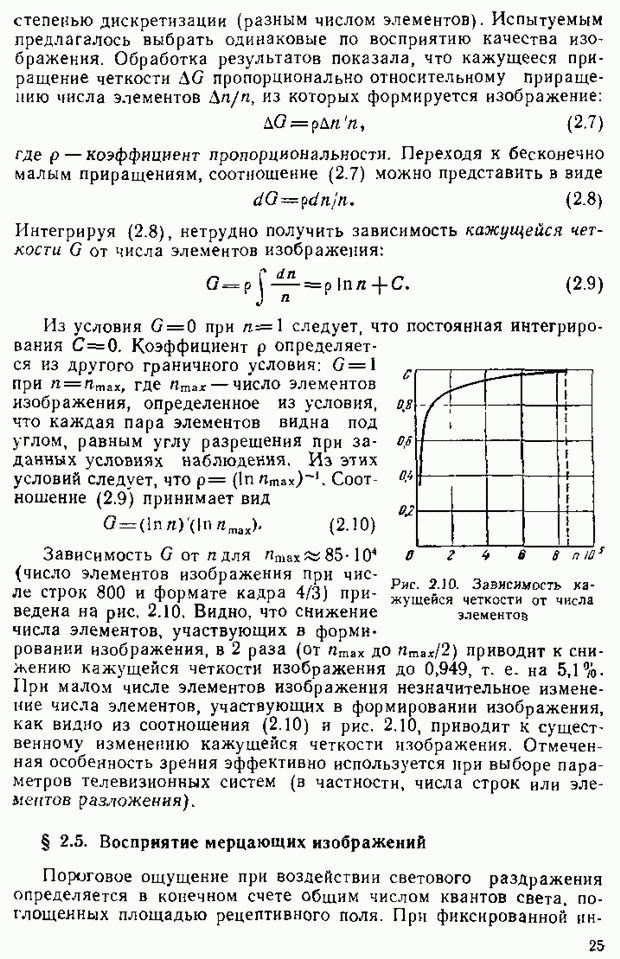
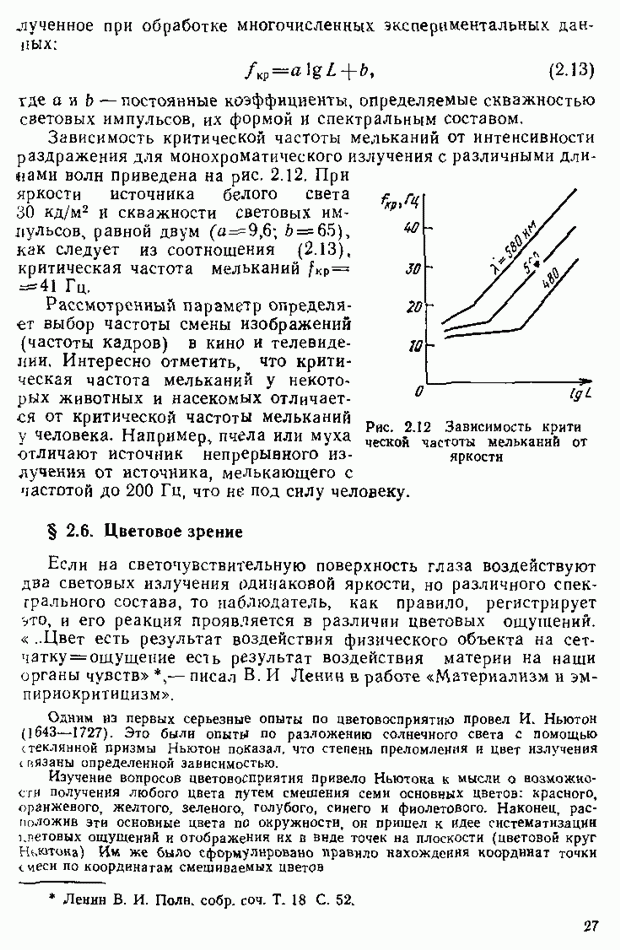
- § 2.4. Разрешающая способность глаза
- § 2.5. Восприятие мерцающих изображений
- § 2.6. Цветовое зрение
- § 2.7. Цветовые измерения и расчеты
- § 2.8. Объемное восприятие пространства
- ГЛАВА 3. ОСНОВЫ ТЕЛЕВИЗИОННОЙ ПЕРЕДАЧИ ИЗОБРАЖЕНИЙ
- § 3.2. Основные параметры последовательного разложения
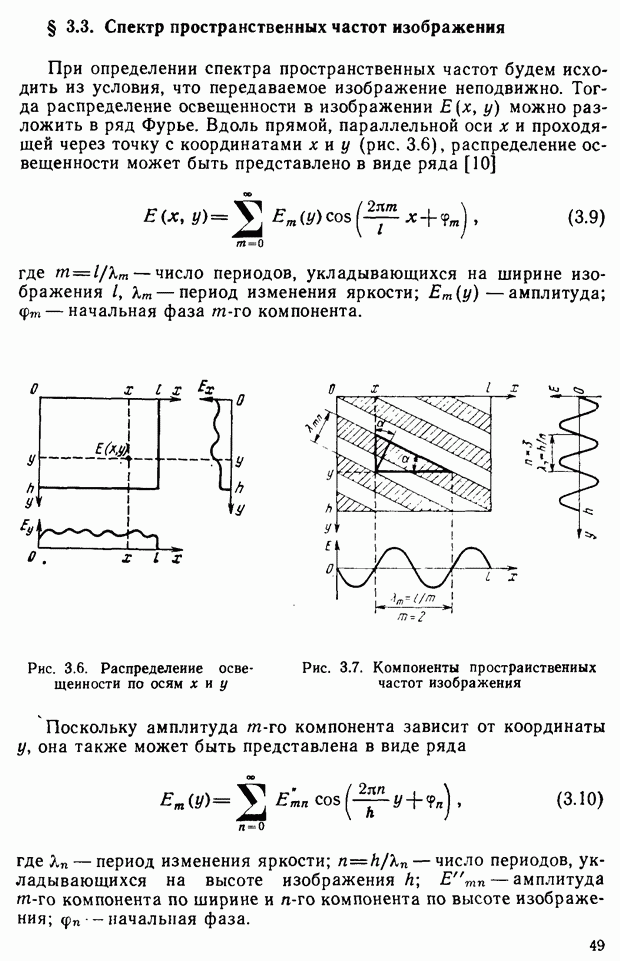
- § 3.3. Спектр пространственных частот изображения
- § 3.4. Пространственная фильтрация изображения в телевизионной системе
- § 3.5. Временная фильтрация изображения в телевизионной системе
- § 3.6. Амплитудная характеристика и чувствительность телевизионной системы
- § 3.7. Спектральные характеристики телевизионной системы
- § 3.8. Частотный спектр сигнала изображения
- § 3.9. Сигналы цветного телевидения
- § 3.10. Выбор параметров разложения
- ГЛАВА 4. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- § 4.2. Принципы накопления заряда
- § 4.3. Устройство и принцип действия видикона
- § 4.4. Видиконы с оксидно-свинцовой мишенью
- § 4.5. Кремкиконы
- § 4.6. Многосигнальные видиконы
- § 4.7. Преобразователи изображений на базе ППЗ-структур
- § 4.8. Принципы построения линейных и матричных ППЗ-преобразователей
- ГЛАВА 5. ПРИНЦИПЫ ПОСТРОЕНИЯ ТЕЛЕВИЗИОННЫХ СИСТЕМ И УСТРОЙСТВ
- § 5.2. Передающие камеры цветного телевидения
- § 5.3. Параметры полного цветового телевизионного сигнала в системе SECAM
- § 5.4. Кодирование сигналов
- § 5.5. Декодирование сигналов
- § 5.6. Телевизионный приемник
- ГЛАВА 6. СИНХРОНИЗАЦИЯ В ТЕЛЕВИЗИОННЫХ СИСТЕМАХ
- § 6.2. Управление частотой и фазой процессов с помощью синхронизирующих импульсов
- § 6.3. Временное преобразование несинхронных телевизионных сигналов в синхронные
- § 6.4. Амплитудная селекция сигналов синхронизации
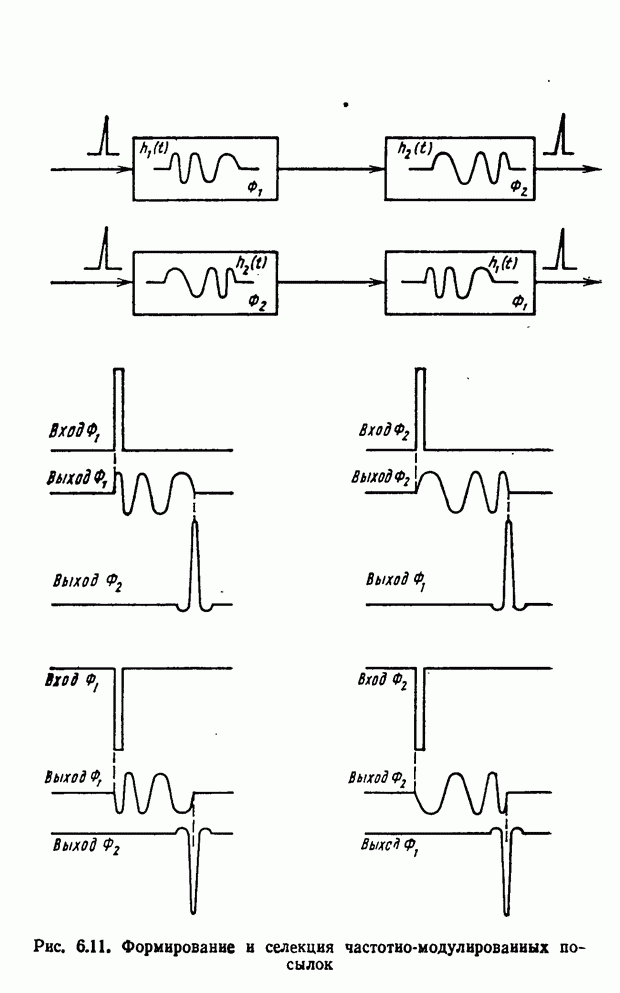
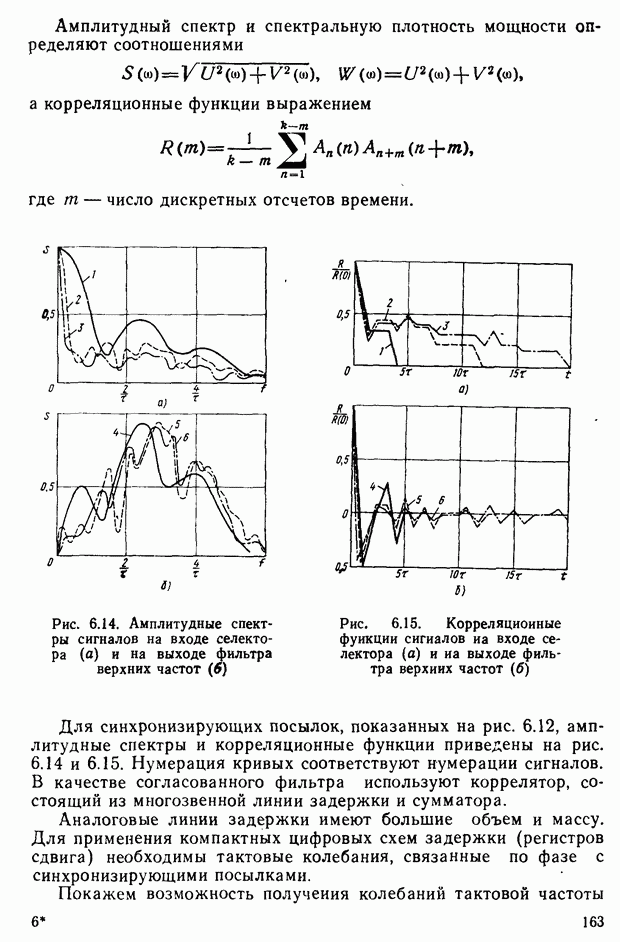
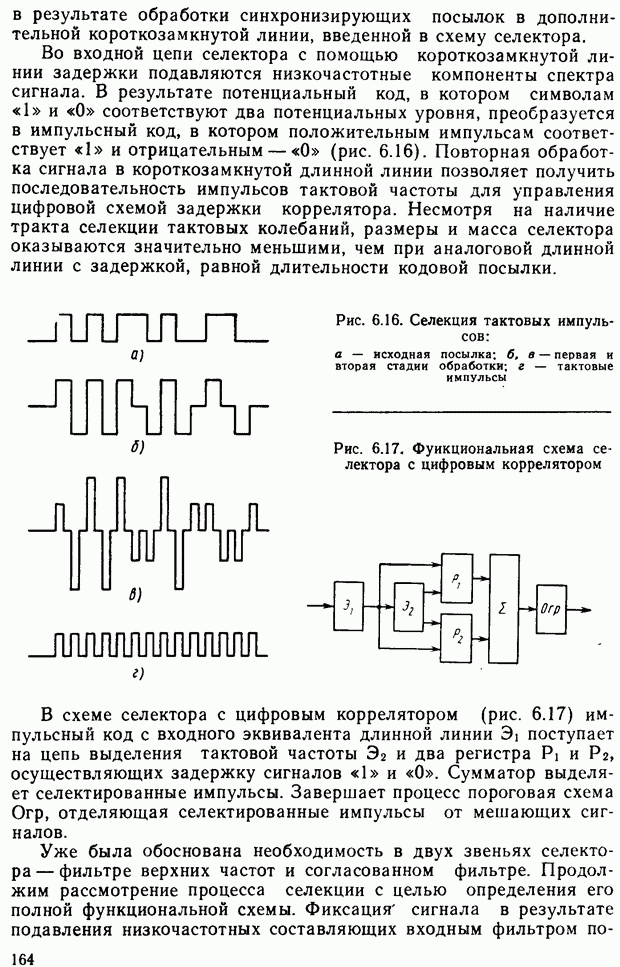
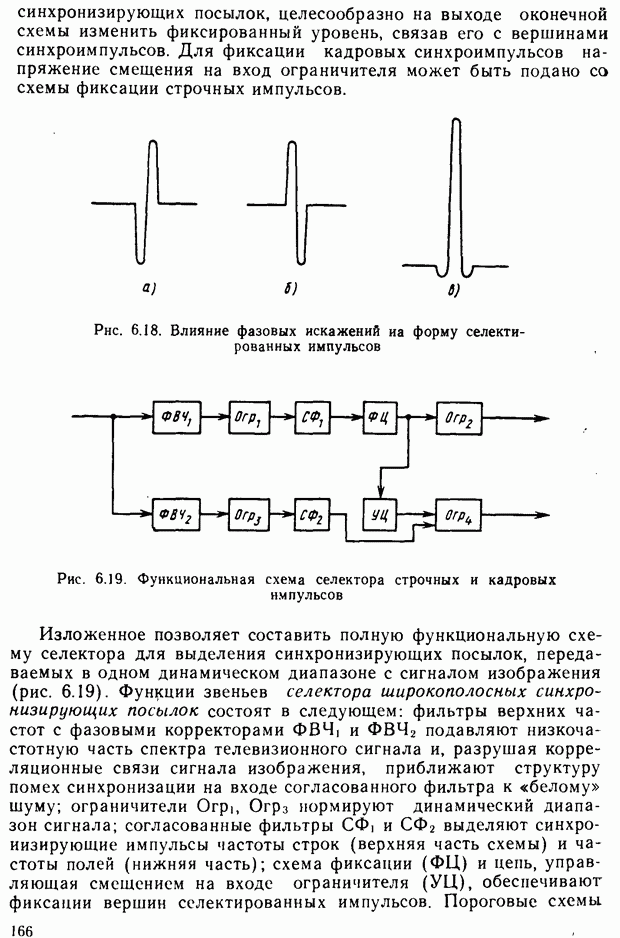
- § 6.5. Селекция и обработка сложных сигналов синхронизации
- ГЛАВА 7. ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ ИЗОБРАЖЕНИЯ
- § 7.1. Кодирование телевизионных сигналов
- § 7.2. Устройства цифровой обработки сигналов
- § 7.3. Временные преобразования цифровых сигналов
- § 7.4. Кодирование сигналов изображения с учетом статистических связей
- ГЛАВА 8. СИСТЕМЫ ВИДЕОЗАПИСИ
- § 8.1. Принципы магнитной записи сигналов изображения
- § 8.2. Преобразование телевизионного сигнала в режимах записи и воспроизведения
- § 8.3. Обработка сигнала, воспроизводимого видеомагнитофоном
- § 8.4. Использование видеомагнитофонов в вещательном телевидении
- ГЛАВА 9. УСТРОЙСТВА ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ
- § 9.2. Люминесцентные экраны
- § 9.3. Трехлучевой масочный кинескоп
- § 9.4. Кинескоп с компланарным расположением прожекторов
- § 9.5. Плоский экран
- ГЛАВА 10. ТЕЛЕВИДЕНИЕ В НАРОДНОМ ХОЗЯЙСТВЕ
- § 10.1. Классификация и области использования телевидения
- § 10.2. Системы наблюдения, контроля и обучения
- § 10.3. Системы обнаружения и визуализации
- § 10.4. Системы анализа и обработки изображений
- ЗАКЛЮЧЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ