| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.2. РАСЧЕТ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ
Принципиально ОИТ могут проектироваться с МС любого типа. Однако преимущественная область применения ОИТ — повышение напряжения весьма мощных или коротких импульсов. В обоих этих случаях ОИТ должен обладать малой индуктивностью рассеяния и выводов. Этим определяется как необходимость применения в ОИТ тороидальных МС, так и специфичная компоновка ОИТ, позволяющая решить обе задачи, причем индуктивность выводов устраняется практи-. чески полностью. По этим причинам далее рассматриваются ОИТ с тороидальной МС.
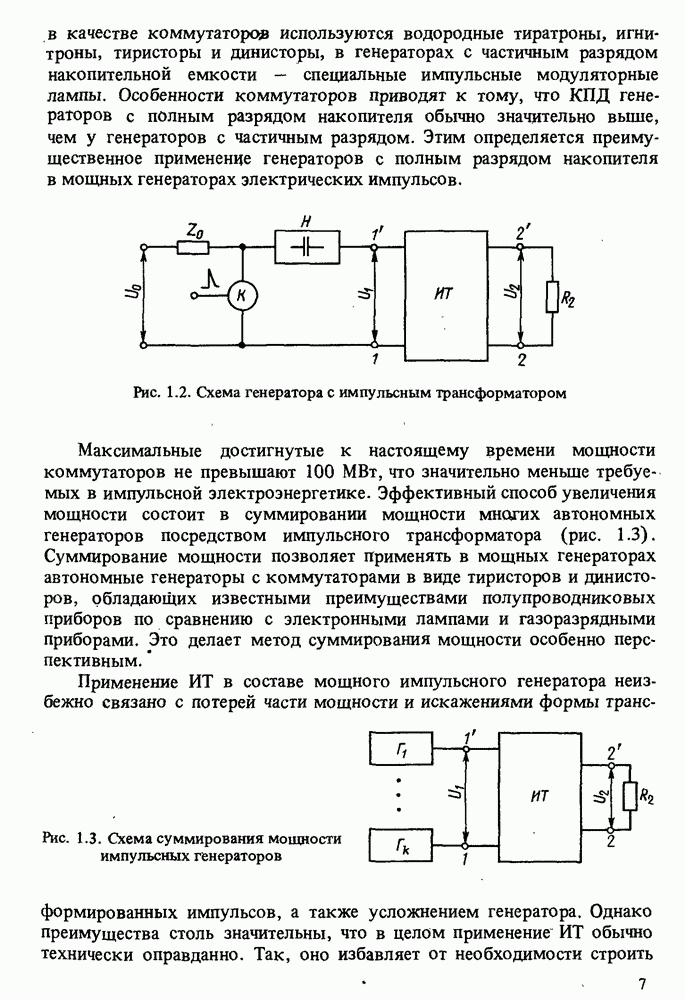
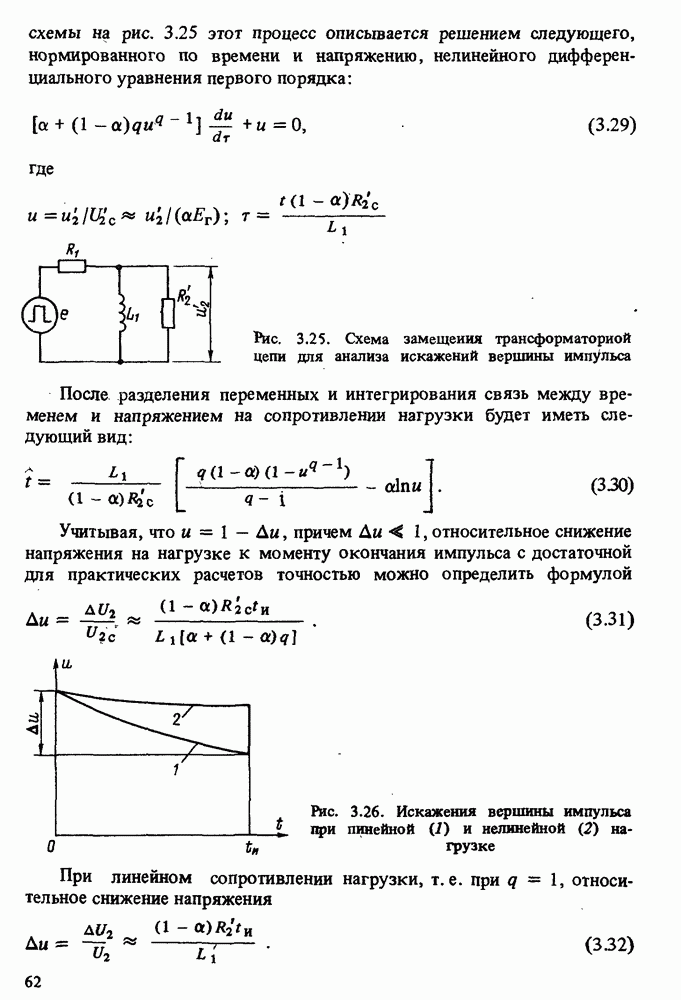
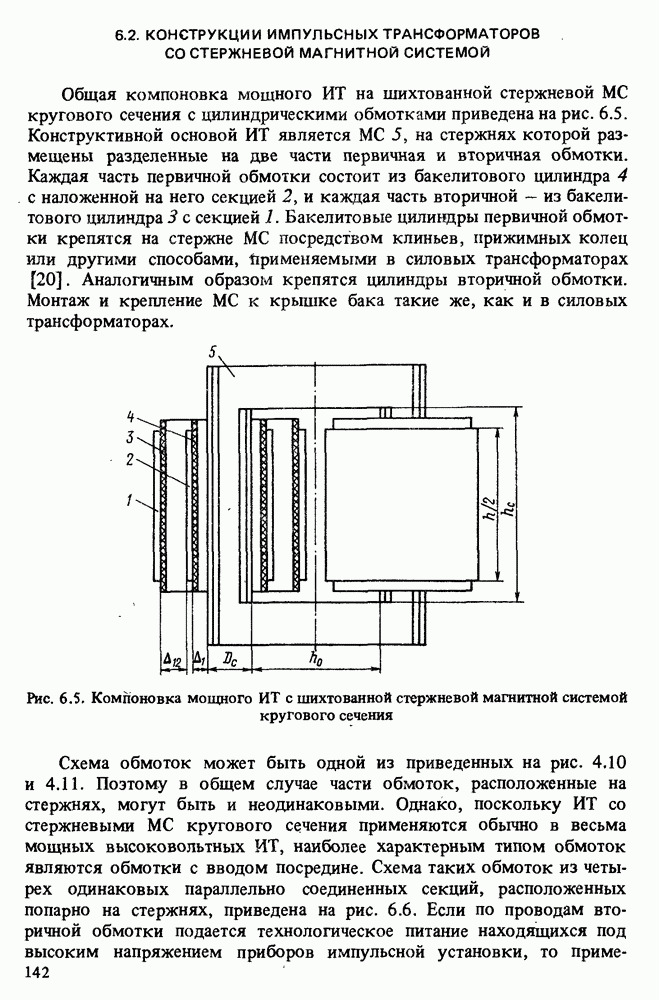
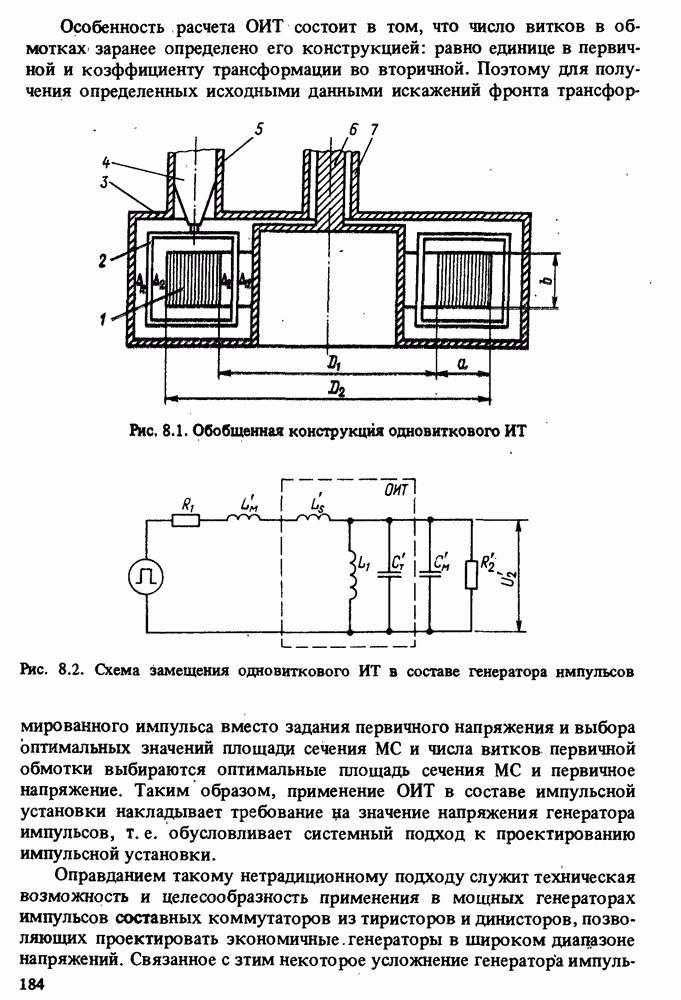
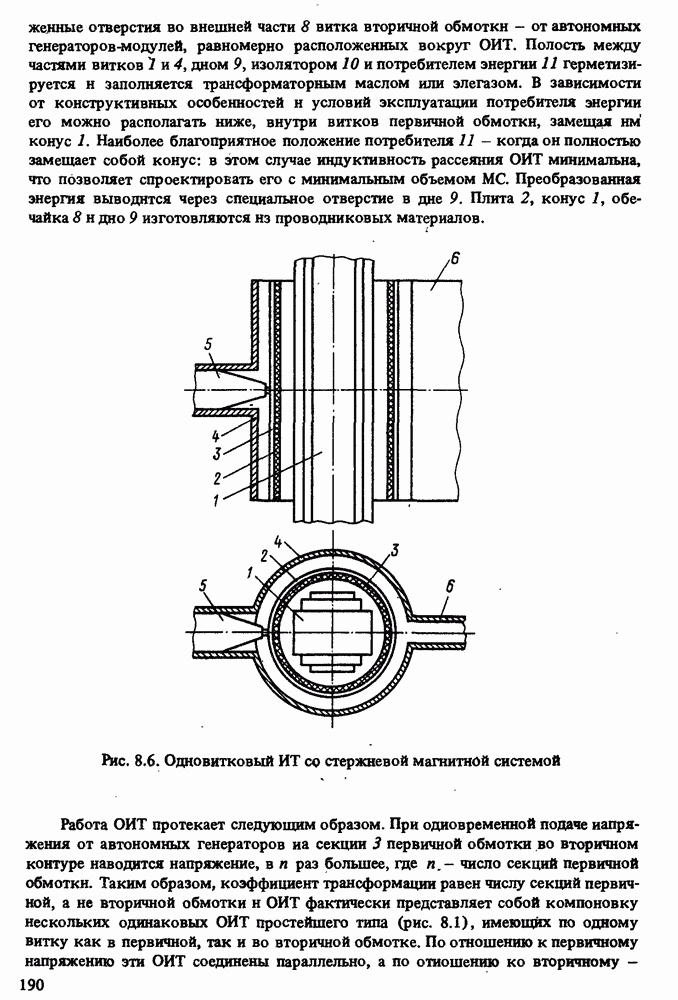
Обобщенная конструкция ОИТ с тороидальной МС приведена на рис. 8.1, где 1 - МС; 2 - вторичная обмотка; 3 - виток первичной обмотки, имеющий вид полого тороида и являющийся одновременно масляным или злегазовым баком; 4, 5 — выводы высокого (вторичного) напряжения; 6 и 7 — вводы низкого (первичного) напряжения. Схема замещения ОИТ в составе генератора импульсов приведена на рис. 8.2, где все обозначения соответствуют принятым ранее.
Электромагнитные параметры ОИТ можно рассчитывать по формулам

а площадь сечения МС — по формуле

Особенность расчета ОИТ состоит в том, что число витков в обмотках заранее определено его конструкцией: равно единице в первичной и коэффициенту трансформации во вторичной. Поэтому для получения определенных исходными данными искажений фронта трансформированного импульса вместо задания первичного напряжения и выбора оптимальных значений площади сечения МС и числа витков первичной обмотки выбираются оптимальные площадь сечения МС и первичное напряжение. Таким образом, применение ОИТ в составе импульсной установки накладывает требование на значение напряжения генератора импульсов, т. е. обусловливает системный подход к проектированию импульсной установки.
Рис. 8.2. (см. скан) Схема замещения одновиткового ИТ в составе генератора импульсов
Оправданием такому нетрадиционному подходу служит техническая возможность и целесообразность применения в мощных генераторах импульсов составных коммутаторов из тиристоров и динисторов, позволяющих проектировать экономичные генераторы в широком диапазоне напряжений. Связанное с этим некоторое усложнение генератора
импульсов компенсируется как применением наиболее перспективных коммутационных приборов, так и получением наиболее высокого из возможных при применении ИТ импульсного напряжения [47].
Оптимальная площадь сечения МС определяется на основании формул (3.45), (3.46), (8.4), (8.5) и (8.7) с учетом соотношения 

Оптимальное первичное напряжение рассчитывается из формулы (8.7) при найденной по формуле (8.8) оптимальной площади сечения МС, после чего по формуле (8.9) рассчитывается необходимая для получения заданного удлинения фронта и выброса на фронте длина намотки 
В импульсных установках обычно желательно минимальное напряжение генератора, так как это упрощает его конструкцию. Для этого, как видно из формулы (8.7), необходима минимальная площадь сечения МС. Главным фактором, позволяющим уменьшить ее, является коэффициент А [см. формулу (8.8)]. Из выражений (8.8) и (8.10) видно, что при заданных параметрах трансформированного импульса уменьшить площадь сечения и первичное напряжение можно фактически только, снижая коэффициент  и повышая приращение индукции в МС. Вследствие этого, хотя прямоугольное сечение позволяет несколько уменьшить объем МС, целесообразны МС с квадратным сечением, работающие в режиме с максимальным приращением индукции. Из формулы (8.9) видно, что при оптимальном первичном напряжении допустимы две различные длины намотки, соответствующие индуктивной
и повышая приращение индукции в МС. Вследствие этого, хотя прямоугольное сечение позволяет несколько уменьшить объем МС, целесообразны МС с квадратным сечением, работающие в режиме с максимальным приращением индукции. Из формулы (8.9) видно, что при оптимальном первичном напряжении допустимы две различные длины намотки, соответствующие индуктивной  и емкостной реакции трансформаторной цепи. При наиболее вероятном для мощных импульсных систем значении
и емкостной реакции трансформаторной цепи. При наиболее вероятном для мощных импульсных систем значении  и оптимальном значении
и оптимальном значении  эти длины различаются в 5,84 раза. Следовательно, во столько же раз объем МС с оптимальной площадью сечения при емкостной реакции больше объема при индуктивной, т. е. в ОИТ, так же как и в обычных ИТ, желательна индуктивная реакция.
эти длины различаются в 5,84 раза. Следовательно, во столько же раз объем МС с оптимальной площадью сечения при емкостной реакции больше объема при индуктивной, т. е. в ОИТ, так же как и в обычных ИТ, желательна индуктивная реакция.
В зависимости от соотношения параметров, входящих в формулы (8.8) ... (8.10), длина МС может изменяться в широких пределах. Отметим следующие случаи:
1. Длина МС при индуктивной реакции недостаточна для
размещения вторичной обмотки или для того, чтобы обеспечить необходимую продольную электрическую прочности вторичной обмотки. В этом случае приходится принимать длину МС, соответствующую емкостной реакции, что приводит примерно к шестикратному увеличению объема МС.
2. Длина МС достаточна для обеспечения необходимой продольной, электрической прочности при обоих видах реакции, но отношение  меньше предельного допустимого. В этом случае можно допустить некоторое увеличение длины МС для достижения необходимого отношения
меньше предельного допустимого. В этом случае можно допустить некоторое увеличение длины МС для достижения необходимого отношения  Тогда ослабится индуктивная и усилится емкостная реакция. Если первоначально реакция была индуктивной, уменьшится коэффициент затухания, увеличится удлинение фронта и выброс напряжения на фронте. Если реакция первоначально была емкостной, то увеличится коэффициент затухания и удлинение фронта, но выброс на фронте уменьшится или его не будет. В обоих случаях увеличение длины намотки приведет к увеличеию объема МС.
Тогда ослабится индуктивная и усилится емкостная реакция. Если первоначально реакция была индуктивной, уменьшится коэффициент затухания, увеличится удлинение фронта и выброс напряжения на фронте. Если реакция первоначально была емкостной, то увеличится коэффициент затухания и удлинение фронта, но выброс на фронте уменьшится или его не будет. В обоих случаях увеличение длины намотки приведет к увеличеию объема МС.
3. Длина МС достаточна для обеспечения необходимой электрической прочности и размещения вторичной обмотки при индуктивной реакции и отношение  Целесообразно принять максимальное допустимое отношение
Целесообразно принять максимальное допустимое отношение  и рассчитать ОИТ на заведомо достижимую в этом случае индуктивную реакцию, т. е. в пренебрежении всеми емкостями трансформаторной цепи. Этот случай самый благоприятный, так как позволяет получить минимальный объем МС ОИТ.
и рассчитать ОИТ на заведомо достижимую в этом случае индуктивную реакцию, т. е. в пренебрежении всеми емкостями трансформаторной цепи. Этот случай самый благоприятный, так как позволяет получить минимальный объем МС ОИТ.
При этом для определения оптимальной площади сечения МС из формул (1.4), (3.23), (8.4) и (8.7) можно получить уравнение вида (5.15), где

Оптимальная площадь сечения МС

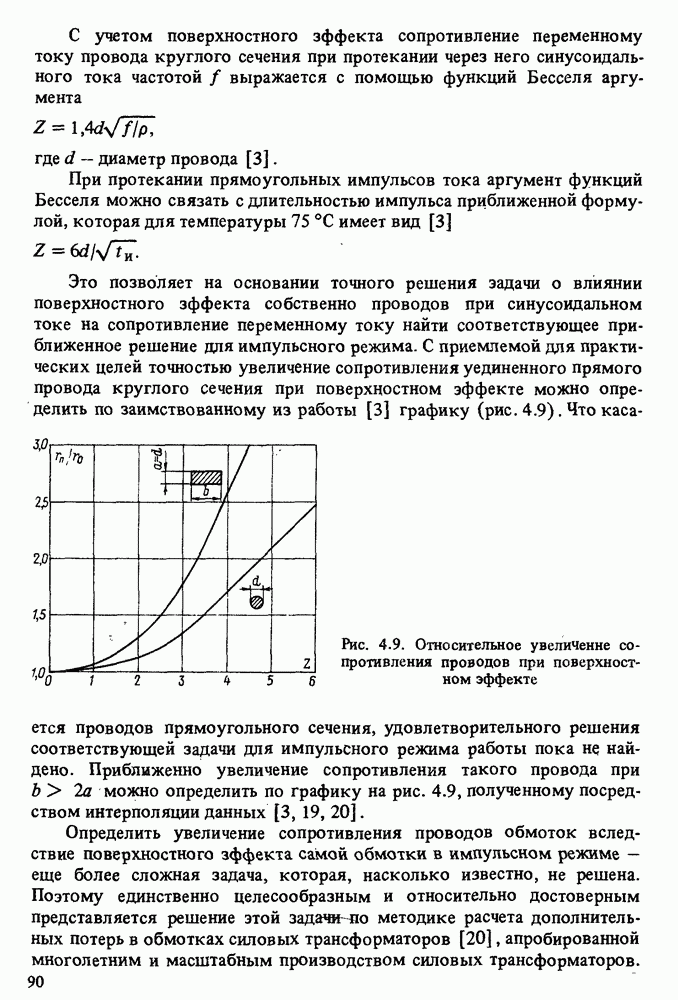
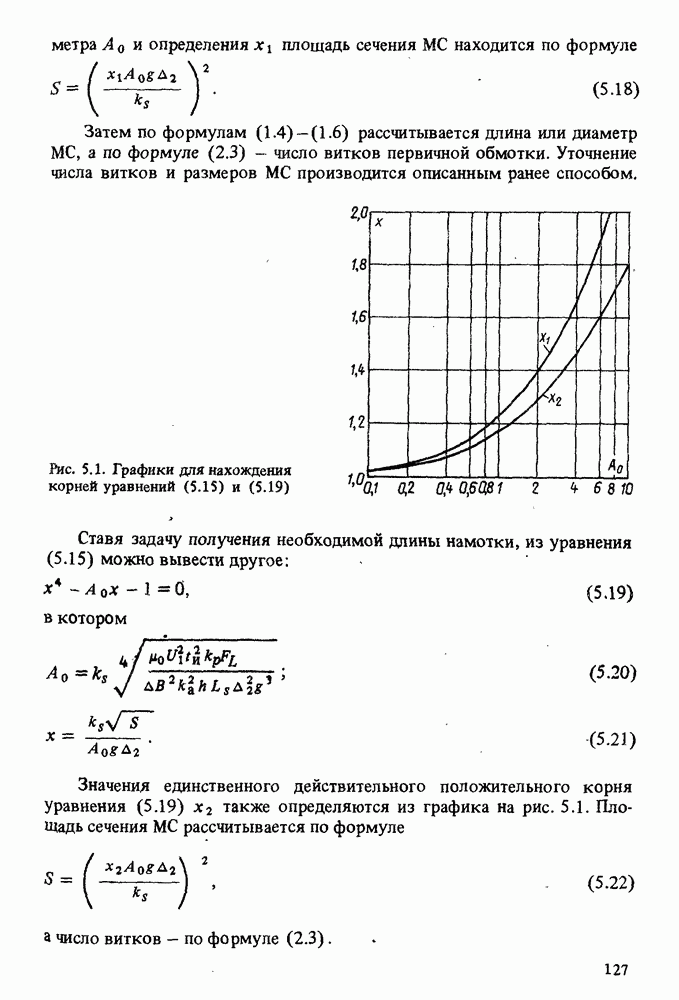
где  — единственный действительный положительный корень уравнения (5.15), определяемый по графику на рис. 5.1.
— единственный действительный положительный корень уравнения (5.15), определяемый по графику на рис. 5.1.
Оптимальное первичное напряжение рассчитывается по формуле (8.7) при подстановке в нее выражения (8.13).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ИМПУЛЬСНЫЙ ТРАНСФОРМАТОР В УСТАНОВКАХ ИМПУЛЬСНОЙ ЭЛЕКТРОЭНЕРГЕТИКИ
- 1.2. ГЕНЕРАТОРЫ МОЩНЫХ ЭЛЕКТРИЧЕСКИХ ИМПУЛЬСОВ
- 1.3. ПОТРЕБИТЕЛИ ИМПУЛЬСНОЙ ЭНЕРГИИ
- 1.4. ТРЕБОВАНИЯ К ИМПУЛЬСНОМУ ТРАНСФОРМАТОРУ
- 1.5. ОБЩИЕ КОНСТРУКТИВНЫЕ СХЕМЫ И КЛАССИФИКАЦИЯ ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ
- 1.6. ИСХОДНЫЕ ДАННЫЕ ДЛЯ ПРОЕКТИРОВАНИЯ ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- ГЛАВА ВТОРАЯ. ЭЛЕКТРОМАГНИТНЫЕ ПРОЦЕССЫ В МАГНИТНОЙ СИСТЕМЕ
- 2.1. ОБЩИЕ СВЕДЕНИЯ О ТРАНСФОРМАТОРАХ С МАГНИТНОЙ СИСТЕМОЙ
- 2.2. ПРИРАЩЕНИЕ ИНДУКЦИИ
- 2.3. МЕТОДЫ УМЕНЬШЕНИЯ ОСТАТОЧНОЙ ИНДУКЦИИ
- 2.4. ПОТЕРИ ЭНЕРГИИ
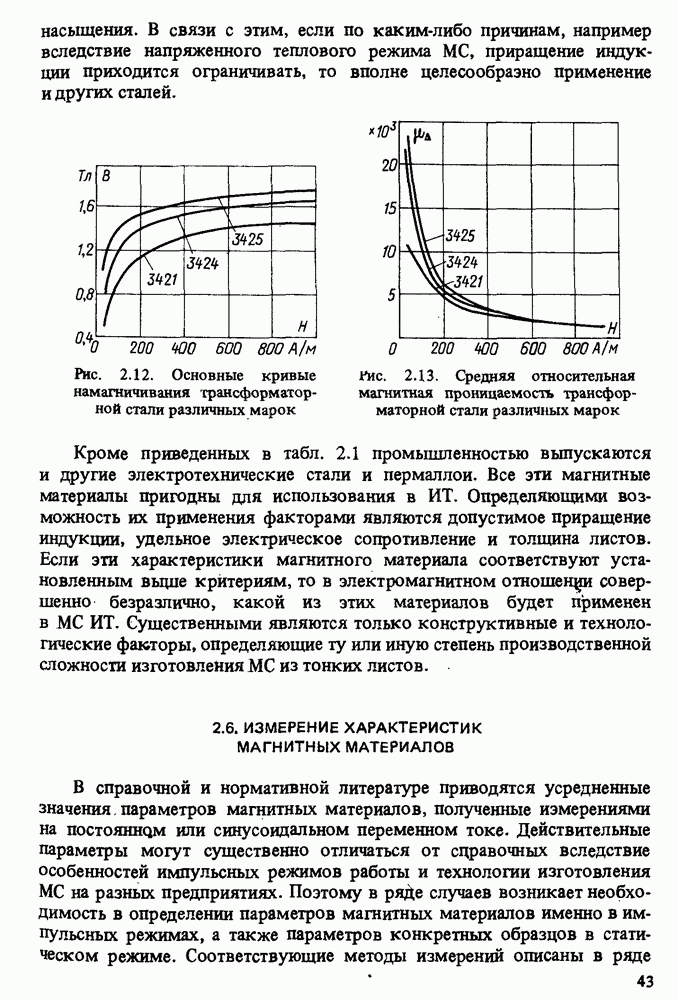
- 2.5. МАГНИТНЫЕ МАТЕРИАЛЫ
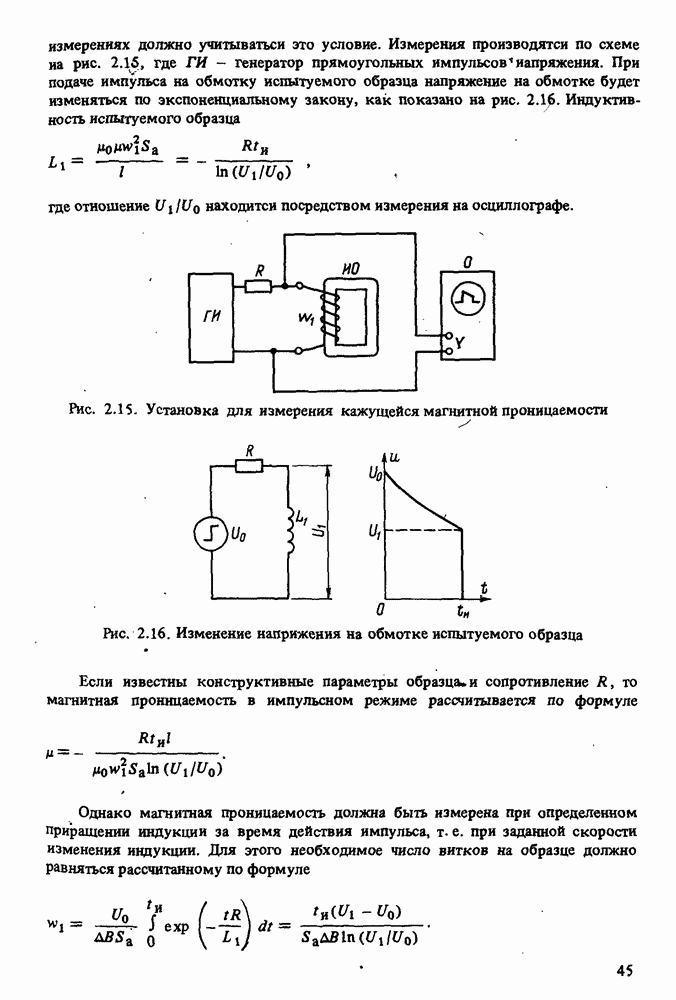
- 2.6. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК МАГНИТНЫХ МАТЕРИАЛОВ
- ГЛАВА ТРЕТЬЯ. РАСЧЕТ ЭЛЕКТРОМАГНИТНЫХ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ ПО ЗАДАННЫМ ИСКАЖЕНИЯМ ФОРМЫ ИМПУЛЬСА
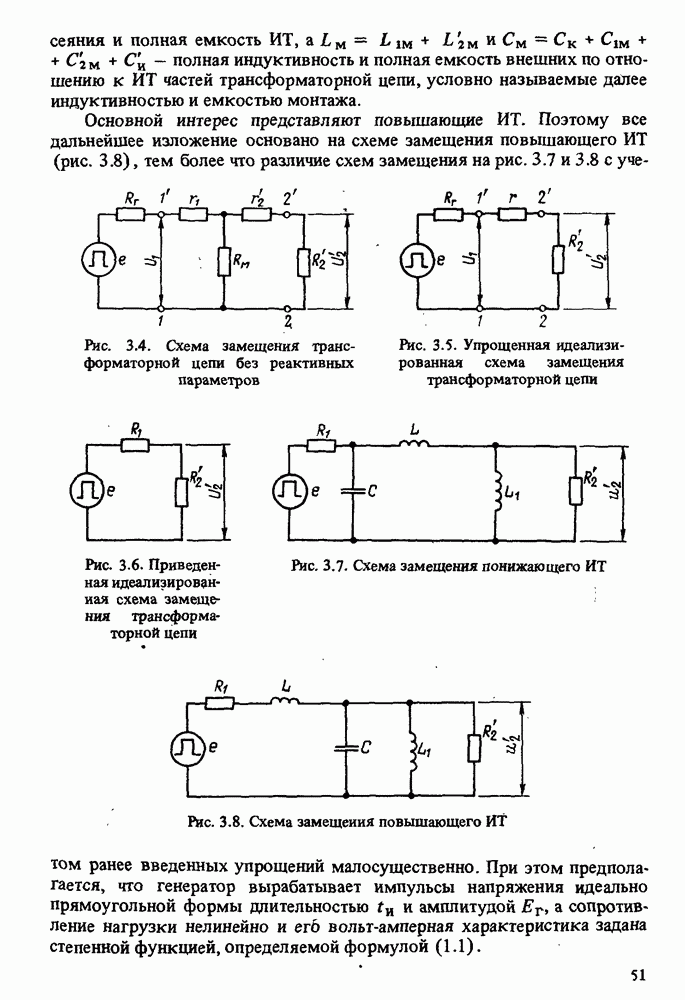
- 3.1. СХЕМА ЗАМЕЩЕНИЯ ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- 3.2. СХЕМА ЗАМЕЩЕНИЯ ТРАНСФОРМАТОРНОЙ ЦЕПИ
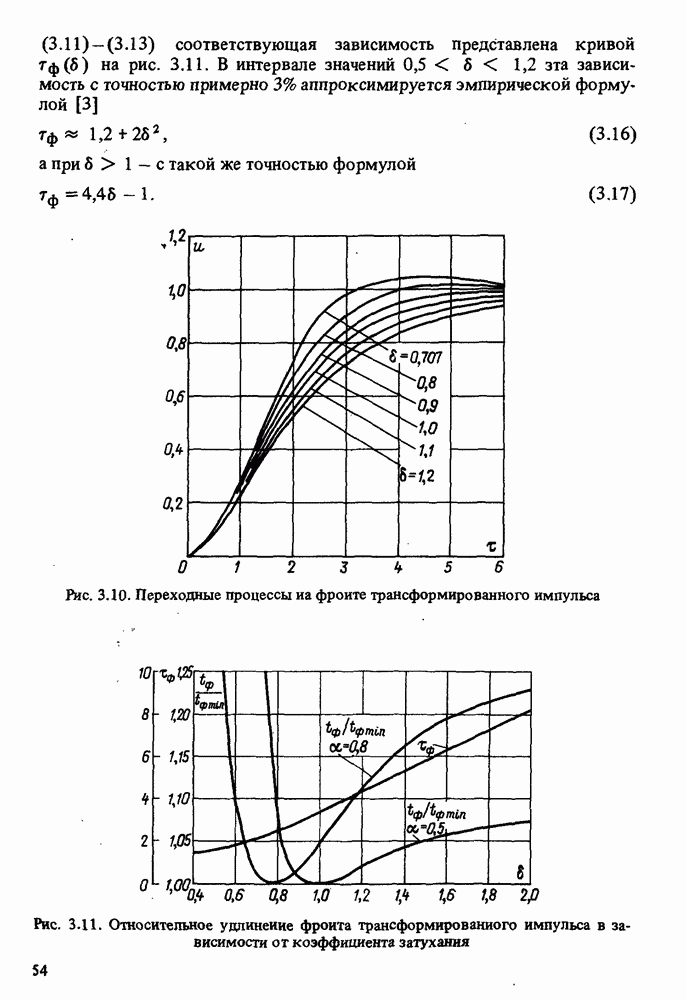
- 3.3. ИСКАЖЕНИЯ ФРОНТА ИМПУЛЬСА
- 3.4. ИСКАЖЕНИЯ ВЕРШИНЫ ИМПУЛЬСА
- 3.5. ИСКАЖЕНИЯ СРЕЗА ИМПУЛЬСА
- 3.6. ЭНЕРГИЯ В РЕАКТИВНЫХ ЭЛЕМЕНТАХ ТРАНСФОРМАТОРНОЙ ЦЕПИ
- 3.7. РАСЧЕТ ЭЛЕКТРОМАГНИТНЫХ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ
- 3.8. КРИТЕРИЙ ОСУЩЕСТВИМОСТИ ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- 3.9. КОРРЕКЦИЯ ИСКАЖЕНИЙ ФОРМЫ ИМПУЛЬСА
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРОМАГНИТНЫЕ ПАРАМЕТРЫ ОБМОТОК
- 4.1. СВЯЗЬ МЕЖДУ ЭЛЕКТРОМАГНИТНЫМИ И КОНСТРУКТИВНЫМИ ПАРАМЕТРАМИ. ИНДУКТИВНОСТЬ НАМАГНИЧИВАНИЯ
- 4.2. ИНДУКТИВНОСТЬ РАССЕЯНИЯ
- 4.3. ДИНАМИЧЕСКИЕ ЕМКОСТИ
- 4.4. СОПРОТИВЛЕНИЕ
- 4.5. ЦИЛИНДРИЧЕСКИЕ ОБМОТКИ
- 4.6. СПИРАЛЬНЫЕ ОБМОТКИ
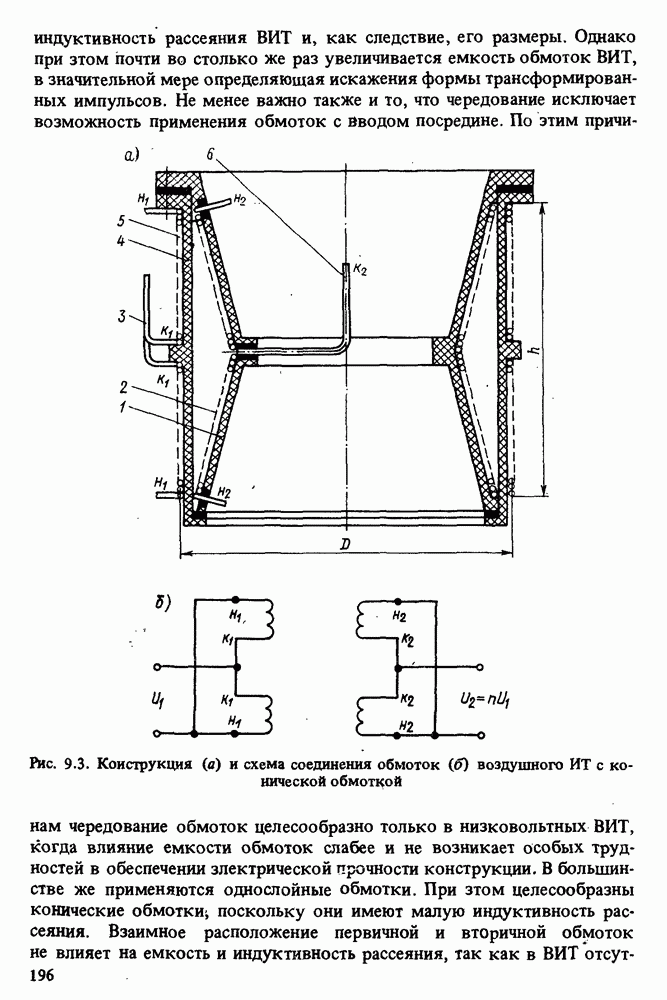
- 4.7. КОНИЧЕСКИЕ ОБМОТКИ
- 4.8. ОБМОТКИ МОЩНЫХ ВЫСОКОВОЛЬТНЫХ ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ
- 4.9. ВЫБОР ИЗОЛЯЦИИ И ПРОВОДОВ
- ГЛАВА ПЯТАЯ. ОСНОВЫ ПРОЕКТИРОВАНИЯ
- 5.2. МИНИМАЛЬНЫЙ ОБЪЕМ МАГНИТНОЙ СИСТЕМЫ
- 5.3. ВЫБОР КОНСТРУКЦИИ
- 5.4. КОНСТРУКТИВНЫЙ РАСЧЕТ
- 5.5. РАСЧЕТ МЕХАНИЧЕСКИХ СИЛ В ОБМОТКАХ
- 5.6. РАСЧЕТ ТЕПЛОВОГО РЕЖИМА
- 5.7. ОЦЕНКА ТЕХНИКО-ЭКОНОМИЧЕСКИХ И ФУНКЦИОНАЛЬНЫХ ПОКАЗАТЕЛЕЙ
- 5.8. О МАШИННОМ ПРОЕКТИРОВАНИИ
- ГЛАВА ШЕСТАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ СО СТЕРЖНЕВОЙ МАГНИТНОЙ СИСТЕМОЙ
- 6.1. ОСНОВНЫЕ СВЕДЕНИЯ О СТЕРЖНЕВЫХ МАГНИТНЫХ СИСТЕМАХ
- 6.2. КОНСТРУКЦИИ ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ СО СТЕРЖНЕВОЙ МАГНИТНОЙ СИСТЕМОЙ
- 6.4. МОЩНЫЙ ВЫСОКОВОЛЬТНЫЙ ИМПУЛЬСНЫЙ ТРАНСФОРМАТОР С ВИТОЙ НЕРАЗРЕЗНОЙ МАГНИТНОЙ СИСТЕМОЙ
- 6.5. ИМПУЛЬСНЫЙ ТРАНСФОРМАТОР СРЕДНЕЙ МОЩНОСТИ С РАЗРЕЗНОЙ МАГНИТНОЙ СИСТЕМОЙ
- ГЛАВА СЕДЬМАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ТОРОИДАЛЬНОЙ МАГНИТНОЙ СИСТЕМОЙ
- 7.2. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ВЕРТИКАЛЬНО УСТАНОВЛЕННОЙ МАГНИТНОЙ СИСТЕМОЙ
- 7.3. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ГОРИЗОНТАЛЬНО УСТАНОВЛЕННОЙ МАГНИТНОЙ СИСТЕМОЙ
- ГЛАВА ВОСЬМАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ОДНИМ ВИТКОМ В ПЕРВИЧНОЙ ОБМОТКЕ
- 8.2. РАСЧЕТ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ
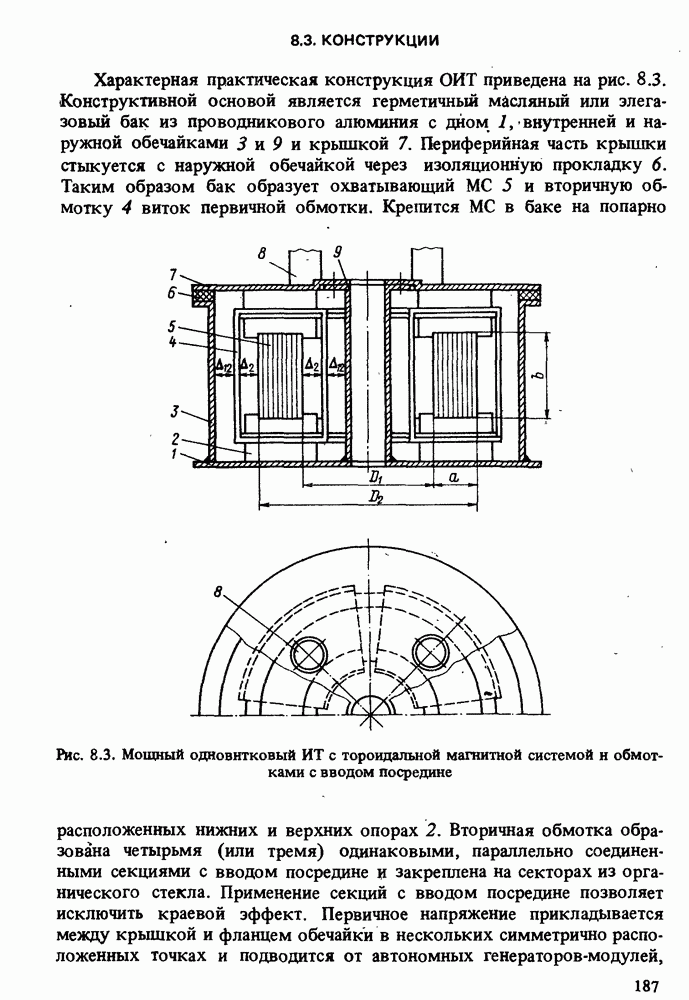
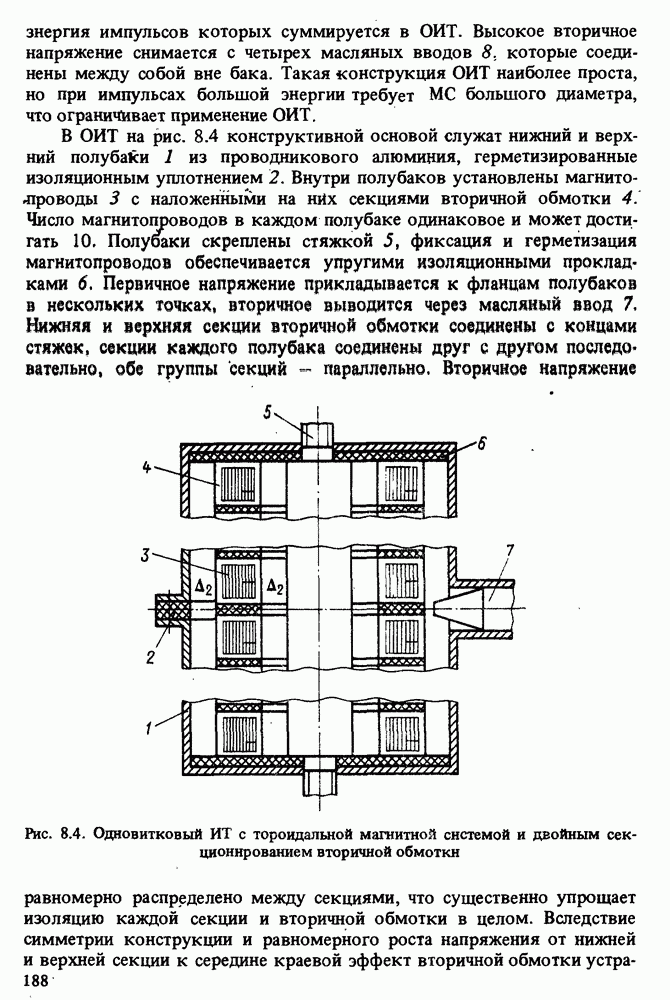
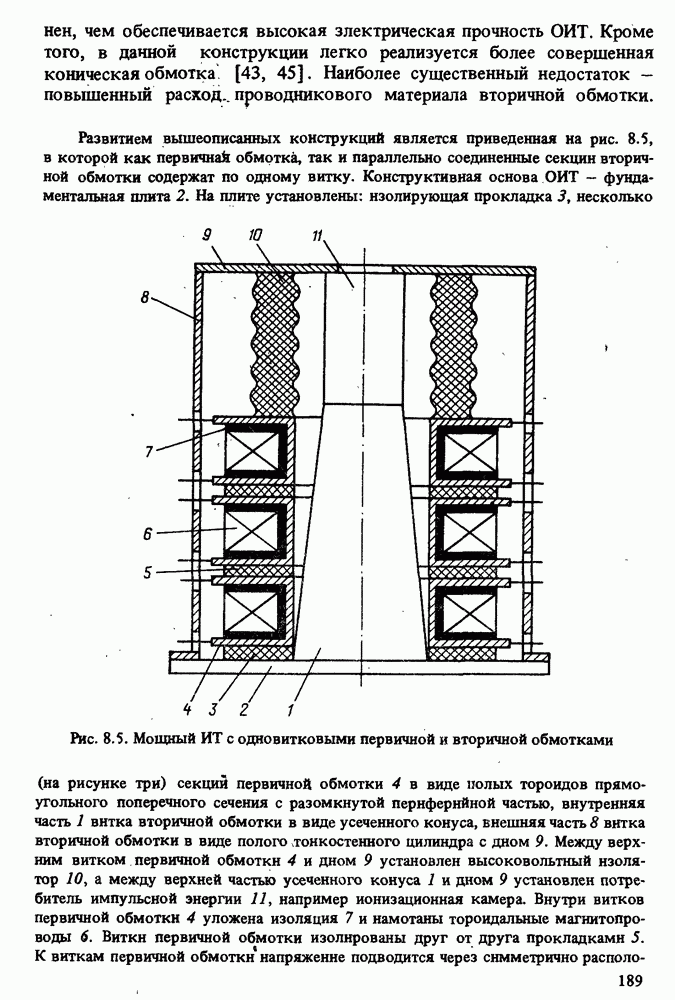
- 8.3. КОНСТРУКЦИИ
- 8.4. ПРИМЕР РАСЧЕТА МОЩНОГО ВЫСОКОВОЛЬТНОГО ОДНОВИТКОВОГО ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- 8.5. ОЦЕНКА ФУНКЦИОНАЛЬНЫХ И ТЕХНИКО-ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
- ГЛАВА ДЕВЯТАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ БЕЗ МАГНИТНОЙ СИСТЕМЫ
- 9.2. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСА
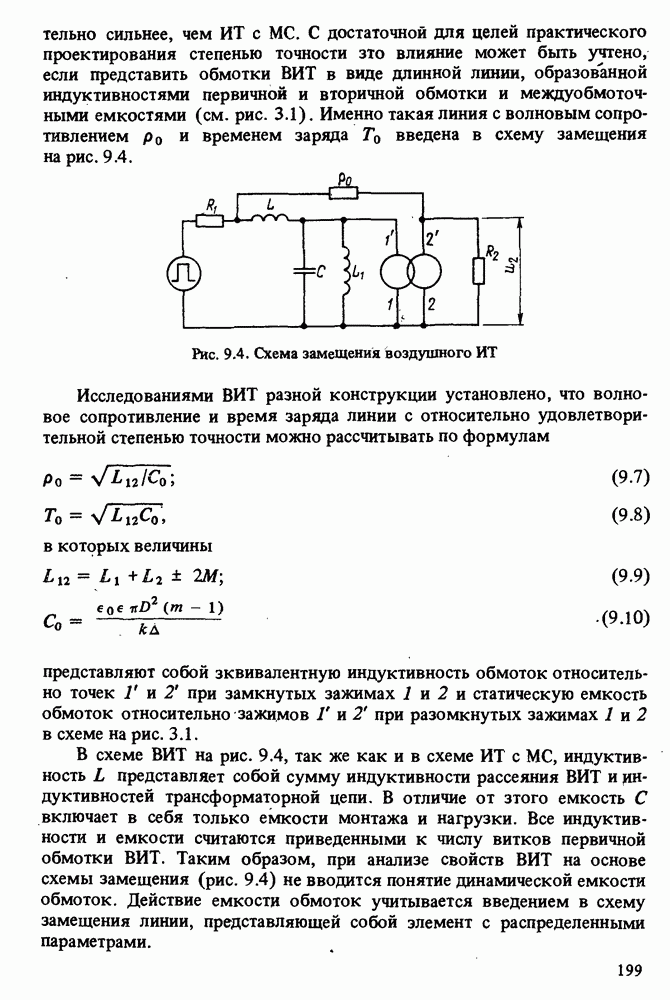
- 9.3. РАСЧЕТ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ
- 9.4. ПРИМЕРЫ ПРИМЕНЕНИЯ И РАСЧЕТА
- СПИСОК ЛИТЕРАТУРЫ